Abstract
To study the effects of liquid properties and interface parameters on gas–liquid two-phase flow in porous media. The volume flow model of gas–liquid two-phase flow in porous media was established, and the interface of the two-phase flow was reconstructed by tracing the phase fraction. The microscopic imbibition flow model was established, and the accuracy of the model was verified by comparing the simulation results with the classical capillary imbibition model. The flow characteristics in the fracturing process and backflow process were analyzed. The influence of flow parameters and interface parameters on gas flow was studied using the single-factor variable method. The results show that more than 90% of the flowing channels are invaded by fracturing fluid, and only about 50% of the fluid is displaced in the flowback process. Changes in flow velocity and wetting angle significantly affect Newtonian flow behavior, while variations in surface tension have a pronounced effect on non-Newtonian fluid flow. The relative position of gas breakthrough in porous media is an inherent property of porous media, which does not change with fluid properties and flow parameters.
1. Introduction
With the impact of renewable resources such as wind and solar energy on conventional fossil energy, the demand space for oil and gas as primary energy sources is further compressed [1]. As the cost of renewable resource development and utilization technologies continues to decline, exploring high-quality development and high return has become the key to sustainable development of oil and gas resources. China is endowed with substantial natural gas resources, and as a clean energy source, natural gas plays a pivotal role in facilitating the country’s goals of carbon peaking and carbon neutrality. It also supports the transition towards a low-carbon, high-quality national energy system [2]. The process of oil and gas exploration is a complex systems engineering challenge, with the flow of hydrocarbons through porous media representing one of its most intricate aspects [3]. Due to the presence of primary water in the reservoir and the intrusion of fracturing fluid, the gas flow in the reservoir behaves as a gas–liquid two-phase flow in a porous media. The storage and flow spaces at the micro and nanoscale significantly enhance interphase interactions, leading to lower gas well flowback rates and accelerated production decline during the development of unconventional gas reservoirs [3,4]. Therefore, understanding the characteristics of gas–liquid two-phase flow in porous media at the microscale is crucial for enhancing the development of unconventional gas reservoirs and promoting their comprehensive utilization.
For the simulation of multiphase flow in porous media, extensive research has been conducted by researchers using both laboratory experiments and numerical simulations. Laboratory experiments are categorized into sand-filled model experiments [5,6] and micro-etching experiments [7,8] based on the method of experimental model construction. The sand-filled experiment uses actual reservoir rock particles to form experimental samples by pressing them in certain ratios. Using this method, physical models with different parameters are constructed for flow analysis. By adjusting the mineral composition and particle size distribution, the effect of particle composition, wetting characteristics, and pore size distribution on the flow process can be reflected to some extent. However, this method mainly studies the flow pattern by monitoring the pressure differences between the inlet and outlet of the rock sample and the fluid flow rate. It does not reflect the real flow process inside the rock sample. Micro-etching experiments combined with CT scanning technology allow for the microscopic scanning of rock samples to obtain the internal flow channel characteristics of rock samples. The fabrication of microscopic flow channels on characteristic plates is achieved using etching techniques. Controlling the injected pore volume flow rate with a microflow pump and simulating the flow processes at the microscale can detect the fluid flow patterns within the microscale channels in real-time. Unfortunately, this method cannot manually modify the interface parameters during the flow process.
For unconventional gas reservoirs, the presence of ultra-low-scale flow channels poses significant challenges for laboratory experimental studies. However, advancements in computational fluid dynamics (CFD) technology now offer a crucial methodology for simulating multiphase flow within porous media at the micro- and nanoscales. At present, the numerical simulation of multiphase flow in porous media in the field of petroleum engineering is divided into two research directions [3,9,10]: one is to study the coupling of continuous and discrete phases between different phases, and to analyze the effects of the boundary layer, surface tension, and wetting angle on the flow process. Secondly, this study investigates the dynamics of particle collisions, mixing processes, and post-collision motion in liquid–solid and gas–solid systems relevant to proppant transport. In this work, we concentrate on gas–liquid two-phase flow within microscale flow spaces. Given the rapid changes at the phase interface between gas and liquid phases, it is essential to employ numerical models capable of accurately capturing these interface dynamics. Some commonly used simulation methods include the Lattice Boltzmann Method (LBM) [11,12,13], the Phase Field Method (PFM) [14,15], the Level Set Method (LSM) [16,17,18], the Interface Tracking Method (FT) [19], and the Volume of Fluid (VOF) method [20,21]. The LBM method is more effective for simulating low-velocity small-scale multiphase flow without tracking the phase interface, but the stability is poor under high-density gas–water ratio conditions. The PFM method has shortcomings in simulating the dissolution of small droplets or bubbles. The LSM has a good ability to describe complex flow channel topology, but the volume conservation on the grid is poor, and there is excessive smoothness in the treatment of phase interfaces at the sharp points of solid particles. The LSM can be seen as a simplification of the PFM, but the physical meaning of the phase field is lost [22]. The FT can prevent the overly-smoothed reconstruction of interfaces at sharp features, but its sensitivity to the topological complexity of the flow channel can lead to instability in computational outcomes. The VOF method reconstructs the phase interface for simulation purposes, allowing it to manage the complex topologies of porous media while maintaining superior volume conservation [23,24].
The simulation dimensions of porous media are typically small, with pore-throat sizes generally in the micron to nanometer range. Unlike at the macroscopic scale, this small size amplifies the influence of factors such as the wettability, flow velocity, and viscosity ratio on flow morphology. Porous media models can be categorized into two-dimensional (2D) and three-dimensional (3D) models. Two-dimensional models, due to their lesser number of computational grids, are convenient for studying flow patterns. In contrast, 3D models have significantly larger computational dimensions and a greater number of discrete grid elements compared to 2D models; their spatial attributes make them more suitable for analyzing the spatial aggregation distribution characteristics of fluids [25,26]. Various numerical simulation methods for multiphase flow have been applied to both types of models. The choice of model does not affect the analysis of microscale flow characteristics, although the selection of the numerical simulation method and the setting of computational parameters are critical [10].
In our study, based on the VOF model in computational fluid dynamics combined with the modeling method of porous media at the microscale, a numerical simulation research method of gas–liquid two-phase flow in porous media is formed. On this basis, the flow differences between gas-driven water and water-driven gas processes were studied. The influence of liquid properties on the flow process was discussed, and the effects of flow rate, wetting angle, and surface tension on the gas–liquid flow shape were analyzed.
2. Two-Phase Flow Simulation Method
2.1. VOF Model
Based on the conventional flow equation, VOF introduces the concept of phase fraction to form a phase fraction equation. During the solution process, pressure, velocity, and phase fraction are solved, and the phase interface shape is reconstructed using the numerical value of the phase fraction. The numerical value of the phase fraction is related to the proportion of fluid in the grid. The defined phase fraction is represented by the symbol α. The value range of α is between [0, 1]; when α = 0, it indicates that the cell is all gas phase, when α = 1, it indicates that the cell is all liquid phase. When the value of α ranges from 0 to 1 it indicates the presence of gas and water phases in the cell, as shown in Figure 1.
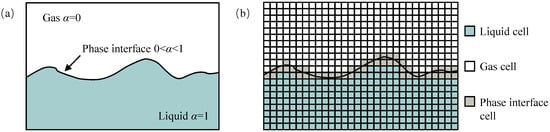
Figure 1.
(a) Phase fraction interface in the VOF model; (b) cell type of the computational region.
The equation of continuity for the flow of a mutually immiscible two-phase fluid in a porous media and the equation of momentum considering the effect of gravity is expressed as follows:
where U represents the velocity tensor, m/s; p represents the pressure in the grid, Pa; ρ represents the average density of phases in the grid, kg/m3; τ represents the shear stress at the two-phase interface, Pa−1; F represents the surface tension of the two-phase interface, N/m; g represents the acceleration of gravity, taken as 9.8 m/s2.
The average density is defined as follows:
Regarding the shear stress at the interface between two phases, when the wetting phase fluid is a Newtonian fluid
where μ represents the average viscosity in a grid, Pa·s.
The calculation formula for the average viscosity in the cell is as follows:
where μl represents the viscosity of the liquid phase in the grid, Pa·s; μg represents the viscosity of the gas phase in the grid, Pa·s.
When the wetting phase fluid is a non-Newtonian fluid, the shear stress and fluid viscosity are related to the shear rate. The power rate model is used to calculate the non-Newtonian fluid viscosity [27,28]:
where k represents the power coefficient, dimensionless; n represents parameters related to fluid properties, dimensionless; γ represents the shear rate, s−1; the subscript i represents the i-th column in the x-axis direction; the subscript j represents the j-th row in the y-axis direction.
Any cell for the computational region satisfies Σα = αl + αg = 1.
The surface tension in Equation (2) is defined by the continuous surface force model [29] as follows:
where κN represents the curvature at the two-phase interface, m−1; σ represents the interfacial tension coefficient, N/m; ρw represents the liquid phase density in the grid, kg/m3; ρg represents the gas phase density in the grid, kg/m3.
The value of κN is related to the divergence of the unit normal vector n at the phase interface [25]:
The value of the phase fraction α is related to the fluid properties, independent of the flow process. The phase fraction field equation for incompressible two-phase flow can be expressed as follows:
Equation (11) is the phase equation of the VOF model.
For incompressible systems, where pressure acts as a relative value and the differential pressure serves as the primary driving force, the cell pressure is defined to simplify the momentum equation, Equation (2), as follows:
where h represents the center position vector of a grid.
Gradient calculation for Equation (12):
Bringing Equation (13) to Equation (2) for simplification:
Equations (1), (11), and (14) together form the mathematical model for the VOF model of the two-phase flow system.
2.2. Numerical Method
The VOF model is implemented using the open-source CFD toolkit OpenFOAM-11, and the VOF model is solved using the interFoam solver. OpenFOAM uses the finite volume method to discretize the VOF model, the second-order upstream interpolation function to discretize the spatial terms, and the first-order Eulerian format to discretize the time terms. The phase equations are solved utilizing the Multi-Dimensional Universal Limiter with Explicit Solution (MULES) algorithm. For the coupled pressure-velocity field, the solution procedure employs the Pressure-Implicit with Splitting of Operators (PISO) method.
Berea sandstone and Fontainebleau sandstone serve as two frequently adopted models in the field of porous media and are extensively utilized for investigating fluid flow behaviors within such media. The primary differentiations between these models reside in their respective porosities and permeabilities. Tailored to specific research goals, the Berea sandstone model is predominantly employed to examine the flow dynamics of hydrocarbons within porous media. Conversely, the Fontainebleau sandstone model is favored for studies concerning carbon dioxide sequestration and nuclear waste disposal. For the purposes of this study, data from the standard Berea sandstone model have been selected; CINEMA 4D-R17 professional modeling software was used to build a 10 mm × 3 mm model of porous media, as shown in Figure 2a. The gray areas depict solid particles and the white areas depict flow channels. A structured hexahedral mesh is generated for the pore medium model using the snappyHexMesh toolbox in OpenFOAM, as shown in Figure 2b. The left side of the model is designated as the inlet, the right side is the outlet, and the solid particles are the walls. The inlet and outlet and wall boundary conditions are set as shown in Table 1. The pore walls were subjected to complete wetting conditions, and the Coulomb number C0 was set to 0.3 with a fixed time step. The values of the fluid parameters and computational parameters in the model are listed in Table 2, and the gas phase properties use the same parameters as for methane gas.
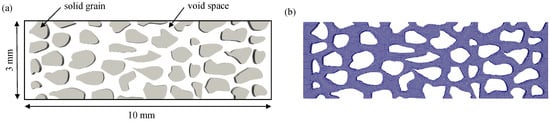
Figure 2.
(a) Porous media model; (b) generation of hexahedral mesh (16,100 cells).

Table 1.
Boundary condition settings in OpenFOAM.

Table 2.
Fluid parameters and calculation parameters.
2.3. Model Validation
To validate the accuracy of the VOF model calculations, a microscale capillary model, as depicted in Figure 3, was established to simulate the position of the gas–liquid interface during the capillary action. The accuracy and applicability of the numerical simulation method were verified by comparing the simulation results with the theoretical solutions of classical capillary. Neglecting gravity and inertia forces, the two-phase interface position is determined by the capillary force and viscous force, and its mathematical expression is as follows [25]:
where σ represents the interfacial tension, N/m; θ represents the wetting angle, °; r represents the capillary radius, m; μw represents the viscosity of the wetting phase, Pa·s; μn represents the non-wetting phase viscosity, Pa·s; L represents the length of the capillary, m; x represents the position of the interface between the two phases, m; t represents the capillary action time, s.
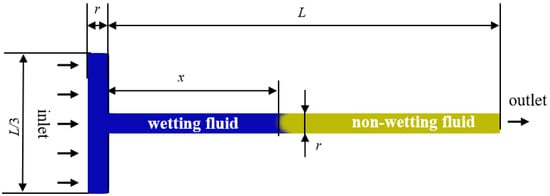
Figure 3.
Capillary percolation model (blue is the wetting phase, yellow is the non-wetting phase).
As depicted in Figure 3, the capillary model features a fluid inlet on the left and a fluid outlet on the right. At the initial moment, the capillary is entirely filled with the non-wetting phase fluid. Subsequently, driven by capillary forces, the wetting phase fluid intrudes from the left-hand side, progressively displacing the non-wetting phase fluid. A critical aspect of this process is the dynamic movement of the contact interface separating the two phases. The capillary length on the right side L is 1000 μm and the capillary diameter r is 30 μm. The boundary conditions are set to no-slip boundary conditions and wetting boundary conditions, and the sides are set to periodic boundary conditions. The wetting phase fluid density is 1000 kg/m3, viscosity 1000 mPa·s. The non-wetting phase fluid density is 0.7 kg/m3, viscosity 10 mPa·s. The surface tension is 0.03 N/m and the wall is set to be fully wetted. The Canny algorithm in MATLAB R2018b software was used to batch process the obtained flow pictures in the capillary at different flow times to obtain the contour lines of the non-wetting phase and to measure the change in the position of the interface between the two phases using the relative size of the pixels.
Figure 4 presents a comparison between the simulation results for the two-phase interface displacement obtained from the capillary percolation model and the theoretical values derived using Equation (15). The data indicate a substantial agreement between the simulation outcomes and the theoretical predictions, validating the applicability of the VOF model for simulating two-phase flow processes at the pore scale.
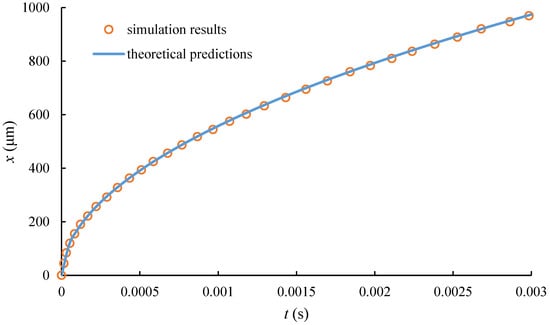
Figure 4.
Comparison of the simulation results of the two-phase interface displacement of the capillary percolation model with the theoretical values.
3. Fracturing and Rejection Process
Fracturing horizontal wells for the hydraulic fracturing and rejection process is a typical gas–liquid two-phase flow process, as shown in Figure 5. The fracturing fluid is pumped into the horizontal well through the surface high-pressure sink and filtered out to the reservoir through the hydraulic fracture; the fluid invades the reservoir matrix pore space under the actions of pumping pressure and capillary force to drive out the gas stored in the pore space. After hydraulic fracturing, the well is opened and the fracturing fluid is returned to the reservoir; the gas in the reservoir repels the fluid due to the production pressure difference, forming a gas flow channel and replacing some of the intruded fluid in the matrix pores. Using the porous media model established in Figure 2, the microscopic flow characteristics of the two stages of fracturing and re-discharge are simulated with the calculated parameters in Table 1 and Table 2 to study the effects of two types of fluids, Newtonian fluid water and non-Newtonian fluid slickwater, on gas flow.
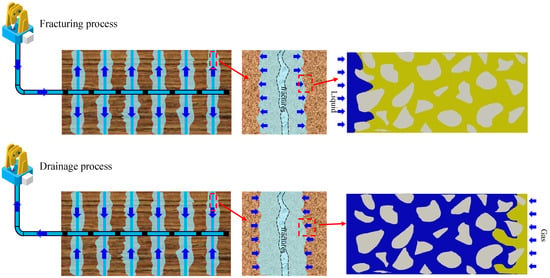
Figure 5.
Schematic diagram of the fracturing and rejection process of a multi-stage fractured horizontal well.
3.1. Fracturing Process Simulation
Figure 6 illustrates the evolution of liquid-phase saturation as water intrudes into the porous medium, displacing the gas. With the injection of water, due to the additional capillary force, the water phase breaks through the small pore size preferentially, and the liquid-phase saturation in the porous medium gradually increases; the increasing relationship between saturation and time is nearly linear. When the water phase breaks through, the liquid-phase saturation reaches a maximum value of 90.42% and remains stable. The gas that could not be displaced becomes primarily concentrated in the dead-end regions of the porous medium. During the simulation, large bubbles were also observed splitting into two small bubbles.
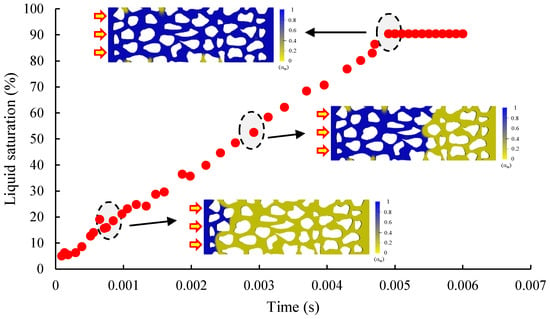
Figure 6.
Simulation of liquid phase saturation changes during water intrusion into porous media.
Figure 7 illustrates the variation in liquid-phase saturation during slickwater intrusion into the porous medium to repel the gas. With the injection of slickwater, the liquid-phase saturation increases linearly and reaches a maximum saturation of 91.47% by the time the liquid phase breaks through and remains stable. Comparing the simulation results depicted in Figure 6 and Figure 7, it is observed that within the time interval of 0–0.002 s, the saturation of slickwater in porous media is slightly higher than that of water, indicating that slickwater more readily enters dead-end positions during the initial stages of flow. Within the subsequent time interval of 0.002–0.005 s, the water occupies a greater proportion of the larger pores, while the slickwater displaces more gas from the dead-end regions of the porous medium. The displacement velocity of the water is marginally faster than that of the slickwater, resulting in a higher water saturation within the porous medium. The water achieves a stable flow earlier than the slickwater. Given that slickwater has a propensity to enter dead-end locations more easily, it exhibits a higher degree of gas displacement compared to water. Ultimately, upon reaching stable flow conditions, the saturation of slickwater in the porous medium is slightly higher than that of water.
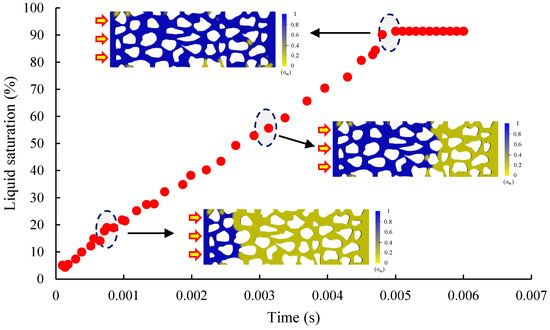
Figure 7.
Simulation of liquid-phase saturation changes during slickwater intrusion into porous media.
In simulations of fracturing fluid intrusion into porous media, the liquid phase acts as the wetting phase, repelling the gas phase along the pore walls and displacing more than 90% of the gas while occupying a larger percolation area. Non-Newtonian fluids are more likely to penetrate the porous medium compared to Newtonian fluids. For non-Newtonian fluids, due to the high initial flow velocity, shear thinning occurs. However, due to complete wetting of the walls, there is little difference in the final liquid-phase saturation between the two types of fluids, as shown in Figure 8. The variation in liquid-phase saturation over time is approximately linear, and the process of liquid-phase intrusion into the porous medium is characterized by “stable displacement” at the microscopic scale.
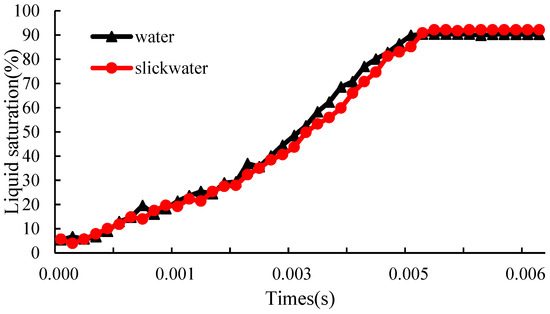
Figure 8.
Comparison of liquid saturation in porous media at different time.
The research phenomenon mentioned above occurs mainly because water is a pressurized fluid, which causes a significant difference in the microscopic flow of water and gas. The liquid as a carrier has a pressure-bearing role; when the liquid percolation is blocked, the agitated pressure will propagate throughout the water column, seeking a breakthrough to form a new percolation channel under the action of the agitated pressure, or break through the narrow throat bundle under the action of the pressure difference, which will appear as an unstable displacement leading edge in the microscopic flow [26]. The liquid phase as the wetting phase is more likely to infiltrate the pore wall to form a water film; the presence of the water film weakens the adsorption of gas molecules onto the wall and increases the content of free gas in the pore [30]. The intrusion of the liquid phase into the formation accelerates the desorption of gas to a certain extent; however, with an increase in liquid-phase saturation in the pore, the thickness of the water film gradually increases, which can lead to the appearance of the gas phase in the liquid-phase trapped pore [31].
3.2. Simulation of the Return Process
Figure 9 shows the variation in the gas saturation when gas breaks through the water phase blockage during the rejection stage. With the injection of gas, the gas saturation in the porous medium increases linearly; the gas phase breaks through the water phase blockade to form a dominant seepage channel when the gas saturation reaches 50.26%. Unlike the fracturing process where the liquid phase intrudes into the porous medium, the gas phase preferentially breaks through in the large-pore diameter pore channel due to the additional capillary force acting as a resistance.
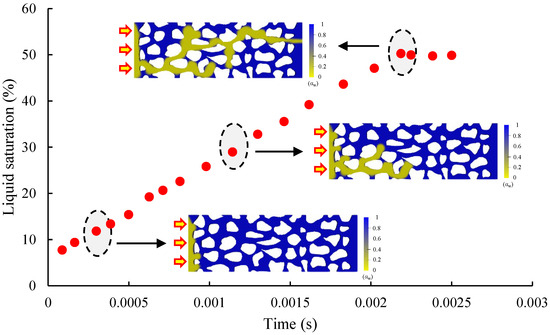
Figure 9.
Simulation of gas saturation changes during gas displacement water.
Figure 10 shows the change in gas saturation during the gas breakthrough of the slickwater closure. With the injection of gas, the gas saturation in the porous medium shows a linear increase; the gas saturation reaches 48.54% when the gas breaks through the slickwater closure to form a dominant seepage channel. The gas–liquid interface of the rejection process shows an obvious fingering phenomenon, and this instability in the flow significantly reduces the rejection efficiency of the fracturing fluid [32]. Without considering the reservoir matrix subjected to compression pore closure, about 50% of the fluid is retained in the porous medium and cannot be discharged; this part of the fluid is retained in the pore space and cannot be discharged, which is the main reason for the low rejection rate of the fracturing fluid. In both fluids with liquid phase properties, the gas breakthrough point is at a high level due to gravity and the breakthrough location is the same in both cases, indicating that the gas will automatically choose the direction of least seepage resistance to flow; this optimal path selection process is not affected by the nature of the fluid [14].
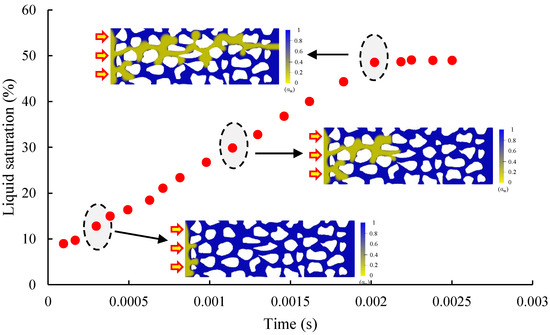
Figure 10.
Simulation of gas saturation changes during gas displacement of slickwater.
Comparing the fracturing process and the rejection process, the time required for gas breakthrough to form a stable seepage flow is half that required for the liquid phase intrusion to form a stable seepage flow, and it therefore takes longer for liquid to enter the porous medium. If we want to improve the efficiency of liquid percolation to replace the gas, we need to consider a reasonable soak time [33].
4. Gas–Liquid Two-Phase Flow Characteristics
Fluid flow in porous media is a complex interaction process; fluid flow velocity affects the flow pattern, wetting angle affects the interface relationship between the fluid and solids, and surface tension affects the interaction between different fluids. In this section the values of flow velocity, wetting angle, and surface tension are varied to study the flow characteristics of gas in Newtonian and non-Newtonian fluids; the porous medium model and simulation parameters are referred to in Figure 2 and Table 2.
4.1. Flow Rate
Gas wells experience frequent changes in their production regime during production, resulting in changes in fluid flow rates which are ultimately reflected as changes in the daily gas production in the gas well. In simulating the effect of gas flow rate changes, three different flow rates are set, as shown in Figure 11. As the percolation velocity increases, the time for the gas to break through the porous medium decreases. Within the porous medium, the gas breaks through in the direction of the minimum seepage resistance, and after breaking through the seepage channel the gas will expand the previous seepage channel and turn to strengthen the already formed seepage channel when a new one cannot be formed.
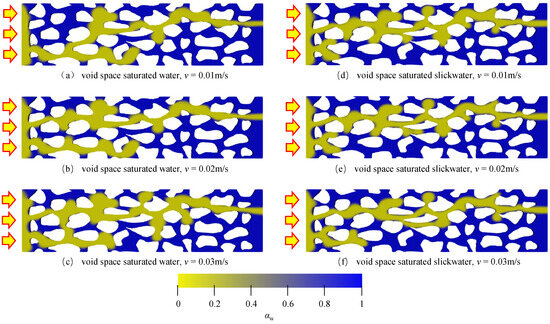
Figure 11.
Effect of flow rate on gas flow pattern in liquid phase fluids of different nature.
The variation in gas saturation as the gas breaks through the porous medium at different flow rates is presented in Figure 12. As the flow rate increases, gas saturation within the porous medium gradually rises, with this trend being particularly pronounced in the water phase. However, the final gas saturation in the slickwater shows little change [34]. Given that most gas wells in the field are fractured using non-Newtonian fracturing fluids, the increase in the fracturing fluid rejection rate achieved by raising the production pressure differential after re-establishing gas flow following a shut-in is not significantly noticeable [4,35,36].
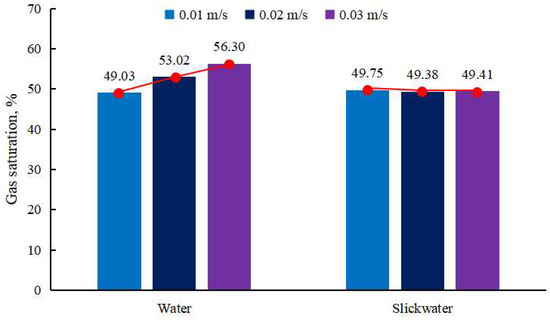
Figure 12.
Variation in gas saturation at different flow rates during gas breakthrough in porous media.
4.2. Wetting Angle
The wetting angle changes the spreading state of the wetting phase on the solid surface in porous media. From the simulation results in Figure 13, it can be seen that a change in the wetting angle has a large effect on the flow pattern of the gas. As the wetting angle increases, the porous medium changes from strongly hydrophilic to neutral wetting, reducing the instability of the leading edge of the gas flow; the pore wall has a weaker ability to adsorb the wetting fluid, enhancing the gas repellent effect and increasing the relative permeability of the gas phase. Similar flow pattern characteristics are shown in both Newtonian and non-Newtonian fluids.
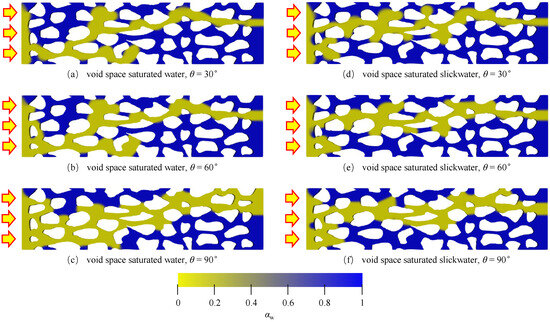
Figure 13.
Effect of wetting angle on gas flow pattern in liquid phase fluids of different nature.
The change in gas saturation within the porous medium at the moment of gas breakthrough for various wetting angle values is presented in Figure 14. It can be seen that, with an increase in the wetting angle, the change in gas saturation in the water phase is larger; the gas-containing saturation increases by 12.01% during the process of changing the water phase from the wetting phase to the non-wetting phase. However, with an increase in the wetting angle, the change in gas saturation in slickwater is not obvious. As the pore radius of an unconventional reservoir is small, it is easy to form a “water lock effect” after contact with the liquid phase. When using a wetting reversal agent to release a water lock, we should consider the nature of the liquid phase that produces the water lock and choose an appropriate wetting reversal agent [37].
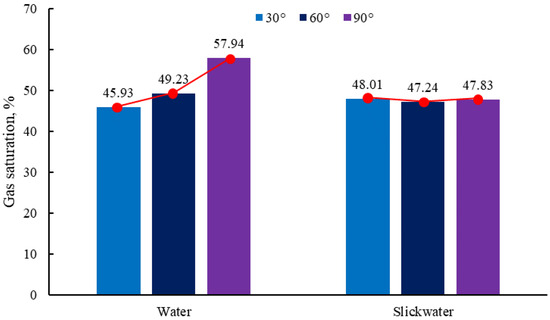
Figure 14.
Variation in gas saturation during gas breakthrough in porous media at different wetting angles.
4.3. Surface Tension
There is a role for surface tension between the interface of two immiscible fluids, the liquid phase and the gas phase. Figure 15 illustrates the flow state of a gas inside a porous medium as the surface tension increases. As the surface tension increases, the liquid becomes more capable of contracting between the phase interfaces; the force required to change the liquid phase morphology is greater, and the flow of the gas at the phase interface is more biased towards being compressed, and therefore the flow pattern is more regular; this change is more pronounced at the gas edges [38]. In slippery water, as the surface tension decreases, the Haynes step phenomenon is evident [39,40], and the gas phase is more likely to form small bubbles that snap off. A comparison of the change in the wetting angle reveals that changing the gas–liquid interaction or the solid–liquid interaction has a greater effect on the choice of gas percolation path, with the gas flowing in the aqueous phase shifting from low to high breakthrough, but preferring high for breakthrough in slippery water, a feature that does not appear in the flow velocity change study.
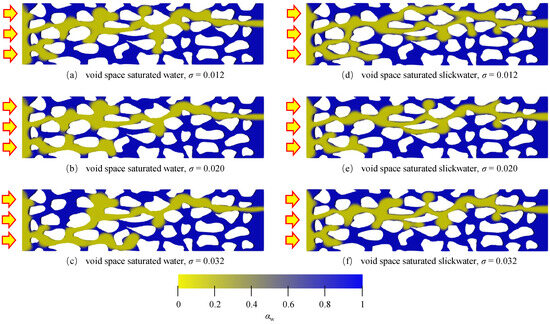
Figure 15.
Effect of surface tension on gas flow patterns in liquid phase fluids of different nature.
Figure 16 shows the variation in gas saturation at the moment of gas breakthrough for different surface tensions. As the surface tension decreases, the gas saturation increases in both liquid-phase fluids, but the increase in the gas saturation in slickwater is more pronounced. Since the lower the surface tension the lower the force required for the gas to repel the liquid phase, the amount of fluid repelled under the same conditions is larger. Selecting fracturing fluids with lower surface tensions is more conducive to fracturing fluid rejection.
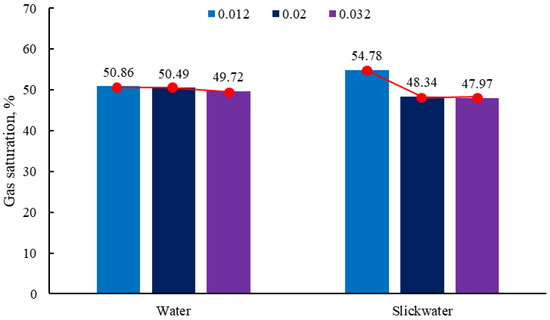
Figure 16.
Variation in gas saturation at different surface tensions during gas breakthrough in porous media.
5. Conclusions
This paper develops a gas–liquid two-phase analysis methodology for microscale fractures, employing fracture modeling and numerical simulations to investigate the behavior of gas-phase flow under various conditions. The key conclusions in this study are summarized as follows:
- The VOF model and porous media modeling techniques can realize the dynamic simulation of gas–liquid two-phase flow at the microscale, and the accuracy of the simulation results is verified using the classical percolation model.
- Liquid-driven gas processes preferentially break through small-pore channels in porous media, occupying more than 90% of the percolation channels in the wetting phase. The gas-driven liquid process preferentially breaks through large-pore channels in porous media and occupy about 50% of the seepage channels after gas breakthrough. The effect of wettability is the main reason for the lower fracturing fluid rejection rate.
- The impact of the flow velocity and wetting angle on gas saturation is pronounced in gas-driven Newtonian fluid flow processes, while surface tension significantly affects gas saturation in gas-driven non-Newtonian fluid flow processes. Gas flow within the porous medium follows the path of least resistance, which is determined by the internal structure of the porous medium and remains unchanged regardless of variations in flow parameters and fluid properties.
This study significantly enhances our understanding of the microscale characteristics of gas–liquid flow and fracturing fluid flowback. By providing novel insights into these phenomena, this research establishes a foundational reference for future investigations into gas–liquid flow dynamics within complex porous media.
Author Contributions
S.Y.: Writing-original draft preparation, software; L.Z.: supervision, methodology; T.L.: conceptualization, writing-reviewing; T.Q.: investigation, data curation; D.H.: visualization, validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the China National Petroleum Corporation Major Science and Technology Project (Grant No. 2023ZZ16-03).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that this study received funding from China National Petroleum Corporation. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication. All Authors were employed by the company PetroChina Southwest Oil & Gas Field Company. The authors declare no conflict of interest.
References
- Zou, C.N.; Xiong, B.; Xue, H.Q.; Zheng, D.W.; Ge, Z.X.; Wang, Y.; Jiang, L.Y.; Pan, S.Q.; Wu, S.T. The role of new energy in carbon neutral. Pet. Explor. Dev. 2021, 48, 411–420. [Google Scholar] [CrossRef]
- Zou, C.N.; Ma, F.; Pan, S.Q.; Lin, M.J.; Zhang, G.S.; Xiong, B.; Wang, Y.; Liang, Y.B.; Yang, Z. Earth energy evolution, human development and carbon neutral strategy. Pet. Explor. Dev. 2022, 49, 411–428. [Google Scholar] [CrossRef]
- Liu, Y.W.; Gao, D.P.; Li, Q.; Wan, Y.Z.; Duan, W.J.; Zeng, X.G.; Li, M.Y.; Su, Y.W.; Fan, Y.B.; Li, S.H.; et al. Mechanical frontiers in shale-gas development. Adv. Mech. 2019, 49, 201901. [Google Scholar]
- Ghanbari, E.; Dehghanpour, H. The fate of fracturing water: A field and simulation study. Fuel 2016, 163, 282–294. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Zheng, J.; He, Y.M.; Zhou, B. Experimental study on seepage law of fractional wet porous media. J. Chengdu Univ. Technol. (Sci. Technol. Ed.) 2021, 48, 9–18. [Google Scholar]
- Long, Y.Q.; Zhu, W.Y.; Huang, X.H.; Wu, J.J.; Song, F.Q. Experimental Study on Oil Displacement of Aqueous Dispersion System of Nano/Micron-sized Polymer Particles in Heterogeneous Reservoir. J. Southwest Pet. Univ. 2015, 37, 129–137. [Google Scholar]
- Zhao, Y.L.; Lu, G.; Zhang, L.H.; Yang, K.; Li, X.H.; Luo, J.X. Physical simulation of waterflooding development in large-scale fractured-vuggy reservoir considering filling characteristics. J. Pet. Sci. Eng. 2020, 191, 10732. [Google Scholar] [CrossRef]
- Guo, F.; Aryana, S.A. An Experimental Investigation of Flow Regimes in Imbibition and Drainage Using a Microfluidic Platform. Energies 2019, 12, 1390. [Google Scholar] [CrossRef]
- Yao, J.; Sun, H.; Li, A.F.; Yang, Y.F.; Huang, C.Q.; Wang, Y.Y.; Zhang, L.; Kou, J.L.; Xie, H.J.; Zhao, J.L.; et al. Modern system of multiphase flow in porous media and its development trend. Chin. Sci. Bull. 2018, 63, 425–451. (In Chinese) [Google Scholar] [CrossRef]
- Woerner, M. Numerical modeling of multiphase flows in microfluidics and micro process engineering: A review of methods and applications. Microfluid. Nanofluid. 2012, 12, 841–886. [Google Scholar] [CrossRef]
- Mora, P.; Morra, G.; Yuen, D.A.; Juanes, R. Influence of Wetting on Viscous Fingering Via 2D Lattice Boltzmann Simulations. Transp. Porous Media 2021, 138, 511–538. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Liu, X.Y.; Zhang, L.H.; Shan, B.C. A basic model of unconventional gas microscale flow based on the lattice Boltzmann method. Pet. Explor. Dev. 2021, 48, 156–165. [Google Scholar] [CrossRef]
- Zhang, L.H.; Xiong, Y.; Zhao, Y.L.; Tang, H.M.; Guo, J.J.; Jia, C.S.; Lei, Q.; Wang, B.H. A reservoir drying method for enhancing recovery of tight gas. Pet. Explor. Dev. 2022, 49, 125–135. [Google Scholar] [CrossRef]
- Liu, J.H.; Ju, Y.; Zhang, Y.Q.; Gong, W.B. Preferential Paths of Air-water Two-phase Flow in Porous Structures with Special Consideration of Channel Thickness Effects. Sci. Rep. 2019, 9, 16204–16217. [Google Scholar] [CrossRef]
- Cogswell, D.A.; Szulczewski, M.L. Simulation of incompressible two-phase flow in porous media with large timesteps. J. Comput. Phys. 2017, 345, 856–865. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Amiri, H.A.A.; Hamouda, A.A. Pore-scale modeling of non-isothermal two phase flow in 2D porous media: Influences of viscosity, capillarity, wettability and heterogeneity. Int. J. Multiph. Flow 2014, 61, 14–27. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhou, H.J.; Li, H.X.; Wen, T.; Zhang, R.H. Gas-water Two-phase Flow Simulation of Low-permeability Sandstone Digital Rock: Level-set Method. Chin. J. Comput. Phys. 2021, 38, 585–594. [Google Scholar]
- Chern, I.L.; Glimm, J.; Mcbryan, O.; Plohr, B.; Yaniv, S. Front tracking for gas dynamics. J. Comput. Phys. 1986, 62, 83–110. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Minakov, A.V.; Guzei, D.V.; Pryazhnikov, M.I.; Filimonov, S.A.; Voronenkova, Y.O. 3D pore-scale modeling of nanofluids-enhanced oil recovery. Pet. Explor. Dev. 2021, 48, 825–834. [Google Scholar] [CrossRef]
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces; University of London: London, UK, 1997. [Google Scholar]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- OpenFOAM. The Open Source CFD Toolbox, 2012, User Guide. Available online: https://www.openfoam.com/documentation/guides/v2012/doc/guide-fvoptions-sources.html (accessed on 25 September 2024).
- Liu, H.H.; Valocchi, A.J.; Werth, C.; Kang, Q.J.; Oostrom, M. Pore-scale simulation of liquid CO2 displacement of water using a two-phase lattice Boltzmann model. Adv. Water Resour. 2014, 73, 144–158. [Google Scholar] [CrossRef]
- Liu, H.H.; Sun, S.L.; Wu, R.; Wei, B.; Hou, J. Pore-Scale Modeling of Spontaneous Imbibition in Porous Media Using the Lattice Boltzmann Method. Water Resour. Res. 2021, 57, e2020WR029219. [Google Scholar] [CrossRef]
- Sontti, S.G.; Atta, A. CFD analysis of microfluidic droplet formation in non-Newtonian liquid. Chem. Eng. J. 2017, 330, 245–261. [Google Scholar] [CrossRef]
- Bao, K.; Lavrov, A.; Nilsen, H.M. Numerical modeling of non-Newtonian fluid flow in fractures and porous media. Comput. Geosci. 2017, 21, cp-494. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Hu, Y.Q.; Zhao, C.N.; Zhao, J.Z.; Wang, Q.; Zhao, J.; Guo, D.; Fu, C.H. Mechanisms of fracturing fluid spontaneous imbibition behavior in shale reservoir: A review. J. Nat. Gas Sci. Eng. 2020, 82, 103498. [Google Scholar] [CrossRef]
- Yang, Y.F.; Wang, K.; Lv, Q.F.; Askari, R.; Wang, C.C. Flow simulation considering adsorption boundary layer based on digital rock and finite element method. Pet. Sci. 2021, 18, 183–194. [Google Scholar] [CrossRef]
- Suo, S.; Gan, Y.X. Tuning capillary flow in porous media with hierarchical structures. Phys. Fluids 2021, 33, 034107–034116. [Google Scholar] [CrossRef]
- Akbarifard, M.G.; Azdarpour, A.; Aboosadi, Z.A.; Honarvar, B.; Nabipour, M. Numerical simulation of water production process and spontaneous imbibition in a fractured gas reservoir—A case study on homa gas field. J. Nat. Gas Sci. Eng. 2020, 83, 103603. [Google Scholar] [CrossRef]
- Cheng, Z.L.; Ning, Z.F.; Wang, Q.; Zeng, Y.; Qi, R.R.; Huang, L.; Zhang, W.T. The effect of pore structure on non-Darcy flow in porous media using the lattice Boltzmann method. J. Pet. Sci. Eng. 2018, 172, 391–400. [Google Scholar] [CrossRef]
- Shen, Y.H.; Ge, H.K.; Meng, M.M.; Jiang, Z.X.; Yang, X.Y. Effect of water imbibition on shale permeability and its influence on gas production. Energy Fuels 2017, 31, 4973–4980. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.F.; Yang, L.F.; Li, J.; Wang, Y.H.; Feng, D.; Yang, J.; Li, P.H. Effects of shut-in timing on flowback rate and productivity of shale gas wells. Nat. Gas Ind. 2017, 37, 48–60. [Google Scholar]
- Zeng, F.H.; Zhang, Q.; Guo, J.C.; Zeng, B.; Zhang, Y.; He, S.G. Mechanisms of shale hydration and water block removal. Pet. Explor. Dev. 2021, 48, 646–653. [Google Scholar] [CrossRef]
- Bui, B.T.; Tutuncu, A.N. Interfacial tension induced-transport in shale: A pore-scale study. J. Pet. Sci. Eng. 2018, 171, 1409–1419. [Google Scholar] [CrossRef]
- Haines, W.B. Studies on the physical properties of soil. J. Agric. Sci. 1930, 20, 97–116. [Google Scholar] [CrossRef]
- Zacharoudiou, I.; Boek, E.S. Capillary filling and Haines jump dynamics using free energy lattice Boltzmann simulations. Adv. Water Resour. 2016, 92, 43–56. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).