Coordinated Optimization of Multi-Regional Integrated Energy Service Providers with Flexible Reserve Resources
Abstract
1. Introduction
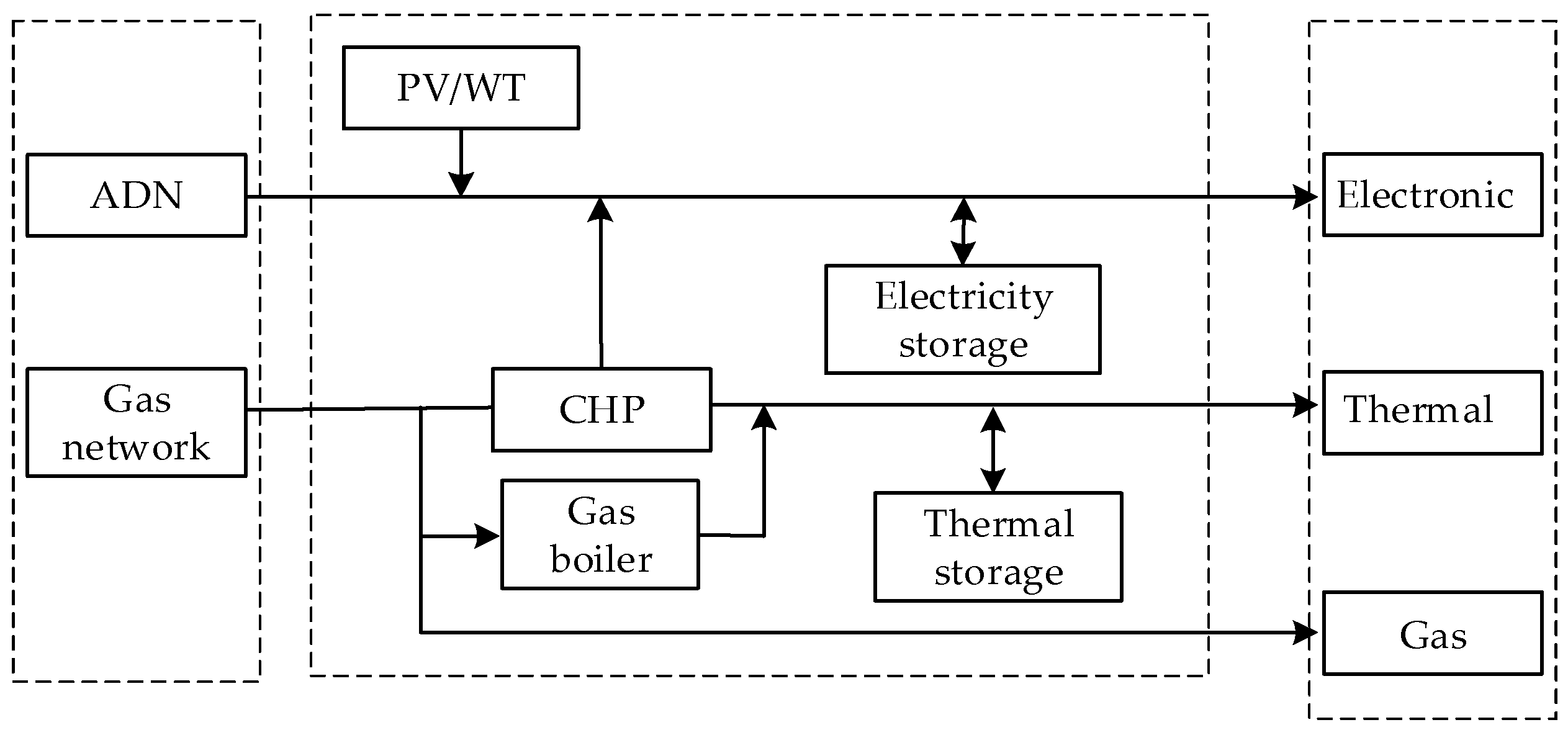
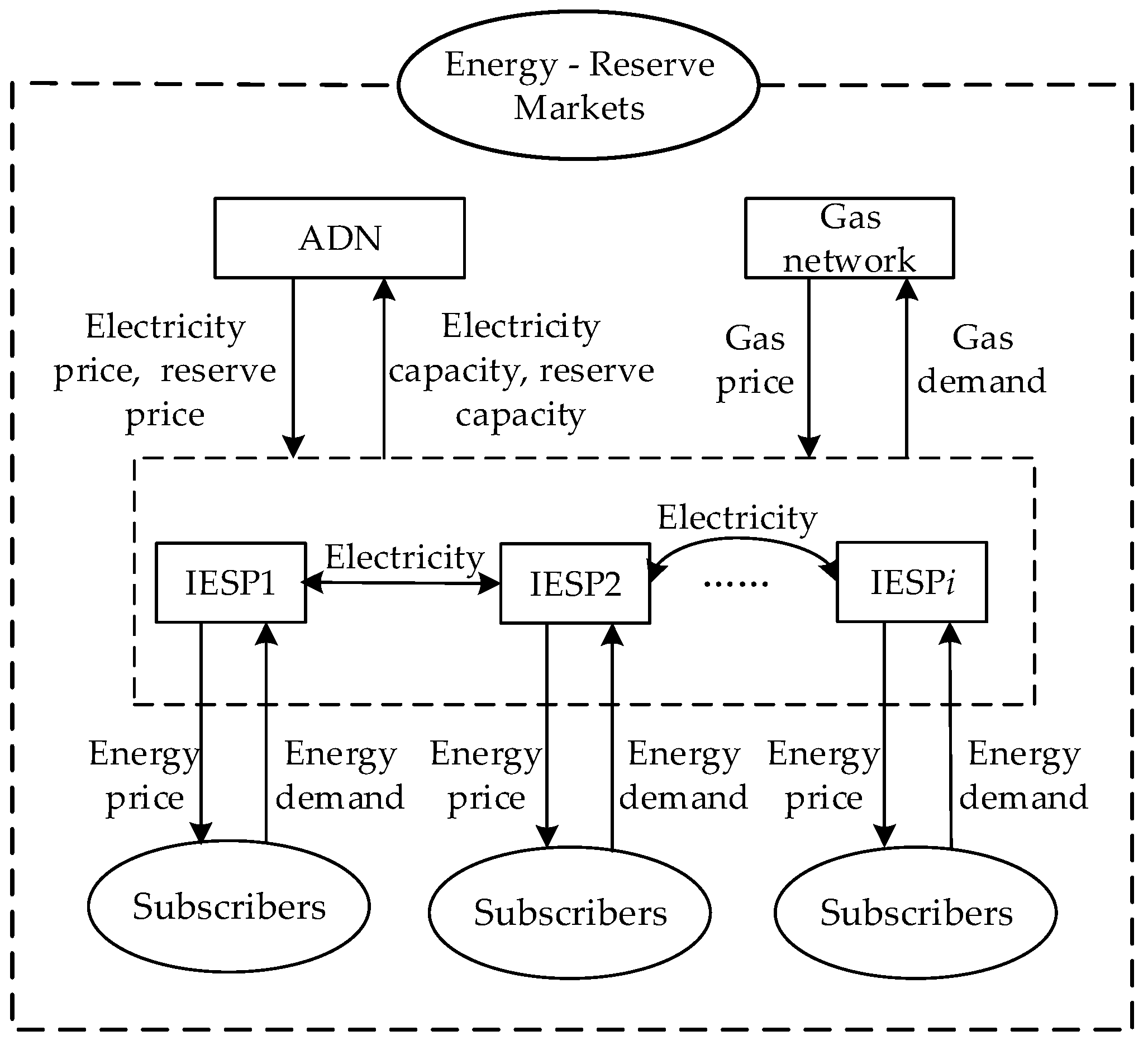
2. Participation of IESPs in Energy and Reserve Market Trading Mechanisms
3. ADN and IESPs Alliance Mixed Game Model
3.1. Gaming Leader ADN
3.1.1. Objective Function of ADN
3.1.2. ADN Constraints
- (1)
- The power balance constraint is as follows:
- (2)
- Reserve capacity constraints are as follows:
3.2. Game Follower IESPs Alliance
3.2.1. Objective Function of the IESPs Alliance
3.2.2. Constraints of the IESPs Alliance
- (1)
- The power balance constraint is as follows:
- (2)
- The demand response constraint is as follows:
- (3)
- The IDR reserve constraints are as follows:
- (4)
- The constraints on energy storage devices are as follows:
- (5)
- The constraints on CHP are as follows:
- (6)
- The gas boiler constraints are as follows:
- (7)
- The reserve constraints of the unit are as follows:
- (8)
- The reserve capacity constraints are as follows:
3.3. IESP Alliance Nash Negotiation Model
3.3.1. SubProblem (P1) Maximization of Alliance Profits
3.3.2. Subproblem (P2) Distribution of Cooperation Profits
4. Model Solving
4.1. Uncertain Scenario Portrayal for Wind, PV, and Loads
- (1)
- The cumulative probability distribution function F(x) into N non-overlapping sub-intervals, each spaced 1/N apart.
- (2)
- t−1 random numbers in the range [0, 1], denoted by , at each equal portion m. Calculate the value of the cumulative probability function corresponding to each random number as follows: .
- (3)
- The incremental sampling value of wind power data is obtained according to the inverse function of the cumulative probability distribution function, i.e.:
- (4)
- The historical output data are added to the incremental sampling values obtained in step (3) to simulate the generation of wind power output data.
- (5)
- If the obtained randomized scenario m has negative power at moment t, i.e., , then take .
- (6)
- An N × t-dimensional matrix is generated to randomly order the data in each column, i.e., N random wind power outflow scenarios are generated.
- (1)
- The cluster number was determined, and samples were randomly selected as initial cluster centers.
- (2)
- The Euclidean distance between each sample and each cluster center is calculated and compared. The nearest cluster center is the cluster to which the sample belongs.
- (3)
- All samples in the same cluster are averaged as the new cluster center coordinates for the cluster
- (4)
- Steps (2) and (3) repeat the calculation until all in-cluster samples no longer change.
- (5)
- The probability of the occurrence of each scene is calculated, with , representing the number of scenes in the wth category divided by the total number of scenes.
4.2. Solving Master–Slave Game Based on KKT Condition
4.3. Solving Cooperative Game Based on ADMM
5. Example Analysis
5.1. Each Subject Transaction Price Analysis
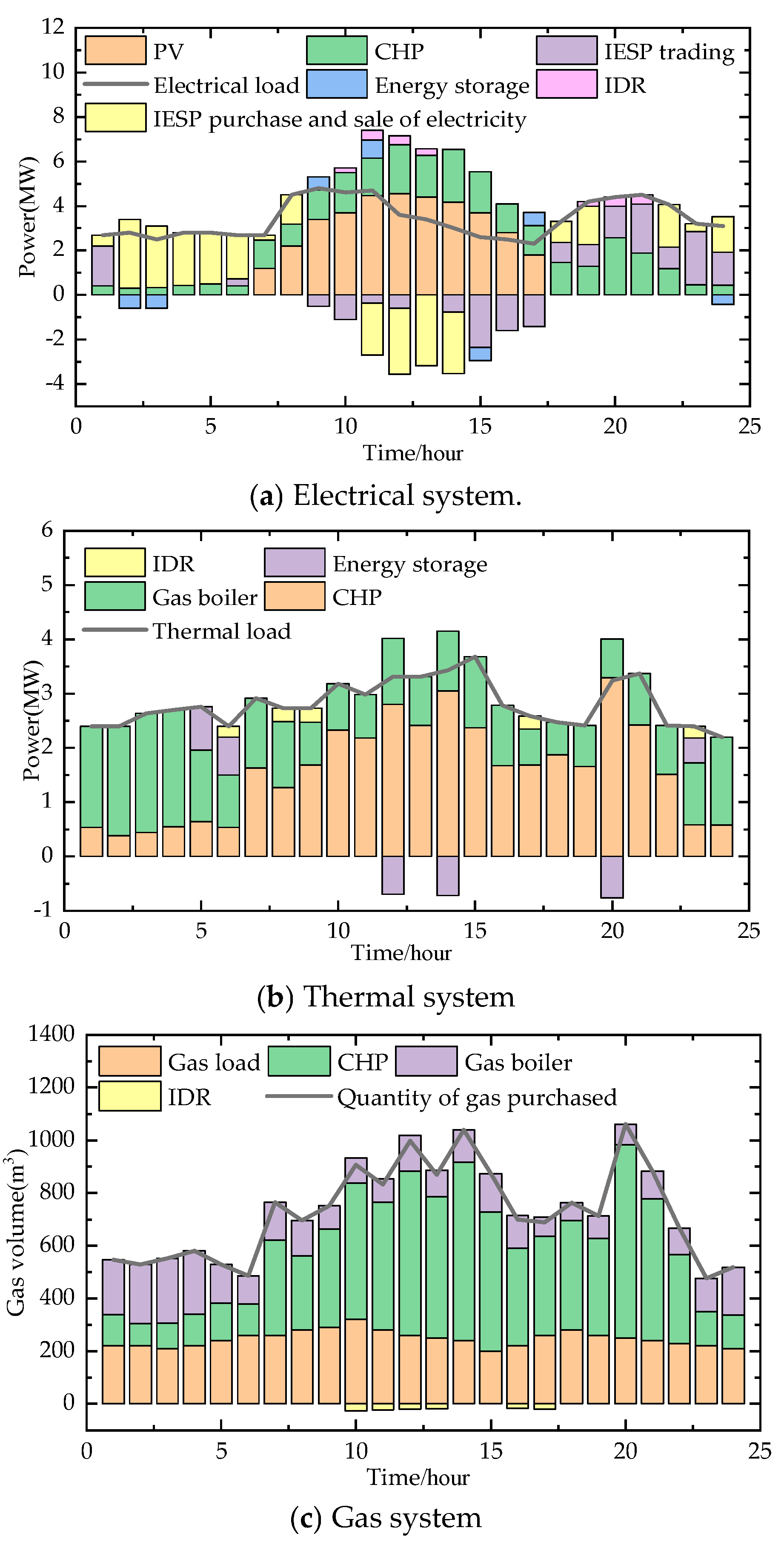
5.2. Analysis of Electrical, Heat, and Gas Balance Results
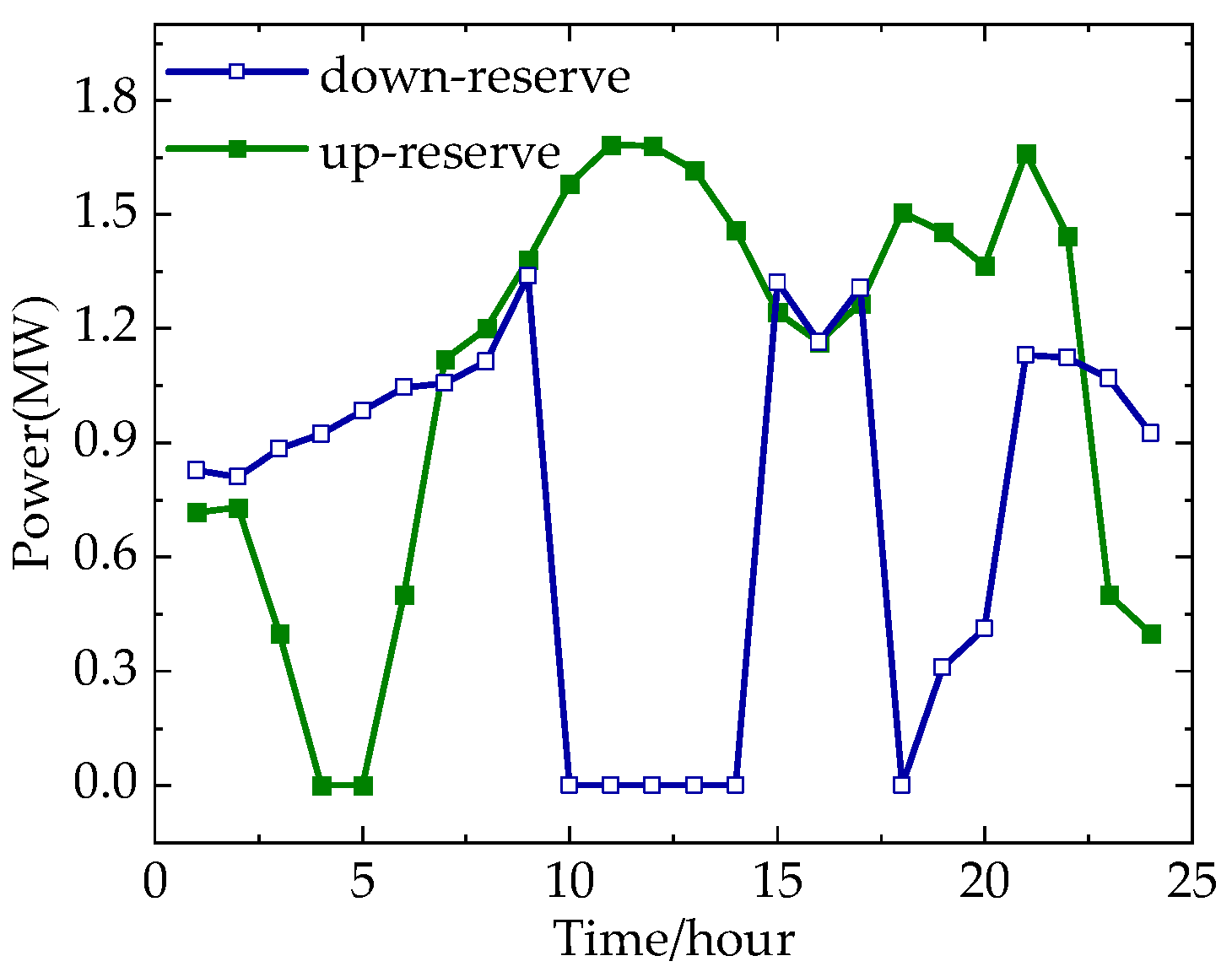
5.3. Analysis of Reserve Capacity Optimization Results
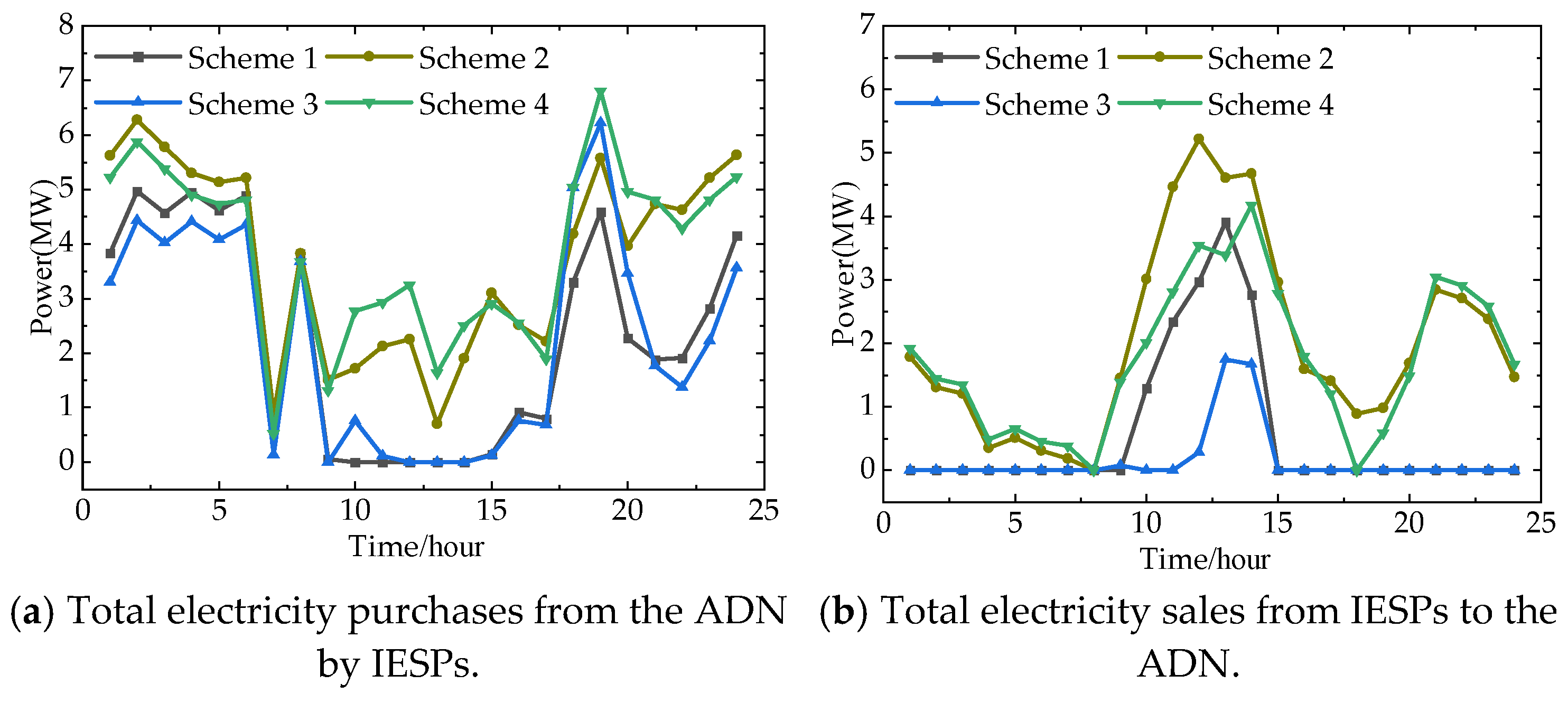
5.4. Analysis of Alternate Transaction Results Between ADN and IESPs
5.5. Scheme Comparison Analysis
5.5.1. Economic Benefit Analysis of IESPs Under Each Scheme
- (1)
- An analysis of the effectiveness of cooperative game: Compared with the scheme 2, scheme 1 considers the cooperative game, and the income of the IESs alliance in the first scheme is 4842 yuan higher than in the second scheme. This is due to the fact that the trading of electricity between IESP members utilizes inter-regional complementarities, which reduces the dependence of IESPs on the ADN and achieves an increase in the total benefits of the IESP alliance. Compared with directly trading with the ADN, the benefits for each IESP increased by 1337 yuan, 779 yuan, and 2726 yuan, respectively.
- (2)
- Demand response effectiveness analysis: Compared with scheme 3, it can be found that scheme 1 considers more incentive demand response and price demand response, which increases the revenue of each IESP alliance by 877 yuan, 1110 yuan, and 1083 yuan. This is because IESPs can transfer or cut the load when the price of electricity is high. At the same time, the implementation of incentive demand response increases the reserve capacity of IESPs, effectively relieves the reserve pressure of CHP, and improves the economy of system operation.
- (3)
- The effectiveness analysis of the cooperative game and demand response is also considered: Compared with scheme 4, scheme 1 considers the cooperation game and demand response, which makes the income of IESPs in each region in scheme 1 increase by 2204 yuan, 1862 yuan, and 3973 yuan, respectively. This is due to the fact that the price of electricity traded between regions is higher than the price of electricity supplied to the ADN. IDR has a short response time to reduce or stop electricity consumption during peak tariffs. When the IESPs have sufficient power, the IESPs provide more power to the ADNs and thus the IESPs increase their revenues.Through the comparison of the above schemes, it is found that the mixed game model of the IESP and ADN alliance considering flexible reserve resources proposed in this paper can effectively improve the economic benefits of each region.
5.5.2. Analysis of Total Transaction Power of IESPs and the ADN Under Each Scheme
6. Conclusions
- (1)
- The mixed game model established in this paper takes into account the uncertainty of new energy and load and collaboratively formulates the unit output plan and reserve capacity scheme of IESPs in each region, as well as the trading power among the subjects. ADN formulates the price of electricity and reserve to guide the IESPs to fully exploit their own flexible reserve resources, alleviate the pressure of reserve on the higher-level grids, and enhance the profitability of the IESPs.
- (2)
- Cooperative gaming can coordinate the scheduling of IESP resources in each region and reduce the dependence on the ADN. Compared to trading directly with ADN, the benefits of each regional IESP are increased by 1337 yuan, 779 yuan, and 2726 yuan, respectively.
- (3)
- The example simulation results show that the flexible reserve resources provided by energy storage and demand response participate in system optimal scheduling, which can improve the flexibility of the CHP group operation and thus improve the economy of system operation. In addition, the method proposed in this paper can provide a reference point for integrated energy systems with large new energy installed capacity and encourage more flexible resources to provide reserve.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Maximum electrical power output of combined heat and power | |
| Thermal power conversion factor for combined heat and power | |
| Electrical power conversion factor for combined heat and power | |
| Maximum creep rate for combined heat and power | |
| Minimum creep rate for combined heat and power | |
| Costs of charging and discharging electrical energy storage | |
| Charge and discharge costs for thermal energy storage | |
| Maximum charging power of electrical energy storage | |
| Maximum discharge power of electric energy storage | |
| Maximum capacity of electrical energy storage | |
| Minimum capacity of electrical energy storage | |
| Electric load demand response costs | |
| Thermal load demand response costs | |
| Gas load demand response costs | |
| Maximum thermal power output of gas boiler | |
| Thermal power conversion factor for gas boiler | |
| Probability of occurrence of scenario w | |
| Penalty factor | |
| Convergence factor |
Abbreviations
| IESP | Integrated energy service provider |
| ADN | Active distribution network |
| IDR | Incentive demand response |
| CHP | Combined heat and power |
| PV | Photovoltaic |
| WT | Wind turbine |
| KKT | Karush–Kuhn–Tucker |
| ADMM | Alternating direction multiplier method |
Appendix A. WT, PV, and Load-Out Scenarios
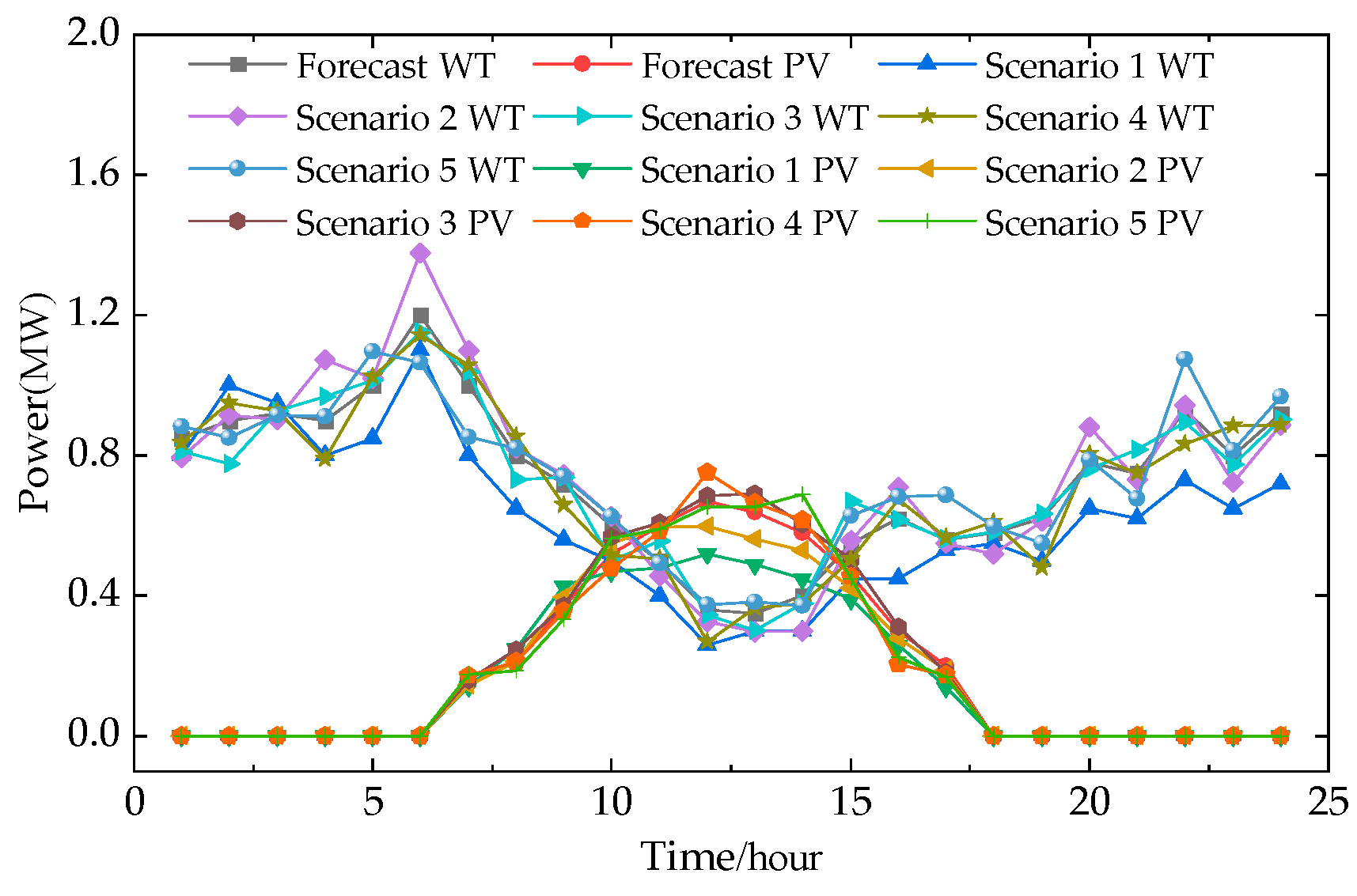

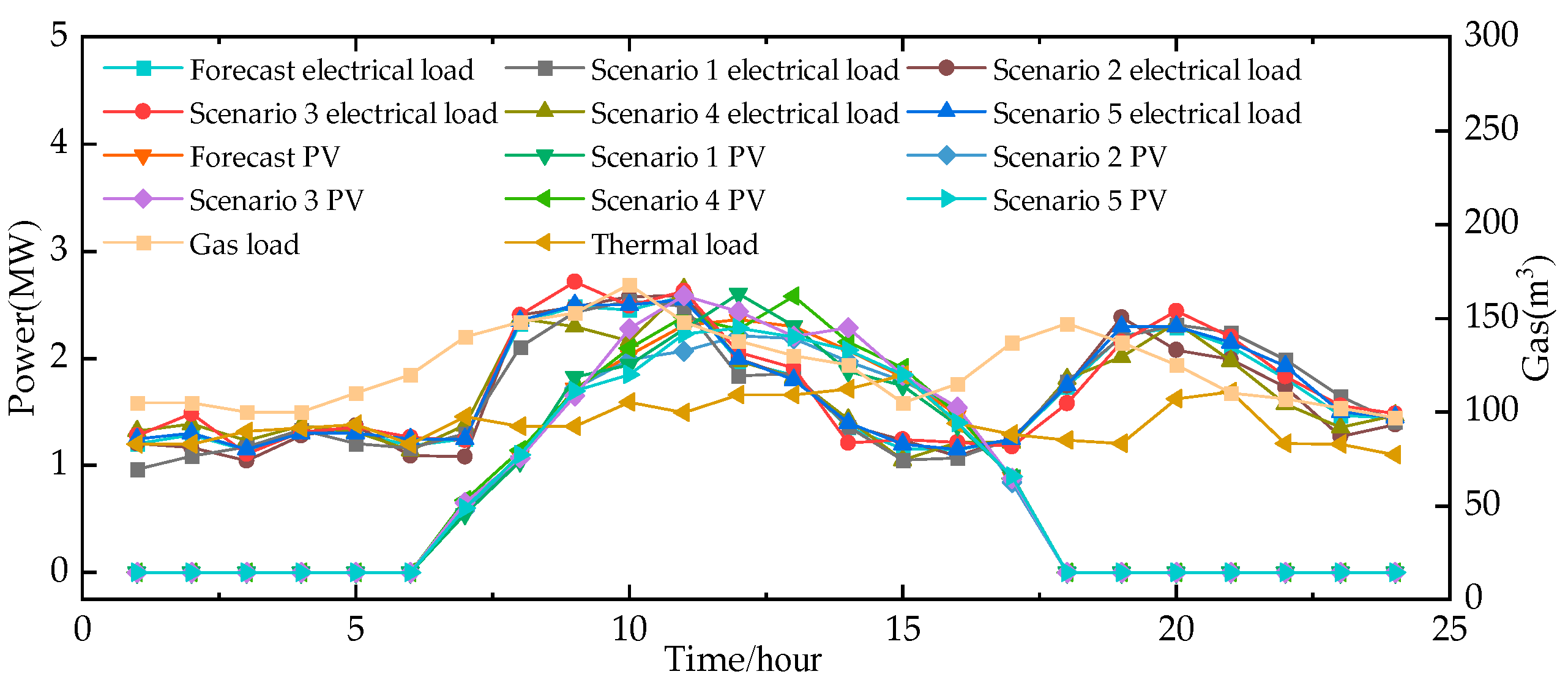
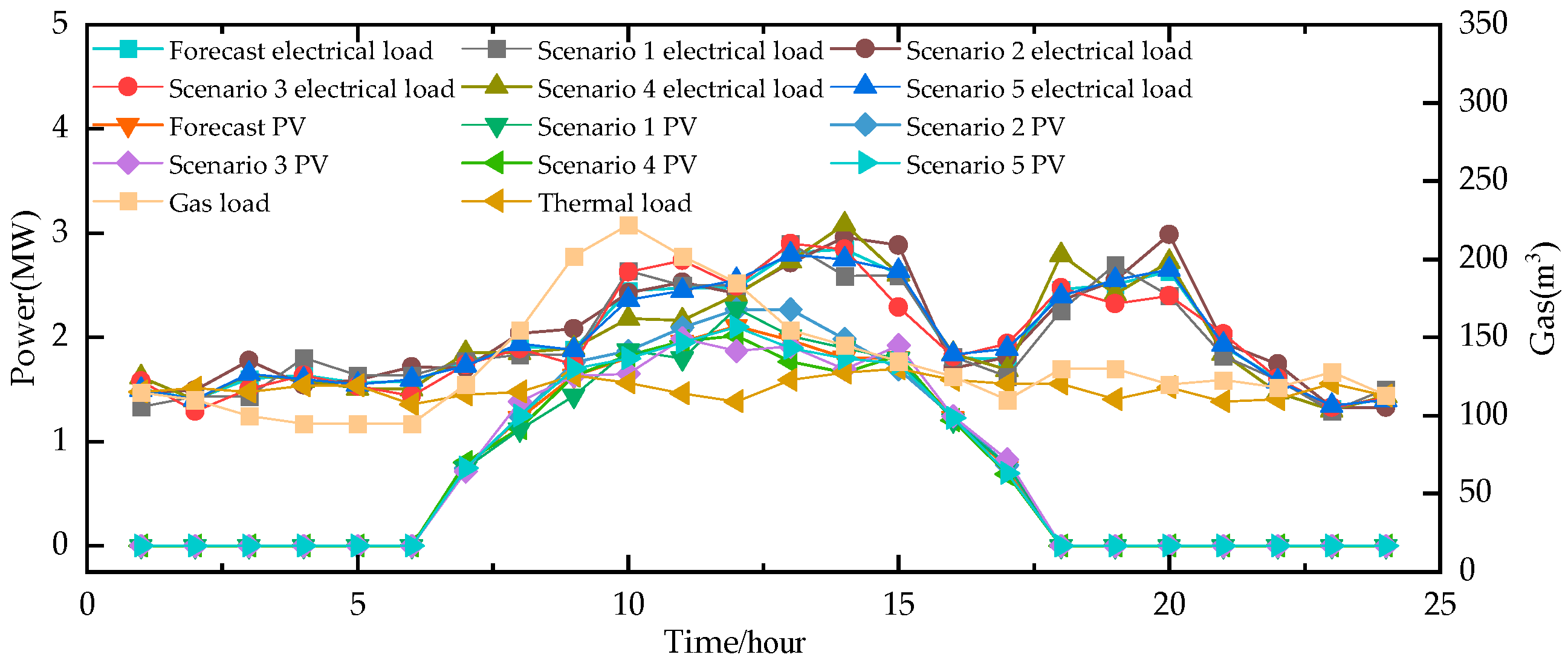

References
- Wang, K.; Niu, D.; Yu, M.; Liang, Y.; Yang, X.; Wu, J.; Xu, X. Analysis and countermeasures of China’s green electric power development. Sustainability 2021, 13, 708. [Google Scholar] [CrossRef]
- Safaei, M.; Al Dawsari, S.; Yahya, K. Optimizing Multi-Channel Green Supply Chain Dynamics with Renewable Energy Integration and Emissions Reduction. Sustainability 2024, 16, 9710. [Google Scholar] [CrossRef]
- Mohandes, B.; Moursi, M.S.E.; Hatziargyriou, N.; Khatib, S.E. A Review of power system flexibility with high penetration of renewables. IEEE Trans. Power Syst. 2019, 34, 3140–3155. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, Q.; Zeng, W. Optimization scheduling of integrated energy service system in community: A bi-layer optimization model considering multi-energy demand response and user satisfaction. Energy 2022, 252, 124063. [Google Scholar] [CrossRef]
- Luo, F.; Shao, J.; Jiao, Z.; Zhang, T. Research on optimal allocation strategy of multiple energy storage in regional integrated energy system based on operation benefit increment. Int. J. Electr. Power Energy Syst. 2021, 125, 106376. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, Q.; Zeng, W. Optimization scheduling of an integrated energy service system in community under the carbon trading mechanism: A model with reward-penalty and user satisfaction. J. Clean. Prod. 2021, 323, 129171. [Google Scholar] [CrossRef]
- Nasrolahpour, E.; Kazempour, J.; Zareipour, H.; Rosehart, W.D. A Bilevel Model for Participation of a Storage System in Energy and Reserve Markets. IEEE Trans. Sustain. Energy 2018, 9, 582–598. [Google Scholar] [CrossRef]
- Zhou, Y.; Hu, W.; Min, Y.; Dai, Y. Integrated Power and Heat Dispatch Considering Available Reserve of Combined Heat and Power Units. IEEE Trans. Sustain. Energy 2019, 10, 1300–1310. [Google Scholar] [CrossRef]
- Yang, R.; Li, K.; Liu, J.; Liu, J.; Xiang, Y. Day-ahead Economic Dispatch Model of Park Integrated Energy System Considering Reserve Allocation of Energy Storage. Electr. Power Constr. 2022, 43, 103–111. [Google Scholar]
- Li, N.; Sun, S.; Zhang, L.; Wang, J.; Qu, Y. The Evaluation Method of the Power Supply Capability of an Active Distribution Network Considering Demand Response. Processes 2024, 12, 2719. [Google Scholar] [CrossRef]
- Chen, Z.; Li, F.; Huang, R. Spinning reserve optimal configuration strategy of a wind power system with demand response. Power Syst. Prot. Control. 2020, 48, 117–122. [Google Scholar]
- Mo, L.; Deng, Z.; Chen, H.; Lan, L. Multi-Objective Co-Operative Game-Based Optimization for Park-Level Integrated Energy System Based on Exergy-Economic Analysis. Energies 2023, 16, 7945. [Google Scholar] [CrossRef]
- Ji, X.; Li, M.; Li, M.; Han, H. Low-carbon dispatch of multi-regional integrated energy systems considering integrated demand side response. Front. Energy Res. 2024, 12, 1361306. [Google Scholar] [CrossRef]
- Sun, H.; Zou, H.; Jia, J.; Shen, Q.; Duan, Z.; Tang, X. Master–Slave Game Optimization Scheduling of Multi-Microgrid Integrated Energy System Considering Comprehensive Demand Response and Wind and Storage Combination. Energies 2024, 17, 5762. [Google Scholar] [CrossRef]
- Yang, S.; Tan, Z.; Lin, H.; De, G.; Zhou, F. Stochastic Optimization and Income Allocation Model for Park Integrated Energy System Considering Cooperation Alliance. Power Syst. Autom. 2020, 44, 36–46. Available online: https://link.cnki.net/urlid/32.1180.TP.20200713.1548.008 (accessed on 3 January 2025).
- Cui, M.; Xuan, M.; Lu, Z.; He, L. Operation Optimization Strategy of Multi Integrated Energy Service Companies Based on Cooperative Game Theory. Proc. CSEE 2022, 10, 3548–3564. [Google Scholar] [CrossRef]
- Zhou, C.; Zheng, C.B. Energy Trading Strategy for Heat and Electricity-Coupled Microgrid Based on Cooperative Game. Appl. Sci. 2022, 12, 6568. [Google Scholar] [CrossRef]
- Khazaei, H.; Aghamohammadloo, H.; Habibi, M.; Mehdinejad, M.; Mohammadpour Shotorbani, A. Novel Decentralized Peer-to-Peer Gas and Electricity Transaction Market between Prosumers and Retailers Considering Integrated Demand Response Programs. Sustainability 2023, 15, 6165. [Google Scholar] [CrossRef]
- Tong, X.; Hu, C.; Zheng, C.; Rui, T.; Wang, B.; Shen, W. Energy Market Management for Distribution Network with a Multi-Microgrid System: A Dynamic Game Approach. Appl. Sci. 2019, 9, 5436. [Google Scholar] [CrossRef]
- Lai, X.; Xie, Z.; Xu, D.; Ying, S.; Zeng, Y.; Jiang, C.; Wang, F.; Wen, F.; Palu, I. Operation Optimization of an Integrated Energy Service Provider with Ancillary Service Provision. Energies 2022, 15, 4376. [Google Scholar] [CrossRef]
- Cui, Y.; Deng, G.; Zhao, Y.; Zhong, W.; Tang, Y.; Liu, X. Economic Dispatch of Power System With Wind Power Considering the Complementarity of Low-carbon Characteristics of Source Side and Load Side. Proc. CSEE 2021, 41, 4799–4815. [Google Scholar] [CrossRef]


| Time Frame | Price (Yuan/kW·h) | |
|---|---|---|
| Valley time | 01:00–06:00; 23:00–24:00 | 0.25 |
| Flat price period | 07:00–09:00; 15:00–17:00; 21:00–22:00 | 0.58 |
| Rush hour | 10:00–14:00; 18:00–20:00 | 1 |
| Parameters | Numerical Value | Parameters | Numerical Value |
|---|---|---|---|
| /MW | 2 | /(kW/m3) | 3.5 |
| /(kW/m3) | 4.5 | /(MW/h) | 0.8 |
| /(MW/h) | 0.8 | /(yuan/kW·h) | 0.01 |
| /(MW/h) | 0.6 | /(MW/h) | 0.6 |
| /(MW·h) | 2 | /(MW·h) | 0.3 |
| /(MW/h) | 0.4 | /(MW/h) | 0.4 |
| /(MW·h) | 1.5 | /(MW·h) | 0.2 |
| /MW | 2 | /(kW/m3) | 9 |
| /(yuan/kW·h) | 0.5 | /(yuan/kW·h) | 0.48 |
| /(yuan/kW·h) | 0.48 | /(yuan/kW·h) | 0.25 |
| /(yuan/kW·h) | 0.25 | /(yuan/kW·h) | 0.005 |
| /(yuan/kW·h) | 0.08 | /(yuan/kW·h) | 0.05 |
| /(yuan/kW·h) | 0.05 |
| Scheme | IESP1 Earnings (Ten Thousand Yuan) | IESP2 Earnings (Ten Thousand Yuan) | IESP3 Earnings (Ten Thousand Yuan) | Total Earnings (Ten Thousand Yuan) |
|---|---|---|---|---|
| 1 | −3.1096 | −3.8904 | −4.9612 | −11.9612 |
| 2 | −3.2433 | −3.9683 | −5.2338 | −12.4454 |
| 3 | −3.1973 | −4.0015 | −5.0695 | −12.2683 |
| 4 | −3.3300 | −4.0766 | −5.3585 | −12.7651 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhong, H.; Zou, X.; Wang, Q.; Li, L. Coordinated Optimization of Multi-Regional Integrated Energy Service Providers with Flexible Reserve Resources. Energies 2025, 18, 284. https://doi.org/10.3390/en18020284
Wang X, Zhong H, Zou X, Wang Q, Li L. Coordinated Optimization of Multi-Regional Integrated Energy Service Providers with Flexible Reserve Resources. Energies. 2025; 18(2):284. https://doi.org/10.3390/en18020284
Chicago/Turabian StyleWang, Xueting, Hao Zhong, Xianqiu Zou, Qiujie Wang, and Lanfang Li. 2025. "Coordinated Optimization of Multi-Regional Integrated Energy Service Providers with Flexible Reserve Resources" Energies 18, no. 2: 284. https://doi.org/10.3390/en18020284
APA StyleWang, X., Zhong, H., Zou, X., Wang, Q., & Li, L. (2025). Coordinated Optimization of Multi-Regional Integrated Energy Service Providers with Flexible Reserve Resources. Energies, 18(2), 284. https://doi.org/10.3390/en18020284






