A Ratchet for Closed Pipes: Asymmetric-Configuration Role on Unidirectional Circulatory Flows
Abstract
1. Introduction
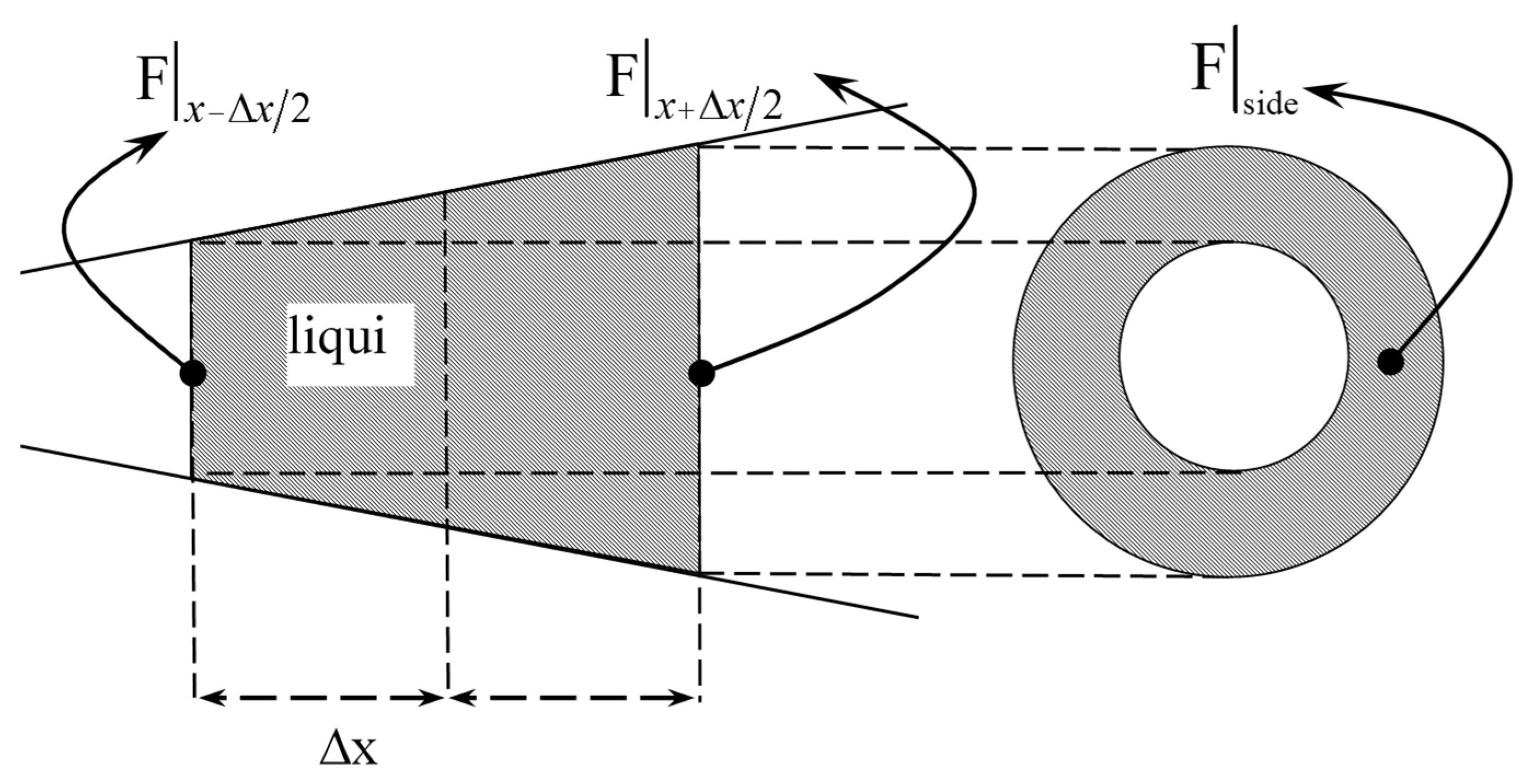
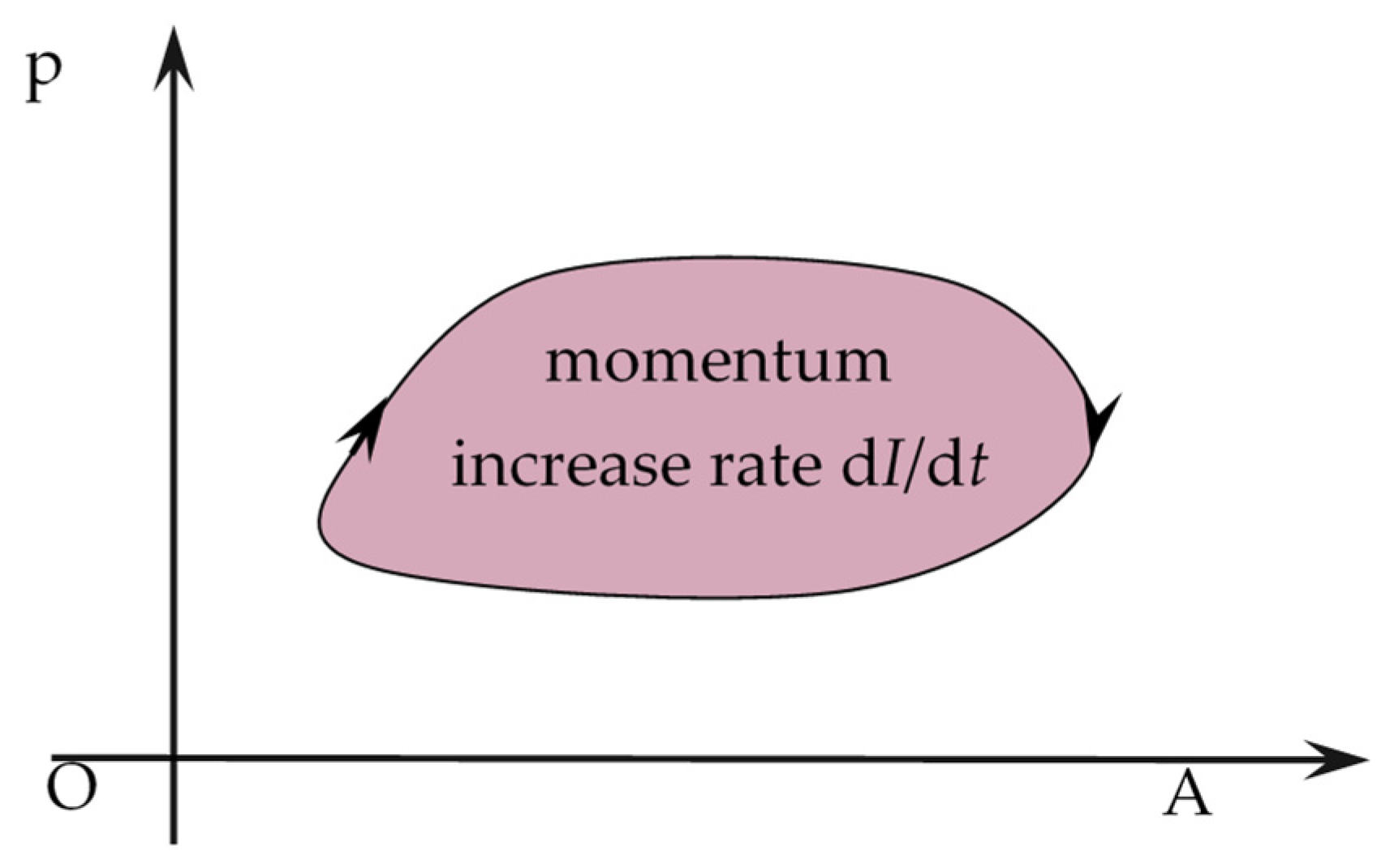
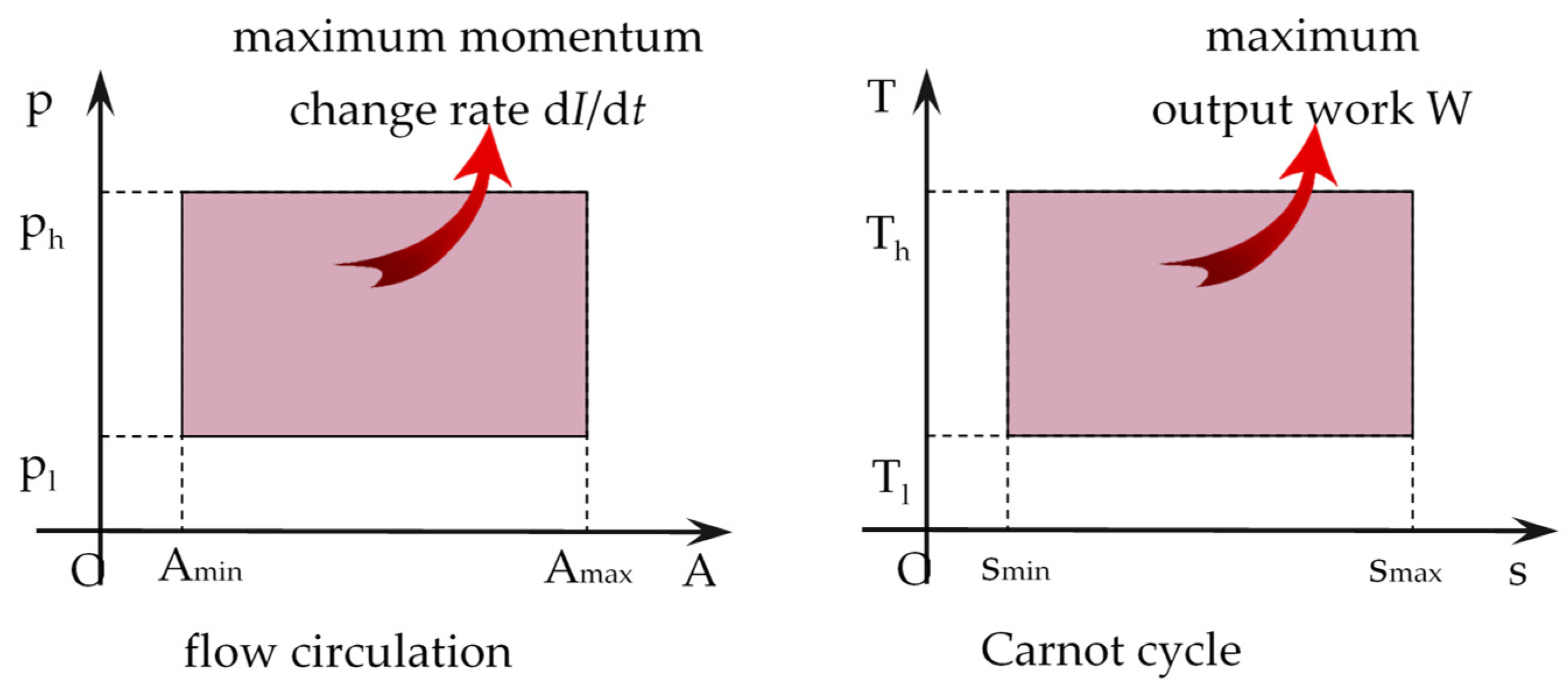
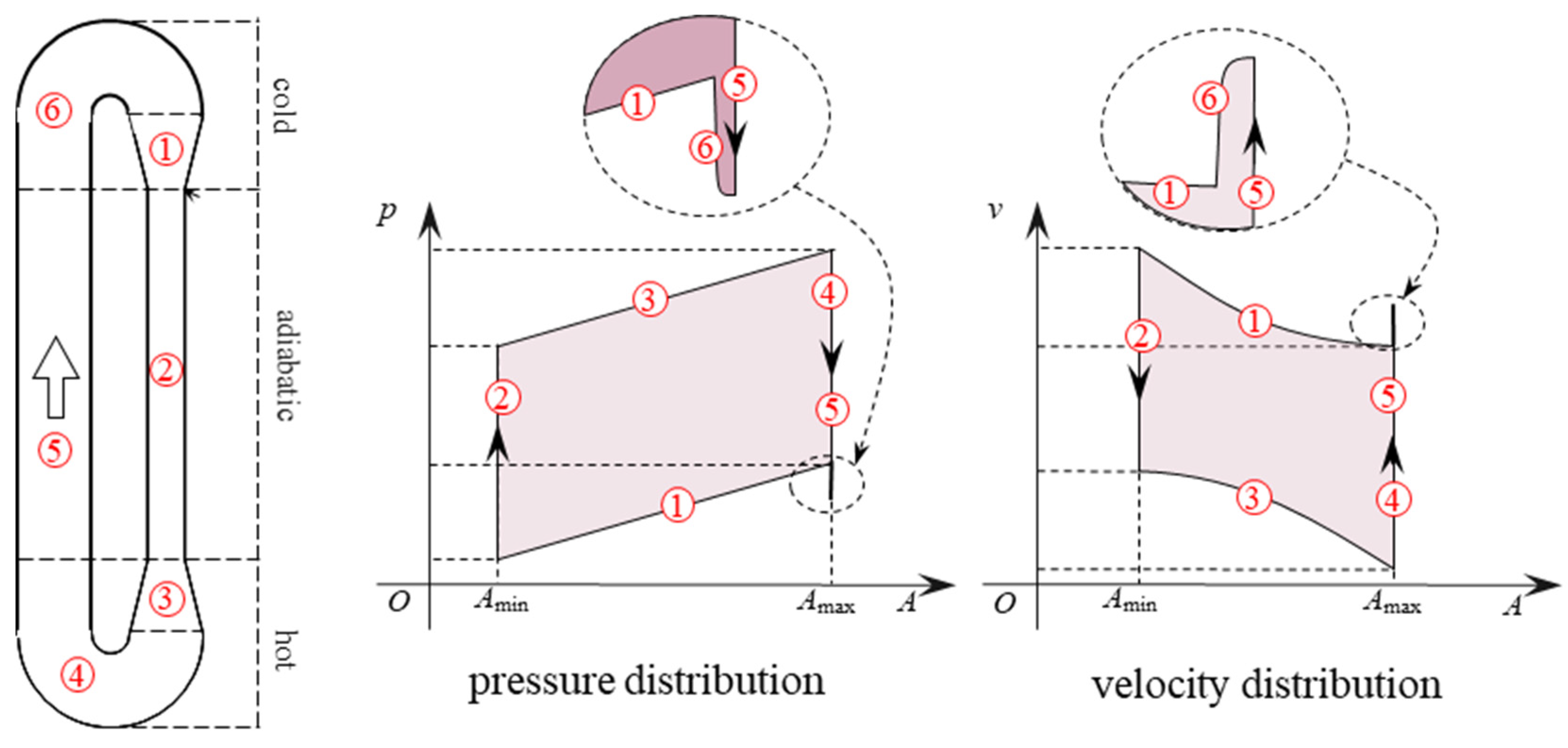
2. Theoretical Analysis
2.1. Ideal Unidirectional Flow
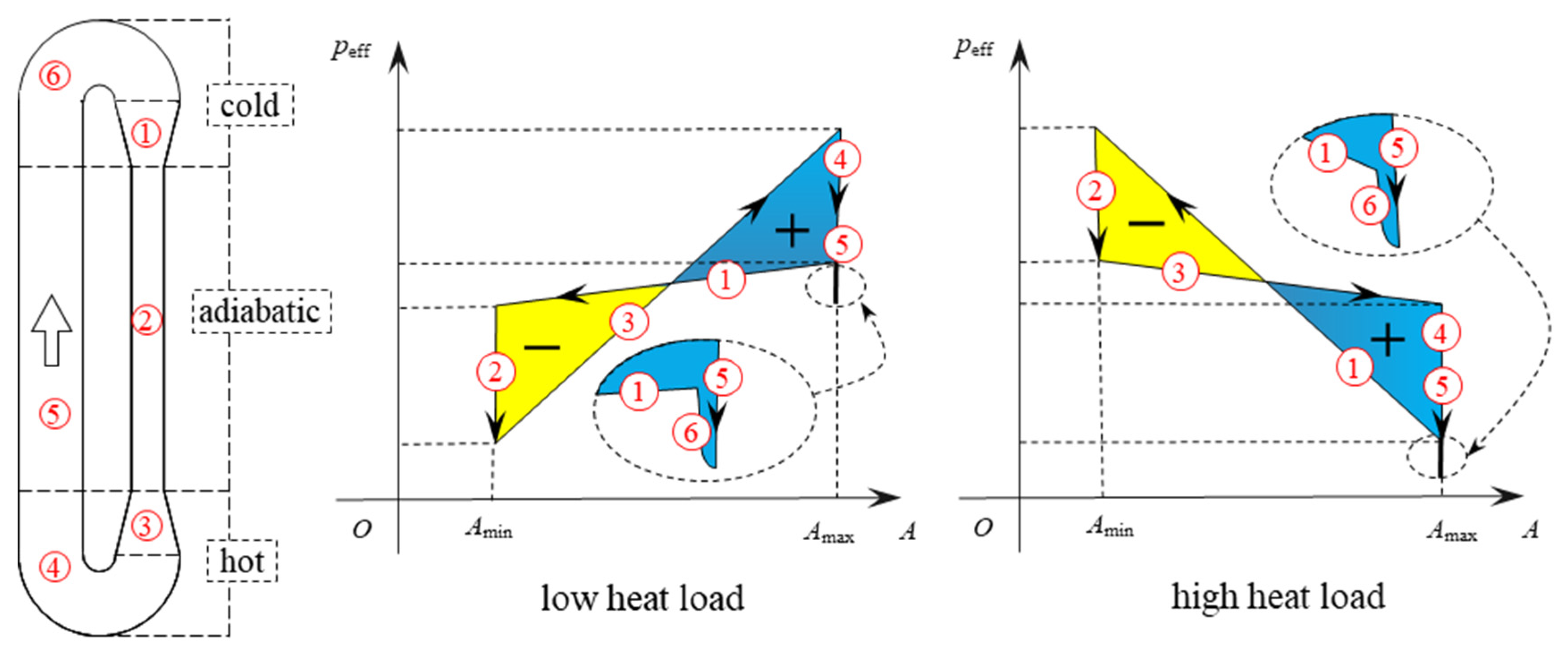
2.2. Two-Phase Effect
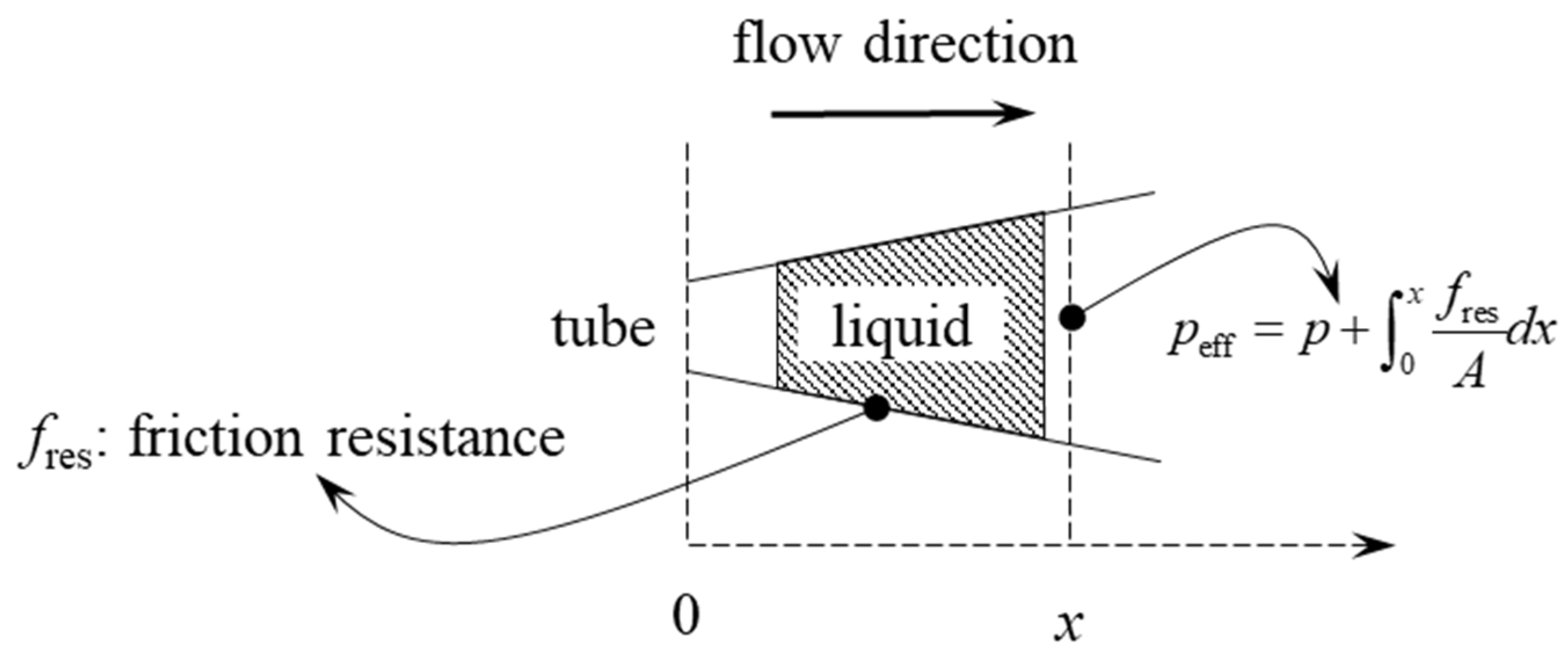
2.3. Friction Effect
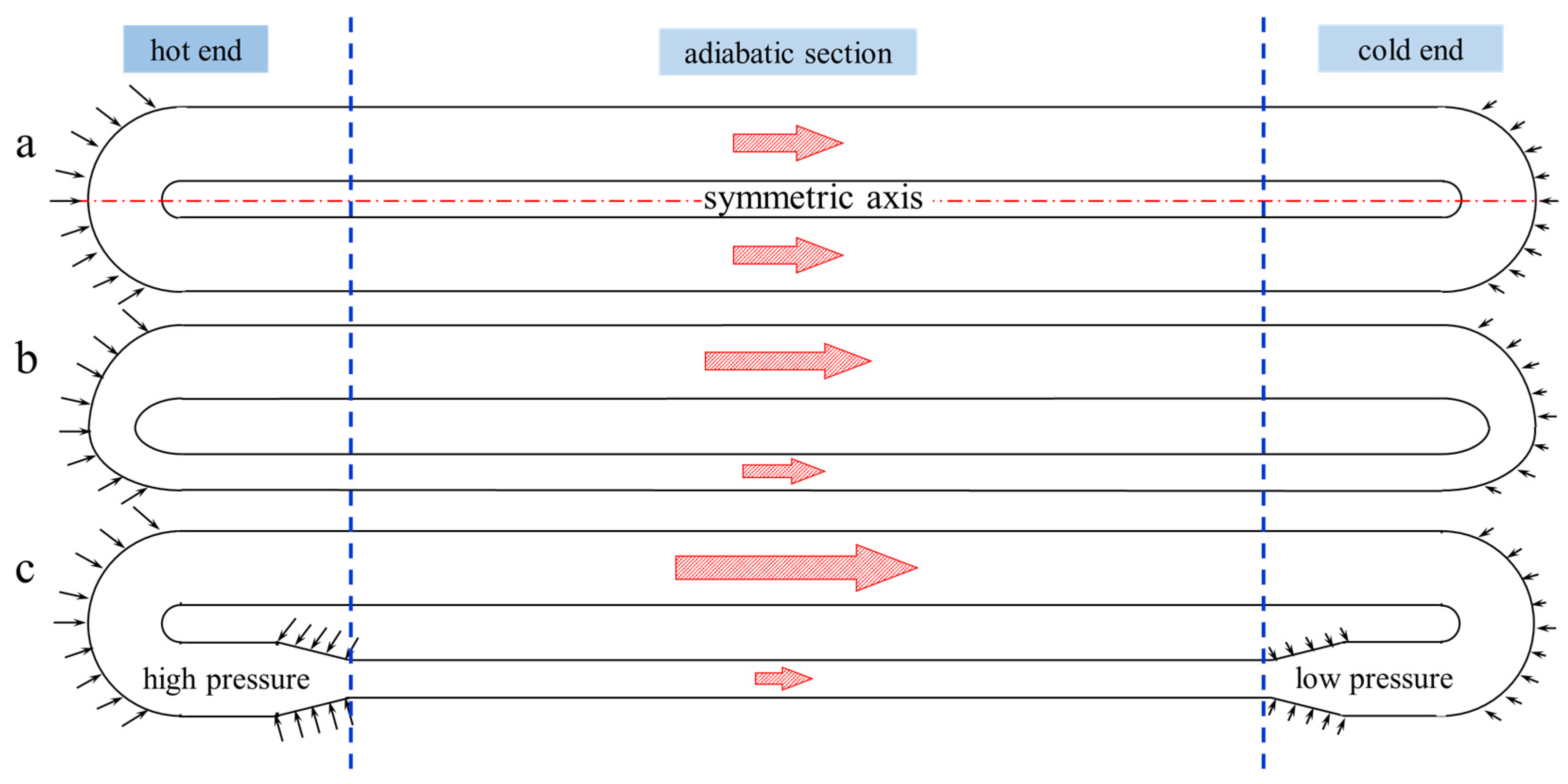
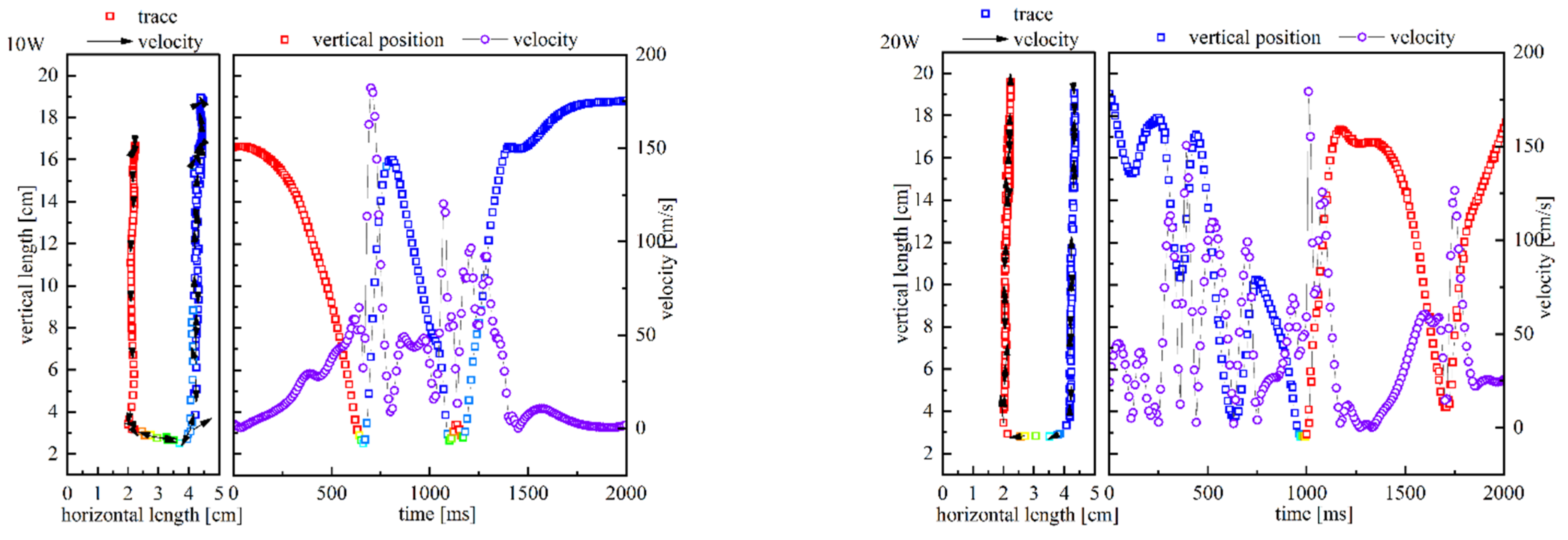
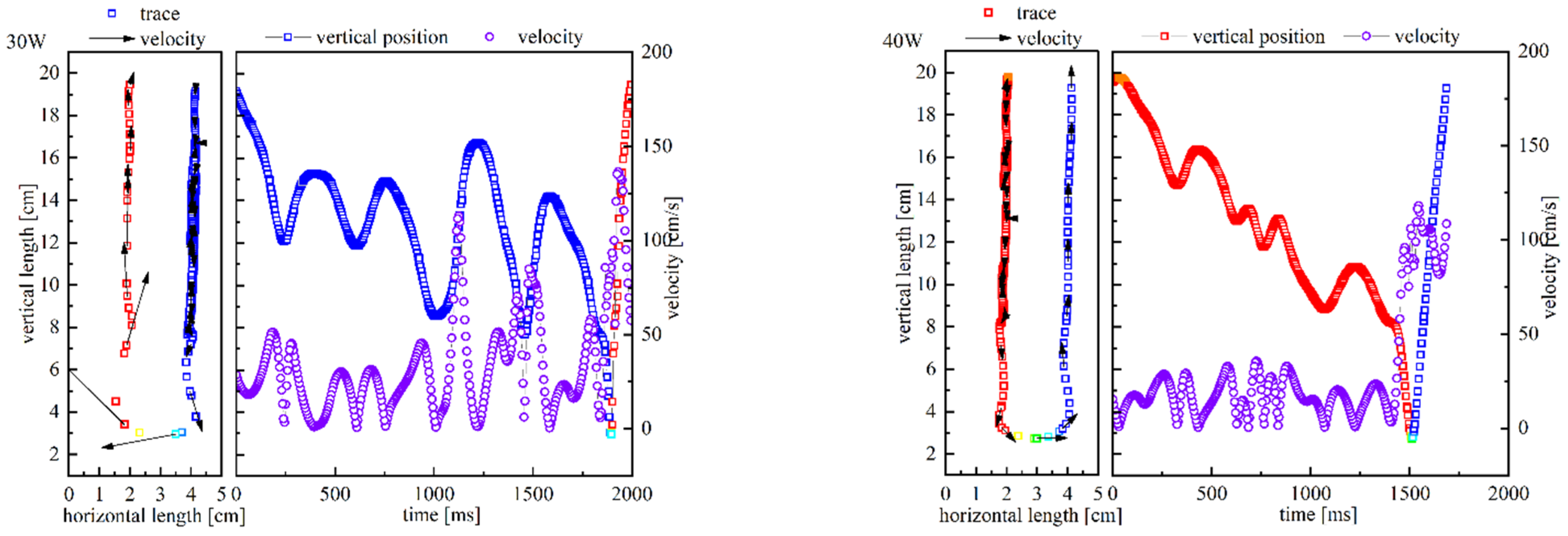
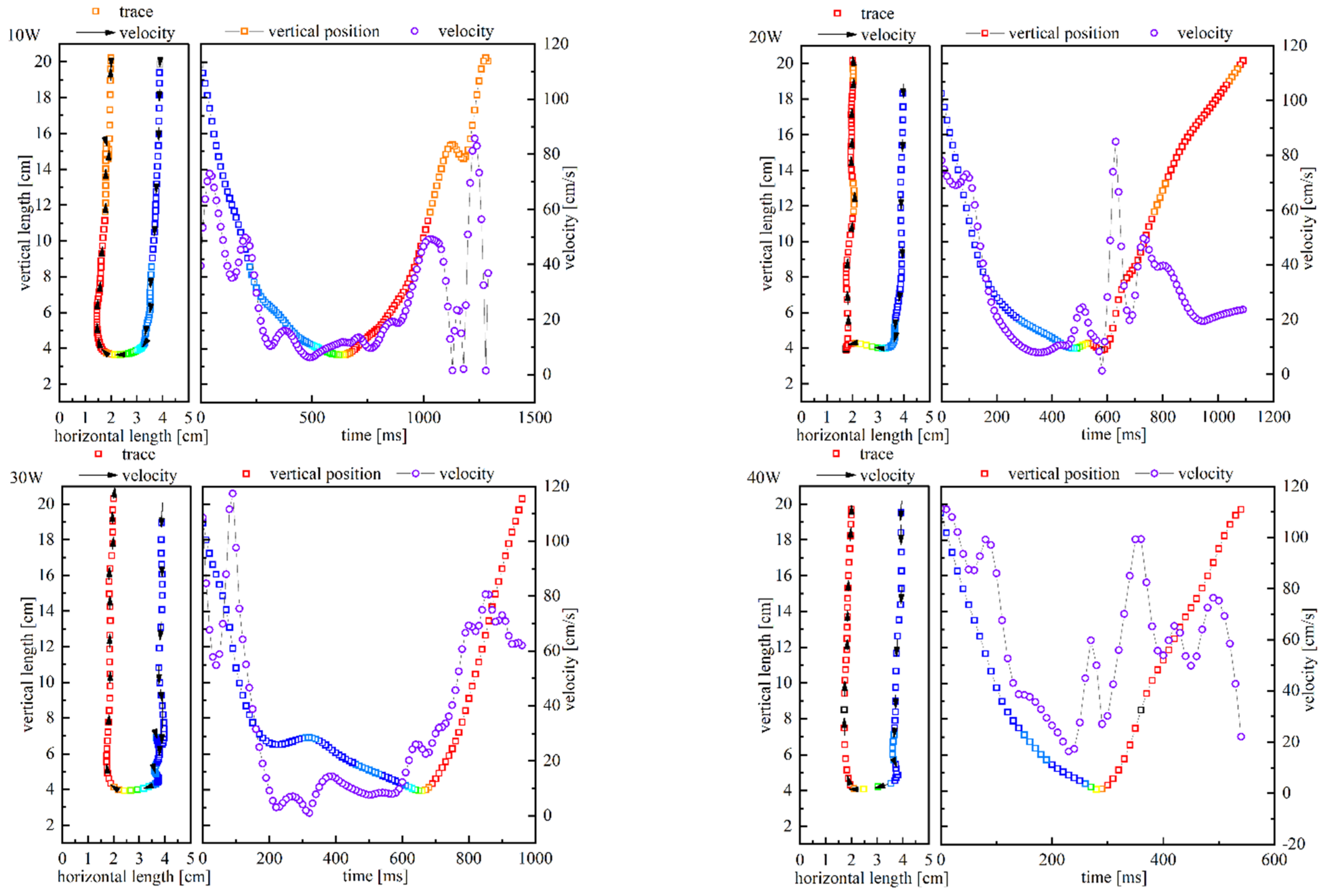
3. Experiments and Results
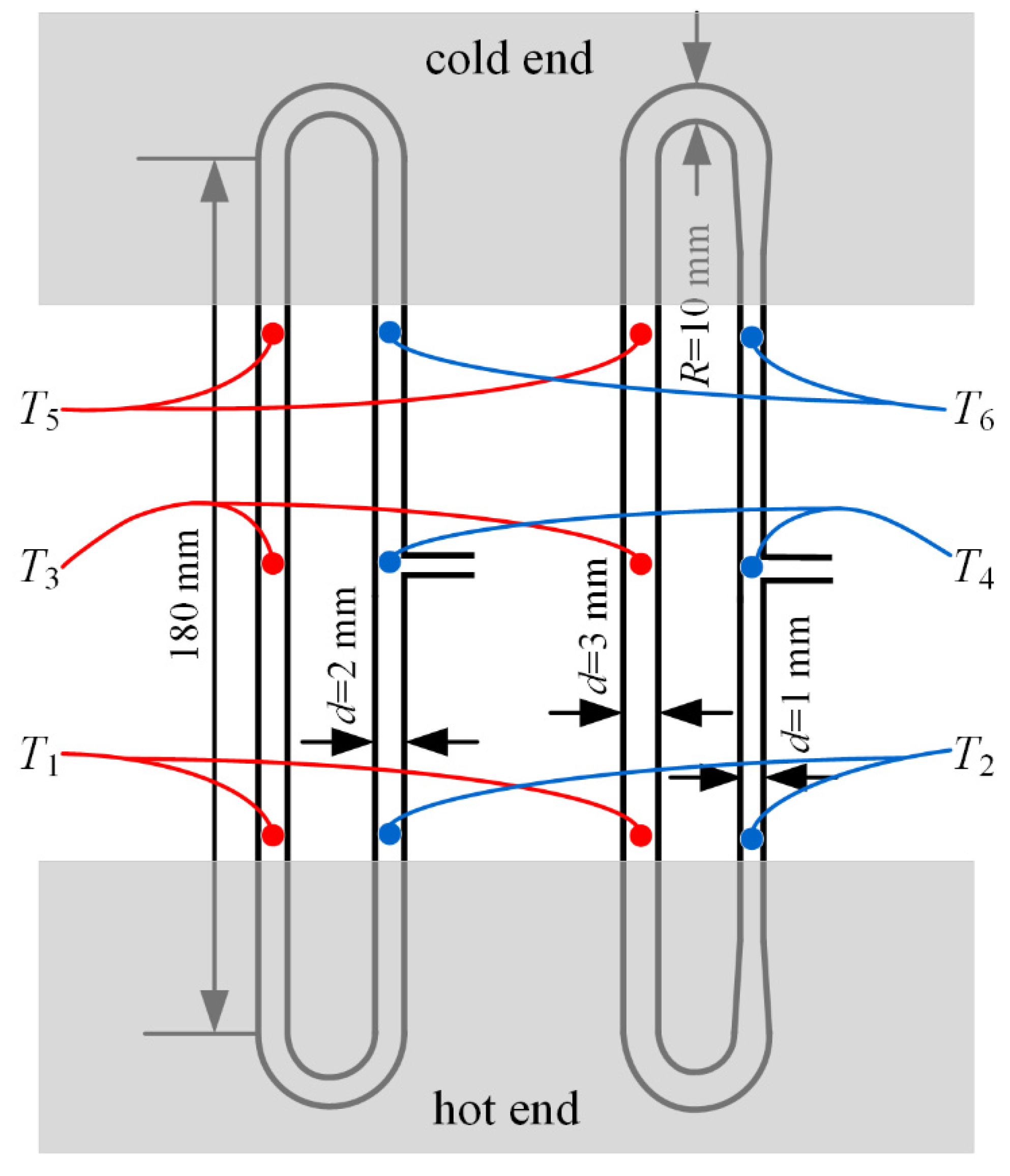
3.1. Experimental Visualization
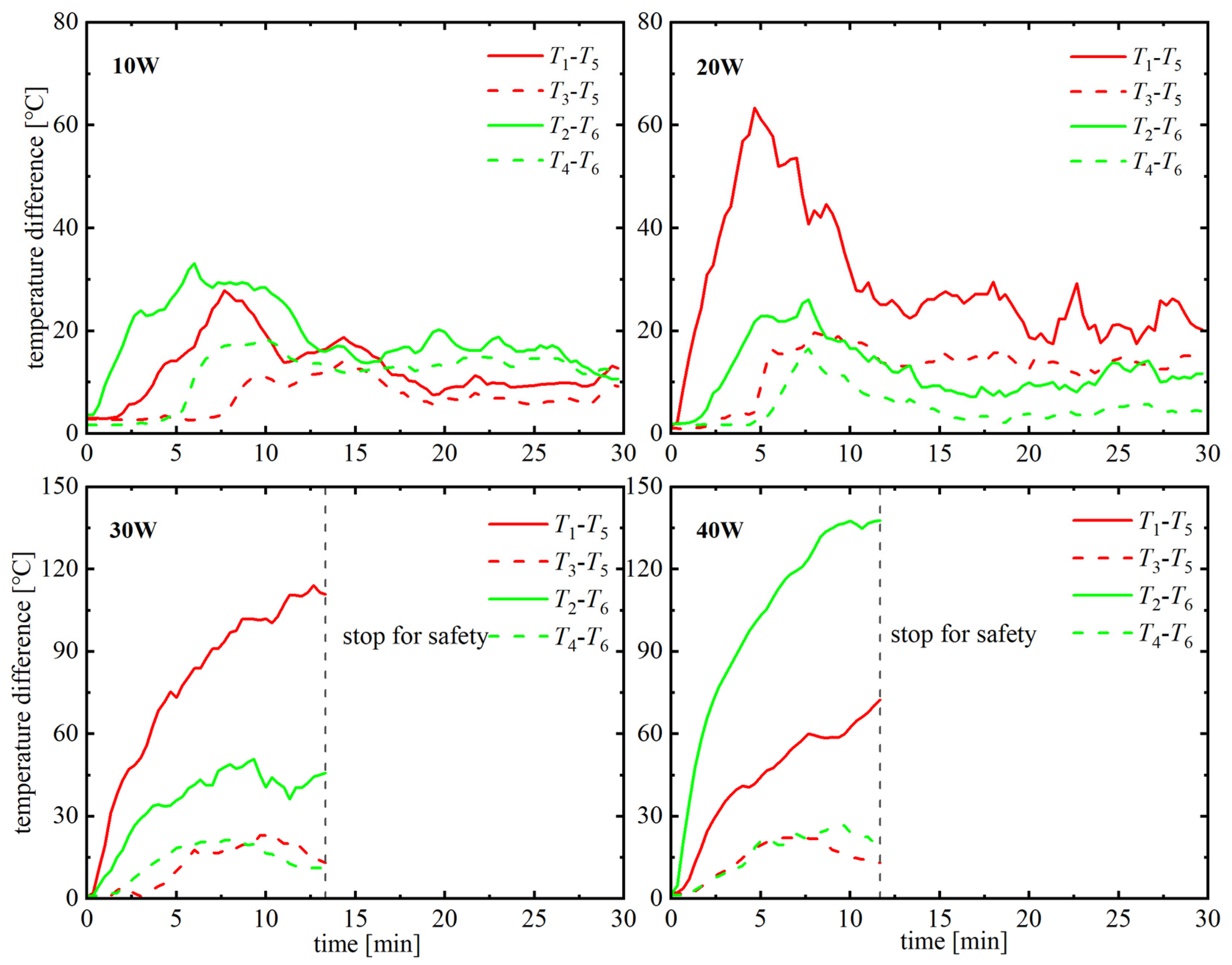
3.2. Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Su, L.; Jiang, J.; Deng, W.; Zhao, D. A Review of Working Fluids and Flow State Effects on Thermal Performance of Micro-Channel Oscillating Heat Pipe for Aerospace Heat Dissipation. Aerospace 2023, 10, 179. [Google Scholar] [CrossRef]
- Priyadarsini, G.D.; Sankad, G. Microfluidic systems with a pulsating heat pipe. Phys. Fluids 2023, 35, 112001. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S. On the interaction between liquid slug and vapor bubble in the chaotic operation of pulsating heat pipe. Phys. Fluids 2023, 35, 054113. [Google Scholar] [CrossRef]
- Hota, S.K.; Lee, K.-L.; Leitherer, B.; Elias, G.; Hoeschele, G.; Rokkam, S. Pulsating heat pipe and embedded heat pipe heat spreaders for modular electronics cooling. Case Stud. Therm. Eng. 2023, 49, 103256. [Google Scholar] [CrossRef]
- Weng, Z.; Du, J.; Jiao, F.; Hong, Y.; He, Y.; Wang, C. Experimental investigation on the heat transfer performance of pulsating heat pipe with self-rewetting Fe3O4-nanofluid. Case Stud. Therm. Eng. 2024, 59, 104456. [Google Scholar] [CrossRef]
- Samana, T.; Kiatsiriroat, T.; Nuntaphan, A. Enhancement of fin efficiency of a solid wire fin by oscillating heat pipe under forced convection. Case Stud. Therm. Eng. 2014, 2, 36–41. [Google Scholar] [CrossRef]
- Bastakoti, D.; Zhang, H.; Li, D.; Cai, W.; Li, F. An overview on the developing trend of pulsating heat pipe and its performance. Appl. Therm. Eng. 2018, 141, 305–332. [Google Scholar] [CrossRef]
- Dilawar, M.; Pattamatta, A. A parametric study of oscillatory two-phase flows in a single turn Pulsating Heat Pipe using a non-isothermal vapor model. Appl. Therm. Eng. 2013, 51, 1328–1338. [Google Scholar] [CrossRef]
- Wang, Y.-N. Micropumps and biomedical applications—A review. Microelectron. Eng. 2018, 195, 121–138. [Google Scholar] [CrossRef]
- Luo, X.; Yang, L.; Cui, Y. Micropumps: Mechanisms, fabrication, and biomedical applications. Sens. Actuators A Phys. 2023, 363, 114732. [Google Scholar] [CrossRef]
- Khandekar, S.; Groll, M. An insight into thermo-hydrodynamic coupling in closed loop pulsating heat pipes. Int. J. Therm. Sci. 2004, 43, 13–20. [Google Scholar] [CrossRef]
- Tong, B.Y.; Wong, T.N.; Ooi, K.T. Closed-loop pulsating heat pipe. Appl. Therm. Eng. 2001, 21, 1845–1862. [Google Scholar] [CrossRef]
- Kwon, G.H.; Kim, S.J. Operational characteristics of pulsating heat pipes with a dual-diameter tube. Int. J. Heat Mass Transf. 2014, 75, 184–195. [Google Scholar] [CrossRef]
- Karthikeyan, V.K.; Khandekar, S.; Pillai, B.C.; Sharma, P.K. Infrared thermography of a pulsating heat pipe: Flow regimes and multiple steady states. Appl. Therm. Eng. 2014, 62, 470–480. [Google Scholar] [CrossRef]
- Zhang, Y.; Faghri, A. Advances and Unsolved Issues in Pulsating Heat Pipes. Heat Transf. Eng. 2008, 29, 20–44. [Google Scholar] [CrossRef]
- Chien, K.-H.; Lin, Y.-T.; Chen, Y.-R.; Yang, K.-S.; Wang, C.-C. A novel design of pulsating heat pipe with fewer turns applicable to all orientations. Int. J. Heat Mass Transf. 2012, 55, 5722–5728. [Google Scholar] [CrossRef]
- Thompson, S.M.; Ma, H.B.; Wilson, C. Investigation of a flat-plate oscillating heat pipe with Tesla-type check valves. Exp. Therm. Fluid Sci. 2011, 35, 1265–1273. [Google Scholar] [CrossRef]
- Feng, C.; Wan, Z.; Mo, H.; Tang, H.; Lu, L.; Tang, Y. Heat transfer characteristics of a novel closed-loop pulsating heat pipe with a check valve. Appl. Therm. Eng. 2018, 141, 558–564. [Google Scholar] [CrossRef]
- Abiev, R.S. Hydrodynamics and Heat Transfer of Circulating Two-Phase Taylor Flow in Microchannel Heat Pipe: Experimental Study and Mathematical Model. Ind. Eng. Chem. Res. 2020, 59, 3687–3701. [Google Scholar] [CrossRef]
- Kwon, G.H.; Kim, S.J. Experimental investigation on the thermal performance of a micro pulsating heat pipe with a dual-diameter channel. Int. J. Heat Mass Transf. 2015, 89, 817–828. [Google Scholar] [CrossRef]
- Liu, S.; Li, J.; Dong, X.; Chen, H. Experimental study of flow patterns and improved configurations for pulsating heat pipes. J. Therm. Sci. 2007, 16, 56–62. [Google Scholar] [CrossRef]
- Holley, B.; Faghri, A. Analysis of pulsating heat pipe with capillary wick and varying channel diameter. Int. J. Heat Mass Transf. 2005, 48, 2635–2651. [Google Scholar] [CrossRef]
- Tseng, C.-Y.; Yang, K.-S.; Chien, K.-H.; Jeng, M.-S.; Wang, C.-C. Investigation of the performance of pulsating heat pipe subject to uniform/alternating tube diameters. Exp. Therm. Fluid Sci. 2014, 54, 85–92. [Google Scholar] [CrossRef]
- Lim, J.; Kim, S.J. Effect of a channel layout on the thermal performance of a flat plate micro pulsating heat pipe under the local heating condition. Int. J. Heat Mass Transf. 2019, 137, 1232–1240. [Google Scholar] [CrossRef]
- Wang, J.; Pan, Y.; Liu, X. Investigation on start-up and thermal performance of the single-loop pulsating heat pipe with variable diameter. Int. J. Heat Mass Transf. 2021, 180, 121811. [Google Scholar] [CrossRef]
- Chen, X.; Li, H.; Han, X.; Liu, X. Thermo-hydrodynamic characteristics of a novel flat-plate micro pulsating heat pipe with asymmetric converging-diverging channels. Int. Commun. Heat Mass Transf. 2024, 152, 107282. [Google Scholar] [CrossRef]
- Geng, X.; Yuan, H.; Oguz, H.N.; Prosperetti, A. Bubble-based micropump for electrically conducting liquids. J. Micromech. Microeng. 2001, 11, 270–276. [Google Scholar] [CrossRef]
- Reay, D.A.; Kew, P.A.; McGlen, R.J. Chapter 2—Heat transfer and fluid flow theory. In Heat Pipes, 6th ed.; Reay, D.A., Kew, P.A., McGlen, R.J., Eds.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 15–64. [Google Scholar] [CrossRef]
- Hagen-Poiseuille Equation—An Overview|ScienceDirect Topics. Available online: https://www.sciencedirect.com/topics/engineering/hagen-poiseuille-equation (accessed on 1 December 2024).
- Spinato, G.; Borhani, N.; Thome, J.R. Understanding the self-sustained oscillating two-phase flow motion in a closed loop pulsating heat pipe. Energy 2015, 90, 889–899. [Google Scholar] [CrossRef]
- Spinato, G.; Borhani, N.; d’Entremont, B.P.; Thome, J.R. Time-strip visualization and thermo-hydrodynamics in a Closed Loop Pulsating Heat Pipe. Appl. Therm. Eng. 2015, 78, 364–372. [Google Scholar] [CrossRef]
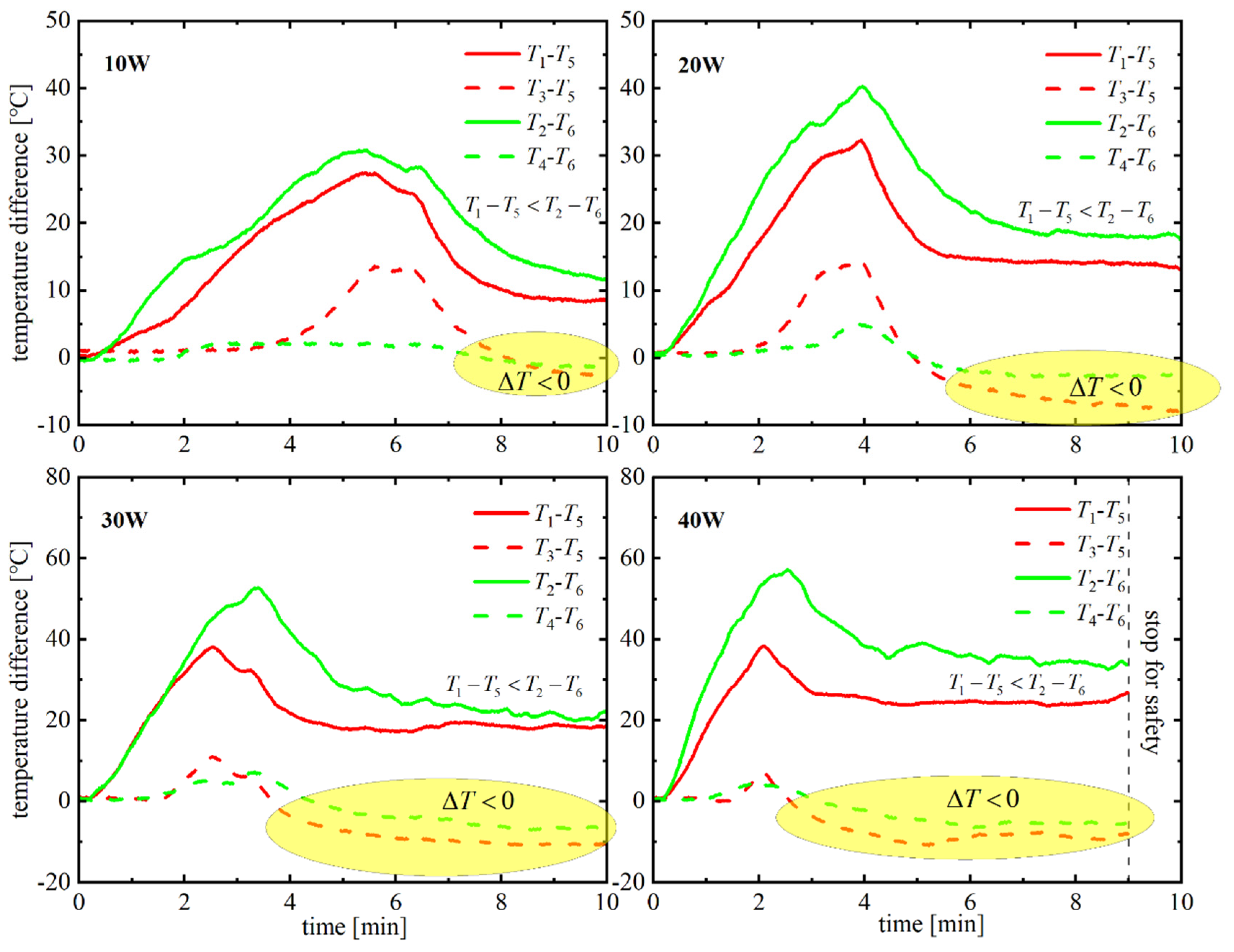
| ∆T | T1–T5 | T2–T6 | T3–T5 | T4–T6 | |
|---|---|---|---|---|---|
| Conditions | |||||
| Varying -diameter | 10 W | 8.7 | 13.0 | −1.9 | −1.0 |
| 20 W | 13.8 | 18.0 | −7.3 | −2.6 | |
| 30 W | 18.4 | 21.1 | −10.7 | −6.6 | |
| 40 W | 24.4 | 34.1 | −8.7 | −5.4 | |
| Constant -diameter | 10 W | 9.9 | 15.6 | 6.8 | 13.7 |
| 20 W | 11.0 | 21.4 | 4.4 | 13.6 | |
| 30 W | - | - | - | - | |
| 40 W | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Liu, Z.; Ji, Y.; Wang, S. A Ratchet for Closed Pipes: Asymmetric-Configuration Role on Unidirectional Circulatory Flows. Energies 2025, 18, 259. https://doi.org/10.3390/en18020259
Bai L, Liu Z, Ji Y, Wang S. A Ratchet for Closed Pipes: Asymmetric-Configuration Role on Unidirectional Circulatory Flows. Energies. 2025; 18(2):259. https://doi.org/10.3390/en18020259
Chicago/Turabian StyleBai, Lihang, Zhang Liu, Yulong Ji, and Shuai Wang. 2025. "A Ratchet for Closed Pipes: Asymmetric-Configuration Role on Unidirectional Circulatory Flows" Energies 18, no. 2: 259. https://doi.org/10.3390/en18020259
APA StyleBai, L., Liu, Z., Ji, Y., & Wang, S. (2025). A Ratchet for Closed Pipes: Asymmetric-Configuration Role on Unidirectional Circulatory Flows. Energies, 18(2), 259. https://doi.org/10.3390/en18020259








