A Double Resistive–Capacitive Approach for the Analysis of a Hybrid Battery–Ultracapacitor Integration Study
Abstract
:1. Introduction
2. General Characteristics of HESSs Based on BES and UC Components
2.1. General Characteristics of BESs
2.2. General Characteristics of UCs
2.3. HESSs Based on BESs and UCs
3. Description of the Test Stand
- PC with LabVIEW 2018 software: Used to develop an application for recording selected experimental data. The application cooperated with National Instruments measurement modules:
- NI 9206: Voltage acquisition at battery terminals.
- NI 9213: Temperature measurement at terminals, battery housing and ambient temperature using K-type thermocouples.
- NI 9401: TTL digital I/O module for controlling relays in charge and load (discharge) circuits.
- TA018 PICO current clamps: Acquired current values for both components.
Adopted Load Cycles
4. Mathematical Models of the BES-UC System Based on a Replacement Double RC Loop Diagram
5. The Process of BES-UC Parameter Identification and Error Analysis
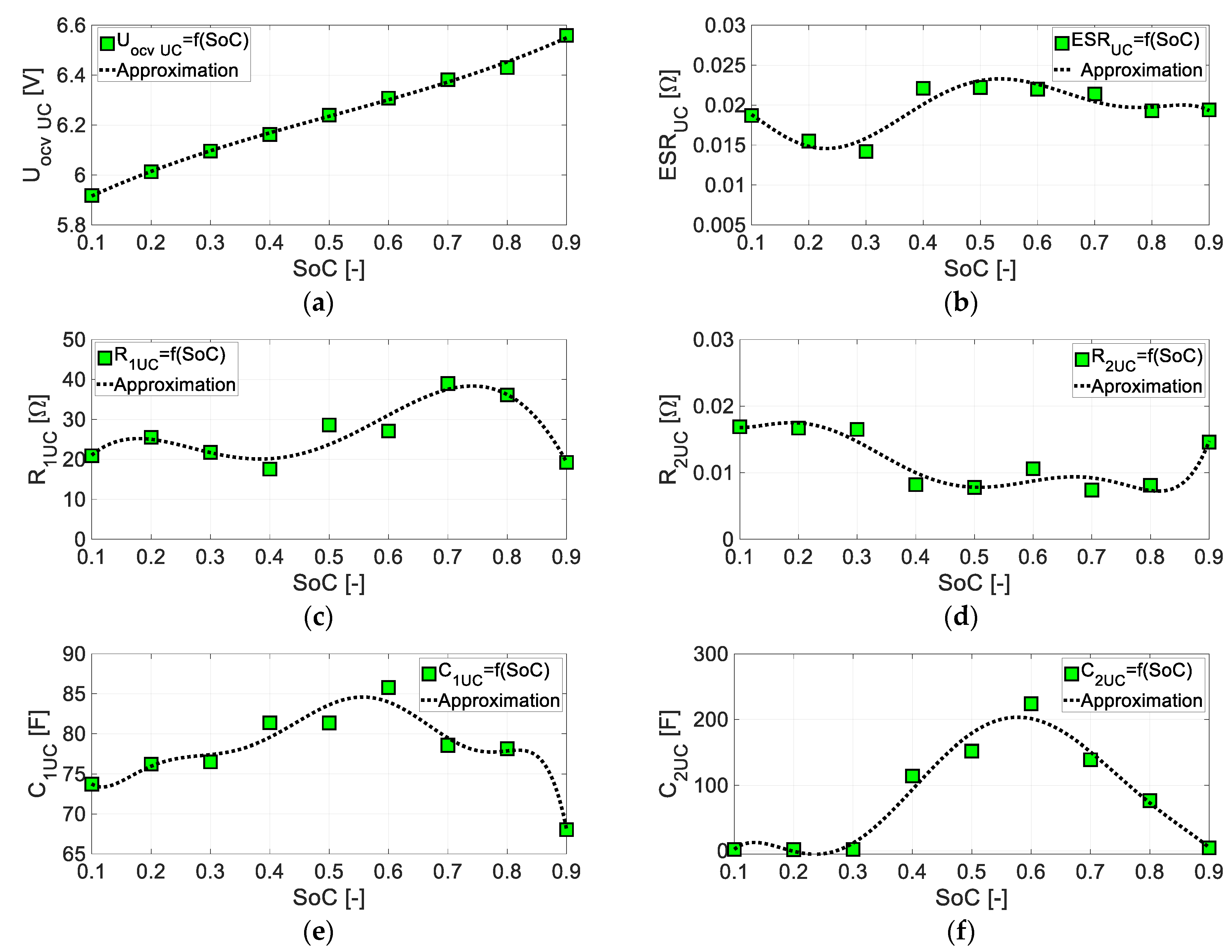
5.1. Identification of BES-UC Model Parameters
- Battery: Ξ0_BES = [R10_BES = 1.0 × 10, R20_BES = 1.0 × 10−2, C10_BES = 1.0 × 10, C20_BES = 1.0, R0_BES = 1.0 × 10−2, UOCV0_BES = 6.0];
- Ultracapacitor: Ξ0_UC = [R10_UC = 1.0, R20_UC = 1.0 × 10−3, C10_UC = 1.0 × 10−3, C20_UC = 1.0 × 10, ESR0_UC = 1.0 × 10−3, EMF0_UC/UOCV0_UC = 6.0].
5.2. Error Analysis
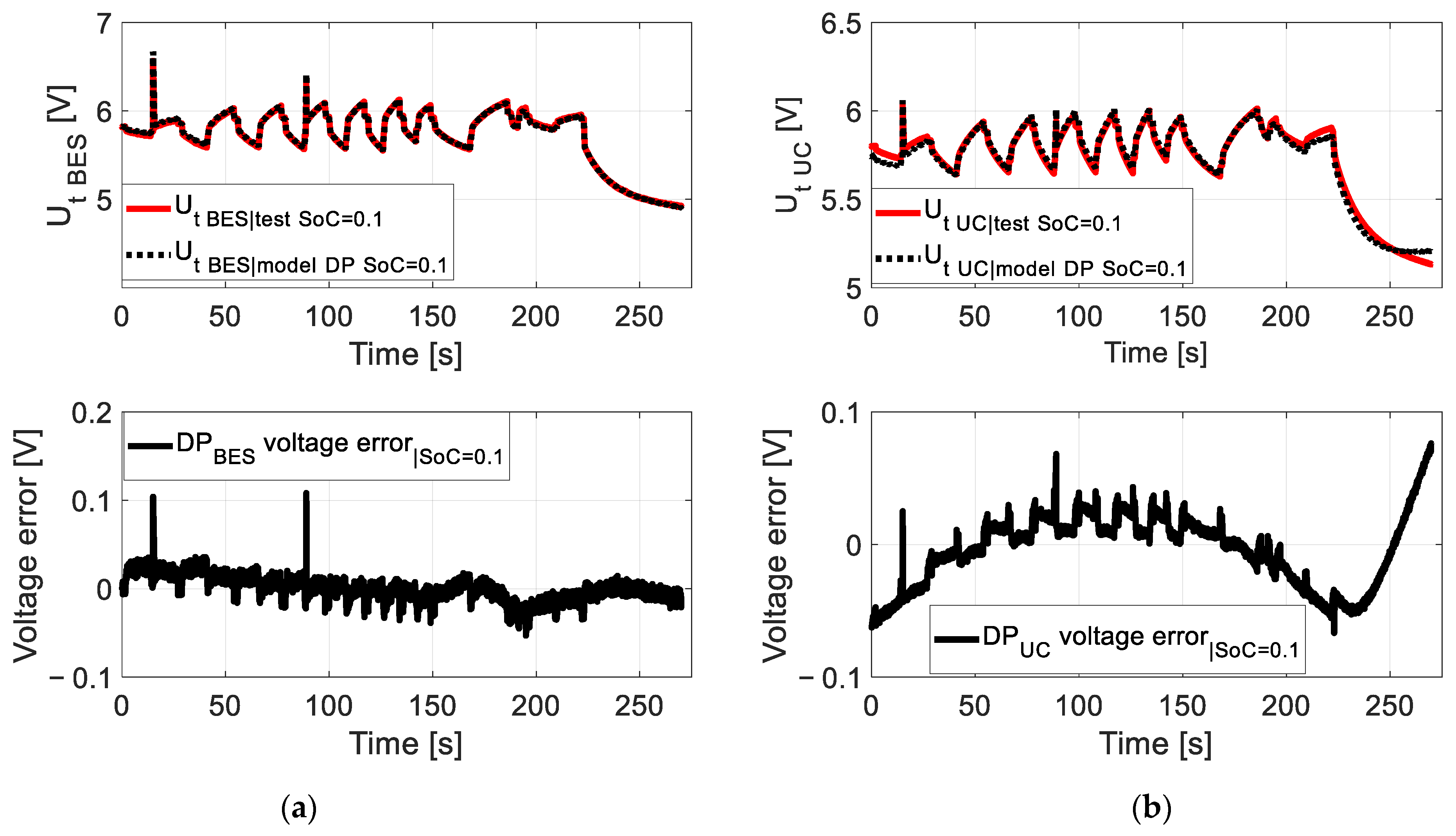
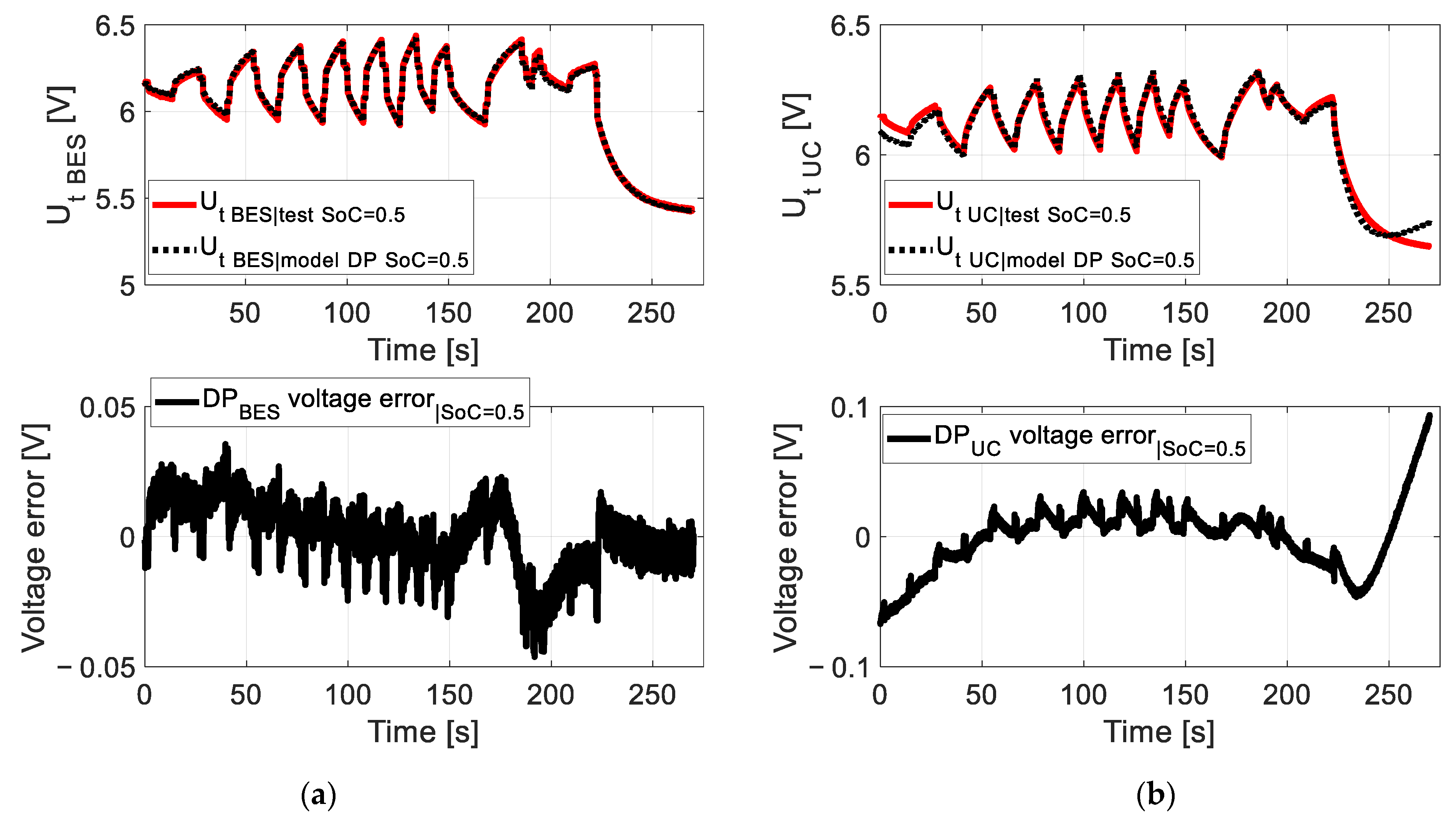
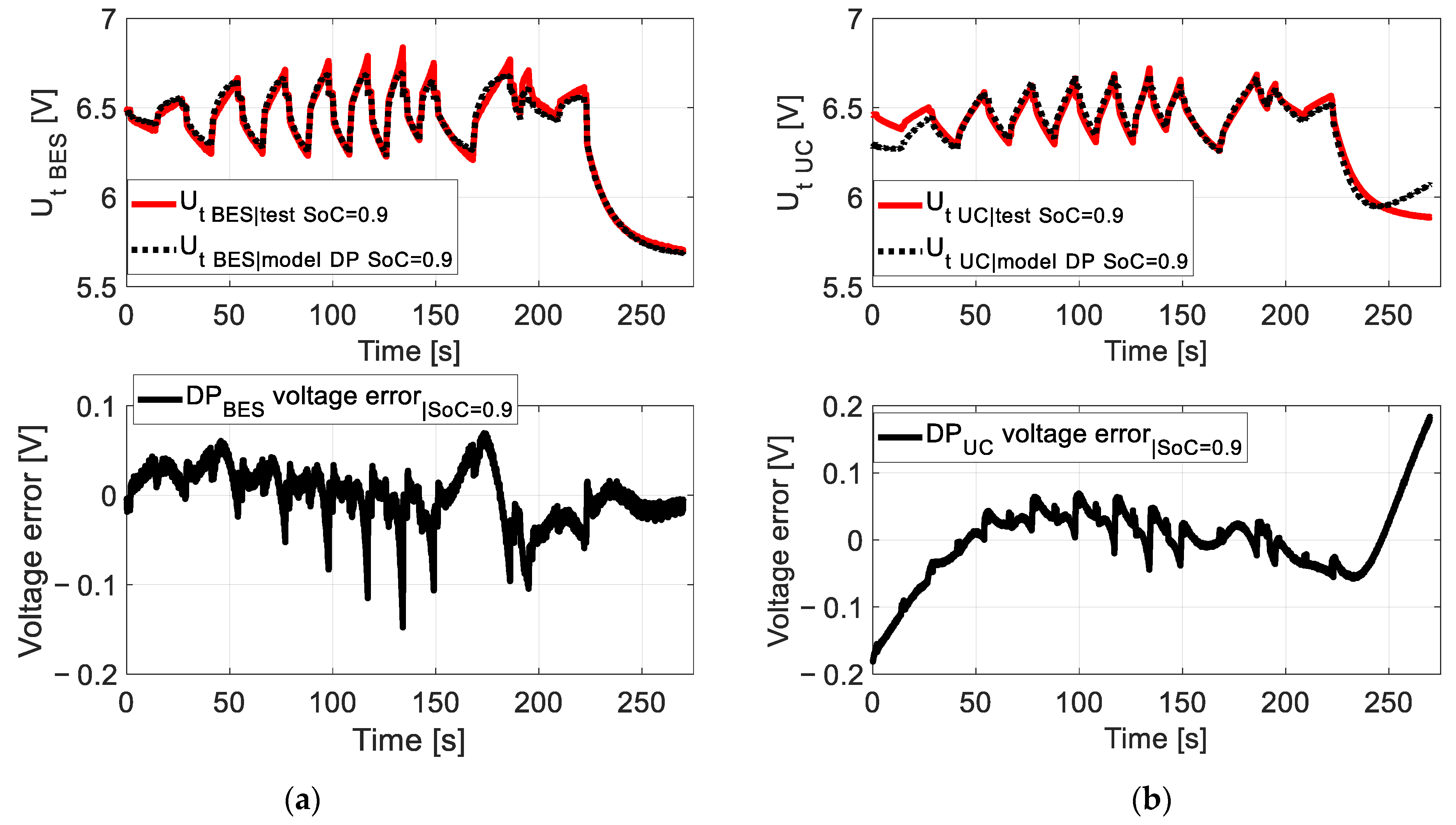
6. Comparison of Results Obtained from the Experiment and the Model for the HESS
- ✓
- ✓
- ✓
- -
- For the battery, they do not exceed 1.1 × 10−3 (at SoC = 0.9).
- -
- For the ultracapacitor, they do not exceed 2.4 × 10−3 (at SoC = 0.9).
7. Conclusions and Recommendations
- -
- The exploration of advanced battery management systems (BMSs) for real-time monitoring and balancing is recommended.
- -
- Integrating hybrid energy storage with smart grids is recommended to optimise energy flow and improve grid stability.
- -
- Exploration of the 2-RC loop modelling process is recommended to ensure the maintenance of accuracy whilst reducing computational intensity for real-time applications.
- -
- The research should be extended beyond VRLA-AGM batteries and Maxwell ultracapacitors to enhance the generalisability of findings to other energy storage technologies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| AGM | Absorbent Glass Mat |
| BES | Battery Energy Storage |
| BEV/EV | Battery Electric Vehicle/Electric Vehicle |
| BMS | Battery Management System |
| DP/2RC | Dual Polarisation/2-Resistive-Capacitance |
| DST | Dynamic Stress Test |
| EKF | Extended Kalman Filter |
| EU | European Union |
| FC | Fuel Cell |
| FTP-75 | Federal Test Procedure |
| GHG | Greenhouse Gas Emission |
| HPPC | Hybrid Pulse Power Characterisation |
| HESS | Hybrid Energy Storage System |
| MAE | Mean Absolute Error |
| MSE | Mean Square Error [–] |
| n.a. | not applicable |
| NRMSE | Normalised Root Mean Square Error [–] |
| OCV | Open-Circuit Voltage [V] |
| PV | Photovoltaic |
| RC | Resistive–Capacitive |
| RES | Renewable Energy Source |
| RLS | Recursive Least Square |
| RMSE | Root Mean Square Error |
| SoC | State of Charge |
| SoH | State of Health |
| TEN-T | Trans-European Transport Network |
| UC | Ultracapacitor |
| UDDS | Urban Dynamometer Driving Schedule |
| UKF | Unscented Kalman Filter |
| VRLA | Valve-Regulated Lead Acid |
| Greek symbols/subscripts/superscripts | |
| C,C1,C2, Cel, Cs2 | Capacitances [F] |
| EBES | The energy stored in the battery [J] |
| EUC + BES | The energy stored in the HESS based on the battery and ultracapacitor [J] |
| EUC | The energy stored in the ultracapacitor [J] |
| err | Error |
| EMF | Electromotive force [V] |
| ESR | Equivalent series resistance [Ω] |
| H | Hessian |
| i | Total pulse current [A] |
| ib | Total loading current flow battery elements [A] |
| ib1,ib2 | Currents flowing through battery elements [A] |
| iuc | Current flowing through ultracapacitor elements [A] |
| j | Sample number [–] |
| J | Jacobian |
| L | Inductance [H] |
| N | Number of data samples [–] |
| UOCV/ OCVBES/ OCVUC | Open-circuit voltage of battery (BES) and ultracapacitor (UC) [V] |
| R0 (Rint) | Ohmic resistance [Ω] |
| R1 | Activation polarisation resistance [Ω] |
| R2 | Concentration polarisation resistance [Ω] |
| Rel, Rsel2 | Resistances [Ω] |
| Qbat | Effective capacity [Ah] |
| Qn | Nominal capacity [Ah] |
| Qmax | Maximum battery capacity [Ah] |
| Qmin | Minimum battery capacity [Ah] |
| Tambient | Ambient temperature [K] |
| Tbody | Body temperature [K] |
| Tterm | Temperature at terminals [K] |
| U1,U2 | Voltage drops [V] |
| Uch | Charging/discharging voltage [V] |
| Udch | Discharging voltage [V] |
| V2 | Variance [-] |
| ∇J | Gradient |
| Ξ | Parameter vector [-] |
| εps | Stationarity condition [-] |
References
- Paris Agreement, United Nations, 2015 (art. 2 par. 1a & art. 4 par. 4). Available online: https://unfccc.int/sites/default/files/resource/parisagreement_publication.pdf (accessed on 20 November 2024).
- European Green Deal, Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions The European Green Deal (COM (2019) 640 Final). Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:b828d165-1c22-11ea-8c1f-01aa75ed71a1.0002.02/DOC_1&format=PDF (accessed on 21 October 2024).
- Transport GHG Emission in EU. Available online: https://www.consilium.europa.eu/en/infographics/fit-for-55-afir-alternative-fuels-infrastructure-regulation/ (accessed on 20 November 2024).
- ChaoJi 3.0 Standard. Available online: https://www.vector.com/int/en/know-how/protocols/gbt-27930/#c204146 (accessed on 22 November 2024).
- White Paper of ChaoJi EV Charging Technology, State Grid Corporation of China Electricity Council Jointly Released June 2020. Available online: https://www.chademo.com/chaoji-gbt-standards-released (accessed on 20 October 2024).
- IEC 61851-23:2014; Electric Vehicle Conductive Charging System—Part 23: DC Electric Vehicle Charging Station. IEC: Geneva, Switzerland, 2014. Available online: https://www.iecee.org/certification/iec-standards/iec-61851-232014 (accessed on 22 November 2024).
- Regulation of The European Parliament and of the Council on the Deployment of Alternative Fuels Infrastructure, and Repealing Directive 2014/94/EU of the European Parliament and of the Council. Available online: https://eur-lex.europa.eu/resource.html?uri=cellar:dbb134db-e575-11eb-a1a5-01aa75ed71a1.0001.02/DOC_1&format=PDF (accessed on 22 November 2024).
- Directives Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32018L2001&from=EN (accessed on 23 November 2024).
- Revision of the Renewable Energy Directive: Fit for 55 Package. Available online: https://www.europarl.europa.eu/RegData/etudes/BRIE/2021/698781/EPRS_BRI(2021)698781_EN.pdf (accessed on 22 November 2024).
- Chmielewski, A.; Gumiński, R.; Mączak, J.; Radkowski, S.; Szulim, P. Aspects of balanced development of RES and distributed micro-cogeneration use in Poland: Case study of muCHP with Stirling engine. Renew. Sustain. Energy Rev. 2016, 60, 930–952. [Google Scholar] [CrossRef]
- Wasim, M.S.; Habib, S.; Amjad, M.; Bhatti, A.R.; Ahmed, E.M.; Qureshi, M.A. Battery-Ultracapacitor Hybrid Energy Storage System to Increase Battery Life Under Pulse Loads. IEEE Access 2022, 10, 62173–62182. [Google Scholar] [CrossRef]
- Jankowska, E.; Kopciuch, K.; Błażejczyk, M.; Majchrzycki, W.; Piórkowski, P.; Chmielewski, A.; Bogdziński, K. Hybrid energy storage based on ultracapacitor and lead acid battery: Case study. In Automation 2018: Advances in Intelligent Systems and Computing; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 743, pp. 339–349. [Google Scholar]
- Piórkowski, P.; Chmielewski, A.; Bogdziński, K.; Możaryn, J.; Mydłowski, T. Research on Ultracapacitors in Hybrid systems: Case Study. Energies 2018, 11, 2551. [Google Scholar] [CrossRef]
- Chariot, Electric Buses. Available online: https://chariot-electricbus.com/cmproduct/battery-electric-buses/ (accessed on 22 November 2024).
- Chariot, Ultracapacitor e-Bus. Available online: https://chariot-electricbus.com/cmproduct/12m-ultracapacitor-chariot-e-bus/ (accessed on 22 November 2024).
- Maxwell. Available online: https://maxwell.com/products/ultracapacitors/ (accessed on 22 November 2024).
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium–ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Chmielewski, A.; Szulim, P.; Gregorczyk, M.; Gumiński, R.; Mydłowski, T.; Mączak, J. Model of an electric vehicle powered by a PV cell—A case study. In Proceedings of the 2017 22nd International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 28–31 August 2017; pp. 1009–1014. [Google Scholar]
- Naresh, P.; Sai Vinay Kishore, N.; Seshadri Sravan Kumar, V. A new configuration for enhanced integration of a battery–ultracapacitor system. Renew. Energy 2024, 229, 120708. [Google Scholar]
- Chien–Hsing, L.; Shih–Hsien, H. Prediction of Equivalent–Circuit Parameters for Double–Layer Capacitors Module. IEEE Trans. Energy Convers. 2013, 28, 913–920. [Google Scholar]
- Kopczyński, A.; Piórkowski, P.; Roszczyk, P. Parameters selection of extended-range electric vehicle powered from supercapacitor pack based on laboratory and simulation tests. IOP Conf. Ser. Mater. Sci. Eng. 2016, 421, 022016. [Google Scholar]
- Esfandyaria, A.; Nortona, B.; Conlona, M.; McCormack, S.J. Performance of a campus photovoltaic electric vehicle charging station in a temperate climate. Sol. Energy 2019, 177, 762–771. [Google Scholar] [CrossRef]
- Akar, F.; Tavlasoglu, Y.; Vural, B. An Energy Management Strategy for a Concept Battery/Ultracapacitor Electric Vehicle with Improved Battery Life. IEEE Trans. Transp. Electrif. 2017, 3, 191–200. [Google Scholar] [CrossRef]
- Demircalı, A.; Sergeant, P.; Koroglu, S.; Kesler, S.; Oztürk, E.; Tumbek, M. Influence of the temperature on energy management in battery–ultracapacitor electric vehicles. J. Clean. Prod. 2018, 176, 716–725. [Google Scholar] [CrossRef]
- Hung, N.B.; Jaewon, S.; Lim, O. A study of the effects of input parameters on the dynamics and required power of an electric bicycle. Appl. Energy 2017, 204, 1347–1362. [Google Scholar] [CrossRef]
- Jia–Sheng, H.; Fei, L.; Chong, Z.; Chang–Yi, C.; Sin–Li, C.; Tsai–Jiun, R.; Chunting, C.M. Hybrid Energy Storage System of an Electric Scooter Based on Wireless Power Transfer. IEEE Trans. Ind. Inform. 2018, 14, 4169–4178. [Google Scholar]
- Hsu, Y.C.; Kao, S.C.; Ho, C.Y.; Jhou, P.H.; Lu, M.Z.; Liaw, C.M. On an Electric Scooter With G2V/V2H/V2G and Energy Harvesting Functions. IEEE Trans. Power Electron. 2018, 33, 6910–6925. [Google Scholar] [CrossRef]
- Chmielewski, A.; Piórkowski, P.; Bogdzinski, K.; Szulim, P.; Guminski, R. Test bench and model research of hybrid energy storage. J. Power Technol. 2017, 97, 406–415. [Google Scholar]
- Chmielewski, A.; Bogdziński, K.; Gumiński, R.; Szulim, P.; Piórkowski, P.; Możaryn, J.; Mączak, J. Operational research of VRLA battery. In Automation 2018: Advances in Intelligent Systems and Computing; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Switzerland, 2018; Volume 743, pp. 783–791. [Google Scholar]
- Czerwiński, A. Akumulatory, Baterie, Ogniwa; Wyd. WKŁ: Sulejówek, Poland, 2012. [Google Scholar]
- Kollmeyer, P.K.; Jahns, T.M. Aging and performance comparison of absorbed glass matte, enhanced flooded, PbC, NiZn, and LiFePO4 12V start stop vehicle batteries. J. Power Sources 2019, 441, 227139. [Google Scholar] [CrossRef]
- Park, J.; Appiah, W.A.; Byun, S.; Jin, D.; Ryou, M.-H.; Lee, Y.M. Semi-empirical long-term cycle life model coupled with an electrolyte depletion function for large-format graphite/LiFePO4 lithium-ion batteries. J. Power Sources 2017, 365, 257–265. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Martinez-Laserna, E.; Rodriguez-Martinez, L.M.; Villarreal, I. Cycle ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2015, 275, 573–587. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Liang, J.; Gan, Y.; Yao, M.; Li, Y. Numerical analysis of capacity fading for a LiFePO4 battery under different current rates and ambient temperatures. Int. J. Heat Mass Transf. 2021, 165, 120615. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.; Park, J. A single particle model with chemical/mechanical degradation physics for lithium ion battery State of Health (SOH) estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J.; Sun, F. Flexible battery state of health and state of charge estimation using partial charging data and deep learning. Energy Storage Mater. 2022, 51, 372–381. [Google Scholar] [CrossRef]
- Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Hsu, C.W.; Tsou, N.T.; Sun, F.; Li, J. Battery degradation prediction against uncertain future conditions with recurrent neural network enabled deep learning. Energy Storage Mater. 2022, 50, 139–151. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Lu, J.; Chen, C.; Shen, W. Battery state-of-charge estimation amid dynamic usage with physics-informed deep learning. Energy Storage Mater. 2022, 50, 718–729. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W. State-of-Health Estimation Based on Differential Temperature for Lithium Ion Batteries. IEEE Trans. Power Electron. 2020, 35, 10363–10373. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; Ma, S.; Lin, X. Characterization of external short circuit faults in electric vehicle Li-ion battery packs and prediction using artificial neural networks. Appl. Energy 2020, 260, 114253. [Google Scholar] [CrossRef]
- Wu, S.; Xiong, R.; Li, H.; Nian, V.; Ma, S. The state of the art on preheating lithium-ion batteries in cold weather. J. Energy Storage 2020, 27, 101059. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Shen, W.; Sun, F. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter. J. Clean. Prod. 2019, 234, 1153–1164. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Hannan, M.A.; Hussain, A.; Hoque, M.M.; Ker, P.J.; Saad, M.H.M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium–ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Linxiao, G.; Denecke, M.E.; Foley, S.B.; Dong, H.; Qi, Z.; Koenig, G.M., Jr. Electrochemical characterization of lithium cobalt oxide within aqueous flow suspensions as an indicator of rate capability in lithiumion battery electrodes. Electrochim. Acta 2018, 281, 822–830. [Google Scholar]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium–Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Yao, L.W.; Aziz, J.A.; Ramli, N. Detail analysis of RC parallel network–based model for high capacity lithium ferro phosphates battery. In Proceedings of the 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK, 27–29 March 2012; pp. 1–6. [Google Scholar]
- Li, S.; Cheng, X. A comparative study on RC models of lithium–ion battery. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia–Pacific (ITEC Asia–Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–4. [Google Scholar]
- Piao, C.; Yang, X. An improved model based on artificial neural networks and Thevenin model for nickel metal hydride power battery. In Proceedings of the International Conference on Optics, Photonics and Energy Engineering (OPEE), Wuhan, China, 10–11 May 2010; pp. 115–118. [Google Scholar]
- Putra, W.S.; Dewangga, B.R.; Cahyadi, A.; Wahyunggoro, O. Current Estimation Using Thevenin Battery Model. In Proceedings of the Joint International Conference on Electric Vehicular Technology and Industrial, Mechanical, Electrical and Chemical Engineering (ICEVT & IMECE), Surakarta, Indonesia, 4–5 November 2015; pp. 5–9. [Google Scholar]
- Gao, W.; Jiang, M. Research on PNGV Model Parameter Identification of LiFePO4 Li–ion Battery Based on FMRLS. In Proceedings of the 6th IEEE Conference on Industrial Electronics and Applications, Beijing, China, 21–23 June 2011; pp. 2294–2297. [Google Scholar]
- Han, Y.; Wang, X. WPT Charging System for Lithium Battery Based on PNGV Model. In Proceedings of the IEEE Transportation Electrification Conference and Expo, Asia–Pacific (ITEC Asia–Pacific), Harbin, China, 7–10 August 2017; pp. 1–5. [Google Scholar]
- Liu, X.; Li, W.; Zhou, A. PNGV Equivalent Circuit Model and SOC Estimation Algorithm for Lithium Battery Pack Adopted in AGV Vehicle. IEEE Access 2018, 6, 23639–23647. [Google Scholar] [CrossRef]
- Bottinger, M.; Paulitschke, M.; Bocklisch, T. Systematic Experimental Pulse Test Investigation for Parameter Identification of an Equivalent Circuit Based Lithium–Ion Battery Model. Energy Procedia 2017, 135, 337–346. [Google Scholar] [CrossRef]
- Cheng, P.; Zhou, Y.; Song, Z.; Ou, Y. Modeling and SOC Estimation of LiFePO4 Battery. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Qingdao, China, 3–7 December 2016; pp. 2140–2144. [Google Scholar]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Inline State of Health Estimation of Lithium–Ion Batteries Using State of Charge Calculation. J. Power Sources 2015, 299, 246–254. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online Estimation of Battery Equivalent Circuit Model Parameters and State of Charge Using Decoupled Least Squares Technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Ke, M.Y.; Chiu, Y.H.; Wu, C.Y. Battery Modelling and SOC Estimation of a LiFePO4 Battery. In Proceedings of the 2016 International Symposium on Computer, Consumer and Control, Xi’an, China, 4–6 July 2016; pp. 208–211. [Google Scholar]
- Pattipati, B.; Balasingam, B.; Avvari, G.V.; Pattipati, K.R.; Bar–Shalom, Y. Open circuit voltage characterization of lithium–ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar] [CrossRef]
- Dusonchet, L.; Favuzza, S.; Massaro, F.; Telaretti, E.; Zizzo, G. Technological and legislative status point of stationary energy storages in the EU. Renew. Sustain. Energy Rev. 2019, 101, 158–167. [Google Scholar] [CrossRef]
- Xiong, R.; Chen, H.; Wang, C.; Sun, F. Towards a smarter hybrid energy storage system based on battery and ultracapacitor—A critical review on topology and energy management. J. Clean. Prod. 2018, 202, 1228–1240. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Delétage, J.Y.; Vinassa, J.M. Behavior and State–of–Health Monitoring of Li–ion Batteries Using Impedance Spectroscopy and Recurrent Neural Networks. Int. J. Electr. Power Energy Syst. 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Lai, Y.; Du, S.; Ai, L.; Cheng, L.Y.; Ji, M. Insight Into Heat Generation Of Lithium–Ion Batteries Based On The Electrochemical–Thermal Model At High Discharge Rates. Int. J. Hydrogen Energy 2015, 40, 13039–13049. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.; Jia, M.; Tang, Y.; Lin, Y.; Zhian, Z.; Liu, Y. An Electrochemical– Thermal Model Based on Dynamic Responses for Lithium Iron Phosphate Battery. J. Power Sources 2014, 255, 130–143. [Google Scholar] [CrossRef]
- Saito, Y.; Shikano, M.; Kobayashi, H. Heat Generation Behavior During Charging and Discharging of Lithium– Ion Batteries After Long– Time Storage. J. Power Sources 2013, 244, 294–299. [Google Scholar] [CrossRef]
- Buller, S.; Karden, E.; Kok, D.; De Doncker, W.R. Modeling the dynamic behavior of supercapacitors using impedance spectroscopy. IEEE Trans. Ind. Appl. 2002, 38, 1622–1626. [Google Scholar] [CrossRef]
- Ramadan, H.S.; Becherif, M.; Claude, F. Extended kalman filter for accurate state of charge estimation of lithium-based batteries: A comparative analysis. Int. J. Hydrogen Energy 2017, 42, 29033–29046. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman Filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J.X. State-of-Charge Estimation of the Lithium-Ion, Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Chia, Y.Y.; Lee, L.H.; Shafiabady, N. A load predictive energy management system for supercapacitor –battery hybrid energy storage system in solar application using the Support Vector Machine. Appl. Energy 2015, 137, 588–602. [Google Scholar] [CrossRef]
- Hredzak, B.; Agelidis, V.G.; Demetriades, G. Application of explicit model predictive control to a hybrid battery ultracapacitor power source. J. Power Sources 2015, 277, 84–94. [Google Scholar] [CrossRef]
- Gu, R.; Malysz, P.; Emadi, A. A Novel Battery/Ultracapacitor Hybrid Energy Storage System Analysis based on Physics-Based Lithium-Ion Battery Modeling. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015. [Google Scholar]
- Rafik, F.; Gualous, H.; Gallay, R.; Crausaz, A.; Berthon, A. Frequency, thermal and voltage supercapacitor characterization and modeling. J. Power Sources 2007, 165, 928–934. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Mellit, A. Artificial intelligence techniques for photovoltaic applications: A review. Prog. Energy Combust. Sci. 2008, 34, 574–632. [Google Scholar]
- Szumanowski, A.; Piórkowski, P.; Chang, Y. Batteries and Ultracapacitors Set in Hybrid Propulsion System. In Proceedings of the 2007 International Conference on Power Engineering, Energy and Electrical Drives, Setubal, Portugal, 12–14 April 2007; pp. 122–127. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Pan, R.; Chen, Z. Modeling and state-of-charge prediction of lithium-ion battery and ultracapacitor hybrids with a co-estimator. Energy 2017, 121, 739–750. [Google Scholar] [CrossRef]
- Jackey, R.; Saginaw, M.; Sanghvi, P.; Gazzarri, J.; Huria, T.; Ceraolo, M. Battery Model Parameter Estimation Using a Layered Technique: An Example Using a Lithium Iron Phosphate Cell; SAE Technical Paper 2013 01–1547; Detroit: Michigan, MI, USA, 2013; pp. 1–14. [Google Scholar]

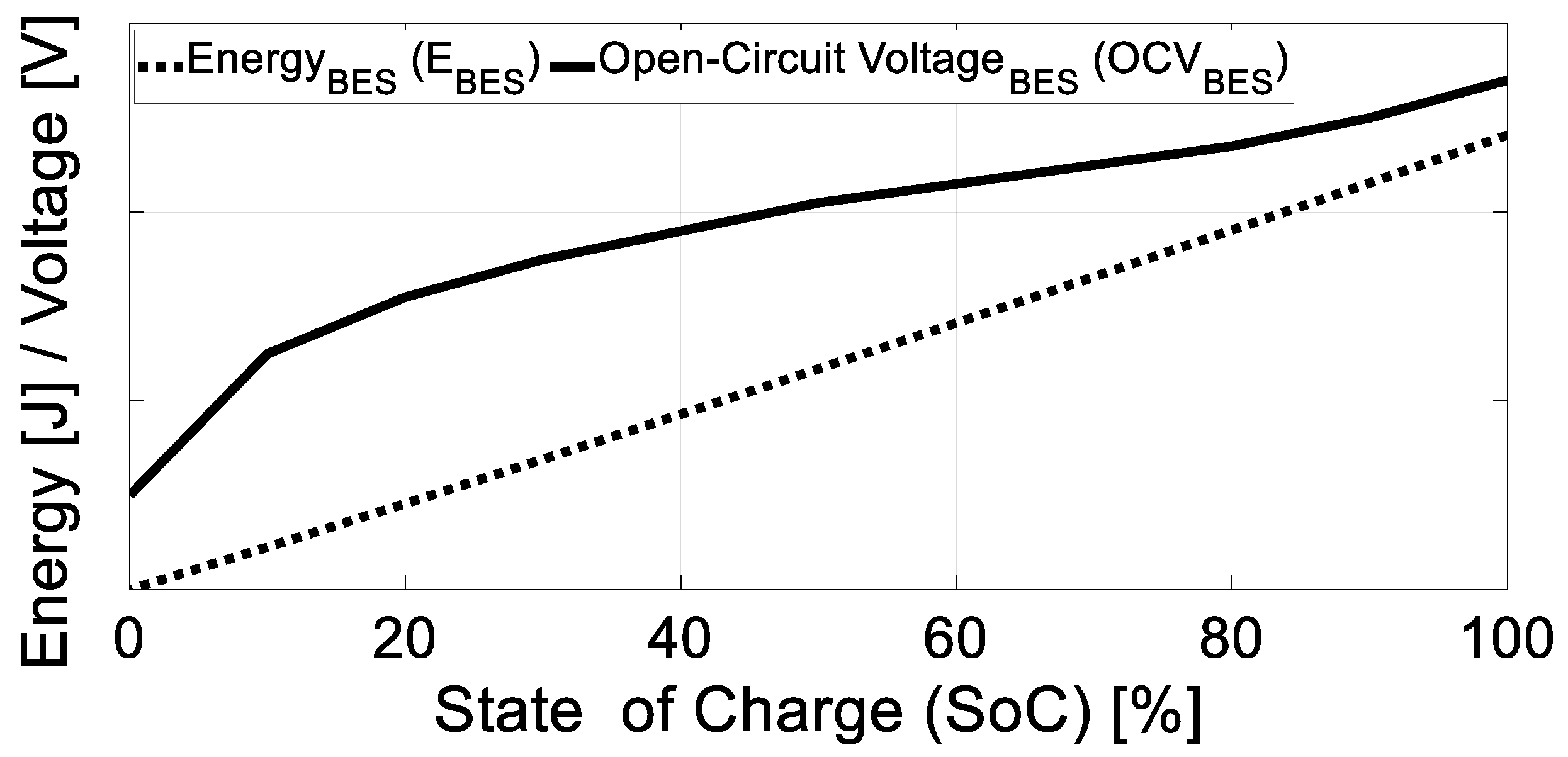
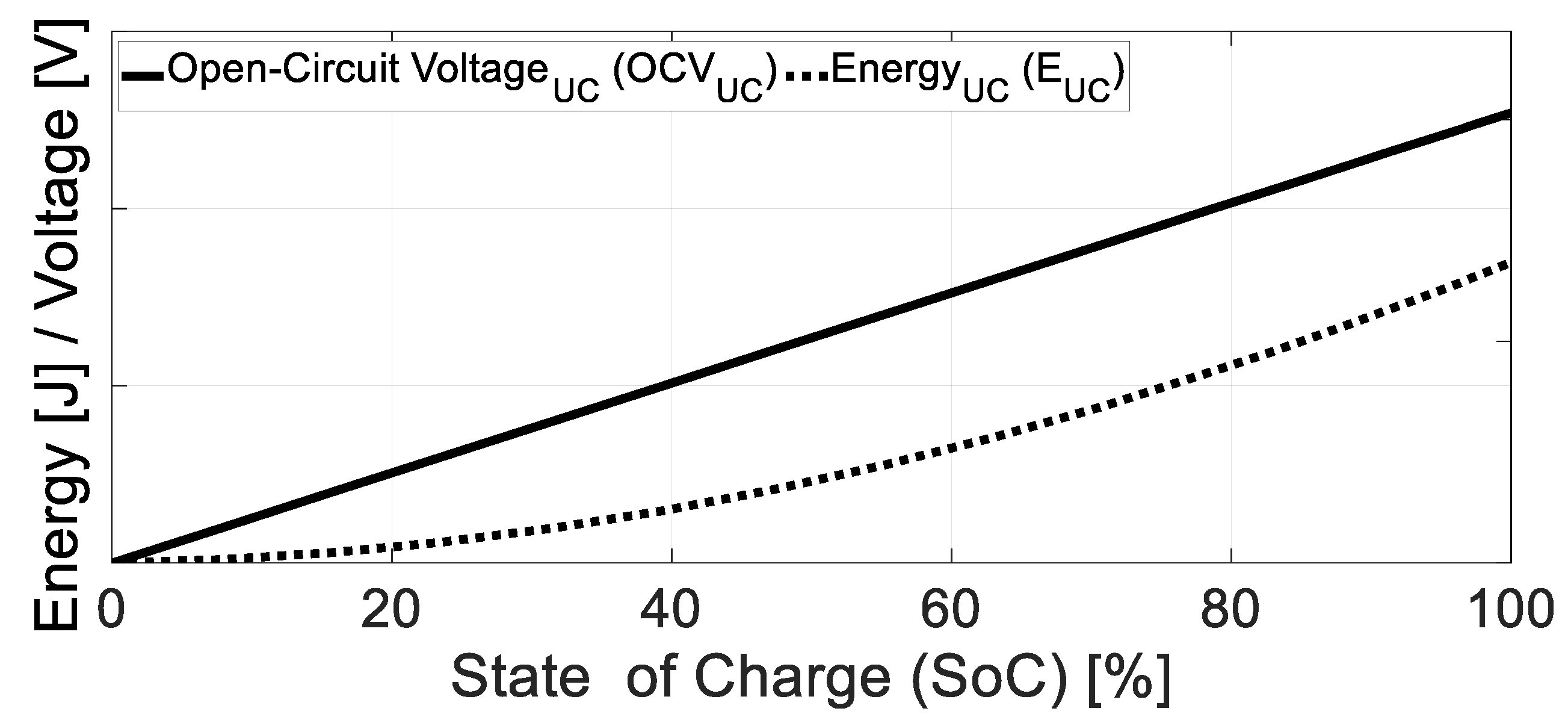
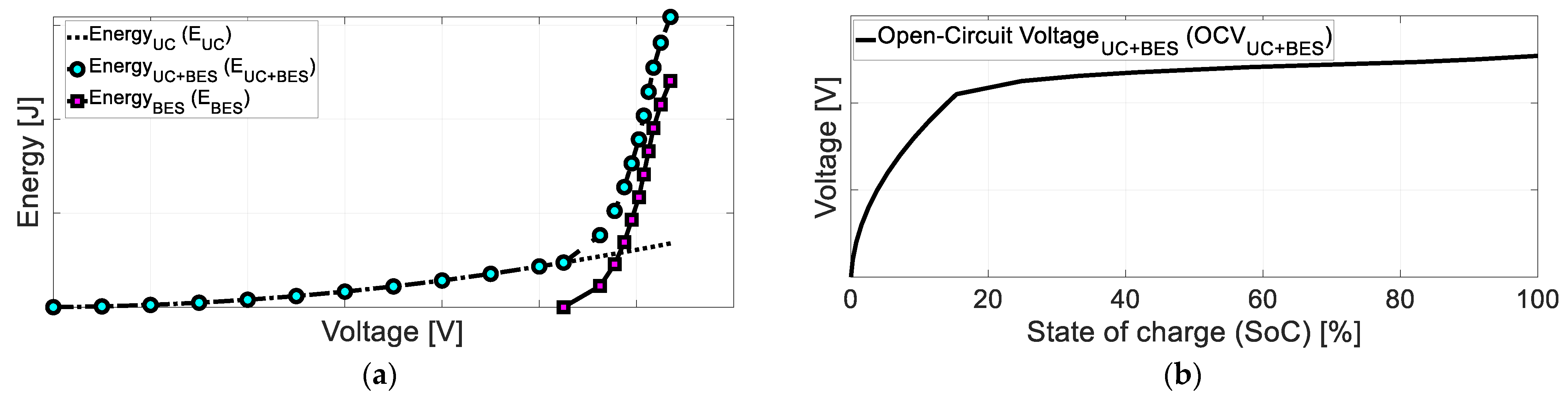

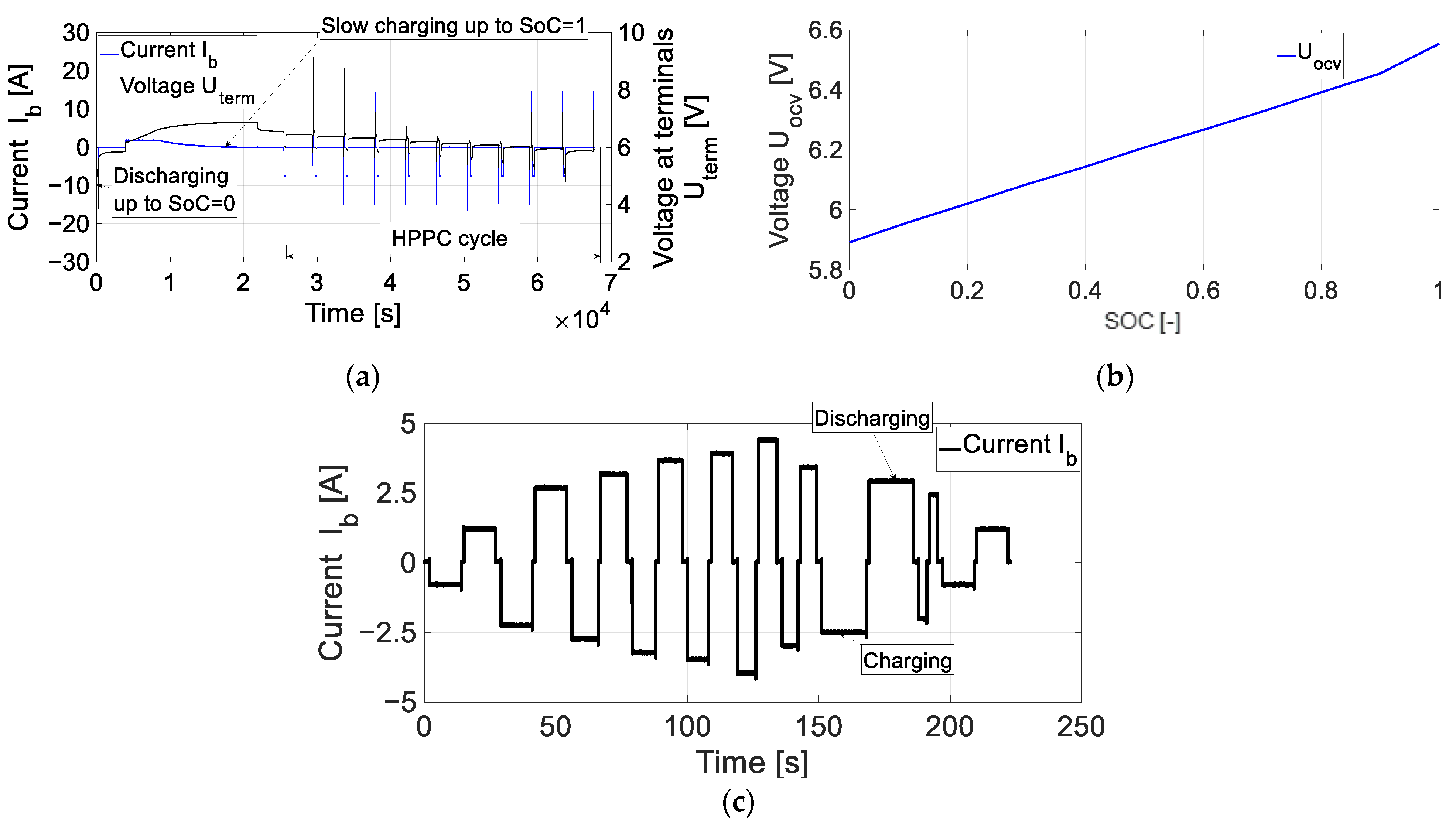
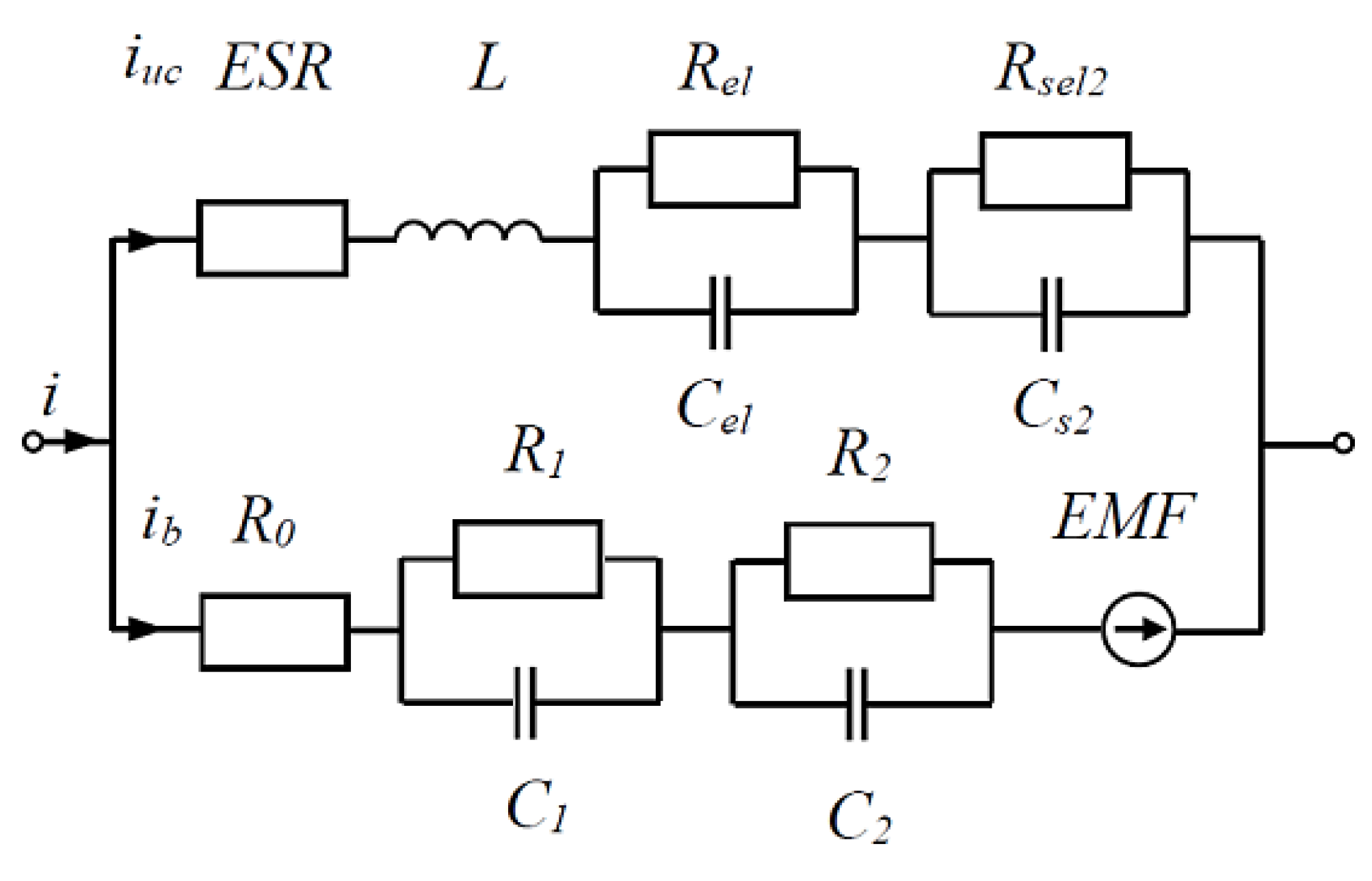



| Battery (VRLA AGM) | Ultracapacitor (Maxwell BMOD0058 E016 B02) | ||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| Nominal voltage | 6 V | Maximum rated voltage | 16 V |
| Minimum voltage | 4.5 V | Minimum voltage | 0 V |
| Maximum voltage | 7.5 V | Maximum voltage | 17 V |
| Capacity | 12 Ah | Capacity | 58 F |
| Internal resistance | 10 mΩ | Initial ESR | 22 mΩ |
| Maximum discharge current | 135 A | Continuous/peak discharge current | 23 A 190 A |
| Dimensions (L × W × H) | 151 mm × 50 mm × 94 mm | Dimensions (L × W × H) | 226.5 mm × 49.5 mm × 75.9 mm |
| Service life | 6–9 years | Service life | 10 years |
| Weight | 1.9 kg | Weight | 0.63 kg |
| Parameter Name | Rint BES | R1 BES | R2 BES | C1 BES | C2 BES | UOCV BES |
|---|---|---|---|---|---|---|
| A | −11 | 4.2 × 10−3 | 26 | 1.8 × 10−4 | 1.3 × 10−4 | 1.1 |
| B | 34 | −1.3 × 10−4 | −84 | −4.1 × 10−4 | −3.1 × 10−4 | −1.7 |
| C | −43 | 1.4 × 10−4 | 1.1 × 10−2 | 3.4 × 10−4 | 2.8 × 10−4 | 5.7 |
| D | 26 | −8.1 × 10−3 | −74 | −1.2 × 10−4 | −9.1 × 10−3 | – |
| E | −7.5 | 2.4 × 10−3 | 27 | 1.6 × 10−3 | 1.2 × 10−3 | – |
| F | 0.91 | −3.7 × 10−2 | −5.5 | 72 | –46 | – |
| G | 0.033 | 55 | 0.53 | – | – | – |
| H | – | – | 0.01 | – | – | – |
| Parameter Name | ESRUC | R1UC | R2UC | C1UC | C2UC | UOCV UC |
|---|---|---|---|---|---|---|
| A | −5.2 | 1 × 10−3 | 8.6 | −5 × 10−4 | −8.4 × 10−4 | 0.87 |
| B | 15 | −3.9 × 10−3 | −24 | 1.6 × 10−5 | 2.7 × 10−5 | −1.3 |
| C | −17 | 4.8 × 10−3 | 24 | −2.2 × 10−5 | −3.4 × 10−5 | 1.3 |
| D | 8.3 | −2.3 × 10−3 | −12 | 1.5 × 10−5 | 2 × 10−5 | 5.8 |
| E | −1.8 | 4.6 × 10−2 | 2.7 | −5.6 × 10−4 | −5.8 × 10−4 | – |
| F | 0.12 | −6.2 | −0.27 | 1.2 × 10−4 | 7.4 × 10−3 | – |
| G | 0.018 | – | 0.027 | −1.2 × 10−3 | −3.3 × 10−2 | – |
| H | – | – | – | 1.2 × 10−2 | – | – |
| Parameter | BES in [47] | BES in [54] | BES in [55] | BES in [57] | HESS in [78] | This Paper |
|---|---|---|---|---|---|---|
| BES equivalent scheme | 1-RC (Thevenin), PNGV, 2-RC (DP), | PNGV | 2-RC (DP) | 2-RC (DP) | 1-RC | 2-RC (DP) |
| UC equivalent scheme | n.a | n.a. | n.a. | n.a. | 1-RC | 2-RC (DP) |
| HESS equivalent scheme | n.a. | n.a. | n.a. | n.a. | 1-RC | 2-RC (DP) |
| Parameter identification method | Genetic algorithm | Kalman filter algorithm | Levenberg–Marquardt algorithm | Extended Kalman filter algorithm | EKF, UKF, RLS | Levenberg–Marquardt algorithm |
| Error indicator name | V2 | Error | RMSE | Error | RMSE, MAE | MSE, NRMSE |
| Error indicator accuracy | 1-RC, PNGV: Medium-high 2-RC (DP): High | PNGV: medium-high | 2-RC (DP): high | 2-RC (DP): high | High: MAE, Medium-high: RMSE | High for MSE, Medium-high for NRMSE |
| Experimental validation test | HPPC, DST | Dynamic test | Pulse test | Normalised FTP-75 test | DST, UDDS | HPPC, Pseudo-random |
| Usability in practical applications | Yes | Yes | Yes | Yes | Yes | Yes |
| Scalability | Yes | Yes | Yes | Yes | Yes | Yes |
| Objects in practical applications | EV | EV | EV | EV | EV | EV, RES integration |
| State of Charge (SoC) | DP ModelBES–UC | |||
|---|---|---|---|---|
| MSEDP–UC | NRMSEDP–UC | MSEDP–BES | NRMSEDP–BES | |
| 0.1 | 0.0006 | 0.7386 | 0.0002 | 0.8978 |
| 0.2 | 0.0009 | 0.6232 | 0.0001 | 0.9111 |
| 0.3 | 0.0016 | 0.4810 | 0.0001 | 0.9113 |
| 0.4 | 0.0017 | 0.4468 | 0.0002 | 0.9046 |
| 0.5 | 0.0004 | 0.7245 | 0.0002 | 0.8931 |
| 0.6 | 0.0010 | 0.5730 | 0.0002 | 0.8778 |
| 0.7 | 0.0007 | 0.6518 | 0.0003 | 0.8623 |
| 0.8 | 0.0007 | 0.6686 | 0.0004 | 0.8416 |
| 0.9 | 0.0024 | 0.4611 | 0.0011 | 0.7597 |
| Role | Application | Description/Recommendation | HESS | BES | UC | |
|---|---|---|---|---|---|---|
| Transportation and Infrastructure | Electromobility operation | Flexible operation of primary energy sources and RES |
| + | + | |
| EV recharging process |
| + | + | |||
| Sustainable development of EV infrastructure | Sustainable development of charging points |
| + | + | + | |
| Aspect | Pros | Cons |
|---|---|---|
| Hybrid energy storage system | Demonstrates efficient integration of battery and ultracapacitor for energy density and power density. | Higher cost and increased system mass due to additional ultracapacitor components. |
| 2-RC circuit model | Provides high accuracy for voltage and parameter estimation. | Accuracy decreases slightly at SoC extremes (e.g., SoC = 0.1 or 0.9). |
| Parameter identification | Effective use of the Levenberg–Marquardt algorithm ensures rapid and accurate parameter optimisation. | Requires careful selection of initial parameters to avoid local minima during optimisation. |
| Error metrics | Low MSE (<0.0024) and reasonable NRMSE values indicate good model reliability. | Lower NRMSE for ultracapacitors compared to batteries suggests scope for further refinement. |
| Experimental validation | Real-world testing using pseudo-random and HPPC cycles validates the model’s accuracy. | Requires specialised equipment and significant computational resources for parameter fitting. |
| Practical application | Applicable for EVs, renewable energy systems and other transport applications. | Increased complexity requires advanced battery management systems for real-world use. |
| Sustainability impact | Supports renewable energy integration and EV infrastructure development. | Limited immediate scalability for cost-sensitive or lightweight applications. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chmielewski, A.; Piórkowski, P.; Bogdziński, K.; Krawczyk, P.; Lorencki, J.; Kopczyński, A.; Możaryn, J.; Costa-Castelló, R.; Ozana, S. A Double Resistive–Capacitive Approach for the Analysis of a Hybrid Battery–Ultracapacitor Integration Study. Energies 2025, 18, 251. https://doi.org/10.3390/en18020251
Chmielewski A, Piórkowski P, Bogdziński K, Krawczyk P, Lorencki J, Kopczyński A, Możaryn J, Costa-Castelló R, Ozana S. A Double Resistive–Capacitive Approach for the Analysis of a Hybrid Battery–Ultracapacitor Integration Study. Energies. 2025; 18(2):251. https://doi.org/10.3390/en18020251
Chicago/Turabian StyleChmielewski, Adrian, Piotr Piórkowski, Krzysztof Bogdziński, Paweł Krawczyk, Jakub Lorencki, Artur Kopczyński, Jakub Możaryn, Ramon Costa-Castelló, and Stepan Ozana. 2025. "A Double Resistive–Capacitive Approach for the Analysis of a Hybrid Battery–Ultracapacitor Integration Study" Energies 18, no. 2: 251. https://doi.org/10.3390/en18020251
APA StyleChmielewski, A., Piórkowski, P., Bogdziński, K., Krawczyk, P., Lorencki, J., Kopczyński, A., Możaryn, J., Costa-Castelló, R., & Ozana, S. (2025). A Double Resistive–Capacitive Approach for the Analysis of a Hybrid Battery–Ultracapacitor Integration Study. Energies, 18(2), 251. https://doi.org/10.3390/en18020251











