Abstract
To address the challenges faced by fuel cell hybrid electric tractors (FCHETs) equipped with a battery and supercapacitor, including the complex coordination of multiple energy sources, low power allocation efficiency, and unclear optimal energy consumption, this paper proposes two energy management strategies (EMSs): one based on hierarchical instantaneous optimization (HIO) and the other based on multi-dimensional dynamic programming with final state constraints (MDDP-FSC). The proposed HIO-based EMS utilizes a low-pass filter and fuzzy logic correction in its upper-level strategy to manage high-frequency dynamic power using the supercapacitor. The lower-level strategy optimizes fuel cell efficiency by allocating low-frequency stable power based on the principle of minimizing equivalent consumption. Validation using a hardware-in-the-loop (HIL) simulation platform and comparative analysis demonstrate that the HIO-based EMS effectively improves the transient operating conditions of the battery and fuel cell, extending their lifespan and enhancing system efficiency. Furthermore, the HIO-based EMS achieves a 95.20% level of hydrogen consumption compared to the MDDP-FSC-based EMS, validating its superiority. The MDDP-FSC-based EMS effectively avoids the extensive debugging efforts required to achieve a final state equilibrium, while providing valuable insights into the global optimal energy consumption potential of multi-energy source FCHETs.
1. Introduction
Tractors, with their superior power performance, play a pivotal role in agricultural production [1,2]. Facing the challenge of global warming, the environmental friendliness and energy efficiency of tractors have become crucial indicators driving the transition of agriculture towards green and sustainable development [3,4]. Traditional tractors rely on internal combustion engines burning fossil fuels, leading to increased carbon emissions and negative environmental impacts [5,6]. Therefore, improving tractor power systems and developing energy-saving technologies are crucial aspects of agricultural emission reduction strategies. Fuel cell systems, with their zero emissions, low noise, high efficiency, and rapid refueling capabilities, are considered one of the most promising options for future new energy power systems [7,8,9]. Applying fuel cell systems to agricultural tractors can effectively enhance the energy efficiency and emission reduction levels of agricultural production, leading the agricultural machinery industry towards a more environmentally friendly and efficient future [10,11].
However, the limitations of fuel cell power system dynamics and low power density cannot meet the dynamic operating requirements of vehicles [12,13]. To overcome this shortcoming, scholars have widely researched the integration of auxiliary energy storage devices such as supercapacitors and batteries with fuel cell systems to form hybrid power systems, improving their dynamic performance and efficiency [14,15]. Based on the configuration of auxiliary energy storage devices, fuel cell hybrid power systems can be divided into three configurations: fuel cell and battery hybrid (FC+B), fuel cell and supercapacitor hybrid (FC+SC), and fuel cell, battery, and supercapacitor hybrid (FC+B+SC) [8]. As the primary non-road mobile machinery in agricultural production activities, tractors face complex and variable environments during field operations, leading to random load influences on their load spectrum [16,17,18,19]. This random load is reflected in the power demand of the driving motor, resulting in random power fluctuations. The FC+B+SC type fuel cell hybrid power system can fully leverage the advantages of each energy storage device to address random power fluctuations, improving system performance. However, the collaborative work of multiple energy sources also brings challenges to control. Maximizing energy utilization efficiency and extending service life have become key research focuses in this area.
Due to the diverse characteristics of energy sources in fuel cell hybrid systems, a reasonable EMS is crucial for coordinating power allocation, improving system economy, and enhancing durability [20]. Extensive research and achievements exist in the field of EMS for fuel cell hybrid systems, which can be primarily categorized into three types: rule-based EMS, optimization-based EMS, and learning-based EMS [7].
Rule-based EMS primarily comprises deterministic rule-based and fuzzy logic rule-based approaches [21]. In rule-based EMS research, Y. Sun et al. [22] designed a rule-based EMS that allocates energy in FC+B type FCHETs by deriving a quadratic utility function and combining it with the Karush–Kuhn–Tucker condition. Simulation results show that this EMS effectively maintains battery SOC, reduces fuel cell performance degradation, and enhances the tractor’s plowing range. V. Martini et al. [23] conducted numerical modeling on FC+B type FCHETs and explored a rule-based EMS. This EMS adopts a strategy where the battery handles dynamic power, while the fuel cell provides steady-state power. The fuel cell output power is adjusted based on the battery’s SOC to ensure normal battery operation. H. Yang et al. [24] proposed a multi-algorithm fusion EMS that integrates thermostat control strategy, power-following strategy, and fuzzy logic control strategy. The proposed EMS can adapt to different initial SOC states, reduce fuel cell power fluctuation amplitude, and achieve a continuous operating time of 2.65 h.
Optimization-based EMS primarily consists of two types: global optimization and instantaneous optimization. Dynamic programming [25,26], Pontryagin’s Minimum Principle [27,28], and genetic algorithms [29,30] are commonly used for solving global optimization problems. Typical methods for instantaneous optimization control include model predictive control strategies [31,32] and equivalent consumption minimization strategies [30,33]. M. Liu et al. [10] proposed an EMS based on a multi-population genetic algorithm for FC+B type FCHETs. Compared with the power-following control strategy, this EMS effectively reduces SOC fluctuation amplitude, increasing the remaining SOC by 11.22% and 6.1% in plowing and transportation scenarios, respectively. The theoretical hydrogen consumption decreased by 26.49% and 36.21%, respectively. Y. Li et al. [34] proposed a hierarchical dynamic programming EMS. The dynamic programming strategy results serve as the upper-level output. The lower-level pre-processes influence variables and screen input variables for a general regression neural network, and realizes the real-time application of the dynamic programming algorithm. Model-in-the-loop and hardware-in-the-loop verification show that the designed tractor simulation model and EMS model are accurate and effective, outperforming the power-following strategy. C. Varlese et al. [35] proposed a novel predictive performance EMS for FC+B type FCHETs. This strategy leverages predictions of average load during the agricultural cycle to achieve stationary fuel cell operation, enhancing fuel cell durability. The test bench analyzes the EMS’s impact on the physical factors of fuel cell operation, emphasizing the advantages of fuel cell systems. X. Lin et al. [36] proposed a decay gradient descent energy reduction power control strategy driven by a self-learning Markov prediction algorithm. This strategy effectively eliminates fuel cell power transients. It achieves a maximum 52.21% reduction in fuel cell usage cost without significantly compromising hydrogen fuel economy. J. Wu et al. [37] proposed an EMS that combines rules and optimization, incorporating rules as constraints into the cost optimization model. This strategy outperforms the comparative strategies under all driving conditions, benefiting from reduced fuel cell system start-stop cycles and increased opportunities for operation in the high-efficiency region. D. Viji et al. [38] proposed a novel hybrid EMS combining Siberian Tiger optimization and the enhanced Wasserstein Generative Adversarial Network. The Siberian Tiger optimization method is used to optimize the parameters of the fuel cell system, while the enhanced Wasserstein Generative Adversarial Network method predicts the vehicle’s power demand. The efficiency value of the proposed method is recorded as 95%, exceeding optimization methods such as particle swarm optimization.
With breakthroughs in artificial intelligence and machine learning, researchers are increasingly exploring the application of AI algorithms and machine learning methods in EMS [39,40]. X. Ren et al. [41] proposed a battery life-conscious energy management predictive control strategy based on a deep reinforcement learning algorithm that predicts the equivalent consumption minimization strategy. Numerical verification and hardware-in-the-loop experimental results comparison show that the proposed strategy effectively achieves a trade-off optimization between energy consumption and battery durability performance. Z. Wang et al. [42] proposed an EMS based on the adversarial deep Q-network algorithm (DQN). Simulation results show that the fuel economy of the DQN and the adversarial DQN are improved by 94.28% and 95.7%, respectively, and that the convergence speed of the adversarial DQN is also improved. Using the NI-PXI real-time simulation test system for simulation, the target vehicle speed is followed, verifying the real-time performance of the strategy.
In summary, compared to road vehicles, research on energy management strategies for FC+B+SC type FCHETs is still relatively limited, with most studies focusing on FC+B type FCHETs. During tractor movement, the overall load profile exhibits non-stationary characteristics, and high-frequency load changes have a significant impact on the lifespan of the battery and fuel cell. Therefore, it is crucial to incorporate high-power devices to handle dynamic power demands. Some research on FC+B+SC type FCHETs remains based on rule-based strategies, which offer advantages in practicality and simplicity. However, these methods are not sufficiently adaptable to comprehensive tractor operating environments and cannot achieve optimal optimization results. The main contributions of this paper are as follows:
- Addressing the high-frequency non-stationary load characteristics during tractor movement and the characteristics of different energy storage devices, this paper proposes an FC+B+SC type FCHET configuration and establishes a system model, aiming to leverage the advantages of each energy storage device while mitigating their drawbacks;
- To effectively manage system energy, this paper proposes a HIO-based EMS. The upper-layer strategy employs a low-pass filter method for energy allocation, utilizing the high-power density of supercapacitors to handle the dynamic power demands of the system. The lower-layer strategy optimizes the instantaneous power distribution between the battery and the fuel cell based on minimizing equivalent fuel consumption;
- To address the multi-state and control variable characteristics of multi-energy source fuel cell hybrid power systems, this paper proposes an MDDP-FSC-based EMS. This strategy employs backward iteration and parallel computation on spatial boundaries, effectively avoiding the extensive debugging efforts required to achieve final state equilibrium.
The structure of this paper is as follows: Section 1 presents the key component parameters and models of the FC+B+SC type fuel cell hybrid electric tractor. Section 2 proposes a HIO EMS based on low-pass filters and equivalent consumption minimization, as well as a global optimization EMS based on MDDP-FSC. Section 3 presents simulation and experimental results to validate the effectiveness and superiority of the proposed energy management strategy design scheme. Finally, Section 4 summarizes the research findings.
2. Modeling
2.1. FCHET Configuration
This study investigates a FCHET featuring a multi-energy source fusion system. As illustrated in Figure 1, the system integrates fuel cells, batteries, and supercapacitors. Leveraging the distinct characteristics of each energy source, the battery is directly connected to the power bus, establishing its voltage as the bus voltage. The fuel cell is connected to the power bus via a series unidirectional DC/DC converter. The supercapacitor is connected to the bus via a series bidirectional DC/DC converter. The drive motor, serving as the tractor’s primary power source, transforms electrical energy from the various energy sources into mechanical energy. This mechanical energy is then delivered to the four wheels and power take-off (PTO) shaft via the mechanical transmission system.
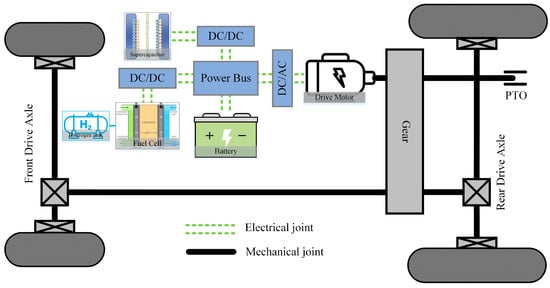
Figure 1.
FCHET structure schematic.
This study employs the Dongfanghong LX904 wheeled tractor (First Tractor Co., Ltd., Louyang China) as a reference model. Based on the tractor’s operating conditions, the key components and parameters of the FCHET are selected and matched, as detailed in Table 1 [23].

Table 1.
Key technical parameters of the FCHET.
2.2. Vehicle Models
2.2.1. Traction Dynamics Model
In mobile traction unit operation, the tractor must overcome both its own motion resistance and the traction resistance imposed by passive farm machinery. The longitudinal dynamic equation for a tractor under traction operation is as follows:
where FD is the total driving force of the tractor, N; FM is the motion resistance, N; FT is the traction resistance of agricultural machinery, N.
2.2.2. Four-Wheel Drive Wheel–Soil Interaction Model
Traction prediction mathematical models can represent the complex relationship between tractor tire driving performance and soil properties [43,44].
where Bn is the tire traction index; i represents front wheels when it is f and rear wheels when it is r; CI is the tire–soil cone index; b is the unloaded tire section width, m; d is the unloaded tire diameter, m; dc is the tire radial deformation, m; h is the tire section height, m; Fz is the tire normal load, N; GTR is the tire traction utilization coefficient; Fw is the tire traction force, N; S is the tire slip ratio; MMR is the tire rolling resistance coefficient; and Fm is the tire motion resistance, N.
Figure 2 illustrates the traction force analysis of a four-wheel drive tractor. Assuming that the coordinates of the tractor’s center of mass and the line of action of the tractive force lie within the same vertical plane perpendicular to the ground, it follows that the load on the driven wheels on both sides of the same drive axle is equal. The moment balance equations for the front and rear drive axles are as follows:
where FA is the drive axle normal load, N; m is the tractor mass, kg; g is the acceleration due to gravity, m/s2; L is the tractor wheelbase, m; a is the longitudinal distance from the center of mass to the rear axle center, m; e is the wheel offset distance, m; and hT is the towing point height, m.
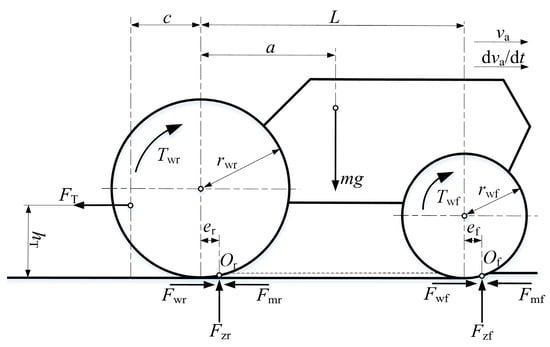
Figure 2.
Longitudinal dynamics of a four-wheel drive tractor.
The total driving force and motion resistance of a four-wheel drive tractor can be calculated based on Equations (2) and (3).
By considering the lack of coordination in the movement of the front and rear axles of a four-wheel-drive tractor, slippage and motion efficiency can be derived. Slip efficiency is used to measure the power loss due to the slippage of the drive wheels, while motion efficiency measures the power loss caused by rolling resistance when the tractor is moving.
where ηS is the slip efficiency; va the actual speed, km/h; vt the theoretical speed, km/h; and ηM is the motion efficiency.
The relationship between the slip efficiency, motion efficiency, and traction force of a four-wheel drive tractor is shown in Figure 3, obtained using the traction performance prediction method for four-wheel drive tractors.
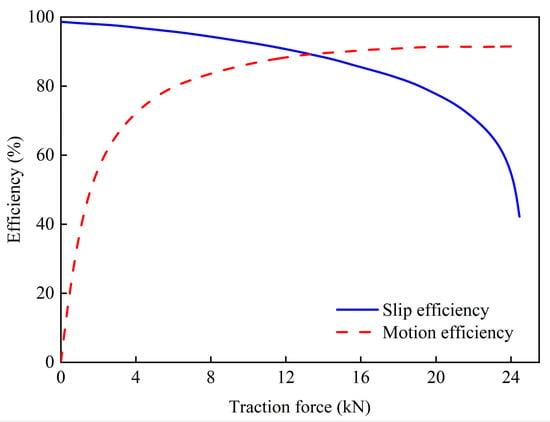
Figure 3.
Slip and motion efficiency.
2.3. Drive Motor Model
During tractor operation, the drive motor’s required speed is dictated by the vehicle’s current speed. However, the required torque is determined by the control strategy. Consequently, the motor’s operation should be constrained within a range of torque values that are feasible for the current speed. The actual torque output of the motor is as follows:
where TDM_Max represents the maximum torque of the drive motor, N·m; ωDM represents the drive motor speed, r·min−1; and TDM represents the drive motor torque, N·m.
The motor efficiency is established using interpolation, based on data obtained from bench tests, as shown in the following equation:
where represents the drive motor efficiency.
According to the power balance, the power at the input end of the motor is related to the traction resistance and the power of each power source, as shown in the following equation:
where PDM represents the motor power, W; ηT represents the efficiency of the mechanical transmission; PFC represents the fuel cell power, W; PBat represents the battery power, W; PSC represents supercapacitor power, W; and ηinv represents the efficiency of the converter.
2.4. Fuel Cell Model
The fuel cell, as the primary energy source for the FCHET, provides stable power by converting the chemical energy of hydrogen and oxygen into electrical energy. Considering the power consumption of auxiliary systems during normal operation, the efficiency model of the fuel cell system is as follows [11]. The discharge efficiency is shown in Figure 4.
where ηFC represents the efficiency of fuel cells.
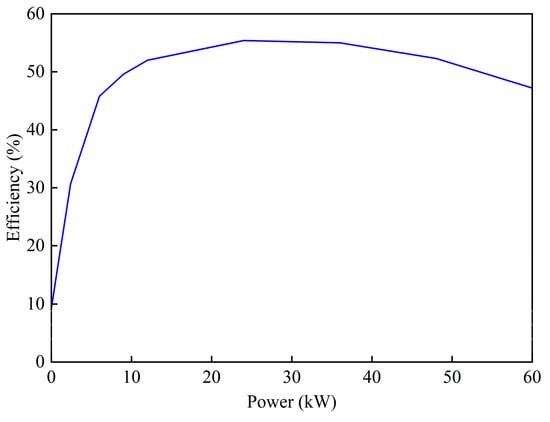
Figure 4.
Fuel cell power–efficiency curve.
Once the fuel cell’s efficiency at the current moment is determined, the hydrogen consumption rate can be calculated using the following equation, based on the fuel cell’s power output and the lower heating value of hydrogen fuel:
where represents the low heat value of hydrogen and represents the hydrogen consumption rate, g/s.
The total mass of hydrogen consumed over the entire operating cycle can be obtained by integrating the hydrogen consumption rate over time.
where t0 represents the start time of operation, s; tf represents the end time of operation, s; and represents the mass of hydrogen consumed, g.
In the realm of FCHET research, the degradation of fuel cell performance is an indispensable area of focus [45,46,47]. Voltage degradation has a direct impact on the output power, which can be evaluated by calculating the standard deviation of power values obtained from five consecutive steps [36]. The rate of voltage degradation in a fuel cell can be expressed as follows:
where UFCD represents the fuel cell voltage degradation, μV.
2.5. Battery Model
The battery functions as a buffer energy source, enhancing the efficiency of the fuel cell system [48]. It is modeled as an open-circuit voltage source in series with an internal resistance [37]. The relationship between the battery’s internal resistance, open-circuit voltage, and SOC is shown in Figure 5. The battery’s output characteristics are described by the following equation:
where UBat represents the battery voltage, V; UBat_OC represents the open-circuit voltage of the battery, V; IBat represents the battery current, A; RBat represents the charge–discharge internal resistance of battery, Ω; and PBat represents the battery power, W.
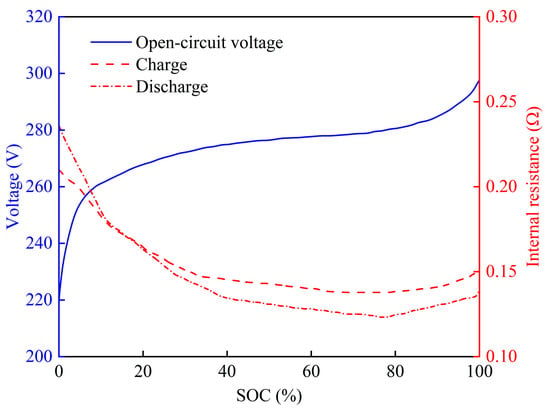
Figure 5.
Open-circuit voltage and internal resistance curve of battery.
The remaining charge is a crucial indicator of the battery’s ability to deliver the normal energy output. The SOC, defined as the ratio of the battery’s current remaining charge to its rated capacity, can be calculated using the following equation:
where SOCBat represents the SOC of battery at time t; SOCBat_0 represents the initial SOC of the battery; and QBat represents the rated capacity of the battery, A·s.
2.6. Supercapacitor Model
Supercapacitors possess the advantages of rapid charge and discharge, high power density, and long lifespan. They significantly enhance the dynamic performance of the FCHET and improve the overall energy utilization efficiency of the system. The model consists of an ideal equivalent capacitance and an equivalent series internal resistance [49], and its output characteristics are as follows:
where PSC represents supercapacitor power, W; USC represents supercapacitor voltage, V; ISC represents supercapacitor current, A; QSC represents supercapacitor charge, C; QSC_0 represents initial supercapacitor charge, C; RSC represents equivalent internal resistance value, Ω; and CSC represents equivalent capacitance, F.
Supercapacitor SOC is used to characterize the remaining available energy of the supercapacitor and can be expressed as follows:
where USC_Min and USC_Max represent the minimum and maximum allowable voltages of the supercapacitor, respectively.
3. EMSs
3.1. HIO
This section proposes a HIO EMS based on low-pass filtering and minimizing equivalent energy consumption, as shown in Figure 6. The proposed strategy consists of two layers: upper and lower. In the upper-layer strategy, by considering the high-power density of supercapacitors, a power allocation method based on a low-pass filter is proposed to provide dynamic power. A fuzzy logic is set up to ensure that the supercapacitor SOC remains within a reasonable range. In the lower-layer strategy, an equivalent energy consumption minimization strategy is considered in order for the fuel cell and battery to meet the remaining power demand of the vehicle while achieving optimal instantaneous power allocation for the battery and fuel cell, thereby improving the system economy.
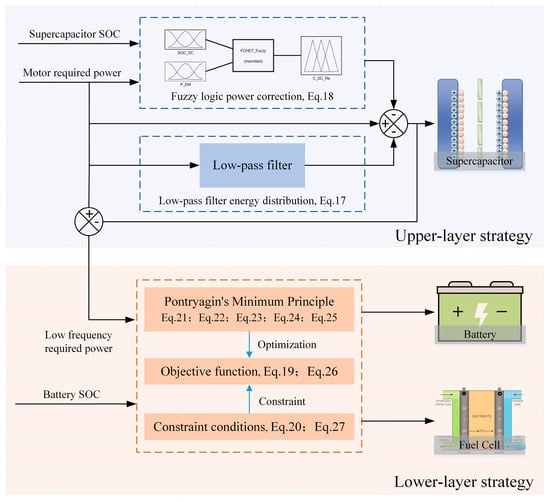
Figure 6.
Hierarchical instantaneous optimization EMS.
3.1.1. Upper-Layer Strategy
Field trials and soil tank experiments have established that the load on the power source during plowing operations exhibits stationary, normally distributed, random behavior [17,18]. In the context of a fuel cell electric tractor, this translates to a fluctuating demand power requirement for the drive motor, comprising a steady power component and a dynamic power component. To accommodate this fluctuating demand, a low-pass filter is designed to selectively pass components of the demand power below a predetermined frequency cutoff. The dynamic portion of the demand power is then supplied by the supercapacitor, leveraging its high-power density. The transfer function of this low-pass filter can be expressed as follows:
where τ represents the time constant.
Tractor movement in the field can be divided into two main stages: posture adjustment and load operation. The power demand corresponds to the low-power and high-power stages, respectively. These two stages constantly switch during field movement. When using the above method for supercapacitors, it is necessary to ensure that the supercapacitor has sufficient capacity to charge and discharge during the switching between these two stages. To ensure that the supercapacitor SOC remains within a suitable range, sufficient for providing dynamic power, and to alleviate the pressure on the fuel cell and battery during field movement, a fuzzy control-based supercapacitor power correction method is proposed.
As shown in Figure 6, the inputs to this fuzzy control are the current supercapacitor SOC (SOC_SC) and the driving motor’s required output power (P_DM). The supercapacitor correction coefficient (C_SC_Re) changes from a constant value to a real-time variable output of the fuzzy control. The input and output membership functions are determined. The input membership function for supercapacitor SOC, the input membership function for driving motor power demand, and the output membership function for the correction coefficient are shown in Figure 7 and Figure 8.
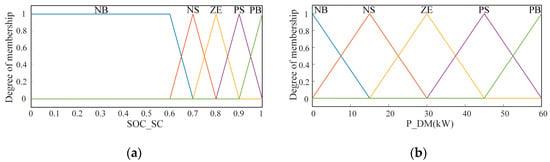
Figure 7.
Input membership function. (a) Supercapacitor SOC; (b) drive motor power demand.
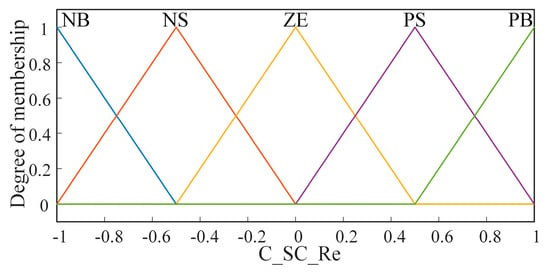
Figure 8.
Output membership function for correction factor.
To maintain the supercapacitor SOC within a suitable range based on the tractor’s operating characteristics, this paper finally establishes a rule base, as shown in Table 2.

Table 2.
Fuzzy control rule table.
Based on the above fuzzy control low-pass filter method for supercapacitors, the supercapacitor can effectively handle high-frequency dynamic power demands and power fluctuations during transitions between field movement stages, while ensuring that the supercapacitor capacity is maintained within the most reasonable range. The power demand of the supercapacitor can be expressed as:
where PSC_Fil represents the supercapacitor power allocated by the low-pass filter; CSC_Re represents the supercapacitor power correction coefficient; and PSC_Re represents the supercapacitor correction reference power.
3.1.2. Lower-Layer Strategy
The lower-layer strategy can allocate the output power of the fuel cell and battery through an equivalent energy consumption minimization strategy, thereby enhancing the economy of the FCHET. In this paper, the battery energy in the fuel cell hybrid tractor is supplied by the fuel cell. According to the equivalent energy consumption minimization strategy, the battery’s energy consumption is converted into hydrogen consumption. By optimizing the power of the fuel cell and battery, the hydrogen consumption is minimized. By setting the battery SOC as the state variable x(t) and the battery power as the control variable u(t), the system’s objective function C(u,x) can be obtained.
where represents the equivalent hydrogen consumption rate.
The constraints for each component during operation when using the equivalent fuel consumption minimization strategy are as follows:
where and represent the lower and upper limits of the battery SOC, respectively; and represent the minimum and maximum power output of the battery, respectively; and and represent the minimum and maximum power output of the fuel cell, respectively.
According to Pontryagin’s Minimum Principle, a co-state variable λ(t) is introduced, and the Hamiltonian equation H is constructed.
where represents the rate of change in the battery SOC and λ(t) represents the equivalent coefficient.
According to Pontryagin’s Minimum Principle, the necessary condition for the objective function C to achieve its minimum value is:
and the following condition must be satisfied:
Combining Equation (14) with Equation (23):
From the above equation, we can see that the co-state variable λ(t) is related to the open-circuit voltage and internal resistance of the battery. To facilitate the analysis of the relationship between the co-state variable, battery power, and fuel cell hydrogen consumption, we can transform the Hamiltonian equation into a form related to battery power.
where s(t) represents the equivalent factor.
The physical meaning of the Hamiltonian equation in energy management problems is the equivalent fuel consumption at the current moment. Therefore, the instantaneous equivalent hydrogen consumption of the system per unit time, along with the battery SOC adjustment factor cBat, is introduced to ensure that the battery SOC remains within a reasonable range.
The battery’s energy is supplied by the fuel cell; therefore, the battery is set to be energy sustaining.
where μ is a fixed constant, its value influences the charging and discharging process of the battery, and is chosen to balance the battery’s SOC value.
3.2. MDDP-FSC
Dynamic programming (DP) is a powerful numerical method for solving optimal control problems, effectively handling constraints and nonlinearities while finding global optimal solutions. To enhance the evaluation performance of dynamic programming, the final states of the state variables are constrained. The optimal control problem for FCHET energy management can be expressed as follows: find a feasible control sequence uk, where k = 0, 1, …, N that minimizes the cost-to-go function in Equation (28) and satisfies the constraints of Equation (29).
where for all k = 0, 1, …, N − 1; gN(xN) represents the cost at the final time step N; gk(xk, uk) represents the cost at time step k; xk+1 represents the state variable at time step k + 1; xk represents the number of state variables at time step k; N is the number of stages after the time domain of the target operating condition is discretized; Xk represents the constraint on the state variable at time step k; xIC represents the initial condition of the state variable; T represents the set of final constraints for the state variables; uk represents the control variable at time step k; and Uk represents the constraint on the control variable at time step k.
According to DP theory, the multi-stage optimization problem of the control strategy can be decomposed into a series of stage-by-stage optimization problems. By using a backward approach, the minimum cost-to-go function Jk(xi) for each stage can be obtained.
- The cost-to-go function J at the final time step N:
- The cost function is computed recursively for each time step k from N − 1 to 0.
After calculating the optimal control variables corresponding to each state variable at the initial time step based on backward iteration, starting from the initial state of the state variables x0, a forward iteration is performed based on the relationship between the state variables and optimal control variables at each time step, thus determining the optimal solution for the cost-to-go function.
When evaluating the advantages and disadvantages of EMSs, to avoid extensive debugging for battery and supercapacitor charge balancing, this paper employs a multi-dimensional, state variable, feasible space-solving method using level set functions. This method can identify the space that does not comply with the final state constraints of the state variables, thereby addressing the problem of large gradients caused by setting the cost-to-go function with state variable penalty functions and achieving the system charge balance [50,51].
- The level set function I at the final time step N:where h(x) is represented by the target set T.
- The level set function is computed recursively for each time step k from N − 1 to 1.
- For each grid point xi, find a set of control variables such that the system’s iterative trajectory at the next time step will be located within the feasible space of the control variables calculated using backward iteration.And find a candidate control variable that minimizes the level set function.
- Calculate the optimal cost based on the optimal candidate control variable. Update the optimal cost according to the following rule if and only if there is at least one valid candidate control variable .
If the grid point is not reachable backward, then calculate the cost based on the control variable .
Repeat steps (2) to (4) until k = 0.
For FCHET, the optimization objective focuses on vehicle economy. Therefore, the energy management problem for FCHET based on dynamic programming becomes a problem of finding a control sequence that minimizes the cost-to-go function.
To ensure the normal operation of each subsystem, the following constraints must be satisfied, as shown in the equation below:
where and represent the lower and upper limits of the supercapacitor SOC, respectively, and and represent the minimum and maximum power output of the supercapacitor, respectively.
Figure 9 illustrates the solution process for the multi-dimensional final state constrained global optimization strategy based on MDDP-FSC. To evaluate the advantages of the proposed hierarchical instantaneous optimization energy management strategy and analyze its optimal energy consumption potential, this paper utilizes the FCHET configuration scheme presented herein. For this analysis, battery and supercapacitor SOC are chosen as state variables, while fuel cell output power, battery output power, and gear number serve as control variables. Table 3 presents the selected state variables, control variables, and grid partitioning employed in this study.
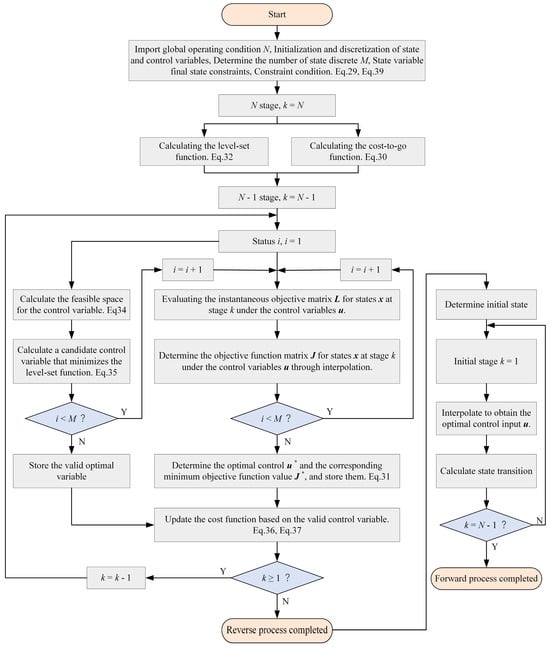
Figure 9.
Schematic diagram of MDDP-FSC solution process.

Table 3.
State and control variables in dynamic programming.
4. Simulation and Validation
4.1. HIL Test Platform
To verify the rationality and effectiveness of the FCHET energy management strategy, this paper constructs an HIL test platform based on the Power ECU rapid control prototyping and the NI real-time simulation machine, building upon our team’s earlier research findings [31]. This platform utilizes the corresponding Simulink plugins of Power ECU-Toolbox and NI-Veristand Blocks to configure the proposed control strategy and the FCHET model with respective I/O modules. The compiled code files are then written into the controller and the NI real-time simulator. Real-time simulation is conducted within NI-Veristand, and the HIL testing process is monitored in real-time using Power CAL V1.32 and NI-Veristand 2020. The HIL test platform is shown in Figure 10.

Figure 10.
HIL test platform.
4.2. Operation Load
The plowing operation load of the tractor is obtained from the tractor load spectrum. According to the probability distribution characteristics of the load, it is known that the tractor plowing load follows a normal distribution [52]. Based on the probability function and autocorrelation function of the load for the Dongfanghong LX904 tractor, a FCHET with random load plowing conditions is established. The tractor’s plowing operation includes two main stages: the posture adjustment stage and the plowing stage. The speed during the posture adjustment stage is set to 3.5 km/h. To reflect the diversity of tractor implements, the plowing stage considers two speeds: 9 km/h and 6 km/h, and the two following load states are set: 100% and 80%. The plowing operation conditions are shown in Figure 11.
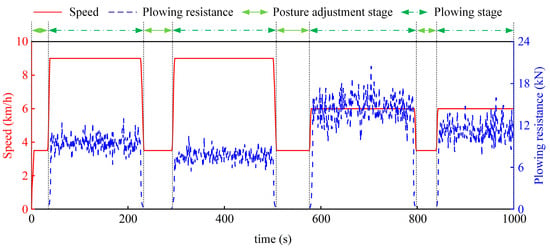
Figure 11.
Plowing operation conditions.
4.3. Feasibility Analysis
As seen in Figure 12a, the drive motor primarily overcomes rolling resistance during the posture adjustment stage, requiring 4.98 kW of power. During the plowing stage, the power demand ranges from 25 kW to 55 kW and exhibits a normal distribution, consistent with the load distribution characteristics of tractor plowing operations. Figure 12b shows that the operating points during the working phase are all located above 90% of the drive motor’s efficiency range, indicating a good match between the FCHET’s mechanical transmission system and the drive motor’s operating range, allowing the drive motor to maintain high efficiency during operation.
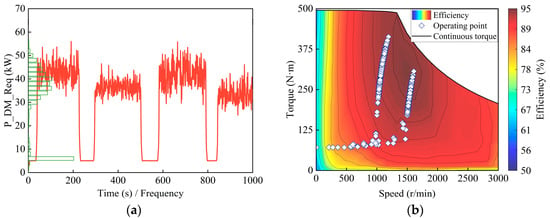
Figure 12.
Drive motor. (a) Power required and (b) operating point.
To analyze the differences in power allocation among different configurations of FCHET power sources, this paper selects the FC+B configuration based on the instantaneous optimization strategy as a reference. Figure 13 shows the power output of each energy source under instantaneous optimization for both configurations. Comparing Figure 13a–c, it can be observed that the fuel cell and battery power curves exhibit similar trends for both configurations, demonstrating the effectiveness of the proposed instantaneous optimization strategy. In terms of dynamic power provision, the FC+B+SC configuration primarily utilizes the supercapacitor to handle the dynamic power of the driving motor. In contrast, the FC+B configuration, lacking a supercapacitor, exhibits a characteristic where the fuel cell provides dynamic power when the fuel cell output power is between 24 kW and 36 kW, while the battery provides dynamic power in the other intervals.
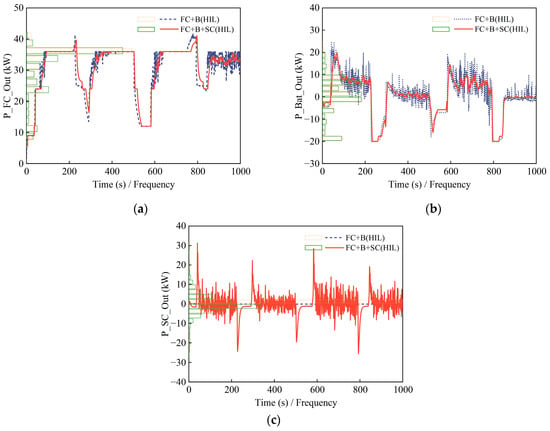
Figure 13.
Power output curves under instantaneous optimization. (a) Fuel cell; (b) battery; and (c) supercapacitor.
Figure 13a demonstrates that, under instantaneous optimization, the fuel cell operates within its high-efficiency range for both configurations. The bar chart indicates that the fuel cell primarily operates between 20 kW and 40 kW for both configurations. Comparing the two configurations, the FC+B+SC configuration achieves a higher average efficiency of fuel cell power distribution due to the collaborative effect of the battery and supercapacitor. Figure 13c shows that the power distribution of the supercapacitor follows a normal distribution, like the load distribution characteristics of the tractor, highlighting its advantage in handling dynamic power demands.
Figure 14 shows the energy consumption of each energy source under the instantaneous optimization strategy for both configurations. To minimize the influence of the supercapacitor SOC on the comparative analysis, the initial battery SOC is set to 60% and the initial supercapacitor SOC is set to 81%. Since the FC+B configuration does not have a supercapacitor, a straight line with the same initial value is used as a reference for comparison in the figure.
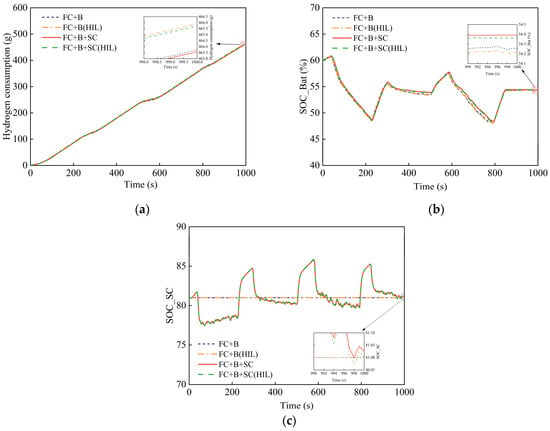
Figure 14.
Energy consumption curves under instantaneous optimization. (a) Hydrogen consumption; (b) battery SOC; and (c) supercapacitor SOC.
The experimental results were compared with the simulation outcomes. As shown in Figure 14, the HIL experiments revealed very close agreement between the simulated data and the actual measurements regarding the hydrogen consumption of the fuel cell, as well as the SOC of both the battery and supercapacitor. Under the equivalent fuel consumption strategy, both configurations displayed similar trends in fuel cell hydrogen consumption and battery SOC variations. Importantly, compared to the FC+B configuration, the addition of a supercapacitor did not increase hydrogen consumption. On the contrary, as indicated by the data in Table 4, the battery’s SOC improved while hydrogen consumption decreased. In summary, both the simulation and HIL experimental results support the effectiveness of the proposed control strategy.

Table 4.
Energy consumption comparison under instantaneous optimization.
Figure 15 presents a comparative analysis of voltage degradation in two different configurations of fuel cell systems. The results indicate that the FC+B+SC configuration significantly reduces cumulative voltage degradation compared to the FC+B configuration. This evidence strongly supports the effectiveness of the FC+B+SC configuration in mitigating the performance decline in fuel cells. Therefore, the addition of a supercapacitor under fuzzy logic low-pass filter control effectively improves the operating conditions of the battery and fuel cell, thereby extending their lifespan. Furthermore, the results from the HIL experiments were in very close agreement with the simulation outcomes.
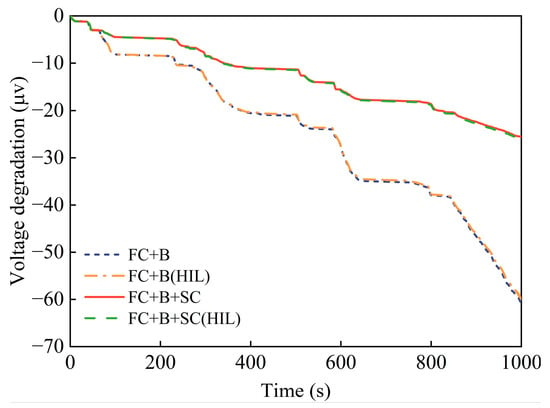
Figure 15.
Fuel cell voltage degradation.
4.4. Robustness Analysis
To verify the ability of the proposed control strategy to maintain supercapacitor and battery charge within an appropriate range and ensure continuous power output under varying initial SOC conditions, simulation experiments were conducted for this paper. The initial SOC values of the battery and supercapacitor are set near their respective operating limits. Figure 16 presents the energy consumption curves for both high and low initial SOC levels, while Table 5 summarizes the simulation results for these conditions.
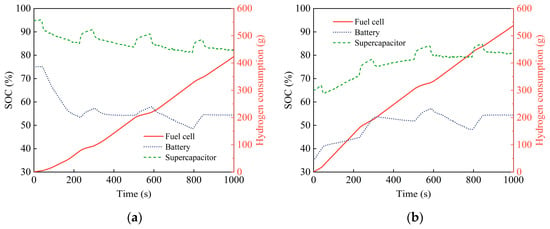
Figure 16.
Energy consumption performance under different initial SOCs. (a) High-level; (b) low-level.

Table 5.
Energy consumption comparison under different initial SOC conditions.
The energy consumption curves and simulation results demonstrate that the proposed energy management strategy effectively adjusts the charge levels of the battery and supercapacitor to within a reasonable range, even under varying initial SOC conditions, ensuring normal system operation.
4.5. Assessment and Potential Analysis
To investigate the energy consumption potential of the global optimal control strategy for FCHET and evaluate the proposed HIO-based EMS, this section compares the EMS based on MDDP-FSC with the proposed EMS. To obtain the global optimal cost as a reference for the control strategy in this paper, the power rate of change in the power sources is not constrained. Figure 17 shows the power output of each energy source under the two control strategies.
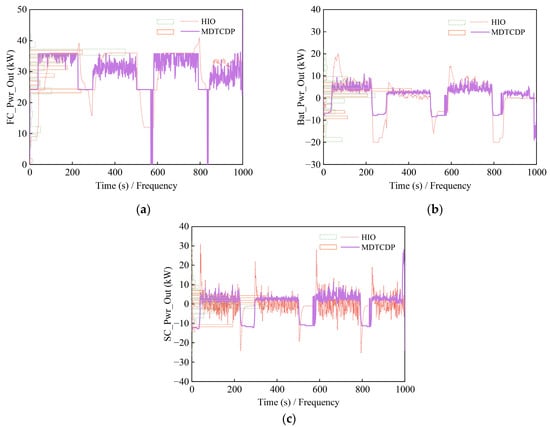
Figure 17.
Power output profiles for different control strategies. (a) Fuel cell; (b) battery; and (c) supercapacitor.
Comparing Figure 17a–c, it can be observed that under the MDDP-FSC-based control strategy, the optimal cost is obtained by backward solution, but the power output of each power source fluctuates frequently. Specifically, during the operation stage, when the fuel cell output power remains between 24 kW and 36 kW, the power above or below this range is provided by the supercapacitor and battery. Due to the capacity advantage of the battery compared to the supercapacitor, the average value of the main power range provided by the battery is relatively higher. The simulation results align with the functionality of the designed system. The HIO-based control strategy, with its upper fuzzy logic low-pass filter controller, effectively addresses the issue of fuel cells and batteries experiencing dynamic power, resulting in a smoother power output.
Figure 17a demonstrates that both control strategies effectively maintain the fuel cell operating region within its high-efficiency range. The bar chart shows that the fuel cell power output of the HIO-based EMS is mainly concentrated between 20 kW and 40 kW, while the fuel cell power output of the MDDP-FSC-based EMS is more concentrated within the fuel cell’s high-efficiency zone. This indicates that the MDDP-FSC-based strategy can more precisely control the fuel cell’s output power, ensuring it consistently operates within its optimal range.
Notably, during the attitude adjustment stage, the MDDP-FSC-based control strategy demonstrates frequent switching of fuel cell power output between the 24 kW power point and zero power point. This demonstrates the global optimization advantage of this strategy, namely its ability to adjust the fuel cell’s output power based on the overall operating conditions to achieve optimal energy consumption performance. This finding provides new insights for optimizing future EMSs for FCHETs, suggesting that a more precise power control strategy could further enhance fuel cell utilization efficiency and reduce system energy consumption.
Figure 18 presents the energy consumption of each energy source under the two control strategies. To conduct a more precise comparative analysis, the initial SOC for the battery and supercapacitor are set at 60% and 80%, respectively. The final state variable interval is defined based on the simulation results of the HIO-based EMS and the MDDP-FSC state variable discretization precision. Specifically, the final battery SOC interval is set to [0.543, 0.548], and the final supercapacitor SOC is set to [0.805, 0.810]. As shown in Table 6, the final SOC values of the battery and supercapacitor are within the state variable discretization interval under both control strategies, demonstrating the final state constraint capability of the MDDP-FSC-based EMS.
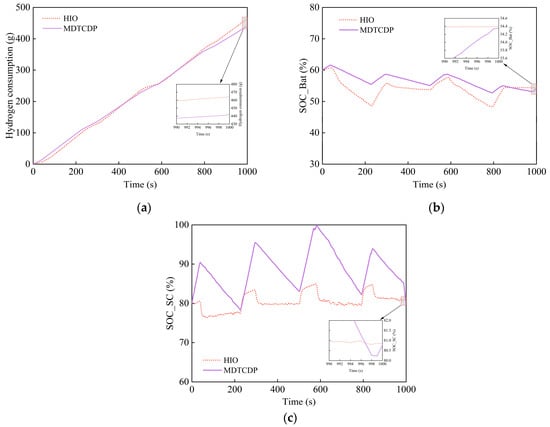
Figure 18.
Energy consumption curves for different control strategies. (a) Hydrogen consumption; (b) battery SOC; and (c) supercapacitor SOC.

Table 6.
Energy consumption comparison under different control strategies.
Given that the difference in the final SOC values of the battery and supercapacitor is negligible, it can be disregarded in terms of its impact on the energy consumption comparison. Regarding hydrogen consumption, the HIO-based EMS consumes 464.23 g of hydrogen, while the MDDP-FSC control strategy consumes 441.95 g. The proposed HIO EMS achieves 95.20% of the hydrogen consumption of MDDP-FSC, showcasing effective energy management. The specific results are summarized in Table 6.
5. Conclusions
This paper proposes two EMSs for FCHETs equipped with batteries and supercapacitors: one based on HIO and another based on MDDP-FSC. By combining theoretical analysis with experimental validation, this research effectively addresses the challenges of coordinating multi-energy source characteristics, suboptimal power distribution efficiency, and unclear optimal energy consumption in FCHETs. The main conclusions are summarized as follows:
- Based on the tractor’s operational load characteristics, this paper designs an FCHET energy source configuration that utilizes the fuel cell for stable power, the supercapacitor for dynamic power, and the battery as an auxiliary energy source to improve fuel cell efficiency. Additionally, models for longitudinal dynamics and the energy source system were developed.
- To overcome the challenges of coordinating multi-energy source characteristics and suboptimal power distribution efficiency, this paper proposes an HIO-based EMS. The upper-layer strategy utilizes a low-pass filter to split the drive motor power into high- and low-frequency components, employing the supercapacitor to handle the high-frequency dynamic power. A fuzzy logic-based supercapacitor power regulator is implemented to ensure that the supercapacitor’s SOC remains within an appropriate range during different stages of tractor operation. The lower-layer strategy allocates low-frequency stable power based on the principle of minimizing equivalent consumption. A HIL simulation platform is developed to validate the feasibility of the proposed EMS. Simulations were conducted on different FCHET configurations under plowing conditions. Simulation results show that the addition of supercapacitors effectively mitigates the load change cycling stress on the fuel cell and the charge–discharge cycling stress on the battery, thereby improving their lifespans. Additionally, the average efficiency of fuel cell power distribution is enhanced, resulting in improved energy consumption. Moreover, the system maintains reasonable charge levels for both the battery and supercapacitor under different initial SOC conditions.
- To further evaluate the superiority of the proposed EMS and explore the global optimal energy consumption of multi-energy source FCHETs, this paper proposes an MDDP-FSC-based EMS. Simulation results indicate that, with identical initial SOC values and negligible final SOC differences between the two EMSs, the proposed EMS achieves a hydrogen consumption level of 95.20% compared to the MDDP-FSC-based EMS. This approach employs a constrained terminal state boundary solution method, effectively reducing the impact of terminal SOC differences on the comparative evaluation of control strategy superiority. Additionally, the results from the MDDP-FSC-based EMS provide new insights for future research on FCHET EMS.
In conclusion, this research provides a theoretical foundation and technical support for the development of FCHET control systems. However, due to limitations in experimental conditions, validating the practical effectiveness of the proposed control strategies on an FCHET prototype will be a focus of further research.
Author Contributions
Conceptualization, S.L. and M.L.; methodology, S.L.; software, S.L. and Y.L.; validation, S.L., W.L. and T.Z.; formal analysis, W.L. and T.Z; investigation, S.L. and S.H.; resources, M.L. and L.X.; data curation, Y.L.; writing—original draft preparation, S.L.; writing—review and editing, M.L.; visualization, Y.L. and S.H.; supervision, M.L.; project administration, M.L.; funding acquisition, M.L. and L.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program, grant number 2022YFD2001200; the National Agricultural Major Scientific and Technological Project, grant number NK202216010401; the Henan Province Key Science and Technology Special Project, grant number 221100110800; and the China National Machinery Industry Corporation Youth Science and Technology Fund, grant number QNJJ-ZD-2022-03. We also thank the anonymous reviewers for providing critical comments and suggestions that improved the manuscript.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
We extend our gratitude to the aforementioned funding bodies for their generous support. Additionally, we thank the anonymous reviewers whose insightful comments and suggestions greatly enhanced the quality of this manuscript.
Conflicts of Interest
Author Mengnan Liu was employed by the YTO Group Corporation R&D Center. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Mocera, F.; Somà, A.; Martelli, S.; Martini, V. Trends and Future Perspective of Electrification in Agricultural Tractor-Implement Applications. Energies 2023, 16, 6601. [Google Scholar] [CrossRef]
- Ali, D.; de Castro, R.; Ehsani, R.; Vougioukas, S.; Wei, P. Unlocking the Potential of Electric and Hybrid Tractors via Sensitivity and Techno-Economic Analysis. Appl. Energy 2024, 377, 124545. [Google Scholar] [CrossRef]
- Gonzalez-de-Soto, M.; Emmi, L.; Benavides, C.; Garcia, I.; Gonzalez-de-Santos, P. Reducing Air Pollution with Hybrid-Powered Robotic Tractors for Precision Agriculture. Biosyst. Eng. 2016, 143, 79–94. [Google Scholar] [CrossRef]
- Pascuzzi, S.; Łyp-Wrońska, K.; Gdowska, K.; Paciolla, F. Sustainability Evaluation of Hybrid Agriculture-Tractor Powertrains. Sustainability 2024, 16, 1184. [Google Scholar] [CrossRef]
- Liu, W.; Yang, R.; Li, L.; Zhao, C.; Li, G. Energy and Environmental Evaluation and Comparison of a Diesel-Electric Hybrid Tractor, a Conventional Tractor, and a Hillside Mini-Tiller Using the Life Cycle Assessment Method. J. Cleaner Prod. 2024, 469, 143232. [Google Scholar] [CrossRef]
- Jeon, H.-H.; Baek, S.-Y.; Baek, S.-M.; Choi, J.-Y.; Kim, Y.-S.; Kim, W.-S.; Kim, Y.-J. Efficiency Analysis of Powertrain for Internal Combustion Engine and Hydrogen Fuel Cell Tractor According to Agricultural Operations. Sensors 2024, 24, 5494. [Google Scholar] [CrossRef] [PubMed]
- Oladosu, T.L.; Pasupuleti, J.; Kiong, T.S.; Koh, S.P.J.; Yusaf, T. Energy Management Strategies, Control Systems, and Artificial Intelligence-Based Algorithms Development for Hydrogen Fuel Cell-Powered Vehicles: A Review. Int. J. Hydrogen Energy 2024, 61, 1380–1404. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhou, Y.; Pan, B.; Wang, R.; Wang, L.; Yan, X. Energy Management Strategies for Fuel Cell Hybrid Electric Vehicles: Classification, Comparison, and Outlook. Energy Convers. Manag. 2022, 270, 116179. [Google Scholar] [CrossRef]
- Li, X.; Ye, T.; Meng, X.; He, D.; Li, L.; Song, K.; Jiang, J.; Sun, C. Advances in the Application of Sulfonated Poly(Ether Ether Ketone) (SPEEK) and Its Organic Composite Membranes for Proton Exchange Membrane Fuel Cells (PEMFCs). Polymers 2024, 16, 2840. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Li, Y.; Xu, L.; Wang, Y.; Zhao, J. General Modeling and Energy Management Optimization for the Fuel Cell Electric Tractor with Mechanical Shunt Type. Comput. Electron. Agric. 2023, 288, 129874. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M.; Yan, X.; Liu, M.; Xu, L. Power Allocation Strategy for Fuel Cell Distributed Drive Electric Tractor Based on Adaptive Multi-Resolution Analysis Theory. Energy 2023, 284, 129350. [Google Scholar] [CrossRef]
- Li, Q.; Chen, W.; Zhang, N.; Luo, Z.; Chen, B. Dynamic Response Characteristics of Proton Exchange Membrane Fuel Cell During Transient Loading: An Experiment Study. Int. J. Hydrogen Energy 2024, 92, 1–13. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, B.; Xiao, G.; Jin, D. Dynamic Response Characteristics and Water-Gas-Heat Synergistic Transport Mechanism of Proton Exchange Membrane Fuel Cell During Transient Loading. Energy 2024, 302, 131852. [Google Scholar] [CrossRef]
- Das, H.S.; Tan, C.W.; Yatim, A.H.M. Fuel Cell Hybrid Electric Vehicles: A Review on Power Conditioning Units and Topologies. Renew. Sustain. Energy Rev. 2017, 76, 268–291. [Google Scholar] [CrossRef]
- Teng, T.; Zhang, X.; Dong, H.; Xue, Q. A Comprehensive Review of Energy Management Optimization Strategies for Fuel Cell Passenger Vehicle. Int. J. Hydrogen Energy 2020, 45, 20293–20303. [Google Scholar] [CrossRef]
- Berriri, M.; Chevrel, P.; Lefebvre, D.; Yagoubi, M. The Influence of Soil Physical Properties on the Load Factor for Agricultural Tractors in Different Paddy Fields. Agriculture 2023, 13, 2073. [Google Scholar] [CrossRef]
- Yang, M.; Sun, X.; Deng, X.; Lu, Z.; Wang, T. Extrapolation of Tractor Traction Resistance Load Spectrum and Compilation of Loading Spectrum Based on Optimal Threshold Selection Using a Genetic Algorithm. Agriculture 2023, 13, 1133. [Google Scholar] [CrossRef]
- Ortopan, M.; Simonović, V.; Tasić, N.; Veg, E.; Zlatanović, I.; Gubeljak, N. Analyzing Site-Specific Tractor Draft Force in Different Passes During Plowing. Teh. Vjesn. 2024, 31, 228–232. [Google Scholar] [CrossRef]
- Mattetti, M.; Maraldi, M.; Lenzini, N.; Fiorati, S.; Sereni, E.; Molari, G. Outlining the Mission Profile of Agricultural Tractors through CAN-BUS Data Analytics. Comput. Electron. Agric. 2021, 184, 106078. [Google Scholar] [CrossRef]
- Hemmati, R.; Saboori, H. Emergence of Hybrid Energy Storage Systems in Renewable Energy and Transport Applications—A Review. Renew. Sustain. Energy Rev. 2016, 65, 11–23. [Google Scholar] [CrossRef]
- Shen, Y.; Xie, J.; He, T.; Yao, L.; Xiao, Y. CEEMD-Fuzzy Control Energy Management of Hybrid Energy Storage Systems in Electric Vehicles. IEEE Trans. Energy Convers. 2024, 39, 555–566. [Google Scholar] [CrossRef]
- Sun, Y.; Xia, C.; Han, J. Research on Energy Management of Fuel-Cell Electric Tractor Based on Quadratic Utility Function. J. Energy Eng. 2023, 149, 4022044. [Google Scholar] [CrossRef]
- Martini, V.; Mocera, F.; Somà, A. Numerical Investigation of a Fuel Cell-Powered Agricultural Tractor. Energies 2022, 15, 8818. [Google Scholar] [CrossRef]
- Yang, H.; Sun, Y.; Xia, C.; Zhang, H. Research on Energy Management Strategy of Fuel Cell Electric Tractor Based on Multi-Algorithm Fusion and Optimization. Energies 2022, 15, 6389. [Google Scholar] [CrossRef]
- Bao, S.; Sun, P.; Zhu, J.; Ji, Q.; Liu, J. Improved Multi-Dimensional Dynamic Programming Energy Management Strategy for a Vehicle Power-Split Hybrid Powertrain. Energy 2022, 256, 124682. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, J.; Song, J.; Ye, J. Research on Energy Management Strategy of Fuel Cell Vehicle Based on Multi-Dimensional Dynamic Programming. Energies 2022, 15, 5190. [Google Scholar] [CrossRef]
- Quan, R.; Guo, H.; Li, X.; Zhang, J.; Chang, Y. A Real-Time Energy Management Strategy for Fuel Cell Vehicle Based on Pontryagin’s Minimum Principle. iScience 2024, 27, 109473. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wei, H.; Xiao, G.; Zhang, Y. Real-Time Energy Management Strategy for a Plug-in Hybrid Electric Bus Considering the Battery Degradation. Energy Convers. Manag. 2022, 268, 116053. [Google Scholar] [CrossRef]
- Ding, N.; Prasad, K.; Lie, T.T. Design of a Hybrid Energy Management System Using Designed Rule-Based Control Strategy and Genetic Algorithm for the Series-Parallel Plug-in Hybrid Electric Vehicle. Int. J. Energy Res. 2021, 45, 1627–1644. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, Y.; Zhang, H.; Wang, D.; Chen, L. Equivalent Consumption Minimization Strategy Based on Global Optimization of Equivalent Factor for Hybrid Tractor. Sci. Rep. 2024, 14, 12911. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, L.; Zhao, C.; Xu, H.; Yan, X. Research on Energy Management Strategy for Hybrid Tractors Based on DP-MPC. Energies 2024, 17, 3924. [Google Scholar] [CrossRef]
- Varlese, C.; Ferrara, A.; Hametner, C.; Hofmann, P. Experimental Validation of a Predictive Energy Management Strategy for Agricultural Fuel Cell Electric Tractors. Int. J. Hydrogen Energy 2024, 77, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, M.; Liu, M.; Li, H.; Zhao, B.; Yan, X. Dual-Source Cooperative Optimized Energy Management Strategy for Fuel Cell Tractor Considering Drive Efficiency and Power Allocation. Agriculture 2024, 14, 1455. [Google Scholar] [CrossRef]
- Li, Y.; Liu, M.; Wang, Y.; Xu, L.; Lei, S. Energy Management Optimization and Validation of a Hydrogen Fuel Cell-Powered Agricultural Tractor Based on Hierarchical Dynamic Programming. IEEE Access 2024, 288, 21382–21401. [Google Scholar] [CrossRef]
- Martini, V.; Mocera, F.; Somà, A. Design and Experimental Validation of a Scaled Test Bench for the Emulation of a Hybrid Fuel Cell Powertrain for Agricultural Tractors. Appl. Sci. 2023, 13, 8582. [Google Scholar] [CrossRef]
- Lin, X.; Zhou, Q.; Tu, J.; Xu, X.; Xie, L. Self-Learning Markov Prediction Algorithm Based Aging-Oriented Gradient Drop Power Control Strategy for the Transient Modes of Fuel Cell Hybrid Electric Vehicles. Appl. Energy 2024, 376, 124198. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Ruan, J.; Liang, Z.; Liu, K. Rule and Optimization Combined Real-Time Energy Management Strategy for Minimizing Cost of Fuel Cell Hybrid Electric Vehicles. Energy 2023, 285, 129442. [Google Scholar] [CrossRef]
- Viji, D.; Dhanka, S.; M.B., B.; Thomas, M. Hybrid STO- IWGAN Method Based Energy Optimization in Fuel Cell Electric Vehicles. Energy Convers. Manag. 2024, 305, 118249. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous Reinforcement Learning of Energy Management with Deep Q Network for a Power Split Hybrid Electric Bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Ahmadi, P.; Raeesi, M.; Changizian, S.; Teimouri, A.; Khoshnevisan, A. Lifecycle Assessment of Diesel, Diesel-Electric and Hydrogen Fuel Cell Transit Buses with Fuel Cell Degradation and Battery Aging Using Machine Learning Techniques. Energy 2022, 259, 125003. [Google Scholar] [CrossRef]
- Ren, X.; Ye, J.; Xie, L.; Lin, X. Battery Longevity-Conscious Energy Management Predictive Control Strategy Optimized by Using Deep Reinforcement Learning Algorithm for a Fuel Cell Hybrid Electric Vehicle. Energy 2024, 286, 129344. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, S.; Luo, W.; Xu, S. Deep Reinforcement Learning with Deep-Q-Network Based Energy Management for Fuel Cell Hybrid Electric Truck. Energy 2024, 306, 132531. [Google Scholar] [CrossRef]
- Tiwari, V.K.; Pandey, K.P.; Pranav, P.K. A Review on Traction Prediction Equations. J. Terramech. 2010, 47, 191–199. [Google Scholar] [CrossRef]
- Roşca, R.; Cârlescu, P.; Ţenu, I.; Vlahidis, V.; Perşu, C. The Improvement of a Traction Model for Agricultural Tire–Soil Interaction. Agriculture 2022, 12, 2035. [Google Scholar] [CrossRef]
- Meng, X.; Sun, C.; Mei, J.; Tang, X.; Hasanien, H.M.; Jiang, J.; Fan, F.; Song, K. Fuel Cell Life Prediction Considering the Recovery Phenomenon of Reversible Voltage Loss. J. Power Sources 2024, 625, 235634. [Google Scholar] [CrossRef]
- Tang, X.; Shi, L.; Zhang, Y.; Li, B.; Xu, S.; Song, Z. Degradation Adaptive Energy Management Strategy for FCHEV Based on the Rule-DDPG Method: Tailored to the Current SOH of the Powertrain. IEEE Trans. Transp. Electrific. 2024, 1. early access. [Google Scholar] [CrossRef]
- Tang, X.; Shi, L.; Li, M.; Xu, S.; Sun, C. Health State Estimation and Long-Term Durability Prediction for Vehicular PEM Fuel Cell Stacks Under Dynamic Operational Conditions. IEEE Trans. Power Electron. 2024, 40, 4498–4509. [Google Scholar] [CrossRef]
- Zhang, R.; Li, X.; Sun, C.; Yang, S.; Tian, Y.; Tian, J. State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications. Batteries 2023, 9, 335. [Google Scholar] [CrossRef]
- Ahmadi, S.; Bathaee, S.M.T.; Hosseinpour, A.H. Improving Fuel Economy and Performance of a Fuel-Cell Hybrid Electric Vehicle (Fuel-Cell, Battery, and Ultra-Capacitor) Using Optimized Energy Management Strategy. Energy Convers. Manag. 2018, 160, 74–84. [Google Scholar] [CrossRef]
- Sundström, O.; Ambühl, D.; Guzzella, L. On Implementation of Dynamic Programming for Optimal Control Problems with Final State Constraints. Oil Gas Sci. Technol. Rev. Inst. Fr. Pét. 2010, 65, 91–102. [Google Scholar] [CrossRef]
- Elbert, P.; Ebbesen, S.; Guzzella, L. Implementation of Dynamic Programming for N-Dimensional Optimal Control Problems with Final State Constraints. IEEE Trans. Control Syst. Technol. 2013, 21, 924–931. [Google Scholar] [CrossRef]
- Liu, M.; Xu, L.; Zhou, Z. Design of a Load Torque Based Control Strategy for Improving Electric Tractor Motor Energy Conversion Efficiency. Math. Probl. Eng. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).