Lithium-Ion Battery Degradation Based on the CNN-Transformer Model
Abstract
1. Introduction
2. Materials and Methods
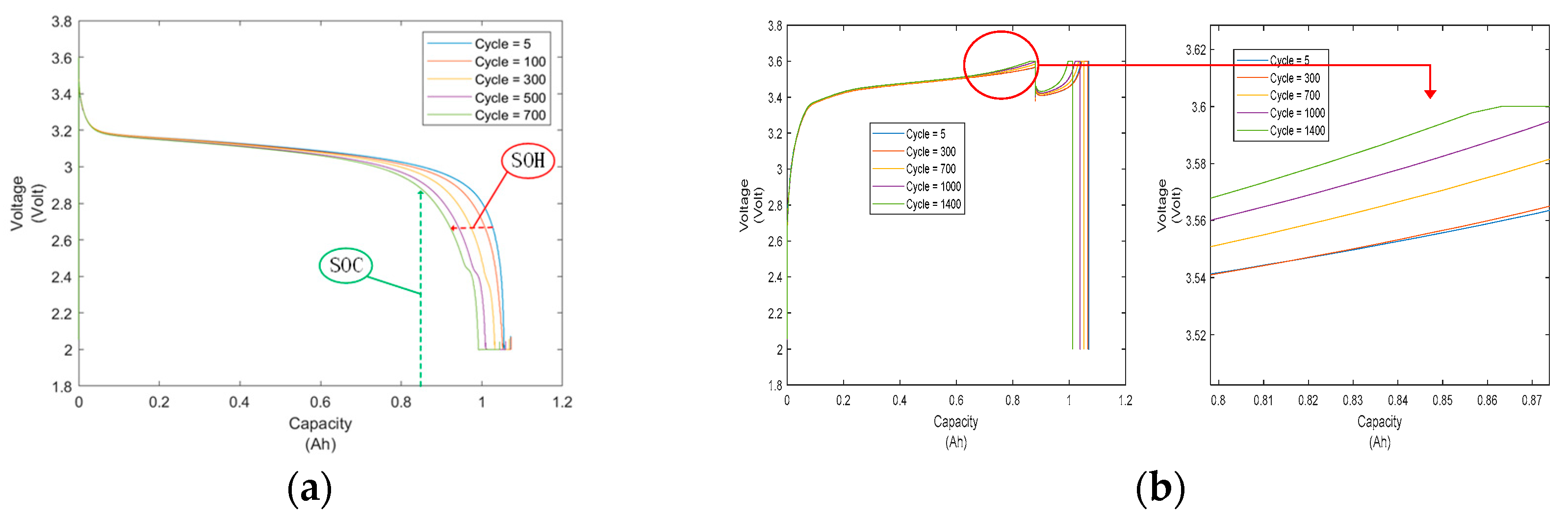
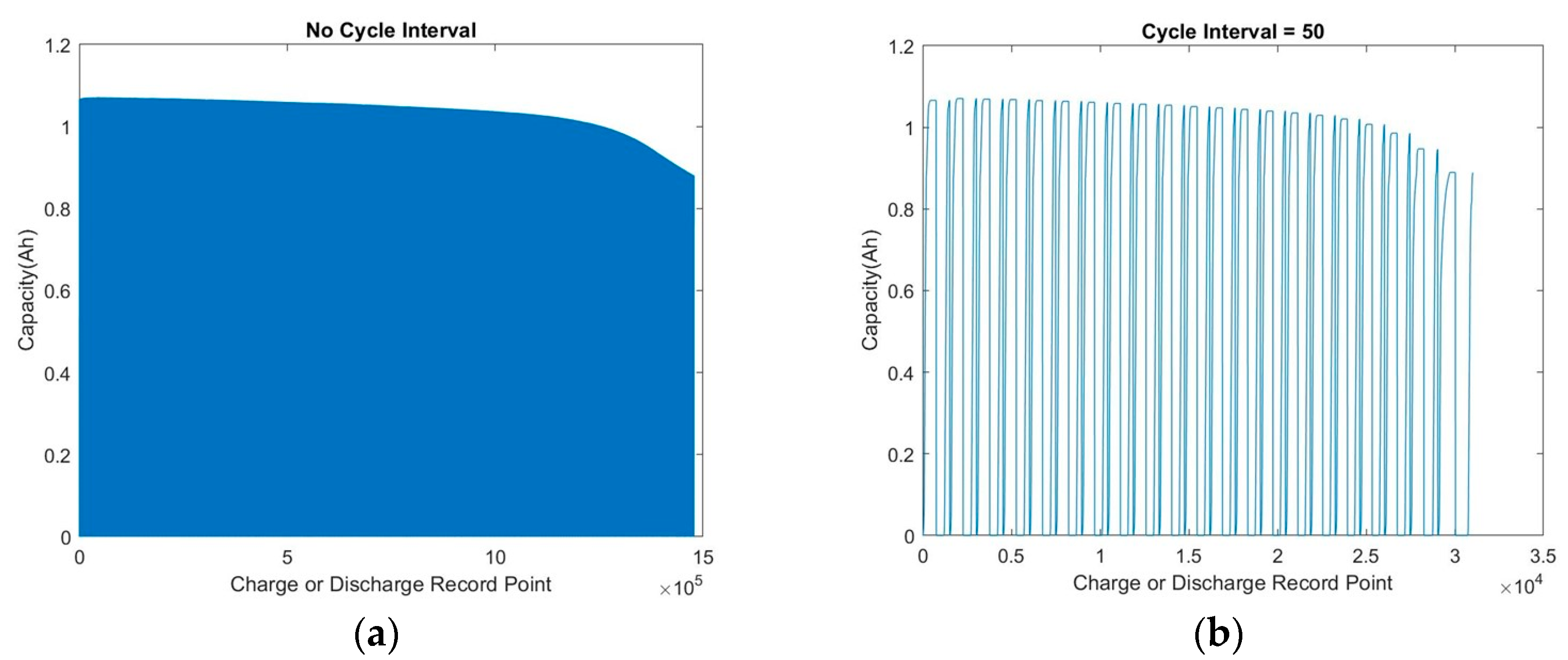
2.1. Battery Instruction
2.2. Hardware and Software
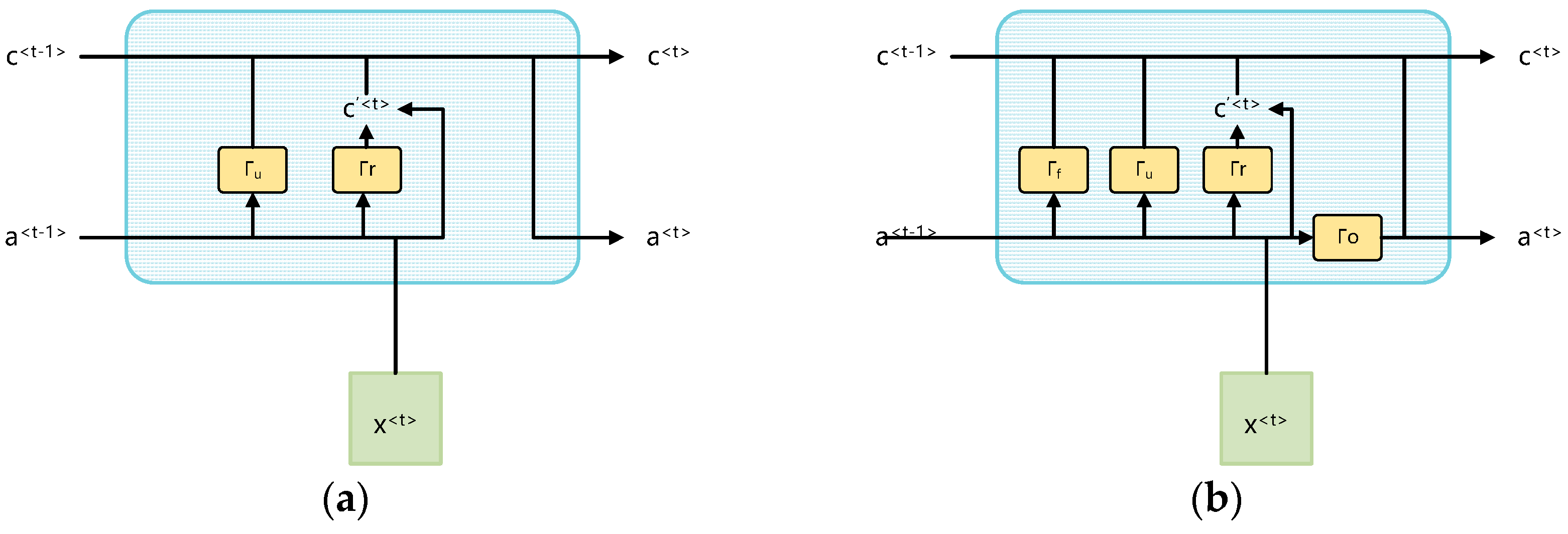
2.3. Methods
- Step 1:
- The preliminary data processing was conducted using Matlab software, including the deletion of erroneous battery data. Voltage and current data from individual batteries were extracted, and the battery capacity for each charge–discharge cycle was calculated in advance. Data used for model training and validation were packaged and stored in .mat files.
- Step 2:
- The battery data were imported from the .mat files into the PyCharm software for training and validation. The model parameters were set and the model training was proceeded with to obtain the final results.
- Step 3:
- The final results were then imported back into the Matlab software for further analysis and processing alongside other battery data.
3. Results
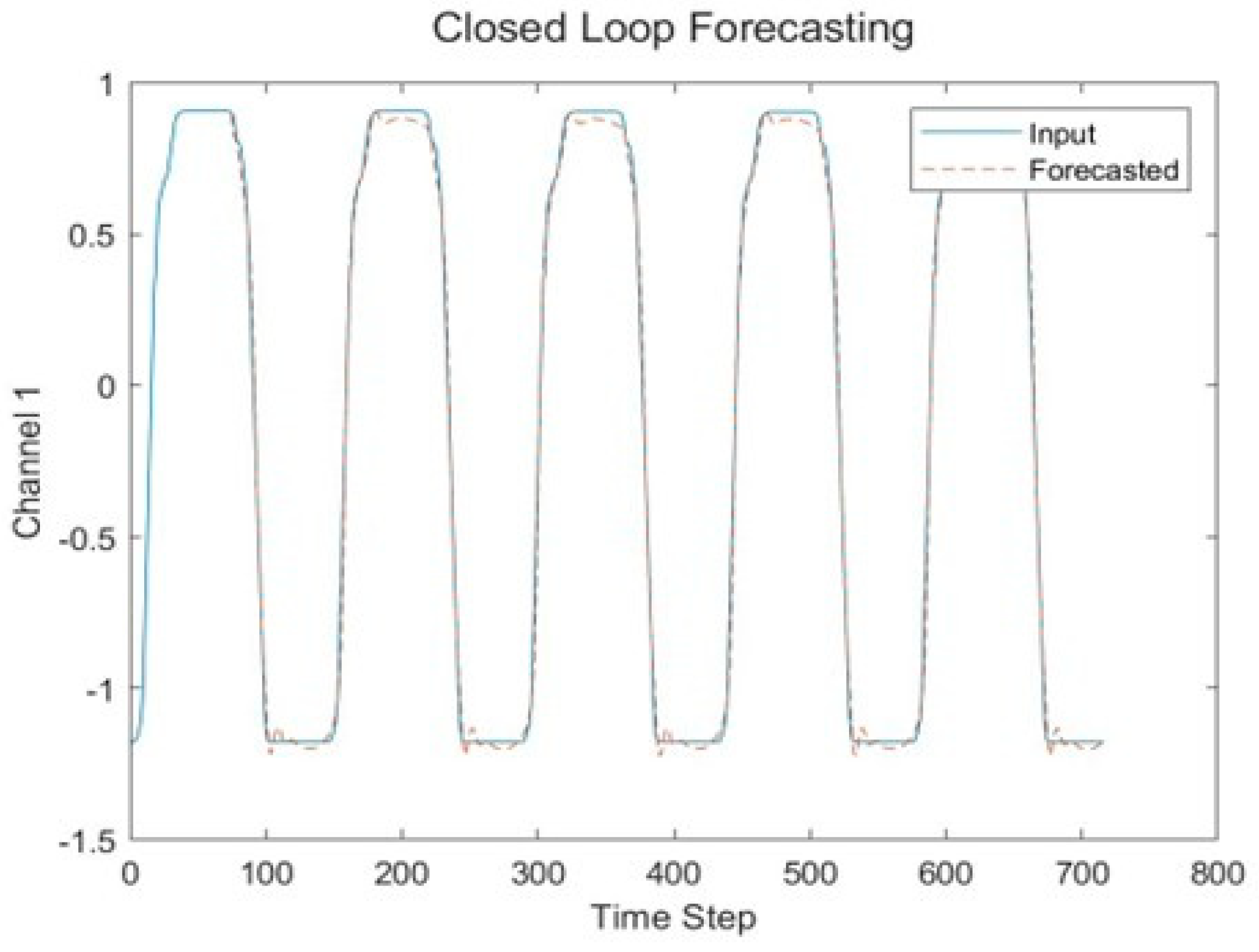
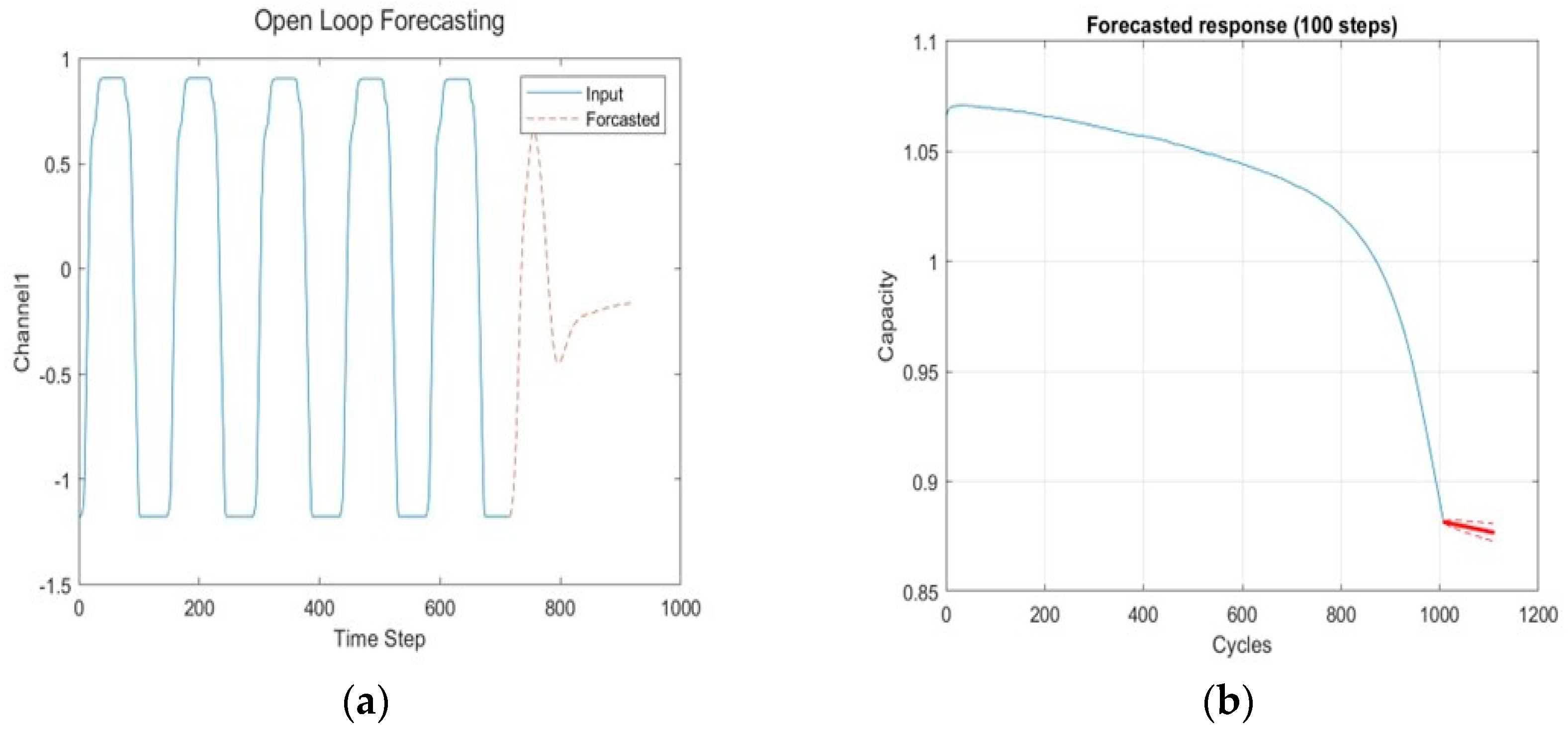
3.1. Training a Single-Battery Model and Using the Model for Prediction
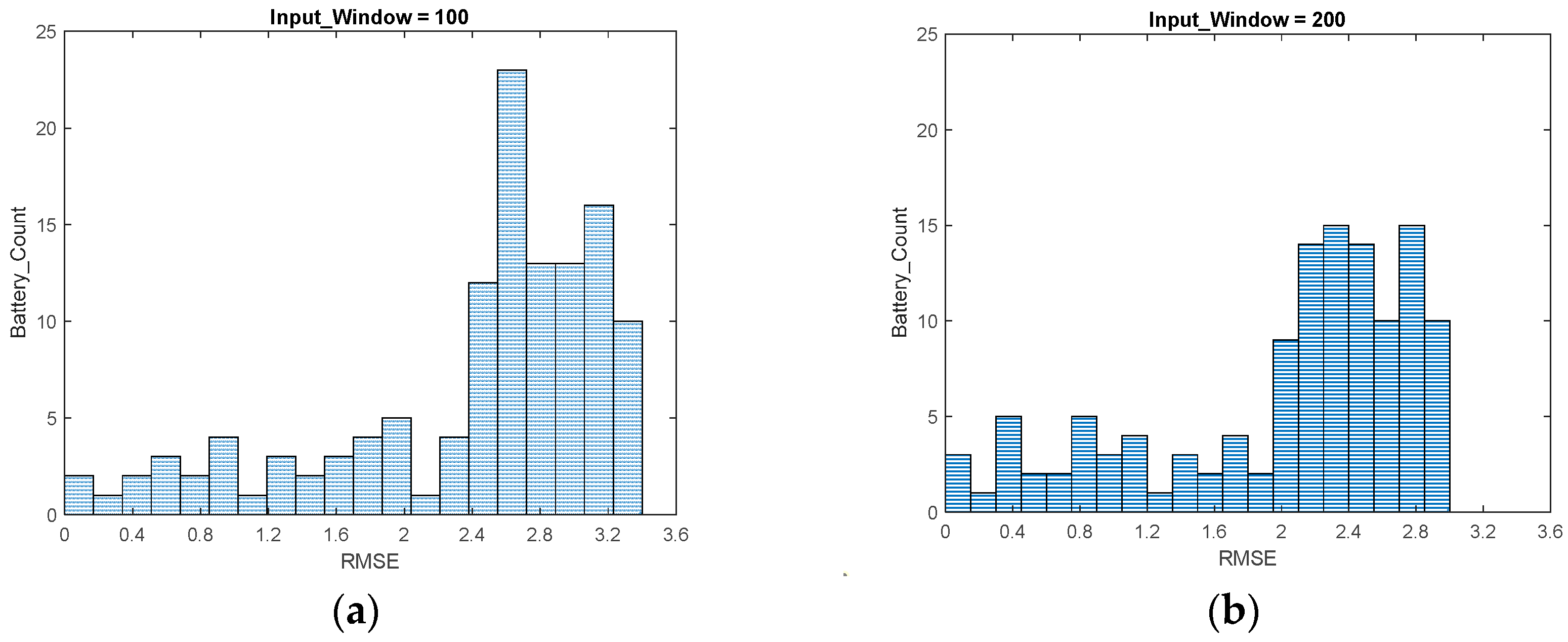
3.2. Statistical Results of Joint Model Training and Model Prediction for 124 Batteries
4. Experiments and Discussions
4.1. Get Enough Data
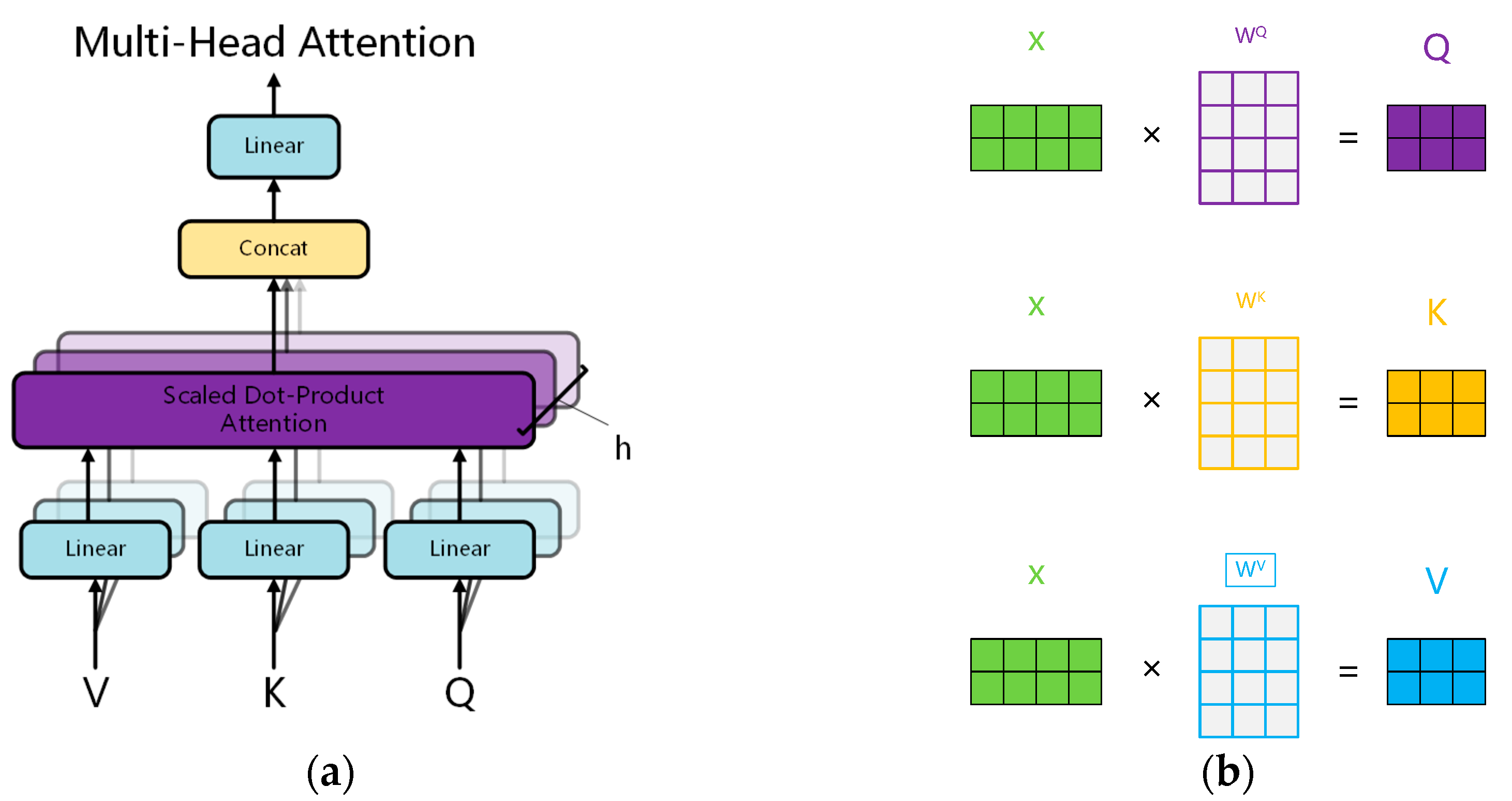
4.2. Transformer Model Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, W.; Xu, H.; Zhang, H.; Wei, F.; Zhang, T.; Wu, Y.; Huang, L.; Fu, J.; Jing, C.; Cheng, J.; et al. Designing ternary hydrated eutectic electrolyte capable of four-electron conversion for advanced Zn–I 2 full batteries. Energy Environ. Sci. 2023, 16, 4502–4510. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Martyushev, N.V.; Kukartsev, V.V.; Konyukhov, V.Y.; Oparina, T.A.; Sevryugina, N.S.; Gozbenko, V.E.; Kondratiev, V.V. Determination of the Performance Characteristics of a Traction Battery in an Electric Vehicle. World Electr. Veh. J. 2024, 15, 64. [Google Scholar] [CrossRef]
- Xiao, W.; Yoo, K.; Kim, J.H.; Xu, H. Breaking Barriers to High-Practical Li-S Batteries with Isotropic Binary Sulfiphilic Electrocatalyst: Creating a Virtuous Cycle for Favorable Polysulfides Redox Environments. Adv. Sci. 2023, 10, 2303916. [Google Scholar] [CrossRef] [PubMed]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Noura, N.; Boulon, L.; Jemeï, S. A review of battery state of health estimation methods: Hybrid electric vehicle challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Cui, Y.; Zuo, P.; Du, C.; Gao, Y.; Yang, J.; Cheng, X.; Yin, G. State of health diagnosis model for lithium ion batteries based on real-time impedance and open circuit voltage parameters identification method. Energy 2018, 144, 647–656. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Lu, D.D.C.; Wang, G.; He, T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Gao, Y.; Wang, F.; Mu, B.; Zhang, W. Accelerated fading recognition for lithium-ion batteries with Nickel-Cobalt-Manganese cathode using quantile regression method. Appl. Energy 2019, 256, 113841. [Google Scholar] [CrossRef]
- Hsu, C.W.; Xiong, R.; Chen, N.Y.; Li, J.; Tsou, N.T. Deep neural network battery life and voltage prediction by using data of one cycle only. Appl. Energy 2022, 306, 118134. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Battery health prediction under generalized conditions using a Gaussian process transition model. J. Energy Storage 2019, 1, 320–328. [Google Scholar] [CrossRef]
- Hosseininasab, S.; Lin, C.; Pischinger, S.; Stapelbroek, M.; Vagnoni, G. State-of-health estimation of lithium-ion batteries for electrified vehicles using a reduced-order electrochemical model. J. Energy Storage 2022, 52, 104684. [Google Scholar] [CrossRef]
- Berecibar, M.; Devriendt, F.; Dubarry, M.; Villarreal, I.; Omar, N.; Verbeke, W.; Van, M.J. Online state of health estimation on NMC cells based on predictive analytics. J. Power Sources 2016, 320, 239–250. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A data-driven approach with uncertainty quantification for predicting future capacities and remaining useful life of lithium-ion battery. IEEE Trans. Ind. Electron. 2020, 68, 3170–3180. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Zeng, A.; Chen, M.; Zhang, L.; Xu, Q. Are transformers effective for time series forecasting? In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 26 June 2023. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 18 May 2021. [Google Scholar]
- Ding, Y.; Jia, M.; Miao, Q.; Cao, Y. A novel time–frequency Transformer based on self–attention mechanism and its application in fault diagnosis of rolling bearings. Mech. Syst. Signal Process. 2022, 168, 108616. [Google Scholar] [CrossRef]
- Han, Z.; Zhao, J.; Leung, H.; Ma, K.F.; Wang, W. A review of deep learning models for time series prediction. IEEE Sensors J. 2019, 21, 7833–7848. [Google Scholar] [CrossRef]
- Lucu, M.; Mrtinez-Laserna, E.; Gandiaga, I.; Camblong, H. A critical review on self-adaptive Li-ion battery ageing models. J. Power Sources 2018, 401, 85–101. [Google Scholar] [CrossRef]
- Hosen, M.S.; Jaguemont, J.; Van Mierlo, J.; Berecibar, M. Battery lifetime prediction and performance assessment of different modeling approaches. iScience 2021, 24. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium-ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Ren, X.; Liu, S.; Yu, X.; Dong, X. A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 2021, 234, 121236. [Google Scholar] [CrossRef]
- Yang, X.G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent neural networks for time series forecasting: Current status and future directions. Int. J. Forecast 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Li, X.; Bi, F.; Yang, X.; Bi, X. An echo state network with improved topology for time series prediction. IEEE Sens. J. 2022, 22, 5869–5878. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Chen, G.; Liu, B.; He, Z.; Gao, F. A fast estimation algorithm for lithium-ion battery state of health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- Ullah, I.; Liu, K.; Yamamoto, T.; Al Mamlook, R.E.; Jamal, A. A comparative performance of machine learning algorithm to predict electric vehicles energy consumption: A path towards sustainability. Energy Environ. 2022, 33, 1583–1612. [Google Scholar] [CrossRef]
- Hong, J.; Lee, D.; Jeong, E.R.; Yi, Y. Towards the swift prediction of the remaining useful life of lithium-ion batteries with end-to-end deep learning. Appl. Energy 2020, 278, 115646. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Braatz, R.D. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Attia, P.; Deetjen, M.; Witmer, J. Accelerating battery development via early prediction of cell lifetime. Elastic 2018, 2, 2. [Google Scholar]


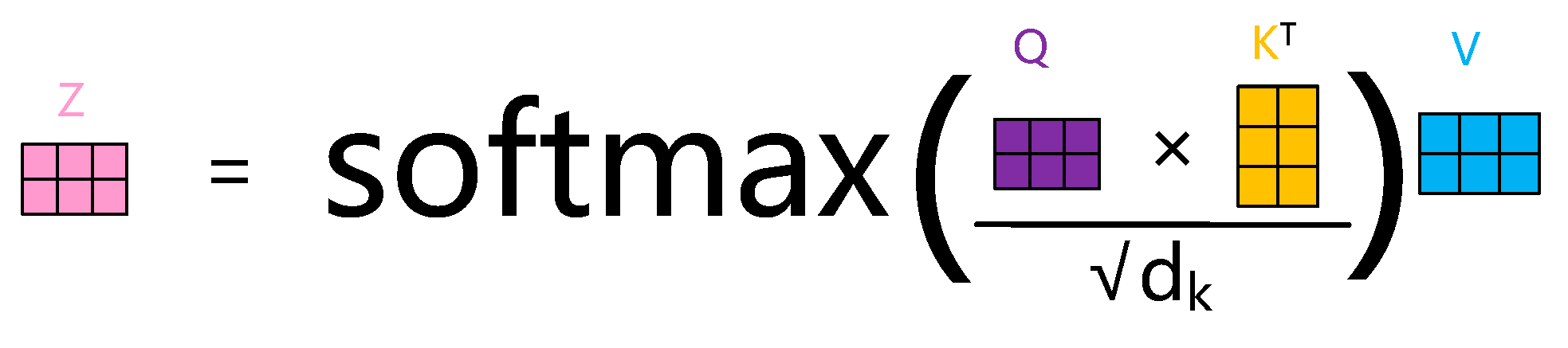



| Attribute | Description |
|---|---|
| Cell chemistry (cathode) | LiFePO4 |
| Cell chemistry (anode) | Graphite |
| Nominal capacity | 1.1 Ah |
| Nominal voltage | 3.3 V |
| Voltage window | 2.0V–3.6 V |
| Environmental temperature | 30 °C |
| Recommended fast-charge current | 3.6 C (4 A) |
| Cell manufacturer and type | A123 APR18650M1A |
| Hardware/Software | Model/Version |
|---|---|
| CPU | AMD 3900X (75 W) |
| GPU | NVIDIA rtx2060 (115 w) |
| Memory | 32G (2666 Hz) |
| Disk | SN750 (1 Tb) |
| OS | Windows 10 Enterprise LTSC |
| GPU Driver Version | 531.14 |
| CUDA Version | 12.1 |
| Python | 3.10 |
| Pytorch | 2.0.0 + cu118 |
| Matlab | 9.8.0.1323502 (R2020a) |
| Pycharm | 2021.1.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Wang, L.; Liao, N.; Xu, Z. Lithium-Ion Battery Degradation Based on the CNN-Transformer Model. Energies 2025, 18, 248. https://doi.org/10.3390/en18020248
Shi Y, Wang L, Liao N, Xu Z. Lithium-Ion Battery Degradation Based on the CNN-Transformer Model. Energies. 2025; 18(2):248. https://doi.org/10.3390/en18020248
Chicago/Turabian StyleShi, Yongsheng, Leicheng Wang, Na Liao, and Zequan Xu. 2025. "Lithium-Ion Battery Degradation Based on the CNN-Transformer Model" Energies 18, no. 2: 248. https://doi.org/10.3390/en18020248
APA StyleShi, Y., Wang, L., Liao, N., & Xu, Z. (2025). Lithium-Ion Battery Degradation Based on the CNN-Transformer Model. Energies, 18(2), 248. https://doi.org/10.3390/en18020248





