Safe Reinforcement Learning for Buildings: Minimizing Energy Use While Maximizing Occupant Comfort

Abstract

With buildings accounting for 40% of global energy consumption, heating, ventilation, and air conditioning (HVAC) systems represent the single largest opportunity for emissions reduction, consuming up to 60% of commercial building energy while maintaining occupant comfort. This critical balance between energy efficiency and human comfort has traditionally relied on rule-based and model predictive control strategies. Given the multi-objective nature and complexity of modern HVAC systems, these approaches fall short in satisfying both objectives. Recently, reinforcement learning (RL) has emerged as a method capable of learning optimal control policies directly from system interactions without requiring explicit models. However, standard RL approaches frequently violate comfort constraints during exploration, making them unsuitable for real-world deployment where occupant comfort cannot be compromised. This paper addresses two fundamental challenges in HVAC control: the difficulty of constrained optimization in RL and the challenge of defining appropriate comfort constraints across diverse conditions. We adopt a safe RL with a neural barrier certificate framework that (1) transforms the constrained HVAC problem into an unconstrained optimization and (2) constructs these certificates in a data-driven manner using neural networks, adapting to building-specific comfort patterns without manual threshold setting. This approach enables the agent to almost guarantee solutions that improve energy efficiency and ensure defined comfort limits. We validate our approach through seven experiments spanning residential and commercial buildings, from single-zone heat pump control to five-zone variable air volume (VAV) systems. Our safe RL framework achieves energy reduction compared to baseline operation while maintaining higher comfort compliance than unconstrained RL. The data-driven barrier construction discovers building-specific comfort patterns, enabling context-aware optimization impossible with fixed thresholds. While neural approximation prevents absolute safety guarantees, reducing catastrophic safety failures compared to unconstrained RL while maintaining adaptability positions this approach as a developmental bridge between RL theory and real-world building automation, though the considerable gap in both safety and energy performance relative to rule-based control indicates the method requires substantial improvement for practical deployment.

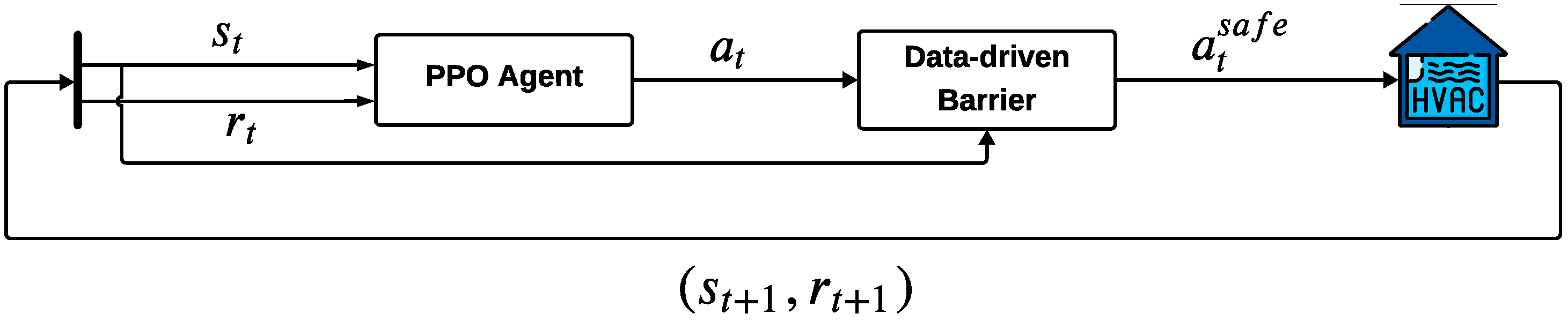
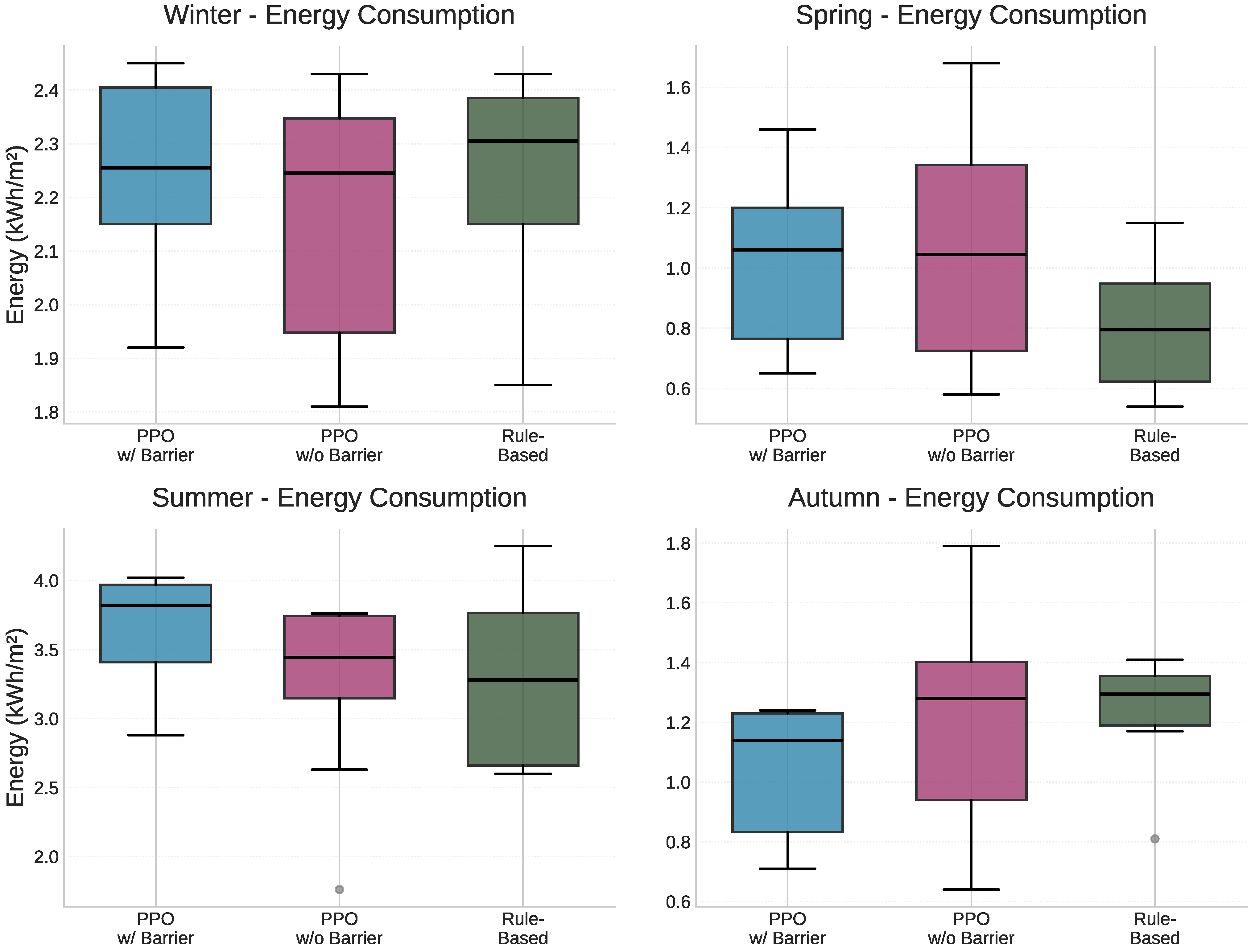1. Introduction

Heating, ventilation, and air conditioning (HVAC) controls typically rely on standardized comfort criteria like Fanger’s thermal comfort model, which forms the basis for key standards, including EN ISO 7730 [1] and ASHRAE 55 [2,3,4]. This model employs the Predicted Mean Vote (PMV) and Predicted Percentage of Dissatisfied (PPD) indices to quantify comfort boundaries. Human thermal comfort depends on physical activity, clothing insulation, air temperature, mean radiant temperature, and air velocity [5,6]. The PMV model, based on extensive field studies, quantifies how these variables impact thermal perception [3]. Significant variations exist based on age and gender [7,8,9], and psychological factors contribute to subjective differences in thermal perception [10,11]. The PPD extends the PMV by predicting the percentage of thermally dissatisfied occupants. Comfort limits vary seasonally, with the temperature range between 20 and 25 °C generally identified as acceptable across seasons [10], forming a subset of specifications outlined by Nikam et al. [12].

Maintaining thermal comfort corridors is essential for system acceptance, as user intervention in energy-optimized controls can undermine system performance. Comfort preferences fluctuate due to psychological factors and environmental conditions [10], necessitating adaptive solutions—particularly in shared spaces where consensus is needed. HVAC systems are crucial for ensuring thermal comfort but come with a significant energy demand. HVAC systems are particularly energy-intensive [13], accounting for 40% of energy use in non-residential buildings [14] and 75% in residential buildings [15]. Buildings account for 30–40% of global energy consumption and a third of CO₂ emissions [15,16,17,18]. Therefore, improving the energy efficiency of HVAC operation is essential to reducing overall energy use and emissions.

Climate change concerns have intensified research on balancing thermal comfort with energy efficiency [10], making the reduction in HVAC energy consumption while maintaining comfort a critical challenge for energy management systems. Learning systems offer the potential to continuously optimize both comfort and energy efficiency by incorporating evolving user preferences. Balancing comfort priorities, however, is critical: insufficient attention to comfort affects occupant health and productivity, while over-prioritization increases energy costs. This balance is particularly significant given current climate challenges and the fact that people spend approximately 90% of their time indoors [5,19]. An acceptable combination of environmental conditions according to PMV and PPD methodologies remains essential [13].

In recent years, reinforcement learning (RL) [20] has received considerable attention for data-driven learning of building control policies [21]. RL is a computational approach to learning from interaction, where an agent learns to make decisions by receiving rewards or penalties from its environment through trial and error [20]. Due to the complexity of modern building control policies in orchestrating competing objectives (cf. energy consumption, occupant comfort), RL offers a feasible approach to efficient data-driven learning of (near-)optimal control policies [22]. Moreover, due to the complexity of modern building environments, providing an accurate model of the building or the HVAC system is an intractable task that may result in inaccurate dynamics, which compromises controller efficiency and leads to sub-optimal control performance. RL can tackle this problem due to its model-free nature and provide a controller that can act (near-)optimally without having any knowledge of the system dynamics [22].

1.1. Research Problem and Contributions

The BOREALIS project [23] aims to develop RL solutions for creating greener, more energy-efficient buildings. While BOREALIS primarily focuses on optimizing artificial lighting control systems to reduce energy consumption while maintaining occupant comfort, the underlying challenge of balancing energy efficiency with user comfort extends across all building control systems. This paper addresses a parallel challenge in HVAC systems, where similar trade-offs between energy consumption and thermal comfort create complex optimization problems that can benefit from the RL methodologies being developed within the BOREALIS framework.

Many RL studies for HVAC controls incorporate both energy consumption and thermal comfort in their reward functions, creating complexity due to these conflicting objectives [21,24]. Balancing these goals with weighted reward functions raises questions about proper quantification and relative importance [25]. Our approach utilizes neural barrier certificates [26] to restrict the action space to options that are both optimal and respect thermal comfort constraints. This data-driven method eliminates the need for explicit thermal comfort modeling while transforming the constrained RL problem into an unconstrained formulation. By maintaining adherence to comfort boundaries, the agent becomes more efficient at optimizing the single-objective function of energy consumption. Moreover, this approach eliminates the requirement for explicit system dynamics in formulating the forward invariance property of barrier certificates [27], transforming it into a purely data-driven learning problem that attempts to achieve improved safety performance while indicating comparable energy efficiency without prior knowledge of system or constraint dynamics. This methodology, while applied here to HVAC systems, offers insights that can inform the broader BOREALIS objective of developing generalizable RL techniques for sustainable building control across multiple domains.

In addressing our research problem, we are guided by the following research questions:

RQ1

What is the applicability and effectiveness of safe reinforcement learning with neural barrier certificates in the building control domain?

RQ2

What is the impact of pre-training, random and non-random episode generation, and the length of training on a safe RL agent’s performance?

RQ3

To what extent does safe RL control with neural barrier certificates improve upon or match the performance of baseline controllers?

We thereby deliver the following contributions:

C1

Demonstrates the applicability of safe RL with neural barrier certificates in the building control domain, validating its effectiveness for handling thermal comfort constraints while optimizing energy consumption.

C2

Provides empirical evidence of the method’s performance across multiple BOPTEST test cases, different control levels (air handling unit (AHU) duct pressure and supply temperature), and varying episode lengths and learning intervals.

C3

Demonstrates that pre-trained barrier functions improve learning efficiency and performance compared to non-pretrained approaches in HVAC control applications.

C4

Shows that safe RL with neural barrier certificates achieves energy and safety performance comparable to a Proximal Policy Optimization (PPO) agent and a Rule-based Controller (RBC), establishing its viability as an alternative control approach for buildings.

1.2. Research Methodology

This study follows an experimental research methodology, employing controlled experiments to establish cause-and-effect relationships and validate theoretical concepts with empirical evidence [28]. We implement a safe RL controller with neural barrier certificates for HVAC systems and systematically evaluate its performance across multiple BOPTEST [29] test cases with varying control configurations. The investigation encompasses different episode lengths, learning intervals, and the impact of pre-training barrier functions on controller performance. The results are benchmarked against established baselines, including a PPO agent and an RBC controller. Based on the identified research gap that we will discuss in Section 2, we formulate the following hypothesis:

Hypothesis (H1).

Safe RL with neural barrier certificates achieves energy efficiency comparable to or better than classical controllers while maintaining thermal comfort constraints through learned barrier certificates.

This is investigated against the null hypothesis:

Hypothesis (H0).

Safe RL with neural barrier certificates does not achieve competitive energy efficiency compared to classical controllers and/or fails to maintain thermal comfort constraints effectively.

Our experimental design allows us to test whether the neural barrier certificate approach can successfully balance energy optimization with constraint satisfaction in real building control scenarios, while also examining the practical benefits of pre-training for deployment efficiency.

Article Organization: Following the introduction, Section 2 reviews existing literature on RL-based building control and safe reinforcement learning approaches. Section 3 provides foundational concepts in reinforcement learning and its application to building control systems. Section 4 presents the neural barrier certificate framework and formulates its application to constrained HVAC control problems. Section 5 details the experimental design, including BOPTEST test cases, control configurations, and evaluation metrics, then presents results comparing the safe RL controller against baseline controllers while analyzing the impact of pre-training on performance. Finally, Section 6 summarizes the contributions and suggests future research directions.

2. Related Work

Model-based approaches have been extensively explored for HVAC control, particularly through proportional–integral–derivative (PID) controllers [30,31,32,33] to manage building energy and air quality. Optimal control formulations for HVAC systems have also been investigated [34,35,36], aiming to lower energy costs and enhance occupant comfort. In addition, fuzzy control strategies have been proposed [37,38] to handle uncertainties arising from external and internal variations. Model predictive control (MPC) further advances these efforts by leveraging predictive models to balance energy consumption and comfort [39,40,41], where adaptive frameworks and grey-box models are employed. Iterative learning control (ILC) has likewise been used to refine MPC output [42].

Model-based approaches for HVAC control face significant challenges due to the complexity of underlying building dynamics, varying occupant behavior, and external environmental factors, often necessitating simplified models that fail to capture nuanced interactions. They also struggle to accommodate changing building characteristics and occupancy patterns while remaining highly sensitive to uncertainties such as weather, occupancy estimates, and internal heat gains [43]. RL addresses these limitations by learning optimal strategies through direct interaction with the environment, requiring no explicit model and allowing continuous adaptation to evolving conditions, thereby overcoming the rigidity of traditional model-based approaches [43].

Various RL methods have been leveraged to optimize HVAC energy usage and maintain occupant comfort [24]. Deep deterministic policy gradients (DDPG) have been used to manage HVAC control [44,45], relying on deep neural networks to capture occupant comfort and energy interactions. Azuatalam [46] proposed a PPO controller that integrates thermal comfort as a penalty to balance energy efficiency and demand response. Asynchronous advantage actor–critic (A3C) was employed to reduce energy consumption while maintaining multi-zone thermal comfort [47], with comfort penalties embedded in the reward. Deep Q-networks (DQN) [48,49] have accounted for occupant-driven factors (e.g., behavior and indoor air quality) while minimizing energy use. Clustering-based RL was introduced [50] to segment data for more robust training. Q-learning under model uncertainty, aided by Bayesian-convolutional neural networks (BCNNs), was investigated by Lork et al. [51] to refine set-point decisions while upholding comfort requirements. The combination of MPC and RL has also been explored [52]. Nguyen et al. [53] used phasic policy gradient (PPG), which is an actor-critic method. The reward function was designed such that the agent is penalized for both high energy consumption and for violating the occupant comfort temperature range. They used a conditional reward function, which only considers comfort penalties during working hours, allowing the agent to prioritize energy savings at other times. One of the main challenges in deep reinforcement learning (DRL) applications is real-world deployment. To directly address this, Solinas et al. [54] utilized Imitation Learning to solve the cold-start problem. This enabled the agent to be deployed directly online and begin improving energy efficiency from day one, avoiding the high costs of white-box models and the poor initial performance of standard online learning. To enable proactive and cost-aware HVAC control, Liu et al. [55] proposed a multi-step predictive DRL (MSP-DRL) framework. Their primary contribution is the integration of a highly accurate weather prediction model, named GC-LSTM, directly into the decision-making process of a DDPG agent. The GC-LSTM model was specifically designed with a Generalized Correntropy loss function to robustly handle the non-Gaussian nature of real-world temperature data.

Kadamala et al. [56] investigated the effectiveness of transfer learning for HVAC control. Their primary contribution is a systematic evaluation of pre-training and fine-tuning methodology. They first trained a foundation model on a source building and then transferred its core network weights to new agents, which were fine-tuned for different target environments. To enhance the proactivity of DRL-based HVAC controllers, Shin et al. [57] proposed a hybrid framework named WDQN-temPER that integrates weather forecasting directly into the learning process. Their primary contribution is twofold: first, they use a gated recurrent unit (GRU) to predict future outdoor temperatures, which is then fed as a state variable to a DQN agent, enabling it to make forward-looking decisions. Second, they introduce temPER, a novel prioritized experience replay technique that gives higher learning priority to transitions where a large change in outdoor temperature occurred. Ding et al. [58] proposed CLUE, a model-based reinforcement learning framework. Their approach utilizes a Gaussian process (GP) to model building dynamics, which explicitly quantifies predictive uncertainty. To mitigate the GP’s high data requirements, they employ a meta-kernel learning technique that pre-tunes the model on data from other buildings. This uncertainty estimate is then used by the controller to discard unsafe action trajectories and activate a rule-based fallback mechanism to ensure robust performance under high model uncertainty. To enable personalized and safely deployable HVAC control, Chen et al. [59] proposed a human-in-the-loop framework that integrates meta-learning with model-based offline reinforcement learning. Their method first employs meta-learning to train a thermal preference model on a diverse dataset of human feedback, allowing for rapid adaptation to a new occupant’s subjective comfort with only a few interactions. Concurrently, a building dynamics model is learned from a static offline dataset using an ensemble of neural networks, where the disagreement among models serves as an uncertainty penalty in the reward function. The key contribution is a practical control strategy that avoids risky online exploration by constraining the agent to known, safe operating regions, while still delivering a highly personalized thermal environment. This dual approach effectively decouples the challenges of fast user adaptation and safe policy learning, presenting a viable pathway for deploying user-centric, intelligent HVAC systems.

Cui et al. [60] proposed a novel hybrid framework that synergistically combines reinforcement learning with active disturbance rejection control (ADRC). Their core contribution is the decomposition of the control problem into a main-auxiliary structure. A twin delayed deep deterministic policy gradient (TD3) agent is designated as the main controller, responsible for optimizing thermal comfort by managing zone-specific supply airflows. Simultaneously, an ADRC-based auxiliary controller manages indoor air quality by regulating the fresh air ratio, while actively estimating and compensating for system-wide disturbances. Gehbauer et al. [61] proposed a grid-interactive RL controller that jointly actuates electrochromic (EC) facades and HVAC using a standardized functional mock-up interface (FMI) based co-simulation toolchain. Their distributed distributional deterministic policy gradient agent (D4PG) consumes 4 h forecasts (weather, occupancy, and TOU prices) to minimize combined energy and demand costs while respecting comfort, and is pre-trained across multiple climate zones before virtual deployment. Benchmarking on simple and high-fidelity Modelica emulators against MPC and heuristic baselines showed RL achieving lower costs than heuristic control and competitive demand reduction, while the open-source functional mock-up interface—machine learning center (FMI-MLC) framework enables rapid interfacing with third-party simulators for practical off-site training. Xue et al. [62] proposed a hybrid multi-agent DRL controller, a genetic algorithm multi-agent DDPG (GA–MADDPG) for multi-zone HVAC. Each zone agent sets its temperature set-point; the reward combines an energy term with zone-specific PMV comfort terms. A key idea is allocating the shared cooling energy to zones via weights and using a genetic algorithm (GA) to optimize these weights to maximize the sum of agents’ average rewards. Li et al. [63] developed a model-free control strategy using reinforcement learning to optimize temperature set-points. Their approach employs the PPO algorithm to learn an adaptive policy that dynamically adjusts thermostat settings based on time-of-use (TOU) electricity prices, occupant comfort, and environmental conditions. The primary contribution is the integration of a policy-based RL agent with an active thermal energy storage (ATES) system, which was validated on a high-fidelity TRNSYS-MATLAB co-simulation platform. Yu et al. [64] introduced online comfort-constrained control via feature transfer (OCFT), a deployment-time safety wrapper for policy transfer in HVAC. OCFT learns expressive nonlinear feature maps from source buildings and, on the target, adapts a lightweight parametric surrogate via online set-membership updates combined with nested convex body chasing. At each control step, a robust action filter minimally perturbs the transferred policy’s proposal so the model-predicted next-step temperature remains within tightened comfort bounds, with slack variables to handle temporary infeasibility due to disturbances and actuator limits. The method further provides finite-time safety guarantees, including an upper bound on the number of comfort violations under bounded worst-case disturbances and, under mild stochastic assumptions, a finite stopping time beyond which all constraints are satisfied. While OCFT provides strong safety assurances, it assumes the availability of historical source-building data (or a surrogate model trained on such data); if these data are unavailable or of poor quality, applicability is reduced, and performance—particularly during initial deployment—may deteriorate. Although these methods successfully optimize energy efficiency and maintain occupant comfort, they require complex reward functions that encode and weigh multiple objectives. Crafting such functions is non-trivial, as the relative importance of energy versus comfort can be subjective and difficult to quantify, often leading to a tedious tuning process [42]. Controllers based on ADRC [60] or meta-learning [59] effectively manage disturbances and personalization but still frame the problem as a multi-objective optimization. Similarly, approaches using PPO for demand response [63] embed comfort as a weighted penalty. This reliance on weighting and penalties means that comfort is treated as a “soft” constraint, which can be violated if the agent determines that doing so maximizes its cumulative reward. While safety is a growing concern, many solutions rely on probabilistic models or offline datasets to indirectly ensure safe operation [58,59,64]. In contrast, our approach requires no historical data or pretraining—neither for initializing the RL agent nor for learning safety constraints—enabling fully online deployment from scratch, without building-specific logs. To streamline the learning process and provide stronger safety guarantees, we adopt a safe RL approach in which the agent is only tasked with maximizing energy efficiency, while occupant comfort constraints are enforced separately as “hard” constraints. Additionally, this data-driven approach enables neural networks to learn constraints as barrier certificates without requiring explicit mathematical models. We thus remove the need to encode or weight comfort in the reward function, ensuring optimal energy usage without compromising occupant comfort.

Table 1. Comparison of safe RL and reward weighting approaches for HVAC control.

Category	Approach	Pros	Cons
Safe RL	CLUE [58]	- Explicit uncertainty quantification via GP - Rule-based fallback for safety - Meta-kernel learning for efficiency - Discards unsafe trajectories	- High data requirements for GP - Computational complexity - Requires data from other buildings
	Human-in-the-loop  [59]	- Fast adaptation to user preferences - Avoids risky online exploration - Personalized thermal comfort - Constrains to safe operating regions	- Requires diverse offline dataset - Complex ensemble modeling - Limited to previously seen regions
	OCFT [64]	- Deployment-time safety wrapper - Finite-time safety guarantees - Minimal-adjustment action filter - Online set-membership adaptation	- Needs historical source-building data
	This paper (Hard Constraints)	- No reward tuning needed - Attempts to enforce hard constraints - Simplified learning process - Data-driven barrier certificates	- May sacrifice some energy efficiency - Relying on neural networks’ prediction of safety
Reward Weighting	DDPG [44,45]	- Deep networks capture complex interactions - Continuous action space - Well-established algorithm	- Requires careful reward weighting - Comfort as soft constraint - Sample inefficiency
	PPO [46,63]	- Stable training - Integrates demand response - Works with ATES systems	- Comfort as weighted penalty - Subjective weight selection - Potential comfort violations
	A3C [47]	- Multi-zone thermal comfort - Parallel training efficiency - Asynchronous updates	- Complex reward engineering - Comfort penalties in reward - Difficult multi-objective balance
	DQN [48,49]	- Accounts for occupant behavior - Considers air quality - Discrete action space	- Multiple factors to weigh - Soft comfort constraints - Action discretization limitations
	Q-learning with BCNNs [51]	- Handles model uncertainty - Bayesian approach - Refines set-point decisions	- Comfort as soft requirement - Computational complexity - Requires reward weighting
	PPG [53]	- Conditional reward function - Context-aware (working hours) - Dynamic prioritization	- Still requires weight tuning - Comfort violations possible - Complex reward structure
	TD3-ADRC [60]	- Separation of concerns - Active disturbance rejection - Specialized controllers	- Multi-objective optimization - Complex architecture - Controller coordination overhead
	EC facade + HVAC (D4PG) co-simulation [61]	- Joint actuation of electrochromic facades and HVAC - Uses short-term forecasts (weather, occupancy, TOU) - FMI-MLC co-simulation enables off-site training - Competitive cost/demand reduction vs. baselines	- Comfort as soft, weighted penalty - Pretraining and hyperparameter tuning overhead
	GA–MADDPG (multi-agent) zone-energy allocation [62]	- Optimizes per-zone energy weights (${\alpha }_i$) via GA - Multi-agent setpoint control with inter-zone coupling - TRNSYS–MATLAB co-simulation; thermal comfort (PMV) reward - Lower energy than MPC and plain MADDPG (meets comfort)	- Comfort as soft, weighted penalty - GA outer loop

summarizes and contrasts various safe RL and reward weighting approaches, highlighting their distinct advantages and disadvantages and thereby motivating our adopted safe RL method.

3. Background and Preliminaries

A reinforcement learning problem consists of an agent and an environment in which the agent aims to learn an optimal policy by interacting with the environment. The agent takes an action $a_t\in \mathcal{A}$, where $\mathcal{A}$ is the set of all possible actions, called the action space, based on the current state $s_t\in \mathcal{S}$, where $\mathcal{S}$ is the set of all states (observations), called the state space, and the current policy, which is the mapping from current state to an action $\pi \left(a_t\right|s_t)$. After taking the action $a_t$, the agent receives the reward $r_t$ and the next state $s_{t+1}$ according to the transition probability $P\left(s_{t+1}\right|s_t,a_t)$ from this interaction with the environment. The reward function is the feedback from the environment on how good or bad the action taken by the agent was.

For a given trajectory $\tau =(s_0,a_0,\dots )$, the discounted return is defined as

$$R\left(\tau \right)=\sum _{t=0}^{\infty }{\gamma }^t{r}_t,$$

(1)

where $\gamma \in [0,1)$ is the discount factor that determines the importance of future rewards [20]. Thus, the central RL problem can be expressed as follows:

$${\pi }^{\ast }=arg\underset{\pi }{max}J\left(\pi \right)$$

(2)

where ${\pi }^{\ast }$ is the optimal policy and

$$J\left(\pi \right)={\mathbb{E}}_{\tau \sim \pi }\left[R\left(\tau \right)\right]$$

(3)

is the expected return. Value functions measure the expected cumulative discounted reward of taking an action in a given state and acting according to a specific policy after that. There are two types of value functions: (i) the on-policy value function determines the expected return starting from state s and acts according to a policy $\pi$, while (ii) the on-policy action-value function gives the expected return of starting from state s, takes an action a, and acts according to the policy $\pi$.

$$\begin{array}{c}\hfill \begin{array}{c}{V}^{\pi }\left(s\right)={\mathbb{E}}_{\tau \sim \pi }\left[R\left(\tau \right)\right|s_0=s]\mathrm{On-policy\; value\; function}\hfill \\ Q^{\pi }|(s,a)={\mathbb{E}}_{\tau \sim \pi }\left[R\left(\tau \right)\right|s_0=s,a_0=a]\mathrm{On-policy\; action-value\; function}\hfill \end{array}\end{array}$$

(4)

The value function and action-value function follow the Bellman principle: the value of a state (or state–action pair) equals the immediate expected reward plus the discounted value of subsequent states [65].

The advantage function $A(s,a)$ measures how much better a specific action a is compared to an average action that would be taken in state s under the current policy $\pi$:

$$A^{\pi }(s,a)=Q^{\pi }(s,a)-V^{\pi }\left(s\right).$$

(5)

A positive advantage value indicates that an action a is better than the policy’s expected performance from state s. In practice, the true advantage function $A^{\pi }(s,a)$ is unknown because it depends on the true value functions $Q^{\pi }$ and $V^{\pi }$, which are typically intractable to compute exactly. Moreover, in policy gradient methods, advantage estimates are crucial for reducing variance while maintaining unbiased gradient estimates. Therefore, we must estimate advantages from sampled trajectories using function approximation and empirical returns. Consider the finite-horizon return from time t:

$${\widehat{R}}_t=\sum _{k=0}^{T-t-1}{\gamma }^k{r}_{t+k},$$

(6)

where T is the length of the trajectory.

Monte-Carlo (MC) Estimation: The MC advantage estimator uses the empirical return:

$${\widehat{A}}_t^{MC}={\widehat{R}}_t-V\left(s_t\right),$$

(7)

This estimator is unbiased but suffers from high variance due to the stochasticity of the entire trajectory.

Temporal Difference TD(0) Estimation: The one-step TD advantage estimator uses bootstrapping:

$${\widehat{A}}_t^{TD\left(0\right)}=r_t+\gamma V\left(s_{t+1}\right)-V\left(s_t\right).$$

(8)

This estimator has lower variance but introduces bias through the value function approximation.

Generalized Advantage Estimation (GAE): GAE [66] provides a principled trade-off between bias and variance:

$$\begin{array}{c}\hfill \begin{array}{c}\widehat{A}={\displaystyle \sum _{l=0}^{\infty }}{\left(\gamma \lambda \right)}^l{\delta }_{t+l}\lambda \in [0,1]\hfill \\ {\delta }_t=r_t+\gamma V\left(s_{t+1}\right)-V\left(s_t\right)\hfill \end{array}\end{array}$$

(9)

where ${\delta }_t=r_t+\gamma V\left(s_{t+1}\right)-V\left(s_t\right)$ is the TD residual and $\lambda \in [0,1]$ controls the bias-variance trade-off. The geometric weighting ${\left(\gamma \lambda \right)}^l$ exponentially decays the contribution of future TD residuals. When $\lambda =0$, GAE reduces to TD(0); when $\lambda =1$, it becomes equivalent to the MC estimator. GAE’s key advantage lies in its ability to smoothly interpolate between these extremes, allowing one to balance bias and variance.

Proximal Policy Optimization

Policy gradient methods work by directly optimizing the policy parameters $\theta$ in the direction that maximizes the expected cumulative reward, $J\left(\theta \right)$. The gradient is estimated as:

$${\nabla }_{\theta }J\left({\pi }_{\theta }\right)=\mathbb{E}\left[{\nabla }_{\theta }log{\pi }_{\theta }\left(a_t\right|s_t){\widehat{A}}^{{\pi }_{\theta }}(s_t,a_t)\right]$$

(10)

where ${\pi }_{\theta }\left(a_t\right|s_t)$ is the policy and ${\widehat{A}}_t$ is an estimate of the advantage function. A major issue with this approach is that a single update step can be excessively large. A large gradient update can drastically change the policy, leading it to a “bad” region of the policy space from which it may never recover. This makes the training process highly unstable. PPO introduces a first-order method to constrain the policy update. Instead of a hard constraint, PPO modifies the objective function to penalize large changes to the policy. The ratio (Equation (11)) indicates how much more likely the new action $a_t$ is under the new policy ${\pi }_{\theta }\left(a_t\right|s_t)$ compared to the old one ${\pi }_{{\theta }_{old}}\left(a_t\right|s_t)$. PPO ensures that the ratio stays close to 1, preventing the new policy from deviating too far from the old one. PPO uses clipping to discourage the policy from changing aggressively.

$$\rho \left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t)}}$$

(11)

The objective function of the PPO [67] is as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}L\left(\theta \right)={\displaystyle \frac{1}{\left|D\right|}}{\displaystyle \sum _{s,a\in D}}min\hfill & (\rho \left(\theta \right)A^{{\pi }_{{\theta }_k}}(s,a),\hfill \\ \hfill & \mathrm{clip}\left(\rho \left(\theta \right),1-ϵ,1+ϵ\right)A^{{\pi }_{{\theta }_k}}(s,a)),\hfill \end{array}\end{array}$$

(12)

where $ϵ$ determines the size of the trust region. If the advantage is positive, indicating a better-than-average action, the objective is capped to prevent the agent from making an overly large and potentially destabilizing policy change. Conversely, if the advantage is negative for a worse-than-average action, the objective is also clipped to stop the agent from over-reacting and making that action extremely unlikely, which could harm future exploration. By always taking the minimum of the unclipped and clipped objectives, the algorithm guarantees that each policy update remains within a trusted “proximal” region around the previous policy, promoting a smooth and reliable learning process.

4. Methodology and Problem Formulation

In the following, we detail the underlying methodology of our proposal, viz., safe RL by capitalizing on learned neural barrier certificates to eventually learn control policies that ensure occupant comfort.

4.1. Safe Reinforcement Learning for HVAC Control

The HVAC control problem is modeled as a Markov decision process (MDP) $M=(\mathcal{S},\mathcal{A},P,R)$ solved through RL. In this framework, the environment provides states $s_t\in \mathcal{S}$ to the agent, consisting of continuous HVAC system variables including operative zone temperature and occupancy $s_t={[T_t,O_t]}^{\top }$, where O is either 0 or 1 (no presence or presence of people, respectively) and T is a real number. The reward function serves as feedback from the environment, evaluating the quality of the agent’s actions. The reward function is defined as $r_t(s_t,a_t)=-(C_t+E_t)$, where $C_t,E_t$ are the HVAC system cost and energy, respectively. The agent selects an action (e.g., temperature set-points or heat pump modulation signals) $a_t\in \mathcal{A}$ according to a policy $\pi \left(a\right|s)$, which maps states to actions. The objective is to find the policy that maximizes the expected cumulative reward $J\left(\pi \right)=\mathbb{E}\left[{\sum }_{t=0}^{\infty }{\gamma }^t{r}_t(s_t,a_t)\right]$. Both the state and action spaces can be either discrete or continuous, with further details discussed in Section 5.

While the agent aims to minimize HVAC energy consumption, it must also maintain thermal comfort. Though comfort depends on multiple factors, including temperature, humidity, and clothing levels [68], this study focuses primarily on indoor temperature with respect to thermal comfort bound between 18 to 24 degrees. This constraint transforms the RL problem into a constrained RL problem. Figure 1 illustrates the process flow for the thermal management system control mechanism. A deep RL agent is trained to control the HVAC system; simultaneously, a barrier certificate is trained in a data-driven manner to prevent the agent from violating the safety constraints (thermal comfort). During early training, safety violations occur frequently since the barrier and RL agent learn simultaneously. As the barrier improves with more data, violations progressively decrease. The barrier function manipulates the RL agent’s objective function by penalizing violations of occupant comfort to advance policy improvement in the direction of safe and optimal actions.

This approach ensures that the agent’s learning is driven towards actions that maintain occupant comfort while minimizing energy consumption, allowing us, in turn, to train an agent specifically to minimize energy consumption while maintaining occupant comfort.

4.2. Safe Reinforcement Learning Through Neural Barrier Certificates

Consider the dynamical system $s_{t+1}=f(s_t,a_t)$, where $s\in \mathcal{S}$ and $a\in \mathcal{A}$ are the state and control input, respectively. The constraint function is defined as $C\left(s_t\right)\le 0$ and we define the set of safe states as ${\mathcal{S}}_{safe}=\left\{s\right|C\left(s_t\right)\le 0\}$ and the set of unsafe states as ${\mathcal{S}}_{unsafe}=\left\{s\right|C\left(s_t\right)>0\}$, respectively; the set of initial states is defined as ${\mathcal{S}}_{init}\subset \mathcal{S}$. We assume that ${\mathcal{S}}_{init}\subseteq {\mathcal{S}}_{safe}$.

Barrier certificates are mathematical constructs that define forward invariant sets in state space. The forward invariant property of the barrier certificates can be used to guarantee the safety of dynamical systems [27]. The function $h^{\pi }:\mathcal{S}\to \mathbb{R}$ is a barrier certificate [26] of a given policy $\pi \left(a_t\right|s_t)$ if it satisfies

$$\begin{array}{c}\hfill \begin{array}{ccc}& \forall \hfill & s\in {\mathcal{S}}_{init}:h^{\pi }\left(s\right)\le 0,\hfill \\ & \forall \hfill & s\in {\mathcal{S}}_{unsafe}:h^{\pi }\left(s\right)>0,\hfill \\ & \forall \hfill & s\in \mathcal{S}:h^{\pi }\left(s_{t+1}\right)-h^{\pi }\left(s_t\right)\le -\alpha \left(h^{\pi }\left(s_t\right)\right),\hfill \end{array}\end{array}$$

(13)

where $\alpha$ is a strictly increasing function with $\alpha \left(0\right)=0$; typically $\alpha \left(h^{\pi }\right)=\lambda h^{\pi }$ for some $0<\lambda <1$. If a barrier certificate $h^{\pi }$ exists for a system under policy $\pi$ with an initial state $s_0\in {\mathcal{S}}_{init}$, then the system’s trajectory remains within the safe set due to forward invariance [27]. Since the system transition function $f(·)$ is needed but unknown, we approximate the barrier certificate using a neural network parameterized by $\mathsf{\Phi }$. The dataset D collected from agent–environment interactions is partitioned into $D_{init}$ (initial states) and $D_{unsafe}$ (unsafe states). The loss function of the neural network is designed to penalize violations of the properties of the control barrier functions [26]. The safety loss corresponds to the first property of Equation (13),

$$J_{\mathrm{Safe}}\left(\mathsf{\Phi }\right)={\displaystyle \frac{1}{|D_{init}|}}\sum _{s\in D_{init}}max(0,h^{\pi }(s;\mathsf{\Phi })),$$

(14)

where $D_{\mathrm{init}}$ is the set of initial state samples. The unsafe loss function corresponds to the second property,

$$J_{\mathrm{Unsafe}}\left(\mathsf{\Phi }\right)={\displaystyle \frac{1}{|D_{unsafe}|}}\sum _{s\in D_{unsafe}}max(0,-h^{\pi }(s;\mathsf{\Phi })),$$

(15)

where $D_{\mathrm{unsafe}}$ is the set of unsafe state samples. The invariant loss corresponds to the forward invariant property (third property),

$$J_{\mathrm{Invt}}\left(\mathsf{\Phi }\right)={\displaystyle \frac{1}{\left|D\right|}}\sum _{s,s^{\prime }\in D}max(0,h^{\pi }(s^{\prime };\mathsf{\Phi })-(1-\lambda )h^{\pi }(s;\mathsf{\Phi })),$$

(16)

where D is the set of all state samples. The barrier loss is the sum of all three loss functions.

$$J_h\left(\mathsf{\Phi }\right)=J_{\mathrm{Safe}}\left(\mathsf{\Phi }\right)+J_{\mathrm{Unsafe}}\left(\mathsf{\Phi }\right)+J_{\mathrm{Invt}}\left(\mathsf{\Phi }\right).$$

(17)

The parameter $\mathsf{\Phi }$ is updated by minimizing Equation (17) using gradient descent.

4.3. Policy Learning

Barrier certificate constraints are applied to the policy optimization problem. In this paper, the PPO is chosen to solve the optimization problem. The objective function of the PPO [67] is Equation (12). The policy constraint is derived from the invariant property of the barrier certificate, which ensures that the agent remains within the safe region. The policy optimization problem then becomes

$$\underset{\theta }{max}L\left(\theta \right)\mathrm{s}.\mathrm{t}.\rho \left(\theta \right)·J_{\mathrm{Invt}}\left(\mathsf{\Phi }\right)\le 0.$$

(18)

Importance sampling is applied since the invariant loss is computed using data from the old policy. The optimization problem in Equation (18) can be transformed into an unconstrained problem using the Lagrangian dual [26],

$$\underset{\nu \ge 0}{min}\underset{\theta }{max}F(\nu ,\theta )=L\left(\theta \right)-\nu \rho \left(\theta \right)J_{\mathrm{Invt}}\left(\mathsf{\Phi }\right).$$

(19)

The value function is also learned by minimizing the loss function

$$J_V={\displaystyle \frac{1}{\left|D\right|}}\sum _{s\in D}{(V_{\psi }\left(s_t\right)-\widehat{R_t})}^2,$$

(20)

where $\psi$ is the critic network parameter and ${\widehat{R}}_t$ is the estimated return.

4.4. Safety Mechanism Overview

This framework can be understood as creating an invisible boundary around comfortable temperature zones. The barrier certificate $h(s;\mathsf{\Phi })$, which is itself a neural network with parameters $\mathsf{\Phi }$, learns to approximate the constraint function directly from building operation data rather than requiring manual design of the barrier function. The parameterized barrier $h(s;\mathsf{\Phi })$ functions as a learned topographical map where negative values indicate safe (comfortable) temperatures and positive values signal unsafe (uncomfortable) conditions. Crucially, unlike traditional hard constraints that define fixed temperature thresholds, $h(s;\mathsf{\Phi })$ learns a smooth, continuous safety landscape that adapts to the specific thermal dynamics of each building. The learning process occurs through three complementary objectives. When the system starts at a comfortable temperature, Equation (14) ensures $h(s;\mathsf{\Phi })\le 0$, confirming that the barrier recognizes this as safe. As the temperature approaches unsafe regions, Equation (15) trains $h(s;\mathsf{\Phi })$ to output positive values. Moreover, Equation (16) enforces the forward invariance property, ensuring that once comfortable, the system tends to remain comfortable. When the PPO agent proposes an action that would lead the system toward uncomfortable temperatures, the term $\nu \rho \left(\theta \right)J_{\mathrm{Invt}}\left(\varphi \right)$ in Equation (19) becomes large, effectively preventing unsafe actions during policy optimization.

5. Experiments and Discussion

In this section, we present a comprehensive training and evaluation of the safe reinforcement learning controller through systematic testing across diverse operational scenarios. Our experimental design aims to assess both the performance characteristics and practical viability of the safe RL-based approach and to compare it to conventional control strategies. The section includes: (1) experimental setup for single-zone and multi-zone building test cases, (2) training results showing learned policies and barrier certificates, (3) performance comparisons with PPO and RBC controllers for energy consumption and cost, (4) safety violation analysis during training and evaluation phases, and (5) discussion of key findings and practical implementation considerations.

5.1. Experimental Design

We evaluate our safe RL approach using two BOPTEST [29,69] test cases representing different control complexity levels. For Experiments 1–5, we use the BESTEST Hydronic Heat Pump scenario modeling a 192 m² residential home with five occupants (present 07:00–20:00 weekdays, 24 h weekends; only Experiment 5 considers occupancy state). The RL agent observes normalized zone temperature (where $T=-1$ represents the lower setpoint, $T=+1$ represents the upper setpoint, with valid range $T\in (-\infty ,+\infty )$) and controls heat pump modulation through 12 discrete levels. For Experiments 6–7, we employ a five-zone Chicago office building with variable air volume (VAV) system, totaling 1655 m². The agent observes zone temperatures, internal heat gains, and outdoor temperature, with Experiment 6 controlling AHU parameters and Experiment 7 managing core zone setpoints. All variables are normalized to [−1, 1] for learning efficiency, with rewards based on BOPTEST KPIs targeting energy and cost reduction [29].

Table 2. Experimental configurations and research question mapping.

Exp.	Description	Building Type	Floor Area	Control Variable(s)	Comfort Zone	RQs
1	Without pre-trained barrier; random episodes	Single-zone (Brussels)	192 m2	Heat pump (12 bins)	18–21 °C	RQ1, RQ2
2	Pre-trained barrier (20 episodes)	Single-zone (Brussels)	192 m2	Heat pump (12 bins)	18–21 °C	RQ1, RQ2
3	Training with diverse random episodes	Single-zone (Brussels)	192 m2	Heat pump (12 bins)	18–21 °C	RQ1, RQ2
4	Training with repeated identical episodes	Single-zone (Brussels)	192 m2	Heat pump (12 bins)	18–21 °C	RQ1
5	Occupancy-aware barrier adaptation	Single-zone (Brussels)	192 m2	Heat pump (12 bins)	18–21 °C (occ.) 15–30 °C (unocc.)	RQ1
6	Multi-zone AHU system control	5-zone office (Chicago)	Total: 1655 m2 Core: 985 m2 N/S: 208 m2 ea. E/W: 131 m2 ea.	Supply air temp. Duct pressure	18–24 °C	RQ1
7	Multi-zone core zone control	5-zone office (Chicago)	(Same as Exp. 6)	Heating setpoint Cooling setpoint	18–24 °C	RQ1, RQ3

details the experimental configurations and their mapping to research questions from Section 1.

Table 3. Hyperparameters for our experiments. The actor and critic networks share the same architecture parameters.

Number Of Hidden Layers	2	Size of Hidden Layers	256
Learning Rate	0.0003	GAE parameter	0.95
Policy Clip	0.2	PPO Activation Function	ReLU
Barrier Activation Function	$tanh$	Lagrangian Initial Value	1
Optimizer	Adam

shows all hyperparameters for the PPO agent and barrier neural network.

5.2. Experimental Results

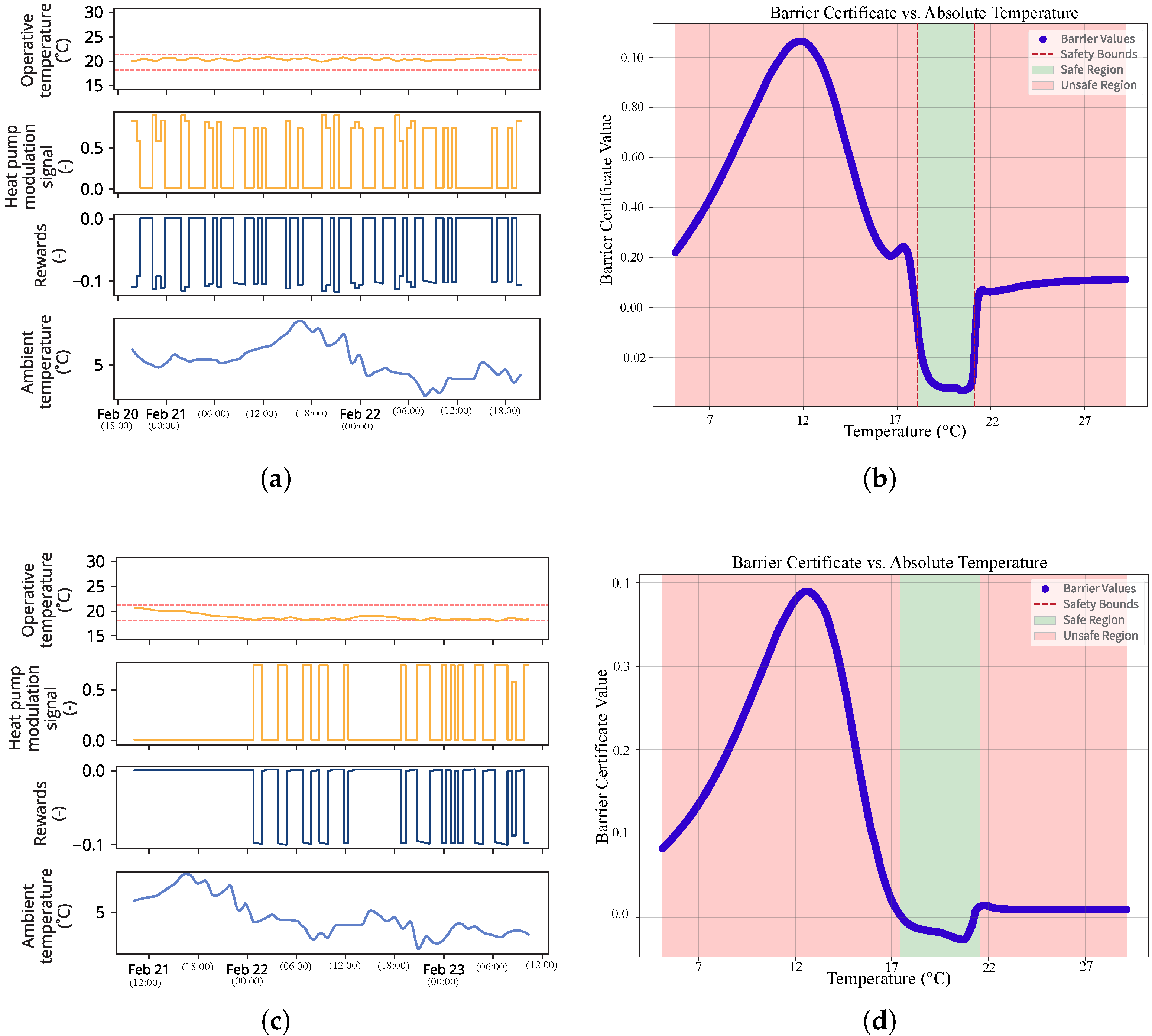
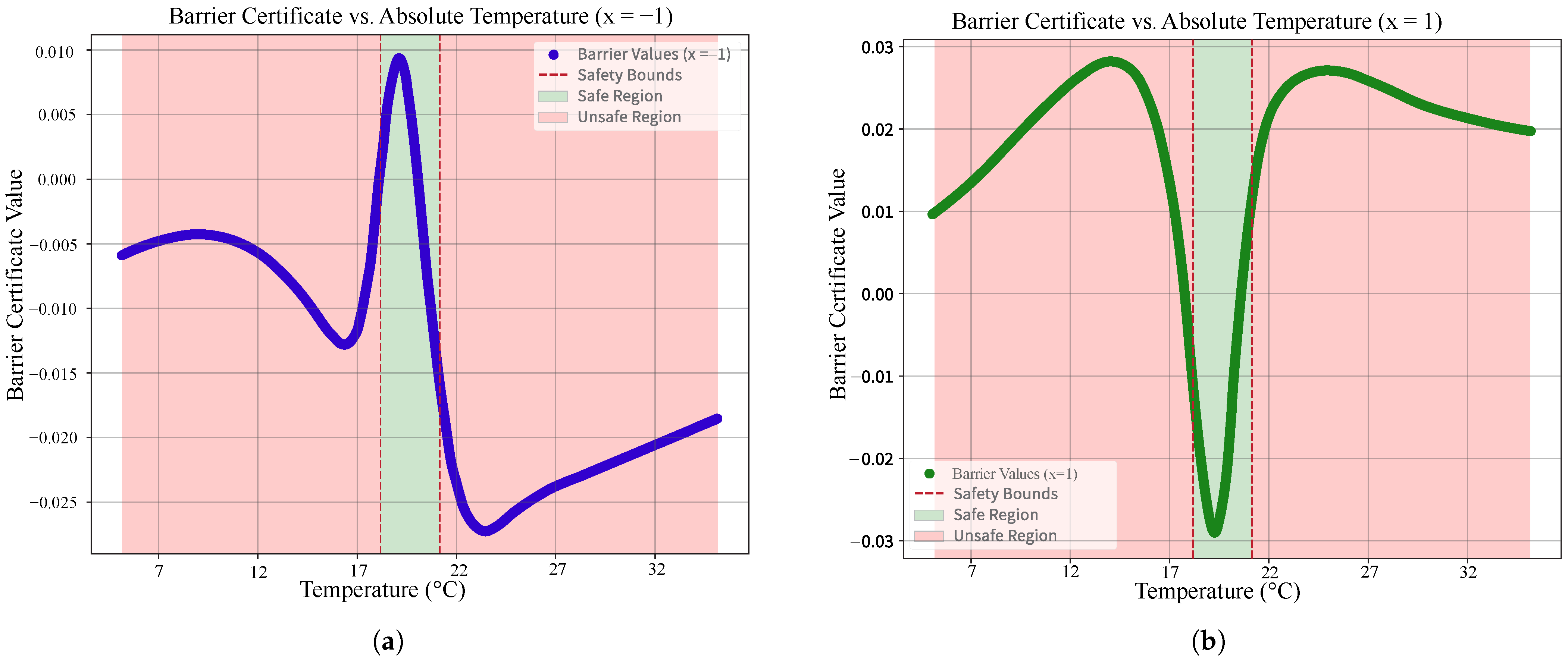
For the first experiment (Experiment 1), the length of the episode is considered to be 2 days, and episodes are randomly generated. The agent interacts with the environment every 30 min and collects data for training. Figure 2a shows the learned policy after training for 188 days, which indicates that the agent learned the best possible policy with respect to the barrier certificate that is shown in Figure 2b. The trained barrier certificate clearly distinguishes between safe and unsafe temperature regions, showing negative values (below zero) only within the comfortable temperature range of 18–21 °C and positive values in the unsafe regions.

Next, we investigated the impact of a pre-trained barrier certificate on the previous experimental setup (Experiment 2). The barrier certificate was trained separately for 20 episodes. The agent successfully learned the safe policy (Figure 2c) within 150 days of training; the corresponding learned barrier certificate is displayed in Figure 2d.

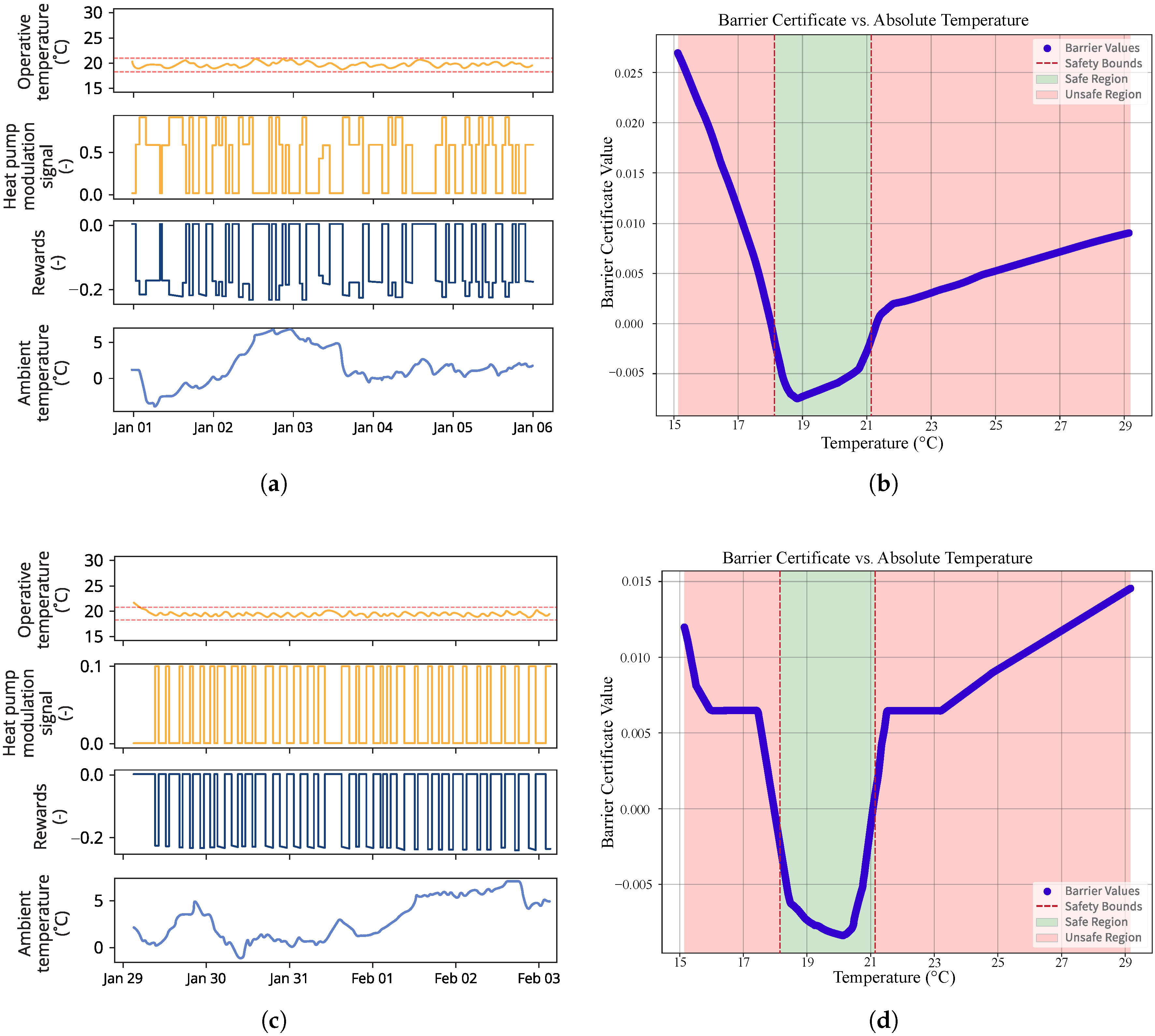
Figure 3 shows training results using 5-day episodes with different training methods: Figure 3a,b show the agent trained on repeated identical days (Experiment 3), while Figure 3c,d show performance with randomly generated daily conditions (Experiment 4). The difference in using either 2- or 5-day episodes shows that in the latter case, learned policies are less conservative in that they tend to violate the barrier more frequently to maximize the reward.

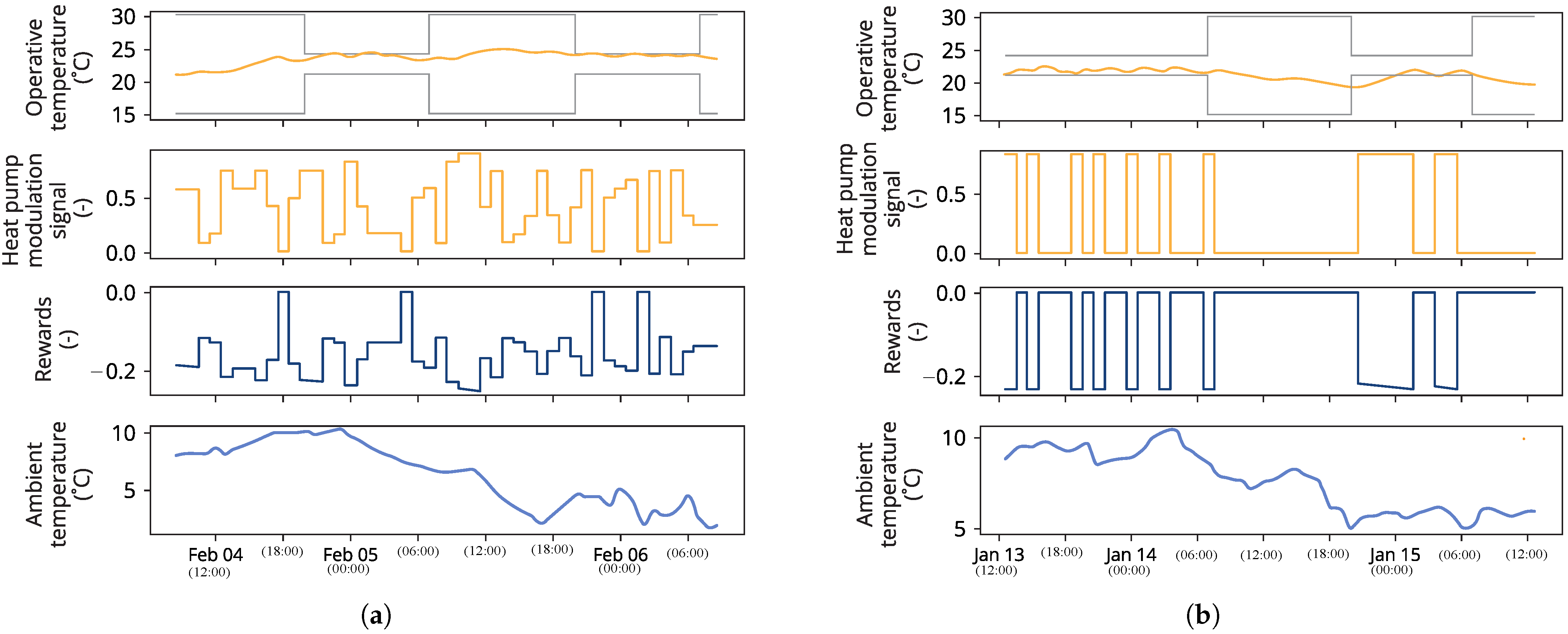
In Experiment 5, we trained an occupancy-aware barrier certificate (pre-trained for 20 episodes) that enforces different comfort bounds: 18–21 °C during occupied hours and 15–30 °C during unoccupied hours. Initially, the agent disregarded occupancy status (Figure 4a), but after further training, it learned to minimize actions during occupied hours (Figure 4b), improving energy efficiency while maintaining comfort. 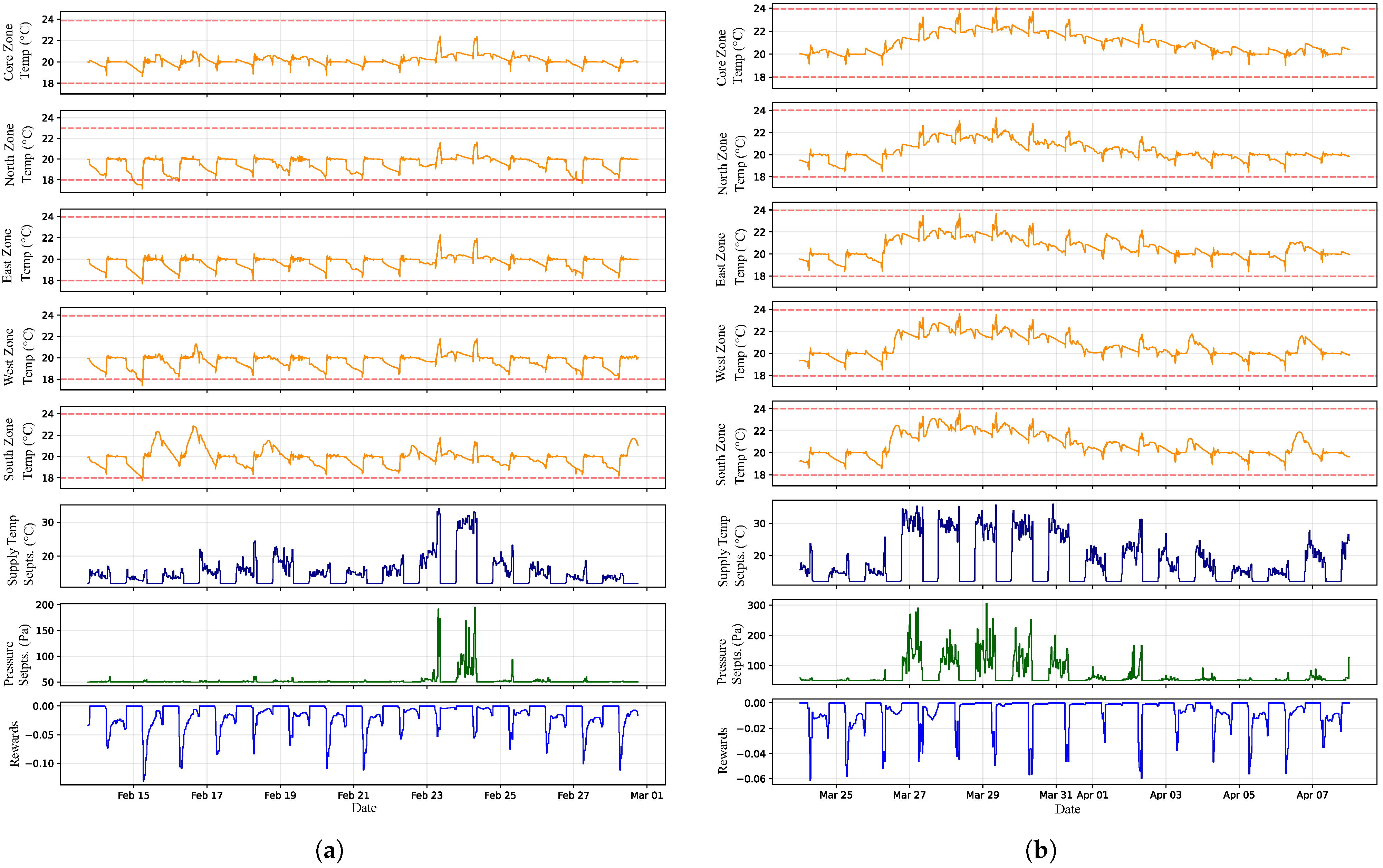Figure 5 illustrates the barrier certificates for both occupied and unoccupied states. For the next set of experiments (6 and 7) on multi-zone test cases, the safety constraint for the agent is that the temperature for each zone must be within the range of 18–24 °C, and the reward function is for the agent to reduce the cost and energy. In Experiment 6, the episode duration is 15 days, and the agent takes an action every 30 min; the learning frequency is every 1.5 days. The agent is tasked to reduce the cost and energy consumption and keep the temperature within the safety constraints for all zones by controlling the pressure setpoint and supply temperature setpoint. Figure 6 shows the learned policy during the training for the agent and final episode of the training (Figure 6a) and one evaluation episode (Figure 6b) in this environment. The agent managed to keep the temperature within the safe zone despite having some violations during the final episodes of training. In the evaluation episode, the agent had some violations but managed to keep the temperature within the safe bounds during the episode.

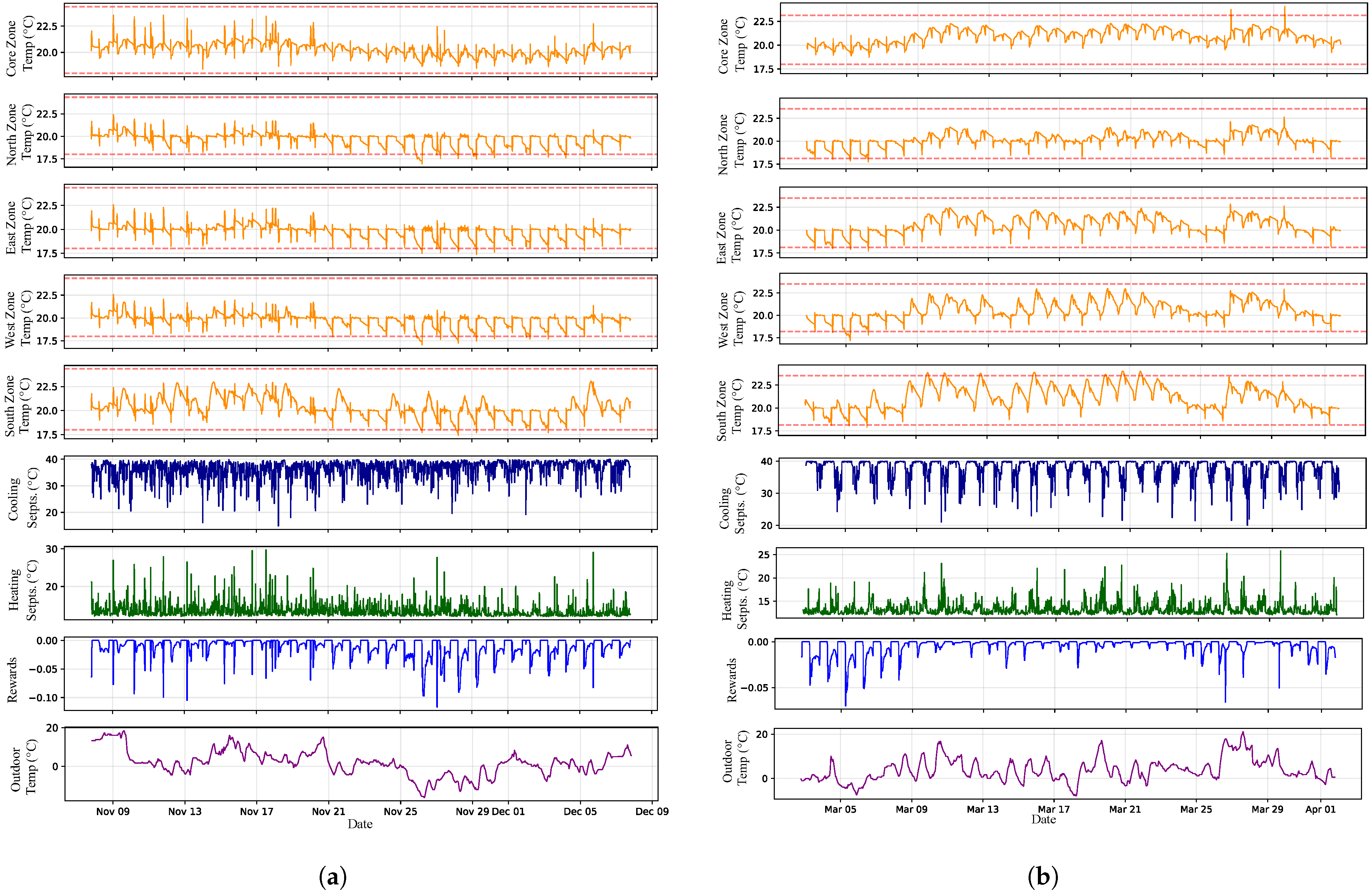
In the next experiment, the agent controls heating and cooling setpoints with an extended 30-day episode duration, maintaining the same 30 min sampling interval but with learning updates every 2 days. The objective focuses on maintaining the core zone temperature within 18–24 °C through setpoint manipulation. Figure 7 presents the final training episode (Figure 7a) and an evaluation episode (Figure 7b) from the multi-zone office environment. The agent successfully maintained the designated temperature bounds with only minor violations throughout the training episodes. 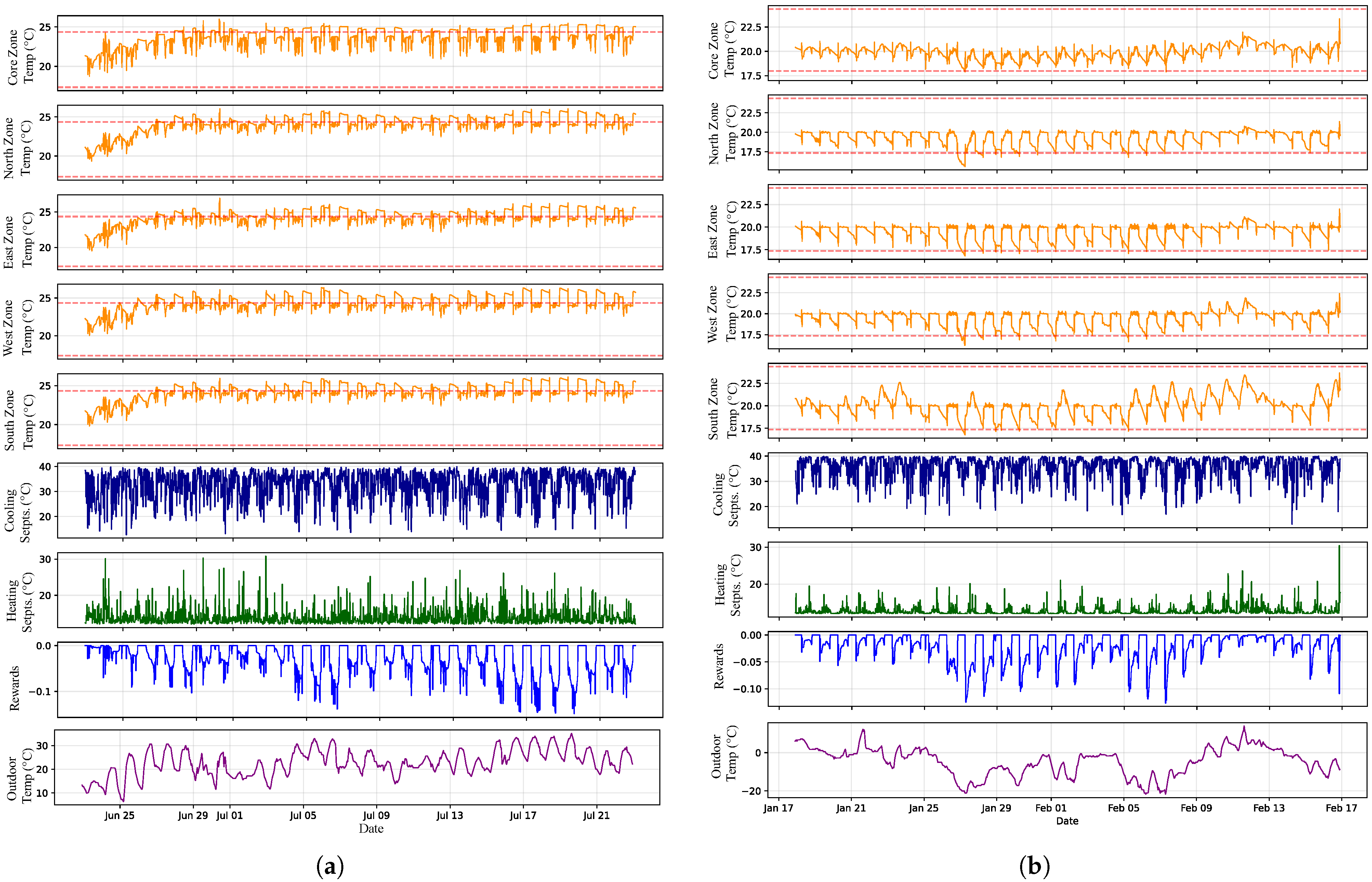Figure 8 shows the agent’s performance under both summer and winter conditions. While the agent successfully maintained safety bounds during cold winter periods, it violated safety constraints under summer cooling conditions.

Our experimental evaluation progressed through a series of increasingly complex scenarios to assess the safe RL controller’s capabilities. Initial experiments with 2-day episodes demonstrated that the agent could learn effective control policies while respecting temperature constraints (18–24 °C), with the barrier certificate clearly delineating safe and unsafe regions. Notably, pre-training the barrier certificate reduced learning time by approximately 20% (from 188 to 150 days), suggesting computational benefits for this approach. When we extended episode lengths to 5 days, an interesting pattern emerged: the agent developed less conservative policies, more frequently approaching barrier boundaries to optimize rewards. This behavior was particularly pronounced when training with randomly generated daily conditions versus repeated patterns.

The introduction of occupancy-aware barriers marked a significant advancement in the controller’s sophistication. By allowing relaxed temperature bounds during unoccupied hours (15–30 °C versus 18–21 °C when occupied), we observed the agent’s ability to learn context-dependent strategies. Initially, the agent ignored occupancy status, but through continued training, it developed an energy-efficient policy that minimized control actions during occupied periods while exploiting the relaxed constraints during unoccupied times. This learning progression was successfully scaled to multi-zone buildings with 15 and 30-day episodes, where the agent managed multiple zones simultaneously while maintaining zone-specific temperature constraints (18–24 °C) and optimizing for cost reduction. Throughout all experiments, the 30 min control interval remained constant, providing consistent temporal resolution for the agent’s decision-making process.

The final sets of experiments showcased the agent’s ability to perform in more complex and real-world-like scenarios, where inter-zone thermal dynamics and multiple control variables significantly increased the challenge. In Experiment 6, the agent successfully managed a five-zone office building by controlling centralized AHU parameters, demonstrating its capability to handle system-level control decisions that affect all zones simultaneously. Experiment 7 explored an alternative control strategy where the agent manipulated zone-level heating and cooling setpoints, providing more direct but localized control. These experiments not only validated the scalability of the safe RL approach from single-zone residential to multi-zone commercial buildings but also demonstrated its flexibility in adapting to different control architectures.

5.3. Comparative Study

To enhance the robustness of the evaluation of our safe RL agent, we conducted an additional set of comparative experiments using the configurations of experiments (7) as outlined in Table 2, but instead, each controller was evaluated in each season of the year to better investigate its energy and safety performance. This approach allows for more comprehensive data collection and demonstrates stronger evidence of performance. The safe PPO agent is compared against two baselines: (1) a PPO agent trained with reward weighting, (2) RBC with static setpoints, as described in [70]. The RBC controller acts as a supervisory controller for setting the set-points for local PID controllers in the test case. PPO uses a comparable reward function to the safe RL agent but incorporates an additional BOPTEST [29] KPI for thermal violation penalties, tuned according to [70]. This test case was chosen for the comparative study since it enables us to investigate the agent’s performance in both cooling and heating scenarios. Our evaluation methodology employs a more rigorous generalization test than typical approaches in the literature. While previous work, such as [70], evaluates agents on full annual cycles with stochastic weather variations, we randomly sample episodes throughout the year. This approach ensures that our agent performs well across diverse seasonal conditions rather than optimizing for average annual performance. This evaluation strategy provides a more realistic assessment of deployment readiness, as real-world controllers must maintain efficiency at all points during the year.

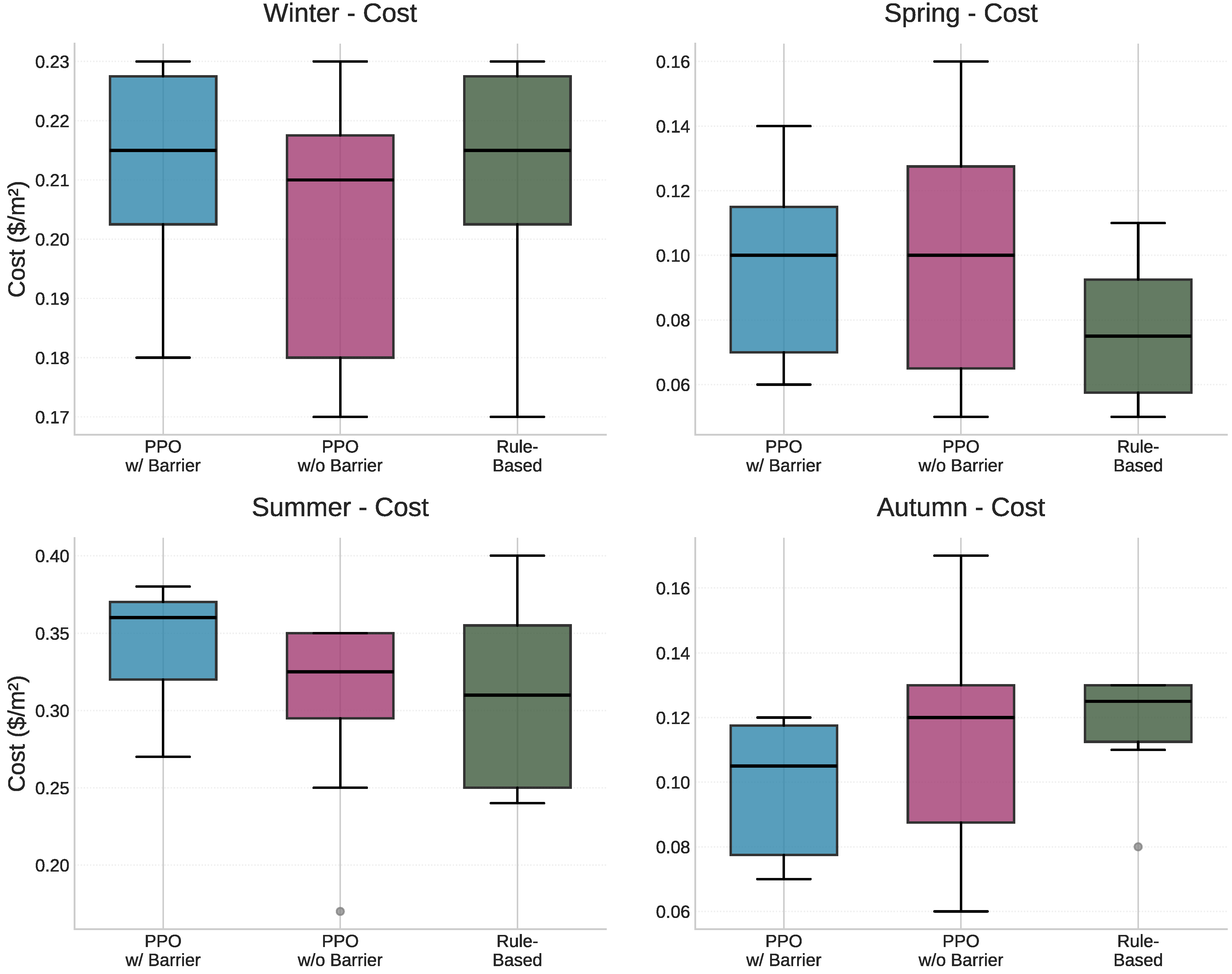
According to

Table 4. Energy consumption and cost analysis by season.

Controller	Metric	Seasonal Performance
		Winter	Spring	Summer	Autumn
PPO w/Barrier	Energy (kWhm−2)	2.25 [2.15–2.40]	1.06 [0.77–1.20]	3.82 [3.41–3.97]	1.14 [0.83–1.23]
	Cost (USD/m2)	0.21 [0.20–0.23]	0.10 [0.07–0.11]	0.36 [0.32–0.37]	0.11 [0.08–0.12]
PPO w/o Barrier	Energy (kWhm−2)	2.25 [1.95–2.35]	1.04 [0.73–1.34]	3.45 [3.15–3.74]	1.28 [0.94–1.40]
	Cost (USD/m2)	0.21 [0.18–0.22]	0.10 [0.07–0.13]	0.33 [0.29–0.35]	0.12 [0.09–0.13]
Rule–Based	Energy (kWhm−2)	2.31 [2.15–2.39]	0.79 [0.62–0.95]	3.28 [2.66–3.76]	1.29 [1.19–1.35]
	Cost (USD/m2)	0.21 [0.20–0.23]	0.08 [0.06–0.09]	0.31 [0.25–0.35]	0.12 [0.11–0.13]

, PPO with barrier certificate demonstrates consistent performance across seasons. The controller achieves a median winter consumption of 2.25 kWhm⁻² (IQR: 2.15–2.40) at USD 0.21/m² (IQR: 0.20–0.23), and spring consumption of 1.06 kWhm⁻² (IQR: 0.77–1.20) at USD 0.10/m² (IQR: 0.07–0.11). Summer shows the highest consumption among all controllers at 3.82 kWhm⁻² (IQR: 3.41–3.97) costing USD 0.36/m² (IQR: 0.32–0.37), indicating a conservative cooling strategy prioritizing comfort. Autumn performance reaches 1.14 kWhm⁻² (IQR: 0.83–1.23) at USD 0.11/m² (IQR: 0.08–0.12), showing competitive efficiency with relatively narrow IQRs suggesting stable control.

PPO without barrier shows more aggressive cost optimization, achieving 10% lower summer consumption at 3.45 kWhm⁻² (IQR: 3.15–3.74) costing USD 0.33/m² (IQR: 0.29–0.35), saving USD 0.03/m² compared to the barrier version. Winter performance matches the barrier version at 2.25 kWhm⁻² (IQR: 1.95–2.35) and USD 0.21/m² (IQR: 0.18–0.22), though with wider variability. Spring consumption of 1.04 kWhm⁻² (IQR: 0.73–1.34) shows the widest IQR span (0.61 kWhm⁻²), indicating higher operational uncertainty. Autumn performance deteriorates to 1.28 kWhm⁻² (IQR: 0.94–1.40) at USD 0.12/m² (IQR: 0.09–0.13), representing 12% higher energy use than the barrier version. The RBC excels in mild conditions, achieving the best spring performance at 0.79 kWhm⁻² (IQR: 0.62–0.95) costing USD 0.08/m² (IQR: 0.06–0.09), representing 24–25% energy savings and 20% cost reduction versus PPO variants. Summer performance of 3.28 kWhm⁻² (IQR: 2.66–3.76) at USD 0.31/m² (IQR: 0.25–0.35) positions it between the two PPO approaches, though with the widest summer IQR (1.10 kWhm⁻²). Winter consumption of 2.31 kWhm⁻² (IQR: 2.15–2.39) matches all controllers’ cost at USD 0.21/m² (IQR: 0.20–0.23). Autumn shows 1.29 kWhm⁻² (IQR: 1.19–1.35) at USD 0.12/m² (IQR: 0.11–0.13), with the narrowest autumn energy IQR (0.16 kWhm⁻²) indicating predictable transitional season performance. Figure 9 and Figure 10 show the energy and cost performance of each controller in each season.

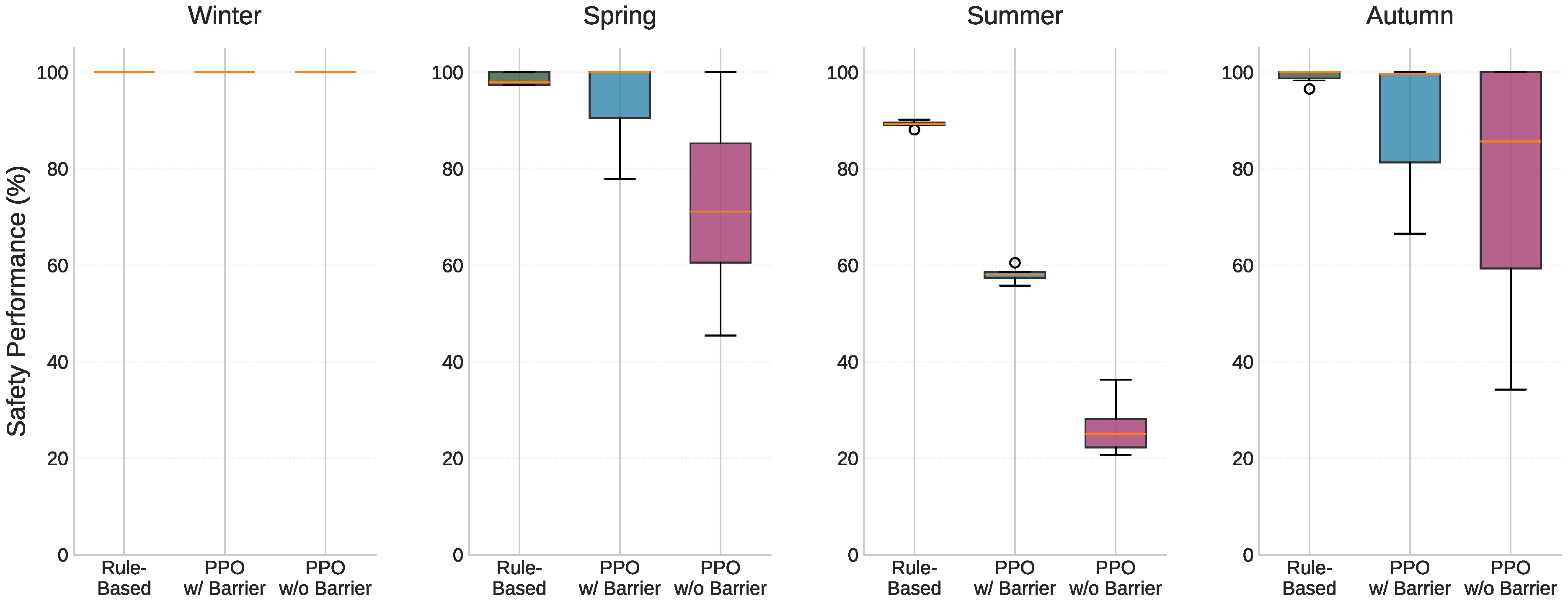
As for the safety performance analysis (

Table 5. Safety performance analysis by season.

Controller	Median Safety Rate (%) [IQR: Q1–Q3]
	Winter	Spring	Summer	Autumn
Rule-Based	100.0 [100.0–100.0]	97.8 [97.4–100.0]	89.3 [89.0–89.5]	100.0 [98.7–100.0]
PPO w/Barrier	100.0 [100.0–100.0]	99.9 [90.5–99.9]	58.1 [57.4–58.6]	99.6 [81.3–99.6]
PPO w/o Barrier	100.0 [100.0–100.0]	71.1 [60.6–85.2]	25.0 [22.2–28.1]	85.6 [59.3–100.0]

), RBC demonstrates the best safety compliance, maintaining 97.8% (spring) and 100% (autumn) safety rates with minimal variability, indicating highly predictable comfort delivery. Even during challenging summer conditions, it sustains 89.3% compliance with narrow (IQR: 89.0–89.5%), suggesting its conservative fixed rules prioritize occupant comfort over energy savings. This aligns with its slightly higher energy consumption but provides reliable comfort assurance.

The safe PPO shows moderate safety performance with higher variability. Spring safety at 99.9% (IQR: 90.5–99.9%) and autumn at 99.6% (IQR: 81.3–99.6%) indicate that the barrier function provides meaningful constraint enforcement, though the wide IQR ranges suggest inconsistent protection across different operating conditions. The dramatic summer degradation to 58.1% (IQR: 57.4–58.6%) reveals that even with barrier constraints, the controller struggles to maintain comfort during peak cooling demands, potentially explaining its higher summer energy consumption as it attempts to recover from constraint violations.

PPO without barrier exhibits the poorest safety performance, particularly the alarming 25.0% summer compliance (IQR: 22.2–28.1%), meaning that comfort constraints are violated 75% of the time during peak cooling season. Spring performance shows 71.1% compliance (IQR: 60.6–85.2%), with an IQR span of 24.6 percentage points, indicating high variability. Autumn demonstrates even greater unpredictability at 85.6% median compliance (IQR: 59.3–100.0%), where the 40.7 percentage point IQR span suggests performance can range from barely acceptable (59.3%) to perfect compliance. This aggressive optimization explains its energy savings but reveals the critical trade-off: the 10% summer energy reduction compared to barrier PPO comes at the cost of acceptable comfort conditions. During winter, all controllers achieve perfect 100% safety compliance (IQR: 100.0–100.0%), reflecting the wider comfort bounds typical of heating seasons. This relaxed constraint environment reveals interesting performance dynamics: the unconstrained PPO achieves competitive energy efficiency at 2.25 kWhm⁻² (matching the barrier variant), while the RBC consumes slightly more at 2.31 kWhm⁻². The PPO-with-barrier’s identical winter consumption to its unconstrained counterpart (2.25 kWhm⁻² at USD 0.21 m⁻²) suggests that winter comfort bounds are sufficiently relaxed that the barrier function rarely activates. However, the barrier variant maintains tighter IQR bounds (2.15–2.40 vs. 1.95–2.35 kWhm⁻²), demonstrating more consistent control behavior. This consistency reflects the barrier function’s design to prioritize safety assurance over energy optimization as per Equation (18), maintaining predictable operation even when natural conditions ensure safety. In summary, the seasonal analysis reveals critical trade-offs between energy efficiency and occupant comfort across different weather conditions. The RBC provides the most reliable comfort, with median safety rates ranging from 89.3% (summer) to 100% (winter/autumn), maintaining narrow IQRs, indicating predictable performance. PPO without barrier achieves lower energy costs but suffers from unacceptable safety performance, particularly in the summer (25.0% compliance, IQR: 22.2–28.1%). PPO with barrier offers a compromise with better safety than unconstrained PPO, yet still exhibits not perfect summer safety rates of 58.1% (IQR: 57.4–58.6%), while maintaining high compliance in other seasons (99.6–100%). Figure 11 shows the safety performance of each controller in each season.

5.4. Discussion

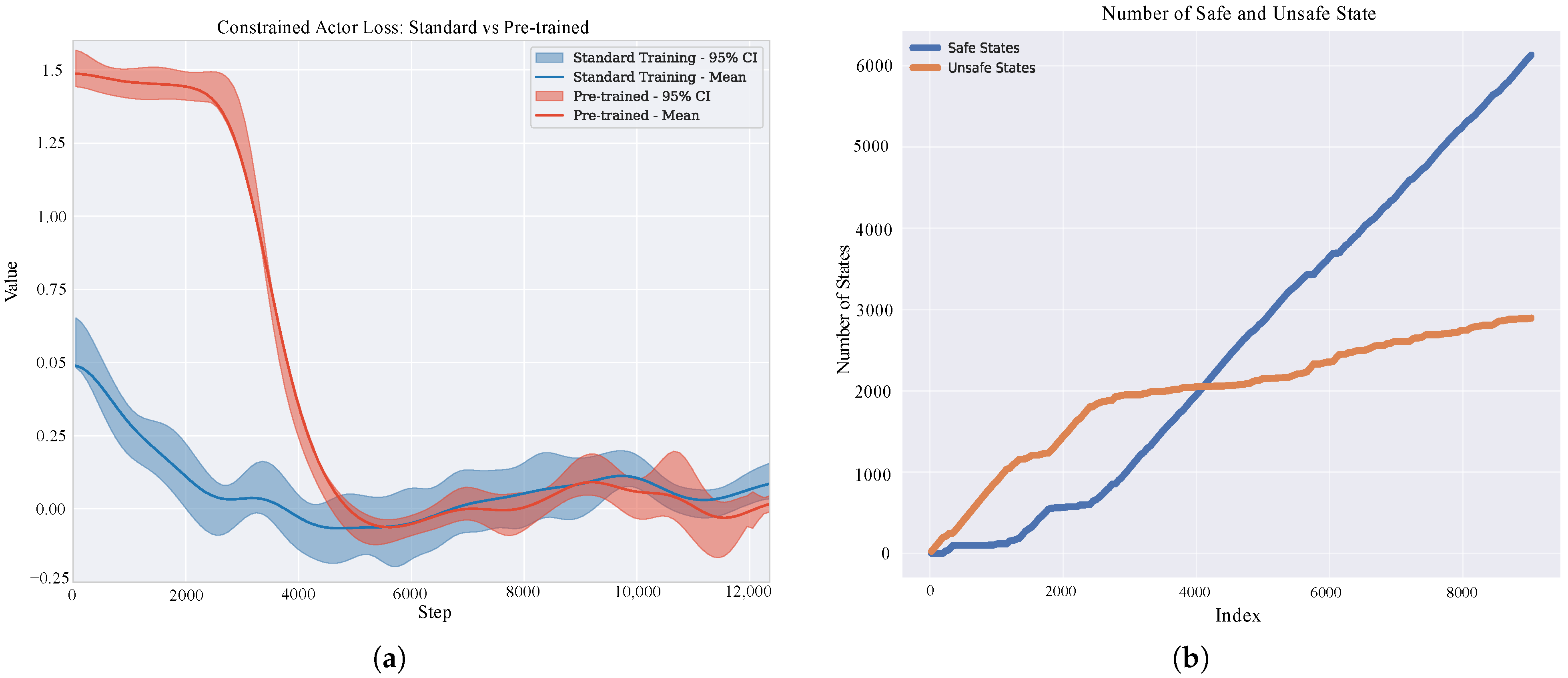
Our experiments with safe RL for HVAC control revealed several important findings that highlight both the potential and challenges of this approach. Figure 12 shows some statistics from our training runs. Specifically, Figure 12b shows the number of safe and unsafe states for the agent as gathered in the dataset. At the early stages of training, the number of unsafe states is higher than safe states. As training continues, however, the number of unsafe states decreases, and the safe states increase. However, the number of unsafe states does not reach zero since we use a neural network to approximate the barrier certificate in a model-free fashion. This approach can achieve near-zero safety violations, but due to the approximation error, it will never be zero [71]. Figure 12a presents the constrained loss function (cf. Equation (19)) for two agents that were trained with and without a pre-trained barrier certificate over 10 runs, respectively. The pre-trained agent shows higher initial loss due to the pre-training phase occurring without agent intervention. After approximately 3000 steps, the loss rapidly converges and stabilizes at a lower value, while the non-pre-trained approach continues to show significant oscillations. This pattern illustrates the key advantage of pre-training: despite higher initial loss values, the pre-trained approach achieves faster stabilization and more consistent performance once active training begins. The pre-training produced a less conservative agent that developed a more optimal policy than the agent without pre-training (Figure 2). This shows that pre-training can lead to a less conservative agent that achieves a more optimal and safe policy with fewer training steps. This finding highlights the fundamental trade-off between strict safety adherence and performance optimization in constrained reinforcement learning. Our results show that while static-day training achieves safety faster, agents trained on varied days exhibit greater robustness through better generalization (cf. Figure 3).

As for the occupancy-aware control, the agent with a pre-trained barrier certificate is trained to incorporate occupancy information, establishing different safety constraints for occupied and unoccupied periods. During occupied hours, the safe temperature region is set between 18–21 °C, while during unoccupied hours, this range expands to 15–30 °C. This configuration provides greater flexibility for the agent to maximize its reward function, as it can suspend actions during unoccupied periods and only adjust temperatures when the space is occupied. For this scenario, we also employed a pre-trained barrier certificate. The grey lines in Figure 4 illustrate the comfort bounds for both occupied and unoccupied hours. Figure 4b demonstrates that the agent trained with this barrier certificate stops taking actions immediately upon reaching unoccupied hours and maintains this inactive state until occupancy resumes. The agent then actively works again to maintain temperatures within the safe bounds (cf. 18–21 °C) during occupied hours by taking the appropriate actions.

To implement the safe RL controller in a more complex scenario, we chose an environment with five thermal zones and the same goals to keep the temperature in a certain range (18–24 °C) and minimize energy consumption. The results in Figure 6 and Figure 7 demonstrate that the safe RL controller successfully maintained temperatures within the specified range while minimizing energy consumption. We evaluated different control levels in these experiments, ranging from low-level AHU parameter adjustments to high-level setpoint modifications. This evaluation confirms the agent’s ability to maintain safety constraints while optimizing energy performance across varying control complexities. The final two experiments demonstrate the agent’s capability to operate safely in complex multi-zone environments where safety constraints are more challenging to satisfy due to increased system dimensionality and inter-zone dependencies.

The seasonal performance analysis reveals a fundamental challenge in deploying RL for building control: the inherent trade-off between safety guarantees and energy optimization varies significantly across operating conditions. While the barrier function improves safety compliance compared to unconstrained RL, it still achieves only 58.1% summer compliance, suggesting that current barrier implementations may be insufficient for extreme conditions. However, the barrier-based approach demonstrates clear potential, more than doubling summer safety rates compared to unconstrained PPO (58.1% vs. 25.0%) and achieving near-perfect compliance in transitional seasons (99.6% autumn, 99.9% spring), indicating that the framework is directionally correct and could benefit from further refinement. During favorable conditions like winter, when all controllers naturally achieve perfect compliance, both PPO variants show identical median consumption (2.25 kWhm⁻²), but the barrier function provides notably more consistent performance, demonstrating operational stability despite minimal safety risk. The unconstrained PPO’s severe comfort violations during summer (25.0% compliance) demonstrate that purely reward-driven optimization is unsuitable for safety-critical applications, despite achieving 10% energy savings. Notably, the RBC’s superior safety performance (89.3%) and competitive efficiency, particularly during mild seasons (0.79 kWhm⁻² in spring), suggest that domain knowledge encoded in simple heuristics remains valuable when conditions are predictable. Safe RL consistently outperforms unconstrained PPO across seasons—achieving 99.6% vs. 85.6% in autumn, 99.9% vs. 71.1% in spring, and, most critically, 58.1% vs. 25.0% in summer—demonstrating that barrier certificates provide meaningful safety improvements and represent a promising direction for making RL viable in real-world building control applications. Nevertheless, the 31.2% point gap between safe RL and RBC performance in summer (58.1% vs. 89.3%) indicates that barrier functions must evolve to incorporate domain expertise to match the reliability of traditional control methods. In summer, the RBC achieves both the lowest energy use (3.28 kWhm⁻²) and the highest median safety (89.3%), indicating that our PPO-with-barrier controller is inferior in this regime. This pattern reflects fundamental differences in summer cooling challenges: high solar and conductive gains create sustained peak loads that saturate HVAC capacity, while the tight comfort ceiling (24 °C) leaves minimal margin for reactive control. Under these conditions, the RBC’s anticipatory scheduling and conservative deadband operation prove more effective than the safe RL agent’s boundary-seeking behavior. While the safe RL agent registers more violations, the observed zone temperatures hover around 25 °C Figure 8a, suggesting boundary-hugging rather than gross discomfort. The reward function inherently drives the RL agent toward the comfort boundary to maximize energy efficiency. However, the neural barrier’s approximation errors can lead to comfort violations during boundary-hugging operation, where the agent operates close to constraint limits. Under thermal stress, this approximation uncertainty becomes more apparent—yet the resulting temperature deviations remain within reasonable bounds when executed by the real system. The RBC deadband approach naturally provides safety margins that prevent such violations and damps cycling. These observations motivate forecast-aware margin tightening and deadband-informed barrier design, as well as limited pre-cooling heuristics or a hybrid fallback to improve summer robustness without sacrificing efficiency.

Table 6. Summary of experiments: training conditions, duration, and safety outcomes.

Experiment	Ep.	Samp.	Description	TD	#Ep. (Train)	S/U
(1) Without Pre-trained Barrier	2 d	30 m	No pre-trained barrier certificate, random episode generation for a single-zone building in Brussels.	188	94	96/0
(2) Pre-trained Barrier	2 d	30 m	Pre-trained barrier certificate (20 episodes) for a single-zone building in Brussels. Faster convergence, less conservative.	150	75	90/6
(3) Random Episodes	5 d	1 h	Training with diverse, randomly selected episodes for better generalization, for a single-zone building in Brussels.	125	25	116/4
(4) Non-random Episodes	5 d	1 h	Training with repeated identical episodes (same day). Faster convergence but overfitting, for a single-zone building in Brussels.	50	10	120/0
(5) Occupancy-aware	2 d	1 h	Barrier adapts to occupancy: 18–21 °C (occupied), 15–30 °C (unoccupied). Reduces actions in unoccupied periods for a single-zone building in Brussels.	160	80	44/4
(6) 5-zone office	15 d	30 m	Training on a longer episode and a more complex environment with 5 zones in Chicago. The agent controlled the supply air temperature and duct pressure to regulate the temperature for all zones and reduce cost and energy consumption.	1 year	24	720/0
(7) 5-zone office	30 d	30 m	The agent controlled the cooling and heating setpoints for the core zone of a multi-zone office situated in Chicago.	1.2 year	15	1440/0

Abbreviations: Ep.—Episode Length; Samp.—Sampling Interval; Desc.—Description; TD—Training Duration; #Ep. (train)—total training episodes; S/U—Safe vs. Unsafe states with the learned policy during training; All experiments used a fixed seed (12,345) to enable exact replication.

summarizes our experiments by our most relevant metric, the number of safe vs. unsafe states.

5.5. Research Questions and Hypotheses

After thoroughly discussing our results in the previous section, we will now provide answers to our research questions (cf. Section 1.1). In addition, we will also review how our hypotheses (cf. Section 1.2) compare with the results of our study.

5.5.1. Answering RQ1

The experimental results demonstrate applicability across the tested building control scenarios, including both residential and commercial settings. The approach was implemented in both residential and commercial settings, scaling from a simple single-zone to a complex five-zone office. This scalability was matched by flexibility in control architectures, as the safe RL agent effectively managed direct equipment control through heat pump modulation in the residential experiments (Experiments 1–5), centralized system control via AHU supply temperature and duct pressure setpoints that affect all zones in Experiment 6, and localized control through the core zone’s heating and cooling setpoints in Experiment 7. Furthermore, the agent demonstrated remarkable adaptability to varying operational contexts, maintaining fixed comfort bounds of 18–21 °C in basic scenarios (Experiments 1–3), implementing sophisticated occupancy-aware control with dynamic constraints, and managing temperature constraints of 18–24 °C across all zones in the multi-zone building, even when only controlling core zone setpoints or central AHU parameters. This versatility across building types, control levels, and operational requirements suggests that safe RL with neural barrier certificates could be a viable solution for various building automation challenges. While these results are promising, broader validation across different building types, climates, and HVAC systems would be needed to establish general applicability.

5.5.2. Answering RQ2

Based on our experimental findings, pre-training, episode generation strategies, and training duration significantly influence safe RL agent performance. Pre-training the barrier certificate for 20 episodes proved highly beneficial—despite showing higher initial loss values (Figure 12a), pre-trained agents achieved rapid convergence and stabilization after approximately 3000 steps, while non-pre-trained agents continued exhibiting significant oscillations throughout training. This pre-training approach produced less conservative agents that can drive the system to the safe set boundaries to achieve a performance but this may lead to more safety violations (Experiments 1 and 2). The choice between random and non-random episode generation revealed a fundamental trade-off: static-day training achieved safety compliance faster with quicker convergence, but agents trained on randomly generated varied days exhibited superior robustness and generalization capabilities, making them more suitable for real-world deployment where conditions constantly change. Regarding sampling time, our experiments revealed interesting trade-offs in control granularity. Comparing Experiment 1 (30 min sampling) with Experiment 3 (1 h sampling), the more fine-grained control provided the agent with more data points and greater flexibility to regulate temperature precisely. While this finer control resolution could potentially lead to increased energy consumption due to more frequent actuator adjustments and might create more opportunities for safety violations, the less frequent adjustment may lead to safety violations as well due to slower response times when temperature drifts occur. This creates a fundamental trade-off: frequent sampling allows rapid corrections but increases the risk of over-control and oscillations that breach safety bounds, whereas infrequent sampling reduces intervention opportunities but may fail to respond quickly enough to disturbances.

5.5.3. Answering RQ3

The safe RL controller with neural barrier certificates demonstrates improvements over baseline controllers, primarily addressing the critical safety-performance trade-off in HVAC control. Compared to unconstrained PPO, the barrier method achieves dramatic safety improvements—increasing summer comfort compliance from 25.0% to 58.1% and autumn compliance from 85.6% to 99.6%, while accepting modest energy penalties of 11% in summer (3.82 vs. 3.45 kWhm⁻²) and maintaining comparable costs (USD 0.36 vs. USD 0.33/m²). Against the RBC, it trades some reliability for adaptability, achieving competitive winter efficiency (2.25 vs. 2.31 kWhm⁻²) but falling short in spring performance (1.06 vs. 0.79 kWhm⁻²) and average safety consistency across all seasons (89.4% vs. 96.8%). The barrier approach essentially redefines the performance frontier: rather than universally dominating existing methods, it occupies a crucial middle ground that makes learning-based control deployable by preventing catastrophic comfort violations (avoiding the unacceptable 25% summer safety of unconstrained PPO) while preserving 85–90% of potential energy savings. This positions safe RL with barrier certificates as a practical bridge between the reliability of RBC and the optimization potential of unconstrained learning, making it particularly valuable for real-world applications where both efficiency and guaranteed comfort are non-negotiable requirements.

5.5.4. Comparison of Hypotheses and Findings

Our experimental results supported H1 and allowed us to reject the null hypothesis H0. The safe RL agent achieved competitive energy performance, demonstrating efficiency comparable to the RBC across most seasons, with particularly strong performance in autumn while showing some limitations in spring operations. Overall energy costs remained within competitive ranges throughout the year. In terms of safety performance, the safe RL agent achieved substantially better results than standard PPO across all seasons, with the most dramatic improvements observed during summer, when unconstrained PPO exhibited catastrophic comfort violations. While not matching the near-perfect safety record of RBC, the barrier certificates effectively enforced comfort constraints and prevented the severe violations observed in unconstrained learning. We reject H0 and accept H1 with the clarification that safe RL achieves safety performance significantly better than standard PPO while maintaining energy efficiency comparable to RBC, successfully positioning itself as a viable middle ground between aggressive optimization and conservative rule-based approaches.

5.6. Key Findings and Lessons Learned

Our research demonstrates that safe RL capitalizing on neural barrier certificates can be effectively implemented for HVAC control applications. One critical insight gained concerns the exploration trade-off: if an agent explores insufficiently, it typically results in overly conservative behavior that prioritizes safety at the expense of energy efficiency. Conversely, excessive exploration can produce an agent with aggressive behavior focused primarily on reward minimization. In our pre-trained agent implementation, we observed less conservative behavior due to the initial pre-training phase, but allowing this agent to explore the action space too extensively led to safety constraint violations. While our approach achieved near-zero violations during evaluation, we found that violations can never be completely eliminated due to inherent approximation errors in neural barrier certificates. This limitation highlights the practical challenges in providing absolute safety guarantees when using neural networks to implement safety constraints. Additionally, our occupancy-aware safe RL agent successfully maintained different thermal comfort bounds based on occupancy status, demonstrating that incorporating contextual information can significantly improve agent behavior. This contextual awareness enables more differentiated control strategies that minimize energy efficiency during unoccupied periods and maintain thermal comfort during occupied periods while optimizing energy consumption at the same time.

Our comparative analysis revealed several critical insights about safe RL deployment in HVAC control. First, seasonal variations fundamentally alter the performance landscape—while RBCs excel during mild spring conditions due to well-tuned fixed parameters, learning-based approaches demonstrate clear advantages during transitional seasons where adaptive behavior is crucial. The barrier certificate approach proved more effective than reward shaping alone, preventing the catastrophic comfort violations that plague unconstrained PPO, particularly during extreme summer conditions where standard RL completely fails to maintain acceptable comfort. Conversely, winter conditions revealed the opposite dynamic—all controllers achieved perfect safety compliance due to wider comfort bounds typical of heating seasons, exposing the barrier function’s stabilizing effect rather than conservatism. During these cold months, both PPO variants achieved similar energy consumption, but the unconstrained PPO exhibited higher variability and less predictable control behavior when exploiting its unrestricted action space, while the barrier-constrained variant maintained tighter operational bounds through its safety-first approach. This seasonal asymmetry highlights that agents trained with hard constraints inherently operate more consistently than their unconstrained counterparts, prioritizing operational stability and guaranteed safety compliance over aggressive optimization strategies even when environmental conditions pose minimal risk. However, our results also exposed the limitations of neural barrier approximations, which cannot match the near-perfect safety guarantees of rule-based systems whose strict, hardcoded rules ensure consistent comfort delivery, though at the expense of adaptability. However, the model-free nature of our barrier-based approach offers significant practical advantages, requiring no explicit system models or manual tuning while maintaining the ability to learn and adapt to building-specific dynamics, suggesting that achieving both the learnability of RL agents and the absolute safety of deterministic controllers remains an open challenge.

Table 6 highlights the effect of different training settings, with an emphasis on training length and the number of safe vs. risky states encountered. The results show that pre-training the barrier certificate (Experiment 2) increases convergence speed and decreases dangerous conditions as compared to training without it (Experiment 1). Randomly produced episodes (Experiment 3) increase generalization but result in more safety violations than repeated episodes (Experiment 4), which have faster convergence but are prone to overfitting. The occupancy-aware approach (Experiment 5) adapts successfully to various comfort restrictions, decreasing energy consumption and needless control operations. These results highlight the trade-off between exploration, safety adherence, and policy optimization in safe RL. In the final sets of experiments (6 and 7), we show that the agent can be used in more complex environments. Moreover, the comparative study showcased the effectiveness of the agent compared to baseline controllers.

5.7. Practical Implications

This paper addresses the critical building management challenge of ensuring occupant comfort while minimizing energy consumption. Our approach implements safe RL using neural barrier certificates, which fundamentally reframes the control problem—comfort requirements become explicit hard constraints rather than weighted reward components, eliminating the complex tuning process that plagues traditional RL deployments [21,24]. For practitioners, this means a more principled and interpretable control strategy that learns building-specific dynamics directly from operational data, adapting to seasonal variations and occupancy patterns without requiring mathematical models. The barrier approach substantially improves upon unconstrained learning by preventing catastrophic comfort violations, though our results reveal important limitations: the method requires significant training data and computational resources, and neural approximation errors prevent absolute safety guarantees, achieving 58.1–100% comfort compliance depending on seasonal conditions. Despite these constraints, the approach offers a viable pathway toward deployable learning-based HVAC control, particularly in applications where the balance between automation benefits and occasional comfort deviations is acceptable.

Additionally, this work demonstrated the applicability of safe RL across different control complexities, from system-level AHU control to zone-specific setpoint management. Our findings showcase the practical flexibility of the safe RL approach in real-world building automation systems. The agent successfully managed both centralized AHU parameters that affect all zones simultaneously, demonstrating the capability for system-wide optimization, and localized heating and cooling setpoints for individual zones, showing effectiveness in zone-level control strategies. This flexibility allows building operators to deploy safe RL at different control hierarchies depending on their existing infrastructure.

Building characteristics and sensor quality influence performance, potentially requiring facility-specific calibration. While the study results emphasize the energy benefits of implementing the learning system in a legacy building, the effectiveness of using RL for newly constructed, highly energy-efficient buildings still needs to be tested and quantified. Thermal insulation, thermal bridge-free construction, ventilation with heat recovery, and airtightness significantly reduce the heat demand of a building and cause longer time constants that require longer episodes for training. For this reason, future work will vary the length of the episodes and evaluate them as a function of different building energy efficiency standards. With improved building envelopes, ensuring summer comfort through shading becomes more important. The learning system could therefore be adapted to other trades.

From a deployment perspective, these summer results indicate that barrier-based RL, while promising, requires further development before matching traditional control reliability in extreme conditions. The 31 percentage point safety gap suggests that current barrier methods may be suitable for moderate climates or as auxiliary controllers but not yet as standalone replacements for rule-based systems in challenging thermal conditions.

Although there is significant potential for energy optimization and comfort maintenance, practical deployment considerations must be carefully addressed. Integrating neural network-based controllers with existing building management systems might be challenging due to limited interfaces and processing capability. Implementing edge computing to process sensor data and execute trained policies locally may incur additional hardware costs beyond initial training fees. Building operators may need a transition time with human oversight to check the system’s judgments before complete automation, potentially requiring dual-control systems throughout installation. When comparing the cost of implementation to predicted energy savings, organizations should consider integration requirements, staff training, and any disruptions during installation. Our study aims to improve energy efficiency and occupant comfort by modernizing outdated building infrastructure using data-driven methods. Our technique provides non-invasive energy-efficiency enhancements and ensures a high level of comfort.

Despite the promising results of our safe RL controller, it is crucial to acknowledge that building hull design remains a fundamental determinant of energy performance. The building envelope establishes the inherent energy efficiency potential that no control system can transcend. These architectural elements are primarily optimized during the design and construction phases, creating the baseline thermal dynamics within which any control system must operate. Our work is thus complementary to good building design: while the hull determines the fundamental energy demand characteristics, our intelligent control approach addresses the last mile of optimization–ensuring that whatever efficiency potential the building possesses is fully realized through adaptive, occupancy-aware control strategies.

6. Conclusions

This work demonstrated that safe RL effectively transforms multi-objective HVAC control into a single-objective problem with safety constraints, achieving near-perfect thermal comfort compliance while optimizing energy consumption without complex reward functions. Our neural barrier certificate provides a data-driven method to enforce comfort constraints without explicit thermal modeling through data collection. Through comprehensive experimental evaluation, we successfully addressed all three research questions posed in this study. Our findings demonstrated the broad applicability and effectiveness of safe RL with neural barrier certificates across diverse building control scenarios (RQ1), revealed the impact of pre-training and episode generation strategies on agent performance (RQ2), and confirmed that safe RL achieves competitive performance compared to established baseline controllers (RQ3). These results enabled us to reject the null hypothesis and validate our approach as a viable alternative for building climate control. Our work delivers four key contributions to the field: we demonstrated the applicability of safe RL with neural barrier certificates in building control, validating its effectiveness for handling thermal comfort constraints while optimizing energy consumption across both residential and commercial buildings. We provided empirical evidence of the method’s performance across multiple BOPTEST test cases, different control levels (from direct equipment control to AHU parameters), and varying episode lengths and learning intervals. Our experiments showed that pre-trained barrier functions improve learning efficiency and produce less conservative policies compared to non-pretrained approaches. We established that safe RL occupies a middle ground in the control landscape, accepting modest energy penalties compared to unconstrained PPO and RBCs in exchange for dramatically improved safety over standard RL, though still falling short of rule-based safety performance.

Our experiments revealed that pre-trained barrier certificates can achieve better performance while maintaining the comfort bounds, though violations cannot be reduced to zero due to the neural barrier certificate’s inherent approximation error. Additionally, our occupancy-aware framework dynamically adjusts comfort constraints based on building occupancy, demonstrating better energy savings while maintaining comfort during occupied periods. Moreover, our experiments on complex multi-zone scenarios demonstrated that the agent is capable of handling complex environments while achieving acceptable safety performance. Through comparative study, the agent traded energy efficiency for improved safety compliance compared to unconstrained RL, achieving this balance through a model-free approach without requiring explicit system models, though safety performance still lags behind traditional RBC. Across seasons, the comparative results show that in winter—when all controllers satisfy comfort—the barrier-PPO and PPO exhibit identical median energy (2.25 kWhm⁻²), with the barrier variant offering steadier operation; in spring and autumn, the safe agent achieves near-perfect compliance (99.9%/99.6%) while unconstrained PPO falls short (71.1%/85.6%); and in summer, while unconstrained PPO uses 10% less energy, its 25.0% compliance renders it impractical; barrier-PPO raises safety to 58.1% but still trails RBC, which achieves both superior safety (89.3%) and energy efficiency. These outcomes suggest that safety-aware RL is a promising middle ground—delivering substantial safety gains over unconstrained RL with competitive efficiency—while further refinement is needed to match rule-based reliability under extreme conditions.

These contributions address key challenges in sustainable building management by enforcing comfort as a hard constraint while optimizing for energy efficiency. This approach has direct applications in intelligent building management systems where occupant preferences vary over time. While we focused on HVAC control, future research should address additional dimensions such as lighting and plumbing (e.g., hot water) while considering broader and potentially adaptive safety aspects. Additionally, extending the barrier certificate framework to handle multi-modal comfort preferences and incorporating human feedback mechanisms could make these systems more responsive to actual occupant needs while maintaining energy efficiency goals. Despite promising results and achieving acceptable performance, safe RL in building domain still requires more advancements in sample efficiency, robustness, and computational efficiency before becoming widely applicable in real-world building management systems.