Evaluation of Development Performance and Adjustment Strategies for High Water-Cut Reservoirs Based on Flow Diagnostics: Application in the QHD Oilfield
Abstract
1. Introduction
2. Methods
2.1. Flow Diagnostics Method
- (1)
- TOF Equation
- (2)
- Tracer Concentration Equation
2.2. Quantitative Diagnostic Evaluation System for Water Injection Development Performance
- (1)
- Time-of-Flight (TOF): Quantitatively describes the injection sweep range, defines displacement fronts, and assesses displacement intensity.
- (2)
- Dynamic Lorenz coefficient: Characterizes the uniformity of displacement and the heterogeneity of flow distribution within an injection–production pattern.
- (3)
- Injection–Production Communication Volume: Measures the degree of inter-well connectivity and the effective sweep efficiency of the injected fluids.
- (4)
- Inter-well Fluid Allocation Factor: Assesses the dynamic correspondence and fluid transfer architecture between injectors and producers.
- (a)
- Time-of-Flight (TOF)
- (b)
- Dynamic Heterogeneity
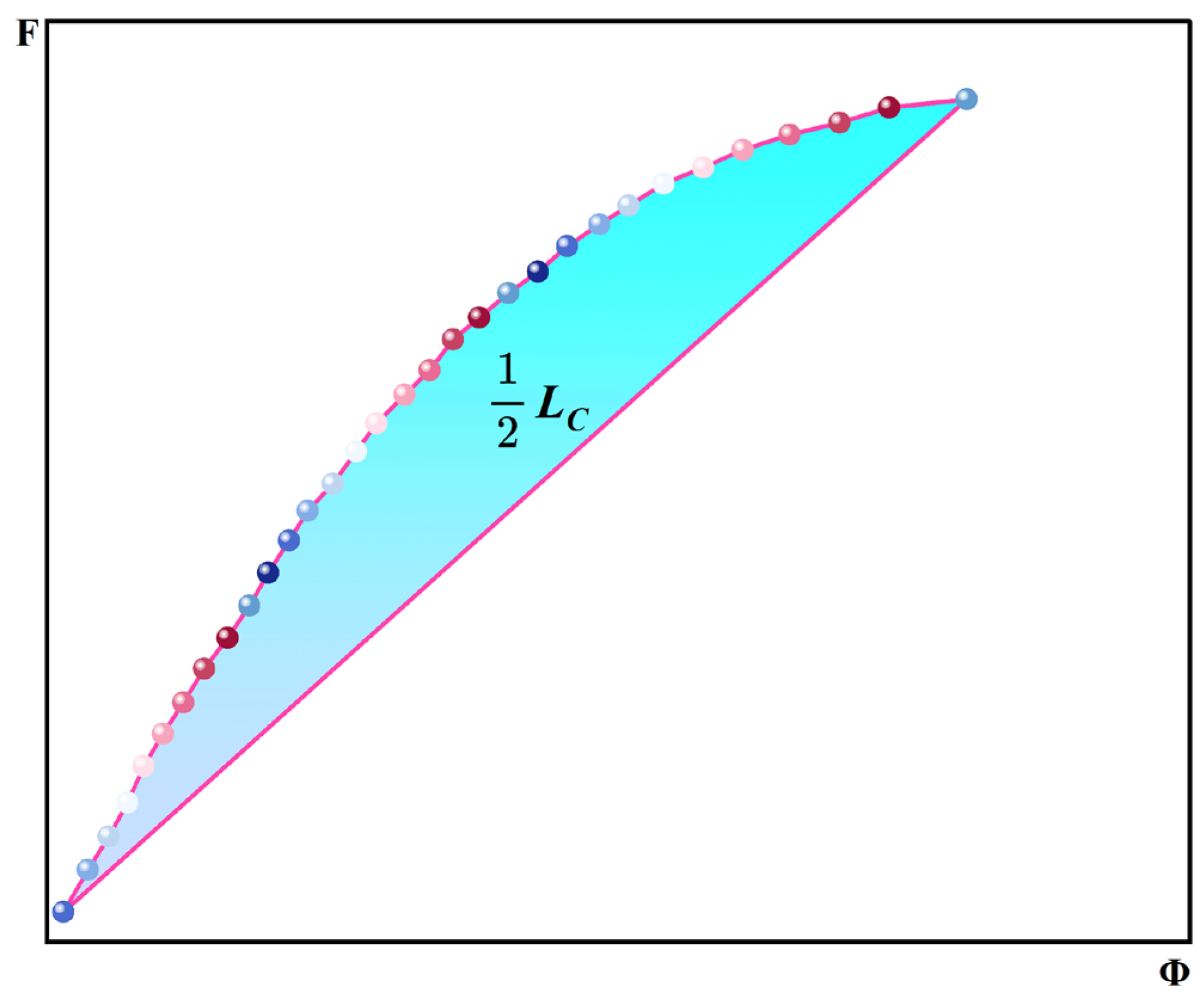
- (1)
- F-Φ Diagnostic Curve
- (2)
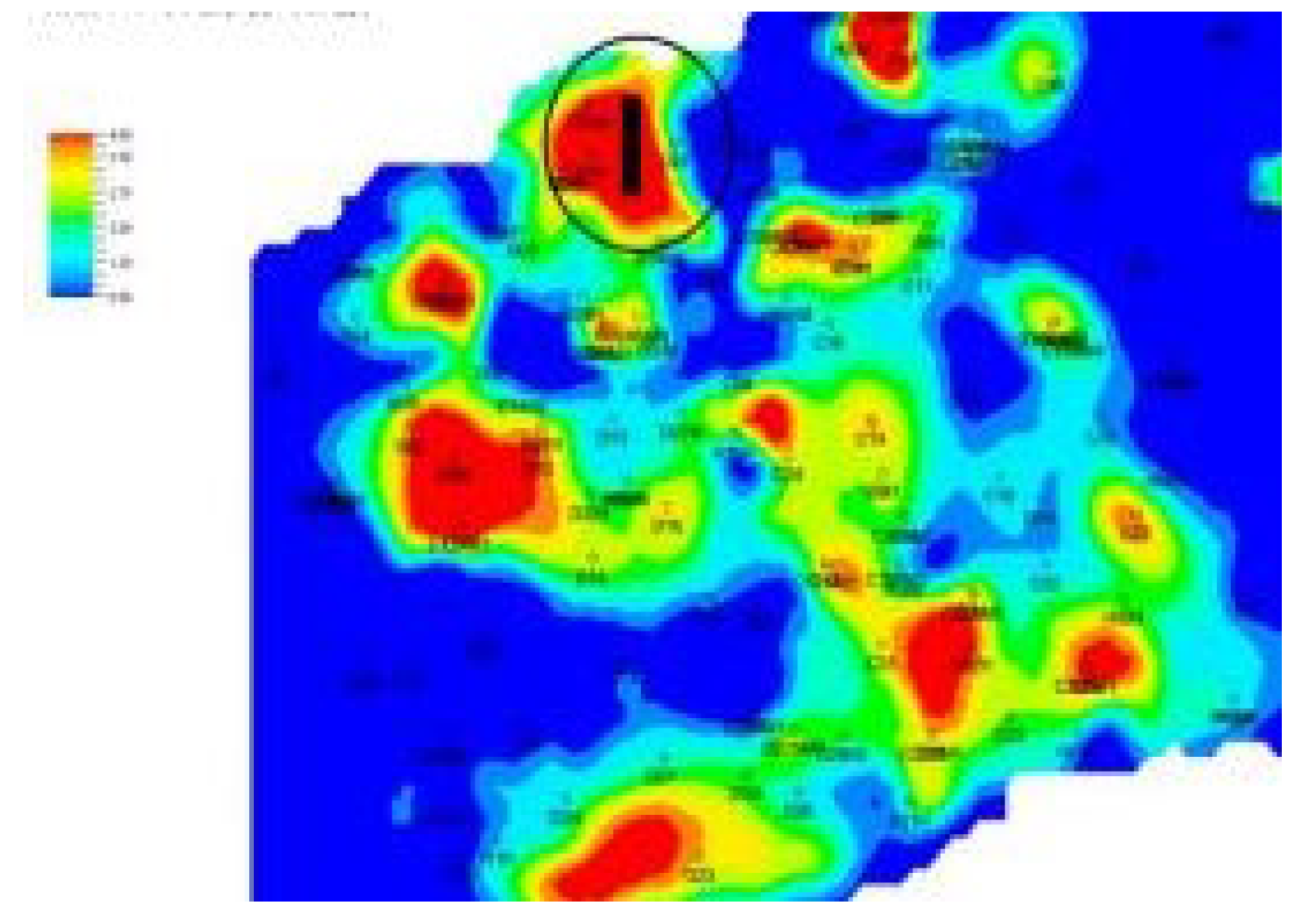
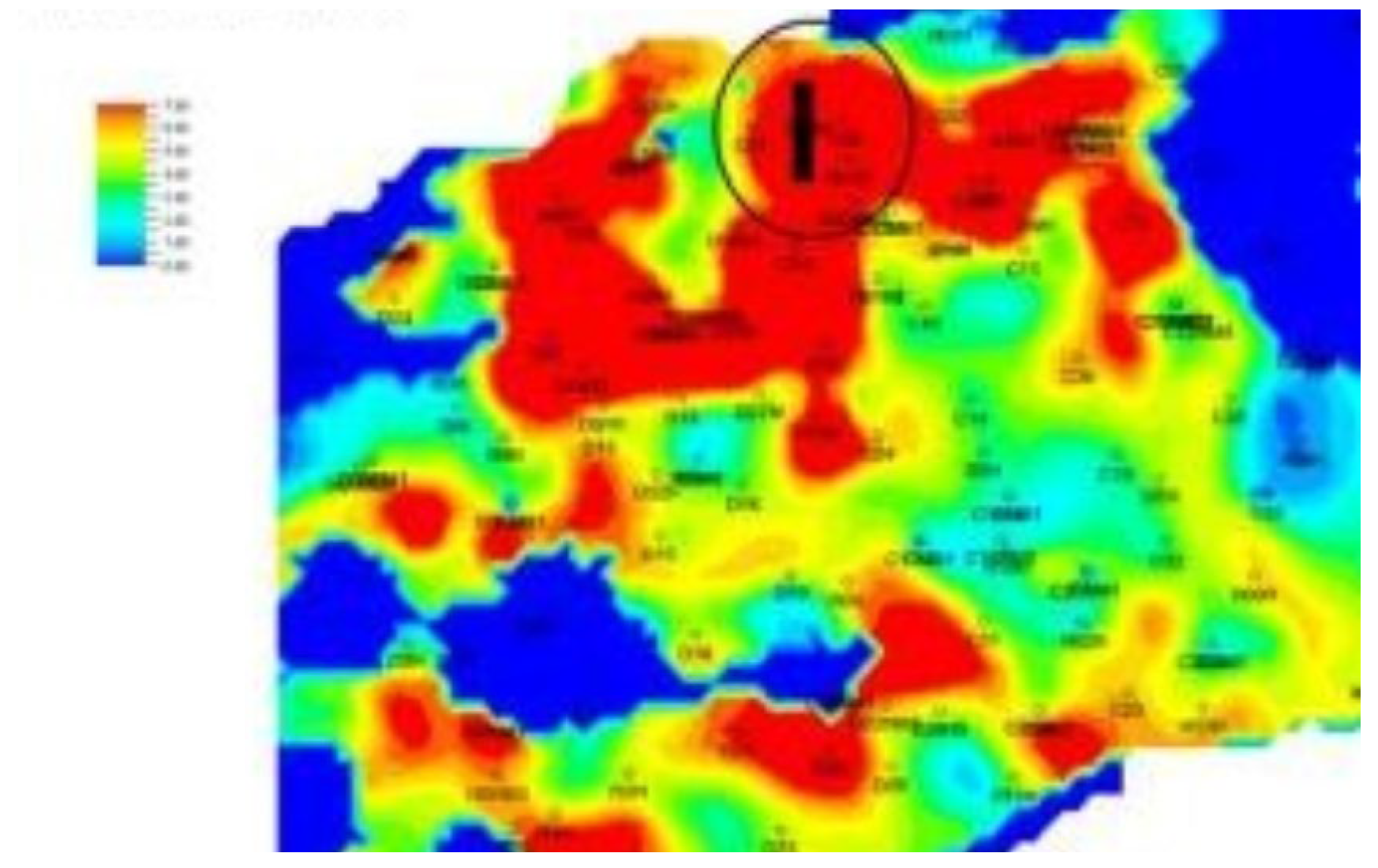
- Dynamic Lorenz Coefficient
- (3)
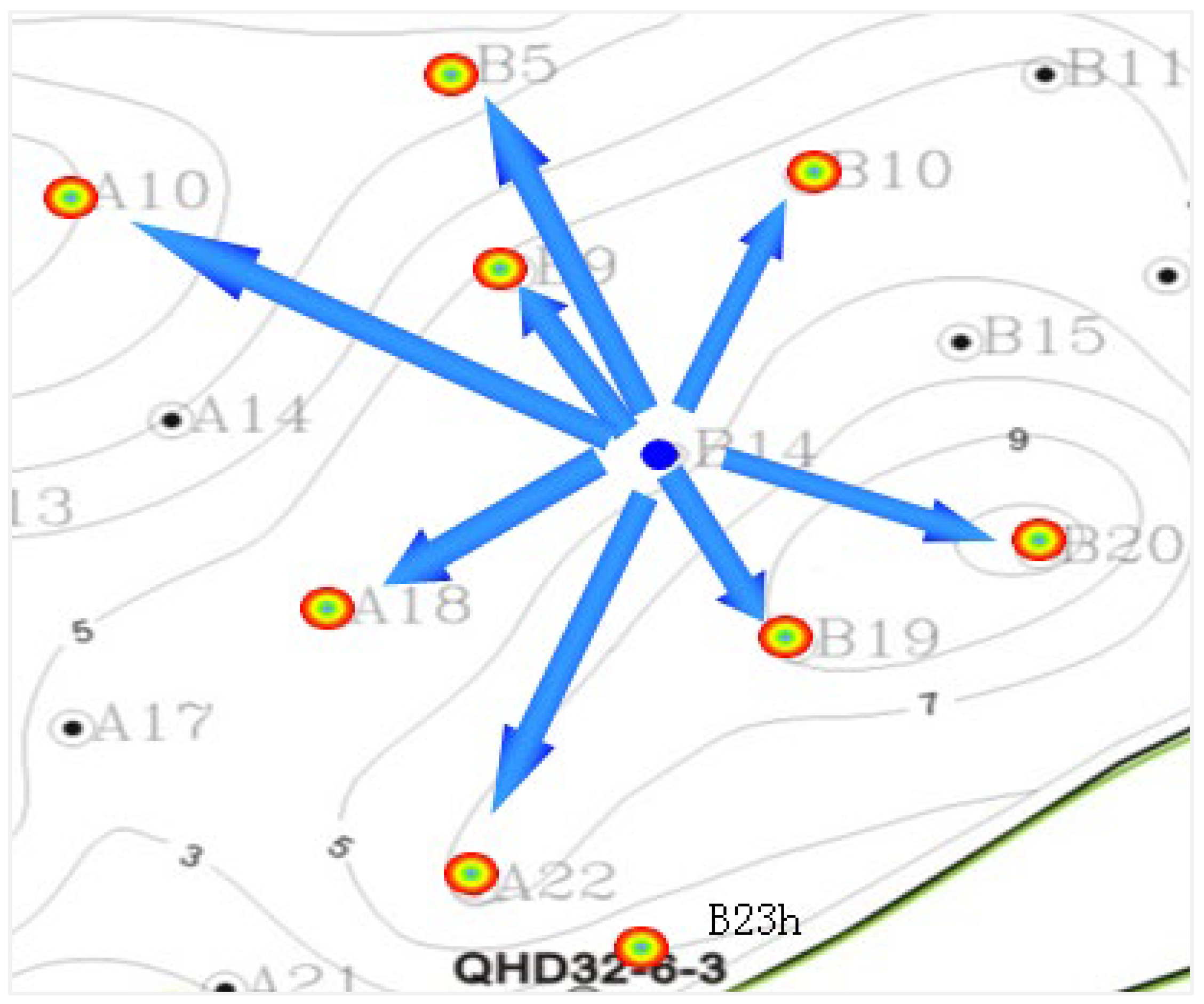
- Injection–Production Communication Volume
- (4)
- Inter-Well Fluid Allocation Factor
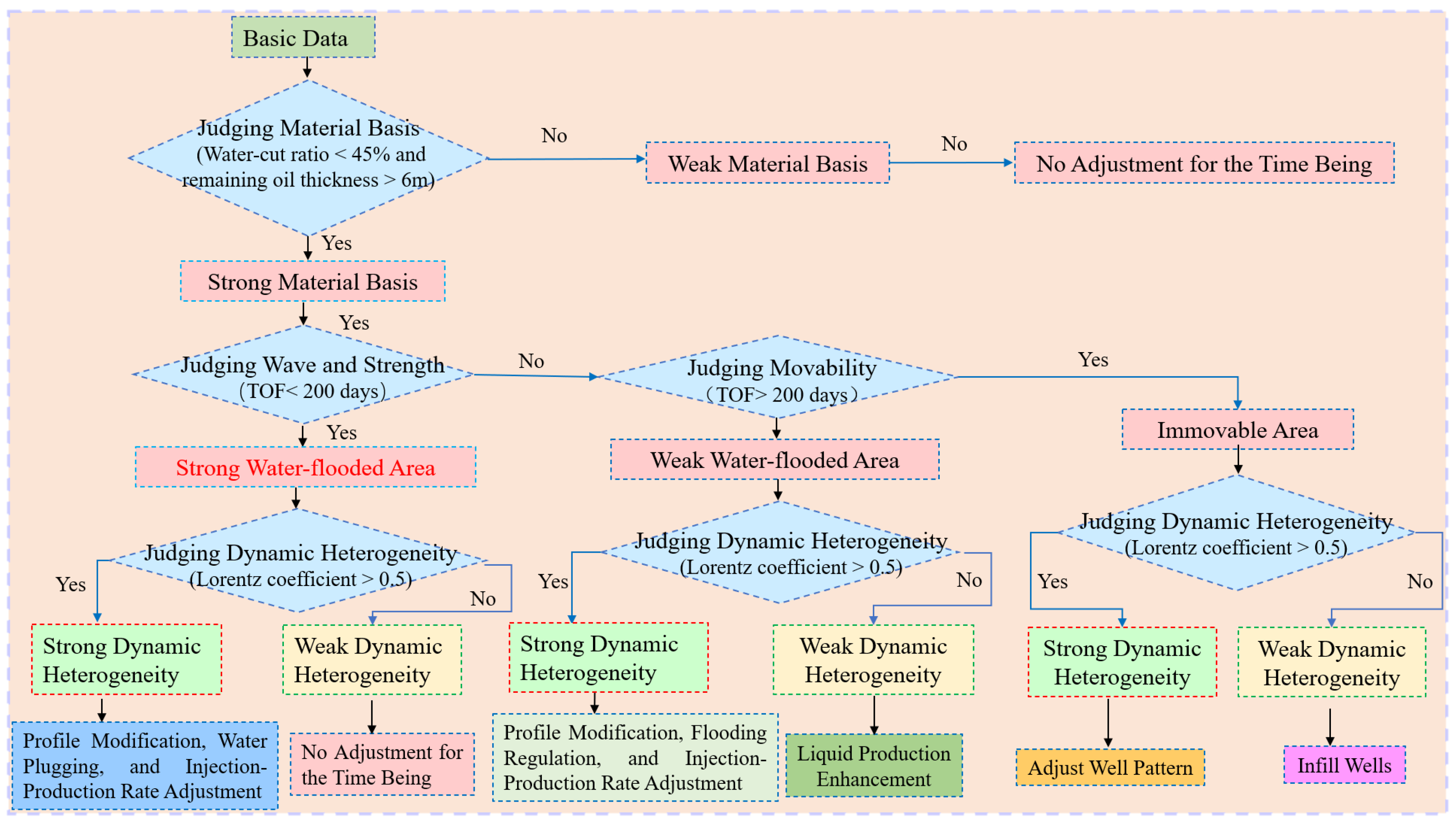
2.3. Hierarchical Adjustment Strategies for Water Injection Development
2.4. Limitations and Uncertainty Considerations
3. Block Application and Practice
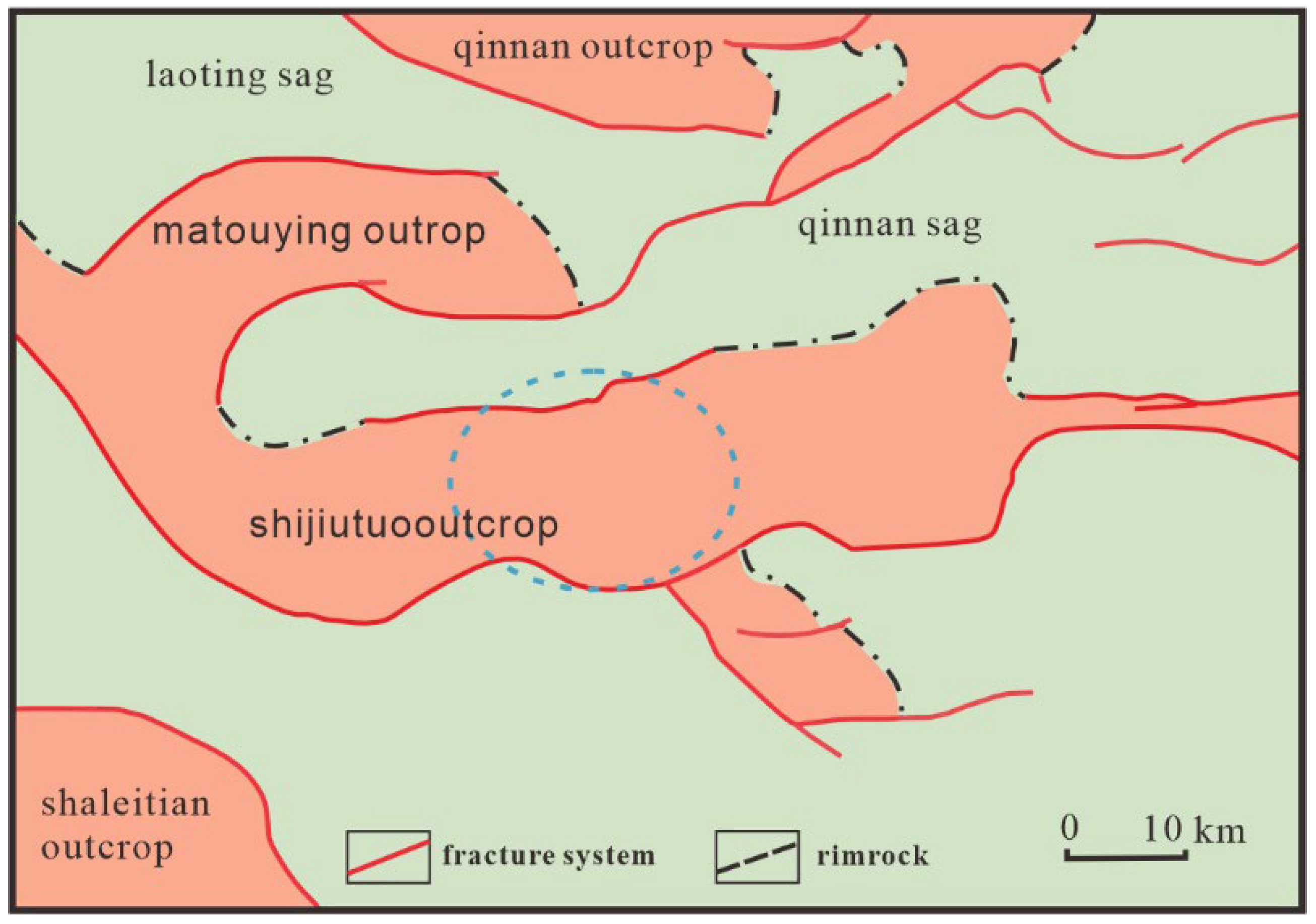
3.1. Block Overview
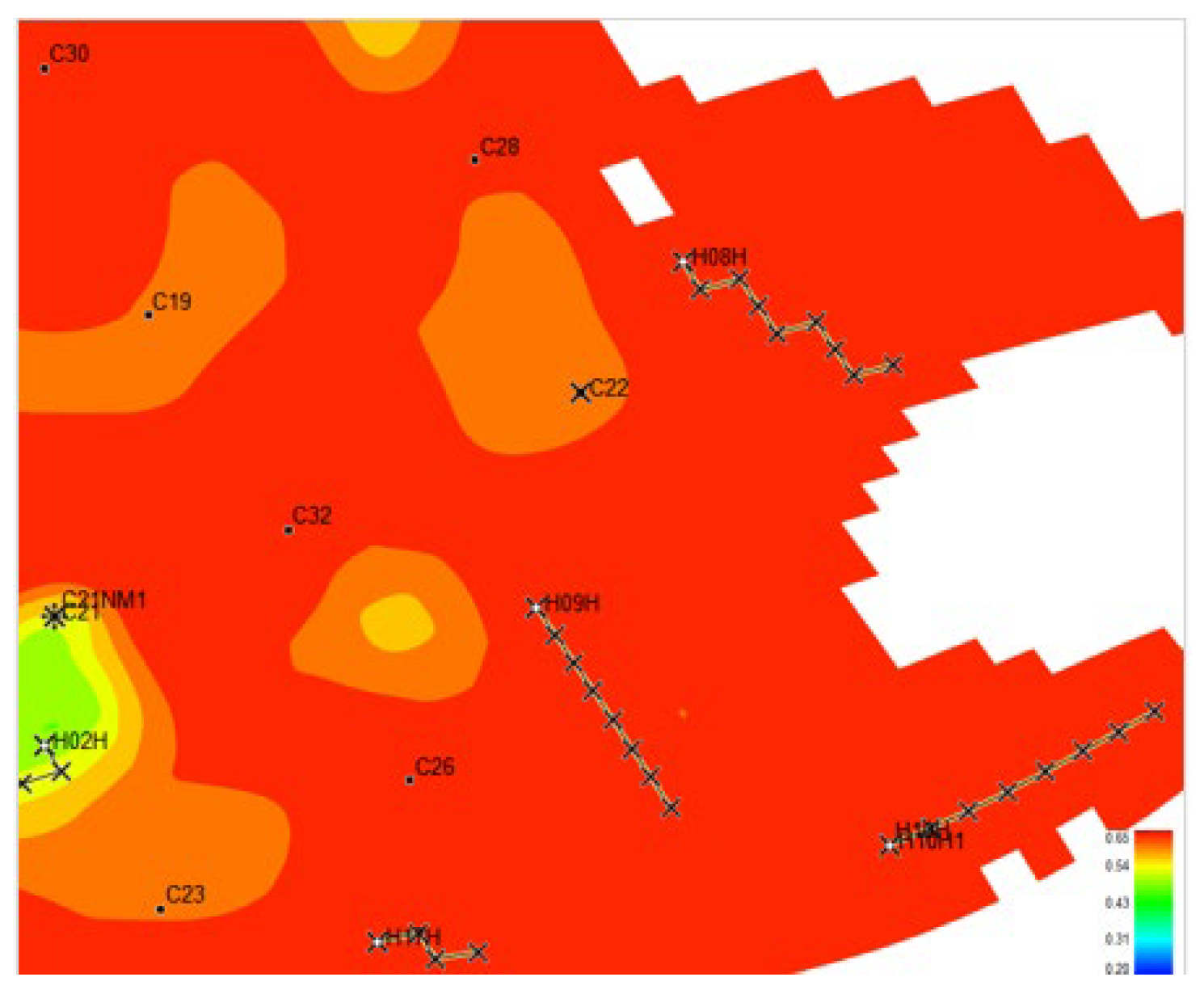
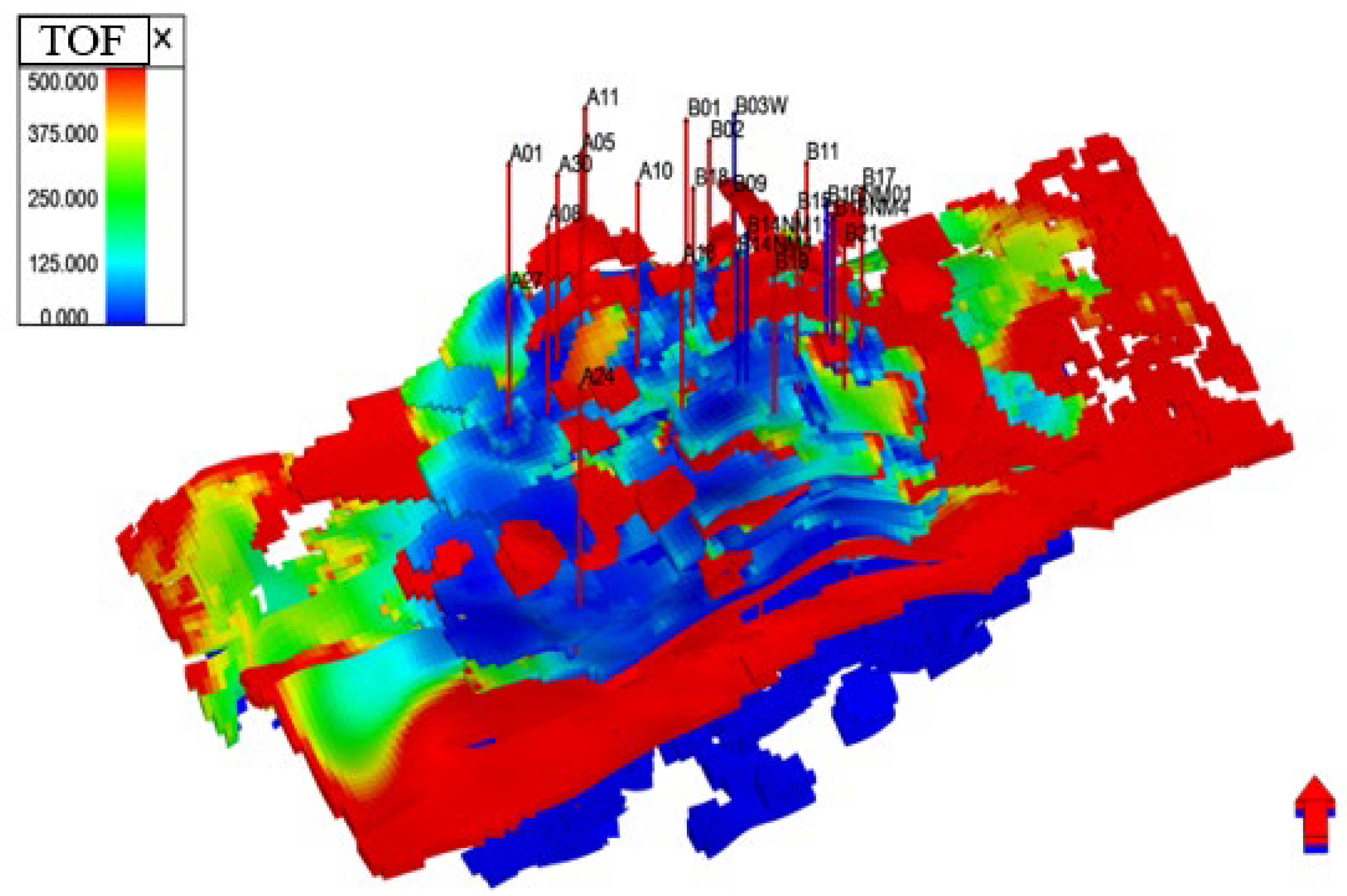
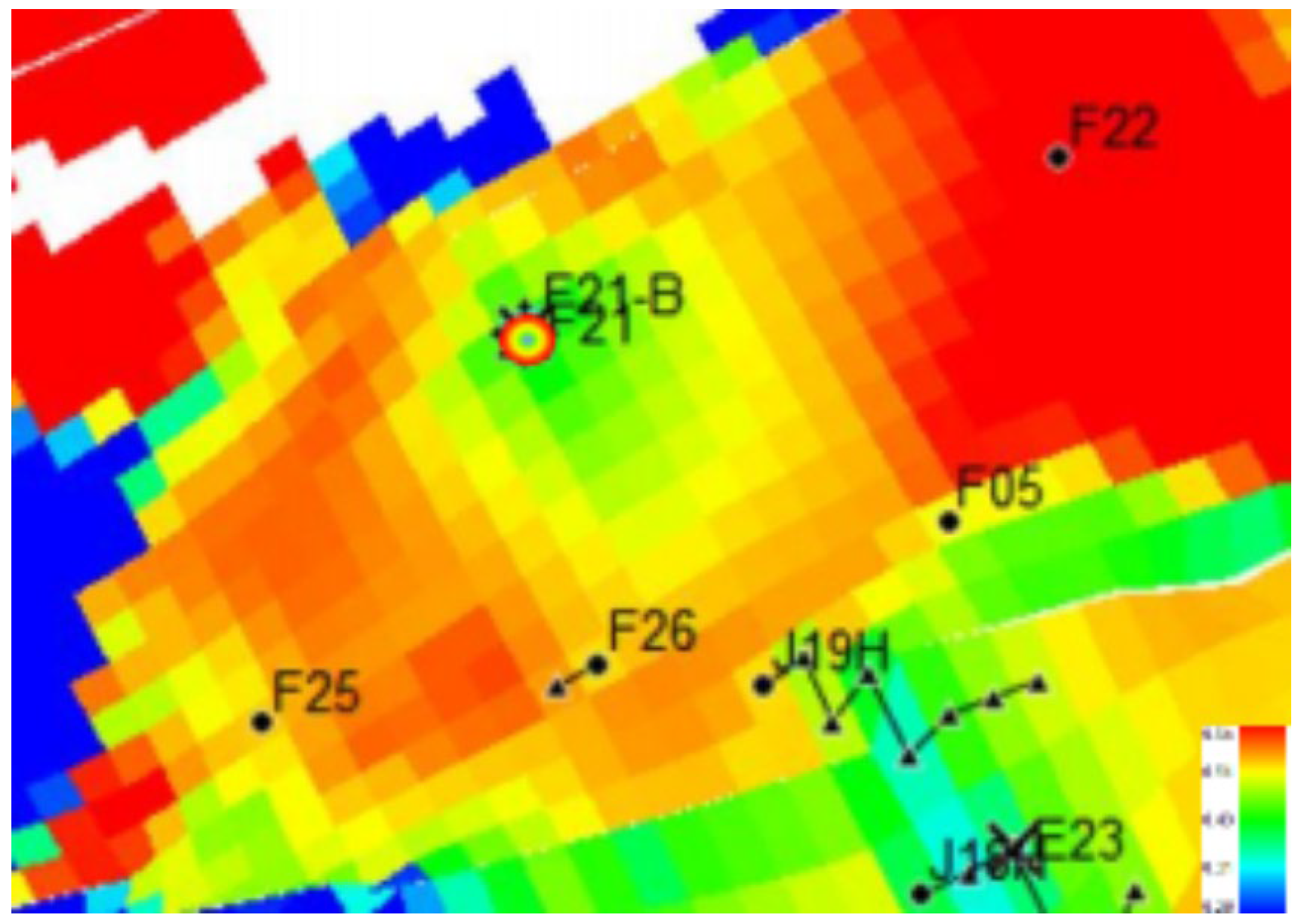
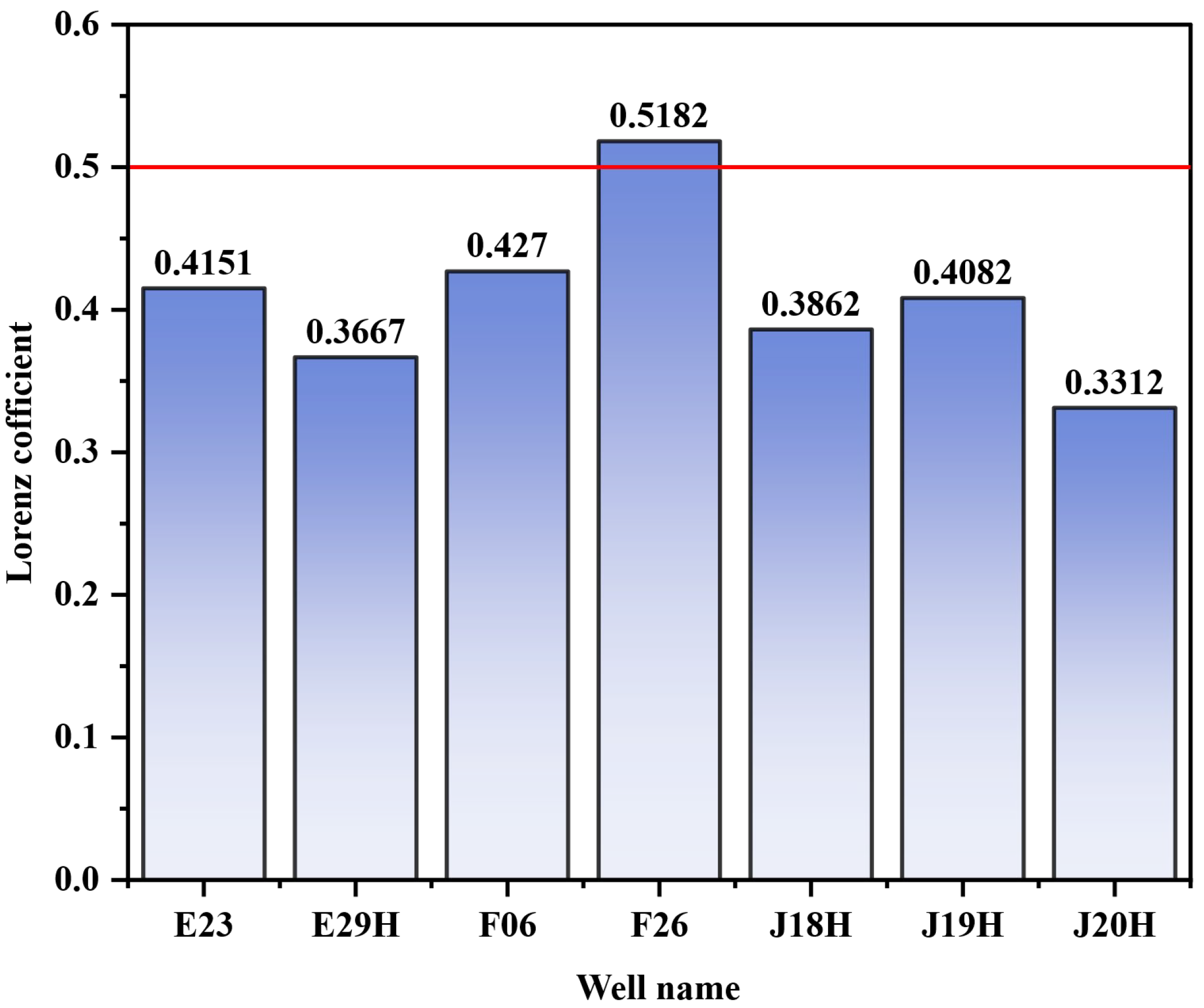
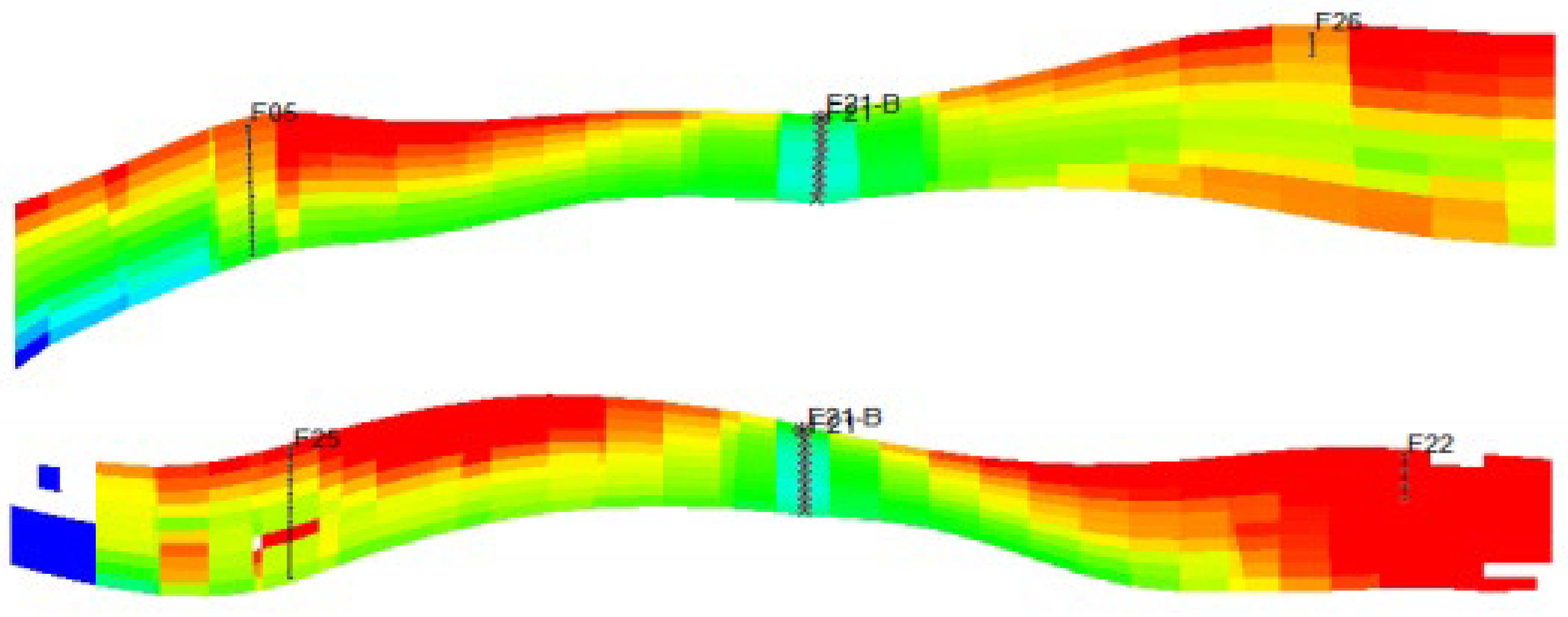
3.2. Water Injection Development Performance Evaluation in Target Block
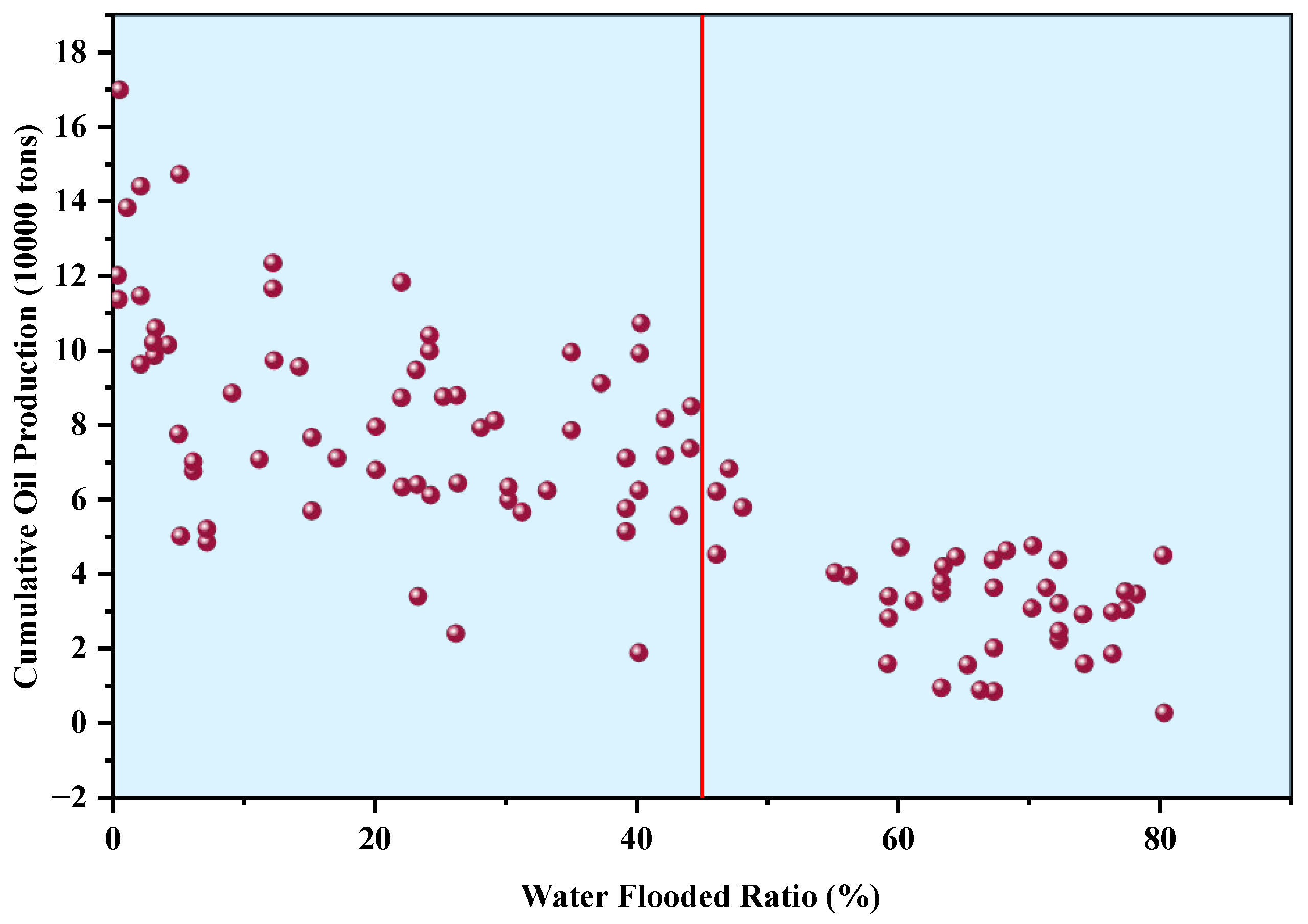
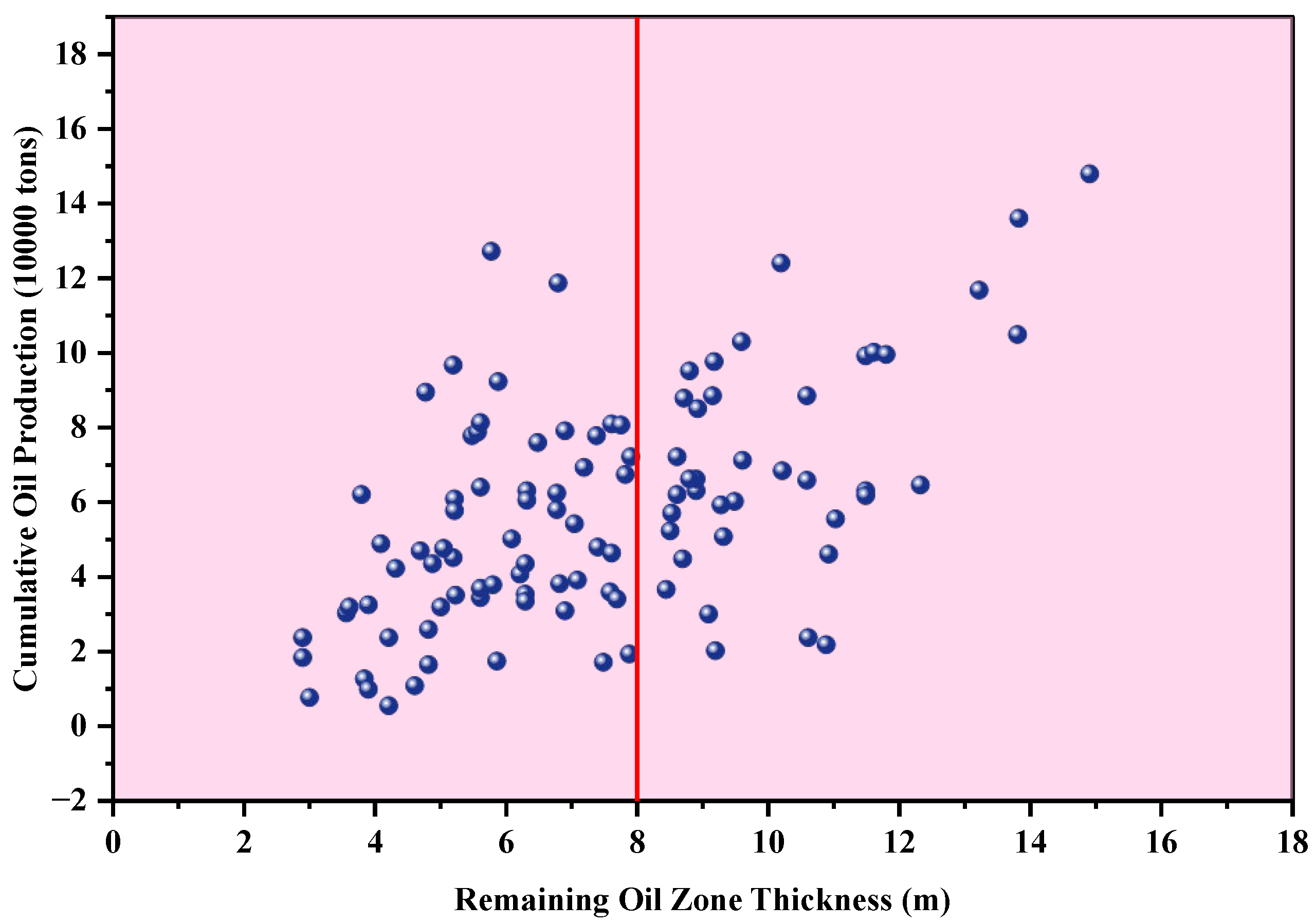
3.3. Adjustment Thresholds
3.3.1. Infill Drilling Thresholds
3.3.2. Conformance Control and Displacement Adjustment Thresholds
3.3.3. Liquid Lifting Thresholds
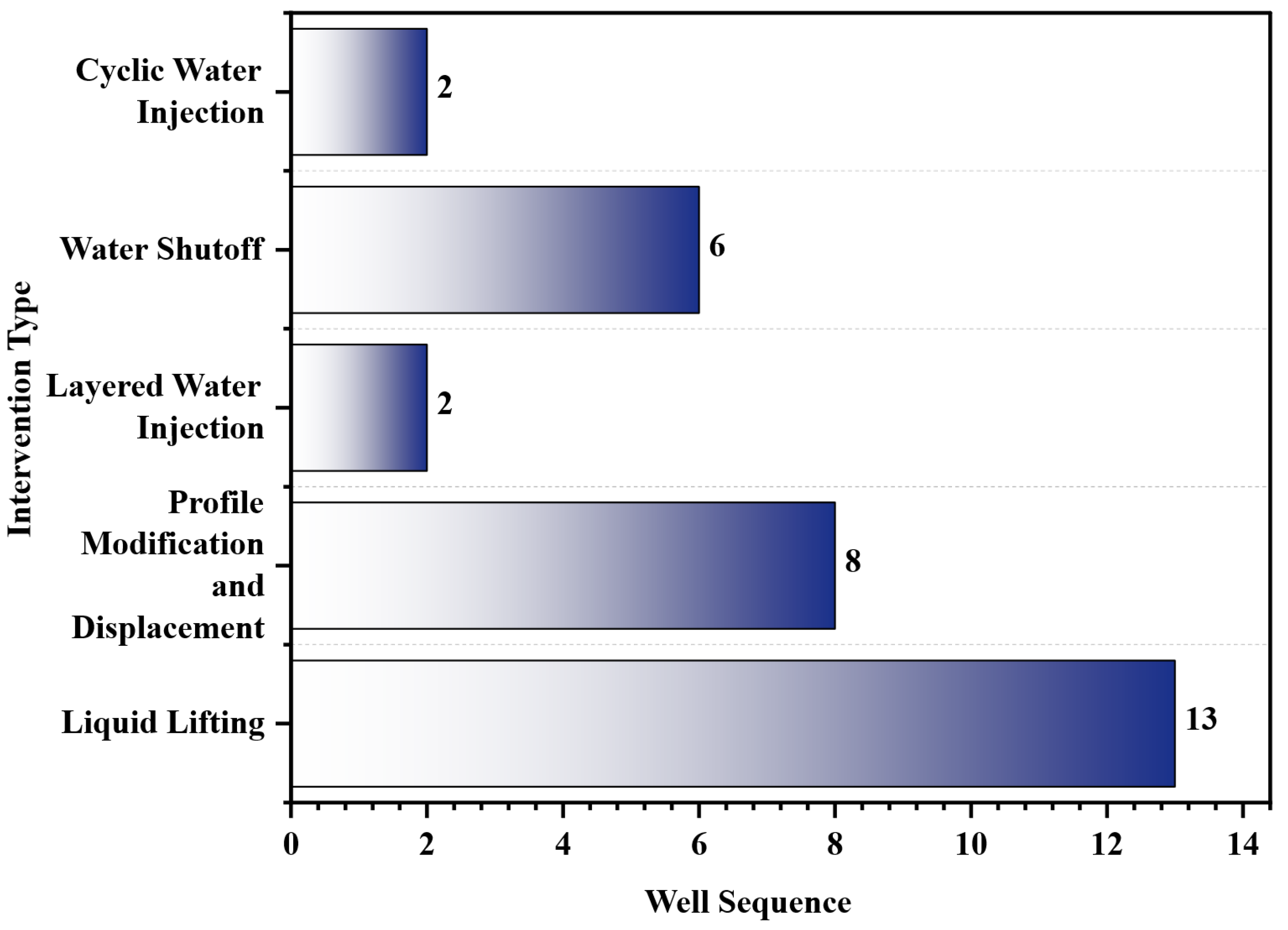
3.4. Adjustment Strategies and Schemes
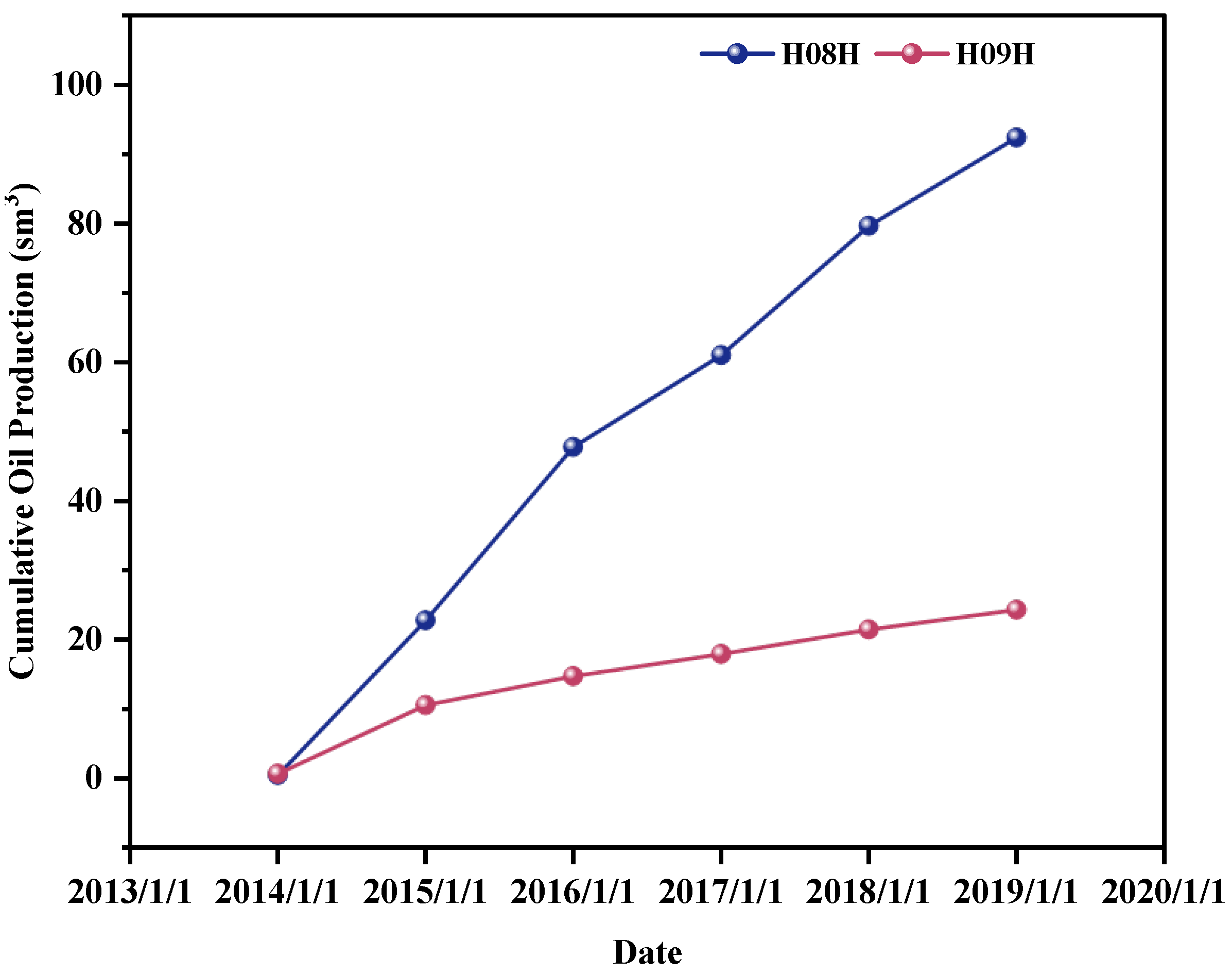
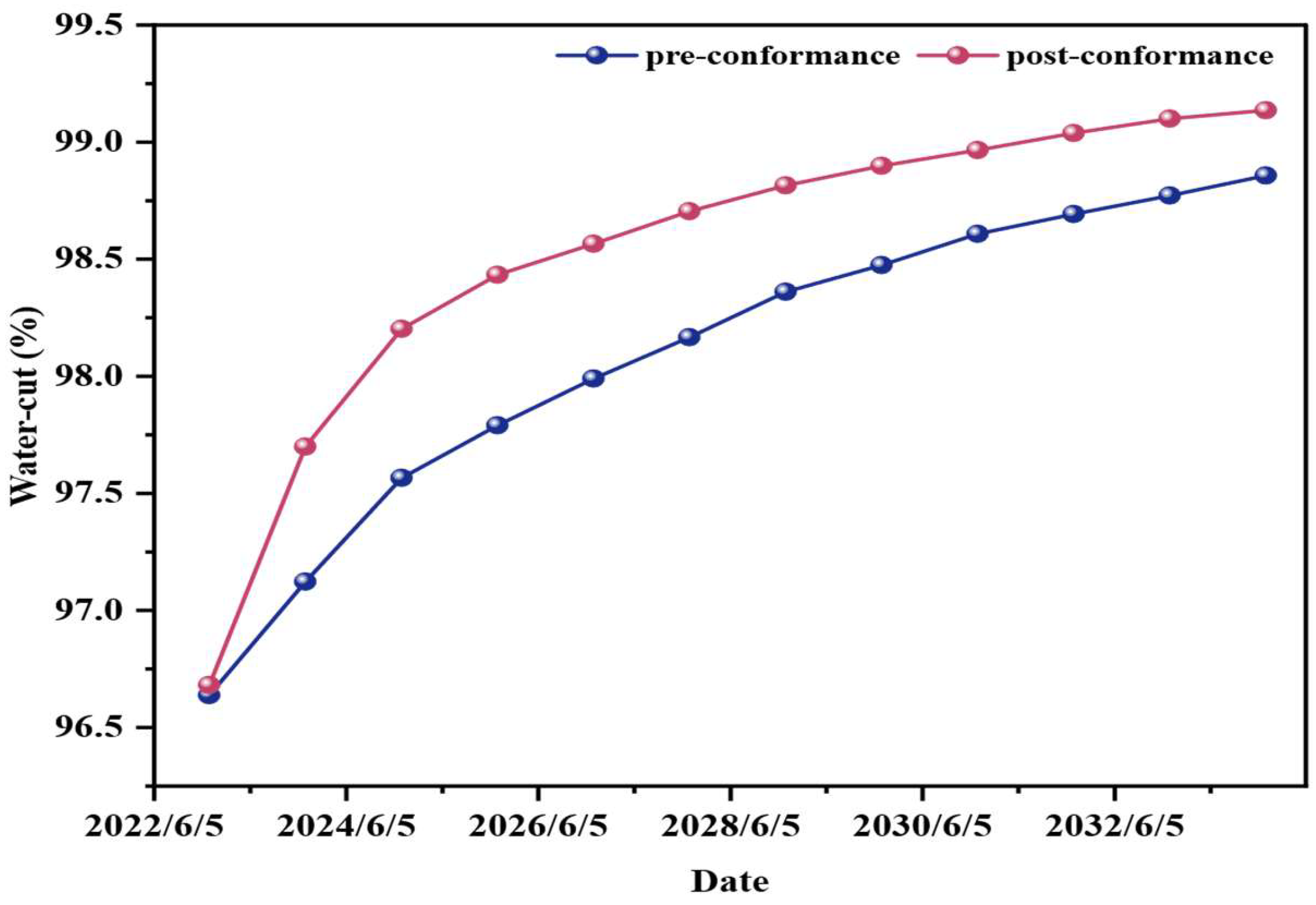
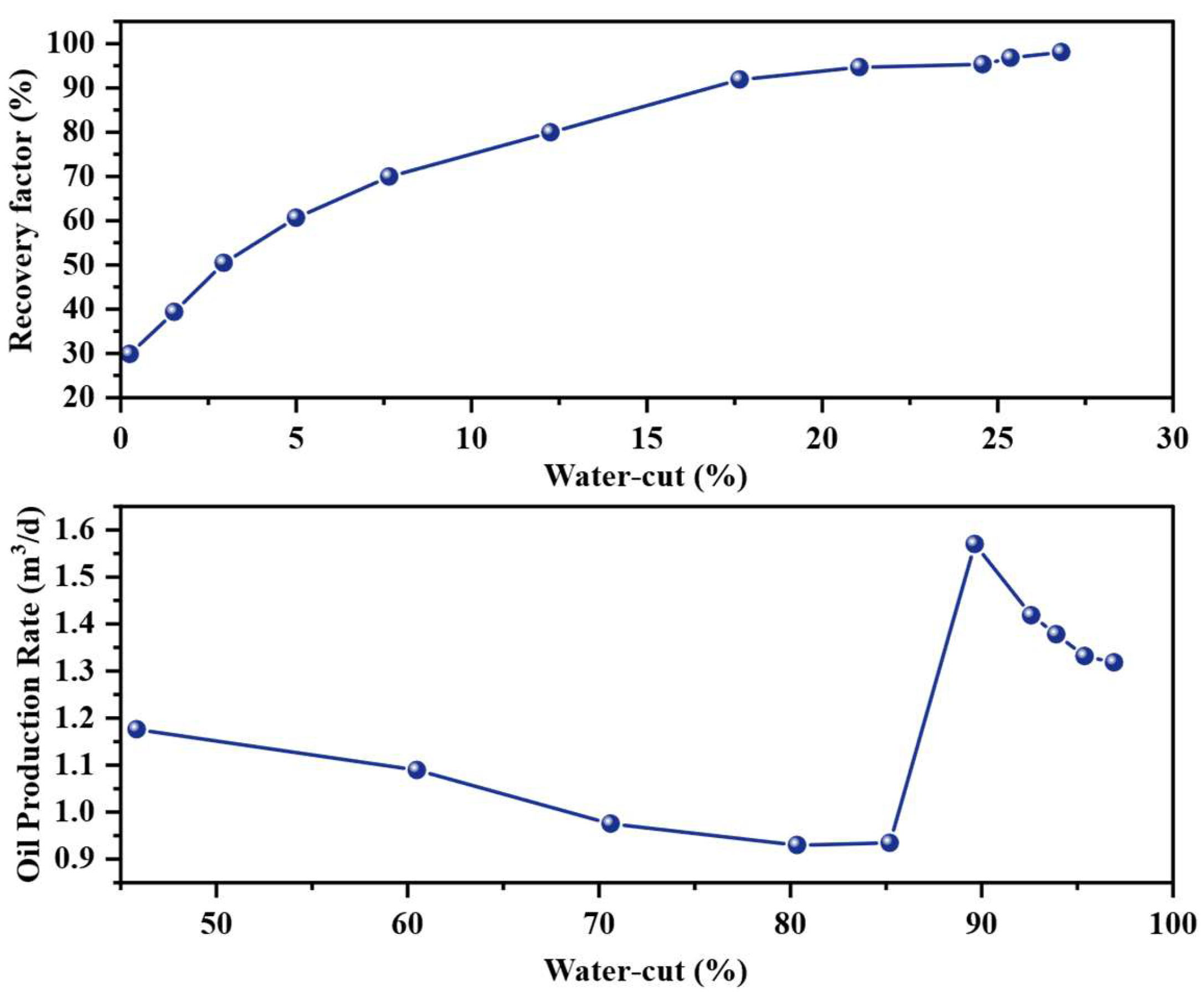
3.5. Adjustment Effects
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yuan, S.; Han, H.; Wang, H.; Luo, J.; Wang, Q.; Lei, Z.; Xi, C.; Li, J. Research progress and potential of new enhanced oil recovery methods in oilfield development. Pet. Explor. Dev. 2024, 51, 963–980. [Google Scholar] [CrossRef]
- Feng, G.; Zhou, Y.; Yao, W.; Liu, L.; Feng, Z.; Yi, Y.; Feng, Y. Countermeasures to Decrease Water Cut and Increase Oil Recovery from High Water Cut, Narrow-Channel Reservoirs in Bohai Sea. Geofluids 2021, 2021, 6671098. [Google Scholar] [CrossRef]
- Temizel, C.; Canbaz, C.H.; Tran, M.; Abdelfatah, E.; Jia, B.; Putra, D.; Irani, M.; Alkouh, A. A comprehensive review heavy oil reservoirs, latest techniques, discoveries, technologies and applications in the oil and gas industry. In Proceedings of the SPE International Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2018. [Google Scholar]
- Liu, J.; Liu, S.; Gao, P.; Zhang, Q.; Liu, Y.; Chen, X.; Zhong, L.; Lin, Y. Efficient development strategies for heavy oil reservoirs with a focus on rational utilization of water resources. Sep. Purif. Technol. 2025, 362, 131943. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Y.; Zhang, L.; Zhang, Q.; Guo, Z.; Wang, B.; Sun, T. Remaining oil distribution characteristics in an oil reservoir with ultra-high water-cut. Energy Geosci. 2024, 5, 100116. [Google Scholar] [CrossRef]
- Ma, K.; Li, A.; Guo, S.; Pang, J.; Xue, Y.; Zhou, Z. Techniques for improving the water-flooding of oil fields during the high water-cut stage. Oil Gas Sci. Technol. Rev. d’IFP Energ. Nouv. 2019, 74, 69. [Google Scholar] [CrossRef]
- Shi, H.; Liu, Y.; Jiang, L.; Zheng, J.; Gan, L. Integrated Solutions for the Redevelopment Plan of Offshore Mature-Oilfield. In Proceedings of the International Petroleum Technology Conference, Virtual, 23 March–2 April 2021. [Google Scholar]
- Liu, H. Challenges and development direction for deep development of high water-cut mature oilfields. Pet. Geol. Oilfield Deve. Daqing 2024, 43, 15–24. (In Chinese) [Google Scholar]
- Arps, J.J. Analysis of decline curves. Trans. AIME 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Miao, F.; Zhang, H.; Zhang, Y. New method for evaluating waterflooding effect by decline rate index. Fault-Block Oil Gas Field 2015, 22, 353–355. (In Chinese) [Google Scholar]
- Miguel, P.R.; Joanna, Z.; Stefano, Z.; Alejandro, S.; Eduardo, T. Fluid dynamics analysis and performance of polymer flow regulators for polymer flooding in multilayered reservoirs. J. Pet. Sci. Eng. 2022, 208, 109680. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, X.; Bi, Y.; He, H.; Gu, X.; Liu, T.; Zhao, L. Analysis of Channeling-Path Phenomena in a Complex Fault-Block Reservoir with Low Recovery Factor and High Water-Cut Ratio. Fluid Dyn. Amp; Mater. Process. 2022, 19, 361–377. [Google Scholar]
- Zhao, P.; He, S.; Cai, M.; Tao, Z.; Zhao, M.; Wu, X.; Ni, T.; Guo, Q.; Wei, P.; Wang, Q.; et al. Streamline simulation based vector flow field characterization and reconstruction method for high water cut reservoir. In Proceedings of the International Petroleum Technology Conference, Shanghai, China, 26–28 August 2020. [Google Scholar]
- Guan, C.; Zhang, J.; Li, X. Quantitative Research on Development Status of Heterogeneous Reservoirs in Offshore Oilfields. In Proceedings of the International Petroleum Technology Conference, Riyadh, Saudi Arabia, 21–23 February 2022. [Google Scholar]
- Li, L.; Yuan, X.; Dai, D.; Yan, C.; Ping, F.; Wang, W. Evaluation of Water Injection Development Effect in Block B of the Bohai Sea. Chem. Eng. Manag. 2024, 7, 152–156. (In Chinese) [Google Scholar]
- Ning, L.; Yang, L.; Zheng, X.; Zhang, J.; Liu, Y.; Ma, J. Evaluation on injection-production connectivity of low-permeability reservoirs based on tracer monitoring and numerical simulation. Xinjiang Pet. Geol. 2021, 42, 735. [Google Scholar]
- Kulkarni, K.N.; Datta-Gupta, A.; Vasco, D. A Streamline Approach for Integrating Transient Pressure Data into High-Resolution Reservoir Models. SPE J. 2001, 6, 273–282. [Google Scholar] [CrossRef]
- Wen, H.; Sun, N.; Liu, Y. Index system evaluating water flooding development effect of oilfield at ultra-high water cut stage. J. Pet. Explor. Prod. Technol. 2017, 7, 111–123. [Google Scholar] [CrossRef][Green Version]
- Chu, Q.; Chen, X.; Shi, P. Developed effects analyses and quantitative evaluating method for QinJiaTun Complex fault-block oilfield. Pet. Geol. Oilfield Dev. Daqing 2016, 35, 58–63. (In Chinese) [Google Scholar][Green Version]
- Li, Z.; Guo, Q.; Zhuang, T.; He, S. Evaluation method of producer development effect in high water-cut reservoirs. Pet. Geol. Recovery Effic. 2022, 29, 85–93. (In Chinese) [Google Scholar][Green Version]
- Wang, C.; Sun, Z.; Sun, Q.; Zhang, L.; Zhang, X. Comprehensive evaluation of waterflooding front in low-permeability reservoir. Energy Sci. Eng. 2021, 9, 1394–1408. [Google Scholar] [CrossRef]
- Shahvali, M.; Mallison, B.; Wei, K.; Gross, H. An Alternative to Streamlines for Flow Diagnostics on Structured and Unstructured Grids. SPE J. 2012, 17.3, 768–778. [Google Scholar] [CrossRef]
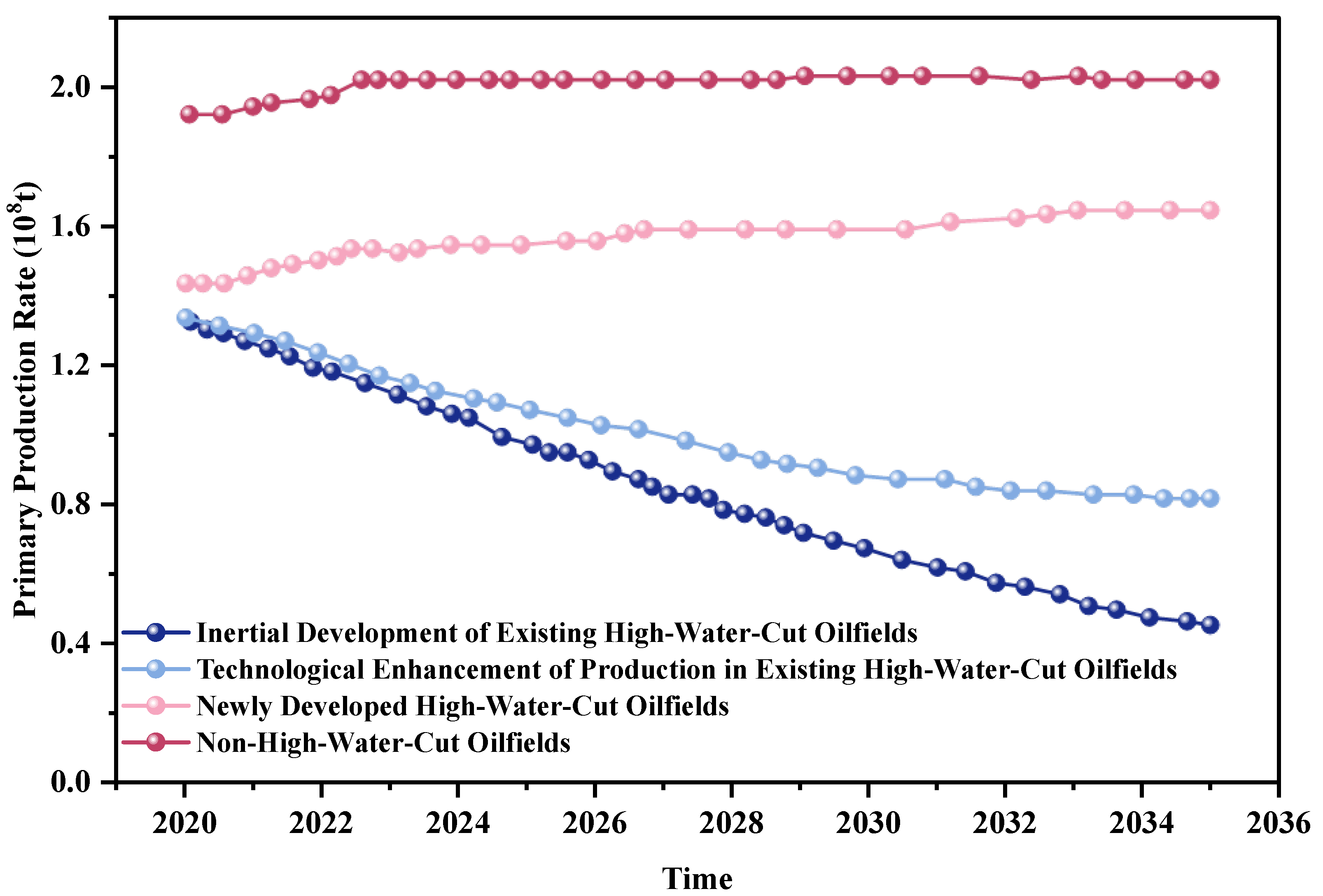
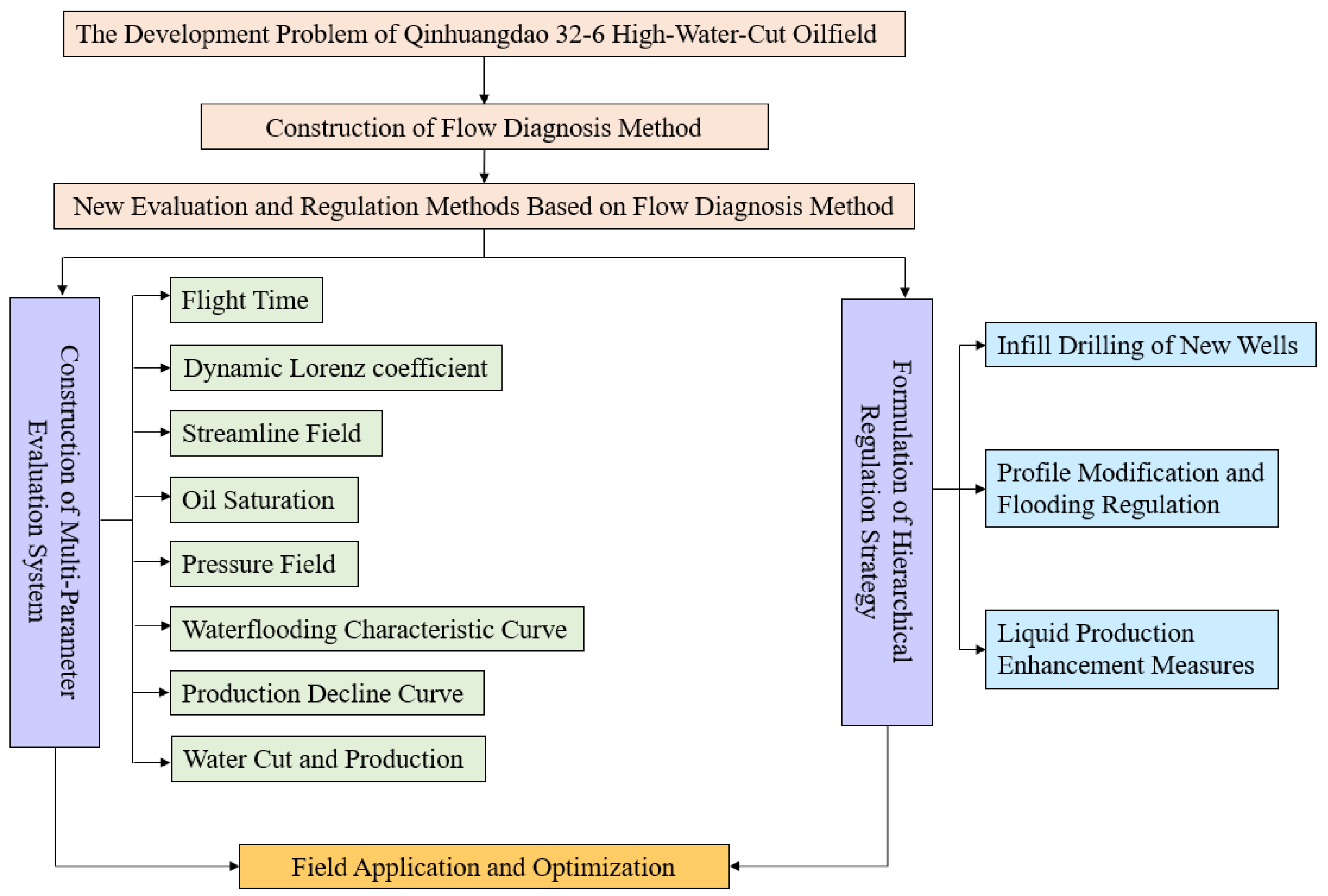
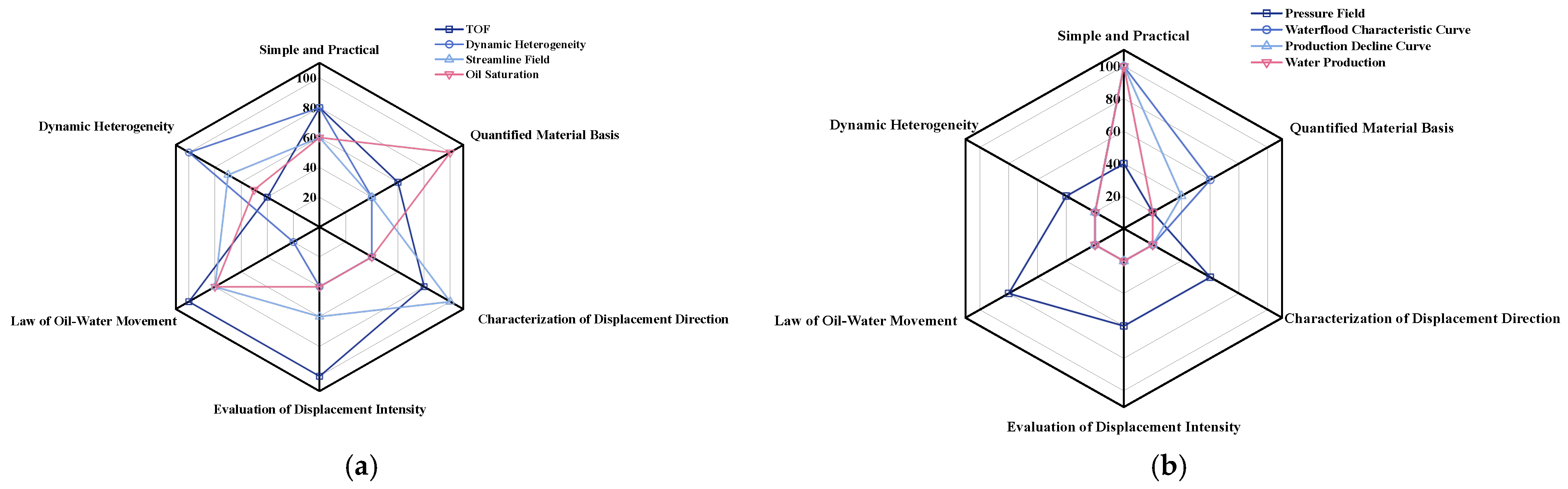


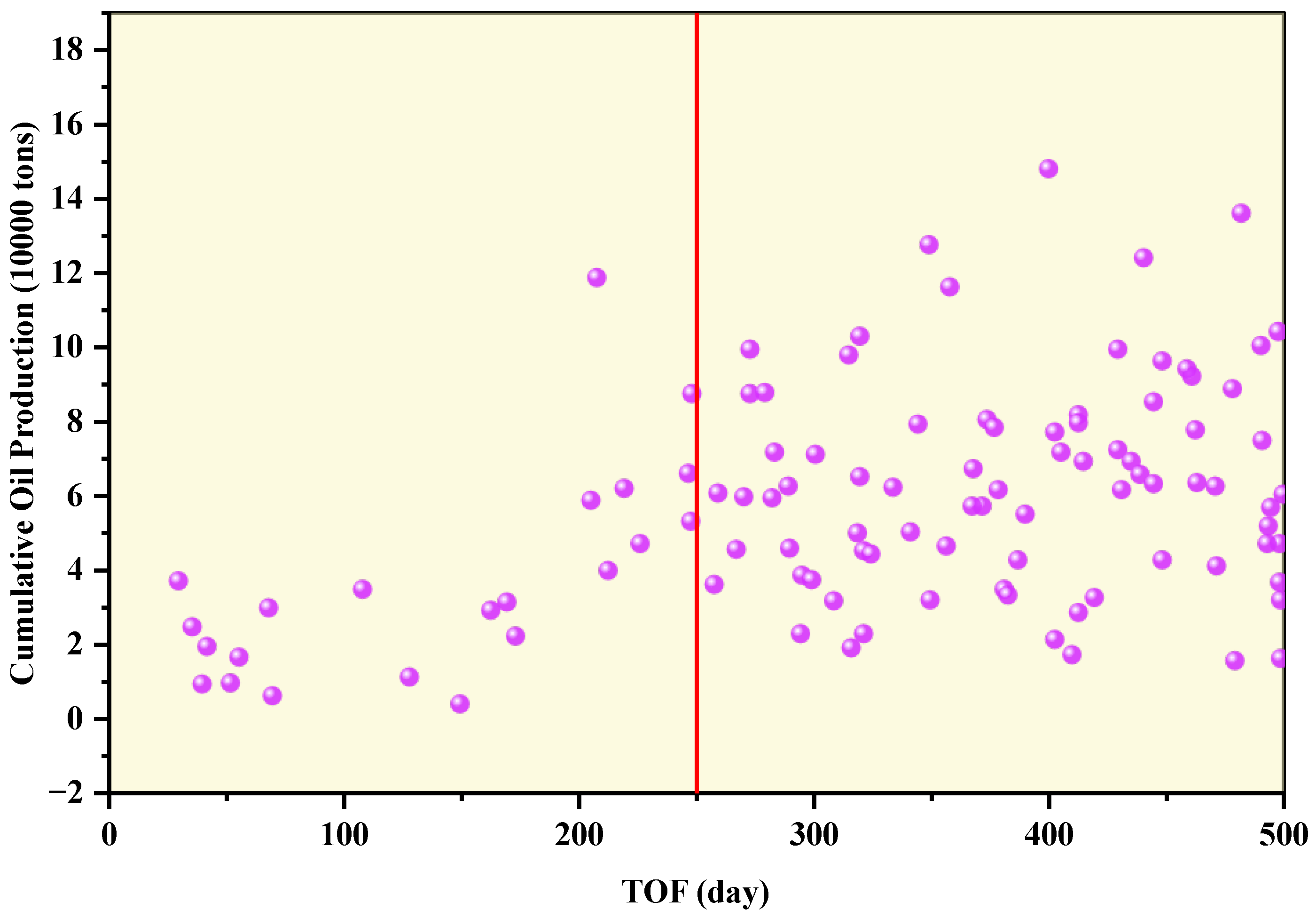
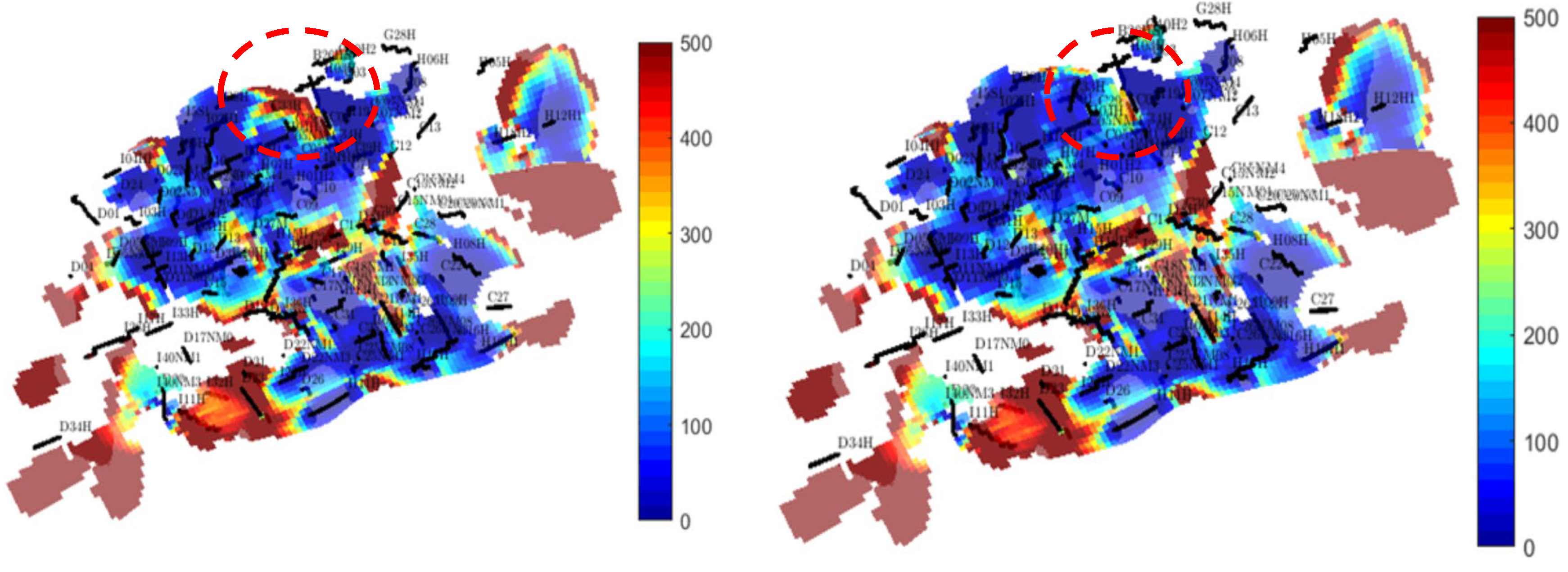
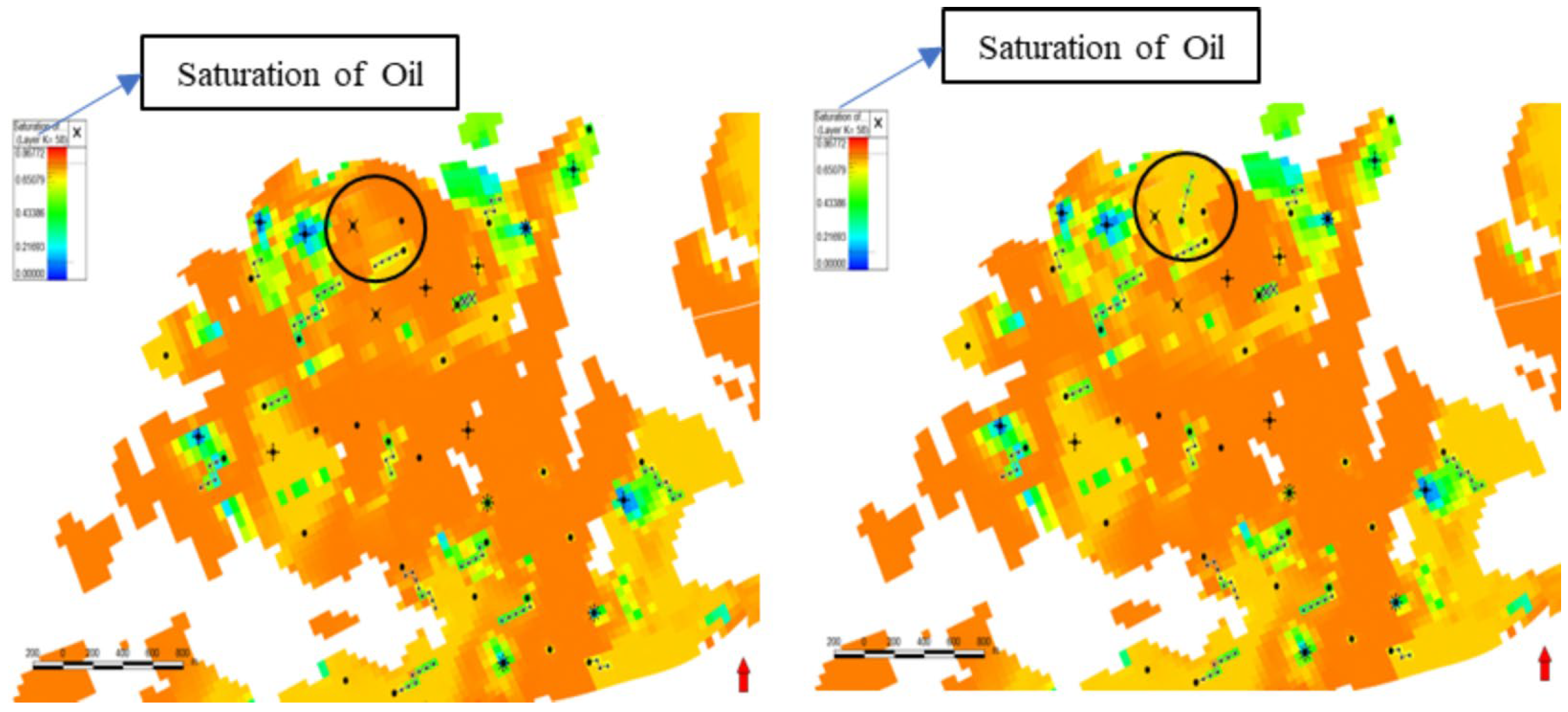
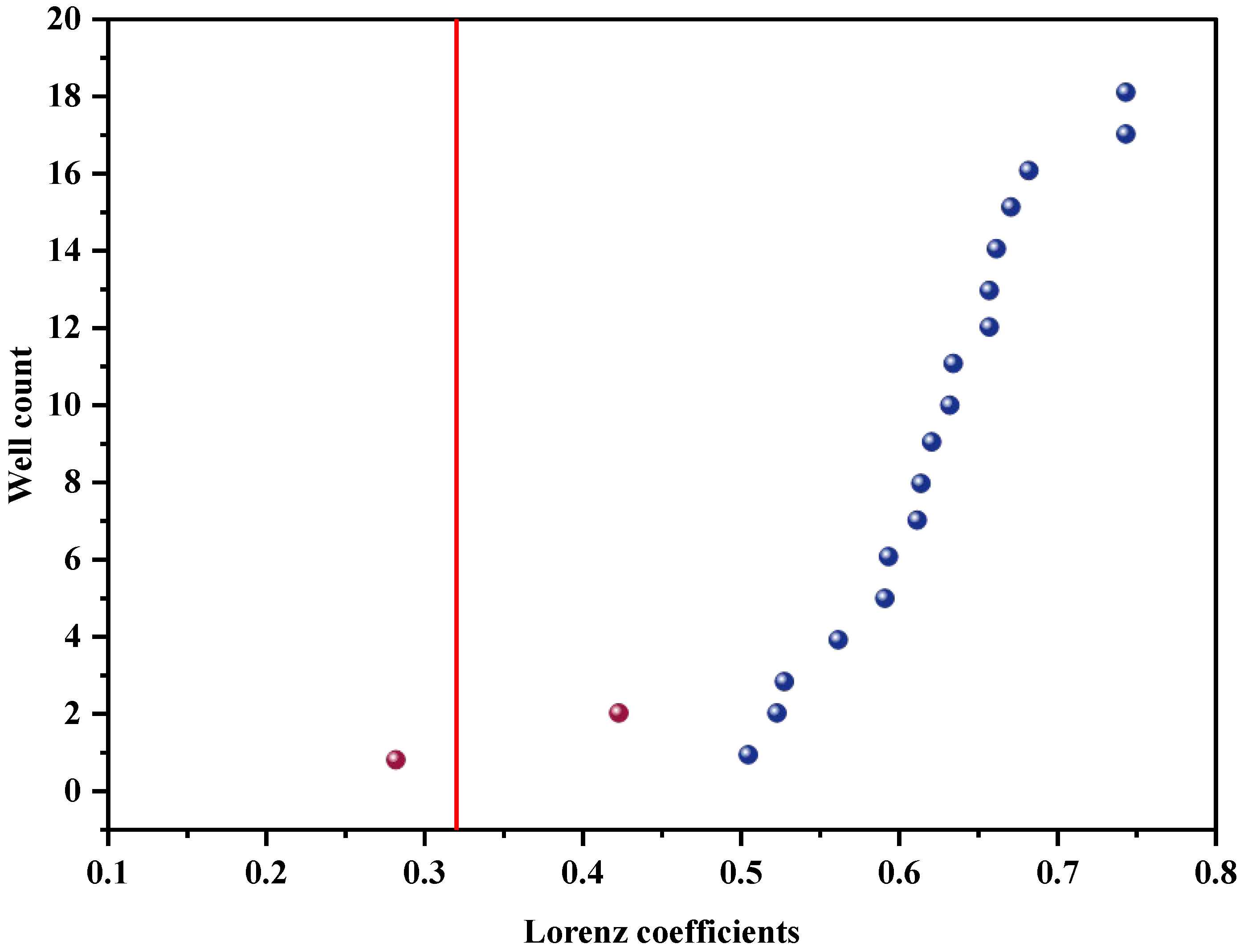



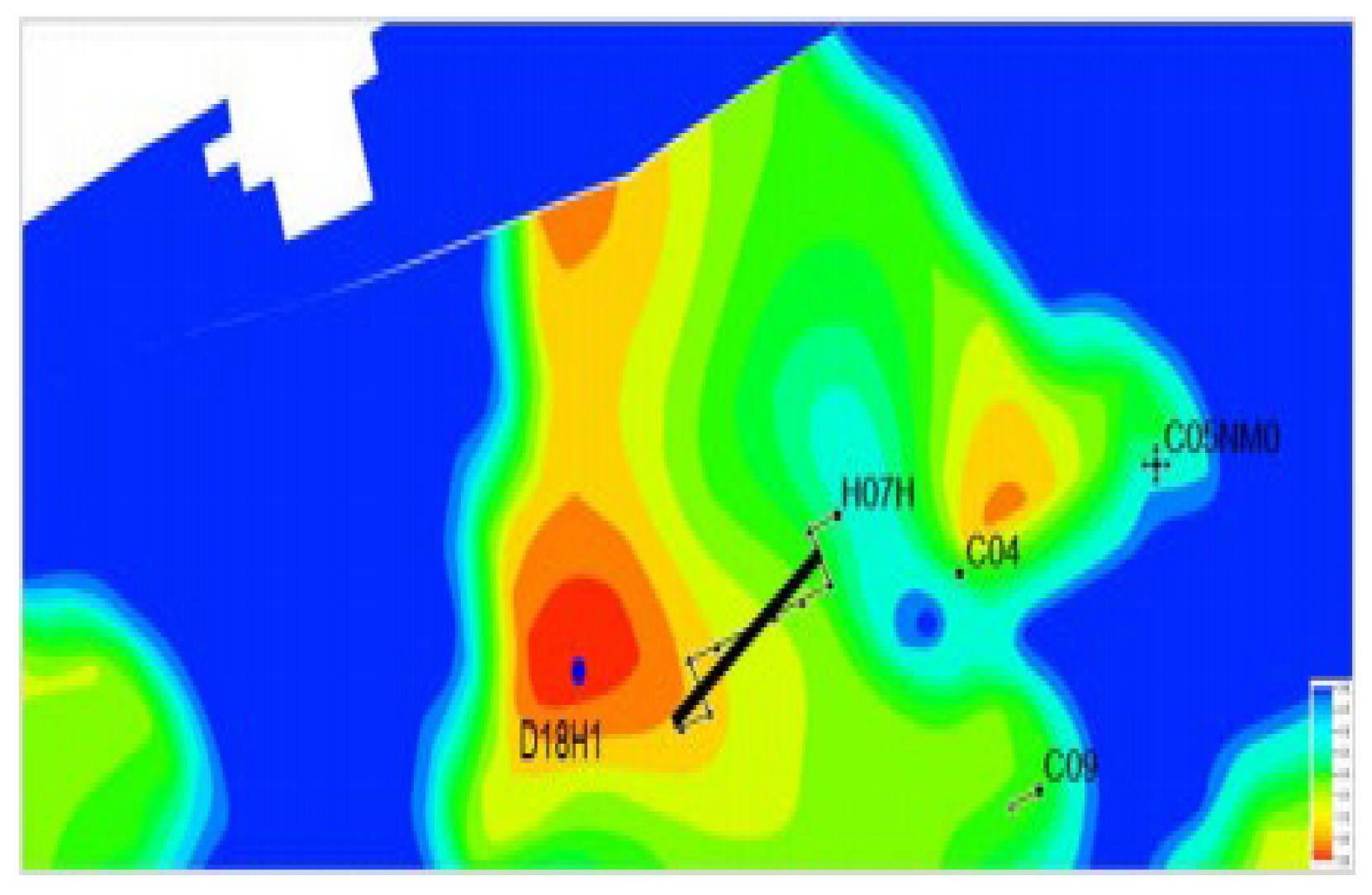
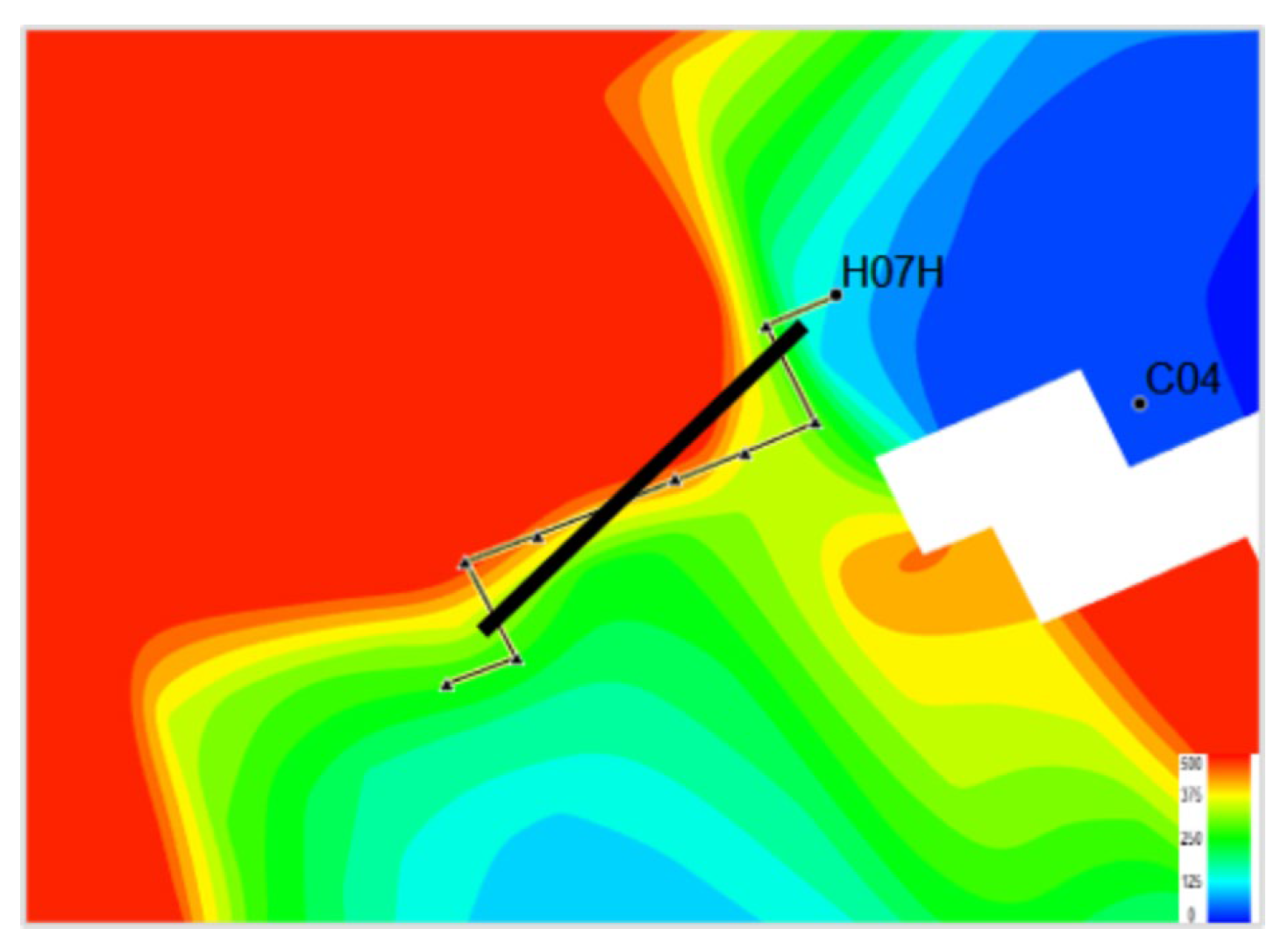
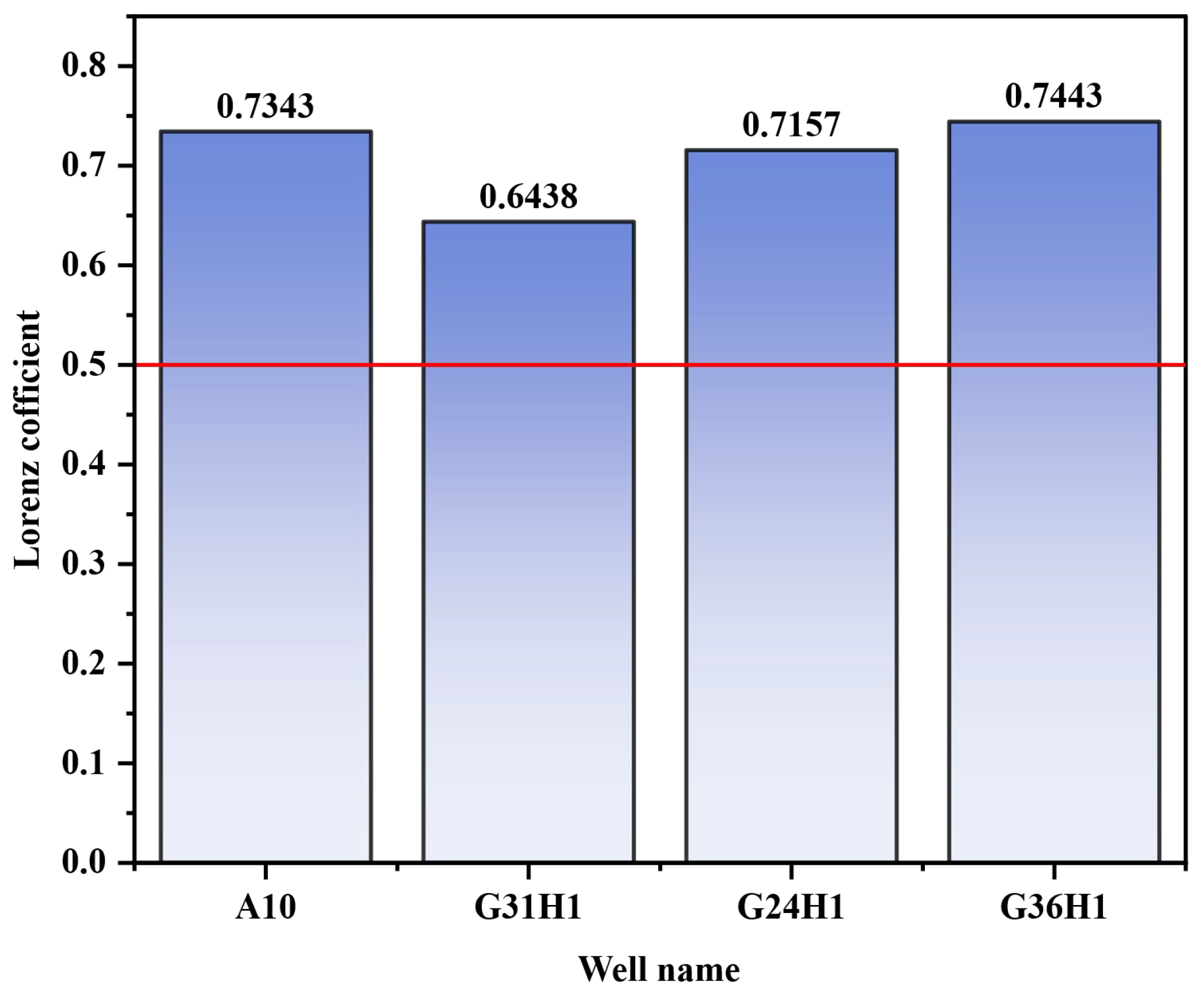

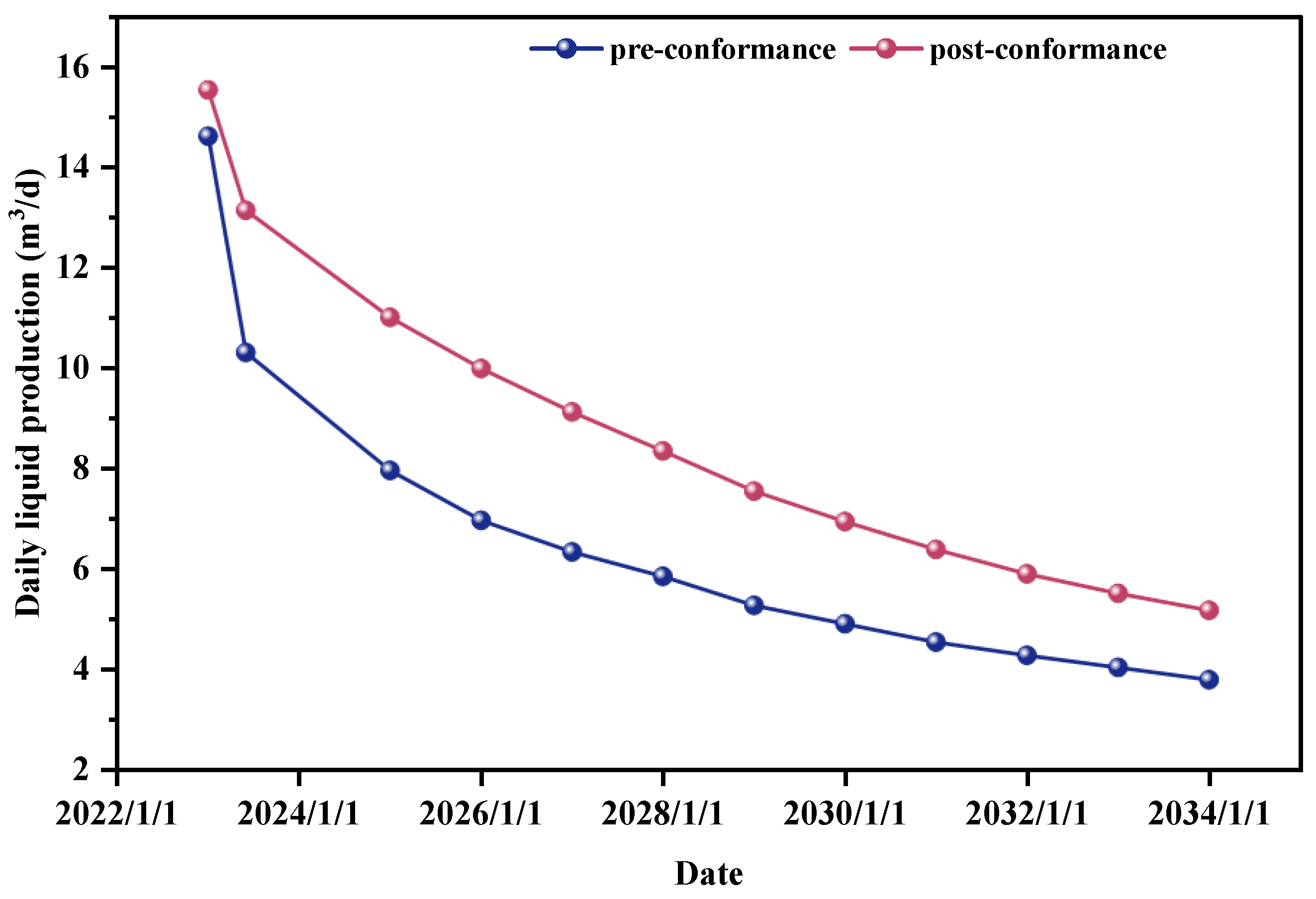
| Method | Evaluation Parameters | Features | Advantages | Application |
|---|---|---|---|---|
| Traditional Reservoir Engineering | Waterflood Characteristic Curves, Production Decline Curves | Traditional curve-fitting methods are computationally efficient but possess low diagnostic accuracy, with their application being constrained by empirical assumptions. | Wide applicability; relies on empirical and engineering judgment. | Daqing Oilfield, Qinjiatun Oilfield Bohai Oilfield [18,19,20] |
| Reservoir Numerical Simulation | Saturation, Streamlines, Flow Velocity, etc. | Reservoir numerical simulation is computationally intensive and time-consuming, making it difficult to satisfy real-time diagnostic needs. However, it excels at meticulously characterizing the internal physical dynamics and remaining oil distribution within the reservoir, though its application scale is generally restricted to localized studies. | High accuracy; capable of evaluating multi-parameter changes during the waterflooding process; offers 3D visualization. | Gangxi Oilfield, Jilin Oilfield [21] |
| Flow Diagnostics (The proposed method) | TOF, Dynamic Lorenz Coefficient, Streamlines, Oil Saturation, Pressure Field, Waterflood Characteristic Curve, Production Decline Curve | The flow diagnostics method is computationally efficient, provides targeted diagnostics, and its application is both flexible and scalable. | Rapid evaluation of waterflood performance for different well groups at various times. Facilitates the screening of candidate interventions and remedial actions. | QHD Oilfield |
| Brief Description | Functional Objective | Role in Decision-Making in Reservoir Development |
|---|---|---|
| Continuity equation for single-phase flow | Ensures mass conservation in steady-state incompressible flow, deriving baseline velocity fields. | Supports initial sweep efficiency evaluation for well pattern screening |
| Multiphase pressure equation | Solves pressure and velocity in oil–water systems, accounting for mobility contrasts from relative permeability. | Identifies flow paths; aids conformance control (TOF < 50 days). |
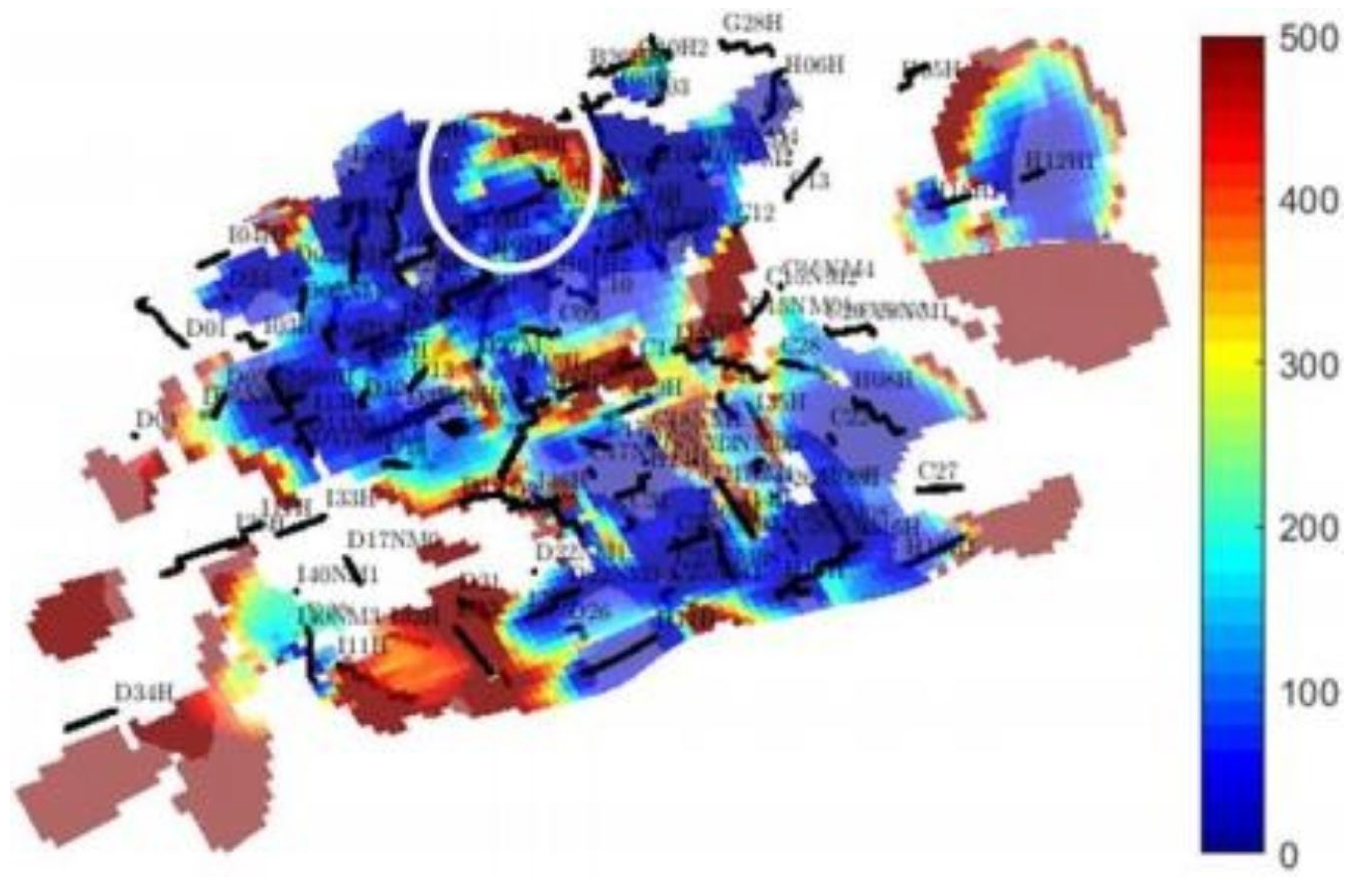
| Time-of-flight (TOF) along streamline | Computes particle travel time based on interstitial velocity and streamline distance. | Quantifies intensity; flags unswept areas for infill (TOF > 200 days). |
| Differentiated TOF equation | Derives partial differential form for direct numerical solution without streamline tracing. | Accelerates tortuosity assessment for flow field planning. |
| Forward TOF equation | Measures transit time from nearest injector to grid block along streamline. | Defines sweep volume; guides modification for channeling. |
| Backward TOF equation | Measures transit time from grid block to nearest producer. | Defines drainage; supports lift optimization (TOF > 200 days). |
| Tracer concentration equation | Models advective transport of tracers along velocity fields, neglecting diffusion. | Tracks allocation; quantifies heterogeneity for oil targeting. |
| Steady-state tracer equation | Solves equilibrium concentration distribution from injectors. | Maps swept regions; informs connectivity adjustments. |
| Injector tracer equation | Computes concentration gradients from specific injectors. | Quantifies control volumes; balances injection allocation. |
| Producer tracer equation | Computes concentration gradients to specific producers. | Quantifies drainage; enables communication volume for shutoff. |
| Intervention Well Number | Treatment Well Number | Distance to Water Well (m) | Treatment Duration (d) | Treatment Rate (m/d) | TOF | Maximum Lorenz Coefficient | Average Lorenz Coefficient | Lorenz Coefficient Surge Factor |
|---|---|---|---|---|---|---|---|---|
| D08Well Group (NmI3Segment) /2020.9.2 | D07 | 437 | 10 | 43.78 | 14 | 0.6621 | 0.62 | 1.068 |
| D13 | 311 | 62 | 5.02 | 58 | ||||
| D27M | 346 | 66 | 5.24 | 78 | ||||
| D28H | 257 | 41 | 6.26 | 30 | ||||
| C04 | 352.1 | 105 | 3.35 | 139 | ||||
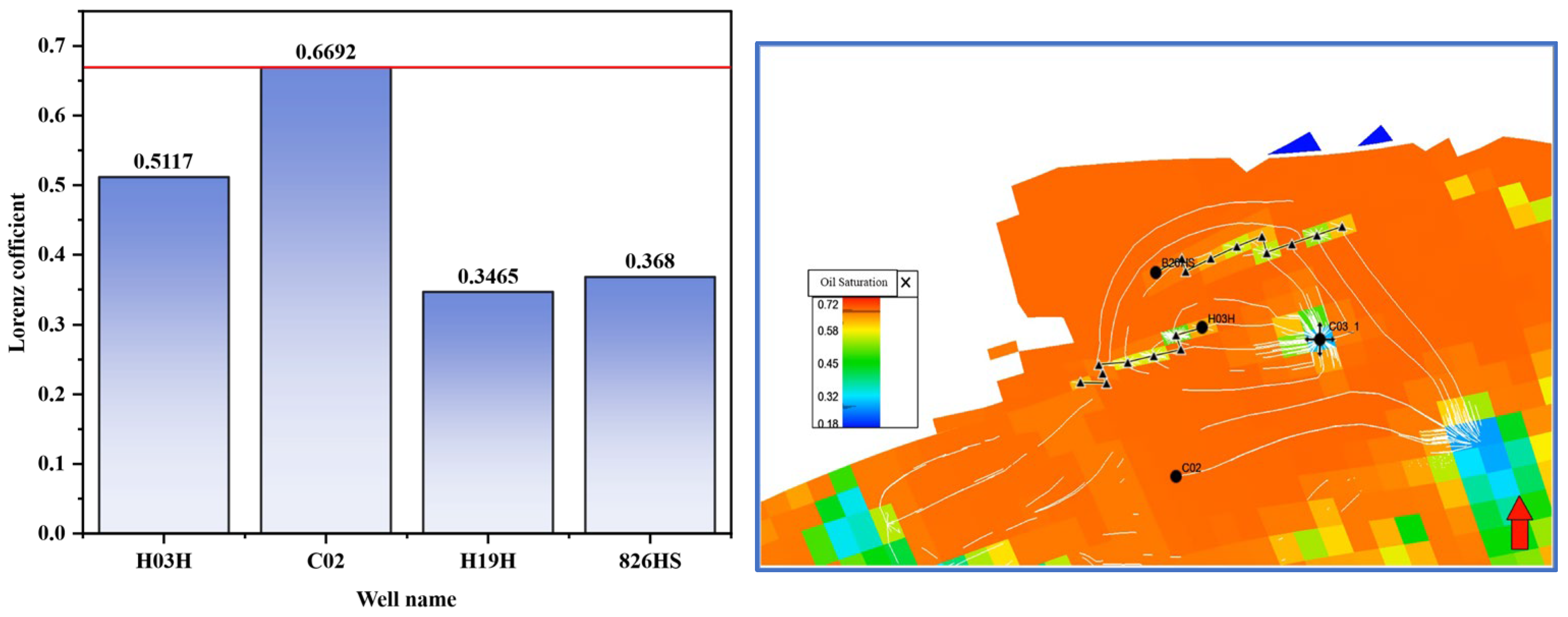
| C03Well Group (NmISegment) /2019.7.18 | H03H | 400 | 32 | 12.5 | 32 | 0.6692 | 0.71 | 0.943 |
| C02 | 370 | 38 | 9.7 | 33 | ||||
| H19H | 250 | 47 | 5.3 | 54 | ||||
| B26HS | 270 | 37 | 7.3 | 26 |
| Production Well | Water Zone Thickness (m) | Remaining Oil Zone Thickness (m) | Reservoir Thickness Ratio (%) | Pre-Intervention Production Rate (m3) | Pre-Intervention Water Cut (%) | Post-Intervention Production Rate (m3) | Post-Intervention Water Cut (%) | TOF |
|---|---|---|---|---|---|---|---|---|
| A01 | 20 | 86.96 | 20 | 90 | 95 | 83 | 75 | 264 |
| A05 | 63 | 75.90 | 14 | 93 | 45 | 93 | 31 | 273 |
| A10 | 43 | 66.15 | 20 | 94 | 40 | 95 | 20 | 273 |
| B09 | 78 | 89.66 | 20 | 95 | 50 | 95 | 30 | 322 |
| B15 | 76 | 91.57 | 23 | 76 | 40 | 83 | 17 | 304 |
| B23H | 10 | 83.33 | 36 | 71 | 75 | 70 | 39 | 350 |
| G29H | 20 | 100.00 | 15 | 56 | 45 | 68 | 30 | 270 |
| G34H | 8 | 72.73 | 22 | 95 | 38 | 95 | 16 | 292 |
| C01 | 55 | 66.27 | 21.8 | 89 | 52.7 | 92 | 30.8 | 275 |
| C24 | 37 | 75.51 | 7.6 | 88 | 27.0 | 94 | 19.4 | 261 |
| C30 | 41 | 71.93 | 9.8 | 91 | 30.7 | 92 | 21.0 | 214 |
| D07 | 57 | 76.00 | 49.3 | 86 | 77.5 | 87 | 28.2 | 329 |
| D28H | 3 | 50.00 | 29.7 | 70 | 124.4 | 78 | 94.7 | 253 |
| H02H | 3 | 100.00 | 14.4 | 96 | 39.6 | 94 | 25.2 | 287 |
| H03H | 12 | 100.00 | 47.6 | 70 | 70.0 | 84 | 22.4 | 323 |
| H04H | 10 | 100.00 | 22.1 | 95 | 44.8 | 96 | 22.6 | 343 |
| H09H | 7 | 100.00 | 9.6 | 94 | 27.3 | 95 | 17.7 | 211 |
| H10H | 7 | 100.00 | 26.4 | 75 | 54.6 | 81 | 28.2 | 283 |
| H11H | 14 | 100.00 | 18.1 | 94 | 42.2 | 94 | 24.0 | 268 |
| H17H | 5 | 100.00 | 30.1 | 76 | 53.8 | 84 | 23.7 | 240 |
| I09H | 8 | 66.67 | 27.4 | 83 | 110.9 | 77 | 83.5 | 343 |
| I09H1 | 18 | 81.82 | 20.3 | 97 | 38.5 | 97 | 18.2 | 237 |
| I28H | 13 | 59.09 | 21.8 | 86 | 42.4 | 89 | 20.6 | 247 |
| I33H | 14 | 66.67 | 24.2 | 95 | 58.9 | 92 | 34.7 | 277 |
| I36H | 4 | 66.67 | 25.2 | 86 | 56.0 | 89 | 30.8 | 252 |
| B26HS | 4 | 50.00 | 12.3 | 93 | 30.7 | 95 | 18.4 | 257 |
| Intervention Recommendations | Implementation Well Group | Implementation Time | Implementation Effectiveness | |
|---|---|---|---|---|
| Monthly Incremental Oil Production (10,000 m3) | Cumulative Incremental Oil Production (up to October 2024) | |||
| Liquid Lifting | G34H | 22 January 2024 | 0.0 | 0.0153 |
| G44H | 2024 August 22 | 0.0606 | 0.1324 | |
| G46H | 27 August 2024 | 0.0409 | 0.0741 | |
| G37H | 19 September 2024 | 0.0164 | 0.0164 | |
| G47H | 13 August 2024 | 0.0192 | 0.1088 | |
| D13 | 28 May 2024 | 0.0228 | 0.1175 | |
| I16H | 17 March 2024 | 0.0032 | 0.0119 | |
| D28H | 3 June 2024 | 0.0398 | 0.2757 | |
| Profile Modification and Displacement | C03 | 20 August 2024 | 0.1104 | 0.6973 |
| C05 | 22 August 2024 | 0.0737 | 0.5523 | |
| C06 | 20 August 2024 | 0.1161 | 0.7248 | |
| C29 | 20 August 2024 | 0.1100 | 0.6993 | |
| Water Shutoff | B17 | 1 March 2024 | 0.012 | 0.0956 |
| B21 | 7 March 2024 | 0.0094 | 0.0412 | |
| I18H | 30 March 2024 | 0.0032 | 0.0119 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Guo, Y.; Wu, L.; Jiang, L.; Wang, S.; Ning, S.; Kang, Z. Evaluation of Development Performance and Adjustment Strategies for High Water-Cut Reservoirs Based on Flow Diagnostics: Application in the QHD Oilfield. Energies 2025, 18, 5310. https://doi.org/10.3390/en18195310
He Y, Guo Y, Wu L, Jiang L, Wang S, Ning S, Kang Z. Evaluation of Development Performance and Adjustment Strategies for High Water-Cut Reservoirs Based on Flow Diagnostics: Application in the QHD Oilfield. Energies. 2025; 18(19):5310. https://doi.org/10.3390/en18195310
Chicago/Turabian StyleHe, Yifan, Yishan Guo, Li Wu, Liangliang Jiang, Shouliang Wang, Shangshu Ning, and Zhihong Kang. 2025. "Evaluation of Development Performance and Adjustment Strategies for High Water-Cut Reservoirs Based on Flow Diagnostics: Application in the QHD Oilfield" Energies 18, no. 19: 5310. https://doi.org/10.3390/en18195310
APA StyleHe, Y., Guo, Y., Wu, L., Jiang, L., Wang, S., Ning, S., & Kang, Z. (2025). Evaluation of Development Performance and Adjustment Strategies for High Water-Cut Reservoirs Based on Flow Diagnostics: Application in the QHD Oilfield. Energies, 18(19), 5310. https://doi.org/10.3390/en18195310






