Feasibility Study of Flywheel Mitigation Controls Using Hamiltonian-Based Design for E3 High-Altitude Electromagnetic Pulse Events
Abstract
1. Introduction
2. System Models
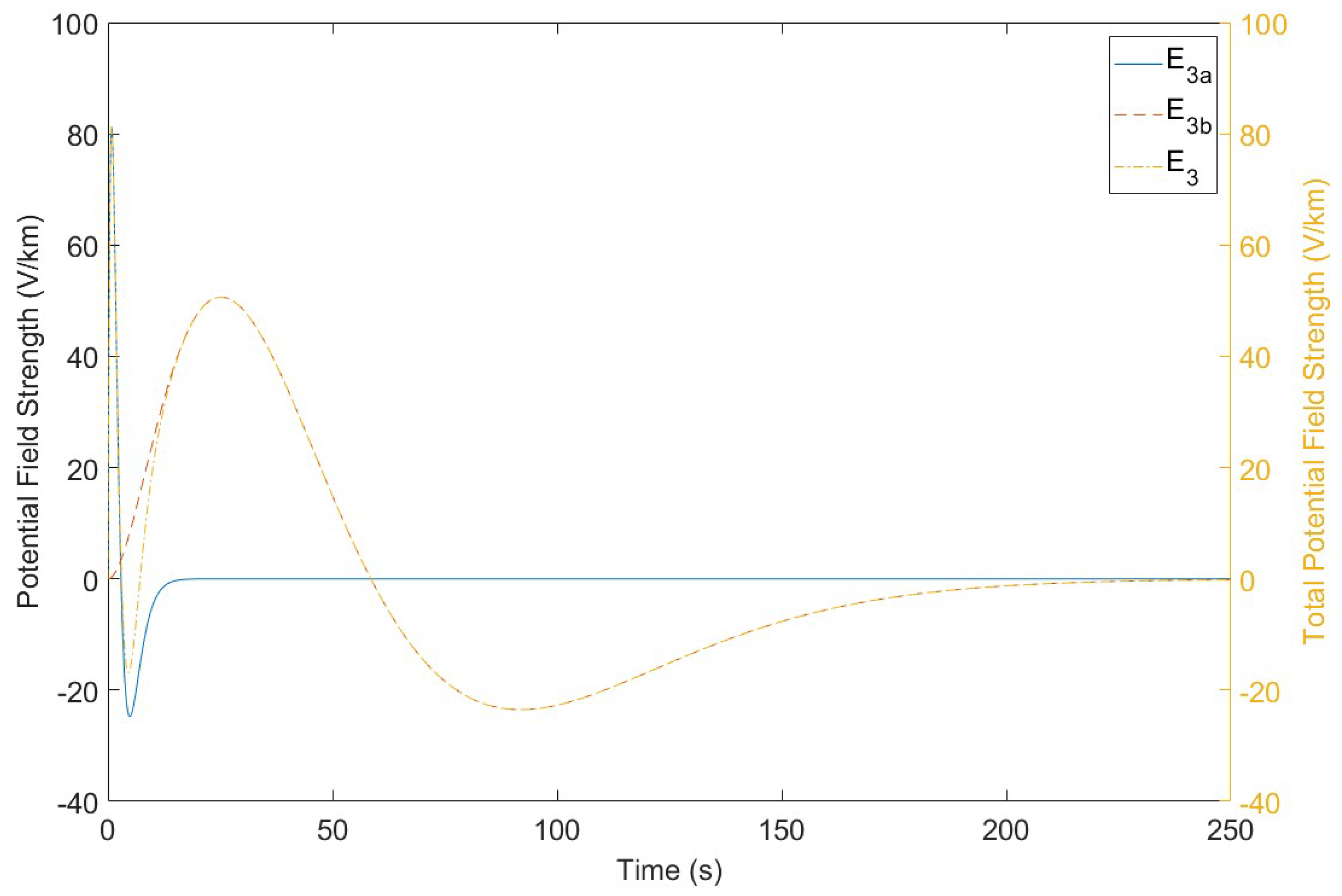
2.1. HEMP Insult Model
2.2. Per-Phase Transformer Model
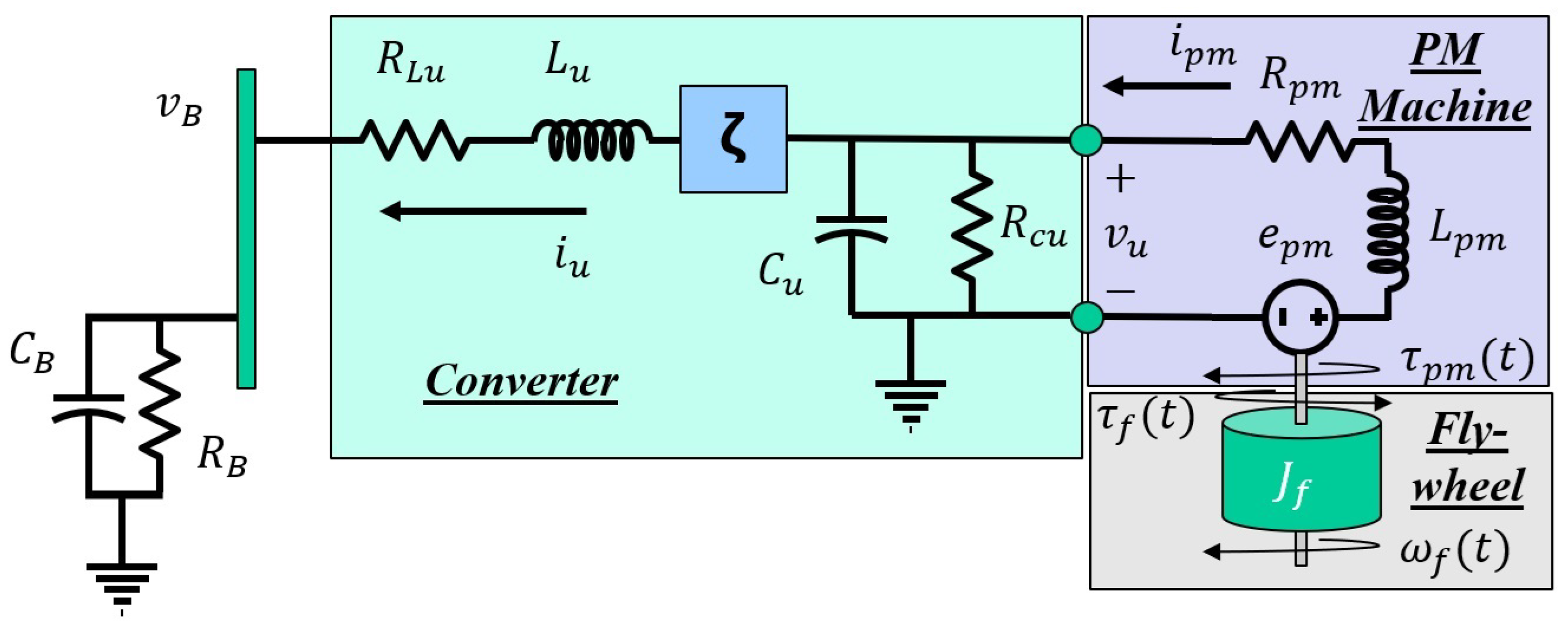
2.3. Flywheel Model
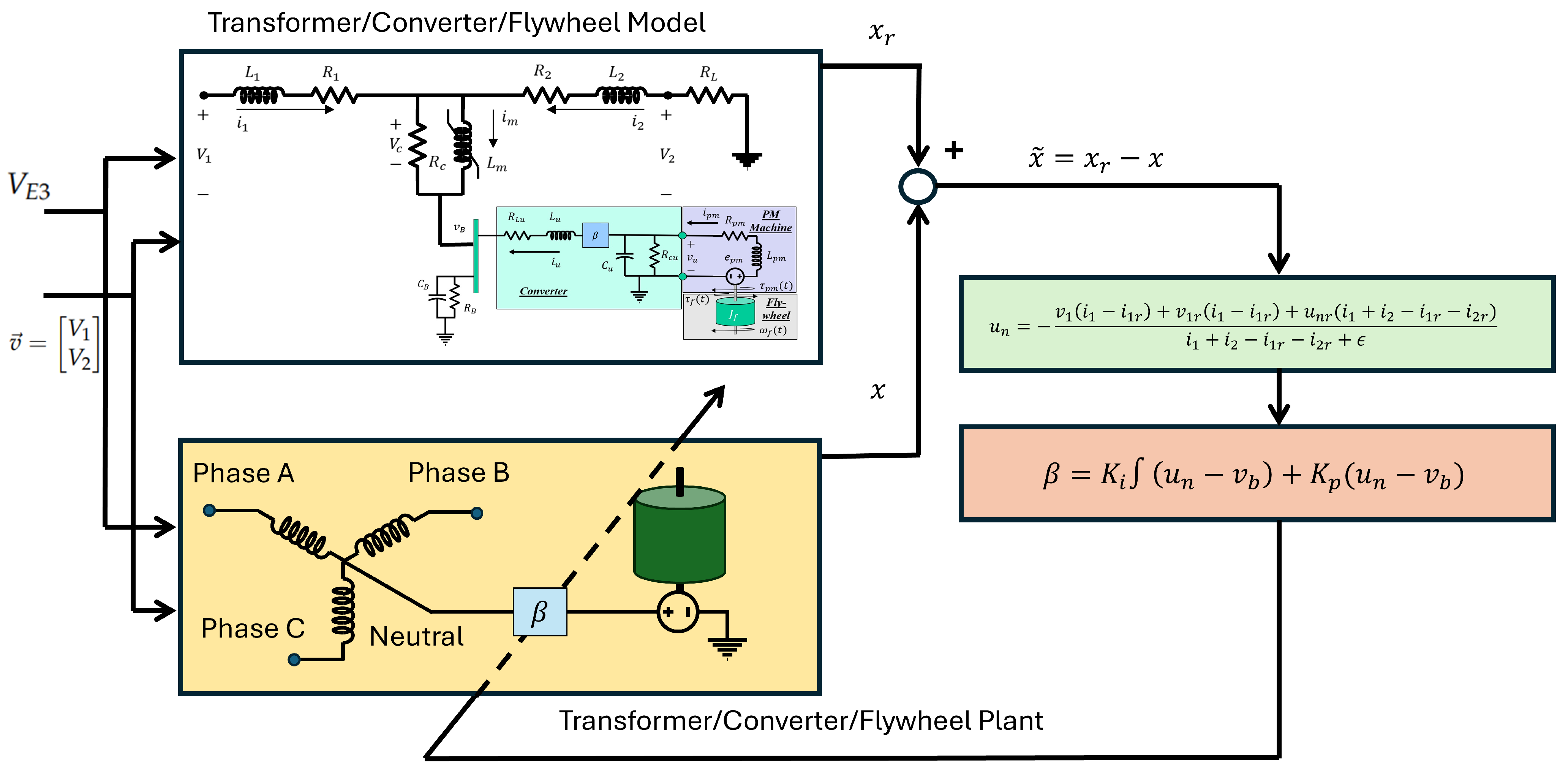
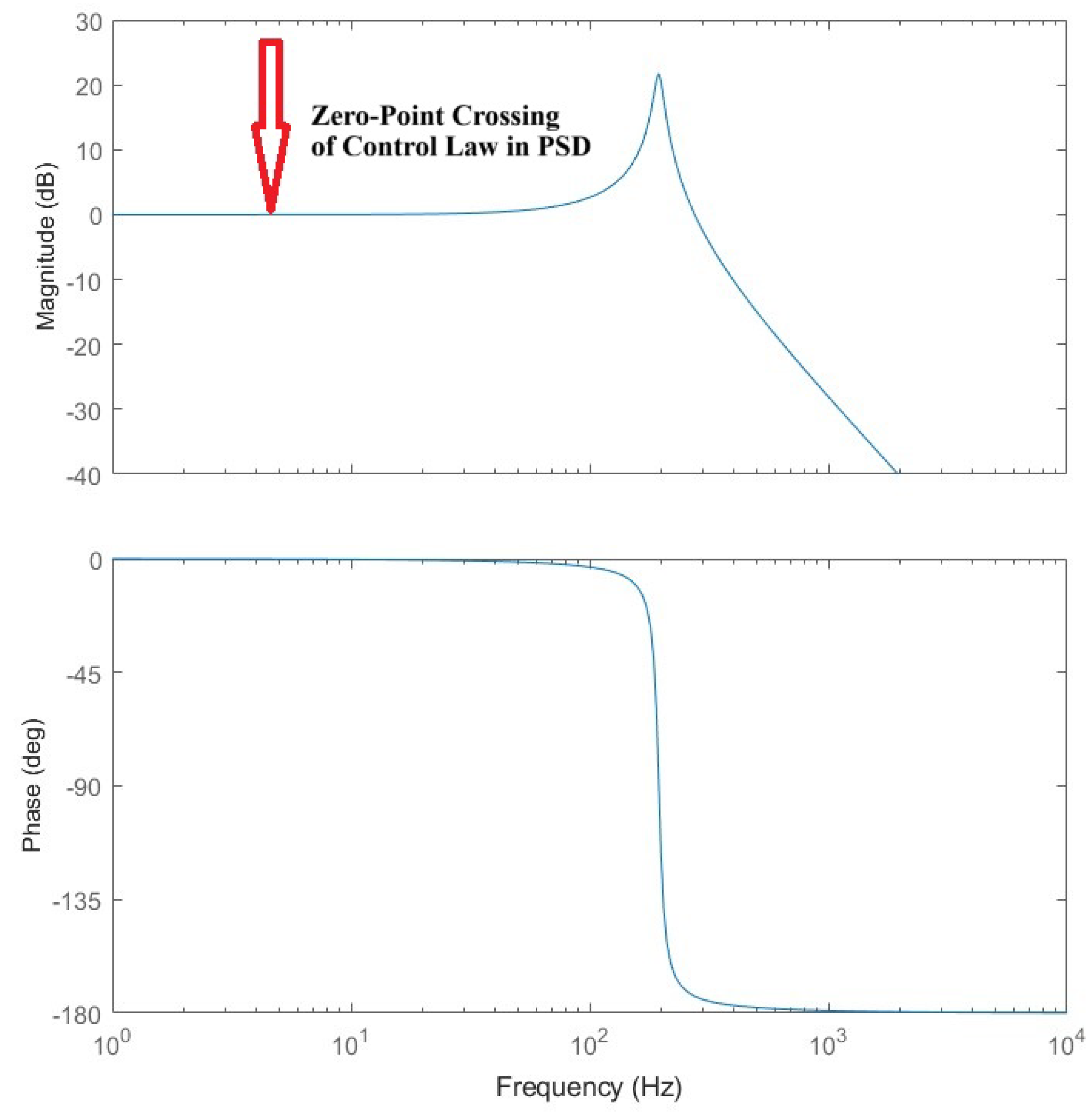
3. Control Law Development
- The Hamiltonian of the system must be positive definite about the equilibrium point.
- The time derivative of the Hamiltonian must be negative definite about the equilibrium point.
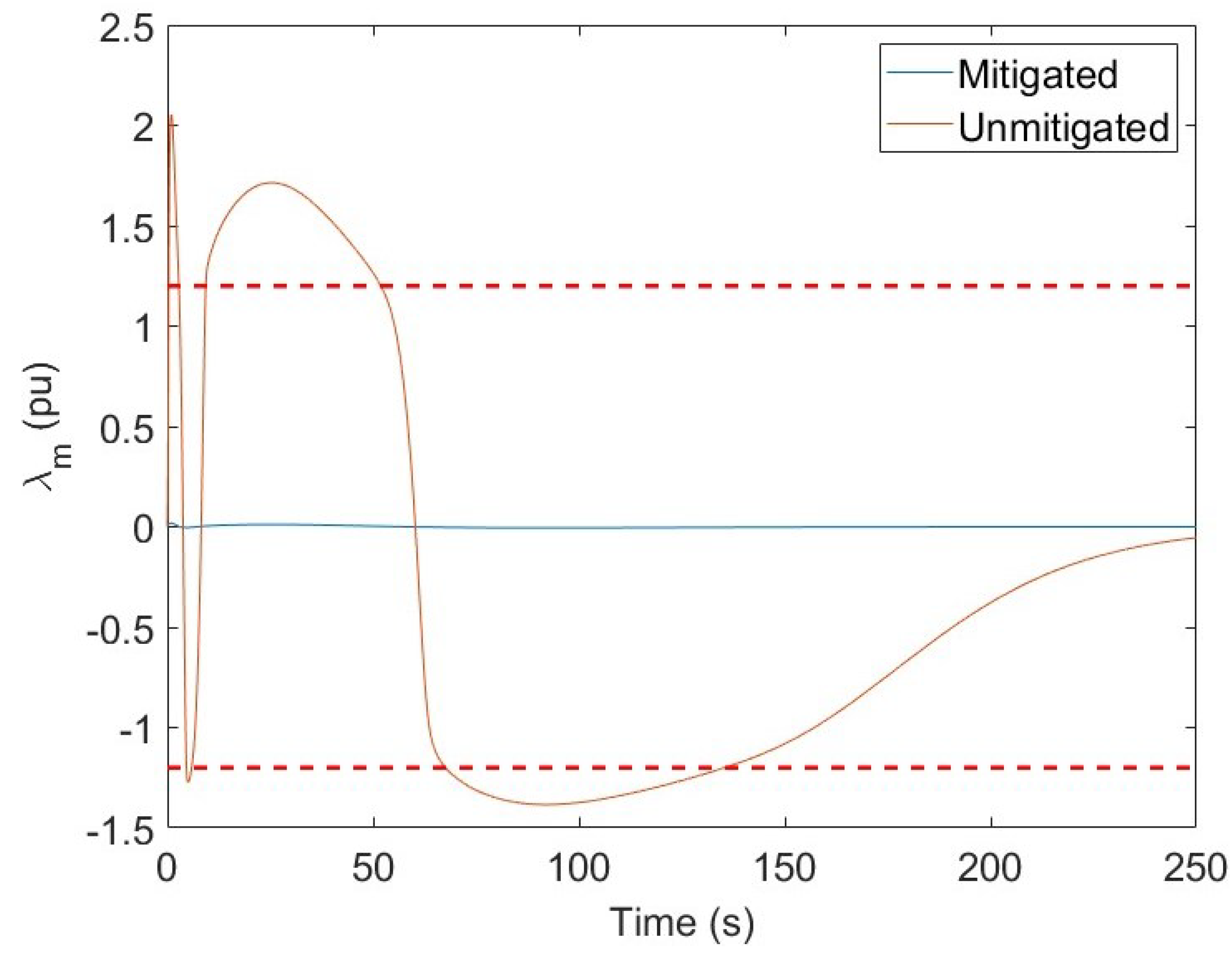
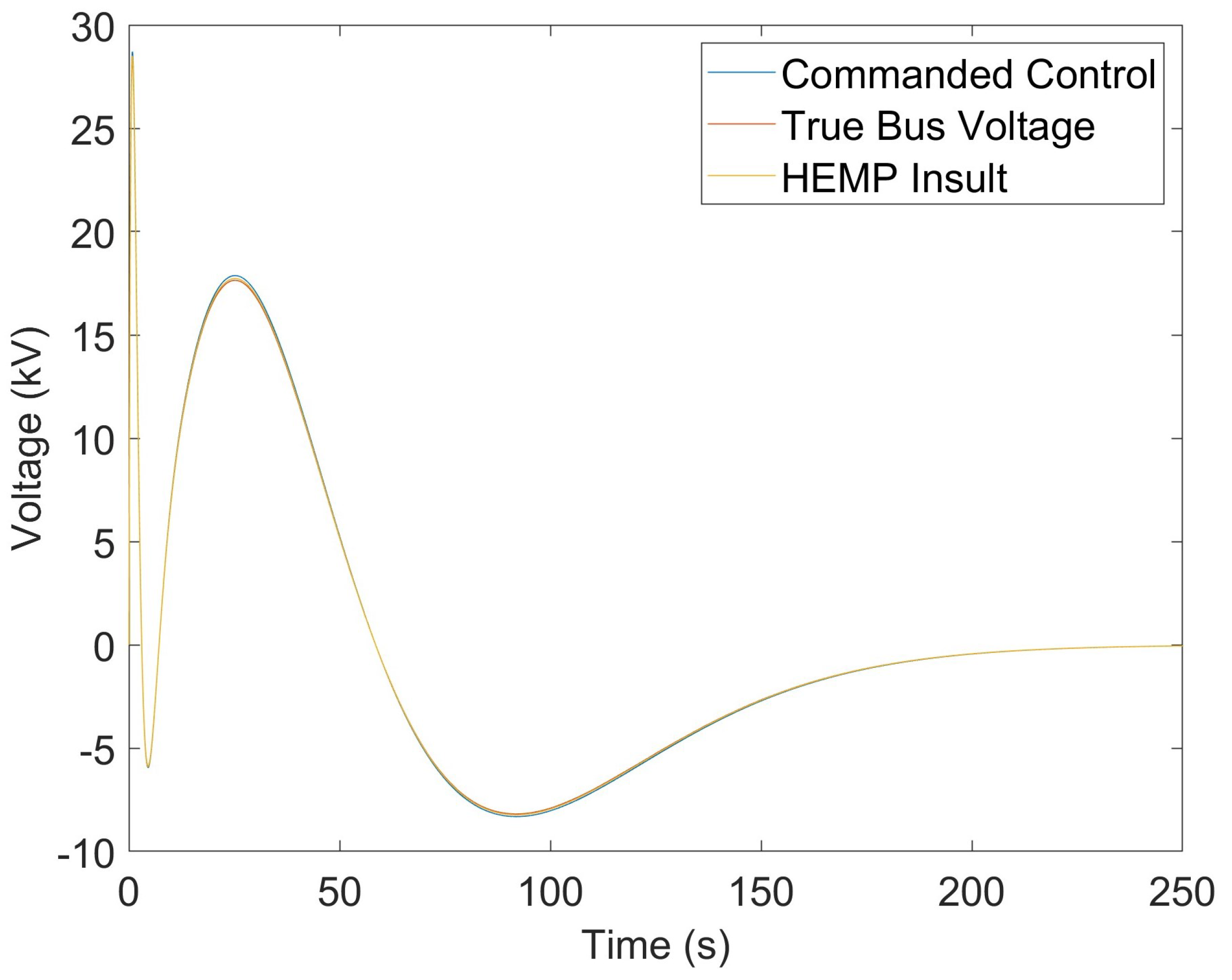
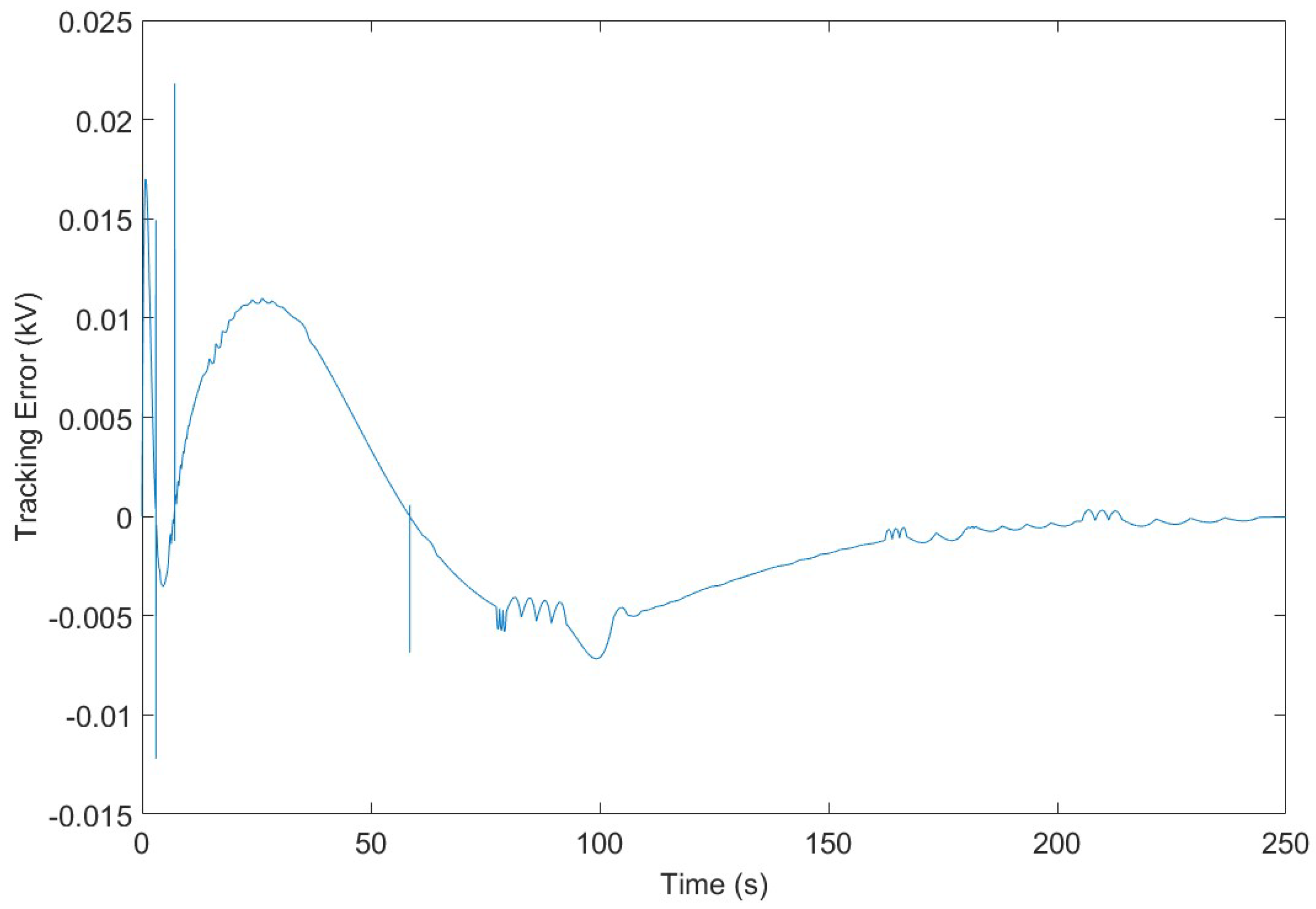
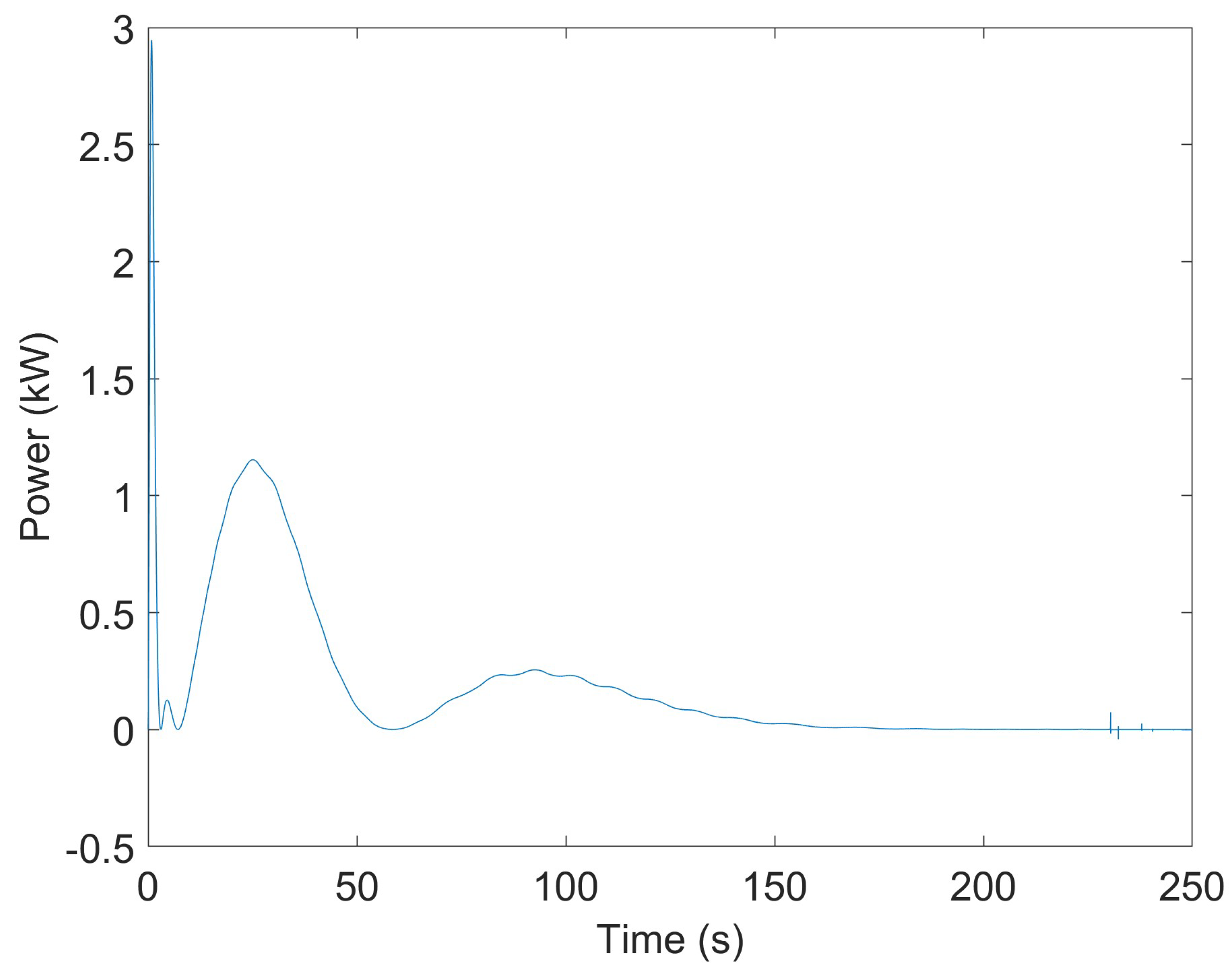
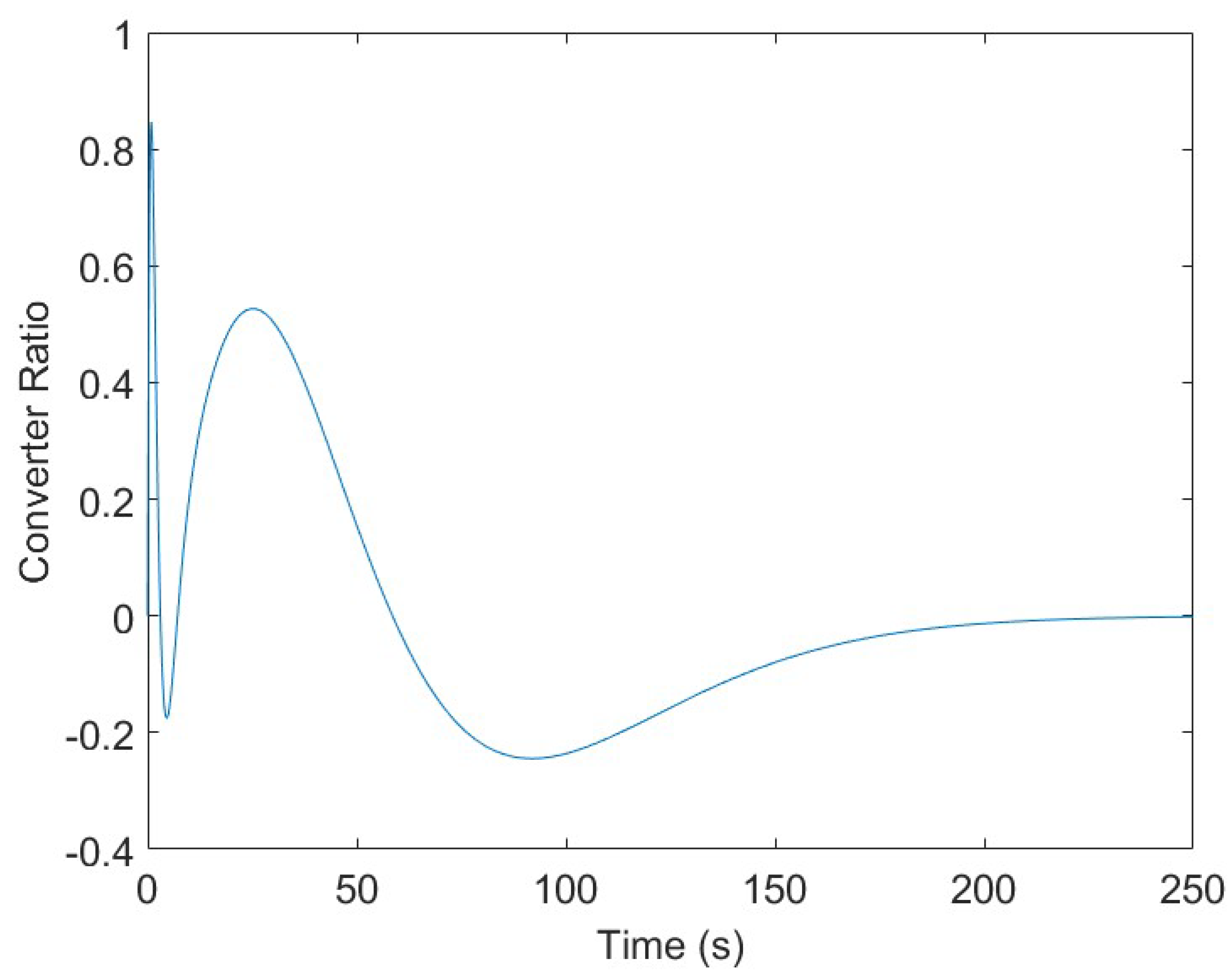
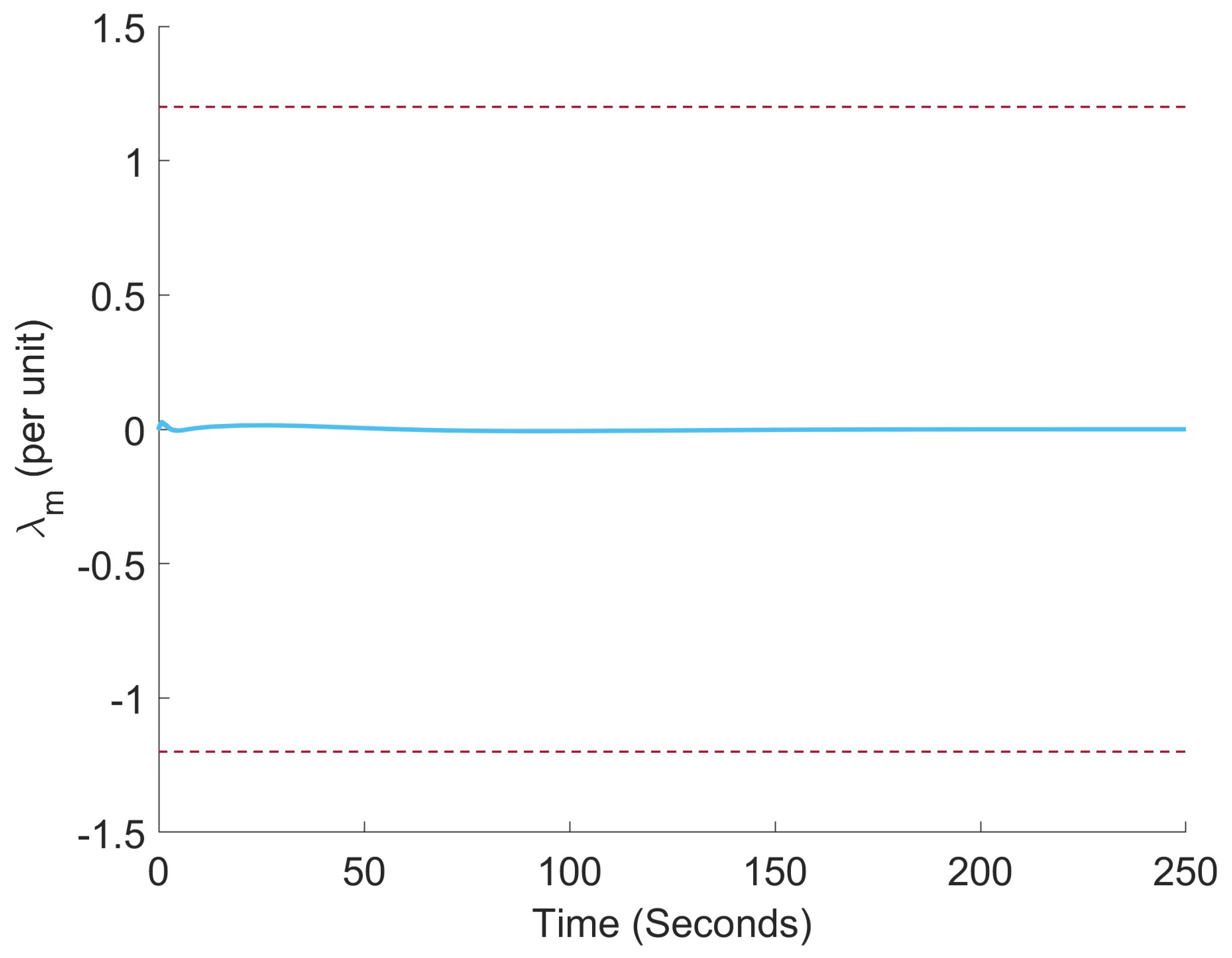
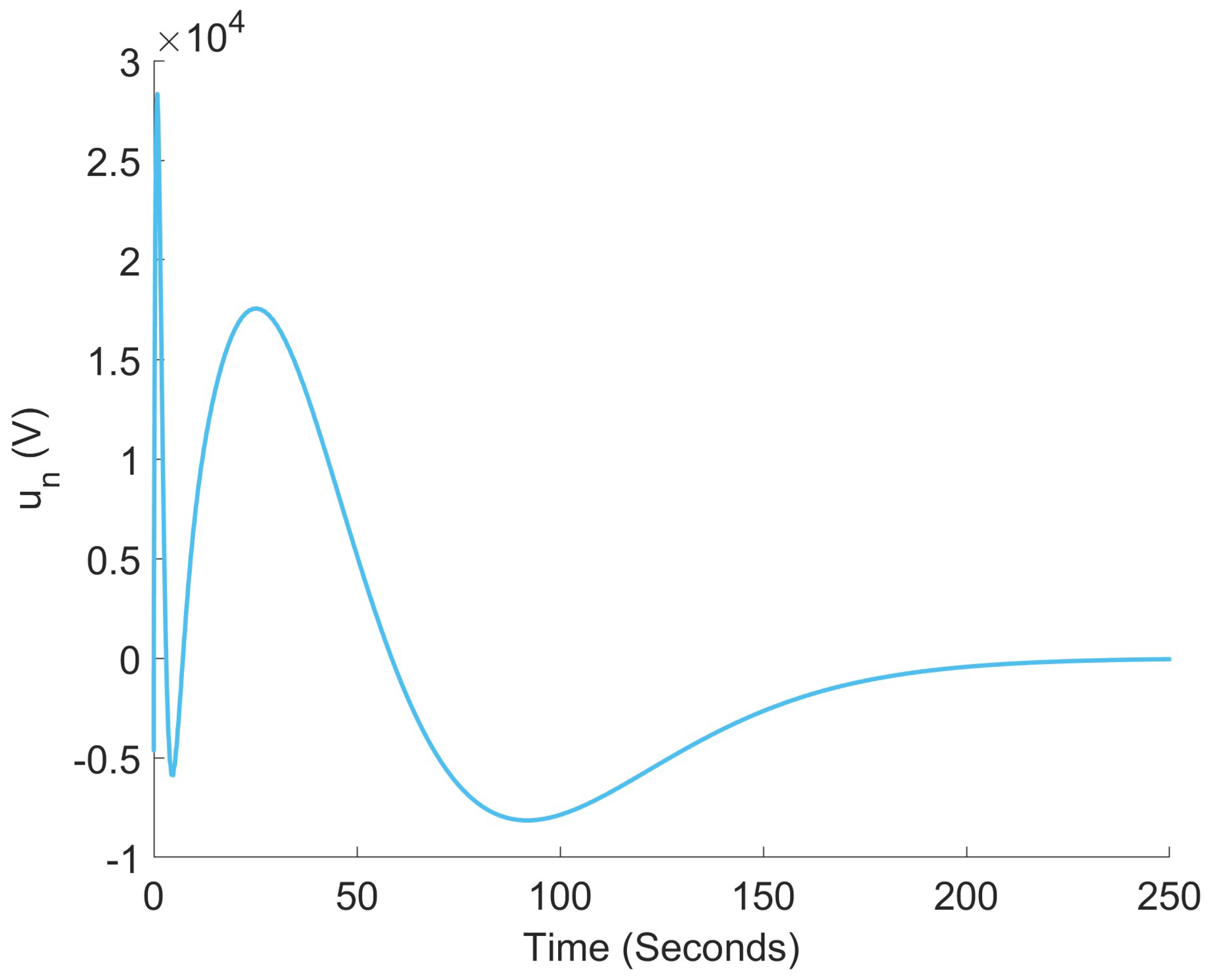
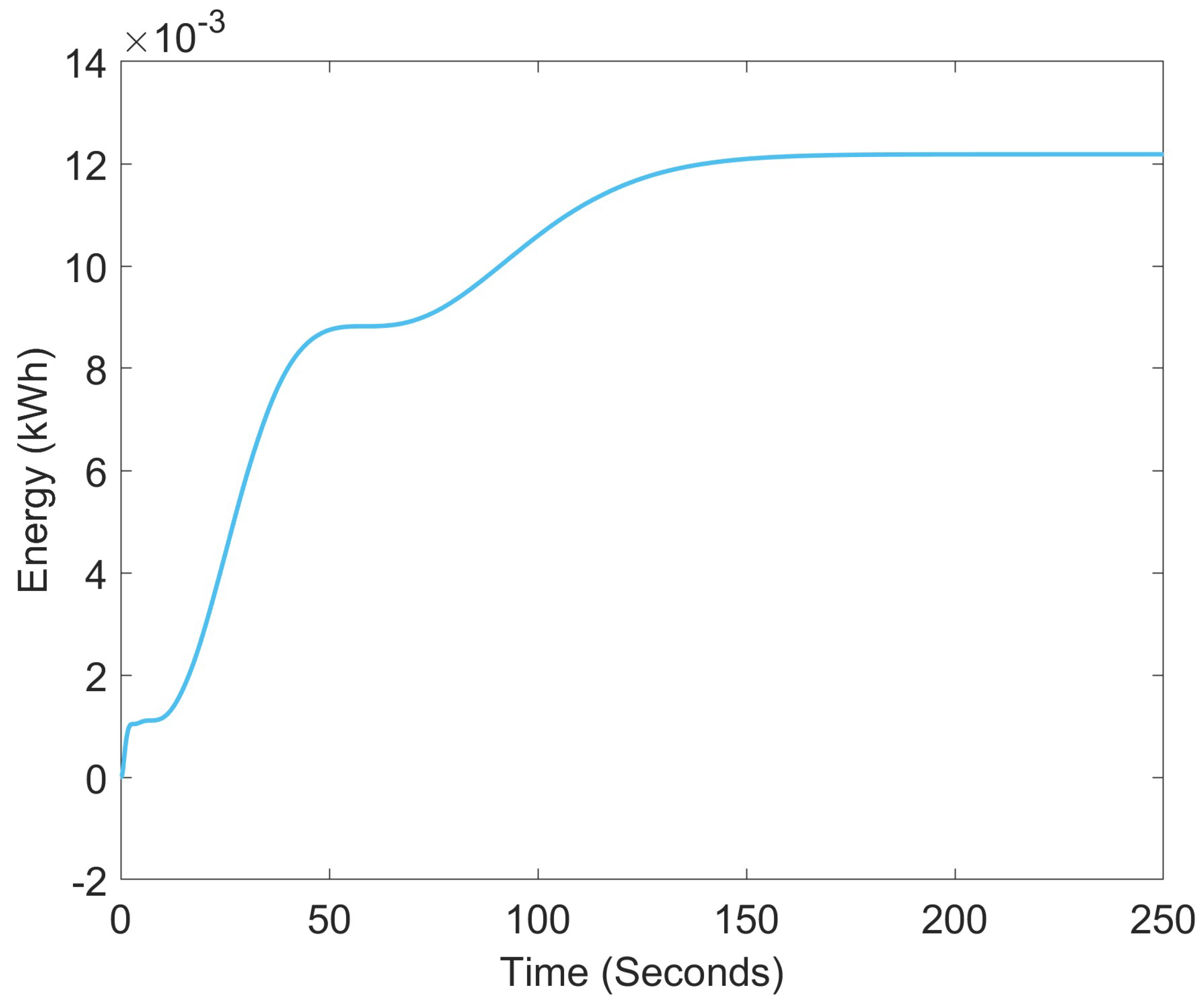
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foster, J.S., Jr.; Gjelde, E.; Graham, W.R.; Hermann, R.J.; Kluepfel, H.M.; Lawson, R.L.; Soper, G.K.; Wood, L.L.; Woodard, J.B. Report of the Commission to Assess the Threat to the United States from Electromagnetic Pulse (emp) Attack: Critical National Infrastructures; Technical Report; Electromagnetic Pulse (EMP) Commission: McLean, VA, USA, 2008. [Google Scholar][Green Version]
- Foster, R.A.; Frickey, S.J. Strategies, Protections and Mitigations for Electric Grid from Electromagnetic Pulse Effects; Technical Report; Idaho National Lab. (INL): Idaho Falls, ID, USA, 2016. [Google Scholar][Green Version]
- Wang, D.; Li, Y.; Dehghanian, P.; Wang, S. Power grid resilience to electromagnetic pulse (EMP) disturbances: A literature review. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar][Green Version]
- IEC 61000-2-9; Electromagnetic Compatibility (EMC)—Part 2: Environment—Section 9: Description of HEMP Environment—Radiated Disturbance. Basic EMC Publication; IEC (International Electrotechnical Commission): Geneva, Switzerland, 1996. Available online: https://webstore.iec.ch/en/publication/4141 (accessed on 17 August 2025).[Green Version]
- Sanabria, D.E.; Bowman, T.; Guttromson, R.; Halligan, M.; Le, K.; Lehr, J. Early-Time (E1) High-Altitude Electromagnetic Pulse Effects on Trip Coils; Technical Report SAND2020-12133; Sandia National Labs: Albuquerque, NM, USA, 2020. [Google Scholar][Green Version]
- Savage, E.; Gilbert, J.; Radasky, W. The Early-Time (E1) High-Altitude Electromagnetic Pulse (HEMP) and Its Impact on the U.S. Power Grid; Technical Report Meta-R-320; Metatech: Goleta, CA, USA, 2010. [Google Scholar][Green Version]
- Hansen, C.W.; Catanach, T.A.; Glover, A.M.; Huerta, J.G.; Stuart, Z.; Guttromson, R. Modeling Failure of Electrical Transformers due to Effects of a HEMP Event; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2020. [Google Scholar][Green Version]
- Shetye, K.; Overbye, T. Modeling and Analysis of GMD Effects on Power Systems: An overview of the impact on large-scale power systems. IEEE Electrif. Mag. 2015, 3, 13–21. [Google Scholar] [CrossRef]
- Faxvog, F.R.; Jensen, W.; Fuchs, G.; Nordling, G.; Jackson, D.B.; Groh, B.; Ruehl, N.; Vitols, A.P.; Volkmann, T.L.; Rooney, M.R.; et al. Power grid protection against geomagnetic disturbances (GMD). In Proceedings of the 2013 IEEE Electrical Power & Energy Conference, Halifax, NS, Canada, 21–23 August 2013; pp. 1–13. [Google Scholar] [CrossRef]
- Brouillette, D. Physical Characteristics of HEMP Waveform Benchmarks for Use in Assessing Susceptibilities of the Power Grid, Electrical Infrastructures, and Other Critical Infrastructure to HEMP Insults; Department of Energy Memo; U.S. Department of Energy: Washington, DC, USA, 2021. [Google Scholar]
- Donnelly, T.J.; Wilson, D.G.; Robinett, R.D.; Weaver, W.W. Top-Down Control Design Strategy for Electric Power Grid EMP (E3) Protection. In Proceedings of the 2023 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 13–14 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Morari, M. Robust stability of systems with integral control. IEEE Trans. Autom. Control 1985, 30, 574–577. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Amiryar, M.E.; Pullen, K.R. A review of flywheel energy storage system technologies and their applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef]
- Hadjipaschalis, I.; Poullikkas, A.; Efthimiou, V. Overview of current and future energy storage technologies for electric power applications. Renew. Sustain. Energy Rev. 2009, 13, 1513–1522. [Google Scholar] [CrossRef]
- Schoenung, S.M.; Hassenzahl, W.V. Long- vs. Short-Term Energy Storage Technologies Analysis: A Life-Cycle Cost Study: A Study for the DOE Energy Storage Systems Program; Technical Report; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2003. [Google Scholar]
- Schoenung, S.M.; Eyer, J. Benefit/Cost Framework for Evaluating Modular Energy Storage; Sandia Report SAND2008-0978; Sandia National Laboratories (SNL): Albuquerque, NM, USA, 2008. [Google Scholar]
- Goris, F.; Severson, E.L. A review of flywheel energy storage systems for grid application. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1633–1639. [Google Scholar]
- Robinett, R.D., III; Wilson, D.G. Nonlinear Power Flow Control Design: Utilizing Exergy, Entropy, Static and Dynamic Stability, and Lyapunov Analysis; Springer: London, UK, 2011. [Google Scholar]
- Crouch, P.E.; van der Schaft, A.J. (Eds.) The variational criterion. In Variational and Hamiltonian Control Systems; Springer: Berlin/Heidelberg, Germany, 1987; pp. 60–84. [Google Scholar] [CrossRef]
- Wilson, D.; Weaver, W.; Robinett, R., III; Young, J.; Glover, S.; Cook, M.; Markle, S.; McCoy, T. Nonlinear Power Flow Control Design Methodology for Navy Electric Ship Microgrid Energy Storage Requirements. In Proceedings of the 14th International Naval Engineering Conference, Glasgow, UK, 2–4 October 2018; Volume 2018. [Google Scholar]
- Choudhury, S. Flywheel energy storage systems: A critical review on technologies, applications, and future prospects. Int. Trans. Electr. Energy Syst. 2021, 31, e13024. [Google Scholar] [CrossRef]
- Bolund, B.; Bernhoff, H.; Leijon, M. Flywheel energy and power storage systems. Renew. Sustain. Energy Rev. 2007, 11, 235–258. [Google Scholar] [CrossRef]
- Nguyen, X.P.; Hoang, A.T. The flywheel energy storage system: An effective solution to accumulate renewable energy. In Proceedings of the 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 March 2020; pp. 1322–1328. [Google Scholar]
- Overbye, T.J.; Faxvog, F.R.; Jensen, W.; Fuchs, G.; Nordling, G.; Jackson, D.B.; Groh, B.; Ruehl, N.; Vitols, A.P.; Volkmann, T.L.; et al. Power Grid Geomagnetic Disturbance (GMD) Modeling with Transformer Neutral Blocking and Live Grid Testing Results. In Proceedings of the 2013 Minnesota Power Conference, Minneapolis, MN, USA, October 2013. [Google Scholar]
- Gurevich, V. Protection of Power Transformer from High Altitude Electromagnetic Pulse. Int. J. Res. Stud. Electr. Electron. Eng. 2020, 6, 17–24. [Google Scholar] [CrossRef]
- Lehman, C.A.; Robinett, R.D., III; Weaver, W.W.; Wilson, D.G. Solid State Transformer Controls for Mitigation of E3a High-Altitude Electromagnetic Pulse Insults. Energies 2025, 18, 1055. [Google Scholar] [CrossRef]
- Lehman, C.A.; Weaver, W.W.; Wilson, D.G.; Robinett, R.D. Active Controls of a Multi-Frequency Multi-Bus Microgrid Network Using Hamiltonian-Based Techniques. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; pp. 1144–1150. [Google Scholar]
- Lehman, C.A.; Robinett, R.D., III; Wilson, D.G.; Weaver, W.W. Comparison of Optimal Control Mitigation Techniques for E3 HEMP Insults Utilizing the Transformer Neutral Path. In Proceedings of the IEEE ECCE 2025, Philadelphia, PA, USA, 19–23 October 2025. [Google Scholar]
- Segaran, D. Dynamic Modelling and Control of Dual Active Bridge Bi-Directional Dc-Dc Converters for Smart Grid Applications. Ph.D. Thesis, RMIT University, Melbourne, VIC, Australia, 2024. [Google Scholar]
- Xue, L.; Mu, M.; Boroyevich, D.; Mattavelli, P. The optimal design of GaN-based dual active bridge for bi-directional plug-in hybrid electric vehicle (PHEV) charger. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 602–608. [Google Scholar]
- Chen, Y.; Zang, B.; Wang, H.; Liu, H.; Li, H. Research on Composite Rotor of 200 kW Flywheel Energy Storage System High Speed Permanent Magnet Synchronous Motor for UPS. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; pp. 398–403. [Google Scholar] [CrossRef]





| Parameter | Description | Value |
|---|---|---|
| Moment of Inertia of Flywheel | 25 kg m2 | |
| Torque Constant | 20 Nm/A | |
| Armature Resistance | 0.1 | |
| Armature Inductance | 0.1 mH | |
| Converter Capacitance | 1 mF | |
| Converter Resistance | 10 M | |
| Line Inductance | 10 mH | |
| Line Resistance | 0.1 | |
| B | Shaft Windage |
| Power Draw | Energy Draw/Storage | Bandwidth | |
|---|---|---|---|
| Control Law Requirement | 2.93 kW | 12.3 Wh | 4.9 Hz |
| System Flywheel | 100 kW | 9.75 kWh | 80 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehman, C.A.; Robinett, R.D., III; Wilson, D.G.; Weaver, W.W. Feasibility Study of Flywheel Mitigation Controls Using Hamiltonian-Based Design for E3 High-Altitude Electromagnetic Pulse Events. Energies 2025, 18, 5294. https://doi.org/10.3390/en18195294
Lehman CA, Robinett RD III, Wilson DG, Weaver WW. Feasibility Study of Flywheel Mitigation Controls Using Hamiltonian-Based Design for E3 High-Altitude Electromagnetic Pulse Events. Energies. 2025; 18(19):5294. https://doi.org/10.3390/en18195294
Chicago/Turabian StyleLehman, Connor A., Rush D. Robinett, III, David G. Wilson, and Wayne W. Weaver. 2025. "Feasibility Study of Flywheel Mitigation Controls Using Hamiltonian-Based Design for E3 High-Altitude Electromagnetic Pulse Events" Energies 18, no. 19: 5294. https://doi.org/10.3390/en18195294
APA StyleLehman, C. A., Robinett, R. D., III, Wilson, D. G., & Weaver, W. W. (2025). Feasibility Study of Flywheel Mitigation Controls Using Hamiltonian-Based Design for E3 High-Altitude Electromagnetic Pulse Events. Energies, 18(19), 5294. https://doi.org/10.3390/en18195294







