Modeling the Duration of Electricity Price Spikes Using Survival Analysis

Abstract

Electricity price spikes are the most important characteristic of the electricity price time series. Operationally, they result from various stresses in the power system or the strategic bidding behavior of market participants. These high prices are important as they represent economic opportunities in the form of profits and savings. Theoretically, price spikes are defined as prices that exceed a threshold over a typically short duration. This definition serves as the basis for several established modeling approaches in the literature. In general, the threshold component determines the design of a price spike model, often overlooking the duration aspect. Therefore, this paper presents a simple yet informative model to quantify the duration of electricity price spikes using historical price data from different market jurisdictions. We approach the problem through the lens of survival analysis, a widely used technique for evaluating time-to-event data. Specifically, we use the Kaplan–Meier (KM) estimator, which enables a nonparametric evaluation of the survival (duration) of price spikes over time. We refer to this as the price spike duration model.

1. Introduction

Electricity price spikes are a prominent feature observed in the price time series of any electricity market, whether with a real-time (RT) or day-ahead (DA). They typically occur during periods of high operational stress in the power system [1] or as a result of strategic bidding by market participants [2]. These spikes are characterized by their magnitude and duration. Accordingly, electricity price spikes are defined as prices that exceed a threshold over a certain, often brief, time window [3,4]. These characteristics distinguish price spikes from normal electricity prices, making them an important area of analysis for different market participants, including generators, industrial loads, and retailers.

In terms of magnitude, modeling price spikes is closely tied to the definition of a price spike threshold. From an operational perspective, market participants require such a threshold to capture the extreme price dynamics in the market. To some extent, the definition for these thresholds can be generic [5] based either on statistical (variable) estimations from the price time series or on the selection of a strategic economic (fixed) cut-off point. In either case, market participants must identify a cut-off point that distinguishes price spikes from normal prices to maximize economic benefits in the form of profits or savings.

Variable thresholds account for price fluctuations over time to identify price spikes. For instance, statistical thresholds based on the mean plus or minus one [6,7], two [7,8,9,10], or three standard deviations [11,12] are commonly used in the literature. Similarly, quartile- and interquartile-based methods are employed to distinguish price spikes from normal prices [13,14,15]. Other approaches involve filtering for the highest prices, such as the top 1% [16] or peaks over threshold [17]. More sophisticated variants of these variable threshold methods have also been proposed in [4,18,19,20]. Given the dynamic nature of the electricity price time series, variable thresholds offer a flexible framework for quantifying price spike magnitude in contrast to fixed thresholds, which do not adapt to changes in the price regime.

Fixed thresholds for price spikes, also known as economic thresholds [21], are based on specific selection criteria influenced by factors such as expert knowledge, market structure, or the economic objectives of particular market participants. These thresholds vary across markets; however, commonly observed values in the literature include 80 AUD/MWh [22]; 100 AUD/MWh, and/or 300 AUD/MWh [5,23,24,25,26]; 5000 AUD/MWh [26]; 250 AUD/MWh, and 500 AUD/MWh [25]; 80 to 150 EUR/MWh [27]; and 150 USD/MWh and 200 USD/MWh [9]. Significant efforts have been made to model the magnitude of price spikes for applications such as forecasting [14] or “outlier” detection and removal [28,29,30]. However, while spike magnitude has been extensively covered through different threshold-based methods, the price spike duration aspect remains less explored.

The second key feature of price spikes is their duration, defining when the spike regime determined by the threshold starts and ends. Some models incorporate duration implicitly within parametric and nonparametric frameworks. For example, machine-learning-based models quantify consecutive spikes over time using an existence index (${\mathbb{I}}_{\mathrm{spike}}\left(t\right)$), which can take the form of a binary [8] or discrete [9] feature. The authors of [8] define ${\mathbb{I}}_{\mathrm{spike}}\left(t\right)$ as one if price spikes occur within the same day before time t, and zero otherwise. The authors of [9] redefine ${\mathbb{I}}_{\mathrm{spike}}\left(t\right)$ as a time distance metric that counts for the number of consecutive spikes between $t-1$ and $t-24$, or 25 otherwise. In both definitions, ${\mathbb{I}}_{\mathrm{spike}}\left(t\right)$ is built under the assumption that price spikes last for multiple hours but no longer than a day [9,10]. This time constraint assumes that price spikes tend to persist and cluster over relatively short periods [19]. Beyond the context of machine learning, price spike duration and persistence have also been incorporated in parametric models.

Parametric predictive models capture the persistence of price spikes by incorporating the history of past events. One example is the autoregressive conditional hazard (ACH) model introduced by [5], which explicitly models the probability of spike occurrence as a function of past spike events, which enables capturing the temporal dependence through a dynamic hazard rate. The model also considers the effects of exogenous variables. Likewise, Ref. [25] uses a Poisson autoregressive model to account for temporal dependence, incorporating the historical arrival (time between spikes) and survival (spike duration) times of spikes, along with exogenous variables, to forecast the probability of occurrence of price spikes. The Hawkes model employed by the work from [15] incorporates time dependency through a self-excitation component, which is extended across different model variants. Similarly, the authors of [17] propose an autoregressive conditional duration peaks-over-threshold model that incorporates both spike intensity and magnitude via the conditional duration between events, along with a set of covariates. They also introduce a Hawkes intensity-based model combined with the peaks-over-threshold model, where spike intensity is dynamically modeled based on the history of past occurrences, and spike magnitude is included in the self-exciting process, accounting for the effects of covariates. Both models fall within the self-exciting marked point process framework, which is used to generate forecasts of returns and value at risk. A multivariate Hawkes model is proposed by the authors of [31] to capture the interdependency of price spikes across interconnected transmission regions. The model jointly characterizes spike frequency and magnitude, where the frequency is modeled through a ground conditional intensity component influenced by past spike occurrences, and the spike size is captured via a magnitude component. This model also incorporates the effects of covariates.

In another approach, the authors of [19] propose a zero-inflated Poisson autoregressive model with exogenous variables to capture the persistence of price spikes as discrete events, based on the fact that spikes tend to cluster. Similar observations about the clustering behavior of spikes are derived by the authors of [21], who include the historical duration hazard of simultaneous spikes in a suite of econometric models, primarily based on logistic regression and a generalized skewed variant, alongside the ACH model from [5]. The authors of [23] propose a semiparametric model to forecast the probability of spikes using their arrival and survival times, along with a set of exogenous variables. Here, the arrival and survival times are also expressed through a natural logarithm transformation and a two-hour moving average. Market structural changes motivate the investigation of price spike durations using a smooth transition logit (STL) model, as proposed by the authors of [22]. The model aims to estimate the probability of observing a short spike that lasts no longer than one half-hour interval, assuming increased strategic bidding behavior from generators. Longer spikes of two or more half-hour intervals are included, but not the focus of interest, as they are attributed to broader power system stresses rather than strategic bidding. Both scenarios are captured by the STL model. Spike durations are quantified as a binary dependent variable, as zero and one for short and long spikes, respectively.

As shown, the persistence of price spikes informs various predictive models by capturing the dependency of future spike intensities on historical spike events. In other words, the intensity of a price spike exhibits temporal dependence, or “memory”, which can be modeled alongside other well-known spike determinants. The literature demonstrates that incorporating the history of past spike occurrences is a significant driver of spike intensity, contributing to the explanatory power of other factors such as load or temperature [5,17]. Moreover, the evidence in the literature suggests that spike duration has been investigated through causal inference to understand how market participants’ behavior, such as strategic bidding, influences its length [22]. These findings highlight spike duration as a fundamental dimension of price behavior deserving further attention, or, as stated by the authors of [22], an area still in its early stages.

Incorporating spike persistence into different models can be carried out using a time-to-event (arrival time) and/or time-of-event (survival time) approach. However, despite the foundational definition of a price spike, the literature remains ambiguous regarding its duration. Some authors argue that price spikes tend to occur over a short period of time but no longer than a day [8], yet the notion of “short period of time” has not been investigated. This paper aims to address this gap by applying survival analysis techniques to explore the duration dimension as a fundamental component of the price spike definition under this precise assumption.

Survival analysis is a set of statistical techniques used to model time-to-event phenomena, including hazard rates, across various research disciplines. In the context of power system operations, both parametric and nonparametric methods, such as Cox proportional hazard models (Cox-PH), Kaplan–Meier estimator, and more recently, machine learning approaches, have been commonly applied to model events like outage durations, equipment failures, preventive maintenance scheduling, and operational risk assessment.

These events share a key characteristic with electricity price spikes: they occur infrequently and can therefore be classified as rare events. Several studies have applied survival analysis in power systems, focusing on critical infrastructure such as transformers, cables, and disconnectors. For instance, Refs. [32,33] use a Cox-PH model with various explanatory variables to estimate the failure probability risk of power cables in networks ranging from low to high voltage. Similarly, Ref. [34] applies a Cox-PH model to examine the effects of different covariates on the failure rates of distribution and regional level disconnectors. Instrument transformer failure rates are analyzed in [35] using both the KM and a Cox-PH model to estimate the probability of failure using historical failure data and covariate effects.

In [36], the KM and a Weibull distribution are used to estimate the lifetime of power transformers at various voltage levels. The Weibull distribution and Monte Carlo simulation are also applied to estimate transformer lifetimes due to aging-related outages [37] and combined aging-related and forced outages [38]. A Cox-PH model is used in [39] to study the impact of spatially distributed meteorological conditions on the failure and lifespan of distribution transformers. In [40], the KM estimator is used to analyze the operational cycles of four small hydropower units, and a prognosis model is proposed to estimate their remaining useful life using sensor data and a suite of models, including Cox-PH, Random Survival Forest, and Gradient Boosting Survival. Outage durations in distribution systems caused by various factors are also analyzed using the KM estimator in [41].

The authors of [42] propose a parametric framework for simulating forced generation outages by modeling the times to state change, indicated as the time to failure (time-to-event) and time to repair (time-of- event), using a Weibull distribution. The model quantifies the probability that a generating unit in the system remains in a given state beyond an elapsed time. Building on this generation reliability framework, the authors of [1] incorporate the capacity model with a bootstrapped on-peak/off-peak detrended load model to simulate the demand-to-capacity ratio, a key determinant of electricity price spikes, also investigated by other authors such as [4]. Prices in a low or high regime are probabilistically selected using this ratio, modeled, respectively, via a Brownian motion process and a normal distribution.

The application of survival analysis in power systems is extensive and has potential in the operations of electricity markets. Unlike previous studies that incorporate the time-to-event and/or time-of-event to support prediction or causal inference [22,23,25], our work focuses solely on modeling spike duration using a rich dataset of price data from various day-ahead and real-time markets. Moreover, while prior research [21,22,23] provides some insights into price spike durations in the Australian market, without making it the central outcome of their analysis, our approach differs by applying survival analysis, specifically, the KM estimator, to approximate the problem nonparametrically. Thus, we aim to establish a practical framework for quantifying spike duration based on its fundamental definition, under the assumption, supported by existing literature [8], that spikes last no more than a day. Accordingly, our objective is to answer the following research questions empirically:

I.

For how long do price spikes persist after the onset and end of the spike regime defined by a given threshold?

II.

What does “short period of time” mean in the context of price spike duration?

The remainder of this paper is structured as follows: Section 2 defines the problem formally and introduces the principles of survival analysis as applied to electricity price spike duration. Section 3 presents the numerical results for all the analyzed markets and time periods. In Section 4, we discuss key observations from the numerical results and relate them to our main research question. Conclusions and directions for future work are provided in Section 5.

2. Problem Definition

The problem under investigation analyzes the duration of electricity price spikes (i.e., time-of-event) through the lens of survival analysis, specifically focusing on time of occurrence [43]. This is conceptually analogous to outage duration modeling in critical electrical infrastructure, such as distribution systems [41]. Price spike durations are analyzed in market $\mathcal{M}$ using historical data consisting of time series of electricity prices ${\mathbf{P}}_{t_i}={[P_{t_1},P_{t_2},\cdots ,P_{t_N}]}^{\prime }$ for $i\in \{1,2,\cdots ,N\}$. The magnitude of each price sample $P_{t_i}$ is evaluated against a threshold $\tau$, such that

$$Z_{t_i}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{P}_{t_i}\ge \tau \hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

Expression (1) defines a binary outcome stored in the form of a random variable ${\mathbf{Z}}_{t_i}={[Z_{t_1},Z_{t_2},\cdots ,Z_{t_N}]}^{\prime }$, indicating the occurrence of price spikes based on a threshold $\tau$. The vector ${\mathbf{Z}}_{t_i}$ is fundamental for quantifying the duration of price spikes in a market $\mathcal{M}$. Additionally, (1) can be adapted to capture negative spikes by evaluating $P_{t_i}\le \tau$. The definition of survival times in this section builds on the foundational work of [43] for nonparametric modeling. For a discrete-time random variable T, survival analysis quantifies the probability $\mathcal{P}$ that an event persists beyond time t, as described by the survivorship function $\varrho \left(t\right)$ in (2) [43].

$$\varrho \left(t\right)=\mathcal{P}(T>t)$$

(2)

From the general form in (2), let ${\mathbf{T}}_j,j\in \{1,2,\cdots ,n\}$ be a discrete random variable valued from a set of time point observations occurring at random times $t_0<t_1<\cdots <t_m$ [5]. The survival function $\varrho \left(t\right)$ is a non-increasing function, satisfying $\varrho \left(0\right)=1$ and $\varrho (\infty )=0$ [44].

Extending from (2), we define a price spike duration model to quantify the length (time-of-event) of electricity price spikes (“sp”) using ${\mathbf{T}}_j^{\left(sp\right)}=[T_1^{\left(sp\right)},T_2^{\left(sp\right)},\cdots ,T_n^{\left(sp\right)}]$. Here, ${\mathbf{T}}_j^{\left(sp\right)}$ contains the realizations of spike durations at intervals [$t_0$, $t_1$), [$t_1$, $t_2$),…, [$t_{m-1}$, $t_m$), each corresponding to an equally spaced time period [45]. In our context, quantifying the realizations in ${\mathbf{T}}_j^{\left(sp\right)}$ requires the binary information in ${\mathbf{Z}}_{t_i}$ as defined in (1). This forms the empirical basis for estimating the spike survival probabilities.

Using the observed price spike durations provided by ${\mathbf{T}}_j^{\left(sp\right)}$, we aim to evaluate (2) by estimating the Product Limit estimator $\widehat{\varrho }\left(t\right)$, also known, and hereafter referred to as the KM estimator [43]. This begins with estimating the survival proportion:

$${\widehat{\varrho }}_d={\displaystyle \frac{p_d^{s{p}_{active}}-p_d^{s{p}_{inactive}}}{p_d^{s{p}_{active}}}}$$

(3)

The expression in (3) quantifies the ratio based on the number of active ($p_d^{s{p}_{active}}$) and inactive ($p_d^{s{p}_{inactive}}$) spikes for a specific duration d, for $d\in \{1,2,\cdots ,D\}$ and D is the maximum observed duration in ${\mathbf{T}}_j^{\left(sp\right)}$. Thus, ${\widehat{\varrho }}_d$ represents the conditional survival probability for each spike duration d. This leads to the final form of the KM estimator:

$$\widehat{\varrho }\left(t\right)=\prod _{d=1}^D{\displaystyle \frac{p_d^{s{p}_{active}}-p_d^{s{p}_{inactive}}}{p_d^{s{p}_{active}}}}$$

(4)

Expression (4) estimates the survival probability of price spikes in market $\mathcal{M}$ and provides the final form of the proposed price spike duration model. While price spikes are primarily driven by short-term power system and market operations, longer spikes can also occur under exceptional conditions, such as extreme weather events, which can cause spikes to persist longer than usual, for example, beyond one day [10]. Although (4) can be used to analyze survival probabilities for these rare events, our modeling assumption focuses on spike durations of up to one day, as discussed in Section 1. Our design assumption parallels that made in [22], who propose the STL model to study the effects of market design in short-duration spikes, as noted in Section 1. Therefore, we exclude these rare events from the sample ${\mathbf{T}}_j^{\left(sp\right)}$ by applying right truncation [45]. Specifically, we set $\beta$ as the truncation limit such that any realization $T_j^{\left(sp\right)}>\beta$ is excluded.

The logic of the proposed price spike duration model is illustrated in Figure 1. The user provides as inputs the price vector ${\mathbf{P}}_{t_i}$ corresponding to market $\mathcal{M}$, a selected price spike threshold $\tau$ for each analyzed period, and the truncation limit $\beta$. These inputs are then used in the first process block to estimate the binary vector ${\mathbf{Z}}_{t_i}$, indicated with the symbol “*” in the first column’s output block. In the first column’s last process block, ${\mathbf{Z}}_{t_i}$ is used to quantify price spike durations, which are stored in ${\mathbf{T}}_j^{\left(sp\right)}$. The user may apply a filtering criterion based on $\beta$ criteria (right truncation), as shown in the second column’s first process block. If this decision is applied, as in our case, then ${\mathbf{T}}^{\prime \left(sp\right)}$ will contain only spike durations up to $\beta$, which will be used to estimate $\widehat{\varrho }\left(t\right)$, as shown in the second process block from the second column. Finally, the survival probability $\widehat{\varrho }\left(t\right)$ for different spike durations is estimated using the KM estimator introduced in (4), following the principles of nonparametric estimation. This is the final output observed in the second column’s third block.

A key assumption in our analysis is that we do not evaluate the influence of external determinants on the duration of price spikes when applying the KM estimator. Our analysis focuses exclusively on the duration of price spikes as an intrinsic characteristic of their definition, as provided in Section 1.

3. Numerical Results

This Section discusses the results of the price spike duration model introduced in Section 2. We begin by presenting the data and preprocessing steps, followed by an exploratory data analysis and relevant modeling assumptions. Finally, we investigate price spike durations in each market $\mathcal{M}$ using the KM estimator, as defined by (4) in Section 2.

The price spike duration model in (4) is agnostic to the choice of price threshold $\tau$. For positive spikes, we select $\tau$ = 300 $\alpha$/MWh (the price magnitude in $“\alpha ”$ per energy unit, where $\alpha$ denotes an arbitrary currency in market $\mathcal{M}$), consistent with thresholds used in the recent literature on price spikes, for example, [26]. Moreover, since not all the markets in our study exhibit extreme negative prices, we justify our selection of the negative threshold for price spikes in Section 3.4.3.

Finally, we emphasize that the focus of this study is to evaluate the duration of price spikes across different markets using survival analysis tools. Exploring a wide range of thresholds is beyond the scope of this work, as varying $\tau$ would influence the outcome of (4) each time. Nevertheless, regardless of the selected threshold, it is expected that the survival probability of price spikes will decrease as their duration increases.

3.1. Datasets and Preprocessing

The duration of price spikes is analyzed across different market designs. The datasets cover markets with only a real-time (RT) settlement component; a day-ahead (DA) market with an auction pricing mechanism, typically complemented by intraday and balancing markets; and markets with two-settlement nodal pricing, featuring both RT and DA structures. Specifically, each market $\mathcal{M}$ consists of two Canadian RT markets, i.e., Alberta and Ontario, operated by the Alberta Electric System Operator (AESO) [46], and Ontario’s Independent Electricity System Operator (IESO) [47], respectively. At the time of this study, Ontario’s market transitioned to a DA structure on 1 May 2025 [47], however, our analysis uses price data from the prior RT-only market. Moreover, we use one U.S. market with DA and RT structures operated by the Electric Reliability Council of Texas (ERCOT) [48]; the Belgian DA market zone operated by the European Power Exchange (EPEX Spot) [49], referred to as EPEX-BE; and one Asian RT market, the Singapore Wholesale Electricity Market (SWEM) [50].

The hourly energy prices used in this study are as follows: the AESO pool price [51]; IESO’s Hourly Ontario Energy Price (HOEP) [52], now referred to as the Ontario Electricity Market Price, which is an after-the-fact price adjusted for real-time differences [53]. Since our study uses pre-renewal RT prices, we refer to it as HOEP. Furthermore, the IESO’s DA market estimates the LMPs that account for transmission capacity constraints, which are then averaged to produce a province-wide DA price known as the Ontario Zonal Price [53]. Additionally, we utilize ERCOT’s DA and RT locational marginal prices (LMPs) [54] for the Houston Hub. While ERCOT’s RT market operates at a 5-min dispatch interval, the data used in this study corresponds to hourly average prices. For the EPEX-BE market we use the DA spot prices [55] (following European naming conventions [2]). Finally, we include the Uniform Singapore Energy Price (USEP) from the SWEM [56]. All datasets used in this study provide hourly price data, either natively or in aggregated formats. The only exception is the SWEM, where the USEP is reported at half-hourly intervals and converted to hourly resolution by averaging each pair of half-hourly values. For all datasets except the SWEM, daylight saving time (DST) effects are accounted for using standard practices in electricity price forecasting [57]. Singapore, which operates on Singapore Time (SGT), does not observe DST [58].

Finally, for all markets, we analyze 5 years of data corresponding to the period from 2020 to 2024. The price spike duration model is individually evaluated for each of these years.

3.2. Exploratory Analysis

Table 1. Summary of the price statistics for each market $\mathcal{M}$ and year.

		2020	2021	2022	2023	2024
AESO–Pool price (CAD/MWh)	Mean	46.72	101.93	162.46	133.64	62.78
	Std Dev	92.13	138.96	199.21	183.83	124.2
	Minimum	0	5.07	0	0	0
	Maximum	999.99	999.99	999.99	999.99	999.99
IESO–HOEP (CAD/MWh)	Mean	12.65	26.75	44.96	28.75	32.19
	Std Dev	21.33	31.23	36.95	20.95	27.05
	Minimum	−4.51	−3.94	−4.43	−0.01	0
	Maximum	1258.05	1660.8	689.33	955.14	1394.13
ERCOT–LMP DA (USD/MWh)	Mean	22.92	148.2	69.92	57.3	28.27
	Std Dev	36.62	891.36	92.15	218.4	59.68
	Minimum	3.66	0.06	4.64	1.55	−0.02
	Maximum	2026.17	8995.11	2523.86	4188.23	2215.08
ERCOT–LMP RT (USD/MWh)	Mean	20.49	79.19	62.12	47.97	26.55
	Std Dev	31.05	460.10	146.60	221.20	68.29
	Minimum	−24.39	−31.66	−29.67	−83.53	−31.83
	Maximum	1081.77	8992.61	4840.21	5015.06	3017.15
EPEX-BE–Spot price (EUR/MWh)	Mean	31.88	104.12	244.55	97.28	70.32
	Std Dev	16.54	79.45	134.65	45.86	43.05
	Minimum	−115.31	−70	−100	−120	−140
	Maximum	200.04	620	871	330.36	565.46
SWEM–USEP 1 (SGD/MWh)	Mean	70.01	196.33	291.81	247.52	163.18
	Std Dev	46.16	358.67	255.27	328.06	229.68
	Minimum	0	−5.05	52.49	74.72	−20.14
	Maximum	1254	4499.09	4499.96	4500	4500

¹ Statistics obtained from the pre-processed hourly prices, as explained in Section 3.1.

presents price statistics for the different markets and periods analyzed in this study, with values reported in their corresponding currency. Overall, the USEP exhibits the highest average price levels, followed by the pool price and the spot price; for example, compare the average price between 2020 and 2021 for these markets. In general, the HOEP exhibits the lower average prices for all the periods compared to the other markets.

Overall, the largest standard deviations are observed for the pool price and the USEP, with some specific years showing particularly high variability in other markets, for example, ERCOT (both, DA and RT markets) in 2021 or EPEX-BE in 2022. These observations will be discussed in more detail in later sections of the manuscript. Additionally, minimum and maximum prices are influenced by market-specific design and regulatory framework.

3.3. Right Truncation

Using right truncation, as introduced in Section 2, provides design flexibility in survival analysis, particularly when tailored to specific contexts. This is relevant in the analysis of price spikes, which are typically short-lived events [26], triggered by operational stresses in the power system, or strategic bidding by market participants. Therefore, it is important to assess whether applying (4) remains meaningful for durations significantly beyond a selected spike survival limit of, for example, 24 h, as suggested in the literature [10].

We analyze all the datasets from all markets and all years to look for spike events longer than 24 h. For example, our findings from Alberta show that such extended spikes typically occur under exceptional conditions rather than during routine market operations. In 2022, three spike events exceeded 24 h in duration, two lasting 31 h and one lasting 25 h, occurring in the Summer and Fall seasons, respectively. Here, one of the 31 h events occurred during the transition between Fall and Winter.

In Alberta, Fall and Spring are considered shoulder seasons, when power plants are more likely to undergo planned outages due to milder weather and lower demand, representing operational conditions where spikes can also occur [1]. In contrast, Summer is the hottest season, during which high temperatures can lead to prolonged price spikes under tight grid conditions due to hot weather. This also applies to Winter, where extreme cold snaps are observed in Alberta. While seasonal factors are important in shaping spiking dynamics in the market, they are not limited to specific seasons. For instance, two 12 h spike events in Summer 2023 coincided with the periods when the AESO issued grid alerts (previously referred to as Energy Emergency Alert [59]).

Similar long-duration spike events are observed in the ERCOT DA and RT markets and in the SWEM. In ERCOT, these correspond to the extreme cold weather events of February 2021 [60] with spike durations reaching 168 and 108 h in the DA and RT markets, respectively. Likewise, the EPEX-BE market experienced a 33 h spike event in December 2021, corresponding to the second half of the year, when European markets observed an increasing price volatility [61]. Additionally, this same market observed 162 and 163 h spike events in August of 2022, likely associated as a combination between maximum record hot temperatures [62] and the effects of the 2022 European energy crisis [61]. The SWEM observed spike events of 46 and 34 h in 2021 and 2022, as a combination of high fuel prices, supply shortages, and high demand. Moreover, this same market recorded a 98 h spike event in Spring 2023, attributed to record-high temperatures and supply shortages caused by maintenance outages [63]. In contrast, Ontario’s market shows no spike events exceeding the 24 h duration limit in any of the analyzed years. Based on these observations, which show that such longer spike events are rare and typically driven by exceptional system conditions, we justify the use of right truncation at a 24 h limit ($\beta =24$ in Figure 1) for price spike duration.

3.4. Price Spike Duration Models

The price spike duration models are developed following the methodology introduced in Section 2, and the experiments are conducted using the Lifelines Python package (v0.27.7) for survival analysis [64]. As previously mentioned, we use a price threshold of $\tau$ = 300 $\alpha$/MWh; however, the model is agnostic to the choice of $\tau$. Here, $\alpha$ corresponds to the Canadian Dollar (CAD) for the pool price and the HOEP, the United States Dollar (USD) for ERCOT’s LMPs, the Euro (EUR) for spot price, and the Singapore Dollar (SGD) for the USEP. Finally, duration probabilities are estimated using right truncation at 24 h, based on the discussion in Section 3.3.

3.4.1. Alberta (AESO) and Ontario (IESO) Pool Price and HOEP

Figure 2 presents the results from the price spike duration for both the pool price (Figure 2a) and the HOEP (Figure 2b), corresponding to Alberta’s and Ontario’s electricity markets, respectively, across all analyzed periods. Price spikes tend to last longer in Alberta than in Ontario. In both cases, spike duration is represented by the survival probability $\widehat{\varrho }\left(t\right)$.

In Alberta, longer-duration price spikes are observed throughout all periods; however, their survival probabilities decline as the duration approaches the 24 h mark, as expected. Additionally, Figure 2a shows that, across all periods, the median survival time for spikes in Alberta lies between 2 and 3 h. For example, when $\widehat{\varrho }\left(t\right)\approx 50\%$, the corresponding spike duration is observed to typically fall within this range. Furthermore, in 2020, 2023, and 2024, spike durations of 4 to 5 h are associated with $\widehat{\varrho }\left(t\right)\approx 25\%$, while in 2021 and 2022, this same probability corresponds to durations of 5 h. Notably, during the COVID-19 pandemic year (2020), spike durations of 11 to 14 h exhibited the highest survival probability (10%) compared to the other years.

Figure 2b offers a contrasting view for the Ontario market, where spike survival probabilities drop drastically after one hour across all years, particularly in 2020 and 2021. Some variation is observed for 2022, 2023, and 2024, where 2 h spike durations correspond to survival probabilities of $\widehat{\varrho }\left(t\right)=7.6\%$, $33.3\%$, and $20\%$, respectively. No spike events are observed to persist beyond 2 h in this market.

The comparison of price spike durations between the Alberta and Ontario markets highlights how market structure influences price spike behavior. Ontario’s generation mix is dominated by nuclear and hydro power, accounting for 57% of the transmission interconnected capacity in this market, with less contribution from natural gas (24%), wind (13%), and solar (13%) [65]. Here, the IESO highlights the importance of nuclear and hydro power operating characteristics in making them the ideal technology to meet the baseload in this market [65]. These technologies operate as a reliable and stable source of power, which can help mitigate market operational uncertainty and the likelihood of strategic bidding, known to be associated with the occurrence of price spikes [22,66].

Alberta’s power market relies heavily on natural gas technologies, accounting for more than 60% of its generation mix [67]. For example, natural gas generation supplied 75% of all electricity in 2024 [68]. Here, at the time of this study, Alberta’s market had phased out coal-fired power plants from its generation mix, with most units converted to natural gas power plants. Moreover, Alberta’s market has observed an expansion in wind and solar capacity since 2020, contributing to more than 30% of the province’s generation mix [67,69]. These specifics of the generation mix in Alberta provide an opportunity where both strategic behavior and operational uncertainty can have a stronger contribution to spike-prone price dynamics in this market, as opposed to Ontario’s.

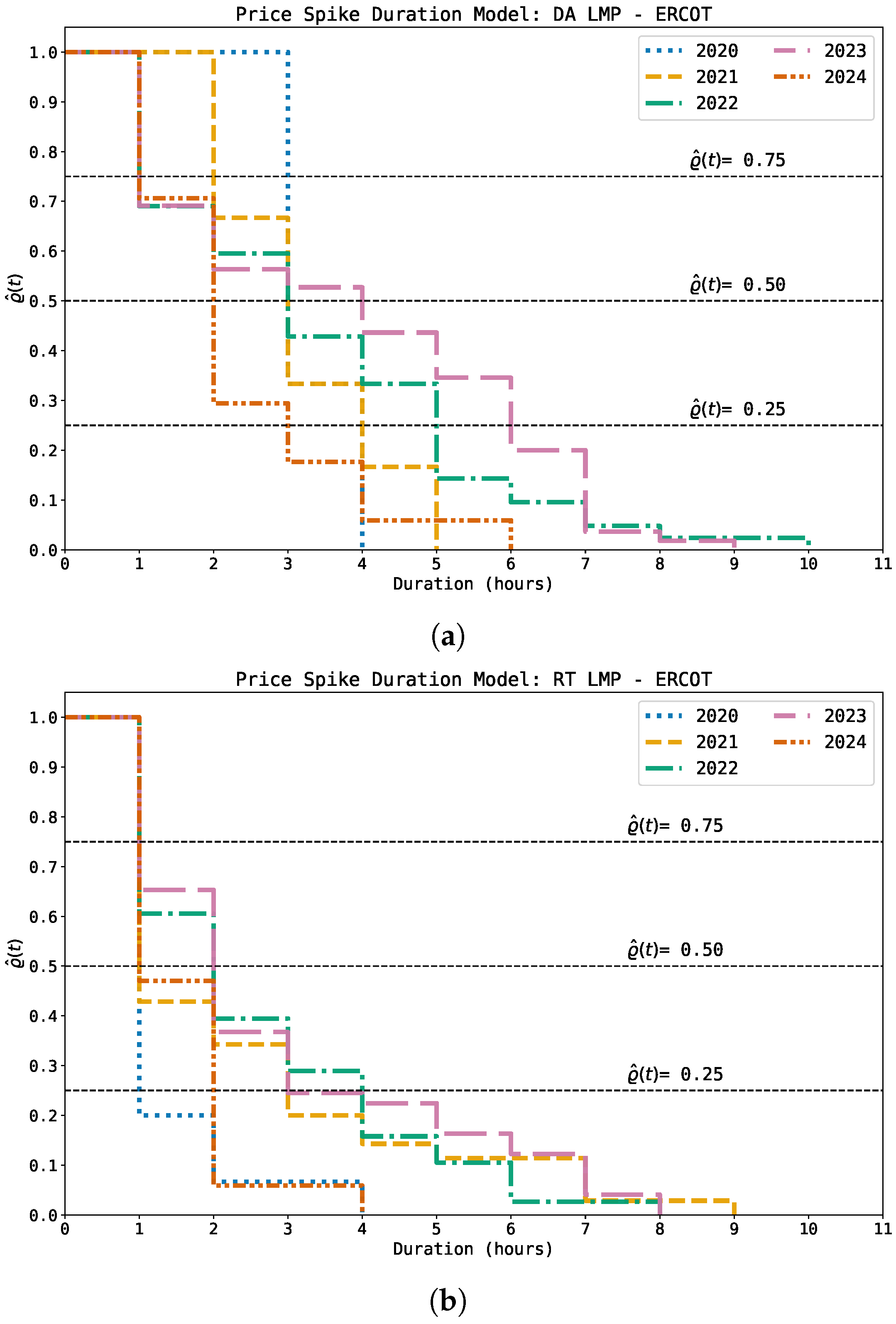
3.4.2. Texas (ERCOT)-DA and RT LMP

The price spike duration model results for ERCOT’s DA and RT markets are shown in Figure 3. Specifically, Figure 3a presents the model for the DA market, where spike durations longer than one hour are observed at $\widehat{\varrho }\left(t\right)=100\%$ for 3 h and 2 h spike events in 2020 and 2021, respectively. Observe that 2020 exhibits fewer transitions between spike durations, for example, from 3 h at $\widehat{\varrho }\left(t\right)=100\%$ to 4 h at $\widehat{\varrho }\left(t\right)=33\%$. Additionally, spike durations between 3 and 6 h are observed at $\widehat{\varrho }\left(t\right)\approx 30\%$ and $\widehat{\varrho }\left(t\right)\approx 45\%$ across all years. This is the only point where survival probabilities converge closely in both the x-axis and the y-axis. Finally, after applying right truncation, following the explanations in Section 2 and Section 3.3, a 5 h spike duration in 2021 corresponds to the longer spike duration observed in this market with 17% survival probability.

Figure 3b shows similar results for the RT market. In 2021, the survival probability drops to $\widehat{\varrho }\left(t\right)=3\%$ to spikes lasting up to 9 h after applying right truncation. Unlike the DA market, all years in the RT market show $\widehat{\varrho }\left(t\right)=100\%$ for 1 h spike events. For 2022, 2023, and 2024, 2 h spike durations correspond to survival probabilities of $\widehat{\varrho }\left(t\right)=61\%$, $65\%$, and $47\%$, respectively, compared to $\widehat{\varrho }\left(t\right)\approx 70\%$ in the DA market for the same years.

A joint comparison between the DA and RT spike duration models in ERCOT is of interest, for example, to determine whether one market tends to exhibit longer spike survival probabilities at specific durations. However, this is not immediately evident from visual inspection of Figure 3. Therefore,

Table 2. Price spike durations in hours [h] for ERCOT, based on a fixed threshold $\tau$ = 300 USD/MWh, are reported alongside their estimated survival probabilities $\widehat{\varrho }\left(t\right)$. Higher values of $\widehat{\varrho }\left(t\right)$ between the DA and RT markets are highlighted in bold.

$\widehat{\mathit{\varrho }}\left(\mathit{t}\right)$		2020		2021		2022		2023		2024
		DA	RT	DA	RT	DA	RT	DA	RT	DA	RT
Duration [h]	1	1	1	1	1	1	1	1	1	1	1
Duration [h]	2	1	0.2	1	0.43	0.69	0.61	0.69	0.65	0.71	0.47
Duration [h]	3	1	0.067	0.67	0.34	0.59	0.39	0.56	0.37	0.29	0.06
Duration [h]	4	0.33	0.067	0.33	0.20	0.43	0.29	0.53	0.24	0.18	0.06
Duration [h]	5	-	-	0.17	0.14	0.33	0.16	0.44	0.22	0.06	-
Duration [h]	6	-	-	-	0.11	0.14	0.11	0.35	0.16	0.06	-
Duration [h]	7	-	-	-	0.11	0.1	0.03	0.20	0.12	-	-
Duration [h]	8	-	-	-	0.03	0.05	0.03	0.04	0.04	-	-
Duration [h]	9	-	-	-	0.03	0.02	-	0.02	-	-	-
Duration [h]	10	-		-	-	0.02	-	-	-	-	-

provides the estimation of $\widehat{\varrho }\left(t\right)$ for the spike durations across all years. In most cases, the DA market shows higher survival probabilities (highlighted in bold) than the RT market for the same durations. We now derive some ideas about these results. Moreover, recall that these two markets operate on different time dimensions, serving different operational purposes.

As pointed out by authors of [70], the DA market is the main floor for forward-looking generation and load scheduling activities; it is also a market observing the larger volume of traded electricity. In contrast, the RT market is a balancing market, responsive to the short-term imbalances in the power system; this market adjusts the deviations from the actual real-time conditions that differ from the planned DA schedules. We further analyze the results from Table 2 using the price spread signal. Following the definition of price spread between DA and RT proposed in the study from [70], we estimate a conditional spike spread $\Delta P_{t_i}^{\left(sp\right)}$ as follows:

$$\Delta P_{t_i}^{\left(sp\right)}=\left\{\begin{array}{cc}{P}_{t_i}^{\left(\mathrm{DA}\right)}-P_{t_i}^{\left(\mathrm{RT}\right)},\hfill & \mathrm{if}{P}_{t_i}^{\left(\mathrm{DA}\right)}\ge \tau \hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(5)

Using the expression in (5), we calculate the positive and negative spike spreads across all the analyzed periods in ERCOT’s DA and RT markets. These quantities are expressed as a percentage of the total number of hours identified by $\Delta P_{t_i}^{\left(sp\right)}$ and are shown in

Table 3. Percentage of positive and negative spike spread hours from the total of hours accounted for $\Delta p_{t_i}^{\left(sp\right)}$ in (5).

	2020	2021	2022	2023	2024
Total of hours accounted by $\Delta p_{t_i}^{\left(sp\right)}$	10	187	142	210	39
Positive spike spread hours [%]	100	80.75	78.17	74.29	74.36
Negative spike spread hours [%]	0	19.25	21.83	25.71	25.64

. Our interest in this metric stems from its ability to reveal underlying market dynamics, particularly given that the DA and RT markets operate on different temporal horizons.

Table 3 shows that the percentage of hours with positive spike spreads consistently exceeds those with negative spreads across all analyzed years. This predominance of positive spreads during DA price spike periods suggests that market participants anticipate future supply scarcity, which is reflected in higher DA prices. Similarly, when accounting for all hours, including those with normal prices, the percentage of positive and negative spreads estimated from $P_{t_i}^{\left(DA\right)}-P_{t_i}^{\left(RT\right)}$ corresponds, respectively, to 66.1 and 33.9% in 2020; 68.3 and 31.7% in 2021; 69.71 and 30.29% in 2022; 64.25 and 35.75% in 2023; and 55.19 and 44.81 % in 2024. In general, this indicates that DA prices tend to be higher across all analyzed periods. For example, under high levels of intermittent generation, such as wind, a predominant percentage of positive spike spreads may be linked to forecast errors arising from wind’s stochastic nature [71], leading to an underestimation of forward-looking wind output. These challenges underscore the operational complexity faced by system operators in managing the integration of intermittent energy sources.

These observations are consistent with the findings of [72], who highlight the challenges associated with integrating increasing volumes of intermittent generation into electricity markets, with particular emphasis on forecast errors. Finally, it is worth noting that ERCOT has integrated approximately 25 GW of wind capacity, representing nearly one-quarter of the total installed generation capacity in the market [73].

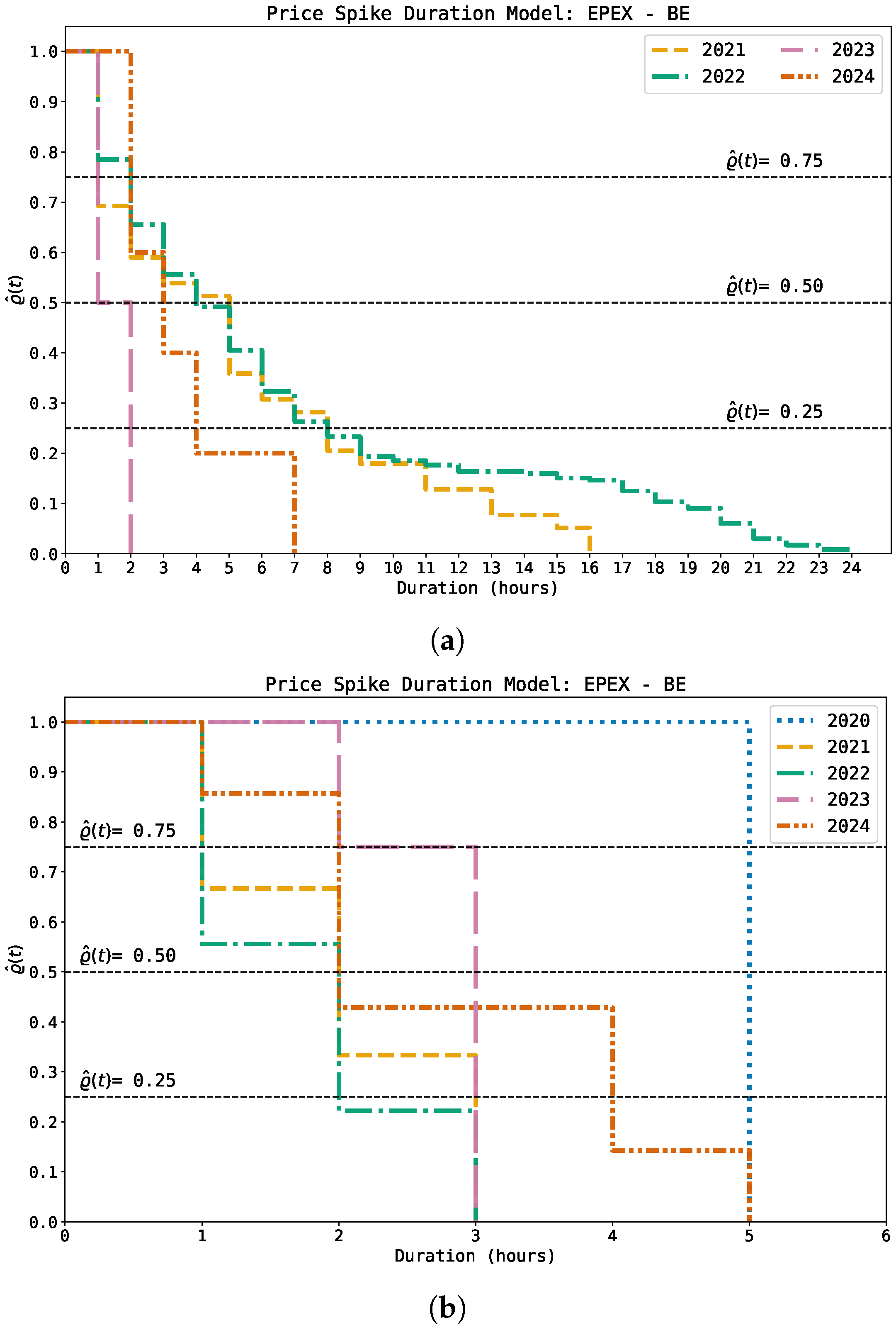
3.4.3. EPEX-BE–Spot Price

Figure 4 presents the results of the DA price spike duration model for the EPEX-BE market. These results estimate the duration of both positive and negative spikes, as shown in Figure 4a and Figure 4b, respectively. Specifically, Figure 4a displays spike durations for the years 2021 to 2024 using a fixed threshold of $\tau$ = 300 EUR/MWh; no spikes were recorded in 2020 above this threshold (see the maximum spot price in Table 1 for that year). In 2024, spike durations at $\widehat{\varrho }\left(t\right)=100\%$ decay after 2 h, similar to the behavior observed in ERCOT’s DA market in 2020 and 2021 (see Figure 3a). In contrast, the remaining years in Figure 4a show a decay after 1 h at $\widehat{\varrho }\left(t\right)=100\%$, consistent with most other markets in this study.

Additionally, the 2023 spike duration model closely resembles those observed in Ontario for 2022 to 2024 (see Figure 2b), although the survival probability for 2 h spike events is higher in the EPEX-BE market ($\widehat{\varrho }\left(t\right)=50\%$) than in Ontario ($\widehat{\varrho }\left(t\right)<50\%$). Furthermore, 2022 exhibits the longest survival probabilities among all years; for example, at $\widehat{\varrho }\left(t\right)\approx 25\%$, spike durations reach approximately 8 to 9 h. Similar observations apply to 2021. It is worth noting that 2023 corresponds to the post-energy crisis period in Europe, during which prices began to stabilize after the 2022 peak, although price levels remained high when compared to those previous to 2021 (i.e., observe the price mean and standard deviations between 2020, 2023, and 2024 in Table 1). Our observations are derived following those presented by authors in [61] for the German market during the same period. 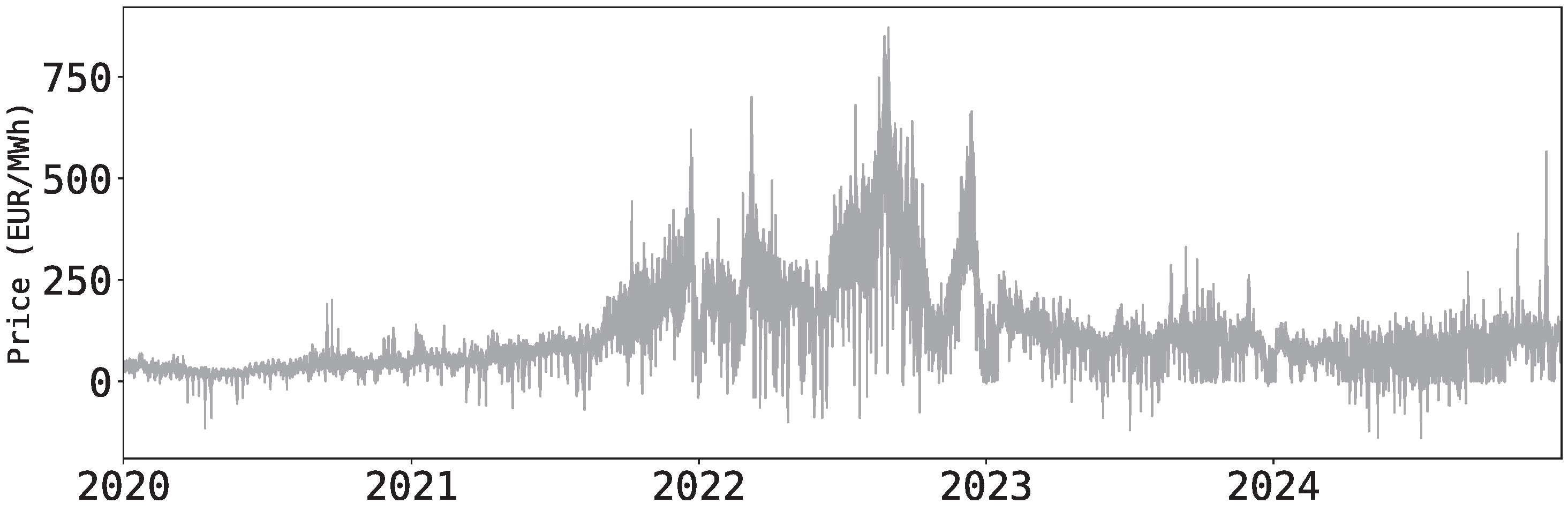To further provide some context on these ideas, Figure 5 shows the price dynamics between the 2020 and 2024 periods in the EPEX-BE market.

The EPEX-BE market exhibits the lowest negative price levels among all the analyzed markets (see Table 1 in Section 3.2). The price spike duration model defined in Section 2 via (4) enables the evaluation of both positive and negative spikes. Hence, we analyze negative price spikes in this market with a fixed threshold of $\tau =-$60 EUR/MWh.

This negative threshold ensures the inclusion of negative spike samples across all years in the study, as it is close to the minimum observed price in 2021 in Table 1. As opposed to considering a threshold like $\tau =\mu -3\sigma$ [11], which would yield −17.72, −134.23, −159.44, −40.32, and −58.83 EUR/MWh, respectively, for each of the corresponding analyzed periods. Comparing these last values with the minimum spot price shown in Table 1 for the EPEX-BE market would exclude the years 2021 and 2022 from the price spike duration model. Additionally, filtering negative spikes as prices below zero [16] captures only negative prices, not necessarily negative price spikes. The model for negative spike durations is shown in Figure 4b.

In 2020, negative spike events lasted 5 h with $\widehat{\varrho }\left(t\right)=100\%$ before dropping to zero, likely reflecting the impact of the COVID-19 pandemic. In 2023, 2 h negative spikes also show $\widehat{\varrho }\left(t\right)=100\%$, decreasing to $\widehat{\varrho }\left(t\right)=75\%$ for 3 h spike events and then to zero. In 2021 and 2022, survival probabilities fall to zero after 3 h durations, with $\widehat{\varrho }\left(t\right)=33\%$ and $\widehat{\varrho }\left(t\right)$ = 22%, respectively. In 2024, 5 h negative spikes exhibit a survival probability of $\widehat{\varrho }\left(t\right)=14.3\%$. Overall, Figure 4 highlights the contrasting behavior of positive and negative spike survival in the EPEX-BE market.

During the evaluation period, negative spikes in the EPEX-BE market tend to occur at lower predicted system load and higher predicted renewable generation volumes. To better account for these two effects jointly, we estimate the net load forecast. These patterns are summarized in Figure 6, which shows a positive correlation between the spot prices and the estimated net load forecasts by day of the week to capture daily seasonality. In general, negative prices tend to appear at lower net load levels. Moreover, they are more frequently observed on weekends, when the net load is typically lower. The lower-left region of Figure 6 also reveals periods of renewable power oversupply. Specifically, the spike events analyzed in this study are more concentrated on weekends (for example, Sundays) than on weekdays, although not necessarily during the lowest net demand levels.

3.4.4. SWEM-USEP

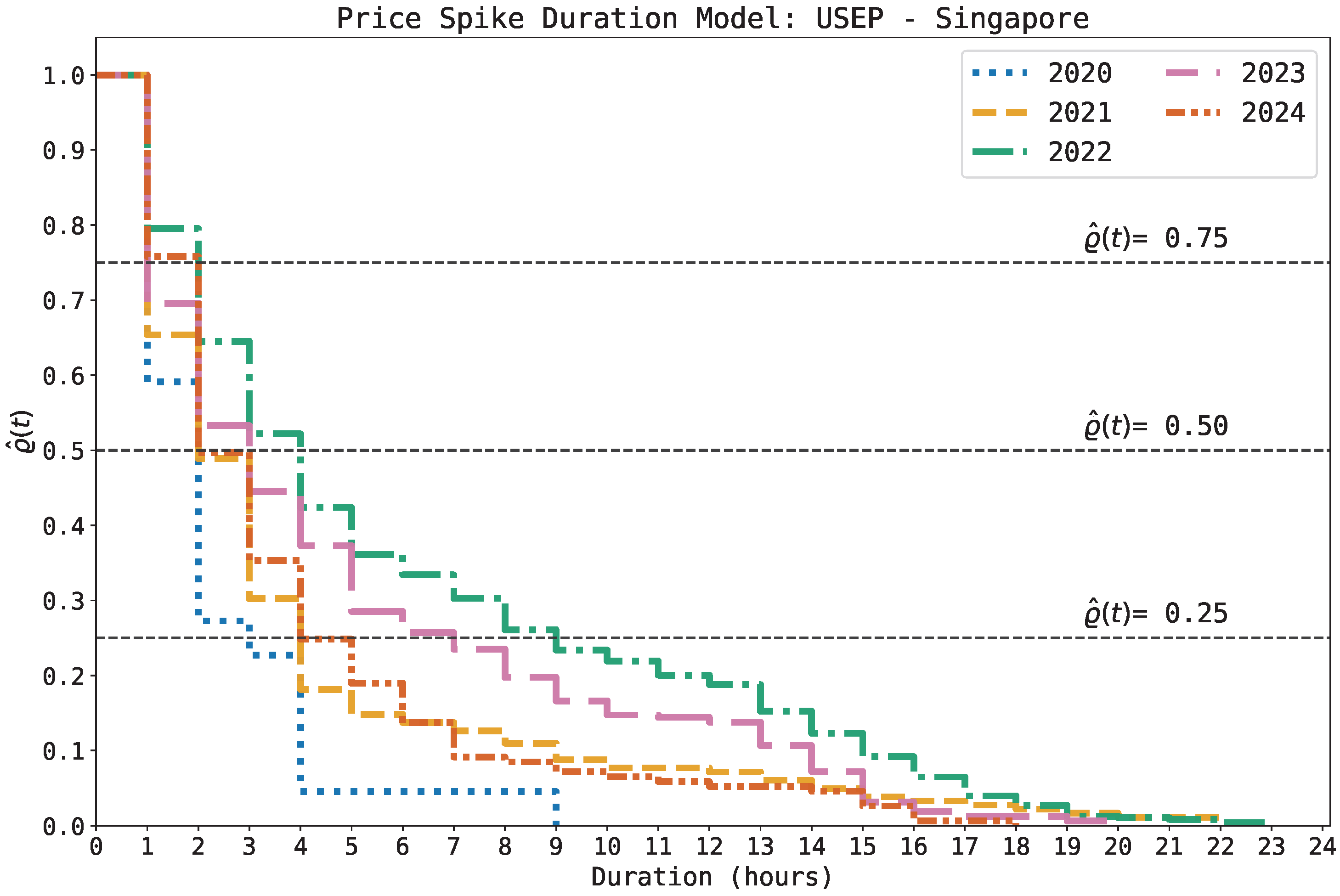
The price spike duration model for the USEP is shown in Figure 7. The survival curve for 2020 displays a noticeably steeper decline compared to other years, particularly beyond the 2 h duration mark. Interestingly, at the $\widehat{\varrho }\left(t\right)\approx 25\%$ survival probability level, spike durations in Singapore’s market during 2022 are comparable to those in the EPEX-BE market (see the same year in Figure 4a) for 8 h and 9 h spike events.

At approximately the same survival probability level ($\widehat{\varrho }\left(t\right)\approx 25\%$), Figure 7 also shows the widest dispersion in spike durations. For example, 7 h and 9 h spike events are observed in 2022 and 2023, respectively, while 3 h, 4 h, and 5 h durations are observed in 2020, 2021, and 2024. With the exception of 2020, the spike duration curves in the SWEM resemble those of Alberta’s market (see Figure 2a).

An interesting feature of the SWEM is its heavy reliance on natural gas, which accounts for approximately 95% of its generation mix. This includes technologies such as combined cycles, cogeneration, and trigeneration systems [63,74]. As a result, the spike events observed in Figure 7 are likely driven by forced and planned outages, associated too with strategic bidding, with minimal influence from variable generation technologies. As previously stated, the spike duration curves between the SWEM and Alberta’s market resemble each other; interestingly, these markets share some important characteristics. For example, they are both organized under an RT-only (single-settlement) framework, with high dependency on natural gas generation. These ideas contrast with markets like ERCOT, where the price spike duration model reflects the impact of high renewable penetration in both of its markets.These observations underscore the importance of market design in shaping the duration and dynamics of price spikes.

4. Discussion

Section 3 presents a variety of results across all analyzed markets and periods, obtained using the price spike duration model introduced in Section 2. In particular, Section 3.4 aims at responding to our first research question in Section 1 using data from different markets and periods. However, our second research question, proposed in Section 1, has not yet been fully addressed. To this end,

Table 4. Positive price spike events duration $d^{(sp,+)}$ based on the median $\widehat{\varrho }\left(t\right)=50\%$; we show those values matching exactly the median or the closest ones to it. These results correspond to those observed in Figure 2, Figure 3, Figure 4a, and Figure 7, for the selected positive spike threshold.

		2020	2021	2022	2023	2024
Pool price AESO	$\widehat{\varrho }\left(t\right)$ [%]	61.54–38.46	47.31	42.58	42.7	39.6
	$d^{(sp,+)}$ [h]	2–3	3	3	3	3
HOEP IESO	$\widehat{\varrho }\left(t\right)$ [%]	100	100	7.69	33.33	20
	$d^{(sp,+)}$ [h]	1	1	2	2	2
LMP DA ERCOT	$\widehat{\varrho }\left(t\right)$ [%]	33.33	66.7–33.33	42.86	52.73	70.59–29.41
	$d^{(sp,+)}$ [h]	4	3–4	4	4	2–3
LMP RT ERCOT	$\widehat{\varrho }\left(t\right)$ [%]	20	43	60.53–39.47	36.73	47.06
	$d^{(sp,+)}$ [h]	2	2	2–3	3	2
Spot price EPEX–BE	$\widehat{\varrho }\left(t\right)$ [%]	–	51.28	49.14	50	60–40
	$d^{(sp,+)}$ [h]	–	5	5	2	3–4
USEP SWEM	$\widehat{\varrho }\left(t\right)$ [%]	59.09	48.9	52.19	53.29	49.67
	$d^{(sp,+)}$ [h]	2	3	4	3	3

reports the duration of positive price spike events $d^{(sp,+)}$ for each market and period, selecting those values equal to or closest (as much as possible) to the median survival probability, i.e., $\widehat{\varrho }\left(t\right)=50\%$.

In general, Table 4 shows that price spike durations fall within the range $1\le d^{(sp,+)}\le 5$ h across all years and most markets, with the majority of spike events lasting between 2, 3, and 4 h, while fewer events last between 1 and 5 h. In general, Ontario’s market displays the shortest spike survival times, while also exhibiting the lowest survival probabilities (near $\widehat{\varrho }\left(t\right)=50\%$) for 2022, 2023, and 2024, respectively.

Interestingly, the EPEX-BE market shows the longest spike survival durations, except in 2020, when no spikes exceeded the selected threshold. In some cases, Table 4 lists two duration values and survival probabilities for a given market and year. This indicates that the survival probability is equidistant from $\widehat{\varrho }\left(t\right)=50\%$ at both the upper and lower bounds; for example, the pool price in 2020. Based on these results, we argue that the term “short period of time” in the definition of a price spike should correspond to a range between 1 and 5 h, with a likely duration, for most markets and periods, falling between 2, 3, and 4 h, at a survival probability of around $50\%$.

Similarly,

Table 5. Negative price spike event duration $d^{(sp,-)}$ based on the median $\widehat{\varrho }\left(t\right)=50\%$; we show those values matching exactly the median or the closest ones to it. These results correspond to those in Figure 4b for the selected negative spike threshold.

		2020	2021	2022	2023	2024
Spot price EPEX-BE	$\widehat{\varrho }\left(t\right)$ [%]	100	66.66–33.33	55.6	75	42.9
	$d^{(sp,-)}$ [h]	5	2–3	2	3	4

presents the price spike durations for negative spikes $d^{(sp,-)}$ at or closest to $\widehat{\varrho }\left(t\right)=50\%$. These results are only representative of the EPEX-BE market, as it is the only one we investigate based on the price statistics from Table 1 in Section 3.2. Overall, we observe that price spike durations fall within the range $2\le d^{(sp,-)}\le 5$ h across the analyzed periods. Most of the negative spike events last between 2 and 3 h, with 2020 and 2024 showing durations of 5 and 4 h, respectively. As this sample represents only one market, general conclusions regarding the duration of negative price spikes are not applicable. However, as negative prices become more prevalent in electricity markets around the world, we expect this study lays the groundwork for future analyses using a more diverse set of markets with increasingly negative price spike behavior dynamics.

Furthermore, the survival of price spike events beyond 24 h is primarily associated with extraordinary circumstances, such as extreme weather events or geopolitical disruptions. In all such cases observed in this study, spike events exhibit low survival probabilities, for example, typically below $\widehat{\varrho }\left(t\right)=25\%$. For transparency, we include in Appendix A the results of the survival model without the application of right truncation, corresponding to the markets and years specified in Section 3.3.

Finally, while parametric models such as ACH, Hawkes processes, or similar variants estimate spike intensity through predefined functional forms, the Kaplan–Meier-based approach proposed in this work offers a nonparametric alternative that directly estimates the empirical distribution of spike durations. This provides a flexible and model-free way to quantify spike duration, advancing existing approaches by focusing on spike survival as a core dimension of spike behavior.

5. Conclusions

Based on the theoretical definition of an electricity price spike, this paper introduced a method to quantify the duration of price spikes using survival analysis techniques, particularly the KM estimator. We referred to it as the price spike duration model. Using a fixed threshold, we evaluated the duration of both positive and negative spikes with a rich dataset comprising five years of electricity prices from various electricity markets with different structures, i.e., real-time and/or day-ahead.

For all markets except some years in Ontario, our results suggested that positive price spikes have a duration of 2, 3, and 4 h at a median survival probability of approximately 50%. However, we did not find sufficient evidence to draw a similar conclusion for negative spikes, leaving this as an open research question. Thus, the empirical evidence supports the notion that price spikes are indeed short-lived events, with a low probability of persisting beyond, for example, 5 h. Moreover, extraordinary price events lasting more than 24 h are less common and generally linked to external instability factors, such as extreme weather conditions or geopolitical/macroeconomic disruptions. Therefore, these events were not considered in the evaluation sample and were removed by the application of right truncation.

The main goal of our study was to propose a price spike duration model, rather than to evaluate spike durations under varying thresholds, as the latter was not the primary focus. However, as discussed in Section 3, the price spike duration model is threshold-agnostic, which allows for a broader evaluation using alternative price spike thresholds. Furthermore, the inclusion of external determinants on the duration of price spikes was also not considered. We acknowledge these as limitations in our work, hoping they motivate further research on the duration of price spikes. Additionally, while the concept of censoring (i.e., right- and left-censoring) is also relevant in survival analysis, it falls outside the scope of this study, based on the proposed modeling assumptions in Section 1. Readers interested in exploring this further are referred to [45]. Finally, we outline different directions for future research, building upon the proposed spike survival model. These include the integration of survival analysis techniques into electricity price spike forecasting, the evaluation of policy impacts on spike durations, and the development of duration-sensitive financial instruments tailored to electricity markets.