Investigation on Dynamic Thermal Transfer Characteristics of Electromagnetic Rail Spray Cooling in Transient Processes

Abstract

Electromagnetic Railguns Face Severe Ablation and Melting Risks Due to Extremely High Transient Thermal Loads During High-Speed Launching, Directly Impacting Launch Reliability and Service Life. To address this thermal management challenge, this study proposes and validates the effectiveness of spray cooling technology. Leveraging its high heat transfer coefficient, exceptional critical heat flux (CHF) carrying capacity, and strong transient cooling characteristics, it is particularly suitable for the unsteady thermal control during the initial launch phase. An experimental platform was established, and a three-dimensional numerical model was developed to systematically analyze the dynamic influence mechanisms of nozzle inlet pressure, flow rate, spray angle, and spray distance on cooling performance. Experimental results indicate that the system achieves maximum critical heat flux (CHF) and rail temperature drop at an inlet pressure of 0.5 MPa and a spray angle of 0°. Numerical simulations further reveal that a 45° spray cone angle simultaneously achieves the maximum temperature drop and optimal wall temperature uniformity. Key parameter sensitivity analysis demonstrates that while increasing spray distance leads to larger droplet diameters, the minimal droplet velocity decay combined with a significant increase in overall momentum markedly enhances convective heat transfer efficiency. Concurrently, increasing spray distance effectively improves rail surface temperature uniformity by optimizing the spatial distribution of droplet size and velocity.

1. Introduction

An electromagnetic railgun is an advanced system that launches projectiles utilizing electromagnetic launch effects. As an innovative weapon platform, it offers multiple advantages, including rapid response, high energy output, precise control, strong concealment (low detectability), and relatively low cost. Due to these benefits, electromagnetic railgun technology has attracted significant worldwide attention in recent years and has become a key research focus in military technology [1].

During launch, the passage of transient current through the rail induces significant heating. This thermal load elevates rail temperature, potentially leading to deformation or melting [2], which compromises the electromagnetic railgun’s effectiveness and safety. Consequently, managing thermal dissipation during continuous firing is critical for extending service life, necessitating the implementation of practical cooling techniques to rapidly reduce rail temperature. Available methods include liquid cooling, air cooling, jet impingement cooling, micro-channel cooling, and spray cooling. Among these active cooling approaches, spray cooling demonstrates exceptionally high heat removal capacity. Therefore, this study investigates an electromagnetic rail spray cooling system through combined experimental and simulation methods.

Using non-contact optical measurement techniques, A.G. Pautsch et al. [3] determined the local average liquid film thickness generated by low-flow single-nozzle and high-flow four-nozzle array sprays. For four-nozzle arrays, it was discovered that although the region with the worst heat transfer performance typically has the thickest liquid film, the region with the thickest liquid film is in the spray overlap region, where variables like localized liquid film velocity and spray flow rate affect the heat transfer capability. Zhao Rui [4] established a mathematical model of spray cooling. It was discovered that for different wall heating powers under liquid film heat transfer, the liquid film is in the single-phase zone when the heating power is low. At this time, the heat is primarily removed from the wall through the flow of the liquid film and air convection heat transfer. Wang et al. [5] discovered that as the wall temperature rose, the thin liquid film evaporation and spray cooling’s capacity to transfer heat increased in the single-phase zone. When spray cooling operates in the non-boiling regime, the relationship between the Nusselt number, Reynolds number, and dimensionless temperature is more clearly defined. To investigate the heat transfer characteristics within this regime, Abbasi et al. [6] conducted an experimental study on the heat transfer efficiency of single-phase flow using a multi-nozzle spray configuration. The findings demonstrated a strong correlation between the normal pressure on the wall and the local heat transfer coefficient of the cooled surface. Cheng et al. [7] reported a contrasting conclusion in their experimental study. They observed that the maximum total heat transfer coefficient at the wall was achieved under specific conditions: a spray height of 4.3 mm, which resulted in a surface spray coverage of merely 12%.

Bhatt et al. [8] examined the impact of cooling medium specific heat capacity and surface tension on spray cooling heat transfer performance. Their findings demonstrated that employing C₆H₆, C₃H₆O, and C₆H₁₄ as coolants yielded critical heat flux values 20%, 40%, and 30% higher, respectively, compared to pure water. Separately, Cui et al. [9] explored the influence of three inorganic salt additives (NaCl, Na₂SO₄, and MgSO₄) when using water as the base coolant. The results indicated that elevating the salt concentration in the cooling fluid markedly enhanced the heat transfer capacity of the spray cooling system within the boiling heat transfer regime.

To elucidate the heat transfer mechanism of single-phase spray cooling under vibrational conditions, Chen et al. [10] established a closed-loop experimental system specifically designed for spray cooling on vibrating surfaces. Their research experimentally examined the effects of various vibration parameters, including the vibrational Reynolds number (Rev), dimensionless acceleration (Ac), amplitude, and frequency, on the heat transfer performance. In a separate study, Isares et al. [11] proposed a novel hybrid cooling system that integrates a spray of hydrofluoroether (HFE)—an integrated, non-electrically conductive liquid—with forced air convection. A three-dimensional transient heat transfer model for a cylindrical lithium-ion battery module was developed using ANSYS Fluent. Numerical simulations were performed to assess how the liquid injection rate and the configuration of the injectors influence the module’s overall cooling performance.

Li et al. [12] pointed out that the spray cooling system with R134a as a coolant can reduce the cabin wall temperature to 275 K, and the temperature drop rate can reach 1.05 K/s, so that the cabin cooling needs can be realized. Ni et al. [13] attempted to explore the enhancement of the spray cooling of a vapor-liquid separation structure. Focusing on the contradiction between the heat transfer coefficient and critical heat flow, a double-decker surface was proposed to decouple the liquid supply and vapor separation.

Tan et al. [14] developed a high-power spray cooling system and employed a multi-factor orthogonal experimental design, using heat transfer power and energy consumption ratio as evaluation metrics, to systematically investigate the influence of various parameters on system performance. Exploring a different approach, Fu et al. [15] integrated spray cooling with a non-azeotropic mixture (R245fa/R142b) to achieve precise temperature control of heated surfaces, conducting experimental studies on the heat transfer characteristics within the boiling regime. Addressing the thermal management of high-power LEDs, Xiang et al. [16] designed and established a high-performance spray cooling system, experimentally and numerically examining the effects of nozzle configuration, flow rate, and nozzle-to-surface distance on heat transfer.

Jin et al. [17] created a numerical model to analyze evaporative and air cooling processes in an intermittent spray cooling system, focusing on the impact of heat load and liquid film thickness on evaporation time and heat transfer enhancement. For safety-critical applications, Liu et al. [18] proposed an emergency refrigerant spray cooling method targeting the overheating stage of lithium-ion batteries to prevent thermal runaway. They developed a coupled model simulating battery overheating behavior and emergency spray cooling, using numerical simulation to define the onset and range of the decomposition reaction stage for NCM111 ternary batteries.

Li et al. [19] performed a comparative study between standard spray cooling and immersed spray cooling. Their findings demonstrated that with appropriate control of immersion depth and spray pressure, immersion does not impair but can enhance heat transfer, with a maximum enhancement ratio of 12.2%. Myers et al. [20] introduced a thermal management concept for railguns utilizing combined spray and evaporative cooling to remove heat directly from the rail’s inner surface. Experiments revealed that nozzle pressure had the most significant influence on the heat transfer coefficient, which reached a maximum value of 20,000 W/m² at a nozzle pressure of 60 lbf/in².

There have been a lot of investigations about the heat transfer characteristics of spray cooling at different conditions. However, there are few studies on the spray cooling of electromagnetic rail, but it is very important for the thermal management of electromagnetic railguns, and this is the main motivation for this study.

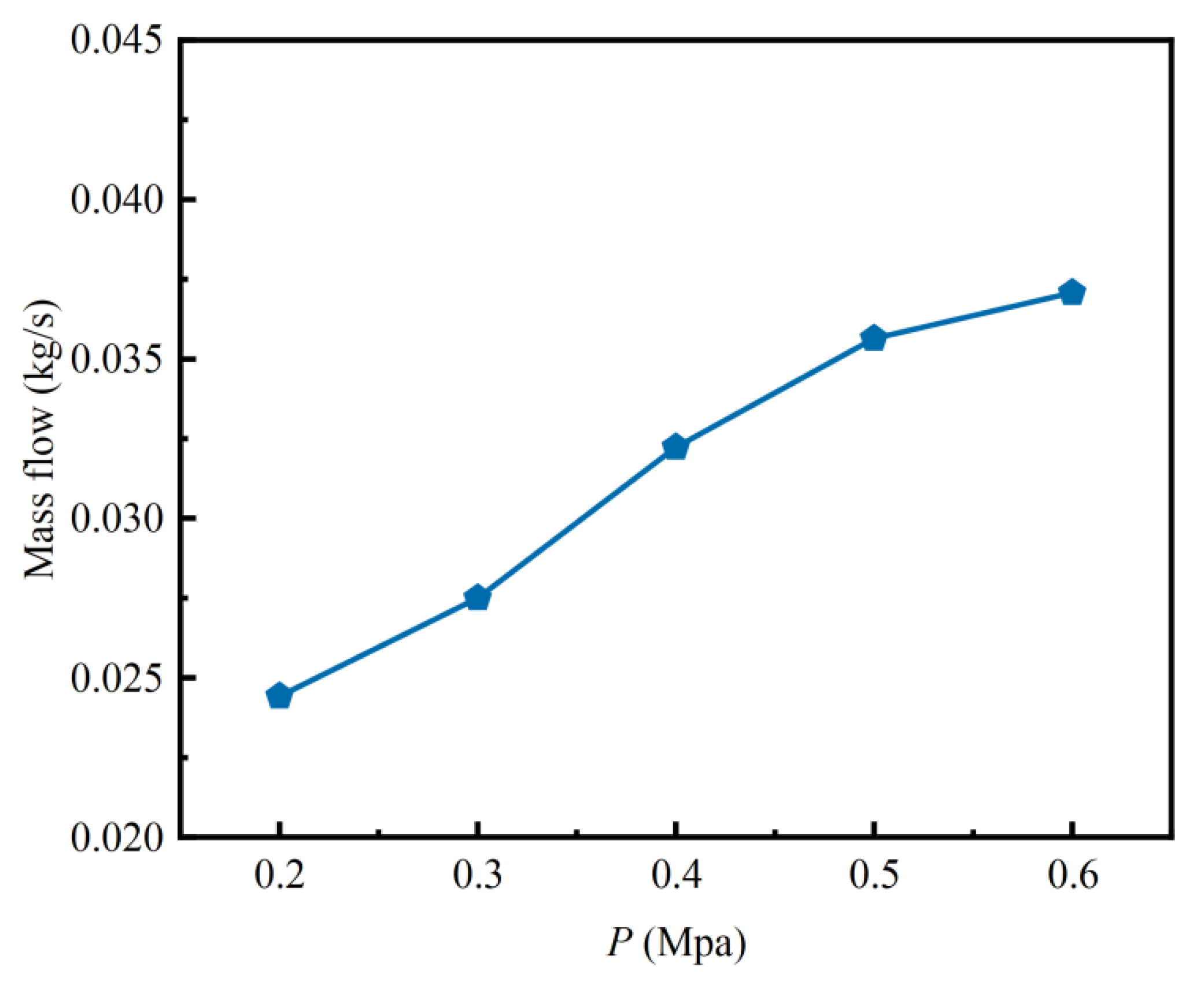
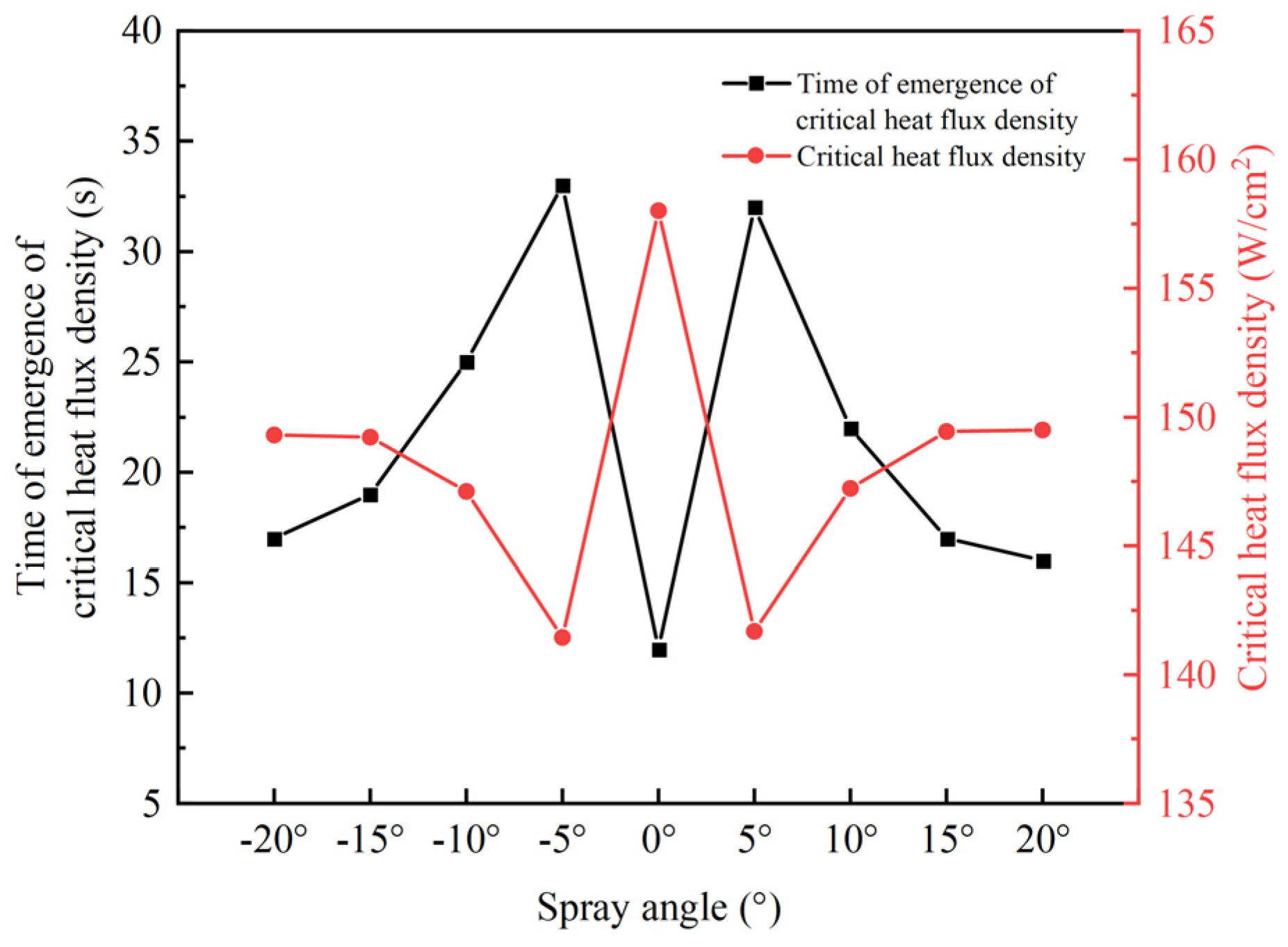
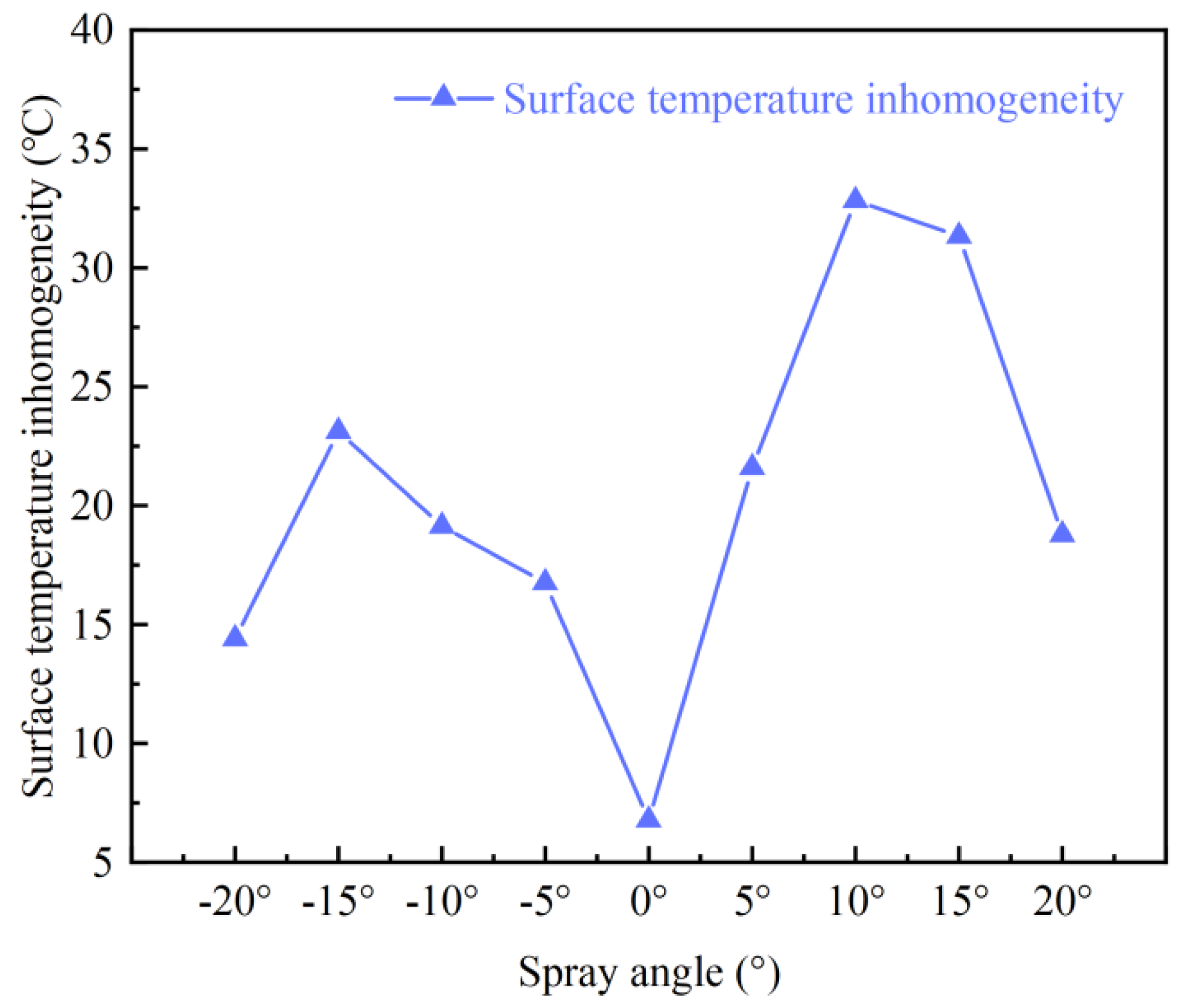
This paper established an experimental setup and conducted a simulation on the heat transfer characteristics of spray cooling on the rail surface. The main objectives are: (i) to analyze the the variation of nozzle flow rate under with inlet pressures, (ii) to study the influence of inlet pressure on the critical heat flux density, average wall heat flux density, average temperature drop and non-uniformity of the wall temperature, (iii) to investigate the effect of the spray angle on the critical heat flux, average wall heat flux density, the average temperature drop and temperature non-uniformity, and (iv) to simulate the impact of spraying cone angle and spray distance on the heat transfer characteristics.

The innovations of this work include: (i) By experimentally investigating the influence of spraying parameters on the cooling effect of the rail surface, the quantitative relationship between nozzle inlet pressure and flow rate can be definited, and the optimal nozzle inlet pressure and spraying angle can be determined, (ii) By simulating the effects of spray cone angle and spray distance on the critical heat flux and temperature uniformity of rail surface, the optimal spray cone angle and spray distance are obtained, and (iii) By optimizing and combining different spray parameters, the best effect of active cooling and thermal management of electromagnetic rail can be achieved.

2. Experimental System and Experimental Method

2.1. Experimental System

In order to investigate the heat transfer characteristics of a spray cooling system, a spray experiment system is designed and established, which is mainly composed of a spray system and a data acquisition system, as shown in Figure 1.

The spray cooling system includes a constant temperature water tank, a pressure pump, three flowmeters, three atomizing nozzles, and an analog rail.

The analog rail is made of copper, and the overall size of the rail is 400 mm × 300 mm × 40 mm.

The experimental procedure involves pressurizing the coolant via a high-pressure circulating pump. This pressurized fluid flows through a regulating valve, instrumentation (pressure sensor, temperature sensor, flow meter), and a swirling pressure atomizer. The atomizer generates a spray of fine droplets directed at the rail surface, where convective heat transfer provides cooling. Post-cooling, the fluid drains via a sump back to the liquid storage tank.

2.1.1. Spray System

The core component of the experimental apparatus is the spray system. Its primary constituents comprise a circulating pressure pump, a stainless steel needle-type regulating valve, a water collection tank (sump), a liquid storage tank, interconnecting piping, and the nozzle assembly. Technical specifications for three representative nozzle models are detailed in

Table 1. Nozzle model and related parameters.

Nozzle Style	Rated Orifice Diameter (mm)	Maximum Unimpeded Aperture (MPa)	The Nozzle Flow Rate (L/min) Under Different Pressure (MPa)				Cone Angle (°) Under Different Pressure (MPa)
			0.2	0.4	0.6	1.0	2	4	6
GO1/8-SS-1.5	1.5	1	1.9	2.5	3.6	4.9	64°	62°	59°
BBG1/8-SS-1.2	1.2	0.9	1.6	1.8	2	2.5	26°	30°	32°
GOG1/8-SS-2.0	2	1	2.3	3.1	4	5.4	116°	120°	118°

.

According to the experimental conditions and purpose of this study, a solid conical nozzle with the model of GO1/8-SS-1.5 was selected for the experiment. The nozzle inlet pressure variation range is 0.2~0.8 MPa, and the spray cone angle is 40°.

For the selected nozzle, the quantitative relationship between nozzle inlet pressure and flow rate was first determined by experiments. Then, the effects of nozzle inlet pressure and spraying angle on the heat flux density, average temperature drop, and temperature non-uniformity of the rail surface were experimentally studied, and the Optimal nozzle inlet pressure and spraying angle were determined, The physical diagram of the nozzle is shown in Figure 2.

In order to achieve the ideal atomization effect of the cooling medium, a circulating pressure pump with a maximum head of 120 m is selected. The flow control valve controls the liquid flow rate and the pressure at the inlet of the nozzle in the experimental system. Considering the adjustment sensitivity and pressure-bearing performance, the experimental system uses a 304 stainless steel needle valve with a pressure range of 0~32 MPa.

2.1.2. Data Acquisition System

Key parameters monitored during the experiment encompass nozzle inlet pressure, flow rate, coolant temperature, temperatures at the back and interior of the copper plate (simulated rail), spraying distance, and spray duration.

Deionized water serves as the working fluid within the system, operating at pressures up to 1.0 MPa. Nozzle inlet pressure is quantified using a MIK-P300 pressure sensor (range: 0–2.0 MPa, accuracy: 0.5%). This sensor’s output is converted to a current signal via a transducer for subsequent data acquisition. Coolant temperature at the nozzle inlet is monitored with a T-type thermocouple (±0.5 °C accuracy).

Temperature gradients through the simulated rail thickness are captured by K-type thermocouples, exhibiting an accuracy of 0.4%. Thermal loading of the simulated rail is achieved using eight cylindrical electric heating rods (diameter: 10 mm, length: 400 mm). Each rod delivers 200 W, with the total input power adjustable via a transformer.

Spatial temperature distribution (both transverse and longitudinal) along the rail is measured using an array of 16 K-type thermocouples. These thermocouples are distributed across 8 measurement holes, with a 25 mm vertical separation between thermocouples within the same hole. The specific arrangement of these 8 holes is illustrated in Figure 3.

To determine the thermal gradient across the rail thickness and the temperature profile on a single cross-section, each measurement borehole contains two thermocouples. One thermocouple is positioned 13 mm from the copper plate’s back surface, while the other is situated 38 mm from it, resulting in a 20 mm separation between these measurement points.

This study employs eight heaters integrated into an aluminum plate to guarantee a uniform copper plate temperature when activating the switch at 430°. Heating occurs sequentially: the aluminum plate is warmed first, subsequently transferring heat to the copper plate. This indirect heating approach prevents localized overheating near the heaters, ensuring thermal uniformity across the copper plate. Figure 3 illustrates the spatial configuration of the copper rail, aluminum plate, and heaters.

Focusing on the high-temperature segment of the electromagnetic railgun rail, this work examines how spray cooling affects heat transfer characteristics at the rail surface. The experimental model’s dimensions, derived from the rail’s geometry and thermal distribution patterns, are not strictly constrained, provided they accommodate the coverage area typical of three nozzles in practical applications.

Electromagnetic launch systems exhibit diverse application scenarios, leading to considerable variation in their specific dimensions. The present study focuses on addressing the fundamental scientific challenges common to the practical application of electromagnetic railguns, which are universal and scale-independent. Consequently, the specific physical size of the railgun is not considered as a variable in the current modeling and analysis.

2.1.3. Cooling Medium Selection

Frequently employed coolants such as methylamine, water, methanol, and freon were considered. Given the open configuration of the experimental spray cooling system, selecting a non-toxic and non-flammable medium was crucial. Among these options, only water and R134a met these safety criteria. Deionized (DI) water was ultimately selected as the coolant for this investigation due to its high specific heat capacity and latent heat of vaporization, coupled with its non-conductive nature, non-toxicity, and non-combustibility. These properties align with electromagnetic railgun operational requirements, ensuring both effective thermal management and operational safety.

2.2. Experimental Methods

Deionized water served as the coolant, and a heated copper plate simulated the high-temperature rail at the electromagnetic railgun launch interface. The experiment aimed to identify optimal spray parameters and examine the influence of spray angle and nozzle inlet flow/pressure on cooling performance. The following procedure was implemented:

• Debug the experimental system, and focus on checking the air-tightness of the spray system pipeline and the insulation of the heating rod.
• Adjust the nozzle height and spraying angle using the mounting bracket to match the experimental setting value before beginning the experiment. To maintain consistent nozzle inlet pressure and flow at the experimental setting value, modify the pipeline’s flow and pressure regulating valve as well.
• Turn on the electric heater to heat the rail. When the temperature is about 430 °C, turn off the switch, and the copper plate temperature distribution is gradually uniform. When the copper plate temperature drops to 400 °C, start the spray system for spray cooling with a temperature of 23 °C.
• When the cooling time of the spray reaches 120 s, close the spray system and record the data under this test condition. When the copper plate temperature drops from 430 °C to 400 °C, open the regulating valve in front of the nozzle, start spraying cooling, and time it. After 120 s of continuous cooling, close the regulating valve and stop spraying cooling.
• Repeat steps (3) and (4) twice. Then, adjust the spray parameters to the next set of working conditions and conduct the next experiment.
• Set up the experimental equipment, handle the experimental data, and compile the findings.

To ensure the accuracy of the research results, the researchers calibrated all testing instruments before the experiment. During the experiment, three parallel experiments were conducted for each experimental condition; the deviations between each group of parallel experiments did not exceed 10%, and the average value of the three groups of parallel experiments was used as the experimental result.

In the present study, except for studying the effect of injection angle on the heat transfer characteristics of the rail surface when the spraying angle changes from −20°to 20°, the spraying angle remained at 0°under all other conditions.

2.3. Experimental Results and Analysis

2.3.1. Data Processing Method

Based on the measured temperature, geometric dimensions, and the thermophysical parameters of the simulated rail, the average heat flux density, rail average temperature drop, and wall temperature non-uniformity can be calculated by using the following equations.

• Average heat flux density:

$$q={\lambda }_{cu}(\overline{t_1}-\overline{t_2})/({\delta }_1-{\delta }_2)$$

(1)

where $q$ is the average heat flux density, ${\lambda }_{cu}$ is the is the thermal conductivity of the copper rail, $\overline{t_1}$ is the average temperature at the cross-section of the rail where point 1 is located, taking the average temperature of the 8 measuring points on that cross-section, $\overline{t_2}$ is the average temperature at the cross-section of the rail where point 2 is located, taking the average temperature of the 8 measuring points on that cross-section, ${\delta }_1$ and ${\delta }_2$ are the distances from the cross-section of measurement points 1 and 2 to the surface of the rail, which are 2 mm and 27 mm respectively.

2.

Average temperature drop of the rail

The average temperature of the cooled rail surface can be calculated by Equation (2):

$$t_{surf}=\overline{t_1}-{\delta }_1(\overline{t_1}-\overline{t_2})/({\delta }_1-{\delta }_2)$$

(2)

where $t_{surf}$ is the average surface temperature of the cooled rail.

The initial temperature of the rail cooling surface is 400 °C, so the average temperature drop of the rail can be expressed as:

$$\Delta T=400-t_{surf}$$

(3)

3.

Non-uniformity of wall temperature

This paper uses the Mean Square Error (MSE) of the temperature at each measuring point on the wall to describe the degree of non-uniformity in temperature distribution [21], where the MSE refers to the average value of the sum of squares of the differences between the temperature at each measuring point on the wall and the average temperature:

$$MSE=\sqrt{\sum {(t_i-t_{surf})}^2/n(n-1)}$$

(4)

where $t_i$ is the wall temperature measured at the i-th temperature measurement point, $t_{surf}$ is the average temperature of the cooled wall surface, n is the number of temperature measurement points arranged on the same section of the rail, in the present study, n = 8.

2.3.2. The Relationship Between Nozzle Inlet Pressure and Nozzle Flow Rate

The flow rate has an important effect on the heat transfer of spray cooling; the nozzle flow rate is closely related to the nozzle inlet pressure, and the relationship between them is shown in Figure 4.

It can be seen from Figure 4 that the nozzle flow rate increases with the increase of spray pressure, but the higher the spray pressure, the slower the growth trend. When the spray pressure increases from 0.2 MPa to 0.5 MPa, the mass flow rate of the nozzle increases from 0.0244 kg/s to 0.0356 kg/s, an increase of 45.90%; for every 0.1 MPa increase in spray pressure, the nozzle flow rate increases by an average of 15.3%. However, when the spray pressure increases from 0.5 MPa to 0.6 MPa, the nozzle flow rate only increases from 0.0356 kg/s to 0.0371 kg/s. Although the spray pressure also increases by 0.1 MPa, the growth rate is only 4.21%. This indicates that continuing to increase the spray pressure no longer has a significant effect on the nozzle flow rate, but the resulting resistance will increase rapidly, and the power consumption of the pressure pump will also increase rapidly.

This is because the relationship between nozzle flow rate and pressure is not linear, but is affected by factors such as fluid properties, nozzle geometry, and flow conditions. Establishing this fundamental relationship provides a basis for the subsequent research on how inlet pressure affects the heat transfer performance of the spray cooling system.

At the same time, an experimental study on spray cooling of the rail for 120 s at a spraying cone angle of 40° and different inlet pressures was carried out. The specific experimental parameters are shown in

Table 2. Experimental conditions of the spray flow experimental study.

Inlet water temperature (°C)	23
Inlet pressure (MPa)	0.2~0.6
Spray distance (cm)	15
Spray angle (°)	0

.

The experimental data were processed and analyzed, and the results are shown in Figure 5 and Figure 6.

It can be seen from Figure 4 that, during the spray cooling process of 120 s, the average heat flux density first rapidly increases to the critical heat flux (CHF) and then slowly decreases. With the increase of the inlet pressure, the critical heat flux density increases continuously, and the time when the critical heat flux appears gradually advances, but the increase in critical heat flux gradually decreases. When the inlet pressure increases from 0.2 MPa to 0.3 MPa, the critical heat flux increases from 1248.61 W/cm² to 1453.54 W/cm², and the occurrence time of critical heat flux density has been advanced from 41 s to 22 s. However, as the inlet pressure increases from 0.5 MPa to 0.6 MPa, the critical heat flux increases from 1580.16 W/cm² to 1611.76 W/cm², and the critical heat flux density appears almost simultaneously at 12 s.

The reason for this is that, during the initial stages of spray cooling, the temperature of the copper plate is extraordinarily high, and the process is in the nucleate boiling zone. As the droplets come into contact with the plate, they immediately evaporate and vaporize. Consequently, as the inlet pressure increases, the nozzle flow rate increases as well, which leads to an increase in the cooling medium’s vaporization heat absorption per unit time. This, in turn, raises the critical heat flux density. Once the wall’s average heat flux density reaches the critical heat flux density, the cooling process shifts gradually to the single-phase region. The proportion of heat transfer relying on boiling heat transfer decreases gradually, and the wall’s average heat flux density decreases rapidly. Once the cooling process enters the single-phase region, heat transfer mainly relies on the mechanism of liquid film evaporation and convective heat transfer. The average heat flux density of the wall then decreases gradually.

It can be seen from Figure 6 that the inlet pressure of the nozzle has little effect on the unevenness of the track surface temperature. When the inlet pressure increases from 0.2 MPa to 0.6 MPa, the unevenness of the track surface varies between 6.78~7.21 °C. That is, the inlet pressure/nozzle flow rate has little effect on the wall temperature non-uniformity. However, the average temperature drop of the rail surface gradually decreases with the increase of the nozzle inlet pressure, and the heat exchange capacity of the cooling system gradually increases. When the nozzle inlet pressure increases from 0.2 MPa to 0.6 MPa, the average temperature drop increases from 310.74 °C to 342.07 °C. However, as the nozzle inlet pressure is higher than 0.5 MPa, the average temperature drop trend is not obvious, indicating that the enhancement effect of increasing the spray flow rate on the cooling system is not obvious.

The reason for this is that the majority of heat transfer during the cooling process occurs in the stage of nucleate boiling heat transfer. The increase of inlet pressure will shorten the time of the cooling system in the nucleate boiling zone, make it enter the single-phase zone, heat transfer faster, and obtain more heat transfer. When the inlet pressure of the nozzle reaches 0.5 MPa, the critical heat flux cannot be significantly improved by increasing the pressure, the time in the nucleate boiling zone cannot be significantly shortened, and there is no way to improve the heat transfer capacity of the spray cooling system. After the end of cooling, the wall temperature is basically unchanged, and the average temperature drop of the rail is basically unchanged.

Based on the above analysis, increasing the inlet pressure of the nozzle can improve the heat transfer of the spray cooling. However, for the spray cooling system, the inlet pressure has a threshold value of 0.5 MPa. When the inlet pressure reaches the threshold value, increasing the inlet pressure can no longer improve the heat transfer. Therefore, for the spray cooling experimental system, the inlet pressure of 0.5 MPa (corresponding to a spray mass flow of 0.3564 kg/s) is the optimal working condition of the system. Therefore, the subsequent studies were conducted under the condition of a flow rate of 0.3564 kg/s.

2.3.3. The Influence of the Spray Angle of the Atomizing Nozzle

Within the experimental investigation of spray angle impact on cooling performance, the spray angle (θ) is defined as the angle between the nozzle centerline and the normal to the wall centerline. Vertical impingement (θ = 0°) occurs when these two lines coincide. Angles measured below the horizontal plane (relative to the wall normal) are assigned positive values, while those above are negative. Crucially, during angle adjustment, the nozzle centerline must intersect the horizontal centerline of the simulated rail. Figure 7 illustrates the spray angle (θ), spray cone angle (α), wall center normal, and nozzle trajectory. Corresponding experimental parameters are detailed in Table 2.

All tests were performed under fixed conditions: a spray distance of 15 cm, nozzle inlet pressure of 0.5 MPa, and inlet water temperature of 23 °C. The spray angle was systematically varied from −20° to 20° during experimentation.

Similarly, after processing the data, the variation of the average heat flux density of the rail wall with time, the critical heat flux density of the wall at different spraying angles, and the variation of the time when the value appears are obtained, as shown in Figure 8 and Figure 9.

From Figure 8 and Figure 9, it can be seen that when the nozzle vertically sprays onto the rail wall, the heat flux density reaches its highest value of 158 W/cm², which appears at the 12th second after the start of spraying. Therefore, the working condition of vertical spraying is used as a benchmark to study other spraying angle conditions.

In the process of increasing the spraying angle, the critical heat flux density decreases rapidly and then increases, and finally tends to be gentle. When the spraying angle is 5°, the critical heat flux density is the lowest, which is only 88.5% of the benchmark condition. In the process of reducing the spraying angle, the change law of the critical heat flux density is the same as that of the up-regulation process. Under the condition of a spraying angle of -5 °, the critical heat flux density is 89.6% of the benchmark condition. At the same nozzle inclination angle, the critical heat flux density under the condition of down-regulation of spraying angle is higher than that under the condition of up-regulation, but the difference between the two is not apparent, only 1% to 2%. The change rule of the occurrence time of the critical heat flux density is opposite to the change rule of its value.

Figure 10 shows the average temperature drop of the rail after 120 s of spray cooling at different spraying angles.

It can be seen that the average temperature drop of the rail is the largest under the condition of 0° spraying angle, which is 341.5 °C. Besides, the heat transfer capacity of the spray cooling system under other spraying angle conditions is studied. In the process of increasing the inclination angle, the average temperature drop of the rail decreases first and then increases. Regardless of whether the nozzle spraying angle is upward or downward, the heat transfer of the spray cooling system is the lowest under the inclination angle of 10°, which is 95.7% and 92.7% of the heat transfer under the reference condition, respectively.

It can be found that the condition of the minimum critical heat flux density is different from the condition of the minimum heat transfer of the cooling system. This is because although the nozzle inclination angle increases from 5° to 10°, the critical heat flux density of the system does not change much, only 3.8%. However, the heat flux density of the heat transfer in the single-phase region is the largest when the nozzle tilt angle is 5°, which leads to a higher heat transfer rate under the final working condition.

Figure 11 shows the change in the temperature non-uniformity of the rail surface after spray cooling for 120 s under different spray angles.

It is found that the uniformity of surface temperature is best when spraying perpendicular to the rail surface, and the temperature non-uniformity of the rail surface will be significantly affected by changing the inclination angle of the nozzle. Based on the vertical spray condition, the non-uniformity of the other conditions ranges from 213% to 485%. In the process of gradually increasing the inclination angle of the nozzle, the temperature non-uniformity of the rail surface increases first and then decreases. When the nozzle inclination angle is the same, the temperature uniformity of the rail surface under the downward spray angle is better than that under the upward spray angle.

The reason for this phenomenon is that the variation of spray angle changes the contact area between the spray droplets and the rail wall. Taking the horizontal center line of the rail surface as the boundary, the area of one spray area becomes larger, and the area of the other spray area decreases, and the spray flow rate of the two areas is the same, which leads to the change of the spray flow rate per unit area, and results in the deterioration of the temperature uniformity of the rail surface. When the spray angle is downward, the direction of gravity is consistent with the direction of droplet velocity, which strengthens the heat transfer between the droplet and the wall, and also improves the temperature uniformity of the rail surface to a certain extent.

Based on the above analysis, the direction of spray angle adjustment has an obvious effect on the heat transfer and the temperature distribution uniformity of the rail surface. With the increase of the nozzle tilt angle, the heat transfer capacity of the cooling system has a process of decreasing first and then increasing. However, the heat transfer capacity of the cooling system and the temperature uniformity of the rail wall are best when the nozzle sprays vertically onto the rail surface. Therefore, it can be determined that vertical spray is the best working condition of the experimental cooling system.

3. Simulation of Spray Cooling of the Electromagnetic Gun Rail

In this paper, by using the ANSYS 2023 simulation software, a comprehensive study was conducted to analyze the impact of spray parameters on the heat transfer characteristics of a cooling system.

3.1. Physical Model

The calculation domain is a hexahedral spray chamber with a length of 400 mm, a width of 500 mm, and a height of 300 mm, as shown in Figure 12.

A copper plate with a length of 400 mm, a width of 300 mm, and a thickness of 40 mm is selected as the simulated high-temperature section of the rail and placed on one side. The atomized droplets generated by the cooling medium passing through the nozzle are directly sprayed onto the heated wall, while the other surfaces are considered to be under adiabatic conditions. This article does not simulate the internal structure and heat transfer flow of the nozzle, and the nozzle type and nozzle parameters are directly given in the model.

Based on the set geometric size parameters and Fluent software, a geometric model of the spray cooling rail surface was established.

3.2. Mathematical Model

The cooling medium forms a liquid film through the atomizing nozzles and then breaks down into droplets of different diameters. These droplets impinge on the heated surface at various directions and velocities, forming a thin liquid film that enhances heat exchange. Considering the relatively low spray flow rate, the volume fraction of atomized droplets in the computational domain remains below 10–12%. Therefore, the Euler-Lagrangian method is employed, where the ambient gas is treated as the continuous phase and the droplets as the dispersed phase, to simulate the unsteady heat transfer process after the droplets impinge on the wall. This model takes into account the evaporation process involving heat and mass transfer of droplets and liquid films, while ignoring the influence of the droplet volume fraction on the continuous phase and droplet-droplet interactions.

3.3. Initial and Boundary Conditions

• The ambient temperature is 20 °C.
• The operating pressure is standard atmospheric pressure, 101.325 kPa.
• Gravity acceleration g = 9.8 m2/s.
• Pressure outlet boundary conditions are set around the fluid domain and on the back of the atomizing nozzle.
• Set the discrete phase boundary condition as the escape model.
• Simulate the rail surface to be set as a non-slip wall surface.
• Discrete phase boundary conditions using a wall film model.
• The side and back of the rail are considered insulation walls.
• Set the initial temperature of the solid domain of the simulated rail to 400 °C.

3.4. Mesh Division of the Rail

The mesh division result is shown in Figure 13, After meshing and initializing the model, it is necessary to simulate the model with a different number of grids. It is repeated by first solving the model with fewer grids, then refining the grid, and finally solving the refined model. When the difference between the calculation results of the model before and after the mesh refinement is small enough, it is considered that the continuous increase of the number of meshes will not affect the calculation results. It means the mesh independence verification has been completed. Since the spray cooling experimental system mainly studies the droplet motion and the heat transfer between the droplet and the rail surface, the mesh refinement is mainly focused on the near-wall of the rail and the spray area. In this study, the cooling process is chosen to last for 1 s, and the average temperature change of the rail surface, as well as the temperature distribution along the rail surface center line, are used to confirm the grid independence. The simulation results are shown in Figure 14 and Figure 15.

By comparing the calculation results, it is found that when the number of grids reaches 542,700, the average temperature of the wall surface changes with time, and the temperature distribution of the rail centerline basically does not change, indicating that the grid density is enough for the simulation calculation of the spray cooling model. Therefore, this paper selects a grid with a number of 542,700 grids for subsequent simulation analysis.

Due to the large number of grids in this simulation and the strong phase transition near the wall, in order to ensure the convergence of each step in the simulation process, it is necessary to set the time step size smaller in the initial stage. Therefore, in the initial stage of the simulation, the time step size is set to 0.00001 s. After 20,000 steps of simulation calculation, i.e., 2 s of cooling, the time step size is increased to 0.00005 s and the calculation continues to 10,000 steps. At this time, each time step size in the simulation calculation process can converge within 20 iterations. Then increase the time step to 0.0005 s and continue with the 10,000-step calculation. During this process, the convergence of the simulation calculation is still very good. Therefore, in the final stage of simulation calculation, set the time step to 0.001 s to complete the remaining simulation work.

3.5. Model Reliability Verification

In order to verify the reliability of the rail spray cooling simulation model in the subsequent simulation analysis process, this model was used to conduct a simulation under the optimal operating condition obtained from the previous experimental study. Specifically, the optimal operating condition is as follows: spray cone angle of 40°, nozzle inlet pressure of 0.5 MPa, spray flow rate of 3.9 L/min, and spraying perpendicular to the rail surface.

It can be seen from Figure 16 that the simulation results show good agreement with the experimental data. The critical heat flux (CHF) in the experimental data is 158 W/cm², while that in the simulation results is 171.7 W/cm², with a deviation of approximately 8.7%. The occurrence time of CHF in the experimental data is 12 s after the start of cooling, and the occurrence time of CHF in the simulation results is 12.6 s after the start of cooling, with a deviation of 5%. Thus, it can be concluded that the rail spray cooling model established in this study is reliable and can be used for further simulation research in subsequent work.

4. Study on the Influencing Factors of Spray Cooling

4.1. Effect of Spraying Cone Angle on the Heat Transfer Characteristics

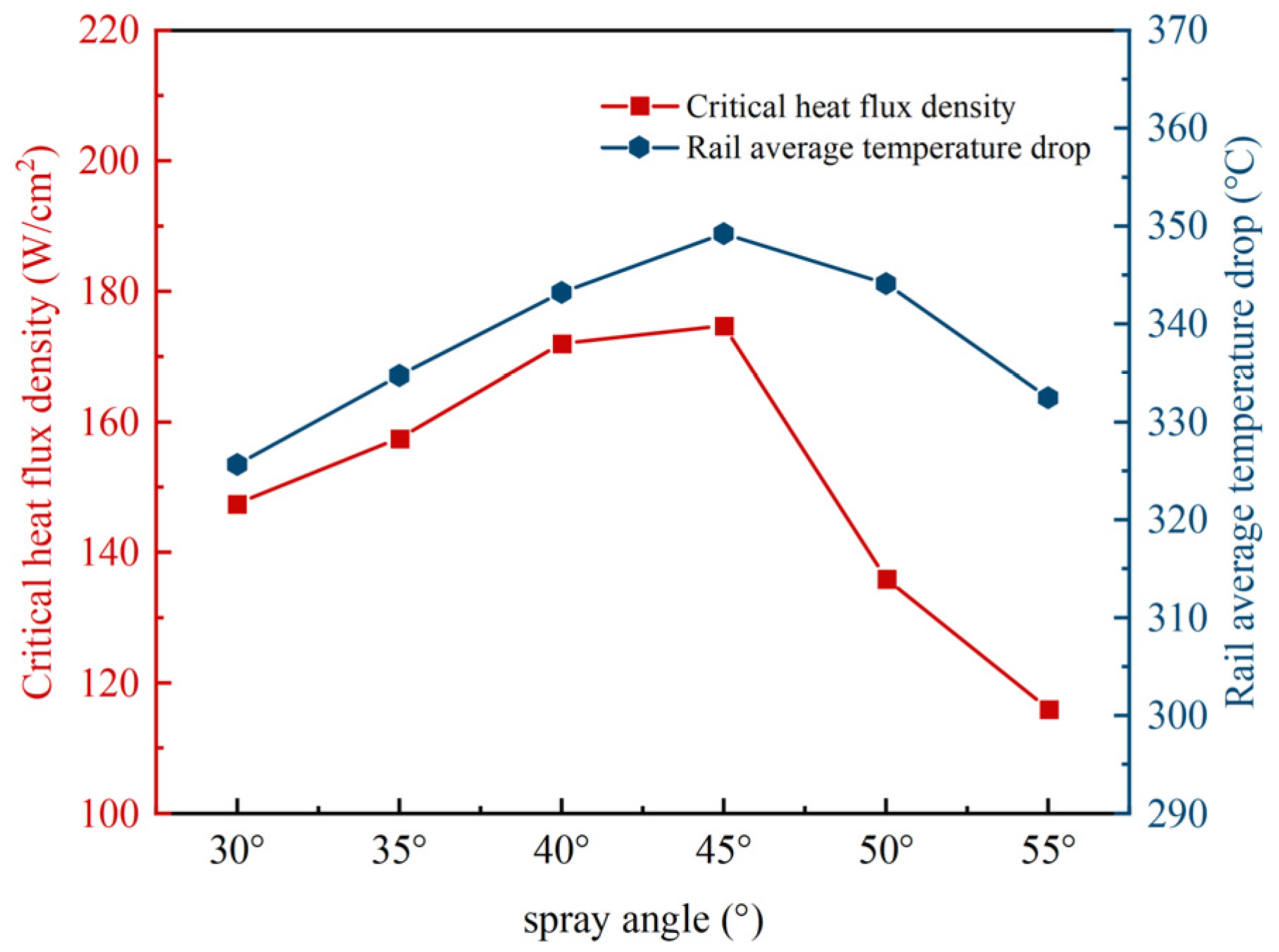
In the present work, the effect of spraying cone angle is investigated under the conditions that the inlet pressure of the nozzle is 0.5 MPa, the spray flow rate of a single nozzle is 3.9 L/min, the spray distance is 15 cm, the spraying angle is 0°, the initial temperature of the rail wall is 400 °C, and the spraying cone angle is increased by 5° as the step length. The spraying conditions with the spraying cone angle ranging from 35° to 55° are simulated, and the results are shown in Figure 17 and Figure 18.

Figure 17 shows the variation of the average heat flux density of the rail heat transfer wall with time under different spraying cone angles. Figure 18 shows the change of critical heat flux density and the rail average temperature under different spraying cone angles.

It can be seen from Figure 17 that the heat transfer process is in the transition boiling stage at the beginning of the cooling process. As the spraying cone angle increases, the heat transfer time in the transition boiling zone gradually shortens. After the start of spray cooling, the larger the spraying cone angle, the faster the heat flux climbs, and the better the heat transfer effect. However, it can be seen from Figure 17 that after entering the nucleate boiling stage, when the spraying cone angle increases from 30° to 55°, the critical heat flux density increases first and then decreases. When the spraying cone angle is 45°, the critical heat flux density reaches the maximum of 174.7 W / cm². As the spray cone angle continues to increase, the critical heat flux decreases. When the spraying cone angle increases to 55°, the critical heat flux decreases to 116.34 W/cm², which is 33.41% less than the maximum value.

The reason is that at the spray distance of 15 cm, the spray area on both sides of the cooling system is almost tangent to the wall when the spraying cone angle is 45°. Therefore, increasing the spraying cone angle will lead to a part of the spray area outside the wall. For a single nozzle, most of the droplets are distributed in the spray edge area. With the increase of the spraying cone angle, the proportion of ineffective droplets will increase, which results in the reduction of the effective spray flow and heat flow density for cooling the wall.

According to Figure 18, the rail average temperature drop increases with the increase of spraying cone angle first, as the cone angle increases to 45°, the rail average temperature drop reaches the maximum value of 348 °C, and then begins to decrease with the increase of spraying cone angle, which means the means that the spray cooling effect is best when the spray cone angle is 45°.

4.2. Effect of Spray Distance on Heat Transfer Characteristics

From the above research, it can be seen that when the spray distance is 15 cm, the spray area is almost tangent to the wall. Continuing to increase the spray distance will make a part of the spray area outside the heat transfer wall. Therefore, this section takes 5 cm as the step length to simulate the spray conditions with spray distances of 5 cm, 10 cm, and 15 cm. The velocity distribution of droplets in the vertical direction under different spray distances, the velocity distribution of droplets in the horizontal direction under different spray distances, and the average velocity variation of droplets under different spray distances are shown in Figure 19, Figure 20 and Figure 21.

It can be seen from Figure 19 and Figure 20 that in the vertical direction, the droplet velocity in the central area of the spray is lower than that at the edge of the spray, and as the spray distance increases, the maximum droplet velocity gradually decreases, while the droplet velocity in the central area of the spray gradually increases, the position where the maximum droplet velocity appears gradually spreads to the edge area of the spray, and the droplet velocity distribution becomes more uniform. In the horizontal direction, the droplet velocity variation of a single nozzle is the same as that in the vertical direction. With the increase of spray distance, the distance between adjacent spray areas decreases, the velocity distribution range of droplets decreases continuously, and the velocity distribution is more uniform.

From Figure 21, it can be seen that the average velocity of the droplet decreases with the increase of spray distance, but the trend of change is not very significant. When the nozzle-wall distance varies from 5 cm to 15 cm, the average velocity of the droplet decreases from 6.24 m/s to 5.95 m/s.

At the same time, the average heat flux density of the rail wall at different spray distances varies with time, and the average temperature drop at different spray distances, as well as the temperature non-uniformity of the wall after spray cooling at different spray distances, are also obtained. The changes are shown in Figure 22, Figure 23 and Figure 24.

It can be seen from Figure 22 and Figure 23 that in the boiling zone, as the spray distance increases, the heat transfer effect of the spray cooling process is enhanced, and the critical heat flux increases from 139.2 W/cm² to 174.7 W/cm², an increase of 25.5%. The reason is that when the spray distance is small, most of the cooling fluid has not broken into droplets when it reaches the wall and still exists in the form of a liquid film.

During the heat transfer in the boiling zone, when the liquid film impinges on the wall surface for heat transfer, a part of the fluid will be lost in the form of a splash before heat transfer, thus reducing the heat transfer. In addition, as the spray distance increases, the average particle size of the droplet gradually increases, but the average velocity attenuation is not obvious, so the momentum of the droplet is larger.

In the transition boiling zone, the heat transfer surface will form a gas film due to the excessive evaporation of the cooling medium, but the droplets with greater momentum can pass through this layer of gas film and the wall for heat transfer. In the nucleate boiling zone, when the droplets collide with the liquid film, the droplets with larger momentum and particle size can bring in more air, which promotes the secondary nucleation in the heat transfer process, so that the entire boiling zone has a better heat transfer effect.

After the cooling process enters the single-phase region, the heat transfer mainly depends on the convective heat transfer, and the particle size with larger momentum has a more obvious disturbance to the liquid film on the heat transfer surface, which strengthens the convective heat transfer process of the liquid film.

From Figure 24, it can be seen that the farther the spray distance is, the smaller the unevenness of the rail surface is. This is because, on the one hand, the increase in spray distance increases the area covered by the spray on the rail wall. On the other hand, at a farther distance from the nozzle, the particle size distribution of the droplets is more concentrated, and the velocity distribution of the droplets is more uniform, which makes the temperature distribution on the wall more uniform.

4.3. Quantitative Uncertainty Analysis

In spray cooling experiments, the heat flux and temperature of the heat transfer surface cannot be directly measured and must instead be indirectly determined by calculating the temperature differences and distances across different cross-sections along the measuring track. Errors in direct measurements propagate to indirect measurements through corresponding functional relationships. In this study, heat flux, track-averaged temperature drop, and wall temperature non-uniformity are considered indirect measurements, while cross-sectional temperature, thermocouple spacing, and nozzle inlet temperature serve as direct measurements.

The combined standard uncertainty of the direct measurements is first evaluated. The standard deviations of the direct measurements are calculated according to Equation (5), based on three repeated measurements and with a t-value of 1.32. The Type A uncertainties for cross-sectional temperature, thermocouple spacing, and nozzle inlet temperature, determined via Equation (6), are 1.9 °C, 0.04 mm, and 0.37 °C, respectively. Neglecting the estimation uncertainty, the Type B uncertainties for these direct measurements are 1.3 °C, 0.01 mm, and 0.25 °C, respectively. Using Equation (7), the combined standard uncertainties for the three direct measurements—cross-sectional temperature, thermocouple spacing, and nozzle inlet temperature—are calculated to be 2.3 °C, 0.04 mm, and 0.45 °C, respectively.

$$u_a=\sqrt{\sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2/\left(n\left(n-1\right)\right)}$$

(5)

$$U_a=t_p\ast u_a$$

(6)

$$u=\sqrt{u_A^2+u_B^2}$$

(7)

Assume that the indirect measurement y has the following functional relationship with n mutually independent direct measurements:

$$y=f(x_1,x_2\dots x_n)$$

(8)

Then, the uncertainty of y can be calculated using the error propagation formula in Equation (9), where the terms in the equation represent the uncertainties of the direct measurement values. By substituting the calculation formulas of heat flux, average temperature drop of the rail, and wall temperature non-uniformity into Equation (9) and performing calculations for each set of data, the maximum uncertainties of the indirectly measured values (heat flux, average temperature drop of the rail, and wall temperature non-uniformity) are obtained as 3.86%, 2.30%, and 3.57% respectively.

$${\delta }_y=\sqrt{\sum _{i=1}^n{\left({\displaystyle \frac{𝜕f}{{𝜕x}_i}}\right)}^2{\delta }_{x_i}^2}$$

(9)

5. Conclusions

In this paper, an experimental setup of a rail spray cooling system is established, and a numerical simulation is conducted; the heat transfer characteristics of rail spray cooling are investigated. The main conclusions are as follows:

• The nozzle flow rate is positively correlated with the nozzle inlet pressure. The increase of nozzle inlet pressure will lead to an increase in the flow rate of the cooling medium per unit time and heat absorption during the evaporation, improving the heat transfer capacity of the spray cooling system. However, when the inlet pressure is greater than 0.5 MPa, the heat transfer capacity is no longer significantly improved.
• Spraying angle has a certain impact on the heat transfer capacity of the spray cooling system and the temperature distribution uniformity of the rail surface. When the spray angle increases upward or downward, the uniformity of droplet distribution on the rail surface will become worse, leading to the deterioration of the heat transfer effect and the uniformity of temperature distribution. As a result, as the nozzle sprays vertically on the rail surface, the heat transfer capacity and the temperature uniformity of the rail surface are the best.
• The simulation results show that when the spray cone angle is 45°, the critical heat flux reaches the maximum value of 174.7 W/cm², and the average temperature drop has also reached its maximum value of 349.2 °C.
• Under the simulation conditions, when the spray distance is 15 cm, the droplet size and velocity distribution are the most uniform, and the uniformity of the rail surface temperature is the best. Therefore, the optimal spray distance is 15 cm in this paper.