A Study on the Optimal Design of Subsurface Pumping Energy Storage Under Varying Reservoir Conditions
Abstract
1. Introduction
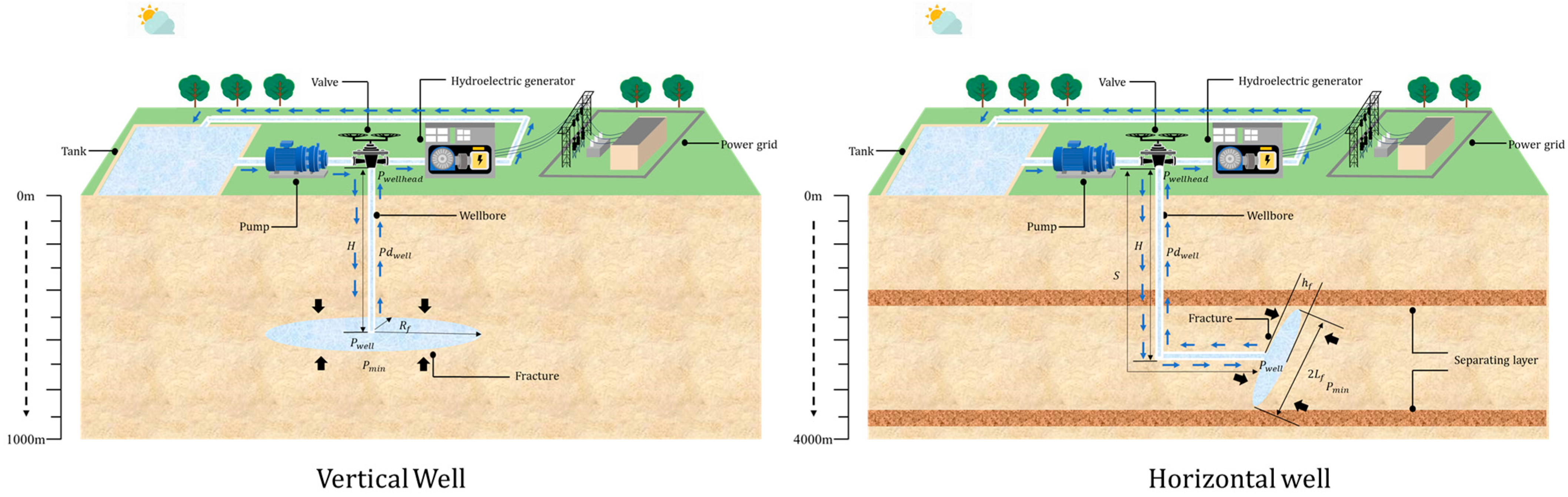
2. Model Description
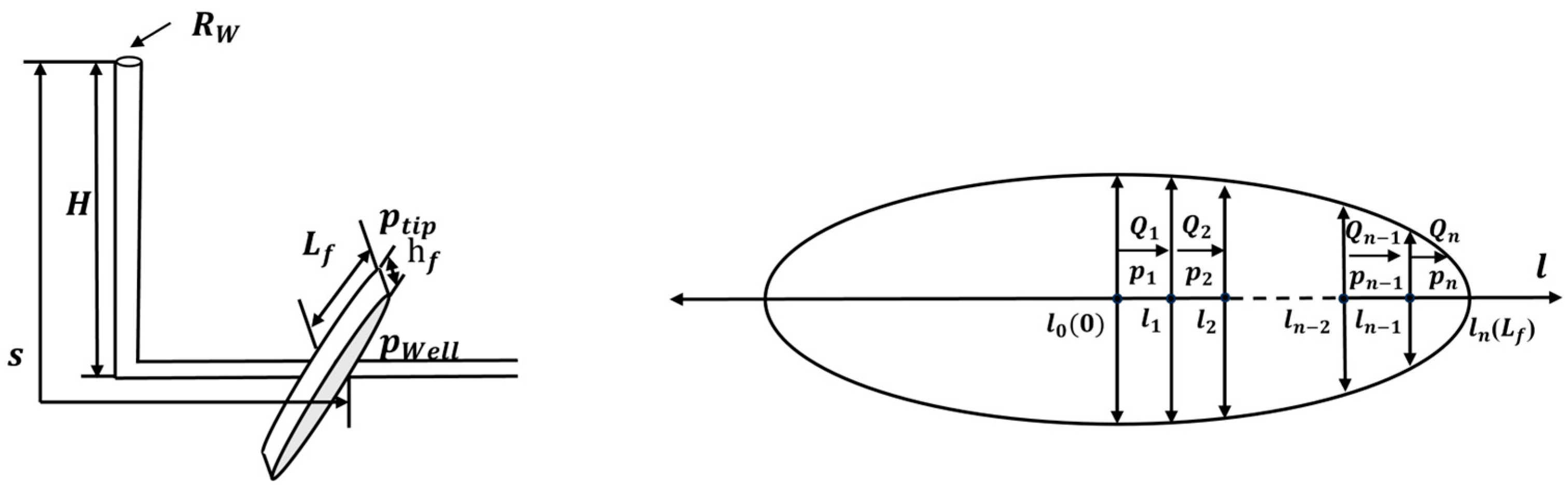
2.1. Shallow Reservoir Model
2.2. Deep Reservoir Model
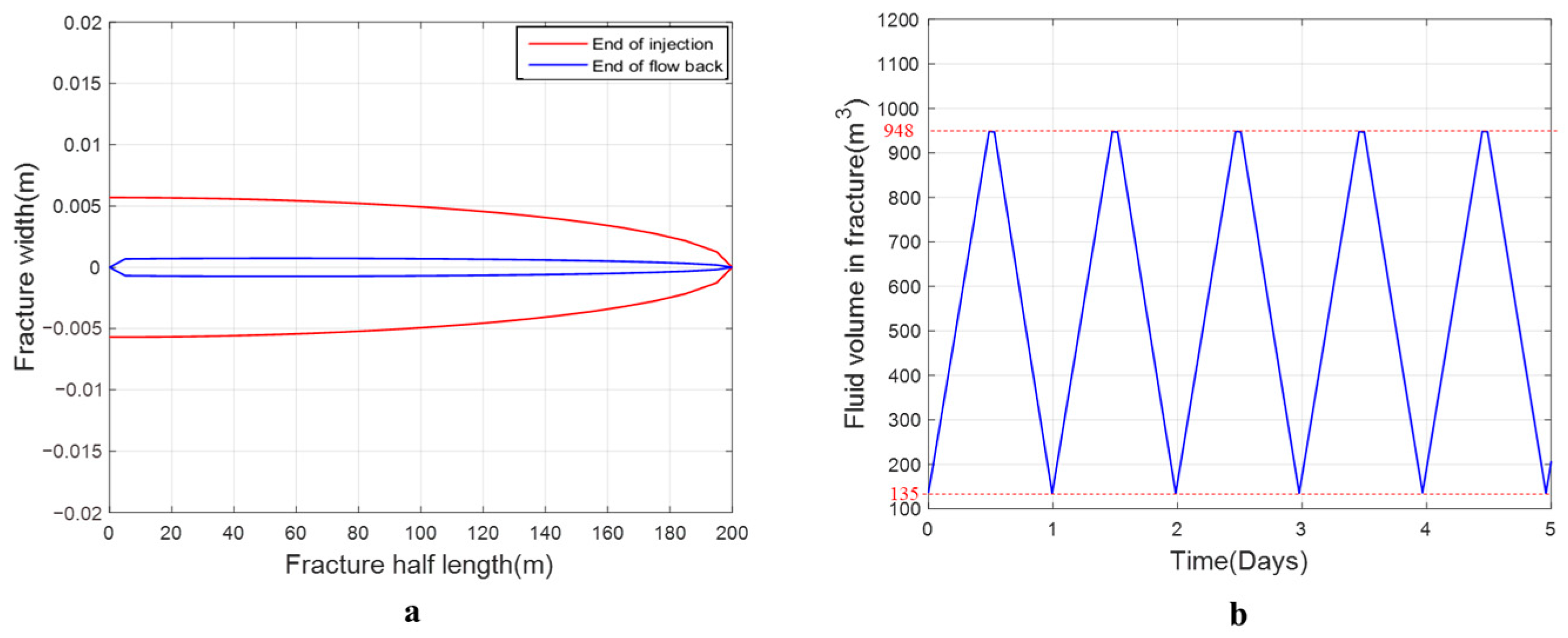
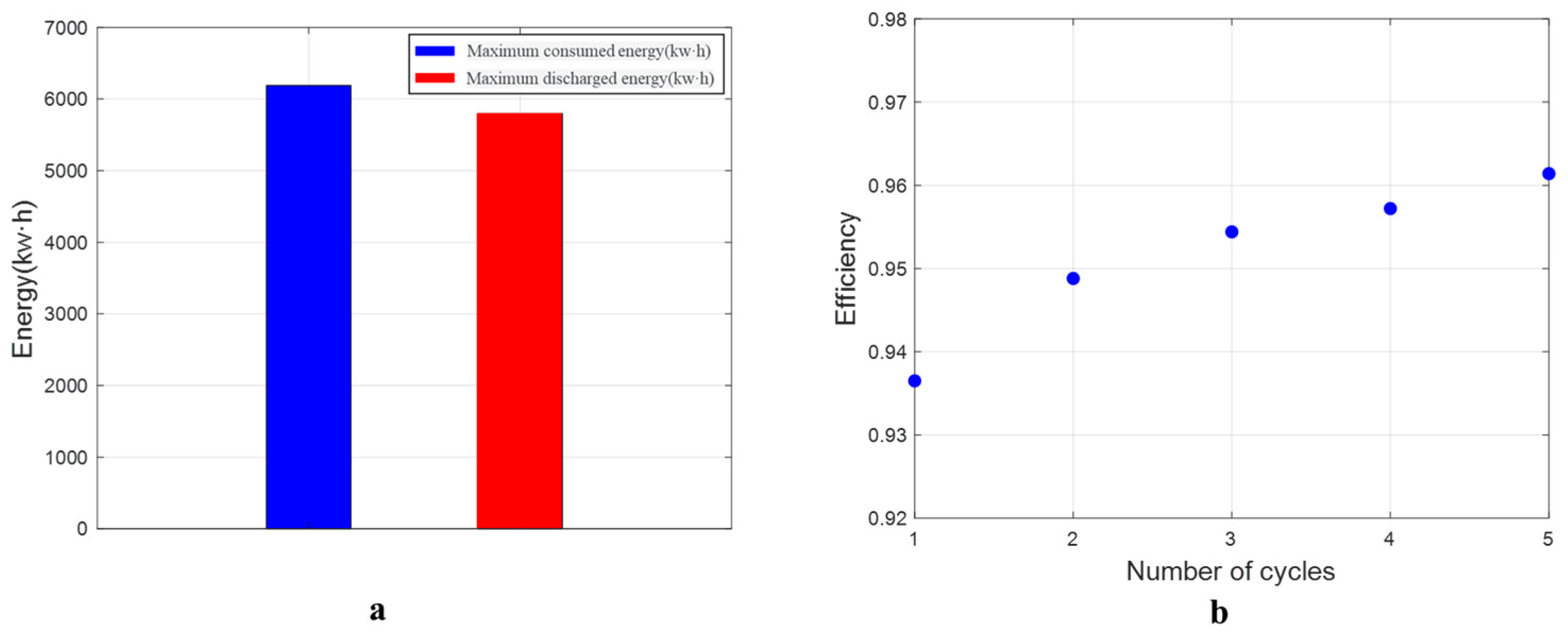
3. Base Case
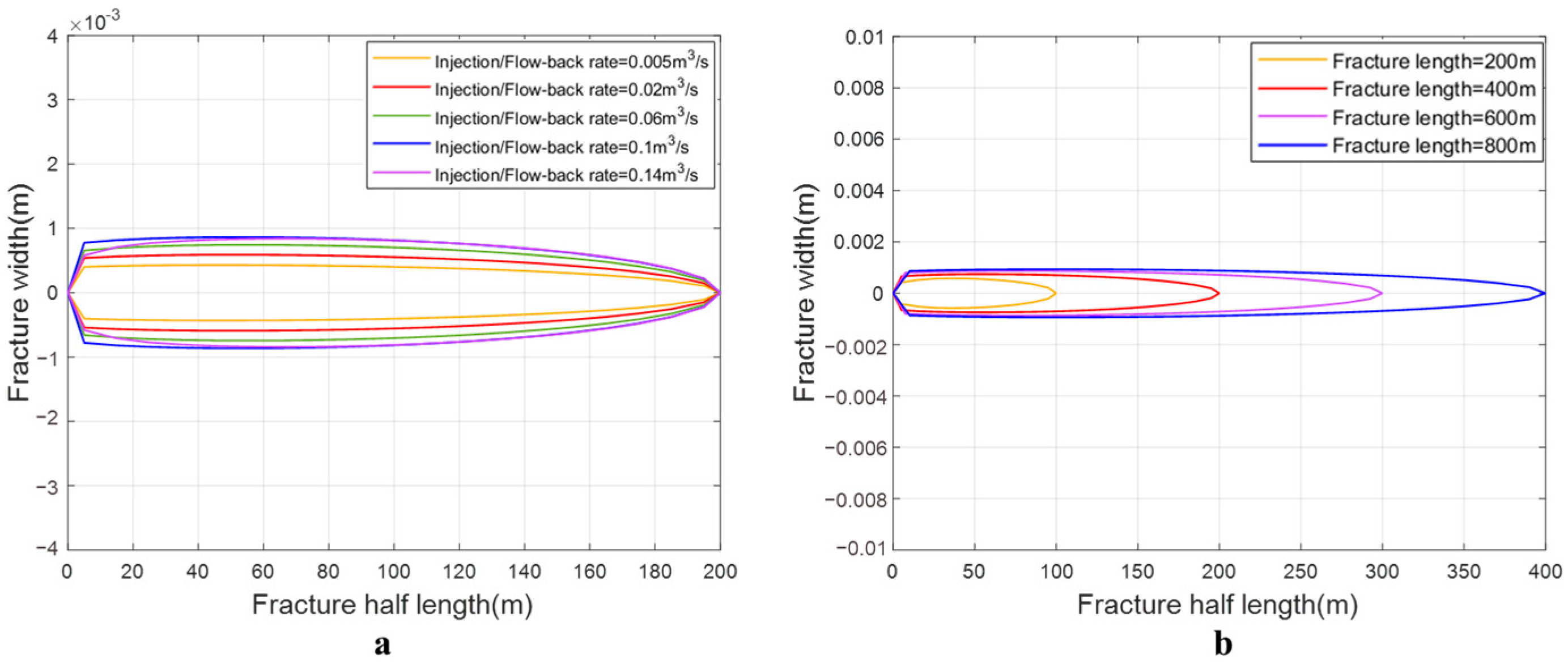
3.1. Shallow Reservoir Case
3.2. Deep Reservoir Case
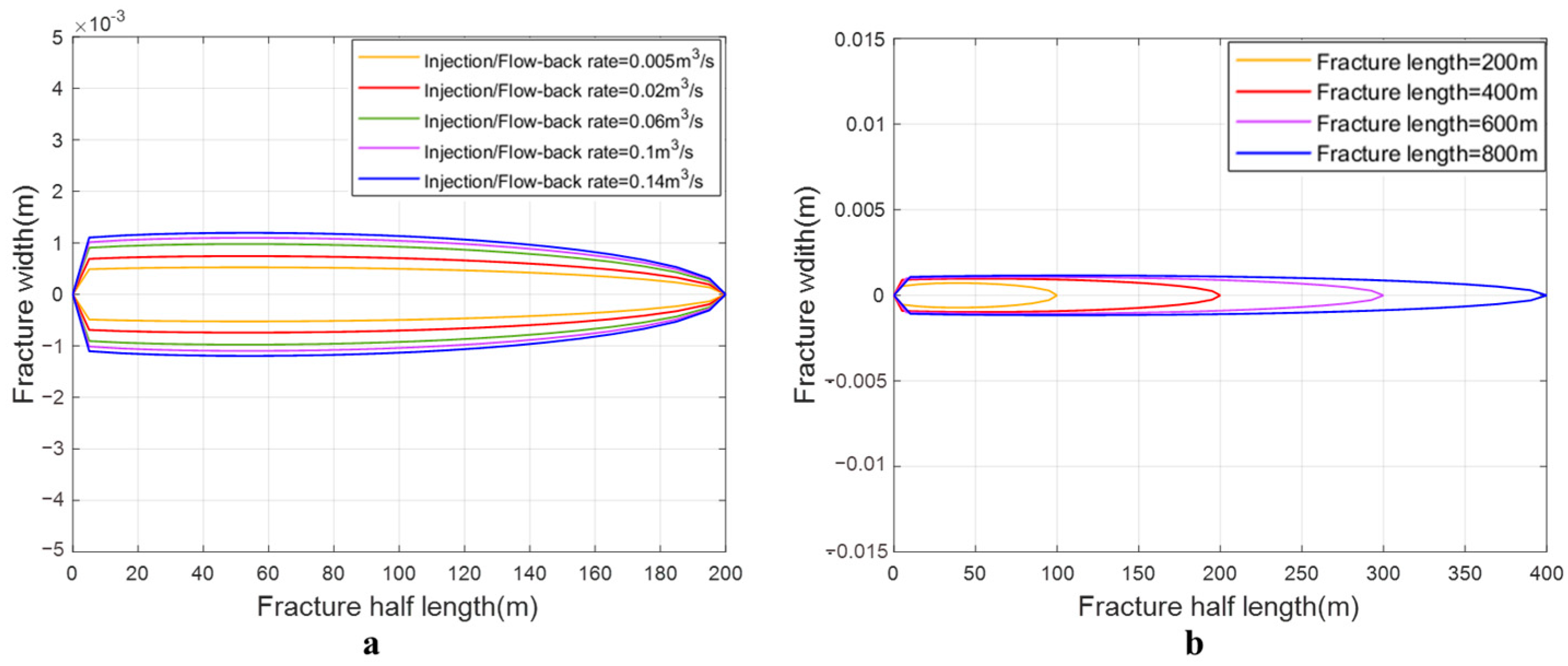
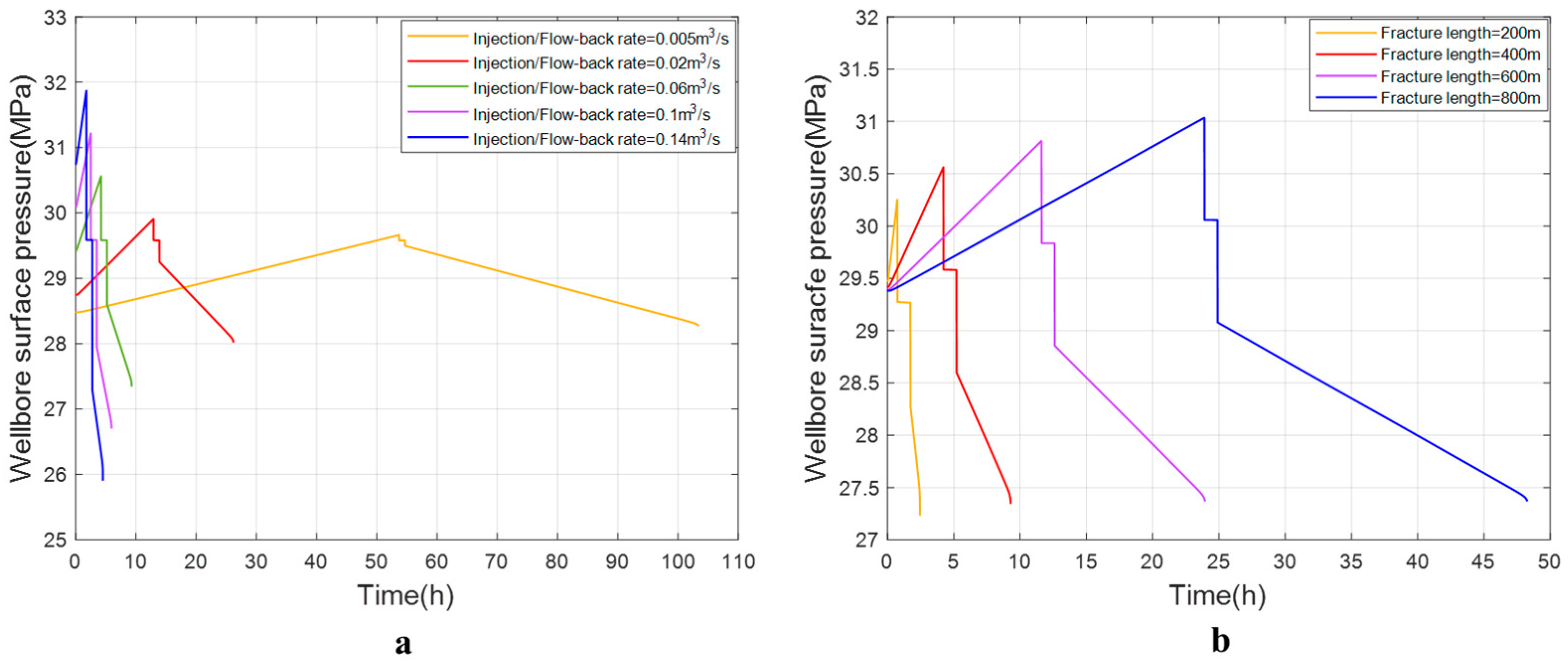
4. Parameter Design
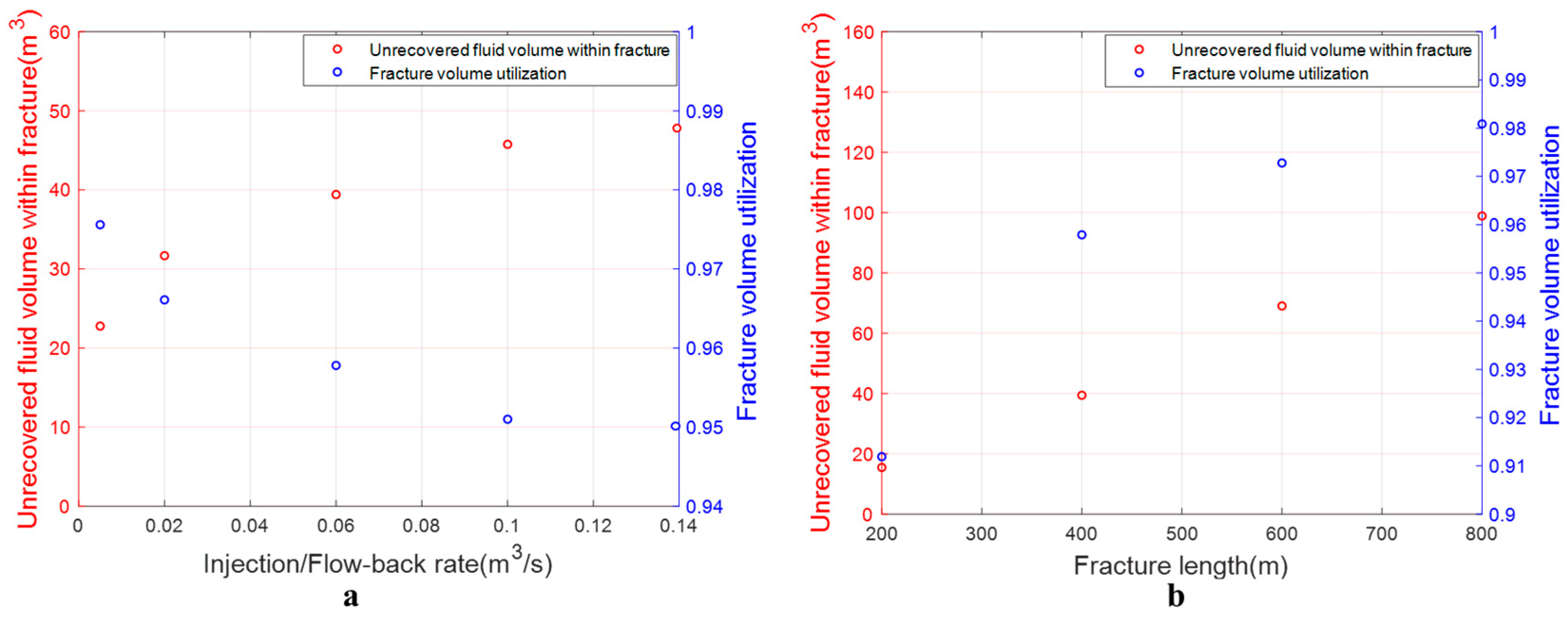
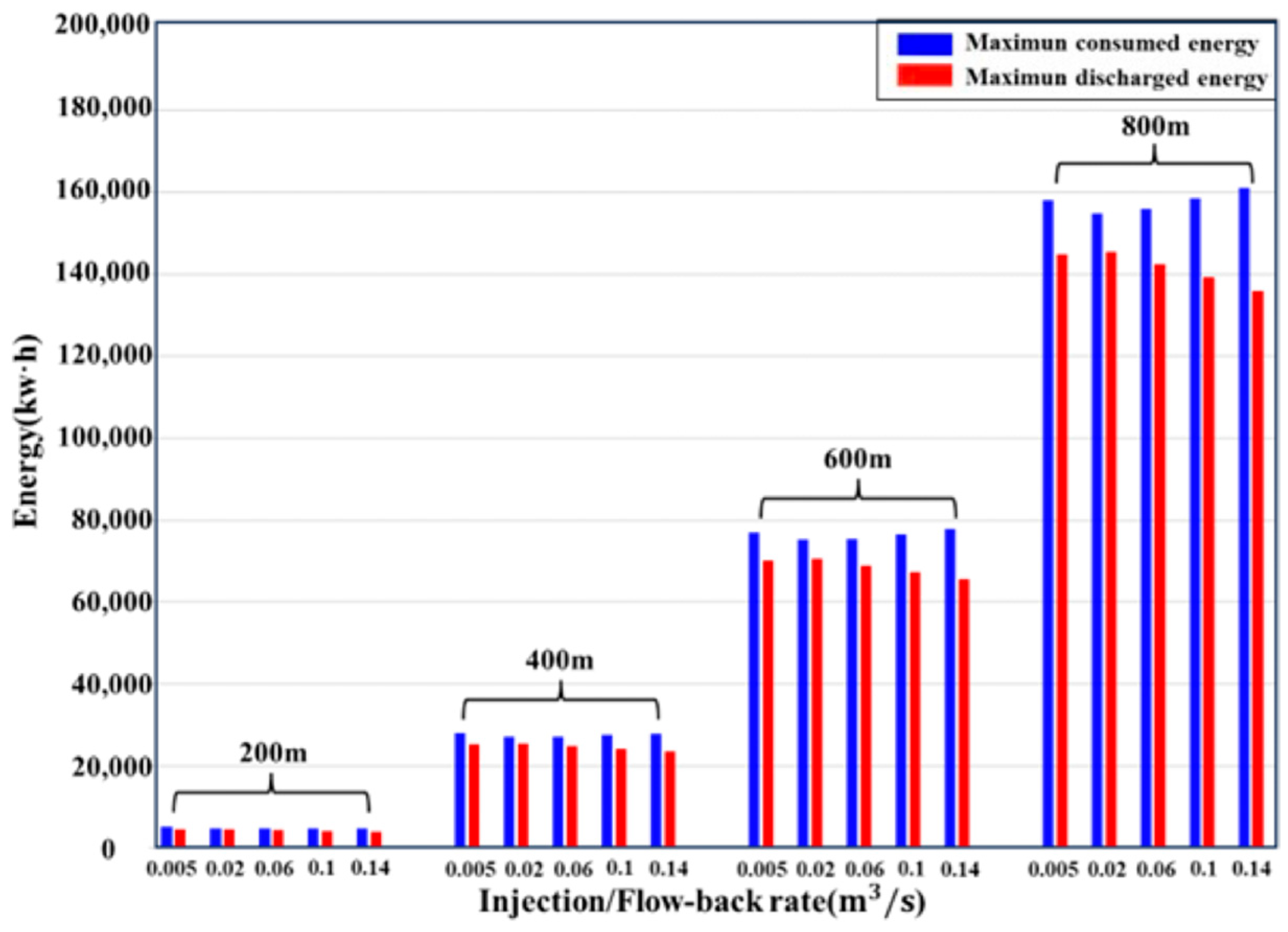
4.1. Shallow Reservoir
4.2. Deep Reservoir
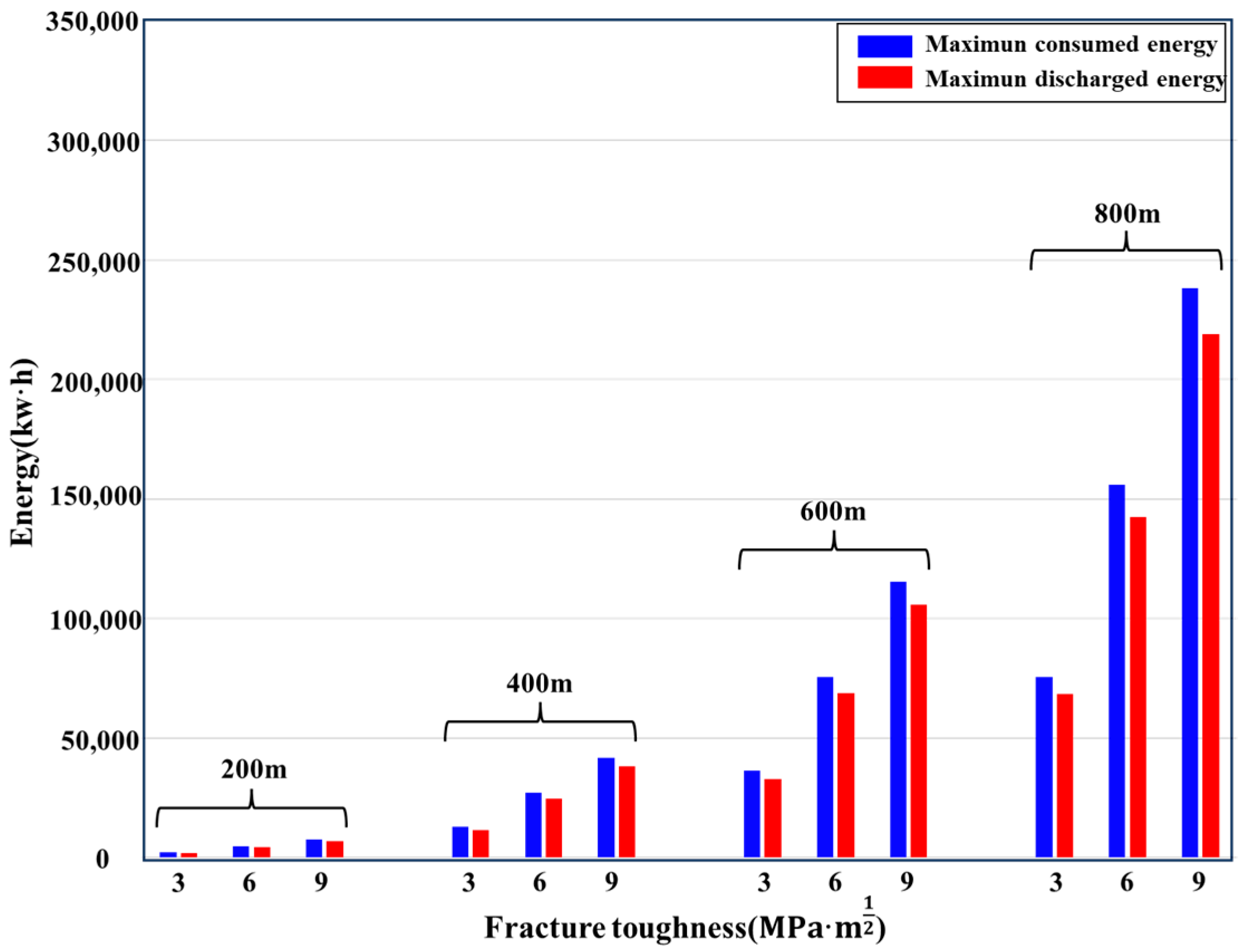
4.3. Fracture Toughness
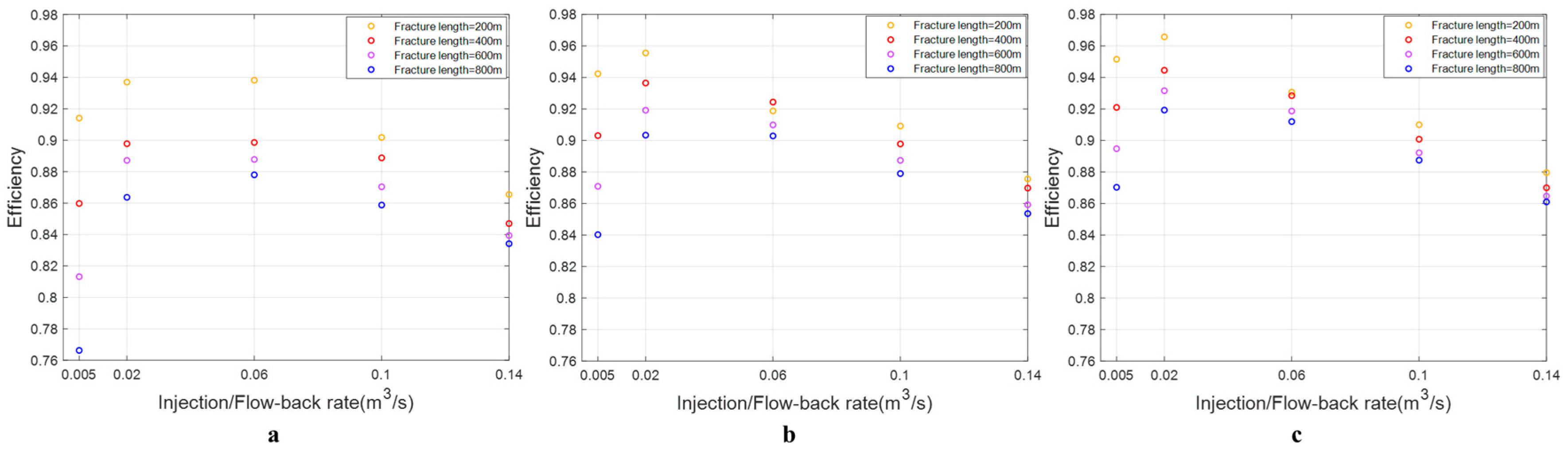
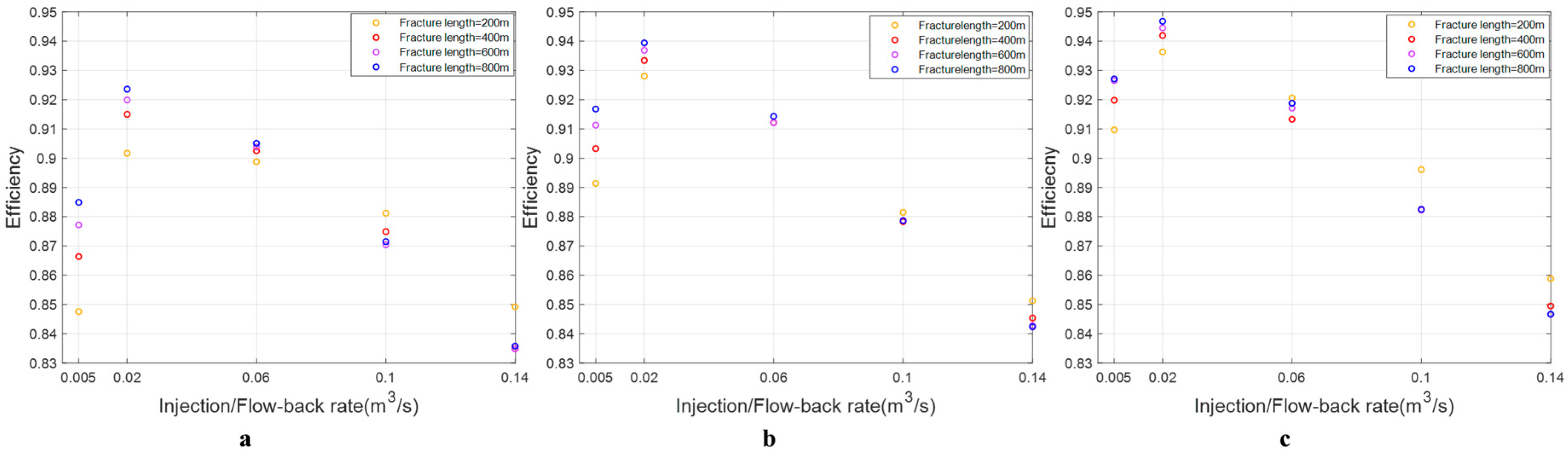
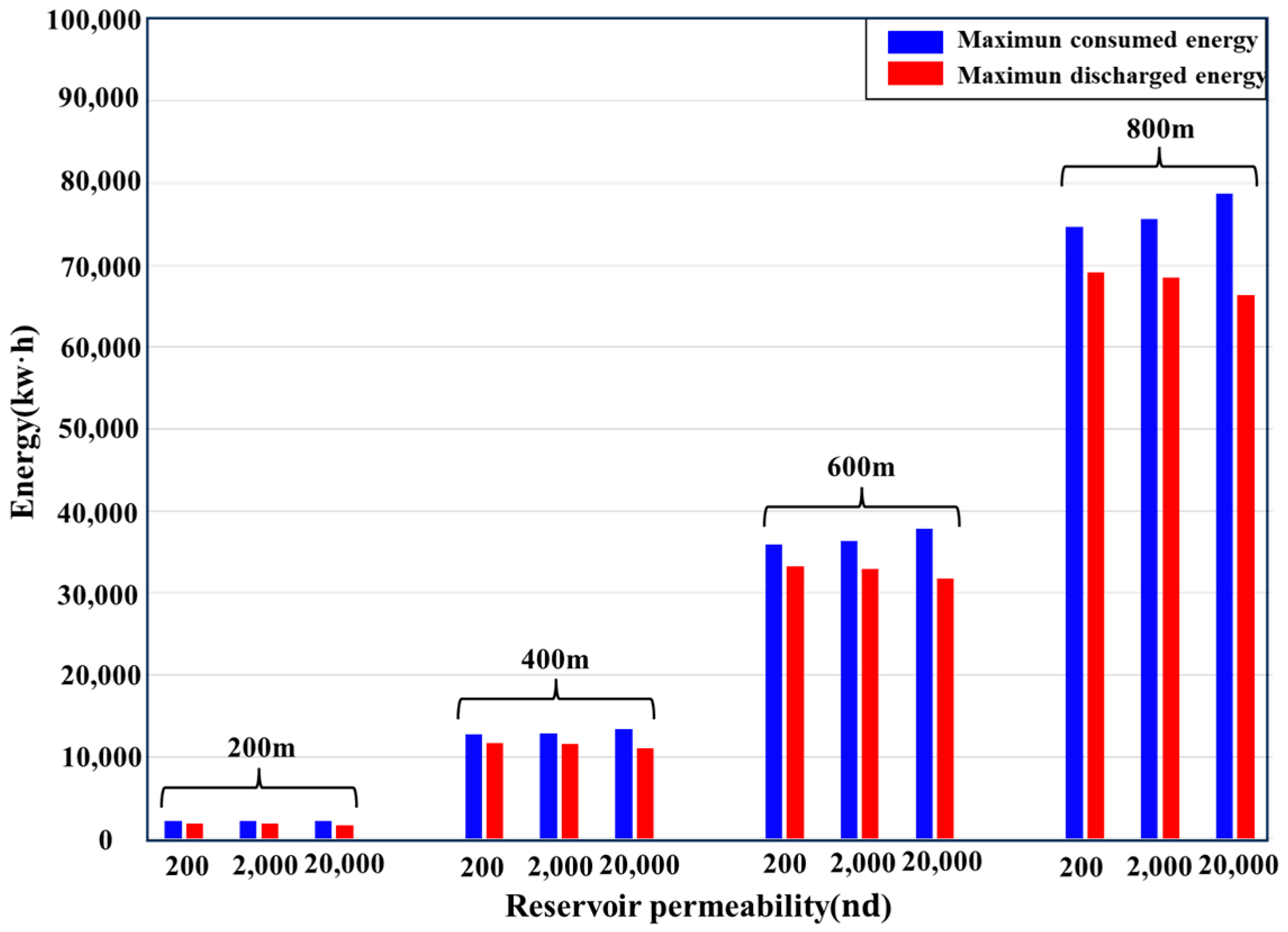
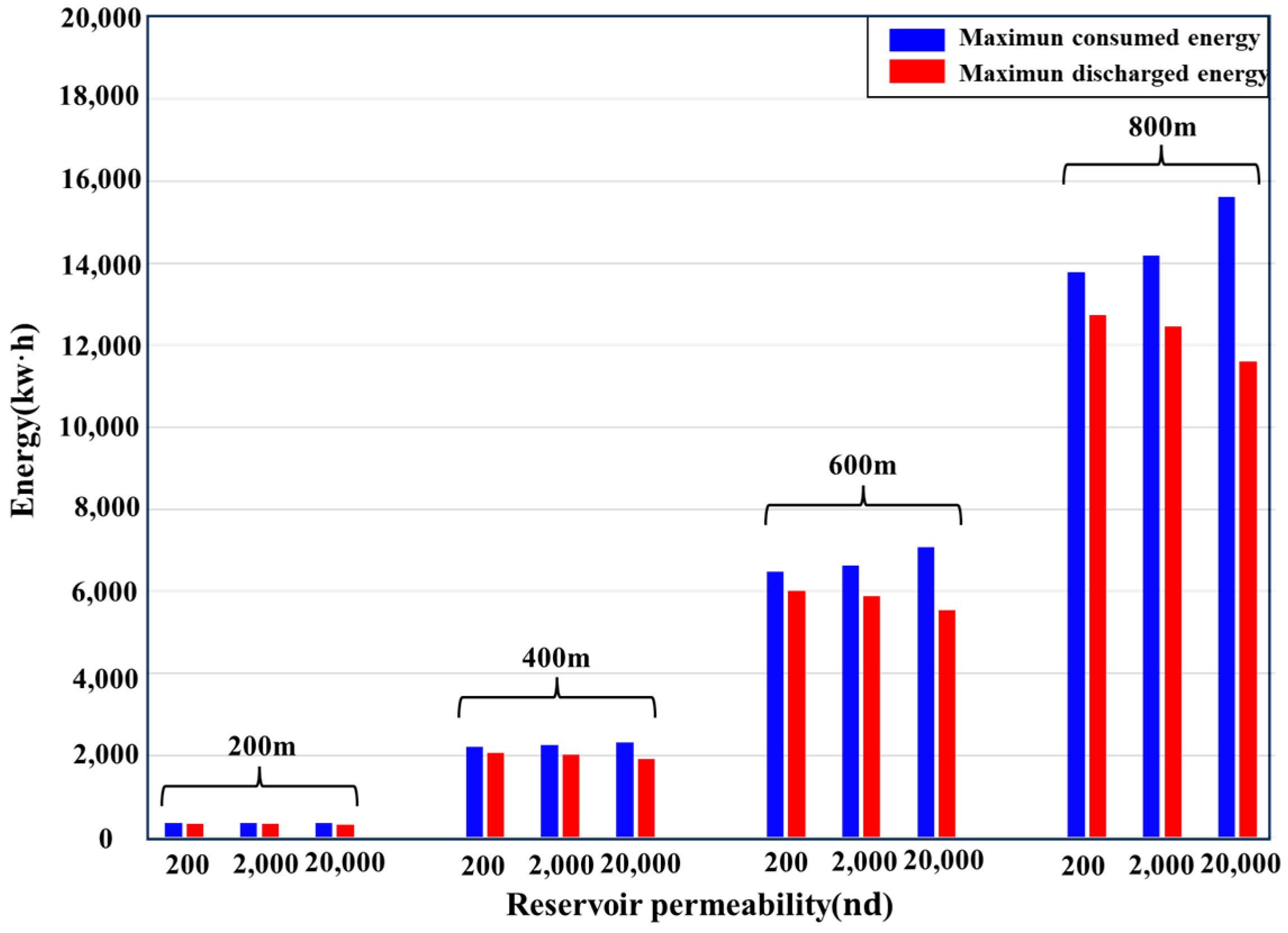
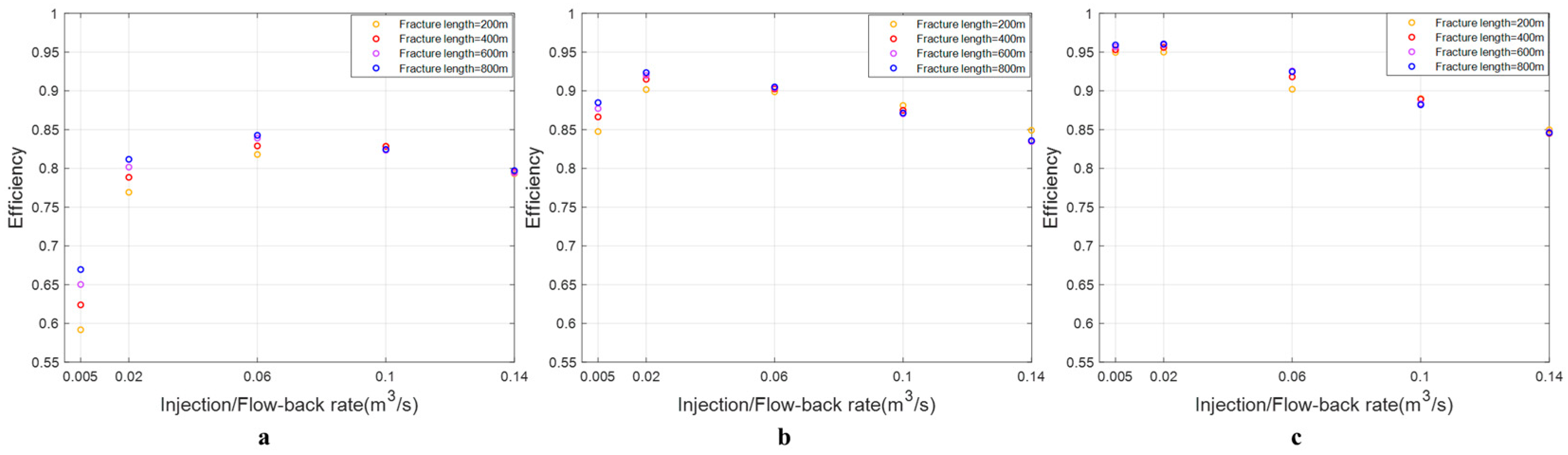
4.4. Reservoir Permeability
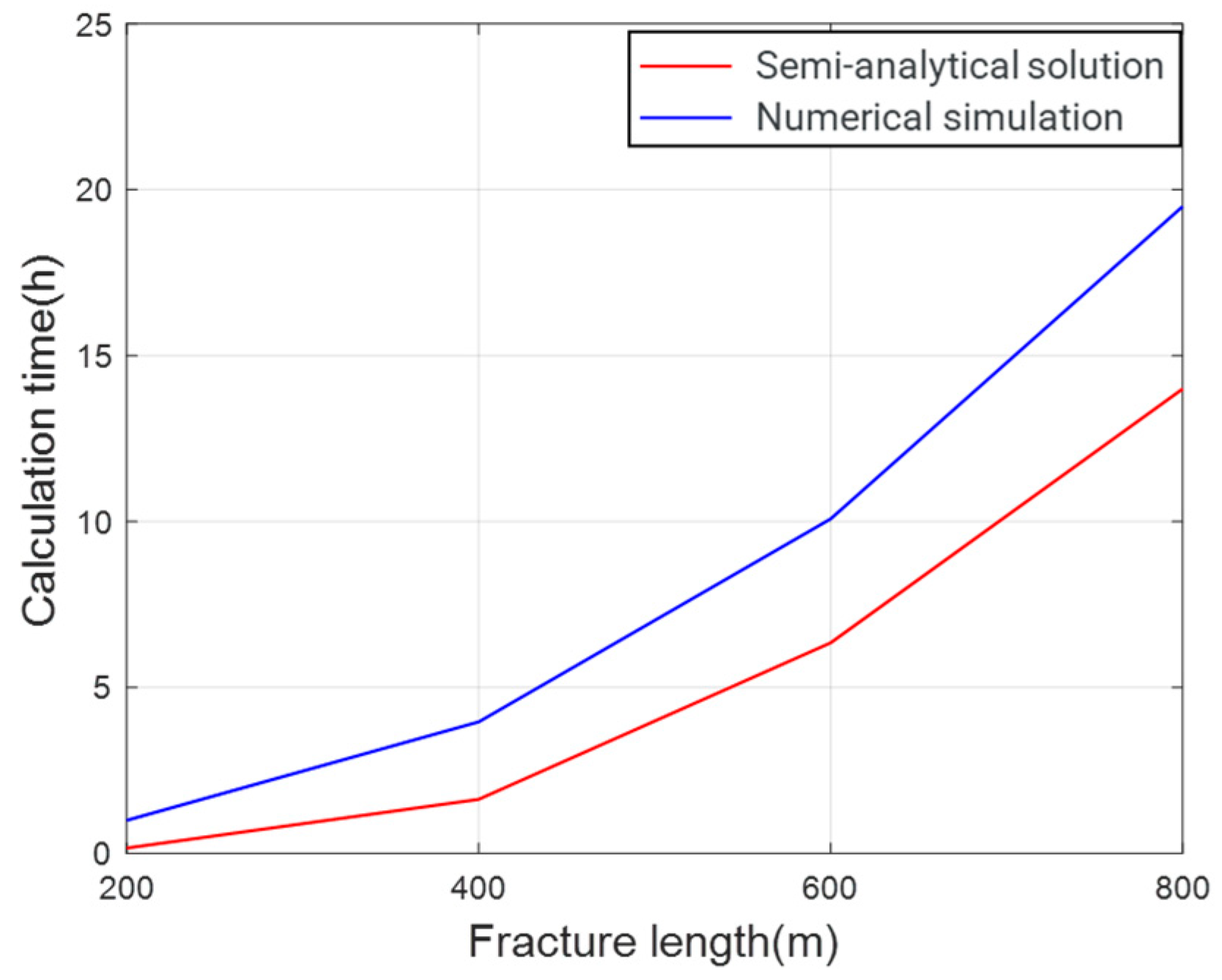
5. Discussion
6. Conclusions
- The effects of changes in injection/flow-back rates and fracture size on energy storage efficiency in reservoirs with different fracture toughness are essentially the same.
- Choosing reservoirs with higher fracture toughness not only fulfills larger-scale energy storage requirements but also enhances energy storage efficiency.
- Lowering reservoir permeability will enhance energy storage efficiency. Additionally, it will minimize the efficiency gap between the optimal injection/flow-back rate and various fracture sizes.
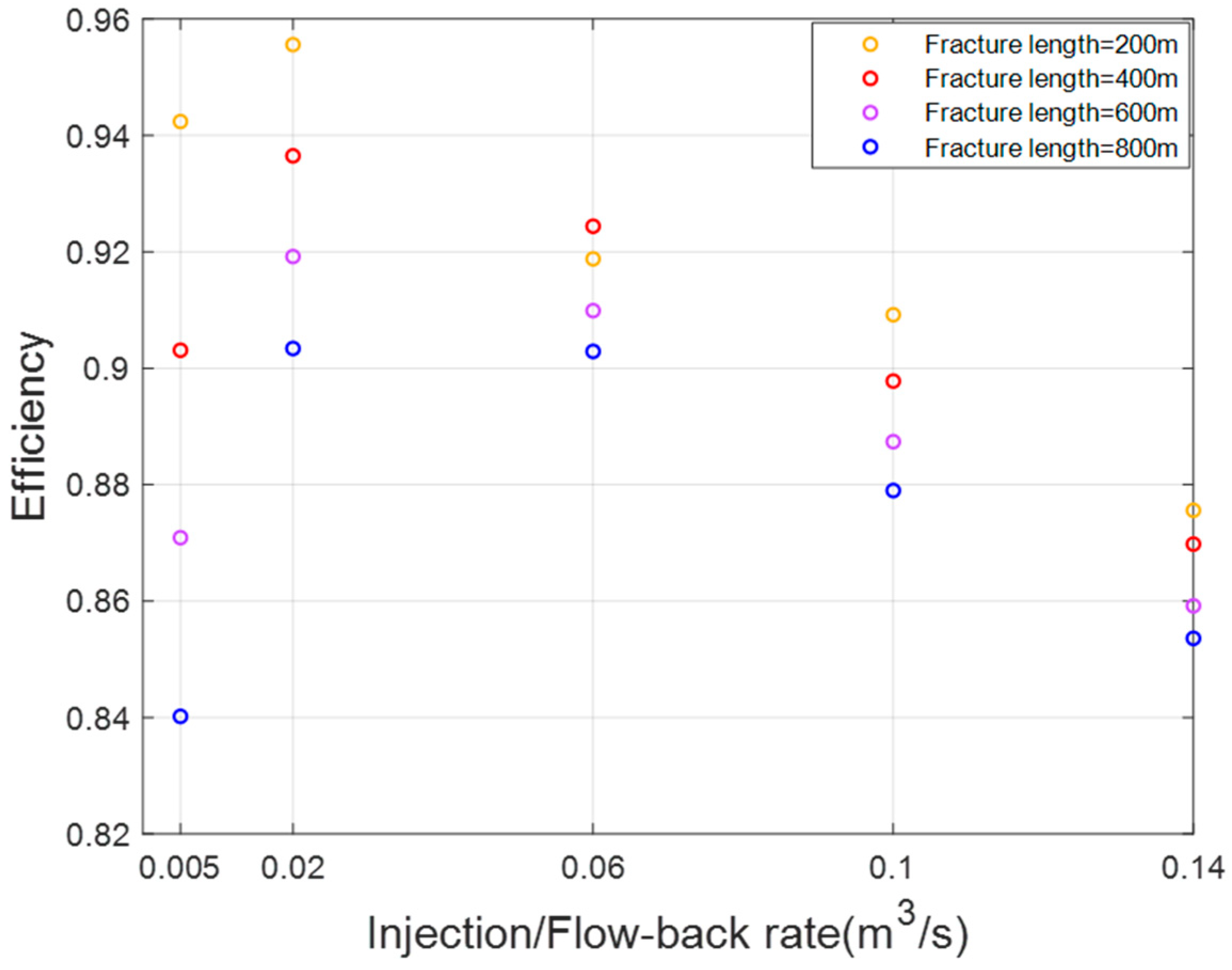
- For shallow circular fractures, smaller fracture sizes exhibit higher energy storage efficiency across all various injection/flow-back conditions.
- For deep elliptical fractures, the optimal fracture size shows an opposite trend with the increase in injection/flow-back rate.
- The impact of injection/flow-back rate on energy storage efficiency in fractures of different sizes remains consistent, with efficiency initially increasing and then decreasing as the injection/flowback rate rises.
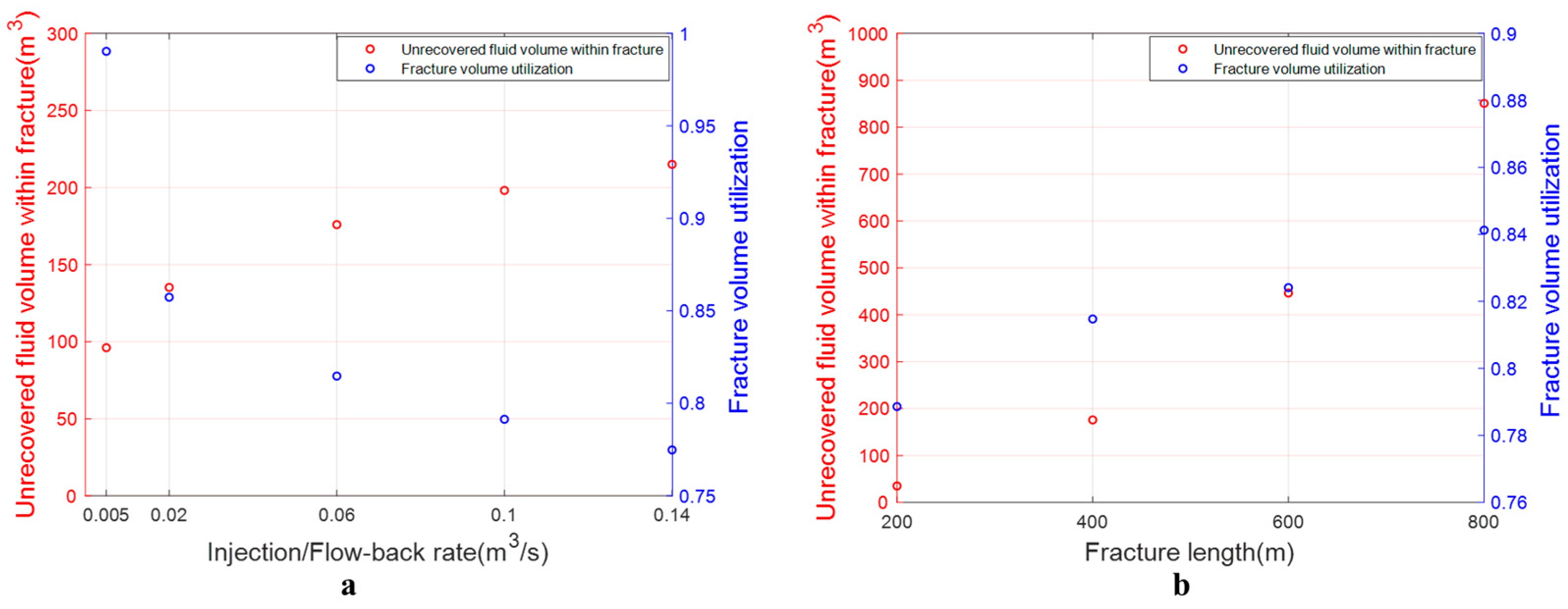
- Although the fluid recovery rate within the fractures cannot reach 100% during the energy discharged process and is influenced by the flowback rate, its impact on the scale of energy storage remains within an acceptable range.
- Employing moderate injection/flow-back rates in larger fractures is the optimal strategy for subsurface pumping energy storage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mclarnon, F.R.; Cairns, E.J. Energy storage. Ann. Rev. Energy 1989, 14, 241–271. [Google Scholar] [CrossRef]
- Baker, J.; Collinson, A. Electrical energy storage at the turn of the Millennium. Power Eng. J. 1999, 6, 107–112. [Google Scholar] [CrossRef]
- Dti Report. In Status of Electrical Energy Storage Systems; DG/DTI/00050/00/00. URN NUMBER 04/1878; UK Department of Trade and Industry: London, UK, 2004; pp. 1–24. Available online: https://www.osti.gov/etdeweb/biblio/20562504#:~:text=This%20report%20presents%20an%20overview%20of%20the%20status,the%20interest%20of%20the%20UK%20electricity%20supply%20industry (accessed on 1 August 2025).
- Australian Greenhouse Office. Advanced Electricity Storage Technologies Programme; Australian Greenhouse Office: Canberra, Australia, 2005; pp. 1–35. ISBN 1-921120-37-1. [Google Scholar]
- Walawalkar, R.; Apt, J.; Mancini, R. Economics of electric energy storage for energy arbitrage and regulation. Energy Policy 2007, 5, 2558–2568. [Google Scholar] [CrossRef]
- Rahman, M.; Oni, A.O.; Gemechu, E.; Kumar, A. Assessment of energy storage technologies: A review. Energy Convers. Manag. 2020, 223, 113295. [Google Scholar] [CrossRef]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, H. Feasibility study of energy storage using hydraulic fracturing in shale formations. Appl. Energy 2024, 354, 122251. [Google Scholar] [CrossRef]
- Hu, Z.W.; Wang, H.Y. Feasibility study of geothermal assisted energy storage using hydraulic fracturing. Geoenergy Sci. Eng. 2024, 242, 213220. [Google Scholar] [CrossRef]
- Hu, Z.W.; Wang, H.Y.; Zheng, S. Numerical modelling of energy storage using hydraulic fracturing in shale formations. Geoenergy Sci. Eng. 2025, 244, 213424. [Google Scholar] [CrossRef]
- da Rosa, A.V.; Ordóñez, J.C. Fundamentals of Renewable Energy Processes; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Herzog, A.V.; Lipman, T.E.; Kammen, D.M. Renewable energy sources. Encycl. Life Support Syst. (EOLSS) Fore-Run. Vol.-Perspect. Overv. Life Support Syst. Sustain. Dev. 2001, 76, 8–62. [Google Scholar]
- Moriarty, P.; Honnery, D. Can renewable energy power the future? Energy Policy 2016, 93, 3–7. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling tech-nology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Choudhury, S. Flywheel energy storage systems: A critical review on technologies, applications, and future prospects. Int. Trans. Electr. Energy Syst. 2021, 31, e13024. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J.; Krupke, C. Overview of Current Development in Compressed Air Energy Storage Technology. Energy Procedia 2014, 62, 603–611. [Google Scholar] [CrossRef]
- Li, H.; Ma, H.; Liu, J.; Zhu, S.; Zhao, K.; Zheng, Z.; Zeng, Z.; Yang, C. Large-scale CAES in bedded rock salt: A case study in Jiangsu Province, China. Energy 2023, 281, 128271. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A.; Ramadan, M. Critical Review of Flywheel Energy Storage System. Energies 2021, 14, 2159. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C. A review of pumped hydro energy storage. Prog. Energy 2021, 3, 022003. [Google Scholar] [CrossRef]
- Li, H.; Ma, H.; Yang, C.; Zhao, K.; Hu, Z.; Daemen, J. Acoustic emission characteristics of rock salt under multi-stage cyclic loading. Int. J. Fatigue 2023, 176, 107911. [Google Scholar] [CrossRef]
- Akpoti, K.; Obahoundje, S.; Mortey, E.M.; Diawuo, F.A.; Antwi, E.O.; Gyamfi, S.; Domfeh, M.K.; Kabo-Bah, A.T. Technological advances in prospecting sites for pumped hydro energy storage. In Pumped Hydro Energy Storage for Hybrid Systems; Academic Press: New York, NY, USA, 2023; pp. 105–118. [Google Scholar]
- Hannan, M.; Wali, S.; Ker, P.; Rahman, M.A.; Mansor, M.; Ramachandaramurthy, V.; Muttaqi, K.; Mahlia, T.; Dong, Z. Battery energy-storage system: A review of technologies optimization objectives constraints approaches and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Bunger, A.P.; Lau, H.; Wright, S.; Schmidt, H. Mechanical model for geomechanical pumped storage in horizontal fluid-filled lenses. Int. J. Numer. Anal. Methods Géoméch. 2023, 47, 1349–1372. [Google Scholar] [CrossRef]
- Wang, H.Y.; Yi, S.T.; Sharma, M.M. A computationally efficient approach to modeling contact problems and fracture closure using superposition method. Theor. Appl. Fract. Mech. 2018, 93, 276–287. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, M.; Yang, H.; Wang, D.; Ramos, M.A.; Hu, T.S.; Xu, Q. Friction Challenge in Hydraulic Fracturing. Lubricants 2022, 10, 14. [Google Scholar] [CrossRef]
- Daneshy, A.A. Experimental Investigation of Hydraulic Fracturing Through Perforations. J. Pet. Technol. 1973, 25, 1201–1206. [Google Scholar] [CrossRef]
- Gottschling, J.C. Openhole vs. Cased-Hole Hydraulic Fracturing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005; p. SPE-97172-MS. [Google Scholar]
- Hanson, M.E.; Anderson, G.D.; Shaffer, R.J.; Thorson, L.D. Some Effects of Stress, Friction, and Fluid Flow on Hydraulic Fracturing. Soc. Pet. Eng. J. 1982, 22, 321–332. [Google Scholar] [CrossRef]
- Hanson, M.E.; Shaffer, R.J.; Anderson, G.D. Effects of Various Parameters on Hydraulic Fracturing Geometry. Soc. Pet. Eng. J. 1981, 21, 435–443. [Google Scholar] [CrossRef]
- Barree, R.D.; Gilbert, J.V.; Conway, M.W. An Effective Model for Pipe Friction Estimation in Hydraulic Fracturing Treatments. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low-Permeability Reservoirs Symposium, Oklahoma City, OK, USA, 9–10 April 2009; p. SPE-122917-MS. [Google Scholar]
- Ba Geri, M.; Imqam, A.; Flori, R. A critical review of using high viscosity friction reducers as fracturing fluids for hydraulic fracturing applications. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium/Production and Operations Symposium, Oklahoma City, OK, USA, 9–10 April 2019; p. D021S004R001. [Google Scholar]
- Smith, C.G.; Khiat, S.; Albadraoui, D. An Effective Technique to Reduce Bottomhole Friction Pressure During Hydraulic Fracturing Treatments. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 13–15 February 2008. [Google Scholar]
- Nizamidin, N.; Kim, A.; Belcourt, K.; Angeles, M.; Kim, D.H.; Matovic, G.; Lege, E. New casing friction model for slickwater: Field data validation, application, and optimization for hydraulic fracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 1–3 February 2022; p. D021S003R005. [Google Scholar]
- Nguyen, H.T.; Lee, J.H.; Elraies, K.A. A review of PKN-type modeling of hydraulic fractures. J. Pet. Sci. Eng. 2020, 195, 107607. [Google Scholar] [CrossRef]
- Kovalyshen, Y.; Detournay, E. A Reexamination of the Classical PKN Model of Hydraulic Fracture. Transp. Porous Media 2010, 81, 317–339. [Google Scholar] [CrossRef]
- Fjær, E.; Holt, R.M.; Horsrud, P.; Raaen, A.M.; Risnes, R. Mechanics of hydraulic fracturing. Dev. Pet. Sci. 2008, 53, 369–390. [Google Scholar]
- Lukawski, M.Z.; Anderson, B.J.; Augustine, C.; Capuano, L.E.; Beckers, K.F.; Livesay, B.; Tester, J.W. Cost analysis of oil, gas, and geothermal well drilling. J. Pet. Sci. Eng. 2014, 118, 1–14. [Google Scholar] [CrossRef]
- Xu, S.; Guo, J.; Feng, Q.; Ren, G.; Li, Y.; Wang, S. Optimization of hydraulic fracturing treatment parameters to maximize economic benefit in tight oil. Fuel 2022, 329, 125329. [Google Scholar] [CrossRef]
- Marongiu-Porcu, M.; Economides, M.J.; Holditch, S.A. Economic and physical optimization of hydraulic fracturing. J. Nat. Gas Sci. Eng. 2013, 14, 91–107. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, S.; Khatod, D. Optimal installation of small hydropower plant—A review. Renew. Sustain. Energy Rev. 2011, 15, 3862–3869. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, S.K.; Khatod, D.K. Costing of a Small Hydropower Projects. Int. J. Eng. Technol. 2012, 4, 239–242. [Google Scholar] [CrossRef]
- Aggidis, G.; Luchinskaya, E.; Rothschild, R.; Howard, D. The costs of small-scale hydro power production: Impact on the development of existing potential. Renew. Energy 2010, 35, 2632–2638. [Google Scholar] [CrossRef]
- Viswanathan, V.; Mongird, K.; Franks, R.; Li, X.; Sprenkle, V.; Pacific Northwest National Laboratory. 2022 grid energy storage technology cost and performance assessment. Energy 2022, 2022, 1–151. [Google Scholar]
- Zheng, S. Development of a Fully Integrated Equation of State Compositional Hydraulic Fracturing and Reservoir Simulator. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2021. [Google Scholar]



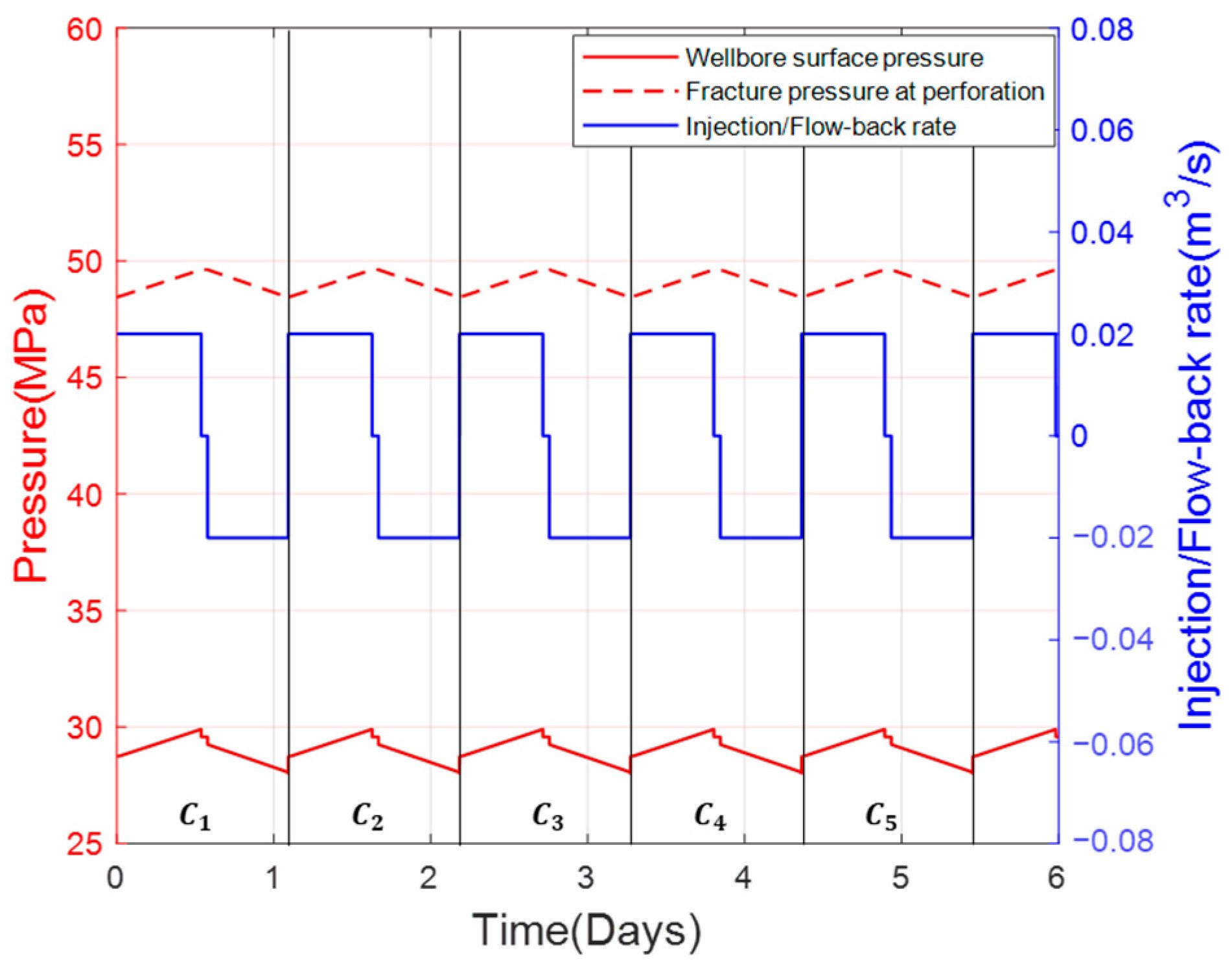
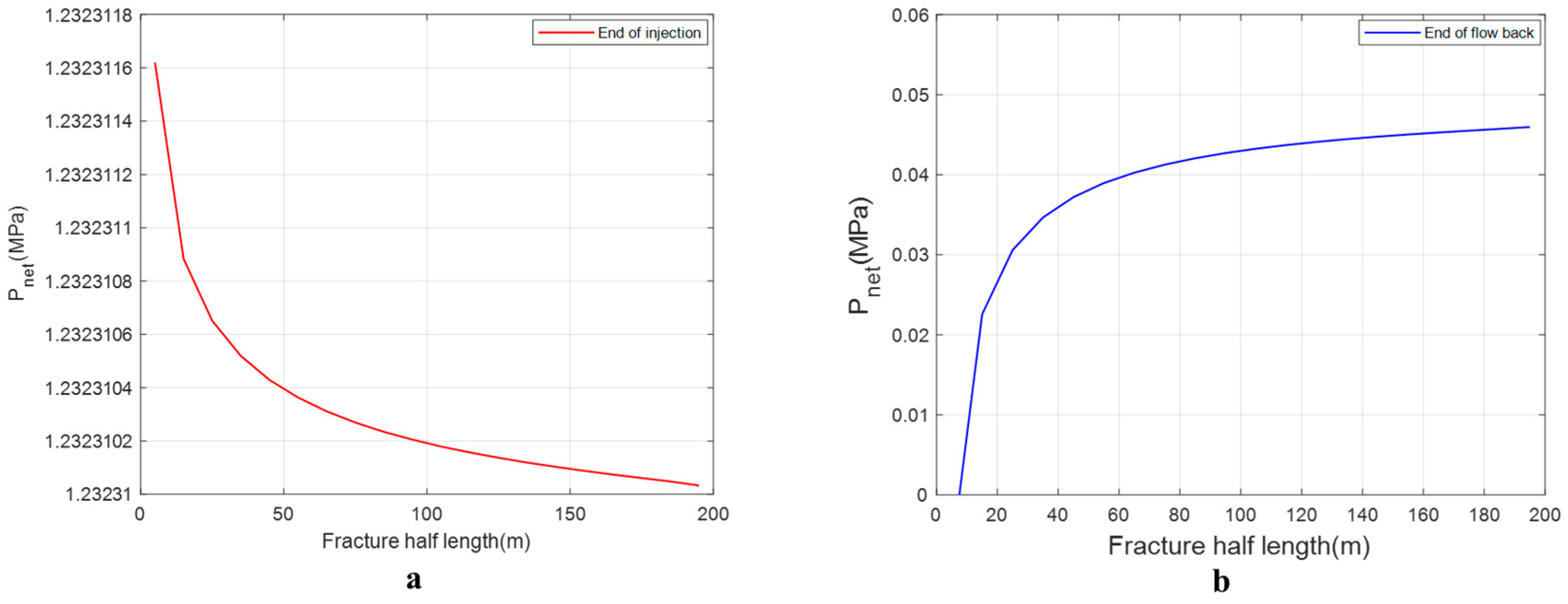

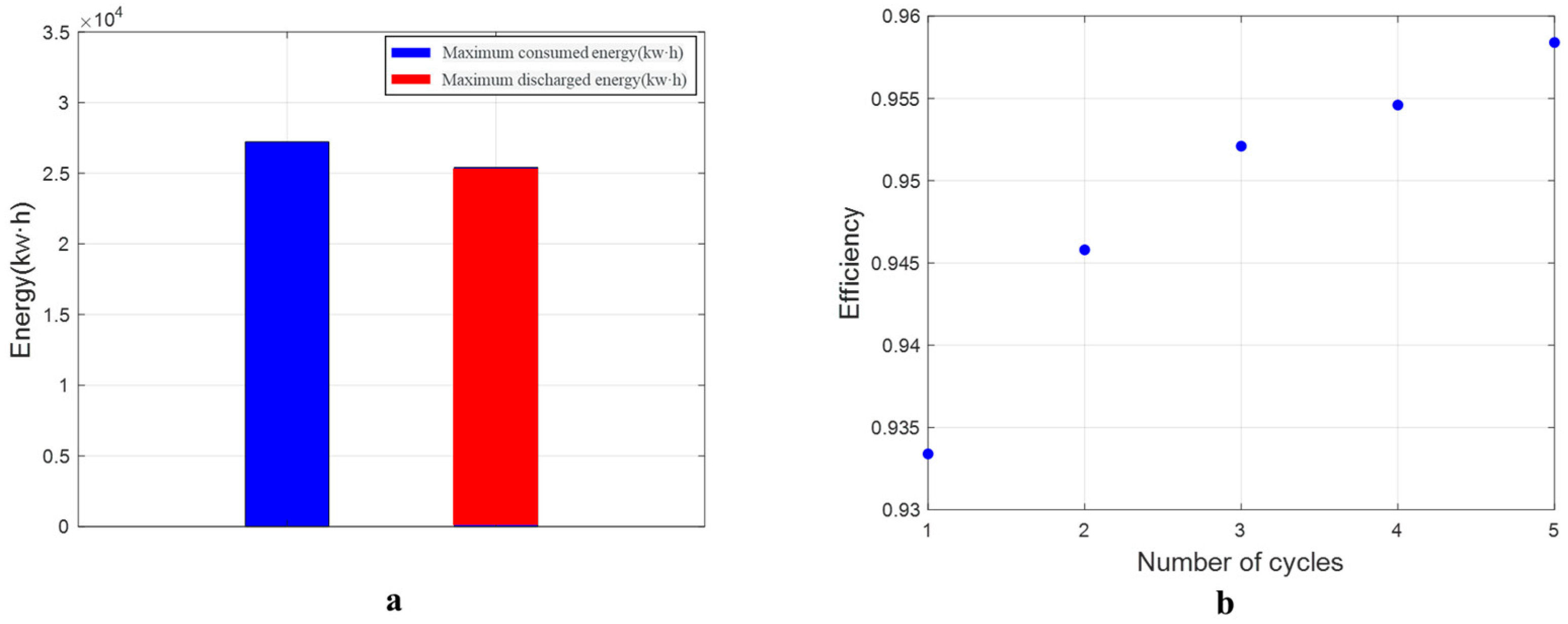
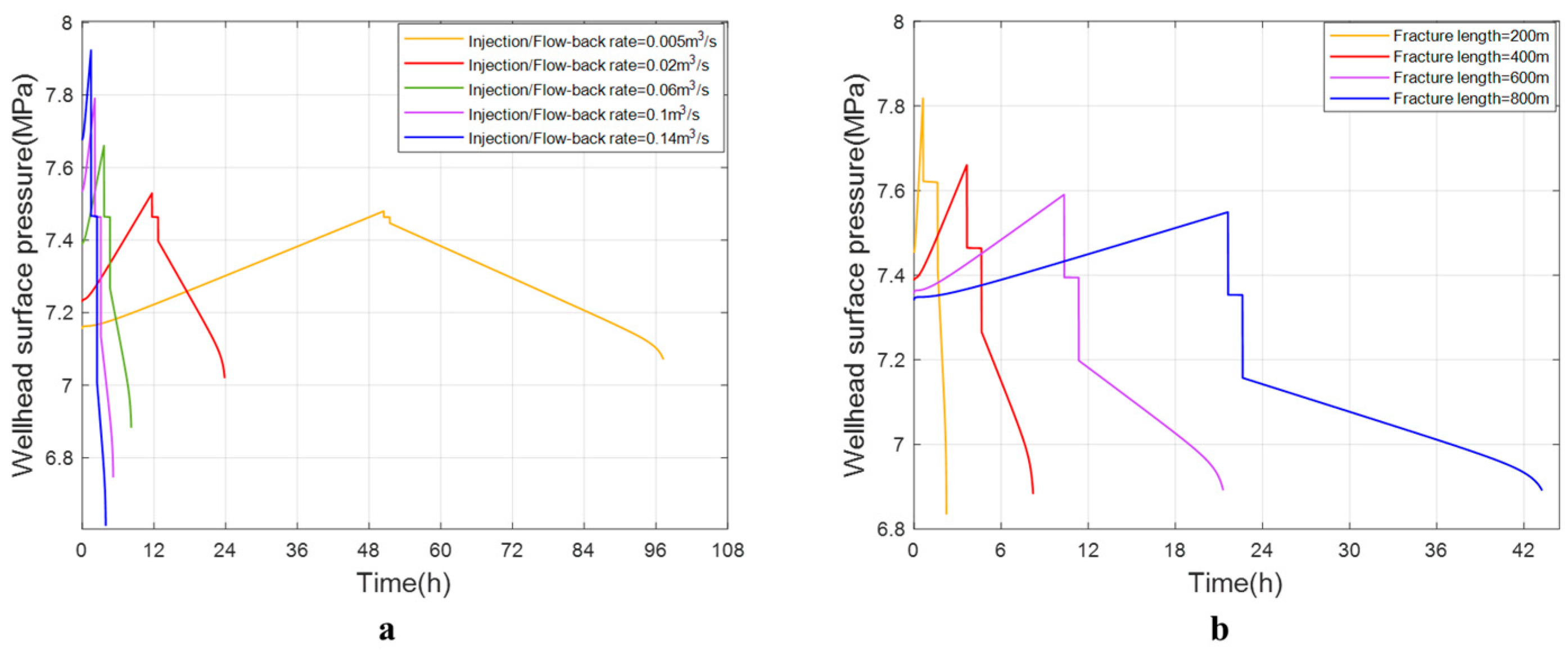









| Parameters | Value Range |
|---|---|
| Number of cycles | 5 |
| Time step (s) | 60 |
| Shut-in time per cycle (h) | 1 |
| Injection/flow-back rate (m3/s) | 0.02 |
| Minimum principal stress gradient (MPa/m) | 0.0242 |
| Pore stress gradient (MPa/m) | 0.0113 |
| Penny-shaped fracture vertical depth (m) | 500 |
| Elliptical fracture vertical depth (m) | 2000 |
| Elliptical fracture measure depth (m) | 2500 |
| Poisson’s ratio | 0.33 |
| Young’s modulus (GPa) | 15 |
| Fracture toughness (MPa·m1/2) | 6 |
| Penny-shaped fracture radius (m) | 200 |
| Elliptical fracture height (m) | 80 |
| Elliptical fracture length (m) | 400 |
| Reservoir permeability (md) | 0.002 |
| Total compressibility (MPa−1) | 0.00011 |
| Fluid viscosity (cp) | 1 |
| Fluid density (kg/m3) | 1023 |
| Initial porosity | 0.1 |
| Initial contact time(s) | 6000 |
| Wellbore roughness (m) | 1.6 × 10−6 |
| Reynolds number conversion value | 4000 |
| parameters | Value Range |
| Number of cycles | 5 |
| Fracture Radius (m) | Injection/Flow-Back Rate (m3/s) |
|---|---|
| 200 | 0.005, 0.02, 0.06, 0.1, 0.14 |
| 400 | 0.005, 0.02, 0.06, 0.1, 0.14 |
| 600 | 0.005, 0.02, 0.06, 0.1, 0.14 |
| 800 | 0.005, 0.02, 0.06, 0.1, 0.14 |
| CAPEX ($USD) | |
|---|---|
| Geological/Geophysical Surveys | $1,200,000 |
| Drilling and Completion | $6,000,000 |
| Fracture Creation | $40,000,000 |
| Fracturing Monitoring | $1,200,000 |
| Tank | $8,000,000 |
| Water Injection Pump | $6,000,000 |
| Pelton Turbine | $16,000,000 |
| Power Conversion System | $8,000,000 |
| Transformers and Electrical Equipment | $4,000,000 |
| Control System | $2,400,000 |
| Construction and Commissioning | $8,000,000 |
| TOTAL CAPEX | $100,800,000 |
| CAPEX/kWh | $252/kWh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Wang, H. A Study on the Optimal Design of Subsurface Pumping Energy Storage Under Varying Reservoir Conditions. Energies 2025, 18, 5252. https://doi.org/10.3390/en18195252
Hu Z, Wang H. A Study on the Optimal Design of Subsurface Pumping Energy Storage Under Varying Reservoir Conditions. Energies. 2025; 18(19):5252. https://doi.org/10.3390/en18195252
Chicago/Turabian StyleHu, Zhiwen, and Hanyi Wang. 2025. "A Study on the Optimal Design of Subsurface Pumping Energy Storage Under Varying Reservoir Conditions" Energies 18, no. 19: 5252. https://doi.org/10.3390/en18195252
APA StyleHu, Z., & Wang, H. (2025). A Study on the Optimal Design of Subsurface Pumping Energy Storage Under Varying Reservoir Conditions. Energies, 18(19), 5252. https://doi.org/10.3390/en18195252





