Detection and Evaluation of Shield Damage Defects in Power Cables Using an Improved Dual-Frequency Time–Frequency Domain Reflectometry
Abstract
1. Introduction
2. Methodology
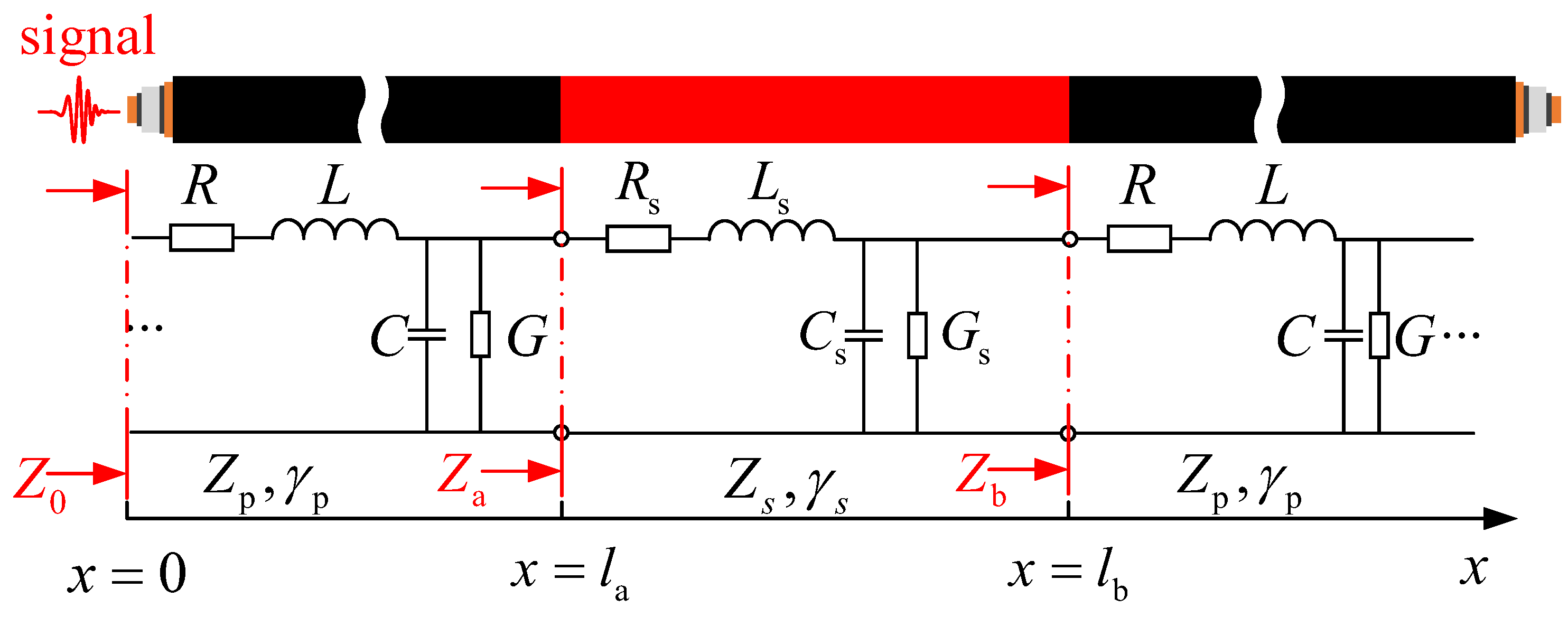
2.1. Basic Theory of TFDR and Modeling of Cable Shield Hole Defects
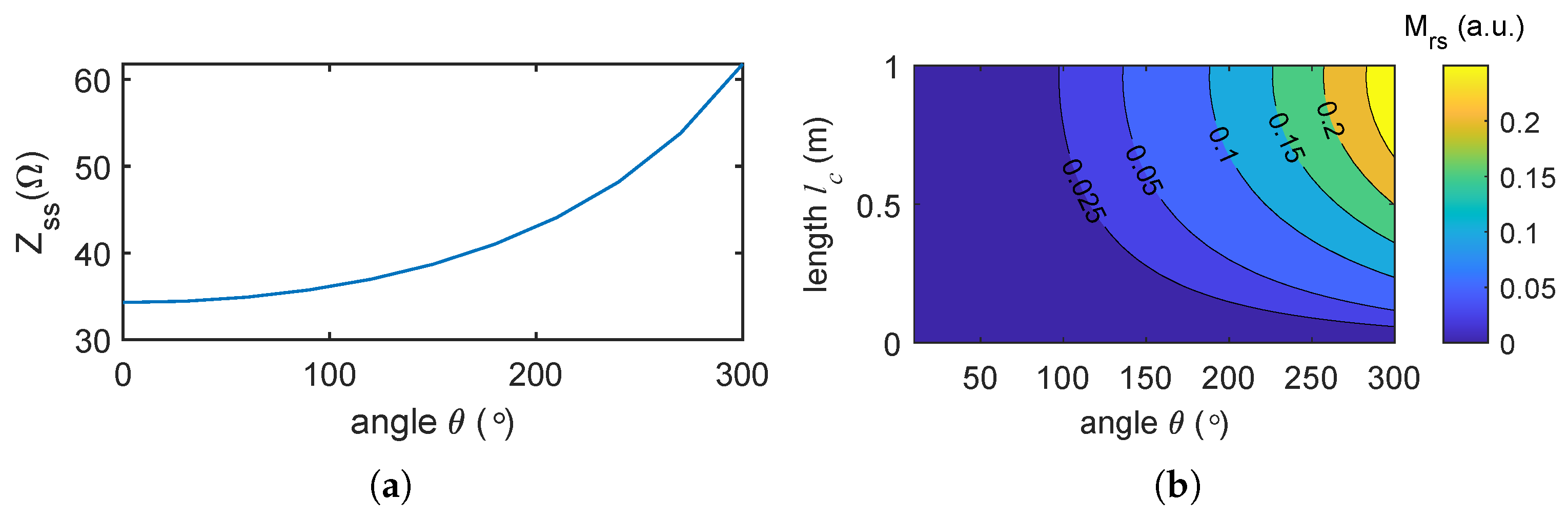
2.2. Evaluation of Shield Hole Sizes Using Improved Dual-Frequency TFDR
| Algorithm 1 Size Assessment of Cable Shield Hole |
Block 1: Measurement Setup
|
3. Simulation Validation
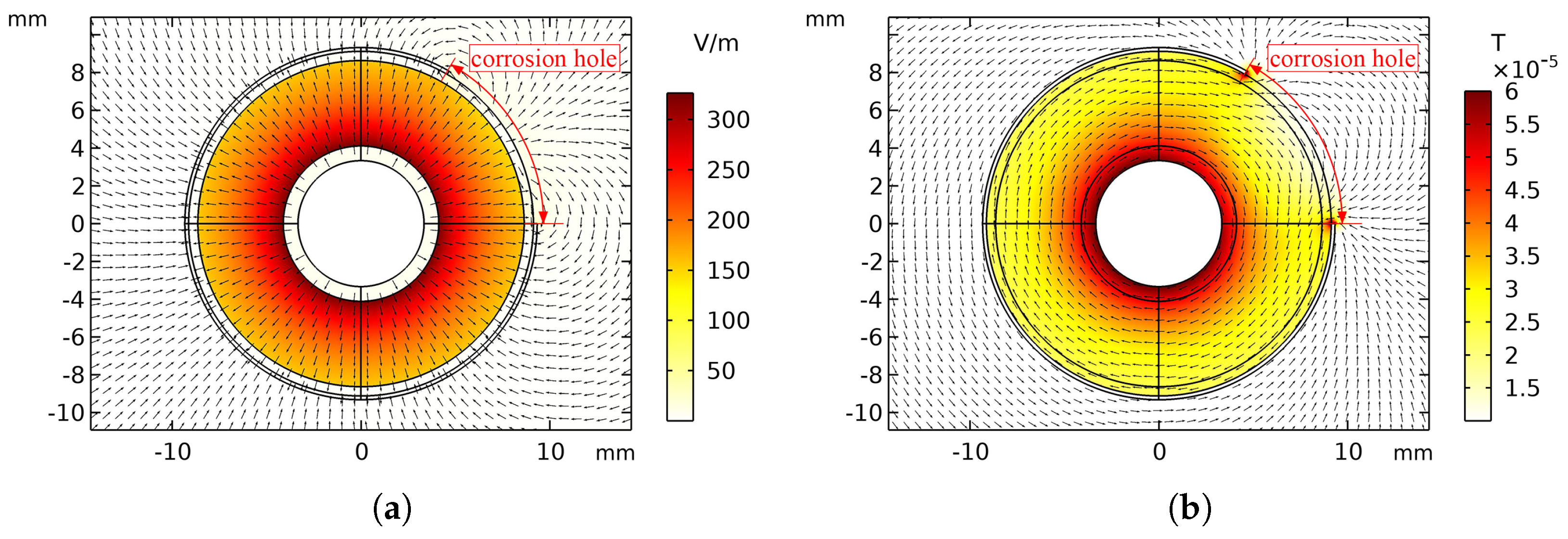
3.1. Modeling and Analyzing the Cable Shield Hole Defects
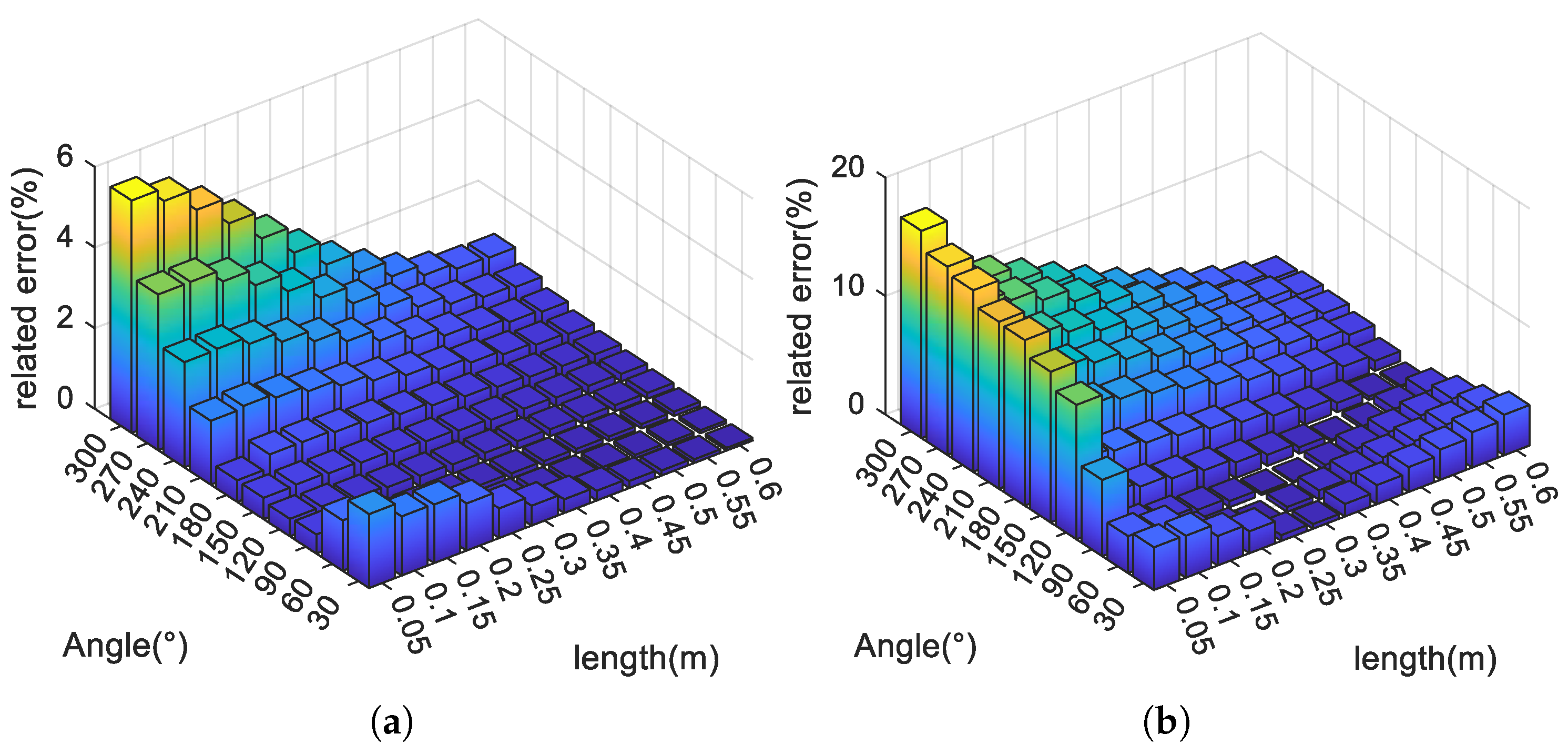
3.2. Simulation of Long Cables with Shield Hole Defects
4. Experiments and Results
5. Conclusions
- 1.
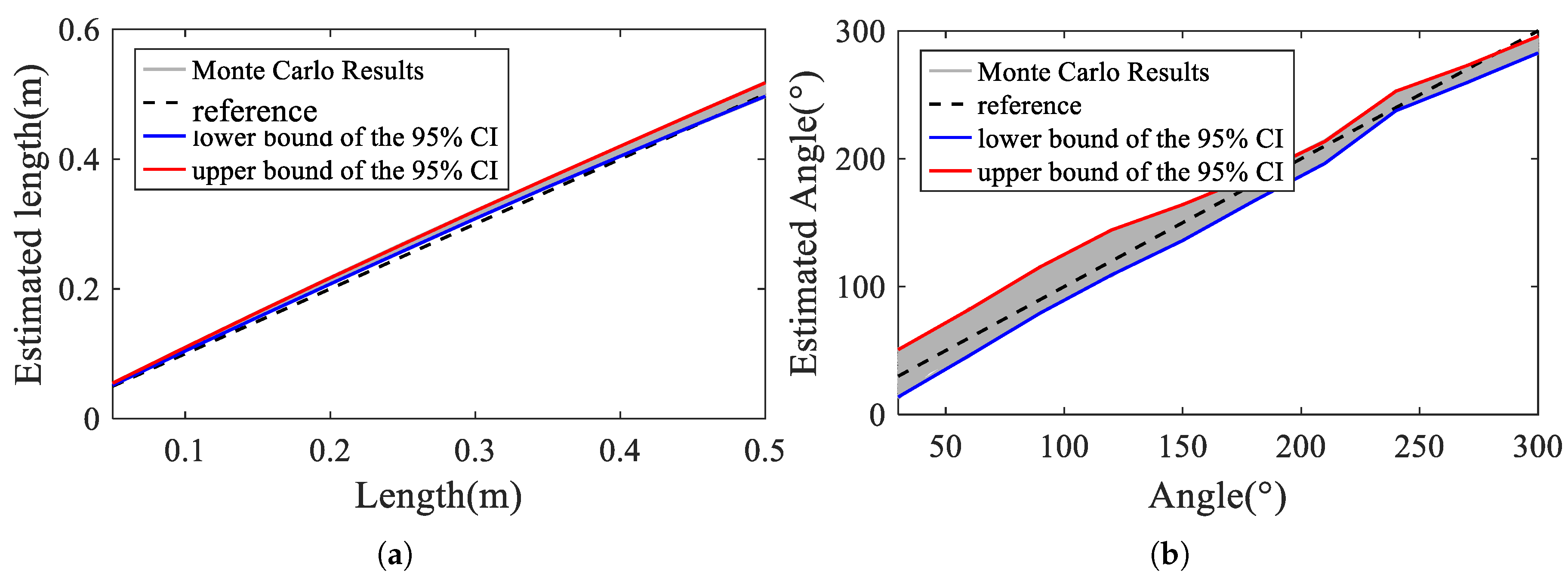
- In the long cable simulation results, the estimated error of defect angles and lengths increased with the increase in defect angle. When the defect angle is lower than 300°, the proposed method has a high accuracy and robustness.
- 2.
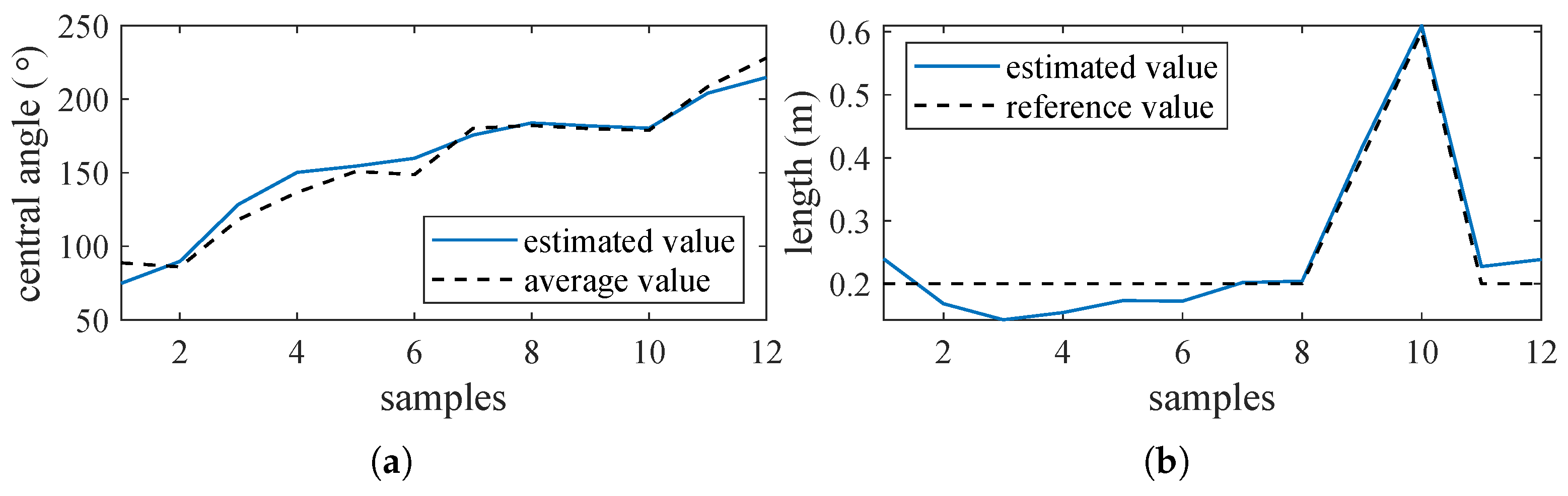
- In the experimental results, the maximum relative errors for regular defects were 11% in length estimation and 5% in angle estimation. For irregular defects, the proposed method was able to estimate both defect length and average angle, with errors of 8.7% and 9.06%, respectively. In multiple-defect scenarios, the method remained effective, yielding maximum relative errors of 14.43% for length and 11.97% for angle.
- 3.
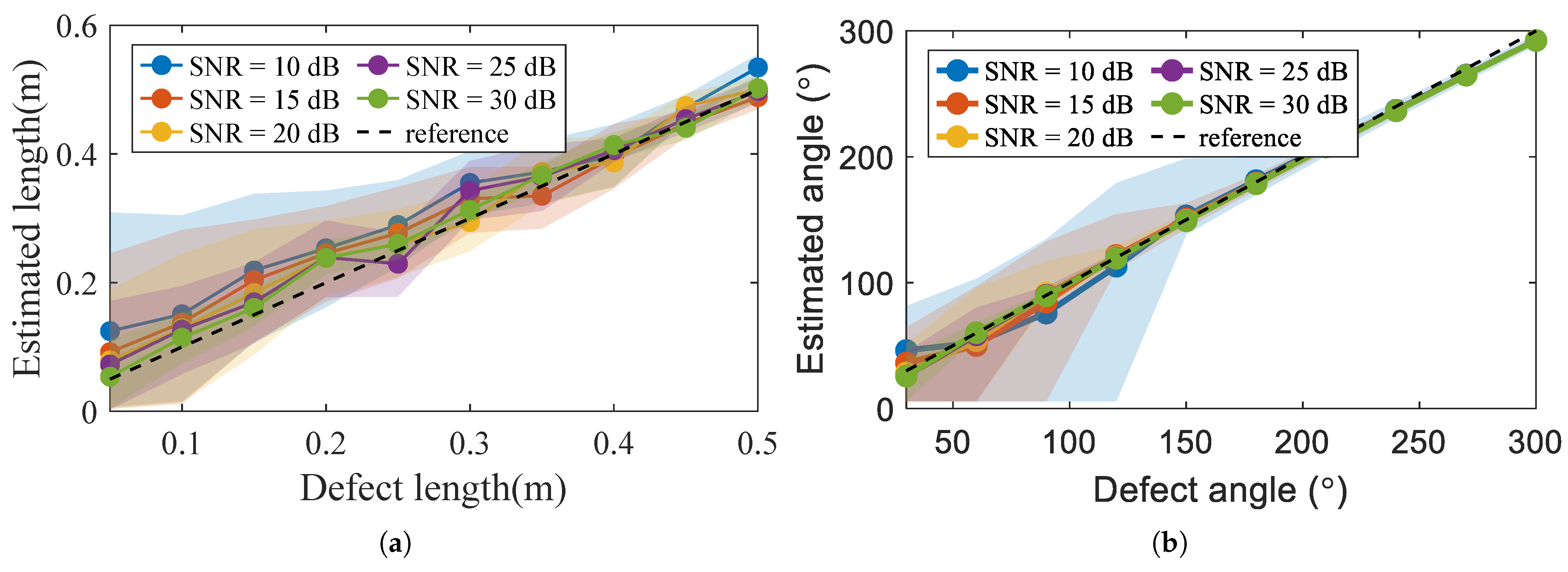
- In practical measurements, the proposed method requires the signal source and data acquisition device to have a bandwidth of at least 100 to ensure estimation accuracy. The on-site SNR is not lower than 20 dB, and excessive noise can lead to larger errors.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tu, H.; Peng, C.; Chen, Y.; Li, L.; Deng, H.; Liu, G. Characteristic impedance modeling of nuclear power instrumentation and control cable shield breakage. Energies 2025, 18, 3008. [Google Scholar] [CrossRef]
- Shao, Q.; Fan, S.; Zhang, Z.; Liu, F.; Fu, Z.; Lv, P.; Mu, Z. Artificial intelligence in cable fault detection and localization: Recent advances and research challenges. Energies 2025, 18, 3662. [Google Scholar] [CrossRef]
- IEEE 1617-2022; IEEE Guide for Assessment, Mitigation, and Control of Corrosion of Metallic Shields for Extruded Dielectric Cables Rated 5 kv to 46 kv. IEEE: New York, NY, USA, 2022.
- Liang, H.; Liu, Y.; Sheng, G.; Jiang, X. Fault-cause identification method based on adaptive deep belief network and time–frequency characteristics of travelling wave. IET Gener. Transm. Distrib. 2019, 13, 724–732. [Google Scholar] [CrossRef]
- Jiang, K.; Zhou, K.; Ren, X.; Xu, Y. Frequency domain sampling optimization of cable defect detection and location method based on exponentially increased frequency reflection coefficient spectrum. Energies 2025, 18, 2428. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, K.; Ren, X.; Xu, Y. Moisture localization and diagnosis method for power distribution cables based on dynamic frequency domain reflectometry. Energies 2025, 18, 2430. [Google Scholar] [CrossRef]
- Abboud, L.; Cozza, A.; Pichon, L. A matched-pulse approach for soft-fault detection in complex wire networks. IEEE Trans. Instrum. Meas. 2012, 61, 1719–1732. [Google Scholar] [CrossRef]
- Mu, H.B.; Zhang, H.T.; Zou, X.Y.; Zhang, D.N.; Lu, X.; Zhang, G.J. Sensitivity improvement in cable faults location by using broadband impedance spectroscopy with dolph-chebyshev window. IEEE Trans. Power Deliv. 2022, 37, 3846–3854. [Google Scholar] [CrossRef]
- Song, E.; Shin, Y.J.; Stone, P.E.; Wang, J.; Choe, T.S.; Yook, J.G.; Park, J.B. Application of time-frequency domain reflectometry for detection and localization of a fault on a coaxial cable. IEEE Trans. Electromagn. Compat. 2009, 54, 2493–2500. [Google Scholar]
- Lee, S.H.; Park, J.B.; Choi, Y.H. Wavelet-transform-based time-frequency domain reflectometry for reduction of blind spot. Meas. Sci. Technol. 2012, 23, 065004. [Google Scholar] [CrossRef]
- Lim, H.; Kwon, G.Y.; Shin, Y.J. Fault detection and localization of shielded cable via optimal detection of time-frequency-domain reflectometry. IEEE Trans. Instrum. Meas. 2021, 70, 3521510. [Google Scholar] [CrossRef]
- Lim, H.; Lee, Y.H.; Bang, S.S.; Shin, Y.J. Application of enhanced optimal-detection of time-frequency domain reflectometry on hts cable with high-resolution. IEEE Trans. Appl. Supercond. 2023, 33, 9000306. [Google Scholar] [CrossRef]
- Zou, X.; Mu, H.; Wang, R.; Fan, K.; Cheng, Z.; He, Y.; Zhang, G. An efficient accuracy improvement method for cable defect location based on instantaneous filtering in time-frequency domain. Measurement 2024, 226, 114178. [Google Scholar] [CrossRef]
- Manet, A.; Kameni, A.; Loete, F.; Genoulaz, J.; Pichon, L.; Picon, O. Equivalent circuit model of soft shield defects in coaxial cables using numerical modeling. IEEE Trans. Electromagn. Compat. 2017, 59, 533–536. [Google Scholar] [CrossRef]
- Zou, X.Y.; Mu, H.B.; Zhang, H.T.; Qu, L.Q.; He, Y.F.; Zhang, G.J. An efficient cross-terms suppression method in time-frequency domain reflectometry for cable defect localization. IEEE Trans. Instrum. Meas. 2022, 71, 3511610. [Google Scholar] [CrossRef]
- Lee, C.K.; Shin, Y.J. Detection and assessment of i&c cable faults using time-frequency R-CNN-based reflectometry. IEEE Trans. Ind. Electron. 2021, 68, 1581–1590. [Google Scholar]
- Zhao, K.; Grivet-Talocia, S.; Manfredi, P.; Yan, Y.; Li, H. Size assessment of power cable shield corrosion defects using double-frequency time–frequency-domain reflectometry. IEEE Trans. Instrum. Meas. 2025, 74, 3513911. [Google Scholar] [CrossRef]
- Papaleonidopoulos, I.C.; Karagiannopoulos, C.G.; Theodorou, N.J. Evaluation of the two-conductor hf transmission-line model for symmetrical indoor triple-pole cables. Measurement 2006, 39, 719–728. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar] [CrossRef]
- Khan, A.S. Microwave Engineering: Concepts and Fundamentals, 1st ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]







| Component | Radius (mm) | Electric Parameters |
|---|---|---|
| Core | 3.335 | = 5.98 S/m |
| Inner semiconductor | 4.115 | |
| XLPE | 8.635 | = 2.3 |
| Outer semiconductor | 9.125 | |
| Shield | 9.325 | = 5.98 S/m |
| Sheath | 12.115 | = 2.25 |
| Sample | (°) | (°) | (m) | (°) |
|---|---|---|---|---|
| 1 | 90 | 0.2 | 88.69 | |
| 2 | 90 | 0.2 | 85.97 | |
| 3 | 120 | 0.2 | 118.18 | |
| 4 | 135 | 0.2 | 136.62 | |
| 5 | 150 | 0.2 | 150.90 | |
| 6 | 150 | 0.2 | 148.72 | |
| 7 | 180 | 0.2 | 180.22 | |
| 8 | 180 | 0.2 | 182.16 | |
| 9 | 180 | 0.4 | 179.99 | |
| 10 | 180 | 0.6 | 178.85 | |
| 11 | 210 | 0.2 | 208.49 | |
| 12 | 225 | 0.2 | 228.01 |
| Type | Defect Size | and Confidence Interval (cm) | Relative Error (%) | and Confidence Interval (°) | Relative Error (%) |
|---|---|---|---|---|---|
| Regular defects | 30 cm, 90° | 32.54 ± 1.2 | 8.47 | 85.9 ± 2.19 | 4.56 |
| 30 cm, 180° | 32.38 ± 1.94 | 7.93 | 174.01 ± 4.57 | 3.33 | |
| 40 cm, 90° | 44.27 ± 1.45 | 10.68 | 86.93 ± 2.21 | 3.41 | |
| 40 cm, 180° | 39.06 ± 2.03 | 2.35 | 181.87 ± 3.55 | 1.04 | |
| 50 cm, 90° | 53.95 ± 2.02 | 7.09 | 88.04 ± 1.48 | 2.18 | |
| 50 cm, 180° | 54.38 ± 2.13 | 8.76 | 175.17 ± 4.16 | 2.68 | |
| 60 cm, 190° | 66.50 ± 1.68 | 10.83 | 184.24 ± 4.29 | 3.03 | |
| 60 cm, 230° | 55.19 ± 2.88 | 8.02 | 229.54 ± 6.14 | 0.2 | |
| Irregular defects | 40 cm, 225° | 37.26 ± 2.46 | 6.85 | 238.83 ± 7.4 | 6.15 |
| 40 cm, 202.5° | 42.46 ± 2.6 | 6.15 | 211.8 ± 5.16 | 4.59 | |
| 50 cm, 216° | 54.35 ± 2.76 | 8.7 | 196.43 ± 3.95 | 9.06 |
| Algorithm | Defect 1 | Defect 2 (40 cm, 180°) | |||
|---|---|---|---|---|---|
| and Confidence Interval (cm) |
Relative Error (%) | and Confidence Interval (°) |
Relative Error (%) | ||
| No Comp. | 30 cm, 90° | 33.56 ± 1.85 | 16.1 | 145.38 ± 3.32 | 19.2 |
| 30 cm, 180° | 44.63 ± 2.23 | 11.58 | 126.74 ± 3.47 | 29.59 | |
| 40 cm, 90° | 52.12 ± 2.17 | 30.3 | 138.97 ± 3.84 | 22.79 | |
| 50 cm, 90° | 48.35 ± 2.18 | 20.87 | 125.83 ± 2.63 | 30.1 | |
| 50 cm, 180° | 26.72 ± 1.78 | 33.2 | 105.41 ± 2.76 | 41.44 | |
| 60 cm, 190° | 35.14 ± 2.01 | 12.15 | 90.25 ± 2.44 | 49.86 | |
| 60 cm, 230° | 46.98 ± 2.37 | 17.45 | 88.76 ± 1.97 | 50.59 | |
| With Comp. | 30 cm, 90° | 42.52 ± 2 | 6.3 | 165.24 ± 4.09 | 8.2 |
| 30 cm, 180° | 35.43 ± 2.04 | 11.43 | 159.92 ± 3.85 | 11.16 | |
| 40 cm, 90° | 35.75 ± 1.93 | 10.63 | 161.85 ± 3.49 | 10.08 | |
| 50 cm, 90° | 43.23 ± 2.12 | 8.3 | 173.36 ± 3.38 | 3.69 | |
| 50 cm, 180° | 34.23 ± 1.88 | 14.43 | 195.26 ± 4.11 | 8.48 | |
| 60 cm, 190° | 33.28 ± 1.98 | 16.8 | 161.72 ± 3.29 | 10.16 | |
| 60 cm, 230° | 44.15 ± 2.3 | 10.38 | 158.45 ± 2.91 | 11.97 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, K.; Grivet-Talocia, S.; Manfredi, P.; Yan, Y.; Li, H. Detection and Evaluation of Shield Damage Defects in Power Cables Using an Improved Dual-Frequency Time–Frequency Domain Reflectometry. Energies 2025, 18, 5214. https://doi.org/10.3390/en18195214
Zhao K, Grivet-Talocia S, Manfredi P, Yan Y, Li H. Detection and Evaluation of Shield Damage Defects in Power Cables Using an Improved Dual-Frequency Time–Frequency Domain Reflectometry. Energies. 2025; 18(19):5214. https://doi.org/10.3390/en18195214
Chicago/Turabian StyleZhao, Kun, Stefano Grivet-Talocia, Paolo Manfredi, Yuan Yan, and Hongjie Li. 2025. "Detection and Evaluation of Shield Damage Defects in Power Cables Using an Improved Dual-Frequency Time–Frequency Domain Reflectometry" Energies 18, no. 19: 5214. https://doi.org/10.3390/en18195214
APA StyleZhao, K., Grivet-Talocia, S., Manfredi, P., Yan, Y., & Li, H. (2025). Detection and Evaluation of Shield Damage Defects in Power Cables Using an Improved Dual-Frequency Time–Frequency Domain Reflectometry. Energies, 18(19), 5214. https://doi.org/10.3390/en18195214







