An Enhanced Method to Estimate State of Health of Li-Ion Batteries Using Feature Accretion Method (FAM)
Abstract
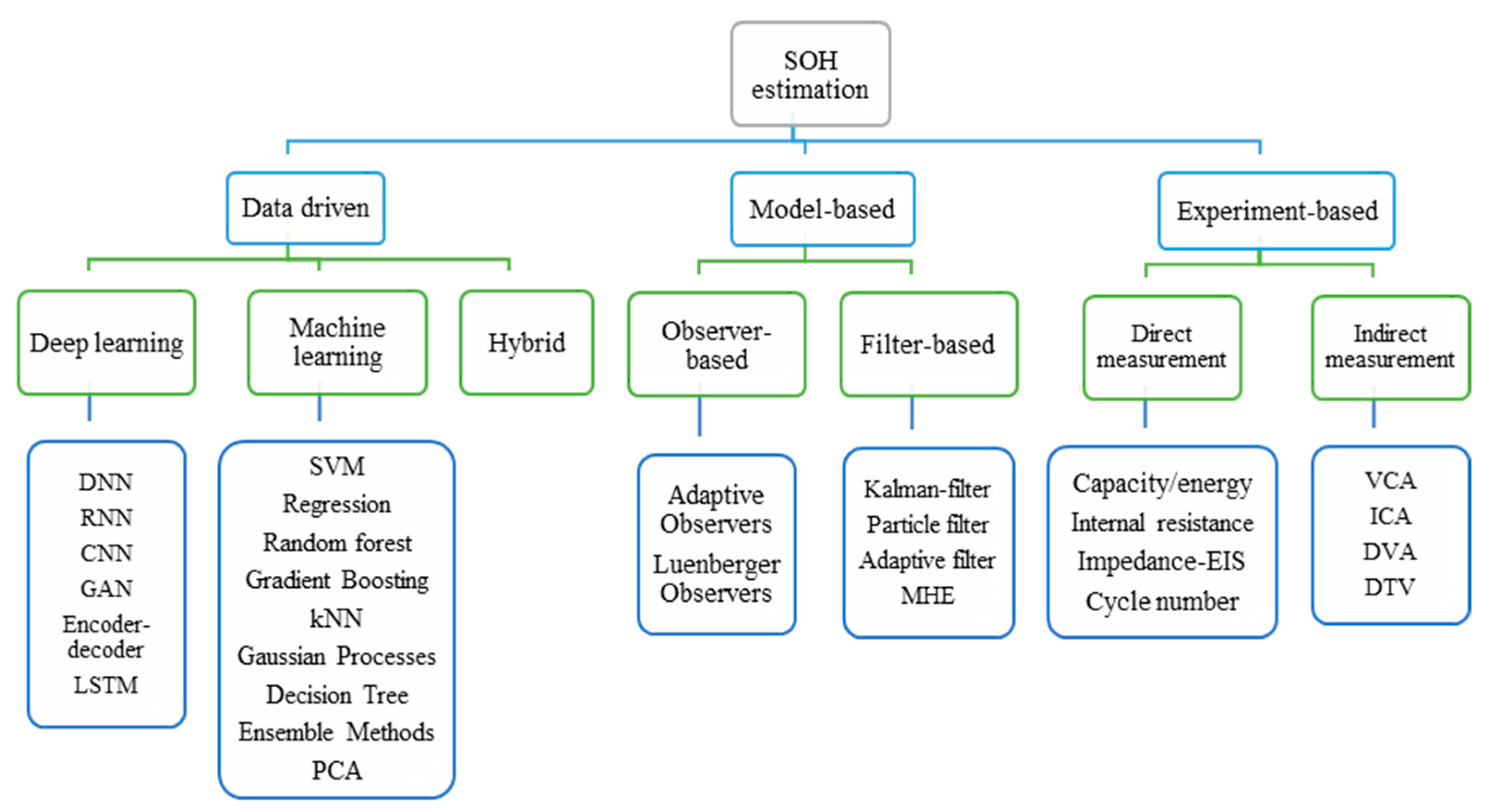
1. Introduction
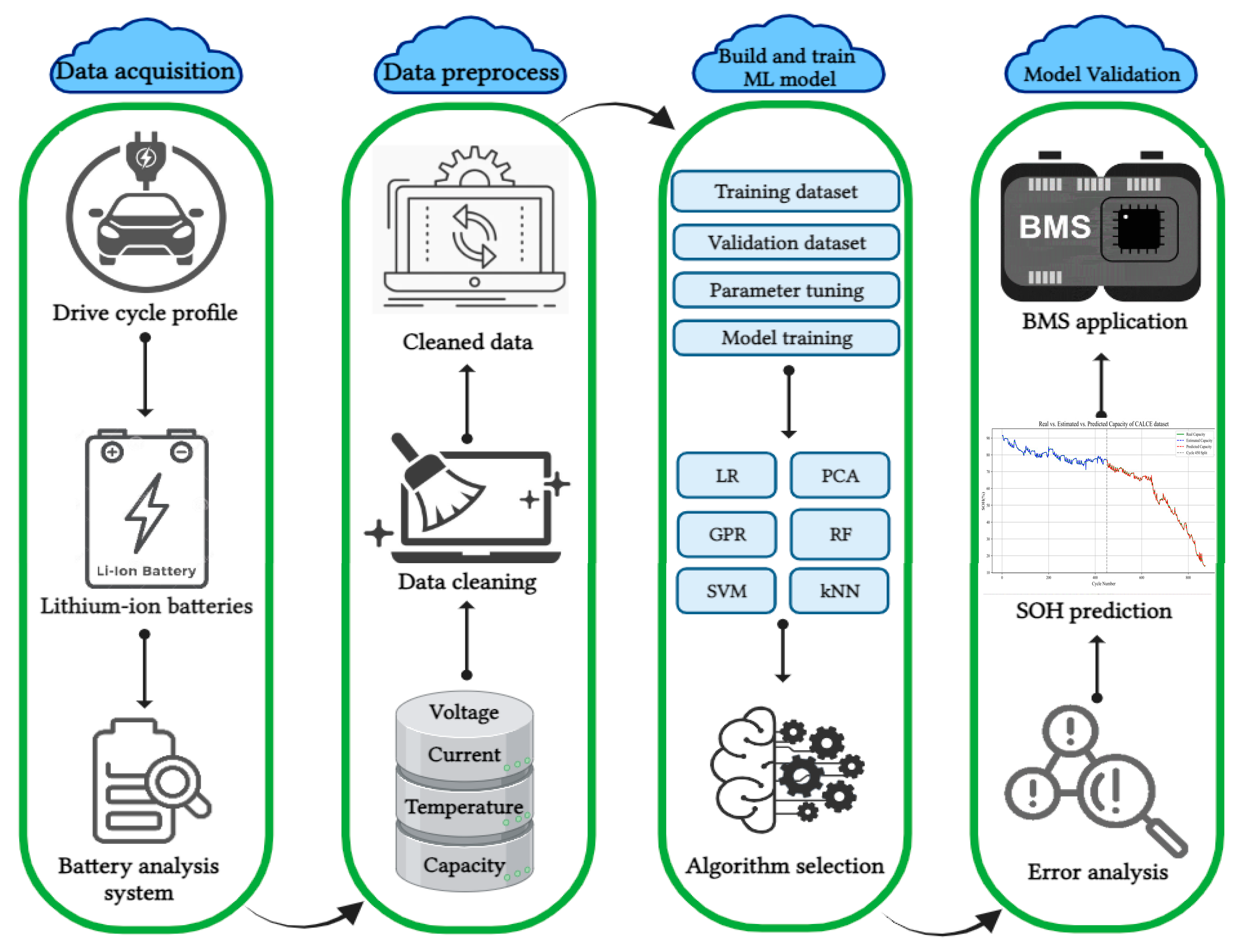
2. Data Preparation and HI Extraction
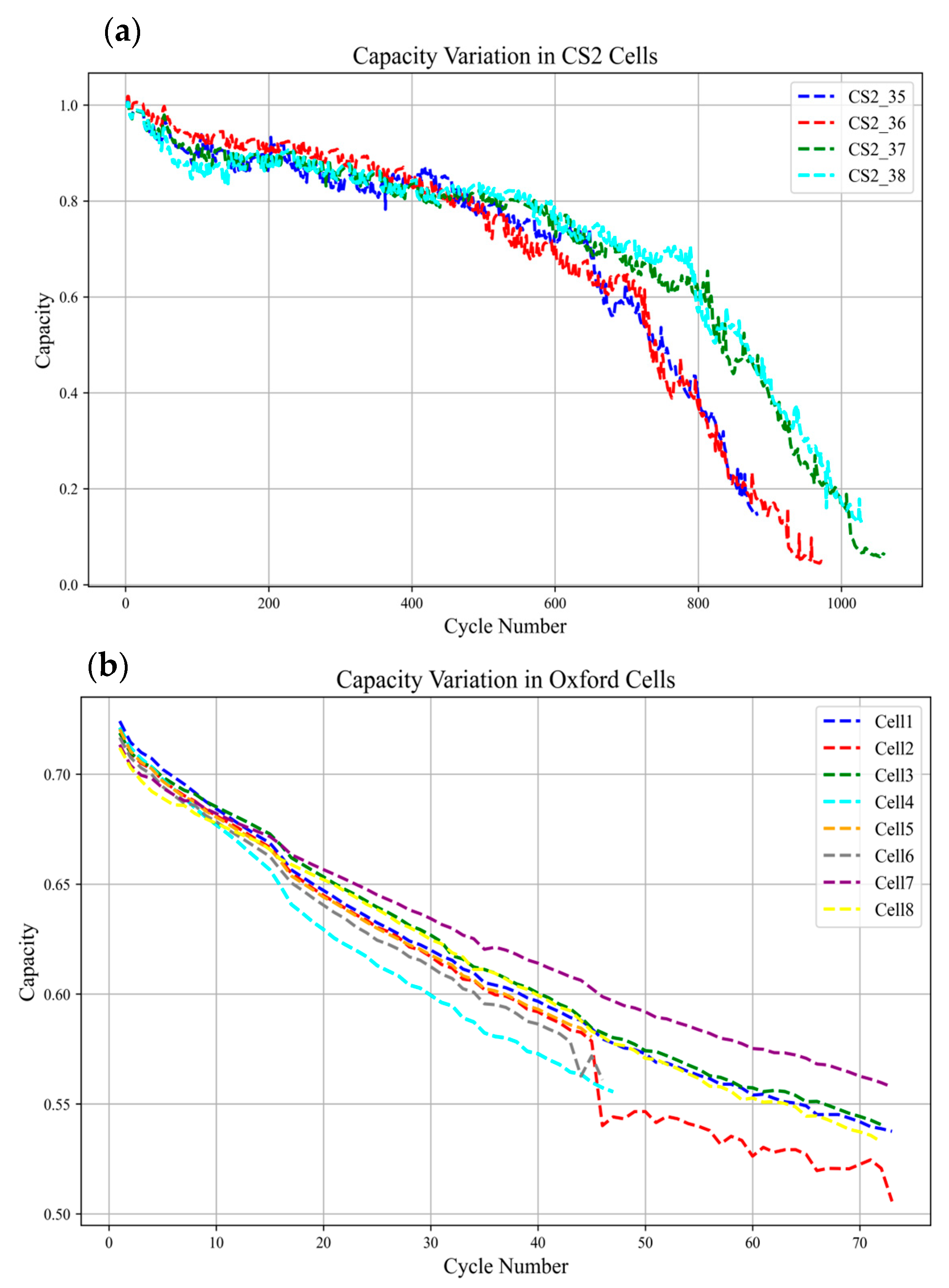
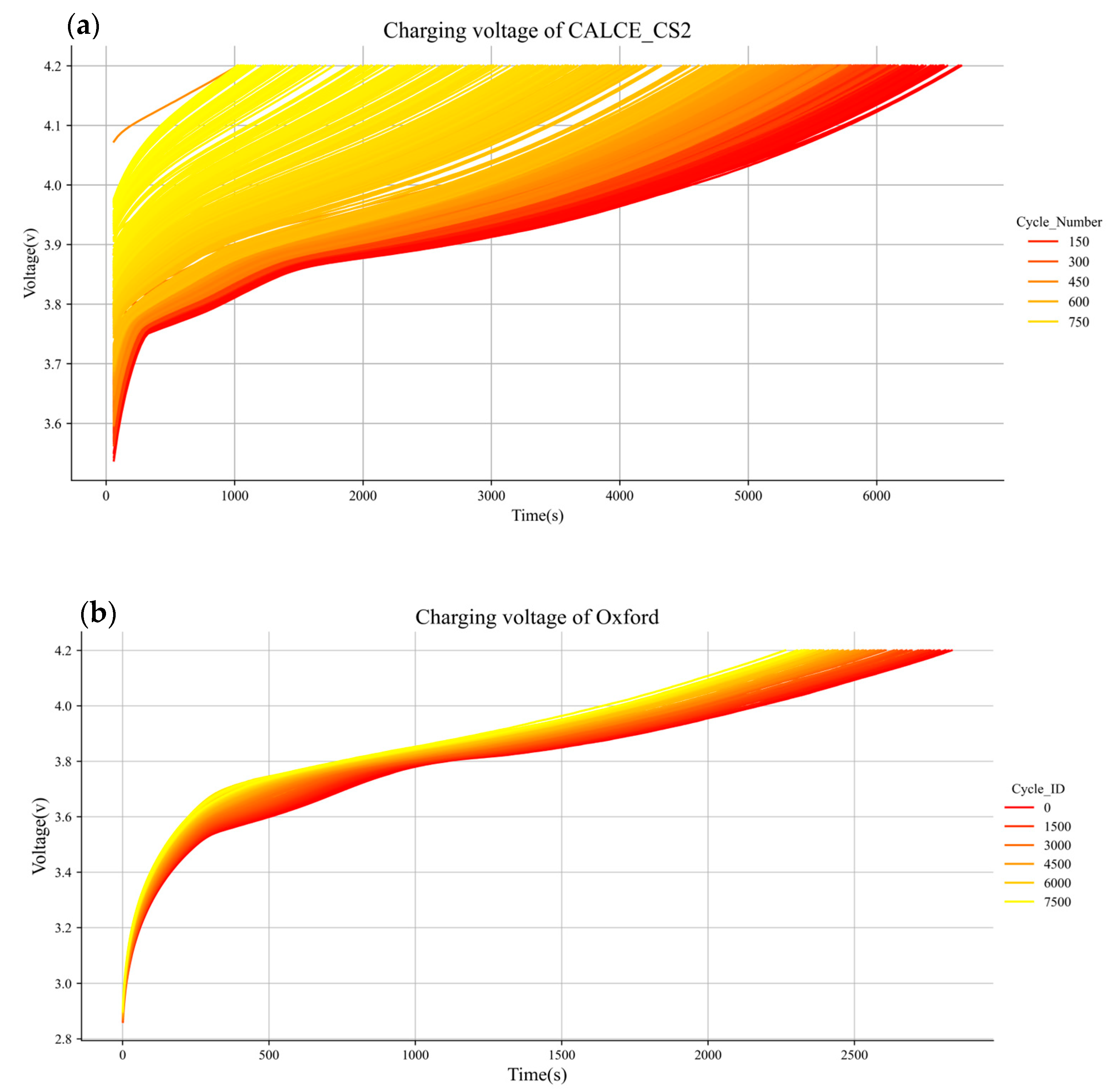
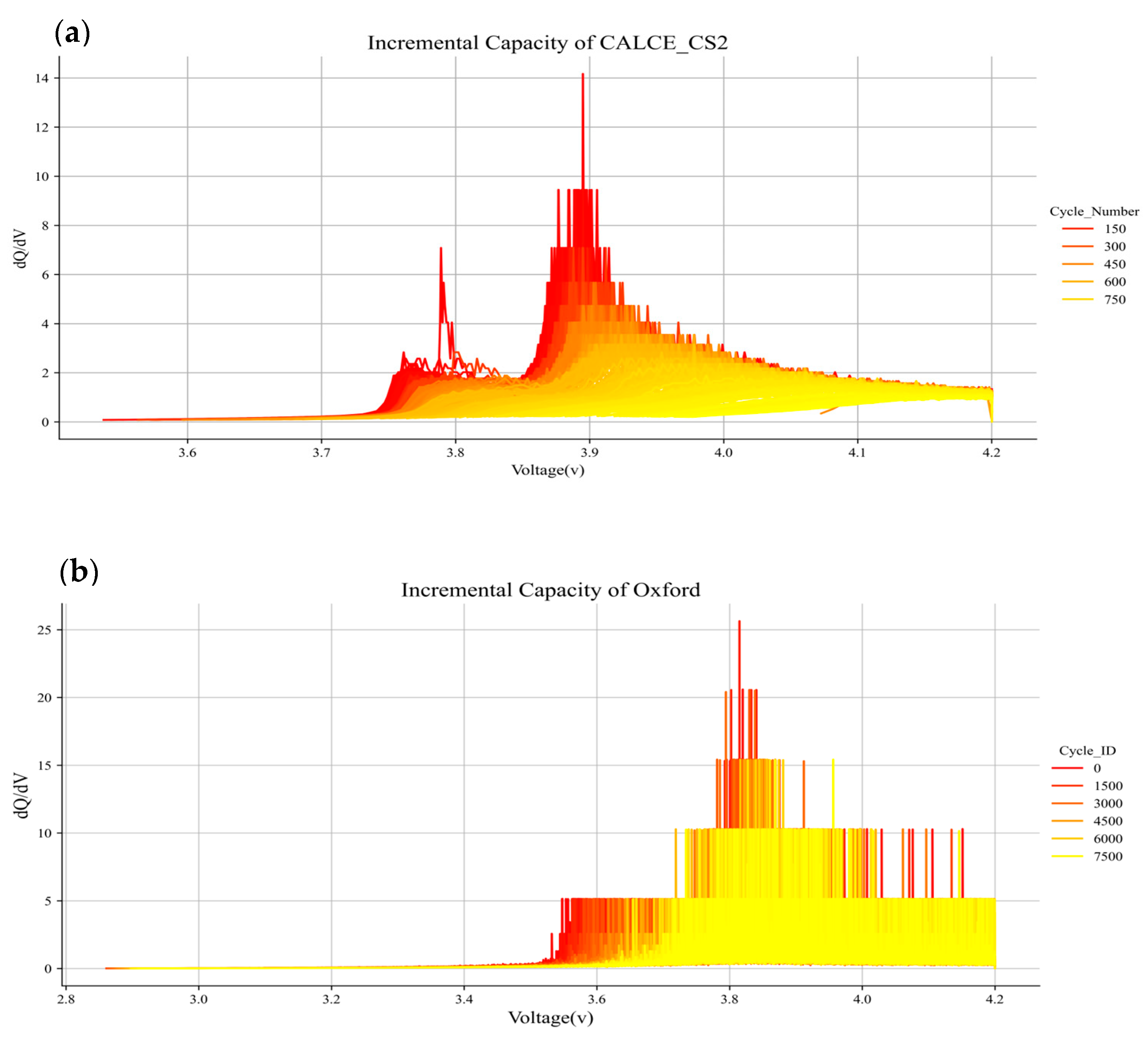
2.1. Battery Data Set
2.2. Voltage Variation
2.3. Incremental Capacity Changes
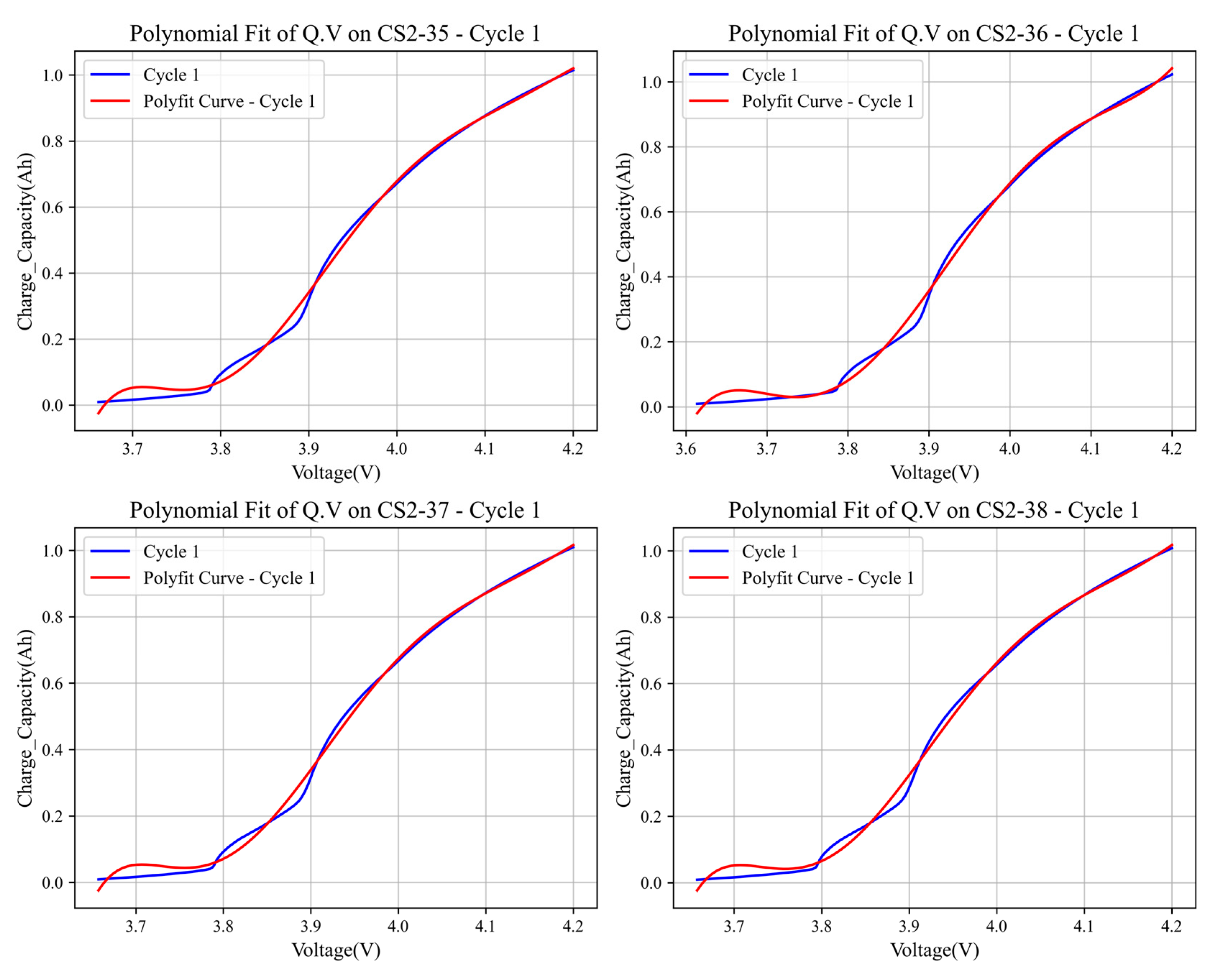
2.4. Coefficients of Polynomial Fit Function in Capacity–Voltage Curve (Q.V)
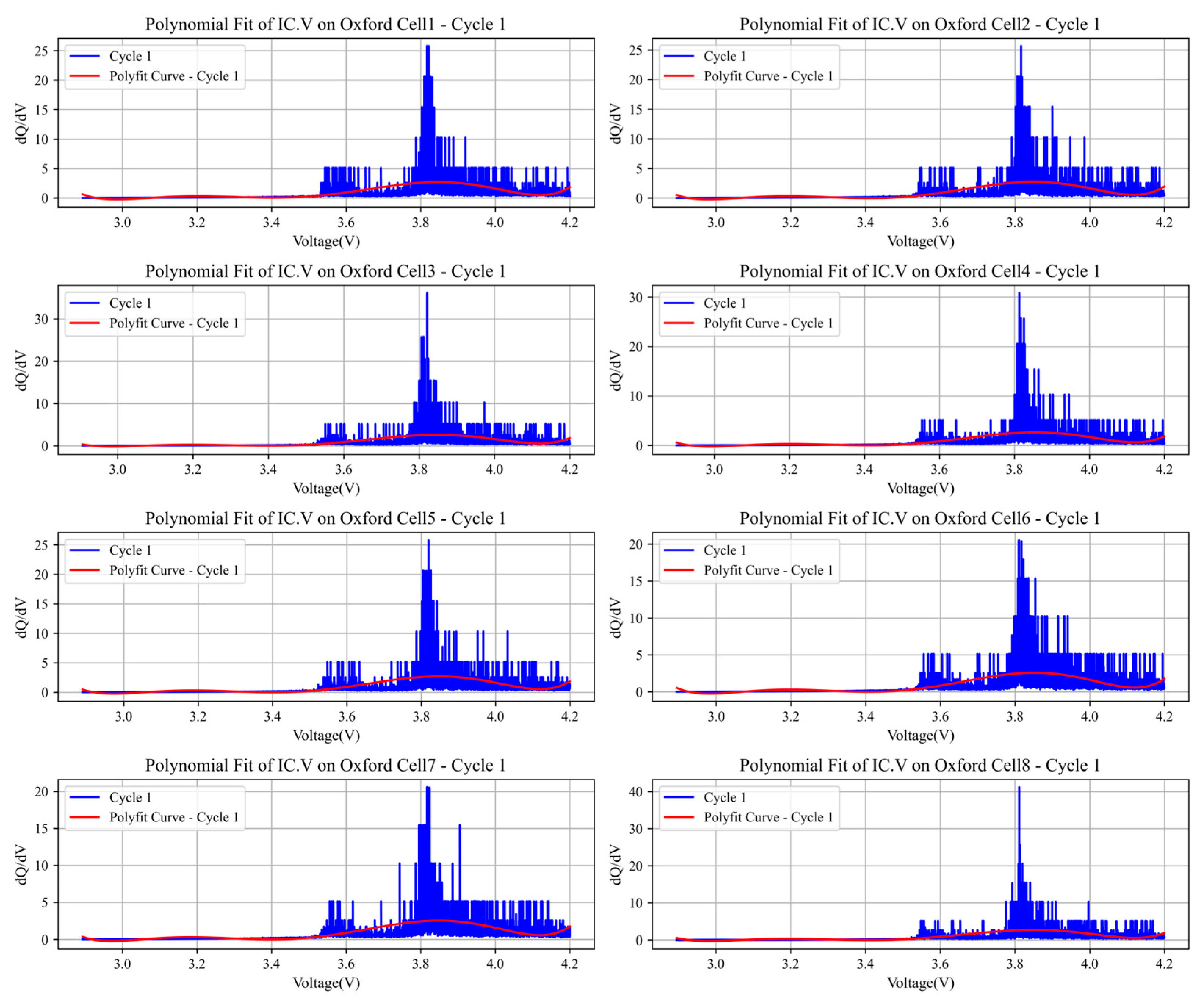
2.5. Coefficients of Polynomial Fit Function in Incremental Capacity–Voltage Curve (IC.V)
2.6. Machine Learning Algorithm
2.6.1. Support Vector Regression (SVR)
2.6.2. Gaussian Process Regression (GPR)
2.6.3. Random Forest Regression (RFR)
2.6.4. Extra Trees Regression (ETR)
2.6.5. LASSO Regression
2.7. Evaluation Criteria
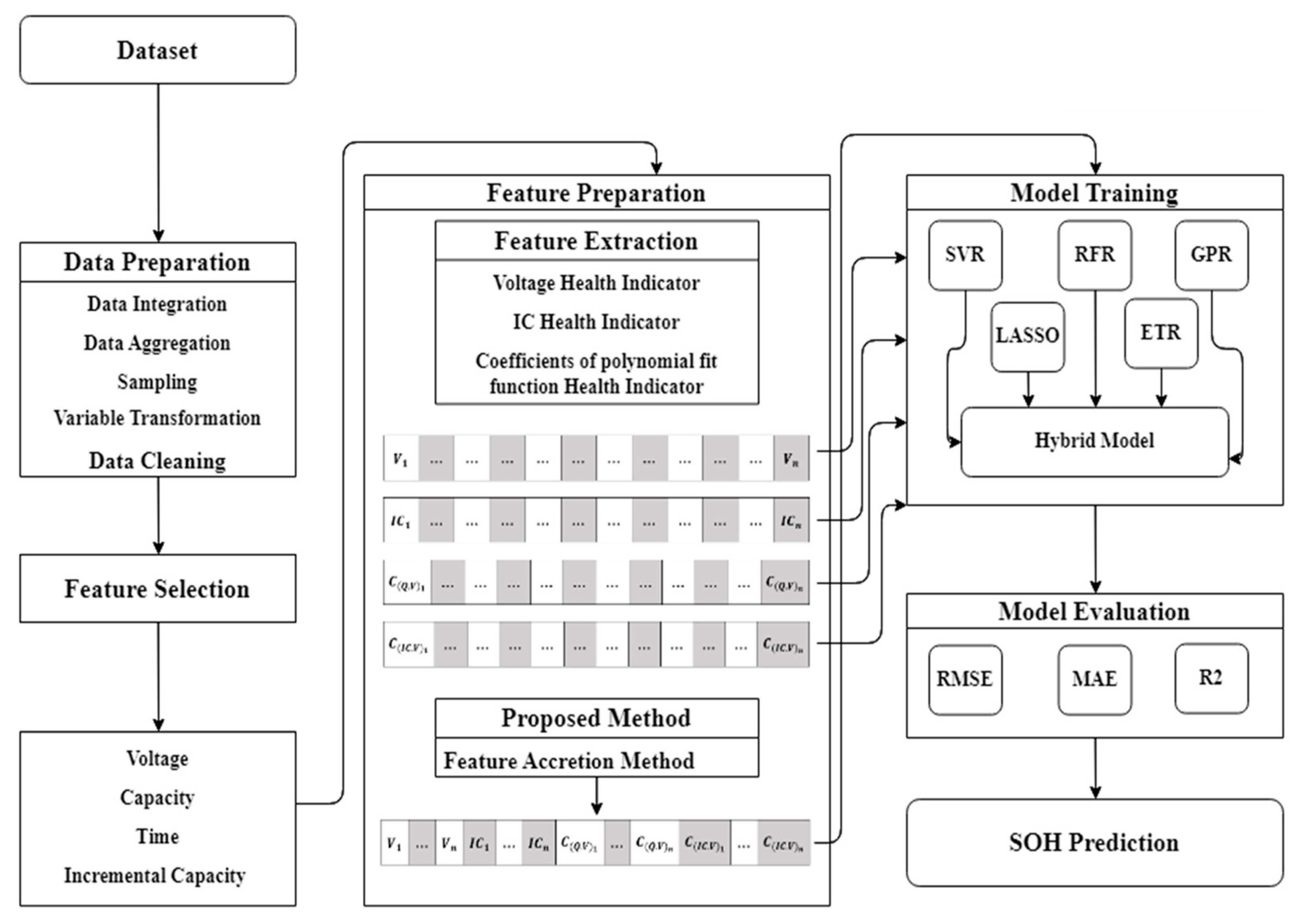
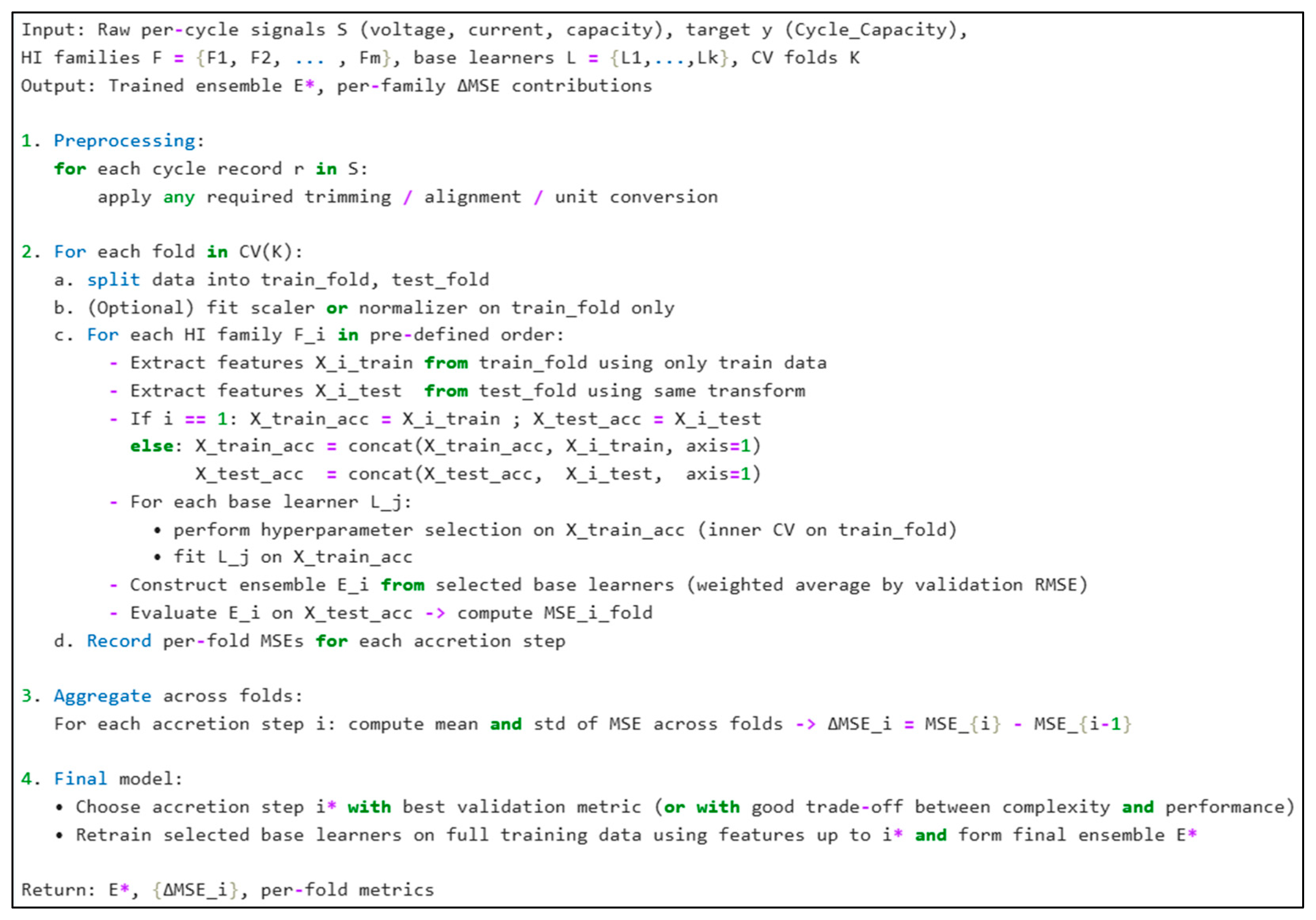
3. Methodologies of the Feature Accretion Method (FAM)
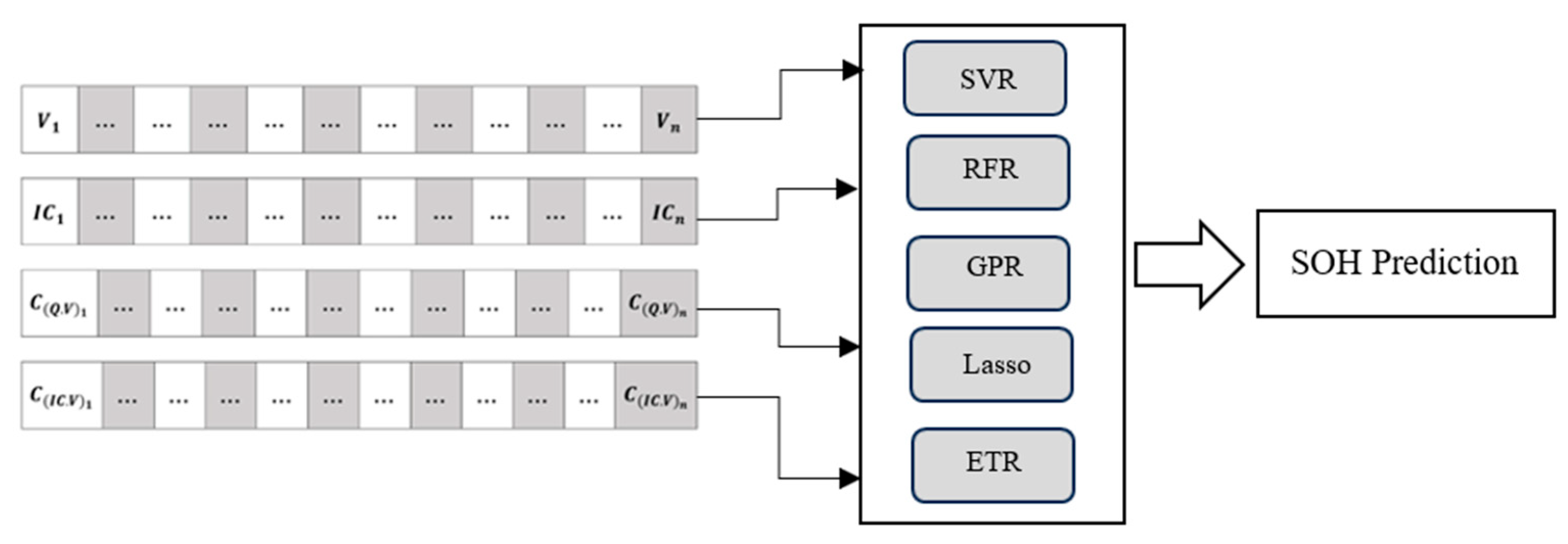
3.1. Individual Health Indicator-Based Battery Capacity Prediction
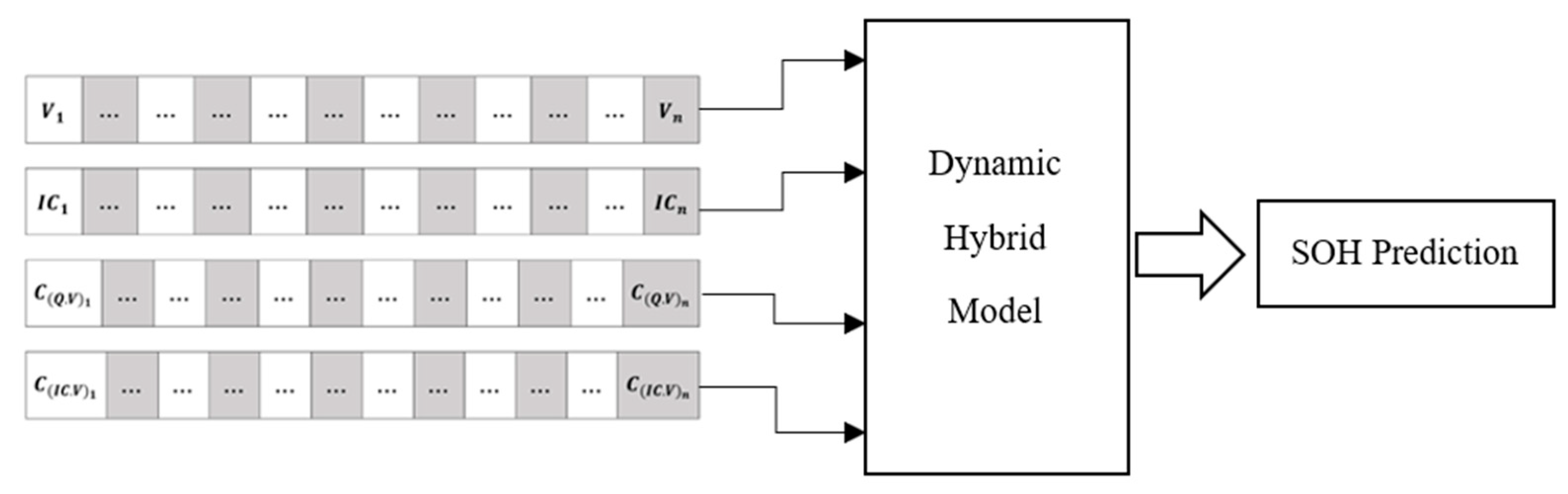
3.2. Dynamic Hybrid Model Health Indicator-Based Battery Capacity Prediction
3.3. Feature Accretion Method-Based Battery Capacity Prediction
4. Results and Discussion
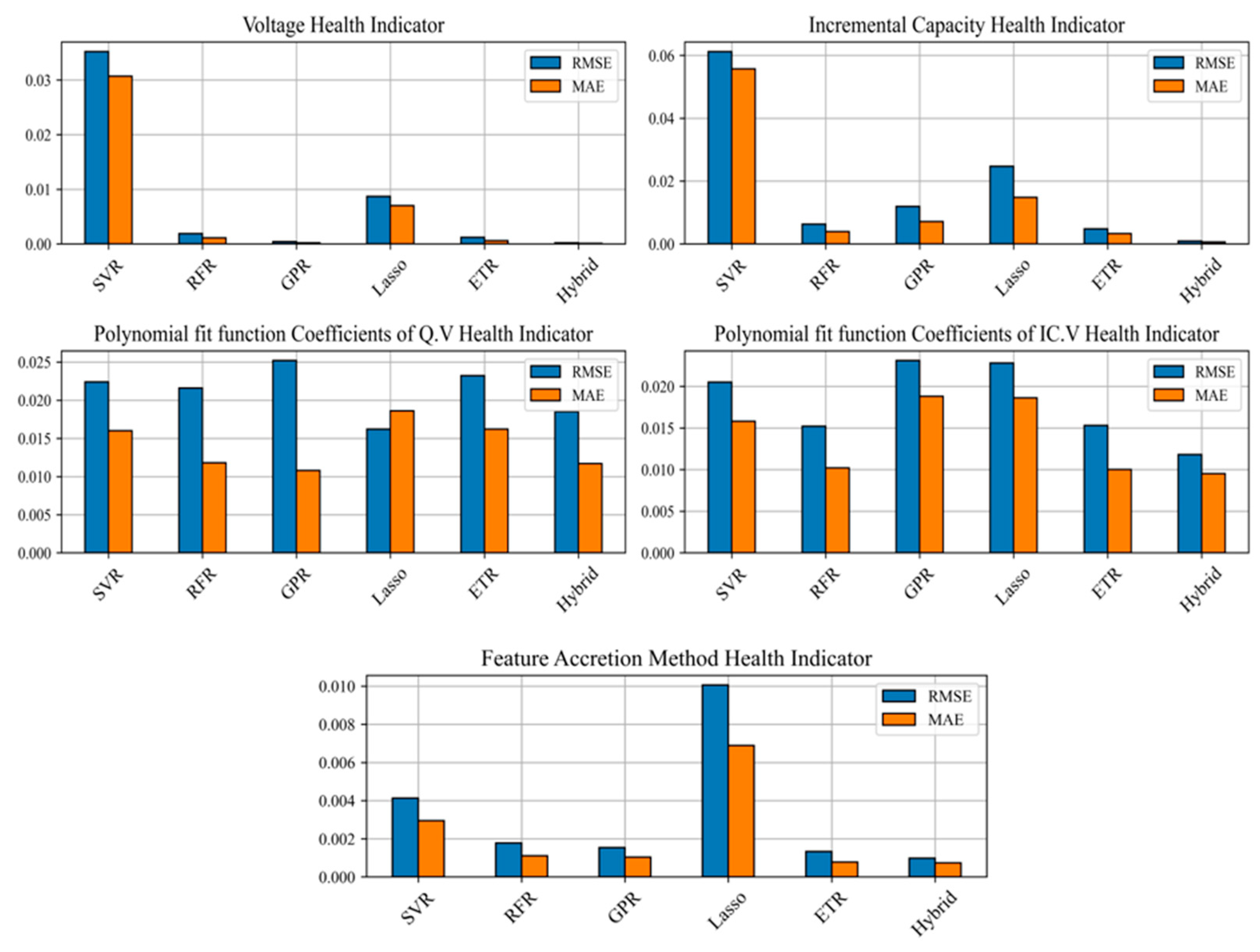
4.1. Comparison of Individual Models with Hybrid Model
4.2. Feature Accretion Method (FAM) of Single and Hybrid Models
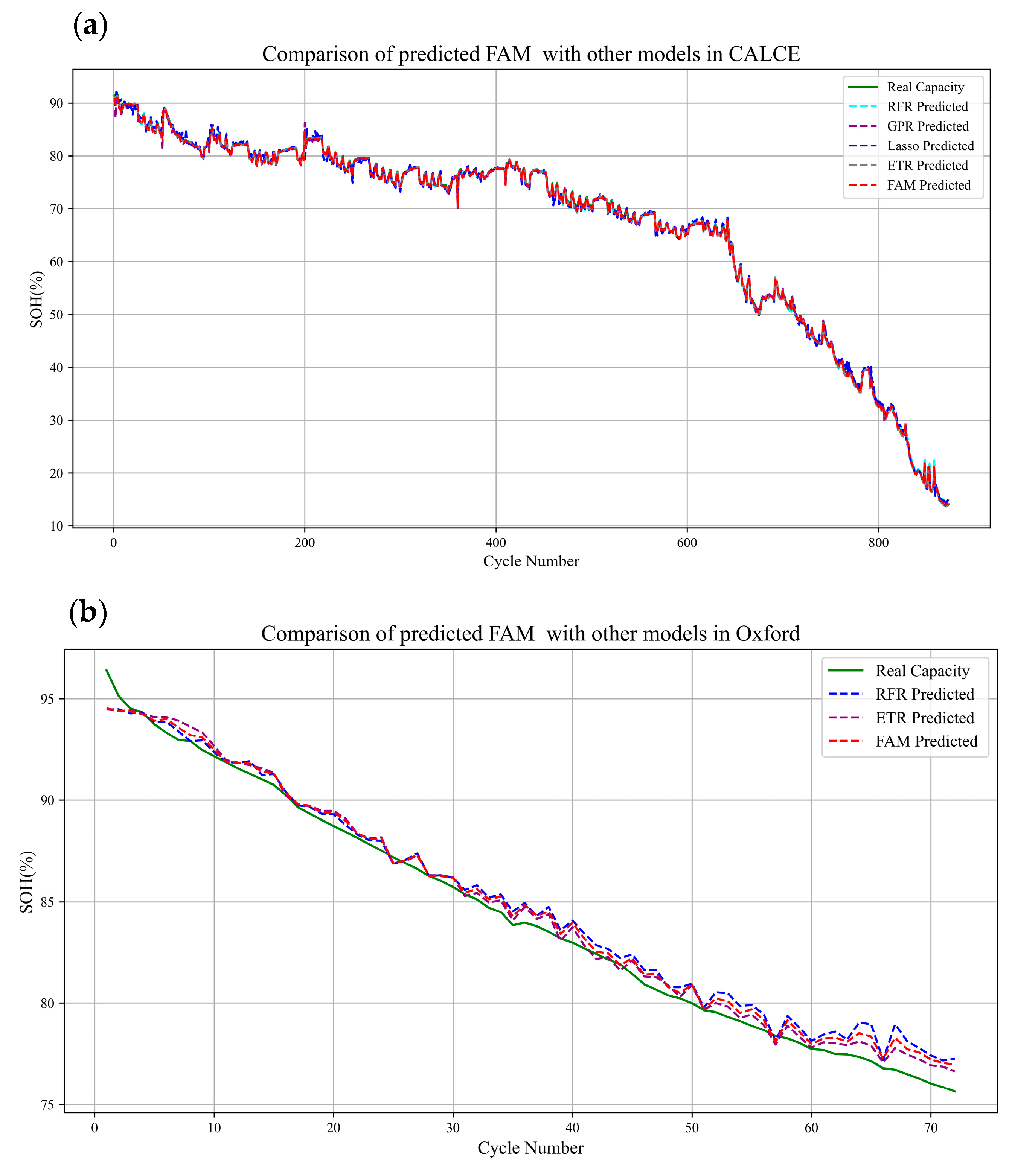
4.3. Comparison with Other Models
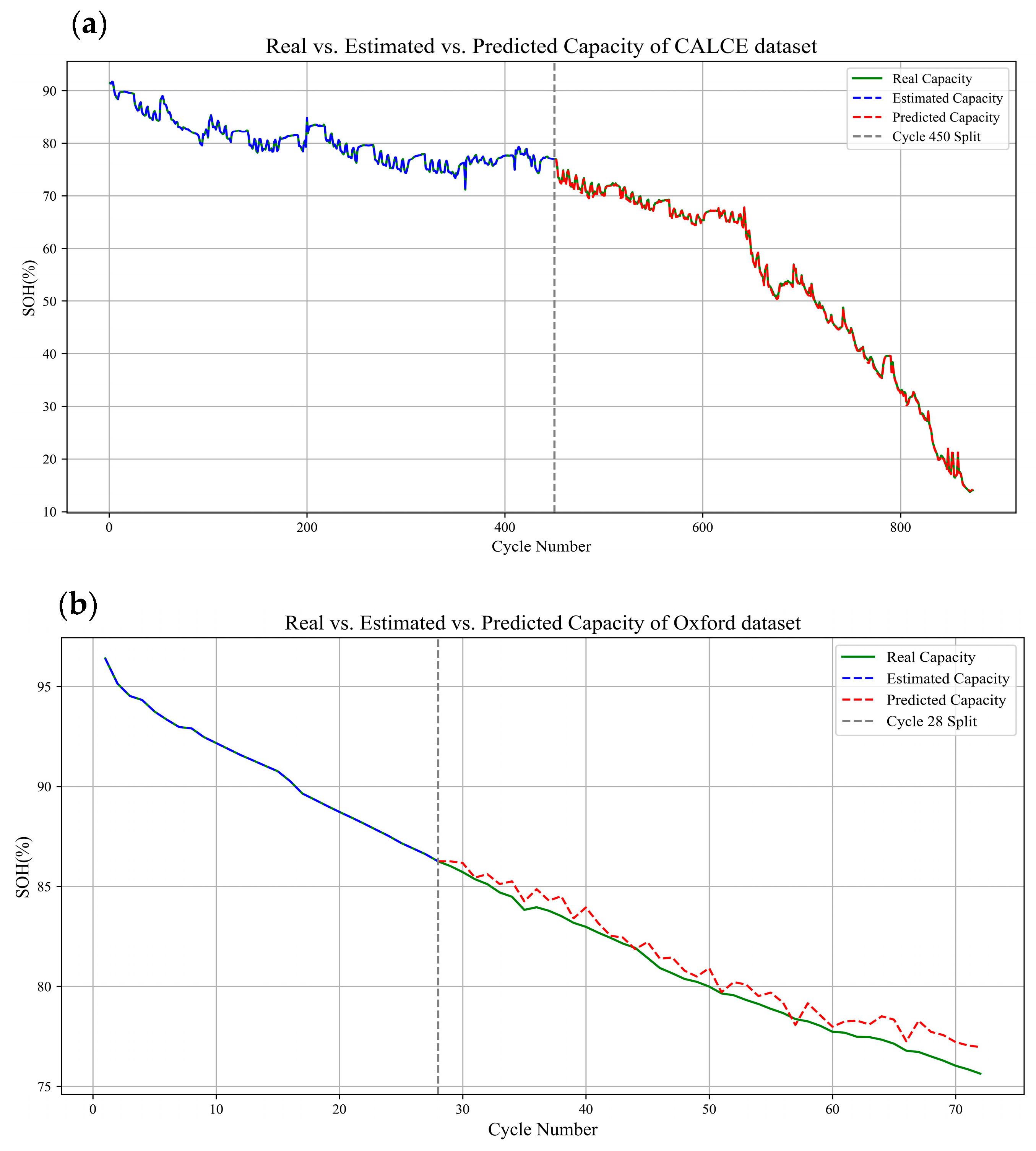
4.4. Analytical Evaluation of FAM on Existing Datasets
4.5. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ETR | Extra Trees Regression |
| FAM | Feature Accretion Model |
| SOH | State of Health |
| GPR | Gaussian Process Regression |
| RFR | Random Forest Regression |
| SVR | Support Vector Regression |
| IC | Incremental Capacity |
| IC/Q | Coefficients of polynomial fit functions on IC |
| Q/V | Coefficients of polynomial fit functions on capacity |
| CALCE | Center for Advanced Life Cycle Engineering |
| BMS | Battery Management System |
References
- Nanaki, E.A.; Koroneos, C.J. Climate Change Mitigation and Deployment of Electric Vehicles in Urban Areas. Renew. Energy 2016, 99, 1153–1160. [Google Scholar] [CrossRef]
- Jeffry, L.; Ong, M.Y.; Nomanbhay, S.; Mofijur, M.; Mubashir, M.; Show, P.L. Greenhouse Gases Utilization: A Review. Fuel 2021, 301, 121017. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M.; Rosado, P. CO2 and Greenhouse Gas Emissions. In Our World in Data; University of Oxford: Oxford, UK, 2020. [Google Scholar]
- Khatua, A.; Kumar, R.R.; De, S.K. Institutional Enablers of Electric Vehicle Market: Evidence from 30 Countries. Transp. Res. Part A Policy Pract. 2023, 170, 103612. [Google Scholar] [CrossRef]
- Costa, E.; Wells, P.; Wang, L.; Costa, G. The Electric Vehicle and Renewable Energy: Changes in Boundary Conditions that Enhance Business Model Innovations. J. Clean. Prod. 2022, 333, 130034. [Google Scholar] [CrossRef]
- Rouholamini, M.; Wang, C.; Nehrir, H.; Hu, X.; Hu, Z.; Aki, H.; Strunz, K. A Review of Modeling, Management, and Applications of Grid-Connected Li-Ion Battery Storage Systems. IEEE Trans. Smart Grid 2022, 13, 4505–4524. [Google Scholar]
- Sun, H.; Yang, D.; Du, J.; Li, P.; Wang, K. Prediction of Li-Ion Battery State of Health Based on Data-Driven Algorithm. Energy Rep. 2022, 8, 442–449. [Google Scholar]
- Han, X.; Garrison, J.; Hug, G. Techno-Economic Analysis of PV-Battery Systems in Switzerland. Renew. Sustain. Energy Rev. 2022, 158, 112028. [Google Scholar]
- See, K.W.; Wang, G.; Gandoman, T.S.; Van Mierlo, J.; Omar, A.; Van Den Bossche, F.; Omar, N. Critical Review and Functional Safety of a Battery Management System for Large-Scale Lithium-Ion Battery Pack Technologies. Int. J. Coal Sci. Technol. 2022, 9, 36. [Google Scholar] [CrossRef]
- Tran, M.K.; Panchal, S.; Khang, T.D.; Panchal, K.; Fraser, R.; Fowler, M. Concept Review of a Cloud-Based Smart Battery Management System for Lithium-Ion Batteries: Feasibility, Logistics, and Functionality. Batteries 2022, 8, 19. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar]
- Yang, S.; Liu, X.; Li, S.; Zhang, C. Advanced Battery Management System for Electric Vehicles; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Lin, C.; Xu, J.; Mei, X. Improving State-of-Health Estimation for Lithium-Ion Batteries via Unlabeled Charging Data. Energy Storage Mater. 2023, 54, 85–97. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Y.; Yang, F.; Peng, W. State of Health Estimation of Lithium-Ion Battery with Automatic Feature Extraction and Self-Attention Learning Mechanism. J. Power Sources 2023, 556, 232466. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, N.; Zhang, Y.; Qi, L.; Li, R. Battery SOH Prediction Based on Multi-Dimensional Health Indicators. Batteries 2023, 9, 80. [Google Scholar] [CrossRef]
- Gong, D.; Gao, Y.; Kou, Y.; Wang, Y. State of Health Estimation for Lithium-Ion Battery Based on Energy Features. Energy 2022, 257, 124812. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Z.; Zhai, Z.; Shang, Z.; Yan, R.; Chen, X. Explainability-Driven Model Improvement for SOH Estimation of Lithium-Ion Battery. Reliab. Eng. Syst. Saf. 2023, 232, 109046. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Hoque, M.M.; Ker, P.J.; Saad, M.H.M.; Ayob, A. A Review of State of Health and Remaining Useful Life Estimation Methods for Lithium-Ion Battery in Electric Vehicles: Challenges and Recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Vennam, G.; Sahoo, A.; Ahmed, S. A Survey on Lithium-Ion Battery Internal and External Degradation Modeling and State of Health Estimation. J. Energy Storage 2022, 52, 104720. [Google Scholar] [CrossRef]
- Singh, S.P.; Singh, P.P.; Singh, S.N.; Tiwari, P. State of Charge and Health Estimation of Batteries for Electric Vehicles Applications: Key Issues and Challenges. Glob. Energy Interconnect. 2021, 4, 145–157. [Google Scholar] [CrossRef]
- Kim, T.; Adhikaree, A.; Pandey, R.; Kang, D.-W.; Kim, M.; Oh, C.-Y.; Baek, J.-W. An On-Board Model-Based Condition Monitoring for Lithium-Ion Batteries. IEEE Trans. Ind. Appl. 2019, 55, 1835–1843. [Google Scholar] [CrossRef]
- Schmitt, J.; Rehm, M.; Karger, A.; Jossen, A. Capacity and Degradation Mode Estimation for Lithium-Ion Batteries Based on Partial Charging Curves at Different Current Rates. J. Energy Storage 2023, 59, 106517. [Google Scholar] [CrossRef]
- Ang, E.Y.M.; Paw, Y.C. Linear Model for Online State of Health Estimation of Lithium-Ion Batteries Using Segmented Discharge Profiles. IEEE Trans. Transp. Electrif. 2022, 9, 2464–2471. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, F.; Yang, F. State of Health Prediction of Lithium-Ion Batteries Based on Autoregression with Exogenous Variables Model. Energy 2023, 262, 125497. [Google Scholar] [CrossRef]
- Hoque, M.A.; Nurmi, P.; Kumar, A.; Varjonen, S.; Song, J.; Pecht, M.G.; Tarkoma, S. Data Driven Analysis of Lithium-Ion Battery Internal Resistance Towards Reliable State of Health Prediction. J. Power Sources 2021, 513, 230519. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A Comparative Study of Different Features Extracted from Electrochemical Impedance Spectroscopy in State of Health Estimation for Lithium-Ion Batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; Årén, F.; Gallo-Bueno, A.; Jørgensen, P.B.; Bhowmik, A.; Demortière, A.; Ayerbe, E.; Alcaide, F.; et al. Artificial Intelligence Applied to Battery Research: Hype or Reality? Chem. Rev. 2022, 122, 10899–10969. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Xuebin, L.; Daiwei, Y.; Jun, Z.; Wenjin, Z. Lithium-Ion Battery State of Health Estimation Using Meta-Heuristic Optimization and Gaussian Process Regression. J. Energy Storage 2023, 58, 106319. [Google Scholar] [CrossRef]
- Shu, X.; Chen, Z.; Shen, J.; Shen, S.; Guo, F.; Zhang, Y.; Liu, Y. Ensemble Learning and Voltage Reconstruction Based State of Health Estimation for Lithium-Ion Batteries with Twenty Random Samplings. IEEE Trans. Power Electron. 2023, 38, 5538–5548. [Google Scholar] [CrossRef]
- Meng, J.; Cai, L.; Stroe, D.-I.; Ma, J.; Luo, G.; Teodorescu, R. An Optimized Ensemble Learning Framework for Lithium-Ion Battery State of Health Estimation in Energy Storage System. Energy 2020, 206, 118140. [Google Scholar] [CrossRef]
- Khaleghi, S.; Hosen, M.S.; Van Mierlo, J.; Berecibar, M. Towards Machine-Learning Driven Prognostics and Health Management of Li-Ion Batteries. A Comprehensive Review. Renew. Sustain. Energy Rev. 2024, 192, 114224. [Google Scholar]
- von Bülow, F.; Meisen, T. A Review on Methods for State of Health Forecasting of Lithium-Ion Batteries Applicable in Real-World Operational Conditions. J. Energy Storage 2023, 57, 105978. [Google Scholar] [CrossRef]
- Park, S.; Lee, P.; Kim, D.; Hong, S.; Na, W.; Kim, J. A SOH Estimation Method Based on ICA Peaks on Temperature-Robust and Aging Mechanism Analysis Under High Temperature. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 2646–2649. [Google Scholar]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-Health Estimation for Li-Ion Batteries by Combing the Incremental Capacity Analysis Method with Grey Relational Analysis. J. Power Sources 2019, 410, 106–114. [Google Scholar] [CrossRef]
- Lin, C.; Xu, J.; Shi, M.; Mei, X. Constant Current Charging Time Based Fast State-of-Health Estimation for Lithium-Ion Batteries. Energy 2022, 247, 123556. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.; Chen, L.; Chen, Y.; Xu, B.; Hong, S.; Zhang, C.; Chen, N. State of Health Estimation of Lithium-Ion Battery Aging Process Based on Time-Frequency Fusion Characteristics. J. Power Sources 2024, 596, 234002. [Google Scholar] [CrossRef]
- Ji, S.; Zhu, J.; Lyu, Z.; Yuan, Y.; Yang, H.; Chen, Z.; Yang, X.; Li, P.; Shen, Y.; Hu, Y. Deep Learning Enhanced Lithium-Ion Battery Nonlinear Fading Prognosis. J. Energy Chem. 2023, 78, 565–573. [Google Scholar] [CrossRef]
- Wang, C.; Su, Y.; Ye, J.; Xu, P.; Xu, E.; Ouyang, T. Enhanced State-of-Charge and State-of-Health Estimation of Lithium-Ion Battery Incorporating Machine Learning and Swarm Intelligence Algorithm. J. Energy Storage 2024, 83, 110755. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, C.; Liu, S.; Jin, L.; Xu, Z. Multi-Objective Optimization Estimation of State of Health for Lithium-Ion Battery Based on Constant Current Charging Profile. J. Energy Storage 2024, 83, 110785. [Google Scholar] [CrossRef]
- Li, X.; Yu, D.; Vilsen, S.B.; Stroe, D.-I. Accuracy Comparison and Improvement for State of Health Estimation of Lithium-Ion Battery Based on Random Partial Recharges and Feature Engineering. J. Energy Chem. 2024, 92, 591–604. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.; Liu, C.; Feng, Z.; Xu, Y. Reliability Enhancement of State of Health Assessment Model of Lithium-Ion Battery Considering the Uncertainty with Quantile Distribution of Deep Features. Reliab. Eng. Syst. Saf. 2024, 245, 110002. [Google Scholar] [CrossRef]
- Bai, J.; Huang, J.; Luo, K.; Yang, F.; Xian, Y. A Feature Reuse Based Multi-Model Fusion Method for State of Health Estimation of Lithium-Ion Batteries. J. Energy Storage 2023, 70, 107965. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, R.; Zheng, Y.; Zhang, L.; Guang, H.; Hong, S. Online State of Health Estimation for Lithium-Ion Batteries Based on Gene Expression Programming. Energy 2024, 294, 130790. [Google Scholar] [CrossRef]
- Ye, J.; Xie, Q.; Lin, M.; Wu, J. A Method for Estimating the State of Health of Lithium-Ion Batteries Based on Physics-Informed Neural Network. Energy 2024, 294, 130828. [Google Scholar] [CrossRef]
- Cai, L.; Stroe, D.-I.; Li, J.; Jiang, Y.; Li, X.; Yin, X.; Wu, J. Automatically Constructing a Health Indicator for Lithium-Ion Battery State-of-Health Estimation via Adversarial and Compound Stacked Autoencoder. J. Energy Storage 2024, 84, 110711. [Google Scholar] [CrossRef]
- Wang, L.; Jiang, S.; Mao, Y.; Li, Z.; Zhang, Y.; Li, M. Lithium-Ion Battery State of Health Estimation Method Based on Variational Quantum Algorithm Optimized Stacking Strategy. Energy Rep. 2024, 11, 2877–2891. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, Z.; Wu, T. A State-of-Health Estimation Method for Lithium Batteries under Multi-Dimensional Features. World Electr. Veh. J. 2024, 15, 68. [Google Scholar] [CrossRef]
- Ma, C.; Zhai, X.; Wang, Z.; Wang, H.; Yang, X. State of Health Prediction for Lithium-Ion Batteries Using Multiple-View Feature Fusion and Support Vector Regression Ensemble. Int. J. Mach. Learn. Cybern. 2019, 10, 2269–2282. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W. State-of-Health Estimation Based on Differential Temperature for Lithium Ion Batteries. IEEE Trans. Power Electron. 2020, 35, 10363–10373. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, X.; Liu, Z. State of Health Estimation of Power Batteries Based on Multi-Feature Fusion Models Using Stacking Algorithm. Energy 2022, 259, 124851. [Google Scholar] [CrossRef]
- Lin, M.; Wu, D.; Meng, J.; Wu, J.; Wu, H. A Multi-Feature-Based Multi-Model Fusion Method for State of Health Estimation of Lithium-Ion Batteries. J. Power Sources 2022, 518, 230774. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y.; Yong, J.; Yang, C.; Yan, L.; Zheng, Y. State of Health Estimation of Lithium-Ion Batteries Using Fusion Health Indicator by PSO-ELM Model. Batteries 2024, 10, 380. [Google Scholar] [CrossRef]
- Cai, X.; Liu, T. State of Health Prediction for Lithium-Ion Batteries Using Transformer–LSTM Fusion Model. Appl. Sci. 2025, 15, 3747. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Zhang, X.; Zhou, Z. Lithium-Ion Battery SOH Estimation Method Based on Multi-Feature and CNN-BiLSTM-MHA. World Electr. Veh. J. 2024, 15, 280. [Google Scholar] [CrossRef]
- Yang, X.; Ma, B.; Xie, H.; Wang, W.; Zou, B.; Liang, F.; Hua, X.; Liu, X.; Chen, S. Lithium-Ion Battery State of Health Estimation with Multi-Feature Collaborative Analysis and Deep Learning Method. Batteries 2023, 9, 120. [Google Scholar] [CrossRef]
- Center for Advanced Life Cycle Engineering (CALCE), University of Maryland. Battery Data. Available online: https://calce.umd.edu/battery-data (accessed on 17 August 2025).
- Howey, D.; Birkl, C. Long term battery ageing tests of 8 Kokam (SLPB533459H4) 740 mAh lithium-ion pouch cells. In Oxford Battery Degradation Dataset 1; University of Oxford: Oxford, UK, 2017. [Google Scholar]
- Wang, Z.; Feng, G.; Zhen, D.; Gu, F.; Ball, A.D. State of Health Estimation of Lithium-Ion Batteries from Charging Data: A Machine Learning Method. In Proceedings of the IncoME-VI and TEPEN 2021; Mechanisms and Machine Science, Tianjin, China, 20–23 October 2021; Springer: Cham, Switzerland, 2023; Volume 117, pp. 707–719. [Google Scholar]
- Goh, H.H.; Lan, Z.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C. Estimation of the State of Health (SOH) of Batteries Using Discrete Curvature Feature Extraction. J. Energy Storage 2022, 50, 104646. [Google Scholar] [CrossRef]
- Kostenko, G.; Zaporozhets, A. Transition from electric vehicles to energy storage: Review on targeted lithium-ion battery diagnostics. Energies 2024, 17, 5132. [Google Scholar] [CrossRef]

| Method | Dataset | HIs | Best Performance | Number of HIs | Ref. |
|---|---|---|---|---|---|
| KNN, SVR, | NASA; CALCE; XJTU-EVC | ΔVstd, ΔVcharge-time; ΔVskew | RMSE = 0.13%; MAE = 0.18% | 3 | [13] |
| RFR | Oxford, CALCE | CCCT | RMSE = 0.52%; MAE = 3.30% | 1 | [35] |
| GPR, SSGPR, BRR, LSSVR | Zenodo | Time domain aging features | RMSE = 0.58%, MAE = 0.70% | 13 | [36] |
| LR, RT, SVM | NASA, CALCE, MIT | Mechanistic feature empowerment of IC/QV/DV/ICD | RMSE = 0.10% | 4 | [37] |
| CGM, SOA, GWO, IFA, PSO | NASA, Experimental dataset | I, V, T | RMSE = 0.92%, MAE = 0.75% | 3 | [38] |
| MOWOA-ELM, WOA-ELM, ALO-SVR | Oxford, CALCE | Polynomial fitting of constant current charging curves | RMSE = 0.58%, MAE = 0.44% | 4 | [39] |
| MLR, SVR, GPR | Experimental dataset | Extracted statistic features from partial recharging profiles | RMSE = 0.29% | 15 | [40] |
| LSTM, DenseNet, CNN, ResNet | NASA | CV, CC | RMSE = 8.85; MAE = 7.92% | 2 | [41] |
| KNNR, ERTR, LoR, RFR | Oxford, CALCE | PIVT, TCCD, SampEn, TSVC | RMSE = 0.16%, MAE = 0.14% | 4 | [42] |
| EN, LR, SVR, GPR | Oxford, NASA, CALCE, MIT | Energy-based features in CC, CV and EDVI | RMSE = 0.06%, MAE = 0.05% | 3 | [16] |
| GEP, SVR, LSTM | MIT | ICA, DTV | RMSE = 0.70%, MAE = 0.63% | 2 | [43] |
| PIFNN, FNN, CNN, RNN | Oxford | IC and DT based features | RMSE ≥ 1%, MAE ≥ 0.5% | 2 | [44] |
| CNN, RNN, SVR, EVO-GPR, Encoder-Decoder | NASA, MIT, Experimental data | Reconstructed V | RMSE = 0.63%, MAE = 0.51% | 1 | [45] |
| SVR, RF, XGBoost, Ridge, VQA-optimized stacking | NASA | Capacity declined based HIs | RMSE = 0.71%, MAE = 0.77% | 8 | [46] |
| POA-DELM | NASA | I, T, dQ/dV | RMSE = 2.95%, MAE = 2.08% | 3 | [47] |
| AdaBoost and Stacking algorithms | NASA | Discharge-based features extracted based on SWBFE | RMSE = 0.29%, MAE = 0.31% | 12 | [48] |
| SVR | Oxford, NASA | DT and ICA based extracted HIs | RMSE = 0.23%, MAE = 0.90% | 21 | [49] |
| SVR, LSTM, Sta-Model | NASA | Extracted HIs from CC-CV charging data | RMSE = 0.47%, MAE = 0.57% | 9 | [50] |
| MLR, SVR, GPR | Oxford | V, T, and IC based HIs | RMSE = 0.32%, MAE = 0.42% | 7 | [51] |
| PSO-ELM | NASA | voltage interval time, avg voltage rise, CCCT, current diff, IC | RMSE = 0.43%, MAE = 0.31% | 7 | [52] |
| Transformer-LSTM | MIT | time to cut-off V, CCCT, energy in CC discharge, EDVI | RMSE = 0.13%, MAE = 0.10% | 10 | [53] |
| CNN-BiLSTM-MHA | Experimental dataset | IE, peak value, avg value, std, avg charging T | RMSE = 0.21%, MAE = 0.17% | 5 | [54] |
| LSTM | NASA, Oxford | Multi-feature collaboration from DTV, SVD, ICA, TVC | RMSE = 0.32%, MAE = 0.28% | 6 | [55] |
| Dataset | Oxford | CALCE CS2 |
|---|---|---|
| Number of cells | 8 | 4 |
| From factor | Pouch | Prismatic |
| Cathode | LiCo2/LiNiMnCoO2 | LiCoO2 |
| Capacity rating | 740 mAh | 1100 mAh |
| Voltage ranges | 2.7 V–4.2 V | 2.7 V–4.2 V |
| Depth of discharge | 1% | 6% |
| Charge | CC (2C) | CC-CV (1C) |
| Discharge | Artemis urban driving cycle | CC (1C) |
| Temperature |
| HI | Model | RMSE | MAE | R2 |
|---|---|---|---|---|
| V | SVR | 0.0352 | 0.0307 | 0.9691 |
| RFR | 0.0018 | 0.0011 | 0.9999 | |
| GPR | 0.0004 | 0.0002 | 1 | |
| Lasso | 0.0087 | 0.007 | 0.9983 | |
| ETR | 0.0012 | 0.0006 | 1 | |
| Hybrid | 0.0002 | 0.0001 | 0.9999 | |
| IC | SVR | 0.0612 | 0.0557 | 0.9065 |
| RFR | 0.0063 | 0.0039 | 0.999 | |
| GPR | 0.0119 | 0.0071 | 0.9964 | |
| Lasso | 0.0247 | 0.0148 | 0.9848 | |
| ETR | 0.0048 | 0.0033 | 0.9994 | |
| Hybrid | 0.0008 | 0.0005 | 0.9999 | |
| C (Q.V) | SVR | 0.0195 | 0.0153 | 0.9901 |
| RFR | 0.0167 | 0.0109 | 0.9871 | |
| GPR | 0.0217 | 0.0178 | 0.9927 | |
| Lasso | 0.0282 | 0.0225 | 0.9792 | |
| ETR | 0.0159 | 0.0105 | 0.9934 | |
| Hybrid | 0.0043 | 0.003 | 0.9995 | |
| C (IC.V) | SVR | 0.0205 | 0.0158 | 0.9893 |
| RFR | 0.0152 | 0.0102 | 0.9942 | |
| GPR | 0.0231 | 0.0188 | 0.9865 | |
| Lasso | 0.0186 | 0.0228 | 0.9869 | |
| ETR | 0.0153 | 0.01 | 0.9941 | |
| Hybrid | 0.0118 | 0.0095 | 0.9964 |
| HI | Model | RMSE | MAE | R2 |
|---|---|---|---|---|
| V | SVR | 0.0039 | 0.0033 | 0.9946 |
| RFR | 0.0031 | 0.0026 | 0.9961 | |
| GPR | 0.0017 | 0.0015 | 0.9999 | |
| Lasso | 0.0042 | 0.0033 | 0.993 | |
| ETR | 0.0036 | 0.0029 | 0.9946 | |
| Hybrid | 0.0016 | 0.0014 | 0.9989 | |
| IC | SVR | 0.0164 | 0.0146 | 0.8943 |
| RFR | 0.0076 | 0.0045 | 0.9772 | |
| GPR | 0.0357 | 0.0291 | 0.5022 | |
| Lasso | 0.0297 | 0.0253 | 0.6548 | |
| ETR | 0.0076 | 0.0045 | 0.9771 | |
| Hybrid | 0.0074 | 0.0043 | 0.9784 | |
| C (Q.V) | SVR | 0.0056 | 0.0049 | 0.9898 |
| RFR | 0.0044 | 0.0036 | 0.9936 | |
| GPR | 0.0023 | 0.0019 | 0.9983 | |
| Lasso | 0.0029 | 0.0023 | 0.9973 | |
| ETR | 0.0045 | 0.0035 | 0.9934 | |
| Hybrid | 0.002 | 0.0016 | 0.9986 | |
| C(IC.V) | SVR | 0.0057 | 0.0051 | 0.9893 |
| RFR | 0.0046 | 0.0037 | 0.9931 | |
| GPR | 0.0026 | 0.0021 | 0.9978 | |
| Lasso | 0.0194 | 0.0061 | 0.993 | |
| ETR | 0.0045 | 0.0036 | 0.9931 | |
| Hybrid | 0.0026 | 0.0022 | 0.9976 |
| Method | Model | RMSE | MAE | R2 |
|---|---|---|---|---|
| Feature Accretion Method (FAM) | SVR | 0.0041 | 0.0029 | 0.9995 |
| RFR | 0.0017 | 0.0011 | 0.9999 | |
| GPR | 0.0015 | 0.0010 | 0.9821 | |
| Lasso | 0.0100 | 0.0068 | 0.9973 | |
| ETR | 0.0013 | 0.0007 | 0.9999 | |
| Hybrid | 0.0009 | 0.0007 | 0.9999 |
| Model | Model | RMSE | MAE | R2 |
|---|---|---|---|---|
| Feature Accretion Method (FAM) | SVR | 0.0181 | 0.0117 | 0.8930 |
| RFR | 0.0038 | 0.0027 | 0.9962 | |
| GPR | 0.0392 | 0.0314 | 0.4962 | |
| Lasso | 0.0106 | 0.0090 | 0.9633 | |
| ETR | 0.0038 | 0.0026 | 0.9951 | |
| Hybrid | 0.0033 | 0.0024 | 0.9962 |
| CALCE Dataset | Oxford Dataset | |
|---|---|---|
| Fold Number | MSE | MSE |
| F1 | 0.0006651 | 0.0009689 |
| F2 | 3.2977 × 10−5 | 2.2845 × 10−6 |
| F3 | 1.0361 × 10−5 | 1.8900 × 10−6 |
| F4 | 3.6715 × 10−5 | 1.1490 × 10−6 |
| F5 | 4.2694 × 10−5 | 7.7102 × 10−7 |
| F6 | 1.9333 × 10−5 | 1.4898 × 10−5 |
| F7 | 2.4105 × 10−5 | 1.4238 × 10−5 |
| F8 | 2.0036 × 10−5 | 1.9672 × 10−5 |
| F9 | 1.7701 × 10−5 | 7.3050 × 10−5 |
| F10 | 9.9613 × 10−5 | 0.0203830 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amani, L.; Sheikhahmadi, A.; Vafaee, Y. An Enhanced Method to Estimate State of Health of Li-Ion Batteries Using Feature Accretion Method (FAM). Energies 2025, 18, 5171. https://doi.org/10.3390/en18195171
Amani L, Sheikhahmadi A, Vafaee Y. An Enhanced Method to Estimate State of Health of Li-Ion Batteries Using Feature Accretion Method (FAM). Energies. 2025; 18(19):5171. https://doi.org/10.3390/en18195171
Chicago/Turabian StyleAmani, Leila, Amir Sheikhahmadi, and Yavar Vafaee. 2025. "An Enhanced Method to Estimate State of Health of Li-Ion Batteries Using Feature Accretion Method (FAM)" Energies 18, no. 19: 5171. https://doi.org/10.3390/en18195171
APA StyleAmani, L., Sheikhahmadi, A., & Vafaee, Y. (2025). An Enhanced Method to Estimate State of Health of Li-Ion Batteries Using Feature Accretion Method (FAM). Energies, 18(19), 5171. https://doi.org/10.3390/en18195171






