Two-Phase Flow Simulation of Bubble Cross-Membrane Removal Dynamics in Boiling-Desorption Mode for Microchannel Membrane-Based Generators
Abstract
1. Introduction
2. Numerical Methodology
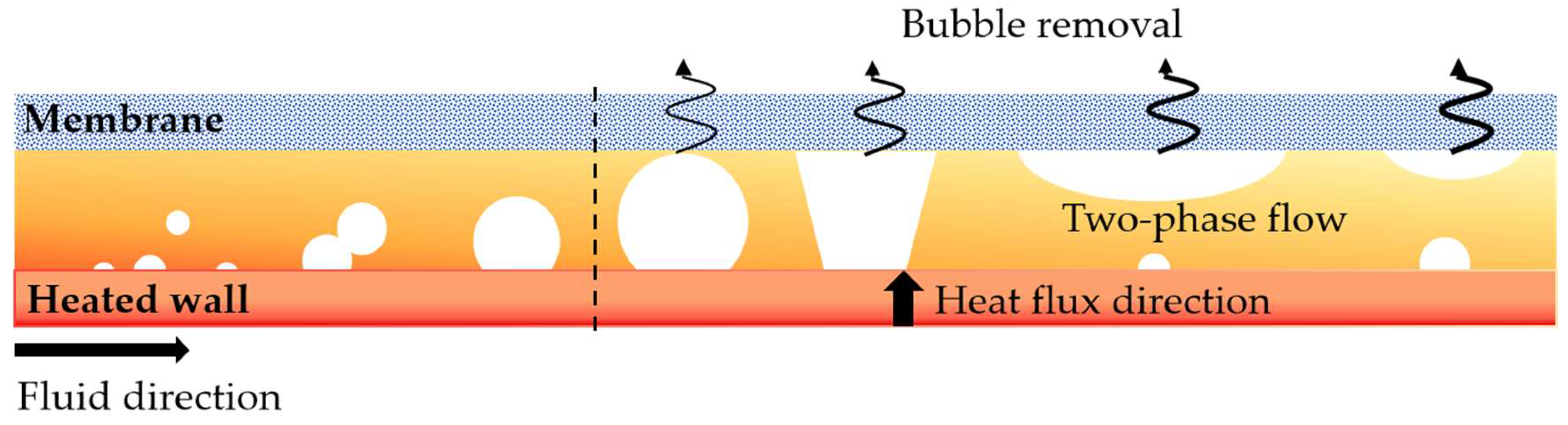
2.1. Problem Description
2.2. Governing Equations
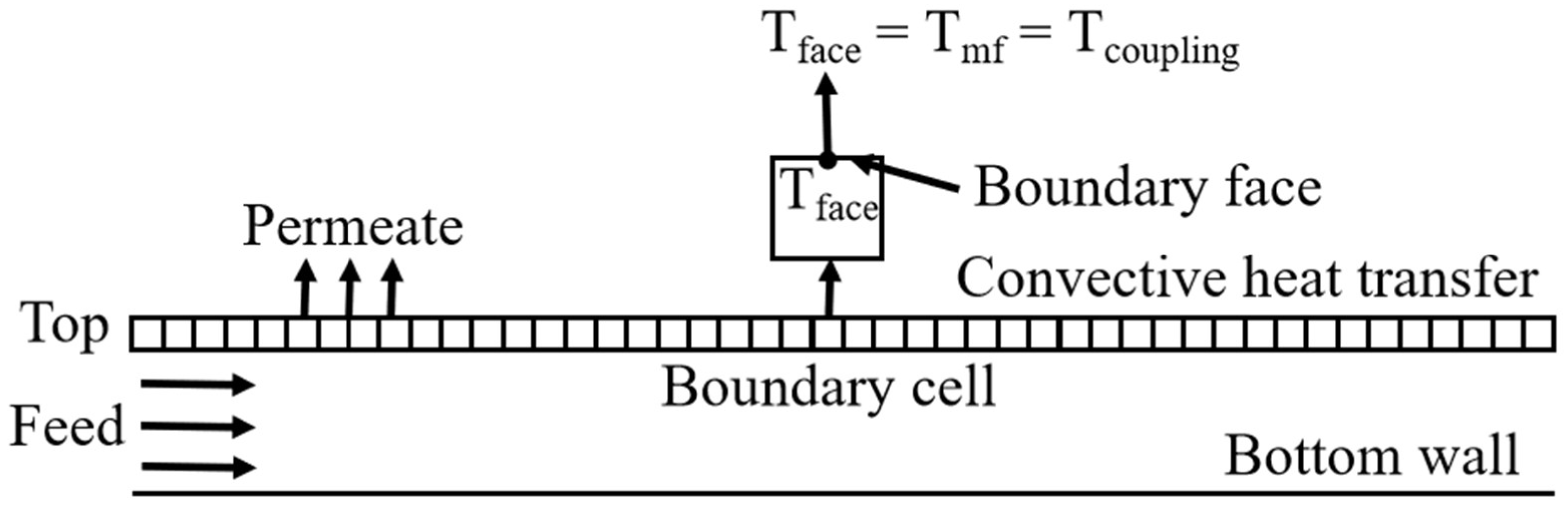
2.3. Bubble Removal Mode
2.4. Solver Setup
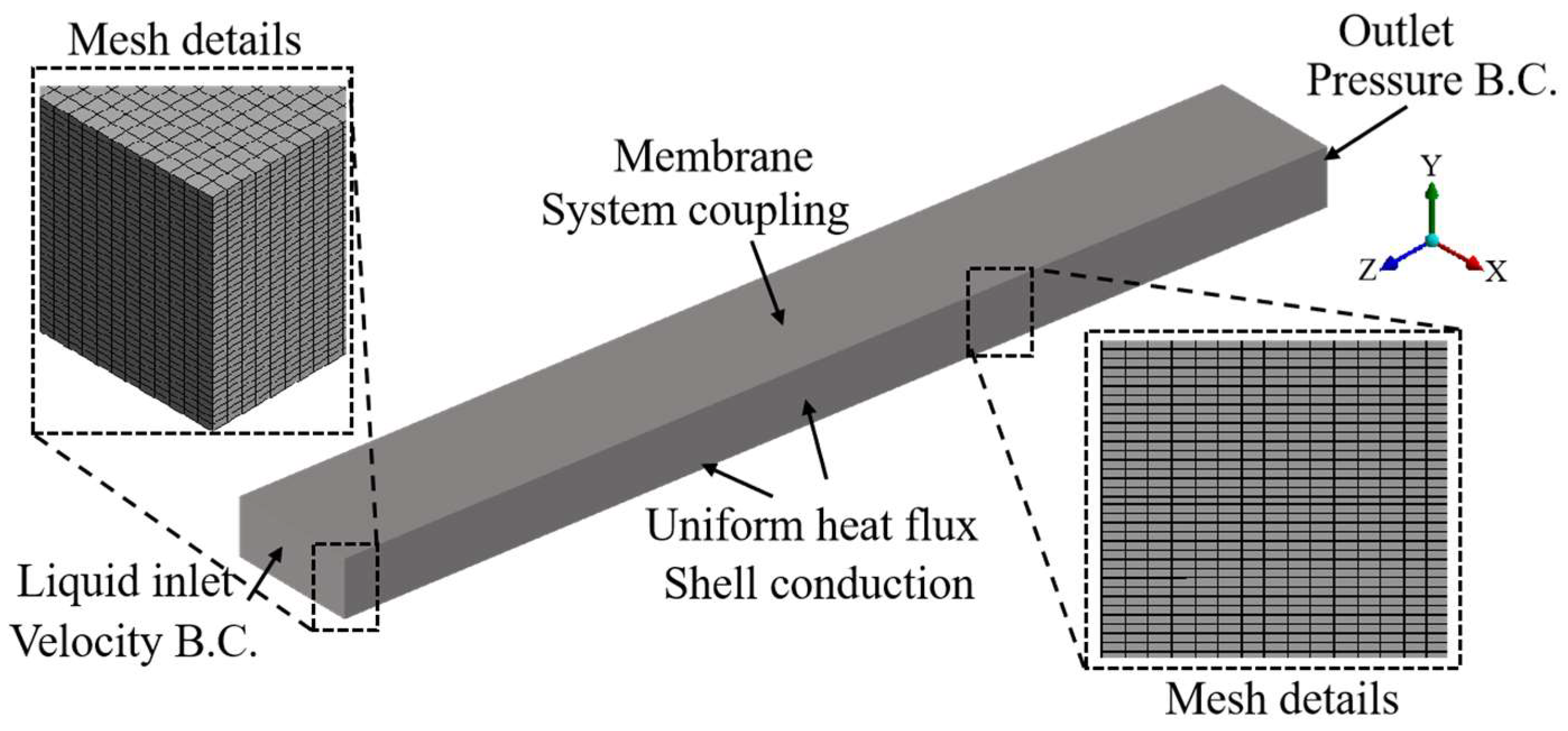
2.5. Computational Domain Configuration
2.6. Grid Independence Test
3. Numerical Model Validation
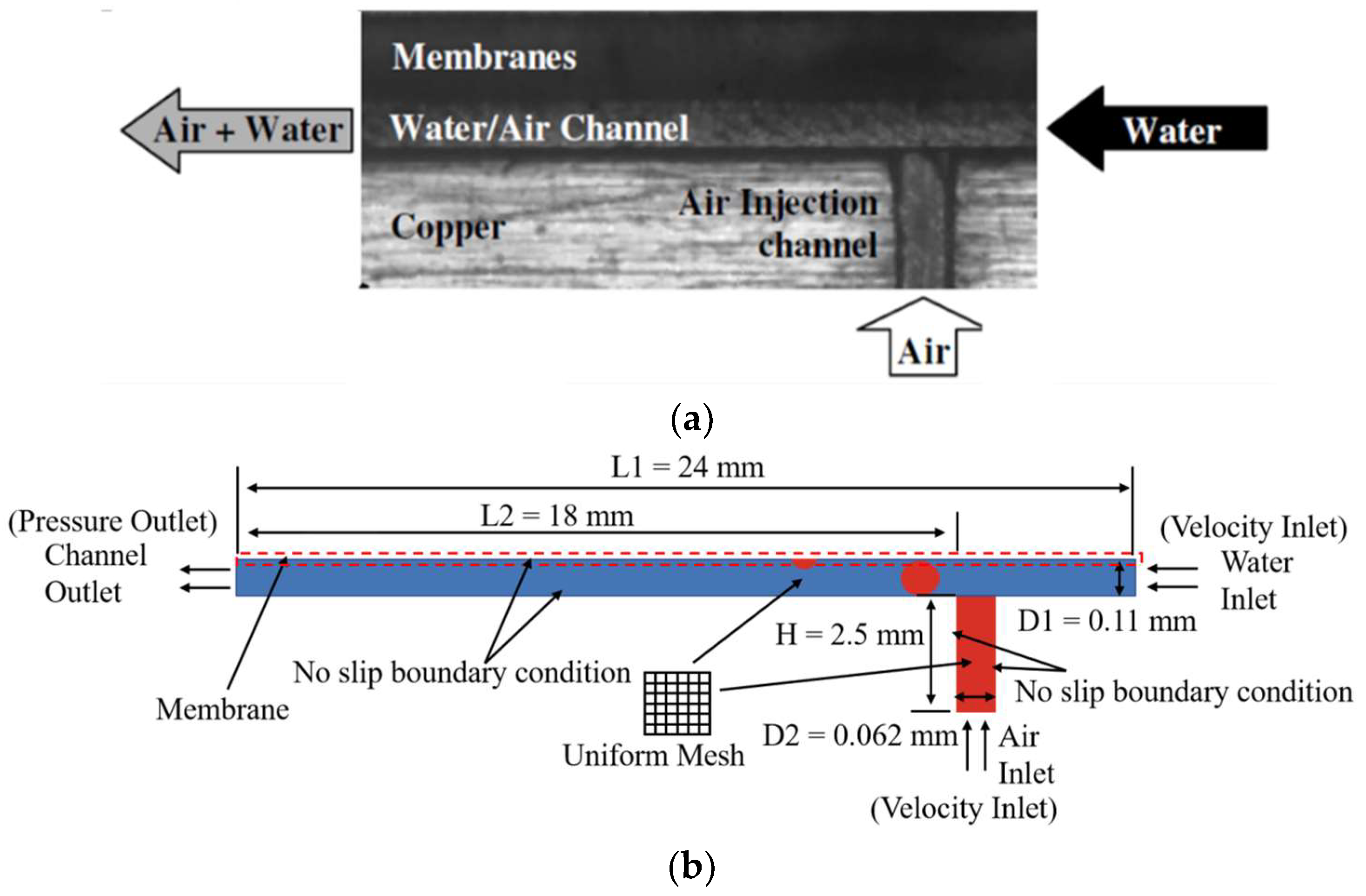
3.1. Bubble Removal Model Validation
3.2. Validation of Phase Change Model
4. Results and Discussions
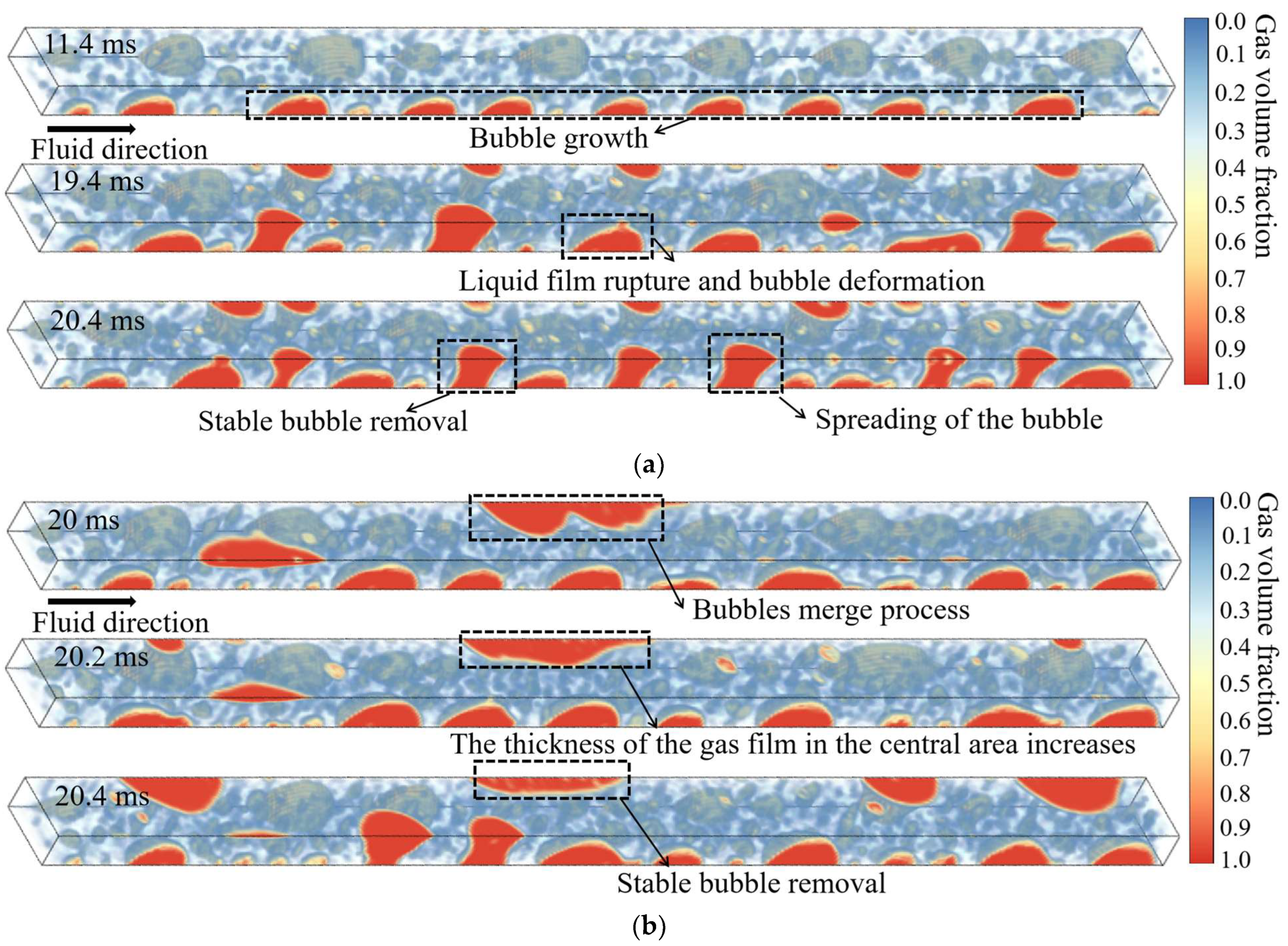
4.1. Overview of Bubble Flow Patterns
4.2. Wall Temperature Distribution
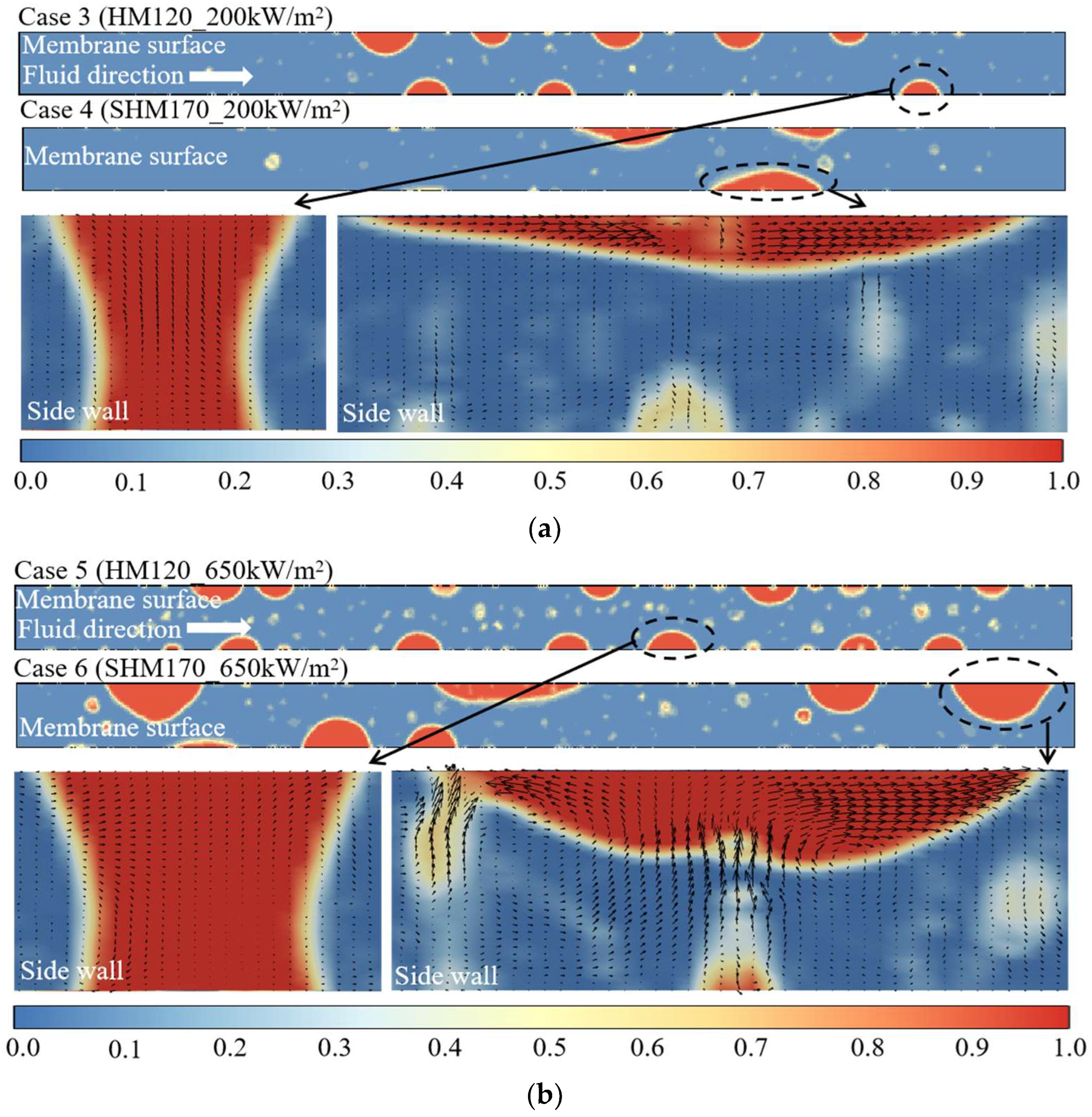
4.3. Analysis of Differences in Venting Volume
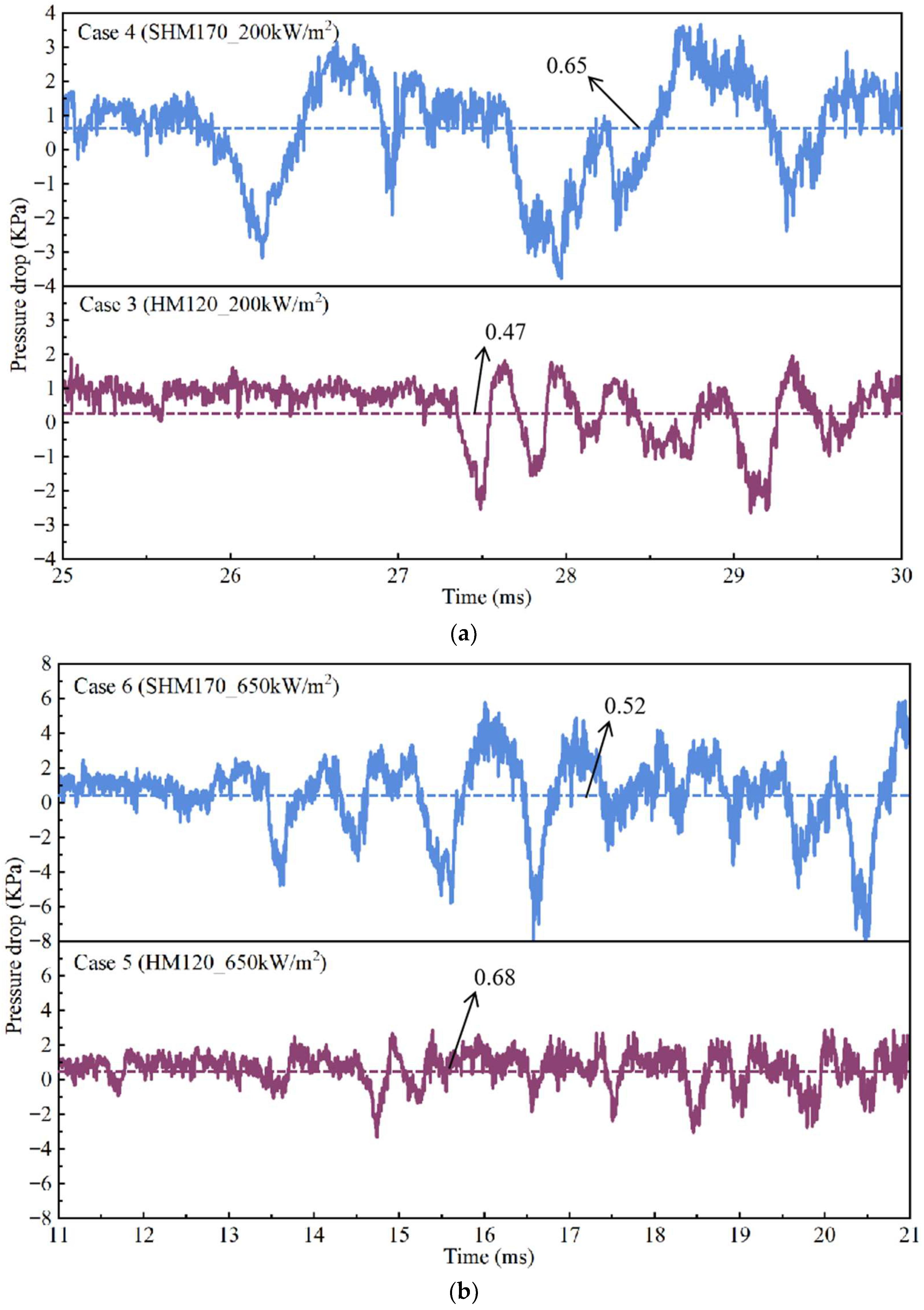
4.4. Pressure Distribution
5. Application Areas and Future Optimization
6. Conclusions
- (1)
- The bubble-venting process proceeds through four distinct, sequential stages: (i) bubble nucleation and growth; (ii) rupture of the liquid film accompanied by bubble deformation; (iii) lateral spreading of the bubble; and (iv) sustained removal of vapor through the membrane. The effect of membrane hydrophobicity on venting dynamics becomes most evident from the third stage onward. While an increase in the heating-wall heat flux does not alter the fundamental sequence of these stages, it does influence key characteristics such as the number of bubbles generated, the timing of transitions between stages, and the probability of bubble coalescence.
- (2)
- Increasing the membrane hydrophobicity in a microchannel membrane-based generator leads to a reduction in wall temperature, with the magnitude of this reduction becoming more pronounced at higher applied heat fluxes.
- (3)
- Increasing membrane hydrophobicity consistently improves venting performance, with the degree of enhancement becoming more significant at higher heat fluxes. The accelerated venting rates achieved by superhydrophobic membranes not only increase the total volume of vapor removed but also shorten the time required to reach a specified removal amount.
- (4)
- The overall pressure fluctuation within the channel results from the superposition of a high-frequency component, generated by bubble growth, and a low-frequency component, arising from flow-rate discontinuities during venting events. The relative contribution of these components is governed by both membrane hydrophobicity and the applied heat flux.
- (5)
- The bubble removal model constructed in this work provides an effective visual and quantitative analysis framework for studying the behavior of bubbles on the membrane surface. Currently, the model simplifies the mass transfer driving force by assuming a constant pressure difference, and verifies its basic feasibility. The future improvement direction lies in coupling the concentration and temperature changes in the lithium bromide solution within the channel to achieve dynamic simulation of the mass transfer driving force, thereby enhancing the prediction accuracy of the model for the real process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Velocity [m/s] | |
| Mass transfer in [kg/s] | |
| Pressure [N/m2] | |
| Acceleration due to gravity [m2/s] | |
| Force [N] | |
| Interface curvature [1/m] | |
| Energy transfer [W] | |
| Latent heat [J/kg] | |
| Transmembrane mass transfer rate [kg/m3/s] | |
| bubble transmembrane desorption rate coefficient | |
| Time step [s] | |
| molecular weight [kg/mole] | |
| membrane thickness [μm] | |
| diffusion term | |
| universal gases constant [J/kg/K] | |
| membrane temperature [K] | |
| membrane pressure [Pa] | |
| molar viscous flow | |
| membrane porosity | |
| membrane pore diameter [μm] | |
| membrane tortuosity | |
| mass transfer driving force [kPa] | |
| Heat transfer across membrane [J/m3/s] | |
| General expression variable | |
| A | Boundary grid |
| B | Boundary grid |
| C | Boundary grid |
| D | Boundary grid |
| E | Boundary grid |
| a | Boundary grid faces |
| b | Boundary grid faces |
| c | Boundary grid faces |
| d | Boundary grid faces |
| e | Boundary grid faces |
| Cl | Liquid-phase cell |
| Cv | Gas-phase cell |
| Grid size | |
| Maximum velocity [m/s] | |
| HM | Hydrophobic membrane |
| SHM | Superhydrophobic membrane |
| Greek | |
| Volume fraction [m3/m3] | |
| Density [kg/m3] | |
| Dynamic viscosity [Pa s] | |
| Surface tension coefficient [N/m] | |
| Thermal conductivity [W/m K] | |
| Subscripts | |
| liquid | |
| vapor | |
| continuum surface tension | |
| boundary face | |
| membrane face | |
| coupling boundary |
References
- IEA. The Future of Cooling; International Energy Agency: Paris, France, 2018. [Google Scholar]
- Khalfallah, E.; Missaoui, R.; El Khamlichi, S.; Ben Hassine, H. Energy Efficient Air Conditioning: A Case Study of the Maghreb; World Bank: Washington, DC, USA, 2016; pp. 14–17. [Google Scholar]
- Popoola, O.; Chipango, M. Improved peak load management control technique for nonlinear and dynamic residential energy consumption pattern. Build. Simul. 2021, 21, 195–208. [Google Scholar] [CrossRef]
- Gao, L.; Zheng, Z.; Tao, L.; Xue, W.; Huang, L.; Liu, R.; Cheng, J. Experiment study of evaporation heat transfer characteristics in plate climbing film evaporator. Cryogenics 2011, 24, 42–45. [Google Scholar]
- Gajghate, S.S.; Barathula, S.; Das, S.; Saha, B.B.; Bhaumik, S. Experimental investigation and optimization of pool boiling heat transfer enhancement over graphene-coated copper surface. Therm. Anal. 2020, 140, 1393–1411. [Google Scholar] [CrossRef]
- Nolwenn, L.P.; Huaylla, F.; Stutz, B.; Perraud, J. Long-term solar heat storage process by absorption with the KCOOH/H2O couple: Experimental investigation. Pergamon Energy 2017, 141, 1313–1323. [Google Scholar]
- Hamid, K.; Wang, C.C.; Tolstorebrov, I.; Hafner, A.; Eikevik, T.M. Experimental study on ammonia/water mixture desorption heat transfer for vapor absorption-compression heat pump. Int. J. Heat Mass Transfer. 2025, 246, 127114. [Google Scholar] [CrossRef]
- García-Hernando, N.; Almendros-Ibáñez, J.A.; Ruiz, G.; De-Vega, M. On the pressure drop in Plate Heat Exchangers used as desorbers in absorption chillers. Energy Convers. Manag. 2011, 52, 1520–1525. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, D.H.; Kim, S.M.; Kim, M.S.; Kim, I.G.; Woo, S.M.; Hong, S.J.; Park, C.W. Heat transfer characteristics of a falling film generator for various configurations of heating tubes in an absorption chiller. Appl. Therm. Eng. 2019, 148, 1407–1415. [Google Scholar] [CrossRef]
- Hu, T.L.; Xie, X.Y.; Jiang, Y. A detachable plate falling film generator and condenser coupling using lithium bromide and water as working fluids. Int. J. Refrig. 2019, 98, 120–128. [Google Scholar] [CrossRef]
- Wirtz, M.; Stutz, B.; Phan, H.T.; Boudehenn, F. Numerical modeling of falling-film plate generator and rectifier designed for NH3-H2O absorption machines. Heat Mass Transfer. 2022, 58, 431–446. [Google Scholar] [CrossRef]
- Thorud, J.D.; Liburdy, J.A.; Pence, D.V. Microchannel membrane separation applied to confined thin film desorption. Exp. Therm. Fluid. Sci. 2006, 30, 713–723. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W. Experimental evaluation on heat/mass transfer and pressure drop of a microchannel membrane-based desorber for compact and efficient H2O/LiBr absorption refrigeration. Int. J. Heat Mass Transfer. 2022, 195, 123198. [Google Scholar] [CrossRef]
- Zhai, C.; Wu, W. Heat and mass transfer performance comparison of various absorbers/desorbers towards compact and efficient absorption heat pumps. Int. J. Refrig. 2021, 127, 203–220. [Google Scholar] [CrossRef]
- Robeson, L.M. Polymer membranes for gas separation. Curr. Opin. Solid State Mater. Sci. 1999, 4, 549–552. [Google Scholar] [CrossRef]
- Isfahani, R.N.; Fazeli, A.; Bigham, S.; Moghaddam, S. Physics of lithium bromide (LiBr) solution dewatering through vapor venting membranes. Int. J. Multiph. Flow 2014, 58, 27–38. [Google Scholar] [CrossRef]
- Venegas, M.; García-Hernando, N.; De-Vega, M. Experimental evaluation of a membrane-based microchannel desorber operating at low desorption temperatures. Appl. Therm. Eng. 2020, 167, 114781. [Google Scholar] [CrossRef]
- Asdrubali, F.; Baldinelli, G.; Presciutti, A. Solar cooling with small-size absorption chillers: Different solutions for summer air conditioning. Ind. E Form.-Spec. Int. Issue IIF-IIR 2008, 7, 34–38. [Google Scholar]
- Venegas, M.; De-Vega, M.; García-Hernando, N.; Ruiz-Rivas, U. Simplified model of a membrane-based rectangular micro-desorber for absorption chillers. Int. J. Refrig. 2016, 71, 108–123. [Google Scholar] [CrossRef]
- Venegas, M.; García-Hernando, N.; De-Vega, M. A parametric analysis on the effect of design and operating variables in a membrane-based desorber. Int. J. Refrig. 2019, 99, 47–58. [Google Scholar] [CrossRef]
- Pual, S.; Bhoumick, M.C.; Roy, S.; Mitya, S. Carbon nanotube enhanced membrane filtration for trace level dewatering of hydrocarbons. Sep. Purif. Technol. 2022, 292, 121047. [Google Scholar] [CrossRef]
- Liu, J.; Xie, B.L.; Mushtaq, N.; Xu, G.R.; Zeev, E.B.; Hu, Y.X. New insights into the role of carbon nanotubes spray-coated on both sides of the PTFE membrane in suppressing temperature polarization and enhancing water flux in direct contact membrane distillation. J. Membr. Sci. 2024, 689, 122184. [Google Scholar] [CrossRef]
- Intrchom, W.; Roy, S.; Mitra, S. Functionalized carbon nanotube immobilized membrane for low temperature ammonia removal via membrane distillation. Sep. Purif. Technol. 2020, 235, 116188. [Google Scholar] [CrossRef]
- Gupta, I.; Chakraborty, J.; Roy, S.; Farinas, E.T.; Mitra, S. Nanocarbon immobilized membranes for generating bacteria and endotoxin free water via membrane distillation. Sep. Purif. Technol. 2021, 259, 118133. [Google Scholar] [CrossRef]
- Ren, J.; Li, J.F.; Xu, Z.S.; Liu, Y.; Cheng, F.Q. Simultaneous anti-fouling and flux-enhanced membrane distillation via incorporating graphene oxide on PTFE membrane for coking wastewater treatment. Appl. Surf. Sci. 2020, 531, 147349. [Google Scholar] [CrossRef]
- Cao, H.; Mao, Y.P.; Wang, W.L.; Jin, Y.; Gao, Y.B.; Zhang, M.M.; Zhao, X.Q.; Sun, J.; Song, Z.L. ZIF-8 based dual scale superhydrophobic membrane for membrane distillation. Desalination 2023, 550, 116373. [Google Scholar] [CrossRef]
- Perez-Raya, I.; Kandlikar, S.G. Discretization and implementation of a sharp interface model for interfacial heat and mass transfer during bubble growth. Int. J. Heat Mass Transfer. 2018, 116, 30–49. [Google Scholar] [CrossRef]
- Sato, Y.; Niceno, B. A sharp-interface phase change model for a mass-conservative interface tracking method. J. Comput. Phys. 2013, 249, 127–161. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Kharangate, C.R.; Mudawar, I. Review of computational studies on boiling and condensation. Int. J. Heat Mass Transfer. 2017, 108, 1164–1196. [Google Scholar] [CrossRef]
- Khan, Z.A.; Ahmad, N.; Sattar, M.; Haq, M.A.; Khan, I.; Ganie, A.H. Cell alternation algorithm for simulating bubble growth in boiling flows through volume of fluid (VOF) method in fluent. Alex. Eng. J. 2022, 61, 13051–13066. [Google Scholar] [CrossRef]
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A comprehensive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Review membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Soukane, S.; Naceur, M.W.; Francis, L.; Alsaadi, A.; Ghaffour, N. Effect of feed flow pattern on the distribution of permeate fluxes in desalination by direct contact membrane distillation. Desalination 2017, 418, 43–59. [Google Scholar] [CrossRef]
- David, M.P.; Steinbrenner, J.; Miler, J.; Goodson, K.E. Visualization and Analysis of Venting from a Single Microchannel Two-phase Copper Heat Exchanger. In Proceedings of the ASME InterPack Conference, San Francisco, CA, USA, 19–23 July 2009; pp. 1–8. [Google Scholar]
- Ramesh, B.; Jayaramu, P.; Gedupudi, S. Subcooled flow boiling of water in a copper microchannel: Experimental investigation and assessment of predictive methods. Int. Commun. Heat Mass Transfer. 2019, 103, 24–30. [Google Scholar] [CrossRef]
- Rajalingam, A.; Chakraborty, S. Fluid flow and heat transfer characteristics of a microstructured microchannel heat sink under flow boiling condition. Appl. Therm. Eng. 2024, 248, 123265. [Google Scholar] [CrossRef]
- Lee, W.H. A Pressure Iteration Scheme for Two-Phase Modeling; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1979; pp. 407–431. [Google Scholar]
- Park, J.; Ryu, J.; Lee, S.J. Penetration of a bubble through porous membranes with different wettabilities. Soft Matter 2019, 15, 5819–5826. [Google Scholar] [CrossRef] [PubMed]



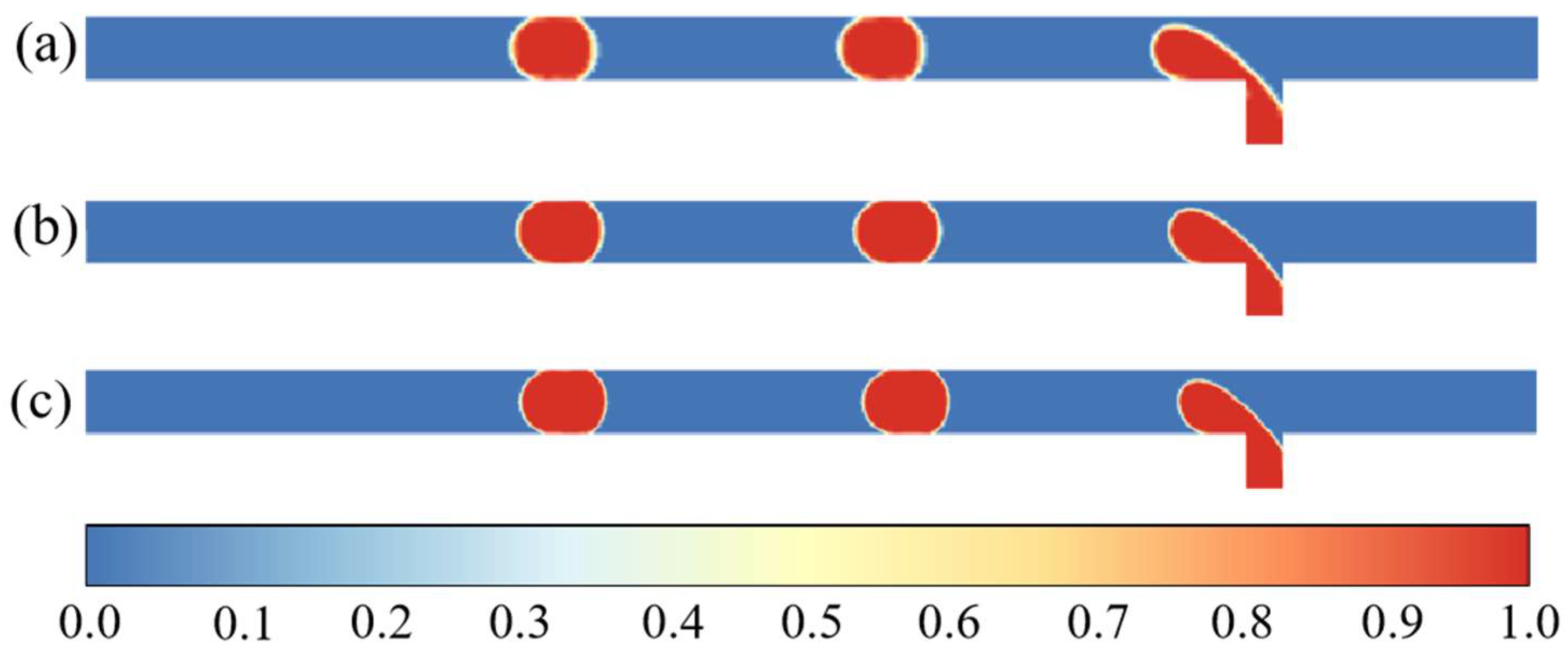

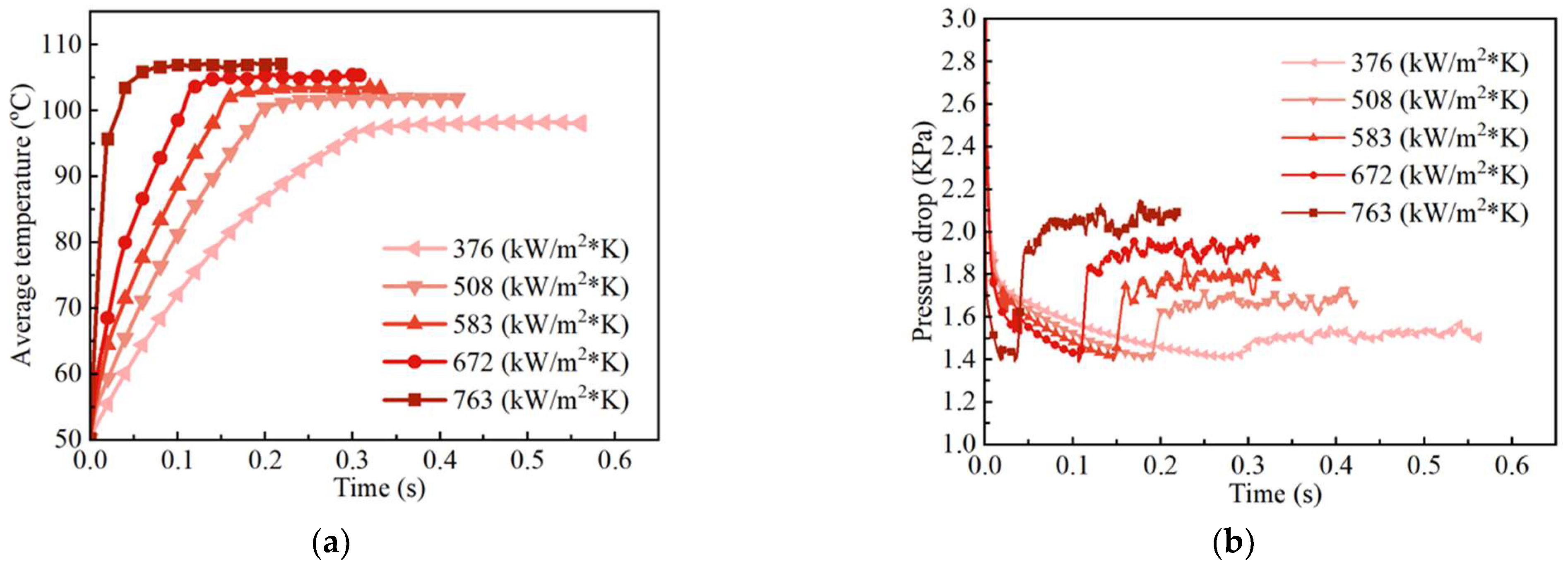
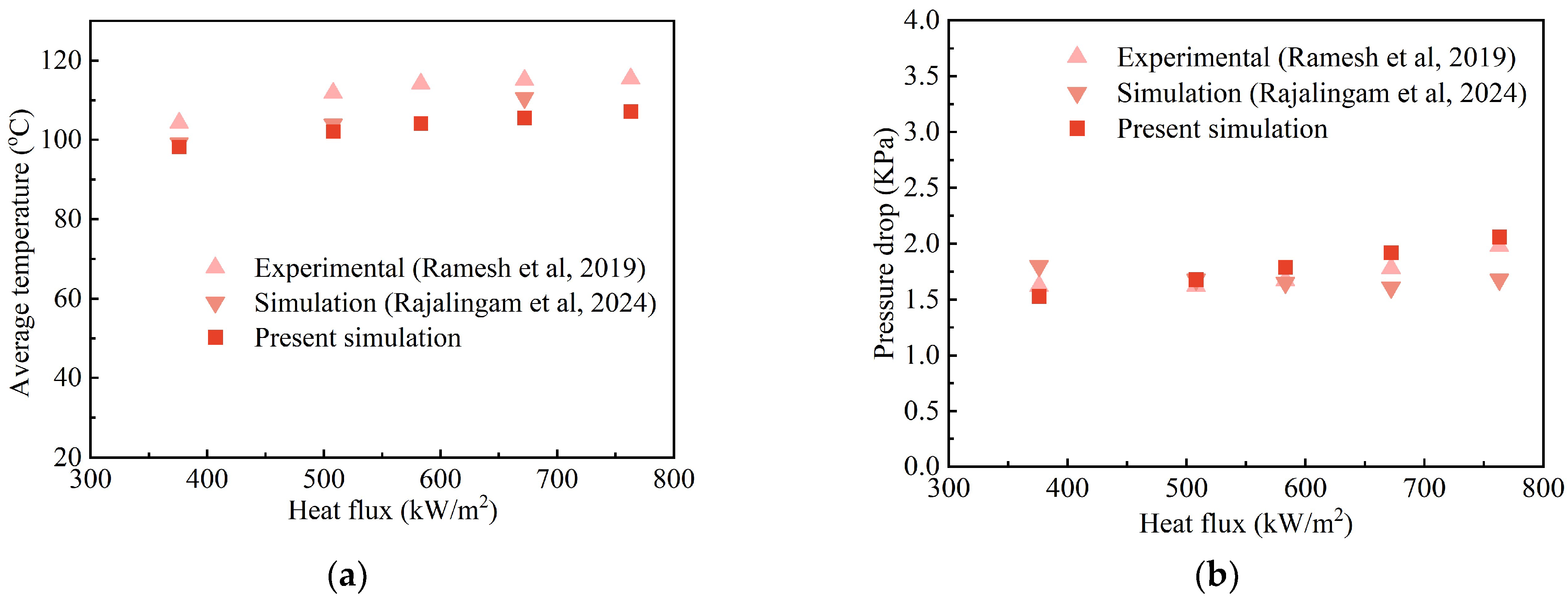



| H2O/LiBr Solution | (kg/m3) | (Pa·s) | (W/m K) | (J/kg K) | (J/kg) | (N/m) |
|---|---|---|---|---|---|---|
| Liquid | 1595 | 1.6 × 10−3 | 0.4776 | 2074 | 2.7 × 106 | 0.085 |
| Vapor | 0.1161 | 1.265 × 10−5 | 0.02429 | 1889 |
| Parameter | Value |
|---|---|
| Porosity | 0.8 |
| Pore size (μm) | 0.45 |
| Thickness (μm) | 60 |
| Mass transfer driving force (kPa) | 0.9 |
| Case | Membrane Contact Angle (°) | Heat Flux (kW/m2) | Initial Condition |
|---|---|---|---|
| 1 | - | 200 | No membrane |
| 2 | - | 650 | |
| 3 | 120 | 200 | Membrane |
| 4 | 170 | 200 | |
| 5 | 120 | 650 | |
| 6 | 170 | 650 |
| No. | Mesh Size-Channel Space (L × W × H) | Avg Tw (K) | e% | ∆P (Pa) | e% |
|---|---|---|---|---|---|
| 1 | 198 × 12 × 15 | 378.41 | 0.03 | 0.389 | 6.68 |
| 2 | 330 × 20 × 25 | 378.30 | 0.0079 | 0.415 | 0.96 |
| 3 | 396 × 24 × 30 | 378.27 | - | 0.419 | - |
| 3 | 396 × 24 × 30 | 378.27 | - | 0.419 | - |
| Two Phase | (kg/m3) | (Pa·s) | (N/m) |
|---|---|---|---|
| Water | 998.2 | 1.003 × 10−3 | 0.072 |
| Air | 1.225 | 1.789 × 10−5 |
| Mesh Size (μm) | Gas Bubble Length (mm) | Percentage Change (%) |
|---|---|---|
| 6 | 0.134 | - |
| 4 | 0.141 | 5.22 |
| 3 | 0.145 | 2.84 |
| Ramesh et al. [36] | |
|---|---|
| Channel dimension | 1 × 0.49 × 40 mm3 |
| Mass flux | 855 kg/m2s |
| Heat flux | 377–763 kW/m2 |
| Working fluid | Water |
| Inlet temperature | 323.15 K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, J.; Gao, H.; Yan, Y. Two-Phase Flow Simulation of Bubble Cross-Membrane Removal Dynamics in Boiling-Desorption Mode for Microchannel Membrane-Based Generators. Energies 2025, 18, 5156. https://doi.org/10.3390/en18195156
Zhai J, Gao H, Yan Y. Two-Phase Flow Simulation of Bubble Cross-Membrane Removal Dynamics in Boiling-Desorption Mode for Microchannel Membrane-Based Generators. Energies. 2025; 18(19):5156. https://doi.org/10.3390/en18195156
Chicago/Turabian StyleZhai, Jianrong, Hongtao Gao, and Yuying Yan. 2025. "Two-Phase Flow Simulation of Bubble Cross-Membrane Removal Dynamics in Boiling-Desorption Mode for Microchannel Membrane-Based Generators" Energies 18, no. 19: 5156. https://doi.org/10.3390/en18195156
APA StyleZhai, J., Gao, H., & Yan, Y. (2025). Two-Phase Flow Simulation of Bubble Cross-Membrane Removal Dynamics in Boiling-Desorption Mode for Microchannel Membrane-Based Generators. Energies, 18(19), 5156. https://doi.org/10.3390/en18195156






