Robust Backstepping Super-Twisting MPPT Controller for Photovoltaic Systems Under Dynamic Shading Conditions
Abstract
1. Introduction
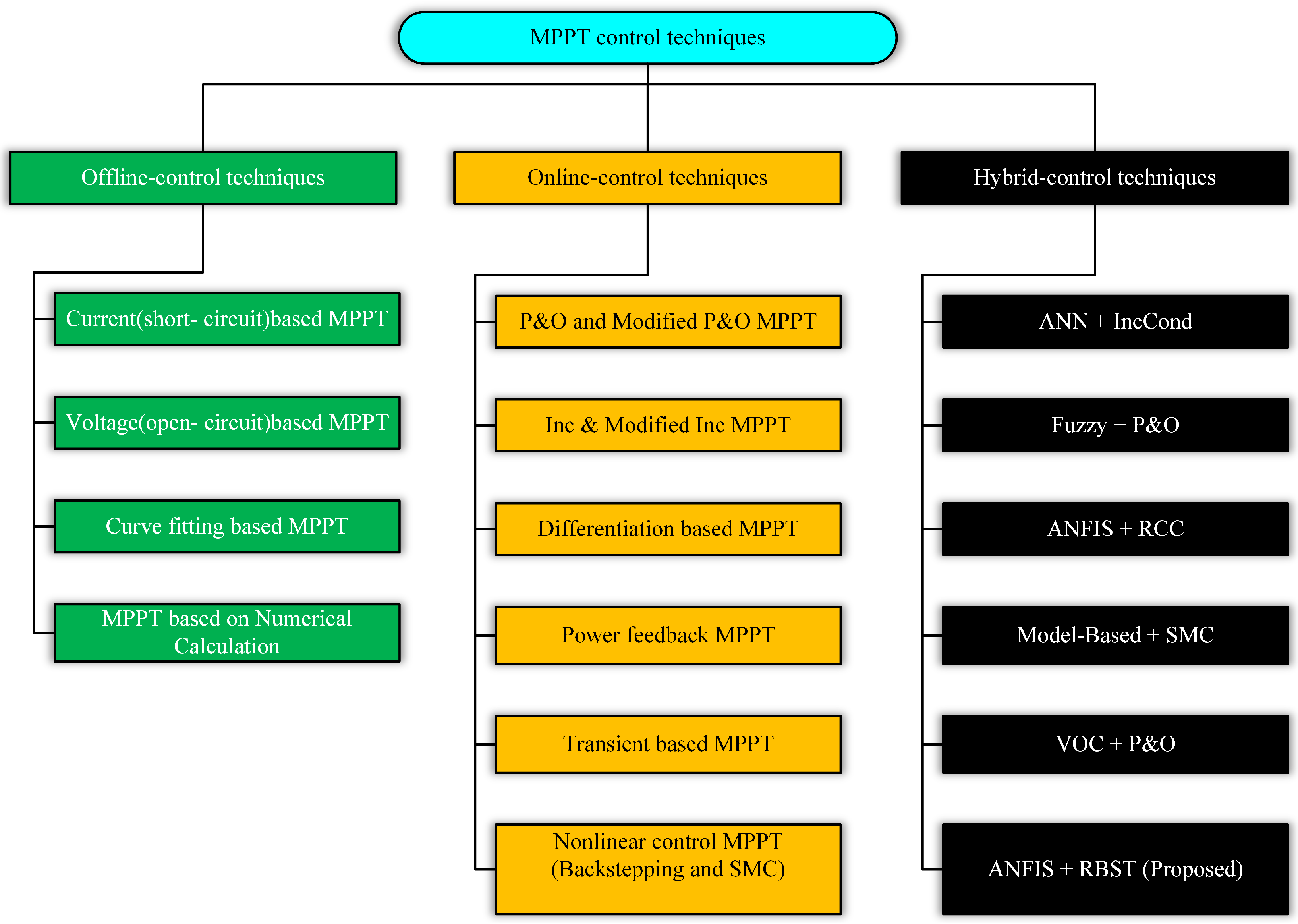
1.1. Model-Based MPPT Control Techniques
1.2. Model-Free MPPT Control Techniques
1.3. Hybrid MPPT Control Techniques
1.4. Motivation and Contribution of This Work
- Hybrid RBST–ANFIS MPPT design: A new hybrid scheme is formulated where ANFIS provides offline estimation and the RBST law ensures online tracking. This integration of intelligent reference generation with Lyapunov-based robust control represents a novel approach in PV MPPT applications.
- Explicit Lyapunov-based RBST formulation: The RBST controller is systematically derived using Lyapunov stability theory, introducing six tuning parameters (–), whose roles are explicitly analyzed in terms of convergence speed, robustness, and chattering reduction.
- Super-twisting within a two-loop backstepping framework: By embedding the super-twisting algorithm inside a two-loop backstepping design, the proposed controller achieves finite-time convergence, eliminates steady-state error, and mitigates chattering compared to classical backstepping and sliding-mode MPPT schemes.
- Duty-cycle boundedness: This method guarantees that the converter duty cycle remains bounded () throughout operation, which is an explicit design constraint often overlooked in nonlinear MPPT schemes.
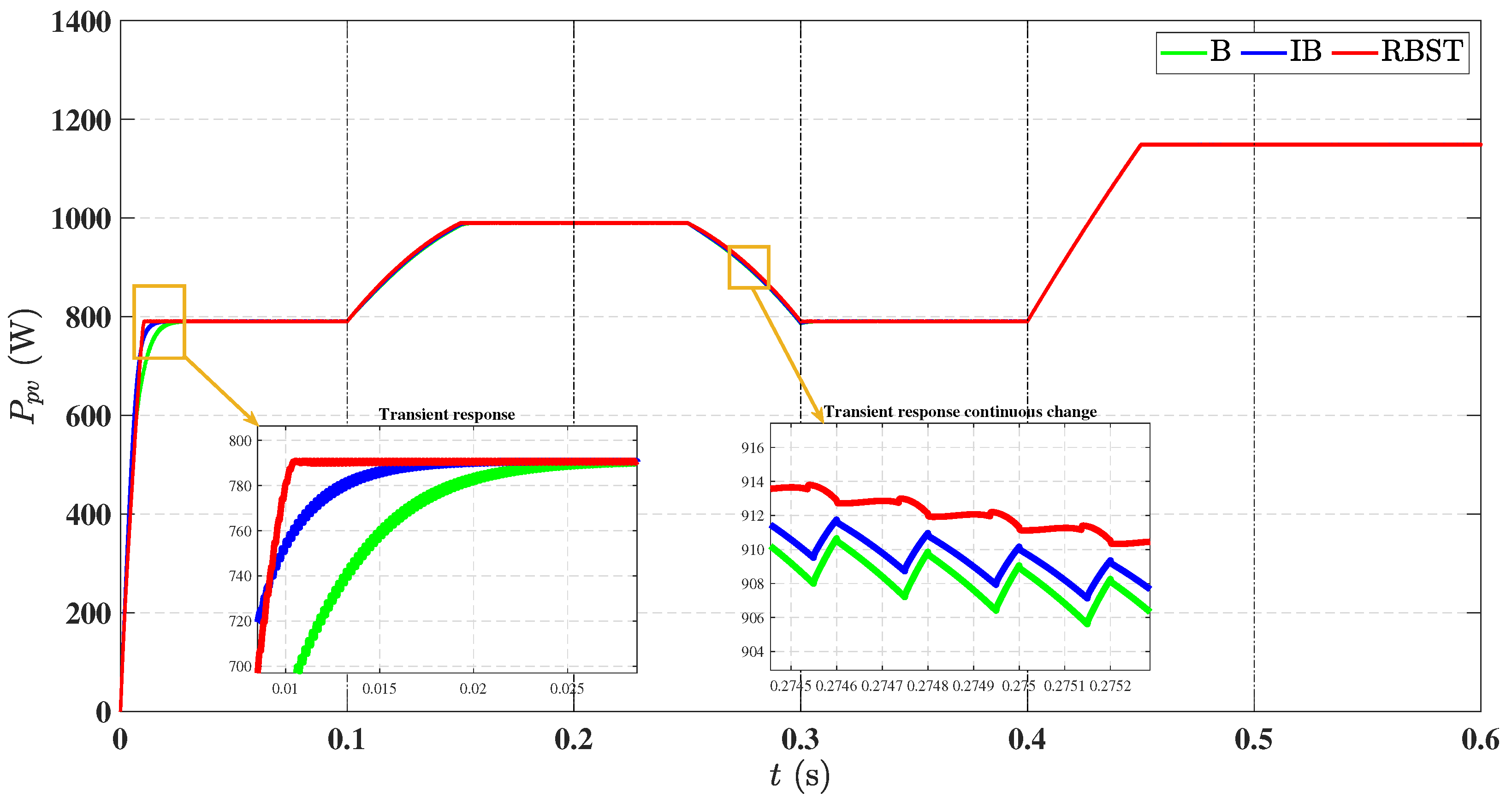
- Superior MPPT performance: Simulation results confirm >99% MPPT efficiency and fast convergence (∼0.018 s rise time) across highly dynamic irradiance and shading conditions, validating both robustness and practicality.
- Integration with a broader research framework: This work also contributes to a wider ongoing PhD project on PV plant development and monitoring, in which the proposed MPPT scheme represents the efficiency-optimization stage that can be linked with geospatial decision support, GIS-based site selection [25], and land surface temperature (LST) downscaling techniques [26], thereby enhancing PV system monitoring and improving overall energy efficiency.
1.5. Organization of This Article
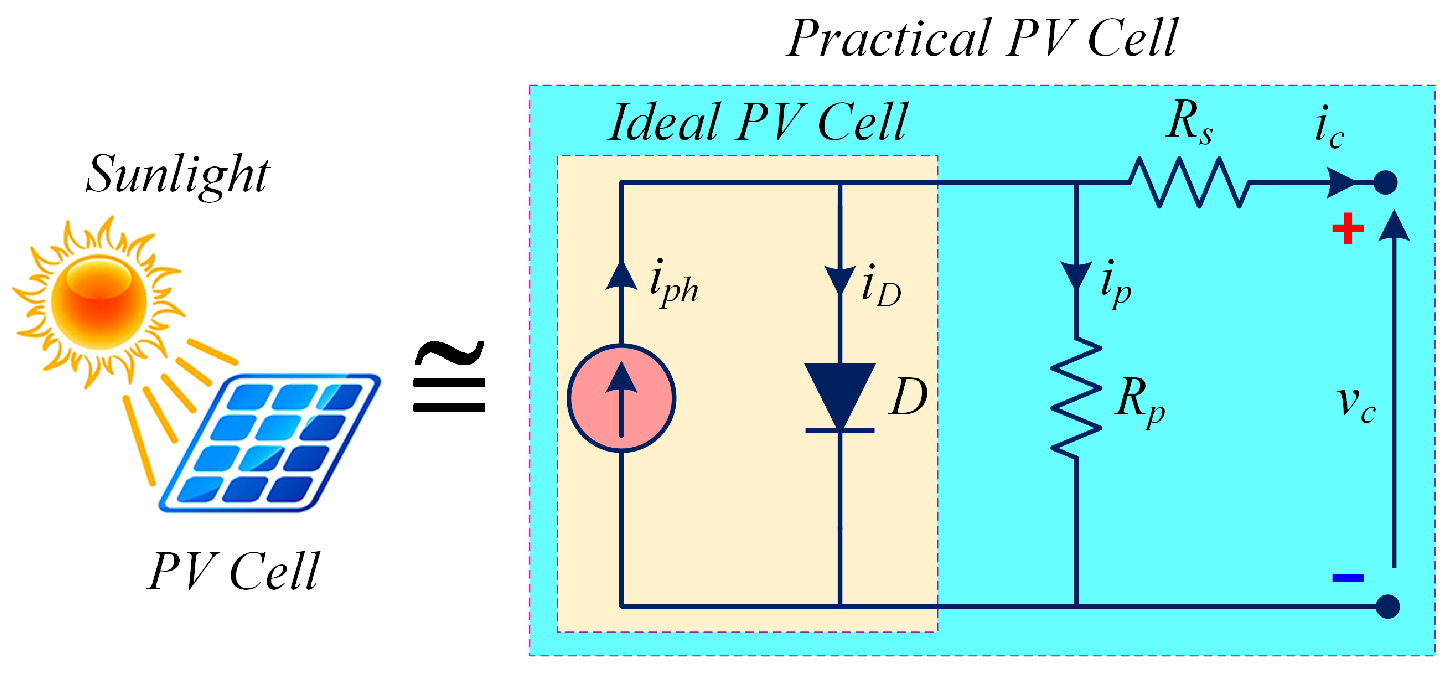
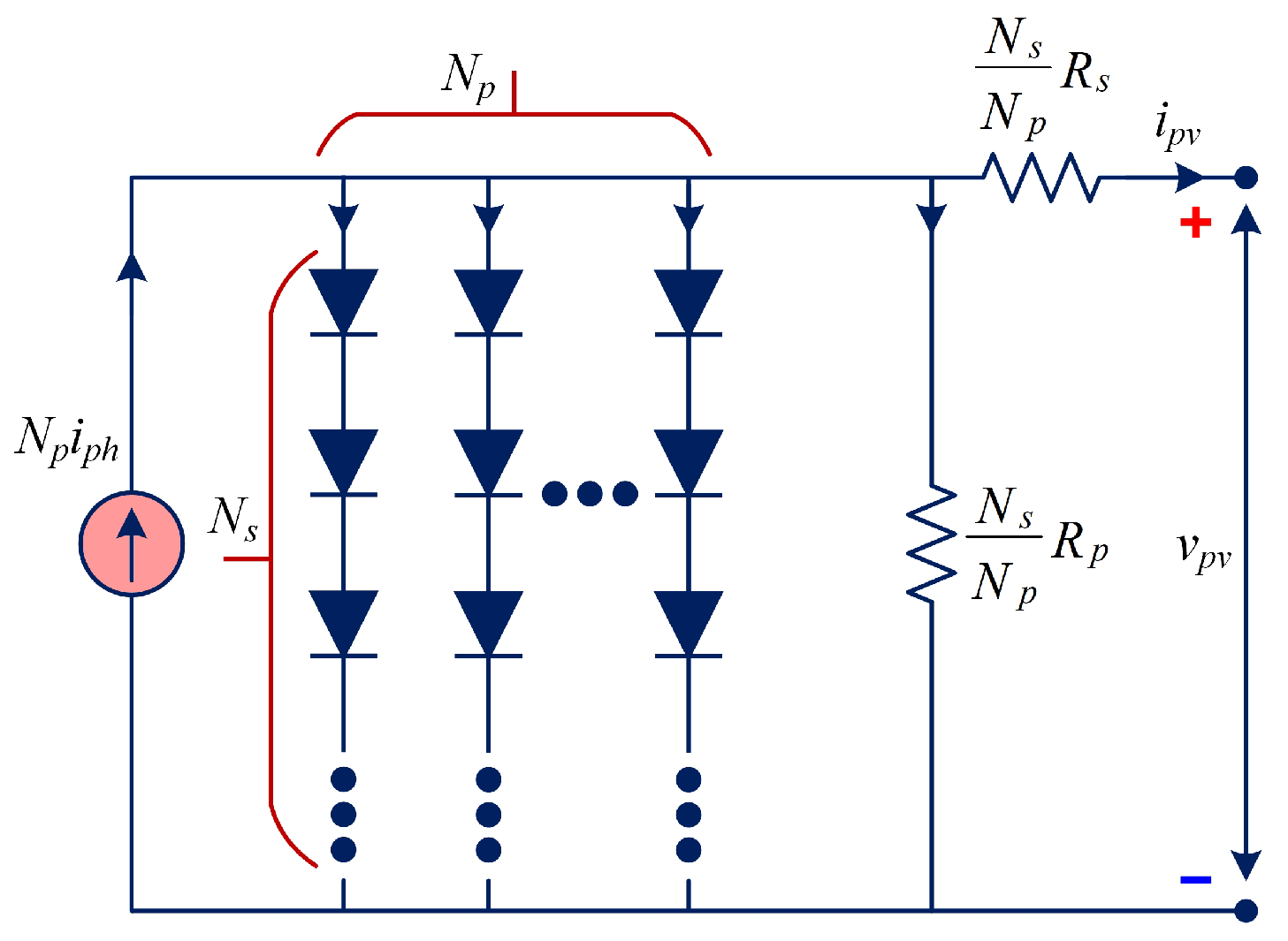
2. Solar Array Mathematical Modeling
3. Mathematical Modeling of DC–DC Power Converter
- Buck Mode: is switched ON and OFF during one switching period, , while remains continuously OFF.
- Boost Mode: is switched ON and OFF during one switching period, while remains continuously ON.
4. ANFIS-Based Reference Peak Power Voltage Generation for MPPT Controller
5. The Proposed Robust Backstepping-Based Super-Twisting MPPT Controller Design
5.1. Robust Backstepping-Based Continuous/Equivalent Control Design
5.2. Super-Twisting-Based Discontinuous Control Design
5.3. Proposed RBST-Based MPPT Control Law
6. Results and Discussion
- Continuously varying irradiance and temperature;
- Sudden step changes in irradiance and temperature;
- Partial shading conditions.
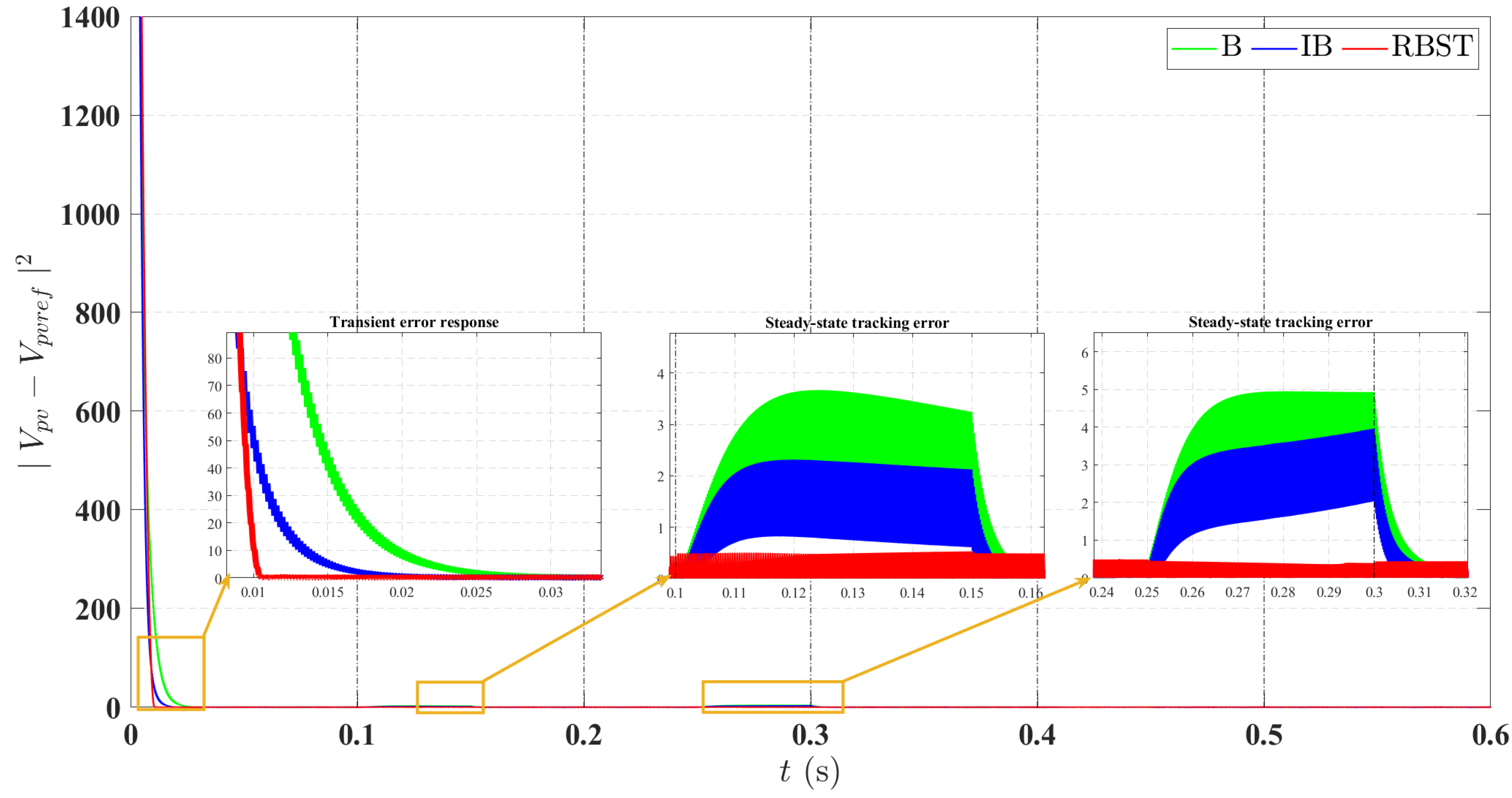
6.1. Continuously Varying Irradiance and Temperature
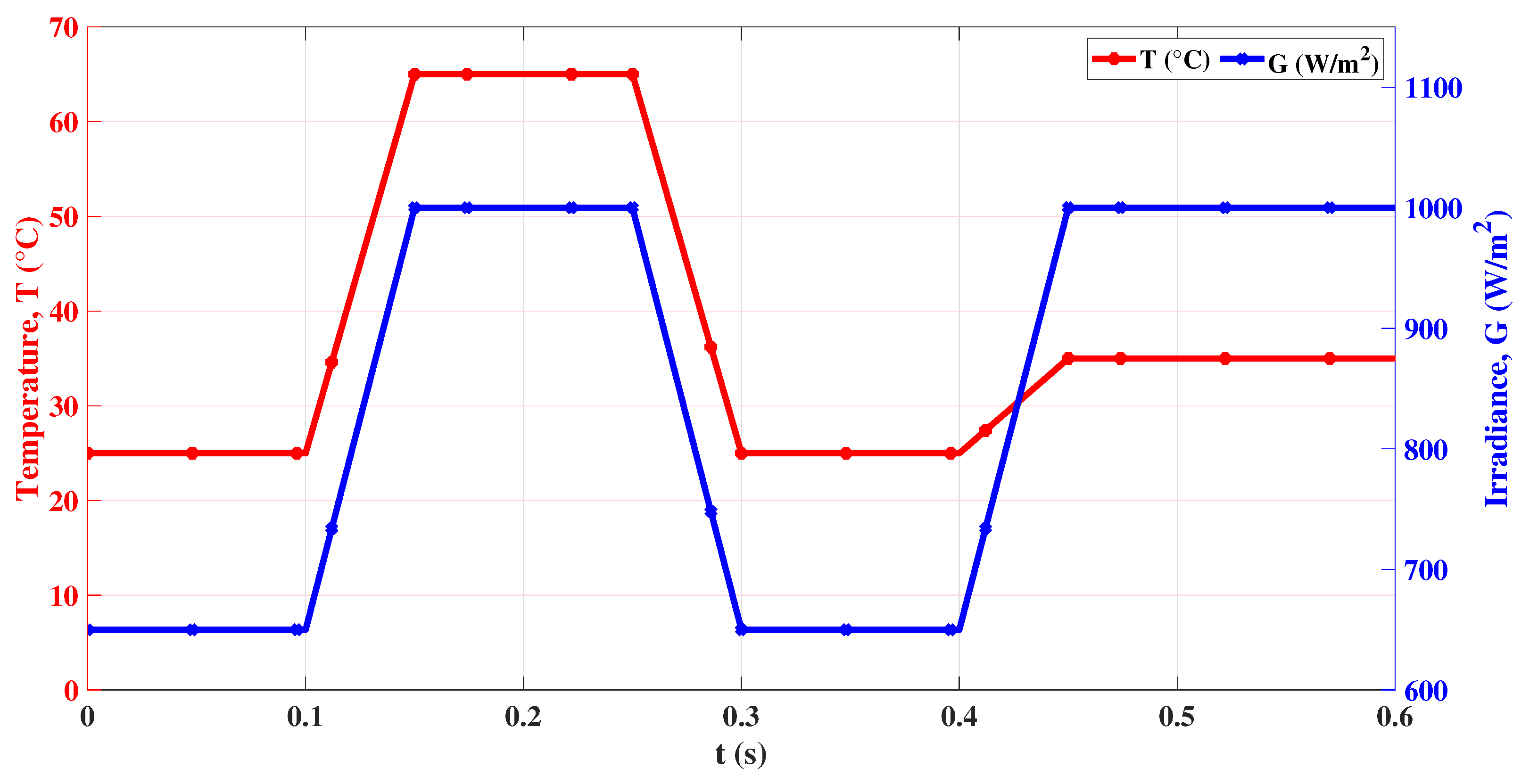
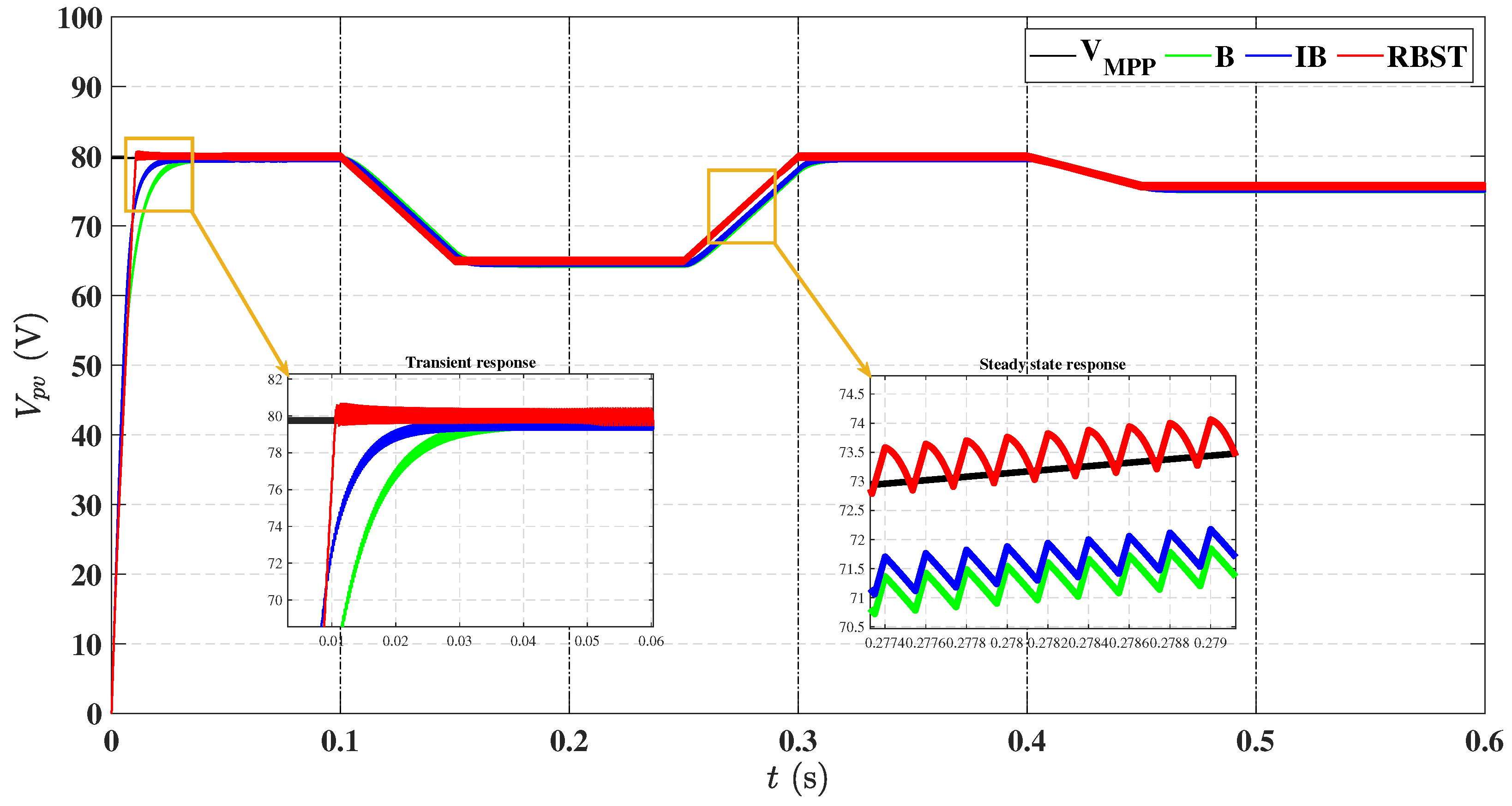
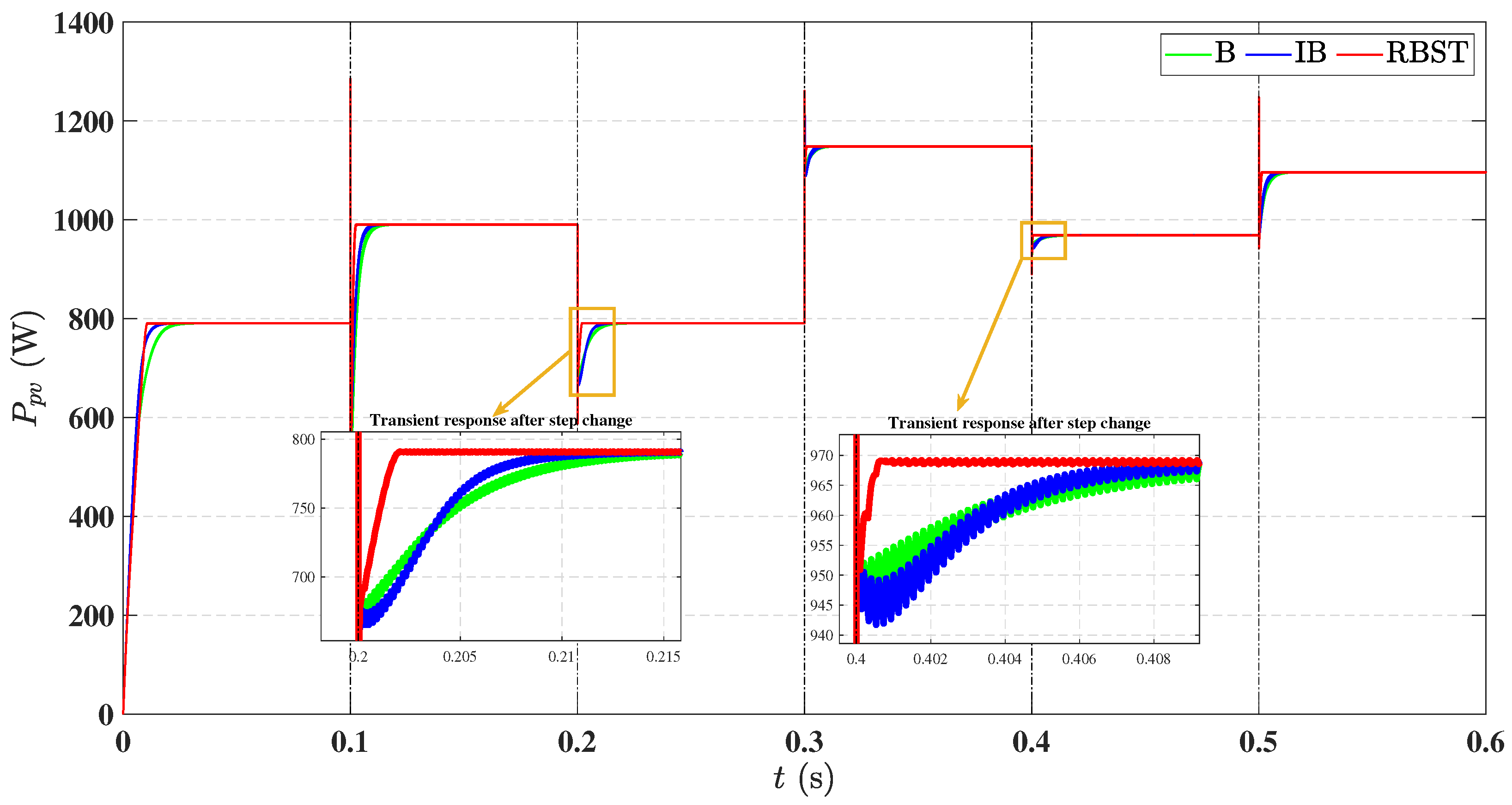
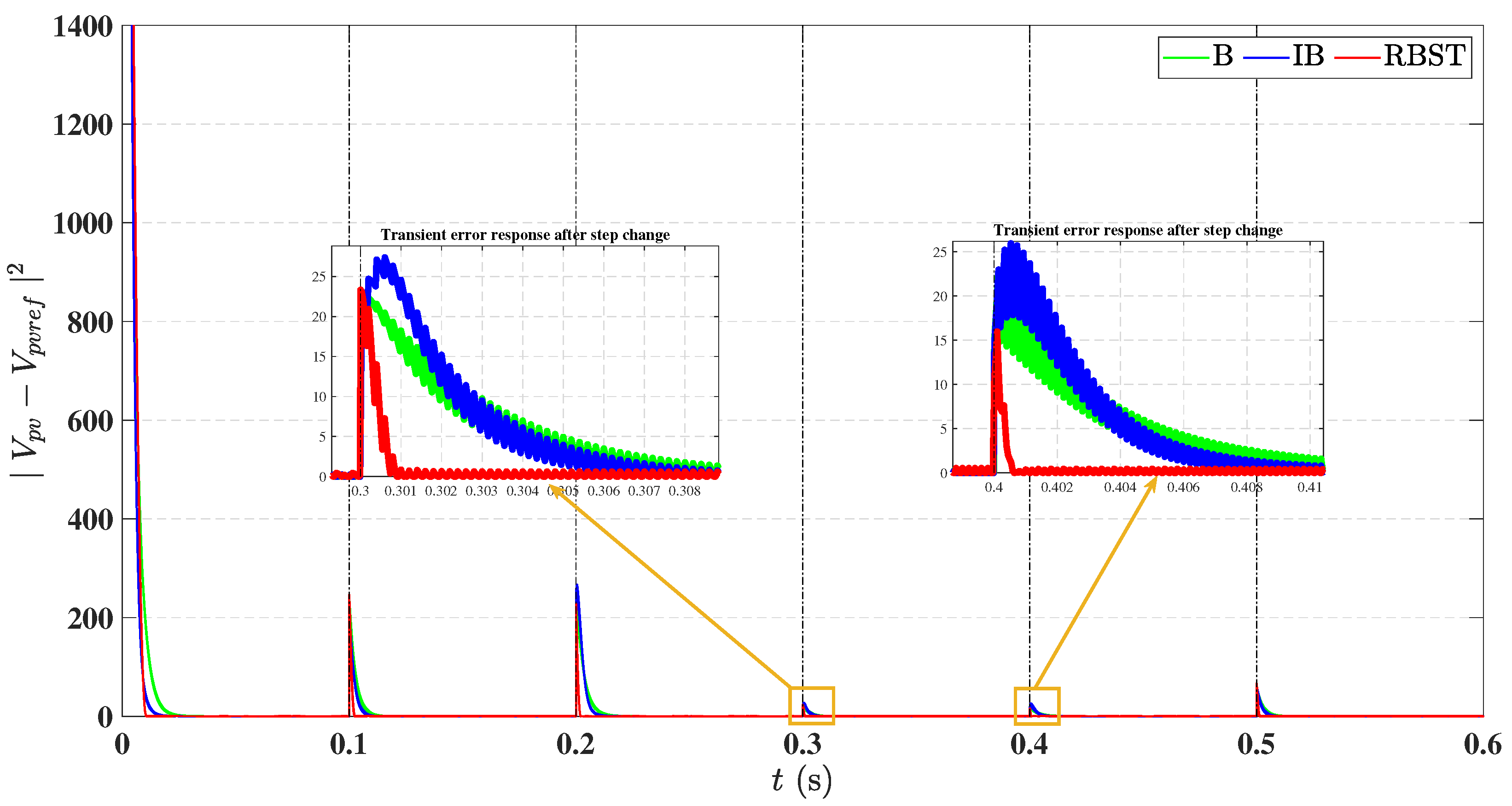
6.2. Sudden Step Changes in Irradiance and Temperature
6.3. Performance Comparison Under Partial Shading Conditions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating Current |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| DC | Direct Current |
| GIS | Geographical Information System |
| LST | Land Surface Temperature |
| MPP | Maximum Power Point |
| MPPT | Maximum Power Point Tracking |
| NIBBPC | Non-inverting Buck–Boost Power Converter |
| OCV | Open-Circuit Voltage |
| P&O | Perturb & Observe |
| PV | Photovoltaic |
| PWM | Pulse Width Modulation |
| RESs | Renewable Energy Sources |
| RBST | Robust Backstepping Super-Twisting |
| SCC | Short-Circuit Current |
| SMC | Sliding Mode Control |
References
- Ahmad, F.F.; Ghenai, C.; Hamid, A.K.; Bettayeb, M. Application of sliding mode control for maximum power point tracking of solar photovoltaic systems: A comprehensive review. Annu. Rev. Control 2020, 49, 173–196. [Google Scholar] [CrossRef]
- Hadj Salah, Z.B.; Krim, S.; Hajjaji, M.A.; Alshammari, B.M.; Alqunun, K.; Alzamil, A.; Guesmi, T. A new efficient cuckoo search MPPT algorithm based on a super-twisting sliding mode controller for partially shaded standalone photovoltaic system. Sustainability 2023, 15, 9753. [Google Scholar] [CrossRef]
- Ali, K.; Khan, L.; Khan, Q.; Ullah, S.; Ahmad, S.; Mumtaz, S.; Karam, F.W.; Naghmash. Robust integral backstepping based nonlinear MPPT control for a PV system. Energies 2019, 12, 3180. [Google Scholar] [CrossRef]
- Harrison, A.; Nguimfack-Ndongmo, J.D.D.; Alombah, N.H.; Kazé, C.V.A.; Kuate-Fochie, R.; Asoh, D.A.; Nfah, E.M. Robust nonlinear MPPT controller for PV energy systems using PSO-based integral backstepping and artificial neural network techniques. Int. J. Dyn. Control 2024, 12, 1598–1615. [Google Scholar] [CrossRef]
- Ali, K.; Khan, Q.; Ullah, S.; Khan, I.; Khan, L. Nonlinear robust integral backstepping based MPPT control for stand-alone photovoltaic system. PLoS ONE 2020, 15, e0231749. [Google Scholar] [CrossRef]
- Ali, K.; Khan, Q.; Khan, L.; Khan, U.A.; Ullah, A. MPPT for photovoltaic system using non-linear hybrid robust integral backstepping controller. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Reisi, A.R.; Moradi, M.H.; Jamasb, S. Classification and comparison of maximum power point tracking techniques for photovoltaic system: A review. Renew. Sustain. Energy Rev. 2013, 19, 433–443. [Google Scholar] [CrossRef]
- Bhatnagar, P.; Nema, R.K. Maximum power point tracking control techniques: State-of-the-art in photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 23, 224–241. [Google Scholar] [CrossRef]
- Lapkitticharoenchai, Y.; Jangwanitlert, A. Lookup table technique by using irradiation intensity and duty cycle for faster MPPT application. In Proceedings of the 2023 8th International Conference on Business and Industrial Research (ICBIR), Bangkok, Thailand, 18–19 May 2023; pp. 1–5. [Google Scholar]
- González-Castaño, C.; Lorente-Leyva, L.L.; Muñoz, J.; Restrepo, C.; Peluffo-Ordóñez, D.H. An MPPT strategy based on a surface-based polynomial fitting for solar photovoltaic systems using real-time hardware. Electronics 2021, 10, 206. [Google Scholar] [CrossRef]
- Mazumdar, D.; Sain, C.; Biswas, P.K.; Sanjeevikumar, P.; Khan, B. Overview of solar photovoltaic MPPT methods: A state of the art on conventional and artificial intelligence control techniques. Int. Trans. Electr. Energy Syst. 2024, 2024, 8363342. [Google Scholar] [CrossRef]
- Kumar, V.; Bindal, R.K. MPPT technique used with perturb and observe to enhance the efficiency of a photovoltaic system. Mater. Today Proc. 2022, 69, A6–A11. [Google Scholar] [CrossRef]
- Ali, Z.; Abbas, S.Z.; Mahmood, A.; Ali, S.W.; Javed, S.B.; Su, C.L. A study of a generalized photovoltaic system with MPPT using perturb and observer algorithms under varying conditions. Energies 2023, 16, 3638. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of the incremental conductance maximum power point tracking algorithm. IEEE Trans. Sustain. Energy 2012, 4, 108–117. [Google Scholar] [CrossRef]
- Moradi, M.H.; Reisi, A.R. A hybrid maximum power point tracking method for photovoltaic systems. Sol. Energy 2011, 85, 2965–2976. [Google Scholar] [CrossRef]
- Yang, C.Y.; Hsieh, C.Y.; Feng, F.K.; Chen, K.H. Highly efficient analog maximum power point tracking (AMPPT) in a photovoltaic system. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 1546–1556. [Google Scholar] [CrossRef]
- Armghan, H.; Ahmad, I.; Armghan, A.; Khan, S.; Arsalan, M. Backstepping based non-linear control for maximum power point tracking in photovoltaic system. Sol. Energy 2018, 159, 134–141. [Google Scholar] [CrossRef]
- Arsalan, M.; Iftikhar, R.; Ahmad, I.; Hasan, A.; Sabahat, K.; Javeria, A. MPPT for photovoltaic system using nonlinear backstepping controller with integral action. Sol. Energy 2018, 170, 192–200. [Google Scholar] [CrossRef]
- Chiu, C.S.; Ouyang, Y.L.; Ku, C.Y. Terminal sliding mode control for maximum power point tracking of photovoltaic power generation systems. Sol. Energy 2012, 86, 2986–2995. [Google Scholar] [CrossRef]
- Koofigar, H.R. Adaptive robust maximum power point tracking control for perturbed photovoltaic systems with output voltage estimation. ISA Trans. 2016, 60, 285–293. [Google Scholar] [CrossRef]
- Pradhan, R.; Subudhi, B. Double integral sliding mode MPPT control of a photovoltaic system. IEEE Trans. Control Syst. Technol. 2015, 24, 285–292. [Google Scholar] [CrossRef]
- Ghaffarzadeh, N.; Bijani, S. Dual surface sliding mode controller for photovoltaic systems enhanced by a ripple domain search maximum power point tracking algorithm for fast changing environmental conditions. IET Renew. Power Gener. 2016, 10, 611–622. [Google Scholar] [CrossRef]
- Zhang, L.; Tao, R.; Bai, J.; Zeng, D. An Improved Sliding Mode Model Reference Adaptive System Observer for PMSM Applications. Expert Syst. Appl. 2024, 250, 123907. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X. Sliding Mode Control of Surface-Mounted Permanent Magnet Synchronous Motor Based on Composite Adaptive Reaching Law. In Proceedings of the 2025 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Jinan, China, 15–17 August 2025; pp. 1–5. [Google Scholar]
- Clementini, E.; Patrizi, R.; Santic, M.; Villante, C. A GeoSpatial Information System for Photovoltaic Plants Development and Monitoring. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 48, 45–50. [Google Scholar] [CrossRef]
- Ali, K.; Clementini, E.; Patrizi, R.; Santic, M.; Villante, C. CNN-Based Downscaling of Land Surface Temperature and Scaling Effect Analysis Using Multi-Sensor Satellite Data: A Case Study in L’Aquila, Italy. In Proceedings of the GeoVisions2025: Symposium on GeoSpatial Technologies: Visions and Horizons, Çanakkale, Turkey, 8–10 October 2025. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive approach to modeling and simulation of photovoltaic arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Ali, K.; Khan, L.; Khan, Q.; Ullah, S.; Ali, N. Neurofuzzy robust backstepping based MPPT control for photovoltaic system. Turk. J. Electr. Eng. Comput. Sci. 2021, 29, 421–436. [Google Scholar] [CrossRef]
- Kim, I.-S. Robust maximum power point tracker using sliding mode controller for the three-phase grid-connected photovoltaic system. Sol. Energy 2007, 81, 405–414. [Google Scholar] [CrossRef]
- Kim, I.-S. Sliding mode controller for the single-phase grid-connected photovoltaic system. Appl. Energy 2006, 83, 1101–1115. [Google Scholar] [CrossRef]
- Rashid, M.H. Power Electronics Handbook: Devices, Circuits and Applications; Elsevier: Oxford, UK, 2010. [Google Scholar]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Almasi, O.N.; Fereshtehpoor, V.; Khooban, M.H.; Blaabjerg, F. Analysis, control and design of a non-inverting buck-boost converter: A bump-less two-level T–S fuzzy PI control. ISA Trans. 2017, 67, 515–527. [Google Scholar] [CrossRef]
- Chen, J.; Maksimović, D.; Erickson, R.W. Analysis and design of a low-stress buck-boost converter in universal-input PFC applications. IEEE Trans. Power Electron. 2006, 21, 320–329. [Google Scholar] [CrossRef]
- Siddique, N.; Adeli, H. Computational Intelligence: Synergies of Fuzzy Logic, Neural Networks and Evolutionary Computing; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Krstić, M.; Kanellakopoulos, I.; Kokotović, P.V. Nonlinear and Adaptive Control Design; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Krstić, M.; Smyshlyaev, A. Boundary Control of PDEs: A Course on Backstepping Designs; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2008. [Google Scholar]
- Slotine, J.-J.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Marquez, H.J. Nonlinear Control Systems: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Li, S.; Yu, X.; Fridman, L.; Man, Z.; Wang, X. Advances in Variable Structure Systems and Sliding Mode Control—Theory and Applications; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
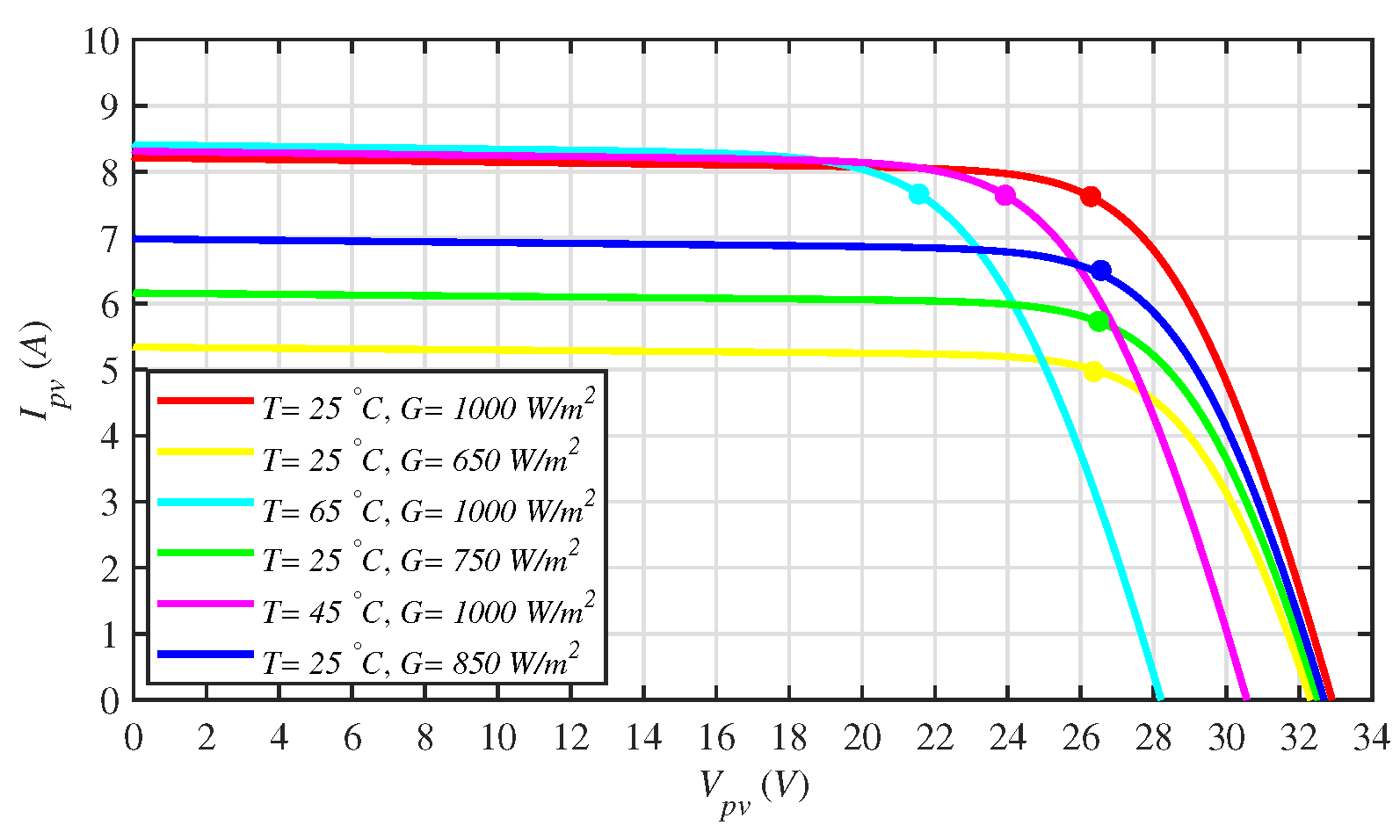
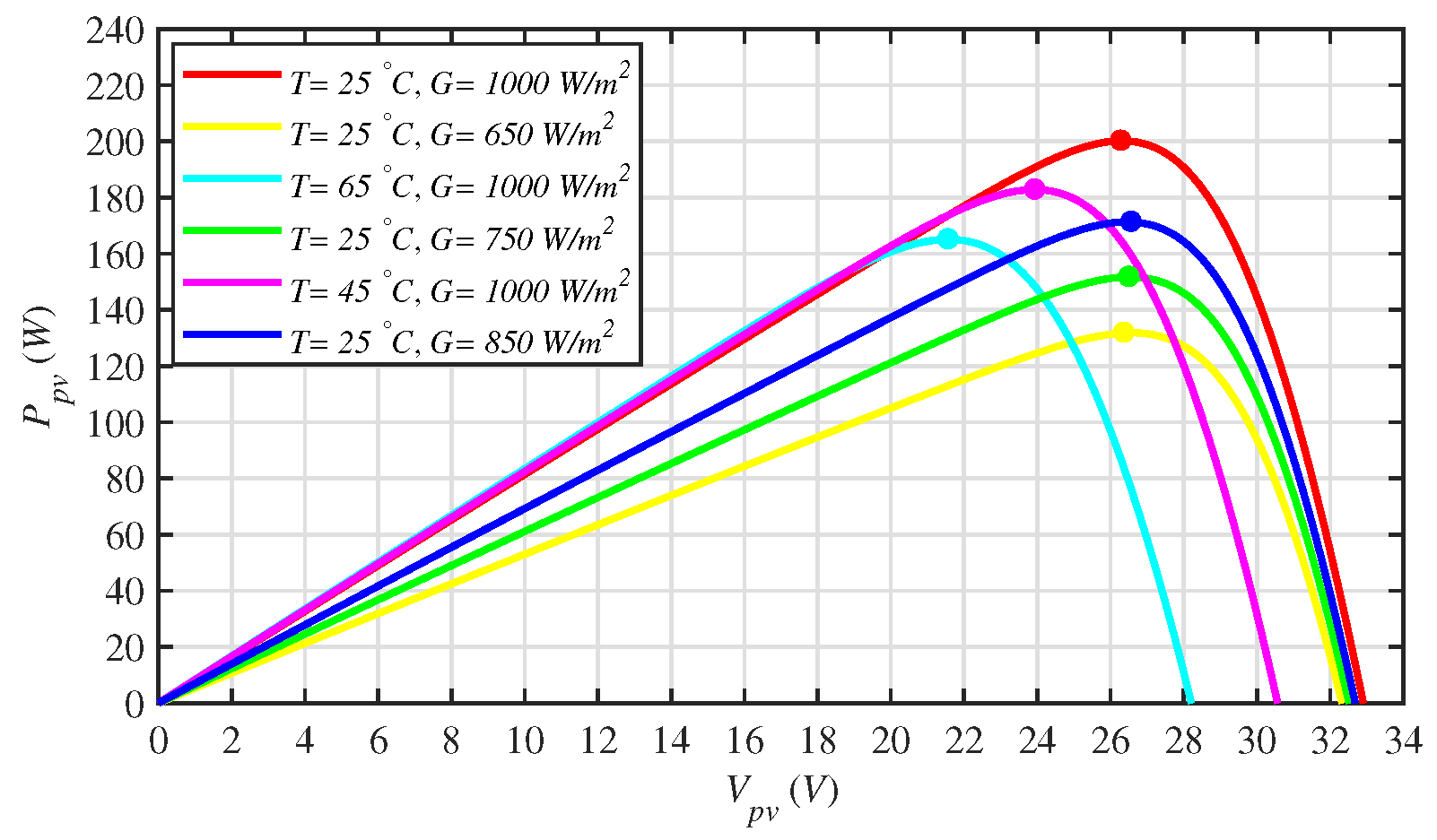
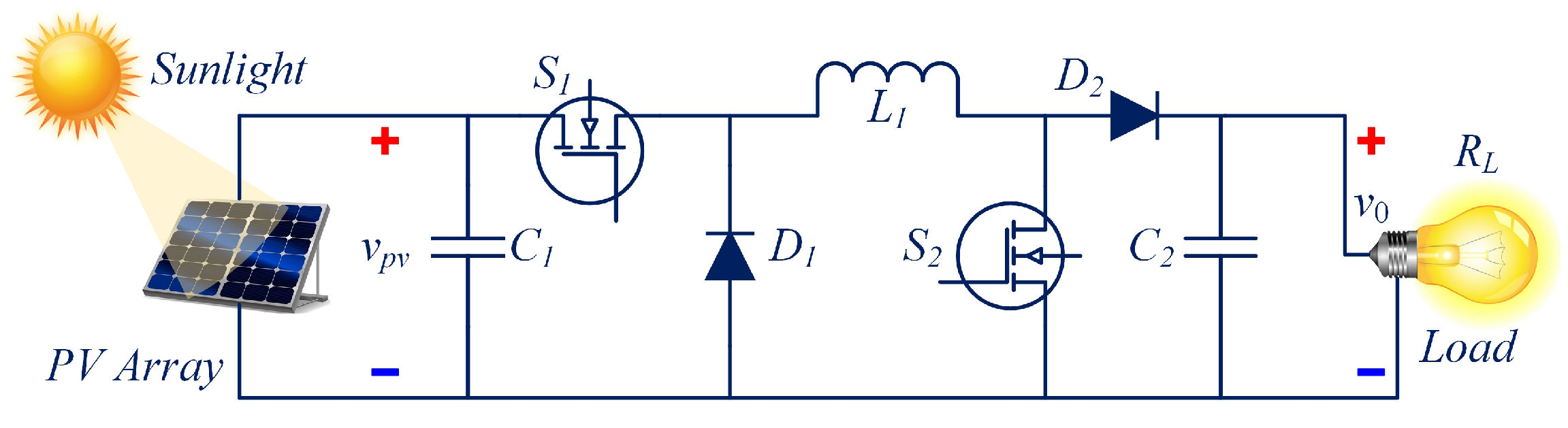
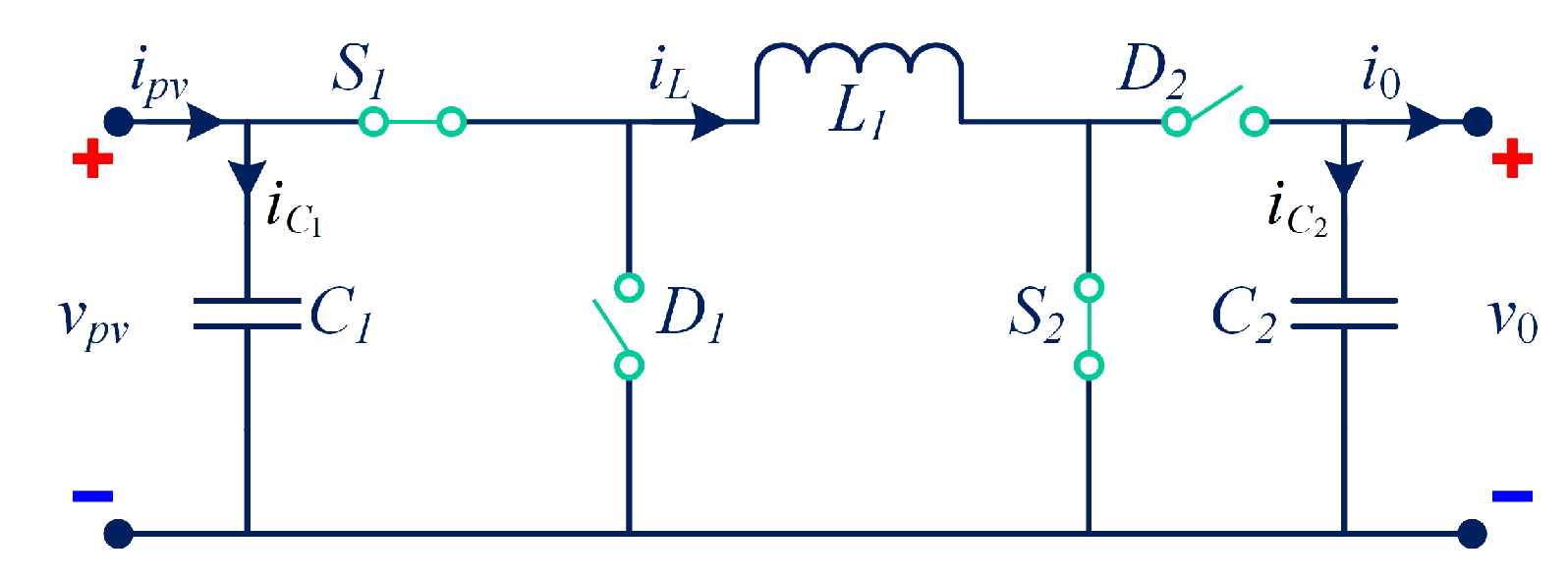
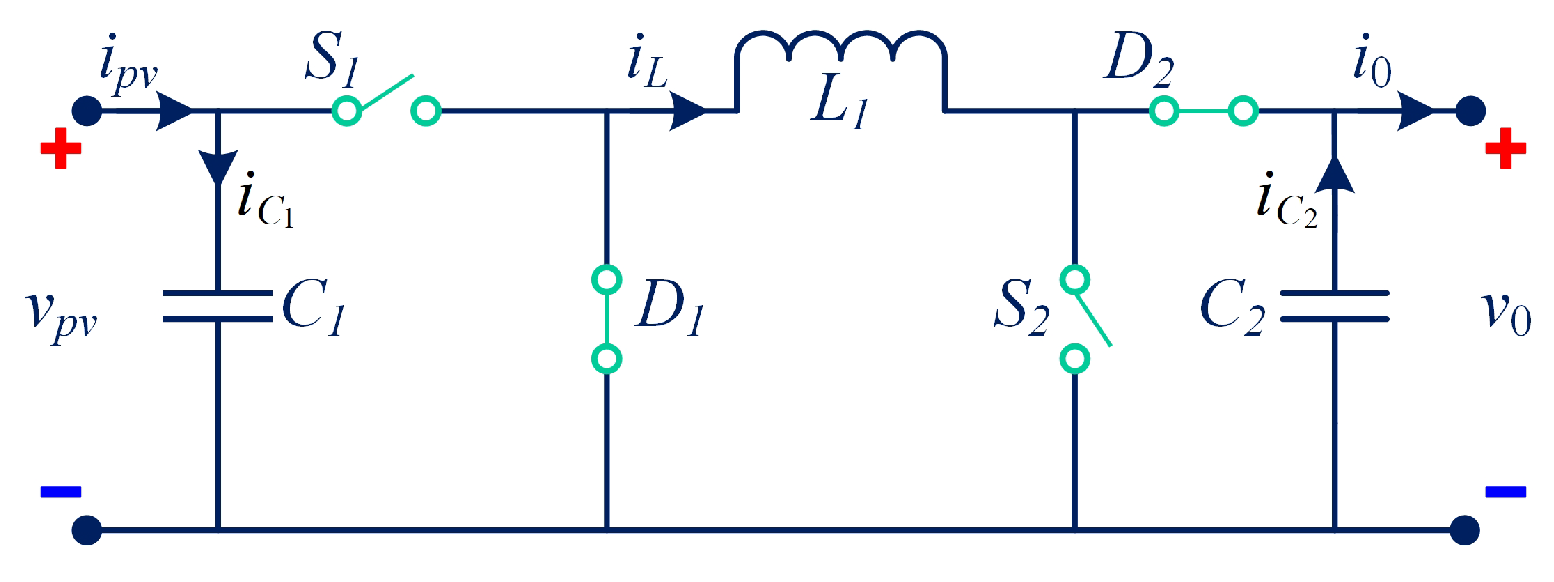
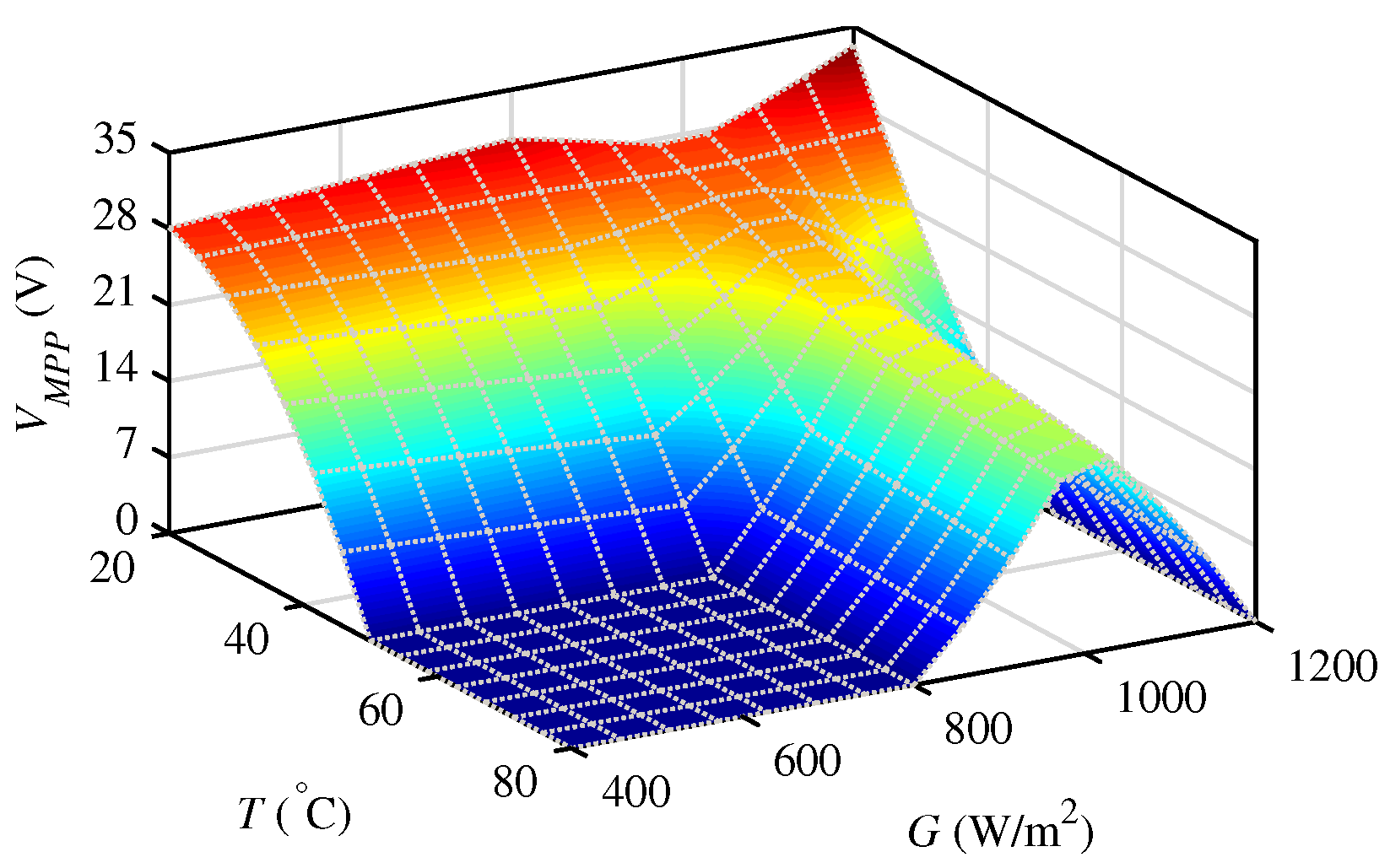
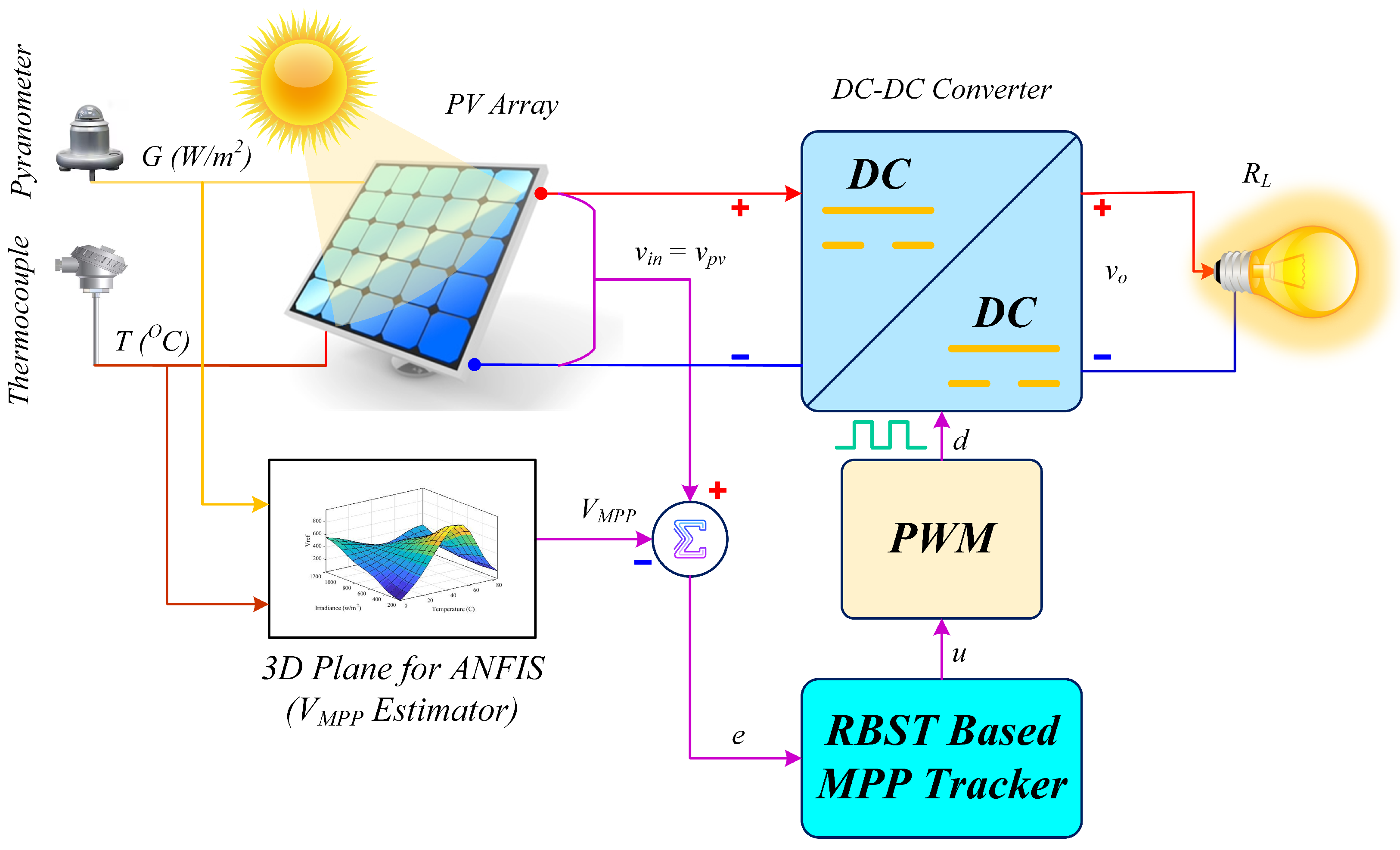

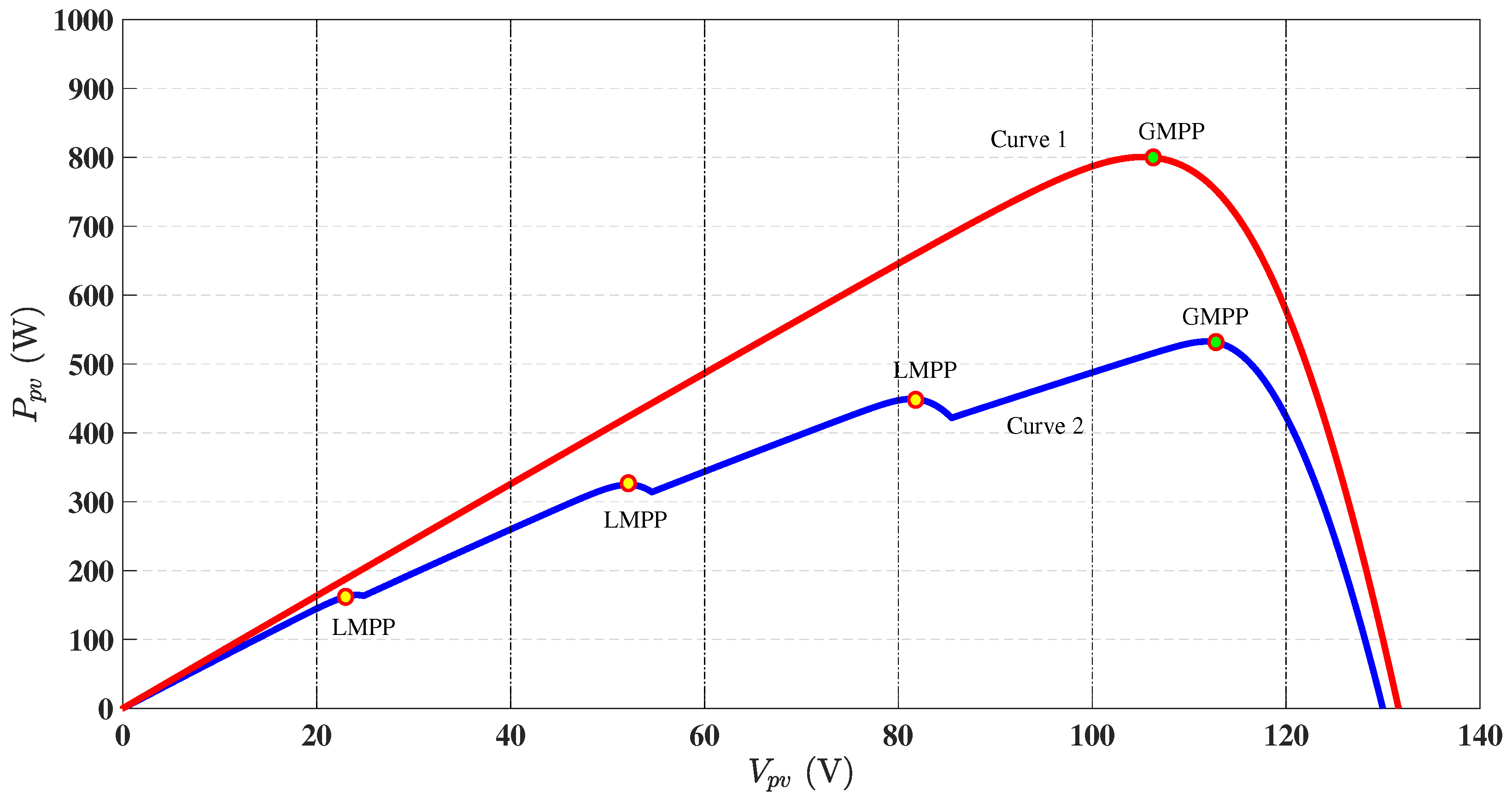
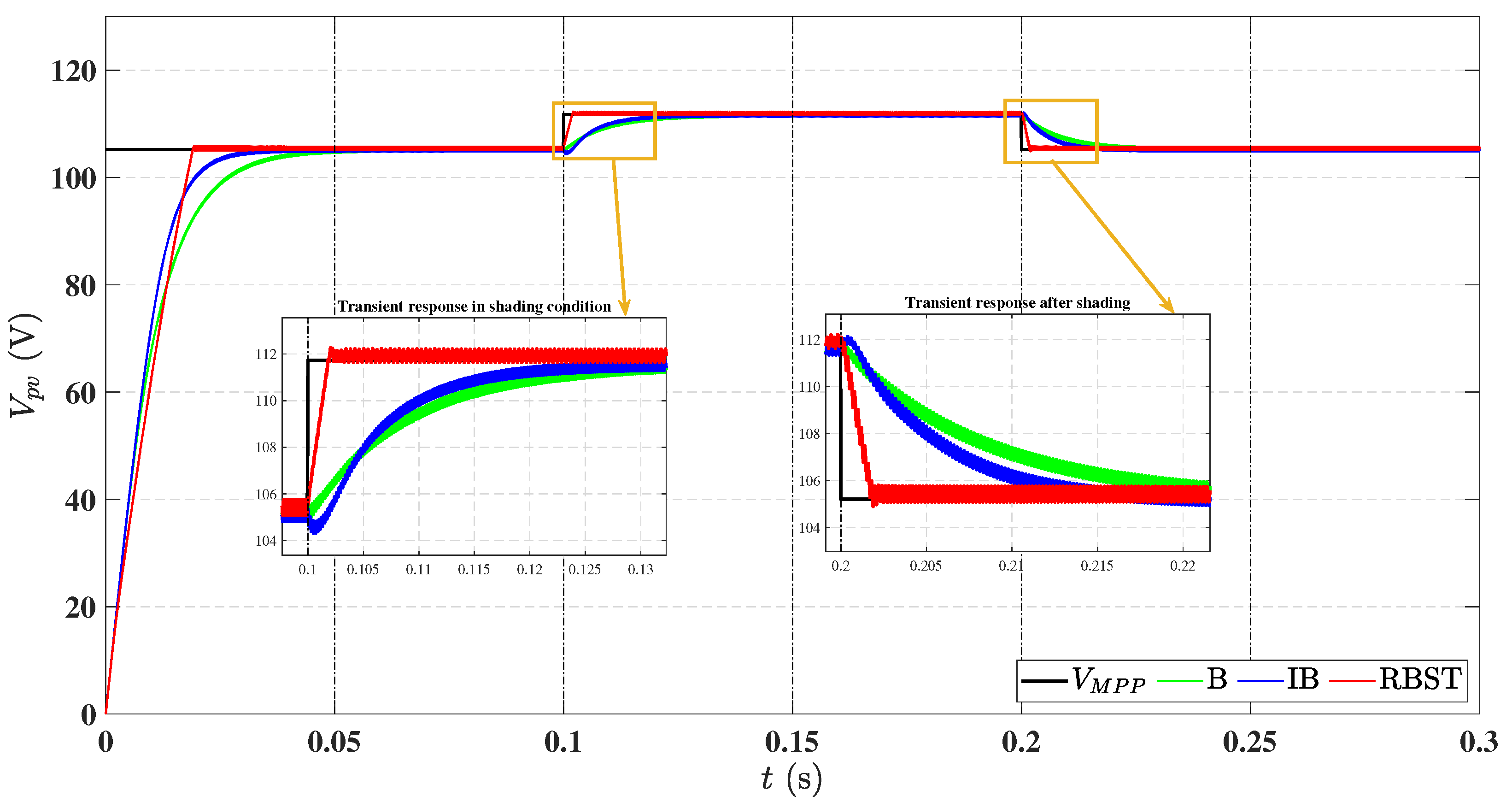
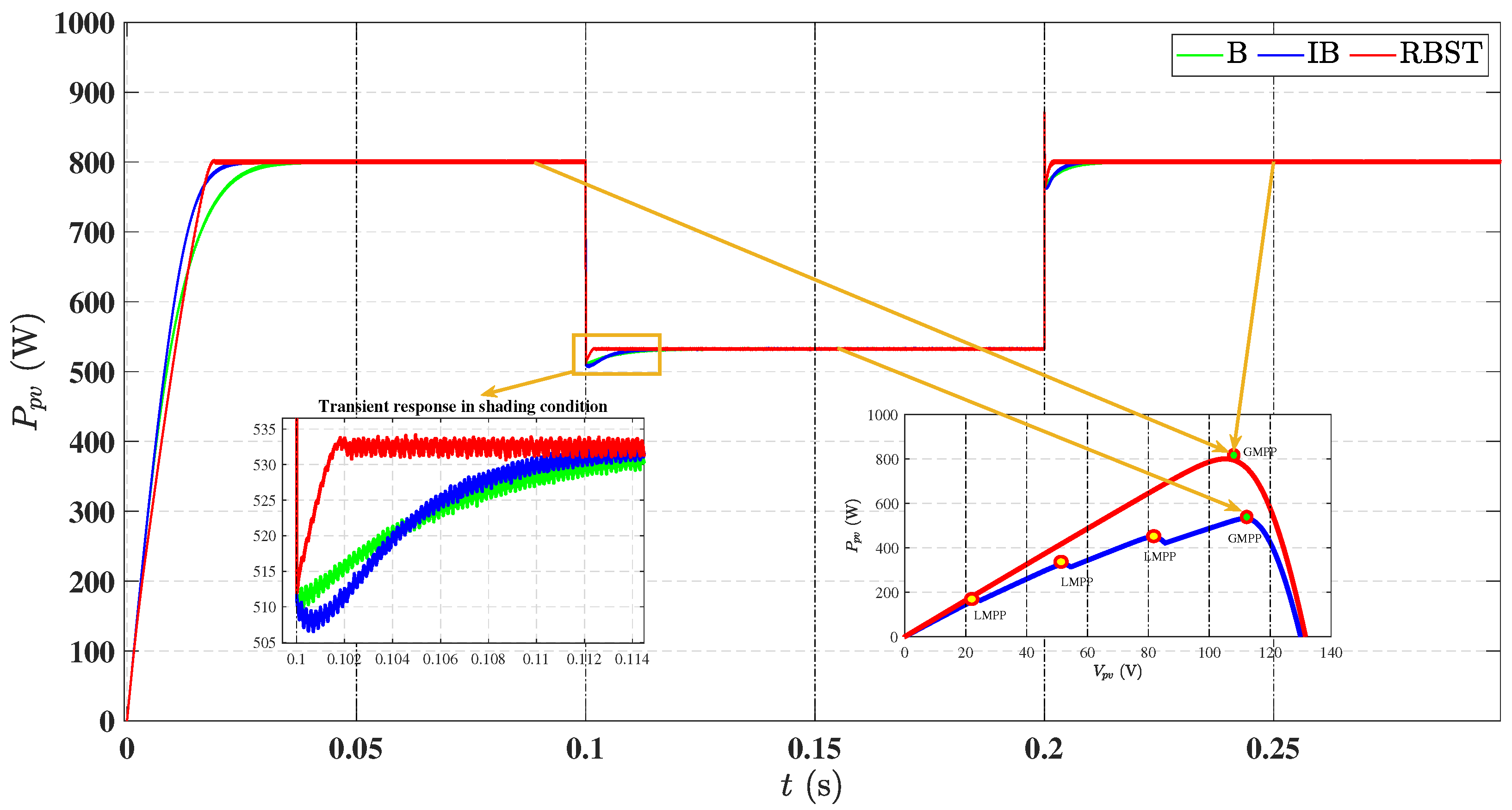

| S. No. | Parameters | Values |
|---|---|---|
| 1 | Number of series-connected cells per module, | 54 |
| 2 | Number of series-connected modules per string | 1 |
| 3 | Number of parallel-connected strings per array, | 1 |
| 4 | Maximum power, | 200.143 W |
| 5 | Voltage @ maximum power, | 26.30 V |
| 6 | Current @ maximum power, | 7.61 V |
| 7 | Open-circuit voltage, | 32.90 V |
| 8 | Short-circuit current, | 8.21 A |
| 9 | Light-generated current, | 8.2288 A |
| 10 | Diode saturation current, | |
| 11 | Temperature coefficient of | −0.35502 °C |
| 12 | Temperature coefficient of | 0.06 °C |
| 13 | Shunt resistance, | 150.6921 |
| 14 | Series resistance, | 0.34483 |
| 15 | Diode ideality factor, | 0.97736 |
| S. No. | Operating Mode Name | (During ) | (During ) |
|---|---|---|---|
| 1 | Buck | Switched ON and OFF | OFF (Continuously) |
| 2 | Boost | ON (Continuously) | Switched ON and OFF |
| 3 | Buck–Boost | Switched ON and OFF | Switched ON and OFF |
| S. No. | Parameters | Values |
|---|---|---|
| 1 | Input capacitor, | 1 |
| 2 | Output capacitor, | 48 |
| 3 | Inductor, L | 20 |
| 4 | Load resistance, | 50 |
| S. No. | Parameters | Description |
|---|---|---|
| 1 | Number of inputs to ANFIS | 2 |
| 2 | Number of outputs of ANFIS | 1 |
| 3 | ANFIS type chosen | TSK (Takagi–Sugeno–Kang) |
| 4 | Membership function type chosen | Triangular (trimf) |
| 5 | No. of membership functions chosen for each input | 3 |
| 6 | Error tolerance for ANFIS training | 0 |
| 7 | Number of epochs chosen for ANFIS training | 10 |
| 8 | Minimal training RMSE | 0.01348 |
| S. No. | Parameters | Values |
|---|---|---|
| 1 | Constant, | 12 |
| 2 | Constant, | 4500 |
| 3 | Constant, | 5100 |
| 4 | Constant, | 70 |
| 5 | Constant, | 0.15 |
| 6 | Constant, | 0.7 |
| Metric | Backstepping (B) | Integral Backstepping (IB) | RBST (Proposed) |
|---|---|---|---|
| Rise Time (s) | 0.054 | 0.038 | 0.018 |
| Mean SSE (V) | 0.7040 | 0.6371 | 0.3015 |
| RMSE (V) | 1.4559 | 1.4412 | 0.5718 |
| Steady-State Error (%) | 0.67 | 0.61 | 0.29 |
| Efficiency (%) | 98.01 | 98.16 | 99.61 |
| Time (s) | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
|---|---|---|---|---|---|---|
| T (°C) | 25 | 65 | 25 | 35 | 25 | 45 |
| G ( /2) | 650 | 1000 | 650 | 1000 | 800 | 1000 |
| (W) | 790 | 990 | 790 | 1149 | 969 | 1096 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, K.; Ullah, S.; Clementini, E. Robust Backstepping Super-Twisting MPPT Controller for Photovoltaic Systems Under Dynamic Shading Conditions. Energies 2025, 18, 5134. https://doi.org/10.3390/en18195134
Ali K, Ullah S, Clementini E. Robust Backstepping Super-Twisting MPPT Controller for Photovoltaic Systems Under Dynamic Shading Conditions. Energies. 2025; 18(19):5134. https://doi.org/10.3390/en18195134
Chicago/Turabian StyleAli, Kamran, Shafaat Ullah, and Eliseo Clementini. 2025. "Robust Backstepping Super-Twisting MPPT Controller for Photovoltaic Systems Under Dynamic Shading Conditions" Energies 18, no. 19: 5134. https://doi.org/10.3390/en18195134
APA StyleAli, K., Ullah, S., & Clementini, E. (2025). Robust Backstepping Super-Twisting MPPT Controller for Photovoltaic Systems Under Dynamic Shading Conditions. Energies, 18(19), 5134. https://doi.org/10.3390/en18195134








