Computational Analysis of the Effects of Power on the Electromagnetic Characteristics of Microwave Systems with Plasma
Abstract
1. Introduction
- (i)
- Extend the plasma model [32] by adding a direct approximation of the link between plasma frequency and MW power;
- (ii)
- Perform an instructive computational analysis of a 2.45 GHz system resembling certain plasma applicators.
2. Computational Method
2.1. Plasma Model
2.2. Plasma Frequency as Function of Power
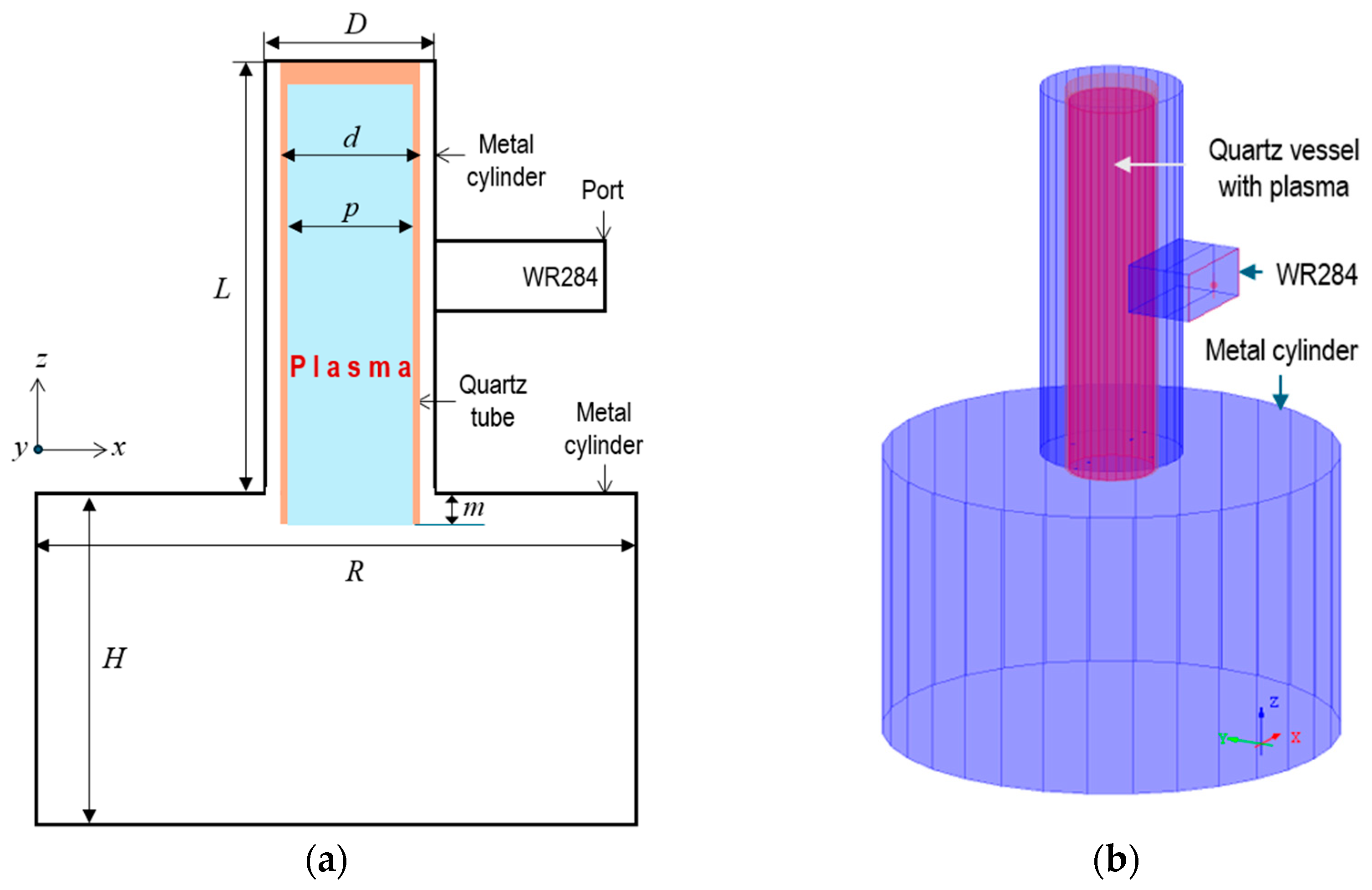
3. Plasma Applicator and Its Model
4. Results of Computational Analysis
4.1. Impact of Microwave Power
4.2. Influence of Plasma Geometry
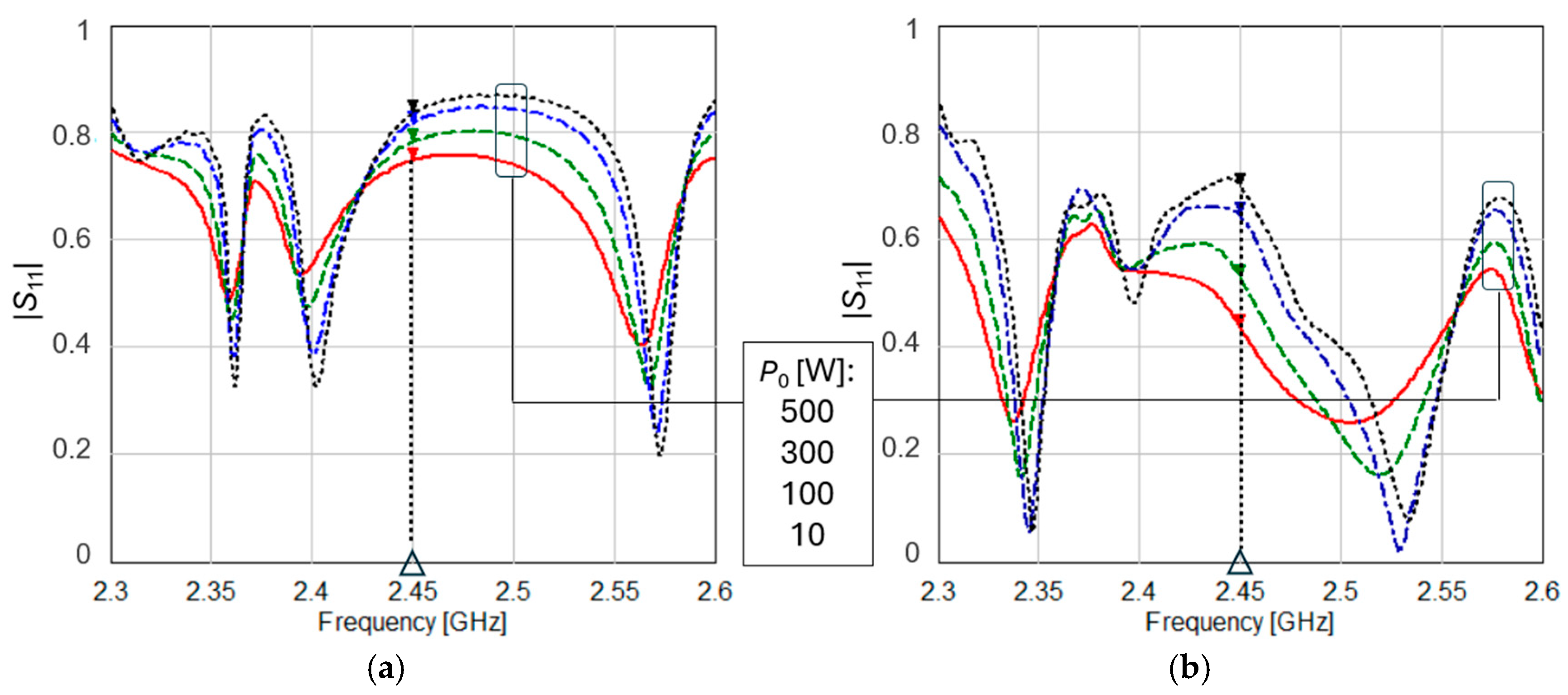
4.3. Effect of Gas
4.4. Effect of Pressure
4.5. Variation in the Electric Field
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hessel, V.; Cravotto, G.; Fitzpatrick, P.; Patil, B.S.; Lang, J.; Bonrath, W. Industrial applications of plasma, microwave and ultrasound techniques: Nitrogen-fixation and hydrogenation reactions. Chem. Eng. Process. 2013, 71, 19–30. [Google Scholar] [CrossRef]
- Penkov, O.V.; Khadem, M.; Lim, W.-S.; Kim, D.-E. A review of recent applications of atmospheric pressure plasma jets for materials processing. J. Coat. Technol. Res. 2015, 12, 225–235. [Google Scholar] [CrossRef]
- Mallik, A.K. Microwave plasma CVD grown single crystal diamonds—A review. J. Coat. Sci. Technol. 2016, 3, 75–99. [Google Scholar] [CrossRef]
- Cohick, Z.; Luo, W.; Perini, S.; Baker, A.; Wolfe, D.; Lanagan, M. A novel, all-dielectric, microwave plasma generator towards development of plasma metamaterials. Appl. Phys. Express 2016, 9, 116201. [Google Scholar] [CrossRef]
- De la Fuente, J.F.; Kiss, A.A.; Radoiu, M.T.; Stefanidis, G.D. Microwave plasma emerging technologies for chemical processes. J. Chem. Technol. Biotechnol. 2017, 92, 2495–2505. [Google Scholar] [CrossRef]
- Tiwari, S.; Caiola, A.; Bai, X.; Lalsare, A.; Hu, J. Microwave plasma-enhanced and microwave heated chemical reactions. Plasma Chem. Plasma Process. 2020, 40, 1–23. [Google Scholar] [CrossRef]
- Achkasov, K. Microwave-induced plasma—From academia to industry. In Proceedings of the 2021 European Microwave Week, Workshop W-07 “High-Power Microwave Industrial Applications”, Utrecht, The Netherlands, 10–15 January 2021. [Google Scholar]
- Bardos, L.; Barankova, H. Microwave Plasma Sources and Methods in Processing Technology; IEEE Press/Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Cho, C.H.; Kim, J.H.; Yang, J.K.; Park, I.S.; Choi, Y.-S.; Kang, I.J. Dry reforming process using microwave plasma generator with high carbon dioxide conversion efficiency for syngas production. Fuel 2024, 361, 130707. [Google Scholar]
- Zhu, H.; Huang, Y.; Yin, S.; Zhang, W. Microwave plasma setups for CO2 conversion: A mini-review. Green Energy Resour. 2024, 2, 100061. [Google Scholar] [CrossRef]
- Magarotto, M.; Sadeghikia, F.; Schenato, L.; Rocco, D.; Santagiustine, M.; Galtarossa, A.; Horestani, A.K.; Capobianco, A.-D. Plasma antennas: A comprehensive review. IEEE Access 2024, 12, 80468. [Google Scholar] [CrossRef]
- Magarotto, M.; Schenato, L.; Santagiustine, M.; Galtarossa, A.; Capobianco, A.-D. Plasma-based intelligent reflecting surface for beam-steering and polarization conversion. IEEE Access 2023, 11, 43546. [Google Scholar]
- Ong, M.Y.; Nomanbhay, S.; Kusumo, F.; Show, P.L. Application of microwave plasma technology to convert carbon dioxide (CO2) into high value products: A review. J. Clean. Prod. 2022, 336, 130447. [Google Scholar] [CrossRef]
- King, D.; Yaran, M.K.; Schuelke, T.; Grotjohn, T.A.; Reinhard, D.K.; Asmussen, J. Scaling the microwave plasma-assisted chemical vapor diamond deposition process to 150–200 mm substrates. Diam. Relat. Mater. 2008, 17, 520–524. [Google Scholar] [CrossRef]
- Rabinovich, A.; Nirenberg, G.; Kocagoz, S.; Surace, M.; Sales, C.; Fridman, A. Scaling up of non-thermal gliding arc plasma systems for industrial applications. Plasma Chem. Plasma Process. 2022, 42, 35–50. [Google Scholar] [CrossRef]
- Sung-Spitzl, H.; Spitzl, R. Scale-up of microwave resonator plasma sources for large area. In Proceedings of the 47th Annual Technical Conference of the Society of Vacuum Coaters, Dallas, TX, USA, 24–29 April 2004; pp. 483–485. [Google Scholar]
- Radoiu, M.; Mello, A. Scaling up microwave excited plasmas—An alternative technology for industrial decarbonization. Plasma Process. Polym. 2024, 21, e2300200. [Google Scholar] [CrossRef]
- Zoubian, F.; Renaut, N.; Latrasse, L. Distributed elementary ECR microwave plasma sources supplied by solid state generators for production of large area plasmas without scale limitation: Plasma density measurements and comparison with simulation. Plasma Res. Express 2021, 3, 025010. [Google Scholar] [CrossRef]
- Fiore, M.; Guissart, A.; Di Modugna, R.; Lobascio, F.; Di Modugno, N.; De Nicolo, T.; Bruno, C. Solid-state generator array for dynamic plasma shaping. In Proceedings of the 59th IMPI’s Microwave Power Symposium, Edmonton, AB, Canada, 24–26 June 2025; pp. 45–47. [Google Scholar]
- Baeva, M.; Hempel, F.; Baierl, H.; Trautvetter, T.; Foest, R.; Loffhagen, D. Two- and three-dimensional simulation analysis of microwave excited plasma for deposition applications: Operation with argon at atmospheric pressure. J. Phys. D Appl. Phys. 2018, 51, 385202. [Google Scholar] [CrossRef]
- Baeva, M.; Stankov, M.; Trautvetter, T.; Methling, R.; Hempel, F.; Loffhagen, D.; Foest, R. The effect of oxygen admixture on the properties of microwave generated plasma in Ar–O2: A modelling study. J. Phys. D Appl. Phys. 2021, 54, 355205. [Google Scholar] [CrossRef]
- Zhang, W.; Tao, J.; Huang, K.; Wu, L. Numerical investigation of the surface wave formation in a microwave plasma torch. IEEE Trans. Plasma Sci. 2017, 45, 2929–2939. [Google Scholar] [CrossRef]
- Bosi, F.; Magarotto, M.; de Carlo, P.; Manente, M.; Trezzolani, F.; Pavarin, D.; Melazzi, D.; Alotto, P.; Bertani, R. Numerical simulation of vibrationally active Ar-H2 microwave plasma. In Proceedings of the 2016 COMSOL Conference, Munich, Germany, 12–14 October 2016. [Google Scholar]
- Nowakowska, H.; Jasiński, M.; Mizeraczyk, J. Electric field distributions and energy transfer in waveguide-based axial-type microwave plasma source. In Proceedings of the 2008 COMSOL Conference, Hannover, Germany, 4–6 November 2008. [Google Scholar]
- Ong, M.Y.; Chia, S.R.; Milano, J.; Nomanbhay, S.; Chew, K.W.; Yusaf, T.; Show, P.L. Simulation of argon-excited microwave plasma reactor for green energy and CO2 conversion application. Appl. Energy 2024, 353, 122160. [Google Scholar] [CrossRef]
- Lejeune, A. Atmospheric plasma modelling applied for thermal plasma assisted processes. In Proceedings of the 2024 COMSOL Conference, Florence, Italy, 22–24 October 2024. [Google Scholar]
- COMSOL Multiphyscis. Available online: https://www.comsol.com (accessed on 8 August 2025).
- Yakovlev, V.V. Examination of contemporary electromagnetic software capable of modeling problems of microwave heating. In Advances in Microwave and Radio Frequency Processing; Willert-Porada, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 178–190. [Google Scholar]
- Celuch, M.; Gwarek, W.K. Properties of the FDTD method relevant to the analysis of microwave power problems. J. Microw. Power Electromagn. Energy 2007, 41, 62–80. [Google Scholar] [CrossRef] [PubMed]
- Celuch, M.; Kopyt, P.; Olszewska-Placha, M. Coupled electromagnetic-thermodynamic simulations of microwave heating problems using the FDTD and FEM methods. In Development of Packaging and Products for Use in Microwave Ovens; Erle, U., Pesheck, P., Lorence, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 459–511. [Google Scholar]
- Williams, C.E.; Yakovlev, V.V. Characterization of microwave plasma in electromagnetic modeling for processing applications. In Proceedings of the 57th IMPI’s Microwave Power Symposium, Denver, CO, USA, 27–29 June 2023; pp. 51–53. [Google Scholar]
- Williams, C.E.; Yakovlev, V.V. Characterization of microwave plasma for electromagnetic modeling in processing applications. J. Microw. Power Electromagn. Energy 2025, 59, 279–290. [Google Scholar] [CrossRef]
- QuickWave, QWED Sp. z o. o. Available online: https://www.qwer.eu (accessed on 8 August 2025).
- Hadidi, K.; Williams, C.E.; Yakovlev, V.V. Computational analysis of electron density effect on power absorption in microwave plasma applicators. In Proceedings of the 59th IMPI’s Microwave Power Symposium, Edmonton, AB, Canada, 24–26 June 2025; pp. 62–64. [Google Scholar]
- Zhang, Q.; Zhang, G.; Wang, L.; Wang, X.; Wang, S.; Chen, Y. Measurement of the electron density in a microwave plasma torch at atmospheric pressure. Appl. Phys. Lett. 2009, 95, 201502. [Google Scholar] [CrossRef]
- Xiao, W.; Liao, Y.; Huang, K. Measuring electron density of atmospheric microwave plasma jet by microwave perturbation method. IEEE Trans. Instrum. Meas. 2022, 71, 8005109. [Google Scholar] [CrossRef]
- Guissart, A.; Richter, T.; Fiore, M.; Muller, R.; Perez-Lopez, E.; Ates, H.; Dingeldein, M.; Baumgaertner, K.-M. Performance study of a solid-state microwave remote plasma source. In Proceedings of the 59th IMPI’s Microwave Power Symposium, Edmonton, AB, Canada, 24–26 June 2025; pp. 42–44. [Google Scholar]
- Latrasse, L.; Radoiu, M.; Nelis, T.; Antonin, O. Self-matching plasma sources using 2.45 GHz solid-state generators: Microwave design and operating performance. J. Microw. Power Electromagn. Energy 2017, 51, 237–258. [Google Scholar] [CrossRef]
- Pauly, S.; Schulz, A.; Walker, M.; Gorath, M.; Baumgärtner, K.; Tovar, G. Modeling and experimental study of remote microwave plasma source for high-rate etching. Chem. Ing. Tech. 2022, 94, 410–416. [Google Scholar] [CrossRef]
- Taylor, K.J.; Yun, S.; Tynan, G.R. Control of plasma parameters by using noble gas admixtures. J. Vac. Sci. Technol. 2004, 22, 2131–2138. [Google Scholar] [CrossRef]
- Hrycak, B.; Czylkowski, D.; Jasinski, M.; Mizeraczyk, J. Tuning characteristics of coaxial microwave plasma source operated with argon, nitrogen and methane at atmospheric pressure. Prz. Elecktrotechniczny (Electr. Rev.) 2012, R 88, 310–312. [Google Scholar]
- Mechenova, V.A.; Yakovlev, V.V. Efficiency optimization for systems and components in microwave power engineering. J. Microw. Power Electromagn. Energy 2004, 39, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Delgado, H.J.; Thursby, M.H. A novel neural network combined with FDTD for the synthesis of a printed dipole antenna. IEEE Trans. Antennas Propag. 2005, 53, 2231–2236. [Google Scholar] [CrossRef]
- Lee, Y.; Filipovic, D.S. ANN based electromagnetic models for the design of RF MEMS switches. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 823–825. [Google Scholar]
- Murphy, E.K.; Yakovlev, V.V. Neural network optimization of complex microwave structures with a reduced number of full-wave analyses. Int. J. RF Microw. Comput.-Aided Eng. 2011, 21, 279–287. [Google Scholar] [CrossRef]
- Williams, C.E.; Murphy, E.K.; Yakovlev, V.V. Machine-learning efficiency optimization of microwave applicators with plasma. Eur. J. Microw. Energy 2024, 1, 44–50. [Google Scholar] [CrossRef]

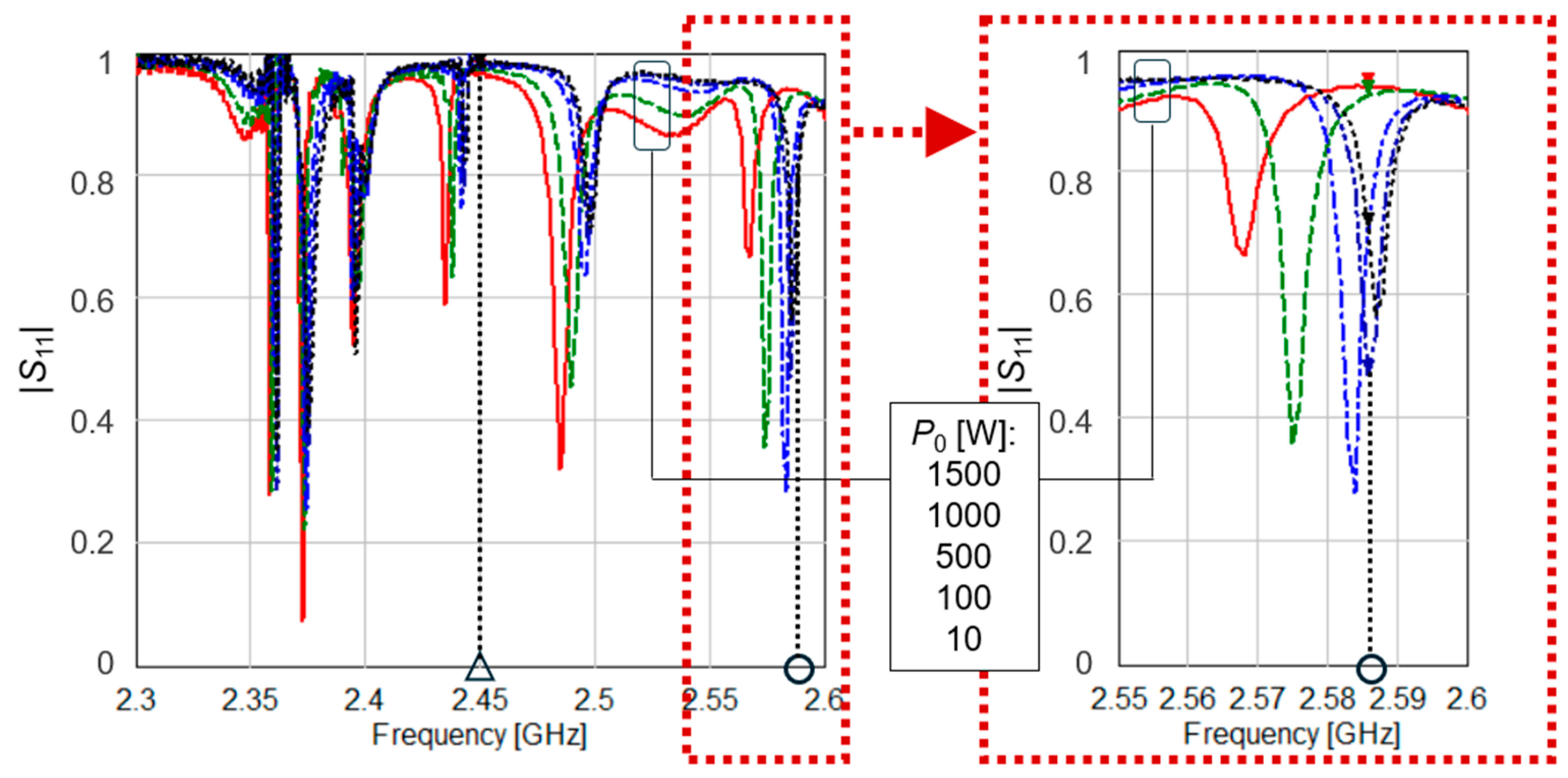
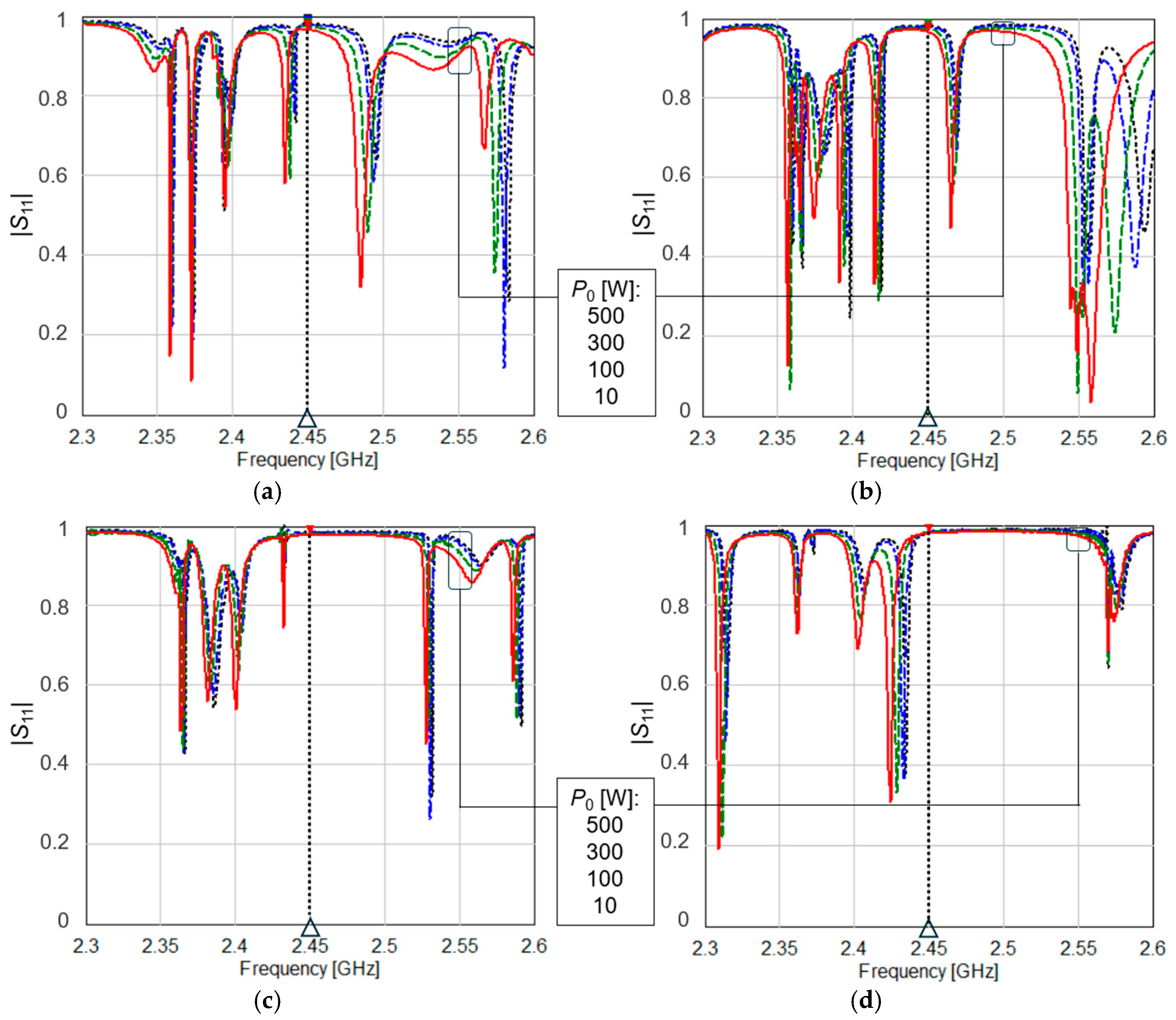

| (8) & (1) and (2) | (9) & (1) and (2) | (10) & (1) and (2) | ||||
|---|---|---|---|---|---|---|
| P0 [W] | [GHz] | [S/m] | [GHz] | [S/m] | [GHz] | [S/m] |
| 10 | 4569 | 10,021 | 85.4 | 3.5 | 2.05 | 0.0020 |
| 100 | 4654 | 10,395 | 113 | 6.13 | 2.09 | 0.0021 |
| 500 | 5029 | 12,138 | 193 | 17.8 | 2.27 | 0.0025 |
| 1000 | 5498 | 14,508 | 260 | 32.4 | 2.48 | 0.0030 |
| 1500 | 5967 | 17,088 | 313 | 47.0 | 2.70 | 0.0035 |
| 2000 | 6436 | 19,880 | 358 | 62.6 | 2.91 | 0.0041 |
| Pressure | γ [GHz] (by (3)) | ||
|---|---|---|---|
| He | Ar | Xe | |
| Low | 0.06 | 0.33 | 0.75 |
| Near atmospheric | 7.2 | 37.8 | 87.5 |
| || | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Power P0 [W] | 10 | 100 | 500 | 1000 | 1500 | 10 | 100 | 500 | 1000 | 1500 |
| ) | 0.971 | 0.981 | 0.983 | 0.991 | 0.980 | 5.7 | 3.8 | 3.4 | 1.8 | 4.0 |
| = 2.485 GHz | 0.322 | 0.809 | 0.954 | 0.965 | 0.976 | 90 | 35 | 9.0 | 6.9 | 4.7 |
| = 2.586 GHz (o) | 0.945 | 0.932 | 0.716 | 0.473 | 0.717 | 11 | 13 | 49 | 78 | 49 |
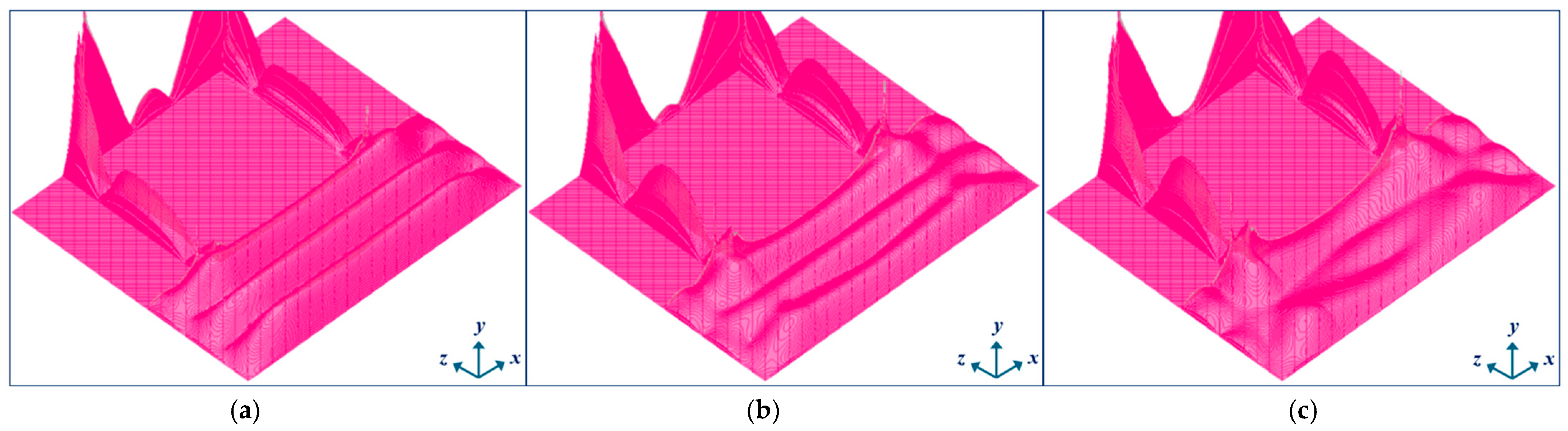
| Figure 7 | P0 [W] | |E|max [V/mm] | Pdiss [W] |
|---|---|---|---|
| (a) | 10 | 8.6 | 0.14 |
| (b) | 300 | 117.2 | 21.0 |
| (c) | 1500 | 431 | 94.4 |
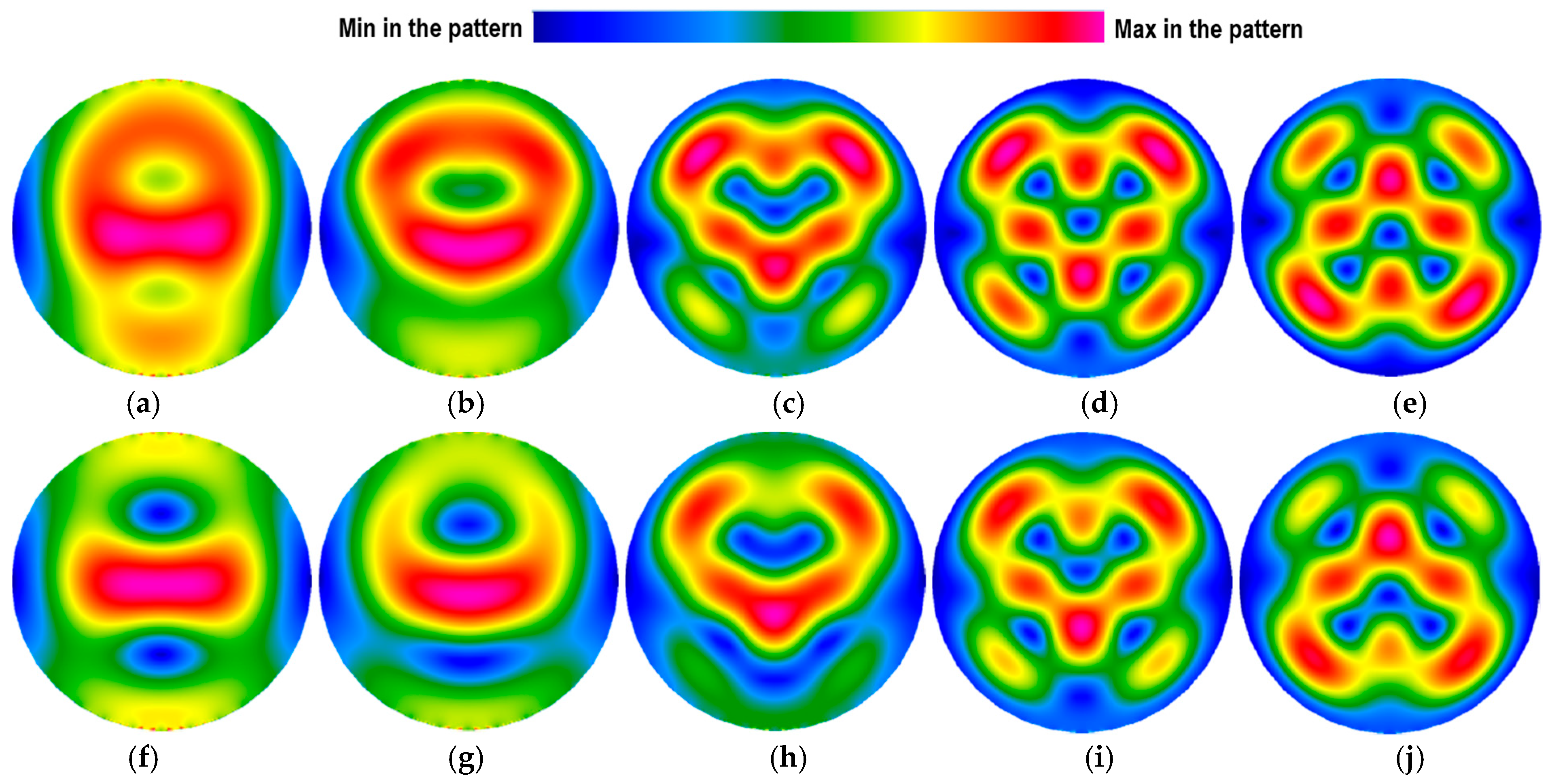
| P0 [W] | |E|max [V/mm] | |
|---|---|---|
| (a–e) | (f–j) | |
| 10 | 1.51 | 2.22 |
| 100 | 5.06 | 7.33 |
| 300 | 14.7 | 15.5 |
| 500 | 29.9 | 27.7 |
| 1500 | 71.4 | 67.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadidi, K.; Williams, C.E.; Yakovlev, V.V. Computational Analysis of the Effects of Power on the Electromagnetic Characteristics of Microwave Systems with Plasma. Energies 2025, 18, 5128. https://doi.org/10.3390/en18195128
Hadidi K, Williams CE, Yakovlev VV. Computational Analysis of the Effects of Power on the Electromagnetic Characteristics of Microwave Systems with Plasma. Energies. 2025; 18(19):5128. https://doi.org/10.3390/en18195128
Chicago/Turabian StyleHadidi, Kamal, Camille E. Williams, and Vadim V. Yakovlev. 2025. "Computational Analysis of the Effects of Power on the Electromagnetic Characteristics of Microwave Systems with Plasma" Energies 18, no. 19: 5128. https://doi.org/10.3390/en18195128
APA StyleHadidi, K., Williams, C. E., & Yakovlev, V. V. (2025). Computational Analysis of the Effects of Power on the Electromagnetic Characteristics of Microwave Systems with Plasma. Energies, 18(19), 5128. https://doi.org/10.3390/en18195128






