Optimal PV Sizing and Demand Response in Greek Energy Communities Under the New Virtual Net-Billing Scheme
Abstract
1. Introduction
2. Methods
2.1. The Virtual Net-Billing Scheme
2.2. Model
2.2.1. The Objective Function
- Capital expenditure (CAPEX) for the PV installation including the purchase and installation cost, annualized using a fixed annuity factor based on the assumed discount rate.
- Operational expenditure (OPEX) such as annual maintenance costs per installed kW.
- Electricity purchase cost for grid-imported energy at a fixed retail price.
- Netted cost charge, reflecting regulatory surcharges applied to self-consumed energy.
- Revenue from surplus energy, compensated at the DAM price minus the export charge, which reflects the cost of the aggregator’s service for the representation of the PV park to the DAM market.
2.2.2. Constraints
- Equation (3) The maximum PV share that a household can own.
- Equation (4) Energy balance at each timestep: consumption (including DR-adjusted demand) must be covered by PV generation, grid import, or export (in the case of surplus).
- Equation (8) Daily DR neutrality, ensuring that load shifts are balanced within a 24 h window.
- Equations (6) and (7). Physical limits on DR flexibility, bounded by a percentage of instantaneous demand.
- For the system is in import mode, allowing energy to be imported from the grid (exported energy is 0);
- For , the system is in export mode, allowing energy to be exported from the grid (imported energy is 0).
2.2.3. Solver and Implementation
2.3. Data
| Dataset | Country | Year | Number of Households | Duration | Sampling Rate | Data | Ref. |
|---|---|---|---|---|---|---|---|
| EMBED | USA | 2017 | 3 | 14–27 days | 12 kHz (house), 1 Hz (appliances) | Appliances | [46] |
| REDD | USA | 2011 | 6 | 3–19 days | 0.5–1 Hz (NILM data) | Household, Appliances | [47] |
| BLUED | USA | 2011 | 1 | 8 days | 12 kHz | Appliances | [48] |
| PLAID | USA | 2013 & 2014 | 56 | 2 weeks | 30 kHz | Appliances | [49] |
| ADRES | Austria | 2009 & 2010 | 30 | 2 weeks | 1 Hz | Household | [50] |
| REFIT | UK | 2015 | 20 | 2 years | 0.125 Hz | Appliances | [51] |
| UK-DALE | UK | 2015 | 5 | Up to 4 years | 16 kHz, 0.17 Hz | Household, Appliances | [52] |
| DRED | The Netherlands | 2015 | 1 | 6 months | 1 Hz, 1 min | Household, Appliances | [53] |
| HES | UK | 2010–2011 | 250 | 1 year | 10 s (household), 2 min | Household, Appliances, Interviews | [54] |
| Dataport | USA | 2014 | 1400 (75 free) | 4 years (full), 6 months (free) | 1 Hz, 1 min, 15 min | Household, Appliances | [55] |
| Smart* | USA | 2014–2016 | 3–114–400 | 4 years | 1 Hz | Household, Occupancy Weather, PV | [56] |
| AMPds | Canada | 2012–2014 | 1 | 2 years | 1 min | Household, Appliances, Weather, water and gas | [57] |
| ECO | Switzerland | 2014 | 6 | 8 months | 1 Hz | Household, Appliances, Occupancy | [58] |
| PRECON | Pakistan | 2018 | 42 | 1 year | 1 min | Household, Appliances | [59] |
| ENERTALK | South Korea | 2016 | 22 | 29–122 days | 15 Hz | Household, Appliances | [60] |
| SustDataED2 | Portugal | 2022 | 1 | 1144 days | 2–10 Hz | Household, Appliances, Weather, PV, Wind, biomass, hydro | [61] |
| IHEPCDS | France | 2006–2010 | 1 | 47 months | 1 min | Household, Appliances | [62] |
| IDEAL | UK | 2020 | 255 | 23 months | 1 Hz | Household | [63] |
| NorPEN | Norway | 2022 | 6 | 2 months | 10 s | Household, Weather, Irradiance, estimated PV, Interviews | [39] |
| IEDL | India | 2020 | 1 | 1 year | 1 min | Household, Appliances | [64] |
| ECD-UY | Uruguay | 2022 | 110,953 | 21 days | 15 min (households), 1 min (appliances) | Household, Appliances | [65] |
| GREEND | Austria/Italy | 2013 | 8 | 1 year | 1 Hz | Household, Appliances | [66] |
| Australian Distribution Network PV Dataset | Australia | 2010–2013 | 300 | 3 years | 30 min | Household, PV | [37] |
| iFlex Dynamic Pricing Dataset | Norway | 2019–2021 | 4483 | 2 winters | 1 h | Household, Weather, PV, Interviews | [67] |
| SHEERM | Portugal | 2021 | 13 | 26–450 days | 15 min | Household, Weather, PV, Price | [43] |
| Ireland Energy Community Load Profiles | Ireland | 2020 | 20 | 1 year | 1 min | Household, Appliances, Weather, PV, BESS | [41] |
| Norwegian Energy Community Dataset | Norway | 2015 | 100 | 1 year | 1 h (households), 1 min (appliances) | Household, Appliances, EV, estimated PV, Weather, Prices | [40] |
| Plegma Dataset | Greece | 2022–2023 | 13 | 3–14 months | 0.1 Hz | Household, Appliances, Interviews | [42] |
2.4. Sensitivity Analysis Design
3. Results
3.1. Baseline Cases
3.2. Sensitivity Analysis Results
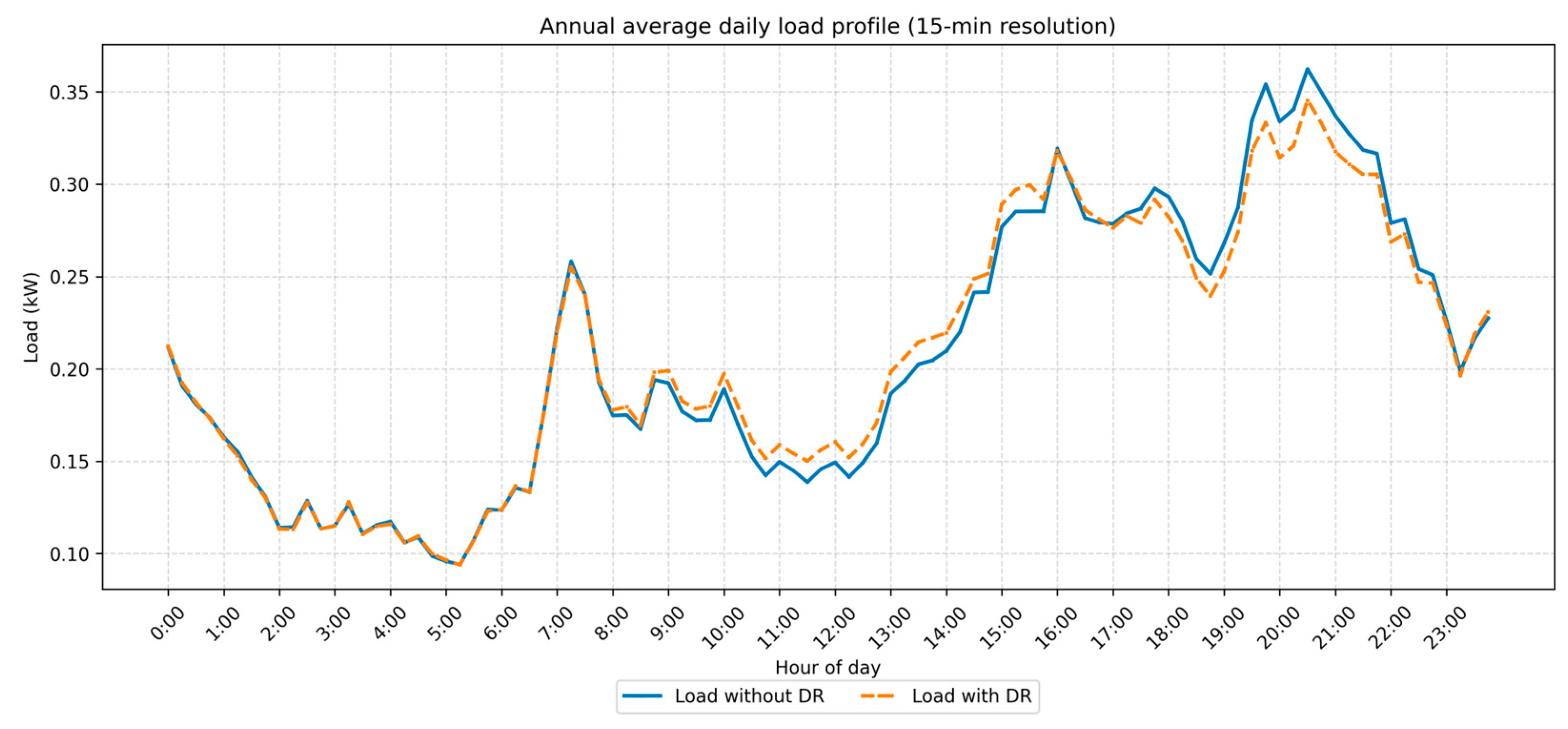
3.3. DR Strategy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CECs | Citizen Energy Communities |
| RECs | Renewable Energy Communities |
| ECs | Energy Communities |
| PV | Photovoltaic |
| BESS | Battery Energy Storage System |
| DR | Demand Response |
| A. Indices and Sets | |
| Index and set of time intervals (15 min resolution) | |
| Index and set of days | |
| Index and set of months | |
| B. Parameters | |
| and time t | |
| Discount rate for cost calculation (%) | |
| Demand response flexibility limit as a fraction of load | |
| PV system degradation rate (%) | |
| C. Variables | |
References
- Kostakis, V.; Giotitsas, C.; Kitsikopoulos, D. Envisioning energy futures through visual images: What would a commons-based energy system look like? Energy Res. Soc. Sci. 2024, 118, 103771. [Google Scholar] [CrossRef]
- European Commission. Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources; European Commission: Brussel, Belgium, 2018; pp. 82–209. Available online: http://data.europa.eu/eli/dir/2018/2001/oj (accessed on 29 April 2025).
- European Commission. Directive (EU) 2019/944 of the European Parliament and of the Council of 5 June 2019 on Common Rules for the Internal Market in Electricity; European Commission: Brussel, Belgium, 2019; pp. 125–199. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32019L0944 (accessed on 29 April 2025).
- Hellenic Parliament. Νόμος 4513/2018—Ενεργειακές Κοινότητες και άλλες διατάξεις; ΦΕΚ A’ 9/23.01.2018; Hellenic Parliament: Athens, Greece, 2018. Available online: https://www.taxheaven.gr/law/4513/2018 (accessed on 29 April 2025).
- Στατιστικά ΓΕΜH. Available online: https://statistics.businessportal.gr/status-changes/legal-types (accessed on 1 July 2025).
- Neij, L.; Palm, J.; Busch, H.; Bauwens, T.; Becker, S.; Bergek, A.; Buzogány, A.; Candelise, C.; Coenen, F.; Devine-Wright, P.; et al. Energy communities—Lessons learnt, challenges, and policy recommendations. Oxf. Open Energy 2025, 4, oiaf002. [Google Scholar] [CrossRef]
- Aghamolaei, R.; Shamsi, M.H.; O’Donnell, J. Feasibility analysis of community-based PV systems for residential districts: A comparison of on-site centralized and distributed PV installations. Renew. Energy 2020, 157, 793–808. [Google Scholar] [CrossRef]
- Sofia, Y.; Katsaprakakis, D.; Sakkas, N.; Condaxakis, C.; Karapidakis, E.; Syntichakis, S.; Stavrakakis, G.M. The Role of Energy Communities in the Achievement of a Region’s Energy Goals: The Case of a Southeast Mediterranean Region. Energies 2025, 18, 1327. [Google Scholar] [CrossRef]
- Friends of the Earth Europe. Corporate Capture of Energy Communities—A Threat for a Citizens Energy Transition in Europe; Friends of the Earth Europe: Brussels, Belgium, 2025; p. 36. Available online: https://friendsoftheearth.eu/wp-content/uploads/2025/04/Report-Corporate-Capture-on-Energy-Communities.pdf (accessed on 10 July 2025).
- Hellenic Parliament. Ελληνική Δημοκρατία Νόμος 5037/2023—Ενεργειακή Aπόδοση και Ενεργειακές Υπηρεσίες, Διαδικασίες Ενεργειακού Ελέγχου, Ενεργειακές Κοινότητες και άλλες διατάξεις; ΦΕΚ A’ 78/28.03.2023; Hellenic Parliament: Athens, Greece, 2023. Available online: https://www.taxheaven.gr/law/5037/2023 (accessed on 29 April 2025).
- Hellenic Parliament. Υπουργείο Περιβάλλοντος και Ενέργειας Κοινή Υπουργική Aπόφαση για το νέο πρόγραμμα φωτοβολταϊκών με εφαρμογή Net-Billing; ΦΕΚ Β’ 5074/05.09.2024.; Hellenic Parliament: Athens, Greece, 2024. Available online: https://ypen.gov.gr/wp-content/uploads/2024/09/FEK-5074B_05_09_2024-net-billing.pdf (accessed on 29 April 2025).
- Energy Communities Repository—Policy database—European Commission. Available online: https://energy.ec.europa.eu/topics/markets-and-consumers/energy-consumers-and-prosumers/energy-communities/energy-communities-repository-policy-database_en (accessed on 10 September 2025).
- Al-Shahri, O.A.; Ismail, F.B.; Hannan, M.A.; Lipu, M.S.H.; Al-Shetwi, A.Q.; Begum, R.A.; Al-Muhsen, N.F.O.; Soujeri, E. Solar photovoltaic energy optimization methods, challenges and issues: A comprehensive review. J. Clean. Prod. 2021, 284, 125465. [Google Scholar] [CrossRef]
- Lopes, R.A.; Martins, J.; Aelenei, D.; Lima, C.P. A cooperative net zero energy community to improve load matching. Renew. Energy 2016, 93, 1–13. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Barbato, A.; Capone, A. Optimization Models and Methods for Demand-Side Management of Residential Users: A Survey. Energies 2014, 7, 5787–5824. [Google Scholar] [CrossRef]
- Weckesser, T.; Dominković, D.F.; Blomgren, E.M.V.; Schledorn, A.; Madsen, H. Renewable Energy Communities: Optimal sizing and distribution grid impact of photo-voltaics and battery storage. Appl. Energy 2021, 301, 117408. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of photovoltaic systems size optimization techniques. Renew. Sustain. Energy Rev. 2013, 22, 454–465. [Google Scholar] [CrossRef]
- Faria, J.; Marques, C.; Pombo, J.; Mariano, S.; Calado, M.d.R. Optimal Sizing of Renewable Energy Communities: A Multiple Swarms Multi-Objective Particle Swarm Optimization Approach. Energies 2023, 16, 7227. [Google Scholar] [CrossRef]
- Magnor, D.; Sauer, D.U. Optimization of PV Battery Systems Using Genetic Algorithms. Energy Procedia 2016, 99, 332–340. [Google Scholar] [CrossRef]
- Bouaouda, A.; Sayouti, Y. Hybrid Meta-Heuristic Algorithms for Optimal Sizing of Hybrid Renewable Energy System: A Review of the State-of-the-Art. Arch. Comput. Methods Eng. 2022, 29, 4049–4083. [Google Scholar] [CrossRef]
- Iqbal, M.; Azam, M.; Naeem, M.; Khwaja, A.S.; Anpalagan, A. Optimization classification, algorithms and tools for renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 39, 640–654. [Google Scholar] [CrossRef]
- Dinh, H.T.; Kim, D.; Kim, D. MILP-based optimal day-ahead scheduling for a system-centric community energy management system supporting different types of homes and energy trading. Sci. Rep. 2022, 12, 18305. [Google Scholar] [CrossRef]
- Lamedica, R.; Santini, E.; Ruvio, A.; Palagi, L.; Rossetta, I. A MILP methodology to optimize sizing of PV—Wind renewable energy systems. Energy 2018, 165, 385–398. [Google Scholar] [CrossRef]
- Fina, B.; Auer, H.; Friedl, W. Profitability of PV sharing in energy communities: Use cases for different settlement patterns. Energy 2019, 189, 116148. [Google Scholar] [CrossRef]
- Volpato, G.; Carraro, G.; Cont, M.; Danieli, P.; Rech, S.; Lazzaretto, A. General guidelines for the optimal economic aggregation of prosumers in energy communities. Energy 2022, 258, 124800. [Google Scholar] [CrossRef]
- Cosic, A.; Stadler, M.; Mansoor, M.; Zellinger, M. Mixed-integer linear programming based optimization strategies for renewable energy communities. Energy 2021, 237, 121559. [Google Scholar] [CrossRef]
- Novoa, L.; Flores, R.; Brouwer, J. Optimal renewable generation and battery storage sizing and siting considering local transformer limits. Appl. Energy 2019, 256, 113926. [Google Scholar] [CrossRef]
- Hascuri, M.; Rami, M.A.; Derrhi, M. PV system sizing with storage management: A comparative study based on Mixed Integer Linear Programming. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 545–550. [Google Scholar] [CrossRef]
- Farrokhifar, M.; Aghdam, F.H.; Alahyari, A.; Monavari, A.; Safari, A. Optimal energy management and sizing of renewable energy and battery systems in residential sectors via a stochastic MILP model. Electr. Power Syst. Res. 2020, 187, 106483. [Google Scholar] [CrossRef]
- Budin, L.; Delimar, M. Renewable Energy Community Sizing Based on Stochastic Optimization and Unsupervised Clustering. Sustainability 2025, 17, 600. [Google Scholar] [CrossRef]
- Kassab, F.A.; Celik, B.; Locment, F.; Sechilariu, M.; Hansen, T.M. Combined Optimal Sizing and Energy Management of a DC Microgrid using MILP. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Tsekouras, G.J.; Vlachos, A.; Rakopoulos, D.; Chatzigeorgiou, I.M.; Kanellos, F.D.; Kontargyri, V. Day Ahead Operation Cost Optimization for Energy Communities. Energies 2025, 18, 1101. [Google Scholar] [CrossRef]
- Attia, A.M.; Al Hanbali, A.; Saleh, H.H.; Alsawafy, O.G.; Ghaithan, A.M.; Mohammed, A. A multi-objective optimization model for sizing decisions of a grid-connected photovoltaic system. Energy 2021, 229, 120730. [Google Scholar] [CrossRef]
- Mariuzzo, I.; Fioriti, D.; Guerrazzi, E.; Thomopulos, D.; Raugi, M. Multi-objective planning method for renewable energy communities with economic, environmental and social goals. Int. J. Electr. Power Energy Syst. 2023, 153, 109331. [Google Scholar] [CrossRef]
- Kazmi, H.; Munné-Collado, Í.; Mehmood, F.; Syed, T.A.; Driesen, J. Towards data-driven energy communities: A review of open-source datasets, models and tools. Renew. Sustain. Energy Rev. 2021, 148, 111290. [Google Scholar] [CrossRef]
- Ratnam, E.L.; Weller, S.R.; Kellett, C.M.; Murray, A.T. Residential load and rooftop PV generation: An Australian distribution network dataset. Int. J. Sustain. Energy 2017, 36, 787–806. [Google Scholar] [CrossRef]
- Australian Government Department of Climate Change, Energy, the Environment and Water. Smart-Grid Smart-City Customer Trial Data. Available online: https://data.gov.au/data/dataset/smart-grid-smart-city-customer-trial-data (accessed on 6 May 2025).
- Vavouris, A.; Guasselli, F.; Stankovic, L.; Stankovic, V.; Gram-Hanssen, K.; Didierjean, S. Descriptor: A Norwegian Positive Energy Neighborhood Dataset of Electrical Measurements and Interviews on Energy Practices (NorPEN). IEEE Data Descr. 2024, 1, 113–121. [Google Scholar] [CrossRef]
- Berg, K.; Löschenbrand, M. A data set of a Norwegian energy community. Data Brief 2022, 40, 107683. [Google Scholar] [CrossRef]
- Khadem, S.; Trivedi, R.; Bahloul, M.; Saif, A.; Patra, S. Comprehensive Dataset on Electrical Load Profiles for Energy Community in Ireland. Sci. Data 2024, 11, 621. [Google Scholar] [CrossRef] [PubMed]
- Athanasoulias, S.; Guasselli, F.; Doulamis, N.; Doulamis, A.; Ipiotis, N.; Katsari, A.; Stankovic, L.; Stankovic, V. The Plegma dataset: Domestic appliance-level and aggregate electricity demand with metadata from Greece. Sci. Data 2024, 11, 376. [Google Scholar] [CrossRef] [PubMed]
- Cecílio, J.; Barros, M.; Oliveira de Sá, A.; Rodrigues, T. SHEERM: Sustainable Household Energy and Environment Resources Management dataset. Zenodo 2024. [Google Scholar] [CrossRef]
- Mutule, A.; Borscevskis, O.; Astapov, V.; Antoskova, I.; Carroll, P.; Kairisa, E. PV Energy Communities in Residential Apartments: Technical Capacities and Economic Viability. Sustainability 2025, 17, 2901. [Google Scholar] [CrossRef]
- Commonen—ΚOΙΝΕΡΓΕΙA. Available online: https://www.commonen.gr/en/ (accessed on 6 May 2025).
- Jazizadeh, F.; Afzalan, M.; Becerik-Gerber, B.; Soibelman, L. EMBED: A Dataset for Energy Monitoring through Building Electricity Disaggregation. In Proceedings of the Ninth International Conference on Future Energy Systems, Karlsruhe, Germany, 12–15 June 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 230–235. [Google Scholar]
- Kolter, J.; Johnson, M. REDD: A Public Data Set for Energy Disaggregation Research. Artif. Intell. 2011, 25, 59–62. [Google Scholar]
- Anderson, K.D.; Ocneanu, A.; Carlson, D.R.; Rowe, A.G.; Berges, M.E. BLUED: A Fully Labeled Public Dataset for Event-Based Non-Intrusive Load Monitoring Research. 2012. Available online: https://api.semanticscholar.org/CorpusID:25397318 (accessed on 9 September 2025).
- Gao, J.; Giri, S.; Kara, E.C.; Bergés, M. PLAID: A public dataset of high-resoultion electrical appliance measurements for load identification research: Demo abstract. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings, Memphis, TN, USA, 3–6 November 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 198–199. [Google Scholar]
- Einfalt, A.; Leitinger, C.; Tiefgraber, D.; Ghaemi, S. ADRES Concept–Micro Grids in Österreich. In Proceedings of the Internationalen Energiewirtschaftstagung an der TU Wien (IEWT), Wien, Austria, 1 January 2009. [Google Scholar]
- Murray, D.; Stankovic, L.; Stankovic, V. An electrical load measurements dataset of United Kingdom households from a two-year longitudinal study. Sci. Data 2017, 4, 160122. [Google Scholar] [CrossRef]
- Kelly, J.; Knottenbelt, W. The UK-DALE dataset, domestic appliance-level electricity demand and whole-house demand from five UK homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [PubMed]
- Uttama Nambi, A.S.; Reyes Lua, A.; Prasad, V.R. Loced: Location-aware energy disaggregation framework. In Proceedings of the 2nd ACM International Conference on Embedded Systems for Energy-Efficient Built Environments, Seoul, Republic of Korea, 4–5 November 2015; pp. 45–54. [Google Scholar]
- Household Electricity Survey. Available online: https://www.gov.uk/government/publications/household-electricity-survey--2 (accessed on 11 August 2025).
- Parson, O.; Fisher, G.; Hersey, A.; Batra, N.; Kelly, J.; Singh, A.; Knottenbelt, W.; Rogers, A. Dataport and NILMTK: A building data set designed for non-intrusive load monitoring. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (Globalsip), Orlando, FL, USA, 14–16 December 2015; IEEE: New York, NY, USA, 2015; pp. 210–214. [Google Scholar]
- Barker, S.; Mishra, A.; Irwin, D.; Cecchet, E.; Shenoy, P.; Albrecht, J. Smart*: An open data set and tools for enabling research in sustainable homes. SustKDD August 2012, 111, 108. [Google Scholar]
- Makonin, S.; Ellert, B.; Bajić, I.V.; Popowich, F. Electricity, water, and natural gas consumption of a residential house in Canada from 2012 to 2014. Sci. Data 2016, 3, 160037. [Google Scholar] [CrossRef]
- Beckel, C.; Kleiminger, W.; Cicchetti, R.; Staake, T.; Santini, S. The ECO data set and the performance of non-intrusive load monitoring algorithms. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings, Memphis, TN, USA, 3–6 November 2014; Association for Computing Machinery: New York, NY, USA, 2014; pp. 80–89. [Google Scholar]
- Nadeem, A.; Arshad, N. PRECON: Pakistan residential electricity consumption dataset. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; pp. 52–57. [Google Scholar]
- Shin, C.; Lee, E.; Han, J.; Yim, J.; Rhee, W.; Lee, H. The ENERTALK dataset, 15 Hz electricity consumption data from 22 houses in Korea. Sci. Data 2019, 6, 193. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.; Quintal, F.; Gonçalves, R.; Nunes, N.J. SustData: A public dataset for ICT4S electric energy research. In Proceedings of the 2nd International Conference on ICT for Sustainability ICT4S 2014, Stockholm, Sweden, 24–27 August 2014; pp. 359–368. [Google Scholar]
- Hebrail, G.; Berard, A. Individual Household Electric Power Consumption; UCI Machine Learning Repository: Irvine, CA, USA, 2006. [Google Scholar]
- Pullinger, M.; Kilgour, J.; Goddard, N.; Berliner, N.; Webb, L.; Dzikovska, M.; Lovell, H.; Mann, J.; Sutton, C.; Webb, J.; et al. The IDEAL household energy dataset, electricity, gas, contextual sensor data and survey data for 255 UK homes. Sci. Data 2021, 8, 146. [Google Scholar] [CrossRef] [PubMed]
- Chavan, D.R.; More, D.S.; Khot, A.M. Iedl: Indian energy dataset with low frequency for nilm. Energy Rep. 2022, 8, 701–709. [Google Scholar] [CrossRef]
- Chavat, J.; Nesmachnow, S.; Graneri, J.; Alvez, G. ECD-UY, detailed household electricity consumption dataset of Uruguay. Sci. Data 2022, 9, 21. [Google Scholar] [CrossRef] [PubMed]
- Monacchi, A.; Egarter, D.; Elmenreich, W.; D’Alessandro, S.; Tonello, A.M. GREEND: An energy consumption dataset of households in Italy and Austria. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014; pp. 511–516. [Google Scholar]
- Hofmann, M.; Siebenbrunner, T. A rich dataset of hourly residential electricity consumption data and survey answers from the iFlex dynamic pricing experiment. Data Brief 2023, 50, 109571. [Google Scholar] [CrossRef] [PubMed]
- Day-Ahead Market—EnExGroup. Available online: https://www.enexgroup.gr/web/guest/markets-publications-el-day-ahead-market#! (accessed on 6 May 2025).
- Wang, J.; Qiu, D.; Wang, Y.; Ye, Y.; Strbac, G. Investigating the impact of demand-side flexibility on market-driven generation planning toward a fully decarbonized power system. Energy 2025, 324, 135692. [Google Scholar] [CrossRef]
- Qiu, D.; Dong, Z.; Ruan, G.; Zhong, H.; Strbac, G.; Kang, C. Strategic retail pricing and demand bidding of retailers in electricity market: A data-driven chance-constrained programming. Adv. Appl. Energy 2022, 7, 100100. [Google Scholar] [CrossRef]
- Papadaskalopoulos, D.; Strbac, G.; Mancarella, P.; Aunedi, M.; Stanojevic, V. Decentralized Participation of Flexible Demand in Electricity Markets—Part II: Application With Electric Vehicles and Heat Pump Systems. IEEE Trans. Power Syst. 2013, 28, 3667–3674. [Google Scholar] [CrossRef]
- Barreto, R.; Faria, P.; Silva, C.; Vale, Z. Clustering Direct Load Control Appliances in the Context of Demand Response Programs in Energy Communities. IFAC-PapersOnLine 2020, 53, 12608–12613. [Google Scholar] [CrossRef]
- Fernandez, E.; Hossain, M.; Nizami, M. Game-theoretic approach to demand-side energy management for a smart neighbourhood in Sydney incorporating renewable resources. Appl. Energy 2018, 232, 245–257. [Google Scholar] [CrossRef]
- Huang, P.; Sun, Y. A collaborative demand control of nearly zero energy buildings in response to dynamic pricing for performance improvements at cluster level. Energy 2019, 174, 911–921. [Google Scholar] [CrossRef]
- Good, N.; Mancarella, P. Flexibility in Multi-Energy Communities With Electrical and Thermal Storage: A Stochastic, Robust Approach for Multi-Service Demand Response. IEEE Trans. Smart Grid 2019, 10, 503–513. [Google Scholar] [CrossRef]
- Chronis, A.-G.; Hatziargyriou, N. The Role of Energy Communities in Enhancing Sustainability in Europe: Successes and Challenges. IEEE Energy Sustain. Mag. 2025, 1, 42–52. [Google Scholar] [CrossRef]
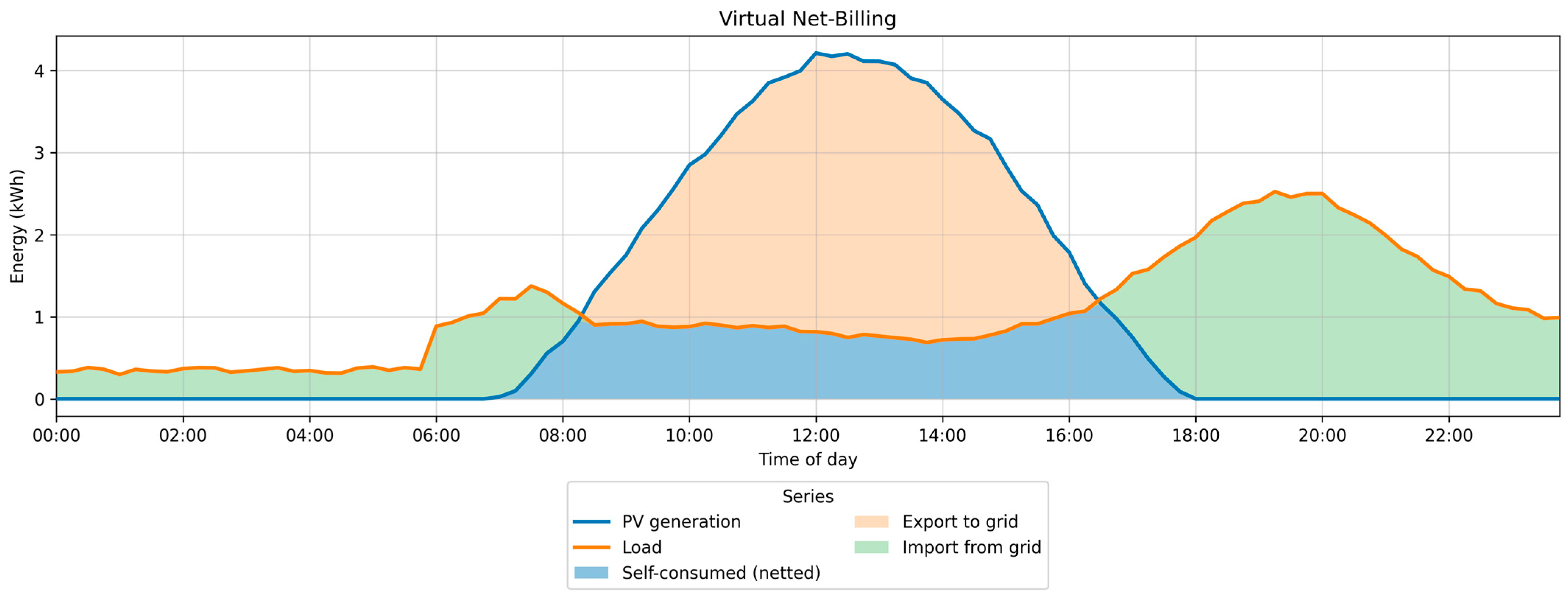
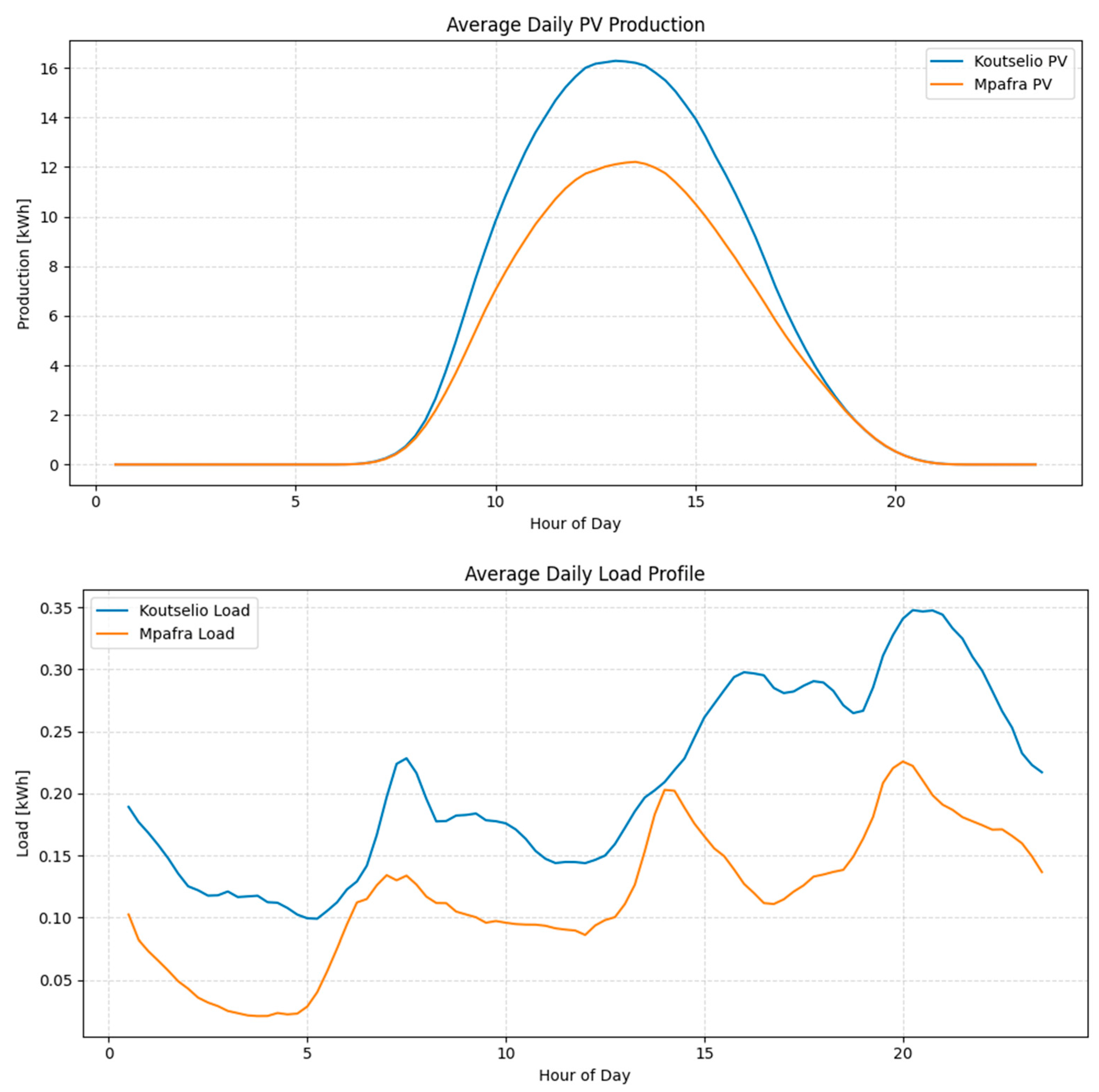


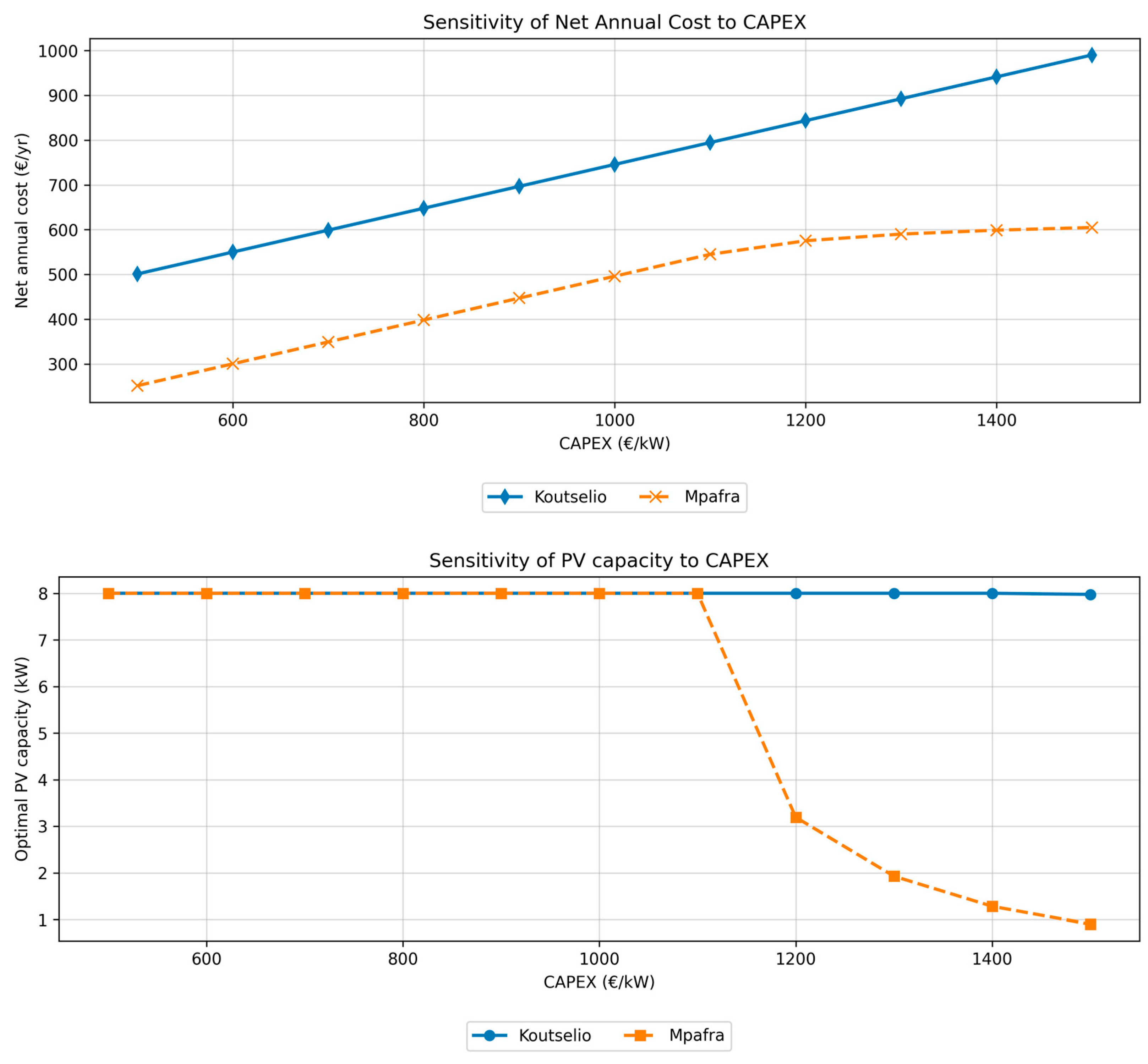
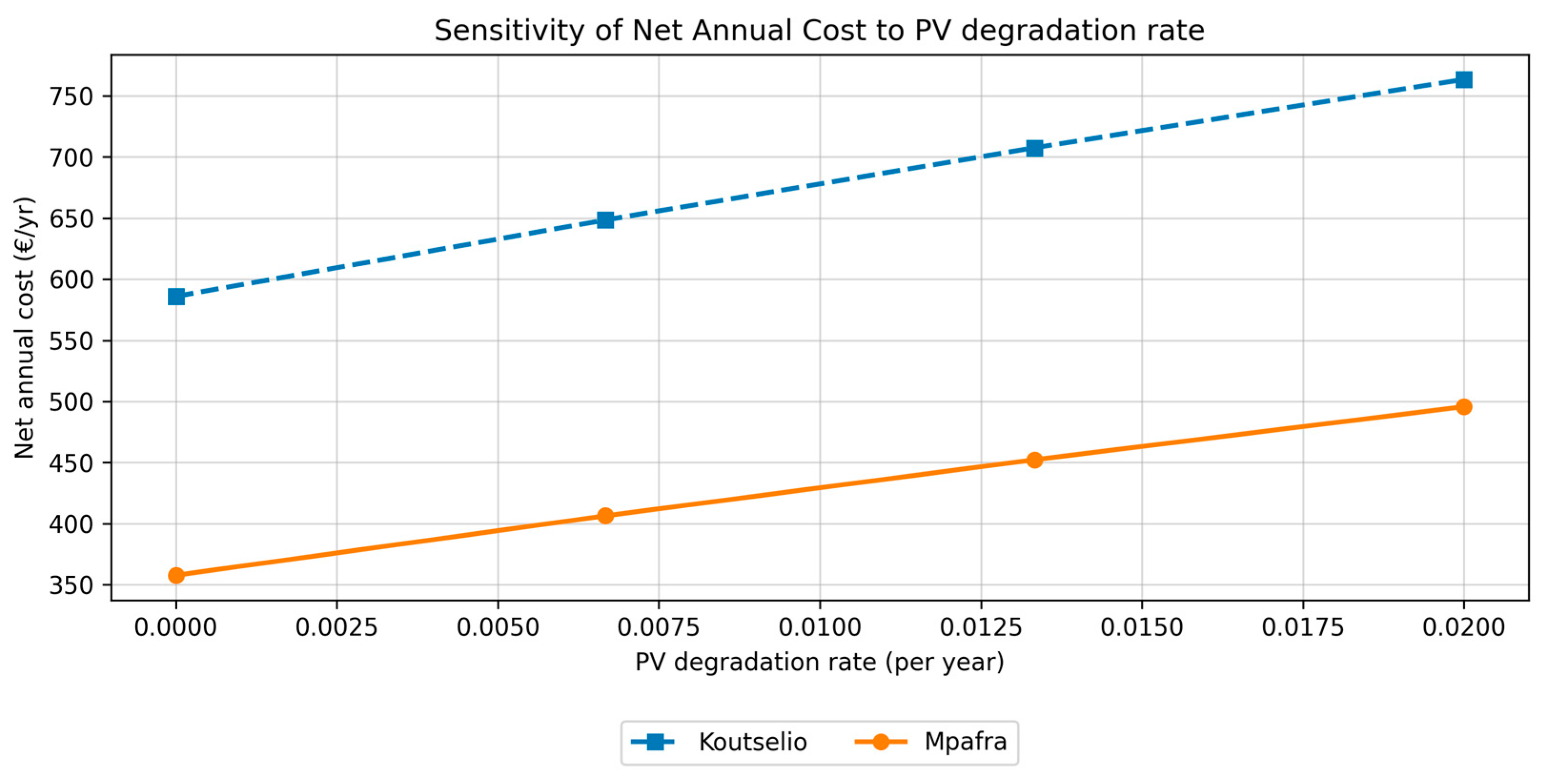



| Reference | Algorithm | Optimization Goal | Assets | DR | Country | Temporal Resolution | Regulatory Framework |
|---|---|---|---|---|---|---|---|
| Fina et al. [25] | MILP | Maximize Net Present Value (NPV) | PV, HVAC, Batteries | No | Austria | 15 min, for 1 year | Based on Austrian market |
| Volpato et al. [26] | MILP | Minimize operational cost | PV, Biogas ICE CHP | Yes | Italy | 60 min, 3 representative days | Aligned with EU directives (RED II & IEMD) |
| Cosic et al. [27] | MILP | Minimize energy cost & CO2 emissions | PV, Batteries | Indirect via dynamic pricing | Austria | 60 min, for 1 year | Compliant with Austrian EAG (Renewable Expansion Act)—shared energy |
| Novoa et al. [28] | MILP | Minimize investment & operating cost, meet ZNE or islanding goals, avoid transformer overloading | PV, Batteries | Indirect via dynamic pricing | USA | 60 min, representative days via k-medoids clustering | Based on SCE utility tariffs (TOU-D-A, TOU-8-B), includes NEM and grid constraints |
| Hascuri et al. [29] | Two MILP types (i) Original (equalities), (ii) Reduced (inequalities only) | Minimize CAPEX (two MILP variants) | PV, Batteries | No | Morocco | 360 min, for 1 year | None indicated |
| Farrokhifar et al. [30] | Stochastic MILP | Minimize net present cost, maximize RES and storage usage, meet demand via DR and V2G | PV, Wind, Batteries, EVs (V2G) | Yes | USA | 60 min, for 1 year | None indicated |
| Budin & Delimar [31] | Two-stage stochastic MILP with unsupervised clustering (load & uncertainty modeling) | Cost reduction & limiting grid impacts | PV, Shared Battery | Indirect via dynamic pricing | Croatia, Germany | 15 min, for 1 year | RED II/RED III—Clean Energy Package, P2P trading |
| Kassab et al. [32] | MILP | Minimize total system cost (CAPEX, O&M, replacement, energy management) | PV, Batteries | No | France | 60 min, for 1 year | None indicated |
| Our study | MILP | Minimize net investment cost (CAPEX, O&M, operation) | PV | Yes | Greece | 15 min, for 1 year | Greek Law 5074/2024 for virtual net-billing in ECs |
| 0.15 | |
| 0.0025 | |
| 8 | |
| 850 | |
| 20 | |
| 2 (%) | |
| 20 | |
| 0.10 | |
| 0.5% |
| Month | Imbalance | ΛΠ1 | ΛΠ2 | ΛΠ3 |
|---|---|---|---|---|
| 1 | −0.027 | 2.034 | 2.142 | 9.177 |
| 2 | 0.335 | 1.555 | 2.002 | 10.029 |
| 3 | 0.976 | 1.456 | 3.019 | 9.852 |
| 4 | 0.114 | 1.386 | 4.365 | 10.056 |
| 5 | −0.423 | 1.844 | 2.781 | 7.039 |
| 6 | −1.080 | 1.916 | 3.006 | 7.398 |
| 7 | −0.251 | 2.964 | 3.461 | 8.778 |
| 8 | −2.999 | 3.162 | 3.269 | 9.398 |
| 9 | −4.932 | 2.896 | 4.534 | 11.691 |
| 10 | −3.046 | 2.501 | 5.927 | 15.430 |
| 11 | −2.060 | 4.091 | 4.386 | 17.502 |
| 12 | 0.779 | 3.384 | 4.439 | 15.560 |
| Parameter | Variation for the Sensitivity Analysis |
|---|---|
| CAPEX | 500–1500 €/kW |
| OPEX | 10–80 €/kW |
| Aggregator’s fee | 0.001–0.005 €/kWh |
| DRcap | 0–50% |
| PV panel degradation rate | 0–2% |
| Scenarios | Koutselio | Mpafra | ||
|---|---|---|---|---|
| Optimal PV Capacity (kW) | Net Cost (€/year) | Optimal PV Capacity (kW) | Net Cost (€/year) | |
| No PV | 0 | 1094.39 | 0 | 614.82 |
| PV | 8 | 682.89 | 8 | 429.84 |
| PV and DR | 8 | 672.33 | 8 | 422.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzigeorgiou, I.-M.; Kitsikopoulos, D.; Papadaskalopoulos, D.A.; Chronis, A.-G.; Xenaki, A.; Andreou, G.T. Optimal PV Sizing and Demand Response in Greek Energy Communities Under the New Virtual Net-Billing Scheme. Energies 2025, 18, 5082. https://doi.org/10.3390/en18195082
Chatzigeorgiou I-M, Kitsikopoulos D, Papadaskalopoulos DA, Chronis A-G, Xenaki A, Andreou GT. Optimal PV Sizing and Demand Response in Greek Energy Communities Under the New Virtual Net-Billing Scheme. Energies. 2025; 18(19):5082. https://doi.org/10.3390/en18195082
Chicago/Turabian StyleChatzigeorgiou, Ioanna-Mirto, Dimitrios Kitsikopoulos, Dimitrios A. Papadaskalopoulos, Alexandros-Georgios Chronis, Argyro Xenaki, and Georgios T. Andreou. 2025. "Optimal PV Sizing and Demand Response in Greek Energy Communities Under the New Virtual Net-Billing Scheme" Energies 18, no. 19: 5082. https://doi.org/10.3390/en18195082
APA StyleChatzigeorgiou, I.-M., Kitsikopoulos, D., Papadaskalopoulos, D. A., Chronis, A.-G., Xenaki, A., & Andreou, G. T. (2025). Optimal PV Sizing and Demand Response in Greek Energy Communities Under the New Virtual Net-Billing Scheme. Energies, 18(19), 5082. https://doi.org/10.3390/en18195082






