Assessing the Technical and Economic Viability of Onshore and Offshore Wind Energy in Pakistan Through a Data-Driven Machine Learning and Deep Learning Approach
Abstract
1. Introduction
- the lack of ML/DL-based wind power modelling in Pakistan, and
- the absence of integrated economic assessments for both onshore and offshore sites.
2. Methods and Data
2.1. Producibility of a Wind Turbine
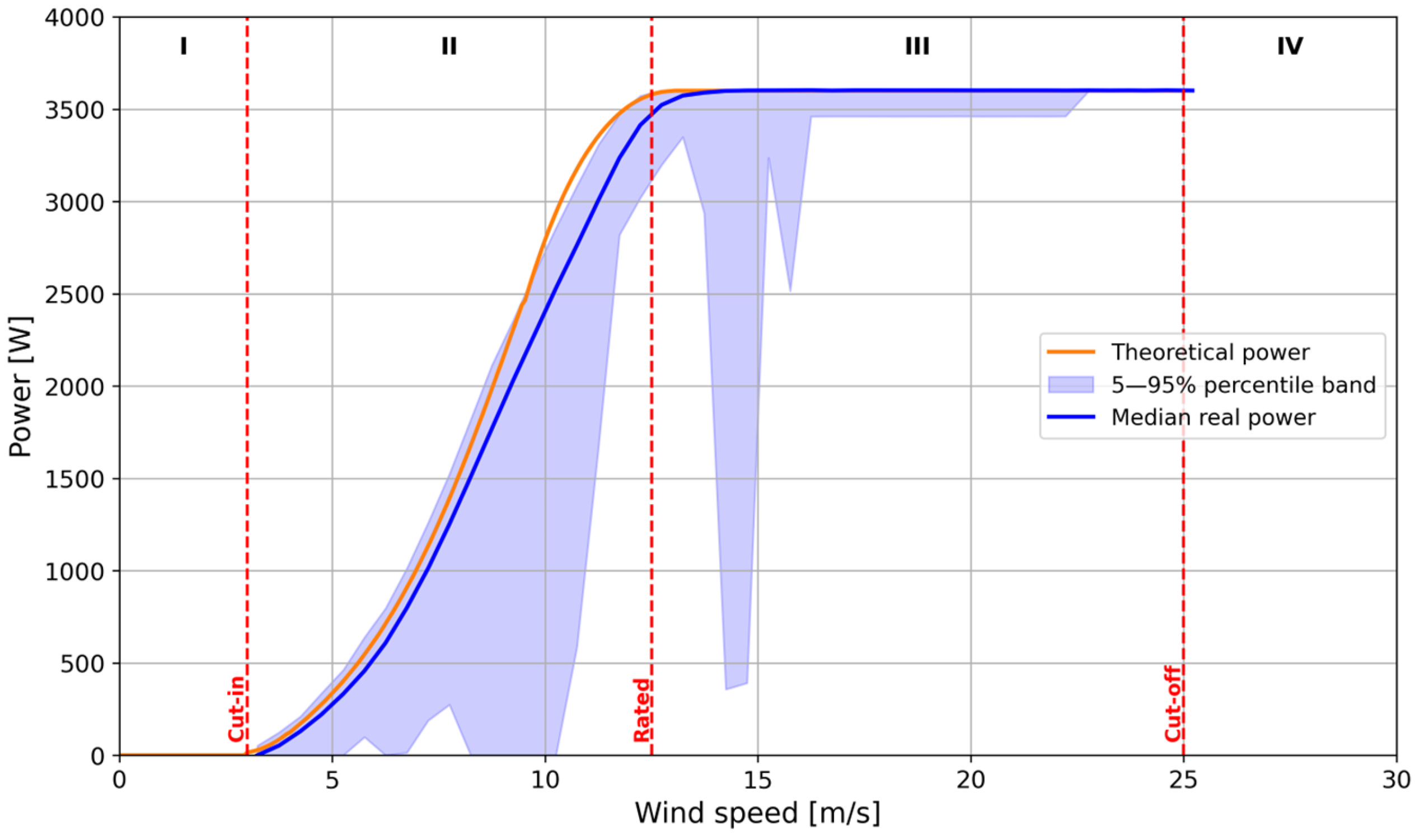
2.1.1. Power Curve
- The region below the cut-in speed , that is, the minimum wind speed at which the turbine starts generating power.
- The region where the power output varies in proportion to the cube of speed, which extends from the cut-in speed to the rated speed .
- The rated power region, beyond the rated speed , is the region in which the turbine produces its maximum constant power output. The turbine operates at rated power throughout this region, until the cut-off speed is reached.
- The region above the cut-off speed of the turbine, after which the turbine is stopped to prevent mechanical or structural damage.

2.1.2. Machine Learning and Deep Learning Models for Wind Power Prediction
- Gradient Boosting (GBoost) [38]: GBoost is a ML model that employs decision trees as weak learners, combining them sequentially to form a strong learner (Figure 2a). This process ensures a more accurate model by progressively reducing errors from previous iterations. Moreover, GBoost utilises residual errors as weight values and optimise the classification performance by using adjustable learning rates and loss functions. However, adding trees sequentially can slow down the learning process when dealing with large datasets.
- Extreme Gradient Boosting (XGBoost) [39]: XGBoost is the advanced version of GBoost, with refinements such as integrating regularisation (L1, L2) [40] by adding a penalty term to the loss function, the computation of second derivatives of the loss function, and parallel optimisation. This combination of characteristics enhances the model’s efficiency and reduces the risk of overfitting.
- Random Forest (RF) [41]: RF is an ensemble learning algorithm based on parallel training with multiple decision trees (Figure 2b). In the training phase of the algorithm, multiple trees are constructed, with each tree being built on a random sample of the dataset. The prediction made by each tree is then averaged. In RF, the number of trees and their depths are higher than those in GBoost and XGBoost. RF demonstrates efficacy in the presence of noisy or highly nonlinear data, such as hourly weather data, because of its robustness and capacity for generalisation.
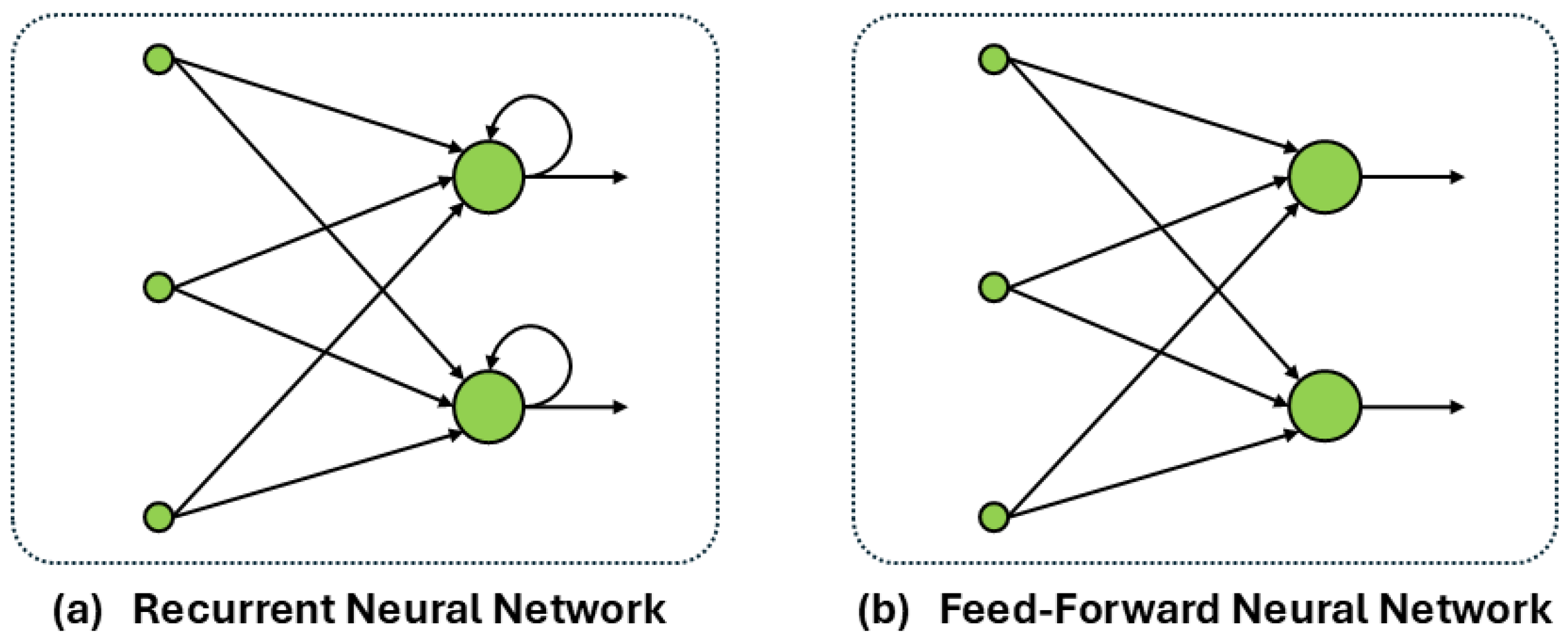
- Multi-Layer Perceptron (MLP) [40]: MLP constitutes the primary DL architecture. It is a feed-forward neural network (Figure 3a) consisting of one or more hidden layers with nonlinear activation functions. Although MLP is capable of modelling complex relationships between inputs and outputs, it does not account for the temporal component in the data, thus limiting its effectiveness in time series analysis.
- Long Short-Term Memory (LSTM) [40]: LSTM is a recurrent neural network architecture employed in the context of DL. In contradistinction to conventional feed-forward neural networks, such as MLP, LSTM employs feedback links (Figure 3b). LSTM networks find application in the analysis and learning of sequential data. Consequently, LSTM networks are a suitable option for data that follows a sequential format.
2.1.3. Energy Performance
2.1.4. Metrics
2.2. Energy Losses
2.2.1. Wake Losses
2.2.2. Grid Losses
2.3. Economic Analysis
2.3.1. CAPEX and OPEX
- Turbine: 1064 EUR2020/kW
- Foundation: 69 EUR2020/kW
- Other (grid connection and installation): 192 EUR2020/kW
- Turbine [49]: 1215 EUR2020/kW
- Foundation: The choice of the type of foundation is dictated by the depth of the seabed . In very shallow waters (<25 m) the monopile is preferred, whereas for intermediate to deep waters (25–55 m), jacket foundations are more suitable. Estimated costs in USD2016/kW are [50]:
- ○
- Monopile:
- ○
- Jacket:
- Installation: Offshore installation is more complex and costly due to the need for specialised vessels and weather constraints. The cost for the installation [48] is estimated in USD2016m as:
- Grid: The cost of grid connection in offshore wind projects depends significantly on the transmission technology adopted, that is, HVAC or HVDC. Once again, HVAC is preferred for shorter distances due to its lower capital cost and simpler infrastructure. HVDC becomes more cost-effective for longer distances, as it minimises transmission losses and allows for more efficient long-distance power transfer, despite higher initial costs. The grid cost can be estimated in USD2019m/kW for the two case as follows [46]:
- Onshore OPEX: 1.5% of CAPEX, annually.
- Offshore OPEX: 2% of CAPEX, annually.
2.3.2. Constant Currency Approach
2.3.3. Levelized Cost Of Energy
2.4. Türkiye SCADA Dataset
2.4.1. Dataset Description
2.4.2. Preprocessing and Model Configuration
- Data loading: The dataset is uploaded using the pandas library, upon which the data points are sorted by timestamp and any duplicates are removed. Following this, rows with missing values (NaN) in the main columns (wind_speed, wind_direction, theoretical_power, active_power) are deleted. No imputation or masking is performed.
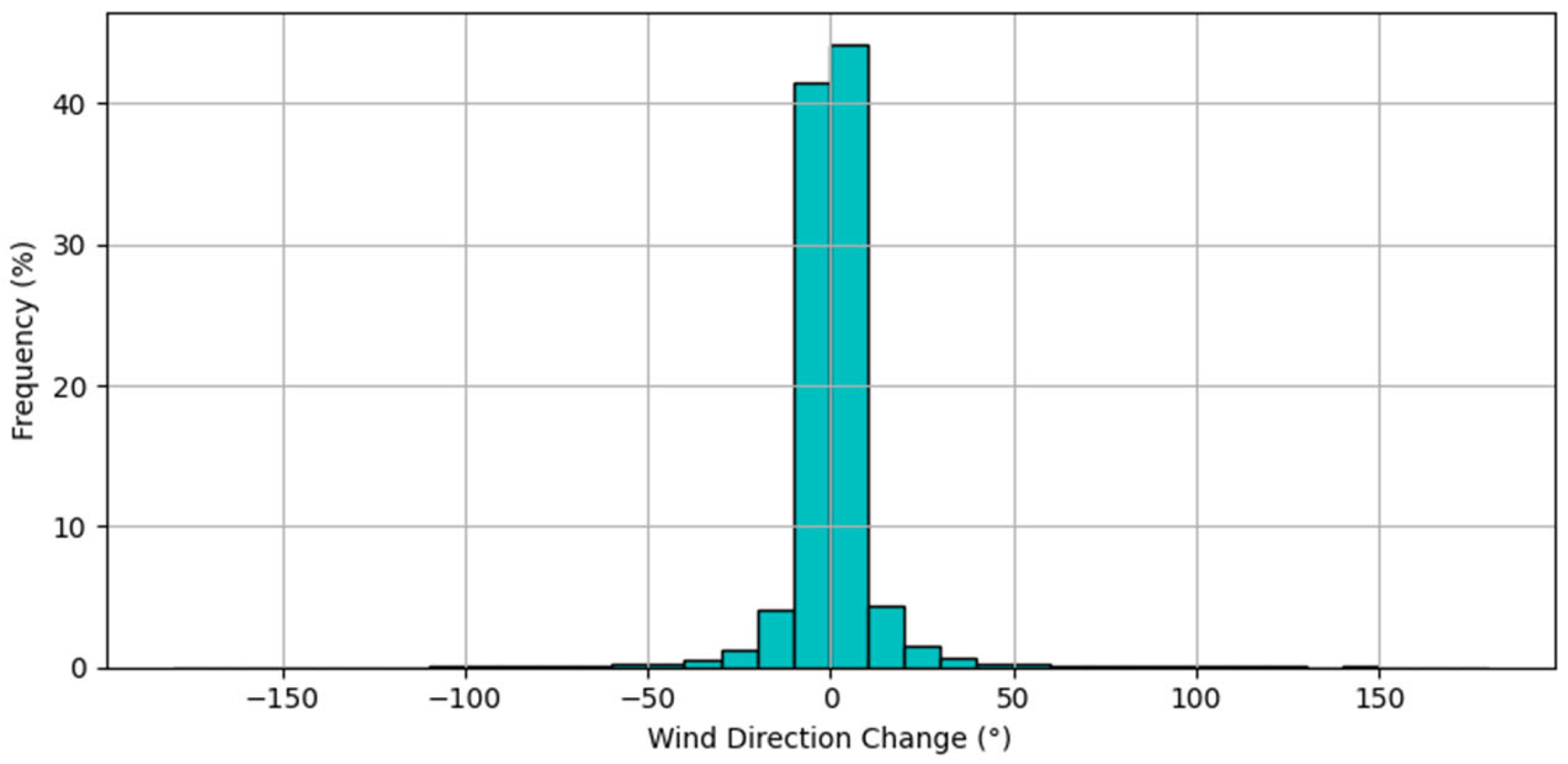
- Calculation of variations: This process entails the calculation of the differences between successive data points on wind speed, wind direction and theoretical power (i.e., the active power calculated via the theoretical power curve). The objective of this calculation is to obtain “d_wind_speed” [m/s], “d_wind_direction” [°] and “d_theoretical_power” [kW].
- Choosing the input features and output of interest: The input features for all the developed models are as follows: “d_wind_speed” [m/s], “d_wind_direction” [°], “d_theoretical_power” [kW], “theoretical_power” [kW], “wind_speed” [m/s]. The incorporation of variations between consecutive timestamps facilitates the capture of temporal dynamics in turbine changes, even for non-sequential models. The output of interest is always “active_power” [kW] for all five models. It is important to note that the present study omitted consideration of certain environmental variables, such as temperature, atmospheric pressure, and air density, due to the unavailability of these variables within the original dataset.
- Outliers removal: The elimination of outliers is achieved through the implementation of a Z-score filter on all features and targets, resulting in the removal of values that deviate by more than three standard deviations from the average value. The percentage of rows that are deleted as a consequence of missing values and outliers removal is 4.9% of the original dataset.
- Inputs standardisation: StandardScaler is utilised for the purpose of standardising the input features. Standardisation is a process that facilitates convergence, thereby ensuring the comparability of data across diverse models.
- Train/test split: The train/test split of the dataset is achieved by employing the train_test_split function, which is utilised across all models to randomly divide the dataset into an 80/20 ratio (80% for training, 20% for testing). In contrast to other models, LSTM employs a data split that is not random but rather follows the timeline, using the initial 80% of the data for training and the remaining 20% for testing, thereby ensuring temporal sequence is respected. Hence, LSTM is the only model that respects the temporal sequence, which is imperative for modelling temporal dependence. All other models treat the data as independent, meaning that the model does not directly capture temporal dependencies.
- Hyperparameter optimisation: the hyperparameters were optimised using a genetic approach (10 generations of 30 individuals), with the DEAP library and exploiting multiprocessing. The implementation of elitism equal to 3 in each of the models ensures the retention and carry-over of the three best individuals from the current generation to the next. Each individual is representative of a set of model hyperparameters, and the fitness function is R2 on the complete dataset.
3. Case Study
3.1. Pakistan Climate
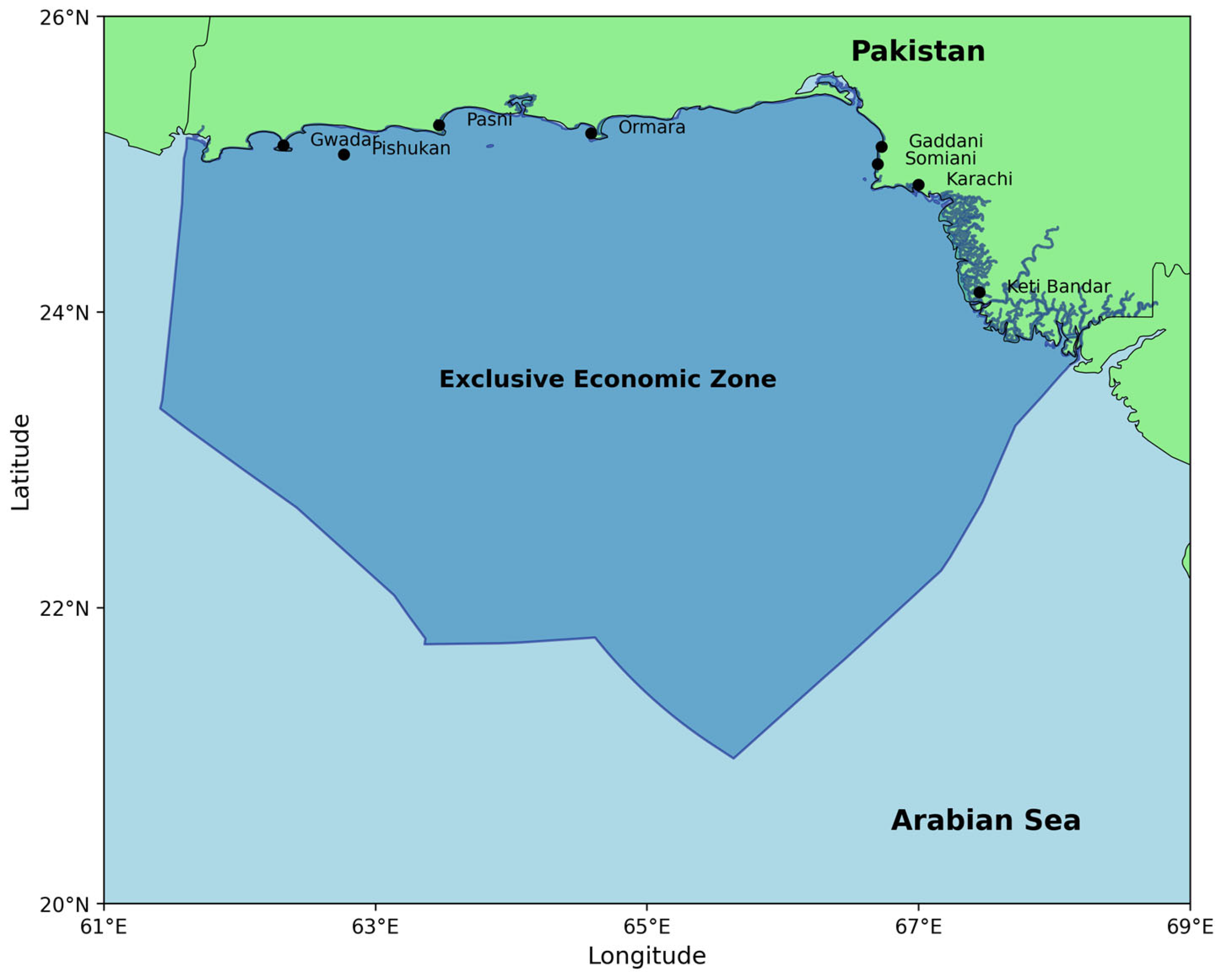
3.2. Pakistan Data
- The windiest onshore coastal site, characterised by the highest annual mean wind speed.
- The windiest offshore site with the shallowest seabed depth, to ensure the feasibility of foundation design.
3.3. Proposed Wind Farm
4. Results and Discussion
4.1. Theoretical and Real Power Curves
4.2. ML and DL Models Performance
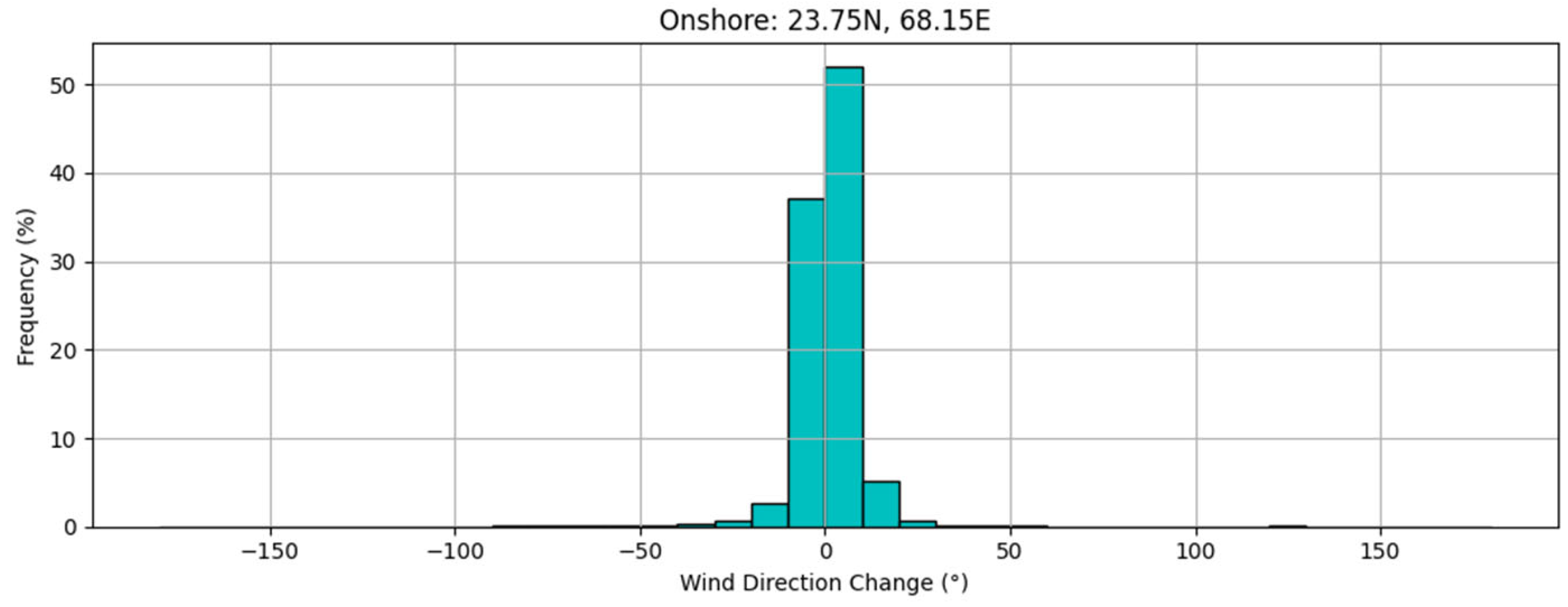
4.3. Selection of Simulation Locations and Wind Patterns
4.4. Producibility of the Proposed Wind Farm
4.5. Economic Analysis Results
- LCOE = 0.120 USD/kWh using the net producibility calculated through the ML model.
- LCOE = 0.097 USD/kWh using the net producibility estimated through the Theoretical Power Curve.
- LCOE = 0.059 USD/kWh using net producibility calculated through the ML model.
- LCOE = 0.048 USD/kWh using the net producibility estimated through the Theoretical Power Curve.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAPEX | Capital Expenditures |
| CF | Capacity Factor |
| CPI | Consumer Price Index |
| DL | Deep Learning |
| EEZ | Exclusive Economic Zone |
| GBoost | Gradient Boosting |
| HVAC | High-Voltage Alternating Current |
| HVDC | High-Voltage Direct Current |
| LCOE | Levelized Cost Of Energy |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| NEPRA | National Electric Power Regulatory Authority |
| OPEX | Operational Expenditures |
| R2 | Coefficient of Determination |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| XGBoost | Extreme Gradient Boosting |
| WACC | Weighted Average Cost of Capital |
References
- Filonchyk, M.; Peterson, M.P.; Zhang, L.; Hurynovich, V.; He, Y. Greenhouse Gases Emissions and Global Climate Change: Examining the Influence of CO2, CH4, and N2O. Sci. Total Environ. 2024, 935, 173359. [Google Scholar] [CrossRef]
- IEA. Global Energy Review 2025; IEA: Paris, France, 2025. [Google Scholar]
- World Energy Transitions Outlook 2024. Available online: https://www.irena.org/Publications/2024/Nov/World-Energy-Transitions-Outlook-2024 (accessed on 27 June 2025).
- Climate Action Support 2024. Available online: https://www.irena.org/Publications/2024/Nov/Climate-Action-Support-2024 (accessed on 27 June 2025).
- Kim, J.; Jaumotte, F.; Panton, A.J.; Schwerhoff, G. Energy Security and the Green Transition. Energy Policy 2025, 198, 114409. [Google Scholar] [CrossRef]
- IRENA. Renewable Capacity Statistics 2025; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2025. [Google Scholar]
- IRENA. Renewable Power Generation Costs in 2024; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2025. [Google Scholar]
- Yu, H.; Wen, B.; Zahidi, I.; Chow, M.F.; Liang, D.; Madsen, D.Ø. The Critical Role of Energy Transition in Addressing Climate Change at COP28. Results Eng. 2024, 22, 102324. [Google Scholar] [CrossRef]
- Qudrat-Ullah, H. A Review and Analysis of Renewable Energy Policies and CO2 Emissions of Pakistan. Energy 2022, 238, 121849. [Google Scholar] [CrossRef]
- Ahmad, R.; Liu, G.; Rehman, S.A.U.; Fazal, R.; Gao, Y.; Xu, D.; Agostinho, F.; Almeida, C.M.V.B.; Giannetti, B.F. Pakistan Road towards Paris Agreement: Potential Decarbonization Pathways and Future Emissions Reduction by a Developing Country. Energy 2025, 314, 134075. [Google Scholar] [CrossRef]
- Adil, L.; Eckstein, D.; Künzel, V. Laura Schäfer Climate Risk Index 2025|Germanwatch e.V. Available online: https://www.germanwatch.org/en/cri (accessed on 30 June 2025).
- Sustainable Development Policy Institute. Annual State of Renewable Energy Report Pakistan 2024; SDPI: Islamabad, Pakistan, 2024. [Google Scholar]
- National Electric Power Regulatory Authority. State of the Industry Report 2024; NEPRA: Islamabad, Pakistan, 2024. [Google Scholar]
- Saulat, H.; Khan, M.M.; Aslam, M.; Chawla, M.; Rafiq, S.; Zafar, F.; Khan, M.M.; Bokhari, A.; Jamil, F.; Bhutto, A.W.; et al. Wind Speed Pattern Data and Wind Energy Potential in Pakistan: Current Status, Challenging Platforms and Innovative Prospects. Environ. Sci. Pollut. Res. 2021, 28, 34051–34073. [Google Scholar] [CrossRef]
- Ali, B.; Abbas, G.; Memon, A.; Mirsaeidi, S.; Koondhar, M.A.; Chandio, S.; Channa, I.A. A Comparative Study to Analyze Wind Potential of Different Wind Corridors. Energy Rep. 2023, 9, 1157–1170. [Google Scholar] [CrossRef]
- Tahir, Z.u.R.; Abdullah, M.; Ahmad, S.; Kanwal, A.; Farhan, M.; Saeed, U.B.; Ali, T.; Amin, I. An Approach to Assess Offshore Wind Power Potential Using Bathymetry and Near-Hub-Height Reanalysis Data. Ocean. Eng. 2023, 280, 114458. [Google Scholar] [CrossRef]
- Desalegn, B.; Gebeyehu, D.; Tamrat, B.; Tadiwose, T.; Lata, A. Onshore versus Offshore Wind Power Trends and Recent Study Practices in Modeling of Wind Turbines’ Life-Cycle Impact Assessments. Clean. Eng. Technol. 2023, 17, 100691. [Google Scholar] [CrossRef]
- Xin, Y.; Bin Dost, M.K.; Akram, H.; Watto, W.A. Analyzing Pakistan’s Renewable Energy Potential: A Review of the Country’s Energy Policy, Its Challenges, and Recommendations. Sustainability 2022, 14, 16123. [Google Scholar] [CrossRef]
- National Transmission and Despatch Company. Indicative Generation Capacity Expansion Plan (IGCEP 2024-34); NTDC: Islamabad, Pakistan, 2024. [Google Scholar]
- Ministry of Energy (Power Division). National Electricity Plan 2023–2027; A Block, Pak Secretariat: Islamabad, Pakistan, 2023. [Google Scholar]
- NEPRA|CTBCM. Available online: https://www.nepra.org.pk/ctbcm.php (accessed on 30 June 2025).
- Wang, Y.; Duan, X.; Song, D.; Zou, R.; Zhang, F.; Li, Y. Wind Power Curve Modeling with Large-Scale Generalized Kernel-Based Regression Model. IEEE Trans. Sustain. Energy 2023, 14, 2121–2132. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Y.; Wang, R.; Ma, R. Modelling Potential Land Suitability of Large-Scale Wind Energy Development Using Explainable Machine Learning Techniques: Applications for China, USA and EU. Energy Convers. Manag. 2024, 302, 118131. [Google Scholar] [CrossRef]
- Karaman, Ö.A. Prediction of Wind Power with Machine Learning Models. Appl. Sci. 2023, 13, 11455. [Google Scholar] [CrossRef]
- Hulio, Z.H. Assessment of Wind Characteristics and Wind Power Potential of Gharo, Pakistan. J. Renew. Energy 2021, 2021, 8960190. [Google Scholar] [CrossRef]
- Burney, S.M.A.; Drakhshan, K.; Karim, S. Forecasting Wind Speed Using Machine Learning ANN Models at 4 Distinct Heights at Different Potential Locations in Pakistan. WSEAS Trans. Comput. 2023, 22, 127–141. [Google Scholar] [CrossRef]
- Tahir, Z.U.R.; Kanwal, A.; Afzal, S.; Ali, S.; Hayat, N.; Abdullah, M.; Saeed, U.B. Wind Energy Potential and Economic Assessment of Southeast of Pakistan. Int. J. Green. Energy 2021, 18, 1–16. [Google Scholar] [CrossRef]
- Dataset. Available online: https://www.kaggle.com/datasets/berkerisen/wind-turbine-scada-dataset (accessed on 28 May 2025).
- Shen, W.; Chen, X.; Qiu, J.; Hayward, J.A.; Sayeef, S.; Osman, P.; Meng, K.; Dong, Z.Y. A Comprehensive Review of Variable Renewable Energy Levelized Cost of Electricity. Renew. Sustain. Energy Rev. 2020, 133, 110301. [Google Scholar] [CrossRef]
- Ozbak, M.; Ghazizadeh-Ahsaee, M.; Ahrari, M.; Jahantigh, M.; Mirshekar, S.; Mirmozaffari, M.; Aranizadeh, A. Improving Power Output Wind Turbine in Micro-Grids Assisted Virtual Wind Speed Prediction. Sustain. Oper. Comput. 2024, 5, 119–130. [Google Scholar] [CrossRef]
- IEC 61400-12-1; Wind Energy Generation Systems—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2022.
- Sireesha, P.V.; Thotakura, S. Wind Power Prediction Using Optimized MLP-NN Machine Learning Forecasting Model. Electr. Eng. 2024, 106, 7643–7666. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind Power Short-Term Prediction Based on LSTM and Discrete Wavelet Transform. Appl. Sci. 2019, 9, 1108. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Sulaiman, M.H. Random Forest Based Wind Power Prediction Method for Sustainable Energy System. Clean. Energy Syst. 2025, 12, 100210. [Google Scholar] [CrossRef]
- Trizoglou, P.; Liu, X.; Lin, Z. Fault Detection by an Ensemble Framework of Extreme Gradient Boosting (XGBoost) in the Operation of Offshore Wind Turbines. Renew. Energy 2021, 179, 945–962. [Google Scholar] [CrossRef]
- Park, S.; Jung, S.; Lee, J.; Hur, J. A Short-Term Forecasting of Wind Power Outputs Based on Gradient Boosting Regression Tree Algorithms. Energies 2023, 16, 1132. [Google Scholar] [CrossRef]
- Singh, U.; Rizwan, M.; Alaraj, M.; Alsaidan, I. A Machine Learning-Based Gradient Boosting Regression Approach for Wind Power Production Forecasting: A Step towards Smart Grid Environments. Energies 2021, 14, 5196. [Google Scholar] [CrossRef]
- Waluyo, N.R.; Astuti, W.; Ihsan, A.F. Anomaly Detection in Gas Pipes with an Ensemble Learning Approach: Combination of Random Forest and GBoost. In Proceedings of the 2024 International Conference on Intelligent Cybernetics Technology and Applications, ICICyTA 2024, Bali, Indonesia, 17–19 December 2024; pp. 55–59. [Google Scholar] [CrossRef]
- Testasecca, T.; Maniscalco, M.P.; Brunaccini, G.; Airò Farulla, G.; Ciulla, G.; Beccali, M.; Ferraro, M. Toward a Digital Twin of a Solid Oxide Fuel Cell Microcogenerator: Data-Driven Modelling. Energies 2024, 17, 4140. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, H.; Zhang, Y.; Zuo, Z. A Comprehensive Review of Wind Power Prediction Based on Machine Learning: Models, Applications, and Challenges. Energies 2025, 18, 350. [Google Scholar] [CrossRef]
- Glossary—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/tools/glossary/index.php?id=Capacity_factor (accessed on 30 June 2025).
- Feng, Y.; Gong, D.; Jiang, S.; Zhao, L.; Cui, N. National-Scale Development and Calibration of Empirical Models for Predicting Daily Global Solar Radiation in China. Energy Convers. Manag. 2020, 203, 112236. [Google Scholar] [CrossRef]
- Das, K.; Kumar, R.; Krishna, A. Analyzing Electric Vehicle Battery Health Performance Using Supervised Machine Learning. Renew. Sustain. Energy Rev. 2024, 189, 113967. [Google Scholar] [CrossRef]
- Dasi, H.; Ying, Z.; Ashab, M.F. Bin Proposing Hybrid Prediction Approaches with the Integration of Machine Learning Models and Metaheuristic Algorithms to Forecast the Cooling and Heating Load of Buildings. Energy 2024, 291, 130297. [Google Scholar] [CrossRef]
- Satymov, R.; Bogdanov, D.; Breyer, C. Techno-Economics of Offshore Wind Power in Global Resolution. Appl. Energy 2025, 393, 125980. [Google Scholar] [CrossRef]
- Bosch, J.; Staffell, I.; Hawkes, A.D. Temporally Explicit and Spatially Resolved Global Offshore Wind Energy Potentials. Energy 2018, 163, 766–781. [Google Scholar] [CrossRef]
- Cavazzi, S.; Dutton, A.G. An Offshore Wind Energy Geographic Information System (OWE-GIS) for Assessment of the UK’s Offshore Wind Energy Potential. Renew. Energy 2016, 87, 212–228. [Google Scholar] [CrossRef]
- Sens, L.; Neuling, U.; Kaltschmitt, M. Capital Expenditure and Levelized Cost of Electricity of Photovoltaic Plants and Wind Turbines—Development by 2050. Renew. Energy 2022, 185, 525–537. [Google Scholar] [CrossRef]
- Bosch, J.; Staffell, I.; Hawkes, A.D. Global Levelised Cost of Electricity from Offshore Wind. Energy 2019, 189, 116357. [Google Scholar] [CrossRef]
- Euro Foreign Exchange Reference Rates. Available online: https://www.ecb.europa.eu/stats/policy_and_exchange_rates/euro_reference_exchange_rates/html/index.en.html (accessed on 1 July 2025).
- Consumer Price Index, 1913-|Federal Reserve Bank of Minneapolis. Available online: https://www.minneapolisfed.org/about-us/monetary-policy/inflation-calculator/consumer-price-index-1913- (accessed on 1 July 2025).
- Dato, P.; Dioha, M.; Hessou, H.; Houenou, B.; Mukhaya, B.; Okyere, M.A.; Odarno, L. Computation of Weighted Average Cost of Capital (WACC) in the Power Sector for African Countries and the Implications for Country-Specific Electricity Technology Cost. Appl. Energy 2025, 397, 126333. [Google Scholar] [CrossRef]
- Wind Turbine Scada Dataset. Available online: https://www.kaggle.com/datasets/berkerisen/wind-turbine-scada-dataset/data (accessed on 27 June 2025).
- Position of the Wind Turbine—40°35’07.6″ N 28°59′25.3″ E—Google Maps. Available online: https://www.google.com/maps/place/40%C2%B035’07.6%22N+28%C2%B059’25.3%22E/@40.5851806,28.9897199,833m/data=!3m1!1e3!4m4!3m3!8m2!3d40.5854444!4d28.9903611!5m1!1e4?hl=en-US&entry=ttu&g_ep=EgoyMDI1MDYyMy4yIKXMDSoASAFQAw%3D%3D (accessed on 27 June 2025).
- N117/3600—Nordex, SE. Available online: https://www.nordex-online.com/en/product/n117-3600/ (accessed on 27 June 2025).
- Chatterjee, J.; Dethlefs, N. Deep Learning with Knowledge Transfer for Explainable Anomaly Prediction in Wind Turbines. Wind. Energy 2020, 23, 1693–1710. [Google Scholar] [CrossRef]
- Zahid, M.; Rasul, G. Thermal Classification of Pakistan. Atmos. Clim. Sci. 2011, 01, 206–213. [Google Scholar] [CrossRef]
- Adeel, M.; Razzak, A.; Riaz, S.M.F.; Iqbal, M.J. Impact of Sea Surface Temperature in the Arabian Sea on the Variability of Summer Monsoon Rainfall over Pakistan Region. Dyn. Atmos. Ocean. 2024, 107, 101482. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service, Climate Data Store. ERA5 Hourly Data on Single Levels from 1940 to Present; Copernicus Climate Change Service (C3S) Climate Data Store (CDS): 2023. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=overview (accessed on 28 May 2025).
- Sharma, P.K.; Warudkar, V.; Ahmed, S. Effect of Atmospheric Stability on the Wind Resource Extrapolating Models for Large Capacity Wind Turbines: A Comparative Analysis of Power Law, Log Law and Deaves and Harris Model. Energy Procedia 2019, 158, 1235–1240. [Google Scholar] [CrossRef]
- Golbazi, M.; Archer, C.L. Methods to Estimate Surface Roughness Length for Offshore Wind Energy. Adv. Meteorol. 2019, 2019, 5695481. [Google Scholar] [CrossRef]
- Levin, N.; Ben-Dor, E.; Kidron, G.J.; Yaakov, Y. Estimation of Surface Roughness (Z0) Cover a Stabilizing Coastal Dune Field Based on Vegetation and Topography. Earth Surf. Process Landf. 2008, 33, 1520–1541. [Google Scholar] [CrossRef]
- IRENA. Renewable Power Generation Costs in 2023; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2024. [Google Scholar]








| Turbine Spacing [D = Rotor Diameters] | 5 × 5 | 10 × 10 | 50 × 50 |
|---|---|---|---|
| 5 | 85% | 70% | 29% |
| 9 | 94% | 86% | 62% |
| 16 | 98% | 96% | 87% |
| 28 | 99% | 98% | 95% |
| Metrics | DATASET: True y = Active Power Predicted y = Theoretical Power |
|---|---|
| R2 | 0.879 |
| MAE | 192.76 W |
| RMSE | 456.19 W |
| Model | Optimal Parameters | R2 Test | R2 Total | MAE Test [kW] | MAE Total [kW] | RMSE Test [kW] | RMSE Total [kW] |
|---|---|---|---|---|---|---|---|
| GBoost | n_estimators = 292, learning_rate = 0.283, max_depth = 10, subsample = 0.791, min_samples_split = 2, min_samples_leaf = 1 | 0.884 | 0.975 | 197.923 | 71.484 | 444.682 | 206.315 |
| XGBoost | n_estimators = 563, max_depth = 10, learning_rate = 0.189, subsample = 0.983, colsample_bytree = 0.978 | 0.884 | 0.976 | 197.732 | 54.843 | 447.061 | 202.255 |
| RF | n_estimators = 556, max_depth = 35, min_samples_split = 2, min_samples_leaf = 1, max_features = 0.933 | 0.901 | 0.970 | 173.024 | 84.105 | 410.574 | 225.545 |
| MLP | hidden_layer_size = 162, activation = tanh, alpha = 0.010, learning_rate = 0.038 | 0.907 | 0.916 | 160.319 | 153.178 | 398.563 | 380.120 |
| LSTM | hidden_layer_size = 70, dropout = 0.009, rec_dropout = 0.137, learning_rate = 0.007 | 0.914 | 0.915 | 201.809 | 157.704 | 395.276 | 381.533 |
| Producibility [GWh/y] | ||||
|---|---|---|---|---|
| Site | Trained RF Model: Gross Production | Theoretical Power Curve: Gross Production | Trained RF Model: Net Production | Theoretical Power Curve: Net Production |
| Offshore | 221.3 | 302.6 | 217.1 | 267.1 |
| Onshore | 244.9 | 333.3 | 240.8 | 294.9 |
| Capacity Factor [%] | ||||
|---|---|---|---|---|
| Site | Trained RF Model: Gross Production | Theoretical Power Curve: Gross Production | Trained RF Model: Net Production | Theoretical Power Curve: Net Production |
| Offshore | 28.1% | 38.4% | 27.5% | 33.9% |
| Onshore | 31.1% | 42.3% | 30.5% | 37.4% |
| Foundation (Jacket) | Grid (HVAC) | Installation | Turbines | Total CAPEX |
|---|---|---|---|---|
| 65.612 | 36.679 | 102.157 | 151.395 | 355.843 |
| Annual OPEX | ||||
| 7.117 |
| Foundation | Turbines | Other CAPEX | Total CAPEX |
|---|---|---|---|
| 8.598 | 132.580 | 23.924 | 165.101 |
| Annual OPEX | |||
| 2.476 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miceli, A.V.; Cardona, F.; Lo Brano, V.; Micari, F. Assessing the Technical and Economic Viability of Onshore and Offshore Wind Energy in Pakistan Through a Data-Driven Machine Learning and Deep Learning Approach. Energies 2025, 18, 5080. https://doi.org/10.3390/en18195080
Miceli AV, Cardona F, Lo Brano V, Micari F. Assessing the Technical and Economic Viability of Onshore and Offshore Wind Energy in Pakistan Through a Data-Driven Machine Learning and Deep Learning Approach. Energies. 2025; 18(19):5080. https://doi.org/10.3390/en18195080
Chicago/Turabian StyleMiceli, Angela Valeria, Fabio Cardona, Valerio Lo Brano, and Fabrizio Micari. 2025. "Assessing the Technical and Economic Viability of Onshore and Offshore Wind Energy in Pakistan Through a Data-Driven Machine Learning and Deep Learning Approach" Energies 18, no. 19: 5080. https://doi.org/10.3390/en18195080
APA StyleMiceli, A. V., Cardona, F., Lo Brano, V., & Micari, F. (2025). Assessing the Technical and Economic Viability of Onshore and Offshore Wind Energy in Pakistan Through a Data-Driven Machine Learning and Deep Learning Approach. Energies, 18(19), 5080. https://doi.org/10.3390/en18195080






