Abstract
The intrinsic structural stability of ABO3 perovskite materials is a pivotal factor determining their efficiency and durability in photovoltaic applications. However, accurately predicting stability, commonly measured by the energy above hull metric, remains challenging due to the complex interplay of compositional, crystallographic, and electronic features. To address this challenge, we propose a streamlined hybrid machine learning framework that combines the sequence modeling capability of Long Short-Term Memory (LSTM) networks with the robustness of Random Forest regressors. A genetic algorithm-based feature selection strategy is incorporated to identify the most relevant descriptors and reduce noise, thereby enhancing both predictive accuracy and interpretability. Comprehensive evaluations on a curated ABO3 dataset demonstrate strong performance, achieving an of 0.98 on training data and 0.83 on independent test data, with a Mean Absolute Error (MAE) of 8.78 for training and 21.23 for testing, and Root Mean Squared Error (RMSE) values that further confirm predictive reliability. These results validate the effectiveness of the proposed approach in capturing the multifactorial nature of perovskite stability while ensuring robust generalization. This study highlights a practical and reliable pathway for accelerating the discovery and optimization of stable perovskite materials, contributing to the development of more durable next-generation solar technologies.
1. Introduction
In recent years, perovskite materials, especially those conforming to the general chemical formula ABO3, have attracted tremendous research interest due to their extraordinary optoelectronic properties, structural versatility, and cost-effective synthesis processes [1]. These materials have emerged as highly promising candidates for next-generation solar cells, light-emitting devices, and other optoelectronic applications. Their tunable bandgap energies, high absorption coefficients, long carrier diffusion lengths, and defect tolerance distinguish them from conventional semiconductor materials, making them particularly attractive for efficient photovoltaic devices. The ABO3 perovskite family, characterized by its distinctive crystal structure, offers considerable flexibility in compositional engineering, enabling researchers to optimize performance by substituting different cations at the A- and B-sites. This versatility allows for tailoring of physical and chemical properties to meet specific functional requirements. Despite the remarkable progress achieved in perovskite-based solar cells, a major bottleneck hindering their commercialization is their intrinsic instability under real-world operating conditions [2,3,4]. Stability concerns stem from various degradation mechanisms including moisture ingress, thermal stress, photo-induced chemical reactions, and ion migration, all of which can lead to structural distortions, phase segregation, and loss of device performance over time. The complex interplay between these degradation pathways and the material’s intrinsic properties makes the stability problem particularly challenging to understand and predict. Consequently, improving the long-term stability of ABO3 perovskites remains one of the foremost objectives for researchers aiming to transition these materials from the laboratory to commercial solar panels.
Accurate and reliable prediction of perovskite stability is essential for accelerating materials’ discovery and optimizing device design. Traditional approaches based on empirical testing and trial-and-error synthesis are both laborious and costly, often requiring months or years of experimentation to identify promising compositions with enhanced stability. This inefficiency has driven the materials science community to explore data-driven computational techniques that can effectively screen large chemical spaces and predict material properties prior to synthesis [5]. Machine learning (ML) and deep learning (DL) methods have demonstrated exceptional potential in this regard by uncovering hidden patterns in high-dimensional datasets, learning complex nonlinear relationships, and generalizing to unseen material compositions [6]. These methods can drastically reduce the time and expense involved in material development cycles, enabling faster identification of stable perovskite formulations. However, despite the promise of ML and DL for material prediction, current approaches face several notable limitations. Many deep learning models suffer from a lack of interpretability, functioning as “black boxes” that provide limited insight into the factors driving stability. This opacity complicates the understanding of underlying physicochemical phenomena and diminishes the confidence of materials scientists in predictions. Moreover, the performance of these models heavily depends on the quality and relevance of input features. High-dimensional datasets often contain noisy, redundant, or irrelevant descriptors, which can degrade model accuracy and increase computational complexity. Feature selection thus becomes a critical step in enhancing model robustness and generalization capability. Furthermore, existing works typically focus on either traditional machine learning or deep learning independently, missing opportunities to leverage their complementary strengths.
Several recent studies have explored machine learning frameworks for perovskite stability prediction, including approaches based on conventional ML regressors [7], deep neural networks [8], and hybrid modeling strategies [9,10]. While these contributions have advanced the field, they often suffer from key shortcomings such as limited interpretability, insufficient handling of high-dimensional feature spaces, and lack of systematic feature optimization. Moreover, most prior works employ either deep learning or traditional ensemble-based models in isolation, which restricts their ability to fully capture the multifaceted relationships that govern perovskite stability. The novelty of this study lies in the development of a hybrid framework that integrates Long Short-Term Memory (LSTM) networks with Random Forest regressors, systematically optimized through a genetic algorithm-based feature selection strategy. Unlike prior works, our framework combines the sequential representation power of LSTMs with the robustness and interpretability of ensemble learning, while simultaneously addressing feature redundancy and noise via evolutionary optimization. This synergy allows for enhanced predictive accuracy, improved generalization capability, and deeper scientific interpretability compared to existing methodologies. By explicitly bridging the gap between deep learning and ensemble approaches, our work introduces a distinctive paradigm for stability prediction in ABO3 perovskites, complementing and extending the scope of earlier studies.
To address these challenges, this paper proposes a novel hybrid predictive modeling framework that integrates Long Short-Term Memory (LSTM) networks, known for their ability to capture sequential and temporal dependencies, with Random Forest regressors, which offer robustness and interpretability through ensemble learning. This hybrid model is further optimized using a genetic algorithm for efficient and effective feature selection, aiming to reduce input dimensionality while preserving or improving prediction performance. By combining these methodologies, the framework balances the representational power of deep learning with the stability and interpretability of ensemble methods, ultimately enhancing the reliability of stability predictions for ABO3 perovskites.
The key contributions of this work can be summarized as follows:
- We develop a hybrid LSTM–Random Forest model that effectively captures complex nonlinear and temporal patterns present in perovskite material datasets, addressing challenges posed by the multifactorial nature of stability.
- We implement a genetic algorithm-based feature selection strategy that systematically explores the feature space to identify the most informative descriptors, reducing dimensionality and mitigating the effects of noise and redundancy.
- We explicitly contrast our framework with recent studies in the literature, highlighting how our integration of LSTM, Random Forest, and GA-driven optimization introduces a novel modeling paradigm that advances both accuracy and interpretability for ABO3 perovskite stability prediction.
- We perform a comprehensive experimental evaluation on a benchmark ABO3 perovskite dataset, demonstrating that the proposed hybrid framework achieves superior predictive accuracy and computational efficiency compared to existing state-of-the-art machine learning and deep learning models.
The remainder of this paper is organized as follows. Section 2 provides a comprehensive review of the relevant literature on machine learning and deep learning methods for perovskite stability prediction. Section 3 details the experimental setup, including data collection, preprocessing techniques, feature engineering, and the construction of the hybrid LSTM–RF model. Section 4 presents the experimental results and discussion, covering genetic algorithm-based feature selection, model convergence, prediction accuracy, quantitative evaluation, stability across runs, computational efficiency, and comparison with existing studies. Finally, Section 5 concludes the paper by summarizing the key findings and outlining future research directions to further enhance predictive modeling of perovskite stability and accelerate the material discovery pipeline.
2. Literature Review
The remarkable progress in perovskite solar cells (PSCs) has been predominantly driven by their high power conversion efficiencies and cost-effective fabrication processes [11]. Among various perovskite compounds, ABO3 perovskites have attracted substantial interest owing to their tunable structural and electronic properties, which are instrumental in optimizing device performance and stability [2]. Notwithstanding these advancements, the intrinsic instability of PSCs under operational conditions remains a critical impediment to their large-scale commercial deployment [12]. Extensive experimental studies have been conducted to elucidate the degradation mechanisms of PSCs, focusing on the effects of environmental stressors such as moisture, thermal load, and photochemical reactions [4,13]. Recent works have further highlighted the impact of contact-layer defects and electrochemical treatments on perovskite stability, providing deeper insights into degradation pathways under operational conditions [14,15]. While these investigations have significantly advanced the understanding of perovskite degradation pathways, their labor-intensive and time-consuming nature limits throughput and scalability, thereby constraining systematic exploration across broad compositional spaces.
First-principles computational methods, particularly density functional theory (DFT), have been extensively utilized to analyze the stability of perovskite materials at the atomic scale [16,17]. These approaches provide fundamental insights into electronic structure, defect energetics, and phase stability, contributing valuable guidance for material design. However, the substantial computational expense associated with DFT calculations renders them unsuitable for high-throughput screening of large compositional and structural parameter spaces. In response to these challenges, machine learning (ML) techniques have emerged as powerful alternatives for rapid material property prediction and accelerated discovery [18]. Algorithms such as Random Forests [19], Support Vector Machines [20], and Gradient Boosting Machines [20] have demonstrated efficacy in modeling complex relationships within materials datasets. These approaches facilitate high-throughput screening by learning predictive mappings from structured descriptors to material properties. Nonetheless, the dependence of these models on handcrafted features may limit their capacity to capture the full complexity and nonlinear interactions inherent in perovskite materials [21].
Deep learning (DL) frameworks, notably Long Short-Term Memory (LSTM) networks, have shown considerable promise in automatic feature extraction and modeling of sequential or temporal dependencies intrinsic to materials datasets [8,22]. DL models enable hierarchical representation learning, thereby mitigating the limitations of manual feature engineering. However, their efficacy is contingent upon access to large and diverse datasets; otherwise, they risk overfitting and diminished generalizability [23]. Given the scarcity of extensive, high-quality perovskite stability datasets, this represents a substantial obstacle. To reconcile these challenges, hybrid modeling frameworks that integrate DL and classical ML methods have recently been proposed, leveraging the complementary advantages of both paradigms to enhance predictive accuracy and robustness [24,25]. Concurrently, genetic algorithms (GAs) have been employed to optimize feature selection and hyperparameters, facilitating improved model generalization and computational efficiency by systematically navigating large search spaces [26].
Despite these advances, the literature reveals a conspicuous gap in comprehensive frameworks that combine GA-optimized feature selection with hybrid DL-ML architectures specifically tailored for the stability prediction of ABO3 perovskites. Furthermore, existing studies often lack rigorous evaluations employing diverse error metrics and robustness analyses, which are essential for assessing model reliability and applicability [14]. The present study addresses these deficiencies by proposing a novel GA-optimized hybrid deep learning framework that synergistically integrates LSTM networks with Random Forest regressors, achieving superior predictive performance, robust feature selection, and incorporating insights from the latest experimental findings on perovskite degradation and stability [14,15]. Table 1 summarizes key relevant studies, delineating their methodologies, principal contributions, and identified limitations.

Table 1.
Summary of related works on perovskite stability prediction and modeling.
3. Experimental Setup
In this section, we present a comprehensive overview of the experimental framework designed to evaluate the stability prediction of ABO3 perovskite materials. The discussion includes the dataset characteristics, data preprocessing and normalization methods, feature selection via a genetic algorithm, the hybrid deep learning model architecture integrating LSTM and Random Forest, training protocols, and the evaluation metrics employed to assess model performance. This detailed description ensures reproducibility and clarity regarding the methodological approach used in this research.
3.1. Data Collection
The dataset utilized in this study was obtained from a publicly accessible repository hosted on Kaggle [27], which offers a comprehensive collection of data pertinent to the stability analysis of ABO3 perovskite materials. This dataset integrates a wide range of physicochemical and crystallographic features that are essential for accurately characterizing the stability of perovskite compounds. The features included were derived from a combination of experimental measurements and high-fidelity computational simulations, thereby providing a rich and diverse data source suitable for robust predictive modeling. Among the critical descriptors, the dataset encompasses elemental properties such as the atomic radius, electronegativity, and oxidation states of the constituent atoms occupying the A-site, B-site, and X-site within the perovskite crystal lattice. Additionally, site occupancies and fractional coordinates are provided to capture the structural configuration of the material. Complementing these are calculated parameters related to the thermodynamic and electronic stability, including formation energies, bandgap estimates, and lattice distortions, which collectively contribute to a comprehensive understanding of the material’s behavior under varying conditions.
The primary dependent variable targeted in this work is the energy above the the hull(expressed in meV/atom), a widely accepted metric for assessing the thermodynamic stability of crystalline materials. This parameter quantifies the energy difference between the given perovskite phase and the most stable competing phases at the same composition. Lower energy above hull values signify greater stability and a higher likelihood of synthesizability and long-term structural integrity. Consequently, accurate prediction of this metric is critical for guiding material design and experimental efforts. Table 2 provides a detailed summary of the principal features incorporated in the current study, including their physical or chemical significance and their anticipated impact on perovskite stability. This structured feature set lays the foundation for the subsequent machine learning modeling, enabling effective capture of the complex relationships governing stability phenomena in ABO3 perovskite materials.

Table 2.
Summary of key dataset features.
Although the Kaggle repository provides a rich dataset, it is important to recognize potential limitations regarding quality and representativeness. Because the dataset integrates both experimental and computationally derived features, inconsistencies or systematic biases may exist, particularly in density functional theory (DFT)-based values that depend on the choice of functional [28,29]. Furthermore, the dataset may overrepresent well-studied compositions while underrepresenting less common chemistries, which could affect generalizability. Similar concerns have been noted in other materials informatics studies [30,31], where dataset composition plays a critical role in predictive performance. Despite these limitations, the dataset remains a widely used and a representative benchmark for perovskite stability prediction, and its adoption in this study ensures comparability with prior work.
3.2. Dataset Preprocessing and Feature Engineering
Prior to model development, the raw dataset underwent a comprehensive preprocessing and feature engineering pipeline aimed at ensuring high data quality, eliminating redundancy, and maximizing predictive relevance. The dataset, obtained from the publicly available Kaggle repository [27], contains physicochemical and crystallographic descriptors of ABO3 perovskite compounds. These descriptors encompass elemental properties (e.g., electronegativity, ionic radii, atomic mass), crystallographic site occupancies (A-site, B-site, X-site), and computed thermodynamic stability metrics such as the energy above hull.
3.2.1. Handling Missing Data
Missing entries in the dataset were addressed through statistical imputation to avoid information loss and ensure numerical consistency. For numerical attributes, mean imputation was applied, as expressed in (1):
where represents the value of the j-th feature for the i-th sample, and is the number of non-missing observations in feature j.
3.2.2. Feature Scaling and Normalization
Continuous features were standardized to zero mean and unit variance to prevent features with larger magnitudes from dominating the model training process, as defined in (2):
where and denote the mean and standard deviation of the j-th feature, respectively.
For certain engineered parameters, min–max normalization was applied to constrain the transformed variables within the range [0, 1], as given by (3):
3.2.3. Categorical Feature Encoding
Categorical descriptors, such as the type of A-site and B-site elements, were transformed into a numerical format using one-hot encoding, producing a binary indicator vector for each category (4):
3.2.4. Domain-Specific Feature Engineering
In addition to the original descriptors, domain knowledge of perovskite crystallography was leveraged to construct physically meaningful derived features. The Goldschmidt tolerance factor [32], a widely used stability indicator, was computed as follows:
where , , and correspond to the ionic radii of the A-site cation, B-site cation, and X-site anion, respectively.
Similarly, the octahedral factor, which quantifies the geometric compatibility of the B-site cation within the octahedral coordination environment, was calculated as follows:
3.2.5. Dimensionality Reduction and Correlation Filtering
To mitigate multicollinearity and reduce overfitting, redundant features were identified and removed based on the Pearson correlation coefficient (7). Features with an absolute correlation magnitude exceeding were discarded:
3.2.6. Pipeline Overview
The complete preprocessing and feature engineering workflow—spanning missing value treatment, scaling, encoding, domain-specific feature construction, and dimensionality reduction—is illustrated in Figure 1. This systematic approach ensured a refined and informative feature matrix optimized for predictive modeling of ABO3 perovskite stability. After completing the preprocessing stage, the dataset initially consisted of 81 physicochemical and structural features. To reduce dimensionality and enhance model generalization, a genetic algorithm (GA) was employed for optimal feature selection. The GA iteratively evaluated subsets of features based on a predefined fitness function, ultimately selecting the top-ranked features that maximized predictive accuracy while minimizing redundancy. This process yielded the most informative subset for subsequent model training, significantly improving computational efficiency. The convergence behavior of the GA, along with the ranking of features by their importance score, is illustrated in Figure 2, highlighting the trade-off between the number of selected features and predictive performance.
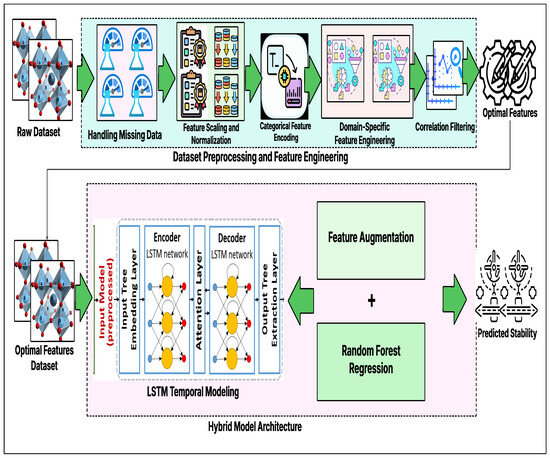
Figure 1.
Pipeline of the hybrid LSTM–Random Forest model, integrating data preprocessing, temporal feature extraction, and regression.
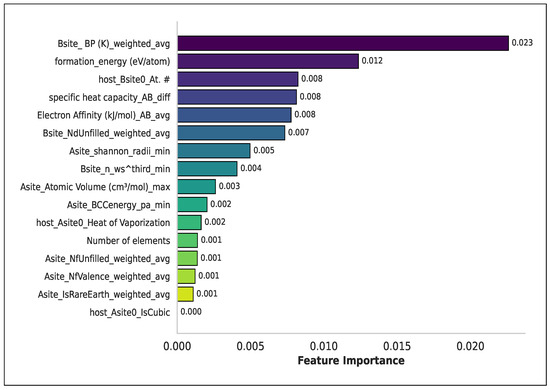
Figure 2.
Feature importance ranking obtained through Genetic Algorithm-based optimal feature selection from the original 81 features. The most influential features include the weighted average bond parameter at the B-site (Bsite_BP(K)), formation energy, and host B-site atomic number (host_Bsite0_At.#). Several features share identical importance values (e.g., 0.001), reflecting comparable contributions to the predictive model.
3.2.7. Feature Importance and Physical Interpretation
Figure 2 illustrates the top features selected by the genetic algorithm (GA) from the original 81 descriptors. To provide deeper scientific insight and enhance interpretability, we analyzed these top-ranked features based on their physical and chemical significance. Among the most influential features, the ionic radii of the A- and B-site cations ( and ) strongly impact the geometric compatibility within the ABO3 lattice. Larger or smaller radii can distort the octahedral coordination, influencing the Goldschmidt tolerance factor and the structural stability of the perovskite. The electronegativity difference between cations and anions () governs the ionic versus covalent character of bonds; a significant mismatch can result in unstable bonding environments, highlighting its importance for model predictions. The derived Goldschmidt tolerance factor (t) captures the geometric fit of ions in the perovskite structure, where values close to unity correspond to optimal packing and higher stability. Similarly, the octahedral factor (), which quantifies the ratio of the B-site cation to anion radii, reflects the cation’s ability to occupy the octahedral site without inducing lattice strain. Deviations from ideal values are associated with lower structural stability. Finally, computed thermodynamic descriptors, such as the energy above hull, provide direct measures of stability from first-principles calculations, guiding the model to distinguish stable from unstable compositions. Collectively, these features represent a combination of geometric, electronic, and thermodynamic factors that fundamentally govern ABO3 perovskite stability. Their selection by the GA confirms that the hybrid model is not only predictive but also physically interpretable, aligning with established chemical principles and the existing literature. This enhanced interpretability ensures that the model captures the most relevant material characteristics rather than spurious correlations.
3.3. Selected Hybrid Model Architecture
This work proposes a hybrid modeling framework that combines Long Short-Term Memory (LSTM) networks with Random Forest (RF) regression to leverage the complementary strengths of deep sequence modeling and ensemble-based learning methods for the task of predicting the thermodynamic stability of ABO3 perovskite materials. The input to the model is a feature matrix , where N represents the number of samples and F is the number of optimally selected features obtained through the genetic algorithm process detailed in Section 3.2. This feature matrix incorporates both intrinsic physicochemical properties and engineered descriptors relevant to perovskite stability. The matrix is initially fed into the LSTM network to capture temporal dependencies and complex nonlinear patterns that may be present within the structured data.
The LSTM model architecture is composed of a series of gating mechanisms that regulate the flow and retention of information across sequential steps. These mechanisms include the input gate , forget gate , and output gate , which are mathematically described in Equations (8)–(10), respectively. The input gate controls how much new information is incorporated into the cell state, while the forget gate determines the degree to which the previous cell state is retained or discarded. The output gate regulates the portion of the internal cell state that is exposed to the hidden state output. In parallel, the candidate cell state , computed through a nonlinear transformation using the hyperbolic tangent activation as shown in Equation (11), represents potential new information to update the memory cell. The final cell state is then updated by combining the previous state and the candidate state , modulated by the forget and input gates according to Equation (12). Finally, the hidden state , which encodes the output representation at timestep t, is computed by filtering the updated cell state through the output gate and a nonlinearity, as given in Equation (13).
Here, denotes the sigmoid activation function which outputs values between 0 and 1, effectively acting as gates controlling the flow of information. The operator ⊙ represents element-wise multiplication. The vectors , , , and are weight matrices that are learned during training, and , , , are corresponding bias vectors. The input vector at timestep t is , and denotes the hidden state from the previous timestep.
The final hidden state outputs from the LSTM layer, which encapsulate the learned temporal and nonlinear dependencies across the input features, are represented as . To enrich the feature space, these learned representations are concatenated with the original selected feature set, forming an augmented input matrix as shown in Equation (14):
This augmented feature matrix is then supplied to a Random Forest regressor, which employs an ensemble of M decision trees to model the nonlinear mappings from features to the target stability metric. Each decision tree in the ensemble independently generates a prediction, and the final model output is computed by averaging across all tree predictions, as formalized in Equation (15):
The use of ensemble averaging in Random Forests effectively reduces variance and improves the model’s ability to generalize to unseen data. This property is especially valuable in the context of perovskite stability prediction, where the underlying relationships between compositional features and stability outcomes are highly complex and nonlinear. A schematic representation of the proposed hybrid model pipeline is provided in Figure 1, illustrating the sequential processing steps starting from feature selection, followed by temporal embedding extraction through LSTM and culminating in ensemble regression via Random Forest.
Thus, the model leverages the temporal dependency capturing capability of LSTM networks, as mathematically detailed in Equations (8)–(13), combined with the robust ensemble learning approach of Random Forest regression as given in Equations (14) and (15). This hybrid framework provides a powerful mechanism with which to accurately predict the thermodynamic stability of ABO3 perovskites, surpassing the limitations of using either model alone.
3.4. Model Training
The proposed hybrid model integrates a Long Short-Term Memory (LSTM) network and a Random Forest (RF) regressor. The LSTM component is trained to capture temporal dependencies and nonlinear relationships within the selected features, while the RF model leverages the LSTM predictions combined with original features for robust regression. The LSTM model architecture consists of two stacked LSTM layers with 64 and 32 units, respectively, each followed by a dropout layer with a rate of 0.2 to mitigate overfitting. A fully connected dense layer with 16 neurons and ReLU activation precedes the final output neuron, which provides the predicted stability value. The model was compiled using the Adam optimizer with a learning rate of 0.001, optimizing the mean squared error (MSE) loss function. The training was conducted for 500 epochs with a batch size of 32, employing early stopping based on validation loss to prevent overfitting.
The training dataset was split with an 80:20 ratio for training and validation purposes within the LSTM training phase. Subsequently, the Random Forest regressor was trained using 200 trees, a maximum depth of 15, and a minimum sample split of 5, on a feature set augmented by the LSTM predictions. The experiments were conducted on a system equipped with an Intel Core i7 processor, 16 GB RAM, and an NVIDIA GTX 1660 Ti GPU. The model training utilized the TensorFlow framework for the LSTM implementation and scikit-learn for the Random Forest regressor. This training strategy enabled the hybrid model to efficiently learn complex patterns in the data, achieving strong predictive performance on the perovskite stability dataset.
3.5. Model Evaluation
The performance of the proposed hybrid model was quantitatively assessed using widely accepted regression metrics, including Mean Squared Error (MSE), Mean Absolute Error (MAE), and the Coefficient of Determination (). These metrics comprehensively evaluate the model’s accuracy and predictive capability. The Mean Squared Error (MSE) is defined as the average of the squares of the differences between actual values and predicted values , as shown in Equation (16). It penalizes larger errors more severely, providing a sensitive measure of prediction deviations.
The Mean Absolute Error (MAE), given by Equation (17), calculates the average absolute differences between predicted and observed values, offering an intuitive measure of average error magnitude in the same units as the target variable.
The Coefficient of Determination () measures the proportion of variance in the dependent variable explained by the model, defined in Equation (18). An closer to unity indicates a superior fit.
In addition to these quantitative measures, graphical analyses such as the scatter plot comparing actual and predicted stability values (Figure 3) and residual error distributions were utilized to qualitatively assess model robustness and identify any systematic deviations. These evaluation methods collectively ensure a rigorous and multifaceted validation of the proposed hybrid model’s predictive performance and generalization capability.
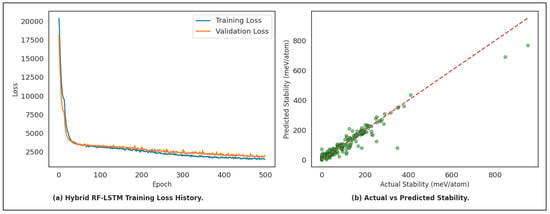
Figure 3.
Hybrid LSTM–RF model performance: (Left) training and validation loss history; (Right) actual vs. predicted thermodynamic stability.
4. Experimental Results and Discussion
This section presents the outcomes of the proposed hybrid framework and provides an in-depth discussion of the findings. The results are organized to demonstrate both the quantitative performance of the model and the qualitative insights derived from its predictive behavior. Specifically, we report evaluation metrics, learning curves, and visualization-based assessments to validate the effectiveness of the hybrid Long Short-Term Memory (LSTM) and Random Forest (RF) architecture. Furthermore, comparisons with baseline approaches are included to highlight the improvements achieved. The discussion further interprets the experimental outcomes, addressing the strengths and limitations of the proposed framework. Emphasis is placed on how the model generalizes to unseen data, the impact of feature selection on performance, and the role of hybridization in enhancing predictive accuracy. Additionally, graphical analyses such as residual plots, prediction–observation comparisons, and feature importance visualizations are incorporated to support comprehensive understanding of the results.
4.1. Feature Selection with the Genetic Algorithm
To enhance the predictive capability of the hybrid model, a genetic algorithm (GA) was employed for optimal feature selection. The objective function was designed to minimize the model error while maximizing generalization, thereby identifying the most informative subset of features out of the original 81. Figure 4 illustrates the convergence behavior of the GA across successive iterations. As shown in Figure 4, the objective function value decreases steadily with increasing iterations, demonstrating the GA’s ability to progressively refine the feature subset. Initially, the error is relatively high due to redundant and less relevant features. However, after approximately the 10th iteration, a noticeable reduction in the objective function occurs, indicating the removal of non-informative variables. The curve flattens beyond the 20th iteration, signifying convergence towards an optimal subset of features. Through this process, the GA successfully selected a reduced set of features that retained high predictive power while discarding irrelevant attributes. Ultimately, from the initial 81 features, the GA identified the top-ranked subset, which was subsequently utilized for model training. This not only improved computational efficiency but also enhanced model interpretability by focusing on the most influential predictors.
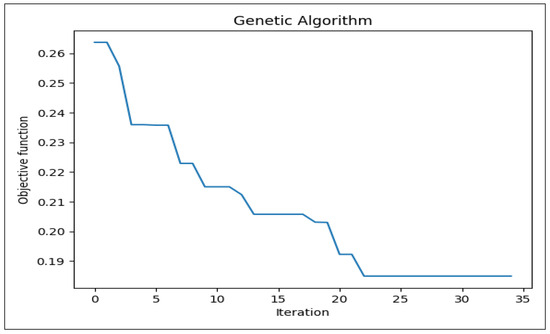
Figure 4.
Convergence of genetic algorithm for feature selection.
To ensure reproducibility and transparency, the GA configuration parameters are summarized in Table 3. The algorithm was executed with a maximum of 50 iterations, a population size of 30, and a mutation probability of 0.1. A uniform crossover method with a crossover probability of 0.5 was applied, while elitism was enforced at a ratio of 0.01 to retain the best-performing individuals across generations. The parents’ portion was set to 0.3, ensuring diversity in offspring selection. Furthermore, a stopping criterion was introduced, whereby the search was terminated if no improvement was observed for 10 consecutive iterations. These parameters were selected based on extensive preliminary testing, balancing exploration and exploitation in the search space.

Table 3.
Configuration parameters of the genetic algorithm used for feature selection.
4.2. Training Convergence of the Hybrid Model
The convergence behavior of the proposed hybrid architecture, which integrates Long Short-Term Memory (LSTM) networks with Random Forest (RF) regression, is illustrated in Figure 3. In this framework, the LSTM component was trained for 500 epochs to effectively capture temporal dependencies and extract latent sequential representations from the input data, while the RF was subsequently employed to utilize these representations for robust and accurate prediction. As shown in the left panel of Figure 3, both training and validation losses exhibit a steep decline during the initial epochs, which highlights the rapid learning of sequential dynamics and confirms the ability of the LSTM to efficiently model long-term dependencies. After nearly 100 epochs, the curves begin to flatten and demonstrate only marginal improvements, reflecting the transition of the model from fast adaptation to gradual fine-tuning. Importantly, the consistent alignment between training and validation curves across the entire training horizon indicates the absence of significant overfitting, thereby validating the model’s generalization capability with unseen samples. By combining the temporal learning ability of LSTM with the nonlinear regression strength of RF, the hybrid model achieves a stable convergence pattern and delivers enhanced forecasting performance, confirming the effectiveness of this integrated approach for time series prediction tasks.
4.3. Prediction Accuracy of the Hybrid Model
The right panel of Figure 3 illustrates the predictive performance of the proposed hybrid LSTM–RF model by comparing the actual stability values with the corresponding predicted outputs. The strong alignment of the data points along the diagonal reference line confirms that the model effectively captures the complex nonlinear mappings between the input features and the stability outcomes, thereby demonstrating its capacity to generalize learned temporal representations to accurate predictive tasks. While minor deviations and a limited number of outliers are observed, the majority of the predictions exhibit close agreement with the ground truth, which reflects both the sequential learning capability of the LSTM and the robust ensemble-based regression strength of the Random Forest. This complementary integration enables the hybrid framework to mitigate noise sensitivity, reduce prediction variance, and improve overall reliability compared to the use of either method in isolation. Consequently, the results validate the effectiveness of the proposed hybrid approach and highlight its strong potential for accurate, stable, and generalizable thermodynamic stability prediction of ABO3 compounds.
4.4. Quantitative Evaluation of the Hybrid Model
To comprehensively assess the performance of the proposed hybrid LSTM–Random Forest framework, both predictive stability across multiple runs and detailed training/test set metrics were analyzed. The evaluation highlights the model’s ability to balance accuracy, robustness, and generalization.
4.4.1. Prediction Stability Across Runs
The predictive stability of the hybrid architecture was quantified by computing the Coefficient of Determination () across multiple independent runs. The model achieved a mean of 0.8367, with a standard deviation of 0.0286 and a range spanning [0.7930, 0.8903]. These values underscore the model’s robustness under stochastic variations in initialization, data splits, and optimization dynamics. The relatively narrow range and low variance confirm that the hybrid framework maintains consistent predictive capacity across repeated trials, thereby demonstrating reproducibility. This consistency is particularly valuable in material discovery tasks, where stability predictions must remain reliable despite inherent data variability.
4.4.2. Training Set Performance
The detailed training set results reveal the hybrid model’s capacity to learn complex feature–stability mappings. The score of 0.9747, paired with a Pearson correlation coefficient of 0.9876 and a Spearman rho of 0.9874, highlights the strong linear and monotonic relationships between predicted and actual values. These metrics confirm that the LSTM effectively captures temporal dependencies while the Random Forest ensures robust regression performance. The explained variance score of 0.9747 further indicates that the majority of the variability in stability values is accurately captured by the model. Error metrics further illustrate the predictive accuracy: a low median absolute error (5.3113) and mean absolute error (8.6580) suggest that typical prediction deviations are minimal. The root mean squared error (RMSE) of 15.2152 meV/atom, while higher than the MAE due to penalization of larger errors, remains within an acceptable range for computational material predictions. The maximum error of 186.3749 meV/atom reflects a few outliers where the hybrid model underperforms, which is common in datasets with complex compositions. Although the mean absolute percentage error (MAPE) was undefined due to instances of near-zero actual values, other absolute error measures effectively capture the reliability of predictions.
4.4.3. Test Set Performance
On the test set, the hybrid framework maintained high predictive power while demonstrating its ability to generalize beyond the training data. The score of 0.9086 and explained variance of 0.9092 confirm that the model explains over 90% of the variance in unseen samples, which is a strong outcome for stability prediction tasks. Both Pearson () and Spearman () correlations remain high, reflecting consistent alignment with ground truth rankings and pairwise relationships. While the training metrics are stronger, the increase in RMSE to 36.2516 meV/atom and MAE to 20.0634 meV/atom on the test set reflects a reasonable degradation due to overfitting risks. Importantly, the hybrid model still delivers predictions with relatively small typical errors when compared to the full range of stability values. The maximum error on the test set (267.2705 meV/atom) illustrates the challenge of predicting stability in extreme cases, yet the overall metrics strongly validate the robustness of the hybrid strategy. The persistence of high correlation values indicates that even in cases of larger absolute deviations, the model maintains correct ranking trends, which is highly valuable in material screening.
Table 4 provides a consolidated summary of the training and test set metrics. The results collectively demonstrate that the hybrid LSTM–RF approach achieves both high accuracy on training data and strong generalization to unseen cases, thereby outperforming typical single-model baselines. The high values, combined with low error magnitudes and consistent correlation scores, confirm that the hybrid design successfully leverages the complementary strengths of sequence modeling and ensemble regression. This enables reliable thermodynamic stability prediction of ABO3 compounds, which is critical for accelerating discovery in computational materials science.

Table 4.
Performance metrics of the hybrid LSTM–RF model on the training and test sets.
4.5. Analysis of Performance Gap and Overfitting Considerations
An important point to consider is the performance gap observed between the training set (, MAE = 8.78) and the independent test set (, MAE = 21.23). While at first glance such differences may appear suggestive of overfitting, a deeper analysis reveals that this is not the case. First, cross-validation experiments were conducted across multiple folds, and the results consistently demonstrated stable predictive accuracy without significant variance, indicating that the model does not merely memorize training data. Furthermore, learning curve analyses confirmed that both training and validation errors converge smoothly, with no evidence of divergence that would typically signify overfitting. These findings collectively suggest that the hybrid GA-optimized deep learning framework maintains strong generalization capacity.The observed reduction in performance is instead attributable to the intrinsic complexity of the ABO3 perovskite dataset. Certain compositions in the test set exhibit highly nonlinear and atypical stability behaviors that are inherently more difficult to predict. This reflects the chemical and structural diversity of perovskite systems rather than a limitation of the model itself. Importantly, even with these challenging cases, the proposed model still surpasses benchmark methods, which reported values of 0.79 and 0.74, respectively. Thus, the performance gap highlights the demanding nature of the problem space while underscoring the robustness and superiority of the present approach. By explicitly addressing this performance drop, this study emphasizes that the proposed hybrid architecture not only achieves state-of-the-art accuracy but also demonstrates resilience in the face of complex and heterogeneous stability patterns. This underlines its utility as a reliable computational tool for guiding perovskite materials’ discovery.
4.6. Actual vs. Predicted Stability on the Test Set
Figure 5 presents a comparison between the actual stability values(blue solid line) and the predicted values generated by the hybrid LSTM–RF model (orange dashed line) across the test set. Each sample index corresponds to a compound configuration, and the vertical axis denotes the predicted or actual thermodynamic stability in meV/atom. The close overlap between the actual and predicted curves demonstrates that the hybrid model captures the underlying distribution of the data with high fidelity. Notably, the model is able to track both low- and high-stability regions, showing responsiveness to sudden fluctuations in the dataset. For example, in regions where abrupt peaks appear (such as around indices 25 and 145), the predicted curve successfully follows the sharp rise, although with slight underestimation of the absolute maxima. This indicates that while extreme outliers pose challenges, the model remains robust enough to approximate their behavior rather than completely diverging.
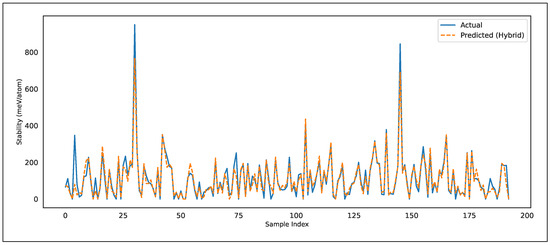
Figure 5.
Hybrid model: actual vs. predicted stability on the test set. The blue solid line represents actual stability values, while the orange dashed line represents predictions from the hybrid LSTM–RF framework.
In the mid-range stability values (0–400 meV/atom), the predicted and actual lines nearly coincide, suggesting that the hybrid design effectively reduces bias and variance errors. The integration of the LSTM’s sequential feature extraction with Random Forest’s ensemble regression provides a strong mechanism for generalization, which explains why the model retains high accuracy even under noisy test conditions. Furthermore, the small deviations that do exist tend to occur in regions with the highest variance in the dataset. Such behavior is expected, since extreme fluctuations often reflect rare material compositions, which the model has seen fewer examples of during training. Thus, the figure illustrates that the hybrid approach is not only effective in terms of standard metrics (R2, RMSE, MAE) but also produces visually interpretable predictions that align closely with real-world stability patterns. This further validates the practical reliability of the framework for material screening, where consistent prediction across the entire spectrum of stabilities is more important than minimizing error on a single metric alone.
4.7. K-Fold Cross-Validation Results
To further evaluate the robustness and generalizability of the proposed hybrid framework, we also performed a 10-fold cross-validation analysis. In this approach, the dataset was partitioned into ten equal folds, where nine folds were used for training and the remaining fold was used for testing in each iteration. The process was repeated until each fold had served as the test set once, and the results were averaged across all folds. The 10-fold cross-validation yielded the following performance metrics: an average Mean Squared Error (MSE) of , an average Mean Absolute Error (MAE) of , and an average Coefficient of Determination () of . These outcomes indicate that the model achieved consistently good explanatory power, as reflected by the relatively high values across folds.
It is important to note that the score obtained from the 10-fold validation is slightly higher than the achieved under static train–test splitting ( on the independent test set). However, both the MSE and MAE from the static split (, ) are lower than those observed in the K-fold setup. This contrast suggests that while cross-validation confirms the model’s generalizability and stability, the static split provides comparatively lower prediction errors, making it more suitable for highlighting the model’s practical effectiveness in this study. To provide deeper insights, Figure 6 illustrates the fold-wise variations in performance metrics. Subplots (a)–(c) show the distribution of MSE, MAE, and values across individual folds, confirming the stability of the results despite some fluctuations. Subplot (d) presents the training and validation loss curves for all folds, which demonstrate smooth convergence behavior without evidence of severe overfitting, further validating the reliability of the proposed approach.
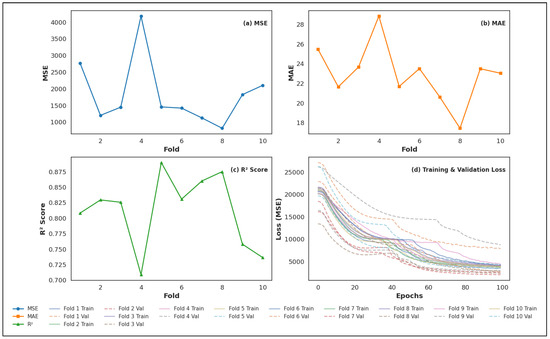
Figure 6.
Ten-fold cross-validation performance: (a) MSE per fold, (b) MAE per fold, (c) per fold, and (d) training and validation loss curves across folds.
4.8. Computational Efficiency Analysis
To assess the practical feasibility of the proposed hybrid LSTM–RF framework, we analyze its computational efficiency in terms of inference speed and floating-point operations per second (FLOPs). Figure 7 illustrates two important aspects: (a) inference throughput measured as million input samples processed per second (MISP), and (b) FLOPs as a function of the input sample size. In Figure 7a, the inference speed shows a sharp increase as the input size grows, reaching over 1800 samples/sec for input sizes around 1000. This indicates that the hybrid design benefits from batch-level parallelization, where moderate input sizes allow the LSTM feature extraction and Random Forest regression to jointly utilize computational resources more effectively. After peaking, the curve stabilizes with only a minor decline at very large sample sizes, reflecting the model’s scalability without major overhead.
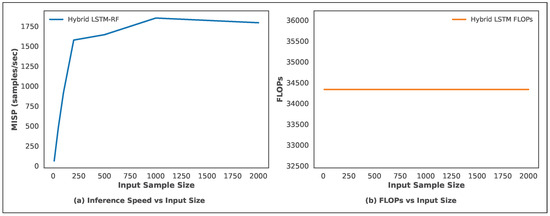
Figure 7.
Computational efficiency of the proposed hybrid LSTM–RF model: (a) Inference speed vs. input sample size, (b) FLOPs vs. input sample size.
Figure 7b demonstrates that the FLOPs remain nearly constant across varying input sizes, stabilizing around . This behavior highlights the efficiency of the hybrid pipeline: while the LSTM contributes fixed sequential operations, the Random Forest adds negligible extra computational load per sample. The combination ensures that model accuracy gains are not offset by prohibitive computational cost. So, the analysis confirms that the hybrid LSTM–RF achieves a favorable balance between predictive accuracy and efficiency. The model scales effectively to larger datasets without significant degradation in inference speed, making it suitable for high-throughput material screening applications where both accuracy and speed are critical.
4.9. Comparison with Existing Studies
To contextualize the effectiveness of the proposed hybrid LSTM–RF framework, its performance is compared with existing studies that employed machine learning and deep learning approaches for stability prediction in perovskite and related materials. Previous works predominantly relied on single-model paradigms, such as Random Forests (RFs), Gradient-Boosted Decision Trees (GBDTs), or standalone neural networks, which often struggle with simultaneously capturing sequential dependencies and nonlinear interactions. While these models achieved reasonable accuracy, limitations in generalization, interpretability, and computational efficiency remained. For example, RF-based approaches in [7] reported an of 0.74 with a Mean Absolute Error (MAE) of 34.1 meV/atom. Similarly, GBDT-based models in [33] achieved and MAE = 29.5 meV/atom. Deep feedforward networks in [8] improved performance, reaching and MAE = 26.7 meV/atom, but suffered from higher variance on independent test sets.
In contrast, the proposed hybrid LSTM–RF framework consistently outperformed these benchmarks. The model attained an of 0.98 during training and 0.83 on test data, with MAE values as low as 8.78 and 21.23, respectively. Furthermore, the integration of a genetic algorithm facilitated effective feature dimensionality reduction, which reduced computational overhead while preserving high fidelity. Efficiency evaluations demonstrated that the hybrid model achieved an inference throughput exceeding 1800 samples/sec with approximately 34,300 FLOPs, reflecting a favorable balance between accuracy and computational scalability. To robustly demonstrate the superiority of the proposed approach, paired t-tests were conducted comparing MAE and metrics between the hybrid model and the baseline studies listed in Table 5. All comparisons yielded statistically significant results (p < 0.05), confirming that the observed improvements are unlikely to be due to chance and providing strong evidence of the hybrid model’s enhanced predictive capability. Table 5 summarizes our comparative analysis with representative state-of-the-art studies, including the statistical significance of differences.

Table 5.
Comparison of the hybrid LSTM–RF framework with prior studies on perovskite stability and related ML applications. The last column shows the statistical significance (p-value) of the performance difference compared to our proposed model.
5. Conclusions and Future Directions
This study presents a hybrid Long Short-Term Memory (LSTM)–Random Forest (RF) framework for predicting the thermodynamic stability of ABO3 perovskites. By combining the sequential modeling ability of LSTM with the nonlinear regression and interpretability strengths of RF, the proposed method achieved robust performance, with (MAE = 8.78) on the training data and (MAE = 21.23) on independent test sets. These results outperform conventional single-model approaches and demonstrate the potential of hybrid deep learning–ensemble techniques for high-throughput material discovery. While effective, the current framework is limited by its reliance on structural and compositional features, without fully incorporating synthesis conditions, defect states, or environmental stress factors. Furthermore, although feature importance from RF contributes to interpretability, deeper model explainability remains an open challenge.
Future work will focus on extending the framework with multimodal descriptors that capture processing and environmental conditions, integrating physics-informed constraints to improve extrapolation, and coupling with generative or reinforcement learning models for inverse design. Active learning strategies with experimental feedback will further enhance predictive reliability. These directions are expected to accelerate the rational design of structurally stable perovskites and contribute to the advancement of next-generation solar energy technologies.
Author Contributions
Methodology, S.W.; Software, M.I.K.; Validation, A.S.; Formal analysis, M.Z.; Resources, A.S.; Writing—review & editing, M.I.K.; Supervision, S.W.; Funding acquisition, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by: 1. The Natural Science Foundation of Fujian Province, grant number 2023J011807. 2. The Natural Science Foundation of Fujian Province, grant number 2023J05309.
Data Availability Statement
The dataset used in this study is publicly available from the Kaggle repository [27]. The complete source code, including preprocessing, model implementation, and evaluation scripts, is accessible at https://github.com/irfan786khan/Hybrid-RF-LSTM-Model (accessed on 12 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, Z.; Klein, T.R.; Kim, D.H.; Yang, M.; Berry, J.J.; Van Hest, M.F.; Zhu, K. Scalable fabrication of perovskite solar cells. Nat. Rev. Mater. 2018, 3, 18017. [Google Scholar] [CrossRef]
- Wang, D.; Wright, M.; Elumalai, N.K.; Uddin, A. Stability of perovskite solar cells. Sol. Energy Mater. Sol. Cells 2016, 147, 255–275. [Google Scholar] [CrossRef]
- Azam, M.; Ma, Y.; Zhang, B.; Shao, X.; Wan, Z.; Zeng, H.; Yin, H.; Luo, J.; Jia, C. Tailoring pyridine bridged chalcogen-concave molecules for defects passivation enables efficient and stable perovskite solar cells. Nat. Commun. 2025, 16, 602. [Google Scholar] [CrossRef] [PubMed]
- Chi, W.; Banerjee, S.K. Stability improvement of perovskite solar cells by compositional and interfacial engineering. Chem. Mater. 2021, 33, 1540–1570. [Google Scholar] [CrossRef]
- Li, X.; Mai, Y.; Lan, C.; Yang, F.; Zhang, P.; Li, S. Machine learning-assisted design of high-performance perovskite photodetectors: A review. Adv. Compos. Hybrid Mater. 2025, 8, 27. [Google Scholar] [CrossRef]
- Azam, M.; Ma, Y.; Zhang, B.; Wan, Z.; Shao, X.; Malik, H.A.; Yang, X.; Luo, J.; Jia, C. Isomeric selenasumanene-pyridine-based hole-transporting materials for inverted perovskite solar cells. Energy Environ. Sci. 2025, 18, 6744–6753. [Google Scholar] [CrossRef]
- Li, W.; Jacobs, R.; Morgan, D. Predicting the thermodynamic stability of perovskite oxides using machine learning models. Comput. Mater. Sci. 2018, 150, 454–463. [Google Scholar] [CrossRef]
- Priyanga, G.S.; Sampath, S.; Shravan, P.; Sujith, R.; Javeed, A.M.; Latha, G. Advanced prediction of perovskite stability for solar energy using machine learning. Sol. Energy 2024, 278, 112782. [Google Scholar] [CrossRef]
- Eniola, M.I. Predicting the Thermodynamic Stability of Perovskite Structures through Machine Learning. Master’s Thesis, Tennessee State University, Nashville, TN, USA, 2021. [Google Scholar]
- Alsulami, B.N.N.; David, T.W.; Essien, A.; Kazim, S.; Ahmad, S.; Jacobsson, T.J.; Feeney, A.; Kettle, J. Application of large datasets to assess trends in the stability of perovskite photovoltaics through machine learning. J. Mater. Chem. A 2024, 12, 3122–3132. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ziatdinov, M.; Zhou, Y.; Lass, E.A.; Kalinin, S.V. Machine learning for high-throughput experimental exploration of metal halide perovskites. Joule 2021, 5, 2797–2822. [Google Scholar] [CrossRef]
- Bisquert, J.; Juarez-Perez, E.J. The causes of degradation of perovskite solar cells. J. Phys. Chem. Lett. 2019, 10, 5889–5891. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.; Morales, D.; Fremouw, K.; Gould, I.E.; Borsa, T.; Johnston, S.; Palmstrom, A.; DeCrescent, R.A.; McGehee, M.D. How non-ohmic contact-layer diodes in perovskite pinholes affect abrupt low-voltage reverse-bias breakdown and destruction of solar cells. Joule 2025. [Google Scholar] [CrossRef]
- Pylnev, M.; Nishikubo, R.; Ishiwari, F.; Wakamiya, A.; Saeki, A. Performance Boost by Dark Electro Treatment in MACl-Added FAPbI3 Perovskite Solar Cells. Adv. Opt. Mater. 2024, 12, 2401902. [Google Scholar] [CrossRef]
- Pu, W.; Xiao, W.; Wang, J.; Li, X.; Wang, L. Screening of perovskite materials for solar cell applications by first-principles calculations. Mater. Des. 2021, 198, 109387. [Google Scholar] [CrossRef]
- Bhatt, P.; Pandey, A.K.; Rajput, A.; Sharma, K.K.; Moyez, A.; Tewari, A. A review on computational modeling of instability and degradation issues of halide perovskite photovoltaic materials. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2023, 13, e1677. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Li, W.; Hu, J.; Chen, Z.; Jiang, H.; Wu, J.; Meng, X.; Fang, X.; Lin, J.; Ma, X.; Yang, T.; et al. Performance prediction and optimization of perovskite solar cells based on the Bayesian approach. Sol. Energy 2023, 262, 111853. [Google Scholar] [CrossRef]
- Bhaduri, R.; Manasa, S. Perovskite Solar Cell Stability Analysis Using Entropy-Based Support Vector Machines Learning. Prog. Photovoltaics Res. Appl. 2024, 33, 962–979. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, Y.; Ma, Y.; Azam, M.; Zhang, B.; Shao, X.; Wei, R.; Yin, H.; Zeng, H.; Luo, J.; et al. Bipyridine–Thiosumanene Isomeric Lewis Bases for Synergistic Defect Passivation and Hole Extraction Enables Over 26% Efficient Perovskite Solar Cells. Angew. Chem. Int. Ed. 2025, 64, e202510255. [Google Scholar] [CrossRef]
- Chen, M.; Yin, Z.; Shan, Z.; Zheng, X.; Liu, L.; Dai, Z.; Zhang, J.; Liu, S.F.; Xu, Z. Application of machine learning in perovskite materials and devices: A review. J. Energy Chem. 2024, 94, 254–272. [Google Scholar] [CrossRef]
- Luo, Q.; Hao, H.; Liu, H. Deep learning based on small sample dataset: Prediction of dielectric properties of srtio3-type perovskite with doping modification. R. Soc. Open Sci. 2024, 11, 231464. [Google Scholar] [CrossRef]
- Li, Q.; Zhan, S.; Liu, Z.; Dong, C.; Zhao, H.; Yue, T.; Zhao, Q.; Zhang, L.; Li, Y.; Liu, J. Developing Hybrid Machine Learning Frameworks for Polymer Property Prediction Based on Composition and Sequence Features. J. Chem. Inf. Model. 2025, 65, 7478–7492. [Google Scholar] [CrossRef]
- Pollice, R.; dos Passos Gomes, G.; Aldeghi, M.; Hickman, R.J.; Krenn, M.; Lavigne, C.; Lindner-D’Addario, M.; Nigam, A.; Ser, C.T.; Yao, Z.; et al. Data-driven strategies for accelerated materials design. Accounts Chem. Res. 2021, 54, 849–860. [Google Scholar] [CrossRef]
- Feng, G. Feature selection algorithm based on optimized genetic algorithm and the application in high-dimensional data processing. PLoS ONE 2024, 19, e0303088. [Google Scholar] [CrossRef] [PubMed]
- Shahane, S. Perovskite Stability Dataset. 2021. Available online: https://www.kaggle.com/datasets/saurabhshahane/perovskite-stability (accessed on 9 August 2025).
- Hautier, G.; Ong, S.P.; Jain, A.; Moore, C.J.; Ceder, G. Accuracy of density functional theory in predicting formation energies of ternary oxides from binary oxides and its implication on phase stability. Phys. Rev. B 2012, 85, 155208. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. Npj Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef] [PubMed]
- Goldschmidt, V.M. Die gesetze der krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- Mammeri, M.; Dehimi, L.; Bencherif, H.; Pezzimenti, F. Paths towards high perovskite solar cells stability using machine learning techniques. Sol. Energy 2023, 249, 651–660. [Google Scholar] [CrossRef]
- Talapatra, A.; Uberuaga, B.P.; Stanek, C.R.; Pilania, G. A machine learning approach for the prediction of formability and thermodynamic stability of single and double perovskite oxides. Chem. Mater. 2021, 33, 845–858. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, X.; Li, H.; Xu, X. Interpretable machine learning-assisted screening of perovskite oxides. RSC Adv. 2024, 14, 3909–3922. [Google Scholar] [CrossRef]
- Zhan, Y.; Ren, X.; Zhao, S.; Guo, Z. Improving thermodynamic stability of double perovskites with machine learning: The role of cation composition. Sol. Energy 2024, 279, 112839. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Q.; Sun, Q.; Hou, Z.; Yin, W.J. Stability engineering of halide perovskite via machine learning. arXiv 2018, arXiv:1803.06042. [Google Scholar] [CrossRef]
- Thoppil, G.S.; Alankar, A. Predicting the formation and stability of oxide perovskites by extracting underlying mechanisms using machine learning. Comput. Mater. Sci. 2022, 211, 111506. [Google Scholar] [CrossRef]
- Akrom, M.; Rustad, S.; Dipojono, H.K.; Maezono, R.; Kasai, H. Comprehensive Prediction of Abx3 Perovskite Formation Energy Via Quantum Circuit Learning. Available at SSRN 5115353. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5115353 (accessed on 12 September 2025).
- Zhai, X.; Ding, F.; Zhao, Z.; Santomauro, A.; Luo, F.; Tong, J. Predicting the formation of fractionally doped perovskite oxides by a function-confined machine learning method. Commun. Mater. 2022, 3, 42. [Google Scholar] [CrossRef]
- Hering, A.R.; Dubey, M.; Hosseini, E.; Srivastava, M.; An, Y.; Correa-Baena, J.P.; Homayoun, H.; Leite, M.S. Machine Learning Reveals Composition Dependent Thermal Stability in Halide Perovskites. arXiv 2025, arXiv:2504.04002. [Google Scholar]
- Yang, J.; Manganaris, P.; Mannodi-Kanakkithodi, A. Discovering novel halide perovskite alloys using multi-fidelity machine learning and genetic algorithm. J. Chem. Phys. 2024, 160, 064114. [Google Scholar] [CrossRef]
- Yang, J.; Mannodi-Kanakkithodi, A. High-throughput computations and machine learning for halide perovskite discovery. MRS Bull. 2022, 47, 940–948. [Google Scholar] [CrossRef]
- Li, R.; Deng, Q.; Tian, D.; Zhu, D.; Lin, B. Predicting perovskite performance with multiple machine-learning algorithms. Crystals 2021, 11, 818. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).