Heat Transfer Characteristics of Multi-Inlet Rotating Disk Cavity
Abstract
1. Introduction
2. Model and Numerical Methods
2.1. Model of the Multi-Inlet Cavity
2.2. Mesh and Boundary Conditions of the Model
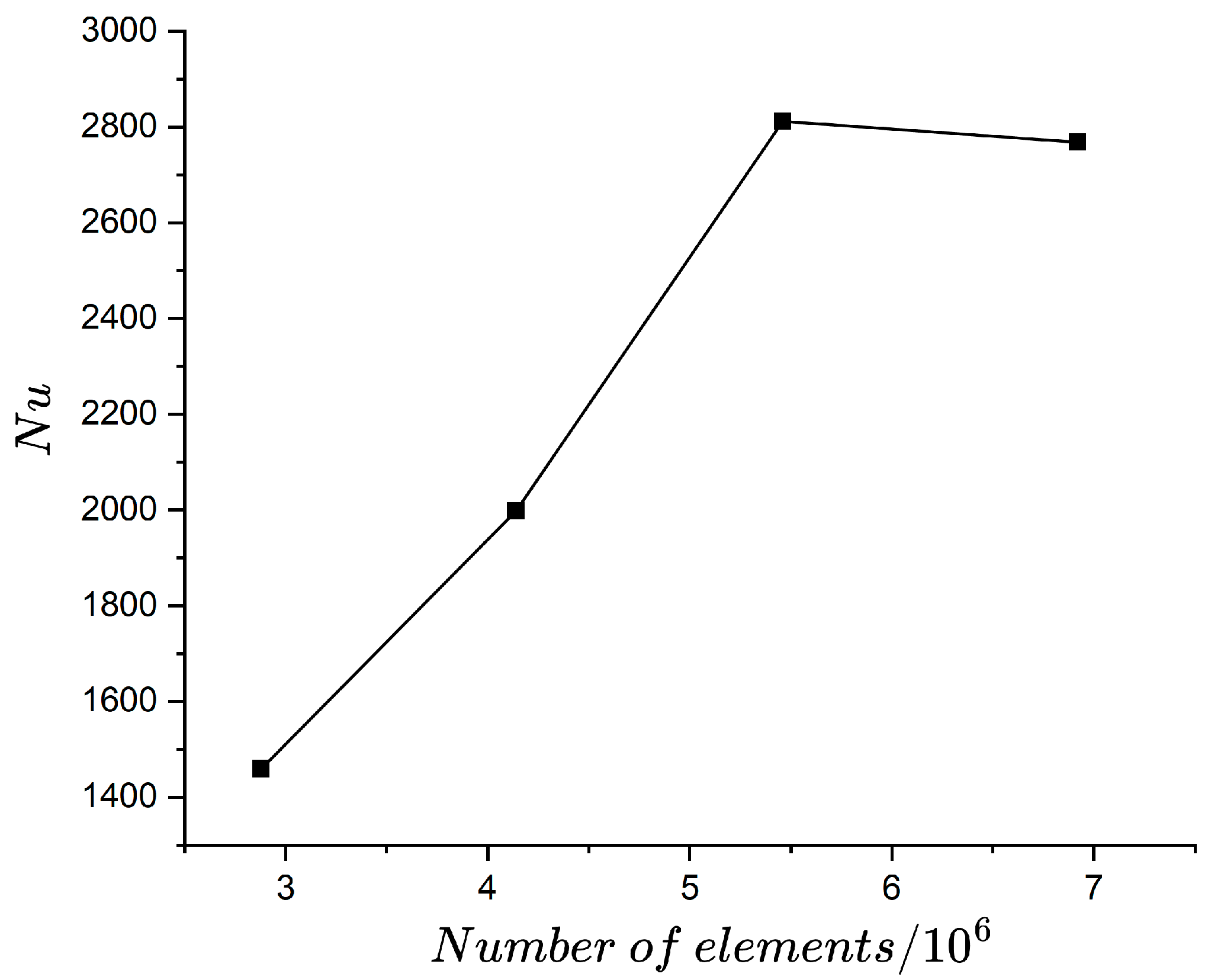
2.3. Numerical Methods and Validation
2.4. Governing Equations
2.5. Parameter Definition
3. Results and Analysis
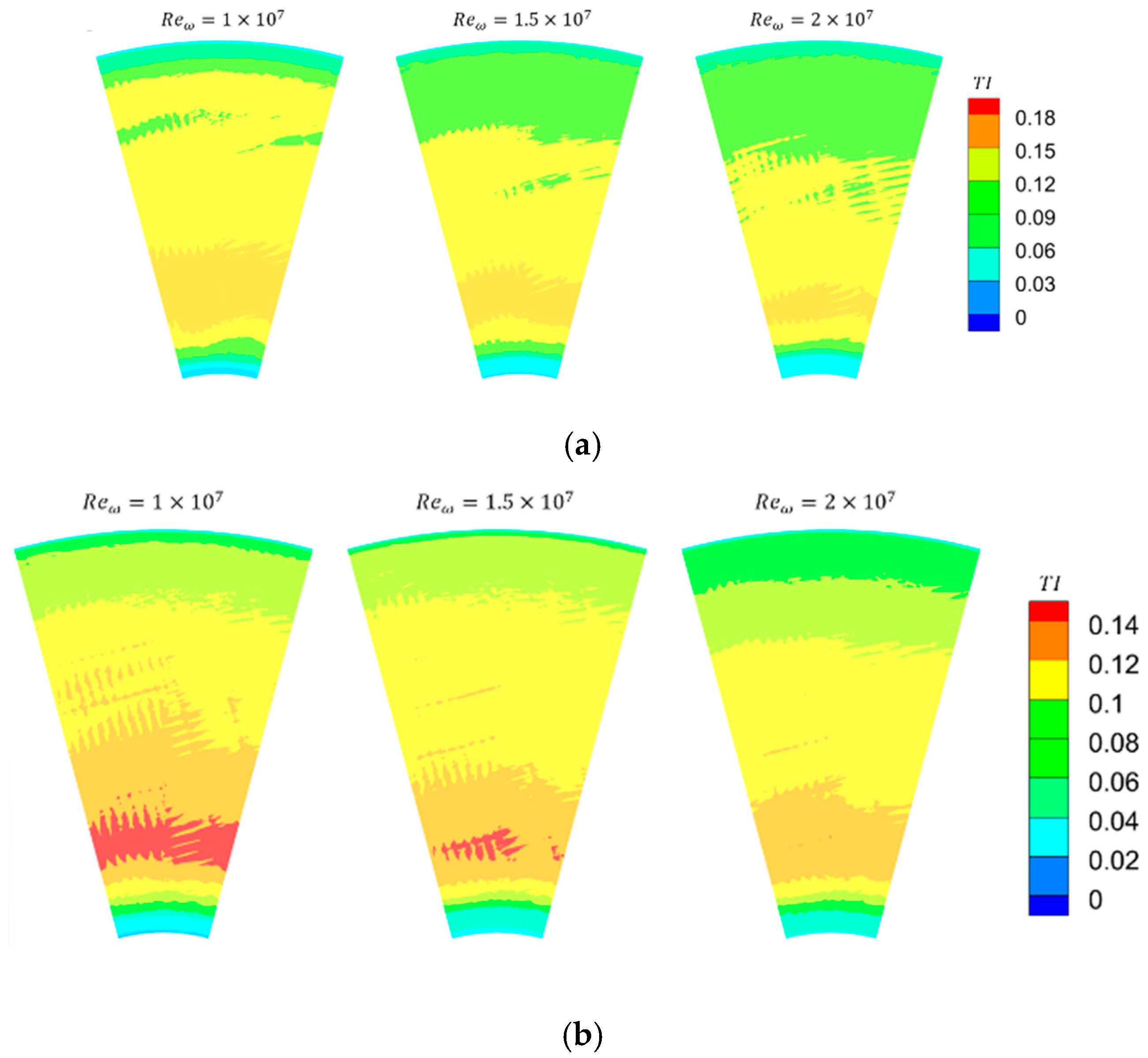
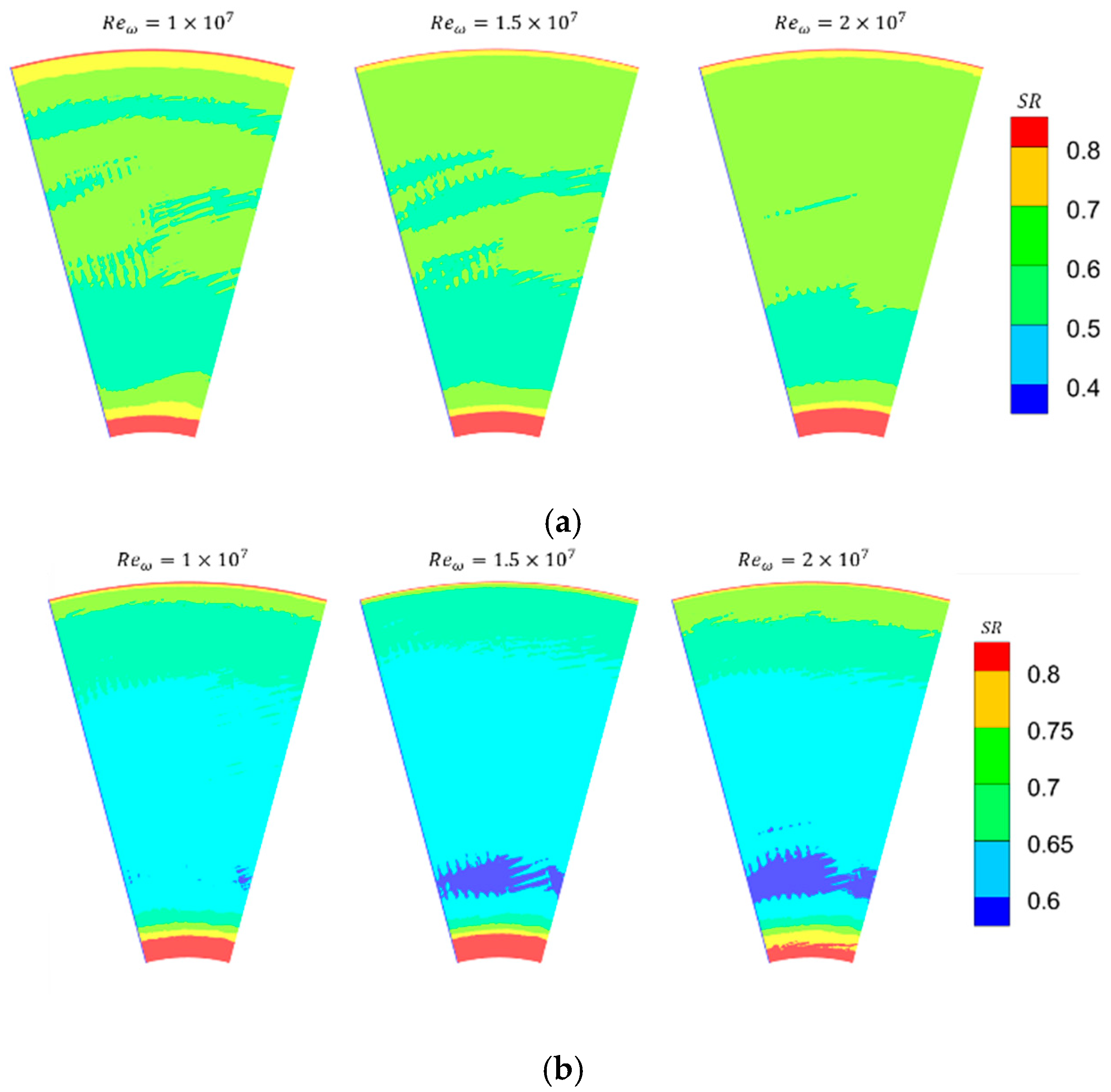
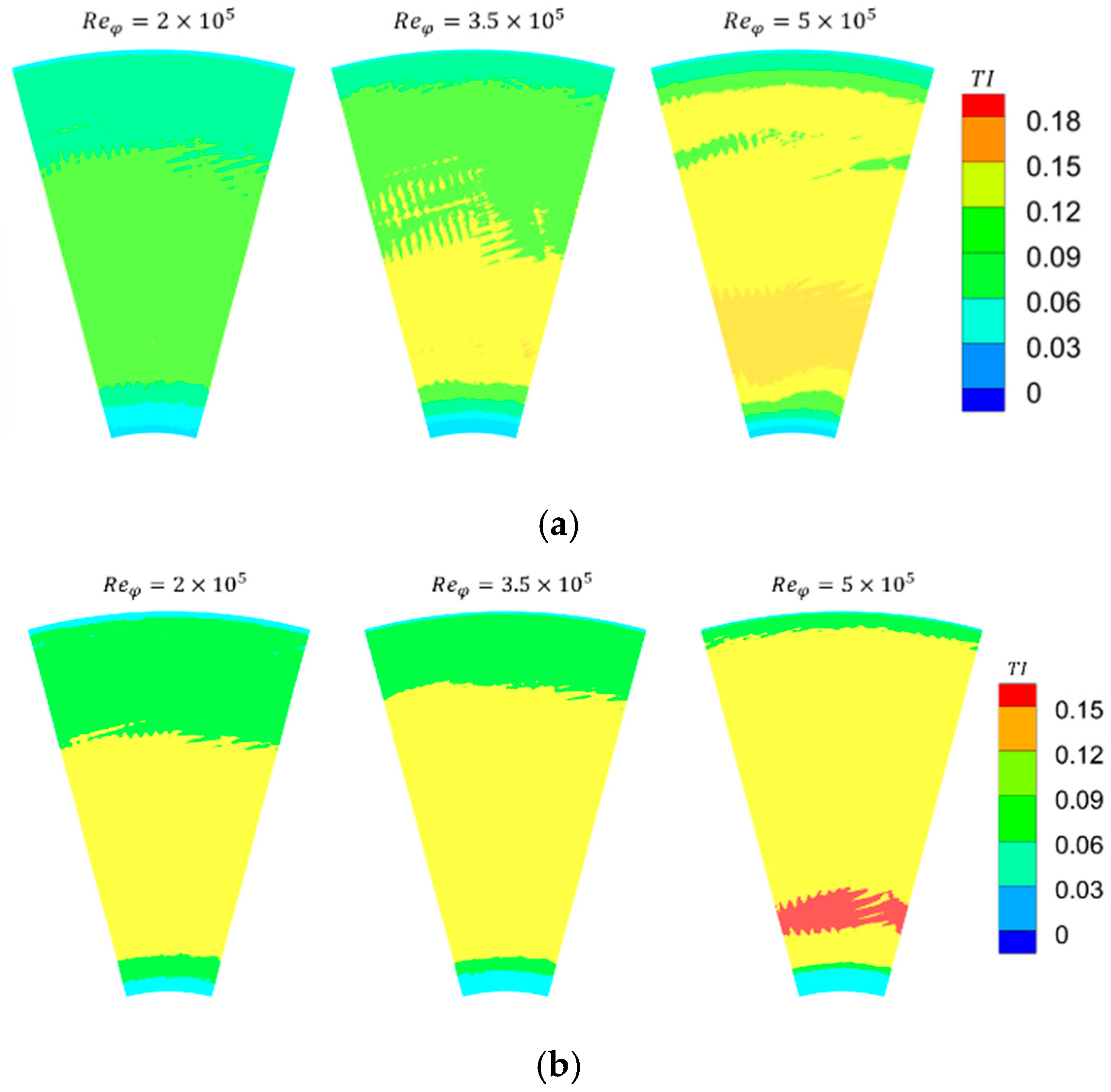
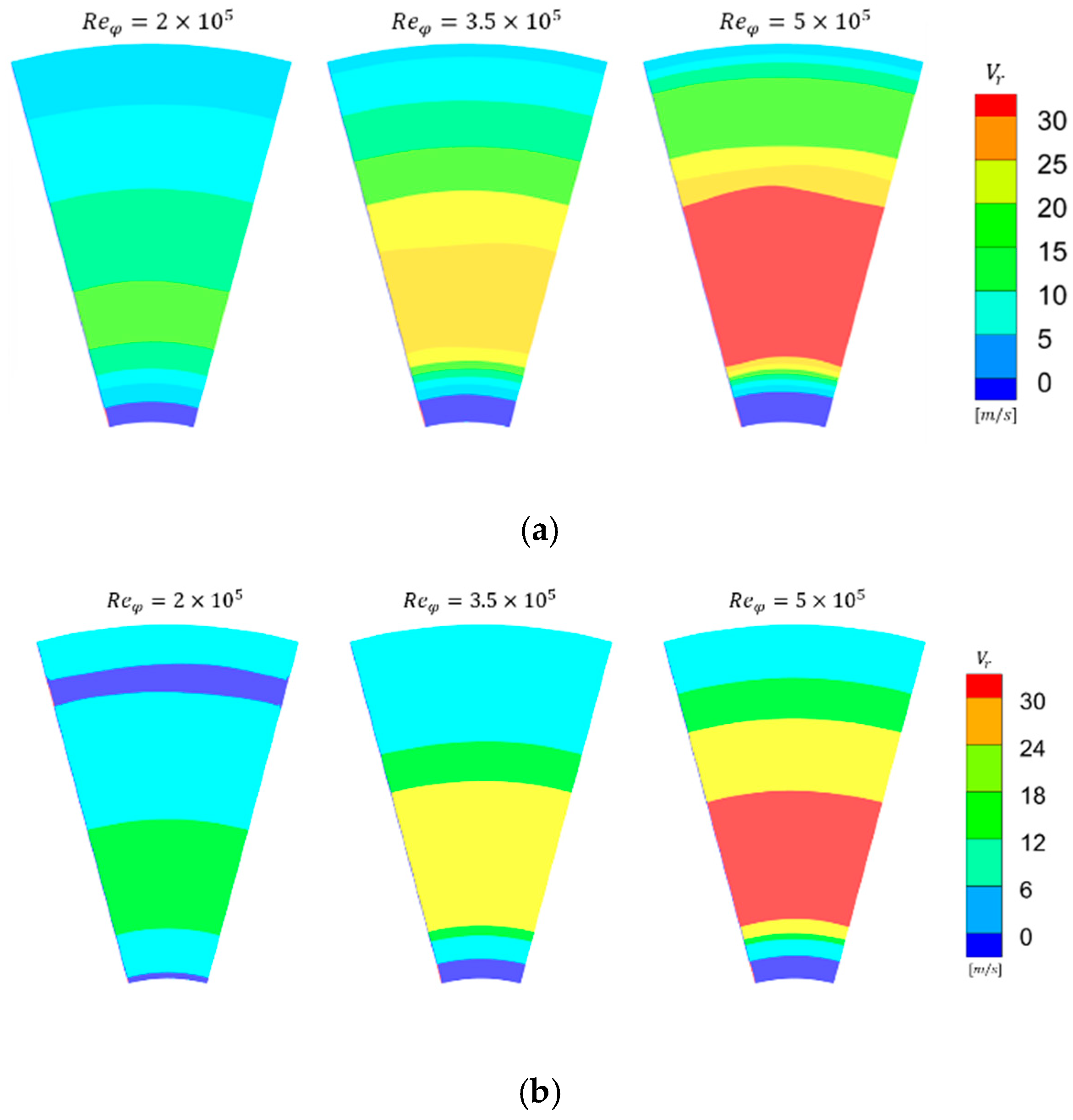
3.1. Flow Structure in the Cavity
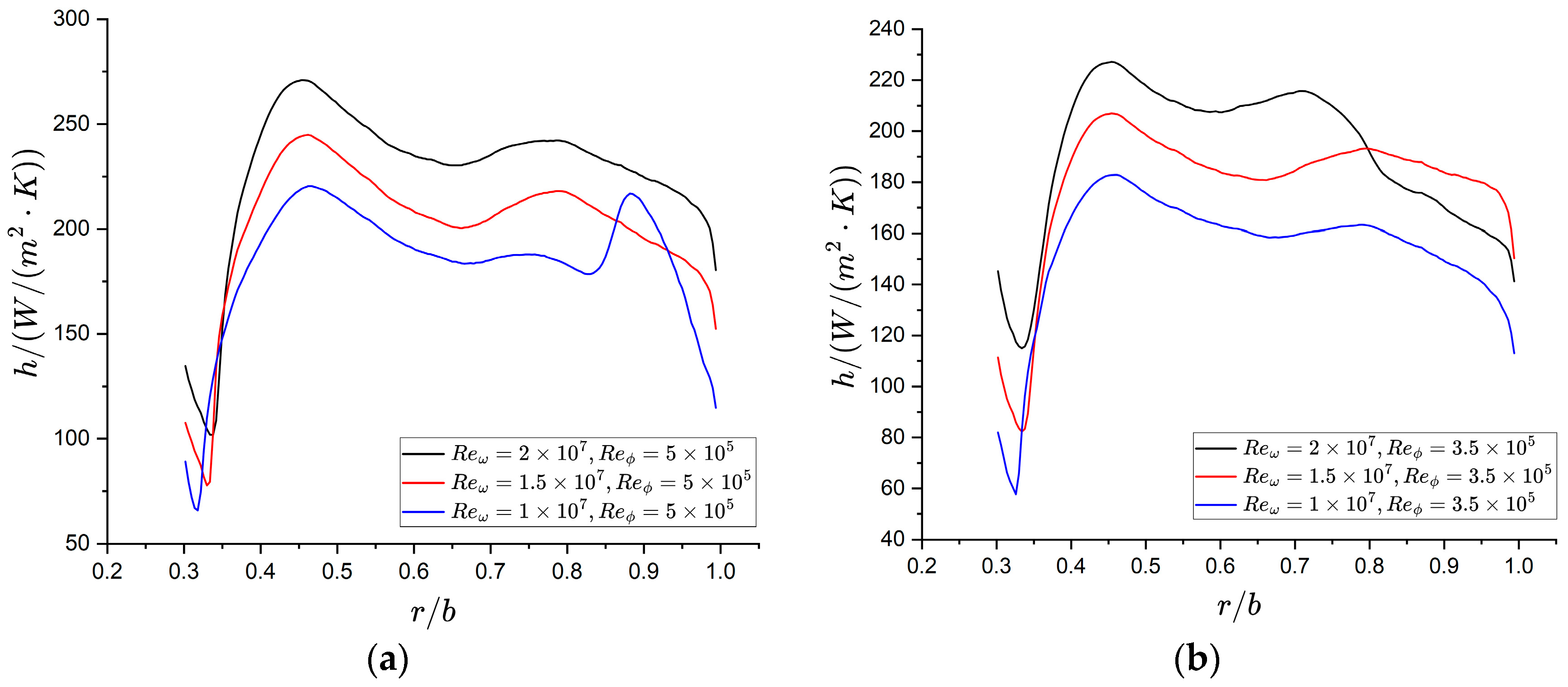
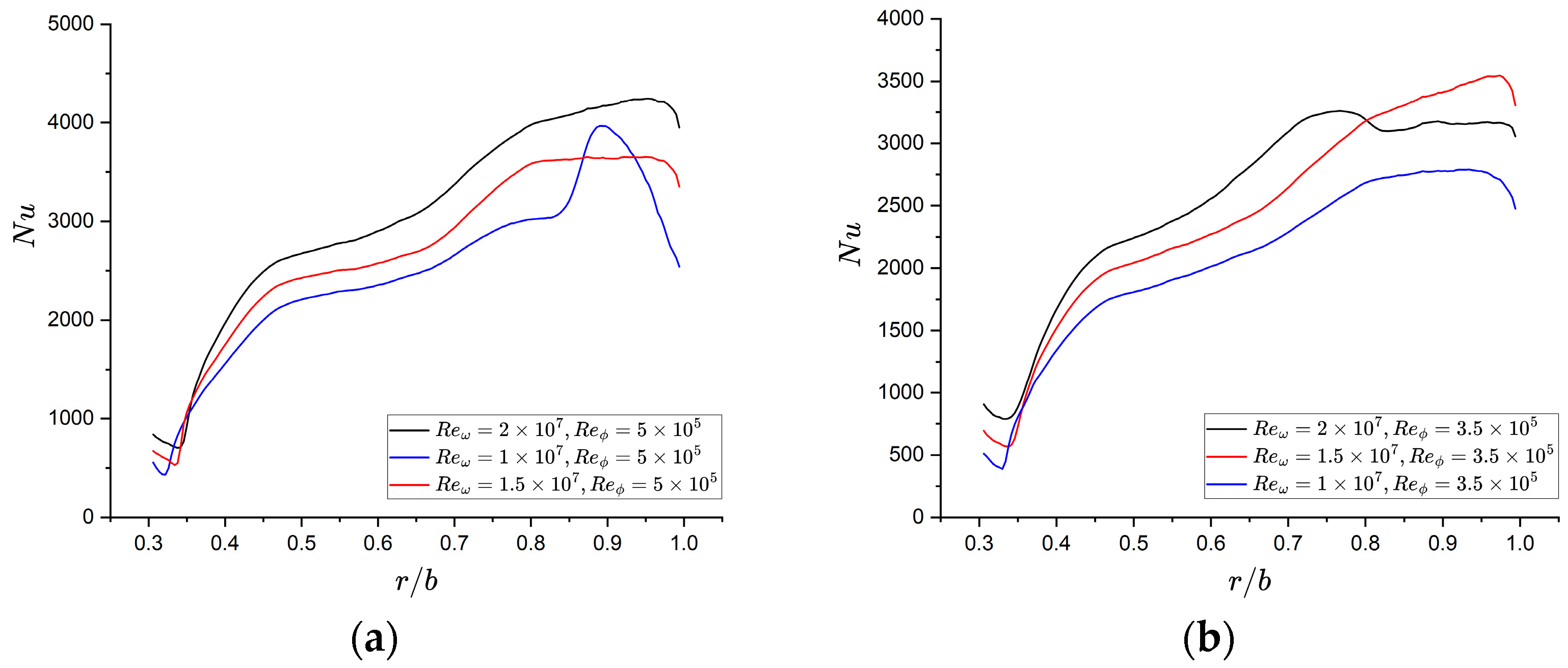
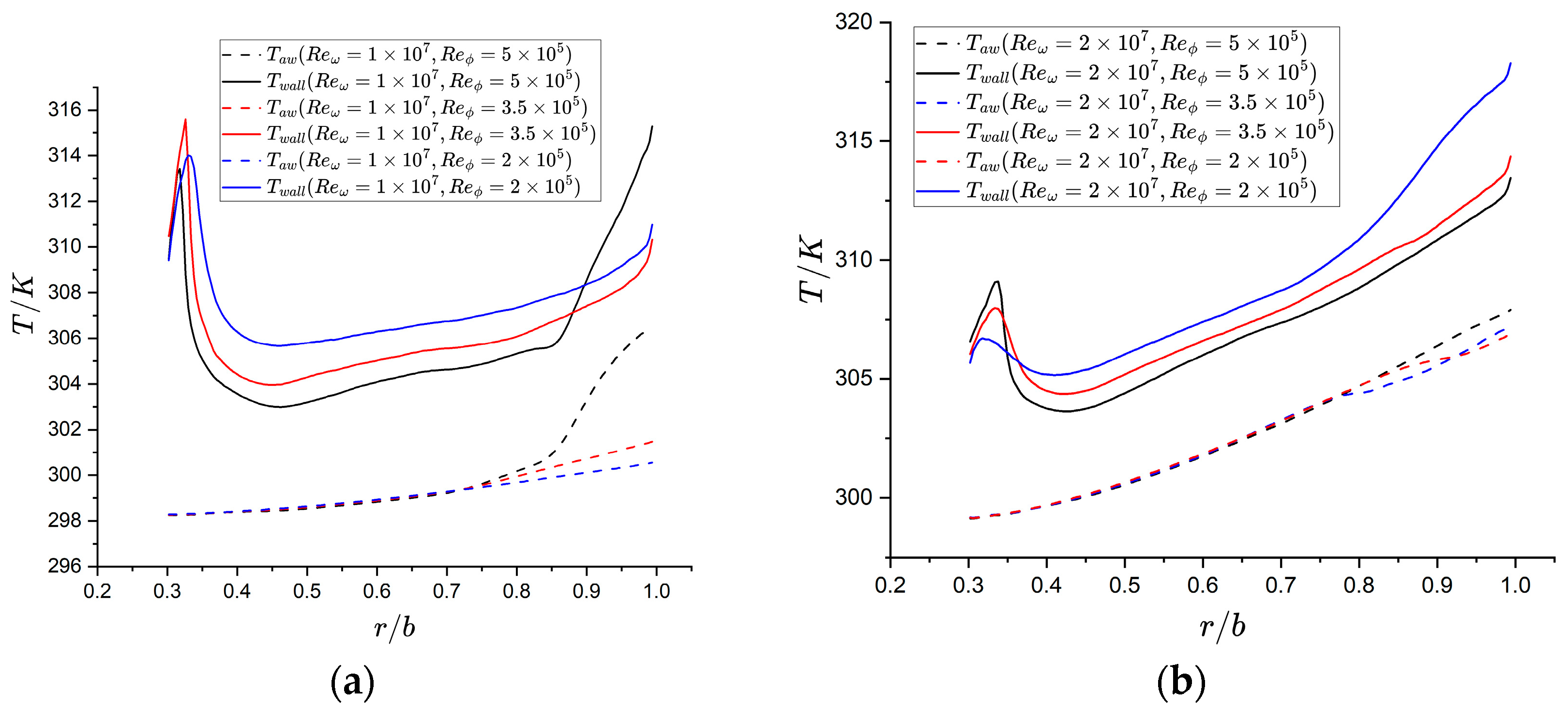
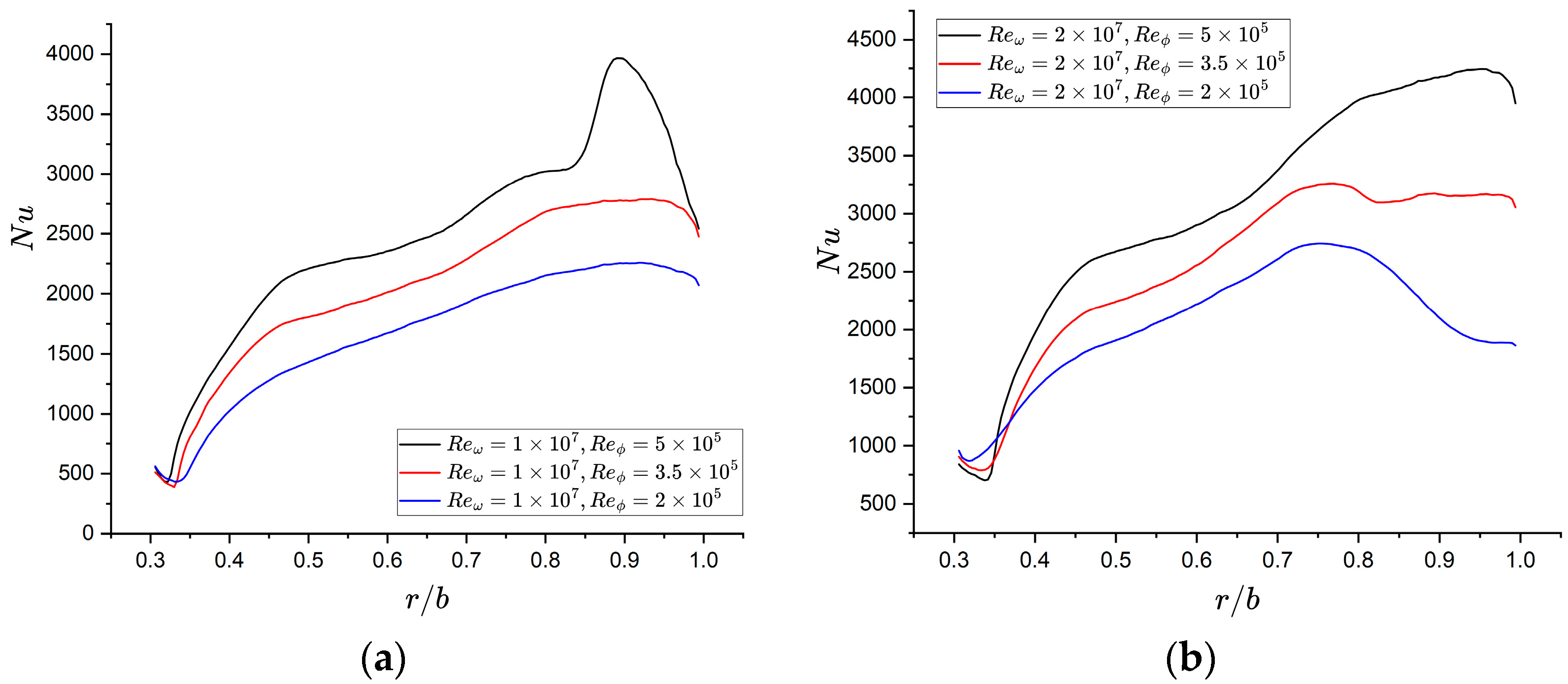
3.2. Influence of Rotation Speed on Heat Transfer
3.3. Influence of Mass Flow Rate on Heat Transfer
4. Conclusions
- A large-scale vortex is induced by the central inlet jet in the low-radius region of the cavity. The flow structure in the high-radius region is significantly influenced by both rotational speed and flow rate. When inertial effects dominate, the high-radius inlet jet induces a vortex on the upstream disk side. When rotational effects dominate, a vortex appears near the downstream disk.
- Increasing the rotational speed generally enhances the wall heat transfer capability. This enhancement occurs because higher rotational speeds amplify the differential rotational linear velocity between the disk surface and nearby wall flow, consequently thinning the boundary layer.
- Increasing the mass flow rate enhances heat transfer through two primary mechanisms: first, it elevates the turbulence intensity of the near-wall fluid; second, the higher radial velocity results in a thinner boundary layer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| LDA | Laser Doppler Anemometry |
| SIMPLE | Semi-Implicit Method for Pressure Linked Equations |
| RNG | Re-Normalization Group |
References
- Lentini, M.; Keller, H. Von Karman Swirling Flows. Siam J. Appl. Math. 1980, 38, 52–64. [Google Scholar] [CrossRef]
- Farthing, P.R.; Long, C.A.; Owen, J.M.; Pincombe, J.R. Rotating Cavity with Axial Throughflow of Cooling Air: Flow Structure. J. Turbomach. 1992, 114, 237–246. [Google Scholar] [CrossRef]
- Bohn, D.; Ren, J.; Tuemmers, C. Investigation of the unstable flow structure in a rotating cavity. In Proceedings of the 51st ASME Turbo Expo 2006, New York, NY, USA, 8–11 May 2006. [Google Scholar]
- Tian, S.; Tao, Z.; Ding, S.; Xu, G. Investigation of flow instability in rotating cavity with axial throughflow of cooling air. J. Beijing Univ. Aeronaut. Astronaut. 2005, 31, 393–396. [Google Scholar] [CrossRef]
- Alexiou, A.; Hills, N.J.; Long, C.A.; Turner, A.B. Heat transfer in high-pressure compressor gas turbine internal air systems: A rotating disc-cone cavity with axial throughflow. Exp. Heat Transf. 2000, 13, 299–328. [Google Scholar] [CrossRef]
- Tian, S.; Tao, Z.; Ding, S.; Xu, G. Computation of buoyancy-induced flow in a heated rotating cavity with an axial throughflow of cooling air. Int. J. Heat Mass Transf. 2008, 51, 960–968. [Google Scholar] [CrossRef]
- Quan, J.; Luo, X.; Peng, Y.; Hu, Y. Numerical Study of Heat Transfer Characteristics Inside Counter-Rotating Disk Cavity. J. Propuls. Technol. 2018, 39, 2813–2819. [Google Scholar] [CrossRef]
- Jackson, R.; Tang, H.; Scobie, J.A.; Owen, J.M.; Lock, G.D. Measurement of Heat Transfer and Flow Structures in a Closed Rotating Cavity. J. Eng. Gas Turbines Power 2022, 144, 051005. [Google Scholar] [CrossRef]
- Bai, L.; Feng, Q.; Liu, S. Numerical investigation of turbulence parameter on flow field of rotating disc cavity with complex geometry. J. Propuls. Technol. 2003, 24, 344–347. [Google Scholar] [CrossRef]
- Guo, J.; Li, Q. Numerical Study of Flow Structure and Heat Transferin Rotating Cavity with Axial Throughflow. J. Propuls. Technol. 2018, 39, 1790–1796. [Google Scholar] [CrossRef]
- Wu, Z.; Luo, X.; Zhu, J.; Zhang, Z.; Liu, J. A Method of Solving Three Temperature Problem of Turbine with Adiabatic Wall Temperature. In Proceedings of the ASME Turbomachinery Technical Conference and Exposition (Turbo Expo)—Sustainable Energy—Accelerating the Transition by Advancing Turbine Technology, New York, NY, USA, 7–11 June 2021. [Google Scholar]
- Li, Z.; Hu, P.; Sui, X.; Zhao, W.; Lin, Q. Flow structures and heat transfer characteristics in a vaneless counter-rotating turbine cavity with different cooling inflows. Proc. Inst. Mech. Eng. Part A J. Power Energy 2023, 237, 656–668. [Google Scholar] [CrossRef]
- Bohn, D.E.; Deutsch, G.N.; Simon, B.; Burkhardt, C. Flow Visualisation in a Rotating Cavity with Axial Throughflow. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8 May 2000. [Google Scholar] [CrossRef]
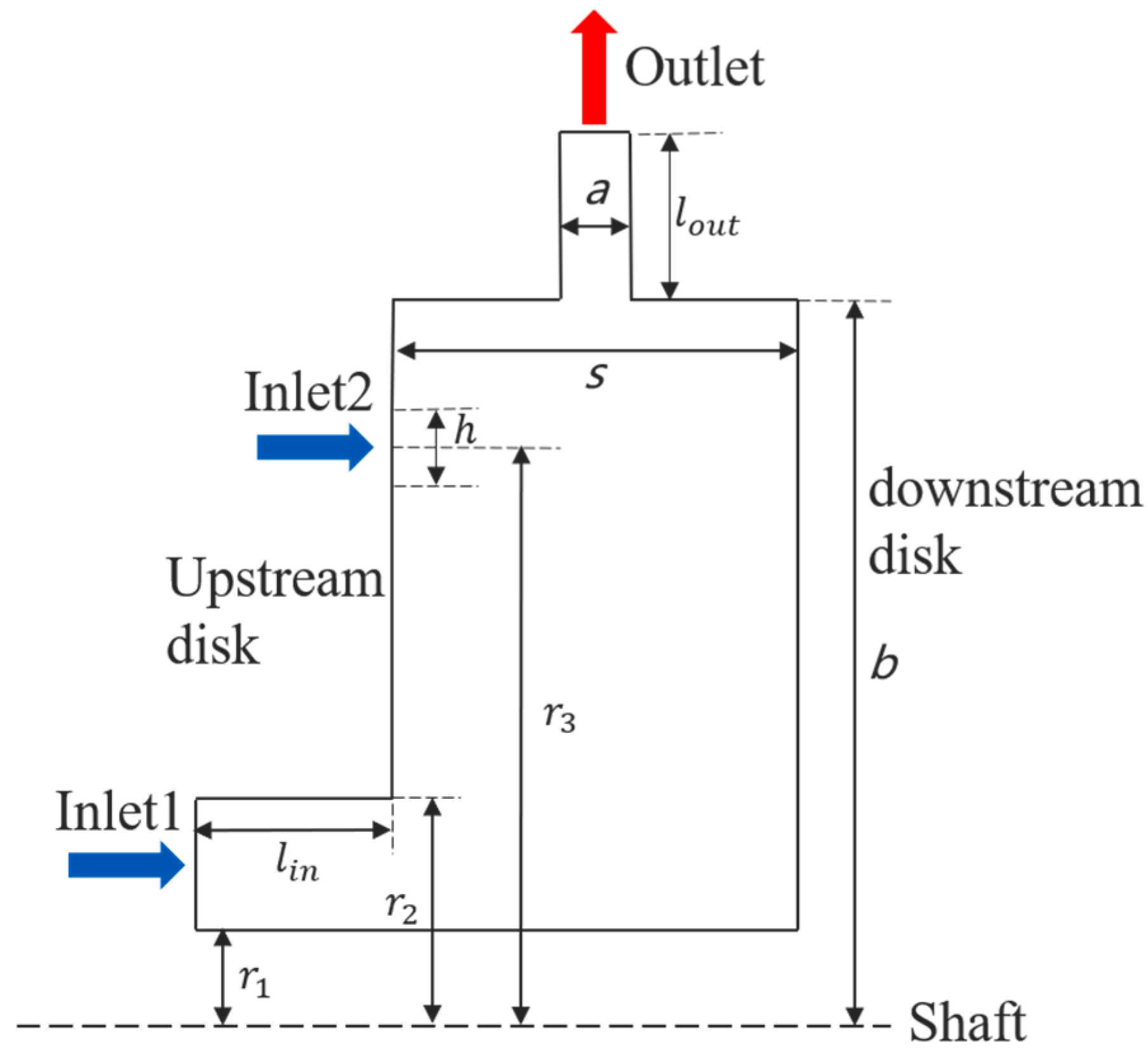


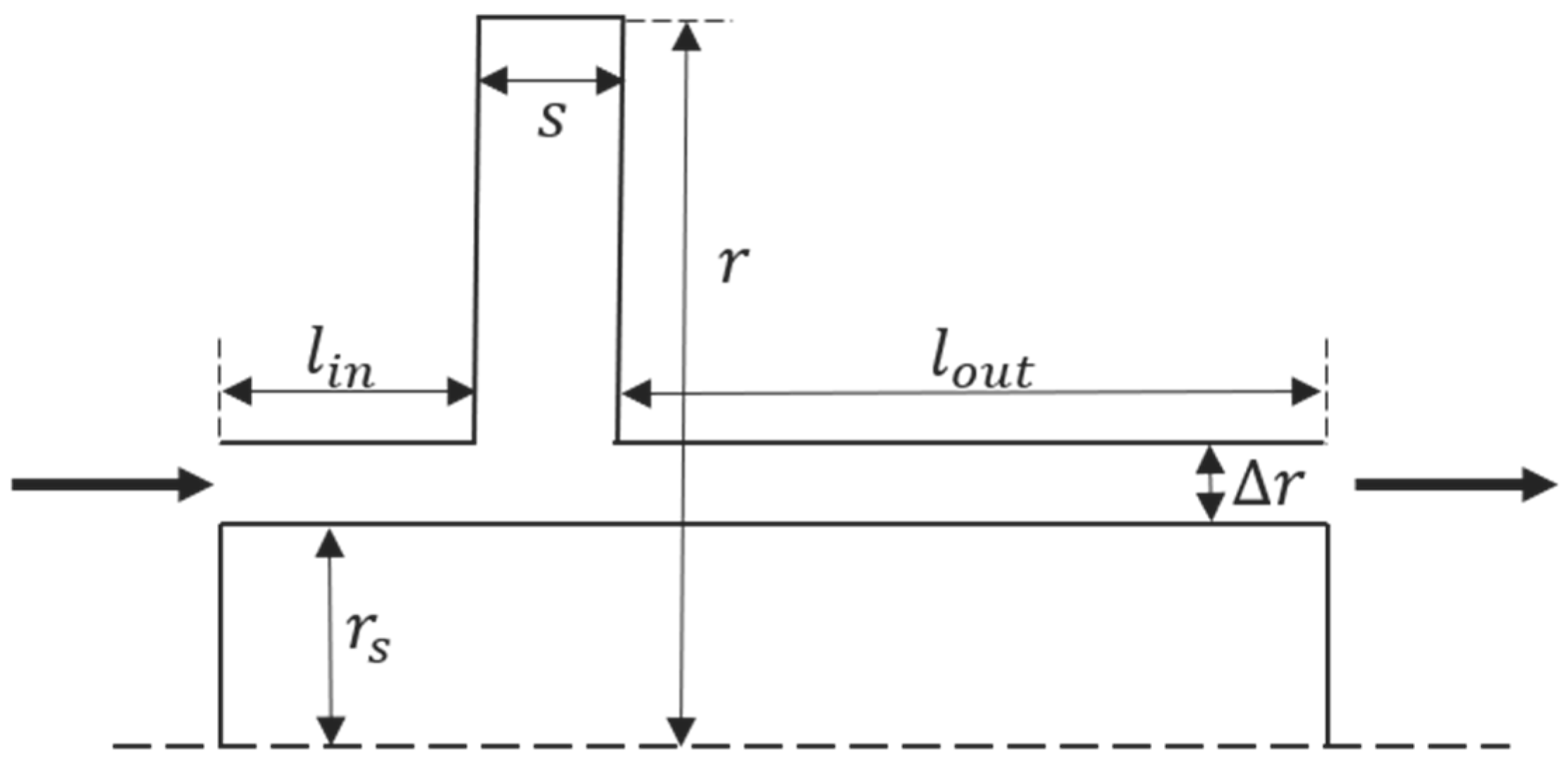




| Edge/mm | Length |
|---|---|
| b | 500 |
| 150 | |
| 172.5 | |
| 400 | |
| 187.5 | |
| s | 100 |
| a | 10 |
| 3 | |
| 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, H.; Li, X.; Ren, J. Heat Transfer Characteristics of Multi-Inlet Rotating Disk Cavity. Energies 2025, 18, 5049. https://doi.org/10.3390/en18195049
Xiao H, Li X, Ren J. Heat Transfer Characteristics of Multi-Inlet Rotating Disk Cavity. Energies. 2025; 18(19):5049. https://doi.org/10.3390/en18195049
Chicago/Turabian StyleXiao, Han, Xueying Li, and Jing Ren. 2025. "Heat Transfer Characteristics of Multi-Inlet Rotating Disk Cavity" Energies 18, no. 19: 5049. https://doi.org/10.3390/en18195049
APA StyleXiao, H., Li, X., & Ren, J. (2025). Heat Transfer Characteristics of Multi-Inlet Rotating Disk Cavity. Energies, 18(19), 5049. https://doi.org/10.3390/en18195049






