Off-Design Performance Modeling of the Natural Gas-Fired Allam Cycle
Abstract
1. Introduction
- The comparison with the Graz cycle [12], for which ηth was estimated to be slightly higher than the Allam cycle (53.5% vs. 52.7%);
- Economic feasibility [13], which was assessed as “quite competitive” in terms of total specific investment costs (about 1300 USD/kW);
- The exergo-economic analysis [14], from which exergetic efficiency and cost of electricity were equal to 50.1% and 91.7 EUR/MWh, respectively;
- Size effect on cycle performance [15], which remains relatively high (ηth > 51%) in the net power range of 400 to 100 MWel;
- Sensitivity to the thermal power recovered from the ASU [15]. The case without heat integration is impacted by 3 pp lower ηth than the base case with heat recovery from the ASU main compressor cooler (about 50% vs. 53%).
2. Brief Review of the Optimized Cycle at Design Point
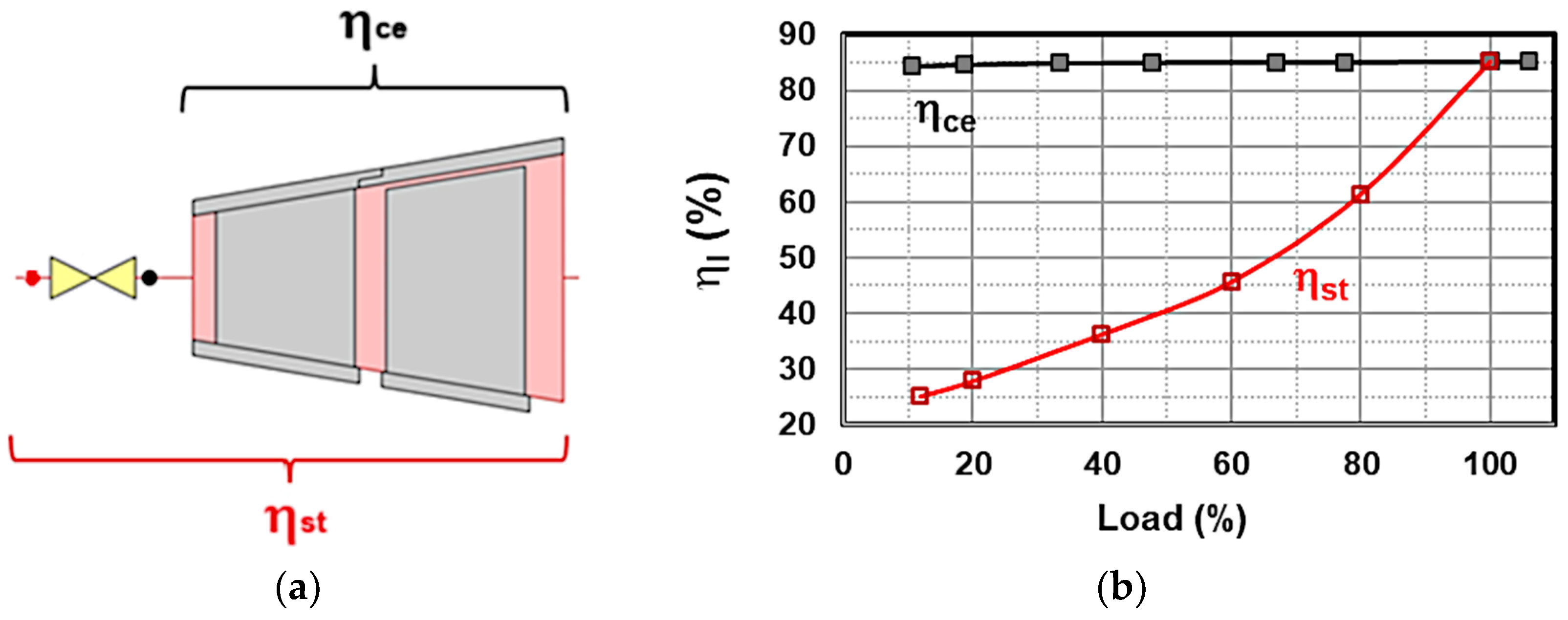
- The turbine was split into seven stages, the first four being cooled; uncooled adiabatic efficiency was set to progressively increase from the first to the seventh stage in the range between 90% and 93%. The number of stages is consistent with the guidelines contained in [25], representing a compromise between expansion efficiency and cooling flow.
- The recuperator was split into three (two-stream) heat exchangers in series, where heat transfer occurs at constant heat capacity, in accordance with the software’s limitations. Nevertheless, the correct temperature difference values on the cold and hot sides were obtained. This approach was also successfully adopted in [20].
- The cold source required for any cooling process was not specified, as was performed by the cycle developers in the original document [26]. The removal of heat to achieve the desired output temperature was simply taken for granted. This applies to both the flue gas stream, which is cooled to reach the Tmin downstream of the recuperator, and the intercooled, two-stage compression of the recirculated CO2 stream.
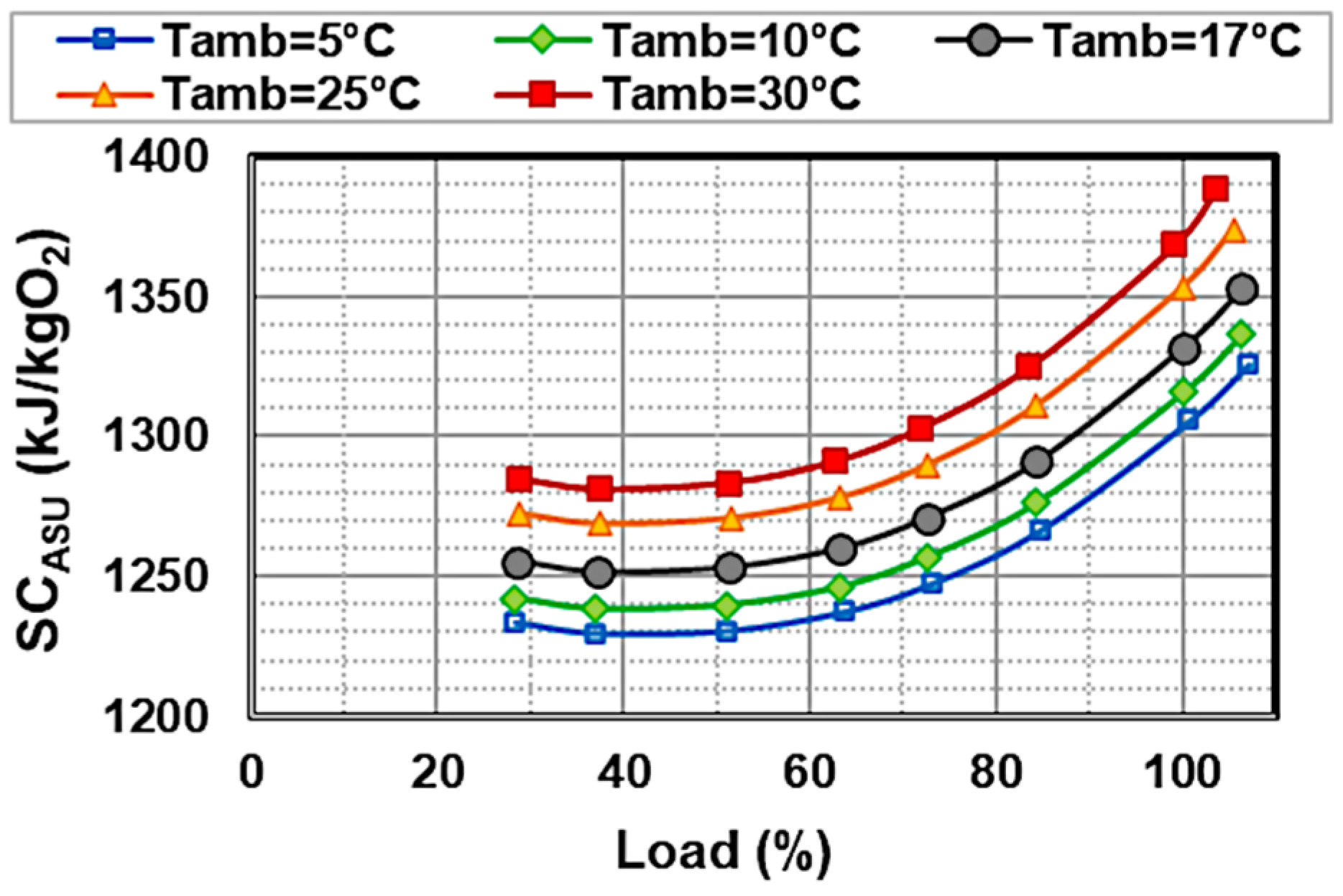
- Power requirements of the ASU to produce high-purity (99.5%) oxygen were estimated without going into the details of the chemical process, which is actually a common practice. The resulting specific consumption (SCASU) of 1330 kJ/kgO2 is in line with values collected by Reale [8], ranging from 1049 to 1447 kJ/kgO2, with most predictions clustering around 1300 ± 50 kJ/kgO2 [27]. In short, a multistage intercooled compression configuration was assumed for both ambient air and oxygen, with two and five stages; the outlet pressure is set by the distillation column and combustor, respectively.
| Design Parameter | Value |
|---|---|
| Minimum cycle temperature (°C) | 17 |
| Turbine inlet pressure (bar) | 303 |
| Turbine inlet temperature (°C) | 1194 |
| Turbine inlet flow (kg/s) | 840 |
| Turbine outlet pressure (bar) | 30 |
| Turbine outlet temperature (°C) | 728 |
| Turbine coolant mass fraction 1 (%) | 12 |
| Turbine exhaust flow (kg/s) | 942 |
| Expansion power (MW) | 447 |
| CO2 compression power (MW) | 73 |
| Fuel input (MW) | 597 |
| Recuperator heat transfer (MW) | 797 |
| ASU penalty (%LHV) | 10.66 |
| Fuel compressor power (MW) | 3.9 |
| Net electric efficiency (%) | 50.4 |

3. Off-Design Model and Assumptions
3.1. Compressors
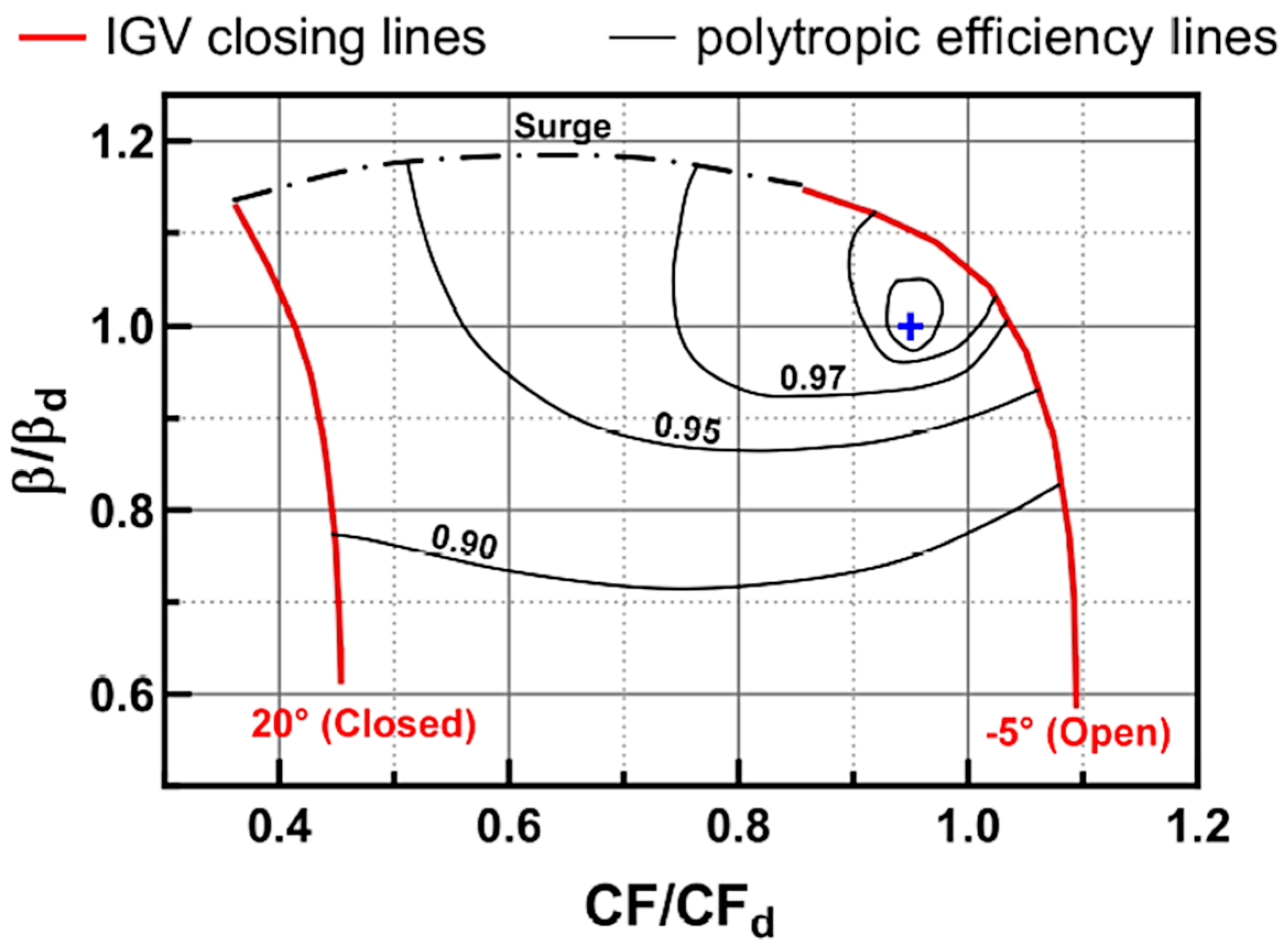
3.2. Turbine
4. Results
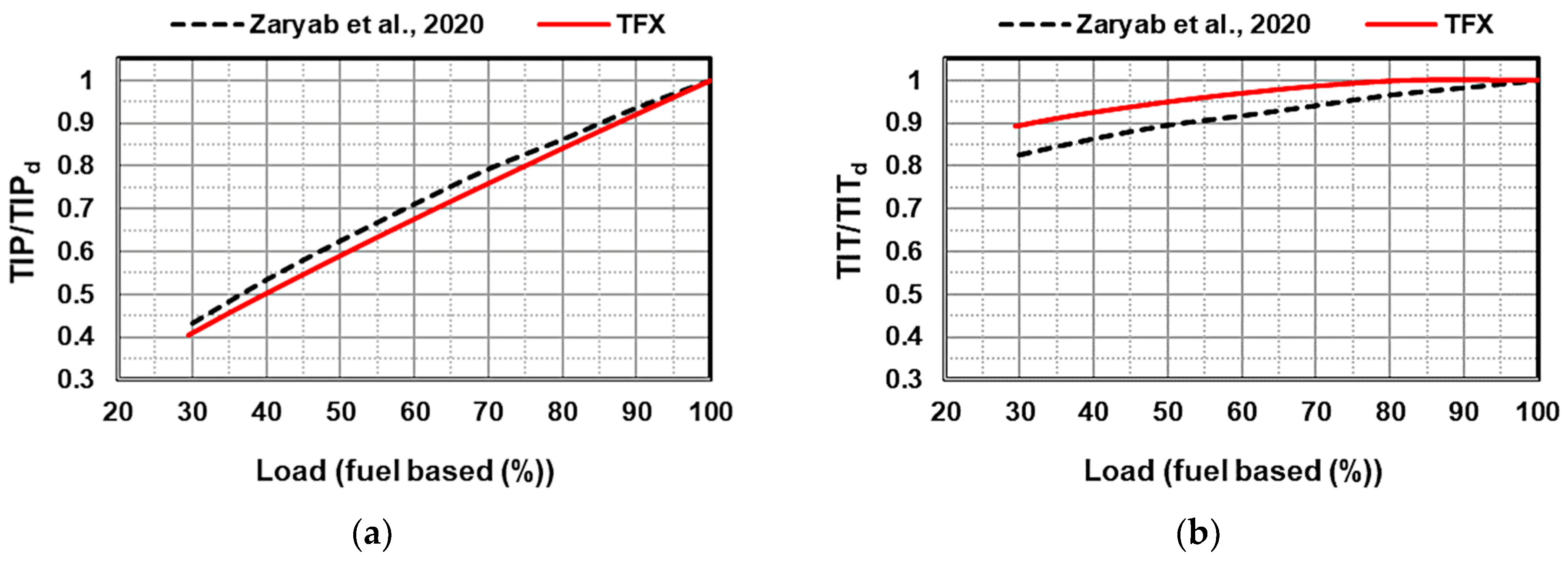
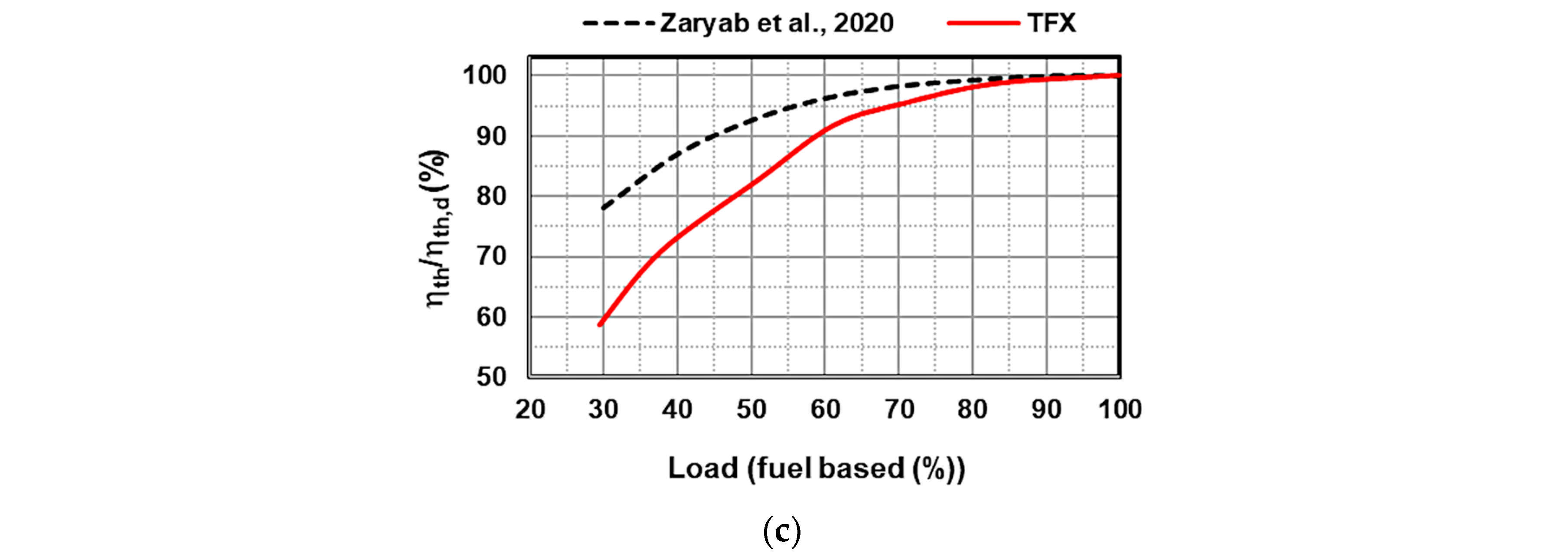
4.1. Validation
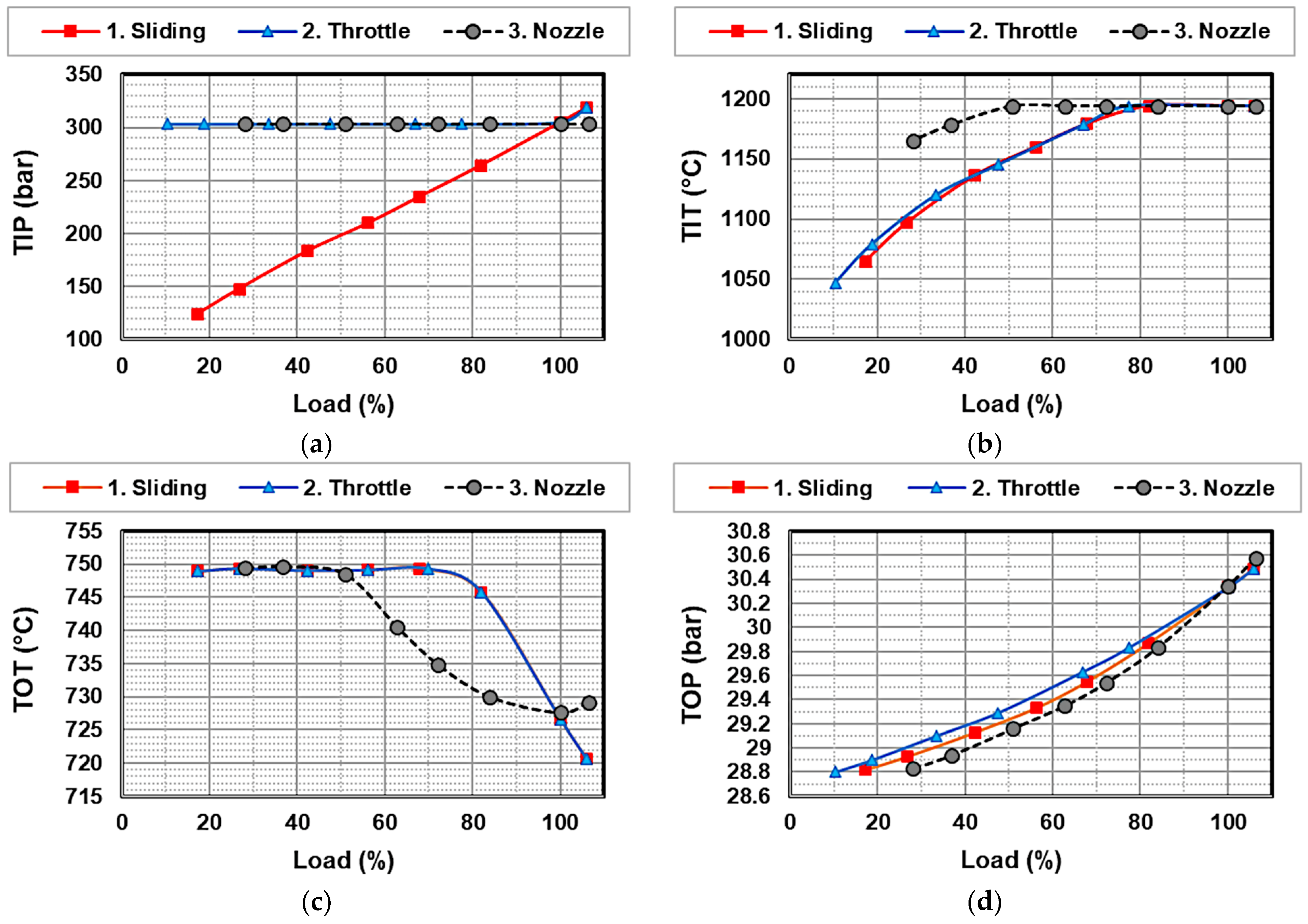
4.2. Part-Load Strategies
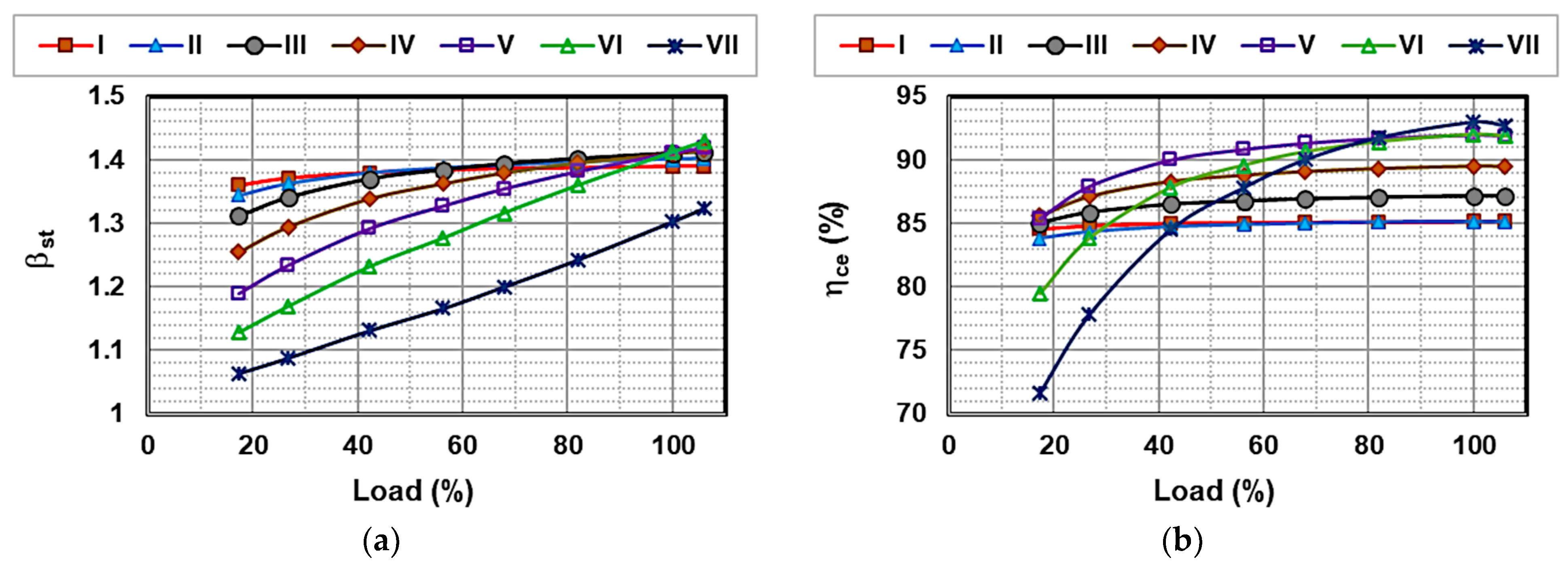
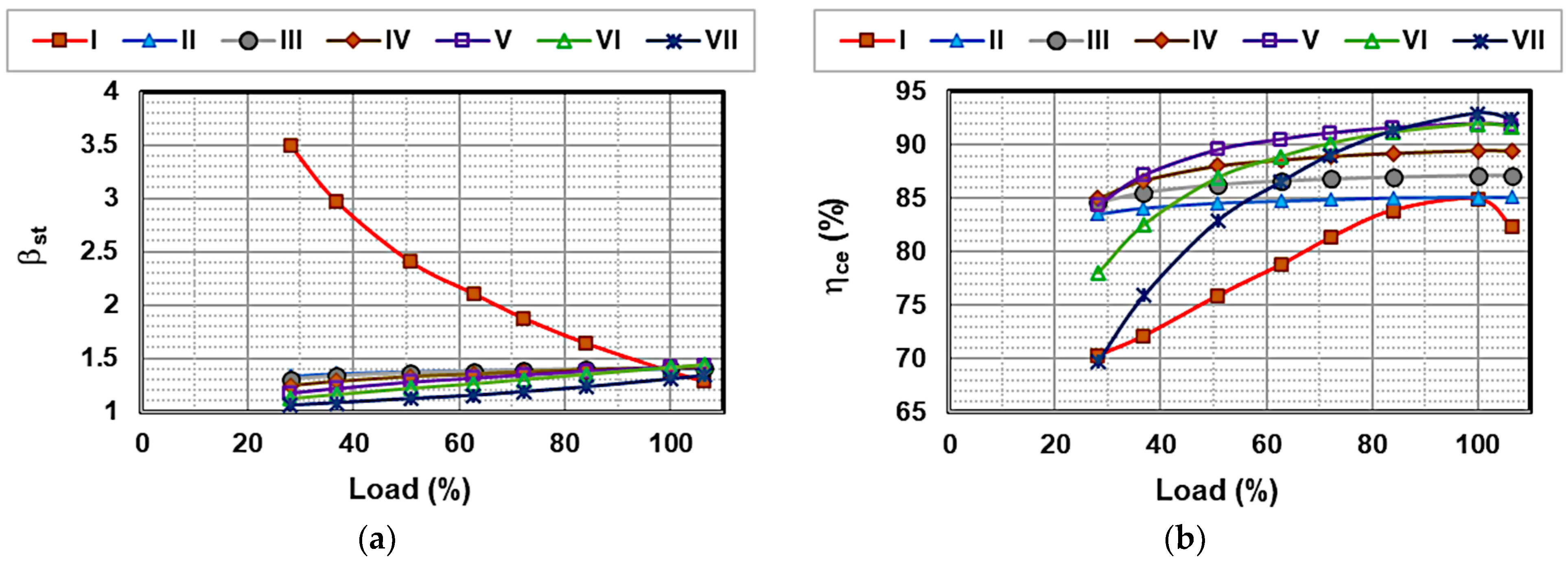
- In the basic version, “IGV+VC” mode prescribes a full admission turbine with sliding pressure control. By reducing the inlet pressure, the turbine can operate efficiently while accommodating a smaller inlet mass flow, according to Equation (8).
- In the intermediate version, a control valve is used at the turbine inlet to maintain the design pressure, whatever the load, by throttling the flow entering the first stage. Note that, if the pressure at the turbine inlet was to slide above the set point, the throttle valve would be wide open, with zero pressure loss. However, this solution may entail operational challenges, as valves are incapable of withstanding the elevated temperatures at the combustor outlet without specialized cooling. Furthermore, the spatial availability for installation is constrained.
- The most advanced solution involves applying nozzle control to modulate the flow area at the inlet of the stage group to maintain design point pressure, regardless of the inlet mass flow rate. This can be achieved by swiveling nozzle vanes, for example. Although costly, this solution could be feasible since the turbine is not directly connected to the compressor shaft.
4.2.1. Main Thermodynamic Parameters
4.2.2. Turbine Stage Characterization
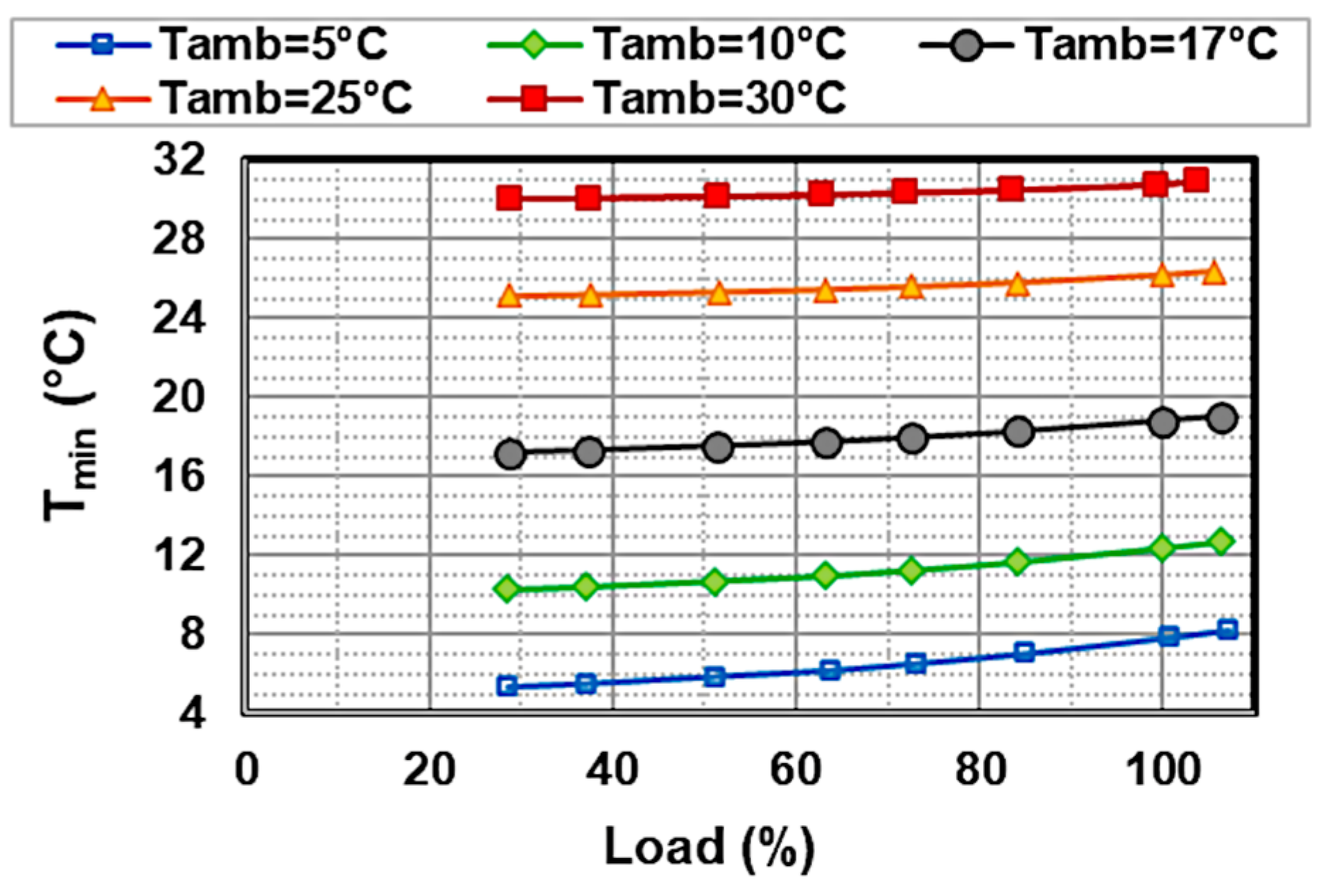
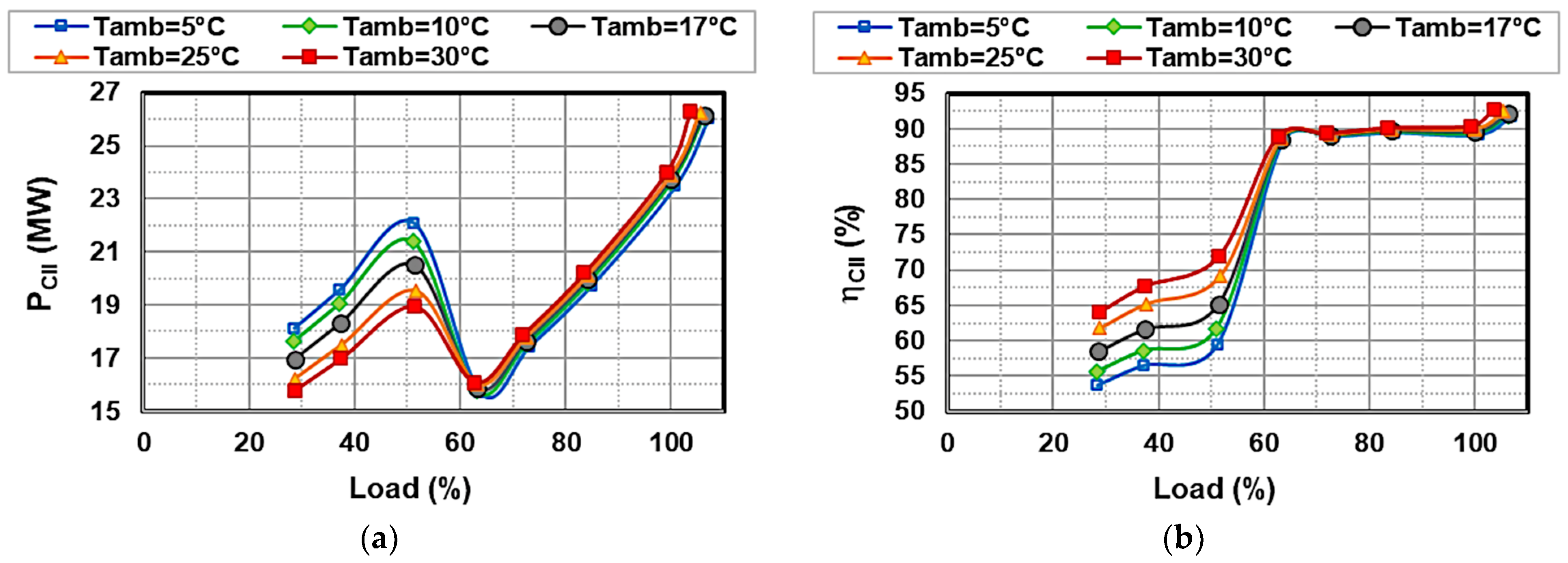
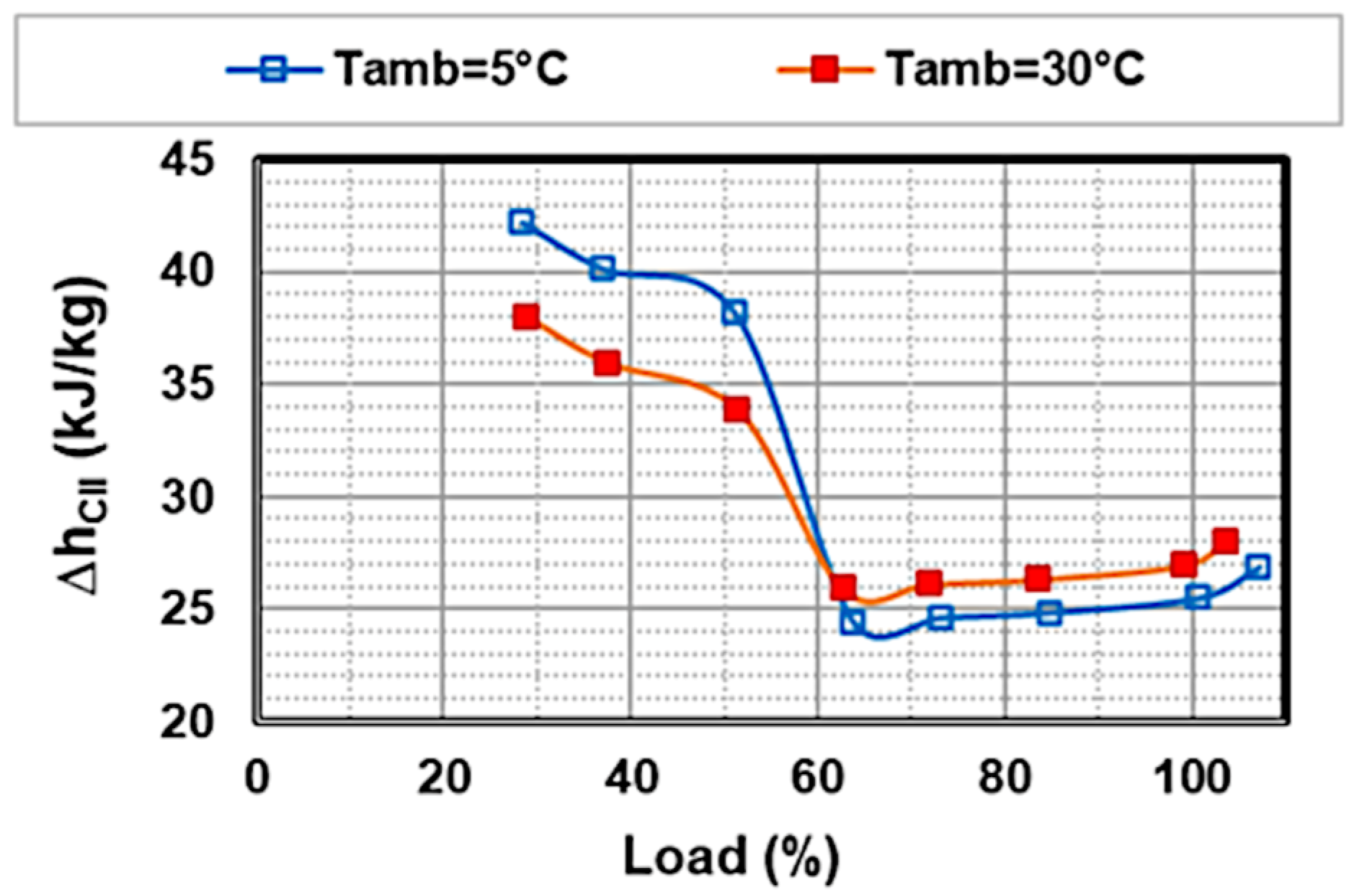
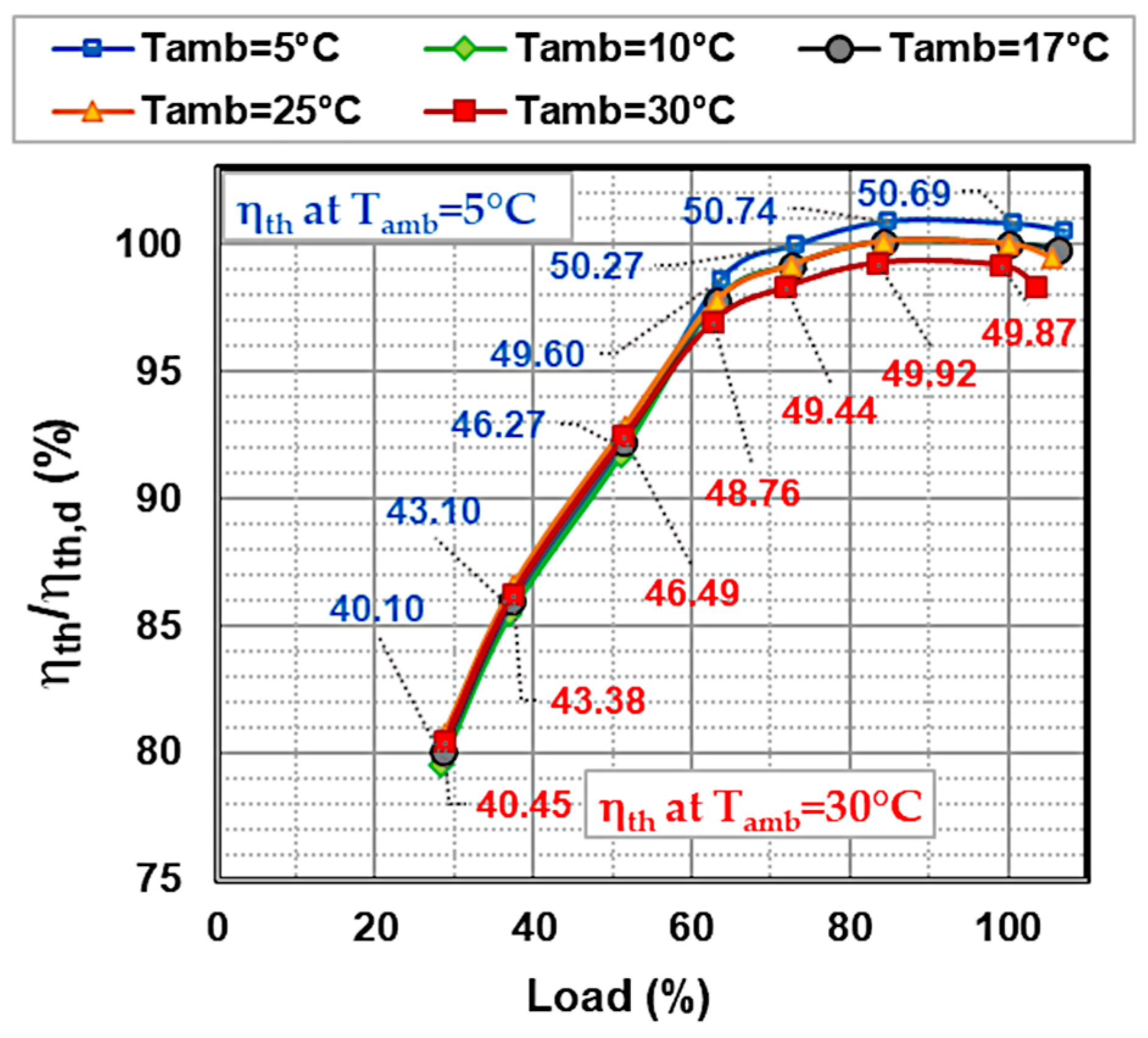
4.3. Influence of Ambient Temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASU | Air separation unit |
| C | Constant |
| CF | Corrected flow |
| CO2 | Carbon dioxide |
| CS | Corrected speed |
| DGV | Diffuser guide vane |
| f | Functional dependence |
| FF | Flow function |
| h | Enthalpy |
| IGV | Inlet guide vane |
| LHV | Lower heating value |
| m | Mass flow rate |
| MW | Molecular weight |
| n | Rotational speed |
| NG | Natural gas |
| O2 | Oxygen |
| P | Power |
| p | Pressure |
| pp | Percentage points |
| R | Gas constant |
| s | Supercritical |
| SC | Specific consumption |
| T | Temperature |
| TFX | Thermoflex prediction |
| TIP | Turbine inlet pressure |
| TIT | Turbine inlet temperature |
| TOP | Turbine outlet pressure |
| TOT | Turbine outlet temperature |
| VC | Variable control |
| β | Pressure ratio |
| Δ | Difference |
| γ | Ratio of specific heat |
| η | Efficiency |
| Subscripts | |
| amb | Ambient |
| C | Compressor |
| ce | Cooled expansion |
| d | Design |
| in | Inlet |
| is | Isentropic |
| min | Minimum |
| od | Off-design |
| out | Outlet |
| ref | Reference |
| st | Stage |
| th | Thermal |
| y | Polytropic |
Appendix A
| Stream Number | p (Bar) | T (°C) | h (kJ/kg) | m (kg/s) |
|---|---|---|---|---|
| 1 | 218.1 | 1099.4 | 1270.3 | 873.6 |
| 2 | 155.8 | 1009.1 | 1147.3 | 909.4 |
| 3 | 110.5 | 935.5 | 1048.2 | 930.8 |
| 4 | 78.34 | 872.5 | 965 | 941.5 |
| 5 | 55.56 | 818.3 | 894.7 | 941.5 |
| 6 | 39.4 | 766.2 | 828 | 941.5 |
| 7 | 303.2 | 1193.8 | 1402.7 | 839.9 |
| 8 | 309.2 | 204 | 68.34 | 881.7 |
| 9 | 309.2 | 204 | 68.34 | 780.1 |
| 10 | 28 | 17 | −104.2 | 941.5 |
| 11 | 28 | 17 | −38.1 | 915 |
| 13 | 28 | 17 | −38.16 | 909 |
| 14 | 49.45 | 62.82 | −7.55 | 909 |
| 15 | 48.48 | 19.54 | −70.72 | 909 |
| 16 | 78 | 57.13 | −50.37 | 909 |
| 17 | 78 | 57.13 | −50.37 | 27.27 |
| 18 | 78 | 57.13 | −50.37 | 881.7 |
| 20 | 76.47 | 16 | −269.6 | 690.7 |
| 21 | 76.47 | 16 | −269.6 | 191.1 |
| 22 | 309.2 | 97.15 | 31.34 | 47.88 |
| 23 | 303.2 | 722.2 | 742.8 | 780.1 |
| 27 | 315.4 | 116.9 | −83.47 | 881.7 |
| 28 | 321.7 | 38.54 | −239.2 | 881.7 |
| 30 | 321.7 | 38.54 | −239.2 | 690.7 |
| 31 | 70 | 25 | 11.93 | 49,976 |
| 32 | 309.2 | 141.8 | 11.93 | 50,212 |
| 33 | 309.2 | 204 | 68.34 | 18.55 |
| 34 | 30.31 | 727.5 | 778.8 | 941.5 |
| 35 | 321.7 | 38.54 | −239.2 | 191.1 |
| 36 | 309.2 | 204 | 68.34 | 15.17 |
| 37 | 309.2 | 204 | 68.34 | 17.86 |
| 38 | 28.56 | 40.54 | −74.98 | 941.5 |
| 39 | 309.2 | 204 | 68.34 | 17.97 |
| 40 | 29.13 | 118.9 | 70.83 | 941.5 |
| 41 | 29.71 | 253 | 214.4 | 941.5 |
| 42 | 309.2 | 204 | 68.34 | 11.17 |
| 43 | 309.2 | 204 | 68.34 | 20.95 |
| 44 | 309.2 | 204 | 68.34 | 10.2 |
| 45 | 309.2 | 204 | 68.34 | 5.976 |
| 46 | 309.2 | 204 | 68.34 | 4.776 |
| 48 | 309.2 | 204 | 68.34 | 49.98 |
| 49 | 309.2 | 204 | 68.34 | 51.7 |
References
- IEA. Global Energy Review 2025; International Energy Agency: Paris, France, 2025. [Google Scholar]
- EMBER. Global Electricity Review 2024; Ember: London, UK, 2024; Available online: https://ember-energy.org/app/uploads/2024/05/Report-Global-Electricity-Review-2024.pdf (accessed on 22 May 2025).
- Friedlingstein, P.; O’sullivan, M.; Jones, M.W.; Andrew, R.M.; Hauck, J.; Landschützer, P.; Le Quéré, C.; Li, H.; Luijkx, I.T.; Olsen, A.; et al. Global Carbon Budget 2024. Earth Syst. Sci. Data 2025, 17, 965–1039. [Google Scholar] [CrossRef]
- Allam, R.J.; Palmer, M.R.; Brown, G.W., Jr. System and Method for High Efficiency Power Generation Using a Carbon Dioxide Circulating Working Fluid. Assignee: 8 Rivers Capital LLC Palmer Labs LLC. U.S. Patent US8596075B2, 3 December 2013. [Google Scholar]
- Allam, R.J.; Fetvedt, J.E.; Forrest, B.A.; Freed, D.A. The oxy-fuel, supercritical CO2 Allam Cycle: New cycle developments to produce even lower-cost electricity from fossil fuels without atmospheric emissions. In Proceedings of the ASME Turbo Expo 2014: Turbomachinery Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Martin, S.; Forrest, B.; Rafati, N.; Lu, X.; Fetvedt, J.; McGroddy, M.; Brown, B.; Allam, R.; Beauchamp, D.; Freed, D. Progress update on the Allam cycle: Commercialization of Net Power and the Net Power demonstration facility. In Proceedings of the 14th International Conference on Greenhouse Gas Control Technologies, GHGT-14, Melbourne, Australia, 21–25 October 2018. [Google Scholar]
- Project Permian. Available online: https://netpower.com/projects/ (accessed on 22 May 2025).
- Reale, F. The Allam Cycle: A Review of Numerical Modeling Approaches. Energies 2023, 16, 7678. [Google Scholar] [CrossRef]
- Allam, R.J.; Palmer, M.R.; Brown, G.W., Jr.; Fetvedt, J.; Freed, D.; Nomoto, H.; Itohb, M.; Okitab, N.; Jones, C., Jr. High efficiency and low cost of electricity generation from fossil fuels while eliminating atmospheric emissions, including carbon dioxide. Energy Procedia 2013, 37, 1135–1149. [Google Scholar] [CrossRef]
- Kindra, V.; Rogalev, A.; Lisin, E.; Osipov, S.; Zlyvko, O. Techno-economic analysis of the oxy-fuel combustion power cycles with near-zero emissions. Energies 2021, 14, 5358. [Google Scholar] [CrossRef]
- Scaccabarozzi, R.; Gatti, M.; Martelli, E. Thermodynamic analysis and numerical optimization of the NET Power oxy-combustion cycle. Appl. Energy 2016, 178, 505–526. [Google Scholar] [CrossRef]
- Wimmer, K.; Sanz, W. Optimization and comparison of the two promising oxy-combustion cycles NET Power cycle and Graz Cycle. Int. J. Greenh. Gas Control 2020, 99, 103055. [Google Scholar] [CrossRef]
- Rogalev, A.; Grigoriev, E.; Kindra, V.; Rogalev, N. Thermodynamic optimization and equipment development for a high efficient fossil fuel power plant with zero emissions. J. Clean. Prod. 2019, 236, 117592. [Google Scholar] [CrossRef]
- Rodríguez Hervás, G.; Petrakopoulou, F. Exergoeconomic analysis of the Allam cycle. Energy Fuels 2019, 33, 7561–7568. [Google Scholar] [CrossRef]
- Martinelli, M.; Chiesa, P.; Martelli, E. Techno-economic assessment of the Allam cycle for different plant sizes, oxygen purities and heat integration with external sources. Fuel 2025, 381, 133383. [Google Scholar] [CrossRef]
- Scaccabarozzi, R.; Gatti, M.; Martelli, E. Thermodynamic optimization and part-load analysis of the NET power cycle. Energy Procedia 2017, 114, 551–560. [Google Scholar] [CrossRef]
- Zaryab, S.A.; Scaccabarozzi, R.; Martelli, E. Advanced part-load control strategies for the Allam cycle. Appl. Therm. Eng. 2020, 168, 114822. [Google Scholar] [CrossRef]
- Fernandes, D.; Wang, S.; Xu, Q.; Chen, D. Dynamic simulations of the Allam cycle power plant integrated with an air separation unit. Int. J. Chem. Eng. 2019, 2019, 6035856. [Google Scholar] [CrossRef]
- Xie, M.; Chen, X.; Chen, L.; Zhou, M.; Liu, Y.; Zeng, L.; Shi, H.; Zhang, F.; Xie, S.; Zhao, Y. Evaluating the feasibility of a novel Allam cycle for co-generating power and water in hot regions. Energy Convers. Manag. 2024, 309, 118447. [Google Scholar] [CrossRef]
- Mitchell, C.; Avagyan, V.; Chalmers, H.; Lucquiaud, M. An initial assessment of the value of Allam Cycle power plants with liquid oxygen storage in future GB electricity system. Int. J. Greenh. Gas Control 2019, 87, 1–18. [Google Scholar] [CrossRef]
- Xie, M.; Zhou, M.; Chen, L.; Zhang, F.; Xiao, N.; Chen, X.; Xie, S.; Shah, N.; Zhao, Y. Techno-economic assessment of the modified Allam cycle configurations with multi-stage pump/compressor for efficient operation in hot regions. Energy Convers. Manag. 2024, 306, 118291. [Google Scholar] [CrossRef]
- Crespi, F.; De Arriba, P.R.; Sánchez, D.; Ayub, A.; Di Marcoberardino, G.; Invernizzi, C.M.; Martínez, G.S.; Iora, P.; Di Bona, D.; Binotti, M.; et al. Thermal efficiency gains enabled by using CO2 mixtures in supercritical power cycles. Energy 2022, 238, 121899. [Google Scholar] [CrossRef]
- Fernandes, D.; Wang, S.; Xu, Q.; Buss, R.; Chen, D. Process and Carbon Footprint Analyses of the Allam Cycle Power Plant Integrated with an Air Separation Unit. Clean Technol. 2019, 1, 325–340. [Google Scholar] [CrossRef]
- Colleoni, L.; Sindoni, A.; Ravelli, S. Comprehensive thermodynamic evaluation of the natural gas-fired Allam cycle at full load. Energies 2023, 16, 2597. [Google Scholar] [CrossRef]
- Allison, T.C.; Moore, J.J.; Cich, S.; White, S.; Pryor, O. Oxy-Fuel Combustion and Advanced Power Generation Turbines. USEA Webinar 2022. Available online: https://usea.org/sites/default/files/event-/SwRI%20USEA%20Webinar%20-%20sCO2%20Oxy-Combustion.pdf (accessed on 10 March 2025).
- Allam, R.; Martin, S.; Forrest, B.; Fetvedt, J.; Lu, X.; Freed, D.; Brown, G.W.; Sasaki, T.; Itoh, M.; Manning, J. Demonstration of the Allam Cycle: An Update on the Development Status of a High Efficiency Supercritical Carbon Dioxide Power Process Employing Full Carbon Capture. Energy Procedia 2017, 114, 5948–5966. [Google Scholar] [CrossRef]
- Haseli, Y.; Sifat, N. Performance modeling of Allam cycle integrated with a cryogenic air separation process. Comput. Chem. Eng. 2021, 148, 107263. [Google Scholar] [CrossRef]
- Marshall, M.; Anguiano, M.; Bensmiller, J.; Replogle, C.; Kerr, T.; Klaerner, G.; Moore, J.J. Detailed design and cost estimation of a 300 MWE oxy-fuel sCO2 turbine. In Proceedings of the ASME Turbo Expo 2025: Turbomachinery Technical Conference and Exposition, Memphis, TN, USA, 16–20 June 2025. [Google Scholar]
- Atlas Copco Gas and Process. Driving Centrifugal Compressor Technology; Atlas Copco Gas and Process: Cologne, Germany, 2022. [Google Scholar]
- El-Masri, M.A. Design of Gas Turbine Combined Cycles and Cogeneration Systems; Thermoflow Inc.: Southborough, MA, USA, 2009; pp. 5.1–5.16. [Google Scholar]
- El-Masri, M.A. GASCAN—An Interactive Code for Thermal Analysis of Gas Turbine Systems. J. Eng. Gas Turbines Power 1988, 110, 201–209. [Google Scholar] [CrossRef]





| Label | Turbine—1st Stage | Compressor | Constraints |
|---|---|---|---|
| 1. Sliding | Full admission with sliding pressure control | IGV closure | TOT ≤ 750 °C Fixed pmin |
| 2. Throttle | Full admission with a throttling valve | ||
| 3. Nozzle | Partial admission with constant inlet pressure |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ambrosio, F.; Colleoni, L.; Ravelli, S. Off-Design Performance Modeling of the Natural Gas-Fired Allam Cycle. Energies 2025, 18, 4771. https://doi.org/10.3390/en18174771
D’Ambrosio F, Colleoni L, Ravelli S. Off-Design Performance Modeling of the Natural Gas-Fired Allam Cycle. Energies. 2025; 18(17):4771. https://doi.org/10.3390/en18174771
Chicago/Turabian StyleD’Ambrosio, Federico, Lorenzo Colleoni, and Silvia Ravelli. 2025. "Off-Design Performance Modeling of the Natural Gas-Fired Allam Cycle" Energies 18, no. 17: 4771. https://doi.org/10.3390/en18174771
APA StyleD’Ambrosio, F., Colleoni, L., & Ravelli, S. (2025). Off-Design Performance Modeling of the Natural Gas-Fired Allam Cycle. Energies, 18(17), 4771. https://doi.org/10.3390/en18174771







