Study on the Gas–Liquid Two-Flow Characteristics Inside a Three-Stage Centrifugal Pump
Abstract
1. Introduction
2. Computational Model and Mesh Generation
2.1. Computational Model
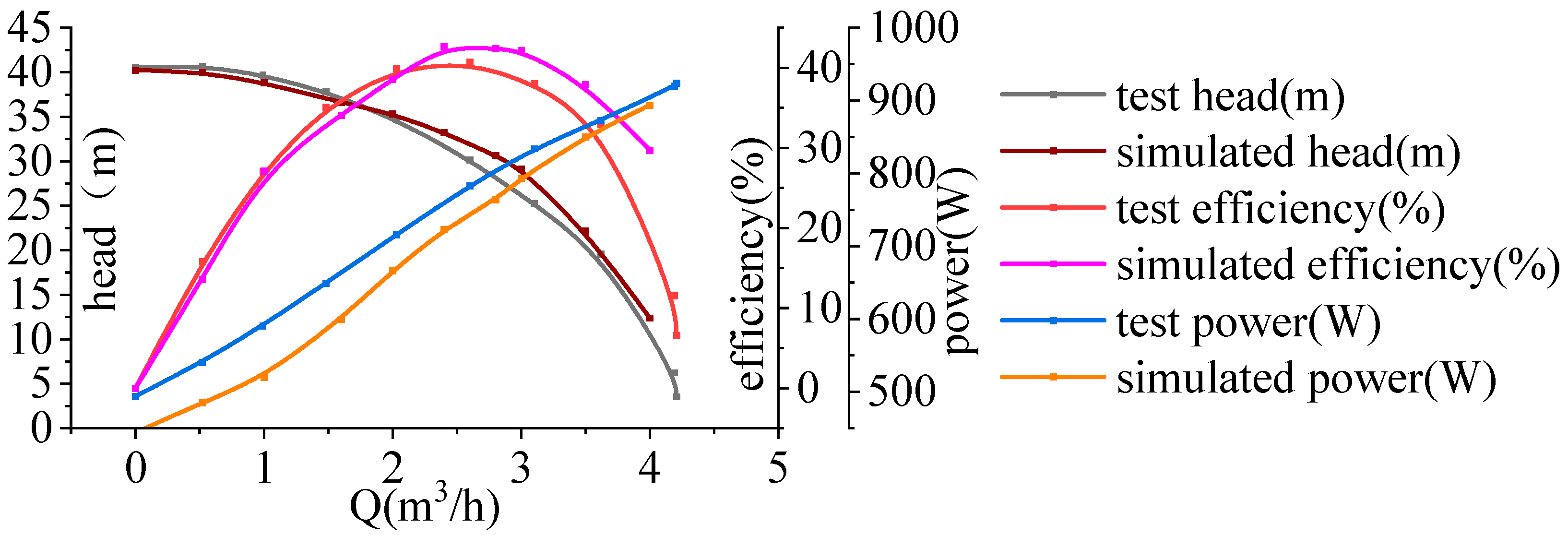
2.2. Turbulence Model, Mesh Generation, and External Characteristics Validation
2.3. Multiphase Flow Model and Boundary Conditions
3. Calculation Result Analysis
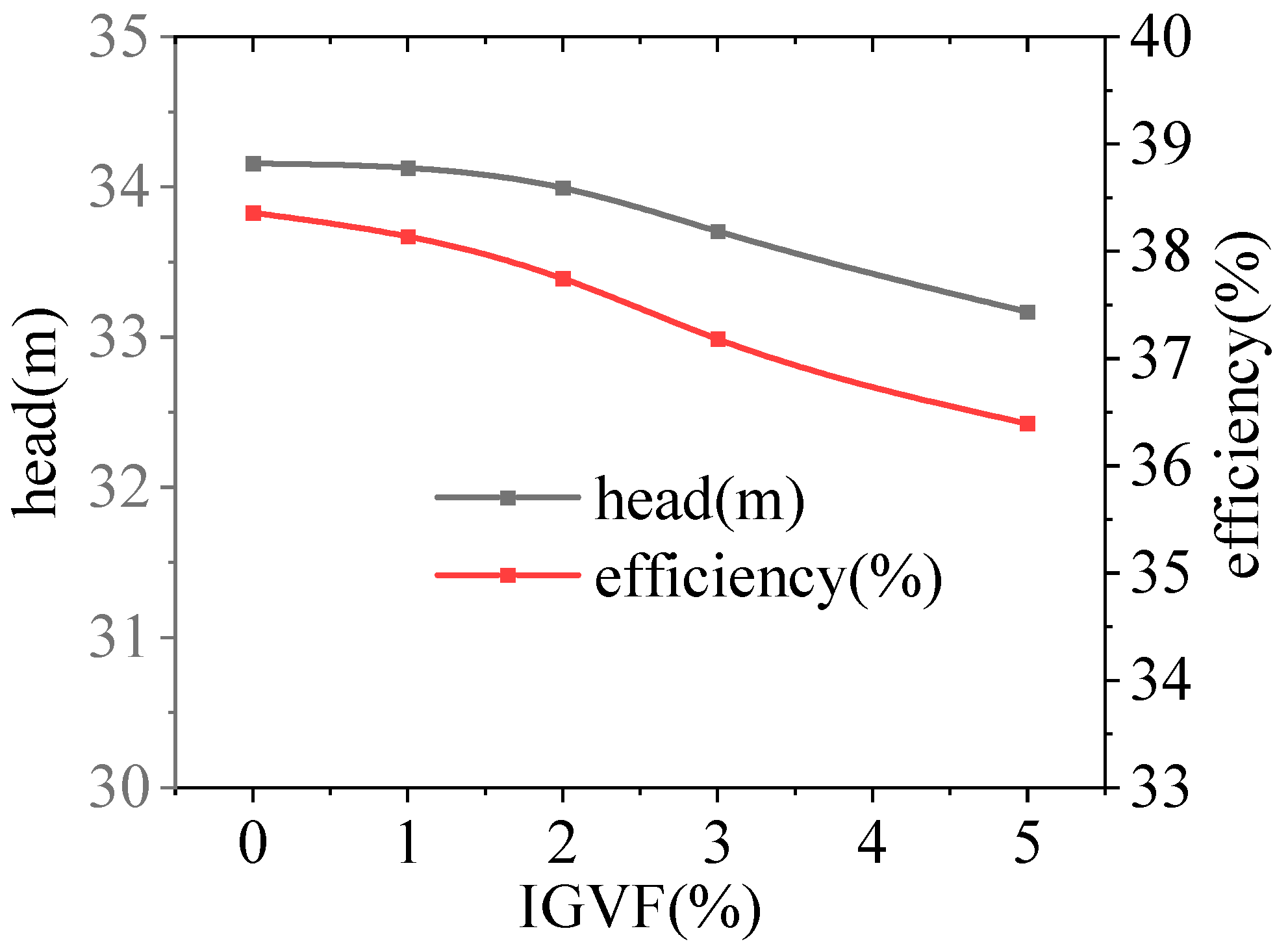
3.1. Characteristic Curve Analysis
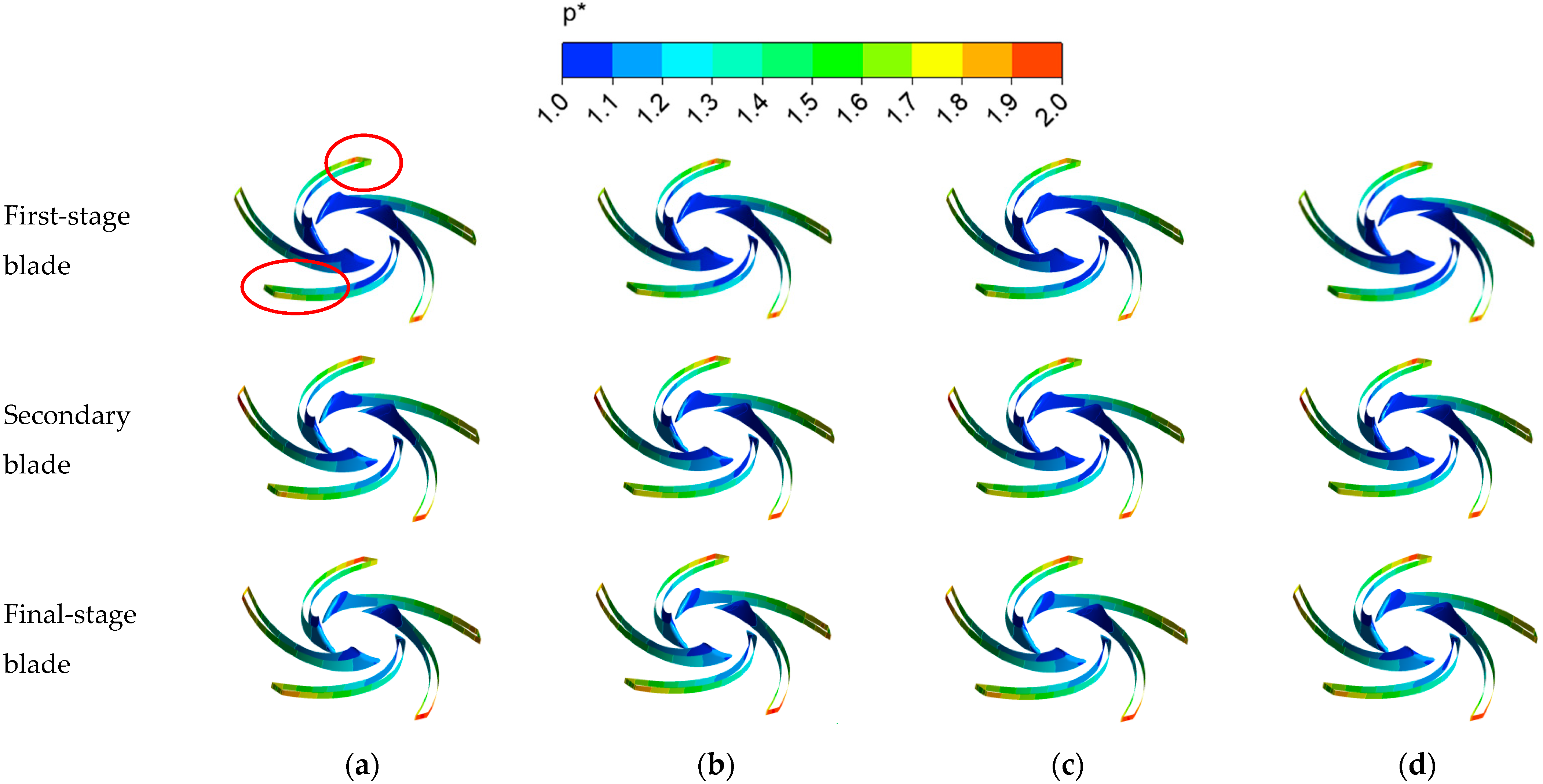
3.2. Impeller Blade Pressure Analysis
3.3. Gas Content Distribution on Blade Surface
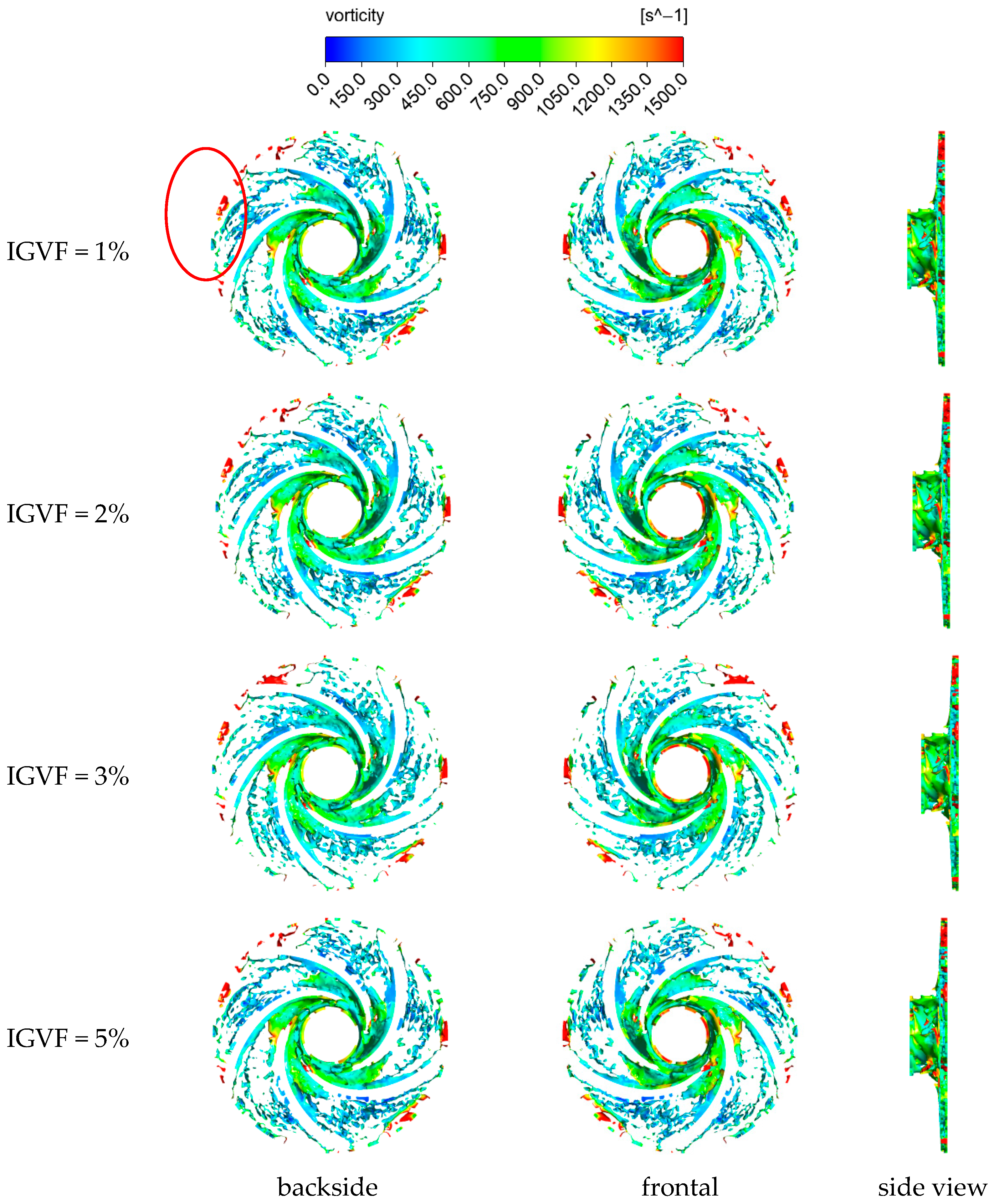
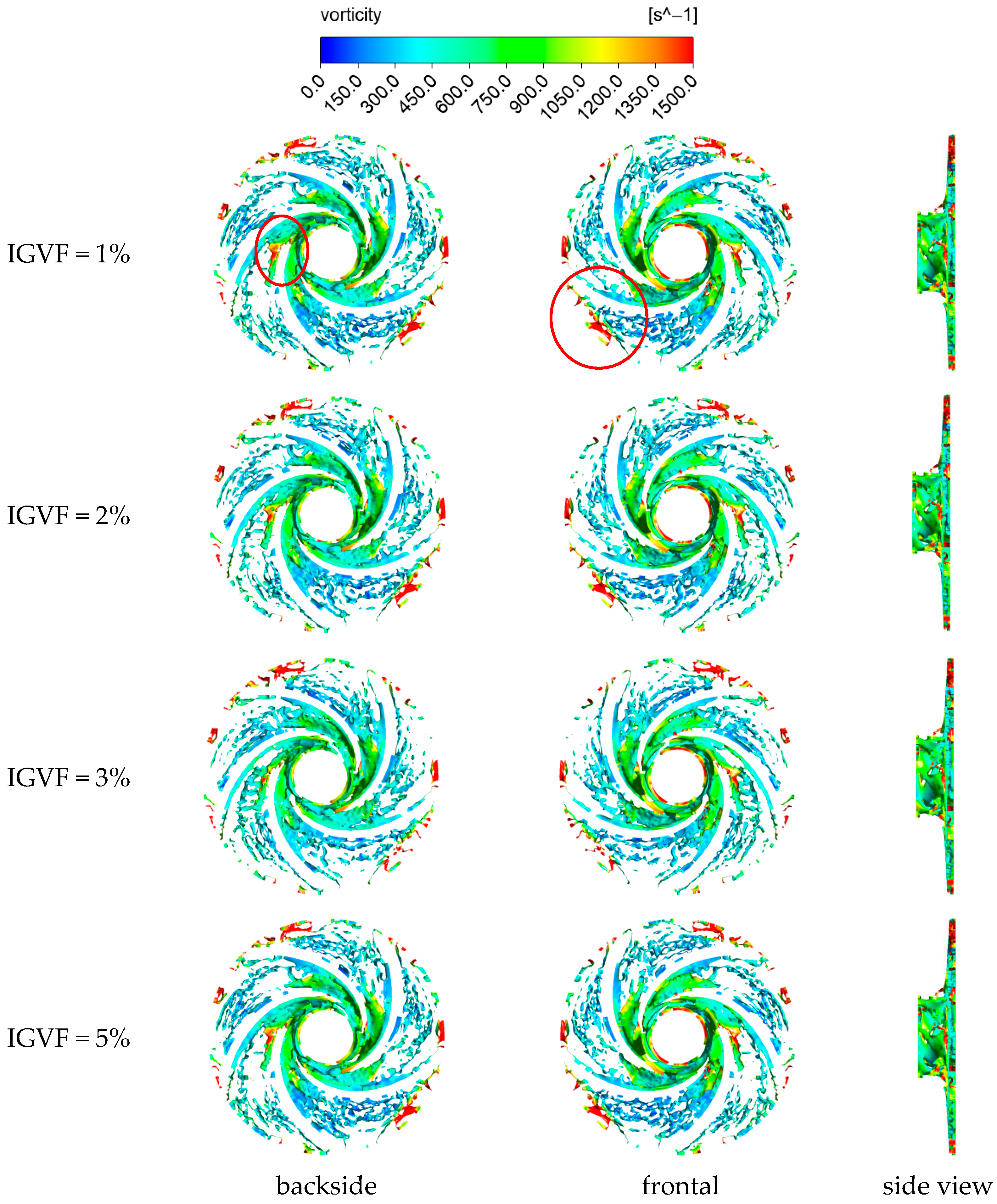
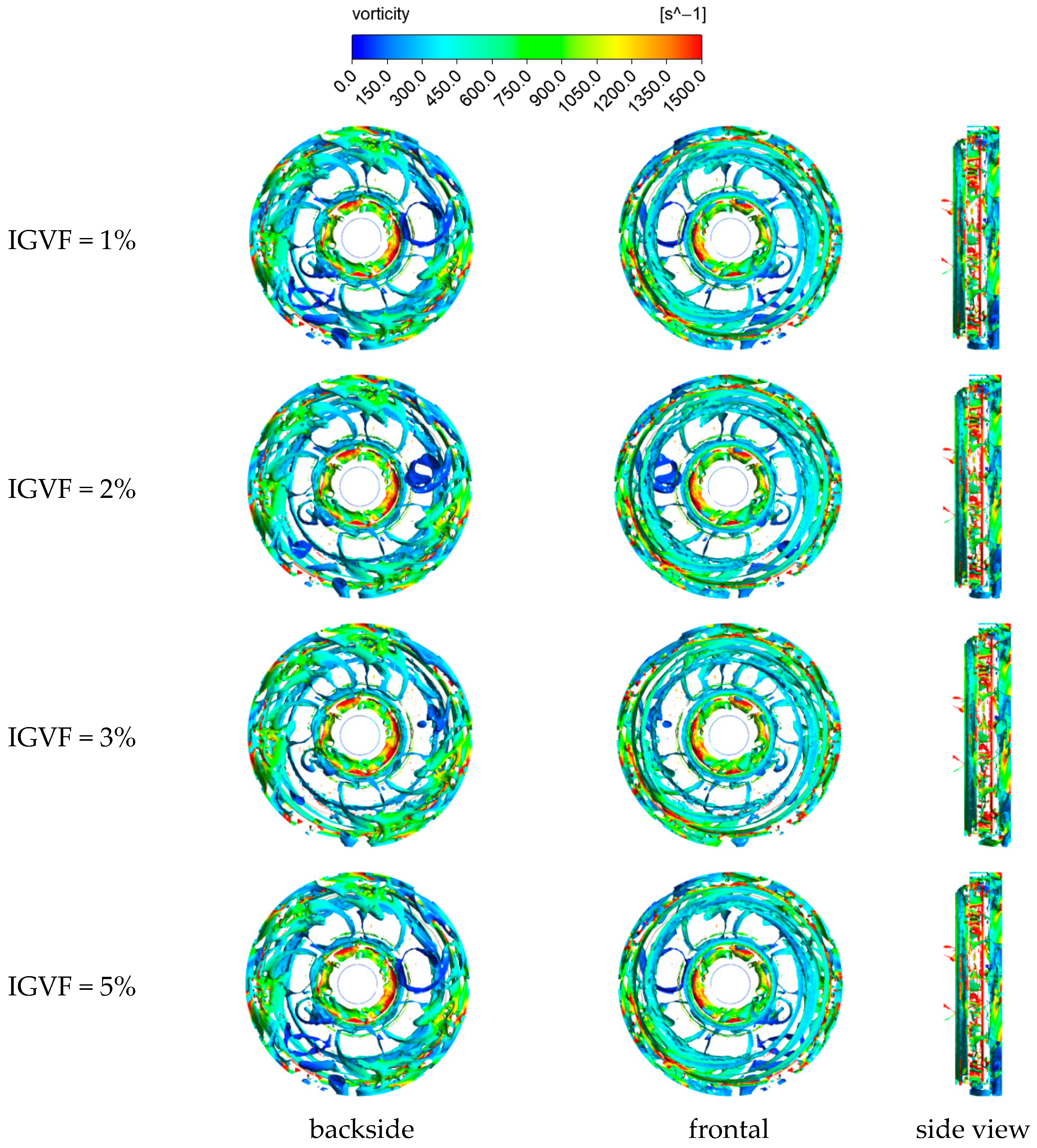
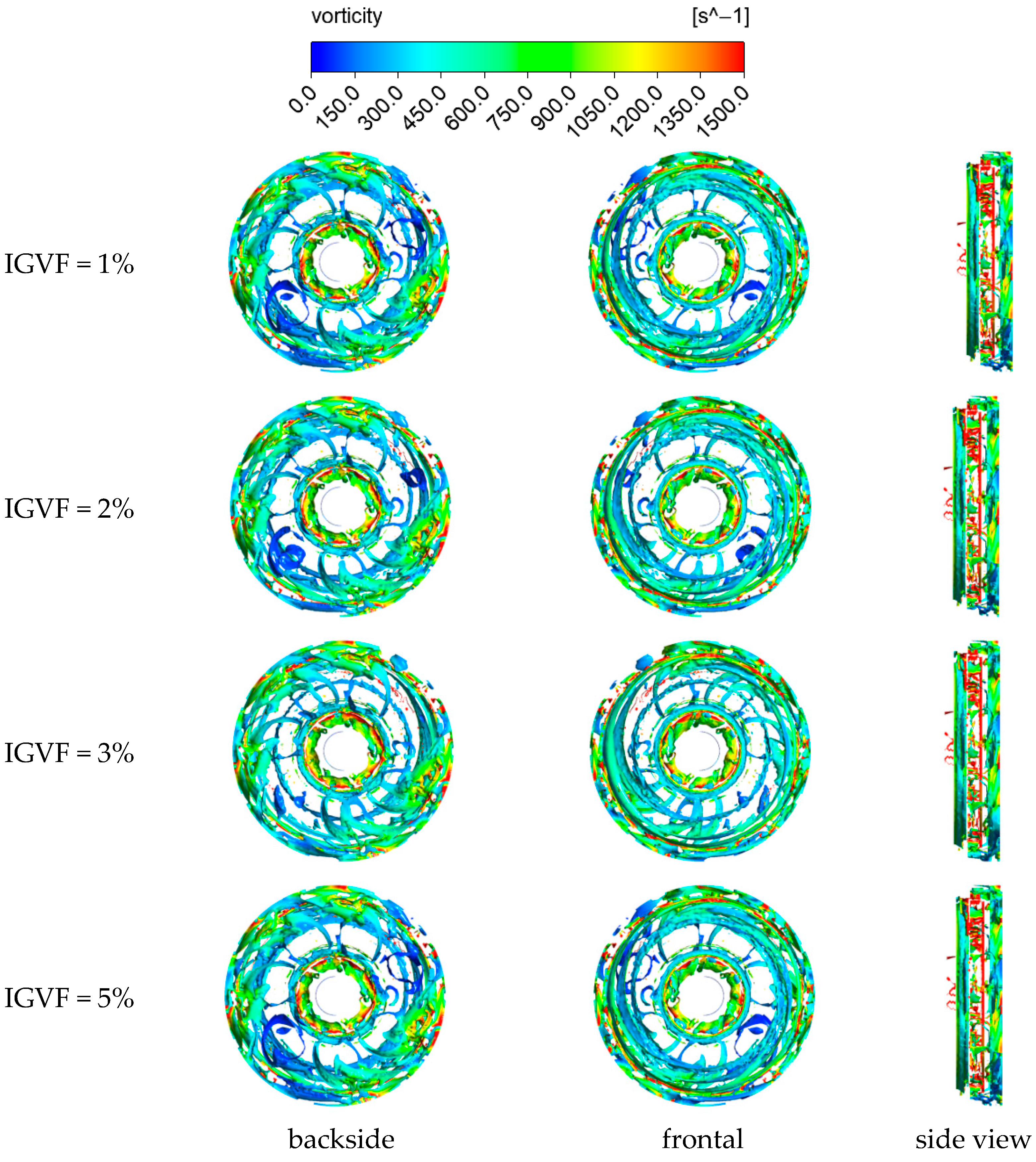
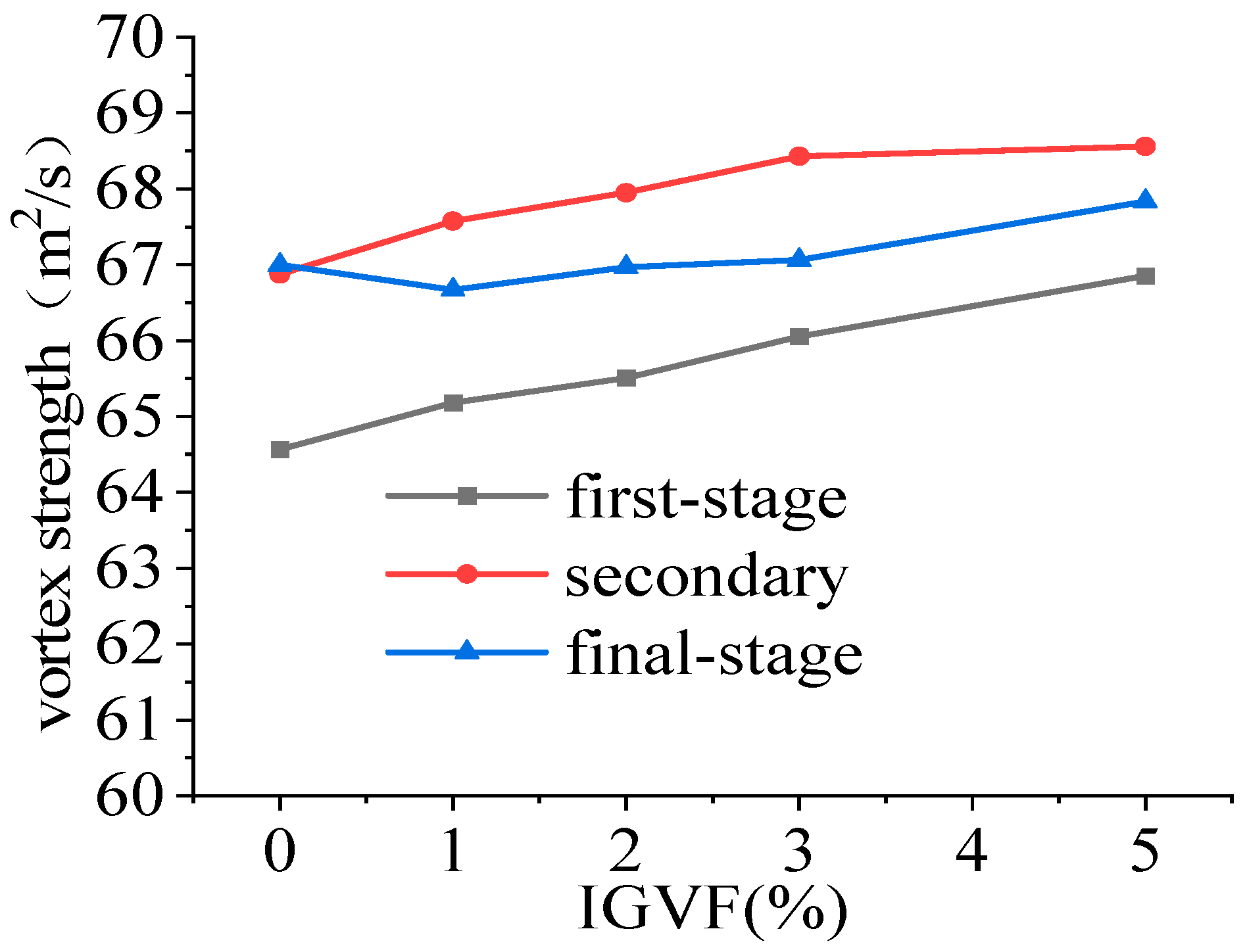
3.4. Vortex Structure Distribution Inside the Impeller
3.4.1. First-Stage Impeller Vortex Structure Distribution
3.4.2. Secondary Impeller Vortex Structure Distribution
3.4.3. Final-Stage Impeller Vortex Structure Distribution
3.5. Guide Vane Vortex Structure Distribution
3.5.1. First-Stage Guide Vane Vortex Structure Distribution
3.5.2. Secondary Guide Vane Vortex Structure Distribution
3.5.3. Final-Stage Guide Vane Vortex Structure Distribution
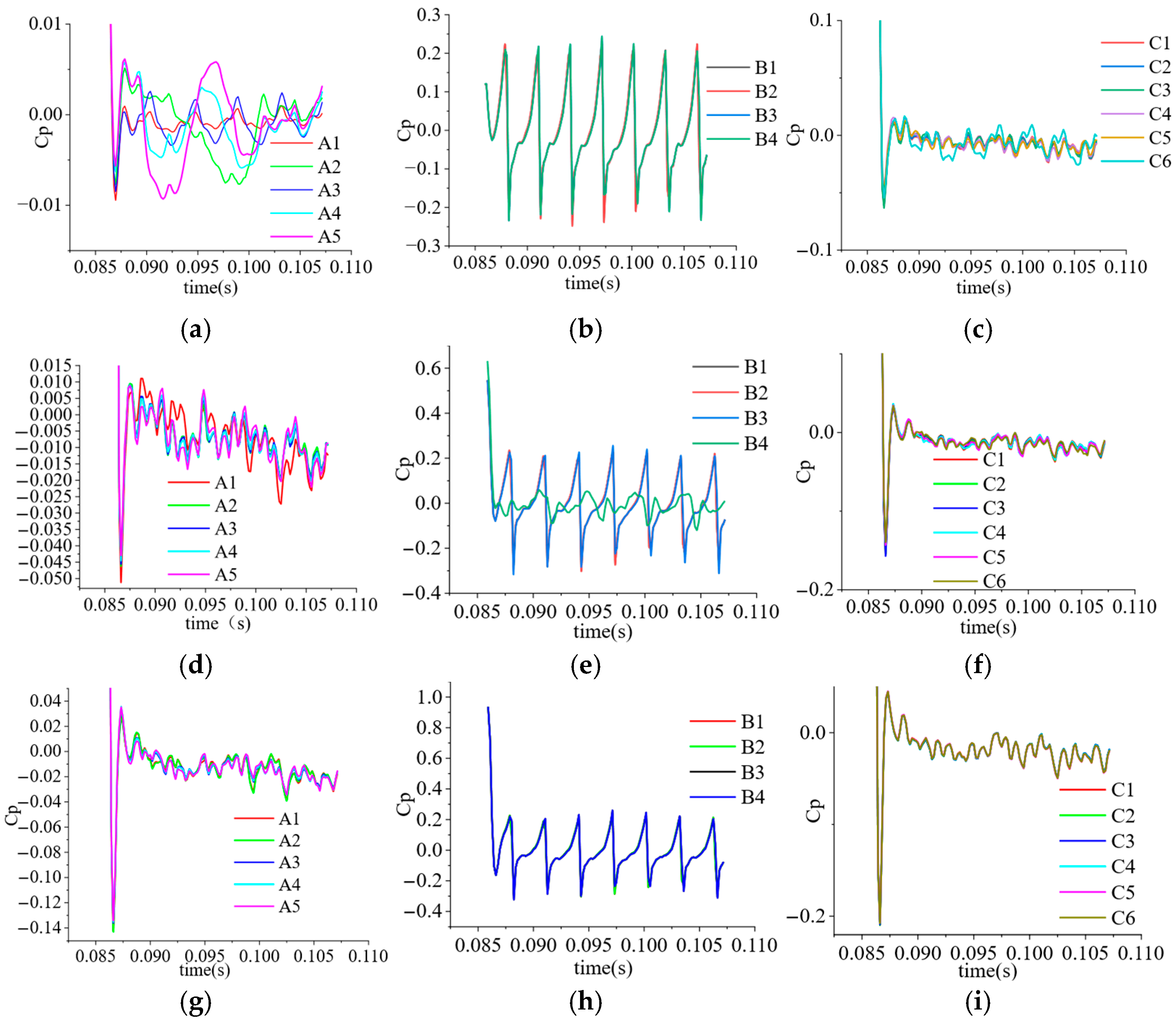
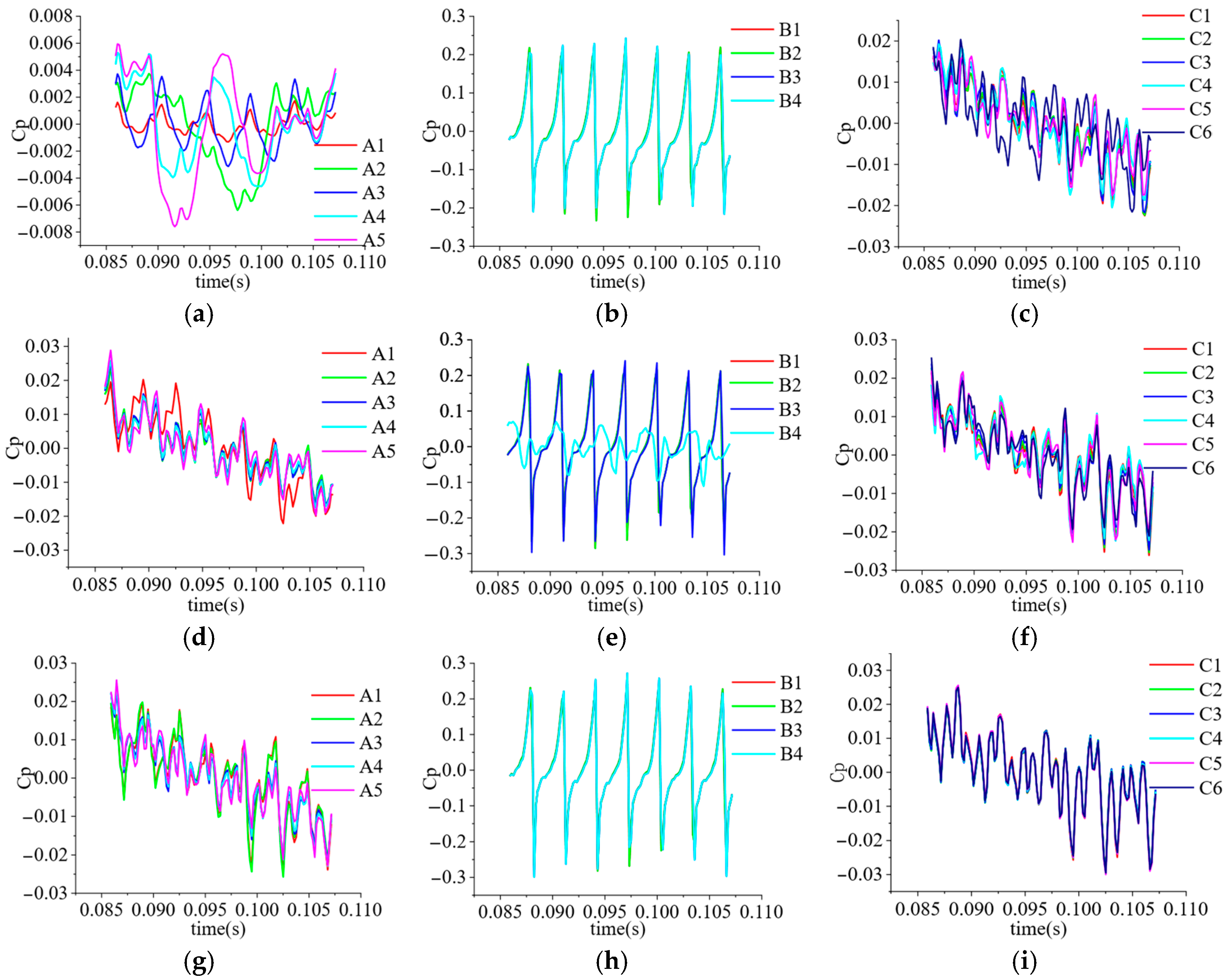
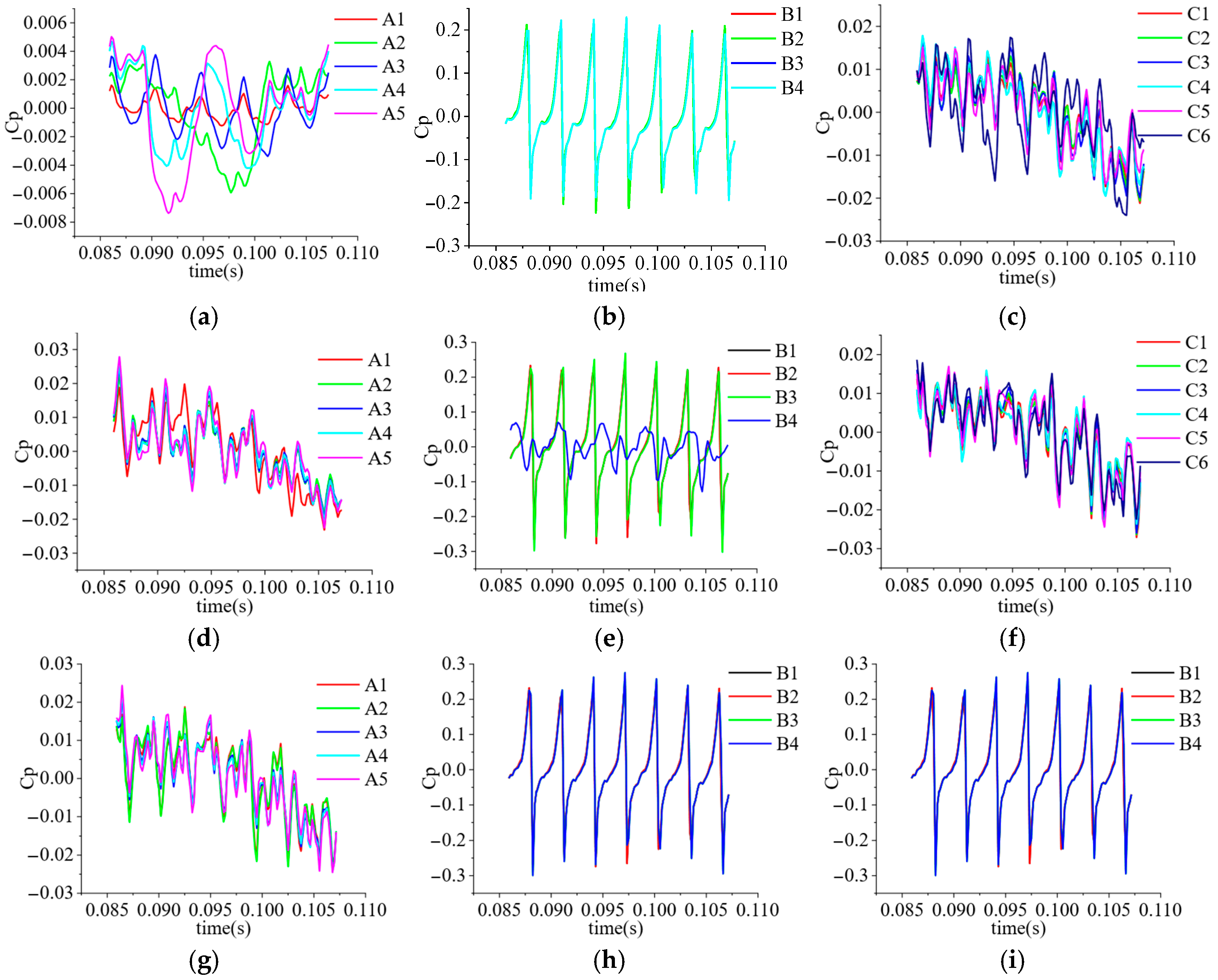
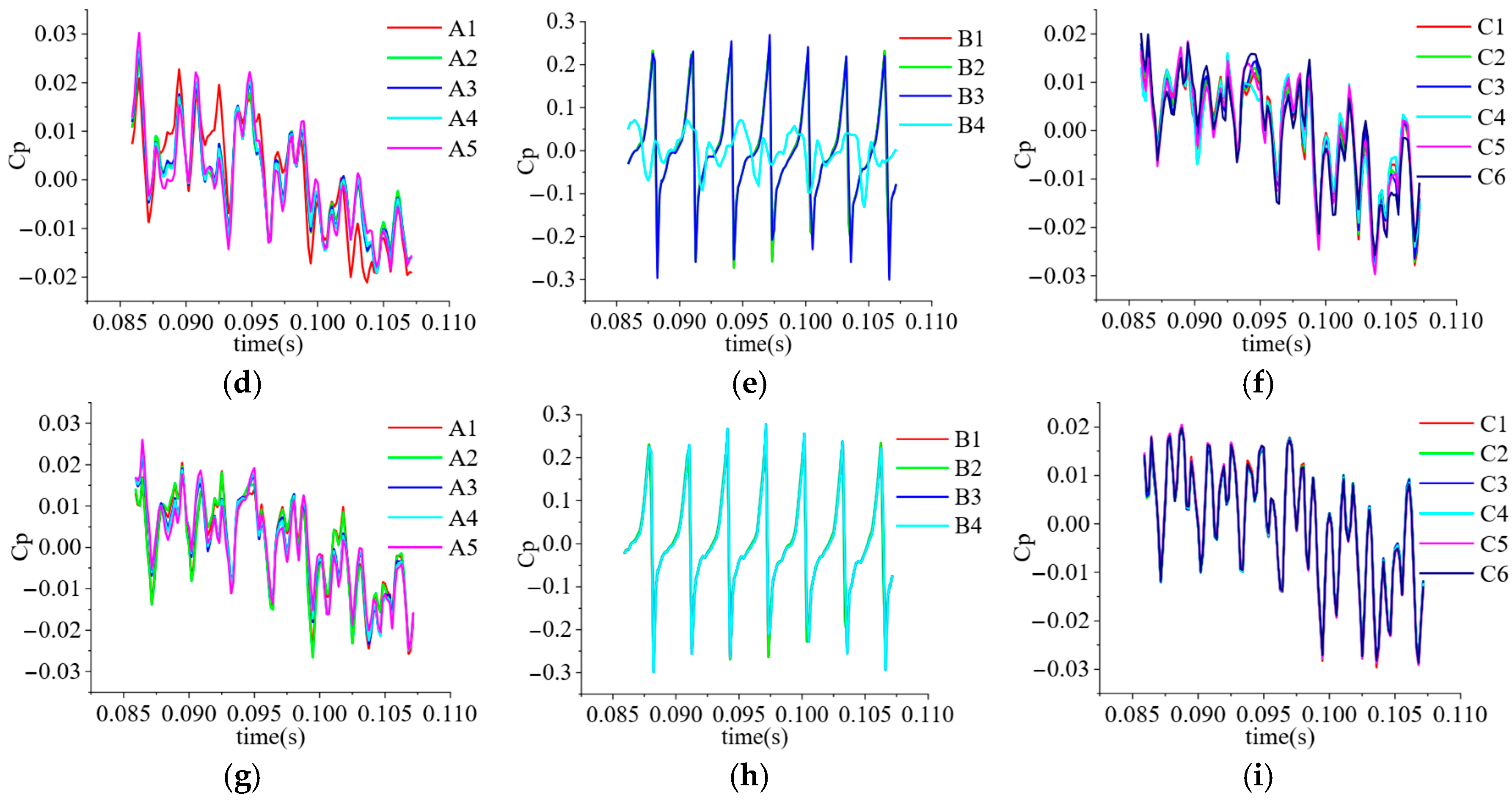
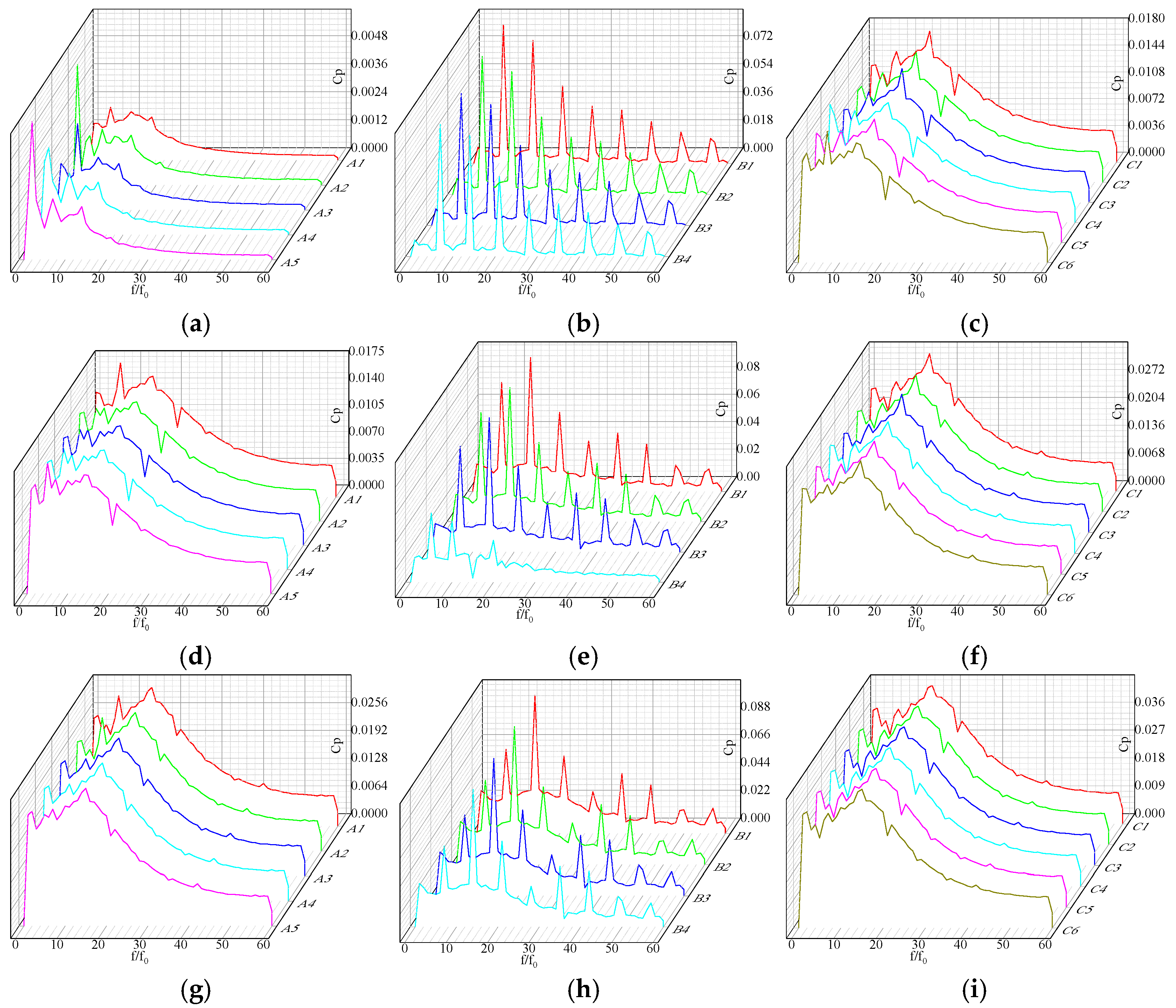
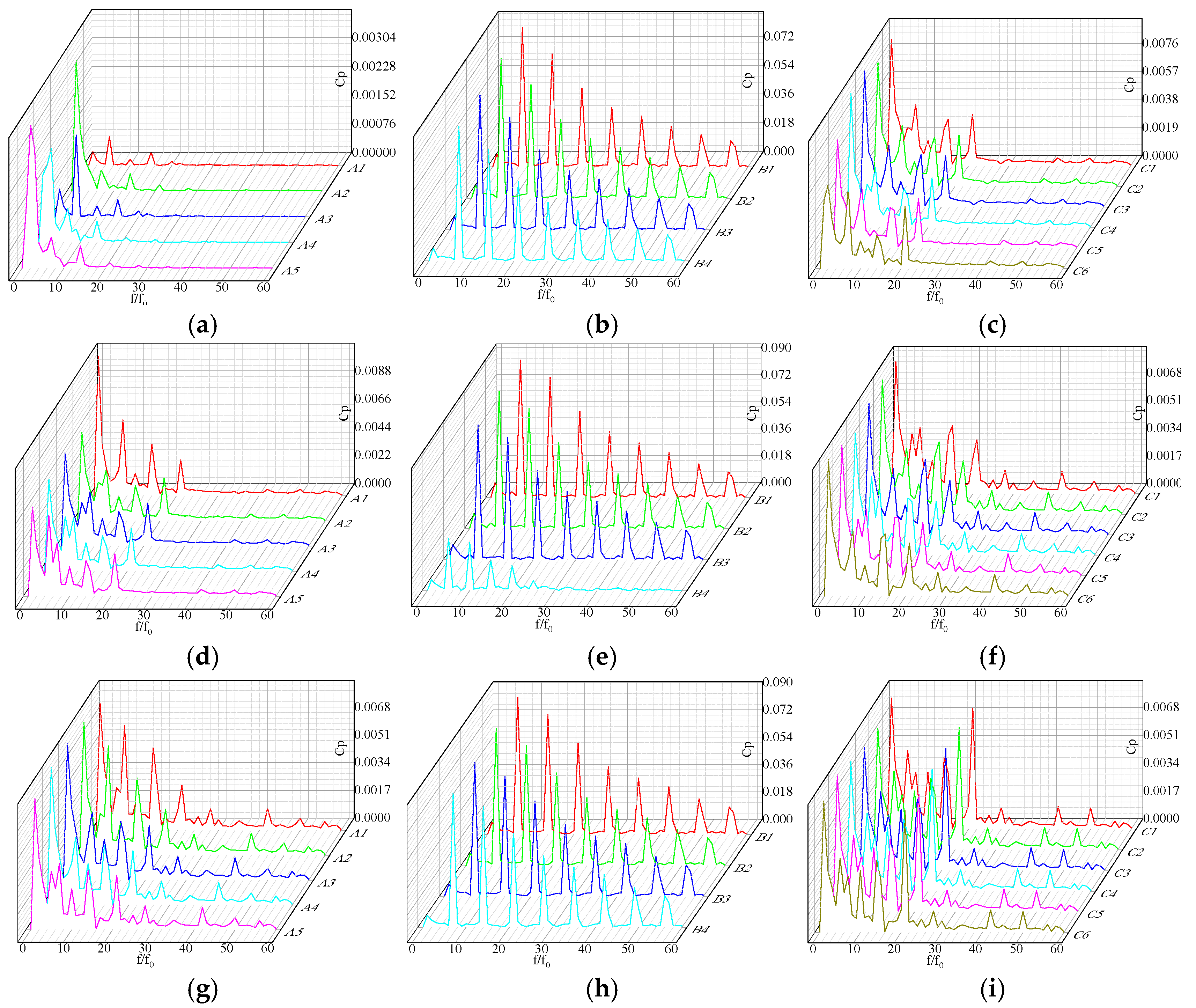
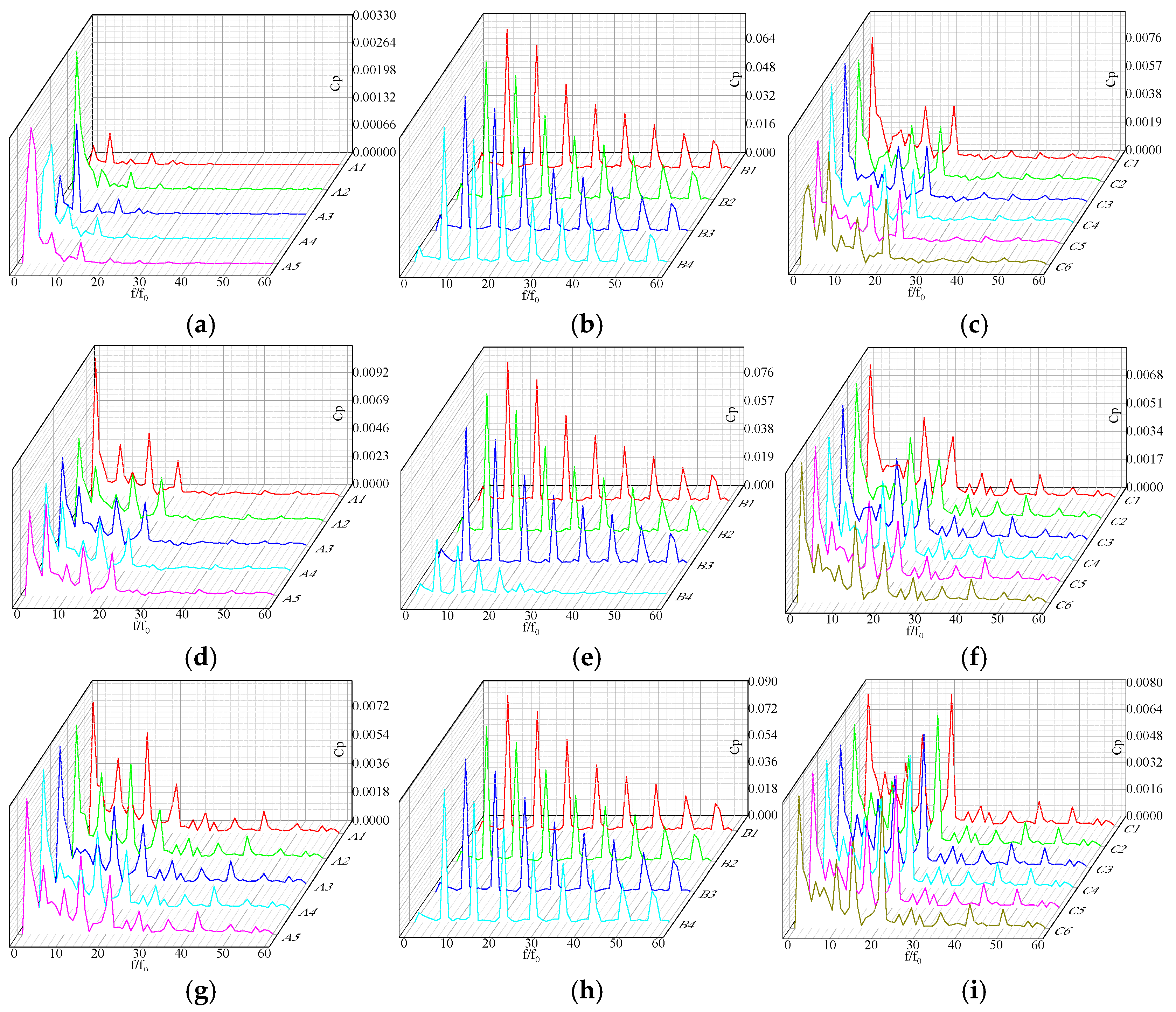
3.6. Pressure Pulsation Analysis
3.6.1. Monitoring Point Setup
3.6.2. Time-Domain Characteristics Analysis of Pressure Pulsation
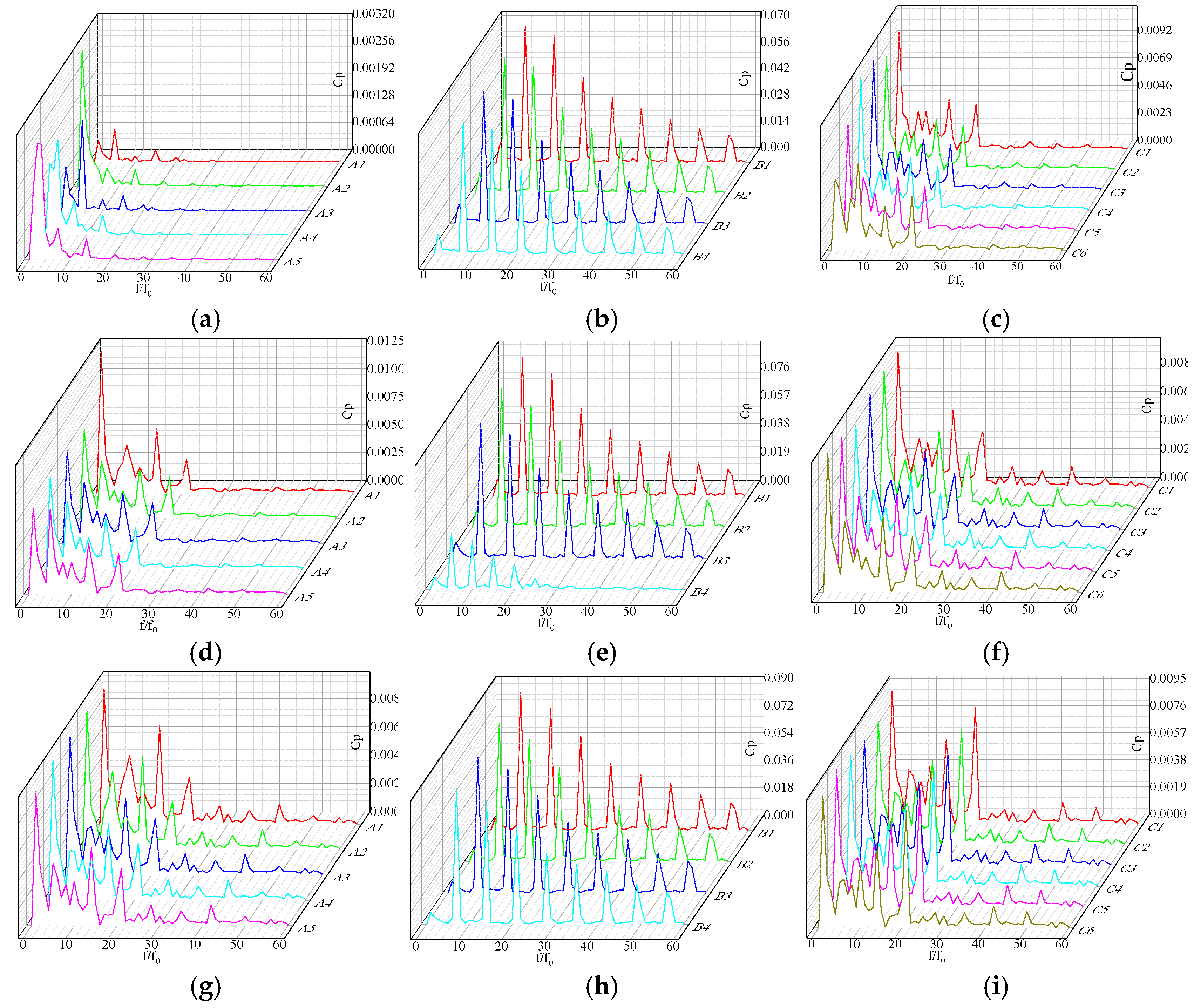
3.6.3. Frequency Domain Characteristics Analysis of Pressure Pulsation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heng, Y.; Chen, Z.; Jiang, Q.; Bois, G.; Zhang, W.; He, K. Performance and internal flow pattern analyses of a specific centrifugal disc pump under air-water two-phase flow conditions. Energy 2024, 309, 132981. [Google Scholar] [CrossRef]
- He, A.; Shao, C. Study on the induced noise of gas-liquid two- phase flow in a centrifugal pump. Appl. Acoust. 2021, 176, 107892. [Google Scholar] [CrossRef]
- Song, X.; Luo, Y.; Wang, Z. Numerical prediction of the influence of free surface vortex air-entrainment on pump unit performance. Ocean Eng. 2022, 256, 111503. [Google Scholar] [CrossRef]
- He, D.; Zhao, L.; Chang, Z.; Zhang, Z.; Guo, P.; Bai, B. On the performance of a centrifugal pump under bubble inflow: Effect of gas-liquid distribution in the impeller. J. Pet. Sci. Eng. 2021, 203, 108587. [Google Scholar] [CrossRef]
- Yan, S.; Luo, X.; Feng, J.; Zhu, G.; Zhang, L.; Chen, S. Numerical simulation of a gas-liquid centrifugal pump under different inlet gas volume fraction conditions. Int. J. Fluid Mach. Syst. 2019, 12, 56–63. [Google Scholar] [CrossRef]
- Yuan, S.; He, W.; Si, Q.; Yuan, J.; Zhang, H.; Cui, Q. Numerical Simulation of Internal Flow in Gas-Liquid Two-Phase Flow Centrifugal Pumps Based on MUSIG Model. J. Drain. Irrig. Mach. Eng. 2021, 39, 325–327. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, K.; Si, Q.; Zhou, B.; Tang, Y.; Jin, Z. Numerical study on Gas-liquid Two-phase Flow in Centrifugal Pumps Based on heterogeneous Flow Model. Trans. Chin. Soc. Agric. Mach. 2017, 48, 89–95. [Google Scholar] [CrossRef]
- Si, Q.; Bois, G.; Liao, M.; Zhang, H.; Cui, Q.; Yuan, S. A comparative study on centrifugal pump designs and two-phase flow characteristic under inlet gas entrainment conditions. Energies 2019, 13, 65. [Google Scholar] [CrossRef]
- Wu, X.; Yang, Y.; Shi, W.; Wu, S.; Jin, Y. Numerical simulation study on flow characteristics of multistage centrifugal pumps under different inlet gas void fractions. Sustainability 2023, 15, 15485. [Google Scholar] [CrossRef]
- Li, C.; Luo, X.; Feng, J.; Sun, S.; Zhu, G.; Xue, Y. Research on the Influence of Inlet Gas Content Rate on the Performance of Deep-sea Multiphase Mixed Transport Pumps. Res. Prog. Hydrodyn. 2020, 35, 248–257. [Google Scholar]
- Cui, Q.; Si, Q.; Bois, G.; Yuan, S.; Yuan, J. Investigation on gas-liquid two-phase flow centrifugal pump performances for different rotational speeds. IOP Conf. Ser. 2019, 240, 16–32. [Google Scholar] [CrossRef]
- Si, Q.; He, W.; Bois, G.; Cui, Q.; Yuan, S.; Zhang, K. Experimental and numerical studies on flow characteristics of centrifugal pump under air- water inflow. Int. J. Fluid Mach. Syst. 2019, 12, 31–38. [Google Scholar] [CrossRef]
- Luo, X.; Yan, S.; Feng, J.; Zhu, G.; Sun, S.; Chen, S. Analysis of Force Characteristics of Gas-Liquid Two-Phase Centrifugal Pump. Trans. Chin. Soc. Agric. Eng. 2019, 35, 66–80. [Google Scholar]
- Guo, Q.; Fei, Z.; Huang, X. Review on Two-Phase Flow in Centrifugal Pumps. J. Drain. Irrig. Mach. Eng. 2025, 43, 238–246. [Google Scholar]
- Fu, Q.; Yuan, S.; Zhu, R.; Chen, J.; Wang, X. Hydraulic characteristics of transient transition process of gas-liquid mixed flow in a centrifugal pump. J. Harbin Eng. Univ. 2012, 33, 1428–1434. [Google Scholar]
- Si, Q.; Guo, Y.; Tian, D.; Ma, W.; Zhang, H.; Yuan, S. Analysis of Internal Flow Characteristics of Semi-open Impeller Centrifugal Pumps under Gas-Liquid Two-Phase Conditions. Trans. Chin. Soc. Agric. Eng. 2021, 37, 30–37. [Google Scholar]
- Tan, M.; Fan, X.; Liu, H.; Wu, X. Research on the Noise Characteristics of Gas-Liquid Two-Phase Flow in Centrifugal Pumps. J. Huazhong Univ. Sci. Technol. 2025, 53, 129–135. [Google Scholar] [CrossRef]
- Verde, W.M.; Biazussi, J.L.; Sassim, N.A.; Bannwart, A.C. Experimental study of gas-liquid two-phase flow patterns within centrifugal pumps impellers. Exp. Therm. Fluid Sci. 2017, 85, 37–51. [Google Scholar] [CrossRef]
- Shao, C.; Zhong, G.; Zhou, J. Study on gas–liquid two-phase flow in the suction chamber of a centrifugal pump and its dimensionless characteristics. Nucl. Eng. Des. 2021, 380, 111298. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, S.; Deng, F.; Liao, M.; Chen, M.; Si, Q. Characteristics of Internal Gas-Liquid Two-Phase Flow in Centrifugal Pumps Based on Dimensional Normalization. J. Drain. Irrig. Mach. Eng. 2021, 39, 451–456+463. [Google Scholar]
- Caridad, J.; Asuaje, M.; Kenyery, F.; Tremante, A.; Aguillón, O. Characterization of a centrifugal pump impeller under two-phase flow conditions. J. Pet. Sci. Eng. 2008, 63, 18–22. [Google Scholar] [CrossRef]
- Pineda, H.; Biazussi, J.; López, F.; Oliveira, B.; Carvalho, R.D.; Bannwart, A.C.; Ratkovich, N. Phase distribution analysis in an electrical submersible pump (ESP) inlet handling water–air two-phase flow using computational fluid dynamics (CFD). J. Pet. Sci. Eng. 2016, 139, 49–61. [Google Scholar] [CrossRef]
- Wang, W.; Li, T. Numerical Analysis of Gas-Liquid Two-Phase Flow in Jet-Type Centrifugal Pumps. Fluid Mach. 2020, 48, 53–57. [Google Scholar]
- Zhang, F.; Zhu, L.; Chen, K.; Yan, W.; Appiah, D.; Hu, B. Numerical simulation of gas–liquid two-phase flow characteristics of centrifugal pump based on the CFD–PBM. Mathematics 2020, 8, 769. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, H.; Deng, F.; Wang, C.; Si, Q. Effect of short blade circumferential position arrangement on gas-liquid two-phase flow performance of centrifugal pump. Processes 2020, 8, 1317. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.; Wang, K.; Zhou, L.; Jiang, X.; Li, Y. Numerical simulation of the sound field of a five-stage centrifugal pump with different turbulence models. Water 2019, 11, 1777. [Google Scholar] [CrossRef]
- Fan, B.; Liang, Z.; Fan, R.; Chen, S. Numerical study on entropy generation of the multi-stage centrifugal pump. Entropy 2022, 24, 923. [Google Scholar] [CrossRef]
- Li, W.; Pan, Y.; Li, H.; Qi, H.; Wu, P.; Lu, D. Research progress on solid-liquid two-phase flow characteristics and erosion of centrifugal pump. J. Drain. Irrig. Mach. Eng. 2023, 41, 109–117. [Google Scholar] [CrossRef]
- Cao, W.; Zhang, Y.; Mao, J.; Cheng, Y.; Zhang, L. Solid-liquid two-phase flow and wear characteristics of high-speed multi-stage deep well pumps. J. Drain. Irrig. Mach. Eng. 2023, 41, 433–439. [Google Scholar]
- Zhang, Z.; Li, Y.; Chen, D. Influence of two-fluid turbulence models on the calculation of solid-liquid two-phase flow field. J. Drain. Irrig. Mach. Eng. 2023, 41, 376–383. [Google Scholar]
- Kong, D.; Pan, Z.; Yang, B. Characteristics of gas-liquid two-phase flow in self-priming pump. J. Drain. Irrig. Mach. Eng. 2022, 40, 15–21. [Google Scholar] [CrossRef]
- Liu, H.; Du, X.; Wu, X.; Tan, M. Numerical simulation on gas-phase characteristics of gas-liquid two-phase flow in pump. J. Drain. Irrig. Mach. Eng. 2022, 40, 238–243. [Google Scholar] [CrossRef]
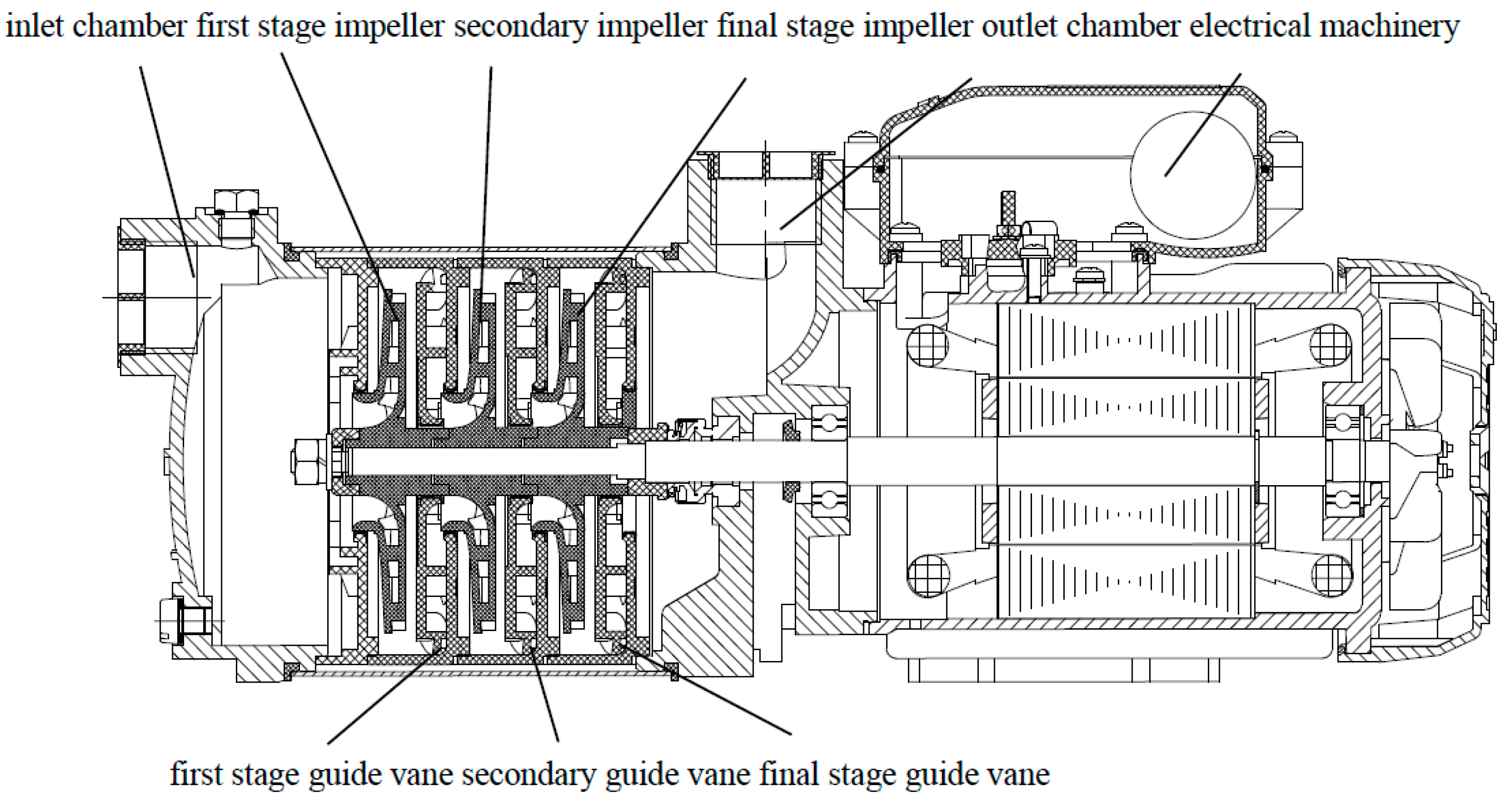
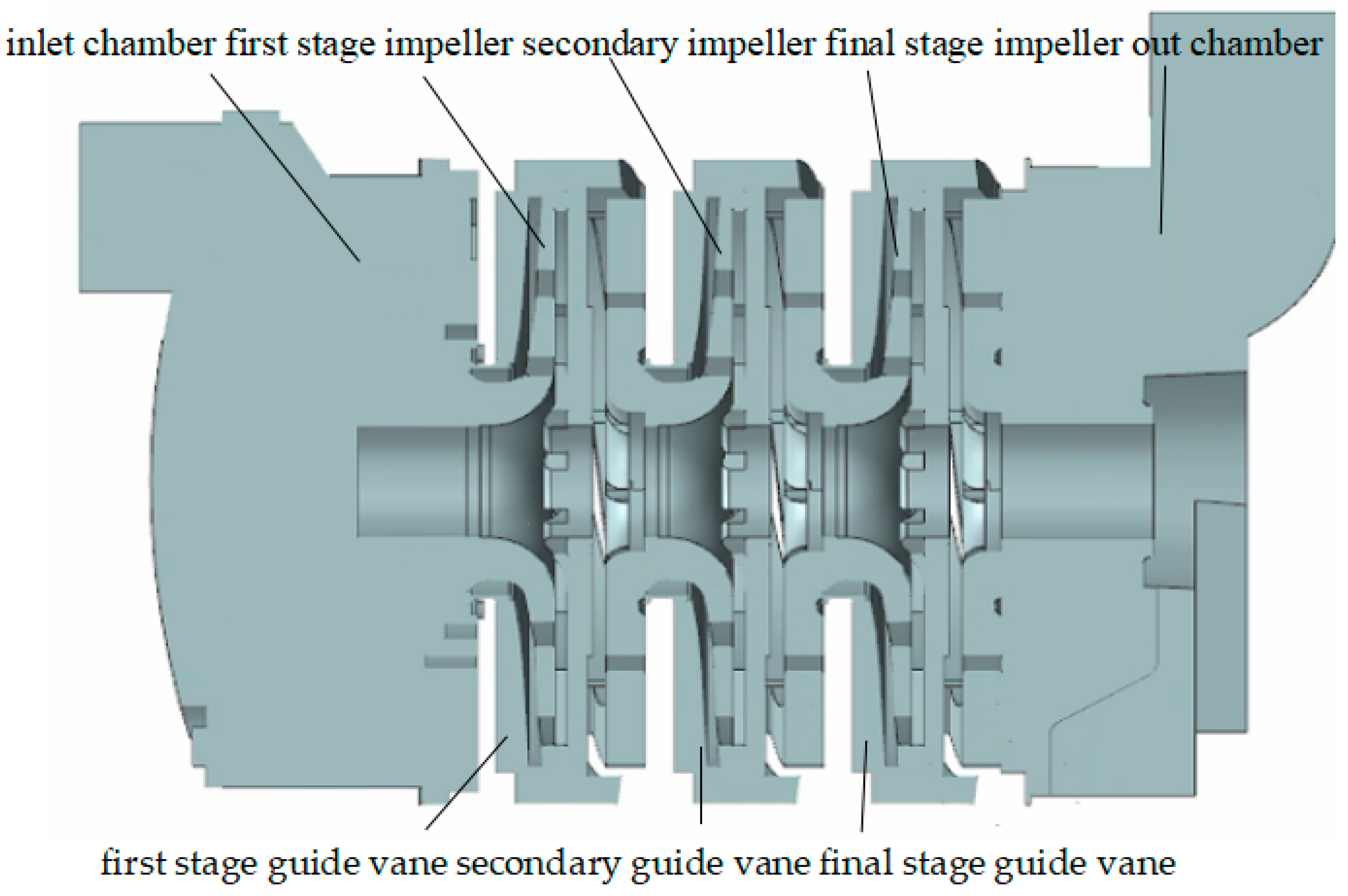
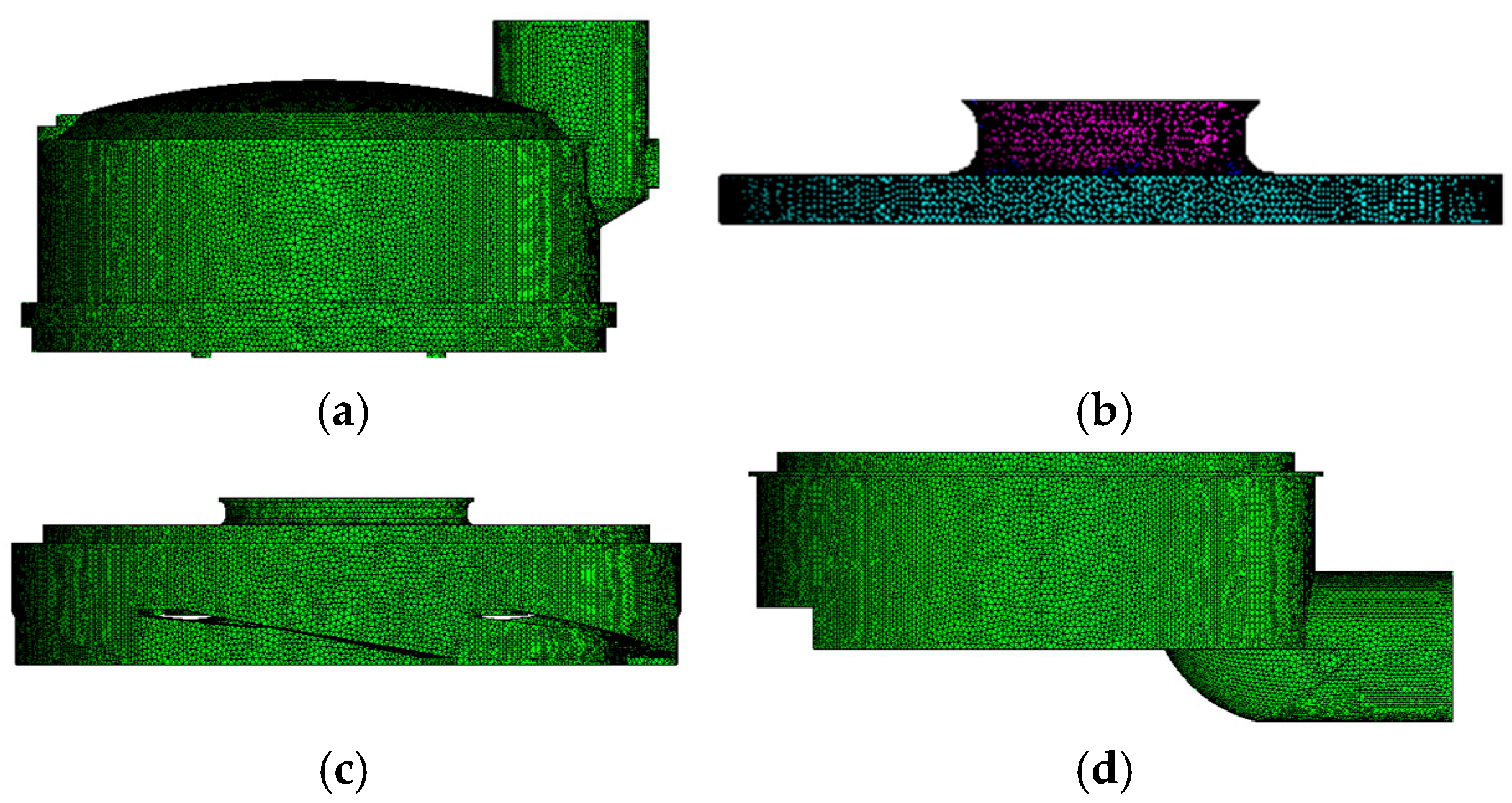
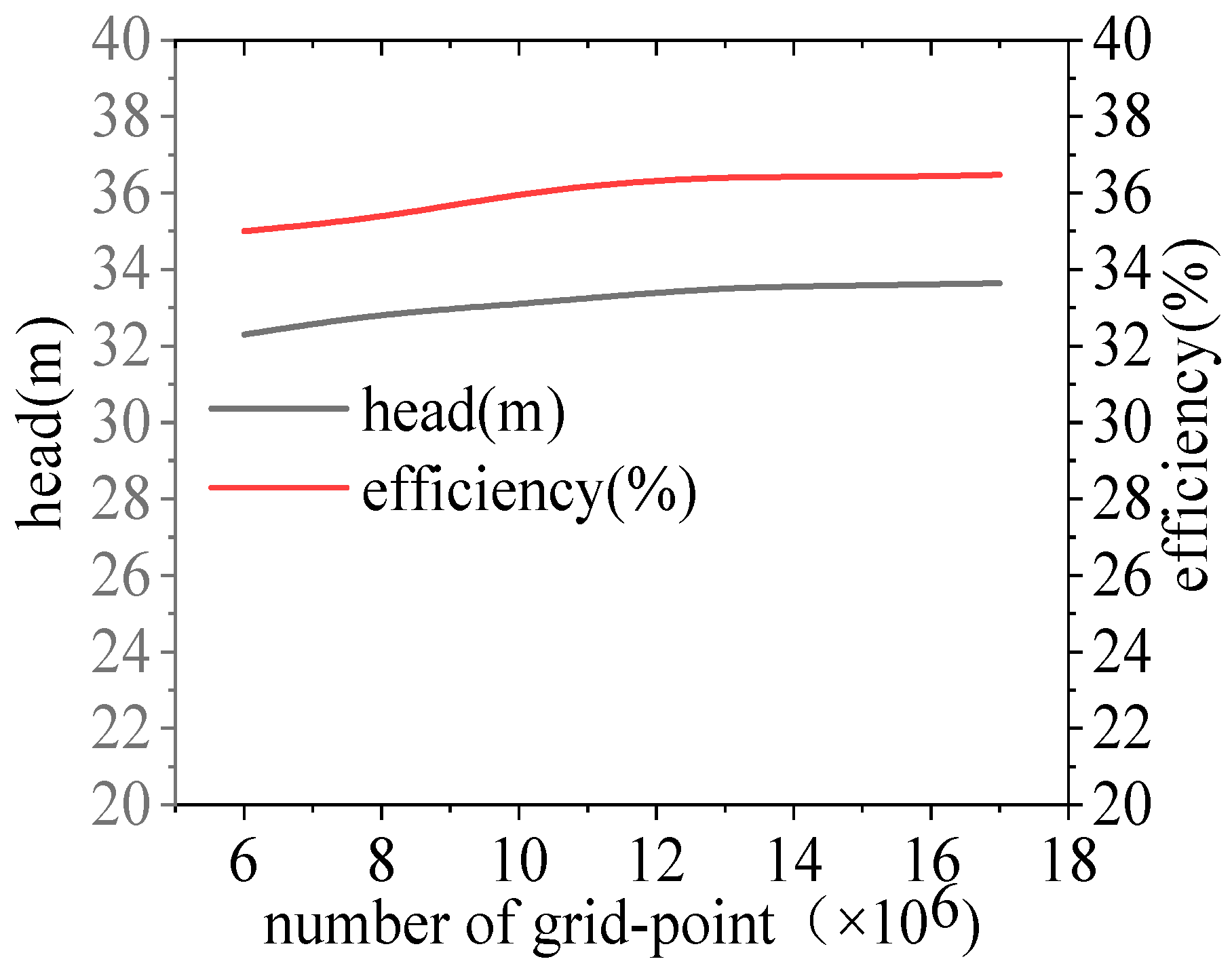





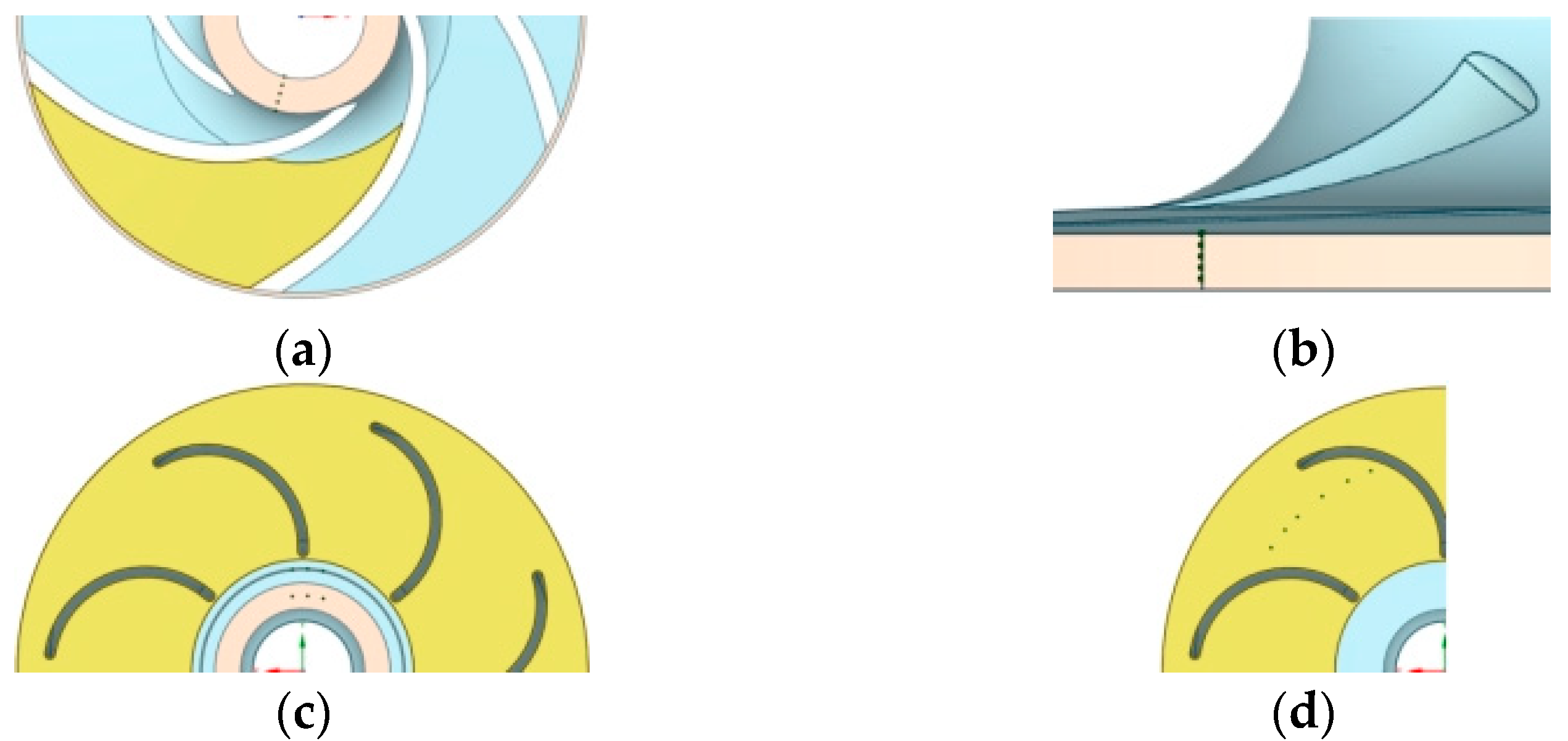

| Parameter | Size |
|---|---|
| inlet diameter of pump | 30 mm |
| outlet diameter of pump | 30 mm |
| inlet diameter of the impeller | 34 mm |
| outlet diameter of the impeller | 98 mm |
| the number of blades | 7 |
| the outlet width of the impeller | 2 mm |
| the base circle diameter of the guide vanes | 110.5 mm |
| the outlet diameter of the guide vanes | 24 mm |
| the number of the guide vanes’ blades | 6 |
| the outlet width of the guide vanes | 6 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Cao, W. Study on the Gas–Liquid Two-Flow Characteristics Inside a Three-Stage Centrifugal Pump. Energies 2025, 18, 4772. https://doi.org/10.3390/en18174772
Zhang X, Cao W. Study on the Gas–Liquid Two-Flow Characteristics Inside a Three-Stage Centrifugal Pump. Energies. 2025; 18(17):4772. https://doi.org/10.3390/en18174772
Chicago/Turabian StyleZhang, Xiang, and Weidong Cao. 2025. "Study on the Gas–Liquid Two-Flow Characteristics Inside a Three-Stage Centrifugal Pump" Energies 18, no. 17: 4772. https://doi.org/10.3390/en18174772
APA StyleZhang, X., & Cao, W. (2025). Study on the Gas–Liquid Two-Flow Characteristics Inside a Three-Stage Centrifugal Pump. Energies, 18(17), 4772. https://doi.org/10.3390/en18174772








