Abstract
Short-term dynamics in auction-based Day-Ahead electricity markets remain insufficiently studied. This paper investigates two such aspects in the Irish Day-Ahead market. First, we address an empirical gap by examining the extent of speculator (financial trader) participation and its evolution over time in a European Day-Ahead setting. Using granular participant-level order and trade data, we quantify speculators’ share of overall market activity and assess how often they are marginal in the auction. Although their share of orders and trades is relatively small, speculators are marginal in a substantial proportion of trading periods and their behaviour changes significantly following a Brexit-related structural shift in market coupling. Second, we introduce a sensitivity-based measure of price inertia defined as the resistance of prices to small changes in demand or supply, adapted to the Day-Ahead auction context, a dimension of market behaviour that has received little prior attention. We find that inertia levels vary considerably and also shift following the structural change. Taken together, these analyses provide empirical evidence that speculators play a non-negligible role in a European auction-based Day-Ahead market, while price inertia offers an additional lens through which to examine short-term market dynamics and their evolution under different market conditions.
1. Introduction
Electricity markets have become a prominent area of academic research in recent decades, driven by transformative developments such as market deregulation, the rapid expansion of renewable generation, and the growing availability of short-term trading opportunities. These changes have spurred research across diverse areas including market power and competition [1,2], price volatility [3], electricity price forecasting [4,5,6,7], portfolio and asset optimisation [8,9], and market dynamics [10]. In many jurisdictions the Day-Ahead (DA) market is one of the main routes to market through which electricity participants hedge or rebalance their positions ahead of physical delivery. DA market prices serve as reference prices for a range of financial derivative contracts and also influence retail electricity pricing. Given its central role, further insights into the functioning of DA markets remain important. This paper contributes to that effort by examining two distinct but interrelated topics within a DA market setting: the activity of financial traders and price inertia, the latter defined as the extent to which market prices resist small shifts in demand or supply. A deeper understanding of these aspects is relevant for regulators evaluating market design and liquidity, as well as for participants active in short-term electricity markets.
As [11] observes, while the role of financial traders in commodity and energy markets has been widely studied, some of the literature exhibits ambiguity in defining financial traders and in specifying the metrics used. In a short-term electricity market context, we refer to financial traders as speculators, defined as participants that neither generate nor consume electricity but instead earn profits or incur losses based on the spread between their buy and sell prices either within the same market or across different market timeframes. While other market participants (e.g., thermal generators, batteries, renewable generation, demand, etc.) may engage in speculative behaviour, we reserve the term speculator for financial traders with no clear consumption or generation role. In several U.S. electricity markets, speculators participate through Virtual Bidding, which allows them to profit from the spread between DA and Real-Time (RT) prices. While Virtual Bidding does not exist in European electricity markets, participants may engage in similar speculative strategies through other mechanisms. For example, in the British market, Net Imbalance Volume (NIV) chasing allows traders to profit from spreads between ex ante prices and balancing market prices [12,13]. Similarly, ref. [2] document speculative behaviour by wind generators in the Iberian market, who exploit price differences across sequential trading periods. In Virtual Bidding related studies, ref. [14] presents instances which would narrow the DA-RT spread with limited system benefits, whereas [15] find a reduction in both the spread and its volatility in California, ref. [16] links lower transaction costs in MISO to greater speculator participation and improved welfare, and [17] highlight reductions in forward premiums constrained by capital and regulatory limits. While this U.S.-focused literature offers valuable insights into price spreads and market efficiency, our study addresses a different and underexplored question: the presence and commercial behaviour of speculators in a European DA market. In contrast to the definitional ambiguity found in some of the broader commodity and energy market literature noted by [11], our analysis offers a clear and transparent framework for identifying speculators and quantifying their presence in a short-term European electricity market setting.
While prior research has examined short-term electricity market price volatility and the occurrence of price spikes, relatively little attention has been given to the concept of price inertia. As introduced earlier, we use this term to describe local price sensitivity to marginal shocks in demand or supply, which is conceptually distinct from volatility: volatility captures variability across periods, whereas inertia reflects price stability in response to incremental changes. We do not address broader notions of inertia that concern long run market stability for example, such as how structural reforms or system integration affect overall price dynamics at the market level. Studies addressing volatility include, among others, refs. [3,18,19,20]. Separately, systematic patterns such as calendar effects have been shown to impact electricity prices [21]. While these reflect broader shifts in demand and supply, our analysis concentrates on marginal, auction-level changes. In terms of inertia in DA markets, studies such as [22,23] touch on the concept indirectly, as their methodologies examine the effect of larger supply shifts on prices. In a DA forecasting context, ref. [24] illustrate how steep supply or demand slopes can generate high price sensitivity to shocks, a similar intuition underlying our measure of price inertia. One rare study to consider market stability explicitly is [25], which finds that increased integration and competition in the Nordic market led to more stable and less volatile prices. While conceptually related, their approach differs methodologically and relies on daily averages, whereas we focus on hourly price data. In this paper, we propose an intuitive and easily understood method for quantifying price inertia in DA markets. Our approach is analogous to liquidity and depth measures familiar from continuous trading, but designed specifically for an auction-based setting.
1.1. Research Questions and Contributions
This paper addresses two distinct but related research questions:
- What is the extent of speculator participation in the market, and how has it evolved over time?
- Can we define a clear and intuitive approach to measuring price inertia, and how has it changed over time?
To address the first question, we use granular participant-level order and trade data to quantify the share of activity attributable to speculators and to measure their influence on price setting, specifically how often their bids or offers equal the market clearing price (i.e., marginality or marginal pricing refers to the mechanism by which short-term electricity market prices are determined [26,27,28,29]). To address the second, we introduce a sensitivity-based method for quantifying DA price inertia using publicly available demand and supply curves. Our findings show that speculators, while a small share of total activity, are frequently marginal in the DA auction. We also observe changes in price inertia after a structural market shift.
The paper contributes in two ways. First, it provides empirical evidence on speculators in a European auction-based DA market, an area largely unexplored in contrast to the extensive U.S. literature. Second, it develops an intuitive and transparent methodology for quantifying DA price inertia, offering a practical lens for assessing how sensitive prices are to small shifts in demand or supply. This metric complements existing volatility measures and has direct relevance for ongoing market design and reform debates e.g., Great Britain’s Review of Electricity Market Arrangements [30,31].
While our methodology is deliberately straightforward and transparent, it is informed by the complexity of the market environment, making an observational, data-driven approach both appropriate and necessary. Key simplifying assumptions are outlined in subsequent sections.
1.2. Paper Structure
The structure of the remainder of the paper is as follows: in Section 2 we present both an overview of the Irish short-term electricity market and related pricing algorithms; we also provide a hypothetical example of a speculator in this setting. In Section 3 we detail the data sources and methodology. Section 4 presents the empirical analyses while in Section 5 we discuss the main findings and note study limitations. In Section 6 we conclude. Supplementary details and materials are available in the accompanying appendices.
2. Market Structure
2.1. Market
The Integrated Single Electricity Market (I-SEM) is the electricity market in Ireland. Although it is a small market (net electricity consumption in Ireland in 2021 was 30 TWh, the equivalent figure for Great Britain was 305 TWh [32]), it typifies spot European wholesale electricity market structures. The Irish electricity market is an example of what is called a multi-settlement electricity market, which is where the bidding and dispatch of electricity for a specific trading period is managed in successive runs. Some of the routes to market, that is, how to buy and sell electrical energy, include
- Day-Ahead (DA) market: at 11 a.m. on day D participants submit orders to buy or sell electricity for hourly delivery periods in the [11 p.m. D, 10 p.m. D + 1] interval. The market coupling algorithm, EUPHEMIA (Section 2.2), takes these inputs, in conjunction with interconnector transmission capacities (and other factors), and determines hourly prices and the direction of energy flow on the interconnectors. If the network is congested then zonal prices will diverge.
- Intraday (ID) market: after the DA auction has cleared additional auctions are held; these auctions, IDA1, IDA2, and IDA3 are similar in nature to the DA with the main differences being that they are held closer to the delivery time and the delivery periods are 30 min intervals; IDA1/IDA2/IDA3 auctions cover the [11 p.m. D, 10:30 p.m. D + 1]/[11 a.m. D + 1, 10:30 p.m. D + 1]/[5 p.m. D + 1, 10:30 p.m. D + 1] time horizons respectively.
- Intraday Continuous (IC) market: this is an important market in other European jurisdictions, but in an Irish electricity market context, it comprises less than half a percent of traded energy volumes over the study timeframe and hence it is ignored here.
- Balancing (B) market: one hour prior to delivery trading opportunities cease and the Transmission System Operator, TSO, takes over (ex-ante in this context means occurring before the delivery period, ex-post means that it occurs after the delivery period). The TSO compares forecast demand versus forecast generation, including what volumes have been traded in the ex ante markets, and dispatches on/off units to ensure that supply meets demand. The prices that result from these dispatch decisions are called settlement imbalance prices (or balancing market prices).
Securing a physical position in the Irish electricity market requires participation in one of the above markets. The market structure therefore provides a non-trivial level of (DA) liquidity.
An important structural market change occurred during the study period. Throughout this period, the electricity markets in Ireland and Great Britain were connected via two interconnectors. Before Great Britain’s departure from the EU, these markets were coupled in the DA and IDA1 auctions; from 1 January 2021 onward, the coupling shifted to the IDA1 and IDA2 auctions [33,34].
2.2. Pricing Algorithm
This section briefly introduces the DA pricing algorithm. Unlike a simple intersection of aggregated demand and supply curves, the actual market clearing process is considerably more complex and a full technical specification (including implementation details) is not publicly available. This combination of algorithmic complexity and limited transparency motivates our use of a deliberately straightforward observational approach when analysing speculator behaviour (Section 3.2). We also note that our price inertia analysis (Section 3.3) relies on a simplifying assumption that abstracts from the full market clearing process.
EUPHEMIA, the Pan-European Hybrid Electricity Market Integration Algorithm, is used to calculate hourly DA prices in a number of European markets. According to the EUPHEMIA Public Description [35]:
- “The algorithm can handle a large variety of order types at the same time”, including Aggregated Hourly Orders, Complex Orders (e.g. with Minimum Income Condition or Load Gradient constraints), Scalable Complex Orders, and Block Orders.
- The algorithm solves a Welfare Maximisation Problem (Master Problem) together with three interdependent sub-problems, one of which is the Price Determination Sub-Problem. In the Master Problem, “EUPHEMIA searches among the set of solutions for a good selection of block and MIC orders that maximises social welfare. Once an integer solution has been found for this problem, EUPHEMIA moves on to determine the market clearing prices.”
From this description it is clear that treating the DA auction simply as the crossing of bid and ask curves, while intuitive, omits the complexities of the actual clearing algorithm. EUPHEMIA is also subject to ongoing incremental changes [36,37], making it a dynamic rather than static construct. In contrast, the algorithm governing the Irish balancing market is fully documented and publicly available [38]. For the British electricity market, Elexon provides similar imbalance pricing guidance in [39].
2.3. Speculators
In the following hypothetical example, the speculator buys in the DA and IDA1 markets and sells in the balancing market. More generally, the opposite scenario also occurs, where a speculator sells in the ex ante markets and buys in the balancing market (speculation may also occur between the DA and intraday markets). Consider a speculator active in a single delivery hour (10:00–11:00). Recall that the DA market settles in hourly blocks, while the IDA1 and balancing markets settle in half-hourly blocks. Suppose the speculator forecasts prices of EURX/MWh in the DA for 10:00–11:00 and in each IDA1 half hour (i.e., 10:00–10:30 and 10:30–11:00), and expects the corresponding balancing market price to be EUR/MWh in each half hour. The speculator decides to buy 50 MW in the DA, and an additional 25 MW in each half-hourly block in the IDA1 market, giving a total ex ante position of 75 MW as shown in Figure 1. Since the speculator neither generates nor consumes electricity, its position in the balancing market is the opposite of these purchases. If its forecasts are correct, its income from the balancing market of EUR will be greater than its total costs of EUR from its DA and IDA1 positions, thereby earning a profit of EUR 1500.
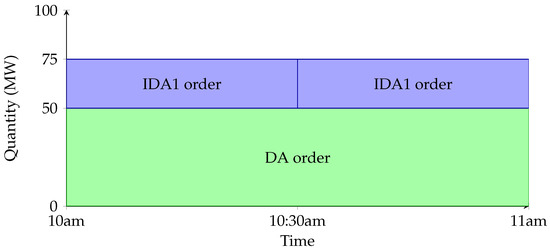
Figure 1.
Speculator hypothetical example.
3. Materials and Methods
In this section we describe the underlying datasets and the empirical analyses. The study period spans a diverse set of energy price regimes, including the COVID-19 pandemic which resulted in a low-price commodity environment at the outset of the pandemic [40,41]. and the European energy crisis. Any reference to accompanying material in the appendices is for replicability and transparency purposes, with the key details captured here.
3.1. Datasets
All datasets used in this study are publicly available and can be accessed through SEMOpx and SEMO [42,43] (with some additional reference material provided in Appendix M). For context, SEMOpx and SEMO are two of the bodies involved in the operation of the Irish electricity market. Some of the datasets they publish include the following:
- Granular Participant Data: For each of the four ex ante markets (Section 2.1), SEMOpx publishes an ETS Bid File containing participant-level order and trade data by trading period. Positive (negative) values denote purchase (sell) orders, with the same convention for trades. For example, the DA ETS Bid File is published on a day + 1 basis and typically exceeds 20,000 rows, with over 300 participants per auction.
- Bid Ask Curve Data: For each ex ante auction, SEMOpx publishes a BidAskCurve file showing an anonymised, monotonic view of buy and sell orders by trading period. Since July 2021 a single file per auction has been published, with bid and ask data in EUR/MWh. Previously, separate files were released: one in GBP/MWh for Northern Ireland (NI) and one in EUR/MWh for the Republic of Ireland (ROI).
- Other Data:
- −
- PUB_MnlyRegisteredCapacity files which provide participant registration data such as registered plant capacity and FuelType (if applicable).
- −
- PUB_30MinImbalCost file containing the balancing market price, , for trading period i. Similarly, MarketResult files containing DA, IDA1, IDA2, and IDA3 market prices (i.e., , , , and ).
In the Irish electricity market, participants may register a variety of unit types, including Supply, Generator, Assetless, and Trading. Because these units can behave flexibly, we follow the steps outlined in Appendix B to identify speculators. As explained there, the procedure was developed iteratively, including interrogation of participant samples to ensure robust cohort allocation. As a further check, we manually reviewed all participants classified as speculators to confirm the appropriateness of their assignment. The procedure does not capture every possible speculative action, and consistent with our conceptual definition in the introduction, does not include participants with obvious generation or consumption roles who may also act speculatively. Nevertheless, it provides a transparent and reproducible framework. Alternative classification approaches are possible, and these caveats are noted in both the Limitations section and Appendix B.
3.2. Market and Speculator Analysis
3.2.1. Quantities
Across the ex ante markets (DA, IDA1, IDA2, IDA3, and IDC), the DA auction dominates, accounting for circa 85% or more of traded volumes. The next largest market is IDA1 (up to about 11%), while IDA2, IDA3, and the Intraday Continuous market together contribute only a negligible share (see Appendix M for supporting information). Given this split, our analysis focuses primarily on DA activity, with IDA1 and the smaller markets providing additional context where relevant. Using the DA ETS Bid Files we derive, for each trading period, two time series:
- Order quantities: the volumes participants were willing to buy or sell.
- Matched quantities: the volumes actually bought or sold.
3.2.2. Marginal Participants
To understand which participants are marginal and whether or not this pattern has changed over time for each trading period (see Appendix D for details), we perform the following:
- We retrieve the bid and ask curves from the relevant BidAskCurve file and determine how they intersect.
- The intersection point(s) are then cross-referenced against the participant order data in the relevant ETS Bid File to determine which unit, or units, are marginal.
A by-product of the marginal analysis is the identification of bid and ask curve intersections. As a result, in addition to identifying marginal participants we also examine how DA bid and ask curves intersect and how these intersection patterns have evolved over time. Given the stepwise nature of the bid and ask curves in the Irish electricity market there are three possible types of intersection: horizontal (the curves are horizontally parallel and intersect over a ranges of quantities), vertical (the curves are vertically parallel and intersect over ranges of prices), and perpendicular (the curves intersect perpendicularly at a single price and quantity point). For a perpendicular intersection, if at the point of intersection the ask curve is horizontal, ACH, we denote it as a perpendicular (ACH) intersection. Similarly, if at the point of intersection the bid curve is horizontal, BCH, we denote it as a perpendicular (BCH) intersection. In Appendix E we provide examples of different bid ask curve intersection types.
3.2.3. Aggregate Speculator Behaviour and Profitability
To examine how aggregate speculator behaviour has evolved, we begin with their DA order (i.e., pre-clearing) quantities referenced in Section 3.2.1. Rather than comparing order quantity distributions across time (e.g., using kernel density estimates), we take a simpler approach that still captures the main trends. For trading period i, let the DA market price be and the standard deviation of DA prices for the corresponding hour over the previous 20 days be . We partition the price domain into three intervals:
- Interval 1: ;
- Interval 2: ;
- Interval 3: .
Here −500 and 3000 are the minimum and maximum permissible DA prices. We note that over the course of the study the maximum DA price rose in stages from EUR 3000/MWh to EUR 5000/MWh; in our analysis, all orders are capped at EUR 3000/MWh. For each interval we calculate the sum of speculator sell orders, and separately buy orders, falling within that range. These values are then aggregated by month, and we plot the monthly totals from November 2018 to December 2022.
Next, we consider aggregate matched (i.e., cleared) speculator quantities. Our main focus is DA, but motivated by the structural market change (Section 2.1) and the hypothetical example (Section 2.3), we also examine IDA1 and balancing market values. Let Speculator denote the set of speculator participants and the matched quantity for trading period i by speculator j in market m. We define
We compute these for each trading period and use pair plots to compare behaviours before and after the structural change (IDA2/IDA3 are omitted given their negligible volumes). Note that the index i in Equations (1)–(3) refers to different temporal granularities depending on the market (hourly for DA, half-hourly for IDA1 and BM), but since the values are expressed in power (MW), we are still comparing like with like in the pair plots.
Ignoring minimal transaction costs, speculator j’s profit or loss is estimated by
where is the price in market m for period i. Since we sum across markets with different temporal granularities, we take the lowest resolution, so i in Equation (4) corresponds to a half-hourly settlement period. The negative sign reflects the buy/sell convention. Given that is expressed in power (MW), when multiplying by prices (EUR/MWh) and accounting for the half hour duration, we multiply by to convert from MW to MWh. We repeat this calculation for all speculators and periods to obtain aggregate profitability.
3.3. Price Inertia Analysis
We measure price inertia in the Irish DA market by applying a small horizontal shift to the bid or ask curve and calculating the resulting intersection price. The difference from the actual market price provides our inertia measure. In principle this would require a full rerun of the EUPHEMIA algorithm. However, given that our shifts are small (1 MW or 10 MW, minor relative to average forecast demand of 4300 MW per period over the study horizon) and the algorithm is not publicly available, we adopt the simplifying assumption that a rerun is unnecessary. This approach is consistent with the existing literature where similar approximations are used in fundamental supply stack models [44,45] and curve-based simulations [24,46]. For trading period i, the process of shifting the DA ask curve by X MW is:
- Retrieve the bid and ask curves from the DA BidAskCurve file.
- Add X MW to each point on the ask curve.
- Identify the intersection with the bid curve; call the resulting price the simulated DA price .
Interpreting the raw price difference time series alone can be misleading given the very different price regimes over the study horizon (see Appendix N Figure A10). To normalise, one option is to divide by , but this fails when prices equal EUR 0/MWh. Instead, we divide by the standard deviation measure (Section 3.2.3), though alternative normalisations are possible. While we report results for positive shifts to the ask curve, we also tested negative shifts and bid curve shifts (±1 MW, ±10 MW); the results were qualitatively similar and are omitted for brevity.
Finally, we extend this baseline approach with two related methods: one that examines the distribution of price inertia and another that uses speculators’ order data to estimate inertia (akin to applying shifts directly to the bid or ask curve). We note that in these extensions the small shift assumption may not always hold.
3.3.1. Price Inertia Distribution
- For each trading period, adjust the ask curve in MW increments until the simulated market price, , differs from the published market price. Let denote the shift required to observe the price change where the MW superscript indicates that we have used MW increments. Use Equation (5) to calculate the associated price difference, which we denote as .
- Repeat with MW decrements to derive the corresponding and Price values.
- For each trading period, define and calculate the Min Shift and Price Impact via
A graphical illustration of this procedure is provided in Appendix J Figure A6. While alternative analytical derivations of Min Shift and Price Impact may be possible, we adopt this simple numerical approach for transparency and reproducibility.
3.3.2. Order Example
This approach involves removing the order data for a single (speculator) participant, reconstructing the bid and ask curves using the remaining participants’ order data, and determining the new intersection price. Implementation details for this alternative approach and related examples are provided in Appendix L.
4. Results
4.1. Market and Speculator Analysis
4.1.1. Quantities
Figure 2 shows stacked area charts of DA sell order and sell matched quantities (Section 3.2.1) in TWh, grouped by FuelType. See Appendix H for details on FuelType notation and month. The dashed vertical line marks the structural market change (Section 2.1); sells are represented by negative quantities. On average, 52% of sell order quantities are matched. For conciseness we omit the buy side plots, but note that about 83% of buy orders are matched. The absence of Coal, Oil, and Distillate categories from matched quantities in certain periods reflects the DA merit order in the Irish market.
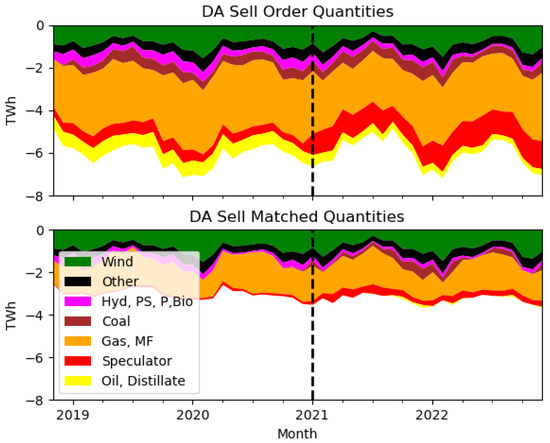
Figure 2.
Irish DA market sell order quantities (top) and sell matched quantities (bottom), in TWh, grouped by FuelType and month. The dashed line marks the Brexit-related structural change.
The speculator sell order and matched quantities (red series) are seen to increase after the structural market change. Pre-change, speculators accounted for ∼10% of DA order quantities and ∼2% of matched quantities; post-change these shares rose to ∼20% and ∼6%. The number of active speculators also increased: before the change an average of 16 (14) submitted sell (buy) orders per day, rising to 30 (24) afterward; this is almost a doubling. For context, the DA market hosted 472 distinct participants over the study period.
Table 1 summarises these statistics. We note in passing that speculators’ relative share is larger in IDA1, averaging 54% (42%) of buy (sell) order quantities and 46% (33%) of buy (sell) matched quantities, though IDA1 is much smaller in size than the DA auction.

Table 1.
Speculator participation in the Irish DA market. Note: DA accounts for circa ≥ 85% of ex ante traded volumes, IDA1 up to ∼11%, and the remainder is split across IDA2, IDA3, and the continuous market.
4.1.2. Marginal Participants
The top plot in Figure 3 shows the percentage of marginal observations, grouped by FuelType and month. Gas and multi-fuel units exhibit a declining tendency to be marginal, falling from about 35% of trading periods before the structural change to around 20% after. In contrast, speculators appear marginal more often, rising from 49% to 66%. That speculators are marginal in a large proportion of trading periods contrasts with their overall minority share of market activity noted earlier.
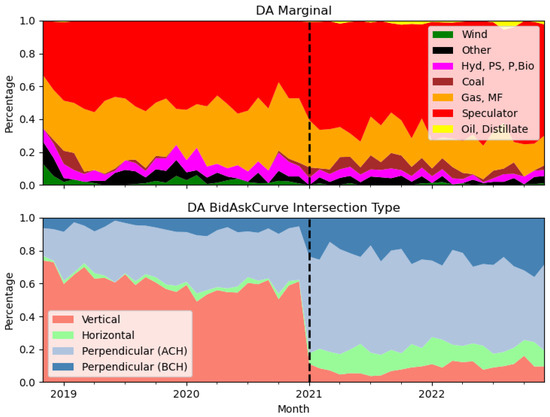
Figure 3.
(Top): percentage of marginal observations in the DA market grouped by FuelType and month. (Bottom): percentage of DA bid and ask curve intersection types by month.
The bottom plot in Figure 3 shows how DA bid and ask curve intersection types (vertical, horizontal, or perpendicular) evolved over time, with a marked change after the structural shift.
4.1.3. Aggregate Speculator Behaviour and Profitability
To examine aggregate pre-clearing behaviour, we sum DA speculator sell order quantities from the top plot in Figure 2 (red series) and split them by price interval (Section 3.2.3), shown in the top plot of Figure 4. For comparison, the bottom plot shows the same breakdown for non-speculators. For speculators, much of the post-change increase in sell orders is concentrated in the interval (orange series), whereas the non-speculator data show no clear step change. Plots of buy orders by interval (Appendix I, Figure A3) show similar patterns, with only a slight, visually imperceptible uptick in non-speculator buy orders within the interval after the structural change. We note in passing that on average 97% of non-speculator buy volumes lie in , highlighting the inelasticity of demand.
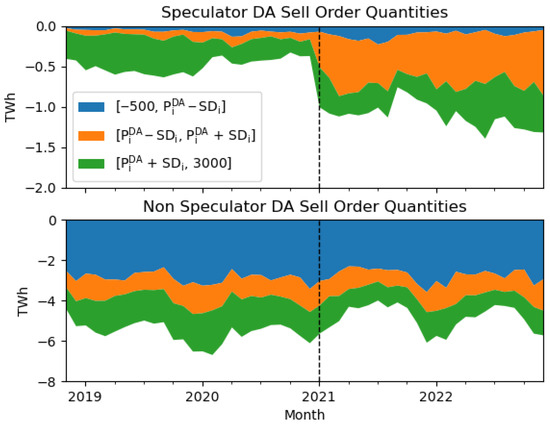
Figure 4.
(Top) plot presents speculator sell order quantities grouped by price interval and month. (Bottom) plot presents corresponding data for non-speculators. Values are in TWh; note the different y-axis scales.
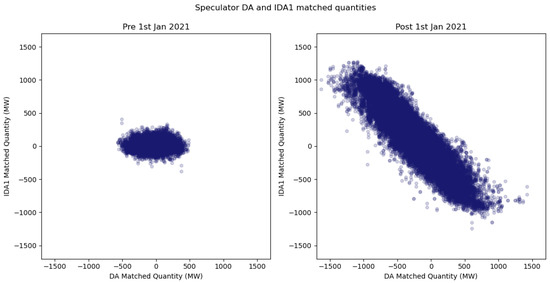
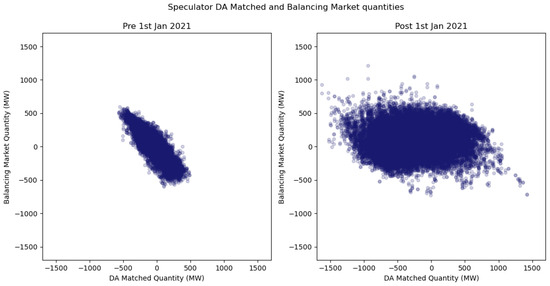
Figure 5 plots Speculator IDA1 Matched Quantities, Equation (2), against DA Matched Quantities, Equation (1), distinguishing pre- and post-change observations. Post-change, the magnitude of DA positions increased, and a negative correlation emerges: DA matched quantities are often partially or fully unwound in IDA1. Similarly, Figure 6 shows balancing market quantities, Equation (3), against DA matched quantities. Here, a negative correlation is evident before the change, whereas post-change the relationship is less clear.
To illustrate aggregate speculator behaviour after January 2021 and highlight their commercial dynamism, Figure 7 presents a two-week granular time series. The top plot shows Speculator DA Matched Quantities (green) and IDA1 Matched Quantities multiplied by (brown), denoted as IDA1 Matched Quantity (inverted). The visible correlation indicates that DA positions are often, though not always, offset in IDA1. The middle plot shows balancing market quantities, which are smaller in magnitude since DA positions are frequently unwound in IDA1. Finally, the bottom plot splits DA matched quantities into buys and sells, revealing heterogeneity across speculators. Taken together, these plots underscore the dynamic and non-stationary nature of speculator activity in the Irish electricity market.
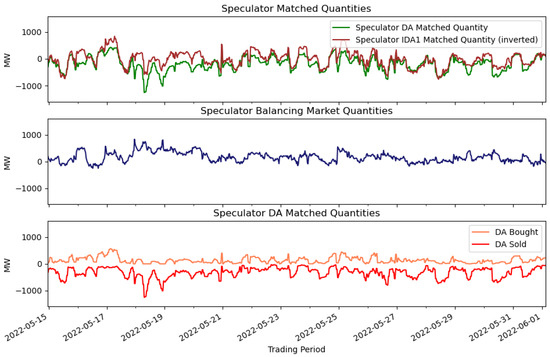
Figure 7.
Speculator time series plots for a sample timeframe (units in MW). The top plot corresponds to Equations (1) and (2), with the latter inverted (i.e., multiplied by ). The middle plot corresponds to Equation (3). In the bottom plot, Speculator DA Buy and Sell Matched Quantities are shown separately.
Using Equation (4), aggregate speculator profit and loss (P&L) from November 2018 to December 2022 is estimated at EUR 76.8 million. Over the same period, close to EUR 21.76 billion of energy was traded in the ex ante markets (see Appendix M. Of this total, EUR 66.2 million relates to 2021–2022. Speculators taking opposing positions in ex ante markets (Appendix G) contributed an estimated EUR 29.9 million. At a granular level (by speculator and trading period), cash flows were positive in about 54% of cases and negative in 46%, underscoring that speculation in short-term electricity markets is not a risk-free activity.
4.2. Price Inertia Analysis
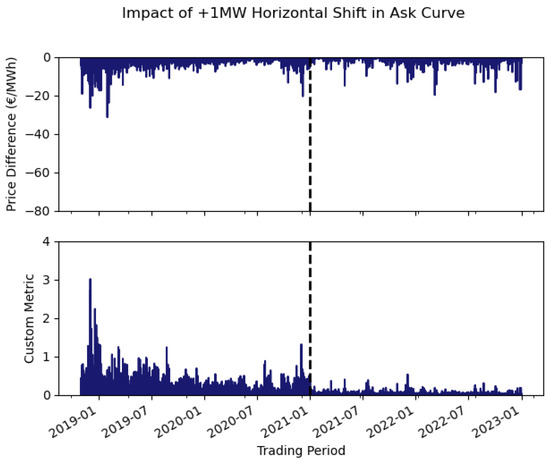
Using bid and ask curves from November 2018 to December 2022, we apply a +10 MW horizontal shift to the ask curve and calculate the percentage of trading periods per day with a price difference of EUR 0/MWh (Equation (5)). Figure 8 shows a clear step change in the share of zero price difference observations after the structural market change.
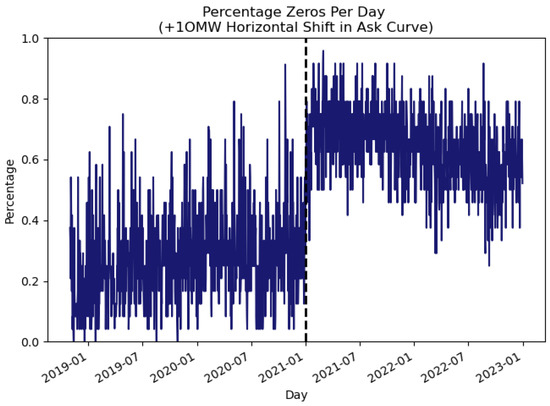
Figure 8.
Percentage of trading periods per day where the price difference values, defined by Equation (5), are EUR 0/MWh.
Figure 9 presents the corresponding time series: the top plot shows price differences by trading period, and the bottom the Custom Metric (Equation (6)). The Custom Metric indicates a reduced impact of horizontal shifts from 2021 onward. Overall, a +10 MW shift altered the market price in about 72% of trading periods before 1 January 2021, compared with 36% after. Where prices changed, the average reduction in DA price was 3.6% pre-change and 0.8% post-change. A two-proportion z-test rejects equality of the pre- and post-change proportions. The associated p-value is ≪0.01.
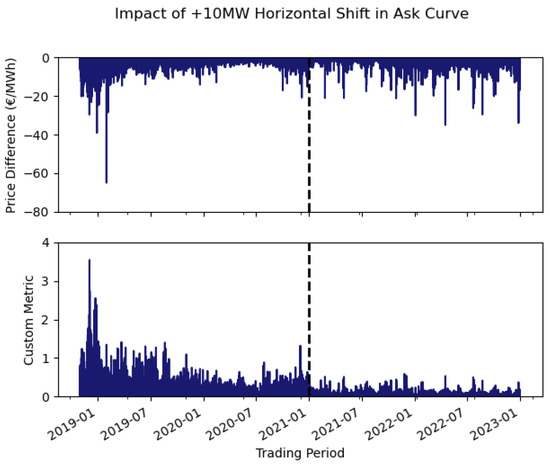
Figure 10 plots the price difference and Custom Metric values against DA prices, highlighting shifts in the distributions before and after the structural change. Supporting material includes histograms of these time series (Appendix J) and the corresponding +1 MW analysis (Appendix K).
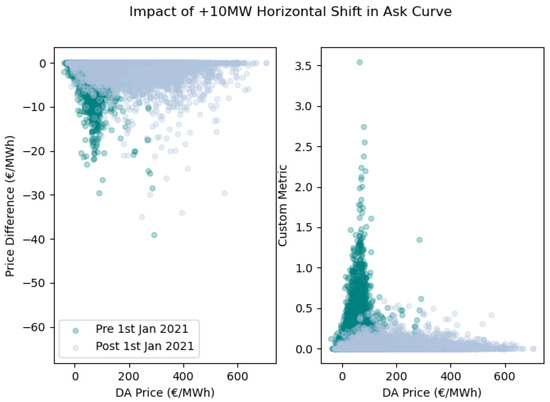
Figure 10.
Scatter plot showing the impact, per trading period, of a +10 MW horizontal shift in the ask curve distinguishing between observations pre and post 1 January 2021.
Figure 11 presents the price inertia distribution analysis described in Section 3.3. The density histogram on the left compares the distributions of the minimum shift required to trigger a market price change before and after 1 January 2021. It shows that, prior to this date, small shifts in the ask curve were more likely to result in a price change than comparable shifts after the change. Finally, in Appendix L, we take a single speculator and simulate its impact on market prices. This approach is conceptually similar to the price inertia method although the assumption of a small shift in the demand or supply curve may not always hold.
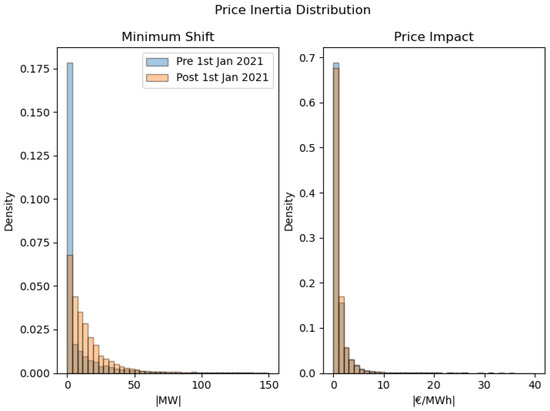
Figure 11.
Price Inertia Distribution. Plot on the left is a histogram of the minimum absolute shift required to trigger a market price change (note: x-axis range restricted for display purposes); plot on the right is the estimated price impact.
5. Discussion
The analysis shows that speculators in the Irish DA market exhibit both dynamism and heterogeneity, with participation undergoing a clear step change after the structural market shift. In particular, buy and sell order volumes within the interval increased. At first sight, the frequency with which speculators were marginal, exceeding their overall market share both before and after the change, may seem counterintuitive, but this is consistent with strategies that place orders close to the market clearing price.
The price inertia analysis provided a simple and transparent metric. A relatively high share of trading periods showed that even small shifts in the ask curve could change the market price, and in some cases the shifts produced substantial movements. This underscores the susceptibility of DA prices to local shocks, a feature familiar to market participants. The shift in inertia levels around the structural change was also notable. Conceptually, the approach is similar to liquidity and depth measures in other markets.
A plausible link between these findings is that, after the structural change, speculators began supplying DA liquidity previously provided through EUPHEMIA’s interconnector scheduling with Great Britain. This resembles one of the motivations for Virtual Bidding noted by [15], namely liquidity provision and price transparency. Much of this additional liquidity occurred near the clearing price, potentially contributing to higher observed inertia. While suggestive, this remains correlation rather than causation, with two main challenges to formal testing:
- Pricing algorithm access: the market clearing process is complex and not fully disclosed, limiting counterfactual analysis; see also [14].
- Market dynamics: outcomes also reflect evolving behaviours of non-speculators [16]; even modest shifts in their bidding or trading strategies, individually or in aggregate, could contribute to the observed changes.
Further research could test the hypothesis more rigorously, for example by forecasting inertia levels and identifying key drivers, though building a model with predictive power may be difficult. More broadly, the results highlight limitations in applying fundamental forecasting to short-term markets: speculators’ adaptive behaviour complicates model input assumptions, and price inertia implies that small demand or supply changes can trigger non-trivial price movements, nonlinearities that may be beyond the reach of fundamental or other forecasting approaches.
Limitations
This study has several limitations that should be acknowledged. First, the analysis focuses on the Irish DA market which, while representative of European auction-based designs, reflects a relatively small system. Second, while our cohort classification provides a transparent framework for identifying speculators, participants in other cohorts may also engage in speculative activity. Third, the market environment is inherently dynamic, making it difficult to isolate speculator effects from those of other participants; our results should therefore be interpreted as correlational rather than causal. In addition, the DA pricing algorithm is complex and only partly disclosed (Section 2.2), preventing full replication of the market clearing process and requiring the simplifying assumptions outlined in Section 3.3. Finally, alternative participant classification approaches are possible; however, given the robustness checks conducted, we consider our process reasonable and sufficient and do not expect materially different results. These limitations constrain the scope of our conclusions but also indicate promising directions for future research.
6. Conclusions
This paper presented two empirical analyses of the Irish DA electricity market, a setting representative of short-term European markets, characterised by non-trivial liquidity, high renewable penetration, and diverse commodity price regimes over the study horizon. The first analysis examined the presence and behaviour of speculators; the second addressed market price inertia.
For speculators, we found that their share of marginal periods was well above their overall market share, that activity increased following a structural market change, and that their behaviour was both dynamic and heterogeneous. The price inertia analysis introduced an intuitive method that highlighted the sensitivity of short-term prices to small shifts in demand or supply. Inertia levels also increased after the structural change, though the underlying causes remain conjectural given the complexity of the auction mechanism and lack of access to the pricing algorithm.
The research has two key implications. First, both sets of findings point to challenges for short-term fundamental modelling approaches in forecasting electricity prices. Second, the price inertia metric provides a useful additional lens for evaluating structural market change proposals in auction-based electricity markets. Overall, our analysis reinforces the view that short-term electricity markets are complex, non-stationary environments shaped by numerous interacting factors.
Author Contributions
Conceptualisation, J.C., A.A., and K.M.; methodology, J.C., A.A., and K.M.; data curation, J.C.; investigation, J.C.; writing—original draft, J.C.; writing—review and editing, A.A. and K.M.; visualisation, J.C., A.A., and K.M.; supervision, A.A. and K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this study are publicly available from SEMOpx (https://www.semopx.com/, accessed on 15 January 2023) and SEMO (https://www.sem-o.com/, accessed on 15 January 2023).
Acknowledgments
During the preparation of this work, after completing a draft manuscript, the author(s) used ChatGPT-4.5 and Gemini 2.0 to refine and suggest alternative wording for certain sentences. Some suggestions were incorporated, others were not. All analysis and results presented in the manuscript are solely the author(s)’ own work. The author(s) take full responsibility for the content of the published article.
Conflicts of Interest
The authors declare no conflicts of interest. It is worth noting that while Joseph Collins reports a relationship with capSpire (a technology consulting and solutions company that specialises in the commodities/energy industry) that includes employment, the manuscript reflects the authors independent research.
Appendix A. Simplifications and Other Considerations
Additional caveats related to the analysis include the following:
- This alternative definition may be of interest for those trading periods in which the published bid and ask curve intersects vertically (Figure A2 Appendix E). Using this definition, while the percentages presented in Section 4.2 (and the graphs in Appendix K) will change, the overall pattern remains the same. That is, a step change in the impact of a small horizontal shift in the ask curve from January 2021 onwards is observed.
- The data pipelines we constructed do not have access to the following datasets:
- −
- DA order data for the first 5 days of the Irish electricity market.
- −
- IDA1/IDA2/IDA3 order data for the first 3 months of the Irish electricity market.
The implications are that our estimates of speculator profitability might be under/over stated for the first 3 months of the Irish electricity market. Given that speculator order/matched quantities were small in the immediately following months, we believe it is reasonable to assume that the under/over estimation would not have a material impact on the profit and loss estimates.
Appendix B. Identifying Speculators
The following steps, developed through trial and error, are used to identify speculators in the Irish electricity market:
- The PUB_MnlyRegisteredCapacity file referenced in Section 3.1 contains a list of registered market participants with ResourceName (an identifier that is unique to each market participant), RegisteredCapacity, and FuelType (categories include wind, multi_fuel, gas, hdyro, peat, coal, pump_storage, biomass, oil, distillate, solar) information. Select ResourceNames where the FuelType is not specified.
- Using the ResourceNames from the previous step, in conjunction with DA order information from the ETS Bid Files, drop or ignore ResourceNames which are
- −
- Always buying in the DA market or
- −
- Always selling in the DA market
The former are likely to correspond to supplier units while the latter are likely to correspond to generator units. We note, however, that speculators could also adopt such strategies (see discussion further below). - Cognisant that some ResourceNames might have commenced commercial operations as demand units and over time switched strategy to that of a supply unit (or vice versa), we endeavour to filter out such units. That is, drop ResourceNames that are predominantly either buying or selling. Note: Picking an arbitrary threshold, if a ResourceName is buying (selling) > 92.5% of trading periods it is active in the DA, then we treat it as a demand (supply) unit and exclude it.
- The final step is to drop ResourceNames which have both a demand and variable renewable generation. For such units, given that the order quantity is the net of demand plus variable renewable generation, it can be expected that their order quantities in contiguous trading periods would exhibit jumps/discontinuities. The approach is to keep track of the number of trading periods in a day which have a similar order quantity, and if over the horizon of interest the proportion of such trading periods is less than some arbitrary threshold (e.g., 7.5%), we drop the ResourceName.
To add to the overall robustness of the approach once the population of speculators have been identified, we perform a cursory manual inspection of each unit (i.e., their positions in the ex ante markets), removing any units from consideration that do not subscribe to speculator type behaviour.
We note the two main shortcomings of the classification approach. First, it does not address speculative actions that may be undertaken by participants with clear generation or consumption roles. Second, a more encompassing algorithm could have incorporated additional ex ante participant information directly into the classification. However, in a subsequent review of participants without FuelType information, the procedure described above performed well with very few exceptions. One such exception was a participant active only from August 2022 (i.e., towards the end of the study period) which was incorrectly assigned to the buy cohort but should have been classified as a speculator. Given the small scale of this participant’s activity, the misclassification has no material impact on the analysis.
Appendix C. Reconciling ETS Bid File and BidAskCurve
Note: This appendix is provided for transparency and reproducibility. Our analysis relies on the published aggregated BidAskCurve, which already incorporates Simple Orders and matched Complex Orders; Complex Orders are therefore not excluded from our dataset or results. The reconciliation below documents how to reproduce the published curves from the ETS Bid File and has no bearing on the empirical results.
Following a significant amount of experimentation, using hourly data from November 2018 to end of December 2022, it has been possible to reconstruct the BidAskCurve data using the ETS Bid File once the following adjustments are made for each trading period
- Complex Orders defined as “a Simple Sell Order or a set of Simple Sell Orders submitted by an Exchange Member in respect of a Unit, covering one or more Trading Periods on a specified Trading Day, and which is subject to: (a) a Minimum Income Condition (with or without a Scheduled Stop Condition) and/or (b) a Load Gradient Condition“ are not part of the ask curve, unless the Complex Order is matched. If a Complex Order is matched then the matched quantity is included in the ask curve at the minimum price point.
- Using the ETS Bid File, we filter orders which have settlement currency of EUR. Calculate the difference between the matched buy quantities and matched sell quantities; depending on the sign, the difference needs to be added to either the bid or ask curve at the maximum or minimum price point. Repeat, but for orders which have a settlement currency of GBP.
It is our assumption that step 2 is a result of EUPHEMIA scheduling flows on the interconnectors joining Great Britain and Ireland. For example, if EUPHEMIA schedules electricity to flow from Great Britain to Ireland then the ETS Bid File will show greater matched purchase quantities than matched sell quantities. In the BidAskCurve file this will correspond to a greater quantity at the minimum price point in the ask curve than is evident from individual participant sell orders in the corresponding ETS Bid File. In addition, we have found that as of July 2021 onwards, when SEMOpx commenced publishing a single combined BidAskCurve (Section 3.1 on page 6), the adjustments described in step 2 are no longer required when reconciling the ETS Bid File and BidAskCurve files.
Appendix D. DA Marginal Units
Consider a single trading period in the Irish electricity DA market. To identify the marginal unit(s) in that trading period:
- From the MarketResult file (Section 3.1), determine the DA market price for the trading period.
- Using the ETS Bid File, select the rows where market participants have an active order in that trading period.
- Iterating through each row in the previous step
- If the market price equals any of the price points in the participant’s order, we flag the participant;
- Otherwise, do nothing.
If one or more participants have been flagged, then we have identified the marginal unit(s) and the process ends. If no units have been flagged, continue to the next step. - Utilising the BidAskCurve file, for that trading period, ascertain how the bid and ask curves intersect. If the curves intersect vertically, determine the two points at which the curves overlap. Denote the prices associated with the overlap as lower_price and upper_price.
- Iterate through each of the rows selected in step 2. If either the lower_price or the upper_price identified in step 4 equals any of the price points in the participant’s order, we flag the participant as being marginal.
Appendix E. Bid Ask Curve Intersection Examples
Figure A1 and Figure A2 provide examples of Bid Ask Curve intersections. In each plot we zoom in on the region where the bid (blue) and ask (red) curves intersect. Figure A1 presents perpendicular (i.e., point) intersections where it can be seen that either the ask or bid curve is horizontal at the point of intersection. The plot on the left in Figure A2 shows a vertical intersection and the DA market price is represented by a black dot.
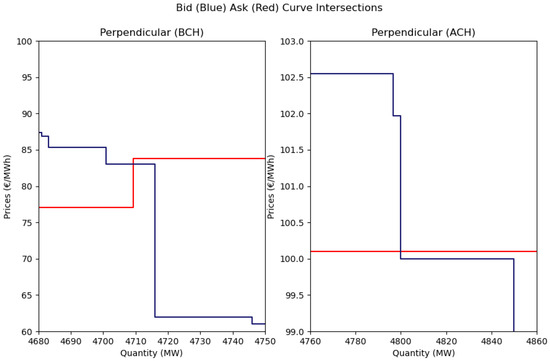
Figure A1.
Plot on the (left,right) shows the Bid Ask Curve intersection for the I-SEM DA trading period 3 p.m.–4 p.m. (4 p.m.–5 p.m.) 31 October 2018.
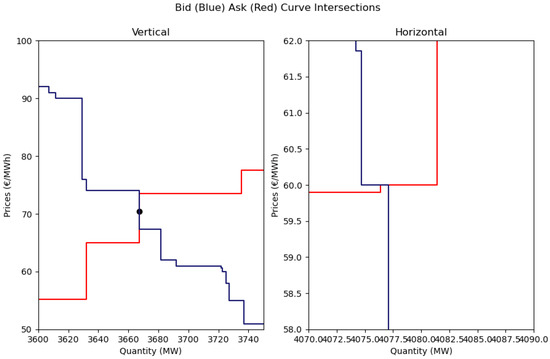
Figure A2.
Plot on the (left,right) shows the Bid Ask Curve intersection for the I-SEM DA trading period 11 p.m.–12 a.m. 30 October 2018 (12 a.m.–1 a.m. 31 October 2018).
Appendix F. Speculators
AU_400137, AU_400139, AU_400143, AU_500104, AU_400140, SU_400314, AU_500101, AU_500126, AU_500012, AU_400118, AU_400100, AU_400122, AU_400002, AU_400128, AU_500110, SU_400136, AU_500114, AU_400103, AU_400138, AU_500109, AU_400003, AU_400006, AU_400101, AU_400135, SU_500082, AU_400105, AU_500001, AU_400005, AU_400010, AU_400141, AU_400111, AU_400125, AU_400106, AU_500115, AU_400114, AU_500121, AU_400112, AU_400132, AU_400119, AU_400116, AU_400113, AU_500122, AU_400134, AU_400117, AU_500105, AU_400011, AU_400009, AU_500113, AU_500111, AU_400136.
Appendix G. Speculator Ex Ante Trading
Consider the following hypothetical scenarios for speculator j in trading period i:
- Scenario 1: the speculator buys 100 MW in DA and sells 100 MW in IDA1; in this situation, the profit or loss equals .
- Scenario 2: the speculator buys 50 MW in DA and sell 150 MW in IDA1; using Equation (4) from Section 3.2, the profit or loss is given by . Rearranging this, this is equivalent to .
That is, in both scenarios, a proportion of the profit or loss is attributable to the loss or gain associated with taking opposing positions in ex ante markets.
Appendix H. FuelType Notation
Categories for the FuelType field in the PUB_MnlyRegisteredCapacity file (Section 3.1) include wind, multi_fuel, gas, hydro, peat, coal, pump_storage, biomass, oil, distillate, and solar (this field can also be unpopulated). When presenting stacked area chart plots in Section 4, we combine some of the FuelType categories and utilise the following notation:
- Wind category represents those ResourceNames (market participants) where the FuelType is wind.
- Other category represents the units which do not have a FuelType (and from their commercial behaviours appear in the main to be either demand or wind participants).
- Gas, MF category corresponds to gas and multi-fuel thermal generation units.
- Hyd, PS, P, Bio denote hydro, pumped storage, peat, and biomass units.
- Speculator represents those units specified in Appendix F.
Appendix I. Buy Order Data Quantities
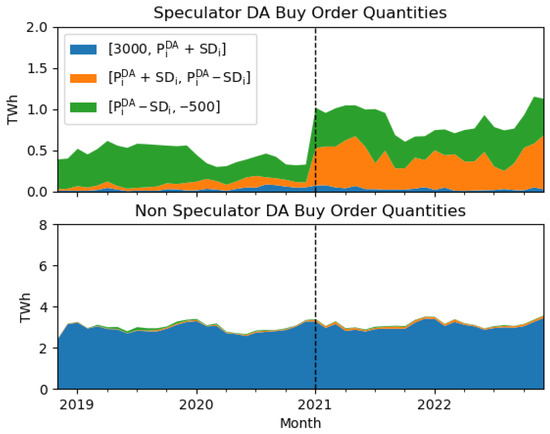
Figure A3.
(Top) plot presents speculator buy order quantities grouped by price interval and month. (Bottom) plot presents corresponding data for non-speculators. Values are in TWh; note the different y-axis scales.
Appendix J. Parallel Shift
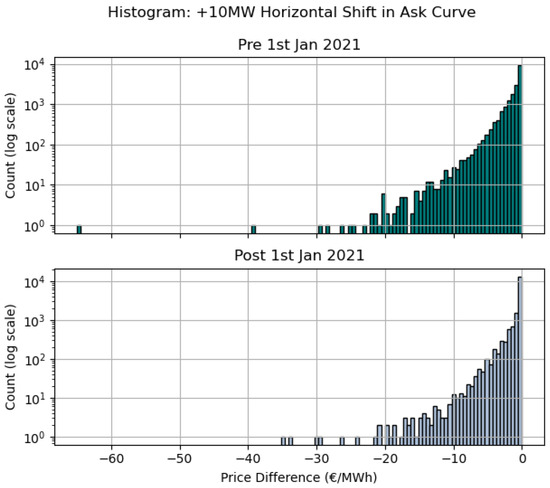
Figure A4.
Histogram of price difference (EUR/MWh), Equation (5), for a +10 MW parallel shift in the ask curve distinguishing between observations pre and post the structural market change. Note that count is on a log scale.
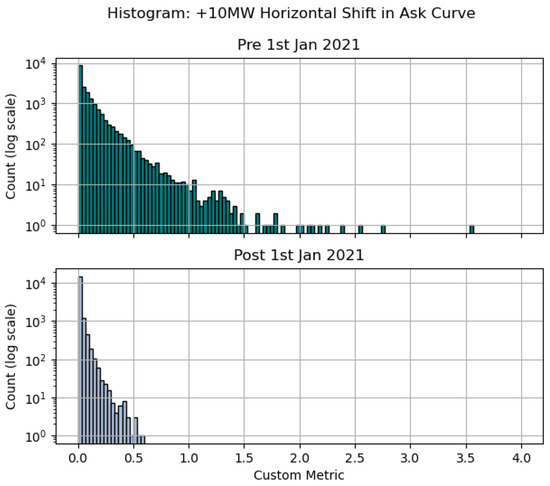
Figure A5.
Histogram of Custom Metric, Equation (6), for a +10 MW parallel shift in the ask curve distinguishing between observations pre and post the structural market change. Note that the count is on a log scale.
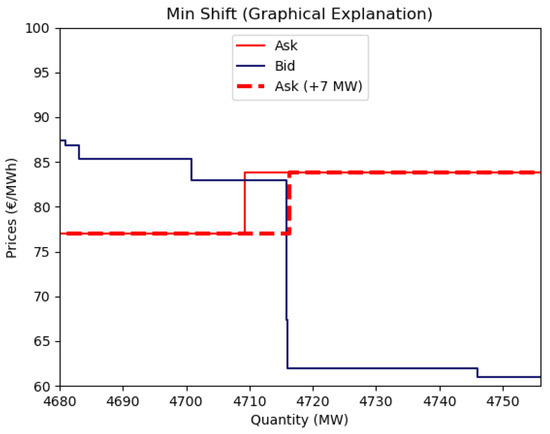
Figure A6.
Graphical illustration of the minimum shift approach described in Section 3.3.1. Solid lines show the original bid and ask curves; the dashed curve shows the ask curve after the minimum horizontal shift needed to change the market clearing price.
Appendix K. +1 MW Parallel Shift in Ask Curve
The top (bottom) plot in Figure A7 shows the price difference (Custom Metric) values per trading period associated with a +1 MW parallel shift in the ask curve. From the underlying data it is observed that in approximately 62% (12%) of all trading periods pre (post) 1 January 2021, the application of a +1 MW horizontal shift in the ask curve results in a changed market price. For those trading periods where the market price changes, there is an average reduction of 2.3% (0.7%) in the DA price pre (post) 1 January 2021.
Appendix L. Simulating Speculator DA Price Impact
To estimate the impact of a single speculator, j, on the DA price for trading period i, the process is as follows
- Retrieve all participant orders for trading period i from the relevant DA ETS Bid File. Convert each of the orders into price and quantity pairs.
- Take the buy price and quantity pairs from step 1 and combine them to produce an aggregated stepwise bid curve. Similarly, take the sell price quantity pairs and combine them to produce an aggregated stepwise ask curve.
- Adjust the stepwise bid and ask curves from step 2 as described in Appendix C.
- Use the bid and ask curves from step 3 to determine the intersection point/price.
- Repeat steps 1 to 4 but this time exclude the order data for speculator j.
We note that steps 1 to 4 can essentially be viewed as a validation step.
By way of example we apply this process to two contiguous trading periods for a particular speculator participant; the results are shown in Figure A8. The figure displays the bid and ask curves for two trading periods on 10 January 2019. The blue lines represent the curves excluding the speculator, while the red lines include them. Since the speculator only submitted sell orders, the red and blue bid curves are identical and hence overlap. For the 4 a.m.–5 a.m. trading period, the speculator placed sell orders of 4 MW at EUR 40/MWh and an additional 4 MW at EUR 50/MWh. In the 5 a.m.–6 a.m. period, similar sell quantities were submitted at EUR 44/MWh and EUR 54/MWh. The DA clearing prices for these periods were EUR 59.16/MWh and EUR 64.09/MWh, respectively. For 4 a.m.–5 a.m., excluding the speculator shifts, the ask curve moves to the left, resulting in a higher intersection price of EUR 61.77/MWh. In contrast, for 5 a.m.–6 a.m., while the ask curve shifts left again, the intersection price remains unchanged. Extending this analysis across all trading periods in which the speculator was active yields Figure A9. However, as noted in Section 3.3, in this broader analysis, the assumption of a small change in the bid or ask curve does not always hold.
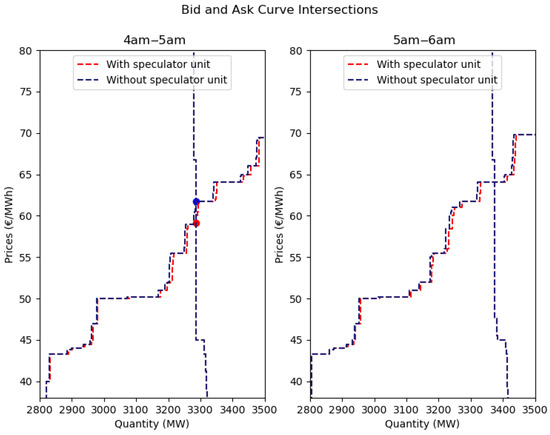
Figure A8.
Day-Ahead bid and ask curve intersections, with and without a single speculator, on 10 January 2019. In the left-hand plot, the red circle marks the original market clearing price, while the blue circle shows the counterfactual price without the speculator. In the right-hand plot, the market and counterfactual prices are identical, so the circles are not shown.
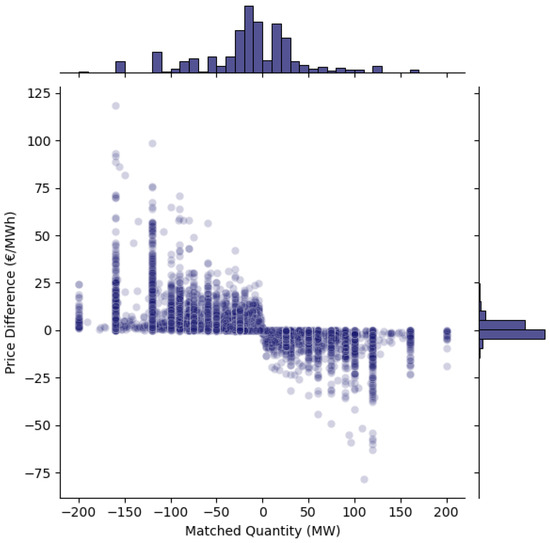
Figure A9.
Impact of a single speculator on the Day-Ahead bid and ask curve intersection. Negative (positive) x-axis values indicate sell (buy) speculator matched quantities. The y-axis represents the price difference: intersection price without the speculator minus the price with the speculator.
Appendix M. SEMO and SEMOpx
Pertinent reports/information from SEMOpx include the following:
- Section 2.1, Structural Market Change, SEMOpx-Bidding.
- Section 3.1, Datasets, SEMOpx Data Publication Guide.
- Section 3.2, Market Shares, Market Summary 2019, Quarterly Report Q4 2020 and December 2022 Market Report.
- Section 3.2, Empirical Analysis (Speculator DA Order Evolution), SEMOpx DAM INFO 12 April 2022 and SEMOpx DAM INFO 30 August 2022.
Similarly, from SEMO, useful reference material includes the following:
Appendix N. Market Prices
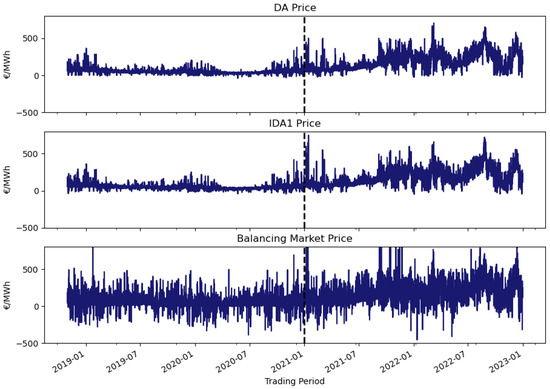
Figure A10.
Time series plots of Irish electricity DA, IDA1, and balancing market prices. The y-axis is cropped to the EUR/MWh range. From November 2018 to December 2022, the BM recorded 56 settlement periods with prices exceeding EUR 800/MWh; the maximum BM price over the period was EUR 4800/MWh.
References
- Wolak, F.A. An empirical analysis of the impact of hedge contracts on bidding behavior in a competitive electricity market. Int. Econ. J. 2000, 14, 1–39. [Google Scholar] [CrossRef]
- Ito, K.; Reguant, M. Sequential markets, market power, and arbitrage. Am. Econ. Rev. 2016, 106, 1921–1957. [Google Scholar] [CrossRef]
- Mayer, K.; Trück, S. Electricity markets around the world. J. Commod. Mark. 2018, 9, 77–100. [Google Scholar] [CrossRef]
- Aggarwal, S.K.; Saini, L.M.; Kumar, A. Electricity price forecasting in deregulated markets: A review and evaluation. Int. J. Electr. Power Energy Syst. 2009, 31, 13–22. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electricity Price Forecasting Using Recurrent Neural Networks. Energies 2018, 11, 1255. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Econometric modelling and forecasting of intraday electricity prices. J. Commod. Mark. 2020, 19, 100107. [Google Scholar] [CrossRef]
- Kaleta, M. Robust Co-Optimization of Medium- and Short-Term Electrical Energy and Flexibility in Electricity Clusters. Energies 2025, 18, 479. [Google Scholar] [CrossRef]
- Canelas, E.; Pinto-Varela, T.; Sawik, B. Electricity portfolio optimization for large consumers: Iberian electricity market case study. Energies 2020, 13, 2249. [Google Scholar] [CrossRef]
- Harder, N.; Qussous, R.; Weidlich, A. Fit for purpose: Modeling wholesale electricity markets realistically with multi-agent deep reinforcement learning. Energy AI 2023, 14, 100295. [Google Scholar] [CrossRef]
- Haase, M.; Zimmermann, Y.S.; Zimmermann, H. The impact of speculation on commodity futures markets–A review of the findings of 100 empirical studies. J. Commod. Mark. 2016, 3, 1–15. [Google Scholar] [CrossRef]
- Tribe, E. BSC Insights: What Is Driving Increases in Electricity Imbalance Volumes. 2019. Available online: https://www.elexon.co.uk/operations-settlement/balancing-and-settlement/elexon-insights-what-is-driving-increases-in-electricity-imbalance-volumes-july-2019/ (accessed on 17 February 2025).
- Nyarko, S. 294/09: Investigations into Net Imbalance Volume Chasing (‘Niv Chasing’) in Gb Electricity Market. 2019. Available online: https://www.elexon.co.uk/documents/groups/panel/2019-meetings/294-september/294-09-investigations-into-niv-chasing-in-gb-electricity-market-shadrack-nyarko/ (accessed on 17 February 2025).
- Parsons, J.; Colbert, C.; Larrieu, J.; Martin, T.; Mastrangelo, E. Financial Arbitrage and Efficient Dispatch in Wholesale Electricity Markets. SSRN Electron. J. 2015. [Google Scholar] [CrossRef]
- Jha, A.; Wolak, F.A. Can Financial Participants Improve Price Discovery and Efficiency in Multi-Settlement Markets with Trading Costs? Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2019. [Google Scholar]
- Mercadal, I. Dynamic competition and arbitrage in electricity markets: The role of financial players. SSRN Work. Pap. 2018. [Google Scholar] [CrossRef]
- Birge, J.R.; Hortaçsu, A.; Mercadal, I.; Pavlin, J.M. Limits to arbitrage in electricity markets: A case study of MISO. Energy Econ. 2018, 75, 518–533. [Google Scholar] [CrossRef]
- Ullrich, C.J. Realized volatility and price spikes in electricity markets: The importance of observation frequency. Energy Econ. 2012, 34, 1809–1818. [Google Scholar] [CrossRef]
- Erdogdu, E. Asymmetric volatility in European day-ahead power markets: A comparative microeconomic analysis. Energy Econ. 2016, 56, 398–409. [Google Scholar] [CrossRef]
- Hellström, J.; Lundgren, J.; Yu, H. Why do electricity prices jump? Empirical evidence from the Nordic electricity market. Energy Econ. 2012, 34, 1774–1781. [Google Scholar] [CrossRef]
- Li, K.; Cursio, J.D.; Jiang, M.; Liang, X. The significance of calendar effects in the electricity market. Appl. Energy 2019, 235, 487–494. [Google Scholar] [CrossRef]
- Sensfuß, F.; Ragwitz, M.; Genoese, M. The merit-order effect: A detailed analysis of the price effect of renewable electricity generation on spot market prices in Germany. Energy Policy 2008, 36, 3086–3094. [Google Scholar] [CrossRef]
- Ciarreta, A.; Espinosa, M.P. Market power in the Spanish electricity auction. J. Regul. Econ. 2010, 37, 42–69. [Google Scholar] [CrossRef]
- Ziel, F.; Steinert, R. Electricity price forecasting using sale and purchase curves: The X-Model. Energy Econ. 2016, 59, 435–454. [Google Scholar] [CrossRef]
- Bask, M.; Widerberg, A. Market structure and the stability and volatility of electricity prices. Energy Econ. 2009, 31, 278–288. [Google Scholar] [CrossRef]
- Fabra, N. Reforming European electricity markets: Lessons from the energy crisis. Energy Econ. 2023, 126, 106963. [Google Scholar] [CrossRef]
- Eurelectric. How Are EU Electricity Prices Formed and Why Have They Soared? 2022. Available online: https://www.eurelectric.org/in-detail/electricity_prices_explained/ (accessed on 17 March 2025).
- EFET. EFET Insight into Marginal Pricing in Wholesale Electricity Markets. 2022. Available online: https://cms.energytradersdeutschland.org/storage/uploads/media/220601-energy-traders-europe-insight-14-spot-trading-electricity.pdf (accessed on 17 March 2025).
- Collins, J.; Amann, A.; Mulchrone, K. Why Gas and Electricity Prices in Ireland Are so Closely Linked. 2022. Available online: https://www.rte.ie/brainstorm/2022/0727/1312565-ireland-gas-electricity-prices-correlation/ (accessed on 17 March 2025).
- REMA. Review of Electricity Market Arrangements. 2022. Available online: https://www.gov.uk/government/consultations/review-of-electricity-market-arrangements (accessed on 17 March 2025).
- The Guardian. ‘I’ve Fallen out with People’: The Bruising Debate over UK Zonal Energy Pricing. The Guardian. 2024. Available online: https://www.theguardian.com/money/2024/oct/07/ive-fallen-out-with-people-the-bruising-debate-over-uk-zonal-energy-pricing (accessed on 23 May 2025).
- Ritchie, H.; Roser, M.; Rosado, P. Energy. Our World in Data. 2022. Available online: https://ourworldindata.org/energy (accessed on 21 March 2025).
- ElectroRoute. Electroroute Brexit Commentary. 2020. Available online: https://electroroute.com/interconnecting-the-dots-on-future-brexit-arrangements/ (accessed on 17 March 2025).
- SEMOpx-Bidding. SEMOpx-Bidding. 2021. Available online: https://www.semopx.com/documents/training/SEMOpx-Bidding.pdf (accessed on 17 March 2025).
- EUPHEMIA. EUPHEMIA Public Description Single Price Coupling Algorithm. 2020. Available online: http://www.nemo-committee.eu/assets/files/euphemia-public-description.pdf (accessed on 21 March 2025).
- Madani, M. Single Day-Ahead Coupling: Important Successes for the Euphemia Lab; N-SIDE: Louvain-la-Neuve, Belgium, 2020. [Google Scholar]
- NEMO. CACM Annual Report 2021; NEMO: Brussels, Belgium, 2021; Available online: https://www.nemo-committee.eu/assets/files/nemo_CACM_Annual_Report_2021_220630-4e7321983974b812f28730a301c9f7d9.pdf (accessed on 17 March 2025).
- Bharatwaj, V.N.; Downey, A. Real-Time Imbalance Pricing in I-SEM—Ireland’s Balancing Market. In Proceedings of the 2018 20th National Power Systems Conference (NPSC), Tiruchirappalli, India, 14–16 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Elexon. A Guide to Electricity Imbalance Pricing in Great Britain; Elexon: London, UK, 2020. [Google Scholar]
- IEA. COVID-19 Impact on Electricity; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/covid-19-impact-on-electricity (accessed on 17 March 2025).
- Kuik, F.; Adolfsen, J.F.; Lis, E.M.; Meyler, A. Energy Price Developments in and Out of the COVID-19 Pandemic—From Commodity Prices to Consumer Prices; European Central Bank: Frankfurt am Main, Germany, 2022. [Google Scholar]
- SEMOpx. SEMOpx Market Platform. 2023. Available online: https://www.semopx.com/ (accessed on 15 March 2023).
- SEMO. Single Electricity Market Operator (SEMO). 2023. Available online: https://www.sem-o.com/ (accessed on 15 March 2023).
- Pape, C.; Hagemann, S.; Weber, C. Are fundamentals enough? Explaining price variations in the German day-ahead and intraday power market. Energy Econ. 2016, 54, 376–387. [Google Scholar] [CrossRef]
- Beran, P.; Pape, C.; Weber, C. Modelling German electricity wholesale spot prices with a parsimonious fundamental model–Validation & application. Util. Policy 2019, 58, 27–39. [Google Scholar]
- Liebl, D. Modeling and forecasting electricity spot prices: A functional data perspective. Ann. Appl. Stat. 2013, 7, 1562–1592. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).