Numerical Investigation of Hydrogen Production via Methane Steam Reforming in Tubular Packed Bed Reactors Integrated with Annular Metal Foam Gas Channels
Abstract
1. Introduction
2. Numerical Method
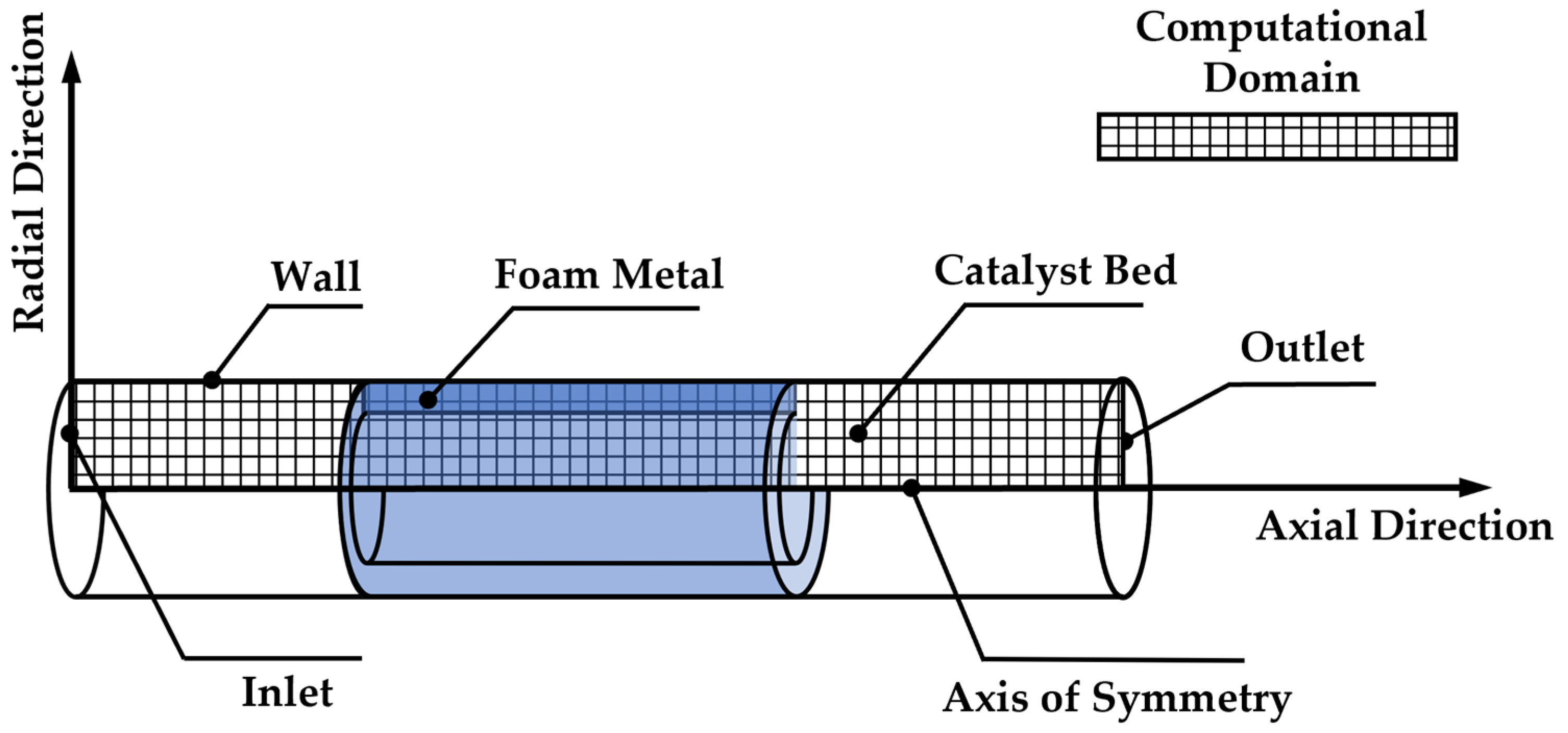
2.1. Physical Model
2.2. Governing Equations
2.3. Boundary Conditions
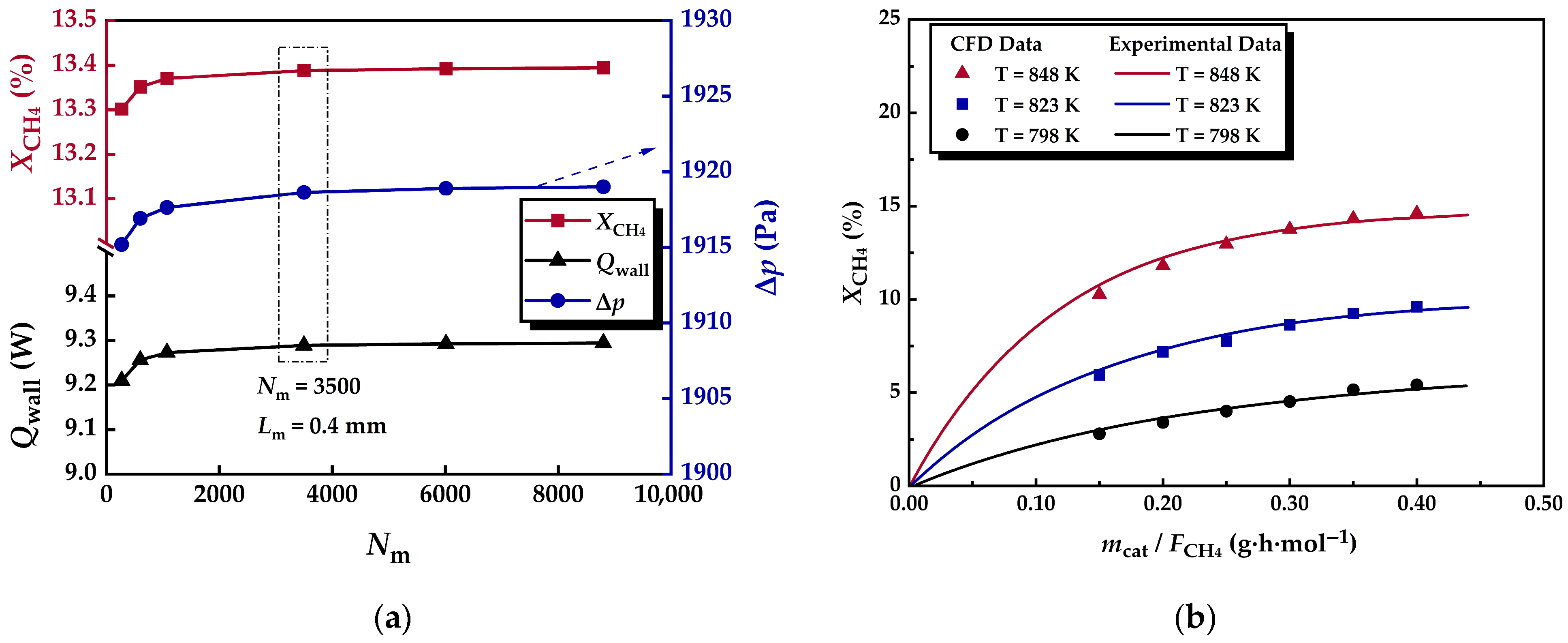
2.4. Mesh and Model Validation
3. Results and Discussion
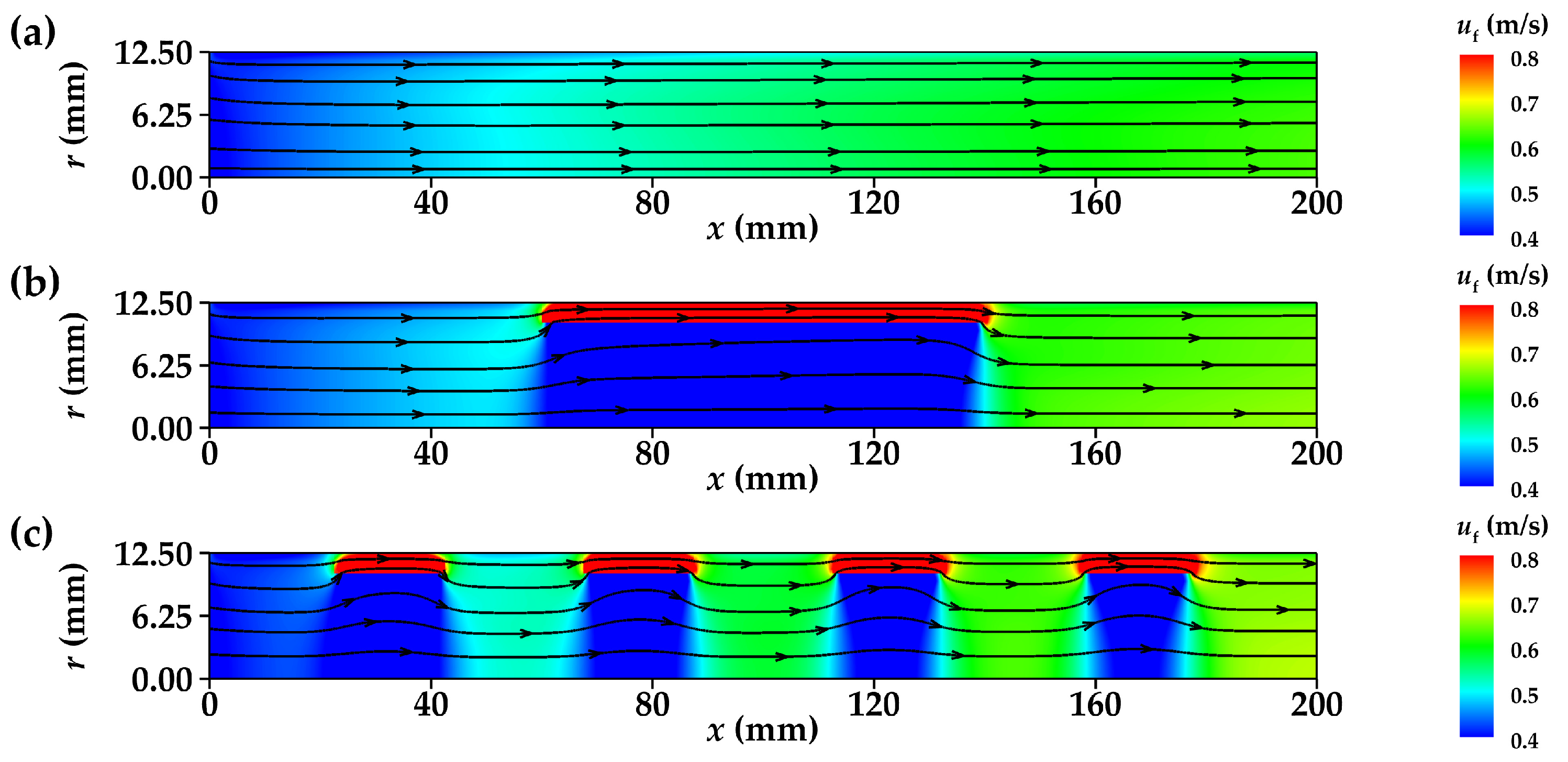
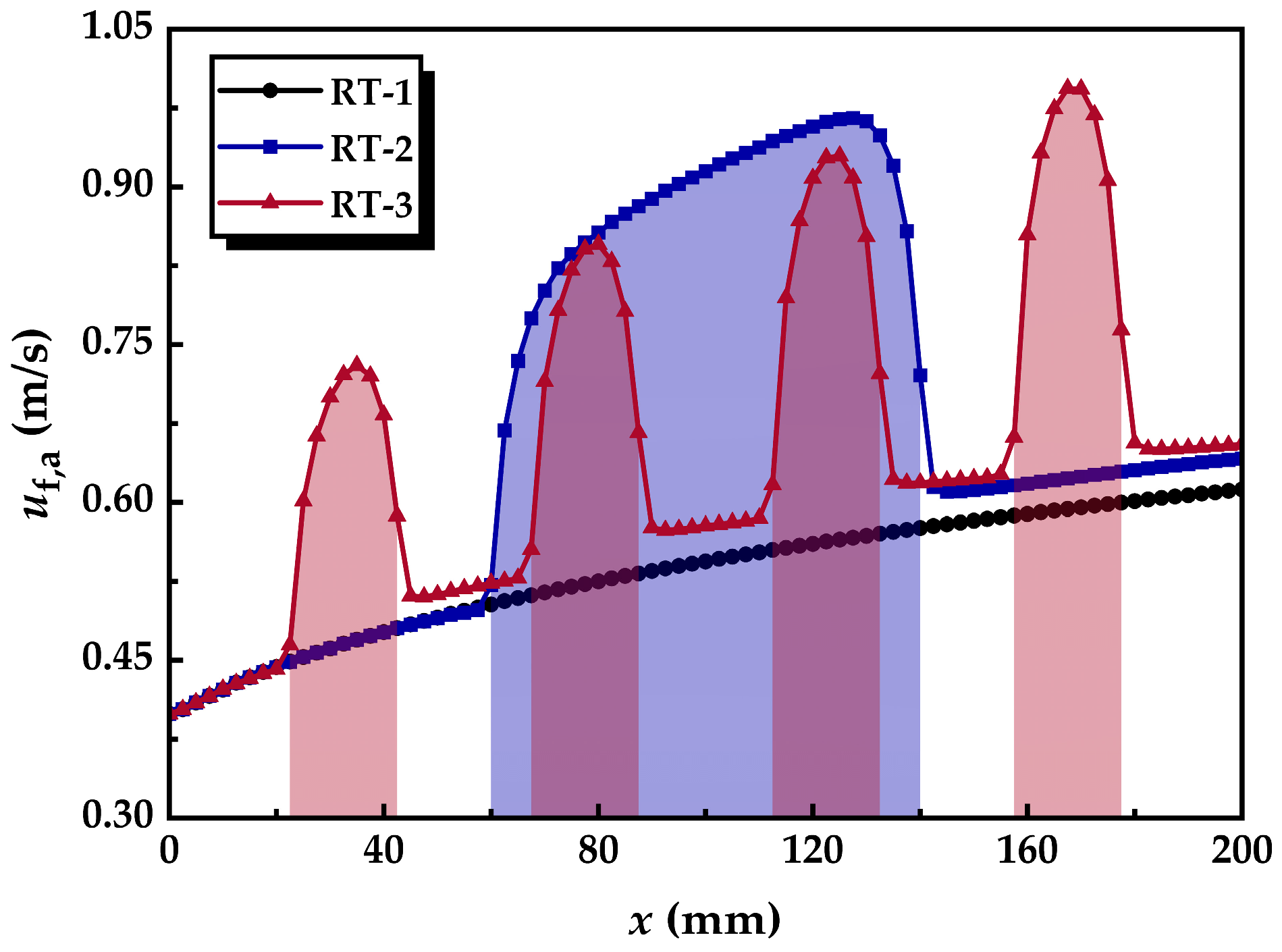
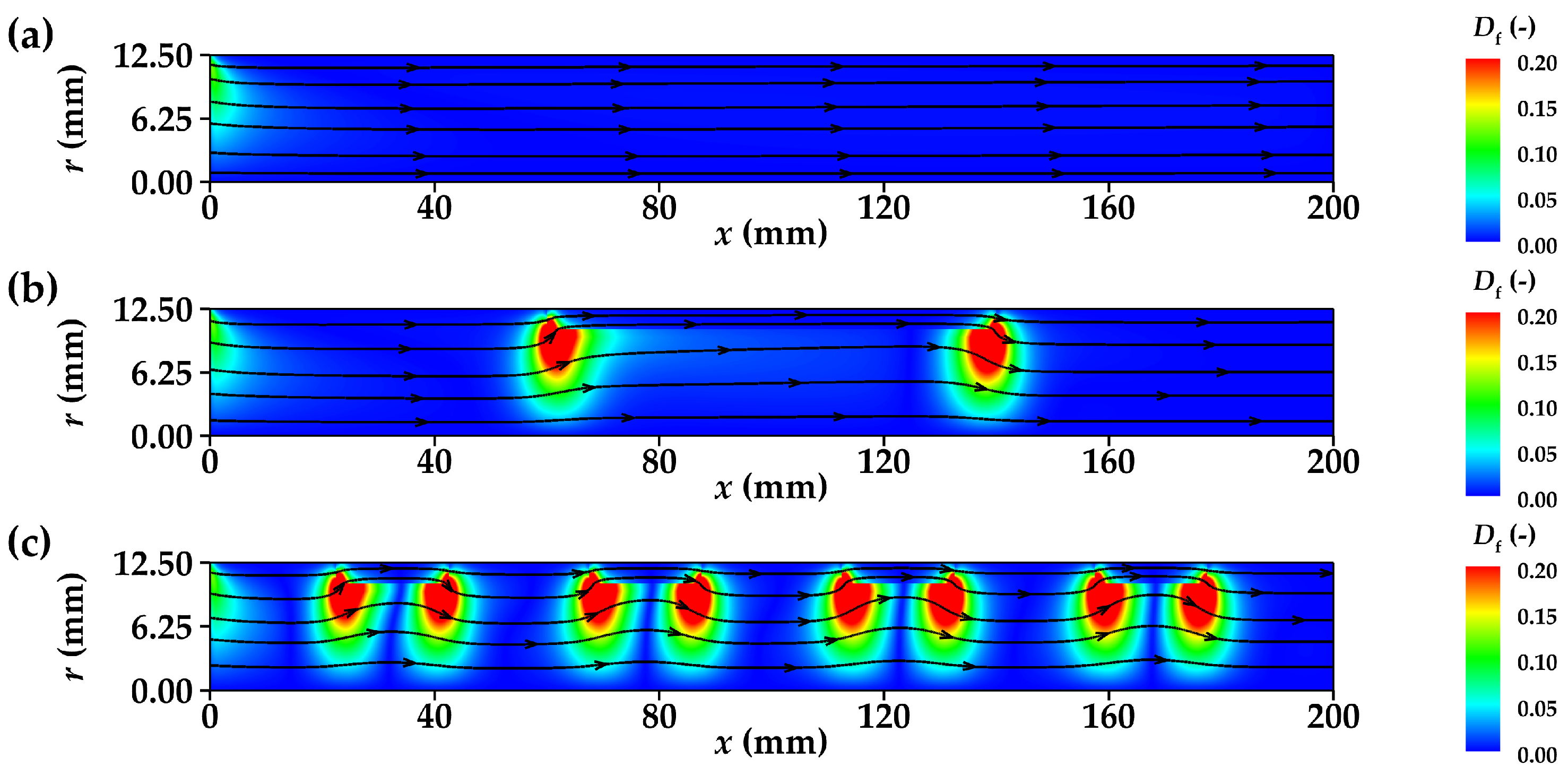
3.1. Flow Characteristics
3.1.1. Velocity Distribution
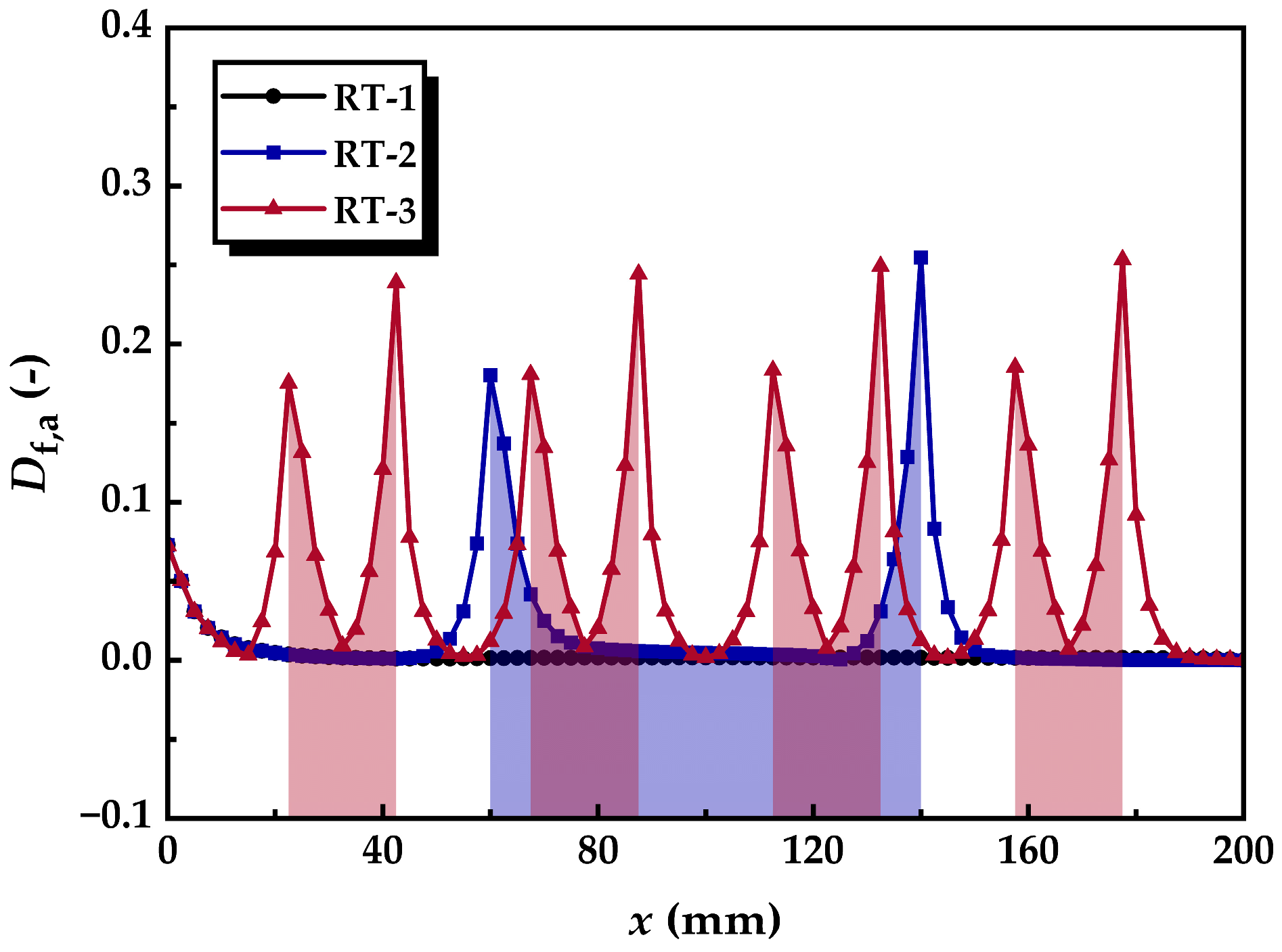
3.1.2. Flow Disturbance Distribution
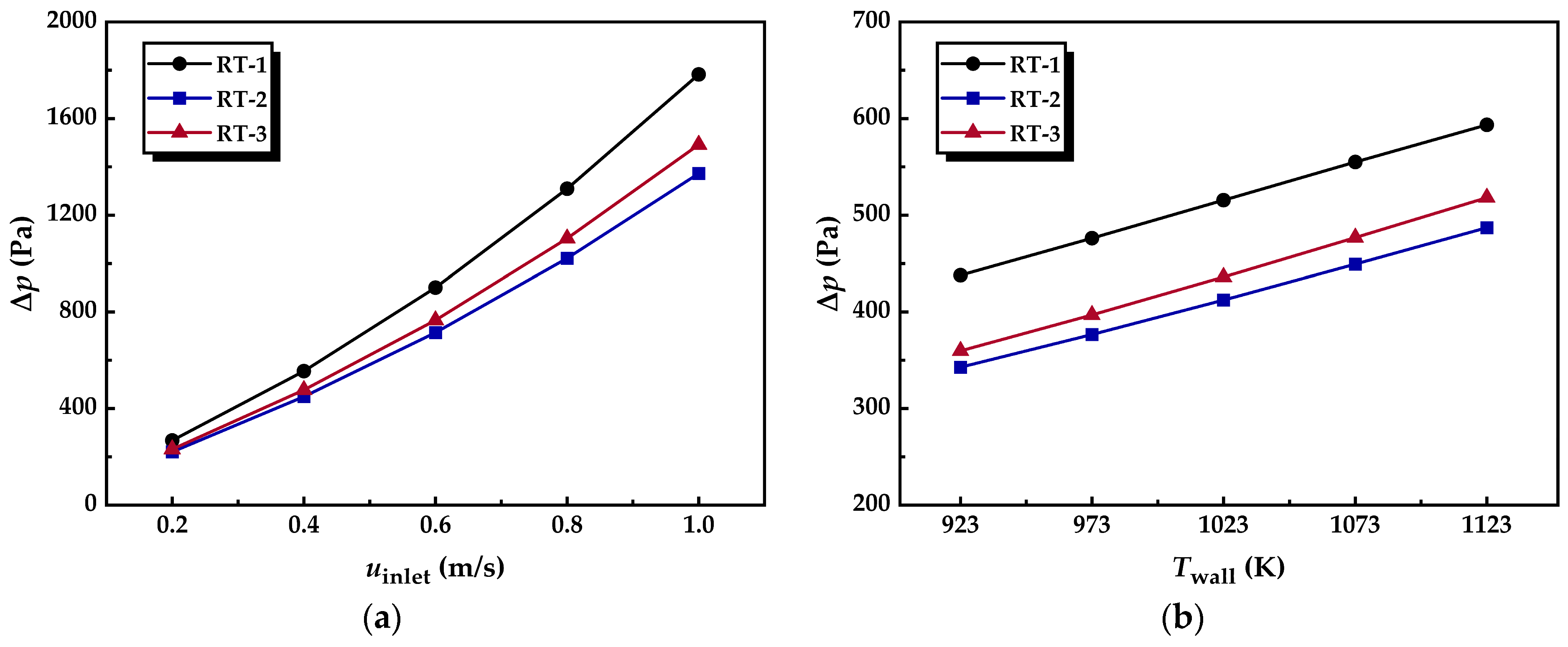
3.1.3. Pressure Drop
3.2. Heat Transfer Characteristics
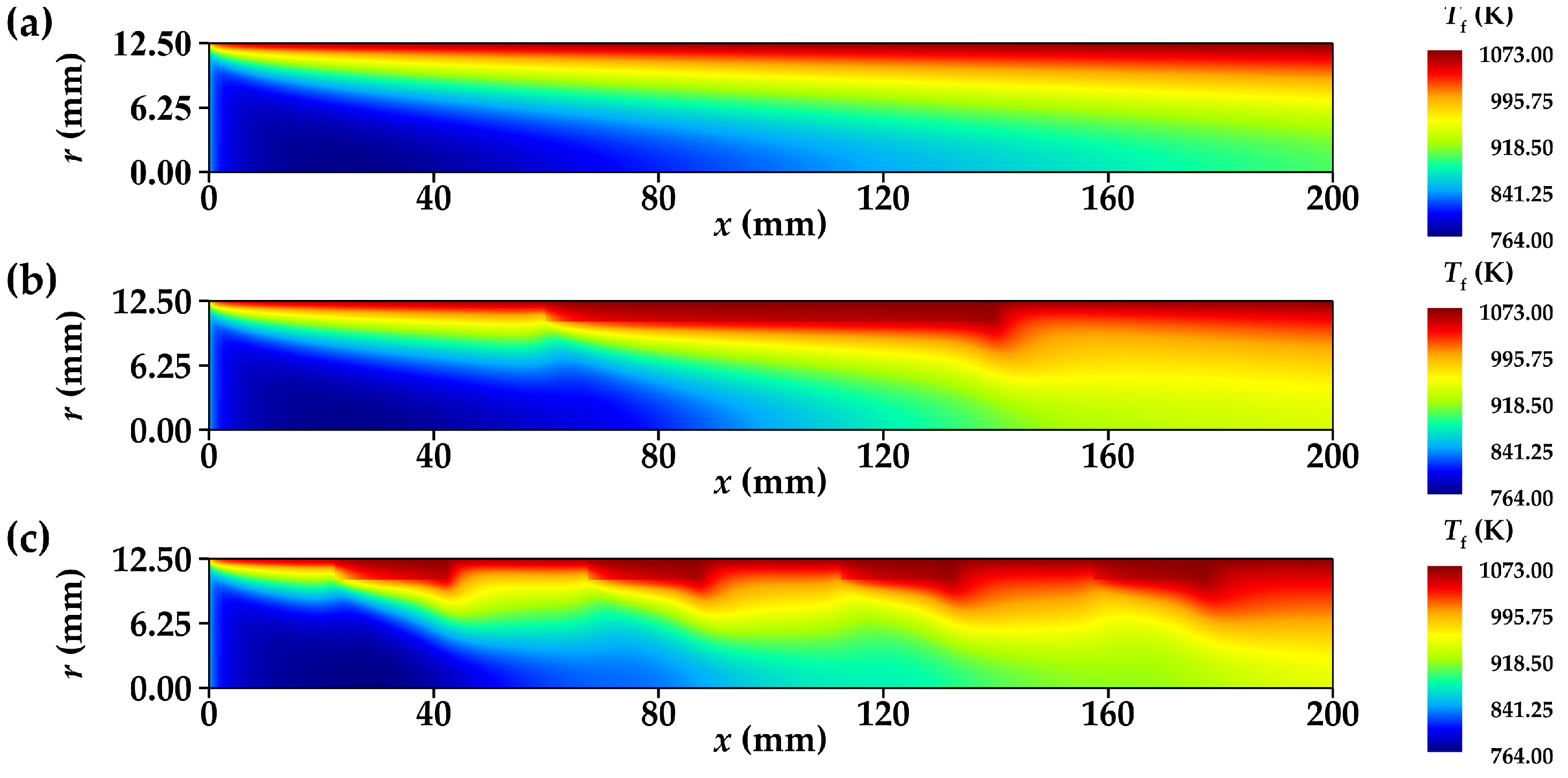
3.2.1. Temperature Distribution
3.2.2. Distribution of Heat Flux Density
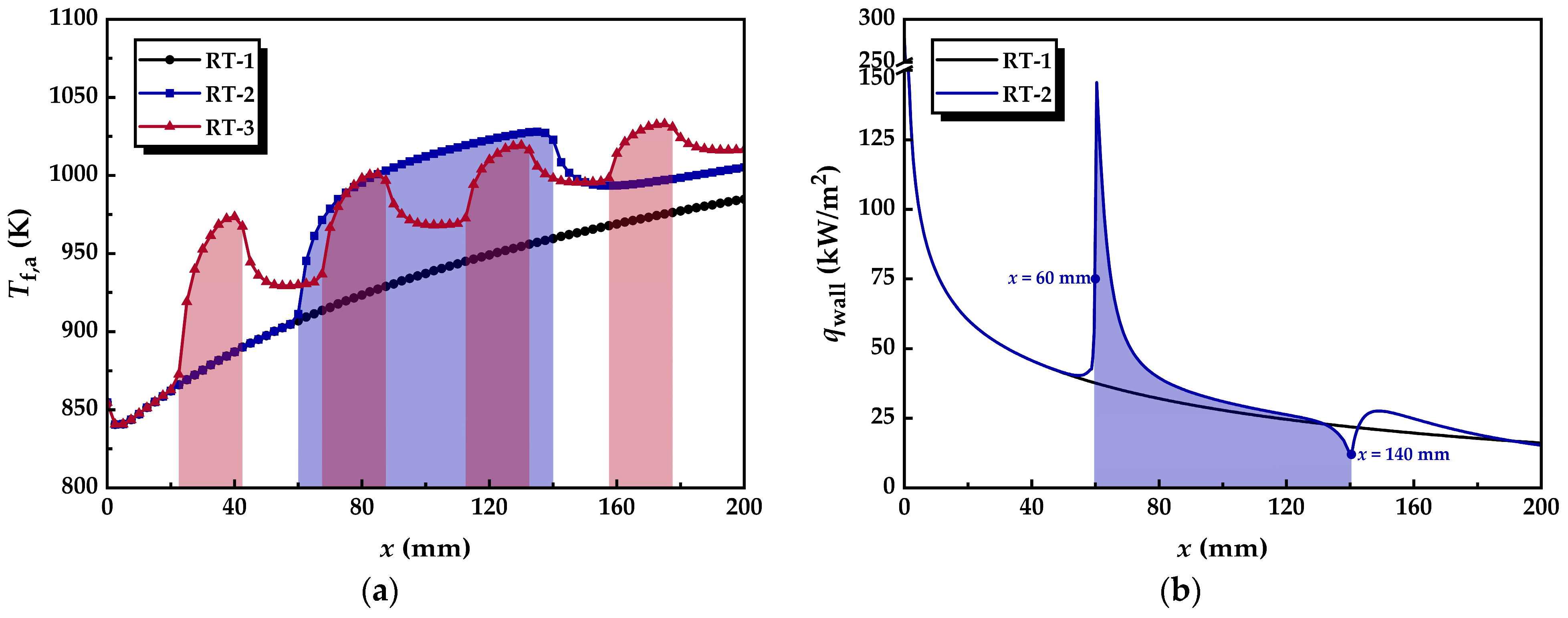
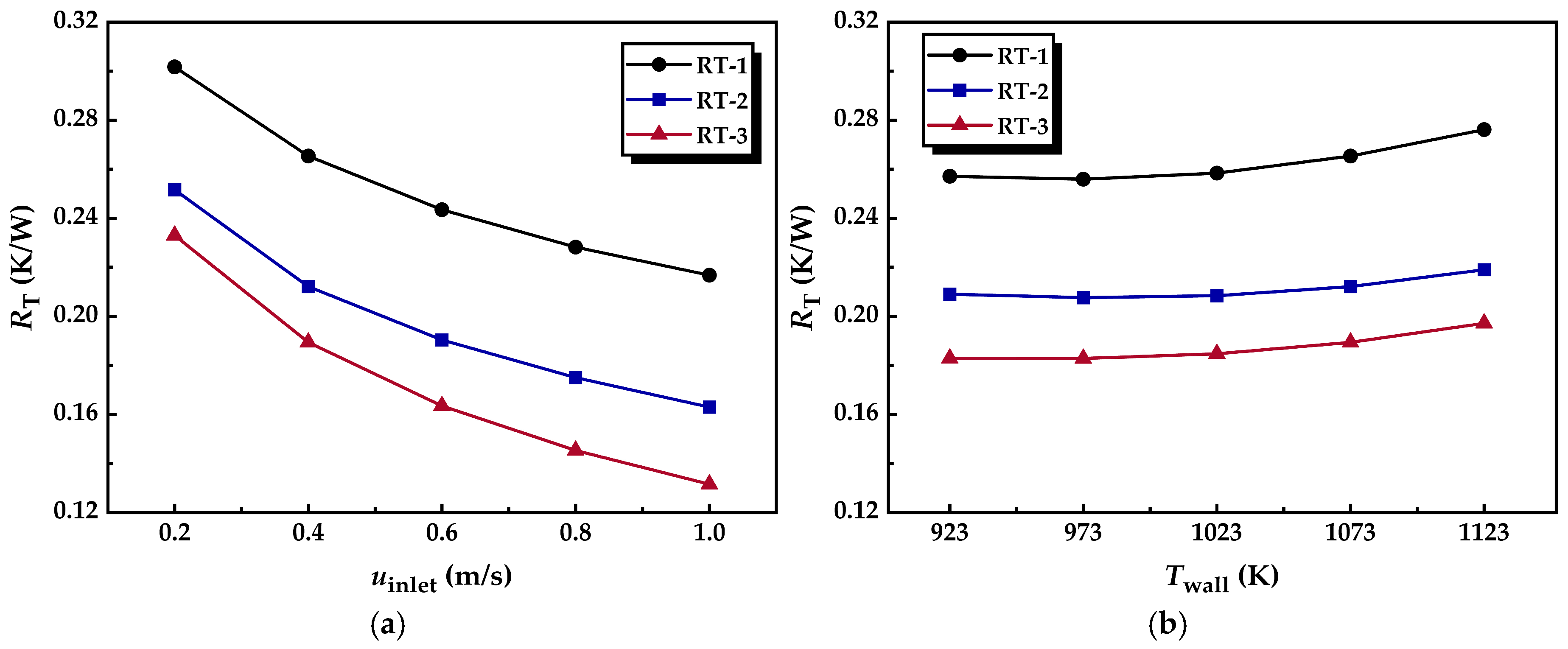
3.2.3. Thermal Resistance
3.3. Reaction Characteristics
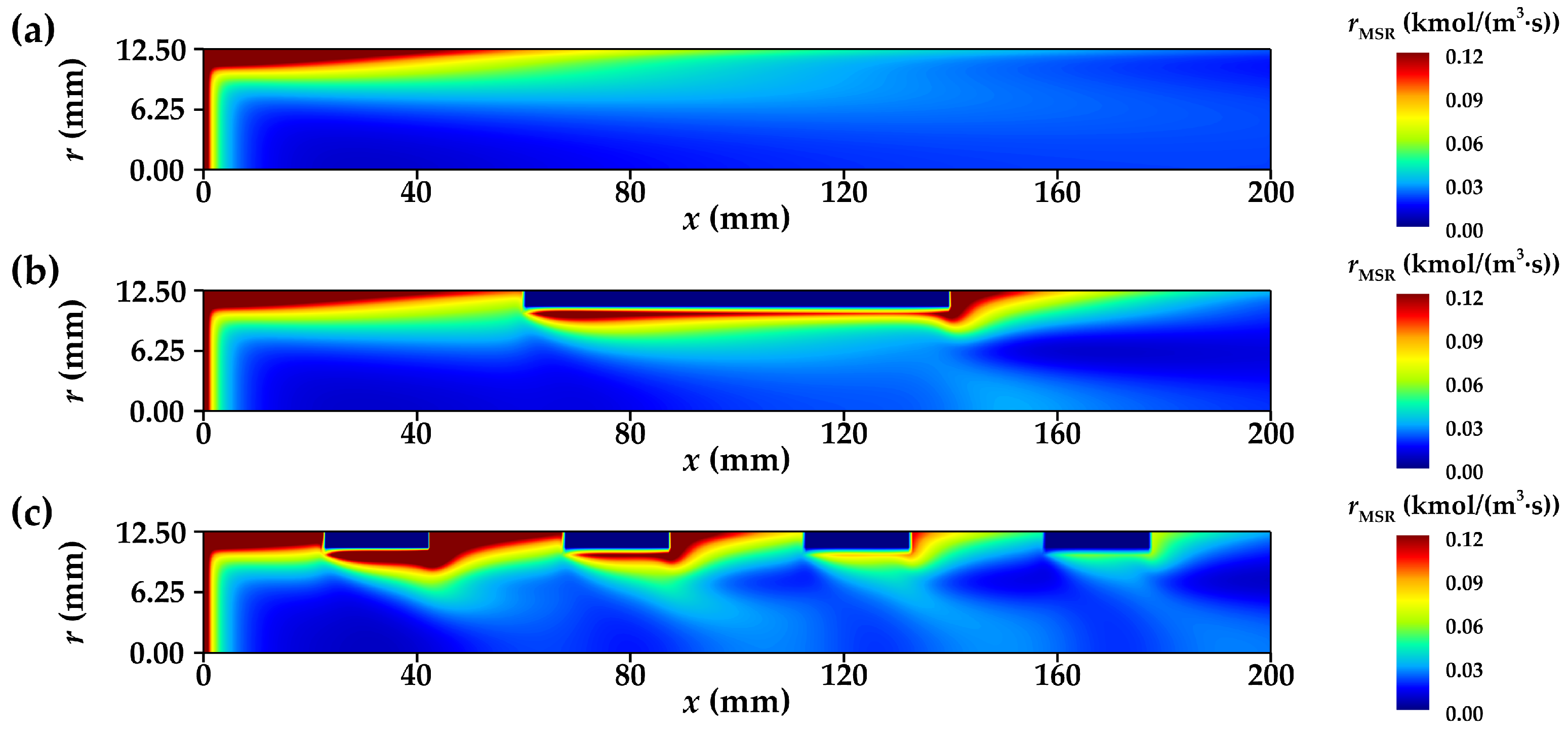
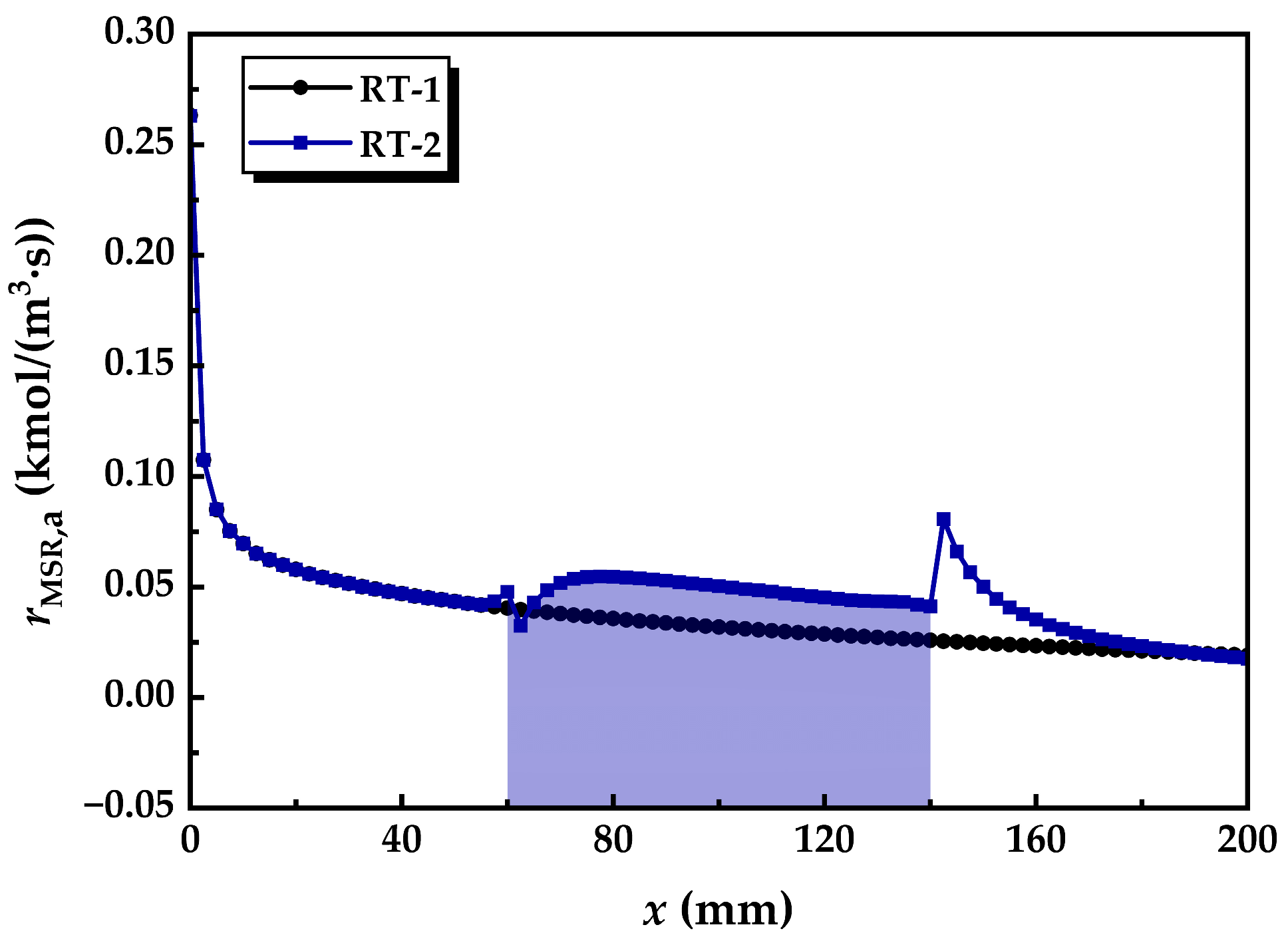
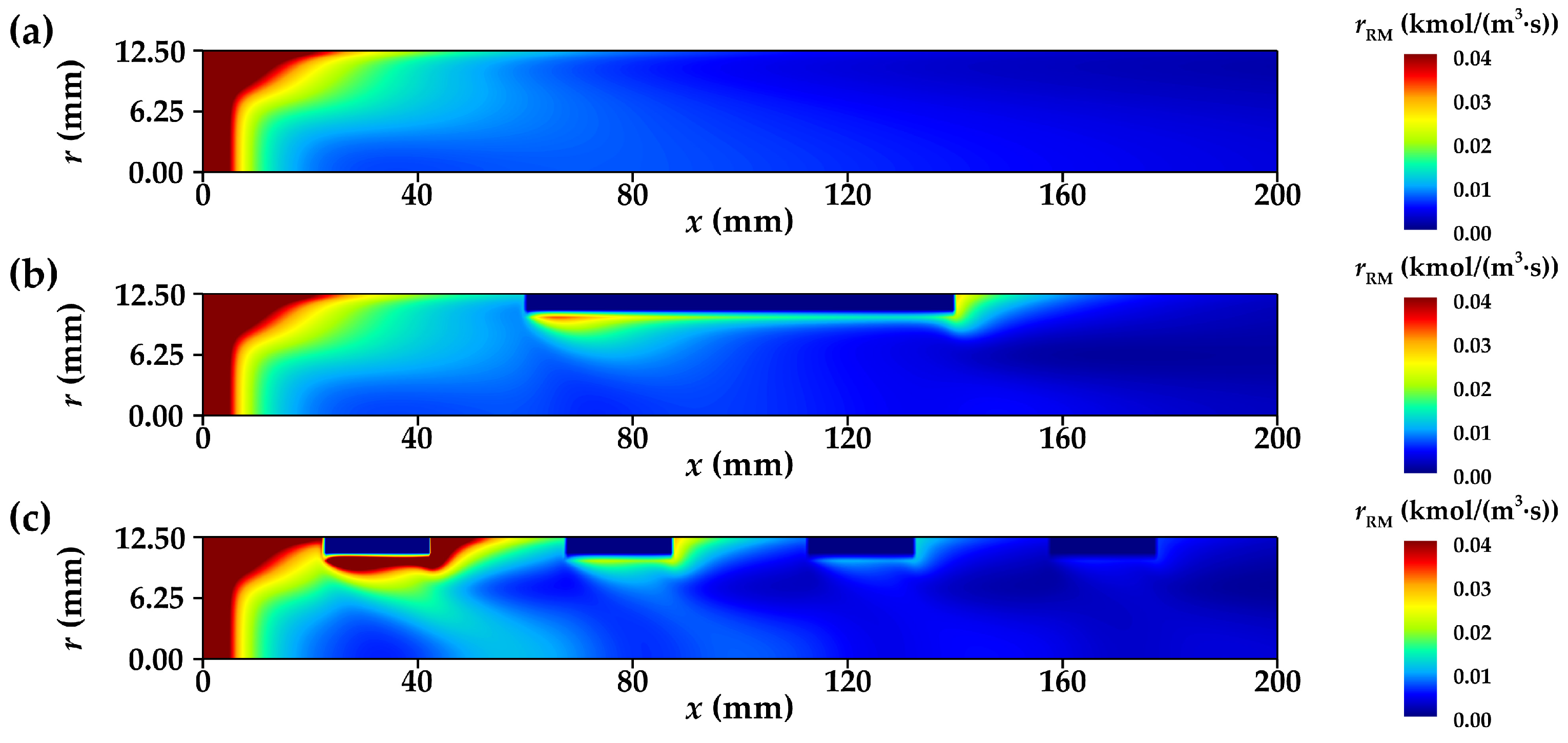
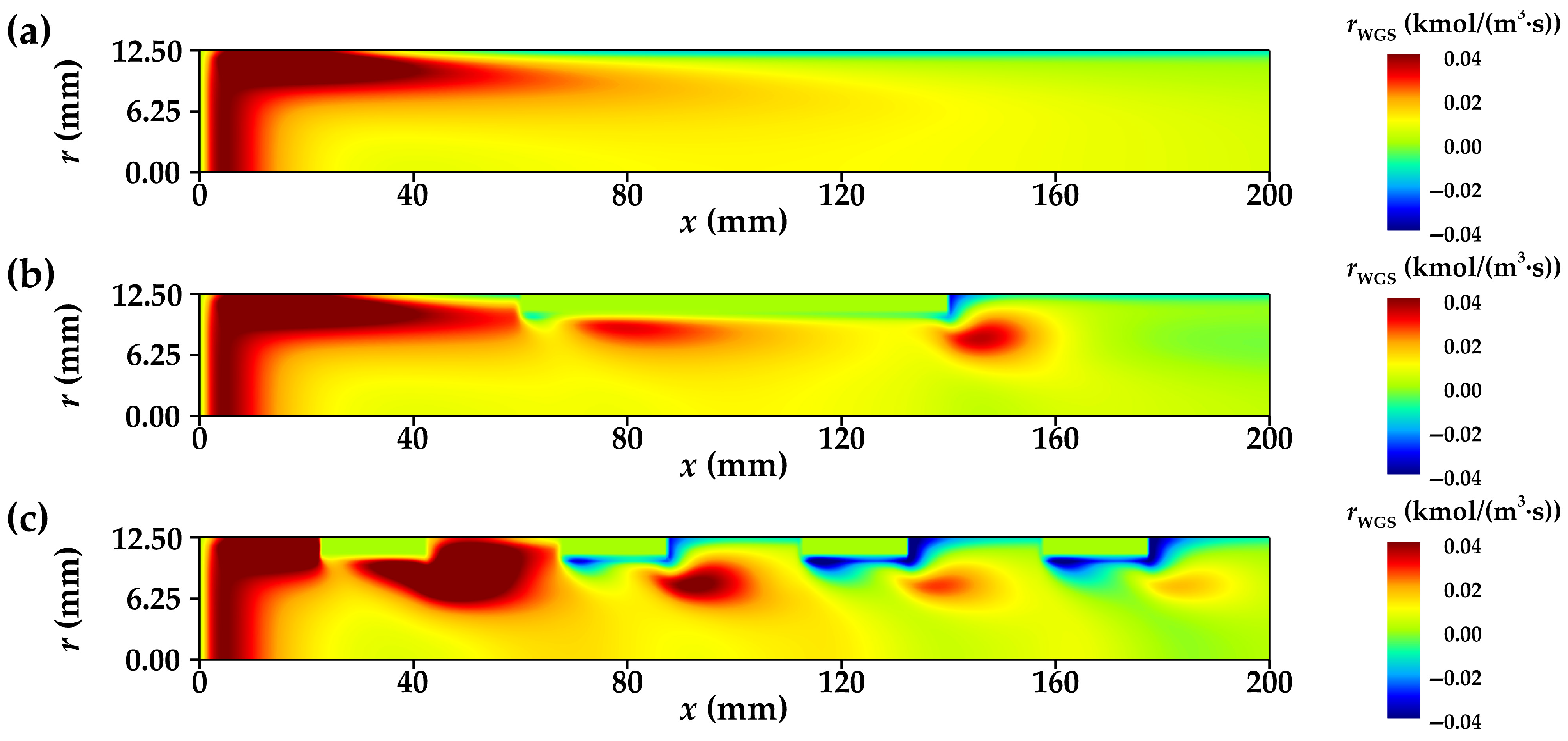
3.3.1. Distribution of Net Reaction Rate
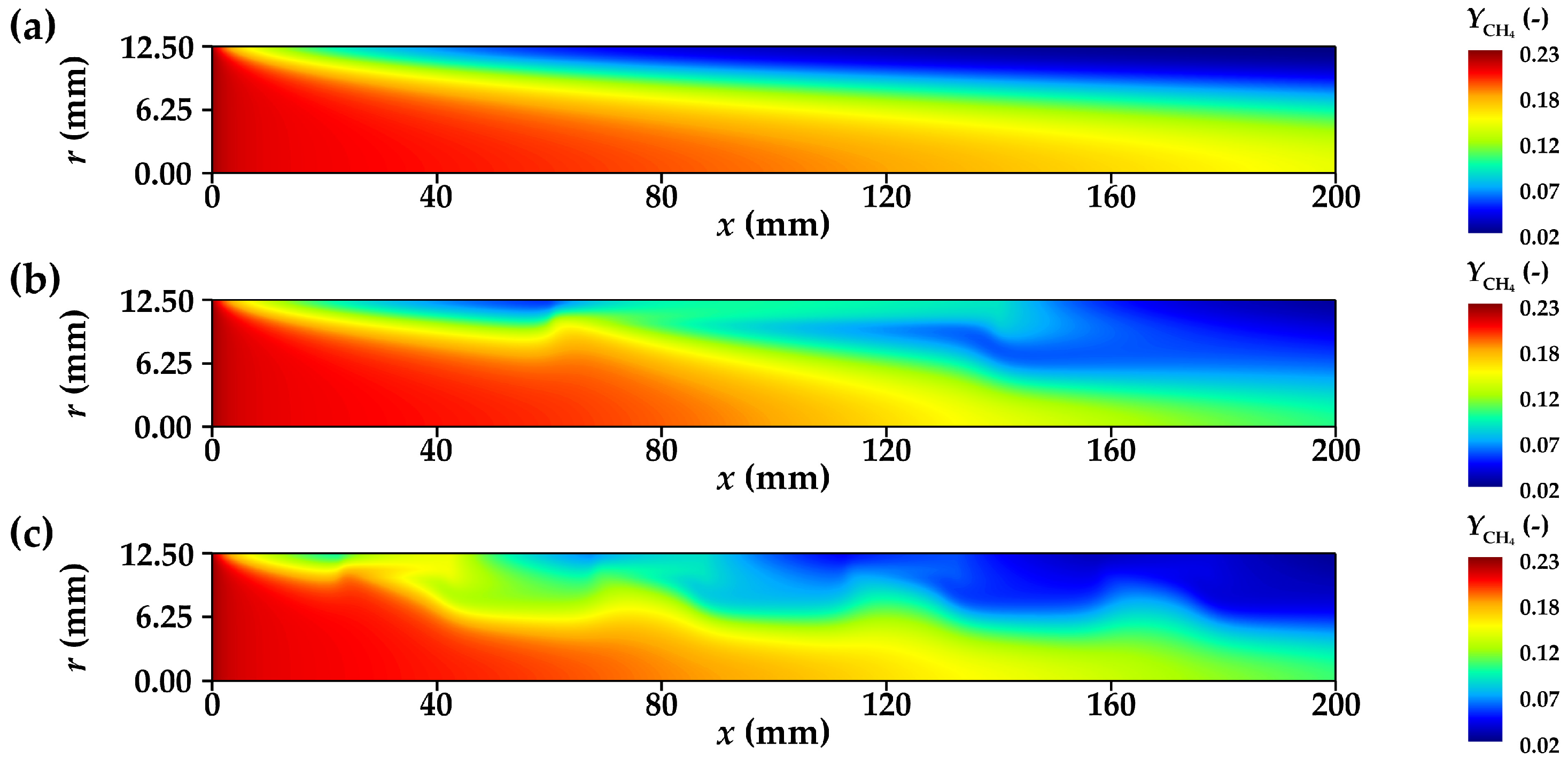
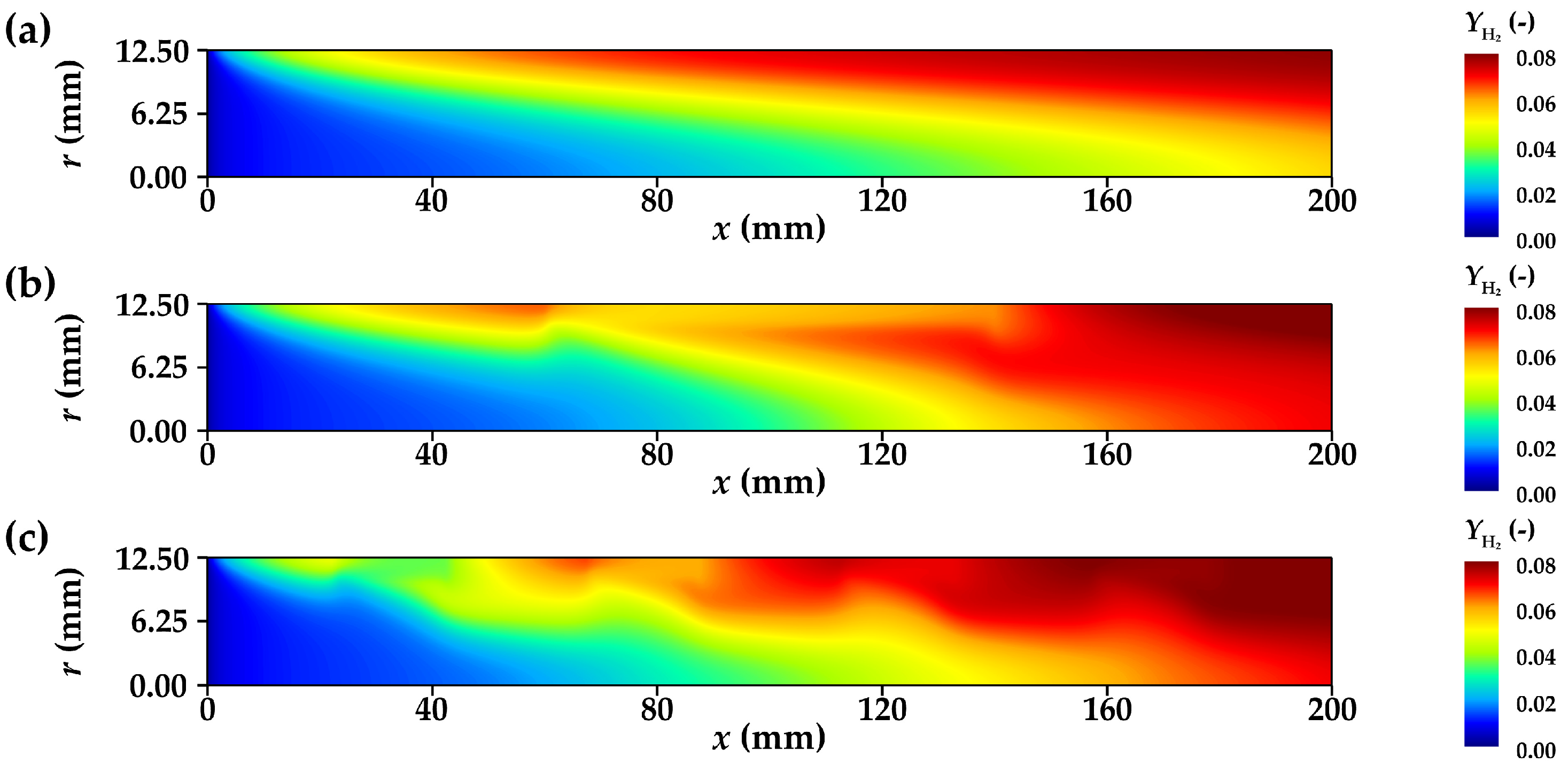
3.3.2. Concentration Distribution of Component Gases
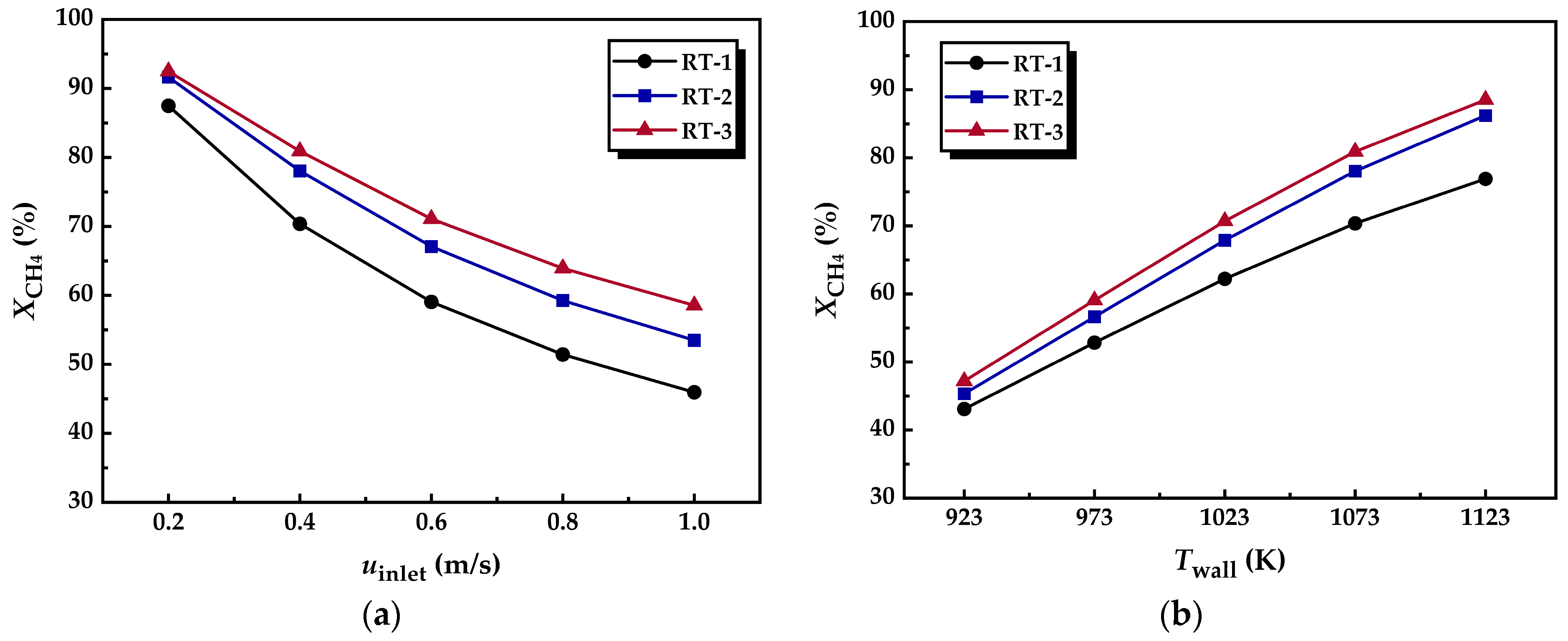
3.3.3. Methane Conversion
4. Conclusions
- The incorporation of annular metal foam gas channels leads to a non-uniform radial distribution of flow resistance within the foam segment, resulting in a flow-splitting effect of the gas mixture. The radial flow induced by the splitting enhances convective heat and mass transfer processes. Additionally, the increased flow proportion through the annular metal foam channels reduces the pressure drop across the reforming tube. In addition, increasing the inlet velocity or decreasing the wall temperature is more beneficial to optimizing the pressure drop of the innovative structure reforming tube.
- Incorporating annular metal foam gas channels reduces the radial thermal conduction resistance within the foam segment. The increased flow proportion through the channel allows the gas mixture to absorb heat more effectively. Moreover, the radial flow resulting from the flow-splitting process enhances convective heat transfer, significantly reducing the overall thermal resistance of the reformer tube.
- The radial flow of fluid and the reduction in thermal resistance within the reforming tube significantly enhance the main reaction rate at multiple locations. Compared to conventional reformers, those equipped with annular metal foam gas channels exhibit higher methane conversion efficiency. Under unfavorable reaction conditions, the annular channel configuration effectively mitigates the negative impacts caused by process deterioration; under favorable conditions, it further amplifies the positive effects on reaction performance. In summary, increasing the inlet velocity or decreasing the wall temperature is conducive to improving the optimization degree of the reaction performance of the innovative structure reforming tube.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| u | velocity (m/s) |
| T | temperature (K) |
| Y | mass fraction |
| Δp | pressure drop (Pa) |
| Q | heat flux (W) |
| XCH4 | methane conversion (%) |
| Df | flow disturbance intensity |
| RT | thermal resistance (K/W) |
| cp | specific heat capacity (J/(kg·K)) |
| Dm | effective mass diffusivity (m2/s) |
| L0 | length of the reforming tube (m) |
| R0 | radius of the reforming tube (m) |
| Greek | |
| ε | porosity |
| η | effectiveness factor |
| ρ | density (kg/m3) |
| λ | thermal conductivity (W/(m·K)) |
| μ | dynamic viscosity (kg/(m·s)) |
| Subscripts | |
| f | gas mixture |
| s | solid phase |
| i (i = MSR, RM, WGS) | chemical reaction |
| i (i = CH4, H2, CO2, CO, H2O) | component gas |
| x | axial direction |
| r | radial direction |
| cat | catalyst |
| foam | metal foam |
| wall | reforming tube wall |
| inlet | reforming tube inlet |
| outlet | reforming tube outlet |
| a | average |
References
- Endo, N.; Goshome, K.; Tetsuhiko, M.; Segawa, Y.; Shimoda, E.; Nozu, T. Thermal Management and Power Saving Operations for Improved Energy Efficiency within a Renewable Hydrogen Energy System Utilizing Metal Hydride Hydrogen Storage. Int. J. Hydrogen Energy 2021, 46, 262–271. [Google Scholar] [CrossRef]
- Parthasarathy, P.; Narayanan, K.S. Hydrogen Production from Steam Gasification of Biomass: Influence of Process Parameters on Hydrogen Yield—A Review. Renew. Energy 2014, 66, 570–579. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I. Review and Evaluation of Hydrogen Production Options for Better Environment. J. Clean. Prod. 2019, 218, 835–849. [Google Scholar] [CrossRef]
- Pizoń, Z.; Kimijima, S.; Brus, G. Enhancing a Deep Learning Model for the Steam Reforming Process Using Data Augmentation Techniques. Energies 2024, 17, 2413. [Google Scholar] [CrossRef]
- Carapellucci, R.; Giordano, L. Steam, Dry and Autothermal Methane Reforming for Hydrogen Production: A Thermodynamic Equilibrium Analysis. J. Power Sources 2020, 469, 228391. [Google Scholar] [CrossRef]
- Hou, K.; Hughes, R. The Kinetics of Methane Steam Reforming over a Ni/α-Al2O Catalyst. Chem. Eng. J. 2001, 82, 311–328. [Google Scholar] [CrossRef]
- Hoang, D.L.; Chan, S.H.; Ding, O.L. Kinetic and Modelling Study of Methane Steam Reforming over Sulfide Nickel Catalyst on a Gamma Alumina Support. Chem. Eng. J. 2005, 112, 1–11. [Google Scholar] [CrossRef]
- Hiramitsu, Y.; Demura, M.; Xu, Y.; Yoshida, M.; Hirano, T. Catalytic Properties of Pure Ni Honeycomb Catalysts for Methane Steam Reforming. Appl. Catal. Gen. 2015, 507, 162–168. [Google Scholar] [CrossRef]
- Tsuda, Y.; Hirano, T.; Echigo, M. Effect of Metal Addition to Ni/CeO2 Catalyst on the Steam Reforming Reaction of Methane. Int. J. Hydrogen Energy 2024, 49, 937–948. [Google Scholar] [CrossRef]
- You, X.; Wang, X.; Ma, Y.; Liu, J.; Liu, W.; Xu, X.; Peng, H.; Li, C.; Zhou, W.; Yuan, P.; et al. Ni-Co/Al2O3 Bimetallic Catalysts for CH4 Steam Reforming: Elucidating the Role of Co for Improving Coke Resistance. ChemCatChem 2014, 6, 3377–3386. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, Z.; Yang, J.; Wang, Q. Numerical Investigation of Hydrogen Production via Methane Steam Reforming in a Novel Packed Bed Reactor Integrated with Diverging Tube. Energy Convers. Manag. 2023, 289, 117185. [Google Scholar] [CrossRef]
- Huang, W.-J.; Yu, C.-T.; Sheu, W.-J.; Chen, Y.-C. The Effect of Non-Uniform Temperature on the Sorption-Enhanced Steam Methane Reforming in a Tubular Fixed-Bed Reactor. Int. J. Hydrogen Energy 2021, 46, 16522–16533. [Google Scholar] [CrossRef]
- Patel, A.; Singh, V.K. Numerical Investigation of a Novel Phase Change Material Based Heat Sink with Double Sided Spiral Fins. Int. Commun. Heat. Mass. Transf. 2022, 138, 106342. [Google Scholar] [CrossRef]
- He, Z.; Yan, Y.; Zhao, T.; Zhang, Z.; Mikulčić, H. Parametric Study of Inserting Internal Spiral Fins on the Micro Combustor Performance for Thermophotovoltaic Systems. Renew. Sustain. Energy Rev. 2022, 165, 112595. [Google Scholar] [CrossRef]
- Kiatpachai, P.; Keawkamrop, T.; Asirvatham, L.G.; Mesgarpour, M.; Dalkılıç, A.S.; Ahn, H.S.; Mahian, O.; Wongwises, S. An Experimental Study of the Air-Side Performance of a Novel Louver Spiral Fin-and-Tube Heat Exchanger. Alex. Eng. J. 2022, 61, 9811–9818. [Google Scholar] [CrossRef]
- Duan, J.; Peng, Z. Numerical Investigation of Nano-Enhanced Phase Change Material Melting in the 3D Annular Tube with Spiral Fins. Renew. Energy 2022, 193, 251–263. [Google Scholar] [CrossRef]
- Jurtz, N.; Flaischlen, S.; Scherf, S.C.; Kraume, M.; Wehinger, G.D. Enhancing the Thermal Performance of Slender Packed Beds through Internal Heat Fins. Processes 2020, 8, 1528. [Google Scholar] [CrossRef]
- Yuan, Q.; Gu, R.; Ding, J.; Lu, J. Heat Transfer and Energy Storage Performance of Steam Methane Reforming in a Tubular Reactor. Appl. Therm. Eng. 2017, 125, 633–643. [Google Scholar] [CrossRef]
- Pashchenko, D.; Mustafin, R.; Mustafina, A. Steam Methane Reforming in a Microchannel Reformer: Experiment, CFD-Modelling and Numerical Study. Energy 2021, 237, 121624. [Google Scholar] [CrossRef]
- Palma, V.; Ricca, A.; Martino, M.; Meloni, E. Innovative Structured Catalytic Systems for Methane Steam Reforming Intensification. Chem. Eng. Process. Process Intensif. 2017, 120, 207–215. [Google Scholar] [CrossRef]
- Suzuki, K.; Iwai, H.; Nishino, T. Electrochemical and Thermofluid Modeling of a Tubular Solid Oxide Fuel Cell with Accompanying Indirect Internal Fuel Reforming; WIT Press: Billerica, MA, USA, 2005. [Google Scholar]
- Mozdzierz, M.; Brus, G.; Sciazko, A.; Komatsu, Y.; Kimijima, S.; Szmyd, J.S. Towards a Thermal Optimization of a Methane/Steam Reforming Reactor. Flow. Turbul. Combust. 2016, 97, 171–189. [Google Scholar] [CrossRef]
- Chen, C.; Diao, Y.; Zhao, Y.; Zhu, T.; Wang, Z.; Han, Y.; Liu, Y. Performance Prediction of a Fin-Metal Foam-Cold Thermal Energy Storage Device: Solidification. Int. J. Heat. Mass. Transf. 2023, 202, 123672. [Google Scholar] [CrossRef]
- Stark, J.R.; Sevart, C.D.; Bergman, T.L. Experimentally Validated Analytical Expressions for the Thermal Resistance of a Novel Composite Fin-Foam Annular Array. Appl. Therm. Eng. 2018, 131, 260–269. [Google Scholar] [CrossRef]
- Samudre, P.; Kailas, S.V. Thermal Performance Enhancement in Open-Pore Metal Foam and Foam-Fin Heat Sinks for Electronics Cooling. Appl. Therm. Eng. 2022, 205, 117885. [Google Scholar] [CrossRef]
- Yang, X.; Wei, P.; Liu, G.; Bai, Q.; He, Y.-L. Performance Evaluation on the Gradient Design of Pore Parameters for Metal Foam and Pin Fin-Metal Foam Hybrid Structure. Appl. Therm. Eng. 2020, 175, 115416. [Google Scholar] [CrossRef]
- Zaio, F.; Ambrosetti, M.; Beretta, A.; Groppi, G.; Tronconi, E. Intensification of Methane Steam Reforming by Cu-Foams Packed with Rh-Al2O3 Catalyst: A Pilot-Scale Assessment. Chem. Eng. Res. Des. 2025, 215, 98–107. [Google Scholar] [CrossRef]
- Ferri, G.; Ambrosetti, M.; Beretta, A.; Groppi, G.; Tronconi, E. Experimental Investigation and 2D Mathematical Modelling of Copper Foams Packed with Rh-Al2O3 Catalysts for the Intensification of Methane Steam Reforming. Catal. Today 2024, 426, 114386. [Google Scholar] [CrossRef]
- Settar, A.; Nebbali, R.; Madani, B.; Abboudi, S. Numerical Investigation on the Wall-Coated Steam Methane Reformer Improvement: Effects of Catalyst Layer Patterns and Metal Foam Insertion. Int. J. Hydrogen Energy 2015, 40, 8966–8979. [Google Scholar] [CrossRef]
- Settar, A.; Abboudi, S.; Lebaal, N. Effect of Inert Metal Foam Matrices on Hydrogen Production Intensification of Methane Steam Reforming Process in Wall-Coated Reformer. Int. J. Hydrogen Energy 2018, 43, 12386–12397. [Google Scholar] [CrossRef]
- Pajak, M.; Mozdzierz, M.; Chalusiak, M.; Kimijima, S.; Szmyd, J.S.; Brus, G. A Numerical Analysis of Heat and Mass Transfer Processes in a Macro-Patterned Methane/Steam Reforming Reactor. Int. J. Hydrogen Energy 2018, 43, 20474–20487. [Google Scholar] [CrossRef]
- Pajak, M.; Brus, G.; Kimijima, S.; Szmyd, J.S. Coaxial Multi-Criteria Optimization of a Methane Steam Reforming Reactor for Effective Hydrogen Production and Thermal Management. Energy AI 2023, 13, 100264. [Google Scholar] [CrossRef]
- Mokheimer, E.M.A.; Ibrar Hussain, M.; Ahmed, S.; Habib, M.A.; Al-Qutub, A.A. On the Modeling of Steam Methane Reforming. J. Energy Resour. Technol. 2015, 137, 012001. [Google Scholar] [CrossRef]
- Lao, L.; Aguirre, A.; Tran, A.; Wu, Z.; Durand, H.; Christofides, P.D. CFD Modeling and Control of a Steam Methane Reforming Reactor. Chem. Eng. Sci. 2016, 148, 78–92. [Google Scholar] [CrossRef]
- Sheu, W.-J.; Chu, C.-S.; Chen, Y.-C. The Operation Types and Operation Window for High-Purity Hydrogen Production for the Sorption Enhanced Steam Methane Reforming in a Fixed-Bed Reactor. Int. J. Hydrogen Energy 2022, 47, 37192–37203. [Google Scholar] [CrossRef]
- Amini, A.; Sedaghat, M.H.; Jamshidi, S.; Shariati, A.; Rahimpour, M.R. A Comprehensive CFD Simulation of an Industrial-Scale Side-Fired Steam Methane Reformer to Enhance Hydrogen Production. Chem. Eng. Process. Process Intensif. 2023, 184, 109269. [Google Scholar] [CrossRef]
- Baek, S.M.; Kang, J.H.; Lee, K.-J.; Nam, J.H. A Numerical Study of the Effectiveness Factors of Nickel Catalyst Pellets Used in Steam Methane Reforming for Residential Fuel Cell Applications. Int. J. Hydrogen Energy 2014, 39, 9180–9192. [Google Scholar] [CrossRef]
- Dixon, A.G. Local Transport and Reaction Rates in a Fixed Bed Reactor Tube: Endothermic Steam Methane Reforming. Chem. Eng. Sci. 2017, 168, 156–177. [Google Scholar] [CrossRef]
- Mancin, S.; Zilio, C.; Diani, A.; Rossetto, L. Experimental Air Heat Transfer and Pressure Drop through Copper Foams. Exp. Therm. Fluid. Sci. 2012, 36, 224–232. [Google Scholar] [CrossRef]
- Xu, J.; Froment, G.F. Methane Steam Reforming, Methanation and Water-gas Shift: I. Intrinsic Kinetics. AIChE J. 1989, 35, 88–96. [Google Scholar] [CrossRef]
- Zanfir, M.; Gavriilidis, A. Catalytic Combustion Assisted Methane Steam Reforming in a Catalytic Plate Reactor. Chem. Eng. Sci. 2003, 58, 3947–3960. [Google Scholar] [CrossRef]
- Dehkordi, A.M.; Memari, M. Compartment Model for Steam Reforming of Methane in a Membrane-Assisted Bubbling Fluidized-Bed Reactor. Int. J. Hydrogen Energy 2009, 34, 1275–1291. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. The Properties of Gases and Liquids; Mcgraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Perry, R.H.; Green, D.W. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Eisfeld, B.; Schnitzlein, K. The Influence of Confining Walls on the Pressure Drop in Packed Beds. Chem. Eng. Sci. 2001, 56, 4321–4329. [Google Scholar] [CrossRef]
- Ngo, S.I.; Lim, Y.-I.; Kim, W.; Seo, D.J.; Yoon, W.L. Computational Fluid Dynamics and Experimental Validation of a Compact Steam Methane Reformer for Hydrogen Production from Natural Gas. Appl. Energy 2019, 236, 340–353. [Google Scholar] [CrossRef]
- Ni, M. 2D Heat and Mass Transfer Modeling of Methane Steam Reforming for Hydrogen Production in a Compact Reformer. Energy Convers. Manag. 2013, 65, 155–163. [Google Scholar] [CrossRef]
- Wang, H.; Duan, X.; Liu, X.; Ye, G.; Gu, X.; Zhu, K.; Zhou, X.; Yuan, W. Influence of Tubular Reactor Structure and Operating Conditions on Dry Reforming of Methane. Chem. Eng. Res. Des. 2018, 139, 39–51. [Google Scholar] [CrossRef]
- Ni, M. 2D Thermal Modeling of a Solid Oxide Electrolyzer Cell (SOEC) for Syngas Production by H2O/CO2 Co-Electrolysis. Int. J. Hydrogen Energy 2012, 37, 6389–6399. [Google Scholar] [CrossRef]
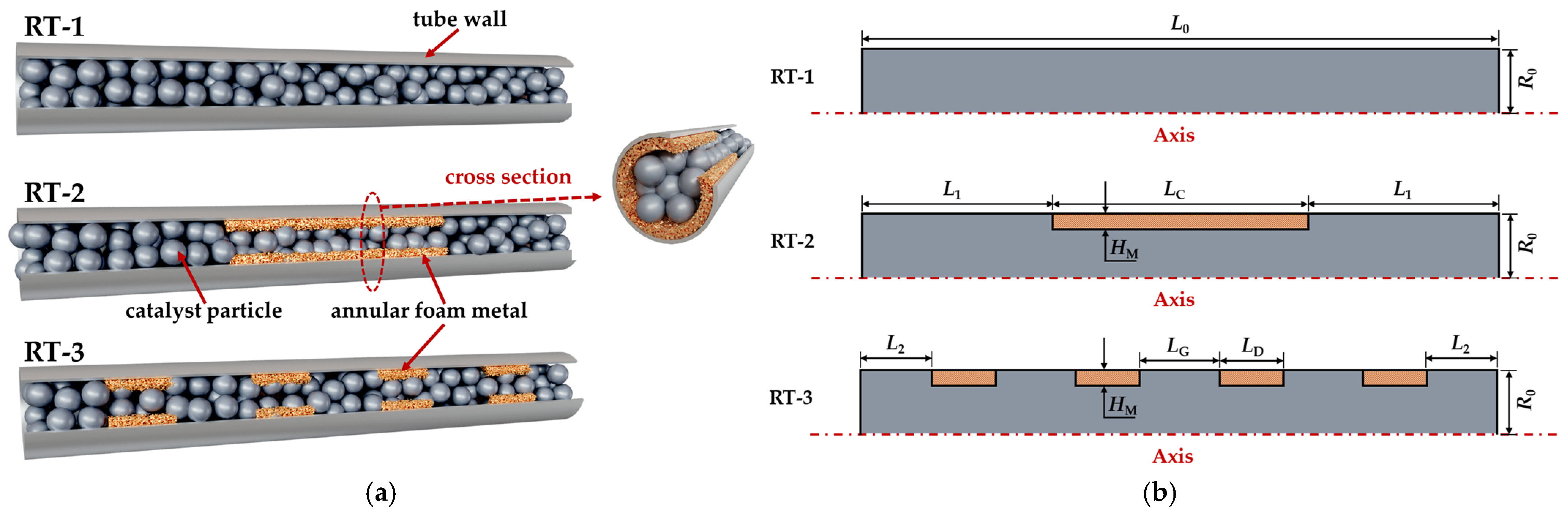
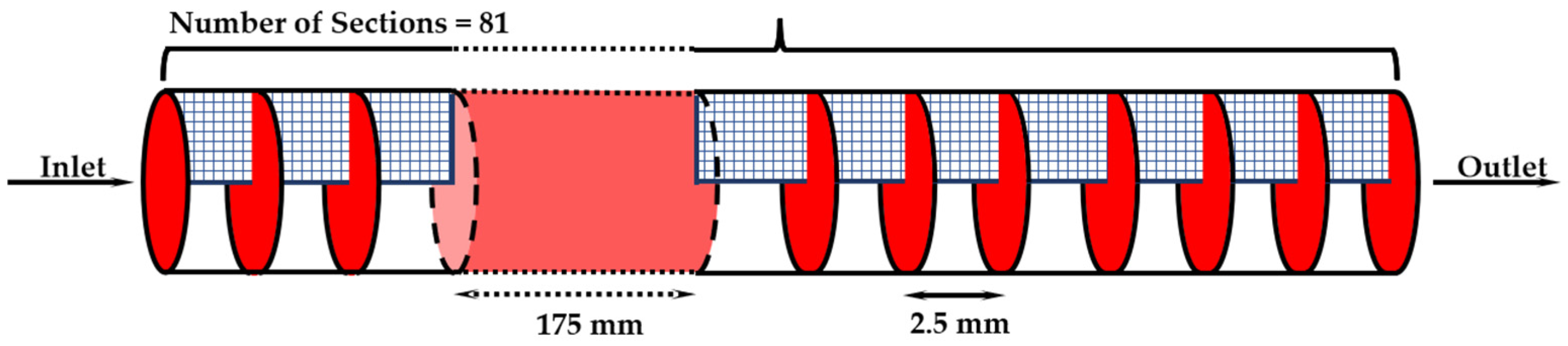
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| L0/(mm) | 200 | LC/(mm) | 80 |
| R0/(mm) | 12.5 | LD/(mm) | 20 |
| L1(mm) | 60 | LG/(mm) | 25 |
| L2/(mm) | 22.5 | HM/(mm) | 2 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| A(kMSR)/(kmol·bar0.5/(kgcat·h)) | 4.225 × 1015 | A(KCH4)/bar−1 | 6.65 × 10−4 |
| A(kRM)/(kmol·bar0.5/(kgcat·h)) | 1.020 × 1015 | A(KH2)/bar−1 | 6.12 × 10−9 |
| A(kWGS)/(kmol/(kgcat·h·bar)) | 1.955 × 106 | A(KCO)/bar−1 | 8.23 × 10−5 |
| EMSR/(J/kmol) | 2.401 × 108 | A(KH2O)/[-] | 1.77 × 105 |
| ERM/(J/kmol) | 2.439 × 108 | ΔHCH4/(J/kmol) | −3.828 × 108 |
| EWGS/(J/kmol) | 6.713 × 107 | ΔHH2/(J/kmol) | −8.290 × 108 |
| ΔHCO/(J/kmol) | −7.065 × 108 | ||
| ΔHH2O/(J/kmol) | 8.868 × 108 |
| uinlet | Tinlet | Twall | Pt | S/C |
|---|---|---|---|---|
| 0.2, 0.4, 0.6, 0.8, 1.0 m/s | 873 K | 1073 K | 5 bar | 3.0 |
| uinlet | Tinlet | Twall | Pt | S/C |
|---|---|---|---|---|
| 0.4 m/s | 873 K | 923, 973, 1023, 1073, 1123 K | 5 bar | 3.0 |
| uinlet (m/s) | Twall (K) | Δp (Pa) of RT-1 | Δp of RT-2 | Δp of RT-3 | RT (K/W) of RT-1 | RT of RT-2 | RT of RT-3 | XCH4 (%) of RT-1 | XCH4 of RT-2 | XCH4 of RT-3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 1073 | 267.73 | 220.59 | 231.41 | 0.30171 | 0.25159 | 0.233 | 87.471 | 91.64 | 92.473 |
| 0.4 | 554.94 | 449.31 | 476.8 | 0.26537 | 0.21214 | 0.18939 | 70.361 | 78.049 | 80.896 | |
| 0.6 | 900.58 | 714.5 | 765.71 | 0.24348 | 0.19042 | 0.1635 | 59.044 | 67.079 | 71.084 | |
| 0.8 | 1309.5 | 1021.9 | 1103.7 | 0.22825 | 0.17507 | 0.14534 | 51.417 | 59.245 | 63.918 | |
| 1.0 | 1783.2 | 1373 | 1491.9 | 0.21678 | 0.16295 | 0.13155 | 45.948 | 53.481 | 58.552 |
| Twall (K) | uinlet (m/s) | Δp (Pa) of RT-1 | Δp of RT-2 | Δp of RT-3 | RT (K/W) of RT-1 | RT of RT-2 | RT of RT-3 | XCH4 (%) of RT-1 | XCH4 of RT-2 | XCH4 of RT-3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 923 | 0.4 | 437.92 | 342.69 | 359.62 | 0.25712 | 0.20905 | 0.18285 | 43.087 | 45.335 | 47.187 |
| 973 | 476.19 | 376.55 | 396.85 | 0.25594 | 0.20764 | 0.18281 | 52.842 | 56.631 | 59.059 | |
| 1023 | 515.55 | 412.28 | 436.12 | 0.25842 | 0.20843 | 0.18473 | 62.206 | 67.872 | 70.702 | |
| 1073 | 554.94 | 449.31 | 476.8 | 0.26537 | 0.21214 | 0.18939 | 70.361 | 78.049 | 80.896 | |
| 1123 | 593.57 | 487.05 | 518.19 | 0.27616 | 0.21901 | 0.19716 | 76.902 | 86.204 | 88.531 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Y.; Zhang, Z.; Wang, Z.; Zhang, G. Numerical Investigation of Hydrogen Production via Methane Steam Reforming in Tubular Packed Bed Reactors Integrated with Annular Metal Foam Gas Channels. Energies 2025, 18, 4758. https://doi.org/10.3390/en18174758
Han Y, Zhang Z, Wang Z, Zhang G. Numerical Investigation of Hydrogen Production via Methane Steam Reforming in Tubular Packed Bed Reactors Integrated with Annular Metal Foam Gas Channels. Energies. 2025; 18(17):4758. https://doi.org/10.3390/en18174758
Chicago/Turabian StyleHan, Yifan, Zihui Zhang, Zhen Wang, and Guanmin Zhang. 2025. "Numerical Investigation of Hydrogen Production via Methane Steam Reforming in Tubular Packed Bed Reactors Integrated with Annular Metal Foam Gas Channels" Energies 18, no. 17: 4758. https://doi.org/10.3390/en18174758
APA StyleHan, Y., Zhang, Z., Wang, Z., & Zhang, G. (2025). Numerical Investigation of Hydrogen Production via Methane Steam Reforming in Tubular Packed Bed Reactors Integrated with Annular Metal Foam Gas Channels. Energies, 18(17), 4758. https://doi.org/10.3390/en18174758





