Investigation of the Effectiveness of a Compact Heat Exchanger with Metal Foam in Supercritical Carbon Dioxide Cooling
Abstract
1. Introduction
1.1. Background on Heat Exchanger Research
1.2. Current Challenges in PCHE Design
1.3. Research Concept, Objectives, and Novelty
2. Numerical Investigation
2.1. Physical Models
2.2. Computational Domain and Boundary Conditions
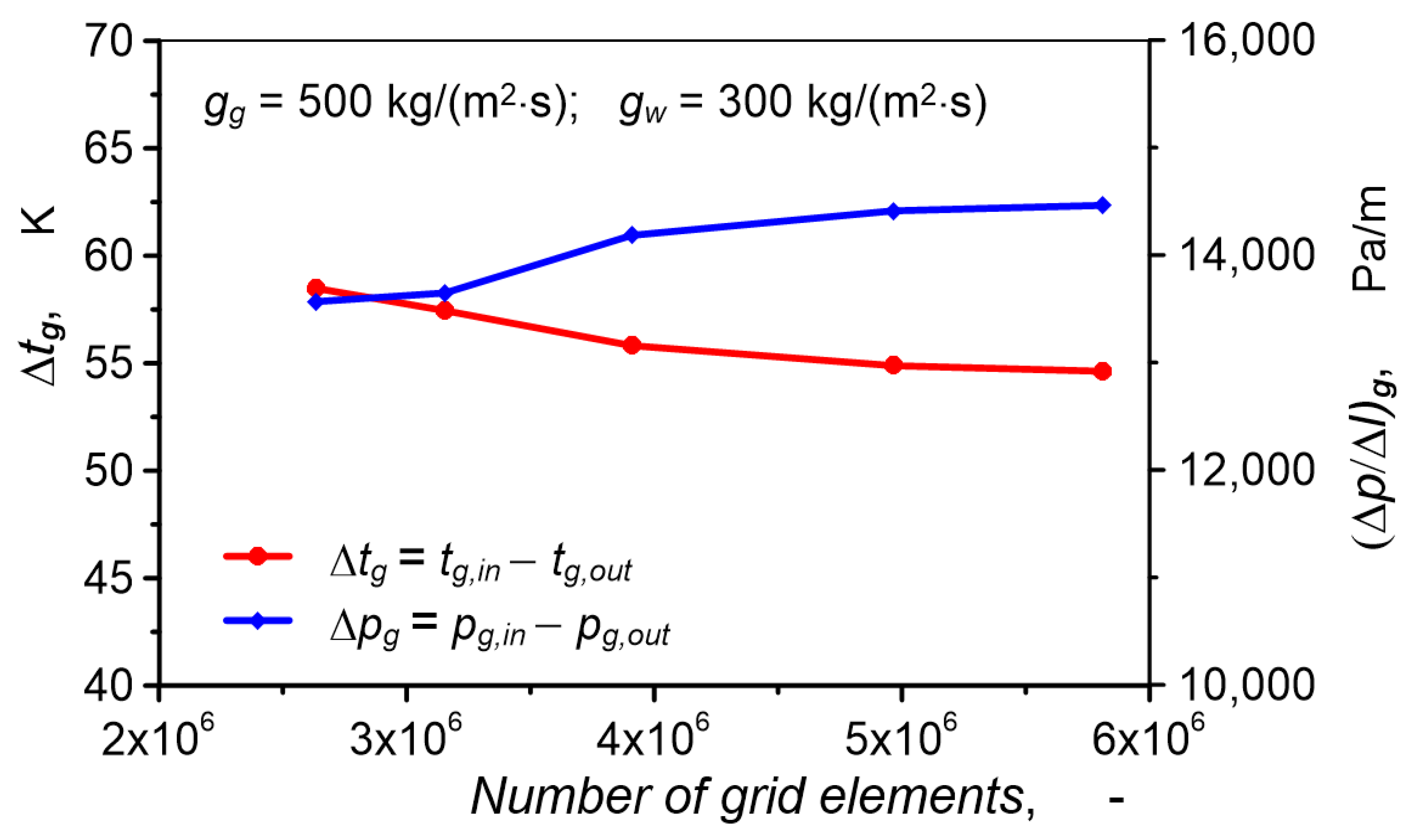
2.3. Numerical Schemes and Validation
2.4. Simulation Conditions
3. Results and Discussion
3.1. Data Reduction
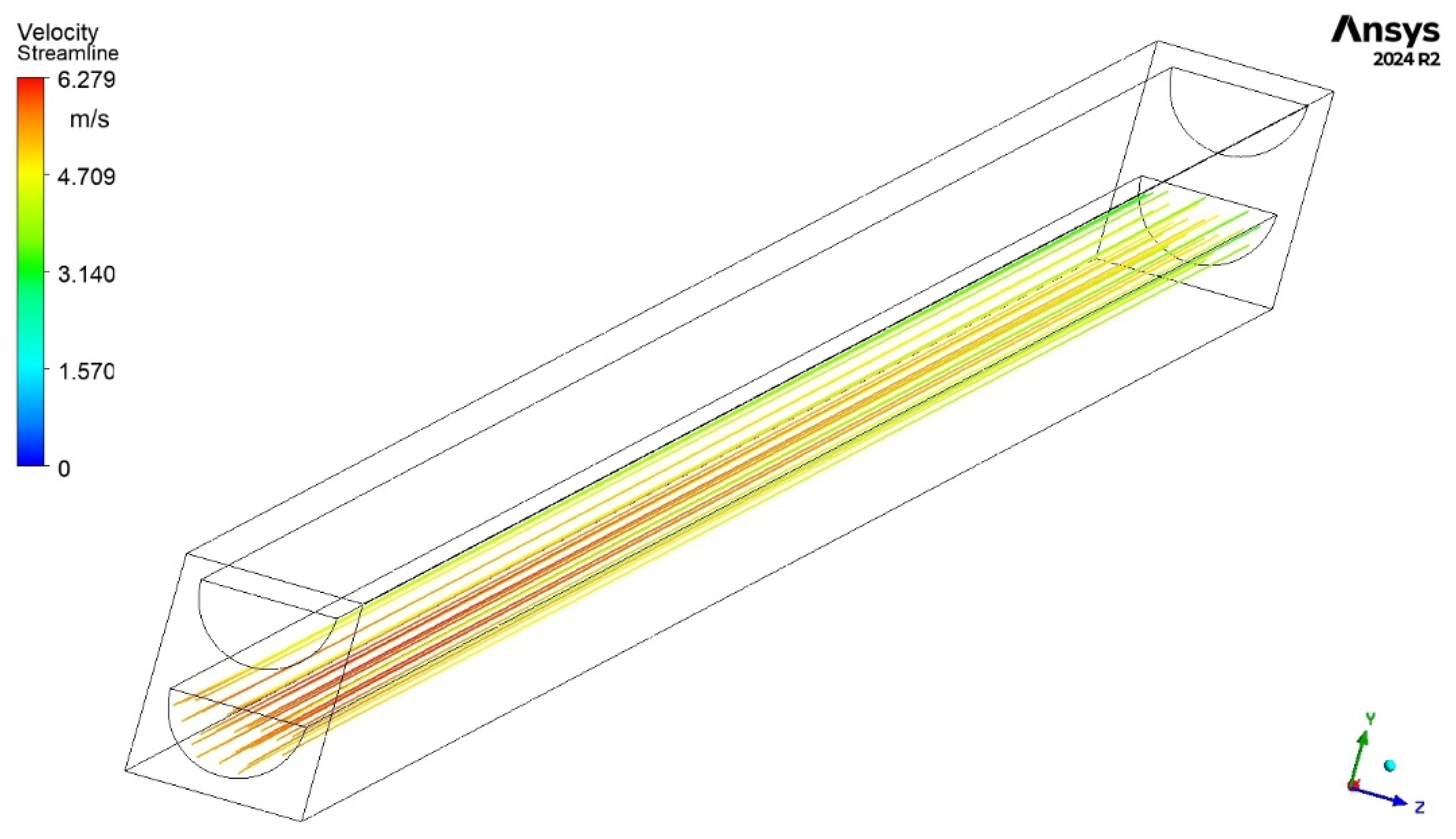
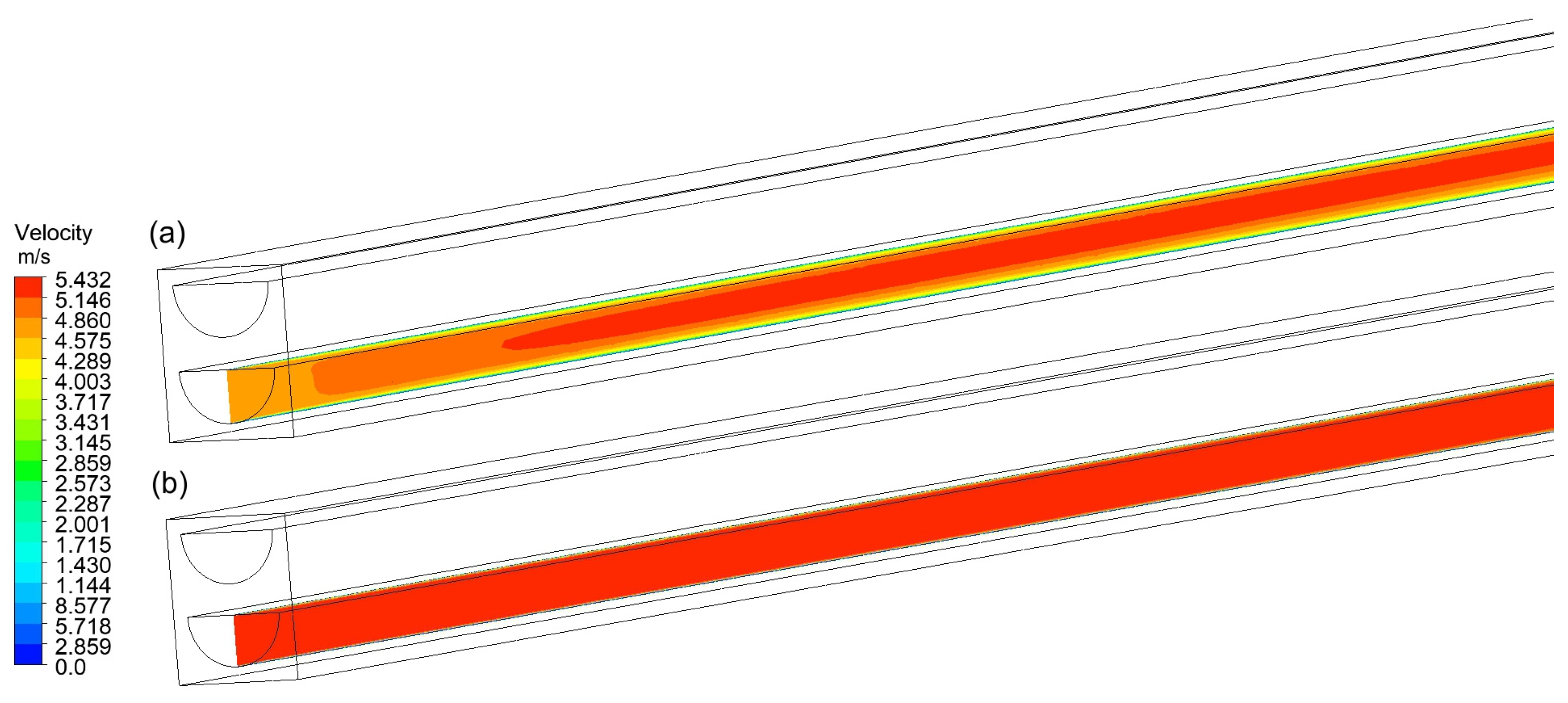
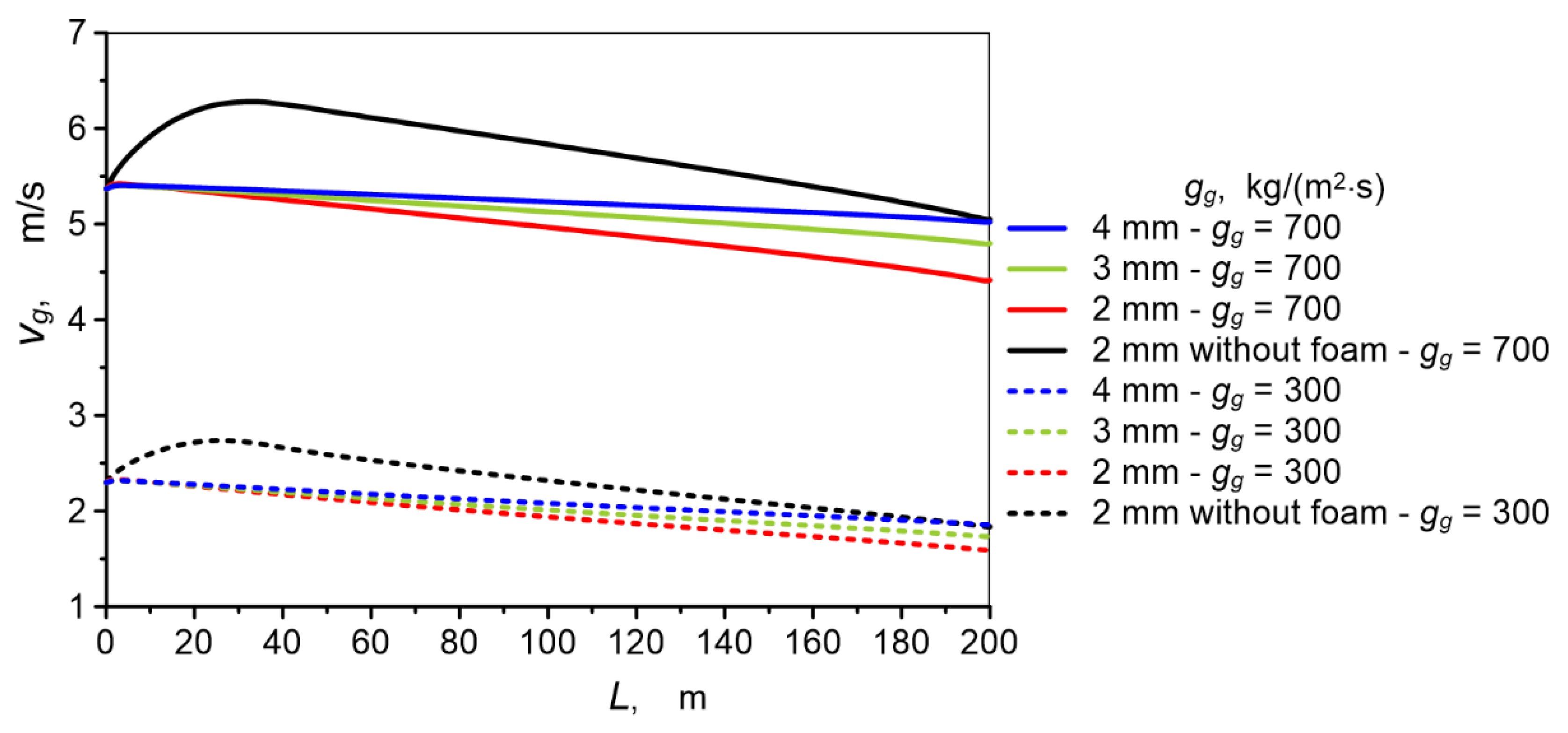
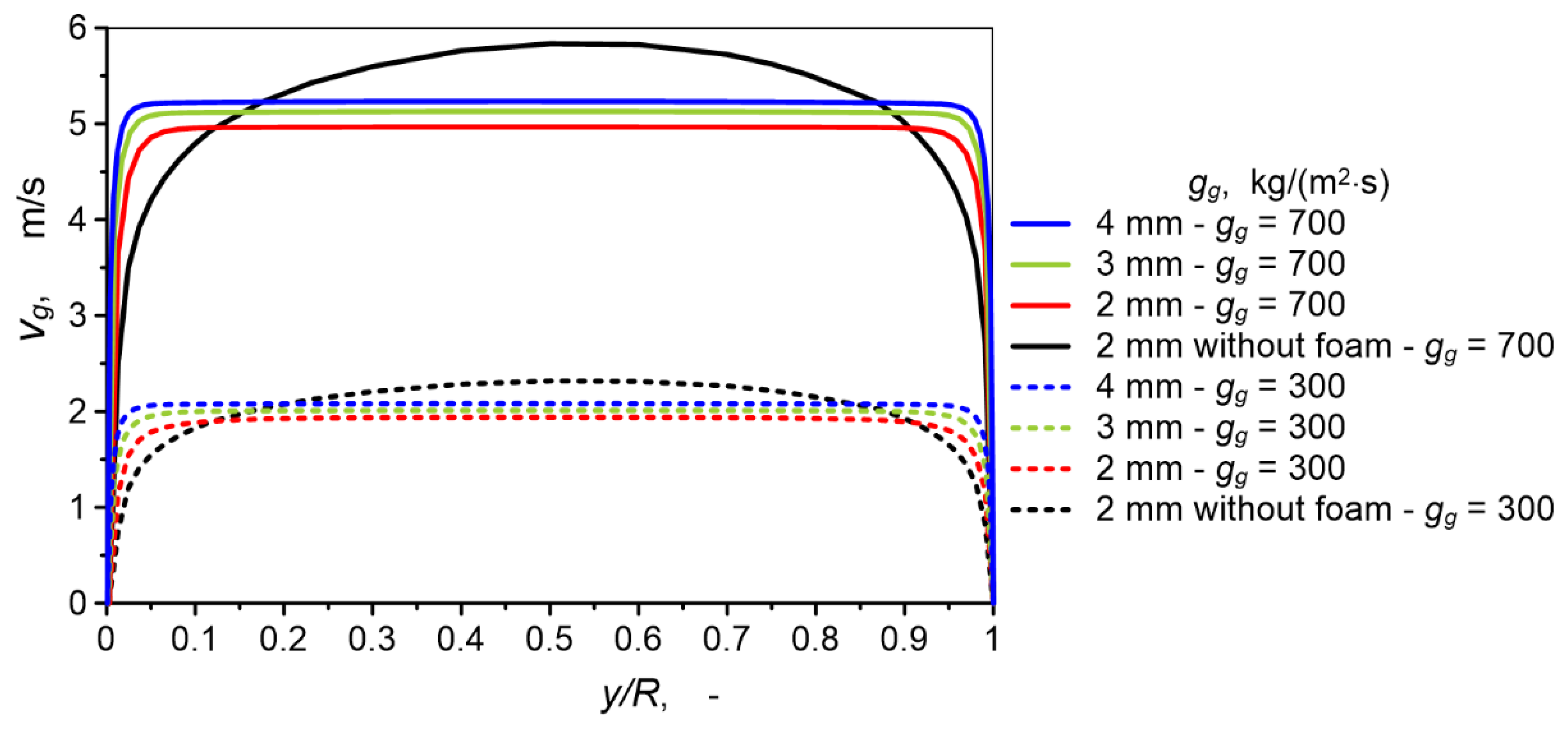
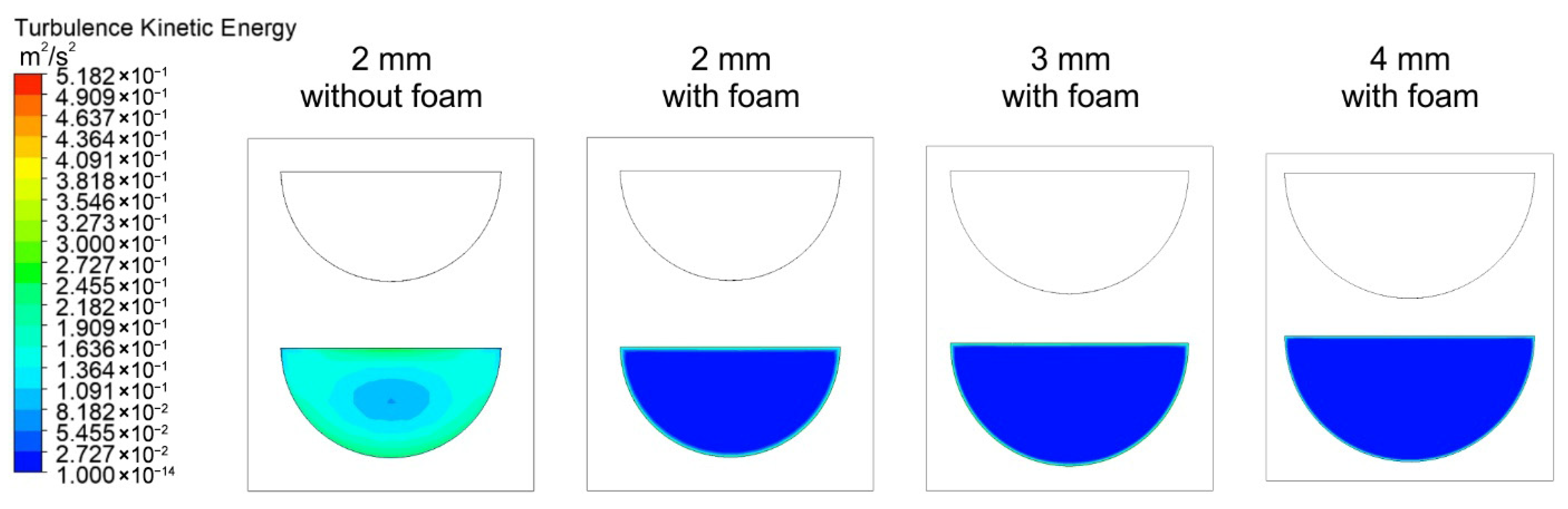
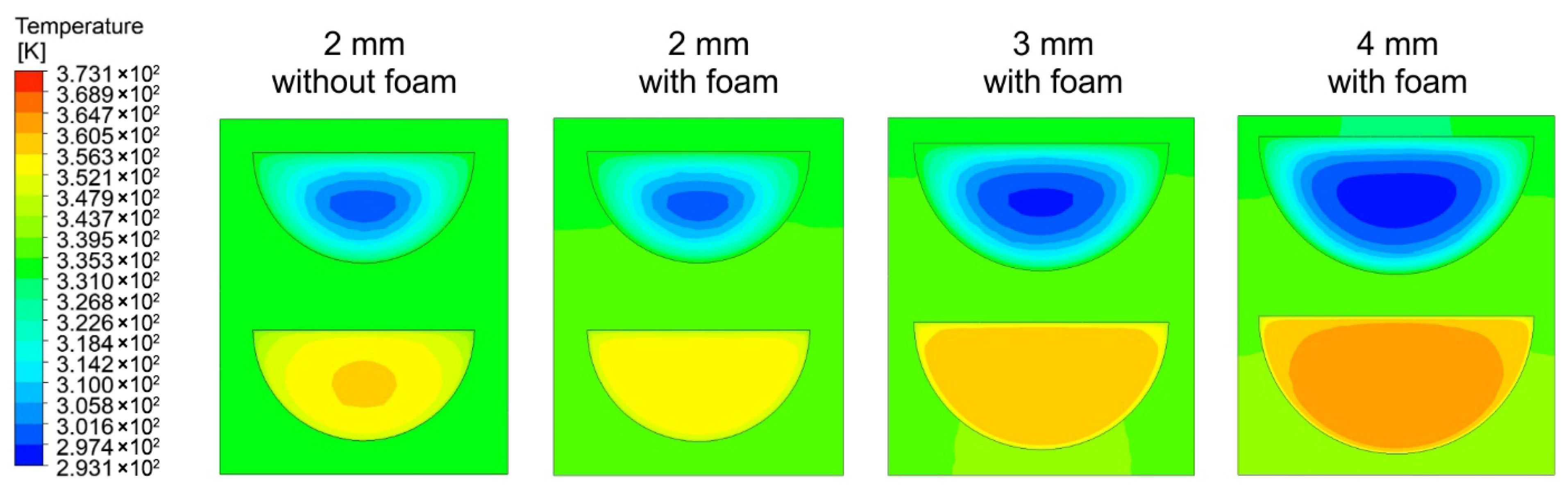
3.2. Flow and Thermal Visualization
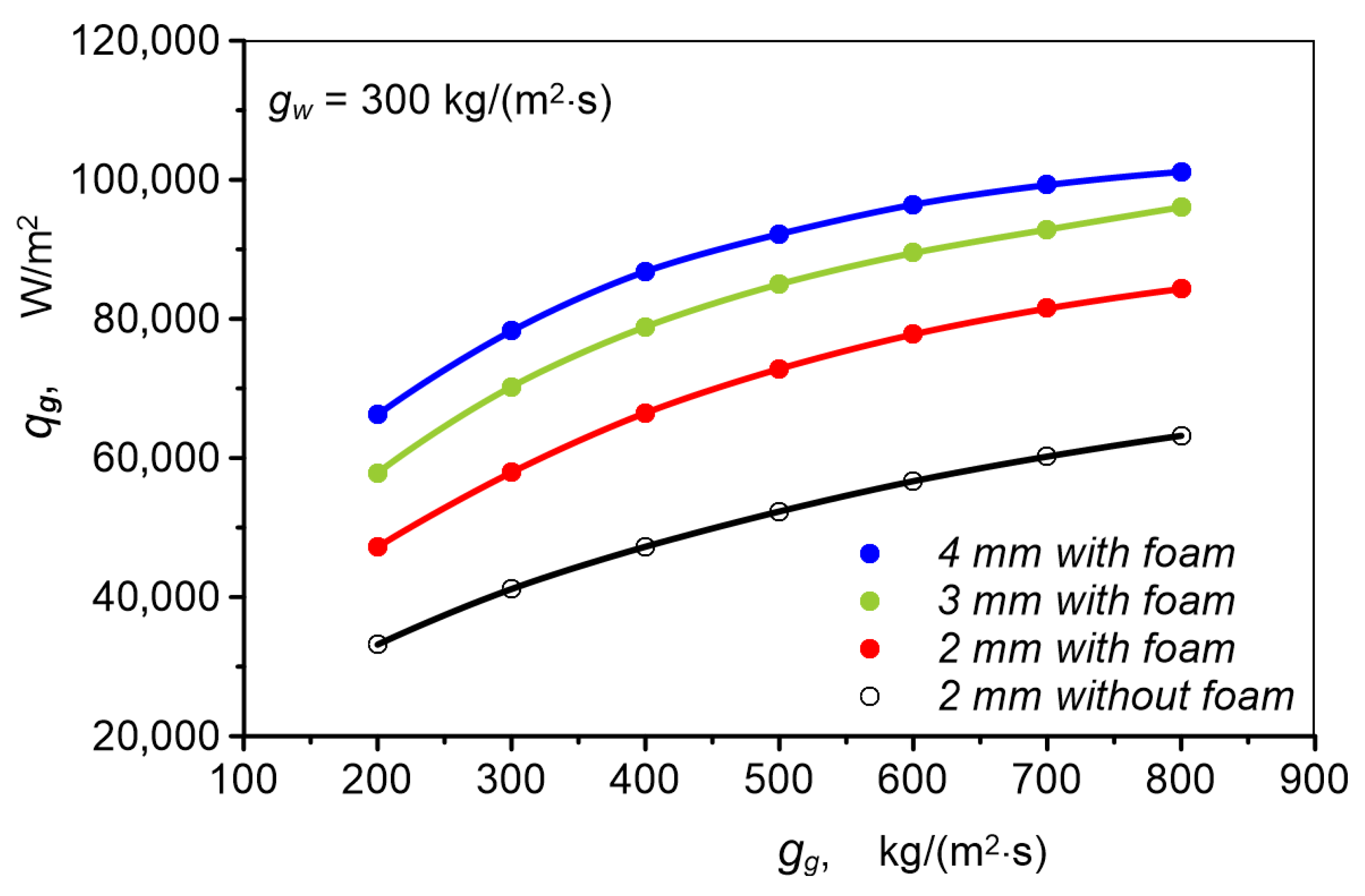
3.3. Heat Transfer
3.4. Pressure Drop
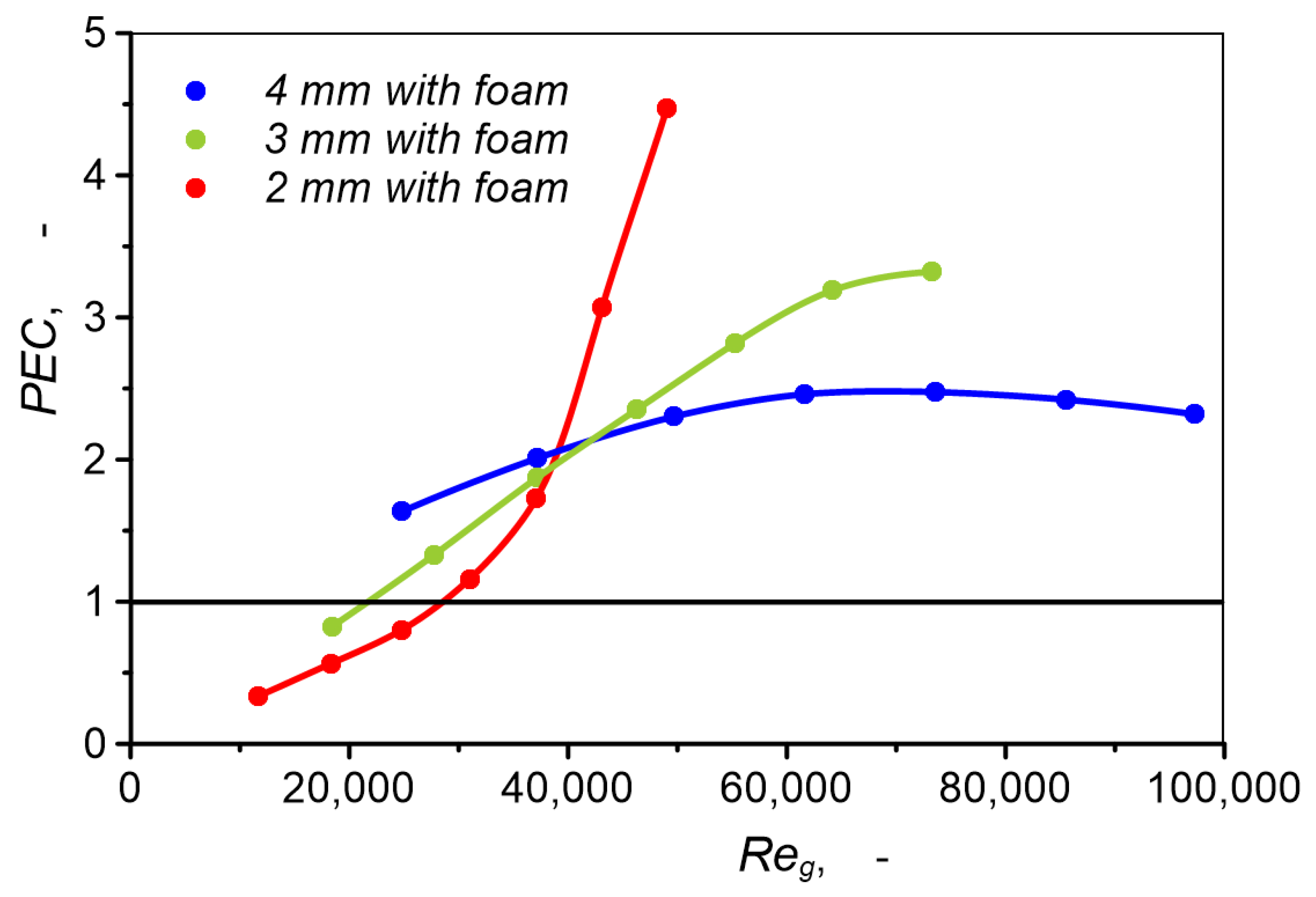
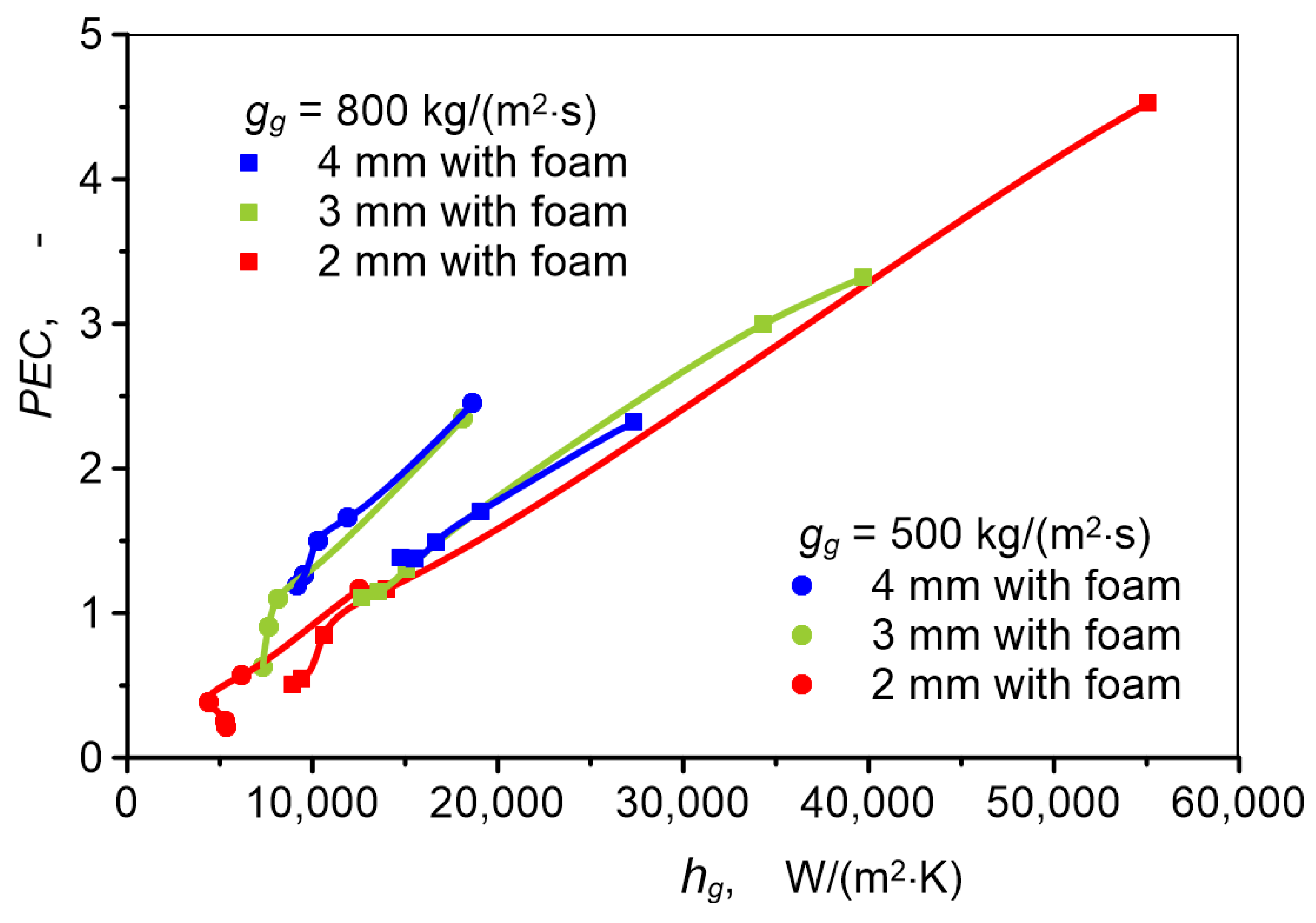
3.5. Heat Exchanger Efficiency
4. Conclusions
- Placing open-cell metal foam in the gas channel causes an increase in heat flux released by the cooled gas compared to cooling in an empty channel of the same diameter. Depending on mass flux, this difference ranges from 33 to 63% in favor of the channel with metal foam.
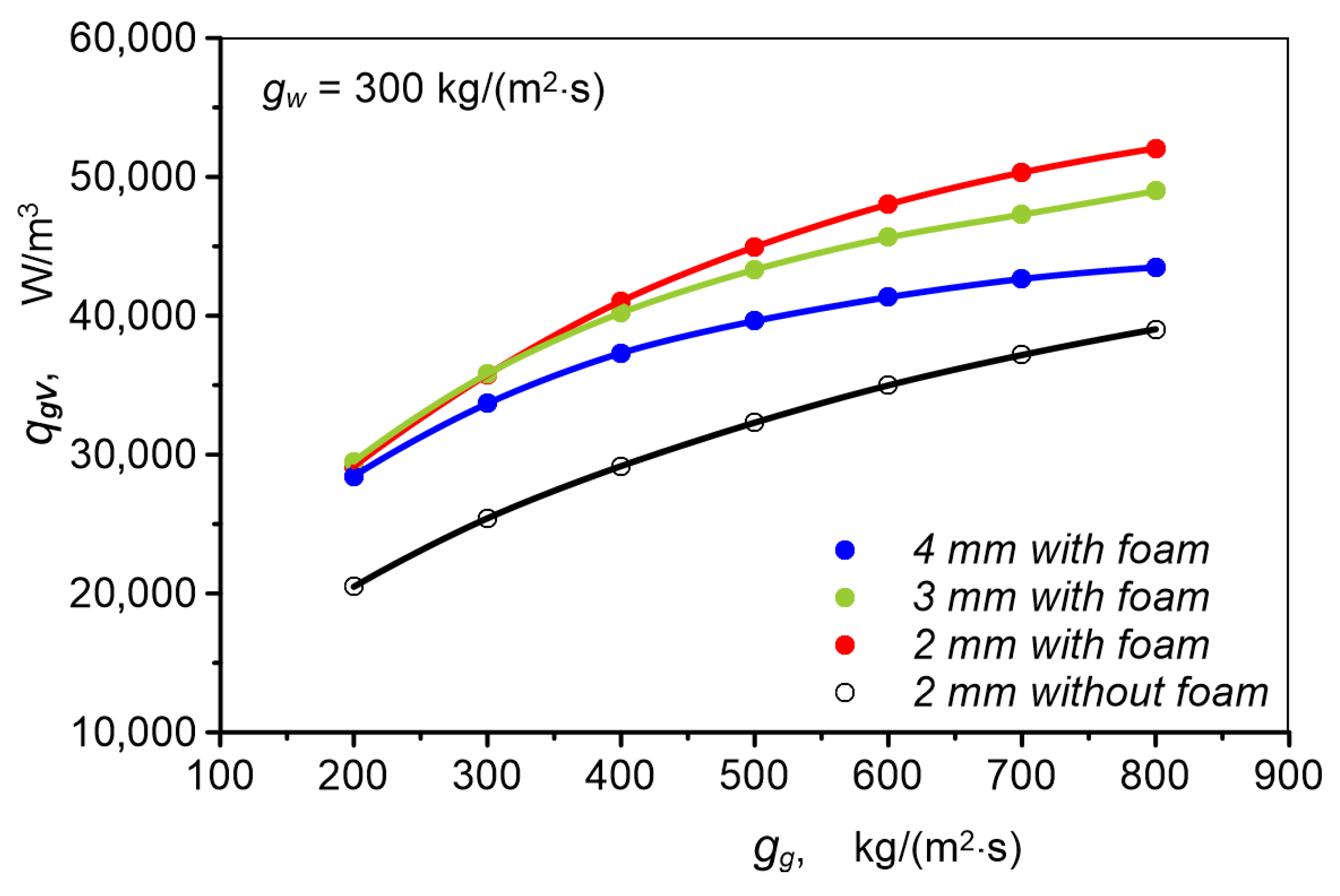
- Heat flux increases with channel diameter. In the case of the presented studies, 20–40% higher heat flux was obtained in a 4 mm diameter channel with metal foam than in a 2 mm channel with metal foam and was 60–84% higher than in a 2 mm channel without foam.
- Increasing channel diameter leads to a decrease in unit heat transfer surface area, therefore the most favorable ratio of heat transfer rate to heat exchanger volume (qgV) is characterized by a heat exchanger with 2 mm diameter channels with metal foam.
- In all analyzed cases, the heat transfer coefficient in channels filled with metal foam achieves significantly higher values than in channels without foam. This difference increases with the mass flux of cooled carbon dioxide. Moreover, the influence of gas mass flux on the heat transfer coefficient value is stronger in a 2 mm channel than in 3 and 4 mm channels. In the case of a 2 mm channel with metal foam, the maximum heat transfer coefficient value is 54.56 kW/(m2·K). For 3 and 4 mm channels, the highest heat transfer coefficient values are 39.69 and 27.33 kW/(m2·K), respectively.
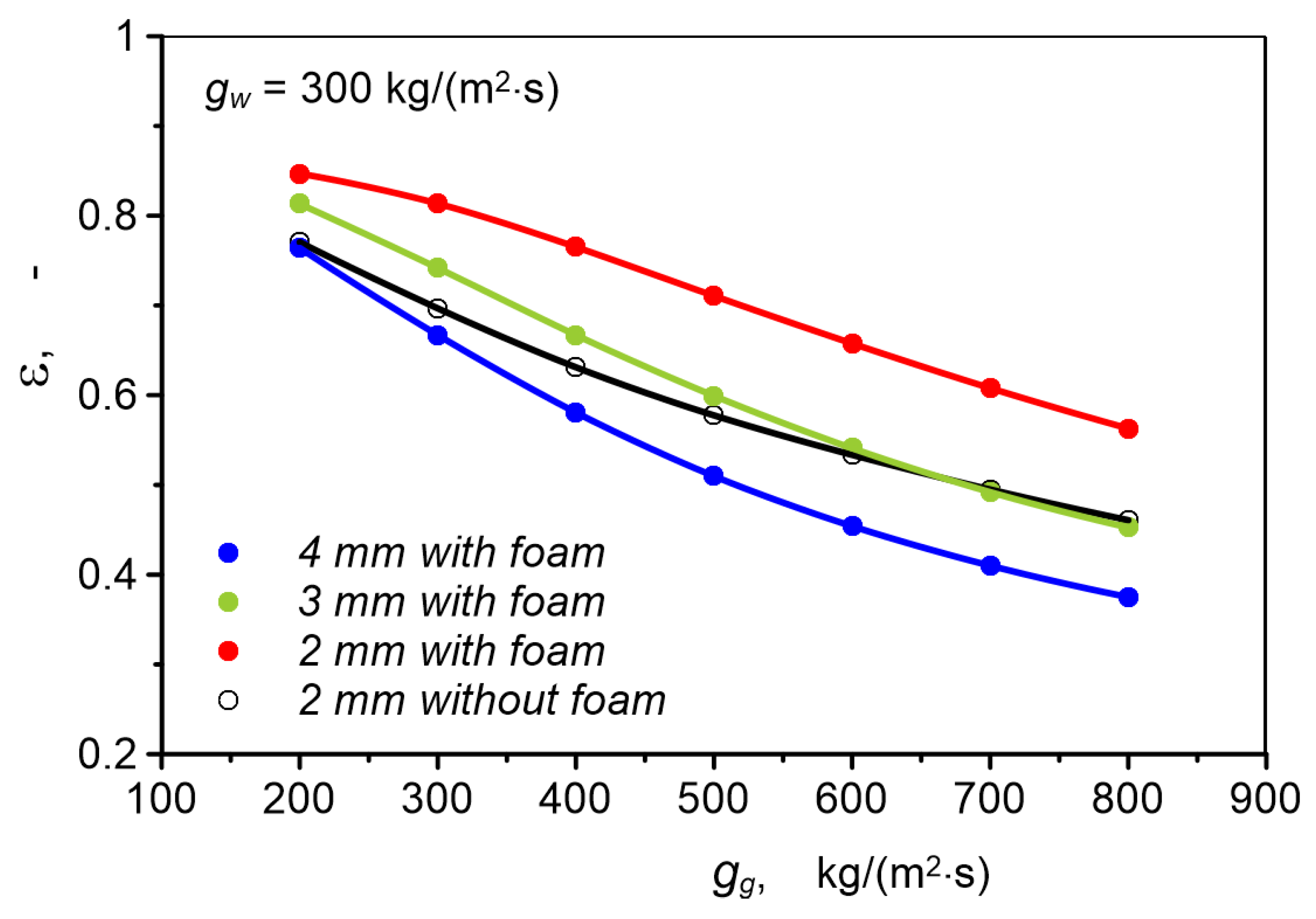
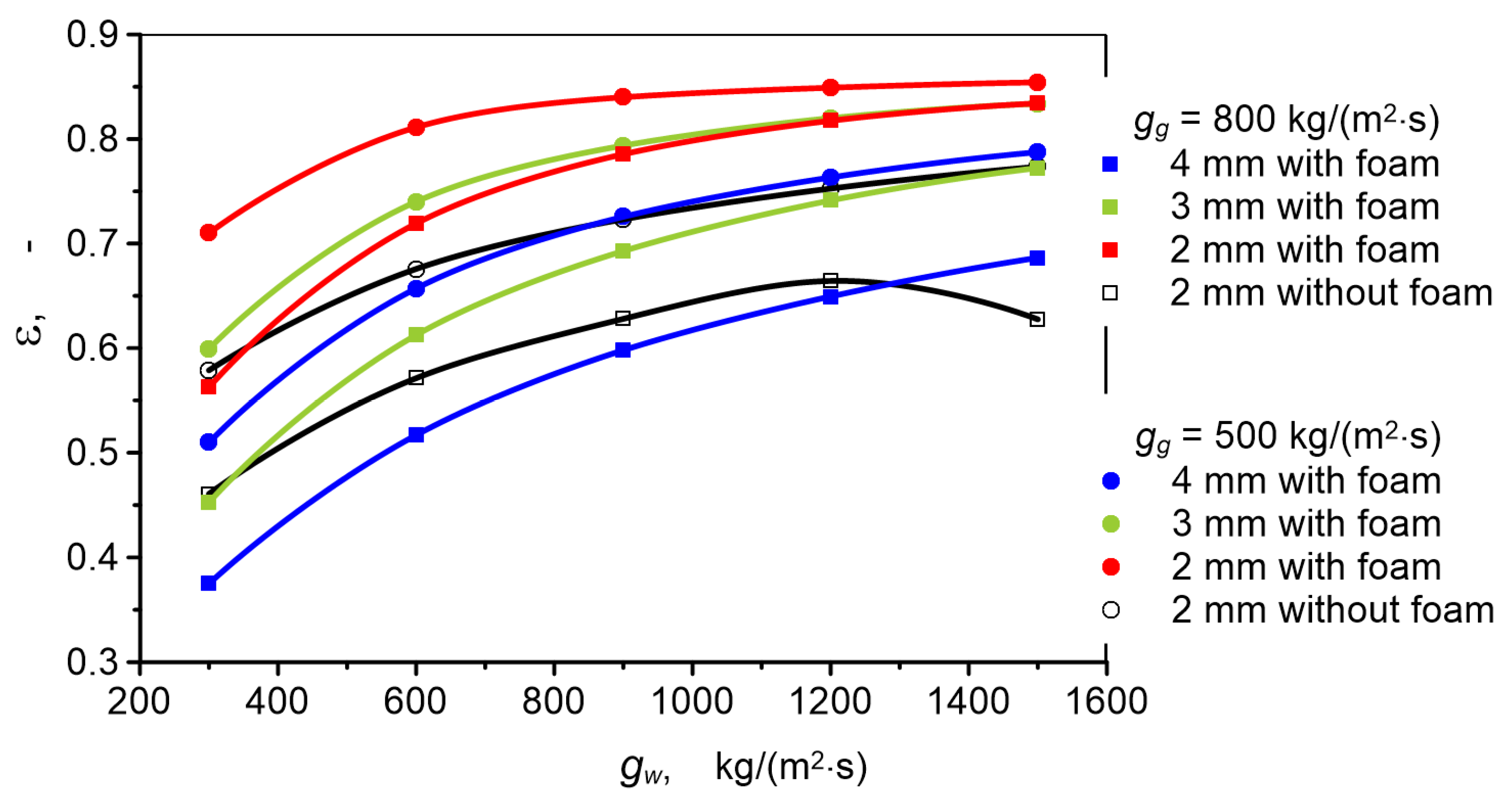
- Heat transfer effectiveness of the studied system with metal foam in a 2 mm diameter channel is 7.6% to 20.7% higher than in the case of a channel without metal foam. For a 3 mm channel, heat transfer effectiveness is lower than for a 2 mm channel with filling. The lowest heat transfer effectiveness characterizes heat transfer in a 4 mm channel. In this case, heat transfer effectiveness in a channel with foam is several percent lower than in an empty channel.
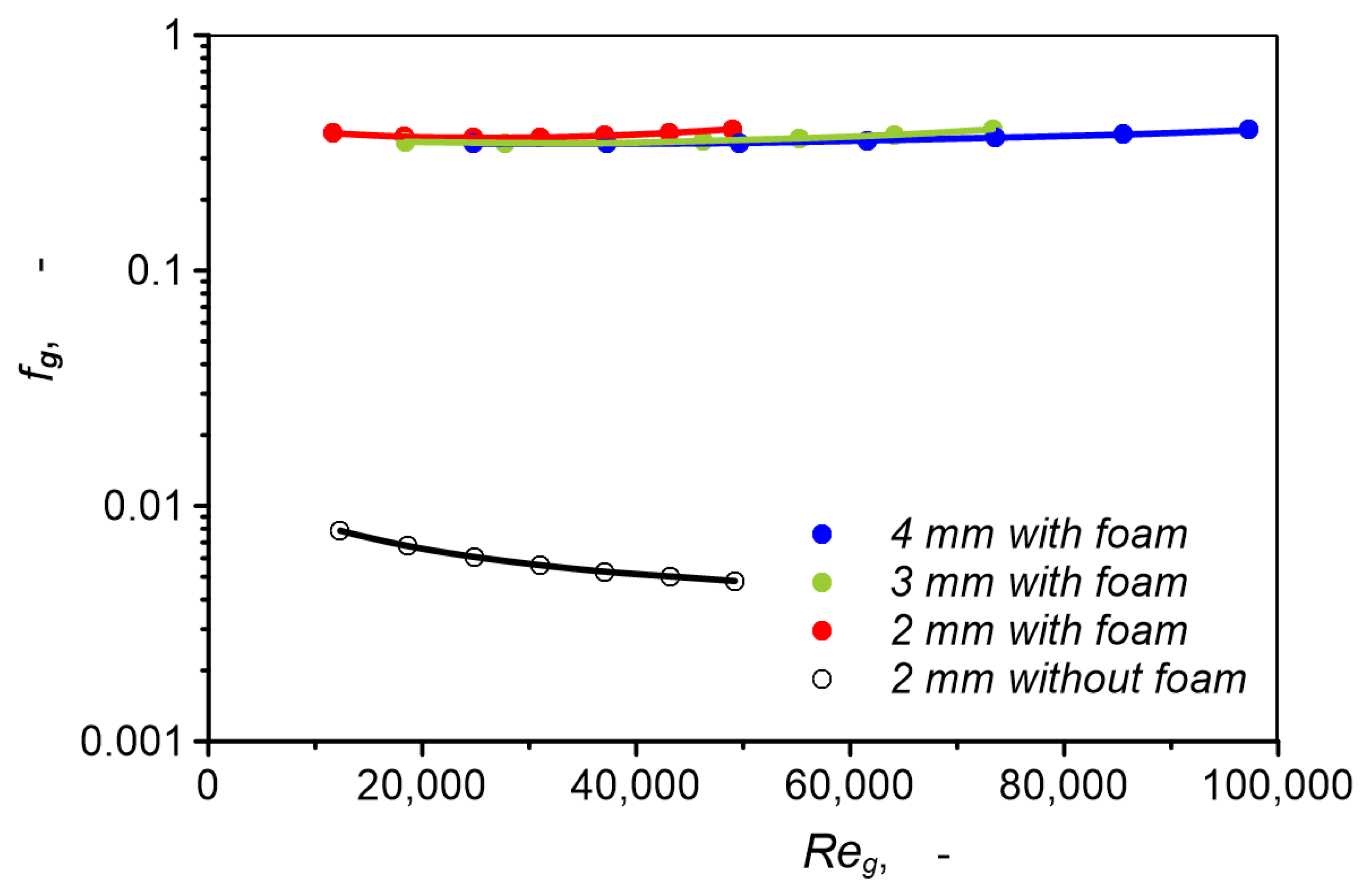
- Pressure drop of supercritical carbon dioxide flow through channels filled with metal foam, in the range of conducted studies, is 45–82 times higher than pressure drop in an empty channel and depends slightly on channel diameter because metal foam parameters have the decisive influence on pressure drop. Increasing channel diameter does not cause a clear decrease in pressure drop and does not contribute to improving hydraulic performance.
- Overall thermal–hydraulic performance of the studied systems strongly depends on flow conditions, expressed by the Reynolds number, heat transfer intensity, and channel diameter. The highest thermal–hydraulic performance is characterized by a 2 mm channel with metal foam, for which the maximum PEC value is 4.47. Under the same heat transfer conditions, PEC for 3 and 4 mm channels is approximately two times lower. The course of thermal–hydraulic performance changes as a function of the Reynolds number is significantly different for individual channels.
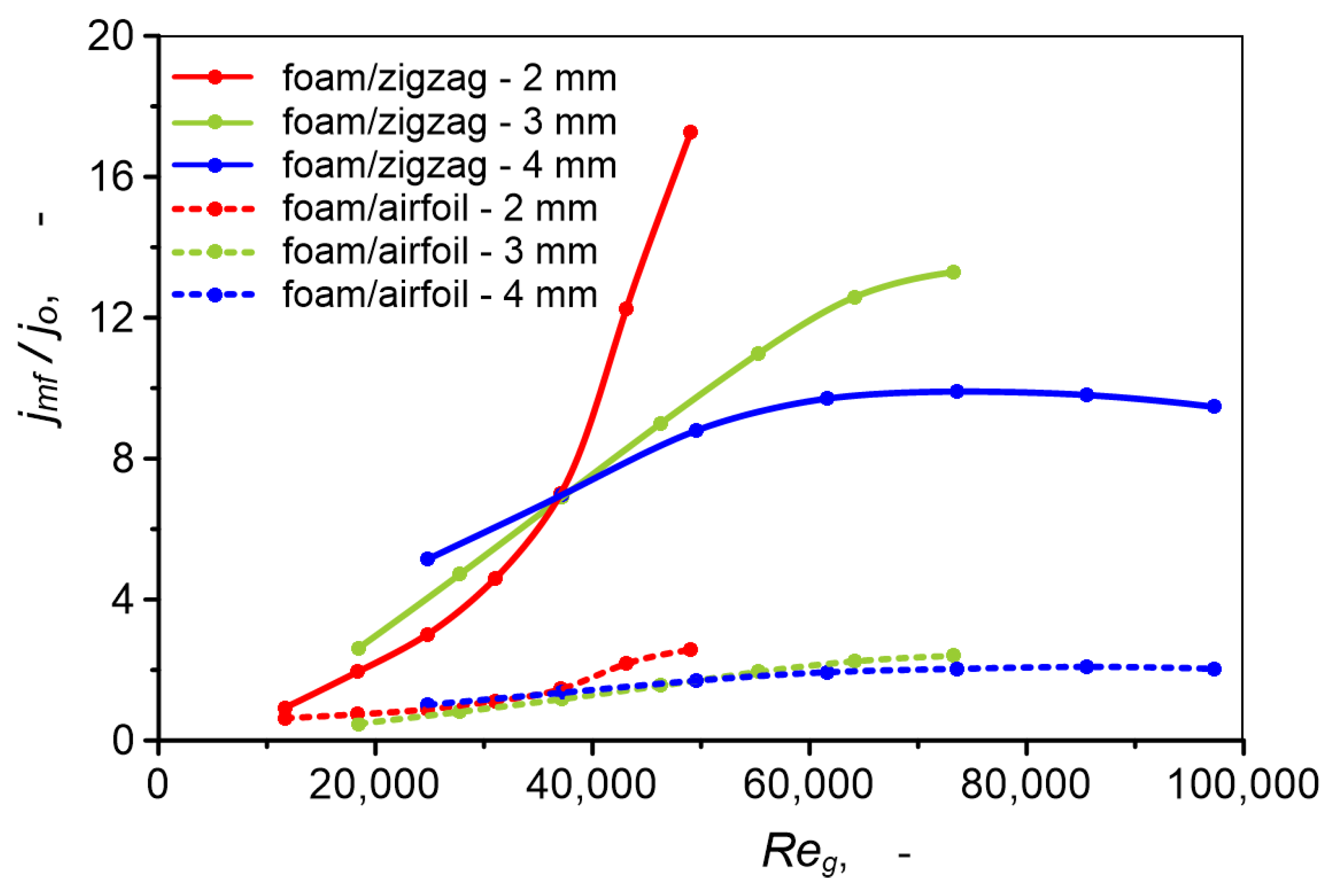
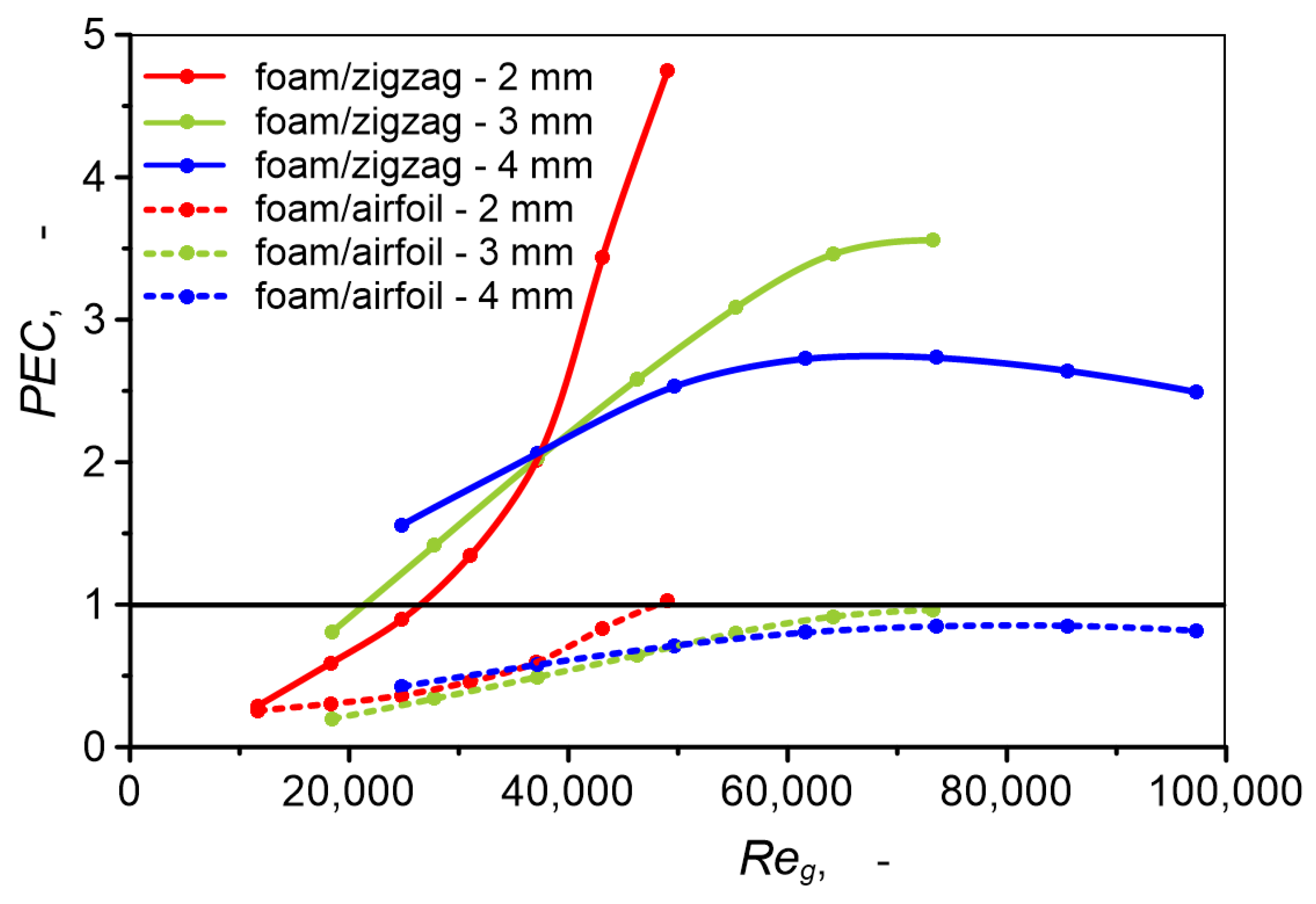
- PCHE heat exchangers with metal foam channels have higher heat transfer performance than PCHE heat exchangers with zigzag channels and airfoil PCHE heat exchangers. Due to high pressure drop, PCHE heat exchangers with metal foam have lower thermal–hydraulic performance than airfoil PCHE heat exchangers.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| aHEx | heat exchanger specific surface area, m2/m3 |
| asf | metal foam specific surface area, m2/m3 |
| c | specific heat, J/(kg·K) |
| CF | foam inertial coefficient, m |
| dc | cell diameter, m |
| d | channel size, m |
| dh | hydraulic diameter, m |
| dl | diameter of foam ligament, m |
| dp | pore diameter, m |
| f | Fanning friction factor, – |
| g | mass flux, kg/(m2·s) |
| h | heat transfer coefficient, W/(m2·K) |
| j | Colburn j-factor, – |
| ks | skeleton thermal conductivity coefficient, W/(m·K) |
| keff | effective thermal conductivity coefficient, W/(m·K) |
| K | foam permeability, m2 |
| L | channel length, m |
| m | mass flow rate, kg/s |
| Nu | Nuselt number, – |
| PEC | Thermal–hydraulic performance, – |
| Pr | Prandtl number, – |
| Re | Reynolds number, – |
| q | heat flux, W/m2 |
| qV | unit heat flux (heat transfer rate per unit volume of the heat exchanger), W/m3 |
| Q | heat transfer rate, W |
| t | temperature, °C |
| v | velocity, m/s |
| Greek Symbols | |
| Δp/Δl | unit pressure drop, Pa/m |
| Δt | temperature difference, K |
| ε | heat transfer effectiveness, – |
| ϕ | porosity of metal foam, – |
| μ | viscosity, Pa∙s |
| Δ | density, kg/m3 |
| ω | pore density, PPI |
| Subscripts | |
| f | fluid (water or sCO2) |
| g | gas (sCO2)/hot fluid |
| in | inlet condition |
| mf | metal foam |
| out | outlet condition |
| s | solid |
| sw | channel wall |
| w | water/cold fluid |
References
- Fu, X.; Zhang, R.; Shi, L.; Wang, Y.; Li, Q.; Cai, W. Micro Segment Analysis and Machine Learning Prediction for Thermal-Hydraulic Parameters of Propane Condensation Flow in a PCHE Straight Channel. Energy 2024, 310, 133261. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Ehsan, M.M. Design and Off-Design Performance Analysis of a Zigzag Channeled Precooler for Indirect Cooling System of Supercritical CO2 Recompression Cycle Incorporated with a Flow-Bypass System. Appl. Therm. Eng. 2023, 226, 120321. [Google Scholar] [CrossRef]
- Baik, S.; Kim, S.G.; Lee, J.; Lee, J.I. Study on CO2—Water Printed Circuit Heat Exchanger Performance Operating under Various CO2 Phases for S-CO2 Power Cycle Application. Appl. Therm. Eng. 2017, 113, 1536–1546. [Google Scholar] [CrossRef]
- Cheng, K.; Zhou, J.; Zhang, H.; Huai, X.; Guo, J. Experimental Investigation of Thermal-Hydraulic Characteristics of a Printed Circuit Heat Exchanger Used as a Pre-Cooler for the Supercritical CO2 Brayton Cycle. Appl. Therm. Eng. 2020, 171, 115116. [Google Scholar] [CrossRef]
- Jin, F.; Chen, D.; Hu, L.; Huang, Y.; Zeng, H.; Wang, J. Thermo-Hydraulic Performance of Printed Circuit Heat Exchanger as Precooler in Supercritical CO2 Brayton Cycle. Appl. Therm. Eng. 2022, 210, 118341. [Google Scholar] [CrossRef]
- Jin, F.; Yuan, D.; Chen, D.; Hu, L.; Huang, Y.; Bu, S. Experimental Study on Cooling Heat Transfer Performance of Supercritical CO2 in Zigzag Printed Circuit Heat Exchanger. Int. J. Heat Mass Transf. 2023, 215, 124538. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Zhang, L.; Yao, M.; Kruizenga, A.; Anderson, M. PDF-Based Modeling on the Turbulent Convection Heat Transfer of Supercritical CO2 in the Printed Circuit Heat Exchangers for the Supercritical CO2 Brayton Cycle. Int. J. Heat Mass Transf. 2016, 98, 204–218. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, Y.; Lee, Y.; Jo, H.J. Condensation Heat Transfer and Applicability Assessment of a Printed Circuit Heat Exchanger as a Condenser in a Cryogenic CO2 Capture and Storage System. Appl. Therm. Eng. 2025, 261, 125133. [Google Scholar] [CrossRef]
- Ren, Z.; Zhao, C.R.; Jiang, P.X.; Bo, H.L. Investigation on Local Convection Heat Transfer of Supercritical CO2 during Cooling in Horizontal Semicircular Channels of Printed Circuit Heat Exchanger. Appl. Therm. Eng. 2019, 157, 113697. [Google Scholar] [CrossRef]
- Ren, Y.; Jiang, R.; Wang, P.; Wu, W.; Yang, Y.; Yang, Q. Experimental Study of a Rectangular Microchannel Printed Circuit Heat Exchanger Using Supercritical Carbon Dioxide and Water Cooling. Appl. Therm. Eng. 2025, 262, 125230. [Google Scholar] [CrossRef]
- Han, Z.; Guo, J.; Huai, X. Theoretical Analysis of a Novel PCHE with Enhanced Rib Structures for High-Power Supercritical CO2 Brayton Cycle System Based on Solar Energy. Energy 2023, 270, 126928. [Google Scholar] [CrossRef]
- Yin, D.; Zhou, Y.; Guo, X.; Wang, D. Numerical Analysis of Wavy PCHEs in Supercritical CO2/Propane Mixture Brayton Cycle. Appl. Therm. Eng. 2023, 235, 121346. [Google Scholar] [CrossRef]
- Saeed, M.; Ali Awais, A.; Berrouk, A.S. CFD Aided Design and Analysis of a Precooler with Zigzag Channels for Supercritical CO2 Power Cycle. Energy Convers. Manag. 2021, 236, 114029. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Ghodrati, P.; Mortazavi, H.; Kang, Y.T. Numerical Analysis of Heat Transfer and Flow Characteristics of Supercritical CO2-Cooled Wavy Mini-Channel Heat Sinks. Appl. Therm. Eng. 2023, 226, 120307. [Google Scholar] [CrossRef]
- Moisseytsev, A.; Sienicki, J.J. Investigation of Alternative Layouts for the Supercritical Carbon Dioxide Brayton Cycle for a Sodium-Cooled Fast Reactor. Nucl. Eng. Des. 2009, 239, 1362–1371. [Google Scholar] [CrossRef]
- Zhou, Y.; Yin, D.; Guo, X.; Dong, C. Numerical Analysis of the Thermal and Hydraulic Characteristics of CO2/Propane Mixtures in Printed Circuit Heat Exchangers. Int. J. Heat Mass Transf. 2022, 185, 122434. [Google Scholar] [CrossRef]
- Lee, S.W.; Shin, S.M.; Chung, S.K.; Jo, H.J. Evaluation of Thermal-Hydraulic Performance and Economics of Printed Circuit Heat Exchanger (PCHE) for Recuperators of Sodium-Cooled Fast Reactors (SFRs) Using CO2 and N2 as Working Fluids. Nucl. Eng. Technol. 2022, 54, 1874–1889. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, P.; Deng, T.; Ke, H.; Lin, Y.; Wang, Q. Thermal-Hydraulic Characteristics of Printed Circuit Heat Exchanger Used for Floating Natural Gas Liquefaction. Renew. Sustain. Energy Rev. 2021, 137, 110606. [Google Scholar] [CrossRef]
- Peng, Z.R.; Zheng, Q.Y.; Chen, J.; Yu, S.C.; Zhang, X.R. Numerical Investigation on Heat Transfer and Pressure Drop Characteristics of Coupling Transcritical Flow and Two-Phase Flow in a Printed Circuit Heat Exchanger. Int. J. Heat Mass Transf. 2020, 153, 119557. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, T.; Ke, H.; Wang, W.; Lin, Y.; Wang, Q. Numerical Investigation on Local Thermal Characteristics of Printed Circuit Heat Exchanger for Natural Gas Liquefication. Energy Procedia 2019, 158, 5408–5413. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Zhang, Y.; Xu, H.; Zeng, W. Experimental and Numerical Analysis of Condensation Heat Transfer and Pressure Drop of Refrigerant R22 in Minichannels of a Printed Circuit Heat Exchanger. Energies 2020, 13, 6589. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y.; Chen, X.; Ma, X.; Yang, S.; Li, S. A Numerical Study on Condensation Flow and Heat Transfer of Refrigerant in Minichannels of Printed Circuit Heat Exchanger. Int. J. Refrig. 2019, 102, 96–111. [Google Scholar] [CrossRef]
- Yoo, J.W.; Nam, C.W.; Yoon, S.H. Experimental Study of Propane Condensation Heat Transfer and Pressure Drop in Semicircular Channel Printed Circuit Heat Exchanger. Int. J. Heat Mass Transf. 2022, 182, 121939. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, L.; Lv, H.; Li, S.; Hou, Y. Experimental and Numerical Investigation of a High-Effectiveness Cryogenic PCHE for Space 80 K Brayton Cryocooler. Int. J. Refrig. 2025, 176, 26–39. [Google Scholar] [CrossRef]
- Tian, Z.; Zhou, X.; Zhao, B.; Shen, W.; Peng, H. Comparative Analyses on Freezing Risk and Novel Anti-Freezing Structure for PCHEs as SLNG Vaporizer. Int. J. Heat Mass Transf. 2024, 229, 125719. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, C.; Jiang, T.; Zhao, B.; Shen, W.; Peng, H. Experimental Study and Dynamic Response Analysis of Thermal–Hydraulic Characteristics in Zigzag PCHE at Ultra-Low Temperature. Appl. Therm. Eng. 2025, 268, 125897. [Google Scholar] [CrossRef]
- Yang, L.; Deng, C.; Li, W.; Zhao, B.; Li, Q.; Cai, W. Study on the Similarity Criterions for Trans-Critical Flow and Heat Transfer of Methane and Nitrogen in PCHE. Int. Commun. Heat Mass Transf. 2024, 159, 107993. [Google Scholar] [CrossRef]
- Chen, J.; Du, W.; Cheng, K.; Li, X.; Guo, J.; Lv, P.; Dong, H. Design Analysis of a Hybrid Printed Circuit Heat Exchanger for Precooling in Hydrogen Refueling Station. Int. Commun. Heat Mass Transf. 2025, 163, 108765. [Google Scholar] [CrossRef]
- Ding, L.; Wang, X.; Niu, M.; Li, B.; Wang, W. Numerical Investigation of Supercritical Flow and Heat Transfer Mechanism in Printed Circuit Heat Exchanger (PCHE) Channels. Int. J. Hydrogen Energy 2024, 62, 31–47. [Google Scholar] [CrossRef]
- Huisseune, H.; De Schampheleire, S.; Ameel, B.; De Paepe, M. Comparison of Metal Foam Heat Exchangers to a Finned Heat Exchanger for Low Reynolds Number Applications. Int. J. Heat Mass Transf. 2015, 89, 1–9. [Google Scholar] [CrossRef]
- Kim, D.Y.; Sung, T.H.; Kim, K.C. Application of Metal Foam Heat Exchangers for a High-Performance Liquefied Natural Gas Regasification System. Energy 2016, 105, 57–69. [Google Scholar] [CrossRef]
- Bamorovat Abadi, G.; Moon, C.; Kim, K.C. Experimental Study on Single-Phase Heat Transfer and Pressure Drop of Refrigerants in a Plate Heat Exchanger with Metal-Foam-Filled Channels. Appl. Therm. Eng. 2016, 102, 423–431. [Google Scholar] [CrossRef]
- Tamkhade, P.K.; Lande, R.D.; Gurav, R.B.; Lele, M.M. Investigations on Tube in Tube Metal Foam Heat Exchanger. Mater. Today Proc. 2023, 72, 951–957. [Google Scholar] [CrossRef]
- Zaib, F.; Ganesan, P.; Zaharinie, T.; Chen, Z.; Naganthran, K. Heat Transfer Performance of a Compact Heat Exchanger Based on Metal Foam and Thermal Interface Material (TIM). Int. J. Heat Mass Transf. 2024, 231, 125861. [Google Scholar] [CrossRef]
- Jadhav, P.H.; Gnanasekaran, N.; Mobedi, M. Analysis of Functionally Graded Metal Foams for the Accomplishment of Heat Transfer Enhancement under Partially Filled Condition in a Heat Exchanger. Energy 2023, 263, 125691. [Google Scholar] [CrossRef]
- Dyga, R.; Troniewski, L. Convective Heat Transfer for Fluids Passing through Aluminum Foams. Arch. Thermodyn. 2015, 36, 139–156. [Google Scholar] [CrossRef]
- Dyga, R.; Brol, S. Investigation of a Modular High-Pressure Heat Exchanger with Metal Foam Packing for a Pneumatic–Hydraulic Drive. Materials 2024, 17, 5557. [Google Scholar] [CrossRef]
- Dyga, R.; Brol, S. Pressure Drops in Two-Phase Gas–Liquid Flow through Channels Filled with Open-Cell Metal Foams. Energies 2021, 14, 2419. [Google Scholar] [CrossRef]
- Yu, P.; Liu, H.; Xue, J.; Zhang, Y.; Che, D. Thermo-Hydraulic Performance of a Cryogenic Printed Circuit Heat Exchanger for Liquid Air Energy Storage. Appl. Therm. Eng. 2023, 219, 119429. [Google Scholar] [CrossRef]
- Yang, X.; Wang, W.; Wang, Z.; Ma, F. Simulation of Pre-Cooling in a High Pressure Hydrogen Refueling Station for Operation Optimization. Int. J. Hydrogen Energy 2024, 86, 434–444. [Google Scholar] [CrossRef]
- Hu, H.; Li, Y.; Lei, R.; Xie, Y.; Li, J. Numerical Investigation on Flow Condensation in Zigzag Channel of Printed Circuit Heat Exchanger. Appl. Therm. Eng. 2024, 252, 123645. [Google Scholar] [CrossRef]
- Ansys Fluent User’s Guide v. 2024/R2. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v242/en/flu_th/flu_th.html (accessed on 2 June 2025).
- Duan, X.; Liu, X.; Huang, X.; Wang, Y.; Ding, C. A Novel Design for Performance Enhancement in Sandwich Heat Transfer Unit with Partially Filled Metal Foam. Int. Commun. Heat Mass Transf. 2025, 165, 109086. [Google Scholar] [CrossRef]
- Torres-Madroñero, J.L.; Lopera-Escobar, J.; Marulanda-Zapata, L.; Fernández-Morales, P.; Nieto-Londoño, C. Numerical Analysis of Non-Regular and Regular Metal Foam Performance in Heat Transfer Enhancing Applications. Appl. Therm. Eng. 2025, 273, 126562. [Google Scholar] [CrossRef]
- Settar, A.; Nebbali, R.; Madani, B.; Abboudi, S. Numerical Investigation of Convective Heat Transfer in a Plane Channel Filled with Metal Foam under Local Thermal Non-Equilibrium. Mech. Ind. 2015, 16, 504. [Google Scholar] [CrossRef]
- Xiong, J.; Sun, J.; Chen, Y.; Nie, Z. Study on the Flow and Heat Transfer Characteristics inside High-Porosity Open-Cell Copper Foams: Experimental and Numerical Explorations. Int. J. Heat Fluid Flow. 2024, 109, 109499. [Google Scholar] [CrossRef]
- Si, W.; Fu, C.; Wu, X.; Deng, X.; Yuan, P.; Huang, Z.; Yang, J. Numerical Study of Flow and Heat Transfer in the Air-Side Metal Foam Partially Filled Channels of Panel-Type Radiator under Forced Convection. Open Phys. 2025, 23, 20250121. [Google Scholar] [CrossRef]
- Hassan, A.M.; Alwan, A.A.; Hamzah, H.K. Metallic Foam with Cross Flow Heat Exchanger: A Review of Parameters, Performance, and Challenges. Heat Transf. 2022, 52, 2618–2650. [Google Scholar] [CrossRef]
- Xu, H.; Gong, L.; Huang, S.; Xu, M. Flow and Heat Transfer Characteristics of Nanofluid Flowing through Metal Foams. Int. J. Heat Mass Transf. 2015, 83, 399–407. [Google Scholar] [CrossRef]
- Xu, H.J.; Gong, L.; Zhao, C.Y.; Yang, Y.H.; Xu, Z.G. Analytical Considerations of Local Thermal Non-Equilibrium Conditions for Thermal Transport in Metal Foams. Int. J. Therm. Sci. 2015, 95, 73–87. [Google Scholar] [CrossRef]
- Zukauskas, A. Convective Heat Transfer in Humans. In Handbook of Single-Phase Convective Heat Transfer; Kakac, S., Shah, R.K., Aung, W., Eds.; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Bhattacharya, A.; Calmidi, V.V.; Mahajan, R.L. Thermophysical Properties of High Porosity Metal Foams. Int. J. Heat Mass Transf. 2002, 45, 1017–1031. [Google Scholar] [CrossRef]
- Dyga, R.; Płaczek, M.; Witczak, S.; Czernek, K. Analysis of Flow Through the Entry Region of a Channel with Metal Foam Packing. In Practical Aspects of Chemical Engineering: Selected Contributions from PAIC 2017; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Kim, I.H.; NO, H.C. Thermal–Hydraulic Physical Models for a Printed Circuit Heat Exchanger Covering He, He–CO2 Mixture, and Water Fluids Using Experimental Data and CFD. Exp. Therm. Fluid Sci. 2013, 48, 213–221. [Google Scholar] [CrossRef]
- Pidaparti, S.R.; Anderson, M.H.; Ranjan, D. Experimental Investigation of Thermal-Hydraulic Performance of Discontinuous Fin Printed Circuit Heat Exchangers for Supercritical CO2 Power Cycles. Exp. Therm. Fluid Sci. 2019, 106, 119–129. [Google Scholar] [CrossRef]


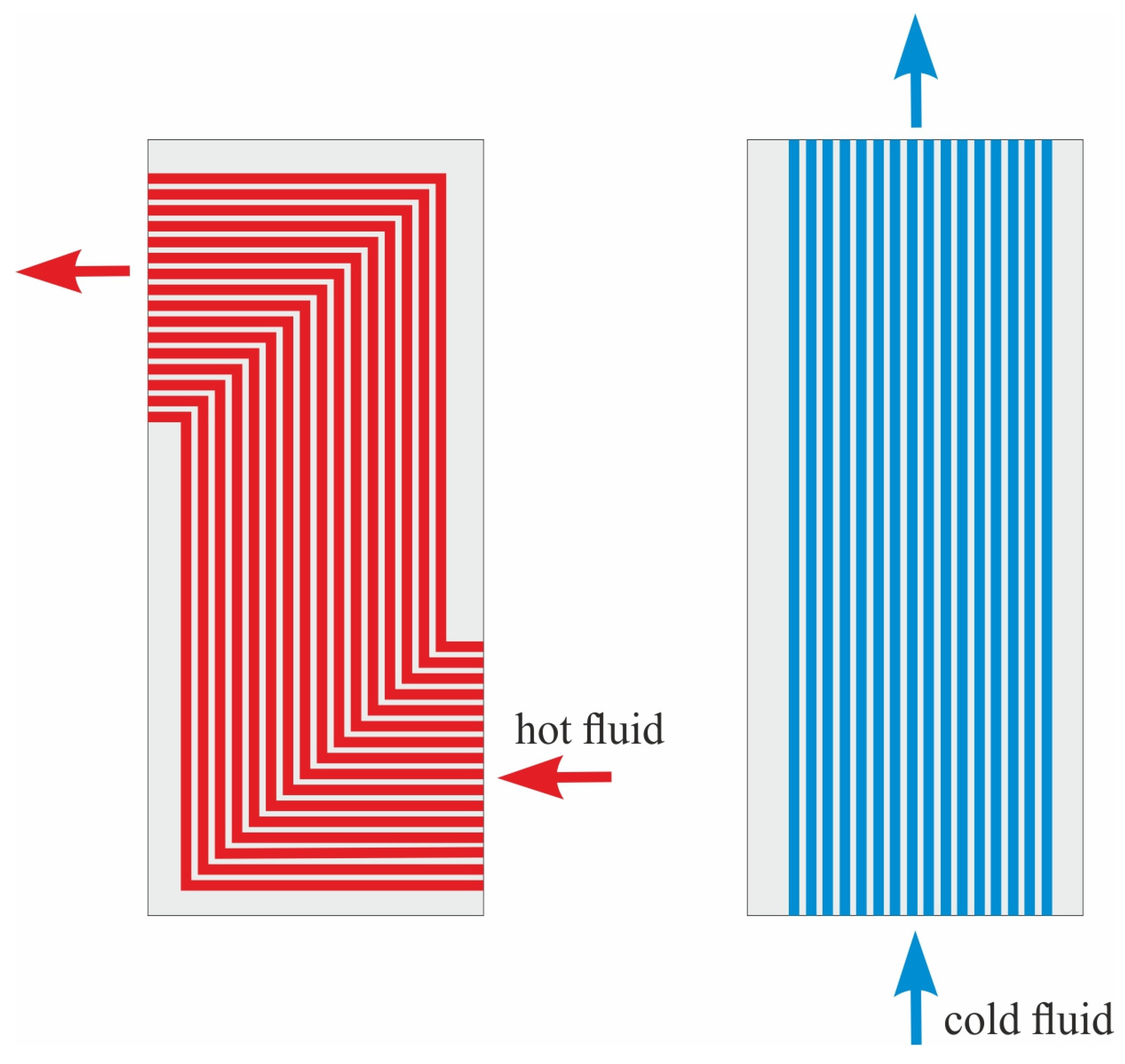
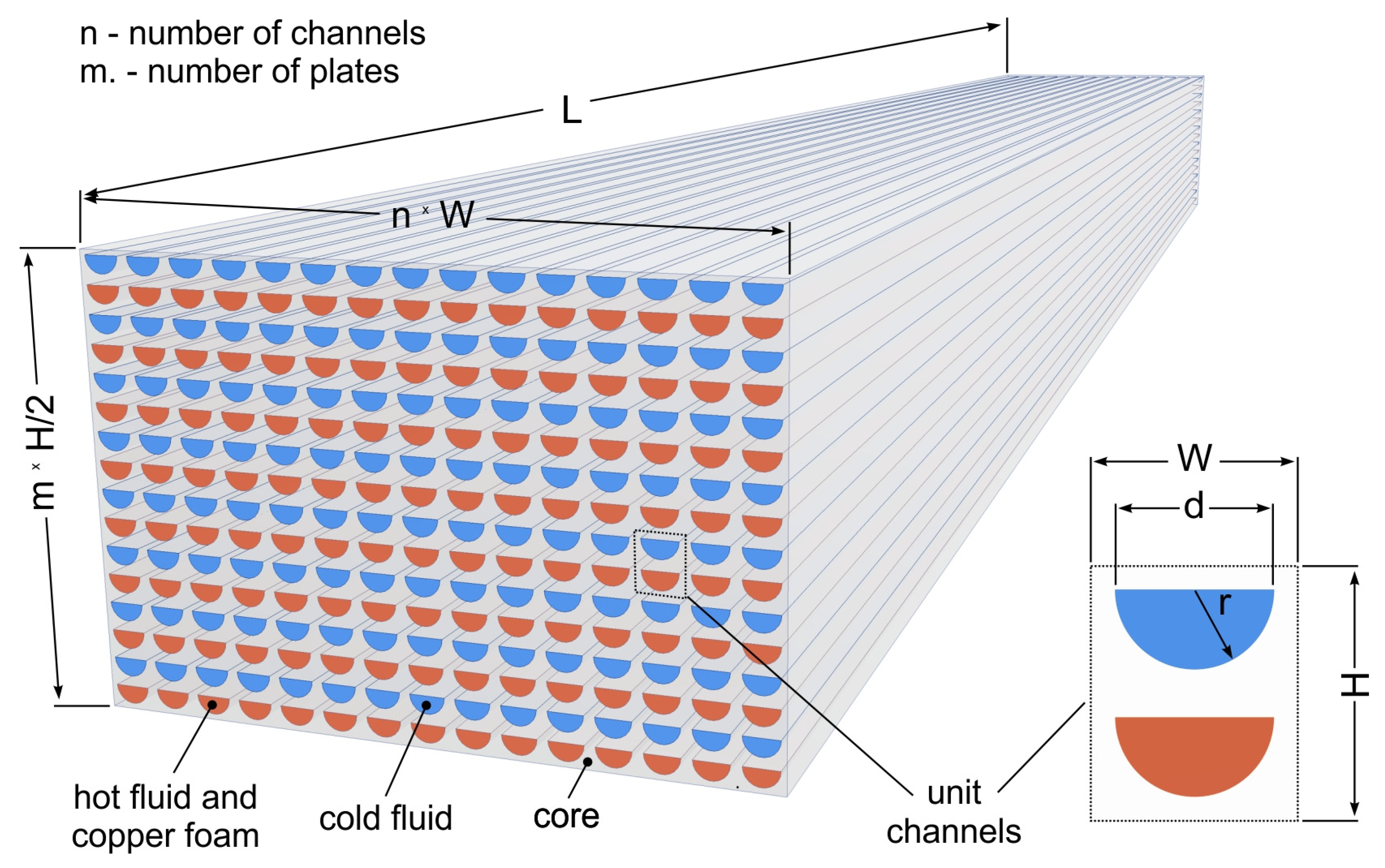
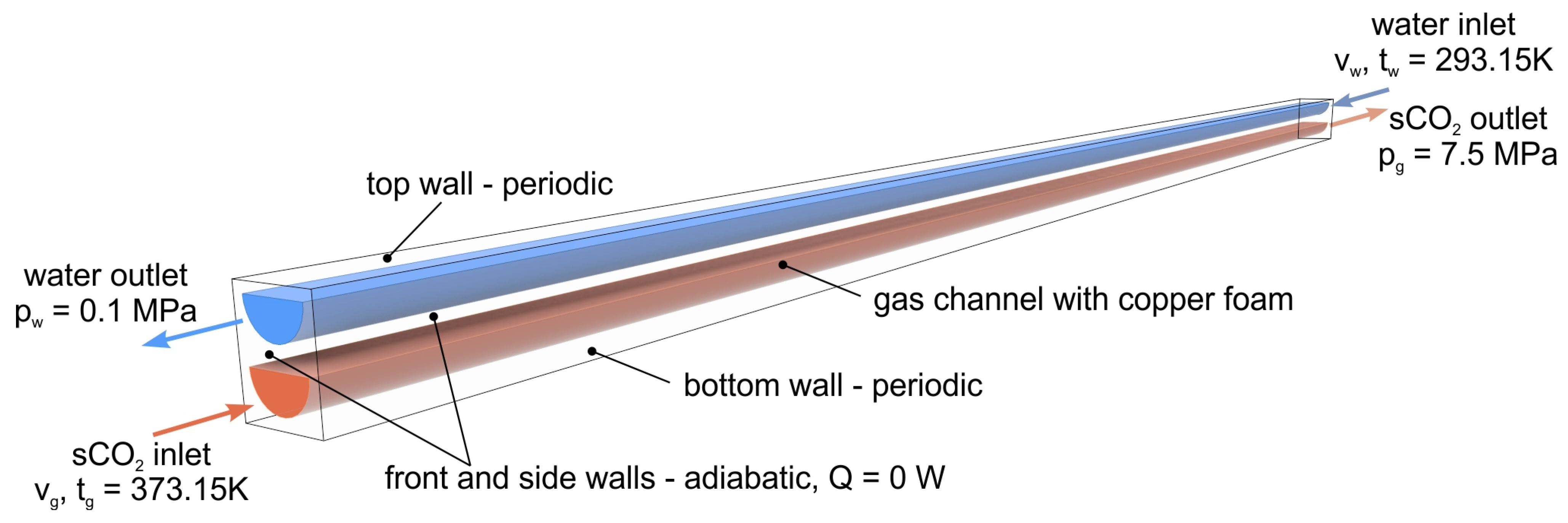
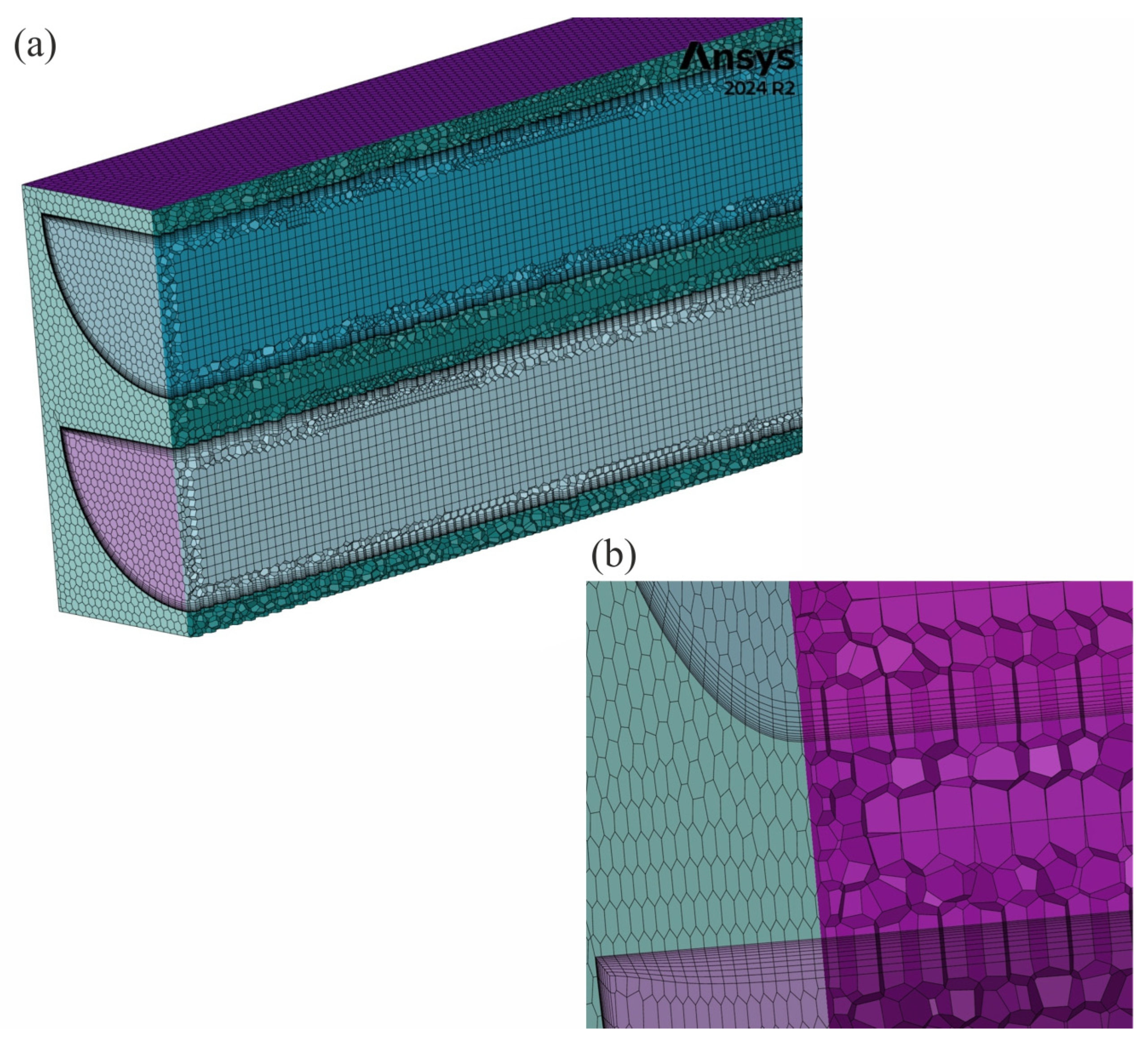






| Source | Fluid Hot/Cold | Fluid Temperature Hot/Cold, [K] | Fluid Pressure [MPa] | Hot Fluid Flow | Cold Fluid Flow | Channel Type/ Diameter |
|---|---|---|---|---|---|---|
| Jin et al. [5] | sCO2/Water | 308.15/ 293.15 | 7.5 | 500 kg/(m2·s) | 500 kg/(m2·s) | zigzag, wavy, airfoil/ 1.22 mm |
| Jin et al. [6] | sCO2/Water | 323–363/ – | 7.5, 8.0, 8.5 | 300, 600 kg/(m2·s) | – | zigzag/2 mm |
| Lee et al. [8] | Liquid CO2/Ethyleneglycol | 318/112 | 1.0 | 40, 60, 80 kg/(m2·s) | 1000 kg/(m2·s) | straight/2, 3, 4 mm |
| Ren et al. [9] | sCO2/Water | 313–373/287–323 | 7.5, 8.1 | 200, 300, 400, 600, 800 kg/(m2·s) | 2000, 2400 kg/(m2·s) | semicircular straight/2.8 mm |
| Ren et al. [10] | sCO2/Water | 343–371/283–293 | 8.1–10.1 | 66.67 × 10−3 kg/s | (250–416) × 10−3 kg/s | rectangular straight/ 3 × 2.28 mm |
| Han et al. [11] | sCO2/sCO2 | 561, 807/400, 548 | 7.88, 7.96 | 506.7, 633.3, 760 kg/(m2·s) | 506.7, 633.3, 760 kg/(m2·s) | straight/0.9 mm |
| Yin et al. [12] | sCO2/propane | 630/ 390–410 | 9.0 | (0.2–0.3) × 10−3 kg/s | 0.3 × 10−3 kg/s | wavy/2 mm |
| Ahmed et al. [2] | sCO2/Water | 338–378/ 283–318 | 7–10 | 149.2 kg/s | – | zigzag/2.2 mm |
| Saeed et al. [13] | sCO2/Water | 343/ 305.2 | 8.0 | (0.5–1.25) × 10−3 kg/s | (2–12) × 10−3 kg/s | zigzag/1.1 mm |
| Li et al. [7] | sCO2/Water | 278–373/ – | 7.5 8.5 | 160–760 kg/(m2·s) | – | straight/1.17 mm |
| Cheng et al. [4] | sCO2/Water | 363–383/ 293–300 | 8.07–8.6 | (0.3–0.5) kg/s | (0.69–1.24) kg/s | zigzag/1.5 mm |
| d, mm | r, mm | S, mm | W, mm | L, mm | aHex, m2/m3 |
|---|---|---|---|---|---|
| 2.0 | 1.0 | 2.6 | 3.2 | 200 | 617.79 |
| 3.0 | 1.5 | 3.6 | 4.2 | 200 | 509.92 |
| 4.0 | 2.0 | 4.6 | 5.2 | 200 | 429.77 |
| Pore density, [PPI] | 40 | 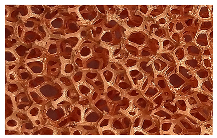 |
| Porosity, – | 0.9 | |
| Effective thermal conductivity, keff [W/(m·K)] | 38.9 | |
| Permeability, K [m2] | 1.464 × 10−7 | |
| Inertial coefficient, CF [m] | 534.3 |
| Boundary | Type of Boundary Condition | Value |
|---|---|---|
| Top and bottom wall | Periodic | – |
| Left, right, front and rear wall | Adiabatic | Q = 0 W |
| Water inlet | Constant velocity and temperature | Tw = 293.15 K vw—Table 4 |
| Water outlet | Constant pressure | pout = 0.1013 × 106 Pa |
| sCO2 inlet | Constant velocity and temperature | Tw = 373.15 K vw—Table 4 |
| sCO2 outlet | Constant pressure | pout = 7.5 × 106 Pa |
| Case | Water Inlet | sCO2 Inlet * |
|---|---|---|
| Constant water mass flux, variable sCO2 mass flux | tw = 293.15 K gw = 300 kg/(m2·s) vw = 0.301 m/s | tg = 373.15 K gg = 200/300/400/500/ 600/700/800 kg/(m2·s) vg = 1.534/2.301/3.068/ 3.835/4.620/5.370/6.136 m/s |
| Constant sCO2 mass flux, variable water mass flux | Tw = 293.15 K gw = 300/600/900/ 1200/1500 kg/(m2·s) vw = 0.301/0.601/0.902/ 1.206/1.503 m/s | Tg = 373.15 K gg = 500 kg/(m2·s) vg = 3.835 m/s |
| Tw = 293.15 K gw = 300/600/900/ 1200/1500 kg/(m2·s) vw = 0.301/0.601/0.902/ 1.206/1.503 m/s | Tg = 373.15 K gg = 800 kg/(m2·s) vg = 6.136 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dyga, R. Investigation of the Effectiveness of a Compact Heat Exchanger with Metal Foam in Supercritical Carbon Dioxide Cooling. Energies 2025, 18, 4736. https://doi.org/10.3390/en18174736
Dyga R. Investigation of the Effectiveness of a Compact Heat Exchanger with Metal Foam in Supercritical Carbon Dioxide Cooling. Energies. 2025; 18(17):4736. https://doi.org/10.3390/en18174736
Chicago/Turabian StyleDyga, Roman. 2025. "Investigation of the Effectiveness of a Compact Heat Exchanger with Metal Foam in Supercritical Carbon Dioxide Cooling" Energies 18, no. 17: 4736. https://doi.org/10.3390/en18174736
APA StyleDyga, R. (2025). Investigation of the Effectiveness of a Compact Heat Exchanger with Metal Foam in Supercritical Carbon Dioxide Cooling. Energies, 18(17), 4736. https://doi.org/10.3390/en18174736






