Experimental Study and Rheological Modeling of Water-Based and Oil-Based Drilling Fluids Under Extreme Temperature–Pressure Condition
Abstract
1. Introduction
2. Experimental Analysis and Procedures
2.1. Equipment
2.2. Materials
2.3. Experimental Design
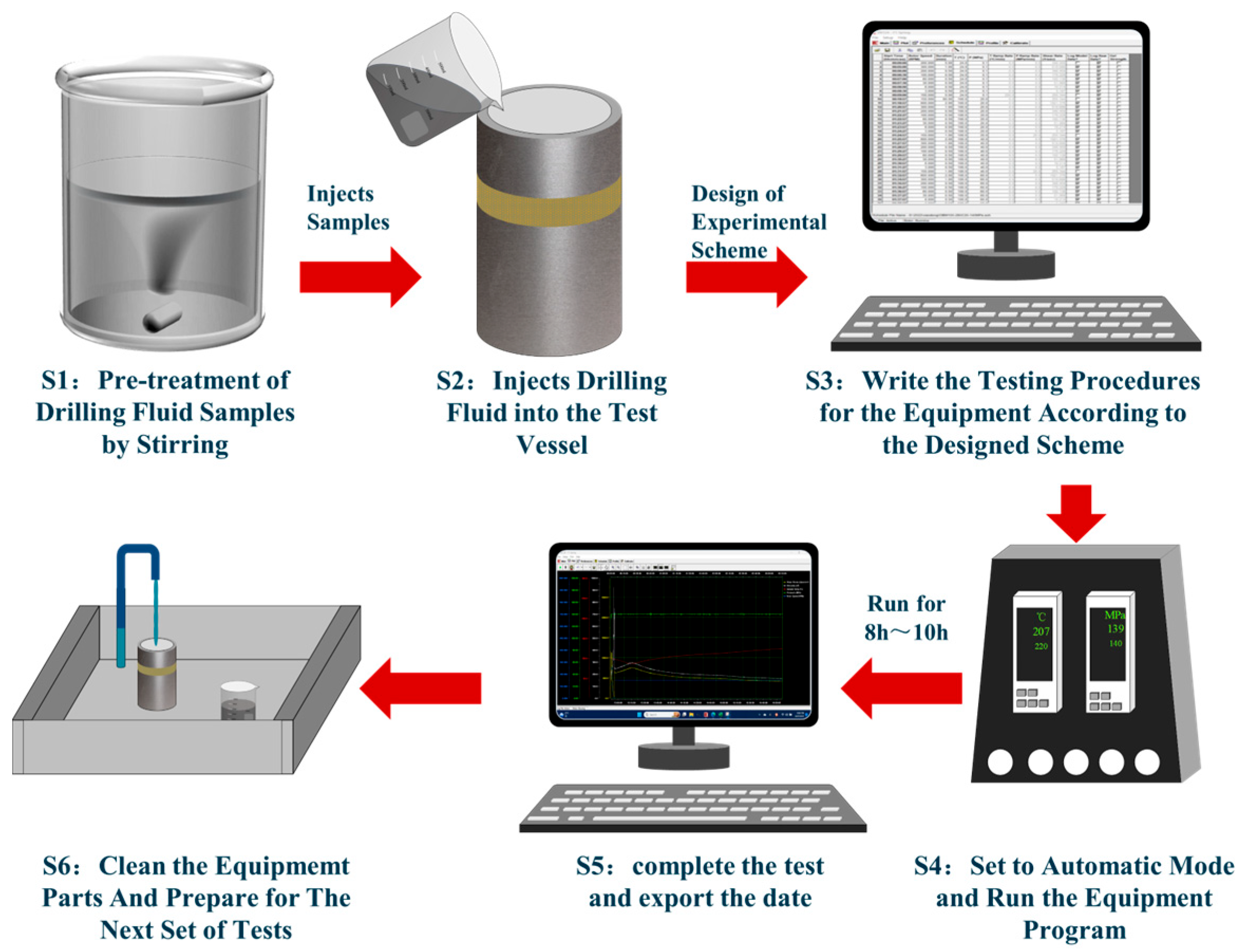
2.4. Experimental Process
3. Results and Discussion
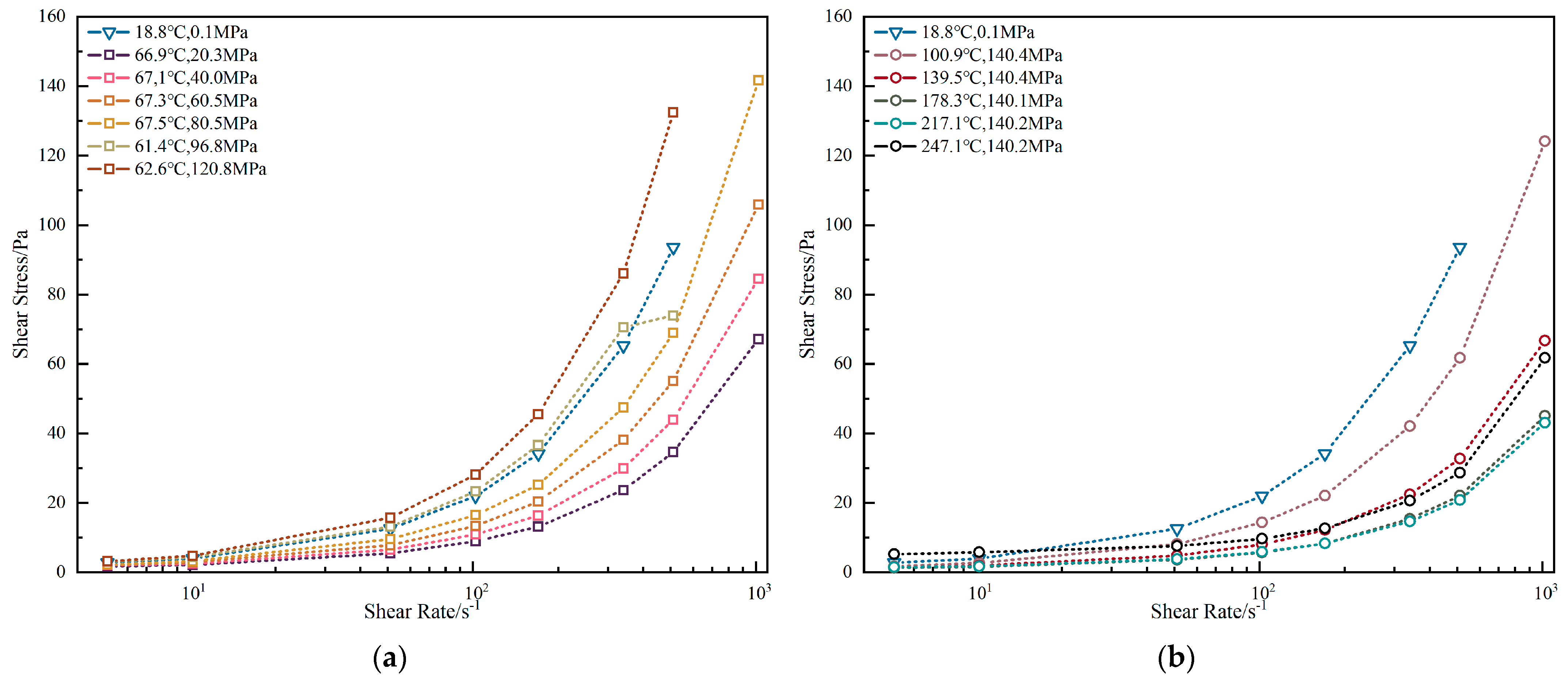
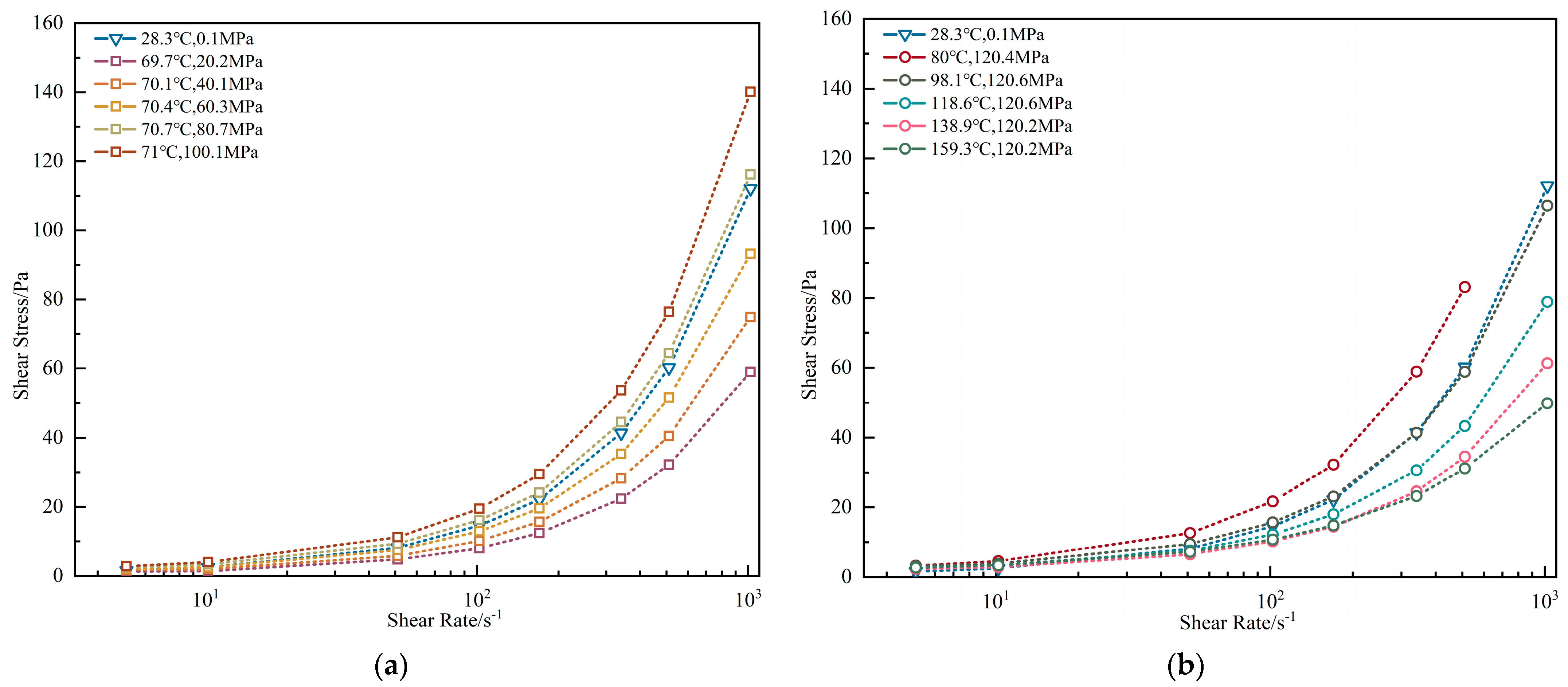
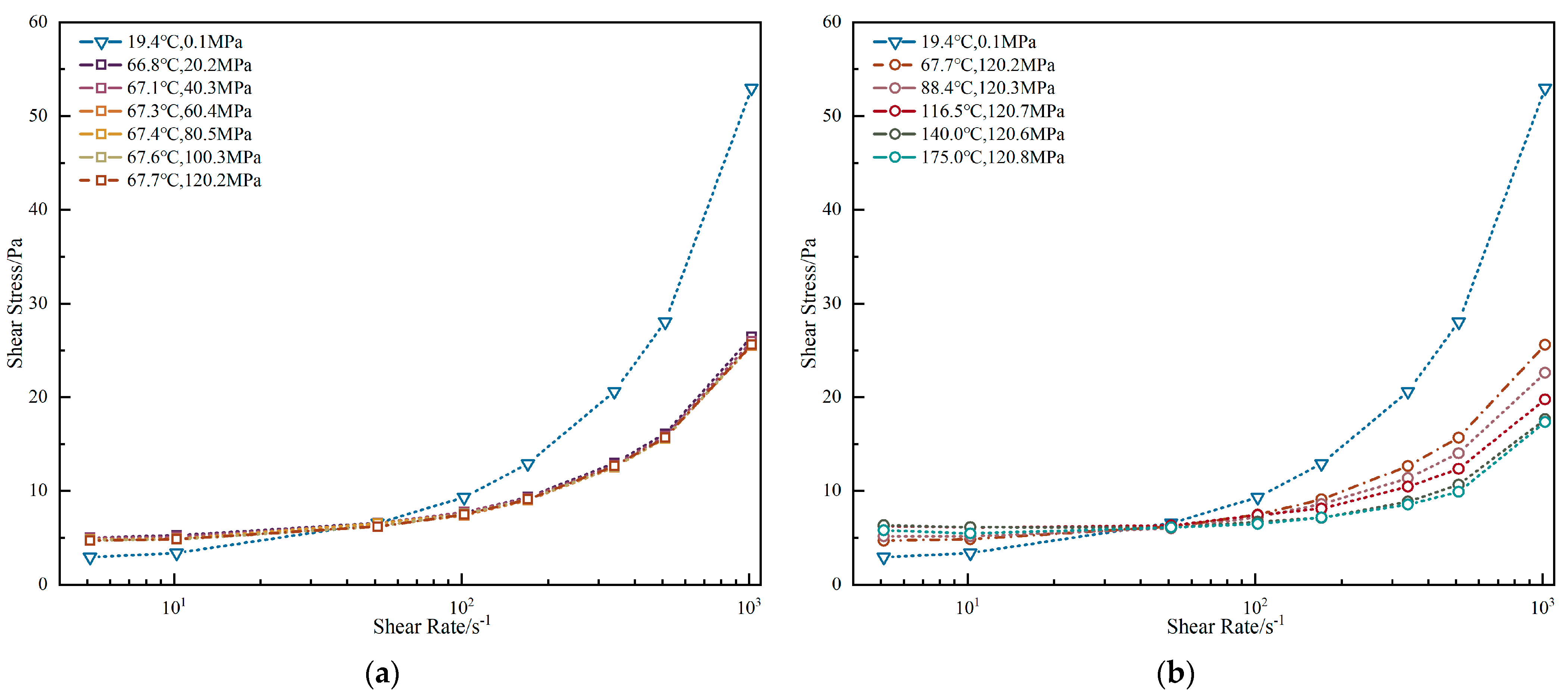
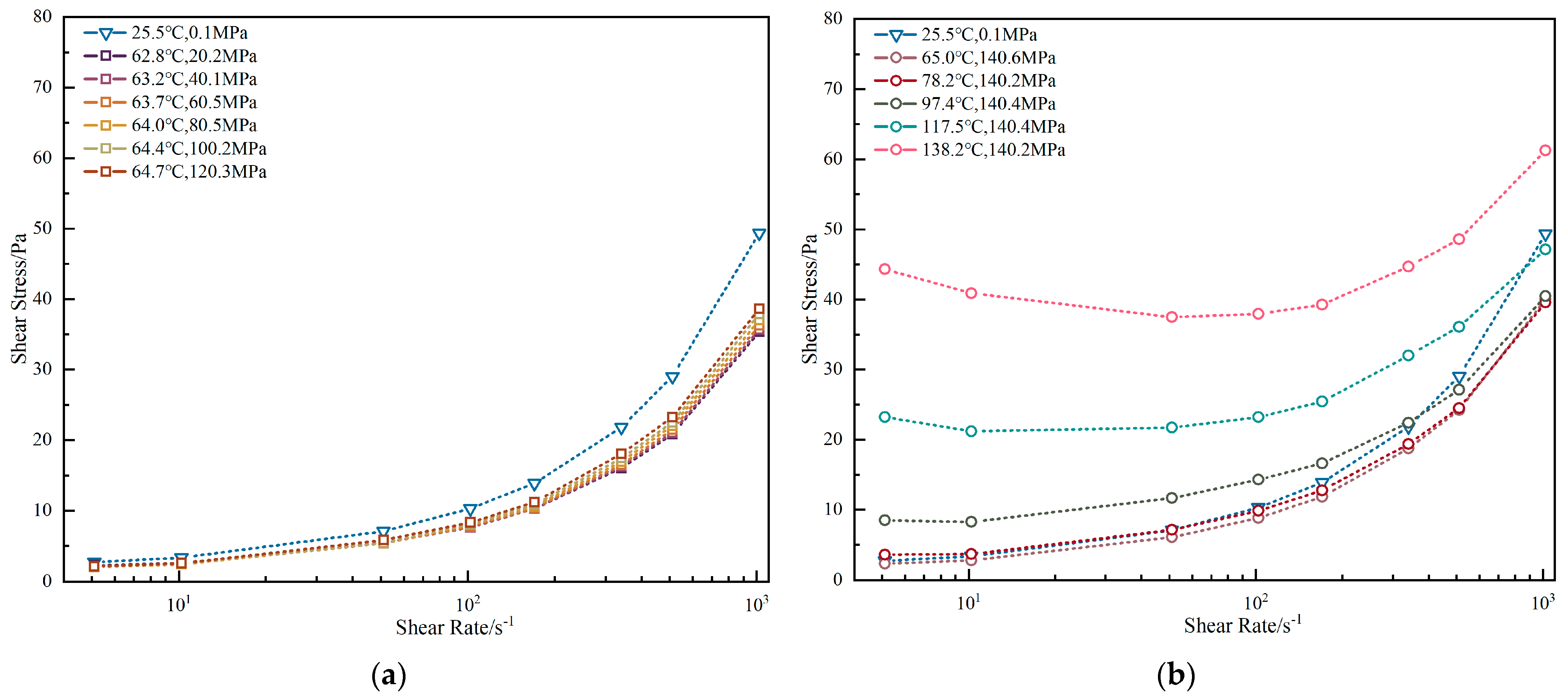
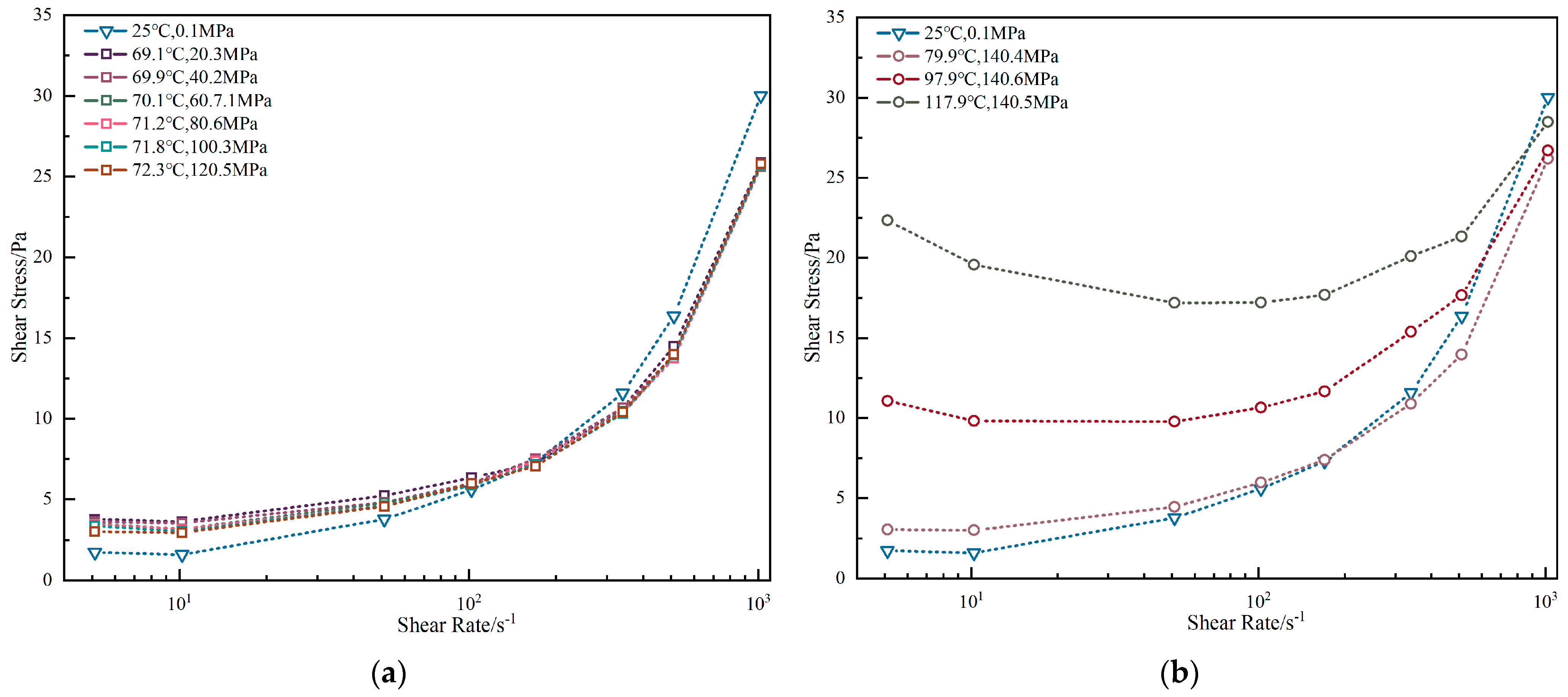
3.1. High-Pressure High-Temperature Behavior
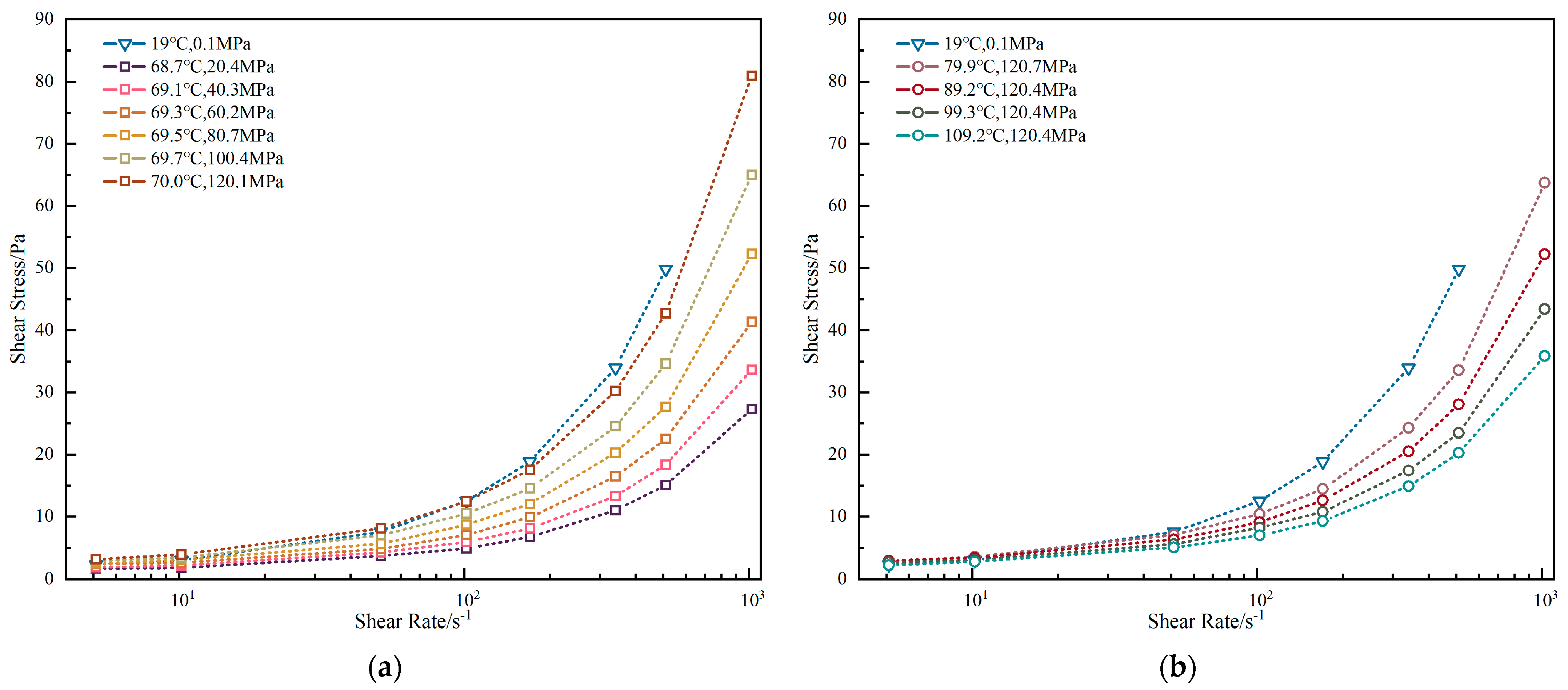
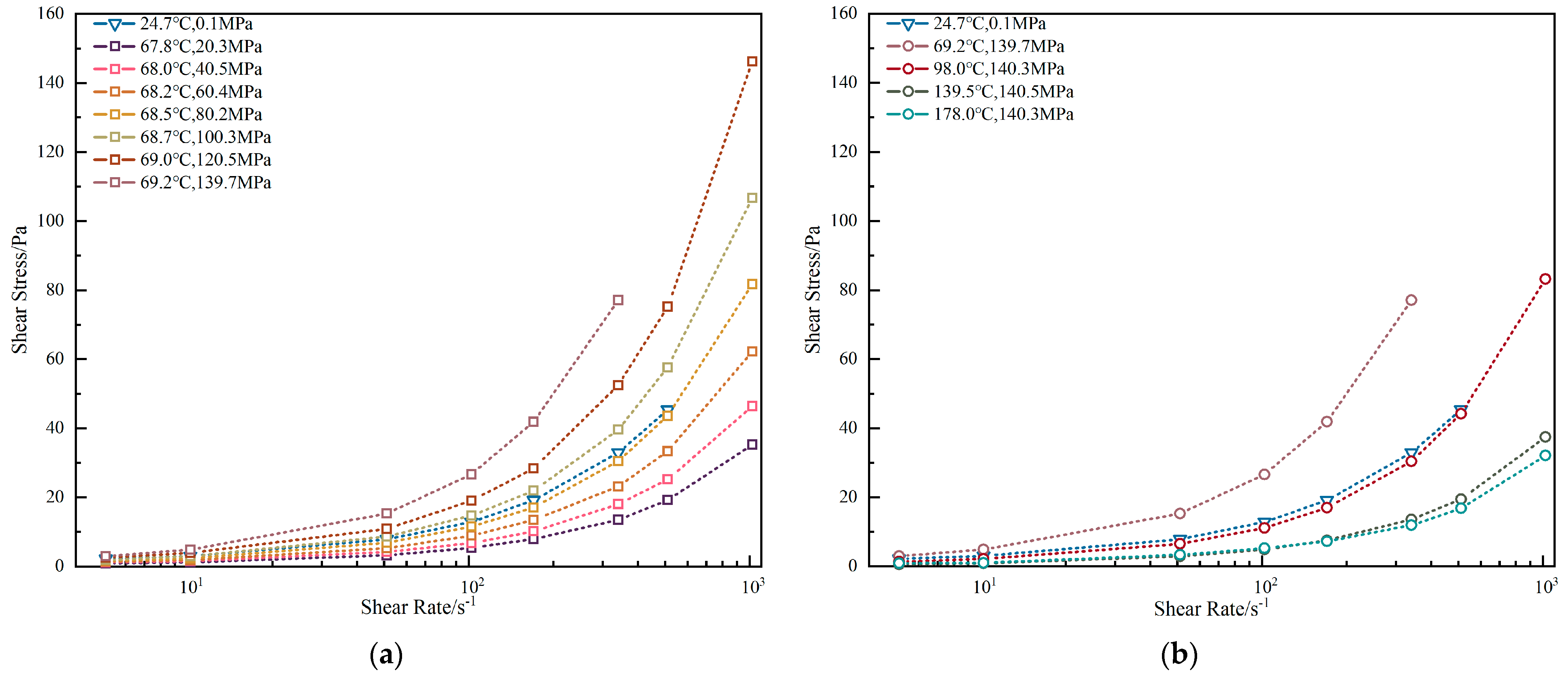
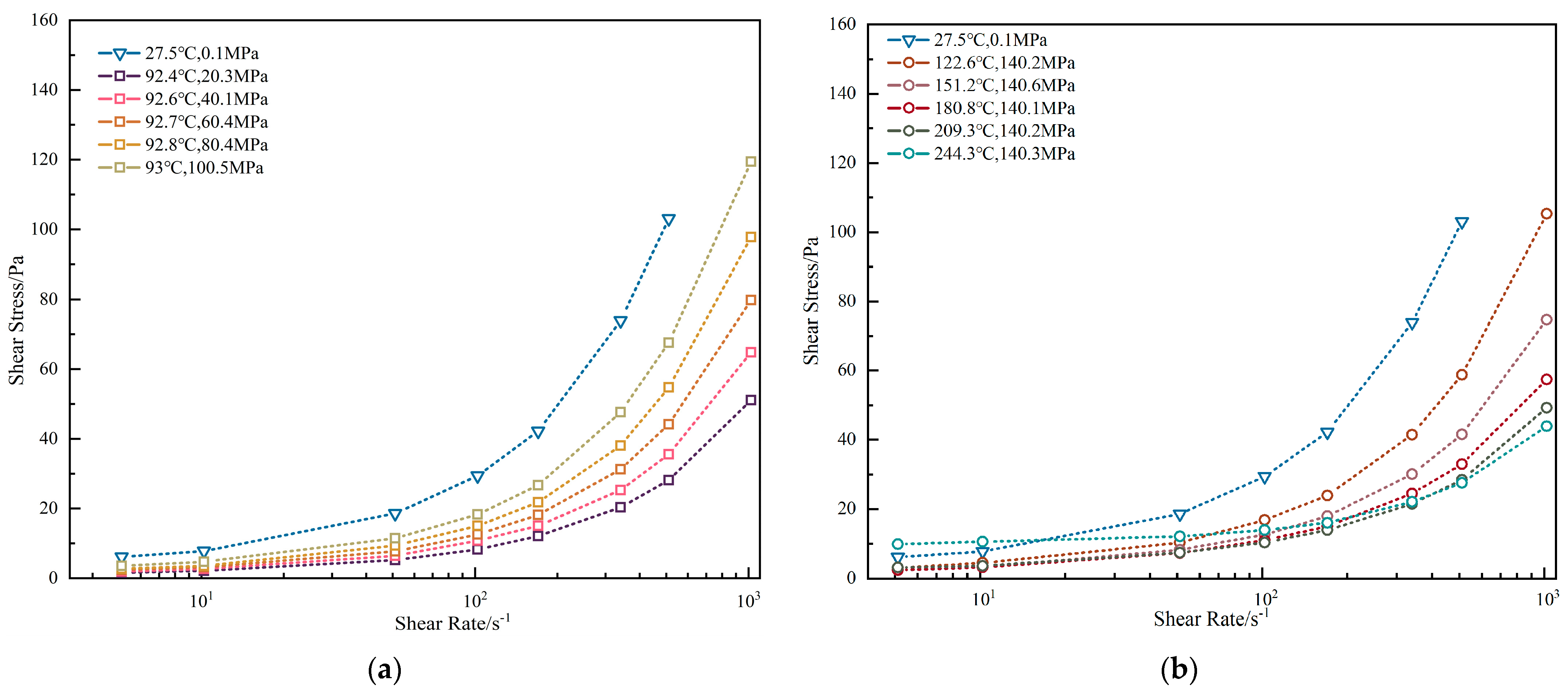
3.1.1. Oil-Base Drilling Fluid
- Validation of the drilling fluid’s pressure-sensitive rheological properties.
- Identification of pressure-induced curve anomalies during bottomhole pressure modeling.
3.1.2. Water-Base Drilling Fluid
3.2. Comparative Analysis
4. Discussion
4.1. Introduction to Optimization Algorithms
- Fast Convergence: Compared with the steepest-descent method, the L-M algorithm can converge to the optimal solution more rapidly.
- Robustness: In the presence of noise and outliers, this algorithm is relatively robust.
- Applicability: It can effectively deal with nonlinear problems with a large number of parameters.
- Global Optimality: Although it does not guarantee finding the global optimal solution, compared with other methods, it is more likely to find the global optimal solution or a solution close to it.
- Applicability: It has strong applicability to complex, high-dimensional, and discontinuous problems.
- Avoidance of Local Optima: Compared with other optimization methods, this type of algorithm is less likely to be confined to local optimal solutions.
4.2. Analysis of the Applicability of Drilling Fluid Rheological Models
4.3. Mathematical Prediction Model for Drilling Fluid Rheological Parameters
- Comprehensive parameterization: Unlike empirical models focusing solely on apparent viscosity (μa) or plastic viscosity (μp), Equation (4) explicitly quantifies all three H-B parameters, which are essential for accurate calculation of the generalized Reynolds number (Reg).
- Thermo-pressure coupling: The inclusion of the cross-term tP captures synergistic interactions between temperature and pressure, reflecting microstructural changes in drilling fluids under HTHP conditions.
4.4. Experimental Verification
5. Conclusions
- Oil-based and water-based drilling fluids exhibit distinct rheological responses to temperature and pressure. Elevated pressure increases shear stress, while higher temperature reduces it, with oil-based fluids showing more significant pressure sensitivity and water-based fluids potentially undergoing gelation at extreme temperatures.
- The Herschel–Bulkley (H-B) model achieves superior fitting accuracy for both fluid types (coefficient of determination > 0.999), outperforming Bingham and power-law models, especially under HTHP conditions.
- The derived H-B parameter prediction model, accounting for temperature-pressure coupling, demonstrates high validation accuracy (R2 > 0.95). It comprehensively quantifies yield stress, consistency coefficient, and flow behavior index, addressing limitations of traditional viscosity-centric models.
- This optimized modeling approach provides a robust tool for engineers to predict annular pressure loss in real-time field operations and optimize drilling fluid design, supporting safer and more efficient deep and ultra-deep drilling. Future research could extend to more diverse fluid formulations and broader HTHP ranges to enhance applicability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. OB-NO 1
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 19.0 | 0.1 | τ0 = 1.91 K = 0.131 n = 0.946 R2 = 1.00 | τ0 = 2.48 K = 0.0930 R2 = 0.999 | K = 0.668 n = 0.663 R2 = 0.984 |
| 68.7 | 20.4 | τ0 = 1.63 K = 0.0486 n = 0.904 R2 = 0.999 | τ0 = 2.14 K = 0.0249 R2 = 0.998 | K = 0.556 n = 0.520 R2 = 0.956 |
| 69.1 | 40.3 | τ0 = 1.91 K = 0.0544 n = 0.919 R2 = 0.999 | τ0 = 2.44 K = 0.0308 R2 = 0.998 | K = 0.628 n = 0.532 R2 = 0.956 |
| 69.3 | 60.2 | τ0 = 2.21 K = 0.0676 n = 0.918 R2 = 1.00 | τ0 = 2.87 K = 0.0381 R2 = 0.999 | K = 0.758 n = 0.533 R2 = 0.956 |
| 69.5 | 80.7 | τ0 = 2.53 K = 0.0747 n = 0.938 R2 = 0.999 | τ0 = 3.16 K = 0.0484 R2 = 0.999 | K = 0.789 n = 0.562 R2 = 0.960 |
| 69.7 | 100.4 | τ0 = 2.94 K = 0.0882 n = 0.946 R2 = 0.999 | τ0 = 3.61 K = 0.0604 R2 = 0.999 | K = 0.886 n = 0.578 R2 = 0.962 |
| 70.0 | 120.2 | τ0 = 3.22 K = 0.105 n = 0.953 R2 = 1.00 | τ0 = 3.95 K = 0.0758 R2 = 0.999 | K = 0.949 n = 0.600 R2 = 0.966 |
| 70.2 | 120.3 | τ0 = 3.28 K = 0.102 n = 0.955 R2 = 1.00 | τ0 = 3.96 K = 0.0751 R2 = 0.999 | K = 0.958 n = 0.597 R2 = 0.965 |
| 79.9 | 120.7 | τ0 = 3.07 K = 0.0846 n = 0.948 R2 = 0.999 | τ0 = 3.69 K = 0.0590 R2 = 0.999 | K = 0.912 n = 0.570 R2 = 0.960 |
| 89.2 | 120.4 | τ0 = 2.97 K = 0.0778 n = 0.930 R2 = 0.999 | τ0 = 3.67 K = 0.0479 R2 = 0.999 | K = 0.968 n = 0.531 R2 = 0.954 |
| 99.3 | 120.4 | τ0 = 2.76 K = 0.0697 n = 0.918 R2 = 0.999 | τ0 = 3.45 K = 0.0394 R2 = 0.998 | K = 0.924 n = 0.512 R2 = 0.951 |
| 109.2 | 120.4 | τ0 = 2.28 K = 0.0783 n = 0.874 R2 = 0.999 | τ0 = 3.19 K = 0.0325 R2 = 0.996 | K = 0.817 n = 0.506 R2 = 0.958 |
Appendix A.2. OB-NO 2
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 24.7 | 0.1 | τ0 = 1.15 K = 0.266 n = 0.820 R2 = 1.00 | τ0 = 3.15 K = 0.0851 R2 = 0.994 | K = 0.652 n = 0.664 R2 = 0.994 |
| 67.8 | 20.3 | τ0 = 0.697 K = 0.0739 n = 0.887 R2 = 1.00 | τ0 = 1.54 K = 0.0336 R2 = 0.997 | K = 0.0336 n = 1.54 R2 = 0.997 |
| 68.0 | 40.5 | τ0 = 0.873 K = 0.0946 n = 0.891 R2 = 1.00 | τ0 = 1.93 K = 0.0443 R2 = 0.998 | K = 0.0443 n = 1.93 R2 = 0.998 |
| 68.2 | 60.4 | τ0 = 1.11 K = 0.111 n = 0.911 R2 = 1.00 | τ0 = 2.25 K = 0.0595 R2 = 0.998 | K = 0.0595 n = 2.25 R2 = 0.998 |
| 68.5 | 80.2 | τ0 = 1.32 K = 0.142 n = 0.915 R2 = 1.00 | τ0 = 2.74 K = 0.0783 R2 = 0.998 | K = 0.423 n = 0.737 R2 = 0.992 |
| 68.7 | 100.3 | τ0 = 1.40 K = 0.192 n = 0.910 R2 = 1.00 | τ0 = 3.37 K = 0.103 R2 = 0.998 | K = 0.500 n = 0.754 R2 = 0.994 |
| 69.0 | 120.5 | τ0 = 2.37 K = 0.187 n = 0.959 R2 = 1.00 | τ0 = 3.54 K = 0.140 R2 = 1.00 | K = 0.647 n = 0.756 R2 = 0.990 |
| 62.6 | 139.7 | τ0 = 1.49 K = 0.386 n = 0.905 R2 = 1.00 | τ0 = 3.23 K = 0.220 R2 = 0.998 | K = 0.804 n = 0.769 R2 = 0.996 |
| 98.0 | 140.3 | τ0 = 1.04 K = 0.137 n = 0.923 R2 = 1.00 | τ0 = 2.34 K = 0.0801 R2 = 0.999 | K = 0.340 n = 0.775 R2 = 0.995 |
| 139.5 | 140.5 | τ0 = 0.474 K = 0.0558 n = 0.937 R2 = 1.00 | τ0 = 0.945 K = 0.0360 R2 = 0.999 | K = 0.139 n = 0.790 R2 = 0.995 |
| 178.9 | 140.3 | τ0 = 0.954 K = 0.0524 n = 0.921 R2 = 0.998 | τ0 = 1.46 K = 0.0302 R2 = 0.997 | K = 0.234 n = 0.684 R2 = 0.985 |
Appendix A.3. OB-NO 3
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 27.5 | 0.1 | τ0 = 4.47 K = 0.459 n = 0.861 R2 = 1.00 | τ0 = 7.75 K = 0.191 R2 = 0.997 | K = 1.92 n = 0.615 R2 = 0.986 |
| 92.4 | 20.3 | τ0 = 1.32 K = 0.121 n = 0.869 R2 = 1.00 | τ0 = 2.75 K = 0.0483 R2 = 0.996 | K = 0.465 n = 0.652 R2 = 0.987 |
| 92.6 | 40.1 | τ0 = 1.70 K = 0.144 n = 0.877 R2 = 1.00 | τ0 = 3.38 K = 0.0612 R2 = 0.997 | K = 0.561 n = 0.659 R2 = 0.987 |
| 92.7 | 60.4 | τ0 = 1.91 K = 0.177 n = 0.878 R2 = 1.00 | τ0 = 3.97 K = 0.0757 R2 = 0.997 | K = 0.684 n = 0.659 R2 = 0.987 |
| 92.8 | 80.4 | τ0 = 1.95 K = 0.225 n = 0.874 R2 = 1.00 | τ0 = 4.59 K = 0.0933 R2 = 0.996 | K = 0.744 n = 0.679 R2 = 0.989 |
| 93.0 | 100.5 | τ0 = 2.36 K = 0.296 n = 0.863 R2 = 1.00 | τ0 = 5.90 K = 0.114 R2 = 0.996 | K = 0.994 n = 0.664 R2 = 0.989 |
| 122.6 | 140.2 | τ0 = 2.52 K = 0.243 n = 0.873 R2 = 1.00 | τ0 = 5.37 K = 0.100 R2 = 0.997 | K = 0.912 n = 0.659 R2 = 0.987 |
| 151.2 | 140.6 | τ0 = 2.03 K = 0.194 n = 0.855 R2 = 1.00 | τ0 = 4.37 K = 0.0704 R2 = 0.995. | K = 0.704 n = 0.649 R2 = 0.988 |
| 180.8 | 140.1 | τ0 = 2.09 K = 0.196 n = 0.814 R2 = 1.00 | τ0 = 4.49 K = 0.0533 R2 = 0.992 | K = 0.811 n = 0.589 R2 = 0.984 |
| 209.3 | 140.2 | τ0 = 2.87 K = 0.163 n = 0.815 R2 = 0.999 | τ0 = 4.86 K = 0.0446 R2 = 0.991 | K = 1.11 n = 0.515 R2 = 0.970 |
| 244.3 | 140.3 | τ0 = 9.94 K = 0.0492 n = 0.944 R2 = 1.00 | τ0 = 10.3 K = 0.0332 R2 = 0.999 | K = 5.35 n = 0.255 R2 = 0.838 |
Appendix A.4. OB-NO 4
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 18.8 | 0.1 | τ0 = 1.54 K = 0.272 n = 0.934 R2 = 1.00 | τ0 = 2.88 K = 0.180 R2 = 0.999 | K = 0.652 n = 0.771 R2 = 0.995 |
| 66.9 | 20.3 | τ0 = 1.63 K = 0.0741 n = 0.979 R2 = 1.00 | τ0 = 1.89 K = 0.0640 R2 = 1.00 | K = 0.431 n = 0.693 R2 = 0.980 |
| 67.1 | 40.0 | τ0 = 1.72 K = 0.0993 n = 0.971 R2 = 1.00 | τ0 = 2.20 K = 0.0810 R2 = 1.00 | K = 0.495 n = 0.707 R2 = 0.983 |
| 67.3 | 60.5 | τ0 = 1.73 K = 0.136 n = 0.959 R2 = 1.00 | τ0 = 2.58 K = 0.102 R2 = 1.00 | K = 0.530 n = 0.734 R2 = 0.988 |
| 67.5 | 80.5 | τ0 = 2.54 K = 0.111 n = 1.03 R2 = 0.999 | τ0 = 1.79 K = 0.136 R2 = 1.00 | K = 0.517 n = 0.779 R2 = 0.986 |
| 61.4 | 96.8 | τ0 = 2.06 K = 0.234 n = 0.974 R2 = 1.00 | τ0 = 6.31 K = 0.152 R2 = 0.942 | K = 0.832 n = 0.732 R2 = 0.969 |
| 62.6 | 120.8 | τ0 = 2.58 K = 0.228 n = 1.02 R2 = 0.999 | τ0 = 2.15 K = 0.253 R2 = 1.00 | K = 0.744 n = 0.809 R2 = 0.992 |
| 100.9 | 140.4 | τ0 = 1.73 K = 0.113 n = 1.01 R2 = 1.00 | τ0 = 1.54 K = 0.120 R2 = 1.00 | K = 0.402 n = 0.801 R2 = 0.991 |
| 139.5 | 140.4 | τ0 = 1.53 K = 0.0519 n = 1.03 R2 = 1.00 | τ0 = 1.17 K = 0.0637 R2 = 1.00 | K = 0.339 n = 0.725 R2 = 0.979 |
| 178.3 | 140.1 | τ0 = 1.42 K = 0.0320 n = 1.04 R2 = 0.999 | τ0 = 1.10 K = 0.0426 R2 = 0.999 | K = 0.334 n = 0.662 R2 = 0.966 |
| 217.1 | 140.2 | τ0 = 1.73 K = 0.0274 n = 1.06 R2 = 0.999 | τ0 = 1.32 K = 0.0403 R2 = 0.999 | K = 0.407 n = 0.623 R2 = 0.955 |
| 247.1 | 140.2 | τ0 = 5.83 K = 0.0116 n = 1.22 R2 = 0.999 | τ0 = 3.93 K = 0.0545 R2 = 0.992 | K = 1.88 n = 0.428 R2 = 0.852 |
Appendix A.5. WB-NO 1
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 28.3 | 0.1 | τ0 = 0.794 K = 0.198 n = 0.914 R2 = 1.00 | τ0 = 2.79 K = 0.109 R2 = 0.999 | K = 0.380 n = 0.806 R2 = 0.997 |
| 69.7 | 20.2 | τ0 = 0.668 K = 0.118 n = 0.895 R2 = 1.00 | τ0 = 1.97 K = 0.0569 R2 = 0.998 | K = 0.296 n = 0.742 R2 = 0.994 |
| 70.1 | 40.1 | τ0 = 0.924 K = 0.142 n = 0.903 R2 = 1.00 | τ0 = 2.44 K = 0.0721 R2 = 0.998 | K = 0.391 n = 0.734 R2 = 0.993 |
| 70.4 | 60.3 | τ0 = 0.977 K = 0.196 n = 0.888 R2 = 1.00 | τ0 = 3.18 K = 0.0900 R2 = 0.997 | K = 0.468 n = 0.743 R2 = 0.994 |
| 70.7 | 80.7 | τ0 = 1.28 K = 0.247 n = 0.887 R2 = 1.00 | τ0 = 4.08 K = 0.112 R2 = 0.997 | K = 0.623 n = 0.732 R2 = 0.994 |
| 71.0 | 100.1 | τ0 = 1.64 K = 0.287 n = 0.892 R2 = 1.00 | τ0 = 4.84 K = 0.135 R2 = 0.998 | K = 0.717 n = 0.740 R2 = 0.994 |
| 72.1 | 108.5 | τ0 = 1.98 K = 0.363 n = 0.875 R2 = 1.00 | τ0 = 3.05 K = 0.187 R2 = 0.998 | K = 1.09 n = 0.658 R2 = 0.993 |
| 80.0 | 120.4 | τ0 = 2.02 K = 0.321 n = 0.887 R2 = 1.00 | τ0 = 4.14 K = 0.158 R2 = 0.998 | K = 0.914 n = 0.704 R2 = 0.993 |
| 98.1 | 120.6 | τ0 = 2.14 K = 0.221 n = 0.889 R2 = 1.00 | τ0 = 4.62 K = 0.102 R2 = 0.997 | K = 0.825 n = 0.672 R2 = 0.987 |
| 118.6 | 120.6 | τ0 = 2.23 K = 0.156 n = 0.894 R2 = 1.00 | τ0 = 3.96 K = 0.0746 R2 = 0.998 | K = 0.774 n = 0.635 R2 = 0.981 |
| 138.9 | 120.2 | τ0 = 1.87 K = 0.149 n = 0.864 R2 = 1.00 | τ0 = 3.64 K = 0.0577 R2 = 0.996 | K = 0.691 n = 0.617 R2 = 0.982 |
| 159.3 | 120.2 | τ0 = 1.66 K = 0.322 n = 0.723 R2 = 1.00 | τ0 = 5.17 K = 0.0461 R2 = 0.982 | K = 0.945 n = 0.552 R2 = 0.990 |
Appendix A.6. WB-NO 2
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 19.4 | 0.1 | τ0 = 3.10 K = 0.0739 n = 0.939 R2 = 0.998 | τ0 = 3.71 K = 0.0484 R2 = 0.998 | K = 0.965 n = 0.534 R2 = 0.953 |
| 66.8 | 20.2 | τ0 = 4.98 K = 0.0408 n = 0.904 R2 = 0.999 | τ0 = 5.41 K = 0.0208 R2 = 0.998 | K = 2.50 n = 0.292 R2 = 0.872 |
| 67.1 | 40.3 | τ0 = 4.93 K = 0.0415 n = 0.898 R2 = 0.999 | τ0 = 5.38 K = 0.0204 R2 = 0.997 | K = 2.48 n = 0.292 R2 = 0.874 |
| 67.2 | 60.4 | τ0 = 4.66 K = 0.0443 n = 0.888 R2 = 0.999 | τ0 = 5.16 K = 0.0202 R2 = 0.997 | K = 2.34 n = 0.298 R2 = 0.878 |
| 67.4 | 80.5 | τ0 = 4.78 K = 0.0425 n = 0.893 R2 = 0.999 | τ0 = 5.25 K = 0.0202 R2 = 0.997 | K = 2.39 n = 0.295 R2 = 0.877 |
| 67.6 | 100.3 | τ0 = 4.61 K = 0.0476 n = 0.878 R2 = 0.999 | τ0 = 5.16 K = 0.0203 R2 = 0.996 | K = 2.30 n = 0.301 R2 = 0.884 |
| 67.8 | 120.2 | τ0 = 4.57 K = 0.0498 n = 0.872 R2 = 0.999 | τ0 = 5.15 K = 0.0204 R2 = 0.996 | K = 2.29 n = 0.302 R2 = 0.886 |
| 87.4 | 120.3 | τ0 = 5.02 K = 0.0288 n = 0.925 R2 = 0.999 | τ0 = 5.29 K = 0.0171 R2 = 0.998 | K = 2.69 n = 0.259 R2 = 0.847 |
| 116.5 | 120.7 | τ0 = 6.07 K = 0.00829 n = 1.07 R2 = 0.998 | τ0 = 5.90 K = 0.134 R2 = 0.998 | K = 3.67 n = 0.192 R2 = 0.758 |
| 146.0 | 120.6 | τ0 = 6.12 K = 0.00110 n = 1.34 R2 = 0.998 | τ0 = 5.59 K = 0.0112 R2 = 0.983 | K = 3.93 n = 0.158 R2 = 0.650 |
| 175.0 | 120.8 | τ0 = 5.83 K = 0.000921 n = 1.36 R2 = 0.994 | τ0 = 5.27 K = 0.0112 R2 = 0.980 | K = 3.55 n = 0.171 R2 = 0.678 |
Appendix A.7. WB-NO 3
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 34.4 | 0.9 | τ0 = 2.30 K = 0.200 n = 0.788 R2 = 0.999 | τ0 = 4.70 K = 0.0452 R2 = 0.990 | K = 0.960 n = 0.541 R2 = 0.980 |
| 62.8 | 20.2 | τ0 = 1.91 K = 0.151 n = 0.779 R2 = 0.999 | τ0 = 3.71 K = 0.0321 R2 = 0.989 | K = 0.811 n = 0.516 R2 = 0.976 |
| 63.2 | 40.1 | τ0 = 1.77 K = 0.160 n = 0.773 R2 = 0.999 | τ0 = 3.66 K = 0.0325 R2 = 0.988 | K = 0.759 n = 0.529 R2 = 0.980 |
| 63.7 | 60.5 | τ0 = 1.63 K = 0.169 n = 0.767 R2 = 0.999 | τ0 = 3.62 K = 0.0332 R2 = 0.988 | K = 0.722 n = 0.540 R2 = 0.982 |
| 64.0 | 80.5 | τ0 = 1.56 K = 0.183 n = 0.759 R2 = 0.999 | τ0 = 3.69 K = 0.0339 R2 = 0.987 | K = 0.714 n = 0.545 R2 = 0.984 |
| 64.4 | 100.2 | τ0 = 1.58 K = 0.188 n = 0.759 R2 = 1.00 | τ0 = 3.77 K = 0.0347 R2 = 0.986 | K = 0.736 n = 0.544 R2 = 0.984 |
| 64.7 | 120.3 | τ0 = 1.53 K = 0.215 n = 0.743 R2 = 1.00 | τ0 = 3.96 K = 0.0354 R2 = 0.985 | K = 0.748 n = 0.547 R2 = 0.987 |
| 65.0 | 140.6 | τ0 = 1.67 K = 0.230 n = 0.738 R2 = 1.00 | τ0 = 4.24 K = 0.0366 R2 = 0.984 | K = 0.824 n = 0.537 R2 = 0.986 |
| 78.2 | 140.2 | τ0 = 2.75 K = 0.240 n = 0.726 R2 = 0.999 | τ0 = 5.37 K = 0.0351 R2 = 0.982 | K = 1.36 n = 0.458 R2 = 0.973 |
| 97.4 | 140.4 | τ0 = 7.59 K = 0.228 n = 0.717 R2 = 0.999 | τ0 = 10.0 K = 0.0312 R2 = 0.980 | K = 4.30 n = 0.290 R2 = 0.925 |
| 117.5 | 140.4 | τ0 = 21.1 K = 0.0481 n = 0.911 R2 = 0.977 | τ0 = 21.6 K = 0.0259 R2 = 0.982 | K = 15.5 n = 0.127 R2 = 0.729 |
| 138.2 | 140.2 | τ0 = 39.9 K = 0.000500 n = 1.54 R2 = 0.869 | τ0 = 38.5 K = 0.0208 R2 = 0.860 | K = 35.3 n = 0.0467 R2 = 0.336 |
| 158.2 | 140.1 | τ0 = 46.2 K = 0.0000000983 n = 2.76 R2 = 0.512 | τ0 = 44.5 K = 0.0172 R2 = 0.473 | K = 46.5 n = 0.0100 R2 = 0.0227 |
Appendix A.8. WB-NO 4
| Temperature (°C) | Pressure (MPa) | Herschel–Bulkley | Bingham | Power-Law |
|---|---|---|---|---|
| 22.8 | 0.1 | τ0 = 36.4 K = 0.159 n = 0.893 R2 = 1.00 | τ0 = 38.2 K = 0.0751 R2 = 0.998 | K = 22.8 n = 0.192 R2 = 0.821 |
| 64.9 | 20.2 | τ0 = 36.6 K = 0.0440 n = 0.956 R2 = 0.999 | τ0 = 36.9 K = 0.0324 R2 = 0.999 | K = 27.9 n = 0.104 R2 = 0.750 |
| 65.5 | 40.3 | τ0 = 36.6 K = 0.0463 n = 0.947 R2 = 0.999 | τ0 = 36.9 K = 0.0319 R2 = 0.999 | K = 27.9 n = 0.103 R2 = 0.753 |
| 66.1 | 60.3 | τ0 = 36.6 K = 0.0470 n = 0.947 R2 = 0.999 | τ0 = 37.0 K = 0.0324 R2 = 0.999 | K = 27.9 n = 0.104 R2 = 0.752 |
| 66.7 | 80.4 | τ0 = 36.6 K = 0.0512 n = 0.937 R2 = 1.00 | τ0 = 37.0 K = 0.0331 R2 = 0.999 | K = 27.8 n = 0.106 R2 = 0.757 |
| 67.2 | 100.0 | τ0 = 36.8 K = 0.0496 n = 0.945 R2 = 0.999 | τ0 = 37.2 K = 0.0339 R2 = 0.999 | K = 27.8 n = 0.107 R2 = 0.755 |
| 67.7 | 119.8 | τ0 = 36.8 K = 0.0538 n = 0.939 R2 = 1.00 | τ0 = 37.2 K = 0.0351 R2 = 0.999 | K = 27.6 n = 0.110 R2 = 0.759 |
| 88.7 | 120.4 | τ0 = 37.5 K = 0.0412 n = 0.945 R2 = 1.00 | τ0 = 37.8 K = 0.0281 R2 = 0.999 | K = 29.5 n = 0.0908 R2 = 0.743 |
| 117.5 | 120.5 | τ0 = 39.7 K = 0.0179 n = 1.02 R2 = 1.00 | τ0 = 39.6 K = 0.0210 R2 = 1.00 | K = 33.1 n = 0.0665 R2 = 0.694 |
| 146.8 | 120.6 | τ0 = 42.5 K = 0.00636 n = 1.14 R2 = 0.998 | τ0 = 42.2 K = 0.0166 R2 = 0.995 | K = 37.1 n = 0.0489 R2 = 0.629 |
| 176.0 | 120.8 | τ0 = 50.6 K = 0.0000466 n = 1.77 R2 = 0.869 | τ0 = 49.9 K = 0.00920 R2 = 0.829 | K = 48.4 n = 0.0172 R2 = 0.264 |
Appendix B. Model Algorithm Pseudocode
| 1. Input Parameters: • Drilling Parameters: H (Well depth, m) t_cycle (Circulation time, h) Q_surface (Surface flow rate, m3/s) T_surface (Surface temperature, °C) G_geo (Geothermal gradient, °C/m) ρ_mud0 (Surface drilling fluid density, kg/m3) • Material Properties: λ_casing (Casing thermal conductivity, W/(m·°C)) λ_cement (Cement sheath thermal conductivity, W/(m·°C)) α_formation (Formation thermal diffusivity, m2/s) • Rheological Model: τ_y (Yield stress, Pa) K_consistency (Consistency index, Pa·s^n) n (Flow behavior index) 2. Spatial Discretization: Δz = BC (Spatial step size, m) N =〔H/Δz〕(Number of grid nodes) • Initialize 2D arrays: P_annulus[N+1][200] (Annular pressure field, Pa) P_pipe[N+1][200] (Drill pipe pressure field, Pa) T_annulus[N+1][200] (Annular temperature field, °C) T_pipe[N+1][200] (Drill pipe temperature field, °C) 3. Main Computation Loop (Temporal Iteration) for t_step in 1 to 200: #Forward Sweep (Top→Bottom) for node in 0 to N: #Geometry Update D_pipe_in[node] = f_diameter(node·Δz, casing_spec) D_pipe_out[node] = f_diameter(node·Δz, drill_string_spec) D_annulus[node] = D_casing[node] D_pipe_out[node] #Mud Density Correction: P = P_annulus[node][t_step-1] T = T_annulus[node][t_step-1] if 1200 ≤ ρ_mud0 ≤ 1600: ρ_mud = (ρ_mud0/1400) × 103 × exp(α1P + β1T + γ1PT) elif 1600 < ρ_mud0 ≤ 2000: ρ_mud = (ρ_mud0/1800) × 103 × exp(α2P + β2T + γ2PT) else: ρ_mud = (ρ_mud0/2400) × 103 × exp(α3P + β3T + γ3PT) #Herschel–Bulkley Model Update τ_eff = τ_y × Φ(T_annulus[node][t_step-1], P_annulus[node][t_step-1]) K_eff = K_consistency × Ψ(T_annulus[node][t_step-1]) n_eff = n × Θ(P_annulus[node][t_step-1]) #Flow Regime Determination Re_annulus = (12^(1-n_eff) × ρ_mud × D_annulus[node]^n_eff × V_annulus^(2-n_eff) / (K_eff × (3 + 1/n_eff)^n_eff) if Re_annulus < Re_critical: ΔP_friction = (4 × K_eff × Δz)/D_annulus[node] × [(3n_eff + 1)/n_eff × V_annulus/D_annulus[node]]^n_eff else: f = Newton-Raphson_Solver(ε/D_annulus[node], Re_annulus) ΔP_friction = f × (ρ_mud × V_annulus2 × Δz)/(2 × D_annulus[node]) #Pressure Update P_annulus[node+1][t_step] = P_annulus[node][t_step] + ρ_mud × g × Δz × sinθ + ΔP_friction #Thermal Calculation t_dimensionless = α_formation × t_cycle / D_annulus[node]^2 if t_dimensionless ≤ 1.5: T_dimensionless = 1.1281√t_dimensionless (1 0.3√t_dimensionless) else: T_dimensionless = (0.4063 + 0.5 ln t_dimensionless)(1 + 0.6/t_dimensionless) T_pipe[node][t_step] = C1exp(-k1Δz) + C2exp(-k2Δz) + (T_injection B·G_geo) + G_geo·Δz # Backward Update (Bottom→Top) for node in N downto 1: # Similar friction calculation for pipe flow P_pipe[node-1][t_step] = P_pipe[node][t_step] ρ_mud × g × Δz × sinθ + ΔP_friction_pipe # Convergence Check if max(|T_annulus[:,t_step] T_annulus[:,t_step-1]|) < 1e-3: converged_step = t_step break |
References
- Sun, J.; Yang, J.; Bai, Y.; Lyu, K.; Liu, F. Research Progress and Development of Deep and Ultra-Deep Drilling Fluid Technology. Pet. Explor. Dev. 2024, 51, 1022–1034. [Google Scholar] [CrossRef]
- Shen, A.; Hu, A.; Qiao, Z.; Zheng, J.; She, M.; Pan, L. Development and Preservation Mechanism of Deep and Ultra-Deep Carbonate Reservoirs. Sci. China Earth Sci. 2024, 67, 3367–3385. [Google Scholar] [CrossRef]
- Wang, C.; Feng, S.; Zhang, Z.; Zhou, B.; Lyu, X.; Zhou, B. Key Technologies for Drilling Design of Well Shendi Take-1. Pet. Drill. Tech. 2024, 52, 78–86. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, K.; Zhong, Y. Seeking Answers from the Depths of the Earth: A Record of Southwest Oil and Gas Field’s Promotion of the Exploration of Chuanke-1 Well in Deep Strata. China Pet. News, 10 August 2023. [Google Scholar]
- Chavez, M.A.; Garcia, G.A.; Pogoson, O.; Li, Y.L.; Cardona, A.H.; Nelson, R.N. Lower Tertiary—A Fully Comprehensive Well Completion Design Methodology to Overcome Reservoir Challenges. In Proceedings of the SPE Artificial Lift Conference-Latin America and Caribbean, Salvador, Brazil, 27–28 May 2015; OnePetro: Baton Rouge, LA, USA, 2013. [Google Scholar]
- Sugisaki, R. Deep-Seated Gas Emission Induced by the Earth Tide: A Basic Observation for Geochemical Earthquake Prediction. Science 1981, 212, 1264–1266. [Google Scholar] [CrossRef] [PubMed]
- Pang, X.-Q.; Jia, C.-Z.; Wang, W.-Y. Petroleum Geology Features and Research Developments of Hydrocarbon Accumulation in Deep Petroliferous Basins. Pet. Sci. 2015, 12, 1–53. [Google Scholar] [CrossRef]
- Li, Q. Numerical Insights into Factors Affecting Collapse Behavior of Horizontal Wellbore in Clayey Silt Hydrate-Bearing Sediments and the Accompanying Control Strategy. Ocean Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Li, Q. Settling Behavior and Mechanism Analysis of Kaolinite as a Fracture Proppant of Hydrocarbon Reservoirs in CO2 Fracturing Fluid. Colloids Surf. A Physicochem. Eng. Asp. 2025, 724, 137463. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, H.; Pang, S. Calculation Method of Drilling Fluid Rheological Parameters and Software Development for Field Application. West-China Explor. Eng. 2008, 20, 72–73. [Google Scholar]
- Karpenko, M. Aircraft Hydraulic Drive Energy Losses and Operation Delay Associated with the Pipeline and Fitting Connections. Aviation 2024, 28, 1–8. [Google Scholar] [CrossRef]
- Zhou, X.; Yu, P.; Qian, X. Optimization of rheological models for cationic polymer drilling fluid system. West-China Explor. Eng. 2009, 21, 43–44. [Google Scholar]
- Frigaard, I.A.; Paso, K.G.; de Souza Mendes, P.R. Bingham’s Model in the Oil and Gas Industry. Rheol. Acta 2017, 56, 259–282. [Google Scholar] [CrossRef]
- Demirdal, B.; Miska, S.; Takach, N.; Cunha, J.C. Drilling Fluids Rheological and Volumetric Characterization Under Downhole Conditions. In Proceedings of the SPE Latin America and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 15–18 April 2007; SPE: Buenos Aires, Argentina, 2007. SPE-108111-MS. [Google Scholar]
- Bailey, T.J.; Bern, P.A.; McEwan, F. Low-Toxicity Oil Muds: A Knowledge of Downhole Rheological Behavior Assists Successful Field Application. SPE Drill. Eng. 1986, 1, 107–114. [Google Scholar] [CrossRef]
- Politte, M.D. Invert Oil Mud Rheology as a Function of Temperature and Pressure; OnePetro: Baton Rouge, LA, USA, 1985. [Google Scholar]
- Srini-Vasan, S.A.C.G.; Gatlin, C. The Effect of Temperature on the Flow Properties of Clay-Water Drilling Muds. J. Pet. Technol. 1958, 10, 59–60. [Google Scholar] [CrossRef]
- McMordie, W.C., Jr.; Bennett, R.B.; Bland, R.G. The Effect of Temperature and Pressure on the Viscosity of Oil-Base Muds. J. Pet. Technol. 1975, 27, 884–886. [Google Scholar] [CrossRef]
- Fisk, J.V.; Jamison, D.E. Physical Properties of Drilling Fluids at High Temperatures and Pressures. SPE Drill. Eng. 1989, 4, 341–346. [Google Scholar] [CrossRef]
- Alderman, N.J.; Gavignet, A.; Guillot, D.; Maitland, G.C. High-Temperature, High-Pressure Rheology of Water-Based Muds; OnePetro: Houston, TX, USA, 1988; pp. 187–195. [Google Scholar]
- Jiang, G.; Wu, X.; Yan, J.; Wu, F.; Wang, S. Study on the Rheology Property of Water Based Drilling Fluid at High Temperature and High Pressure. Drill. Fluid Complet. Fluid 1994, 11, 21–26. [Google Scholar]
- Rommetveit, R.; Bjorkevoll, K.S. Temperature and Pressure Effects on Drilling Fluid Rheology and ECD in Very Deep Wells; OnePetro: Manama, Bahrain, 1997; pp. 297–305. [Google Scholar]
- Quitian-Ardila, L.H.; Andrade, D.E.V.; Franco, A.T. A Proposal for a Constitutive Equation Fitting Methodology for the Rheological Behavior of Drilling Fluids at Different Temperatures and High-Pressure Conditions. Geoenergy Sci. Eng. 2024, 233, 212570. [Google Scholar] [CrossRef]
- Rafieefar, A.; Sharif, F.; Hashemi, A.; Bazargan, A.M. Rheological Behavior and Filtration of Water-Based Drilling Fluids Containing Graphene Oxide: Experimental Measurement, Mechanistic Understanding, and Modeling. ACS Omega 2021, 6, 29905–29920. [Google Scholar] [CrossRef] [PubMed]
- Fakoya, M.F.; Ahmed, R.M. A Generalized Model for Apparent Viscosity of Oil-Based Muds. J. Pet. Sci. Eng. 2018, 165, 777–785. [Google Scholar] [CrossRef]


| Types of Drilling Fluids | Number | Density (g/cm3) | Temperature (°C) | Pressure (MPa) |
|---|---|---|---|---|
| Oil-based | OB-1 | 1.00 | 25~110 | 0.1~120 |
| OB-2 | 1.57 | 25~180 | 0.1~140 | |
| OB-3 | 2.08 | 25~247 | 0.1~140 | |
| OB-4 | 2.25 | 25~247 | 0.1~140 | |
| Water-based | WB-1 | 1.54 | 25~160 | 0.1~120 |
| WB-2 | 1.70 | 25~175 | 0.1~120 | |
| WB-3 | 1.82 | 25~120 | 0.1~140 | |
| WB-4 | 2.15 | 25~120 | 0.1~140 |
| Temperature (°C) | Pressure (MPa) | τ0 | k | n | R2 |
|---|---|---|---|---|---|
| 20.58 | 0.10 | 2.207 | 0.000 | 5.924 | 0.994 |
| 69.17 | 20.30 | 3.830 | 0.017 | 1.031 | 0.998 |
| 69.90 | 40.17 | 3.671 | 0.017 | 1.032 | 0.998 |
| 70.58 | 60.65 | 3.476 | 0.018 | 1.025 | 0.997 |
| 69.78 | 80.57 | 3.435 | 0.018 | 1.030 | 0.997 |
| 69.93 | 100.28 | 3.329 | 0.018 | 1.024 | 0.997 |
| 70.85 | 120.49 | 3.130 | 0.022 | 1.000 | 0.997 |
| 70.85 | 140.38 | 3.120 | 0.025 | 0.986 | 0.996 |
| 79.86 | 140.63 | 4.603 | 0.019 | 1.011 | 0.999 |
| 97.95 | 140.59 | 9.908 | 0.006 | 1.142 | 0.989 |
| Coefficients | A | B | C | D | E | R2 | |
|---|---|---|---|---|---|---|---|
| H-B Parameter | |||||||
| τ0 | 0.238 | −1.918 × 10−2 | 3.582 × 10−4 | −3.930 × 10−3 | 1.318 × 10−5 | 0.998 | |
| K | −3.008 | 0.212 | −1.567 × 10−3 | −3.799 × 10−3 | 4.136 × 10−5 | 0.994 | |
| n | 1.471 | −8.208 × 10−2 | 5.151 × 10−4 | 6.159 × 10−6 | −6.161 × 10−7 | 0.999 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, H.; Cai, C.; Zhang, B.; Luo, J.; Chen, P.; Xiao, D. Experimental Study and Rheological Modeling of Water-Based and Oil-Based Drilling Fluids Under Extreme Temperature–Pressure Condition. Energies 2025, 18, 4687. https://doi.org/10.3390/en18174687
Lei H, Cai C, Zhang B, Luo J, Chen P, Xiao D. Experimental Study and Rheological Modeling of Water-Based and Oil-Based Drilling Fluids Under Extreme Temperature–Pressure Condition. Energies. 2025; 18(17):4687. https://doi.org/10.3390/en18174687
Chicago/Turabian StyleLei, Haishen, Chun Cai, Baolin Zhang, Jing Luo, Ping Chen, and Dong Xiao. 2025. "Experimental Study and Rheological Modeling of Water-Based and Oil-Based Drilling Fluids Under Extreme Temperature–Pressure Condition" Energies 18, no. 17: 4687. https://doi.org/10.3390/en18174687
APA StyleLei, H., Cai, C., Zhang, B., Luo, J., Chen, P., & Xiao, D. (2025). Experimental Study and Rheological Modeling of Water-Based and Oil-Based Drilling Fluids Under Extreme Temperature–Pressure Condition. Energies, 18(17), 4687. https://doi.org/10.3390/en18174687





