Dynamic Behavior of a Glazing System and Its Impact on Thermal Comfort: Short-Term In Situ Assessment and Machine Learning-Based Predictive Modeling
Abstract
1. Introduction
2. Materials and Methods
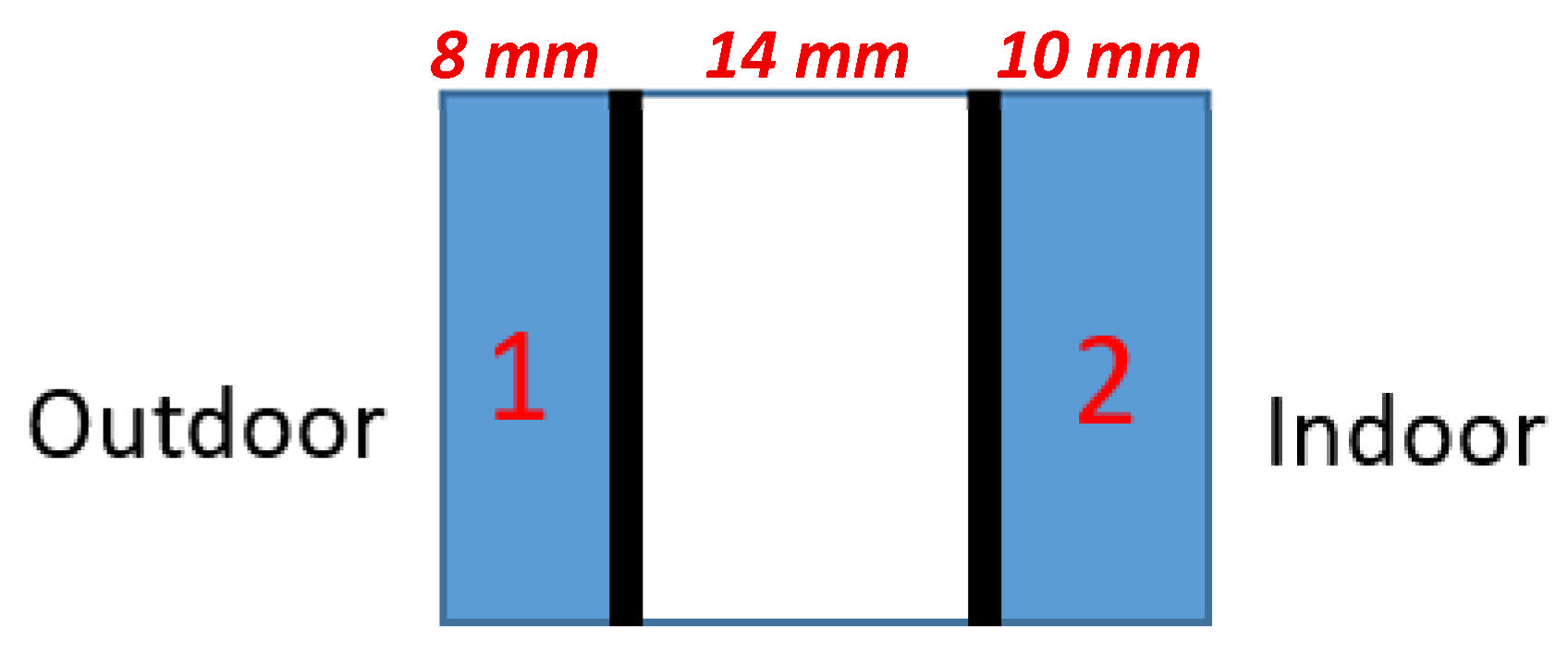
2.1. Glazing Unit
2.2. Measurement Campaign
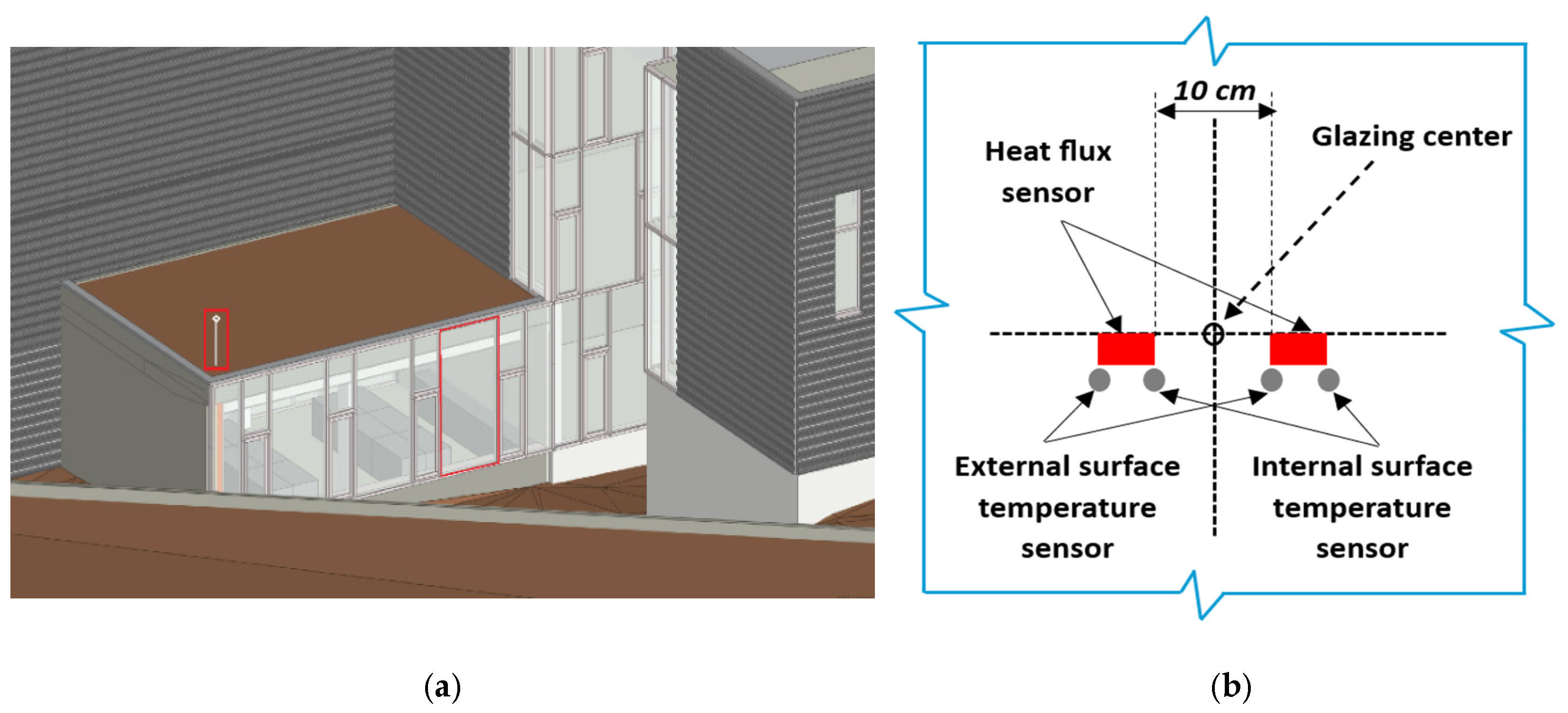
2.3. Measurement Setup
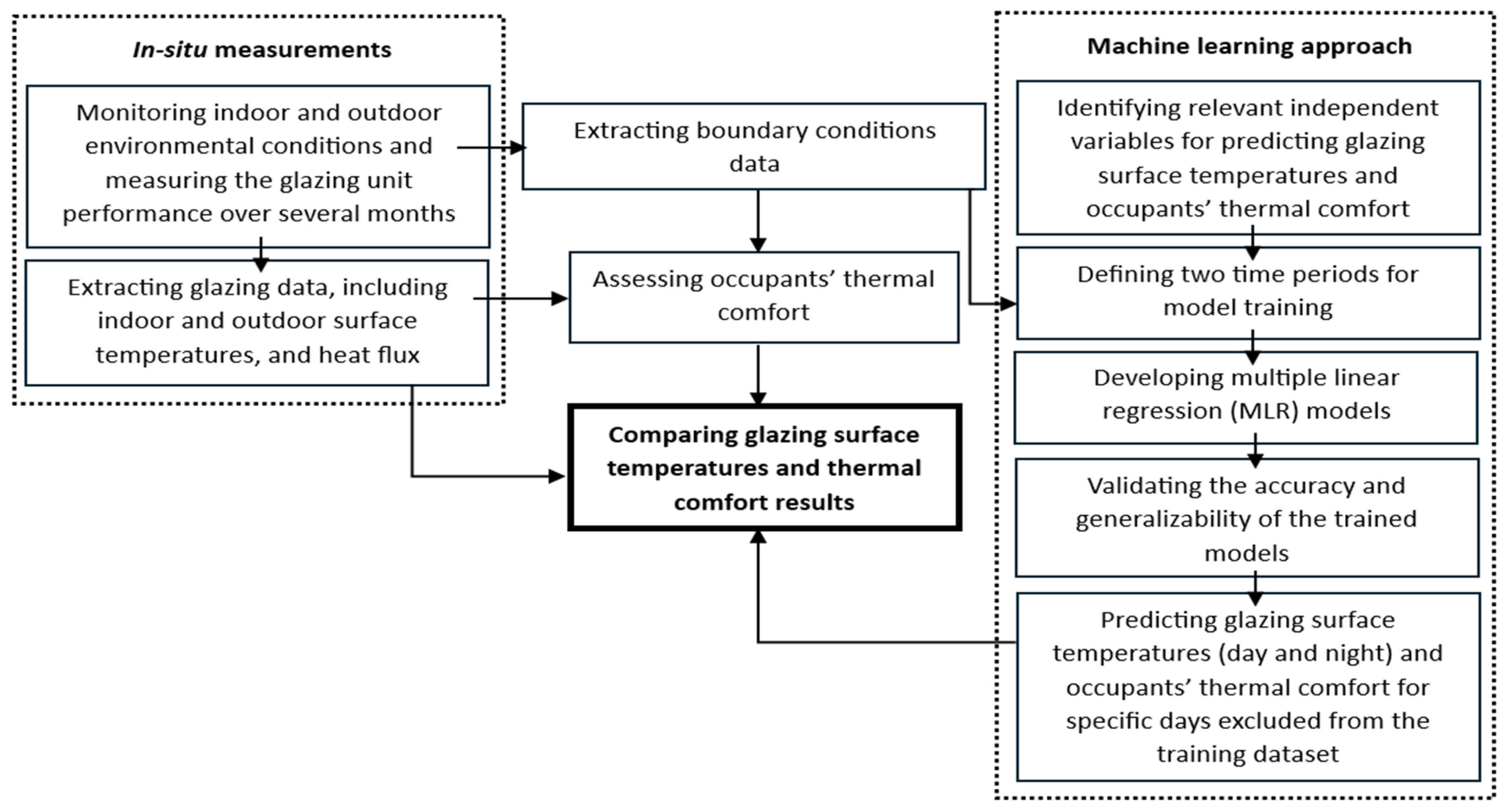
2.4. Machine Learning Approach
2.4.1. Dependent and Independent Variables for Dynamic Performance Analysis of the Glazing Unit
2.4.2. Dependent and Independent Variables for Indoor Thermal Comfort Analysis
3. Results
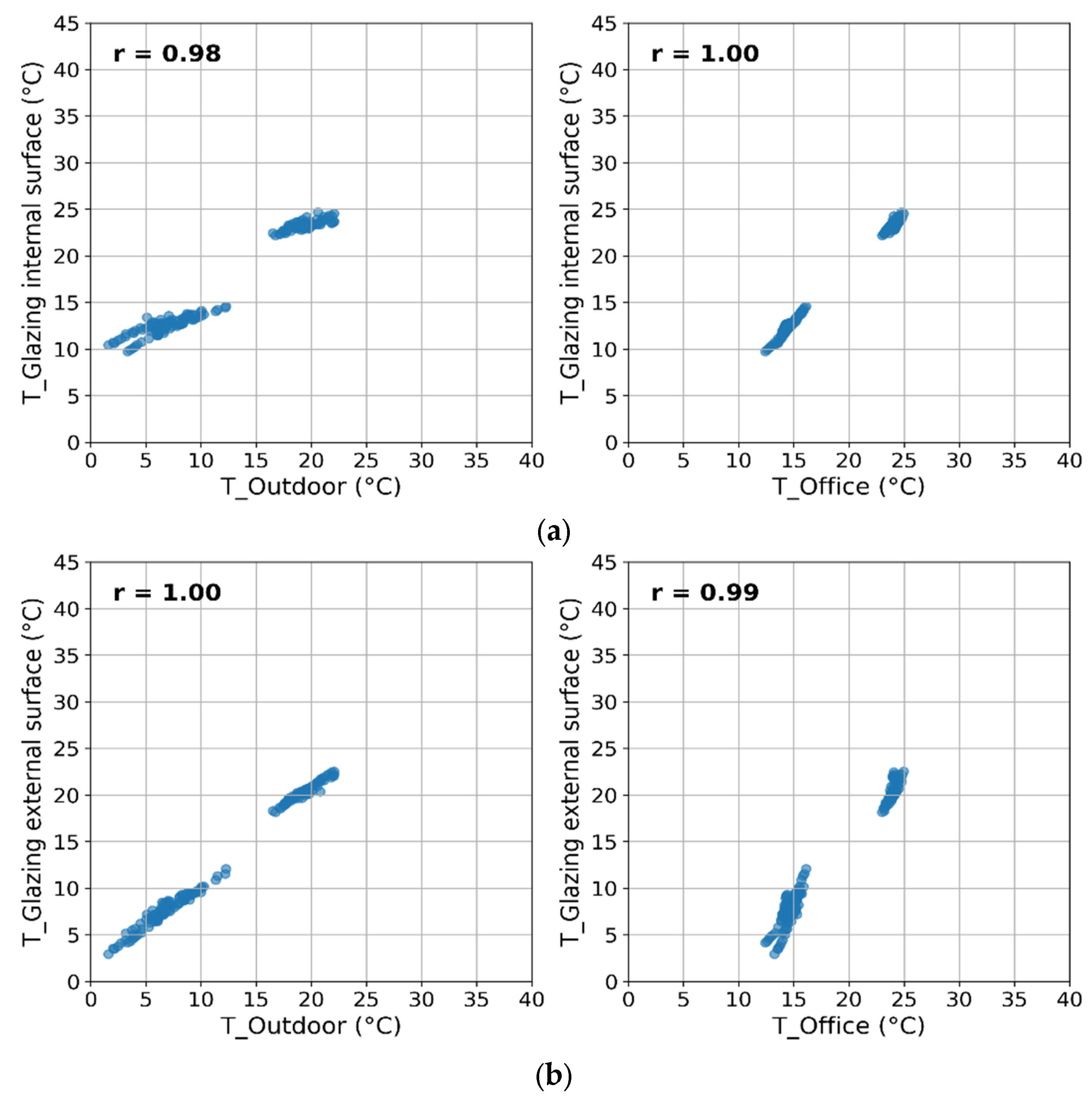
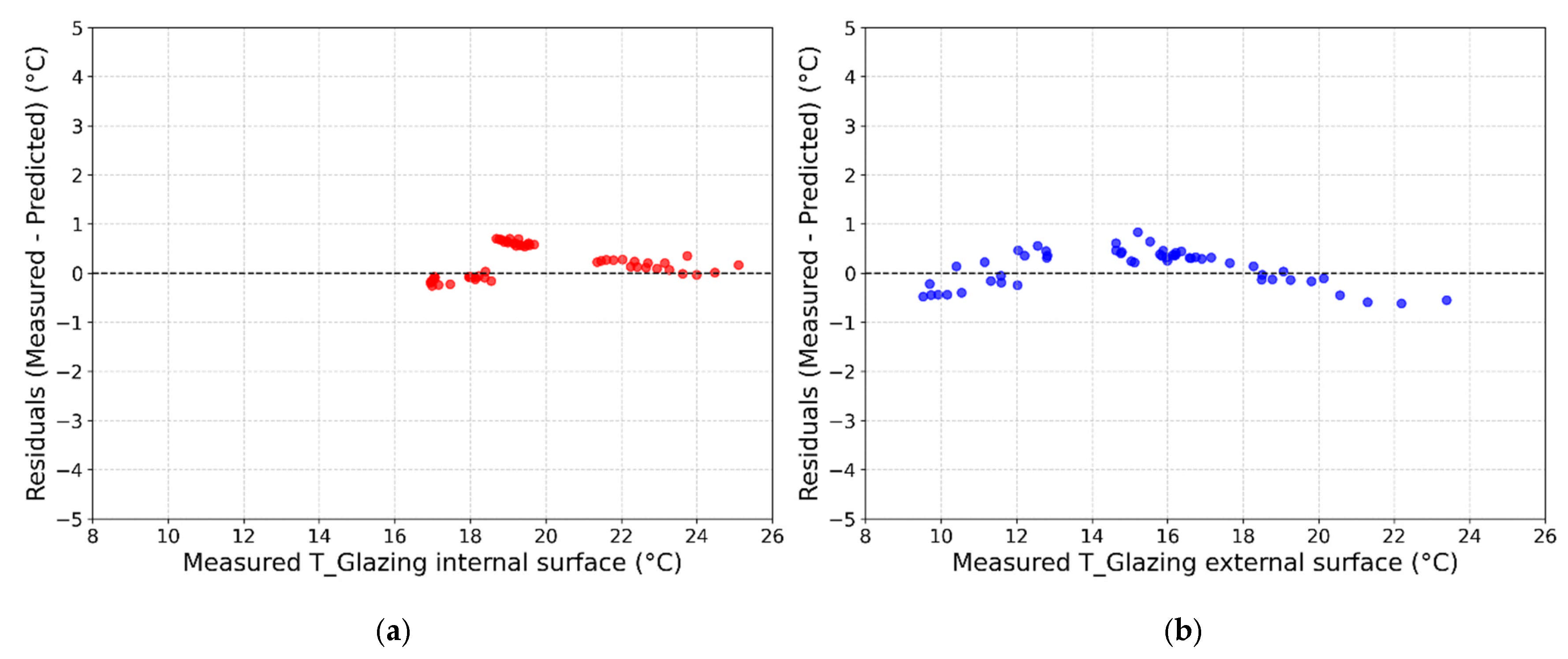
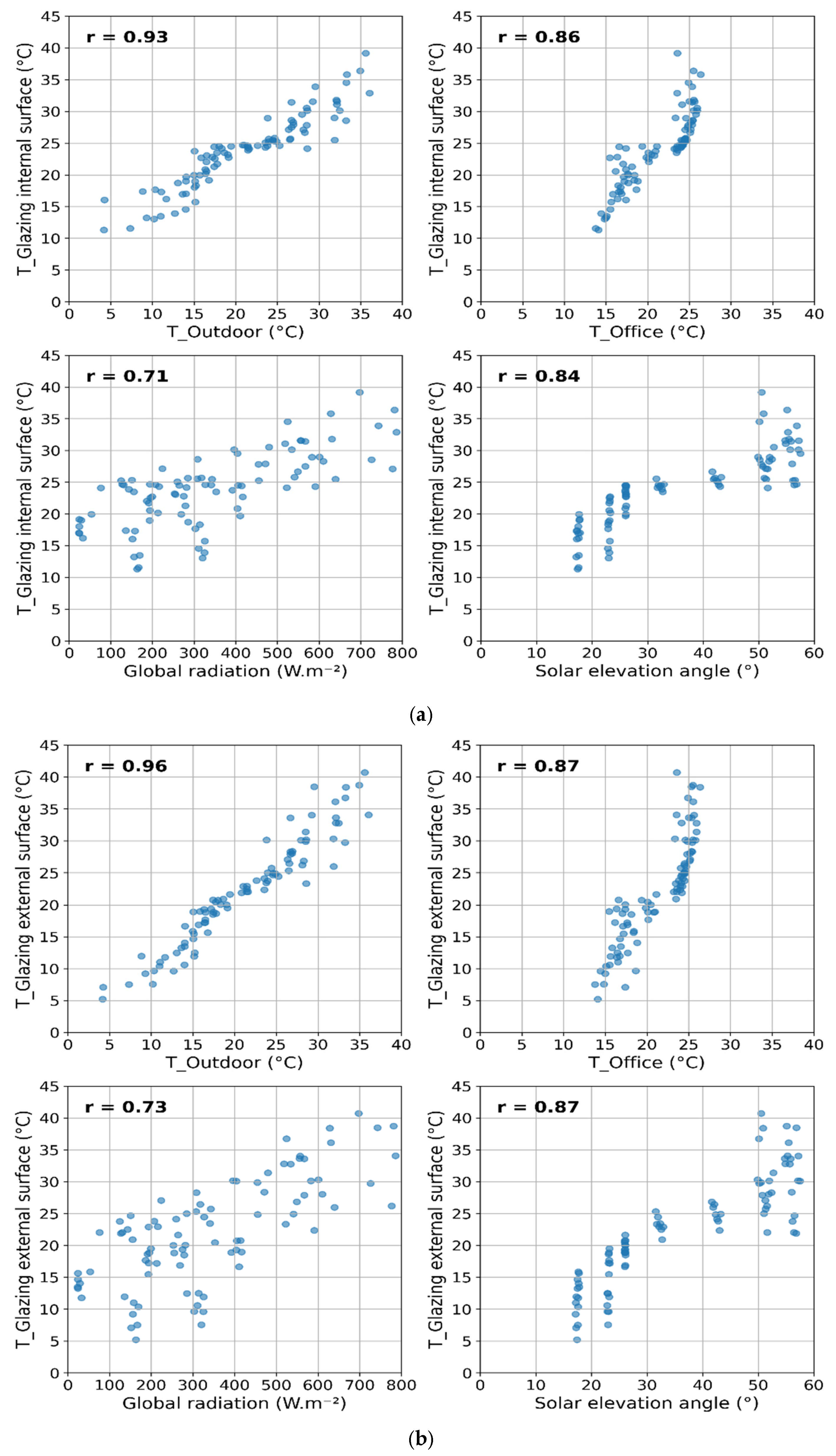
3.1. Dynamic Behavior Evaluation
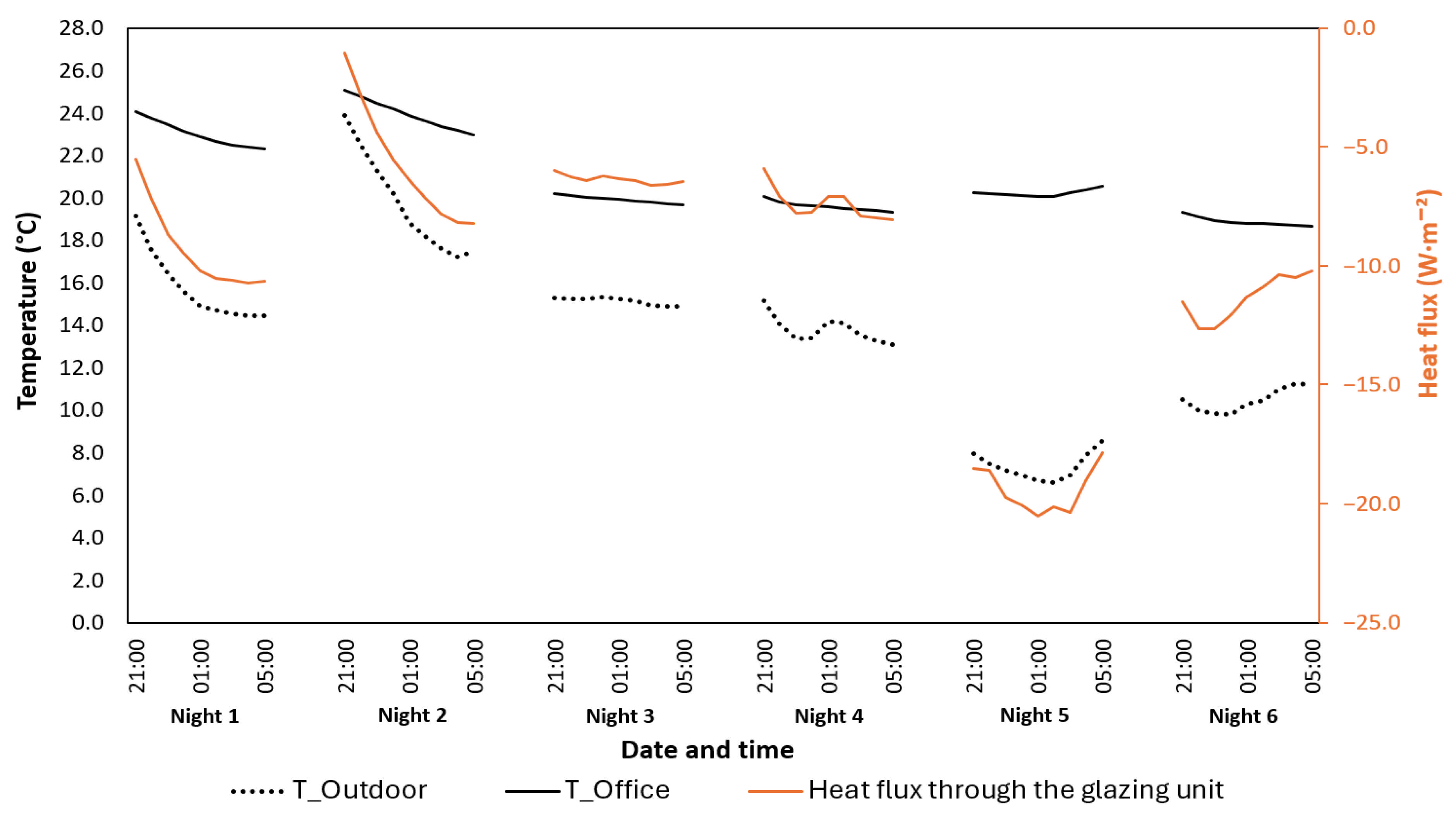
3.1.1. Nighttime Assessment
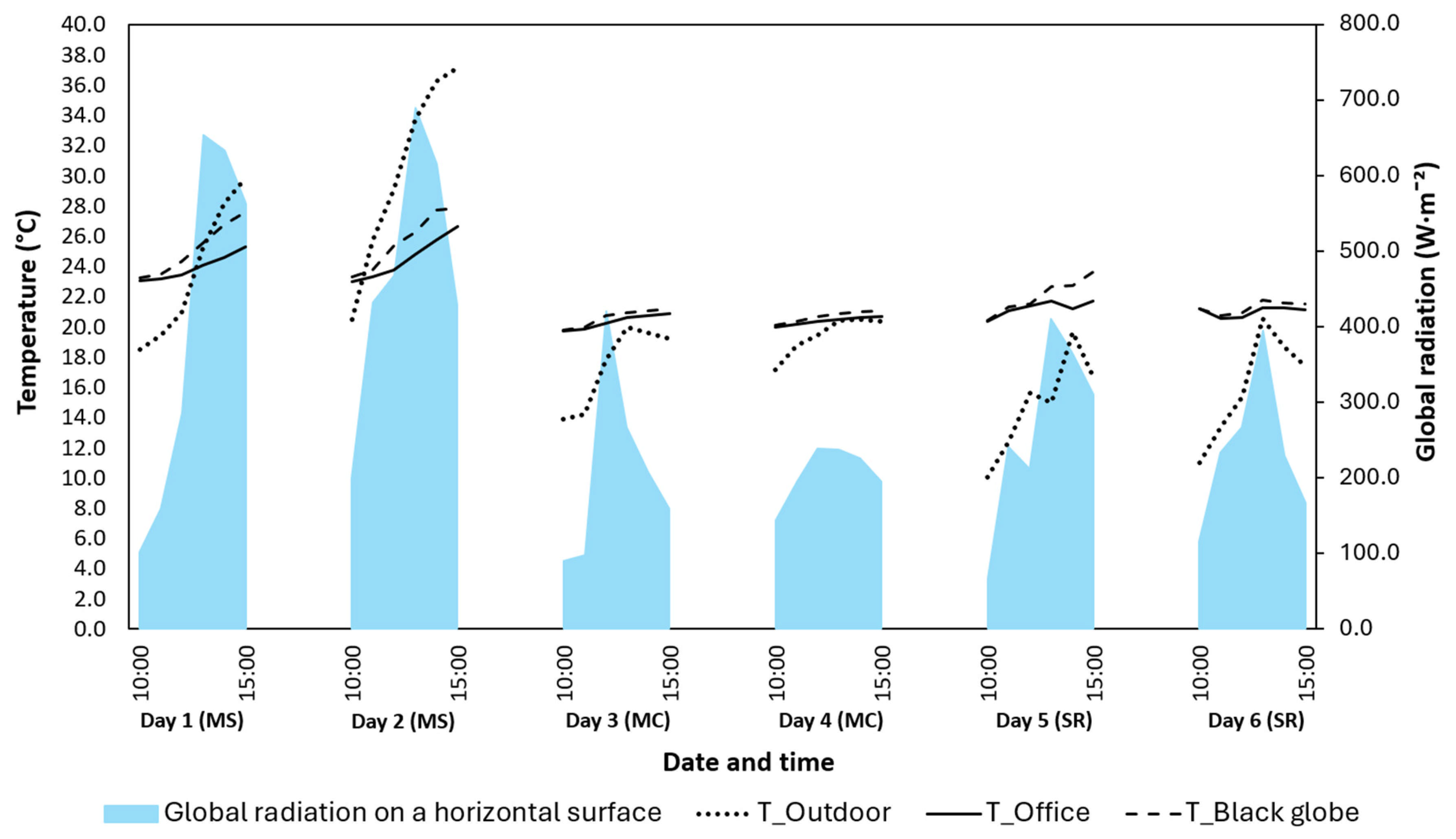
3.1.2. Daytime Assessment
3.2. Thermal Comfort Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | black globe temperature (°C) | ||
| MAPE | Mean Absolute Percentage Error | outdoor ambient temperature (°C) | |
| ML | Machine Learning | office ambient temperature (°C) | |
| MLR | Multiple Linear Regression | operative temperature (°C) | |
| MRT | Mean Radiant Temperature | external surface temperature of the glazing (°C) | |
| MSE | Mean Squared Error | internal surface temperature of the glazing (°C) | |
| NZEBs | Nearly Zero-Energy Buildings | U-value | thermal transmittance () |
| PMV | Predicted Mean Vote | air velocity at the level of the black globe sensor () | |
| PPD | Predicted Percentage Dissatisfied | observed value of the dependent value for the -th data point | |
| RMSE | Root Mean Squared Error | predicted value of the dependent value for the -th data point | |
| SHGC | Solar Heat Gain Coefficient | arithmetic mean of the dependent variable | |
| Abbreviations | emissivity of the black globe sensor (no dimension) | ||
| diameter of the black globe sensor (m) | solar elevation angle (°) | ||
| global horizontal radiation () | Subscripts | ||
| r | Pearson Correlation Coefficient | -th data point () | |
| R2 | Coefficient of Determination | total number of data points | |
| air temperature (°C) |
References
- Salazar, S.L.; Yang, R.; Li, D.; Chagolla-Aranda, M.A.; Chávez-Chena, Y.; Simá, E. Advanced hybrid assessment of glazing systems: A comparative analysis using differential and global methods for precise thermal optimization and energy efficiency in building. J. Build. Eng. 2025, 100, 111711. [Google Scholar] [CrossRef]
- Moghaddam, S.A.; Simões, N.; da Silva, M.G. Review of the experimental methods for evaluation of windows’ solar heat gain coefficient: From standardized tests to new possibilities. Build. Environ. 2023, 242, 110527. [Google Scholar] [CrossRef]
- Wijewardane, S.; Santamouris, M. Smart glazing systems: An industrial outlook. Sol. Compass 2025, 14, 100114. [Google Scholar] [CrossRef]
- Mohammadi, M. Keeping it simple: Field testing and techno-economic assessment of a low-cost secondary quad glazing for enhanced energy efficiency in buildings. Energy Built Environ. 2025, in press. [CrossRef]
- Teixeira, H.; Rodrigues Moret, A.; Aelenei, D.; Gomes, M.G. Literature review of solar control smart building glazing: Technologies, performance, and research insights. Build. Environ. 2025, 274, 112784. [Google Scholar] [CrossRef]
- Song, B.; Yang, L.; Bai, L. Field experimental study of the impact of solar radiation on the thermal comfort of occupants near the glazing area in an office building. Energy Build. 2025, 332, 115422. [Google Scholar] [CrossRef]
- Pavlenko, A.M.; Sadko, K. Evaluation of Numerical Methods for Predicting the Energy Performance of Windows. Energies 2022, 16, 1425. [Google Scholar] [CrossRef]
- Krarti, M.; Ayari, M.A.; Touati, F.; Paurobally, M.R. Energy Benefits of PV-Integrated Dynamic Overhangs for Residential Buildings in Qatar. Energies 2025, 18, 1156. [Google Scholar] [CrossRef]
- Moghaddam, S.A.; Serra, C.; Gameiro Da Silva, M.; Simões, N. Comprehensive Review and Analysis of Glazing Systems towards Nearly Zero-Energy Buildings: Energy Performance, Thermal Comfort, Cost-Effectiveness, and Environmental Impact Perspectives. Energies 2023, 16, 6283. [Google Scholar] [CrossRef]
- Shi, Y.; Xi, X.; Zhang, Y.; Xu, H.; Zhang, J.; Zhang, R. Prediction and analysis of the thermal performance of composite vacuum glazing. Energies 2021, 14, 5769. [Google Scholar] [CrossRef]
- Peng, J.; Tan, Y.; Fang, Y.; Yang, H.; Song, A.; Curcija, C.; Selkowitz, S. Excellent Insulation Vacuum Glazing for Low-Carbon Buildings: Fabrication, Modeling, and Evaluation. Engineering 2024, in press. [CrossRef]
- Pan, Z.; Liu, J.; Wu, H.; Luo, D.; Huang, J. Theoretical-experimental-simulation research on thermal-daylight-electrical performance of PV glazing in high-rise office building in the Greater Bay Area. Appl. Energy 2025, 378, 124739. [Google Scholar] [CrossRef]
- Gumbarević, S.; Milovanović, B.; Dalbelo Bašić, B.; Gaši, M. Combining Deep Learning and the Heat Flux Method for In-Situ Thermal-Transmittance Measurement Improvement. Energies 2022, 15, 5029. [Google Scholar] [CrossRef]
- Khaled Mohammad, A.; Ghosh, A. Exploring energy consumption for less energy-hungry building in UK using advanced aerogel window. Sol. Energy 2023, 253, 389–400. [Google Scholar] [CrossRef]
- Es-sakali, N.; Idrissi Kaitouni, S.; Ait Laasri, I.; Oualid Mghazli, M.; Cherkaoui, M.; Pfafferott, J. Static and dynamic glazing integration for enhanced building efficiency and indoor comfort with thermochromic and electrochromic windows. Therm. Sci. Eng. Prog. 2024, 52, 102681. [Google Scholar] [CrossRef]
- Simões, N.; Moghaddam, S.A.; da Silva, M.G. Review of the Experimental Methods for Evaluation of Windows’ Thermal Transmittance: From Standardized Tests to New Possibilities. Buildings 2023, 13, 703. [Google Scholar] [CrossRef]
- Kuhn, T.E. State of the art of advanced solar control devices for buildings. Sol. Energy 2017, 154, 112–133. [Google Scholar] [CrossRef]
- Ranđelović, D.; Jovanović, V.; Ignjatović, M.; Marchwiński, J.; Kopyłow, O.; Milošević, V. Improving Energy Efficiency of School Buildings: A Case Study of Thermal Insulation and Window Replacement Using Cost-Benefit Analysis and Energy Simulations. Energies 2024, 17, 6176. [Google Scholar] [CrossRef]
- Li, X.; Wu, Y. A review of complex window-glazing systems for building energy saving and daylight comfort: Glazing technologies and their building performance prediction. J. Build. Phys. 2024, 48, 496–540. [Google Scholar] [CrossRef]
- Guattari, C.; De Cristo, E.; Evangelisti, L.; Gori, P.; Jacoby, R.; Fabiani, C.; Laura, A. Energy & Buildings Thermal characterization of building walls using an equivalent modeling approach. Energy Build. 2025, 329, 115226. [Google Scholar] [CrossRef]
- Laukkarinen, A.; Vinha, J. Long-term prediction of hourly indoor air temperature using machine learning. Energy Build. 2024, 325, 114972. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Machine learning for energy performance prediction at the design stage of buildings. Energy Sustain. Dev. 2022, 66, 12–25. [Google Scholar] [CrossRef]
- Paschke, F.; Bishara, N.; Schulz, I.; Kocer, C.; Schneider, J.; Maier, A. In situ Ug-value measurement on three different glazing types. J. Phys. Conf. Ser. 2021, 2069, 012134. [Google Scholar] [CrossRef]
- Dogan, A.; Kayaci, N.; Bacak, A. Machine learning-based predictive model for temperature and comfort parameters in indoor enviroment using experimantal data. Appl. Therm. Eng. 2025, 259, 124852. [Google Scholar] [CrossRef]
- Nardi, I.; Lucchi, E. In Situ Thermal Transmittance Assessment of the Building Envelope: Practical Advice and Outlooks for Standard and Innovative Procedures. Energies 2023, 16, 3319. [Google Scholar] [CrossRef]
- Katić, D.; Krstić, H.; Ištoka Otković, I.; Begić Juričić, H. Comparing multiple linear regression and neural network models for predicting heating energy consumption in school buildings in the Federation of Bosnia and Herzegovina. J. Build. Eng. 2024, 97, 110728. [Google Scholar] [CrossRef]
- Ciulla, G.; D’Amico, A. Building energy performance forecasting: A multiple linear regression approach. Appl. Energy 2019, 253, 113500. [Google Scholar] [CrossRef]
- No, S.T.; Seo, J.S. Analysis of Window Components Affecting U-Value Using Thermal Transmittance Test Results and Multiple Linear Regression Analysis. Adv. Civ. Eng. 2018, 2018, 1780809. [Google Scholar] [CrossRef]
- Ibrahim, S.; Kamaruddin, S.A.; Nasir, N.A.N.M. Heating Load of Residential Buildings Using Multiple Linear Regression Artificial Neural Network. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 92, 28–38. [Google Scholar] [CrossRef]
- Troup, L.; Phillips, R.; Eckelman, M.J.; Fannon, D. Effect of window-to-wall ratio on measured energy consumption in US office buildings. Energy Build. 2019, 203, 109434. [Google Scholar] [CrossRef]
- Jose, D.M.; Vincent, A.M.; Dwarakish, G.S. Improving multiple model ensemble predictions of daily precipitation and temperature through machine learning techniques. Sci. Rep. 2022, 12, 4678. [Google Scholar] [CrossRef]
- Tercha, W.; Tadjer, S.A.; Chekired, F.; Canale, L. Machine Learning-Based Forecasting of Temperature and Solar Irradiance for Photovoltaic Systems. Energies 2024, 17, 1124. [Google Scholar] [CrossRef]
- Mutombo, N.M.A.; Numbi, B.P. Development of a Linear Regression Model Based on the Most Influential Predictors for a Research Office Cooling Load. Energies 2022, 15, 5097. [Google Scholar] [CrossRef]
- Jiang, T.; Hao, F.; Chen, X.; Zou, Z.; Zheng, S.; Liu, Y.; Xu, S.; Yin, H.; Yang, X. Estimating indoor air temperature by obtaining outdoor building window surface temperature using infrared technology: An exploratory approach. Build. Environ. 2024, 251, 111218. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, S.A.; Brett, M.; da Silva, M.G.; Simões, N. Comprehensive in-situ assessment of glazing systems: Thermal properties, comfort impacts, and machine learning-based predictive modelling. Build. Environ. 2025, 279, 113027. [Google Scholar] [CrossRef]
- Song, B.; Bai, L.; Yang, L. The Effects of Exterior Glazing on Human Thermal Comfort in Office Buildings. Energies 2024, 17, 776. [Google Scholar] [CrossRef]
- Dogan, T.; Kastner, P.; Mermelstein, R. Surfer: A fast simulation algorithm to predict surface temperatures and mean radiant temperatures in large urban models. Build. Environ. 2021, 196, 107762. [Google Scholar] [CrossRef]
- Chereches, M.L.; Chereches, N.C.; Ciobanu, A.A.; Hudisteanu, S.V.; Turcanu, E.F.; Bradu, A.; Popovici, C.G. Experimental study on airflow and temperature predicting in a double skin façade in hot and cold seasons in Romania. Appl. Sci. 2021, 11, 12139. [Google Scholar] [CrossRef]
- Long, X.; Jin, Q.; Yu, Z. Multi-objective optimization of PCM-integrated thermochromic glazing to enhance the thermal and daylighting performance. Appl. Therm. Eng. 2025, 266, 125661. [Google Scholar] [CrossRef]
- Teixeira, H.; Gomes, M.G.; Moret Rodrigues, A.; Aelenei, D. Solar responsive building glazing: Experimental analysis of the impact of photochromic glazing on indoor thermal and luminous conditions. J. Build. Eng. 2024, 92, 109812. [Google Scholar] [CrossRef]
- Duan, Q.; Hinkle, L.; Wang, J.; Zhang, E.; Memari, A. Condensation effects on energy performance of building window systems. Energy Rep. 2021, 7, 7345–7357. [Google Scholar] [CrossRef]
- Nguyen, C.K.; Teodosiu, C.; Kuznik, F.; David, D.; Teodosiu, R.; Rusaouën, G. A full-scale experimental study concerning the moisture condensation on building glazing surface. Build. Environ. 2019, 156, 215–224. [Google Scholar] [CrossRef]
- Zozulák, M.; Vertaľ, M.; Zozuláková, S.; Dolníková, E.; Katunský, D. Heat-air-moisture modeling for prediction of interior surface condensation of lift-and-slide window—Case study. Heliyon 2023, 9, e15183. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, X.; Bisby, L. Comparative study of thermal breakage of annealed and tempered glazing with different thicknesses under uniform radiation conditions. Fire Saf. J. 2023, 140, 103867. [Google Scholar] [CrossRef]
- ISO 15099; Thermal Performance of Windows, Doors and Shading Devices—Detailed Calculations. International Organization for Standardization: Geneva, Switzerland, 2003.
- ASHRAE Standard 55-2020; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2020.
- ANSI/ASHRAE Standard 55-2010; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2010.
- d’Ambrosio Alfano, F.R.; Dell’isola, M.; Ficco, G.; Palella, B.I.; Riccio, G. On the measurement of the mean radiant temperature by means of globes: An experimental investigation under black enclosure conditions. Build. Environ. 2021, 193, 107655. [Google Scholar] [CrossRef]
- Tartarini, F.; Schiavon, S.; Cheung, T.; Hoyt, T. SoftwareX CBE Thermal Comfort Tool: Online tool for thermal comfort calculations and visualizations. SoftwareX 2020, 12, 100563. [Google Scholar] [CrossRef]
- Broday, E.E.; Ruivo, C.R.; da Silva, M.G. The use of Monte Carlo method to assess the uncertainty of thermal comfort indices PMV and PPD: Benefits of using a measuring set with an operative temperature probe. J. Build. Eng. 2020, 35, 101961. [Google Scholar] [CrossRef]
- ISO 7726:2025; Ergonomics of the Thermal Environment—Instruments for Measuring and Monitoring Physical Quantities. International Organization for Standardization: Geneva, Switzerland, 2025.
- Moghaddam, S.A.; Mattsson, M.; Ameen, A.; Akander, J.; da Silva, M.C.G.; Simoes, N. Low-Emissivity Window Films as an Energy Retrofit Option for a Historical Stone Building in Cold Climate. Energies 2021, 14, 7584. [Google Scholar] [CrossRef]
- Raschka, S. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. University of Wisconsin–Madison, Madison, WI, USA. 2018. Available online: https://arxiv.org/pdf/1811.12808 (accessed on 28 August 2025).
- Golosov, N.; Cervone, G. Integrating Thermal Infrared Imaging and Weather Data for Short-Term Prediction of Building Envelope Thermal Appearance. Remote Sens. 2024, 16, 3981. [Google Scholar] [CrossRef]
- Hwang, R.; Chiu, H.-C. A Case Study-Based Framework Integrating Simulation, Policy, and Technology for nZEB Retrofits in Taiwan’ s Office Buildings. Energies 2025, 18, 3854. [Google Scholar] [CrossRef]
- Evangelisti, L.; De Cristo, E.; Guattari, C.; Gori, P.; De Rubeis, T.; Monteleone, S. Case Studies in Thermal Engineering Preliminary development of a non-contact method for thermal characterization of building walls: Laboratory evaluation. Case Stud. Therm. Eng. 2025, 69, 106012. [Google Scholar] [CrossRef]
- Hossein, S.; Besharati, Z.; Abdolrasoul, S. Prediction of room temperature in Trombe solar wall systems using machine learning algorithms. Sustain. Energy Storage 2024, 3, 243–249. [Google Scholar]
- Lala, B.; Hagishima, A. A Review of Thermal Comfort in Primary Schools and Future Challenges in Machine Learning Based Prediction for Children. Buildings 2022, 12, 2007. [Google Scholar] [CrossRef]
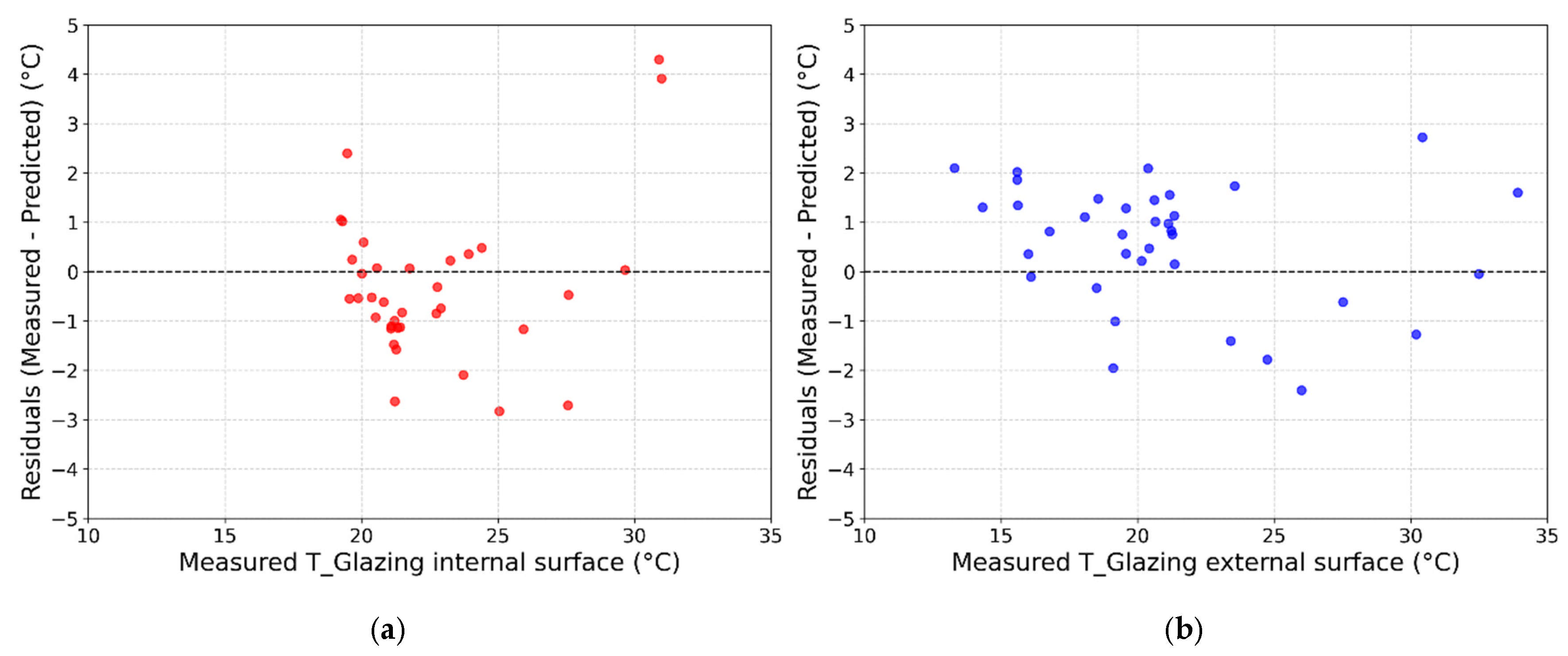
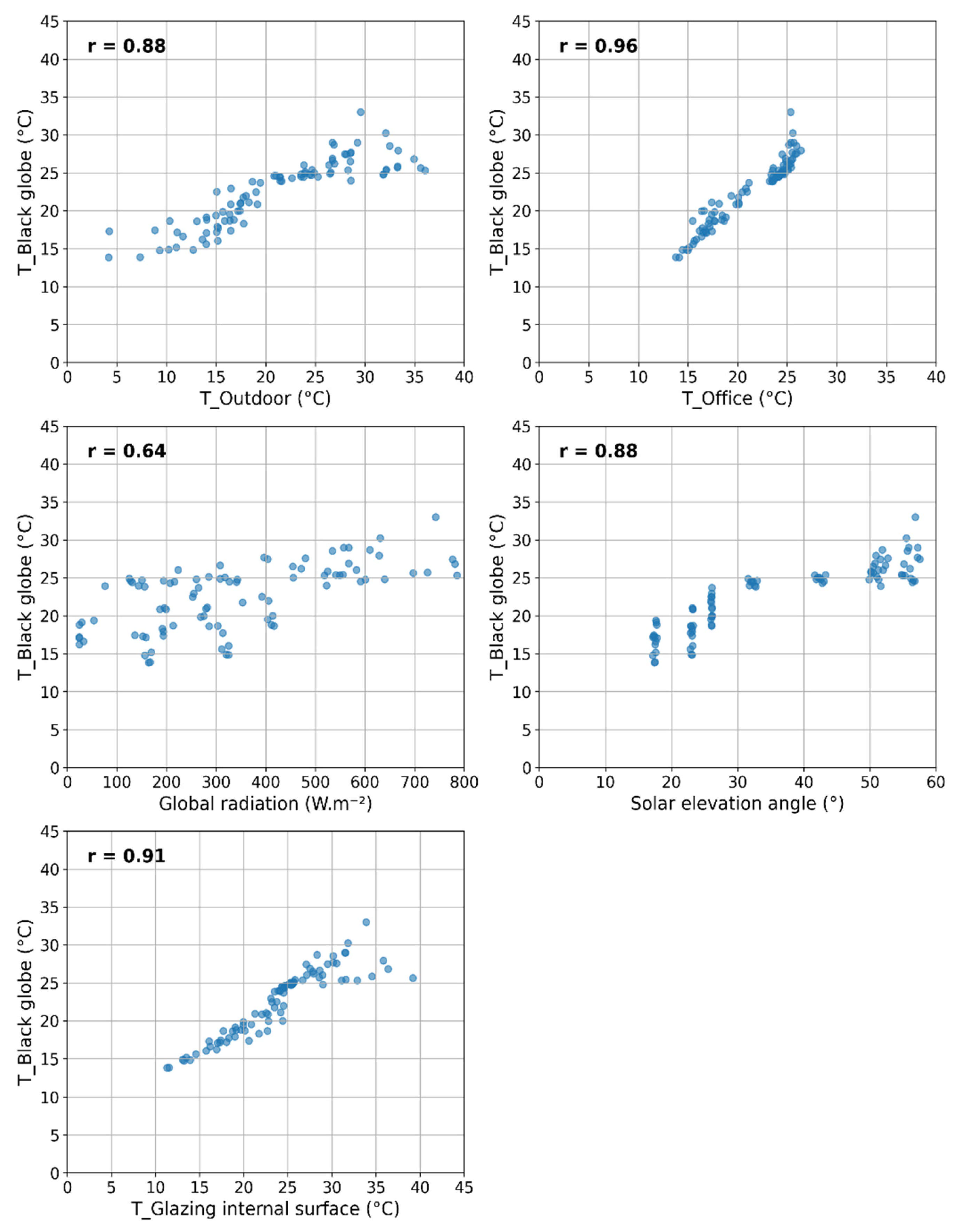
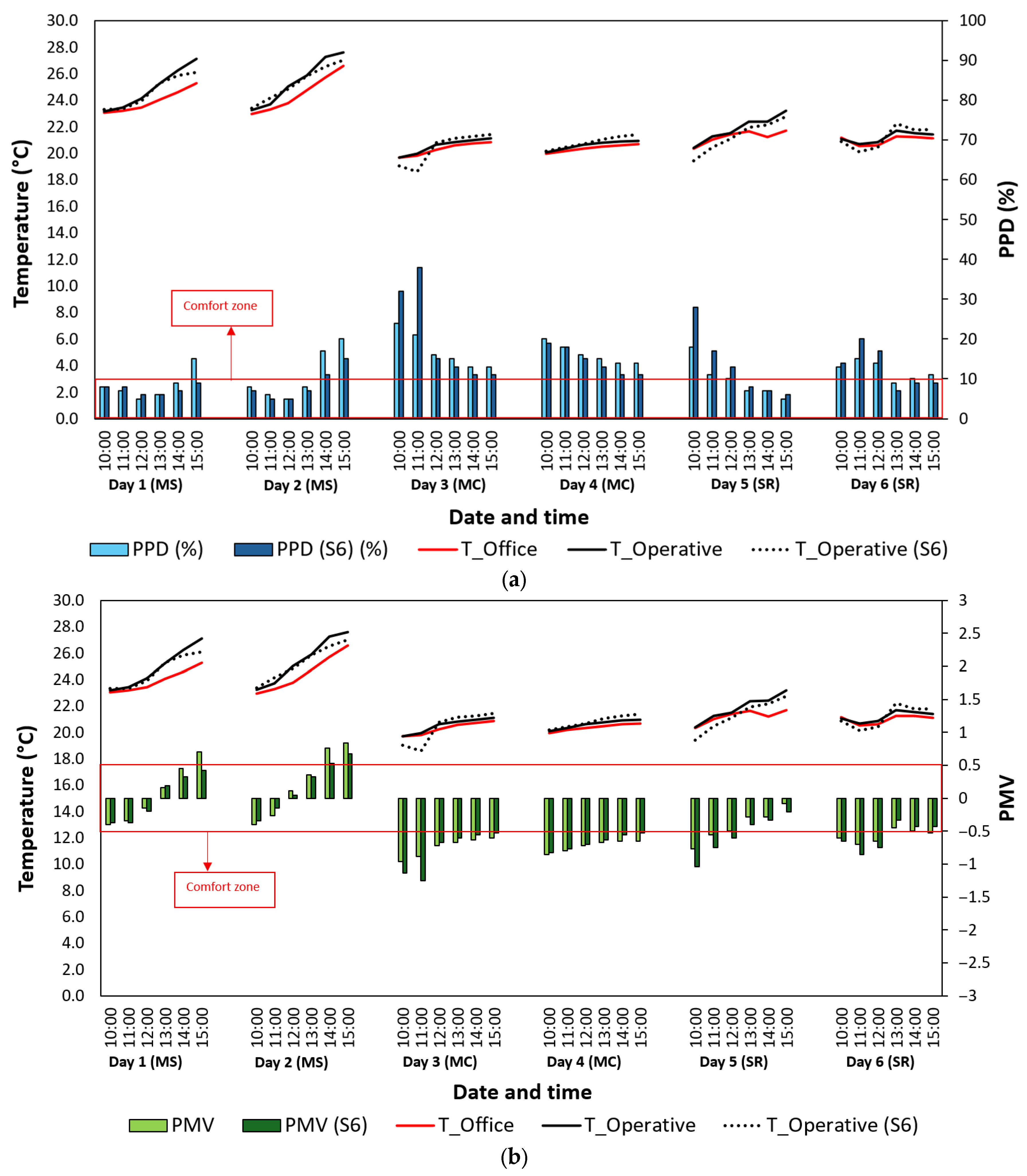
| Scenario | Independent Variables |
|---|---|
| Scenario 1 | and |
| Scenario 2 | , , and () |
| Scenario 3 | , , , and |
| Scenario 4 | , , , , (), (), (), (), (), and () |
| Scenario 5 | , , and |
| Scenario 6 | , , , (), (), and () |
| Scenario 7 | , , , , and |
| Scenario 8 | , , , , , (), (), (), (), (), (), (), (), (), and () |
| Dependent Variable | Scenario | Independent Variables | MSE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|---|
| T_Glazing internal surface | Scenario 1 | and | 0.05 | 0.22 | 1.13 | 0.99 |
| T_Glazing internal surface | Scenario 2 | , , and () | 0.04 | 0.20 | 1.00 | 0.99 |
| T_Glazing external surface | Scenario 1 | and | 0.15 | 0.38 | 3.54 | 0.99 |
| T_Glazing external surface | Scenario 2 | , , and () | 0.14 | 0.37 | 3.40 | 0.99 |
| MSE | RMSE | MAPE | R2 | |
|---|---|---|---|---|
| T_Glazing internal surface (Scenario 2) | 0.13 | 0.36 | 1.62 | 0.98 |
| T_Glazing external surface (Scenario 2) | 0.12 | 0.34 | 2.17 | 0.99 |
| Dependent Variable | Scenario | Independent Variables | MSE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|---|
| T_Glazing internal surface | Scenario 1 | , , , and | 3.89 | 1.97 | 7.26 | 0.81 |
| T_Glazing internal surface | Scenario 2 | , , , , (), (), (), (), (), and () | 2.90 | 1.70 | 6.00 | 0.86 |
| T_Glazing external surface | Scenario 1 | , , , and | 5.27 | 2.29 | 9.73 | 0.87 |
| T_Glazing external surface | Scenario 2 | , , , , (), (), (), (), (), and () | 3.66 | 1.91 | 7.91 | 0.91 |
| MSE | RMSE | MAPE | R2 | |
|---|---|---|---|---|
| T_Glazing internal surface (Scenario 2) | 2.38 | 1.54 | 4.90 | 0.78 |
| T_Glazing external surface (Scenario 2) | 2.12 | 1.46 | 6.35 | 0.91 |
| Scenario | Independent Variables | MSE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|
| Scenario 1 | and | 1.30 | 1.14 | 4.31 | 0.88 |
| Scenario 2 | , , and () | 1.18 | 1.09 | 4.25 | 0.89 |
| Scenario 3 | , , , and | 1.35 | 1.16 | 4.40 | 0.87 |
| Scenario 4 | , , , , (), (), (), (), (), and () | 0.96 | 0.98 | 3.33 | 0.91 |
| Scenario 5 | , , and | 0.43 | 0.66 | 2.29 | 0.96 |
| Scenario 6 | , , , (), (), and () | 0.28 | 0.53 | 1.79 | 0.98 |
| Scenario 7 | , , , , and | 0.47 | 0.69 | 2.08 | 0.96 |
| Scenario 8 | , , , , , (), (), (), (), (), (), (), (), (), and () | 0.30 | 0.55 | 1.70 | 0.97 |
| MSE | RMSE | MAPE | R2 | |
|---|---|---|---|---|
| Black globe temperature (Predicted ) | 0.40 | 0.63 | 2.30 | 0.93 |
| Black globe temperature (Real ) | 0.11 | 0.34 | 1.14 | 0.98 |
| Operative temperature (Predicted ) | 0.24 | 0.49 | 1.77 | 0.95 |
| ) | 0.07 | 0.26 | 0.87 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghaddam, S.A.; Simões, N.; Brett, M.; da Silva, M.G.; Prata, J. Dynamic Behavior of a Glazing System and Its Impact on Thermal Comfort: Short-Term In Situ Assessment and Machine Learning-Based Predictive Modeling. Energies 2025, 18, 4656. https://doi.org/10.3390/en18174656
Moghaddam SA, Simões N, Brett M, da Silva MG, Prata J. Dynamic Behavior of a Glazing System and Its Impact on Thermal Comfort: Short-Term In Situ Assessment and Machine Learning-Based Predictive Modeling. Energies. 2025; 18(17):4656. https://doi.org/10.3390/en18174656
Chicago/Turabian StyleMoghaddam, Saman Abolghasemi, Nuno Simões, Michael Brett, Manuel Gameiro da Silva, and Joana Prata. 2025. "Dynamic Behavior of a Glazing System and Its Impact on Thermal Comfort: Short-Term In Situ Assessment and Machine Learning-Based Predictive Modeling" Energies 18, no. 17: 4656. https://doi.org/10.3390/en18174656
APA StyleMoghaddam, S. A., Simões, N., Brett, M., da Silva, M. G., & Prata, J. (2025). Dynamic Behavior of a Glazing System and Its Impact on Thermal Comfort: Short-Term In Situ Assessment and Machine Learning-Based Predictive Modeling. Energies, 18(17), 4656. https://doi.org/10.3390/en18174656








