Abstract
This article presents an overview of selected research focusing on digital real-time simulation (DRTS) in the context of digital twin (DT) realization with the primary aim of enabling the intelligent fault diagnosis (FD) and condition-based monitoring (CBM) of electrical machines. The concept of standalone DTs in conventional multiphysics digital offline simulations (DoSs) is widely utilized during the conceptualization and development phases of electrical machine manufacturing and processing, particularly for virtual testing under both standard and extreme operating conditions, as well as for aging assessments and lifecycle analysis. Recent advancements in data communication and information technologies, including virtual reality, cloud computing, parallel processing, machine learning, big data, and the Internet of Things (IoT), have facilitated the creation of real-time DTs based on physics-based (PHYB), circuit-oriented lumped-parameter (COLP), and data-driven approaches, as well as physics-informed machine learning (PIML), which is a combination of these models. These models are distinguished by their ability to enable real-time bidirectional data exchange with physical electrical machines. This article proposes a predictive-level framework with a particular emphasis on real-time multiphysics modeling to enhance the efficiency of the FD and CBM of electrical machines, which play a crucial role in various industrial applications.
1. Introduction
Today, the design and implementation of industrial products are almost inconceivable without the initial phase of virtual development supported by digital simulation (DS). DS enables the creation of a reference model that provides a precise description of a physical entity. This is commonly known as a digital twin (DT), which serves as a virtual representation of the product prior to physical prototyping [1,2,3,4]. This approach provides access to a broad range of variables that may not be directly measurable or may require sophisticated instrumentation. Using this method, industrial products can be developed more efficiently and cost-effectively through a comprehensive analysis of their entire lifecycle. An important feature of the DS world is that every test and decision can be implemented, and undesired conditions can be anticipated. This can facilitate tasks such as configuration, FD, and CBM for both preventive and predictive maintenance. Compared with real-world testing, DS offers significant time and cost savings while minimizing waste and reducing potential risks. Conducting experiments in a physical lab requires substantial time owing to the preparation and construction of the experimental test benches. Additionally, laboratory testing is often constrained by facility capabilities, capacity limitations, and lack of flexibility when modifications are required. In a design process that involves multiple iterations, in which each stage depends on the outcomes of the previous test, the resulting time delay can be substantial. Beyond saving time and cost, DS enables the exploration of a much wider range of variants. This gives product developers greater flexibility to innovate, test numerous combinations, and experiment with unconventional approaches, ultimately leading to a more refined and optimized solution. To accurately represent the physical world, the DS must incorporate interactions across multiple physical domains, including electromagnetics, fluid dynamics, mechanics, thermodynamics, and materials science [5]. If DS results fail to accurately represent real-world conditions, they lose their value. Confidence in DS increases when its outcomes align with those obtained from physical tests and field experiences. The core idea of DS relies on solving particularly partial differential equations (PDEs), that is, differential equations in multi-variables of time and space which often represent coupled equations derived from multiphysics modeling. Apart from certain simplified cases in which these PDEs can be solved analytically, their complexity in most real-world scenarios necessitates the utilization of discretization approaches for numerical computation. Over time, various methods have been developed, among which the most widely applied are the finite difference method (FDM), the finite element method (FEM), and the finite volume method (FVM) [6,7]. The finite difference equation for differential operators can be expressed using forward, backward, or central differences, whereas the Galerkin method is commonly employed to formulate finite element equations. The finite volume method (FVM) can be derived from either the FDM or FEM [6]. The FEM has become the standard approach for numerically solving PDEs that describe physical fields, including multiphysics couplings. Consequently, static, transient, and time-harmonic analyses involving both material and geometrical nonlinearities can be efficiently performed [8]. These formulations are widely implemented in many open-source and commercial multiphysics simulation packages (OpenFOAM, FEniCS, Elmer, FreeFEM, ANSYS, COMSOL, STAR-CCM+, etc.) [9].
Electrical machines are widely used in various industrial applications, including electric traction systems, hybrid and electric vehicles, wind and marine energy conversion, power generation, energy storage, shipboard systems, and aerospace electrification. To enhance their design and performance, digital offline simulation (DoS) is frequently used to optimize structural configurations, develop controllers, and analyze the dynamic behavior of innovative electrical machines [10]. The modeling of electrical machines can be broadly categorized into two main approaches: physics-based (PHYB) and data-driven approaches. PHYB models primarily rely on the observation of physical phenomena and aim to represent them using mathematical formulations, which are then solved, either analytically or numerically. By contrast, data-driven models require a large number of data during the training phase, which can be generated from partial PHYB models or experimental measurements [9]. The multiphysics modeling of electrical machines can capture various fields of physics, including electromagnetism, mechanics, vibro-acoustics, and thermal phenomena, and can be composed of several interacting PHYB or data-driven models [11,12,13,14]. Focusing on the electrical and magnetic aspects, the literature commonly reports both simplified PHYB models using circuit-oriented lumped-parameter (COLP) approaches and detailed PHYB (DPHYB) models for electrical machine modeling [10]. The former rely on an electrically and magnetically coupled circuit and are typically used for analyzing the dynamic behavior of electrical machines and electromagnetic transient studies. This type of model assumes perfect symmetry in both the field and construction, a constant air gap that is small relative to the rotor radius, a linear magnetic system, and the omission of hysteresis effects. In contrast, the second method considers complex geometry, magnetic saturation, eddy current, and hysteresis effects in detail and is employed for design purposes [10,15]. Clearly, DPHYB models offer greater accuracy than COLP models, but this comes at the cost of increased computation time. COLP models include the dynamic ‘abc’ and ‘dq0’ reference frame models and the dynamic voltage-behind-reactance model, in which the variables of the stator are described in the ‘abc’ reference frame and the variables of the rotor are given in the ‘dq0’ reference frame [15,16]. The ‘dq0’ reference frame model can be derived from the ‘abc’ reference model by using the Park transform, which eliminates time-varying inductances in the ‘abc’ frame and simplifies the voltage equations in AC electrical machines. The self- and mutual inductances of the ‘abc’ reference model are commonly determined based on the winding function approach (WFA) or modified WFA (MWFA) when some data regarding the geometry of the machine are known [17]. Another approach is to perform basic experimental tests through which it is possible to obtain these parameters for a simplified internal equivalent circuit model [18]. DS of COLP models has been widely conducted using Electromagnetic Transient Program-type (EMTP-type) software, initially developed by H.W. Dommel in the late 1960s. Well-established examples include EMTP-ATP, EMTP-RV, and EMTDC/PSCAD, which are circuit-theory-based simulation tools for studying power system transients and dynamics. The universal COLP machine model was later incorporated into EMTP by H.K. Lauw and W.S. Meyer, enabling the analysis of various types of electric machines within a single modeling framework [19]. The most common formulation methods in EMTP-type tools fall into two main categories: nodal analysis and state-space methods for computing the response of power systems in the time domain. The discretization of ordinary differential equations (ODEs) using integration techniques yields difference equations. The combination of the method of characteristics and trapezoidal rule in a generalized algorithm enabled the accurate simulation of transient networks involving both distributed and lumped parameters in Dommel’s EMTP. However, the use of a constant time-step length presents some problems when modeling switching elements and can produce spikes and numerical oscillations (or chatter). In this regard, critical damping adjustment, in which the integration method is changed to backward Euler for two steps after discontinuity, has been proposed [20]. In this respect, two-stage diagonally implicit Runge–Kutta, a mathematically oscillation-free method, was utilized in Expandable Transient Analysis Program (XTAP) [19]. A guideline for choosing an appreciate integration method for modeling COLP models is presented in [21].
DPHYB models encompass both FEM-based and analytical models. In FEM-based models of electrical machines, Maxwell’s equations must be solved numerically for each mesh element, whether in 2D triangular or 3D tetrahedral configurations. Conversely, analytical models rely on explicit solutions of Maxwell’s equations and are widely employed to aid in design and analysis, particularly when an accurate calculation of the magnetic field distribution across various machine regions is essential. The accurate modeling of electric machines often relies on the FEM. However, finite element analysis (FEA) can be highly time-consuming, particularly during the initial design stages when conducting parametric studies. Several tools have been proposed in the domain of electrical machine design (MotorAnalysis, Flux-2D, Code Carmel, JMAG, Altair Flux/FluxMotor, etc.). Two commonly used analytical models for design purposes are magnetic equivalent circuits (MECs), which rely on a permanence element network, and models derived from the formal resolution of Maxwell’s equations in regions with constant permeability [22,23]. In an MEC-based model, the mesh network must be carefully designed to achieve an accuracy comparable to that of a FEM-based model. When considering the effect of iron magnetic saturation, the differential equation governing the MEC-based model transforms into a nonlinear representation of magnetic scalar potentials. To solve this problem, the Newton–Raphson method is typically employed, often in combination with an adaptive simulation time step [24].
Data-driven modeling has gained significant attention owing to the development of advanced open-source machine learning (ML) and artificial intelligence (AI) tools, user-friendly and affordable computational resources, and extensive training materials. Unlike PHYB models, this approach operates under the premise that the data encapsulate both explicit and implicit physical behaviors. Therefore, when trained on sufficiently large datasets, data-driven models can independently uncover underlying physical relationships. In particular, deep learning has enabled models to achieve near-human or even superhuman performance in tasks once considered out of reach for computers. These models can be typically categorized into six types: supervised and unsupervised linear models, supervised and unsupervised nonlinear models, and unsupervised deep learning approaches [25]. Although the performance of data-driven models depends on the widespread availability of large-scale/big data, the proposed methodology seeks to address the limitations of relying solely on either PHYB or data-driven modeling techniques. This integrated approach, known as hybrid modeling, combines the clarity, theoretical grounding, and insight of PHYB models with the precision, computational efficiency, and pattern recognition capabilities of advanced ML and AI methods. Hybrid modeling can be conceptualized as existing at the intersection of large-scale/big data, physics-informed modeling, and data-driven techniques, as illustrated in Figure 1 [9,26]. For example, instead of relying on computationally intensive FEA, a deep neural network (DNN) is employed as a surrogate model. The DNN was trained in a supervised manner using a large dataset generated from precomputed FEA results. During inference, the outputs of the network intermediate are utilized as inputs for the PHYB post-processing step, which computes characteristic maps and key performance indicators. This hybrid strategy demonstrates a significant reduction in computational time while preserving the flexibility within the simulation workflow of electrical machines [27].
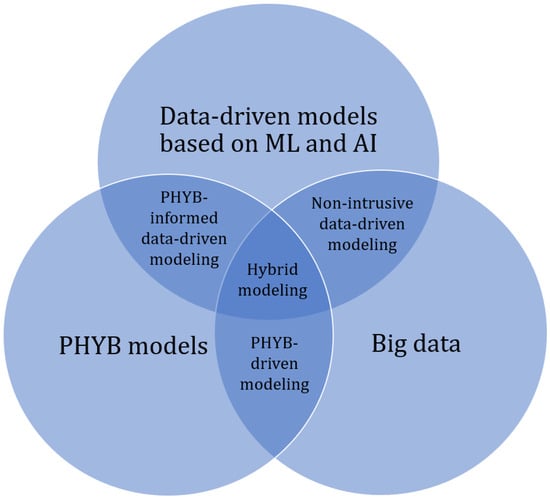
Figure 1.
Scheme for hybrid modeling at the intersection of PHYB models, big data, and data-driven models [9].
The reliability and availability of electrical machines are critical in many industrial sectors, where they operate under specific stresses and loads under real-world conditions, often subject to random variations. CBM plays a pivotal role in preventing failures and minimizing downtime, making it an essential component of most maintenance strategies [28,29]. FD involves the detection, isolation, and identification of faults. The main challenge is to perform the incipient FD online under transient operating conditions as early as possible. FD approaches can be broadly classified into three categories based on the algorithms used: signal-based, model-based, and data-driven. Machine learning techniques have been widely applied to automate data-driven approaches in three main steps: sensor data acquisition, statistical feature extraction, and fault classification [30,31,32,33,34]. Statistical feature extraction involves the analysis of collected data across various domains of time, frequency, and time–frequency. After dimensionality reduction, the extracted features are typically used in small-scale machine learning models for unsupervised clustering, such as K-means clustering, K-nearest neighbors, self-organizing map, supervised classification using random forest, support vector machine, backpropagation neural networks, and decision trees [30,32,35]. However, the selection of meaningful features remains a challenging issue because it is labor-intensive and must be adapted to different fault classification tasks and varying machine operating conditions. Deep learning (DL) has been significant in overcoming the shortcomings of traditional ML methods owing to its ability to automatically extract representative features from raw data and accurately establish nonlinear mappings of different health conditions. Popular DL models and methods utilized in the field of FD include the deep belief network, the stacked autoencoder, and the convolutional neural network [31].
Although learning can be supervised, semi-supervised, or reinforcement learning [36], training a DL model from scratch for classical ML tasks requires a large number of data that cover all possible machine fault conditions. This is a major challenge in practical applications because the measured data for only a few fault conditions can be insufficient. To solve the issue of limited training data, transfer learning (TL) has been introduced, which has shown remarkable capability in obtaining a satisfactory deep architecture by fine-tuning a DL model that has been pre-trained in other tasks [37]. Data-driven methods mostly focus on the design of models, with the same aim as signal-based methods, to extract fault features with high quality and avoid noise interference. Mamba was proposed in the field of DL [38], the core idea of which is the state-space model (SSM), where the coefficient matrices of the SSM are learnable parameters of the model. It achieves the selective processing of input information by parameterizing the input of the SSM [32]. The CBM framework incorporates not only condition monitoring data but also event data. Event data record occurrences such as installations, breakdowns, and overhauls, along with their causes, as well as actions taken on the asset, such as minor repairs, preventive maintenance, or oil changes. Condition monitoring data, on the other hand, consist of measurements that reflect the health status or operational state of an electrical machine. Analyzing event data alone typically falls under the domain of reliability analysis, which involves fitting the data to the probability distributions of time between events and using these models for further assessment. In CBM, however, condition monitoring data are available in addition to event data. Combining these datasets enables a more comprehensive analysis, as it leverages both the occurrence of events and underlying asset conditions. This integrated analysis is achieved by developing mathematical models that accurately represent fault or failure mechanisms. Models built from both data types form the foundation for maintenance decision making, including diagnostics and prognostics [28].
The DoS concept has been widely applied in the development of FD and CBM strategies for electrical machines. This approach primarily focuses on creating models that accurately incorporate various fault types, including bearing defects; static, dynamic, or mixed eccentricity; open or unbalanced circuits; short circuits in stator or rotor windings; insulation degradation; damage to rotor bars and end rings in squirrel-cage induction machines (SCIMs); and demagnetization in permanent magnet synchronous machines (PMSMs) [39,40,41,42]. DoS enhances the clarity of fault signatures in physical variables that are often influenced by noise and the inherent imperfections of the sensors used in experimental test setups. This makes it possible to effectively analyze early-stage faults. A digital real-time simulation (DRTS) corresponds to a DoS that must operate within real-time processing constraints. In other words, the discretized model must be sufficiently swiftly computed to synchronize with real-world timing [43]. Therefore, the selected solver must be optimized to resolve the system equation within a specified time step. DRTS is more advantageous than DoS because it can be linked to external equipment for design, test control, and robustness analysis in a hardware-in-the-loop (H-i-L) framework. H-i-L systems have been essential in the aerospace industry and flight simulations for several decades [44,45]. Their application has expanded significantly in various fields, including powertrain modeling for electric vehicles, energy management in microgrids, power and energy systems, and the dynamic performance analysis of power electronic devices. Recently, this concept was proposed to develop advanced fault diagnosis methods for electrical machines [18,46,47,48]. DRTS contributes to the FD and CBM of electrical machines by incorporating technologies such as virtual reality, DT, data analytics, large-scale/big data, Internet of Things (IoT), and ML, which have been widely adopted in the Industry 4.0 revolution. DT technology, which defines the adaptable mapping of a physical system to a virtual replication [49], is a powerful and emerging technology that enables the representation of the state of health of complex systems and facilitates CBM [50,51]. This article provides an overview of selected papers on the topic of multiphysics DRTS in the context of DTs for the intelligent FD and CBM of electrical machines. Section 2 reviews the definition of DT, its emerging concepts, and the various levels and scales at which it is applied. Section 3 discusses the main challenges of DRTS as an enabling tool within an electrical machine DT platform. Section 4 explores whether a multiphysics RTDS can contribute to the intelligent FD and CBM of electrical machines. Finally, the conclusion summarizes the key points and offers perspectives for future research in this domain.
2. Electrical Machine Digital Twins
2.1. Digital Twin Definition
The notion of a DT can be traced back to NASA in the 1960s, when it emerged as a dynamic representation of the Apollo missions. Following the explosion of an oxygen tank and damage to the main engine during Apollo 13, NASA employed several simulators to investigate the root causes of the malfunction. They enhanced their physical model of the spacecraft by incorporating digital elements, creating an early version of what is now known as a DT. This system allows for continuous data input, supporting both forensic analysis of the incident and the planning of subsequent actions [52]. Since its initial development, the concept of DT has gained significant attention from both academia and the industry. Figure 2 illustrates the timeline of the DT evolution, starting from its inception [53,54]. Numerous reviews and state-of-the-art articles have focused on enabling technologies, existing challenges, and methodologies for leveraging DTs in product lifecycle management and innovation [53,55,56,57]. Scholars and institutions have proposed various definitions and interpretations of DT; comprehensive discussions can be found in [25,53,56,57,58]. For instance, Vrabic et al. [59] characterized DT as a digital counterpart of a physical asset or system enhanced with integrated simulations and service-related data. The digital model aggregates data from multiple sources throughout the product lifecycle, which is regularly updated and represented in different formats to forecast both current and future states in design and operational contexts, thereby supporting improved decision making [56]. According to Tao et al. [55], a DT can be characterized as a high-fidelity simulation that integrates multiphysics and multi-scale modeling, incorporating probabilistic elements. It dynamically mirrors the state of its physical counterpart using a combination of historical information, real-time sensor inputs, and physical modeling.
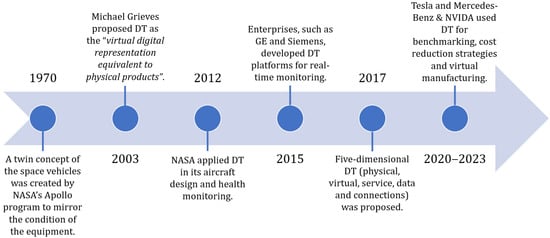
Figure 2.
Timeline of DT evolution [53,54].
Similarly, Rasheed et al. [9,25] defined DT as a virtual model of a physical system that utilizes real-time data and digital simulations to enable monitoring, control, optimization, prediction, and informed decision making. Unlike traditional digital models or digital shadows, DTs are distinguished by a fully bidirectional data flow between their physical and digital counterparts that allows any change in the physical system to be immediately reflected in its digital representation [56]. More recently, Rasheed et al. [25] presented a comprehensive survey of the emerging applications of DT technology in the wind energy industry. Their study presents widely recognized definitions of DT from leading organizations and researchers, including Gartner, NVIDIA, IBM, DNV, GE Digital, Siemens, Oracle, Microsoft, the Digital Twin Consortium, Trauer et al., Grieves and Vickers, and the Industrial Digital Twin Association. Table 1 summarizes these recent definitions based on key aspects: ‘Things,’ which indicates the scope of application covered by each definition; ‘Representation,’ which refers to the realization space of the digital model; ‘Data,’ which outlines how information is utilized; and ‘Purposes,’ which identifies the primary objectives of DT development.

Table 1.
Summary of most popular DT definitions [25].
The definition of DT can fall within its capabilities and levels, which are classified as standalone, descriptive, diagnostic, prescriptive, and autonomous [25,60]. The standalone DT represents the foundational level and is primarily utilized during the design phase. It relies on a DoS approach to enable a cost-effective system evaluation prior to physical construction. At the descriptive level, a CAD model combined with real-time sensor data is used to reflect physical assets. This setup relies on a precise PHYB that supports data interpolation in the targeted areas of interest. At the diagnostic level, powerful ML tools can be applied to the data to support FD and CBM. Using insights from diagnostic DTs, human experts can intervene early to make the necessary adjustments and prevent minor issues from escalating into major problems. Unlike standalone, descriptive, and diagnostic DTs, which do not offer foresight, the predictive DT continuously delivers updated predictions by leveraging real-time data streams from the physical entity. The prescriptive DT is valuable for optimizing asset control, as it generates recommendations based on what-if scenarios, risk assessments, and uncertainty analysis. This capability is especially beneficial for decision support systems, offering guidance to experts, who then determine the appropriate course of action. In the final stage, the DT and its physical counterpart engage in continuous two-way communication. The physical asset updates the DT in real time, whereas the twin, in turn, issues control commands to steer the physical system toward optimal performance. This enables rapid decision making without requiring human intervention. Referred to as the autonomous DT, this fifth level requires a high degree of technological maturity, particularly for deployment in safety-critical applications [25]. Industrial platforms such as General Electric’s ‘Predix,’ Siemens’ ‘MindSphere,’ and ‘ThingWorx’ support the development of DTs by leveraging Internet of Things (IoT) technologies. The IoT extends digital connectivity into the physical environment through the widespread use of radio-frequency identification (RFID) chips embedded in real-world devices [61]. Although the IoT offers significant benefits, it also presents major challenges related to IT infrastructure, connectivity, data privacy, security, trust, and data management [56]. In this context, data analytics plays a critical role in collecting, cleaning, and processing data for further analysis. The data cleaning stage, particularly through imputation techniques, is essential to addressing errors or missing values and ensuring the quality and reliability of the data before analysis.
2.2. Benefits and Constraints
The technical and economic benefits of DTs can be highlighted across five phases of the product lifecycle: product design, manufacturing, operation, maintenance, and recycling [53]. This means that if the DT can replace the physical entity, it can be used during the design, testing, and operation phases. This capability enables a better understanding of how an asset performs under both normal operating conditions and undesired stress, helps to determine material weaknesses, and assesses its suitability for its intended purpose. This has at least two beneficial effects: decreasing the cost of development and testing while increasing the number of situations that can be considered, assessed, and evaluated and extend/augmenting physical objects with software capabilities that will substantially enrich them. The greater the accuracy and fidelity of the DT, the more effectively it can replicate and predict the behavior of the physical asset in all scenarios. Furthermore, the DT approach facilitates the systematic collection and organization of data related to physical assets. This is particularly valuable, as historical records of an asset’s behavior under various conditions can offer insights for optimizing its performance and guiding future improvements. Analyzing and leveraging this information can significantly support the refinement and evolution of products over time [62]. In modern manufacturing, DTs are increasingly integrated into smart factories to model, analyze, and manage diverse processes with greater efficiency. Their adoption offers several advantages, such as real-time machine condition monitoring, enhanced system availability and reliability, advanced CBM capabilities, and the provision of tailored services to stakeholders [9,56]. These advantages are made possible through continuous data acquisition and transmission through IoT platforms. The collected data serve as a foundation for essential functions, including production scheduling, equipment maintenance, logistics, and strategic decision making. Within the framework of Industry 4.0, the overarching objective is to enable intelligent, data-driven decisions that strengthen both profitability and sustainability in smart manufacturing environments [63].
Although the DT approach offers several advantages for enterprises and communities, it also carries significant risks. The core purpose of the DT is to replicate the behavior of a physical entity. Consequently, one major challenge lies in determining the aspects of reality that are critical to accurately representing a digitalized model. Furthermore, DT development and structuring within an enterprise may require considerable time and effort. Secure data collection, communication, manipulation, and representation also require infrastructure that requires competent teams in information technology, which may not be available in a company. In addition, from a security and privacy perspective, a DT gathers and represents a significant amount of information that holds considerable value to the owner of the corresponding physical object. It not only reflects how the object is built and operated but also captures patterns of its usage and behavior. Such data are valuable for both competitive reasons and personal insights. For manufacturers and vendors, understanding how a product is used provides critical intelligence, whereas for users, this usage data can reveal detailed profiles of their preferences and habits. Therefore, clearly defining the ownership of a DT and regulating the collection of behavioral data are essential to ensuring proper security and protection for both users and owners. Another critical concern is software programmability and control, as unauthorized access to an object poses significant risks that can lead to disruptions or even serious accidents that impact both individuals and operations. One can easily imagine scenarios in which DTs might be exploited to interfere with people’s daily lives or manipulate specific environments. Therefore, expanding the use of DTs beyond tightly controlled settings requires the implementation of a strong and reliable security framework capable of detecting malicious activities or harmful actions, whether triggered intentionally by hackers or inadvertently by owners [62].
2.3. Electrical Machine DT Realization
Drawing from the diverse range of existing DT definitions, the authors propose a predictive-level framework with the following vision for the DT design of an electrical machine in the service phase [51,55,58]:
- The DT of an electrical machine is a synchronized, ultra-high-fidelity replica of it, incorporating multiphysics, multi-scale, and probabilistic modeling.
- An automated, bidirectional, real-time flow of data occurs between the DT and the electrical machine through appropriate instrumentation and an IoT platform.
- The twin encompasses data from the service stage of the electrical machine’s lifecycle and remains connected to this phase through to the retirement stage.
Figure 3 represents the scheme of electrical machine DT realization based on IoT and cloud computing technologies for FD and CBM. The physical electrical machine in this configuration is fully instrumented using RFID smart sensors to collect data on voltage, current, vibration, acoustics, temperature, speed, and mechanical torque. Quantities such as the active, reactive, and apparent power can be computed based on the measured stator voltages and currents. The implemented sensors describe the conditions of the electrical machine supplied by an electrical drive. This device adjusts the operating point of the electrical machine based on its health state. The RFID smart sensors and electrical drive are connected via an IoT platform to a cloud computing platform, as shown in Figure 3. The cyber layer of this structure enables secure bidirectional data transfer among smart sensors, electrical drives, and cloud computing platforms. In the next section, the DRTS challenges are discussed, as they are considered a fundamental stage for the predictive-level framework for the DT design of electrical machines in the illustrated configuration (Figure 3).
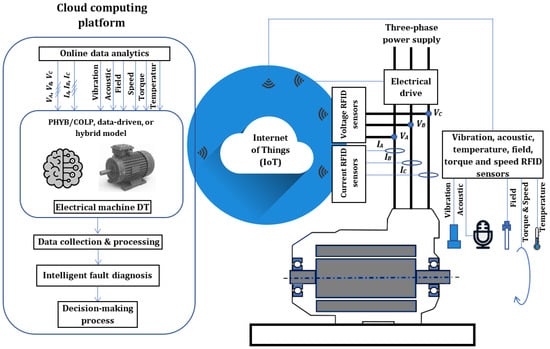
Figure 3.
Scheme of electrical machine DT for intelligent fault diagnosis [4].
3. Electrical Machine DRTS Challenges
3.1. Electrical Machine Models
In addition to DT, other terms have been introduced to clarify its workings in the real world, including physical entities, physical objects, physical things, physical assets, physical processes, physical products, real-world entities, physical systems, and physically manufactured products, as well as its workings in the digitally generated virtual world, including virtual entities, virtual dynamics, virtual representations, digital representations, and digital exact replicas (Table 1). DPHYB, COLP, or data-driven models or a combination of these models can be used to build the DTs of electrical machines. As mentioned in the Introduction, data-driven models, despite exhibiting stable behavior after the training process, require extensive historical data (big data), which can be obtained from the collected information. They are simpler to configure, typically do not require detailed physical entity parameters, and operate faster than real-time models. However, they operate as black boxes, and the presence of biased data can manifest in the model, resulting in unpredictable errors and uncertainties. PHYB and COLP models have significant advantages because they operate based on a solid physics foundation, resulting in estimated errors and uncertainties, which are important criteria for fault management systems.
The PHYB and COLP modeling approaches can be categorized into experimental and numerical models. Experimental modeling involves conducting reduced- or full-scale experiments to determine the main parameters of the electrical machine model [18,64]. To enhance the physical authenticity of a DT, it is necessary to solve the governing equations obtained from the physical modeling. In some cases, analytical solutions can be derived using simplified equations. However, owing to their complexity, numerical solutions are often obtained using computers [9,65,66]. The main aim is to analyze quantities that are commonly difficult or costly to measure directly. These models can be subsequently employed, as shown in Figure 3, as the DTs of electrical machines. The traditional approach involves creating a COLP dynamic ‘dq0’ reference model for AC electrical machines [67,68]. The estimation of model parameters can be used for fault diagnosis (Table 2). Although several techniques have been proposed for the identification of AC electrical machine parameters, they are commonly performed offline, limiting their application to DT realization. Another approach relies on residual computations using parity equations, state observers, or state estimators. This technique has been used extensively in sensor fault detection and diagnosis systems. Such dynamic models are sufficiently simple to be used in DRTS and DT realizations, as presented in [15]. However, they omitted the magnetic saturation effect and assumed a sinusoidal winding distribution. Moreover, the machine is assumed to be perfectly symmetrical. The ‘dq0’ reference frame models are commonly preferred for simulating electromagnetic transients because the ‘abc’ reference frame models have time-varying inductances. This means that to solve the governing equations, the inductance matrices must be inverted at each time step during the digital simulation, in addition to the computational burden of each digital simulation step [15]. Despite the aforementioned inconvenience, the ‘abc’ reference frame has the advantage of being easily applicable for modeling multi-phase electrical machines, regardless of asymmetry in both stator and rotor circuits, and can account for all space harmonics in the electrical machine [69,70,71]. In this regard, it is possible to include certain inherent asymmetries in the physical electrical machines in the model. Induction machines (IMs), which are broadly utilized in the industry, are good examples [72].

Table 2.
COLP modeling of various fault types in ‘dq0’ reference frame.
The equations representing the dynamic of a p-pole, three-phase, wye-connected IM in the ‘abc’ reference frame is given by [87]
with
where , , and denote the voltage, current, and flux linkages, respectively. The subscripts and denote variables related to the stator and rotor circuits, respectively. and represent the stator and rotor resistance matrices, respectively, in diagonal form. and denote stator and rotor winding inductances, respectively. is the angular separation of the stator and rotor’s axes. represents the mutual inductance between the stator and the rotor windings. The superscript ′ represents the variables that refer to stator windings. The relationship between the torque and rotor speed is defined as
where J denotes the moment of inertia (kgm2), B denotes the viscous friction (N.m.s), and . The governing differential algebraic equations represented by (1) and (2) can be reformulated into a first-order ODE (5) for the DS of the IM model in the ‘abc’ reference frame [16]:
with
Relations (1) and (2) can be considered a baseline for modeling various types of faults such as broken rotor bars, end rings, and stator winding ITSCs in IMs (Table 3). For instance, the COLP model of a three-phase IM can be developed to include an ITSC in one of its stator windings [80] (Figure 4). The main parameters of the three-phase IM are modified in (1) and (2) owing to the stator-related matrices of the stator winding ITSC: , , and . In these matrices, the parameters corresponding to the faulty segment are separated from those of the remaining windings. The proposed model can be extended to study the simultaneous occurrence of ITSC faults in the stator windings of IMs [17]. To investigate broken rotor bars or end-ring defects in squirrel-cage induction machines (SCIMs) using the COLP modeling approach, the rotor structure can be represented by the configuration shown in Figure 5. In this model, accounts for the resistance of the rotor bars and end-ring segments, whereas includes self-, leakage, and mutual inductances. Additionally, denotes the mutual inductances between each rotor loop or end-ring segment and each phase of the stator winding [88].

Table 3.
COLP modeling of various fault types in `abc’ reference frame.
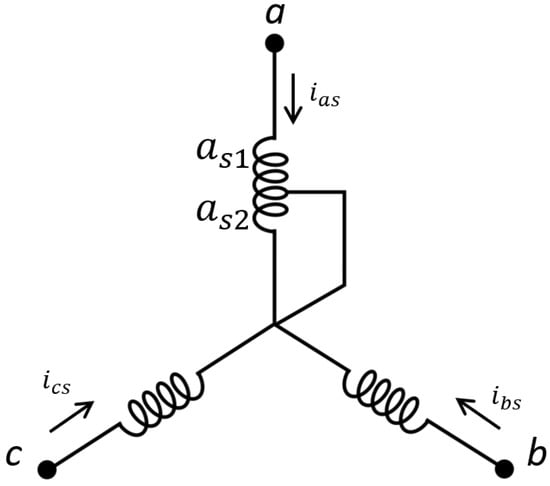
Figure 4.
Stator windings of an IM with an ITSC fault in phase ‘a’ [80].
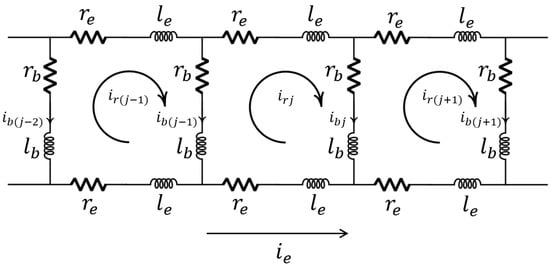
Figure 5.
Equivalent circuit of a squirrel-cage rotor showing rotor loop currents [88].
The COLP modeling approach was initially developed for multi-phase winding structures of IMs, designed to operate even in scenarios where one or more of the stator phases are open-circuit, as discussed in [70]. The winding function approach (WFA) for computing self- and mutual inductances, which considers all space harmonics in a multi-phase IM, is presented. The proposed model includes asymmetry resulting from inter-turn faults in the stator phase windings, as well as any issue and number of failures in the rotor bars and end rings [71]. This type of modeling is crucial to fault diagnosis in AC electrical machines, where in many cases, space harmonics are required for efficient fault identification [107]. A universal mathematical model for a five-phase IM encompassing the influence of higher space and time harmonics in the air-gap field is presented in a similar manner. Given the significant role of space harmonics in AC electrical machines with more than three phases, mathematical relations for computing self- and mutual inductances are derived [108]. To simplify the DRTS of the ‘abc’ reference frame model of the IM based on (5), both and are described through look-up tables as functions of [109]. This modeling approach can be extended to other electrical machine classes, such as permanent magnet synchronous machines (PMSMs) [48] (Table 3). In this regard, the classical ‘abc’ reference frame models of the IM and PMSM can be utilized for the DRTS of stator winding asymmetry faults. This illustrates the efficacy of such simple representations in detecting winding imbalance faults [17,18,110,111].
The use of PHYB models, especially FEM-based models that incorporate spatial and nonlinear aspects, as well as non-sinusoidal winding distribution phenomena inside the machine, can enhance the fault detection performance. These models provide comprehensive information regarding the health states of machines by using residual signals. However, the computational intensity of these models and their size and time-step limitations render them unsuitable for DRTS application. MEC-based models are generally considered to be a middle ground between FEM-based and COLP models in terms of computational performance [10]. The concept of MEC-based modeling relies on the analogy between electric and magnetic circuits. A deeper analysis of the electric and magnetic fields revealed that magnetic circuits typically function in a saturated nonlinear mode, whereas the majority of the elements in electric circuits exhibit linearity. In this regard, the machine’s 2D or 3D structure must be divided into small elements that describe the MEC. Each element of the MEC model includes voltage and current sources and reluctances, which can be expressed as
where l represents the length of the flux tube and A denotes its cross-sectional area. denotes the permeability of the magnetic material. Figure 6 represents the 3D MEC reluctance-based network and the circuit model of its elements. The voltage source, , represents the magnetomotive force (MMF), and the current source, , represents the flux of the permanent magnet. This network must be solved to obtain magnetic scalar potential u at each node. Based on Figure 6b, it is possible to derive the following [10]:
Once the permeance and MMF are computed, the MEC relations can be determined based on classical circuit nodal analysis.
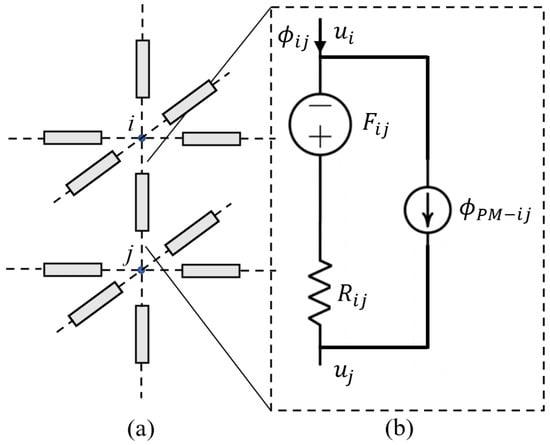
Figure 6.
Scheme of MEC model: (a) 3D reluctance network and (b) equivalent circuit of each element of the network [4].
Flux tubes serve as the foundation for MEC modeling techniques. A flux tube constitutes a geometrical region where all flux lines are perpendicular to their bases and no flux lines cut their sides. This requires knowledge of the machine geometry, including the effects of the stator and rotor slots, skewing, winding connections, and magnetic nonlinearity of the electrical machine cores. Consequently, it produces more accurate results than the COLP modeling technique under both healthy and faulty conditions (Table 4). For instance, permeance network and nonlinear MEC-based models have been introduced for real-time simulation of IMs [112,113]. A DRTS model was developed for PMSMs with shaped poles by utilizing the analytical solution of field equations incorporating space harmonics in the air-gap flux density distribution. The model was constructed under the assumption of linear superposition [114].
Hybrid modeling, as shown in Figure 1, is an emerging research topic that has received significant attention in recent years, especially since traditional multiphysics modeling approaches account for only a fraction of the relevant physical phenomena, which often explains the mismatch between their predictions and experimental observations [26]. With the availability of large number of data, open-source cutting-edge ML and data analytics libraries, and computation resources, the utilization of a hybrid approach to modeling allows for predictions of all aspects owing to its ability to combine the strengths of physics-based models and data-driven approaches, enabling more accurate, robust, and generalizable solutions across various engineering and scientific domains. Some active areas of research in this context include cost function modification to accommodate the Jacobian model, grow-when-required networks, physics-informed machine learning (PIML), embedding hard physical constraints in a neural network, leveraging uncertainty information, developing visual tools for network analysis, and nonparametric modeling approaches for bridging data science and dynamical systems [26]. In particular, PIML, initially introduced by Raissi et al. [115], is a significant advancement at the intersection of ML and PHYB modeling [116]. PIML distribution terms refer to physics-informed, physics-based, physics-guided, physics-infused, and physics-aware machine learning [117]. The architecture of physics-based neural networks (PINNs) is similar to that of conventional ML perceptrons (MLPs), as they consist of an input layer, multiple hidden layers, and an output layer. The main distinction between PINNs and standard MLPs is the inclusion of a differentiation layer (Figure 7). Each layer plays a specific and essential role in the PINN training process. Spatiotemporal data, represented by coordinates x and time t, are provided to the network through the input layer and then processed by the hidden layers. Then, the network predicts the latent solution y of the PDE through the output layer. These predicted values y are subsequently passed to the differentiation layer, where automatic differentiation is applied with respect to both x and t to generate the differential terms of the PDE. This process leads to the formulation of a loss function used to train the network. The total loss function of a PINN is expressed as a combination of a term that penalizes the residuals of the PDE and the term y loss function, which ensures agreement between the model predictions and given data points [118]. This concept has been widely employed in various applications, such as electrical impedance tomography [119], power system dynamic modeling and analysis [120,121], the modeling and prediction of temperature fluctuations in proton exchange membrane electrolysis [122], state estimation in unbalanced distribution power systems [123], high-speed transportation [124], and hydrogen-powered electric aircraft, among others [125]. A new partitioned PINN framework was proposed to enhance both the prediction accuracy and computational efficiency of electromagnetic field analysis in PMSMs. In this regard, separate neural network models were developed for the stator, air-gap, and rotor regions, with strict boundary conditions applied to maintain magnetic field continuity between neighboring subdomains [126]. A PINN architecture was designed to tackle the challenges of developing DTs for PMSMs in intelligent condition-based monitoring [127]. A physics-informed generative adversarial network-based approach was proposed for the optimal design of permanent magnet linear synchronous machines, achieving speeds up to 40 times faster than the FEM method while maintaining comparable accuracy [128].
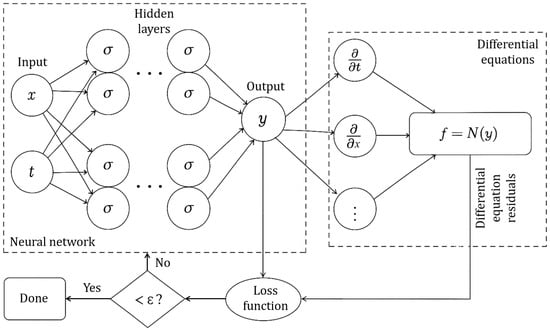
Figure 7.
Schematic representation of a PINN framework [116].

Table 4.
MEC modeling of various fault types.
Table 4.
MEC modeling of various fault types.
| Fault Types | References |
|---|---|
| Broken rotor bar and end ring | [129,130,131] |
| Stator/rotor windings ITSC | [132,133,134] |
| Static, dynamic, or mixed eccentricity | [135] |
| Ball bearing and race | [136,137] |
| Magnetization-related | [138,139,140,141,142,143,144] |
3.2. RTDS Hardware Platforms
A real-time simulation is defined as a process in which computational tasks are completed within the same time interval as the physical processes that are represented. This section explores the main aspects of the practical implementation of RTDS across various hardware platforms, emphasizing the constraints, trade-offs, and architectural capabilities. RTDS assumes that the state of a system changes only at fixed discrete time steps, synchronized with a real-time clock. The execution of RTDS involves three critical stages: receiving/sending signals through input/output (I/O) interfaces; executing computations, particularly solving the ODEs that define machine behavior; and transferring data between processing units and memory. To preserve real-time behavior, all these processes must be completed within the simulation time step. In this regard, among the various implicit and explicit numerical integration methods, the Runge–Kutta (RK), backward Euler, forward Euler, and trapezoidal rule are more widely used in power system simulations, including electrical machines. When selecting an integration method, the key factors include numerical precision, computational time, and resource usage. Higher-order methods, such as RK4, offer better precision but require more computational resources. In contrast, the FE method is faster and simpler but less accurate, especially for larger step sizes [10,145,146].
There are two types of RTDS, H-i-L and S-i-L, in the context of electrical machine DT design. In the H-i-L configuration, a physical component interacts with simulated components on a hardware platform, whereas in the S-i-L configuration, all components are simulated digitally on the same platform, ensuring signal integrity and computational flexibility. H-i-L is advantageous for testing in high-risk or inaccessible environments, whereas S-i-L allows for pure software validation [13,147]. Simulation fidelity is governed by the time-step size. A small time step ensures higher accuracy but increases the risk of overrun if computations cannot be completed in time. This is particularly challenging for high-frequency simulations such as those involving PWM drives, which may require nanosecond-level precision.
Hardware platforms can be categorized into chip single-core processor units (CSPUs), chip multiprocessor units (CMPUs), computer clusters, field-programmable gate arrays (FPGAs), and graphics processing units (GPUs). Each platform presents a unique set of advantages and trade-offs in terms of execution speed, resource usage, scalability, latency, and programming complexity. CMPUs or multicore CPUs include several processing cores within a single chip. Each core executes the instructions in parallel using multithreading. The CMPUs support shared memory and offer high clock speeds, making them suitable for medium-complexity simulations. Their advantages include user-friendly programming with tools like MATLAB/Simulink, cost-effectiveness and wide availability, and effectiveness for models like ’dq0’ and MECs [113,148,149,150,151,152]. Their limitations include high I/O latency owing to PCI bus delays, difficulty in handling time steps smaller than one microsecond, and suboptimal performance for high-frequency simulations [150,153]. Computer clusters consist of multiple interconnected computers (nodes), each with multiple CPUs. They are scalable and suitable for simulating large-scale electric systems such as wind farms. Their architecture is based on a master node that manages the simulation, whereas the slave nodes execute parallel computations. The nodes communicate via high-speed Ethernet or Infiniband links. Challenges include high communication latency, complex programming models involving message-passing interfaces (MPIs), and node synchronization, which can become a bottleneck. Computer clusters are widely employed in the RTDS of electrical machines [148,154,155,156,157].
FPGAs consist of configurable logic blocks, interconnection resources, and I/O interfaces. These platforms allow for deterministic execution and very fine time-step control, making them suitable for the real-time simulation of electric machines and drives. Key features include low-latency I/O interfaces without PCIs, parallel or pipelined architectures for high performance, and support for both fixed-point and floating-point arithmetic operations. The development approach is based on either textual programming languages (e.g., VHDL and Verilog) or schematic/block-based tools such as the Xilinx System Generator. Limitations include limited hardware resources, the need for expertise in digital hardware design, and high costs when scaling with multiple FPGAs. They are widely used in the DRTS of electrical machines and drives [87,112,114,158,159,160,161,162,163,164,165,166]. Multiple interconnected FPGAs or pipelining schemes can be considered for high-order RTDS models [10,68]. Graphics processing units (GPUs) are well suited for handling large-scale numerical simulations owing to their highly parallel architecture and strong floating-point processing capabilities. They consist of numerous cores arranged in blocks and grids, with threads executing instructions in a Single-Instruction, Multiple-Data (SIMD) manner and working alongside a central host CPU. These features make GPUs particularly effective in speeding up FEM simulations and managing models with thousands of ODEs. Additionally, they offer high computational throughput and can be programmed using languages such as Compute Unified Device Architecture (CUDA) or Open Computing Language (OpenCL). However, GPUs have drawbacks, such as significant initialization and data transfer overhead, and tend to be less efficient when applied to small-scale or rapidly changing models. Owing to their inherent parallel processing capabilities, GPUs have been adopted in various numerical analyses related to electrical engineering. Their applications include the numerical field analysis and simulation of electric machines [167,168,169,170,171]. In comparison, CMPUs provide adaptable but moderately performing solutions with higher latency; computer clusters offer scalability but require complex coordination and programming; FPGAs deliver fast, low-latency performance but are constrained by limited resources; and GPUs excel in processing large models, although they are less optimal for high-frequency operations.
4. Intelligent FD and CBM of Electrical Machines
The multiphysics modeling of electrical machines integrates various physical domains, including electromagnetics, thermal dynamics, mechanics, and acoustics. For instance, lumped models (LMs) are typically used to represent magnetic, electrical, electronic, and thermal components, whereas analytical models are applied to describe the vibro-acoustic and mechanical behaviors of a PMSM. Although such coupled modeling approaches are commonly used during the design phase of electrical machines, their applications in FD and CBM remain limited [11,172]. In particular, the resistances in the COLP model presented in [172] were defined as functions of the supply frequency and winding temperature, thereby allowing for improved accuracy. The frequency effect accounts for both skin and proximity effects. A multiphysics model of an induction machine is shown in Figure 8 [173]. This model comprises five interdependent sub-models. All of these sub-models are either analytical or semi-analytical to achieve a good compromise among computational speed, accuracy, and flexibility. The core of this approach is the electromagnetic model, which provides key insights, such as induction in the air gap, radial forces acting on the stator, and current distributions. The outputs of this model can be utilized in two ways. First, they serve as inputs for mechanical vibration and acoustic models, which are designed to predict the vibration behavior of the machine and the resulting electromagnetic noise emissions. Second, the electromagnetic model outputs are fed into the loss model, which quantifies the various losses occurring within the motor. The calculated losses are subsequently used in a fluid flow and thermal coupled (FFTC) model to simulate the evolution of internal motor temperature over time. A dynamic interaction exists between the electromagnetic and FFTC models: the temperature predictions from the FFTC model influence certain electromagnetic parameters, which in turn affect the loss estimations, that is, the same losses that act as heat sources in FFTC analysis.
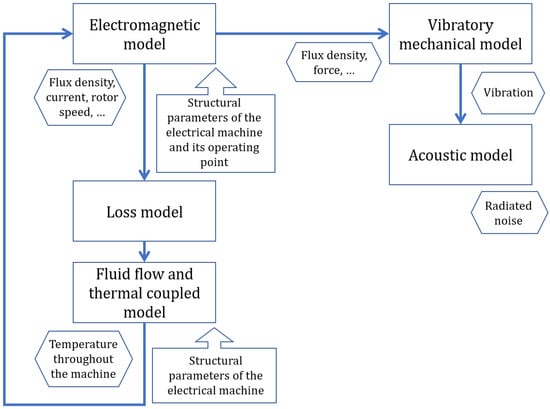
Figure 8.
A schematic of a multiphysics model of an induction machine [173].
In this regard, the DT design procedure for the FD and CBM of complex systems is well defined in [174]. In the first stage, it is essential to establish a high-fidelity reference model (a DT) for the electrical machine. Table 5 summarizes the advantages and disadvantages of PHYB/COLP techniques compared with data-driven models for DT development [9,66]. A multiphysics model that considers all the important aspects of the electrical, mechanical, and thermal behaviors of a physical entity enables the reference model to provide a wide spectrum of signals. Although data-driven models have weaknesses in representing all aspects of complex systems, they can be combined with PHYB/COLP techniques to optimize and solve the ODE governing the model [175,176]. In the second stage, an IoT infrastructure must be built to facilitate the evolution of the DT through available data from sensors installed on a physical electrical machine. In the final stage, the DT data are fused with well-known data-driven models for further processing, FD, and CBM [31]. The main features of the DT of an electrical machine that contribute to intelligent FD and CBM are highlighted as follows:
- DT parameters can be updated in real time based on voltage, current, vibration, acoustic, field, speed, and temperature measurements.
- The DT can be supplied by the measured phase (, and ) or line (, and ) voltages.
- The DT provides a wide range of inaccessible signals that commonly require sophisticated instrumentation.
- More clear fault signatures can be detected in the physical variables of the DT.
- Intelligent FD and CBM become possible by processing the DT data outcomes.
- Remote monitoring and control become feasible via the IoT infrastructure.

Table 5.
Comparison of PHYB/COLP modeling techniques with data-driven approaches for electrical machines DT design [4,9,66].
Table 5.
Comparison of PHYB/COLP modeling techniques with data-driven approaches for electrical machines DT design [4,9,66].
| PHYB/COLP Techniques | Data-Driven Approaches |
|---|---|
| + Solid foundation in physics | − Black-box concept |
| − Need for partial or entire geometric data of the electrical machine | + No need for any knowledge about the electrical machine |
| + No need for data for training | − A lot of data need to be provided for machine learning |
| − Need for optimization algorithms for continuous updates of model parameters | + Neural network update |
| − Numerical instability of the model | + Stable for a trained model |
| + Less prone to bias | − Bias in the data can be reflected in the model |
| − Difficulty in assimilating extensive historical data | + They integrate easily extensive historical data |
| + Developed model can be used for similar electrical machines | − New model needs to be trained for each electrical machine |
| + Several variables are available from the developed model | − Only the trained variables are available |
To achieve a high level of DT performance, it is crucial to adopt a strategy based on multiphysics modeling and integration of the main fault types (Figure 9a). This approach involves coupling all physical phenomena that contribute to lifecycle analysis, including thermal, mechanical, electrical, and chemical aspects. The parameters of the electrical machine DT can be updated using measured signals. Furthermore, the DRTS data can be used for DNN pre-training. The parameters of the DNN, namely, the weights, biases, and hyper-parameters, can then be transferred to a new DNN for fine-tuning using the measured data for FD, as shown in Figure 9b. The DRTS data, measured data, and event data which represent the FD results can be leveraged to perform the intelligent FD and CBM of electrical machines, but they have rarely been investigated in the literature [31,53].
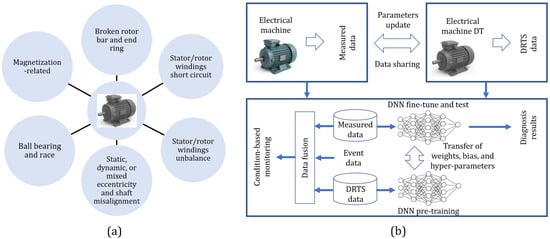
Figure 9.
(a) Integration of the main fault types into the DT of an AC electrical machine. (b) DT-assisted simplified framework for the intelligent FD and CBM of AC electrical machines [31,53].
5. Conclusions and Perspectives
This paper presents a summary of articles focusing on DRTS in the context of emerging DT technologies for intelligent FD and CBM in electrical machines. A predictive-level framework with the following vision is proposed for DT design during the service phase:
- The DT of an electrical machine is a synchronized, ultra-high-fidelity replica of it, incorporating multiphysics, multi-scale, and probabilistic modeling.
- An automated, bidirectional, real-time flow of data occurs between the DT and the electrical machine through appropriate instrumentation and an IoT platform.
- The twin encompasses data from the service stage of the electrical machine’s lifecycle and remains connected to this phase through to the retirement stage.
Based on the above definition, achieving an ultra-high-fidelity replica requires a multiphysics modeling approach with online parameter updating, whether this is a PHYB, data-driven, or hybrid approach. Furthermore, implementing intelligent FD and CBM requires simulation of key fault scenarios using the DT of an electrical machine, which offers a wide range of variables. The model must also operate in real time to ensure proper synchronization and bidirectional data flow with the physical system through the IoT infrastructure. Notably, the PIML approach is an increasingly attractive research direction, aiming to bridge machine learning and PHYB modeling to achieve a precise, real-time DT. In this context, hardware platforms such as GPUs, FPGAs, PC clusters, and CMPUs, which are commonly used in RTDS for electromagnetic transient studies of electrical machines, are well suited to support this requirement.
Author Contributions
These authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research study was funded by the Spanish ‘Ministerio de Ciencia e Innovación’, Agencia Estatal de Investigación and FEDER program in the framework of ‘Proyectos de Generación de Conocimiento 2021’ of ‘Programa Estatal para Impulsar la Investigación Científico-Técnica y su Transferencia’, belonging to ‘Plan Estatal de Investigación Científica, Técnica y de Innovación 2021-2023’ (ref: PID2021-122343OB-I00).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AC | Alternating Current |
| COLP | circuit-oriented lumped-parameter |
| CBM | condition-based monitoring |
| CMPU | chip multiprocessor unit |
| CSPU | chip single-core processor unit |
| CUDA | Compute Unified Device Architecture |
| DNN | deep neural network |
| DoS | digital offline simulation |
| DRTS | digital real-time simulation |
| DS | digital simulation |
| DT | digital twin |
| EMTP | Electromagnetic Transient Program |
| FD | fault diagnosis |
| FDM | finite difference method |
| FEM | finite element method |
| FFTC | fluid flow and thermal coupled |
| FPGA | field-programmable gate array |
| FVM | finite volume method |
| GPU | Graphics Processor Unit |
| H-i-L | hardware-in-the-loop |
| IM | induction machine |
| IoT | Internet of Things |
| MEC | magnetic equivalent circuit |
| ML | machine learning |
| MMF | magnetomotive force |
| MPI | message-passing interface |
| MWFA | modified winding function approach |
| ODE | ordinary differential equation |
| PDE | partial differential equation |
| PHYB | physics-based |
| PIML | physics-informed machine learning |
| PINN | physics-informed neural network |
| PMSM | permanent magnet synchronous machine |
| RFID | radio-frequency identification |
| RK | Runge–Kutta |
| RTDS | Real-Time Digital Simulator |
| PMSG | permanent magnet synchronous generator |
| SCIM | squirrel-cage induction machine |
| SIMD | Single-Instruction, Multiple-Data |
| SSM | state-space model |
| TL | transfer learning |
| TSR | Tip–Speed Ratio |
| MPPT | Maximum Power Point Tracking |
| P-H-i-L | power-hardware-in-the-loop |
| P-i-L | processor-in-the-loop |
| S-i-L | software-in-the-loop |
| WECS | Wind Energy Conversion System |
| WFA | winding function approach |
| WT | Wind Turbine |
| XATP | Expandable Transient Analysis Program |
References
- Semenkov, K.; Promyslov, V.; Poletykin, A.; Mengazetdinov, N. Validation of Complex Control Systems with Heterogeneous Digital Models in Industry 4.0 Framework. Machines 2021, 9, 62. [Google Scholar] [CrossRef]
- Markwirth, T.; Jancke, R.; Sohrmann, C. Dynamic Fault Injection into Digital Twins of Safety-Critical Systems. In Proceedings of the 2021 Design, Automation and Test in Europe Conference and Exhibition (DATE), Virtual, 1–5 February 2021; pp. 446–450. [Google Scholar] [CrossRef]
- Guo, K.; Wan, X.; Liu, L.; Gao, Z.; Yang, M. Fault Diagnosis of Intelligent Production Line Based on Digital Twin and Improved Random Forest. Appl. Sci. 2021, 11, 7733. [Google Scholar] [CrossRef]
- Kia, S.H.; Razik, H.; Dunai, L. Electrical Machines: Real-time Simulation for Intelligent Fault Diagnosis, Prognostics and Health Management. In Proceedings of the IECON 2024—50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Florkowski, M. Digital Twins and Simulations: World of Simulation. In ABB Report; ABB: Zurich, Switzerland, 2019; pp. 8–13. [Google Scholar]
- Chung, T. Computational Fluid Dynamics. Computational Fluid Dynamics, 2nd ed.; McGraw-hill: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Allaire, G. Numerical Analysis and Optimization: An Introduction to Mathematical Modelling and Numerical Simulation; Oxford University Press: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Kaltenbacher, M. Numerical Simulation of Mechatronic Sensors and Actuators: Finite Elements for Computational Multiphysics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Rasheed, A.; San, O.; Kvamsdal, T. Digital Twin: Values, Challenges and Enablers from a Modeling Perspective. IEEE Access 2020, 8, 21980–22012. [Google Scholar] [CrossRef]
- Mojlish, S.; Erdogan, N.; Levine, D.; Davoudi, A. Review of Hardware Platforms for Real-time Simulation of Electric Machines. IEEE Trans. Transp. Electrif. 2017, 3, 130–146. [Google Scholar] [CrossRef]
- Le Besnerais, J.; Fasquelle, A.; Hecquet, M.; Pelle, J.; Lanfranchi, V.; Harmand, S.; Brochet, P.; Randria, A. Multiphysics Modeling: Electro-Vibro-Acoustics and Heat Transfer of PWM-Fed Induction Machines. IEEE Trans. Ind. Electron. 2010, 57, 1279–1287. [Google Scholar] [CrossRef]
- Le Besnerais, J. Vibroacoustic Analysis of Radial and Tangential Air-Gap Magnetic Forces in Permanent Magnet Synchronous Machines. IEEE Trans. Magn. 2015, 51, 8105609. [Google Scholar] [CrossRef]
- Omar Faruque, M.D.; Strasser, T.; Lauss, G.; Jalili-Marandi, V.; Forsyth, P.; Dufour, C.; Dinavahi, V.; Monti, A.; Kotsampopoulos, P.; Martinez, J.A.; et al. Real-time Simulation Technologies for Power Systems Design, Testing, and Analysis. IEEE Power Energy Technol. Syst. J. 2015, 2, 63–73. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Lazzari, M.; Pastorelli, M. A Simplified Thermal Model for Variable-speed Self-cooled Industrial Induction Motor. IEEE Trans. Ind. Appl. 2003, 39, 945–952. [Google Scholar] [CrossRef]
- Matar, M.; Iravani, R. Massively Parallel Implementation of AC Machine Models for FPGA-Based Real-time Simulation of Electromagnetic Transients. IEEE Trans. Power Deliv. 2011, 26, 830–840. [Google Scholar] [CrossRef]
- Wang, L.; Jatskevich, J.; Dinavahi, V.; Dommel, H.W.; Martinez, J.A.; Strunz, K.; Rioual, M.; Chang, G.W.; Iravani, R. Methods of Interfacing Rotating Machine Models in Transient Simulation Programs. IEEE Trans. Power Deliv. 2010, 25, 891–903. [Google Scholar] [CrossRef]
- Agah, G.R.; Rahideh, A.; Faradonbeh, V.Z.; Kia, S.H. Stator Winding Interturn Short-Circuit Fault Modeling and Detection of Squirrel-Cage Induction Motors. IEEE Trans. Transp. Electrif. 2024, 10, 5725–5734. [Google Scholar] [CrossRef]
- Hedayati Kia, S. Detection of Stator and Rotor Asymmetries Faults in Wound Rotor Induction Machines: Modeling, Test and Real-time Implementation. In Emerging Electric Machines; Zobaa, A.F., Aleem, S.H.A., Eds.; IntechOpen: Rijeka, Croatia, 2021; Chapter 3. [Google Scholar] [CrossRef]
- Ametani, A. Numerical Analysis of Power System Transients and Dynamics; The Institution of Engineering and Technology: Stevenage, UK, 2015. [Google Scholar] [CrossRef]
- Watson, N.; Arrillaga, J. Power Systems Electromagnetic Transients Simulation; The Institution of Engineering and Technology: Stevenage, UK, 2003. [Google Scholar] [CrossRef]
- Dinavahi, V.; Lin, N. Hardware Emulation Building Blocks for Power System Components. In Real-Time Electromagnetic Transient Simulation of AC–DC Networks; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 2; pp. 17–77. [Google Scholar] [CrossRef]
- Tiegna, H.; Amara, Y.; Barakat, G. Overview of Analytical Models of Permanent Magnet Electrical Machines for Analysis and Design Purposes. Math. Comput. Simul. 2013, 90, 162–177. [Google Scholar] [CrossRef]
- Devillers, E.; Le Besnerais, J.; Lubin, T.; Hecquet, M.; Lecointe, J.P. A Review of Subdomain Modeling Techniques in Electrical Machines: Performances and Applications. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 86–92. [Google Scholar] [CrossRef]
- Dinavahi, V.; Lin, N. Rotating Machines. In Real-Time Electromagnetic Transient Simulation of AC–DC Networks; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 4; pp. 143–191. [Google Scholar] [CrossRef]
- Stadtmann, F.; Rasheed, A.; Kvamsdal, T.; Johannessen, K.A.; San, O.; Kölle, K.; Tande, J.O.; Barstad, I.; Benhamou, A.; Brathaug, T.; et al. Digital Twins in Wind Energy: Emerging Technologies and Industry-Informed Future Directions. IEEE Access 2023, 11, 110762–110795. [Google Scholar] [CrossRef]
- San, O.; Rasheed, A.; Kvamsdal, T. Hybrid Analysis and Modeling, Eclecticism, and Multifidelity Computing Toward Digital Twin Revolution. GAMM-Mitteilungen 2021, 44, e202100007. [Google Scholar] [CrossRef]
- Parekh, V.; Flore, D.; Schöps, S. Performance Analysis of Electrical Machines Using a Hybrid Data- and Physics-Driven Model. IEEE Trans. Energy Convers. 2023, 38, 530–539. [Google Scholar] [CrossRef]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Frosini, L. Novel Diagnostic Techniques for Rotating Electrical Machines—A Review. Energies 2020, 13, 5066. [Google Scholar] [CrossRef]
- Kumar, R.R.; Andriollo, M.; Cirrincione, G.; Cirrincione, M.; Tortella, A. A Comprehensive Review of Conventional and Intelligence-Based Approaches for the Fault Diagnosis and Condition Monitoring of Induction Motors. Energies 2022, 15, 8938. [Google Scholar] [CrossRef]
- Xia, M.; Shao, H.; Williams, D.; Lu, S.; Shu, L.; de Silva, C.W. Intelligent Fault Diagnosis of Machinery Using Digital Twin-Assisted Deep Transfer Learning. Reliab. Eng. Syst. Saf. 2021, 215, 107938. [Google Scholar] [CrossRef]
- Wang, S.; Xu, Q.; Zhang, K.; Liu, Y.; Liu, H. Selection refines diagnosis: Mamba for acoustic weak fault diagnosis combining feature mode decomposition and selection. Adv. Eng. Inform. 2025, 66, 103421. [Google Scholar] [CrossRef]
- Li, D.; Kakosimos, P.; Peretti, L. Machine-Learning-Based Condition Monitoring of Power Electronics Modules in Modern Electric Drives. IEEE Power Electron. Mag. 2023, 10, 58–66. [Google Scholar] [CrossRef]
- Nasiri, A.; Rahideh, A.; Agah, G.R.; Kia, S.H. Ball-Bearing Fault Detection of Squirrel-Cage Induction Motors Based on Single-Phase Stator Current Using Wavelet Packet Decomposition and Statistical Features. IEEE Trans. Energy Convers. 2025, 40, 1529–1537. [Google Scholar] [CrossRef]
- Kumar, R.R.; Waisale, L.O.; Tamata, J.L.; Tortella, A.; H. Kia, S.; Andriollo, M. Advanced Fault Detection and Severity Analysis of Broken Rotor Bars in Induction Motors: Comparative Classification and Feature Study Using Dimensionality Reduction Techniques. Machines 2024, 12, 890. [Google Scholar] [CrossRef]
- Ouali, Y.; Hudelot, C.; Tami, M. An Overview of Deep Semi-Supervised Learning. arXiv 2020, arXiv:2006.05278. [Google Scholar] [CrossRef]
- Xu, Y.; Sun, Y.; Liu, X.; Zheng, Y. A Digital-Twin-Assisted Fault Diagnosis Using Deep Transfer Learning. IEEE Access 2019, 7, 19990–19999. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. arXiv 2024, arXiv:2312.00752. [Google Scholar]
- Terron-Santiago, C.; Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A. A Review of Techniques Used for Induction Machine Fault Modelling. Sensors 2021, 21, 4855. [Google Scholar] [CrossRef]
- Singh, A.; Grant, B.; DeFour, R.; Sharma, C.; Bahadoorsingh, S. A Review of Induction Motor Fault Modeling. Electr. Power Syst. Res. 2016, 133, 191–197. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, P.; He, S.; Huang, J. A Review of Modeling and Diagnostic Techniques for Eccentricity Fault in Electric Machines. Energies 2021, 14, 4296. [Google Scholar] [CrossRef]
- Usman, A.; Joshi, B.M.; Rajpurohit, B.S. Review of Fault Modeling Methods for Permanent Magnet Synchronous Motors and Their Comparison. In Proceedings of the 2017 IEEE 11th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Tinos, Greece, 29 August–1 September 2017; pp. 141–146. [Google Scholar] [CrossRef]
- Bélanger, J.; Venne, P.; Paquin, J.N. The What, Where, and Why of Real-time Simulation. Planet RT 2010, 1, 37–49. [Google Scholar]
- Mihalič, F.; Truntič, M.; Hren, A. Hardware-in-the-Loop Simulations: A Historical Overview of Engineering Challenges. Electronics 2022, 11, 2462. [Google Scholar] [CrossRef]
- Horri, N.; Pietraszko, M. A Tutorial and Review on Flight Control Co-Simulation Using Matlab/Simulink and Flight Simulators. Automation 2022, 3, 486–510. [Google Scholar] [CrossRef]
- Terron-Santiago, C.; Martinez-Roman, J.; Puche-Panadero, R.; Sapena-Bano, A. Low-Computational-Cost Hybrid FEM-Analytical Induction Machine Model for the Diagnosis of Rotor Eccentricity, Based on Sparse Identification Techniques and Trigonometric Interpolation. Sensors 2021, 21, 6963. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Chinesta, F.; Pineda-Sanchez, M.; Aguado, J.; Borzacchiello, D.; Puche-Panadero, R. Induction Machine Model with Finite Element Accuracy for Condition Monitoring Running in Real Time Using Hardware in the Loop System. Int. J. Electr. Power Energy Syst. 2019, 111, 315–324. [Google Scholar] [CrossRef]
- Yousefzadeh, M.; Hedayati Kia, S.; Hoseintabar Marzebali, M.; Arab Khaburi, D.; Razik, H. Power-Hardware-in-the-Loop for Stator Windings Asymmetry Fault Analysis in Direct-Drive PMSG-Based Wind Turbines. Energies 2022, 15, 6896. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Y.; Lei, G.; Yin, W.; Ba, X.; Zhu, J. Construction Method and Application Prospect of Electrical Machine Digital Twin. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Hosamo, H.H.; Svennevig, P.R.; Svidt, K.; Han, D.; Nielsen, H.K. A Digital Twin Predictive Maintenance Framework of Air Handling Units Based on Automatic Fault Detection and Diagnostics. Energy Build. 2022, 261, 111988. [Google Scholar] [CrossRef]
- Falekas, G.; Karlis, A. Digital Twin in Electrical Machine Control and Predictive Maintenance: State-of-the-Art and Future Prospects. Energies 2021, 14, 5933. [Google Scholar] [CrossRef]
- Allen, B.D. Digital Twins and Living Models at NASA. In Proceedings of the Digital Twin Summit, Virtual, 3–4 November 2021. [Google Scholar]
- Hu, W.; Zhang, T.; Deng, X.; Liu, Z.; Tan, J. Digital Twin: A State-of-the-Art Review of Its Enabling Technologies, Applications and Challenges. J. Intell. Manuf. Spec. Equip. 2021, 2, 1–34. [Google Scholar] [CrossRef]
- Chen, Z.; Choudhury, M.D.; Blincoe, K.; Dhupia, J.S. A Digital Twin Based Framework for Real-Time Machine Condition Monitoring. In Proceedings of the 2023 IEEE 19th International Conference on Automation Science and Engineering (CASE), Auckland, New Zealand, 26–30 August 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital Twin in Industry: State-of-the-Art. IEEE Trans. Ind. Inform. 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of Digital Twin About Concepts, Technologies, and Industrial Applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Trauer, J.; Schweigert-Recksiek, S.; Engel, C.; Spreitzer, K.; Zimmermann, M. What is a Digital Twin?—Definitions and Insights From an Industrial Case Study in Technical Product Developement. Proc. Des. Soc. Des. Conf. 2020, 1, 757–766. [Google Scholar] [CrossRef]
- Vrabič, R.; Erkoyuncu, J.A.; Butala, P.; Roy, R. Digital Twins: Understanding the Added Value of Integrated Models for Through-life Engineering Services. Procedia Manuf. 2018, 16, 139–146. [Google Scholar] [CrossRef]
- Shao, G.; Kibira, D.; Frechette, S. Digital Twins for Advanced Manufacturing: The Standardized Approach. In Digital Twins, Simulation, and the Metaverse: Driving Efficiency and Effectiveness in the Physical World through Simulation in the Virtual Worlds; Grieves, M., Hua, E.Y., Eds.; Springer: Cham, Switzerland, 2024; pp. 145–169. [Google Scholar] [CrossRef]
- Yang, C.; Shen, W.; Wang, X. The Internet of Things in Manufacturing: Key Issues and Potential Applications. IEEE Syst. Man, Cybern. Mag. 2018, 4, 6–15. [Google Scholar] [CrossRef]
- Crespi, N.; Drobot, A.T.; Minerva, R. The Digital Twin: What and Why? In The Digital Twin; Crespi, N., Drobot, A.T., Minerva, R., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 3–20. [Google Scholar] [CrossRef]
- Friederich, J.; Francis, D.P.; Lazarova-Molnar, S.; Mohamed, N. A framework for data-driven digital twins of smart manufacturing systems. Comput. Ind. 2022, 136, 103586. [Google Scholar] [CrossRef]
- Alvarez-Gonzalez, F.; Griffo, A.; Sen, B.; Wang, J. Real-time Hardware-in-the-Loop Simulation of Permanent-Magnet Synchronous Motor Drives Under Stator Faults. IEEE Trans. Ind. Electron. 2017, 64, 6960–6969. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Karamanakos, P.; Rodriguez, J. Digital Twin Techniques for Power Electronics-Based Energy Conversion Systems: A Survey of Concepts, Application Scenarios, Future Challenges, and Trends. IEEE Ind. Electron. Mag. 2023, 17, 20–36. [Google Scholar] [CrossRef]
- Mendes, G.; Ferreira, A. Extending the Multiphysics Modelling of Electric Machines in a Digital Twin Concept. In Proceedings of the 2021 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Cracow, Poland, 22–25 September 2021; Volume 2, pp. 689–693. [Google Scholar] [CrossRef]
- Iranian, M.E.; Mohseni, M.; Aghili, S.; Parizad, A.; Baghaee, H.R.; Guerrero, J.M. Real-time FPGA-Based HIL Emulator of Power Electronics Controllers Using NI PXI for DFIG Studies. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2005–2019. [Google Scholar] [CrossRef]
- Chen, Y.; Dinavahi, V. Hardware Emulation Building Blocks for Real-time Simulation of Large-Scale Power Grids. IEEE Trans. Ind. Inform. 2014, 10, 373–381. [Google Scholar] [CrossRef]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Zhao, Y.; Lipo, T. Modeling and Control of a Multi-phase Induction Machine with Structural Unbalance. IEEE Trans. Energy Convers. 1996, 11, 570–577. [Google Scholar] [CrossRef]
- Toliyat, H.; Lipo, T. Transient Analysis of Cage Induction Machines Under Stator, Rotor Bar and End Ring faults. IEEE Trans. Energy Convers. 1995, 10, 241–247. [Google Scholar] [CrossRef]
- Bouzid, S.; Viarouge, P.; Cros, J. Real-Time Digital Twin of a Wound Rotor Induction Machine Based on Finite Element Method. Energies 2020, 13, 5413. [Google Scholar] [CrossRef]
- Ambrožič, V.; Fišer, R.; Nemec, M.; Drobnič, K. Dynamic Model of Induction Machine with Faulty Rotor in Field Reference Frame. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 142–149. [Google Scholar] [CrossRef]
- Baccarini, L.M.R.; de Menezes, B.R.; Caminhas, W.M. Fault Induction Dynamic Model, Suitable for Computer Simulation: Simulation Results and Experimental Validation. Mech. Syst. Signal Process. 2010, 24, 300–311. [Google Scholar] [CrossRef]
- Bachir, S.; Tnani, S.; Trigeassou, J.C.; Champenois, G. Diagnosis by Parameter Estimation of Stator and Rotor Faults Occurring in Induction Machines. IEEE Trans. Ind. Electron. 2006, 53, 963–973. [Google Scholar] [CrossRef]
- Bossio, G.; De Angelo, C.; Garcia, G.; Solsona, J.; Valla, M. Effects of Rotor Bar and End-Ring Faults Over the Signals of a Position Estimation Strategy for Induction Motors. IEEE Trans. Ind. Appl. 2005, 41, 1005–1012. [Google Scholar] [CrossRef]
- Nemec, M.; Drobnič, K.; Fišer, R.; Ambrožič, V. Simplified model of induction machine with broken rotor bars. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 1085–1090. [Google Scholar] [CrossRef]
- Magagula, G.S.; Nnachi, A.F.; Akumu, A.O. Broken Rotor Bar Fault Simulation And Analysis In D-q Reference Frame. In Proceedings of the 2020 IEEE PES/IAS PowerAfrica, Virtual, 25–28 August 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Jannati, M.; Idris, N.; Salam, Z. A new method for modeling and vector control of unbalanced induction motors. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3625–3632. [Google Scholar] [CrossRef]
- Tallam, R.; Habetler, T.; Harley, R. Transient Model for Induction Machines with Stator Winding Turn Faults. IEEE Trans. Ind. Appl. 2002, 38, 632–637. [Google Scholar] [CrossRef]
- Yassa, N.; Rachek, M. Modeling and detecting the stator winding inter turn fault of permanent magnet synchronous motors using stator current signature analysis. Math. Comput. Simul. 2020, 167, 325–339. [Google Scholar] [CrossRef]
- Choudhary, A.; Meena, D.C.; Patra, A.K. Asynchronous Motor Modeling in Simulink for Stator and Rotor Fault Analysis. In Proceedings of the 2019 International Conference on Green and Human Information Technology (ICGHIT), Kuala Lumpur, Malaysia, 16–18 January 2019; pp. 82–85. [Google Scholar] [CrossRef]
- Guezmil, A.; Berriri, H.; Pusca, R.; Sakly, A.; Romary, R.; Mimouni, M. Detecting Inter-Turn Short-Circuit Fault in Induction Machine Using High-Order Sliding Mode Observer: Simulation and Experimental Verification. J. Control. Autom. Electr. Syst. 2017, 28, 532–540. [Google Scholar] [CrossRef]
- Bindu, S.; Thomas, V.V. Detection of Static Air-Gap Eccentricity in Three-Phase Squirrel Cage Induction Motor Through Stator Current and Vibration Analysis. In Advances in Power Systems and Energy Management: ETAEERE-2016; Springer: Singapore, 2018; pp. 511–518. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, B.; Kanemaru, M.; Lin, C.; Liu, D.; Miyoshi, M.; Teo, K.H.; Habetler, T.G. Model-Based Analysis and Quantification of Bearing Faults in Induction Machines. IEEE Trans. Ind. Appl. 2020, 56, 2158–2170. [Google Scholar] [CrossRef]
- Ishikawa, T.; Seki, Y.; Kurita, N. Analysis for Fault Detection of Vector-Controlled Permanent Magnet Synchronous Motor With Permanent Magnet Defect. IEEE Trans. Magn. 2013, 49, 2331–2334. [Google Scholar] [CrossRef]
- Roshandel Tavana, N.; Dinavahi, V. A General Framework for FPGA-Based Real-time Emulation of Electrical Machines for HIL Applications. IEEE Trans. Ind. Electron. 2015, 62, 2041–2053. [Google Scholar] [CrossRef]
- Didier, G.; Razik, H.; Rezzoug, A. An Induction Motor Model Including the First Space Harmonics for Broken Rotor Bar Diagnosis. Eur. Trans. Electr. Power 2005, 15, 229–243. [Google Scholar] [CrossRef]
- Tang, J.; Chen, J.; Dong, K.; Yang, Y.; Lv, H.; Liu, Z. Modeling and Evaluation of Stator and Rotor Faults for Induction Motors. Energies 2020, 13, 133. [Google Scholar] [CrossRef]
- Zouzou, S.E.; Ghoggal, A.; Aboubou, A.; Sahraoui, M.; Razik, H. Modeling of Induction Machines with Skewed Rotor Slots Dedicated to Rotor Faults. In Proceedings of the 2005 5th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Vienna, Austria, 7–9 September 2005; pp. 1–6. [Google Scholar] [CrossRef]
- Kaikaa, M.Y.; Hadjami, M.; Khezzar, A. Effects of the Simultaneous Presence of Static Eccentricity and Broken Rotor Bars on the Stator Current of Induction Machine. IEEE Trans. Ind. Electron. 2014, 61, 2452–2463. [Google Scholar] [CrossRef]
- Jung, J.H.; Kwon, B.H. Corrosion Model of a Rotor-Bar-Under-Fault Progress in Induction Motors. IEEE Trans. Ind. Electron. 2006, 53, 1829–1841. [Google Scholar] [CrossRef]
- Bossio, G.R.; De Angelo, C.H.; Pezzani, C.M.; Bossio, J.M.; Garcia, G.O. Evaluation of Harmonic Current Sidebands for Broken Bar Diagnosis in Induction Motors. In Proceedings of the 2009 IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Cargèse, France, 31 August–3 September 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Houdouin, G.; Barakat, G.; Dakyo, B.; Destobbeleer, E. A Winding Function Theory Based Global Method for the Simulation of Faulty Induction Machines. In Proceedings of the IEEE International Electric Machines and Drives Conference, IEMDC’03, Chicago, IL, USA,, 12–15 May 2003; Volume 1, pp. 297–303. [Google Scholar] [CrossRef]
- Ojaghi, M.; Sabouri, M.; Faiz, J. Performance Analysis of Squirrel-Cage Induction Motors Under Broken Rotor Bar and Stator Inter-Turn Fault Conditions Using Analytical Modeling. IEEE Trans. Magn. 2018, 54, 8203705. [Google Scholar] [CrossRef]
- Benninger, M.; Liebschner, M.; Kreischer, C. Automated Parameter Identification for Multiple Coupled Circuit Modeling of Induction Machines. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 1307–1313. [Google Scholar] [CrossRef]
- Devanneaux, V.; Dagues, B.; Faucher, J.; Barakat, G. An Accurate Model of Squirrel Cage Induction Machines Under Stator Faults. Math. Comput. Simul. 2003, 63, 377–391. [Google Scholar] [CrossRef]
- Vaseghi, B.; Takorabet, N.; Meibody-Tabar, F. Analytical Circuit-Based Model of PMSM Under Stator Inter-Turn Short-Circuit Fault Validated by Time-Stepping Finite Element Analysis. In Proceedings of the The XIX International Conference on Electrical Machines—ICEM 2010, Rome, Italy, 6–8 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Ilamparithi, T.; Nandi, S. Comparison of Results for Eccentric Cage Induction Motor Using Finite Element Method and Modified Winding Function Approach. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, Delhi, India, 20–23 December 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Faiz, J.; Ojaghi, M. Unified Winding Function Approach for Dynamic Simulation of Different Kinds of Eccentricity Faults in Cage Induction Machines. IET Electr. Power Appl. 2009, 3, 461–470. [Google Scholar] [CrossRef]
- Joksimovic, G.; Durovic, M.; Penman, J.; Arthur, N. Dynamic Simulation of Dynamic Eccentricity in Induction Machines-Winding Function Approach. IEEE Trans. Energy Convers. 2000, 15, 143–148. [Google Scholar] [CrossRef]
- Pal, R.S.C.; Mohanty, A.R. A Simplified Dynamical Model of Mixed Eccentricity Fault in a Three-Phase Induction Motor. IEEE Trans. Ind. Electron. 2021, 68, 4341–4350. [Google Scholar] [CrossRef]
- Wang, C.; Wang, M.; Yang, B.; Song, K. A Model-Based Method for Bearing Fault Detection Using Motor Current. J. Physics: Conf. Ser. 2020, 1650, 032130. [Google Scholar] [CrossRef]
- Ojaghi, M.; Yazdandoost, N. Winding Function Approach to Simulate Induction Motors Under Sleeve Bearing Fault. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (ICIT), Busan, Republic of Korea, 26 February–1 March 2014; pp. 158–163. [Google Scholar] [CrossRef]
- Ojaghi, M.; Sabouri, M.; Faiz, J. Analytic Model for Induction Motors Under Localized Bearing Faults. IEEE Trans. Energy Convers. 2018, 33, 617–626. [Google Scholar] [CrossRef]
- Ajily, E.; Ardebili, M.; Abbaszadeh, K. Magnet Defect and Rotor Eccentricity Modeling in Axial-Flux Permanent-Magnet Machines via 3-D Field Reconstruction Method. IEEE Trans. Energy Convers. 2016, 31, 486–495. [Google Scholar] [CrossRef]
- Strangas, E.; Clerc, G.; Razik, H.; Soualhi, A. Fault Diagnosis, Prognosis, and Reliability for Electrical Machines and Drives; IEEE Press Series; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Pereira, L.A.; Scharlau, C.C.; Pereira, L.F.A.; Haffner, J.F. General Model of a Five-Phase Induction Machine Allowing for Harmonics in the Air Gap Field. IEEE Trans. Energy Convers. 2006, 21, 891–899. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Martinez-Roman, J.; Puche-Panadero, R.; Pineda-Sanchez, M.; Perez-Cruz, J.; Riera-Guasp, M. Induction Machine Model with Space Harmonics for Fault Diagnosis Based on the Convolution Theorem. Int. J. Electr. Power Energy Syst. 2018, 100, 463–481. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Mills, A.R.; Chong, E.; Sun, Z. Current-Residual-Based Stator Interturn Fault Detection in Permanent Magnet Machines. IEEE Trans. Ind. Electron. 2021, 68, 59–69. [Google Scholar] [CrossRef]
- Jeong, H.; Moon, S.; Kim, S.W. An Early Stage Interturn Fault Diagnosis of PMSMs by Using Negative-Sequence Components. IEEE Trans. Ind. Electron. 2017, 64, 5701–5708. [Google Scholar] [CrossRef]
- Tavana, N.R.; Dinavahi, V. Real-time Nonlinear Magnetic Equivalent Circuit Model of Induction Machine on FPGA for Hardware-in-the-Loop Simulation. IEEE Trans. Energy Convers. 2016, 31, 520–530. [Google Scholar] [CrossRef]
- Asghari, B.; Dinavahi, V. Experimental Validation of a Geometrical Nonlinear Permeance Network Based Real-time Induction Machine Model. IEEE Trans. Ind. Electron. 2012, 59, 4049–4062. [Google Scholar] [CrossRef]
- Tavana, N.R.; Dinavahi, V. Real-time FPGA-Based Analytical Space Harmonic Model of Permanent Magnet Machines for Hardware-in-the-Loop Simulation. IEEE Trans. Magn. 2015, 51, 8106609. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar] [CrossRef]
- Farea, A.; Yli-Harja, O.; Emmert-Streib, F. Understanding Physics-Informed Neural Networks: Techniques, Applications, Trends, and Challenges. AI 2024, 5, 1534–1557. [Google Scholar] [CrossRef]
- DENG, W.; NGUYEN, K.T.; MEDJAHER, K.; GOGU, C.; MORIO, J. Physics-informed machine learning in prognostics and health management: State of the art and challenges. Appl. Math. Model. 2023, 124, 325–352. [Google Scholar] [CrossRef]
- Son, S.; Jeong, J.; Jeong, D.; ho Sun, K.; Oh, K.Y. Physics-Informed Neural Network: Principles and Applications. In Recent Advances in Neuromorphic Computing; Bai, K.J., Yi, Y., Eds.; IntechOpen: Rijeka, Croatia, 2024; Chapter 4. [Google Scholar] [CrossRef]
- Smyl, D.; Tallman, T.N.; Homa, L.; Flournoy, C.; Hamilton, S.J.; Wertz, J. Physics Informed Neural Networks for Electrical Impedance Tomography. Neural Netw. 2025, 188, 107410. [Google Scholar] [CrossRef]
- Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Power Systems. arXiv 2020, arXiv:1911.03737. [Google Scholar] [CrossRef]
- Ventura Nadal, I.; Stiasny, J.; Chatzivasileiadis, S. Physics-Informed Neural Networks: A plug and play integration into power system dynamic simulations. Electr. Power Syst. Res. 2025, 248, 111885. [Google Scholar] [CrossRef]
- Zerrougui, I.; Li, Z.; Hissel, D. Physics-Informed Neural Network for modeling and predicting temperature fluctuations in proton exchange membrane electrolysis. Energy AI 2025, 20, 100474. [Google Scholar] [CrossRef]
- Iliadis, P.; Petridis, S.; Skembris, A.; Rakopoulos, D.; Kosmatopoulos, E. Physics-Informed Neural Networks for Enhanced State Estimation in Unbalanced Distribution Power Systems. Appl. Sci. 2025, 15, 7507. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Dinavahi, V. Physics-Informed Machine Learning Modeling and Inferencer-in-The-Loop Based Real-Time Digital-Twin Emulation for a High-Speed Maglev Transportation System. 2025. Available online: https://ssrn.com/abstract=5389685 (accessed on 1 August 2025).
- Zhang, S.; Dinavahi, V.; Liang, T. Towards hydrogen-powered electric aircraft: Physics-informed machine learning based multi-domain modeling and real-time digital twin emulation on FPGA. Energy 2025, 322, 135451. [Google Scholar] [CrossRef]
- Qiao, Z.; Wang, D.; Ni, Y.; Song, K.; Li, Y.; Wang, S. A partitioned modeling approach using a physics-informed neural network for PMSM. Eng. Anal. Bound. Elem. 2025, 179, 106379. [Google Scholar] [CrossRef]
- Son, S.; Lee, H.; Jeong, D.; Oh, K.Y.; Ho Sun, K. A novel physics-informed neural network for modeling electromagnetism of a permanent magnet synchronous motor. Adv. Eng. Inform. 2023, 57, 102035. [Google Scholar] [CrossRef]
- Wu, H.; Niu, S.; Zhang, Y.; Fu, W. Physics-Informed Generative Adversarial Network-Based Modeling and Simulation of Linear Electric Machines. Appl. Sci. 2022, 12, 10426. [Google Scholar] [CrossRef]
- Sizov, G.Y.; Yeh, C.C.; Demerdash, N.A.O. Magnetic Equivalent Circuit Modeling of Induction Machines Under Stator and Rotor Fault Conditions. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 119–124. [Google Scholar] [CrossRef]
- Naderi, P. Modified Magnetic-Equivalent-Circuit Approach for Various Faults Studying in Saturable Double-Cage-Induction Machines. IET Electr. Power Appl. 2017, 11, 1224–1234. [Google Scholar] [CrossRef]
- Hemeida, A.; Billah, M.M.; Kudelina, K.; Asad, B.; Naseer, M.U.; Guo, B.; Martin, F.; Rasilo, P.; Belahcen, A. Magnetic Equivalent Circuit and Lagrange Interpolation Function Modeling of Induction Machines Under Broken Bar Faults. IEEE Trans. Magn. 2024, 60, 8200704. [Google Scholar] [CrossRef]
- Naderi, P.; Shiri, A. Rotor/Stator Inter-Turn Short Circuit Fault Detection for Saturable Wound-Rotor Induction Machine by Modified Magnetic Equivalent Circuit Approach. IEEE Trans. Magn. 2017, 53, 8107013. [Google Scholar] [CrossRef]
- Faiz, J.; Moosavi, S.M.; Abadi, M.B.; Cruz, S.M. Magnetic Equivalent Circuit Modelling of Doubly-Fed Induction Generator with Assessment of Rotor Inter-Turn Short-Circuit Fault Indices. IET Renew. Power Gener. 2016, 10, 1431–1440. [Google Scholar] [CrossRef]
- Roshanfekr, R.; Jalilian, A. An Approach to Discriminate Between Types of Rotor and Stator Winding Faults in Wound Rotor Induction Machines. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on, Mashhad, Iran, 8–10 May 2018; pp. 1067–1070. [Google Scholar] [CrossRef]
- Faiz, J.; Ghasemi-Bijan, M.; Ebrahimi, B.M. Modeling and Diagnosing Eccentricity Fault Using Three-dimensional Magnetic Equivalent Circuit Model of Three-phase Squirrel-cage Induction Motor. Electr. Power Components Syst. 2015, 43, 1246–1256. [Google Scholar] [CrossRef]
- Han, Q.; Ding, Z.; Xu, X.; Wang, T.; Chu, F. Stator Current Model for Detecting Rolling Bearing Faults in Induction Motors Using Magnetic Equivalent Circuits. Mech. Syst. Signal Process. 2019, 131, 554–575. [Google Scholar] [CrossRef]
- Gong, Z.; Desenfans, P.; Pissoort, D.; Hallez, H.; Vanoost, D. Multiphysics Coupling Model to Characterise the Behaviour of Induction Motors With Eccentricity and Bearing Faults. IEEE Trans. Energy Convers. 2024, 39, 146–159. [Google Scholar] [CrossRef]
- Faiz, J.; Mazaheri-Tehrani, E. Demagnetization Modeling and Fault Diagnosing Techniques in Permanent Magnet Machines Under Stationary and Nonstationary Conditions: An Overview. IEEE Trans. Ind. Appl. 2017, 53, 2772–2785. [Google Scholar] [CrossRef]
- Raminosoa, T.; Farooq, J.; Djerdir, A.; Miraoui, A. Reluctance Network Modelling of Surface Permanent Magnet Motor Considering Iron Nonlinearities. Energy Convers. Manag. 2009, 50, 1356–1361. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Saied, S.; Hemmati, S.; Tenconi, A. Inverse Transform Method for Magnet Defect Diagnosis in Permanent Magnet Machines. IET Electr. Power Appl. 2014, 8, 98–107. [Google Scholar] [CrossRef]
- Farooq, J.; Srairi, S.; Djerdir, A.; Miraoui, A. Use of Permeance Network Mmethod in the Demagnetization Phenomenon Modeling in a Permanent Magnet Motor. IEEE Trans. Magn. 2006, 42, 1295–1298. [Google Scholar] [CrossRef]
- Momma, D.; Yoshida, Y.; Tajima, K. Demagnetization Analysis of Ferrite Magnet Motor Based on Reluctance Network Analysis. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–4. [Google Scholar]
- Guo, L.; Xia, C.; Wang, H.; Wang, Z.; Shi, T. Improved Equivalent Magnetic Network Modeling for Analyzing Working Points of PMs in Interior Permanent Magnet Machine. J. Magn. Magn. Mater. 2018, 454, 39–50. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Ojaghlu, P.; Takorabet, N. Irreversible Demagnetization Analysis of RWAFPM Motor Using Modified MEC Algorithm. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 1227–1239. [Google Scholar] [CrossRef]
- Paja, C.A.R.; Romero, A.; Giral, R. Evaluation of Fixed-Step Differential Equations Solution Methods for Fuel Cell Real-Time Simulation. In Proceedings of the 2007 International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; pp. 480–487. [Google Scholar] [CrossRef]
- Grégoire, L.A.; Blanchette, H.F.; Bélanger, J.; Al-Haddad, K. Real-Time Simulation-Based Multisolver Decoupling Technique for Complex Power-Electronics Circuits. IEEE Trans. Power Deliv. 2016, 31, 2313–2321. [Google Scholar] [CrossRef]
- Bouscayrol, A. Different Types of Hardware-In-the-Loop simulation for Electric Drives. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 2146–2151. [Google Scholar] [CrossRef]
- Pak, L.F.; Dinavahi, V. Real-Time Simulation of a Wind Energy System Based on the Doubly-Fed Induction Generator. IEEE Trans. Power Syst. 2009, 24, 1301–1309. [Google Scholar] [CrossRef]
- Champagne, R.; Dessaint, L.A.; Fortin-Blanchette, H.; Sybille, G. Analysis and Validation of a Real-Time AC Drive Simulator. IEEE Trans. Power Electron. 2004, 19, 336–345. [Google Scholar] [CrossRef]
- Dufour, C. A Real-Time Simulator for Doubly Fed Induction Generator based Wind Turbine Applications. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004. Technical Report. [Google Scholar]
- Abourida, S.; Dufour, C.; Belanger, J.; Yamada, T.; Arasawa, T. Hardware-In-the-Loop Simulation of Finite-Element Based Motor Drives with RT-LAB and JMAG. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 3, pp. 2462–2466. [Google Scholar] [CrossRef]
- Dufour, C.; Abourida, S.; Belanger, J. Hardware-In-the-Loop Simulation of Power Drives with RT-LAB. In Proceedings of the 2005 International Conference on Power Electronics and Drives Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; Volume 2, pp. 1646–1651. [Google Scholar] [CrossRef]
- Dufour, C.; Cense, S.; Jalili-Marandi, V.; Bélanger, J. Review of State-of-the-Art Solver Solutions for HIL Simulation of Power Systems, Power Electronic and Motor Drives. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–12. [Google Scholar] [CrossRef]
- Paquin, J.N.; Li, W.; Belanger, J.; Schoen, L.; Peres, I.; Olariu, C.; Kohmann, H. A Modern and Open Real-Time Digital Simulator of All-Electric Ships with a Multi-Platform Co-Simulation Approach. In Proceedings of the 2009 IEEE Electric Ship Technologies Symposium, Baltimore, MD, USA, 20–22 April 2009; pp. 28–35. [Google Scholar] [CrossRef]
- Faruque, M.O.; Dinavahi, V. An Advanced PC-Cluster Based Real-Time Simulator for Power Electronics and Drives. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 3, pp. 2579–2584. [Google Scholar] [CrossRef]
- Pak, L.F.; Faruque, M.O.; Nie, X.; Dinavahi, V. A Versatile Cluster-Based Real-Time Digital Simulator for Power Engineering Research. IEEE Trans. Power Syst. 2006, 21, 455–465. [Google Scholar] [CrossRef]
- Larose, C.; Guerette, S.; Guay, F.; Nolet, A.; Yamamoto, T.; Enomoto, H.; Kono, Y.; Hasegawa, Y.; Taoka, H. A fully digital real-time power system simulator based on PC-cluster. Math. Comput. Simul. 2003, 63, 151–159. [Google Scholar] [CrossRef]
- Chen, H.; Sun, S.; Aliprantis, D.C.; Zambreno, J. Dynamic Simulation of Electric Machines on FPGA Boards. In Proceedings of the 2009 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 3–6 May 2009; pp. 1523–1528. [Google Scholar] [CrossRef]
- Ponce, P.; Ibarra, L.; Molina, A.; MacCleery, B. Real Time Simulation for DC and AC Motors Based on Lab VIEW FPGAs. In Proceedings of the IFAC Proceedings Volumes (IFAC-PapersOnline). IFAC Secretariat, Bucharest, Romania, 23–25 May 2012; Volume 14, pp. 1777–1784. [Google Scholar] [CrossRef]
- Jandaghi, B.; Dinavahi, V. Hardware-in-the-Loop Emulation of Linear Induction Motor Drive for MagLev Application. IEEE Trans. Plasma Sci. 2016, 44, 679–686. [Google Scholar] [CrossRef]
- Schmitt, A.; Richter, J.; Jurkewitz, U.; Braun, M. FPGA-based Real-Time Simulation of Nonlinear Permanent Magnet Synchronous Machines for Power Hardware-in-the-Loop Emulation Systems. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3763–3769. [Google Scholar] [CrossRef]
- Dufour, C.; Belanger, J.; Abourida, S.; Lapointe, V. FPGA-Based Real-Time Simulation of Finite-Element Analysis Permanent Magnet Synchronous Machine Drives. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 909–915. [Google Scholar] [CrossRef]
- Parma, G.G.; Dinavahi, V. Real-Time Digital Hardware Simulation of Power Electronics and Drives. IEEE Trans. Power Deliv. 2007, 22, 1235–1246. [Google Scholar] [CrossRef]
- Kredo, K.; Zenor, J.; Bednar, R.; Crosbie, R. FPGA-Accelerated Simulink Simulations of Electrical Machines. In Proceedings of the 2015 IEEE Electric Ship Technologies Symposium (ESTS), Old Town Alexandria, VA, USA, 21–24 June 2015; pp. 74–79. [Google Scholar] [CrossRef]
- Rajne, P.A.; Ramanarayanan, V. Programming an FPGA to Emulate the Dynamics of DC Machines. In Proceedings of the 2006 India International Conference on Power Electronics, Chennai, India, 19–21 December 2006; pp. 120–124. [Google Scholar] [CrossRef]
- Herrera, L.; Li, C.; Yao, X.; Wang, J. FPGA-Based Detailed Real-Time Simulation of Power Converters and Electric Machines for EV HIL Applications. IEEE Trans. Ind. Appl. 2015, 51, 1702–1712. [Google Scholar] [CrossRef]
- O’Connell, T.C.; Krein, P.T.; Yilmaz, M.; Friedl, A. On the Feasibility of Using Large-Scale Numerical Electric Machine Field Analysis Software in Complex Electric Drive System Design Tools. In Proceedings of the 2008 11th Workshop on Control and Modeling for Power Electronics, Zurich, Switzerland, 17–20 August 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Adzima, A.J.; Krein, P.T.; O’Connell, T.C. Investigation of Accelerating Numerical-Field Analysis Methods for Electric Machines with the Incorporation of Graphic-Processor Based Parallel Processing Techniques. In Proceedings of the 2009 IEEE Electric Ship Technologies Symposium, Baltimore, MD, USA, 20–22 April 2009; pp. 59–64. [Google Scholar] [CrossRef]
- Rodrigues, A.W.O.; Guyomarc’h, F.; Dekeyser, J.L.; Le Menach, Y. Automatic Multi-GPU Code Generation Applied to Simulation of Electrical Machines. IEEE Trans. Magn. 2012, 48, 831–834. [Google Scholar] [CrossRef][Green Version]
- Rodrigues, A.W.D.O.; Chevallier, L.; Menach, Y.L.; Guyomarch, F. Test harness on a preconditioned conjugate gradient solver on GPUs: An efficiency analysis. IEEE Trans. Magn. 2013, 49, 1729–1732. [Google Scholar] [CrossRef][Green Version]
- Liu, Z.H.; Li, X.H.; Wu, L.H.; Zhou, S.W.; Liu, K. GPU-Accelerated Parallel Coevolutionary Algorithm for Parameters Identification and Temperature Monitoring in Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Inform. 2015, 11, 1220–1230. [Google Scholar] [CrossRef]
- Bracikowski, N.; Hecquet, M.; Brochet, P.; Shirinskii, S.V. Multiphysics Modeling of a Permanent Magnet Synchronous Machine by Using Lumped Models. IEEE Trans. Ind. Electron. 2012, 59, 2426–2437. [Google Scholar] [CrossRef]
- Fasquelle, A. Coupled Electromagnetic, Acoustic and Thermal-Flow Modelling of an Induction Motor of Railway Traction. Ph.D. Thesis, Ecole Centrale de Lille, Villeneuve-d’Ascq, France, 2007. [Google Scholar]
- Tao, F.; Zhang, M.; Liu, Y.; Nee, A. Digital Twin Driven Prognostics and Health Management for Complex Equipment. CIRP Ann. 2018, 67, 169–172. [Google Scholar] [CrossRef]
- Lagaris, I.; Likas, A.; Fotiadis, D. Artificial Neural Networks for Solving Ordinary and Partial Differential Equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef]
- Wu, D.; Chamoin, L.; Lisser, A. Solving Large-scale Variational Inequalities with Dynamically Adjusting Initial Condition in Physics-informed Neural Networks. Comput. Methods Appl. Mech. Eng. 2024, 429, 117156. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).