Substantiation of a Rational Model of an Induction Motor in a Predictive Energy-Efficient Control System
Abstract
1. Introduction
- Optimization of energy consumption;
- Integration of digitalization and intellectualization methods and tools;
- Increasing the share of renewable energy sources;
- Reducing the negative impact on the environment;
- Reduction in weight and dimensions;
- Increasing adaptability and modularity.
2. Materials and Methods
3. Results and Discussion
4. The Significance of the Research Findings for Operational and Strategic Management in Industry
5. Conclusions
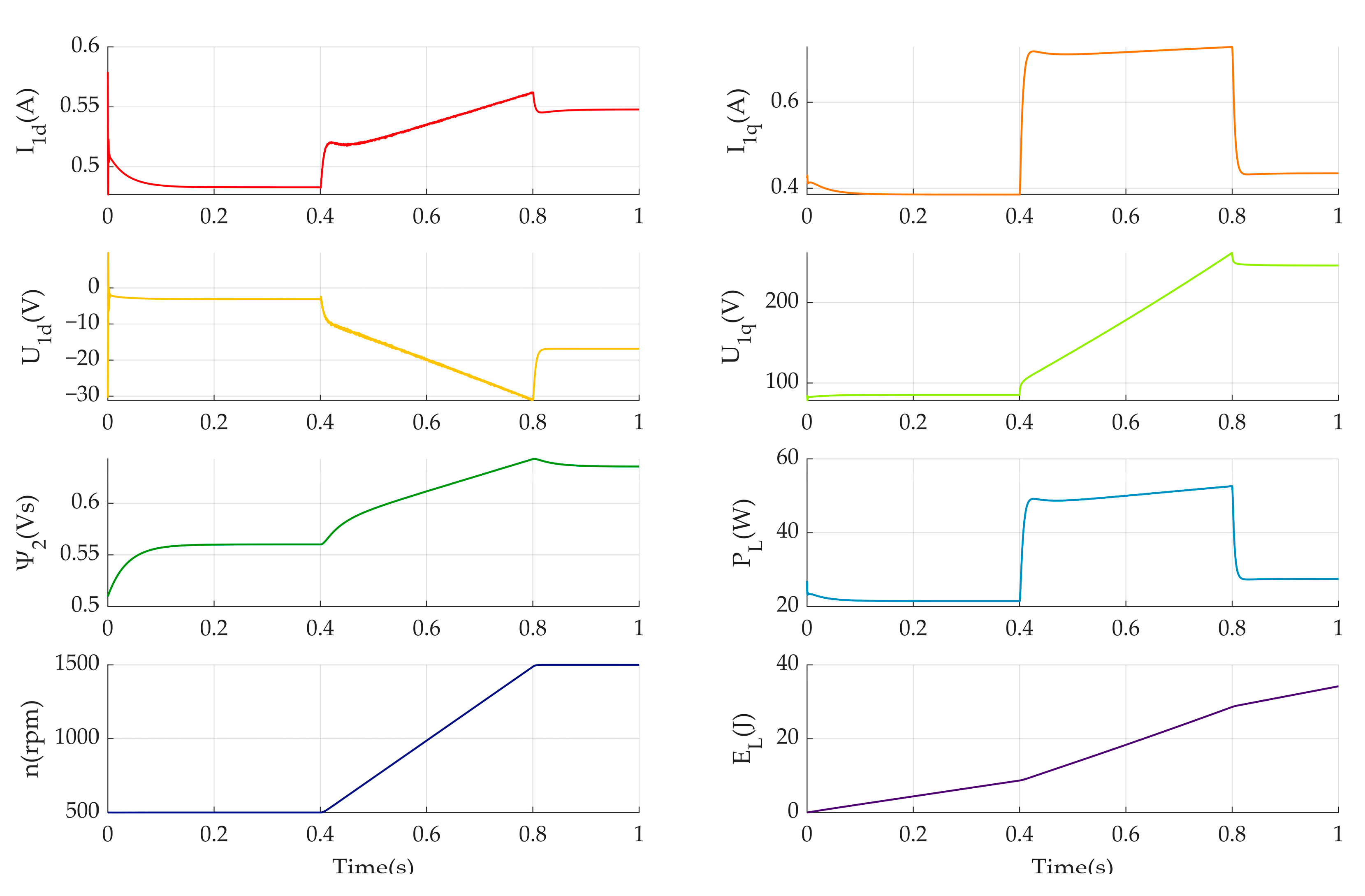
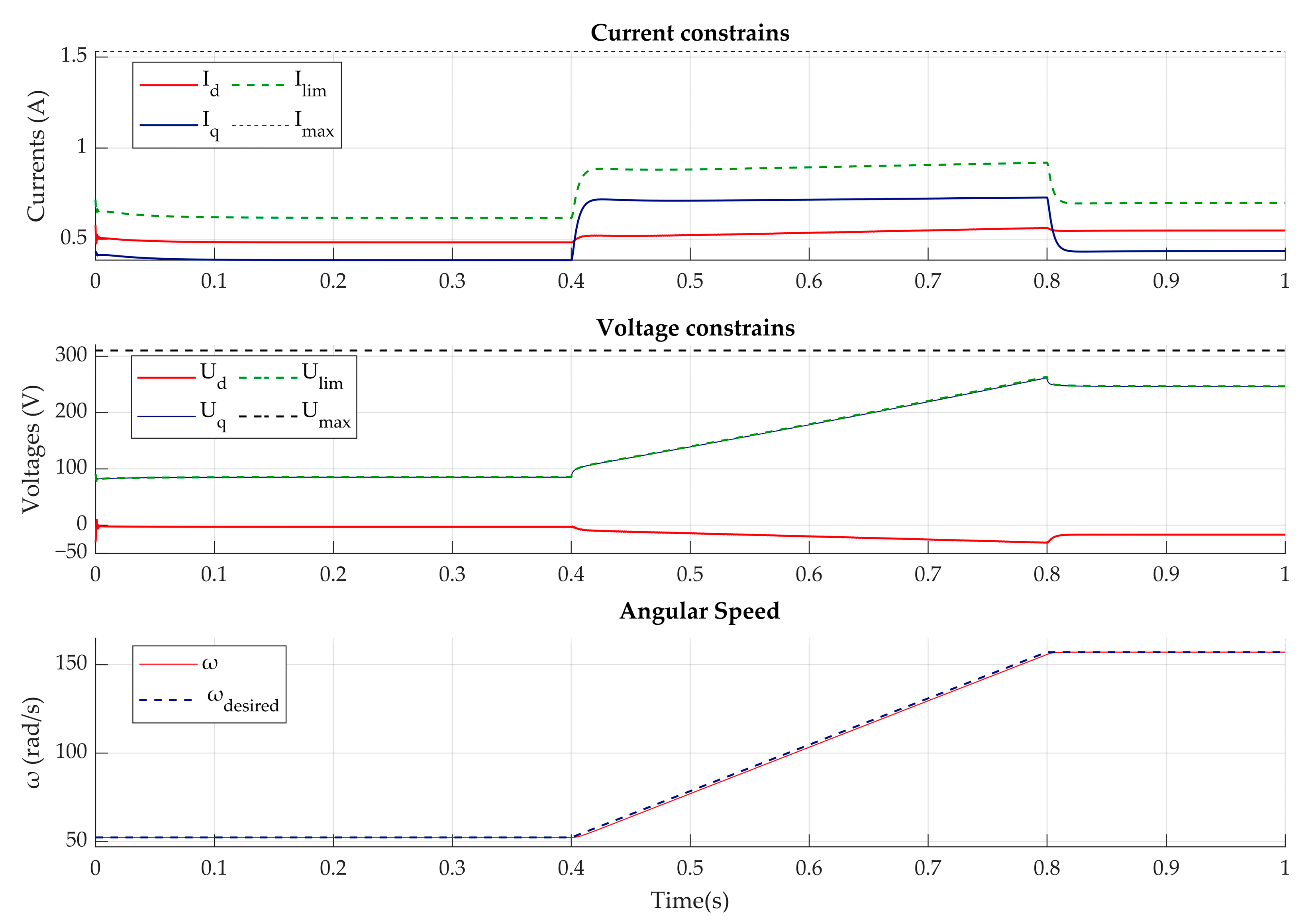
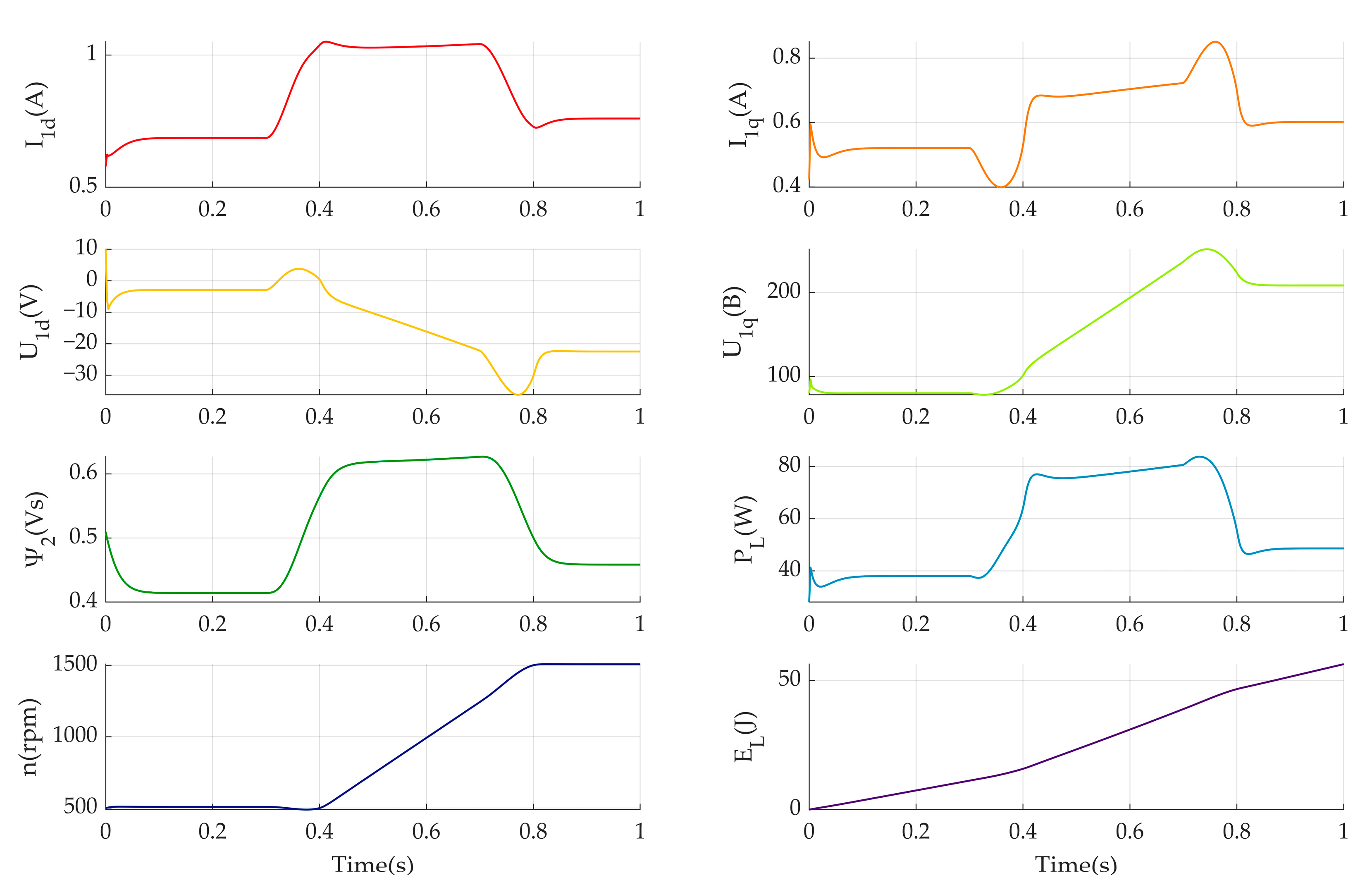
- Three approaches to the implementation of predictive control models based on GRAMPC, fmincon, and the MPC Toolbox have been investigated. This enabled the examination of how the level of detail in induction motor models affects the efficiency of their control.
- The models were simulated in MATLAB, and the relationships between electric energy consumption indicators and the accuracy of maintaining motor speed were established in terms of their impact on the overall energy efficiency of electric drives under dynamic operating conditions. This makes it possible to optimize control strategies.
- Based on the results of computer experiments using predictive methods (GRAMPC, fmincon, and the MPC Toolbox) in MATLAB (v 24.1) and Simulink, it has been determined that under dynamic operating conditions, the most suitable model for controlling induction motors is an equivalent circuit with the parameters , and . This allows for improved control approaches for induction motors.
- Promising directions for further research have been substantiated. These include, on the one hand, unifying the representation of processes across various electric machines with a rotating magnetic field to support the development of standardized energy-efficient control methods, and on the other hand, enhancing the functionality of the GRAMPC algorithm to accommodate complex, time-varying trajectories of desired speed/load torque in real-time optimization of the cost function.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farrag, M.; Lai, C.S.; Darwish, M.; Taylor, G. Improving the efficiency of electric vehicles: Advancements in hybrid energy storage systems. Vehicles 2024, 6, 1089–1113. [Google Scholar] [CrossRef]
- Urbanski, K.; Janiszewski, D. Improving the dynamics of an electrical drive using a modified controller structure accompanied by delayed inputs. Appl. Sci. 2024, 14, 10126. [Google Scholar] [CrossRef]
- Ali, Q.; Di Silvestre, M.L.; Lombardi, P.A.; Riva Sanseverino, E.; Zizzo, G. Electrifying the road to net-zero: Implications of electric vehicles and carbon emission coefficient factors in European power systems. Sustainability 2024, 16, 5084. [Google Scholar] [CrossRef]
- Nazari, Z.; Musilek, P. Impact of digital transformation on the energy sector: A review. Algorithms 2023, 16, 211. [Google Scholar] [CrossRef]
- Rjabtšikov, V.; Rassõlkin, A.; Kudelina, K.; Kallaste, A.; Vaimann, T. Review of electric vehicle testing procedures for digital twin development: A comprehensive analysis. Energies 2023, 16, 6952. [Google Scholar] [CrossRef]
- Papaika, Y.u.A.; Lysenko, O.G.; Rodna, K.S.; Shevtsova, O.S. Information technologies in modeling operation modes of mining dewatering plant based on economic and mathematical analysis. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2020, 4, 82–87. [Google Scholar] [CrossRef]
- Beshta, A.; Balakhontsev, A.; Khudolii, S. Performances of asynchronous motor within variable frequency drive with additional power source plugged via combined converter. In Proceedings of the 2019 IEEE 6th International Conference on Energy Smart Systems (ESS), Kyiv, Ukraine, 17–19 April 2019; pp. 156–160. [Google Scholar] [CrossRef]
- Syrotkina, O.; Kobti, Z.; Aleksieiev, M.; Moroz, B.; Udovyk, I.; Diachenko, G. Mathematical model and method for diagnosing the operability of information and control systems. In Proceedings of the 2022 12th International Conference on Advanced Computer Information Technologies (ACIT), Ruzomberok, Slovakia, 26–28 September 2022; pp. 49–52. [Google Scholar] [CrossRef]
- Nazarova, O.; Osadchyy, V.; Hutsol, T.; Glowacki Sz Nurek, T.; Hulevskyi, V.; Horetska, I. Mechatronic automatic control system of electropneumatic manipulator. Sci. Rep. 2024, 14, 6970. [Google Scholar] [CrossRef]
- May, G.; Stahl, B.; Taisch, M.; Kiritsis, D. Energy management in manufacturing: From literature review to a conceptual framework. J. Clean. Prod. 2017, 167, 1464–1489. [Google Scholar] [CrossRef]
- Vladyko, O.; Maltsev, D.; Gliwiński, Ł.; Dychkovskyi, R.; Stecuła, K.; Dyczko, A. Enhancing mining enterprise energy resource extraction efficiency through technology synthesis and performance indicator development. Energies 2025, 18, 1641. [Google Scholar] [CrossRef]
- Seheda, M.S.; Beshta, O.S.; Gogolyuk, P.F.; Blyznak, Y.u.V.; Dychkovskyi, R.D.; Smoliński, A. Mathematical model for the management of the wave processes in three-winding transformers with consideration of the main magnetic flux in mining industry. J. Sustain. Min. 2024, 23, 20–39. [Google Scholar] [CrossRef]
- Miroshnykov, I.; Cichoń, D.; Shyrin, L.; Dybrin, S.; Dychkovskyi, R. Ensuring the environmental sustainability of molybdenum ore mining. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: London, UK, 2025; Volume 1457, p. 012014. [Google Scholar] [CrossRef]
- Pazynich, Y.; Kolb, A.; Korcyl, A.; Buketov, V.; Petinova, O. Mathematical model and characteristics of dynamic modes for managing the asynchronous motors at voltage asymmetry. Polityka Energetyczna—Energy Policy J. 2024, 27, 39–58. [Google Scholar] [CrossRef]
- Nikolsky, V.; Dychkovskyi, R.; Cabana, E.C.; Howaniec, N.; Jura, B.; Widera, K.; Smoliński, A. The hydrodynamics of translational–rotational motion of incompressible gas flow within the working space of a vortex heat generator. Energies 2022, 15, 1431. [Google Scholar] [CrossRef]
- Kolb, A.; Pazynich, Y.; Mirek, A.; Petinova, O. Influence of voltage reserve on the parameters of parallel power active compensators in mining. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2020; Volume 201, p. 01024. [Google Scholar] [CrossRef]
- Beshta, O.S.; Beshta, O.O.; Khudolii, S.S.; Khalaimov, T.O.; Fedoreiko, V.S. Electric vehicle energy consumption taking into account the route topology. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2024, 2, 104–112. [Google Scholar] [CrossRef]
- Dychkovskyi, R.; Dyczko, A.; Borojević Šoštarić, S. Foreword: Physical and chemical geotechnologies—Innovations in mining and energy. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2024; Volume 567, p. 00001. [Google Scholar] [CrossRef]
- Magdziarczyk, M.; Chmiela, A.; Dychkovskyi, R.; Smoliński, A. The cost reduction analysis of green hydrogen production from coal mine underground water for circular economy. Energies 2024, 17, 2289. [Google Scholar] [CrossRef]
- Fedoreiko, V.; Zahorodnii, R.; Lutsyk, I.; Rutylo, M.; Bureha, N. Modelling of resource-saving control modes of a bioheat generator using neuro-fuzzy controllers. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: London, UK, 2025; Volume 1457, p. 012005. [Google Scholar] [CrossRef]
- Beshta, A.; Aziukovskyi, O.; Balakhontsev, A.; Shestakov, A. Combined power electronic converter for simultaneous operation of several renewable energy sources. In Proceedings of the International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 15–17 November 2017; pp. 236–239. [Google Scholar] [CrossRef]
- Roy, S.; Pandey, R. A review on motor and drive system for electric vehicle. In Planning of Hybrid Renewable Energy Systems, Electric Vehicles and Microgrid. Energy Systems in Electrical Engineering; Bohre, A.K., Chaturvedi, P., Kolhe, M.L., Singh, S.N., Eds.; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Pivniak, H.; Aziukovskyi, O.; Papaika Yu Lutsenko, I.; Neuberger, N. Problems of development of innovative power supply systems of Ukraine in the context of European integration. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2022, 5, 89–103. [Google Scholar] [CrossRef]
- Osadchyy, V.; Nazarova, O.; Hutsol, T.; Glowacki, S.; Mudryk, K.; Bryś, A.; Rud, A.; Tulej, W.; Sojak, M. Adjustable vibration exciter based on unbalanced motors. Sensors 2023, 23, 2170. [Google Scholar] [CrossRef]
- Pivnyak, G.; Olishevska, V.; Olishevskiy, H.; Lutsenko, I.; Lysenko, A.; Sala, D. Comprehensive study on electric vehicles and infrastructure for sustainable development in Ukraine. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2024; Volume 567, p. 01025. [Google Scholar] [CrossRef]
- Statista. Estimated Number of Electric Vehicles in Use Worldwide Between 2016 and 2023, by Type. 2023. Available online: https://www.statista.com/statistics/1101415/number-of-electric-vehicles-by-type/#statisticContainer (accessed on 20 August 2025).
- Lukassek, M.; Dahlmann, J.; Völz, A.; Graichen, K. Model predictive path-following control for truck–trailer systems with specific guidance points—Design and experimental validation. Mechatronics 2024, 100, 103190. [Google Scholar] [CrossRef]
- Windisch, T.; Hofmann, W. A novel approach to MTPA tracking control of AC drives in vehicle propulsion systems. IEEE Trans. Veh. Technol. 2018, 67, 9294–9302. [Google Scholar] [CrossRef]
- Diachenko, G.G.; Aziukovskyi, O.O. Review of methods for energy-efficiency improvement in induction machines. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2020, 1, 80–88. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ali, J.A.; Mohamed, A.; Hussain, A. Optimization techniques to enhance the performance of induction motor drives: A review. Renew. Sustain. Energy Rev. 2017, 81, 1611–1626. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Jena, R.K. Loss model based controller of fuzzy DTC driven induction motor for electric vehicles using optimal stator flux. e-Prime—Adv. Electr. Eng. Electron. Energy 2023, 6, 100304. [Google Scholar] [CrossRef]
- Beshta, O.S.; Fedoreiko, V.S.; Balakhontsev, O.V.; Khudolii, S.S. Dependence of electric drive’s thermal state on its operation mode. Nauk. Visnyk Natsionalnoho Hirnychoho Universytetu 2013, 6, 67–72. Available online: https://nvngu.in.ua/index.php/en/component/jdownloads/finish/44-06/714-2013-6-beshta/0 (accessed on 20 August 2025).
- Winter, M.; Schullerus, G. Analysis of the influence of modelling accuracy on the energy efficiency optimization of induction machines. In Proceedings of the Electromechanical Drive Systems; ETG Symposium, Online, 9–10 November 2021; pp. 1–7. Available online: https://ieeexplore.ieee.org/document/9735207 (accessed on 20 August 2025).
- Shykhov, S.K.; Schullerus, G.; Winter, M. Rational model of the motor in the forecasting control system of dynamic efficiency of the asynchronous drive. In Proceedings of the 4th International Scientific and Technical Internet Conference “Innovative Development of Resource-Saving Technologies and Sustainable Use of Natural Resources”, Petroșani, Romania, 12 November 2021; pp. 52–53. Available online: http://ds.knu.edu.ua:8080/jspui/bitstream/123456789/4139/1/Innovative%20development%20of%20resource-saving%20yechnologies%20and%20sustainable%20use%20of%20natural%20resources.pdf (accessed on 20 August 2025).
- GRAMPC Project Team. GRAMPC Documentation Version 2.2. 2019. Available online: https://sourceforge.net/p/grampc/blog/2019/10/grampc-v22/ (accessed on 20 August 2025).
- Auchterlonie, L.J.; Fletcher, P.N. Results Which Provide Detailed Insight into Microwavescattering Properties of Melting Spongy Hail. Electron. Lett. 1995, 31, 1756–1757. [Google Scholar] [CrossRef]
- Sevier, J.; Minturn, D.; Bernard, D.; Pollard, T. The effect of computational time-delays on pilot performance in real-time flight simulation. In Proceedings of the 4th 22-nd Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1984; pp. 1–87. [Google Scholar] [CrossRef]
- Blinov, I.; Radziukynas, V.; Shymaniuk, P.; Dyczko, A.; Stecuła, K.; Sychova, V.; Miroshnyk, V.; Dychkovskyi, R. Smart Management of Energy Losses in Distribution Networks Using Deep Neural Networks. Energies 2025, 18, 3156. [Google Scholar] [CrossRef]
- Bashynska, I.; Niekrasova, L.; Ivliev, D.; Dudek, M.; Kosenkov, V.; Yakimets, A. Justification for Transitioning Equipment to Direct Current for Smart Small Enterprises with Sustainable Solar Power Autonomy. In Proceedings of the 2024 IEEE 5th KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 7–11 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Barada Mohanty, D.K. Transient stability analysis of induction motor drive using nonlinear model. Futur. Trends Electr. Eng. 2024, 3, 192–204. [Google Scholar] [CrossRef]
- Shcherba, A.; Vinnychenko, D.; Suprunovska, N.; Roziskulov, S.; Dyczko, A.; Dychkovskyi, R. Management of Mobile Resonant Electrical Systems for High-Voltage Generation in Non-Destructive Diagnostics of Power Equipment Insulation. Electronics 2025, 14, 2923. [Google Scholar] [CrossRef]
- Bashynska, I. Ethical aspects of AI use in the circular economy. AI Soc. 2025, 1–9. [Google Scholar] [CrossRef]
- MathWorks Specify Prediction Model for Nonlinear, Model Predictive Control. Available online: https://www.mathworks.com/help/mpc/ug/specify-prediction-model-for-nonlinear-mpc.html (accessed on 20 August 2025).
- MathWorks. Fmincon Options. Available online: https://www.mathworks.com/help/optim/ug/fmincon.html#busog7r-options (accessed on 20 August 2025).
- Polyanska, A.; Pazynich, Y.; Petinova, O.; Nesterova, O.; Mykytiuk, N.; Bodnar, G. Formation of a culture of frugal energy consumption in the context of social security. J. Int. Comm. Hist. Technol. 2024, 29, 60–87. [Google Scholar] [CrossRef]
- Farhani, F.; Zaafouri, A.; Chaari, A. Real time induction motor efficiency optimization. J. Frankl. Inst. 2017, 354, 3289–3304. [Google Scholar] [CrossRef]
- Weis, R.; Gensior, A. A model-based loss-reduction scheme for transient operation of induction machines. In Proceedings of the 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Yu, J.; Pei, W.; Zhang, C. A loss-minimization port-controlled Hamilton scheme of induction motor for electric vehicles. IEEE/ASME Trans. Mechatron. 2015, 20, 2645–2653. [Google Scholar] [CrossRef]
- Dominic, A.; Schullerus, G.; Winter, M. Dynamic energy efficient control of induction machines using anticipative flux templates. Appl. Sci. 2021, 11, 2878. [Google Scholar] [CrossRef]


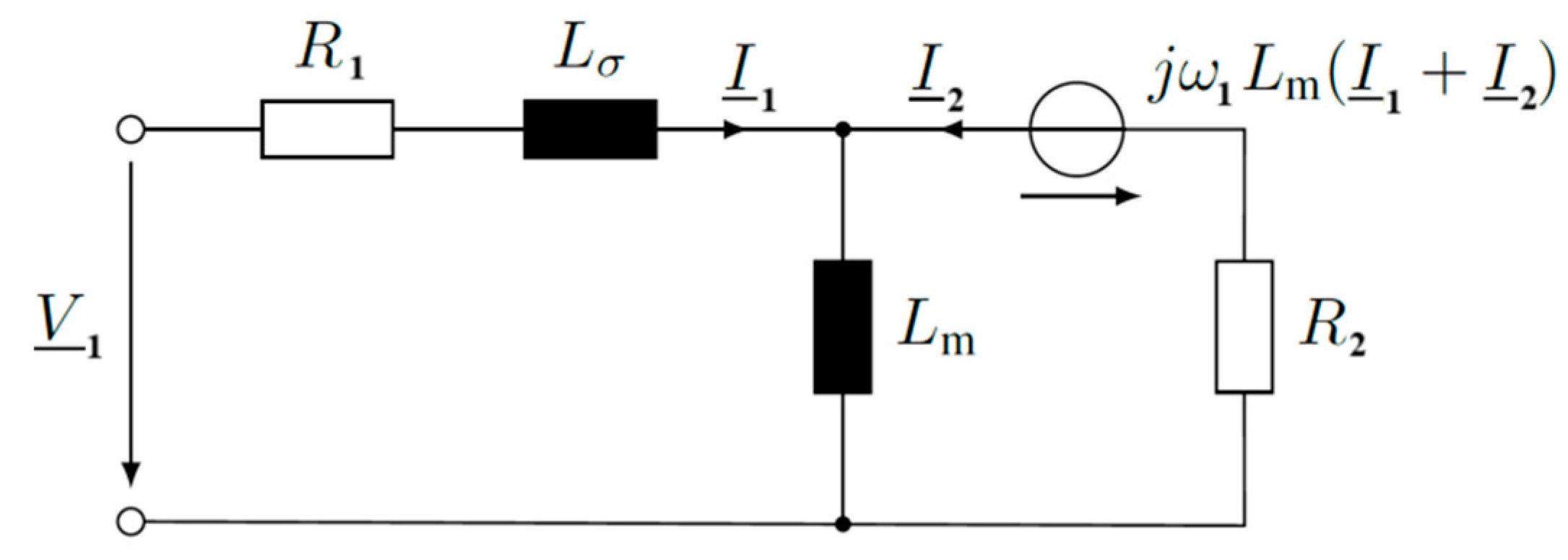


| PN | 370 W | TN | 2.59 Nm |
| Zp | 2 | JM | 22·10−4 kg·m2 |
| nN | 1370 rpm | ||
| R1 | 27.8 Ω | Lσ | 0.6 H |
| R2 | 17.24 Ω | Lμ | 0.142 H |
| RFe | 2300 Ω | tR | 35 ms |
| ωRm,1 | 52.4 rad/s ≅ 500 rpm | ωRm,2 | 157 rad/s ≅ 1500 rpm |
| TL | 0.64 Nm |
| Model Type | Level of Detail | Elapsed Time, s | Control Accuracy (rad/s) |
|---|---|---|---|
| I | 44.12 | 0.15 | |
| II | 24.71 | 0.22 | |
| III | 25.56 | 0.25 | |
| IV | 27.68 | 0.20 | |
| V | 26.86 | 0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diachenko, G.; Laktionov, I.; Sala, D.; Pyzalski, M.; Balakhontsev, O.; Pazynich, Y. Substantiation of a Rational Model of an Induction Motor in a Predictive Energy-Efficient Control System. Energies 2025, 18, 4628. https://doi.org/10.3390/en18174628
Diachenko G, Laktionov I, Sala D, Pyzalski M, Balakhontsev O, Pazynich Y. Substantiation of a Rational Model of an Induction Motor in a Predictive Energy-Efficient Control System. Energies. 2025; 18(17):4628. https://doi.org/10.3390/en18174628
Chicago/Turabian StyleDiachenko, Grygorii, Ivan Laktionov, Dariusz Sala, Michał Pyzalski, Oleksandr Balakhontsev, and Yuliya Pazynich. 2025. "Substantiation of a Rational Model of an Induction Motor in a Predictive Energy-Efficient Control System" Energies 18, no. 17: 4628. https://doi.org/10.3390/en18174628
APA StyleDiachenko, G., Laktionov, I., Sala, D., Pyzalski, M., Balakhontsev, O., & Pazynich, Y. (2025). Substantiation of a Rational Model of an Induction Motor in a Predictive Energy-Efficient Control System. Energies, 18(17), 4628. https://doi.org/10.3390/en18174628








