1. Introduction
1.1. Aim and Background
Wireless Smart Concentrators (WSCs) are designed to aggregate and transmit data from numerous smart meters and Internet of Things (IoT) devices within a localized area to central utility servers. These devices enhance operational efficiency by facilitating accurate data collection, supporting demand response programs, and reducing the need for manual meter readings. In recent years, distribution utilities have focused on optimizing the allocation of WSCs in low-voltage (LV) distribution systems to achieve technical and economic benefits [
1,
2].
For these utilities, optimizing WSCs allocation is a technical challenge and a critical component of strategic planning [
3]. The effective allocation of WSCs ensures that utilities can meet the growing demand for connectivity from consumers, who increasingly rely on smart technologies for energy management and other services [
4]. Data recorded in WSCs can help utilities enhance service quality, reduce operational costs, and improve customer satisfaction.
The growing complexity of urban environments introduces significant challenges to the effective allocation of WSCs. Physical obstacles such as buildings, trees, and varying topographies can degrade signal strength and coverage, leading to uncertainties in wireless communication [
5]. These effects are further exacerbated in densely built areas or regions with heterogeneous spatial characteristics, requiring more sophisticated planning methods.
The optimal allocation of WSCs is carried out in this paper through a Variable Neighborhood Search (VNS) algorithm. This technique offers a dynamic search mechanism with few parameters, making it suitable for complex, spatially variable environments [
6,
7]. Thus, this work aims to demonstrate the advantages of a VNS-based model that optimizes WSC positioning, incorporating realistic communication constraints, such as nonlinear signal attenuation and interference, which vary with urban density.
1.2. Literature Review and Research Gap
The optimal allocation of WSCs in distribution networks has received significant attention in recent years. Traditional approaches based on Mixed-Integer Linear Programming (MILP) provide globally optimal solutions under convexity assumptions and fixed-distance parameters [
1,
3]. However, these models often assume idealized communication conditions and uniform environments, disregarding critical factors such as signal attenuation caused by urban structures, shadowing from vegetation, and variability in building density, especially in vertically growing cities [
8,
9].
To address these limitations, metaheuristic techniques have been adopted due to their robustness in large-scale and combinatorially complex problems. Notably, Particle Swarm Optimization (PSO) and Genetic Algorithms (GAs) have demonstrated potential for WSC and related infrastructure optimization tasks [
10,
11]. These population-based algorithms are particularly effective in high-dimensional spaces, but their performance can degrade in environments with abrupt spatial changes or non-uniform coverage requirements. Furthermore, they often require extensive parameter calibration and may converge slowly when confronted with heterogeneous urban scenarios.
Recent literature surveys [
12,
13] emphasize the need for adaptable and spatially aware algorithms that can respond to dynamic urban features and topological discontinuities. In this context, non-population-based methods, such as Variable Neighborhood Search (VNS), emerge as promising alternatives. VNS systematically explores neighborhoods with increasing distance from the current solution, making it well-suited for discrete optimization problems with complex landscapes and shifting constraints [
6].
Despite these advantages, VNS remains underutilized in the context of communication infrastructure planning, particularly for WSC allocation in urban environments. Recent works have begun to explore its potential in infrastructure-related applications with spatial constraints [
7,
14], but its application to communication networks with nonlinear wireless propagation constraints remains limited.
Moreover, a substantial portion of existing models in the specialized literature simplifies environmental conditions by neglecting nonlinear constraints such as multipath effects, shadowing, and signal fading—critical phenomena in areas with dense building concentrations or vegetation [
8,
9]. These oversimplifications diminish the practical relevance of many prior solutions, particularly in vertically developed urban areas.
From an optimization modeling perspective, the allocation problem becomes a Mixed-Integer Nonlinear Programming (MINLP) formulation when spatially variable propagation coefficients are considered. Such formulations are inherently non-convex and particularly challenging to solve with exact mathematical programming solvers. As highlighted in [
15,
16], non-convex multimodal problems are more effectively addressed by metaheuristic techniques, since commercial solvers often fail to identify globally optimal solutions within reasonable computational times due to the combinatorial explosion of the solution space, the abundance of local optima, and the complexity of nonlinear constraint sets. This difficulty persists even with modern solvers, which frequently demand prohibitively long runtimes without guaranteeing global optimality.
In response to this gap, our study introduces a VNS-based optimization algorithm that explicitly accounts for nonlinear wireless communication constraints, using spatially varying wireless propagation coefficients derived from building density and afforestation levels. This formulation enables more realistic modeling of communication coverage in dense urban areas and supports early-stage planning efforts involving utility companies, urban planners, and technology providers [
17,
18]. By identifying and addressing these methodological limitations, the proposed approach advances the literature on WSC allocation and contributes a scalable, adaptable, and spatially sensitive methodology aligned with the goals of sustainable smart city development [
19].
1.3. Contributions and Paper Organization
The findings of this work provide practical and valuable insights for utility professionals, researchers, and engineers involved in allocating WSCs in low-voltage (LV) distribution networks, particularly in the context of promoting sustainable urban development. The main contributions of this paper are outlined as follows:
- 1.
A VNS algorithm is introduced to minimize investment costs associated with predefined communication technologies. High-level parameters—such as coverage radius—are leveraged to identify optimal solutions, avoiding the need for detailed and computationally demanding modeling of communication channels. As a result, the process is simplified, the computational burden is reduced, and applicability across diverse urban scenarios is ensured.
- 2.
A framework is proposed for WSC allocation that accounts for realistic signal propagation in heterogeneous urban environments, considering factors such as vertical growth and varying building or vegetation densities. The VNS algorithm is employed to ensure efficient and reliable coverage, addressing challenges posed by non-uniform urban layouts.
- 3.
The proposed VNS-based algorithm adapts to varying urban densities by allowing the selection between MILP and MINLP formulations for WSC allocation, depending on the desired modeling detail. Both simplified coverage matrices and detailed propagation-aware constraints are supported, enabling cost and signal quality comparisons across diverse urban settings.
The proposed VNS algorithm is compared with three metaheuristic techniques—namely, Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Tabu Search (TS)—as well as with exact methods, yielding optimal results in shorter computation times.
This paper is organized as follows:
Section 2 introduces the problem of allocating WSC in LV distribution networks.
Section 3 presents the mathematical formulation and the optimization methods employed.
Section 4 presents the implementation of the VNS-based WSC allocation method.
Section 5 presents the results obtained by the proposed VNS algorithm, comparing its performance with GA, PSO, and TS.
Section 6 compares deterministic and metaheuristic approaches to solving the MINLP formulation. Finally,
Section 7 presents the conclusions and outlines future research directions.
2. The WSC Allocation Problem Description
Distribution utilities seek to integrate communication technologies into their systems to enhance distribution network management and provide high-quality service [
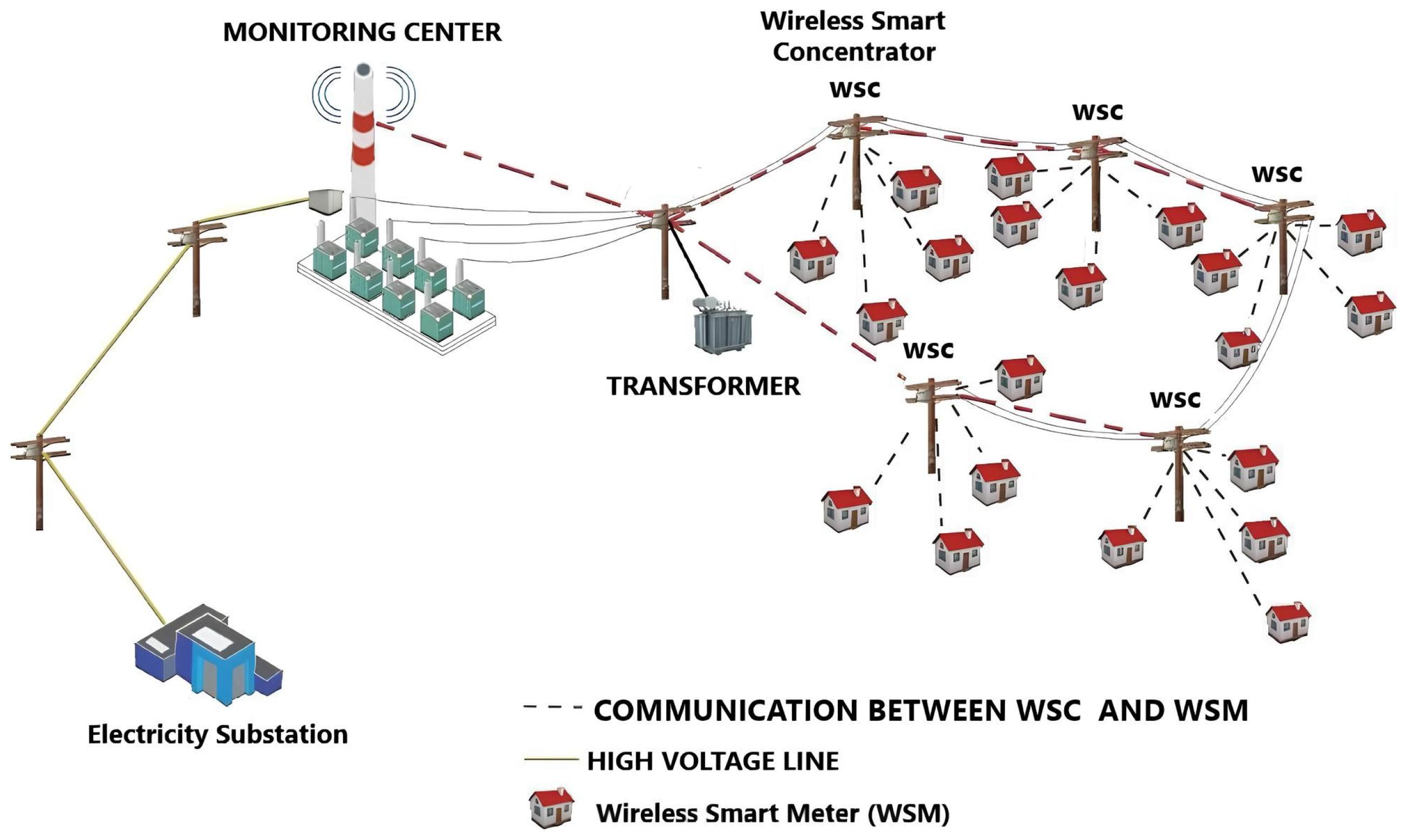
20]. Thus, the advanced metering infrastructure (AMI) with wireless smart meters (WSMs), Wireless Smart Concentrators (WSCs), and a control center facilitates automatic reading and bidirectional communication installed by distribution utilities, as illustrated in
Figure 1. AMI collects and transfers energy consumption data for analysis and decision-making at the utility’s control center [
21,
22].
In this scenario, it is essential to ensure the reliable transmission of information to maintain communication between the WSC and the WSM [
23]. Thus, when selecting sites for installing WSCs in the LV distribution network, it is crucial to consider the limitations of communications technologies regarding the maximum distance between each WSC and WSM, which is the coverage radius of the WSC in the installed location. The coverage radius is calculated based on factors such as the radio frequency power received to maintain communication between the WSC and the WSM of wireless technology as indicated in Equation (
1). In this case, the received power
guarantees communication between a WSC of type
a allocated at node
i and a WSM of type
a installed at location
j, and the distance
between these devices.
and
are, respectively, the transmit power and antenna gain of the WSM of type
a installed at location
j and
is the antenna gain of the WSC of type
a allocated at location
i.
is the propagation coefficient of the region between node
i and location
j, which represents the obstacles that can attenuate the communication signal between the WSC and the WSM, such as large vertical buildings.
is the wavelength of the transmitted wireless signal.
Nonlinear equations that describe signal propagation—particularly those grounded in real-world communication environments—can lead to highly complex and non-convex optimization problems. Implementing such models requires advanced computational techniques, making it difficult for practitioners to integrate these constraints into optimization frameworks. These challenges highlight the trade-off between the accuracy of nonlinear models and their practical feasibility [
24,
25,
26].
Communication technologies often exhibit highly nonlinear behaviors that result in complex constraints, such as Equation (
1) in this work. These constraints can lead to non-convex optimization spaces, making it difficult to achieve a global solution. This issue has been extensively discussed in the literature on smart grid communications, which often highlights the complexity of non-convex spaces and the challenges of modeling nonlinear behaviors [
27]. Moreover, the nature of these constraints can vary depending on the specific technology employed and the environmental factors affecting its performance. This variability complicates the design of a universal optimization approach, necessitating adaptable and computationally efficient methods [
28,
29]. To address these limitations, this work proposes two distinct formulations for the WSC allocation problem. The first one is a MILP model that uses a binary coverage matrix and assumes fixed distances between candidate nodes; thereby restricting the potential installation sites to predefined infrastructure locations. The second one is a MINLP model that introduces variable distances and integrates signal attenuation equations that account for environmental heterogeneity, such as urban density and obstructions. The later formulation allows concentrators to be optimally placed in the vicinity of utility poles, offering greater flexibility to improve communication performance in complex urban environments.
The proposed VNS algorithm is specifically designed to accommodate both formulations. Involved agents can select among the MILP model for faster approximations, the MINLP model for higher physical fidelity, or employ both to analyze trade-offs between cost and signal quality. This flexibility makes the proposed approach suitable for practical deployment by distribution utilities operating in diverse urban settings and under varying technological constraints [
30,
31].
3. Mathematical Formulations for the Optimal Allocation of WSCs
This section presents the mathematical formulations used to model the optimal allocation of WSCs in LV distribution networks. The allocation problem can be approached with different levels of modeling detail depending on the treatment of the distance between WSCs and WSMs. When this distance is considered a fixed parameter, the problem can be formulated as an MILP model using a predefined coverage matrix. Alternatively, when the distance is treated as a decision variable, more realistic and flexible representations are achieved through MINLP models. Two MINLP formulations are presented in this work: a general nonlinear model that explicitly represents signal attenuation but introduces high non-convexity, and a relaxed nonlinear model that simplifies the propagation constraints, making it compatible with general-purpose nonlinear solvers. This layered approach allows utility planners to choose between computational efficiency and modeling accuracy, depending on the complexity of the urban scenario and the available data.
3.1. MILP Formulation Based on Fixed Candidate Locations and Coverage Matrix
A widely used strategy to install WSCs involves considering a gamma parameter (
) to characterize the occupancy density of the environment through which the communication signal will propagate, together with a distance matrix (
D) that contains the distances between each WSC and each WSM [
12]. This strategy establishes a binary coverage matrix
, which indicates whether a WSM is covered by a WSC with communication technology
a installed at node
i.
The first optimization model analyzed in this study is an MILP formulation, adapted from [
32], which assumes that candidate installation points for WSCs are fixed and correspond to existing nodes (e.g., poles) in the LV distribution network. This linear approach simplifies the modeling of wireless signal propagation by using a binary coverage matrix derived from a predefined coverage radius, which can be obtained from simulations or manufacturer specifications.
The objective of the MILP model is to minimize the total cost of deploying WSCs across a set of nodes
, given a set of consumer locations
and available communication technologies
. The total cost includes both investment and maintenance costs, as described by the objective function in Equation (
2). Here,
and
represent the investment and maintenance costs of installing a WSC of technology
a at node
i, and
is a binary variable indicating whether a WSC of type
a is installed at that node.
The MILP model is subject to the following constraints. Equation (
3) limits the total number of installed WSCs to the number of candidate nodes. Equation (
4) ensures that each WSM
is covered by at least one WSC, based on the binary coverage matrix
.
This MILP formulation offers a computationally efficient approach for determining the placement of WSCs, making it particularly suitable for practical applications where simplicity and computational time are critical constraints. It serves as a benchmark for evaluating the performance of the proposed metaheuristic algorithm. Specifically, our VNS algorithm will be compared against this model, as well as against three widely used heuristics: two population-based methods (PSO and GA) and a trajectory-based heuristic (TS), all of which have proven effective in solving similar allocation problems [
33,
34]. Unlike VNS, the implementation details of PSO, GA, and TS are presented separately in
Appendix A,
Appendix B, and
Appendix C, respectively. By leveraging a fixed set of candidate locations and simplifying signal propagation with a binary coverage matrix, this model facilitates rapid and scalable analysis. It provides a solid foundation for comparing alternative solution methods and assessing the cost-effectiveness of wireless communication infrastructure in smart grid applications [
35,
36].
3.2. MINLP Formulations for WSCs Allocation
The MILP model assumes fixed distances and simplifies signal coverage, which may not accurately reflect real urban conditions where buildings, vegetation, and elevation differences can significantly impact signal propagation. The nonlinear models presented in this subsection explicitly incorporate distance as a decision variable, allowing for a more detailed representation of signal attenuation. Two MINLP formulations are proposed: a full MINLP that introduces continuous positioning of WSCs and models received signal power through nonlinear equations; and a simplified MINLP that retains discrete positioning of WSCs but incorporates signal degradation via simplified nonlinear constraints. These types of problems (nonlinear and non-convex) are usually better handled by metaheristic approaches than by exact methods [
37,
38,
39].
3.2.1. Full MINLP with Explicit Nonlinear Received Power and Flexible Positioning
This formulation is given by Equations (
5)–(
13), and must also consider Equations (
1) and (
3) as constraints. It introduces a nonlinear model that treats WSC coordinates (
,
) as decision variables, selected from a predefined set of coordinates (
,
) using binary variables
. The distance
between each WSC and WSM is computed based on Euclidean geometry, and the received power
is modeled explicitly using a standard path-loss model as indicated in Equation (
1). This leads to products of binary and continuous variables (e.g.,
), making the problem highly nonlinear and non-convex. Solving such a formulation requires advanced solvers like KNITRO that support both nonlinear and combinatorial constraints.
Subject to
This approach captures detailed propagation and attenuation characteristics, and allows flexible positioning of Wireless Smart Concentrators (WSCs) near existing infrastructure. However, it is computationally expensive and highly dependent on the solver used, which limits its scalability when applied to large-scale urban networks.
3.2.2. Simplified MINLP with Discrete Positioning and Received Power Constraints
This model is given by Equations (
14)–(
18), and must also consider the constraint given by Equation (
1). It adopts a simplified MILP formulation that replaces the explicit nonlinear function of received power with a set of pre-calculated received power values associated with discrete positions. Here, potential locations are treated as a fixed and finite set, and the distance
is implicitly embedded in the constraints through binary associations.
Instead of modeling the power–distance relationship via algebraic expressions, this approach leverages pre-tabulated power levels or threshold constraints (e.g.,
if
), thus avoiding nonlinear terms involving distance or binary–continuous multiplications. As a result, the model becomes significantly more tractable and can be handled by open-source MINLP solvers such as Bonmin, which are efficient for convex or mildly non-convex problems.
Subject to
This formulation is easier to solve using open-source solvers, such as Bonmin, and offers greater scalability for larger problem instances. The reduced nonlinearity also enables faster convergence. However, it comes at the cost of lower modeling precision, as the power–distance relationship is not explicitly represented, and it offers less flexibility in terms of positioning and signal control.
4. Implementation of the VNS-Based WSC Allocation Method
The implementation of the VNS method for WSC allocation in urban distribution networks is explained step by step below. This robust metaheuristic systematically explores multiple neighborhood structures to escape local optima and enhance solution quality.
4.1. Step 1: Data Preparation and Pre-Optimization Parameter Evaluation
This initial phase involves collecting and processing the following input data.
Geographic Information System (GIS) data: This includes digital urban maps with details on buildings, terrain, and obstructions for accurate signal modeling; predefined candidate sites for WSC installation such as poles or rooftops; and the exact coordinates of smart meters, representing demand points requiring reliable signal coverage.
Wireless Communication Technology (WCT) parameters: The input data includes a list of available WCTs with their specifications such as transmission power, cost, and signal range; parameters for the radio propagation model like path loss exponent and shadow fading, which may vary with urban density and are based on field data or literature; and cost parameters including WSC installation, operation, and technology-specific expenses.
Cost parameters: Fixed costs for installing WSCs, operational costs, and any specific costs associated with each WCT.
Maximum or fixed number of WSCs to be allocated: This is typically a budget or network capacity constraint decided by planners.
Coverage requirements: Minimum signal strength threshold required at each smart meter for reliable communication.
4.2. Step 2: Definition of Parameters and Decision Variables
Parameters and decision variables must be defined according to the selected mathematical model: a MILP problem, which assumes the locations (coordinates of the WSCs) are fixed; and a MINLP model, where the locations of the WSCs are treated as continuous variables.
A single, robust VNS algorithm is designed to solve both formulations. This approach allows for a direct comparison of the solutions obtained when coordinates are fixed versus when they are optimized, using the same powerful metaheuristic framework.
The fixed parameters or input data are provided below:
Base Sets
: The set of N candidate locations for installing WSCs.
: The set of WSMs that must be covered.
: The set of available technologies (in this case, two).
Geographical and Physical Data
Coordinates : The fixed or variable physical location of each candidate site .
Coordinates : The physical location of each meter .
Cost Parameters
: Investment cost for each technology in .
: Maintenance and operation cost for each technology.
: The displacement cost coefficient, used in the MINLP model to penalize moving a WSC from its base location.
Technical and Coverage Parameters
A (Coverage Matrix): This is a precomputed matrix that indicates whether a WSC located at p using technology t covers meter m. This matrix is derived from more fundamental parameters such as transmission power, antenna gains, and distances (calculated based on coordinates).
The decision variables represent the elements to be optimized. They differ slightly between the MILP and MINLP models. These are indicated below.
Binary Solution Vector (x): A binary vector of dimension , used in both models. The first half ( to ) corresponds to installation decisions for Technology 1, and the second half ( to ) corresponds to decisions for Technology 2. An entry of 1 signifies installation, while 0 signifies no installation.
Continuous Coordinate Vector (P): Used only in the MINLP model, this vector stores the final, optimized coordinates for each WSC activated in the solution vector x. In the MILP model, these coordinates are considered fixed to their base locations.
The objective function, , computes the total cost. It is composed of two parts: a linear hardware cost and an optional, nonlinear displacement cost.
Hardware Cost: This component is linear and calculated directly from the binary vector x. For each entry , the corresponding investment and maintenance costs () for the selected technology are added to the total cost.
Displacement Cost: This component is nonlinear and applies only to the MINLP model. For each active WSC p, it calculates a penalty for moving from its base position to its optimized final position . The cost is calculated as . In the MILP model, this cost is zero as locations are fixed.
The total cost is the sum of these two components. To be considered feasible, a solution must satisfy the following constraints:
Location Exclusivity Constraint: This constraint ensures that, for each location p, at most, one technology can be installed. It is enforced by checking that the sum of the decision variables for both technologies at a single location does not exceed 1.
4.3. Step 3: Execution of the VNS Algorithm
At this stage, the necessary parameters are configured and the VNS algorithm is executed. The goal is to efficiently explore the solution space through a systematic search strategy based on neighborhood variation. First, the maximum intensity of the diversification phase (
) and the stopping criterion of the algorithm (
) are defined. Once the parameters are set, the algorithm proceeds with its execution. The general process of the VNS algorithm, illustrated in
Figure 2, consists of the following steps:
Initialization: The algorithm starts by generating an initial feasible solution . Control variables are initialized as follows: and .
Main Loop: The algorithm enters a main loop that continues until the stopping criterion is met, i.e., while .
Neighborhood Loop: Inside the main loop, a nested loop is initiated to explore neighborhood structures. It starts with and continues while .
Shake (Diversification): This step aims to perturb the current solution in order to escape from the current basin of attraction. A random perturbation of strength k is applied to the binary vector , resulting in a new candidate solution .
Local Search: The perturbed solution is subjected to a local improvement process to find a local optimum, . The evaluation within this search is model-dependent:
- –
For the MILP model, the cost of a neighbor is calculated directly from the fixed hardware costs.
- –
For the MINLP model, this step becomes a two-level process. For a given binary vector, a nested continuous optimizer is executed to find the optimal coordinates P for the active WSCs before the total cost can be determined.
The search accepts the first change that results in a cost reduction and continues until no further improvements are found, yielding the local optimum .
Move Decision and Update: This is a critical step where the algorithm decides how to proceed:
- –
Case A—Improvement Found: If , the new solution is better. The best-known solution is updated: , and the current solution is redirected to this new region: . The neighborhood counter is reset to . This reflects the core VNS logic: “If a deeper valley is found, restart exploration from its base.”
- –
Case B—No Improvement: If , the shake did not lead to a better solution. The reference solution remains unchanged, and the neighborhood index is incremented: . The rationale here is “That shake wasn’t enough; let’s try a stronger perturbation.”
Termination: When the main loop ends (i.e., after reaching ), the algorithm terminates. The output is the best solution found during the entire process, denoted by (and for the MINLP case) and its associated cost .
4.4. Step 4: Post-Optimization Validation and Results Evaluation
After the algorithm converges, the correctness and practical applicability of the final WSC configuration must be rigorously evaluated, considering the following criteria:
Radio Coverage Simulation: The final WSC locations and assigned technologies are used to simulate radio coverage across the urban area, leveraging the initially prepared GIS data and propagation models. This visually confirms the actual coverage footprint.
Connectivity Validation: A critical step is to ensure that every smart meter (demand point) is covered by at least one allocated WSC with adequate signal strength. This confirms that the fundamental network connectivity constraint is met, guaranteeing data transmission reliability.
Cost–Benefit Analysis: The total deployment cost of the obtained solution is calculated and compared against predefined budget constraints and, if available, against solutions from baseline metaheuristics or exact solvers.
Sensitivity Analysis (External): While VNS parameter sensitivity is internal, external sensitivity analysis on key input parameters (e.g., variations in estimated signal range, changes in obstacle density, or different cost structures) can be performed to assess the robustness of the final solution under varying real-world conditions.
Output Generation for Planners: The validated solution, including optimal WSC locations (coordinates), assigned technologies, and associated costs, can be presented in easily interpretable formats (e.g., GIS maps, detailed reports) for distribution network planners to facilitate informed decision-making.
5. MILP Allocation with VNS: Performance and Benchmark Comparison
This section compares the performance of the proposed VNS method with that of PSO and GA in solving the WSC allocation problem under the MILP formulation. The problem was solved using the CPLEX solver via AMPL to serve as a benchmark. In this formulation, candidate WSC locations are fixed (e.g., poles), and the distance between WSCs and WSMs is treated as a constant based on preprocessed spatial data. This allows the problem to maintain convexity and ensures all solvers and metaheuristics converge to the same objective value.
The evaluation considered a Danish LV network, adapted from [
40], comprising 15 nodes and 45 consumers. The main variables include installation and maintenance costs, as well as the propagation coefficient (
), which represents the signal communication between WSCs and WSMs in urban environments. Two scenarios were analyzed:
PSO, GA, and VNS were implemented using RSTUDIO-2025.05.1-513.EXE with the MEIGOR toolbox. QGIS was employed to generate spatial overlays of propagation coefficients. All algorithms used the same initial data and network conditions. The hardware setup consisted of an AMD Ryzen 9 5950X processor (Advanced Micro Devices, Inc., Santa Clara, CA, USA) with 16 cores and 32 GB of RAM. Calibration of each metaheuristic ensured a repetition rate of over 70% for the best objective function, with parameter values presented in
Table 1 and
Table 2.
Figure 3 and
Figure 4 display heat maps superimposed on the test distribution network, generated using QGIS software. Warmer colors indicate a higher concentration of vertical buildings or afforestation that can reduce the WSC’s coverage radius. Therefore, in such regions, it becomes necessary to install technologies with a wider coverage radius or a greater number of WSCs to ensure adequate coverage for WSMs installed at consumer locations. In the case of a uniform distribution of vertical constructions, a single color tone is observed, as seen in
Figure 3. These figures also show that the number of WSMs per node remains constant, with the warmer colors in
Figure 4 indicating afforestation or constructions that do not require communication between WSMs and WSCs.
Following the approach by [
42], the results for Case I and Case II are presented in
Table 3. For each metaheuristic technique, the table shows the total time (
) calculated over 30 runs (
), along with the mean time (
) referring to a single run.
The optimal configuration for Case I used two WSCs (nodes 4 and 9) with ZB-Pro technology, at a cost of USD 143.92. VNS achieved this in 63 s total (2.1 s average), outperforming GA (96 s) and PSO (99 s).
For Case II, the optimal allocation included WSCs with ZB-Pro (nodes 3, 5, 11, 15) and ZB-S2C (nodes 6, 9, 13), costing USD 451.07. VNS completed in 189 s, compared to 522 s (GA) and 948 s (PSO). Across both cases, VNS consistently achieved the same quality solution with lower computational cost. Although time is not a constraint in planning, the significant efficiency gains support the adoption of VNS, particularly in dense urban environments.
VNS also has advantages over solvers like CPLEX in terms of usability. It requires tuning of only one key parameter (), whereas CPLEX demands complex formulations and multiple calibrations. VNS abstracts coverage via radius estimation, making it suitable for real-world deployments.
Sensitivity Analysis
A sensitivity analysis was carried out on Case II. The parameter
was varied to observe its effect on solution frequency. After testing different parameters, such as the number of iterations and various local search strategies, it was found that
is the parameter with the most significant influence on the algorithm’s performance, directly affecting the variability of the solutions obtained.
Table 4 shows that settings beyond 0.3 sharply decrease solution repetition below 50%. This confirms that VNS’s effectiveness depends mainly on a single parameter.
Maxdist controls the neighborhood radius. Low values risk getting stuck in local optima; high values dilute the search. In dense urban areas, moderate (e.g., 0.1–0.3) is ideal. Future work could implement adaptive maxdist parameter tuning based on urban density metrics, enabling real-time adjustments.
6. Comparison of Deterministic and Metaheuristic MINLP Models
While the MILP formulation serves as a practical baseline for preliminary network design, a more precise representation of wireless signal propagation in heterogeneous urban environments requires an MINLP model. This formulation captures the inherent nonlinearities of signal attenuation more accurately, allowing for a more realistic analysis of coverage limitations and placement flexibility. This section presents the results of applying the proposed VNS algorithm to the MINLP problem, demonstrating its advantages over both exact solvers and other metaheuristics in complex, non-convex environments. The experiments compared three distinct approaches for solving the MINLP problem for WSC allocation. These include the following:
The BONMIN solver (Basic Open-source Nonlinear Mixed-Integer Programming), a deterministic method commonly applied to non-convex MINLP problems.
The Tabu Search (TS) metaheuristic, known for its performance in combinatorial optimization.
The proposed VNS algorithm, designed to balance exploration and intensification through neighborhood diversification.
Unlike the MILP model, where candidate locations are fixed, and the propagation coefficient is discretized, the MINLP formulation introduces two key enhancements:
These elements enhance the fidelity of the model, more accurately reflecting real-world conditions in dense urban environments with vertical development.
Table 5 summarizes the allocation results obtained using each method, including CPU time and total cost.
6.1. Results with BONMIN Solver
The BONMIN solver successfully identified an optimal solution with a total cost of USD 287.84, requiring 634.97 s to complete. The allocated WSCs were located at nodes 5, 6, 13, and 14, all utilizing the Xbee Pro S2C technology (WCT = 2). While BONMIN guarantees optimality, it demands substantial computational resources and can face difficulties scaling to larger, more complex allocation problems due to the combinatorial explosion of decision variables.
6.2. Results of the VNS and Tabu Search Methods
Both the VNS and Tabu Search metaheuristics produced a superior solution with a total cost of USD 270.29—lower than that obtained by the BONMIN solver—demonstrating that these techniques can identify high-quality solutions beyond the exact solver’s result.
In terms of computational time, VNS completed the optimization in 7.74 s, while Tabu Search was faster, completing it in only 2.62 s. Despite this performance, the VNS algorithm offers several advantages that extend beyond time metrics. It requires tuning only one main parameter (), making it easier to calibrate and apply to diverse urban conditions compared to TS, which typically requires more complex parameter adjustment and memory control mechanisms. While TS was effective in this instance, its tendency to get trapped in local minima under more intricate problem settings can compromise robustness. In contrast, VNS maintains stronger exploratory capabilities by dynamically shifting neighborhoods and avoiding premature convergence.
6.3. Discussion and Comparative Insights
These results highlight key trade-offs between exact and metaheuristic approaches:
Exact methods (e.g., BONMIN) offer mathematically optimal solutions but at a high computational cost, which limits their applicability to large-scale or time-sensitive scenarios.
Metaheuristics (e.g., VNS and TS) deliver near-optimal solutions by exploring high-quality regions of the solution space with substantially lower execution times, making them more suitable for scalable and real-time planning.
Beyond the solver comparison, our findings also reveal important differences between linear and nonlinear problem formulations. In Case II, the linear model used fixed values (3 and 4) for defining coverage, while the nonlinear model allowed to vary continuously within this range. This difference significantly affected the optimization results: the best solution obtained using the linear MILP model yielded a total cost of approximately USD 451.07, while the nonlinear MINLP model—solved via VNS—achieved a much lower cost of USD 270.29. Thus, the MILP-based solution represents a nearly 50% higher cost than that achieved through nonlinear modeling.
This gap illustrates a key limitation of the linear formulation: its inability to capture finer signal propagation dynamics across heterogeneous urban environments. While the linear MILP model is computationally simpler and well-suited for rapid scenario analysis, it may overestimate the required number of WSCs or select suboptimal locations due to its coarse abstraction of signal attenuation. On the other hand, the nonlinear formulation provides enhanced realism by modeling signal loss more precisely as a function of distance and environmental conditions (e.g., urban density), thereby supporting more cost-effective and spatially efficient deployments.
In particular, the VNS algorithm stands out as a flexible, low-cost, and easily tunable approach for solving MINLP problems involving spatial flexibility and nonlinear propagation dynamics. By enabling solution identification within seconds, VNS contributes to energy-efficient computation, reducing the need for extensive CPU usage in data centers and supercomputers. This is particularly important as utilities and planners move toward more sustainable and computationally responsible decision-making processes.
6.3.1. Model-Side Scaling (Variables and Constraints)
In the simplified MINLP (Equations (
14)–(
18)), the number of binary siting variables scales as
(WSC-by-technology). Continuous variables include the installed sites’ coordinates and, if explicitly modeled, auxiliary variables representing received power levels for each WSC–WSM link in order to satisfy the coverage constraint. If coverage links are formed naively, the number of coverage constraints scales as
. However, in power distribution feeders, a distance cap
induces
sparse linking: each WSM only interacts with WSC candidates within a local neighborhood of size
. Under this common engineering assumption, constraints drop to
, which is effectively linear in
M for fixed
k [
43].
6.3.2. BONMIN (Deterministic MINLP) Scaling
Branch-and-bound for MINLP explores a tree whose size can, in the worst case, grow exponentially with the number of binaries; at each node, a nonlinear relaxation must be solved, and its computational cost rises faster than linear with the number of continuous variables and constraints. In practice, this implies that both runtime and memory tend to increase more than proportionally (often polynomial of degree greater than one, and in some cases exponential) with
N,
M, and
T, even when sparsity is exploited [
44]. This is consistent with the observation that BONMIN achieved optimality in the test Danish distribution feeder, but required high CPU time and showed limited scalability for denser or larger systems. Similar scalability limitations of deterministic MINLP solvers have also been reported in power system planning studies [
45].
6.3.3. VNS (Metaheuristic) Scaling
The computational cost of one VNS iteration is dominated by the
evaluation step. In OP
var mode (the MINLP case), evaluation (see “Nested Evaluation” in
Figure 2) first reads the
active WSC set in the candidate
x, then solves a
continuous subproblem whose size depends on the number of active WSCs, not on the full
N. If each WSM links only to nearby active WSCs (bounded
k via
), evaluation scales approximately as
for constraint assembly plus the computational cost of a small continuous solver call whose dimension is proportional to the active sites (often much smaller than
N). Therefore, for a fixed number of VNS iterations and neighborhoods, the overall computational cost of VNS grows roughly linearly in
M (and in
N through the active set), provided locality is enforced. Memory usage is likewise linear in the sparse neighborhood lists and candidate vectors. This behavior is consistent with the Danish power feeder results and with prior reports showing that VNS, GA, and PSO scale efficiently for large allocation problems in smart grids [
46].
6.3.4. Takeaways for Larger Feeders
Deterministic MINLP (BONMIN): Runtime and memory are expected to increase more than linearly with system size due to the combination of many binaries and nonlinear relaxations; scalability is highly sensitive to non-convexity and branching efficiency [
47].
VNS: Computational cost grows close to linear under bounded connectivity (via ), because each iteration evaluates only local interactions and a small continuous subproblem tied to the active facilities, not to all candidates. The memory footprint remains modest (candidate vectors and sparse neighbor lists).
Practical enablers: (i) Precomputing neighbor lists with
, (ii) caching repeated distance/propagation terms during local moves, and (iii) early-stopping rules on neighborhoods, all of which are embedded in the Evaluate routine and algorithmic flow [
46].
In summary, based on the structure of the MINLP formulation and the VNS evaluation pipeline, BONMIN’s computational burden is expected to increase more than proportionally with network size. In contrast, VNS scales much more gently—dominated by local, sparse evaluations and small continuous subproblems—making it the more practical option as LV feeders approach hundreds of nodes. This conclusion aligns with recent findings in the smart grid optimization literature, where metaheuristic approaches consistently demonstrate better computational scalability than deterministic solvers for large, non-convex allocation problems [
45,
46].
7. Conclusions
This study proposed a flexible and computationally efficient algorithm for optimizing the allocation of WSCs in urban environments, with particular emphasis on minimizing infrastructure investment costs while maintaining robust communication coverage. By integrating both MILP and MINLP formulations within a VNS framework, the approach adapts to multiple levels of modeling fidelity and urban complexity.
Unlike conventional models that rely solely on fixed distance thresholds and predefined candidate nodes, our methodology accommodates both discrete and continuous placement options, enhancing the representation of wireless signal propagation—particularly relevant in cities experiencing vertical growth and heterogeneous building densities. The dual MILP–MINLP structure allows planners and utility professionals to balance computational simplicity and physical realism, depending on the spatial and technological constraints of the deployment region.
Simulation results validate the advantages of VNS over both exact solvers and traditional metaheuristics. In the MILP formulation, VNS achieved optimal solutions equivalent to those from CPLEX, PSO, and GA, while reducing execution times by up to 75%. In the more complex MINLP formulation, VNS not only maintained rapid convergence (e.g., 7.74 s) but also outperformed the BONMIN exact solver by identifying lower-cost solutions, even under nonlinear and spatially flexible conditions. These findings highlight the algorithm’s robustness in solving real-world smart grid communication problems under high-dimensional, non-convex constraints.
The methodological contribution of this work lies in demonstrating that metaheuristic-based models—when well-structured—can rival or exceed exact methods in both accuracy and practical usability. The simplicity of configuring only one primary parameter () further promotes operational feasibility, especially for planning teams in utility companies or municipalities lacking access to high-performance computing resources.
Finally, this work contributes to the sustainability agenda by offering a replicable and scalable planning tool that supports the inclusive expansion of smart infrastructure. By improving coverage analysis in urban areas with diverse topographies and enabling energy-efficient computation, the proposed method aligns with the goals of reducing digital divides, promoting smart metering adoption, and advancing equitable urban development.
Directions for Future Research
Building upon the robust framework established in this study, future research can explore several promising avenues:
Integration of Dynamic Urban Scenarios: Investigating the applicability of VNS to allocate WSCs in highly dynamic urban environments, incorporating real-time data on urban expansion, temporary obstacles, and demand fluctuations.
Hybrid Communication Infrastructures: Extending the optimization model to include hybrid communication technologies (e.g., integrating fiber optics or other wired solutions with wireless concentrators) to further enhance network resilience and capacity.
Enhanced Signal Propagation Models: Incorporating more sophisticated and granular signal propagation models (e.g., ray-tracing simulations) to refine WSC placement decisions in extremely complex urban topographies.
Multi-objective Optimization: Exploring multi-objective VNS formulations to simultaneously optimize for cost, reliability, latency, and environmental impact (e.g., electromagnetic field exposure) in WSC deployment.
Additional Communication Parameters: Extending the model to explicitly incorporate factors such as latency, jitter, and packet delivery reliability, thereby enriching the analysis and providing deeper insights into the robustness of the proposed approach.
These directions aim to further broaden the applicability and refine the precision of WSC allocation strategies within the evolving landscape of modern smart grid systems and IoT-based urban monitoring.
Author Contributions
Conceptualization, C.A.S., R.W.-S., and J.D.M.; methodology, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G.; software, C.A.S., R.W.-S., and J.D.M.; validation, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G.; formal analysis, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G.; investigation, C.A.S., R.W.-S., J.D.M., and J.M.L.-L.; resources, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G.; data curation, C.A.S., R.W.-S., and J.D.M.; writing—original draft preparation, C.A.S., R.W.-S., and J.D.M.; writing—review and editing, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G.; visualization, C.A.S., R.W.-S., J.D.M., and J.M.L.-L.; supervision, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G.; project administration, C.A.S., R.W.-S., J.D.M., and J.M.L.-L.; funding acquisition, C.A.S., R.W.-S., J.D.M., J.M.L.-L., and N.M.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank the Federal University of ABC (UFABC) for institutional support. This work was financially supported by the São Paulo Research Foundation (FAPESP), under grant #2024/14894-8; by the Coordination for the Improvement of Higher Education Personnel—Brazil (CAPES)—Funding Code 001, under grants 88887.709682/2022-00, 88887.692379/2022-00, and 88887.939062/2024-00; and by the National Council for Scientific and Technological Development (CNPq), through the Universal Project no. 407244/2023-9 and 309013/2025-9. The authors also acknowledge support from the National Institute of Science and Technology—INCT-INERGE, and the financial support provided by the Colombian Ministry of Science, Technology, and Innovation “MinCiencias” through “Patrimonio Autónomo Fondo Nacional de Financiamiento para la Ciencia, la Tecnología y la Innovación, Francisco José de Caldas” (Perseo Alliance, Contract No. 112721-392-2023).
Conflicts of Interest
The authors declare that they have no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMI | Advanced Metering Infrastructure |
| AMPL | A Mathematical Programming Language |
| GA | Genetic Algorithm |
| GAMS | General Algebraic Modeling System |
| IoT | Internet of Things |
| LV | Low Voltage |
| OF | Objective Function |
| PSO | Particle Swarm Optimization |
| VNS | Variable Neighborhood Search |
| WSCs | Wireless Smart Concentrators |
| MINLP | Mixed-Integer Nonlinear Programming |
| WCTs | Wireless Communication Technologies |
| BONMIN | Basic Open-source Nonlinear Mixed-Integer Programming |
| TS | Tabu Search |
Appendix A. Particle Swarm Optimization
This section presents the structure and implementation of the PSO algorithm used to solve the optimization problem [
34,
48]. Due to the binary nature of the decision variables, a variant called Binary Particle Swarm Optimization (BPSO) is adopted.
Appendix A.1. Adaptation to Binary Search Space
The standard PSO algorithm was originally designed for continuous search spaces, where variables can take any real value. However, the decision variable in our problem is a binary vector (0 or 1). Therefore, the BPSO variant is utilized, adapting key PSO concepts as follows:
Position (x): Represents a binary solution vector where each element corresponds to the activation status of a specific technology at a given site.
Velocity (v): Interpreted as the probability that a bit in the position vector switches to 1, rather than as a physical displacement.
Position Update: The velocity is passed through a sigmoid function to squash it into a probability value between 0 and 1. Each bit is updated based on this probability.
Appendix A.2. Flowchart
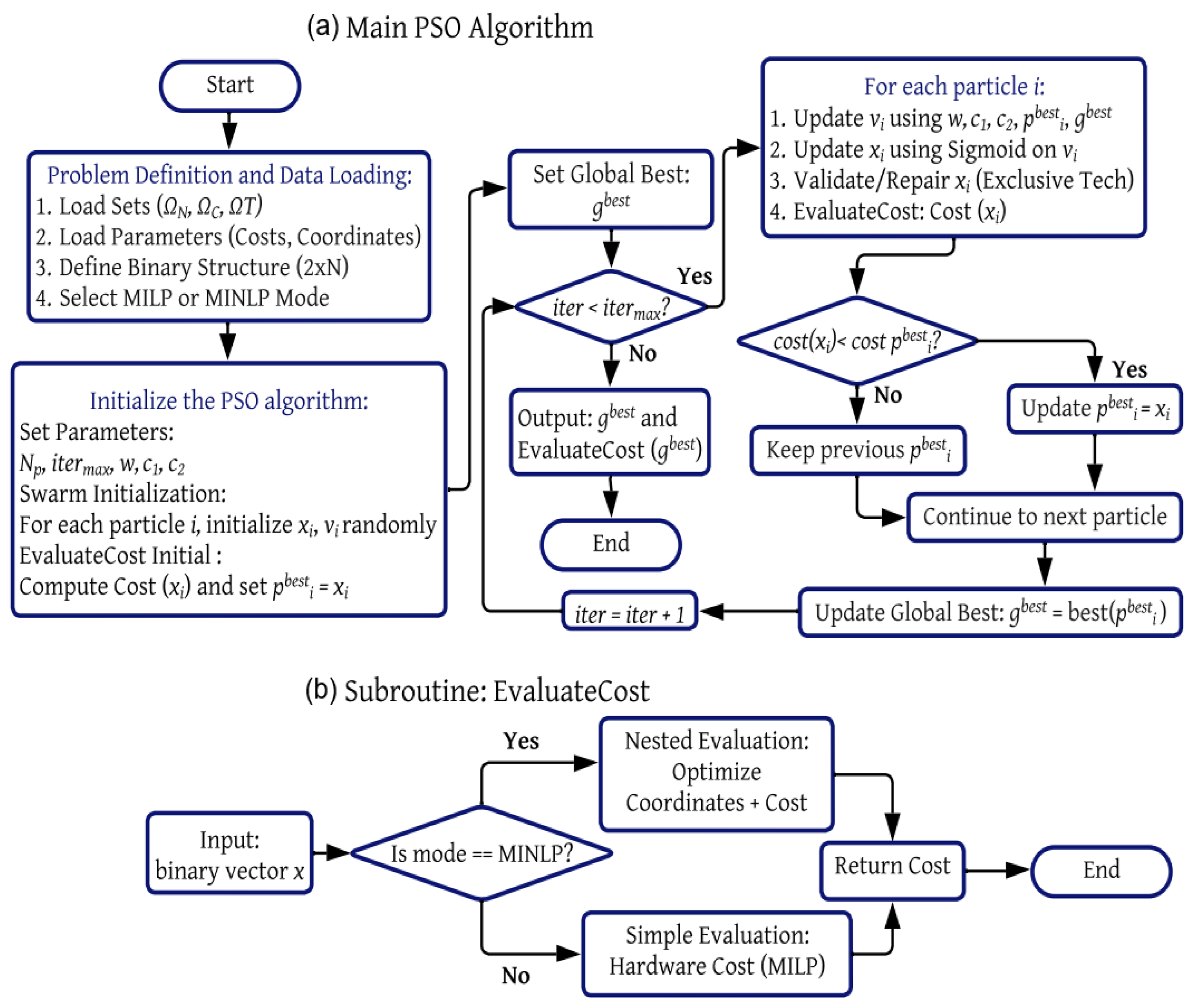
The PSO-based optimization process, illustrated in
Figure A1, consists of four main phases: (0) problem definition and data loading, (1) algorithm initialization, (2) iterative optimization, and (3) termination and output.
Figure A1.
Flowchart of the Particle Swarm Optimization algorithm.
Figure A1.
Flowchart of the Particle Swarm Optimization algorithm.
Appendix A.2.1. Phase 0: Problem Definition and Data Loading
This initial phase is crucial for establishing the structure and parameters of the optimization problem.
Data and Parameter Loading: Input data sets are loaded, including the sets of potential locations (), consumers (), and technologies (), along with associated costs such as investment (), operation and maintenance (), and transportation costs (). Additionally, base coordinates and other relevant data are loaded.
Structure Definition: The algorithm is configured to explore a binary solution vector of dimension , where the first half corresponds to technology 1 and the second half to technology 2. This defines a discrete binary search space.
Operation Mode Selection: The user selects between MILP (fixed coordinates, linear model) and MINLP (variable coordinates, nonlinear model). This choice affects how each solution’s cost is evaluated.
Appendix A.2.2. Phase 1: PSO Initialization
With the problem defined, the PSO algorithm is initialized to begin the optimization process.
Set PSO Parameters: Metaheuristic parameters are defined, including the number of particles, maximum number of iterations (), and the PSO coefficients for inertia (w), cognitive component (), and social component ().
Swarm Initialization: A population of N particles is generated. Each particle is initialized with a random binary position vector () and a random velocity vector ().
Fitness Evaluation and Memory Initialization:
- –
The cost of the initial position of each particle is computed using the cost function.
- –
Each particle’s initial position is stored as its personal best ().
- –
Among all values, the best one is selected and stored as the global best () of the swarm.
Appendix A.2.3. Phase 2: Main Optimization Loop
This is the core iterative process where the swarm explores the solution space until the stopping criterion is met (i.e., reaching ).
- 1.
Velocity Update: For each particle, a new velocity is calculated based on its current velocity (inertia), the direction to its personal best (), and the direction to the global best ().
- 2.
Binary Position Update: The new velocity values are passed through a sigmoid function to obtain probabilities. These are used to update the binary position vector of each particle.
- 3.
Solution Validation and Repair: The new binary vector is validated to ensure it satisfies basic problem constraints (e.g., no simultaneous activation of both technologies at the same site). If violations are found, repair strategies are applied.
- 4.
Fitness Evaluation: The new solution is evaluated using the EvaluateCost subroutine.
- 5.
Update Personal Best (): If the new solution is better than the particle’s previous personal best, is updated.
- 6.
Update Global Best (): Once all particles have been updated, the best in the swarm is compared with the current , and is updated if a better solution is found.
Appendix A.2.4. Key Subroutine: EvaluateCost
The cost evaluation subroutine adapts its behavior based on the selected operation mode:
MILP Mode (Simple Evaluation): The cost is computed as the sum of hardware costs for the activated WSCs, assuming fixed coordinates.
MINLP Mode (Nested Evaluation): For a given binary vector x, a continuous optimization problem is solved to determine the optimal coordinates of the active WSCs. The final cost is the sum of hardware costs and the resulting transportation cost based on optimized coordinates.
Appendix A.2.5. Phase 3: Termination and Output
The algorithm terminates when the iteration counter reaches . The final output is the best solution found, stored in , along with its associated cost .
Appendix B. Genetic Algorithm
The flowchart shown in
Figure A2 outlines the implementation of a GA adapted to the characteristics of the current problem. The process follows the canonical stages of a GA, with tailored modifications to handle binary decision variables and the selection between MILP and MINLP operational modes.
Figure A2.
Genetic Algorithm flowchart.
Figure A2.
Genetic Algorithm flowchart.
Appendix B.1. Phase 0: Problem Definition and Data Loading
As in previous approaches, this initial block is essential to define the problem comprehensively before the optimization process begins.
Input Data Loading: The algorithm loads all necessary input data, including the sets of potential locations (), consumers (), and available technologies (), along with investment costs (), operational and maintenance costs (), and transport costs (), as well as any relevant spatial coordinates.
Chromosome Representation: Solutions are encoded as binary chromosomes of length , where each bit indicates the activation status of a specific technology at a given site. This defines a discrete and constrained binary search space.
Operation Mode Selection: The user selects between the MILP (fixed coordinates, linear formulation) or MINLP (variable coordinates, nonlinear formulation) modes. This decision affects how the cost function is computed.
Appendix B.2. Phase 1: Genetic Algorithm Initialization
Once the problem has been defined, the GA is initialized as follows:
Parameter Configuration: Key hyperparameters are set, including population size, the maximum number of generations, crossover rate, and mutation rate.
Initial Population Generation: A population of feasible chromosomes is randomly generated. Each chromosome must satisfy the exclusivity constraint—only one technology can be active per location.
Appendix B.3. Phase 2: Evolutionary Cycle
This phase represents the core of the GA, where the population evolves over successive generations.
- 1.
Fitness Evaluation: The fitness of each chromosome is computed via the EvaluateCost subroutine. A lower cost corresponds to higher fitness.
- 2.
Selection: Parent chromosomes are selected using methods such as tournament selection. In this strategy, k individuals are randomly sampled and the fittest among them is selected for reproduction. This promotes the survival of the fittest.
- 3.
Reproduction: Crossover and Mutation:
Crossover: Pairs of selected parents are recombined to produce offspring. In one-point crossover, a random cut point is selected and gene segments are exchanged between the parents. This enables inheritance of favorable traits from both individuals.
Mutation: Applied with low probability, mutation flips one or more bits in the offspring. This operator introduces diversity and reduces the risk of premature convergence.
- 4.
Validation and Repair: Offspring chromosomes are verified for feasibility. If any constraints (e.g., mutual exclusivity) are violated, a repair function is invoked to restore validity.
- 5.
Replacement and Elitism: The current population is replaced by the offspring. An elitist strategy ensures that the best individual from the current generation is carried over to the next without modification, preserving the best solution found thus far.
Appendix B.4. Key Subroutine: EvaluateCost
The cost evaluation routine operates consistently with other metaheuristics and adapts to the selected operational mode:
MILP Mode: Cost is directly calculated from the hardware activation costs using fixed site coordinates.
MINLP Mode: For a given chromosome, a nested continuous optimization is executed to determine optimal coordinates for active WSCs. The total cost includes hardware and transport components derived from the optimized layout.
Appendix B.5. Phase 3: Termination and Output
The evolutionary cycle continues until the predefined number of generations is reached. Upon termination, the best chromosome in the final generation—corresponding to the lowest-cost solution—is returned as the optimal result along with its fitness value obtained from EvaluateCost.
Appendix C. Tabu Search Algorithm
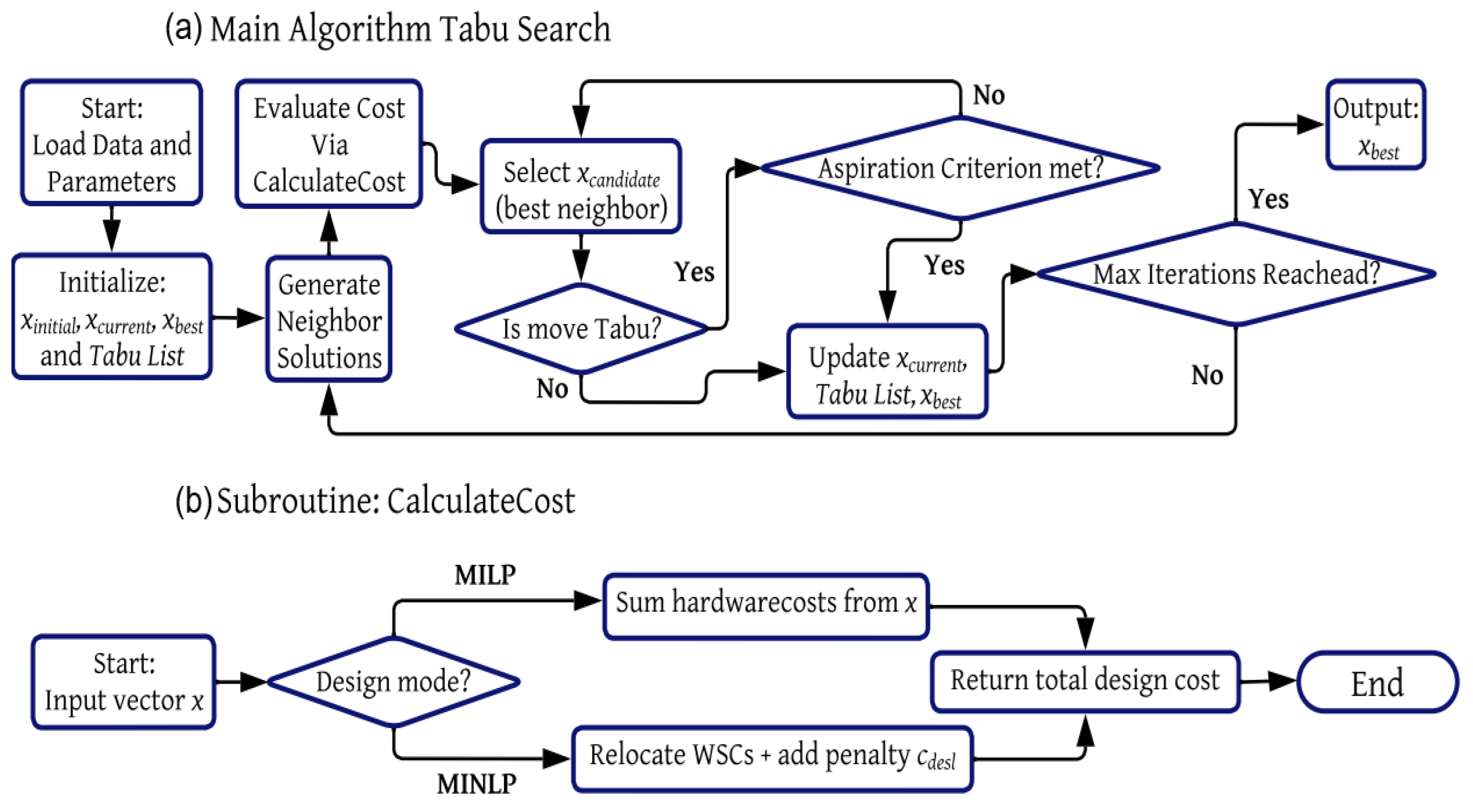
This section presents a detailed description of the Tabu Search (TS) metaheuristic, as illustrated in the flowchart of
Figure A3.
Figure A3.
Tabu Search algorithm flowchart.
Figure A3.
Tabu Search algorithm flowchart.
Appendix C.1. Problem Definition and Data Loading
The algorithm begins with a problem setup phase, which provides all necessary data for evaluating network designs. This includes the following:
Deployment map and components: The input comprises N candidate locations for installing WSCs, 45 fixed consumer locations to be covered, and the technical specifications of two wireless technologies: Xbee S2C and Xbee Pro S2C.
Cost parameters: Each technology has associated installation (), maintenance (), and relocation penalties ().
Solution structure: A network design is represented by a binary solution vector x of size . The first N elements indicate the deployment of Xbee S2C, while the remaining N elements refer to Xbee Pro S2C. A value of 1 at position i denotes the installation of the corresponding technology at location i.
Deployment mode: Two modes are supported:
- –
textitMILP (Mixed-Integer Linear Programming): WSCs are fixed at predefined base coordinates.
- –
MINLP (Mixed-Integer Nonlinear Programming): WSCs can be repositioned within a local vicinity around their base coordinates, incurring a relocation cost.
Appendix C.2. Phase 1: Algorithm Initialization
Search parameters: The algorithm initializes the total number of iterations (MaxIter) and the size of the Tabu List (tenure), which controls the memory horizon.
Initial solution (): A valid random binary vector x is generated, representing an initial WSC deployment.
State initialization: The initial solution is stored as both the current solution () and the best-found solution (). The Tabu List is initially empty.
Appendix C.3. Phase 2: Main Search Loop
The core of the algorithm is an iterative improvement process where neighboring solutions are explored to enhance the network design.
Appendix C.3.1. Neighbor Generation and Evaluation
All neighboring solutions differing from by a single bit flip are generated. Each bit flip corresponds to a physical action:
Each neighbor is evaluated using the CalculateCost subroutine to determine its total deployment cost.
Appendix C.3.2. Selection of Best Candidate
Among all neighbors, the candidate solution with the lowest cost is identified, regardless of whether its cost is higher than —a necessary allowance for escaping local minima.
Appendix C.3.3. Tabu Logic and Aspiration Criterion
The move leading to is checked against the Tabu List:
If the move is not in the Tabu List, it is allowed.
If it is tabued, the Aspiration Criterion is applied: if has a better cost than , the move is accepted regardless.
Appendix C.3.4. State Update
Upon accepting a candidate,
becomes the new ;
The corresponding move is added to the Tabu List;
If improves upon , then is updated.
Appendix C.3.5. Cost Evaluation Subroutine: CalculateCost
This function returns the total cost of a given network design:
In MILP mode, the cost is computed as the sum of hardware costs for active WSCs.
In MINLP mode, the function additionally solves a continuous optimization problem to reposition active WSCs optimally and adds the relocation penalty .
Appendix C.4. Phase 3: Termination
After completing all iterations, the algorithm outputs the best-found solution , representing the lowest-cost configuration of WSCs (including selected technologies and physical positions).
References
- Alaqeel, T.; Suryanarayanan, S. A comprehensive cost-benefit analysis of the penetration of Smart Grid technologies in the Saudi Arabian electricity infrastructure. Util. Policy 2019, 60, 100933. [Google Scholar] [CrossRef]
- Crispim, J.; Braz, J.; Castro, R.; Esteves, J. Smart Grids in the EU with smart regulation: Experiences from the UK, Italy and Portugal. Util. Policy 2014, 31, 85–93. [Google Scholar] [CrossRef]
- Fei, Z.; Li, B.; Yang, S.; Xing, C.; Chen, H.; Hanzo, L. A survey of multi-objective optimization in wireless sensor networks: Metrics, algorithms, and open problems. IEEE Commun. Surv. Tutor. 2016, 19, 550–586. [Google Scholar] [CrossRef]
- Shreenidhi, H.S.; Ramaiah, N.S. A two-stage deep convolutional model for demand response energy management system in IoT-enabled Smart Grid. Sustain. Energy Grids Netw. 2022, 30, 100630. [Google Scholar] [CrossRef]
- Gao, C.; Li, S.; Wei, M.; Duan, S.; Xu, J. A Fair Energy Allocation Algorithm for IRS-Assisted Cognitive MISO Wireless-Powered Networks. Information 2024, 15, 49. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N.; Brimberg, J.; Pérez, J.A.M. Variable Neighborhood Search. In Handbook of Metaheuristics; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 57–97. [Google Scholar] [CrossRef]
- Mrkela, L.; Stanimirović, Z. A Multi-objective variable neighborhood search for the maximal covering location problem with customer preferences. Clust. Comput. 2022, 25, 1677–1693. [Google Scholar] [CrossRef]
- Jayachandran, M.; Rao, K.P.; Gatla, R.K.; Kalaivani, C.; Kalaiarasy, C.; Logasabarirajan, C. Operational concerns and solutions in smart electricity distribution systems. Util. Policy 2022, 74, 101329. [Google Scholar] [CrossRef]
- Gonzalez, D.; Garcia, E.; Martin, F. Performance evaluation of wireless sensor networks in high-rise urban environments. Sensors 2019, 19, 1234. [Google Scholar]
- Wang, W. Deployment and optimization of wireless network node deployment and optimization in smart cities. Comput. Commun. 2020, 155, 117–124. [Google Scholar] [CrossRef]
- Balyan, V.; Gupta, D. Device-to-device and mobile user communication with queuing in NOMA-based network. Int. J. Smart Sens. Intell. Syst. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Sharma, D.K.; Rapaka, G.K.; Pasupulla, A.P.; Jaiswal, S.; Abadar, K.; Kaur, H. A review on smart grid telecommunication system. Mater. Today Proc. 2022, 51, 470–474. [Google Scholar] [CrossRef]
- Ogut, O.; Tzortzi, J.N.; Bertolin, C. Creating a Roadmap to Forecast Future Directions in Vertical Green Structures as a Climate Change Mitigation Strategy: A Critical Review of Technology-Driven Applications. Sustainability 2024, 16, 4543. [Google Scholar] [CrossRef]
- de Armas, J.; Moreno-Pérez, J.A. A Survey on Variable Neighborhood Search for Sustainable Logistics. Algorithms 2025, 18, 38. [Google Scholar] [CrossRef]
- Peng, X.; Jin, Y.; Wang, H. Multimodal Optimization Enhanced Cooperative Coevolution for Large-Scale Optimization. IEEE Trans. Cybern. 2019, 49, 3507–3520. [Google Scholar] [CrossRef] [PubMed]
- Raj, B.; Ahmedy, I.; Idris, M.Y.I.; Noor, R.M. A Hybrid Sperm Swarm Optimization and Genetic Algorithm for Unimodal and Multimodal Optimization Problems. IEEE Access 2022, 10, 109580–109596. [Google Scholar] [CrossRef]
- Ogbodo, E.; Dorrell, D.; Abu-Mahfouz, A. Energy-efficient distributed heterogeneous clustered spectrum-aware cognitive radio sensor network for guaranteed quality of service in smart grid. Int. J. Distrib. Sens. Netw. 2021, 17, 15501477211028399. [Google Scholar] [CrossRef]
- Abbas, S.S.A.; Dag, T.; Gucluoglu, T. Optimizing Mobile Base Station Placement for Prolonging Wireless Sensor Network Lifetime in IoT Applications. Appl. Sci. 2025, 15, 1421. [Google Scholar] [CrossRef]
- Li, X.; Dong, B.; Li, S.; Xie, B.; Xie, L. Accelerating Green Growth: The Impact of Government Environmental Audits on Urban Green Economy. Sustainability 2025, 17, 5289. [Google Scholar] [CrossRef]
- El Maghraoui, A.; El Hadraoui, H.; Ledmaoui, Y.; El Bazi, N.; Guennouni, N.; Chebak, A. Revolutionizing smart grid-ready management systems: A holistic framework for optimal grid reliability. Sustain. Energy Grids Netw. 2024, 39, 101452. [Google Scholar] [CrossRef]
- Shaukat, N.; Ali, S.; Mehmood, C.; Khan, B.; Jawad, M.; Farid, U.; Ullah, Z.; Anwar, S.; Majid, M. A survey on consumers empowerment, communication technologies, and renewable generation penetration within Smart Grid. Renew. Sustain. Energy Rev. 2018, 81, 1453–1475. [Google Scholar] [CrossRef]
- Gallardo, J.L.; Ahmed, M.A.; Jara, N. Clustering Algorithm-Based Network Planning for Advanced Metering Infrastructure in Smart Grid. IEEE Access 2021, 9, 48992–49006. [Google Scholar] [CrossRef]
- Baksh, R.; Itoo, S.; Ahmad, M. A comprehensive and secure scheme for privacy-preserving smart meter data aggregation in the smart grid. Sustain. Energy Grids Netw. 2024, 39, 101461. [Google Scholar] [CrossRef]
- Madisetti, V. Wireless, Networking, Radar, Sensor Array Processing, and Nonlinear Signal Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Clerckx, B.; Huang, K.; Varshney, L.; Ulukus, S.; Alouini, M. Wireless Power Transfer for Future Networks: Signal Processing, Machine Learning, Computing, and Sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1060–1094. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. (CSUR) 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Xu, S.; Qian, Y.; Qingyang Hu, R. Reliable and resilient access network design for advanced metering infrastructures in smart grid. IET Smart Grid 2018, 1, 24–30. [Google Scholar] [CrossRef]
- KOJIMA, H.; TSUCHIYA, T.; FUJISAKI, Y. The Aggregation Point Placement Problem for Power Distribution Systems. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2018, E101.A, 1074–1082. [Google Scholar] [CrossRef]
- Sadati, M.E.H.; Çatay, B.; Aksen, D. An efficient variable neighborhood search with tabu shaking for a class of multi-depot vehicle routing problems. Comput. Oper. Res. 2021, 133, 105269. [Google Scholar] [CrossRef]
- Zhen, T.; Elgindy, T.; Alam, S.S.; Hodge, B.; Laird, C.D. Optimal placement of data concentrators for expansion of the smart grid communications network. IET Smart Grid 2019, 2, 537–548. [Google Scholar] [CrossRef]
- 2019 Index IEEE Transactions on Smart Grid Vol. 10. IEEE Trans. Smart Grid 2019, 10, 6977–7081. [CrossRef]
- Garcia, G.C.; Vargas, R.; Melo, J.D.; Casella, I.R.S. Analysis of the Optimized Allocation of Wireless and PLC Data Concentrators in Extensive Low-Voltage Networks Considering the Increase in the Residential Electric Vehicles Charging. IEEE Access 2023, 11, 140774–140788. [Google Scholar] [CrossRef]
- Nasser Lauar, S.; Mestria, M. Greedy Genetic Algorithm for the Data Aggregator Positioning Problem in Smart Grids. Intel. Artif. 2021, 24, 123–137. [Google Scholar] [CrossRef]
- Palate, B.O.; Guedes, T.P.; Grilo-Pavani, A.; Padilha-Feltrin, A.; Melo, J.D. Aggregator units allocation in low voltage distribution networks with penetration of photovoltaic systems. Int. J. Electr. Power Energy Syst. 2021, 130, 107003. [Google Scholar] [CrossRef]
- Wu, L.; Qu, J.; Shi, H.; Li, P. Node deployment optimization for wireless sensor networks based on virtual force-directed particle swarm optimization algorithm and evidence theory. Entropy 2022, 24, 1637. [Google Scholar] [CrossRef] [PubMed]
- Abdulwahid, H.M.; Mishra, A. Deployment optimization algorithms in wireless sensor networks for smart cities: A systematic mapping study. Sensors 2022, 22, 5094. [Google Scholar] [CrossRef] [PubMed]
- López-Lezama, J.M.; Cortina-Gómez, J.; Muñoz-Galeano, N. Assessment of the Electric Grid Interdiction Problem using a nonlinear modeling approach. Electr. Power Syst. Res. 2017, 144, 243–254. [Google Scholar] [CrossRef]
- Jaramillo Serna, J.d.J.; López-Lezama, J.M. Alternative Methodology to Calculate the Directional Characteristic Settings of Directional Overcurrent Relays in Transmission and Distribution Networks. Energies 2019, 12, 3779. [Google Scholar] [CrossRef]
- Agudelo, L.; López-Lezama, J.M.; Muñoz-Galeano, N. Vulnerability assessment of power systems to intentional attacks using a specialized genetic algorithm. Dyna 2015, 82, 78–84. [Google Scholar] [CrossRef]
- Bhattarai, B.P.; Myers, K.S.; Bak-Jensen, B.; de Cerio Mendaza, I.D.; Turk, R.J.; Gentle, J.P. Optimum aggregation of geographically distributed flexible resources in strategic smart-grid/microgrid locations. Int. J. Electr. Power Energy Syst. 2017, 92, 193–201. [Google Scholar] [CrossRef]
- Haque, K.F.; Abdelgawad, A.; Yelamarthi, K. Comprehensive performance analysis of zigbee communication: An experimental approach with XBee S2C module. Sensors 2022, 22, 3245. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Duan, Q.; Yan, B.; Cheng, S.; Shi, Y. Automated Design of Metaheuristic Algorithms: A Survey. arXiv 2023, arXiv:2303.06532. [Google Scholar]
- Song, T.; Han, X.; Zhang, B. Multi-Time-Scale Optimal Scheduling in Active Distribution Network with Voltage Stability Constraints. Energies 2021, 14, 7107. [Google Scholar] [CrossRef]
- Bratko, I. A short note on logic as a game. Synthese 2019, 36, 595–615. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Y.; Su, X. Integrated optimization of smart building energy consumption in microgrids using linearized real-time control strategies. Sustain. Energy Grids Netw. 2025, 43, 101745. [Google Scholar] [CrossRef]
- Bratko, I.; Bratko, I. A Hybrid Genetic Algorithm and Differential Evolution for the Optimal Design of a Two-Stage Heat Exchanger Network. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Bratko, I.; Bratko, I. The role of artificial intelligence in agriculture: A review of recent applications. Comput. Electron. Agric. 2007, 58, 149–158. [Google Scholar] [CrossRef]
- Dechanupaprittha, S.; Jamroen, C. Self-learning PSO based optimal EVs charging power control strategy for frequency stabilization considering frequency deviation and impact on EV owner. Sustain. Energy Grids Netw. 2021, 26, 100463. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).