Selection and Classification of Small Wind Turbines for Local Energy Systems: Balancing Efficiency, Climate Conditions, and User Comfort
Abstract
1. Introduction
- Efficiency—maximizing energy yield in turbulent conditions using real-world wind data, taking into account TI and terrain features;
- Comfort—reducing noise, vibration, and flicker, improving social acceptance and aesthetics;
- Climate Adaptation—the resilience of MAWTs to climate change, extreme weather events, increasing urban density, and evolving local conditions.
2. Material and Methods
2.1. Meteorological Data and Wind Analysis
2.2. Wind Resource Classification for MAWTs
- -
- Analysis of actual annual energy production from 2 kW MAWTs, based on meteorological data from locations such as Gdynia Redłowo.
- -
- Operational requirements of various turbine types (e.g., cut-in values, rated values, power characteristics, aerodynamic efficiency).
- -
- Urban and landscape context (compact development, rooftops, suburban areas, open spaces). Table 1 presents the proposed wind resource classification for MAWTs.
- -
- Preliminary site selection for MAWTs;
- -
- Turbine type selection (e.g., VAWT instead of HAWT in a high turbulence environment);
- -
- Estimated annual energy production (AEP) without the need for long-term measurements;
- -
- Economic cost-effectiveness assessment (e.g., LCOE—levelized cost of energy) in the context of low and medium wind speeds.
2.3. Typology and Characteristics of MAWTs
- -
- Rotor rotation axis: horizontal (HAWT) or vertical (VAWT);
- -
- Rotor type: classic, shrouded, with diffuser, multi-rotor;
- -
- Blade geometry: curved, straight, helical, composite blades, flexible;
- -
- Mounting type: freestanding, mast-mounted, roof-mounted, building-integrated;
- -
- Operating mode: off-grid, hybrid, with energy storage, or direct energy consumption.
2.3.1. Horizontal Axis Turbines (HAWT)
2.3.2. Vertical Axis Turbines (VAWT)
2.3.3. Diffuser-Augmented Wind Turbines (DAWT)
2.3.4. Compact and Multi-Rotor Turbines (CAWT, WLT)
2.3.5. Building-Integrated Turbines (BIWT)
2.4. Location and Architectural Context
- Open areas—Sparse tree cover, minimal development, good wind exposure (e.g., rural areas, coastlines);
- Suburban areas and outskirts—Moderate exposure, presence of individual buildings, moderate turbulence;
- Urban areas—High development, high turbulence intensity, need for integration with buildings;
- Industrial and campus areas—Possibility of installing large masts, good technical conditions, moderate aesthetic requirements.
- -
- Static roof strength;
- -
- Protection against vibration transmission;
- -
- Noise and structural resonance reduction;
- -
- Wind protection (e.g., minimizing edge vortices).
2.5. Environmental and Social Factors in MAWT Assessment
- -
- Residents are involved in the project (e.g., as prosumers);
- -
- The installation serves a demonstration or educational purpose;
- -
- Noise and visual impact are minimal [48].
3. Results
3.1. Classification of Buildings and Locations for MAWT Integration
3.2. Local Scenarios and Reference Conditions
3.3. Forecasted Annual Energy Production (AEP) for Selected MAWT Types
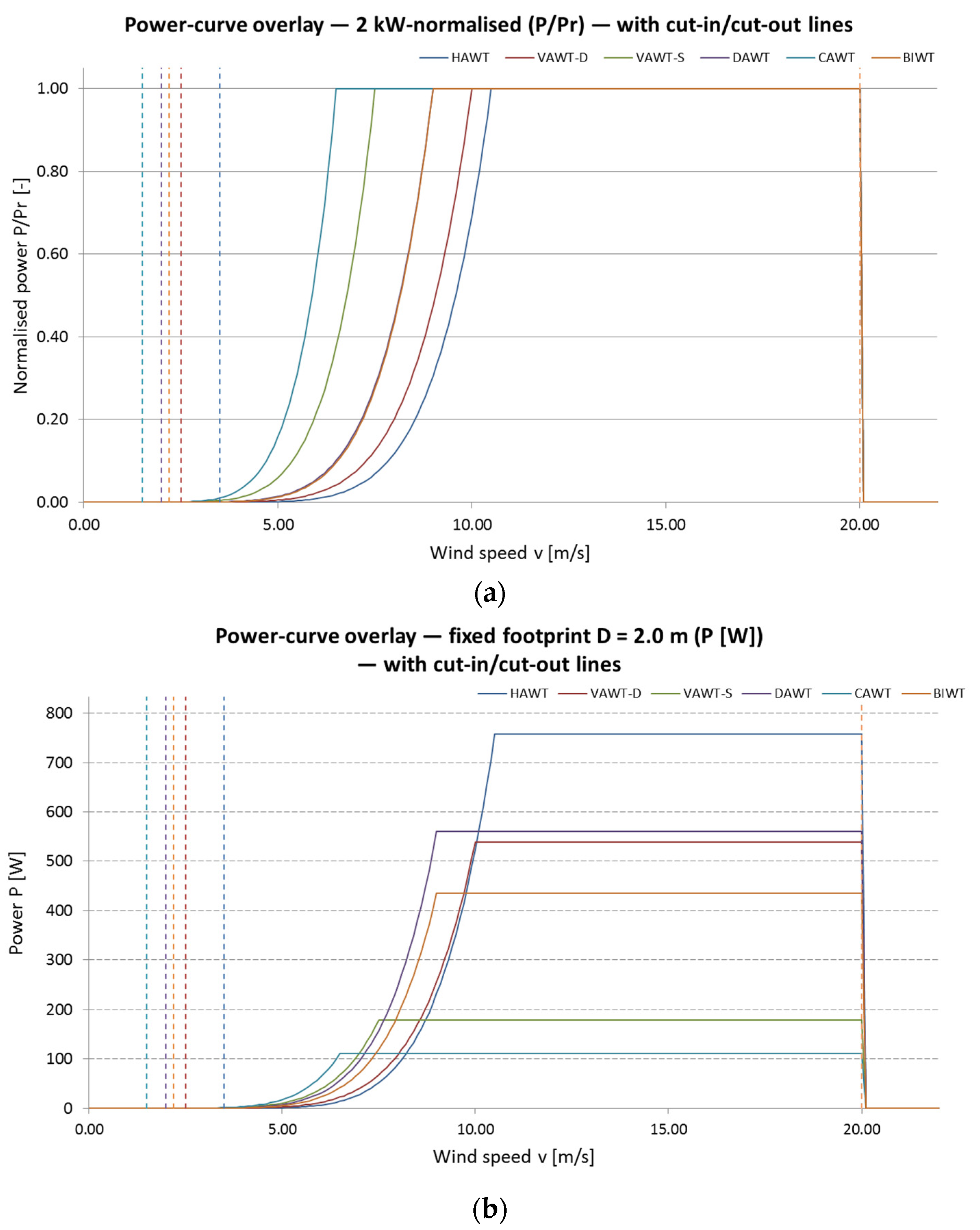
- (i)
- Table 6a—2 kW-normalized curves: Each typology’s power curve is scaled to reach 2 kW at vr while preserving the original cut-in/rated/cut-out thresholds and the (v) shape. This isolates aerodynamic behavior and start-up thresholds.
- (ii)
- Table 6b—Footprint-constrained curves: All typologies are evaluated for a common rotor footprint (D = 2.0 m, swept area ). Here, no rescaling to 2 kW is applied; absolute power is limited by . This view reflects rooftop constraints and yields realistic absolute AEP at the same swept area.
- The original power curve Porig(v) was obtained from manufacturer data or the literature, digitized where necessary, and rescaled so that P(vr) = 2 kW, while retaining its original shape and the manufacturer-specified cut-in, rated, and cut-out wind speeds.
- The manufacturer- or the literature-based performance curve was applied without altering its shape except for the scaling in point 1.
- The probability density f(v) of wind speeds at the considered site was modeled using the Weibull parameters (k, c) in Table 5.
- Annual energy production was computed as
- 5.
- Uncertainty ranges (±1σ) were estimated by propagating the 95% confidence intervals of k and c using Monte Carlo sampling (10,000 iterations).
| (a) | ||||||
| Turbine Type | Reference Model | Rotor Area [m2] | Cut-in [m/s] | Rated [m/s] | Cpmax | AEP [kWh/Year, ±1σ] |
| HAWT | HAWT—Ref. 2 kW | 9.62 | 3.5 | 10.5 | 0.34 | 1254 ± 232 |
| VAWT (Darrieus) | VAWTD–Ref. 2 kW | 3 | 2.5 | 10 | 0.28 | 1033 ± 152 |
| VAWT (Savonius) | VAWTS—Ref. 2 kW | 2.2 | 1.5 | 7.5 | 0.22 | 812 ± 70 |
| DAWT | DAWT—Ref. 2 kW | 4 | 2 | 9 | 0.4 | 1476 ± 176 |
| CAWT | CAWT—Ref. 2 kW | 1.2 | 1.5 | 6.5 | 0.21 | 642 ± 44 |
| BIWT | BIWT—Ref. 2 kW | 2.5 | 2.2 | 9 | 0.31 | 1142 ± 141 |
| (b) | ||||||
| Turbine Type | Reference Model | Rotor Area [m2] | Cut-in [m/s] | Rated [m/s] | Cpmax | AEP [kWh/Year, ±1σ] |
| HAWT | HAWT – Ref. D = 2.0 m | 3.14 | 3.5 | 10.5 | 0.34 | 166 ± 31 |
| VAWT (Darrieus) | VAWTD – Ref. D = 2.0 m | 3.14 | 2.5 | 10 | 0.28 | 172 ± 27 |
| VAWT (Savonius) | VAWTS – Ref. D = 2.0 m | 3.14 | 1.5 | 7.5 | 0.22 | 202 ± 16 |
| DAWT | DAWT – Ref. D = 2.0 m | 3.14 | 2 | 9 | 0.4 | 305 ± 38 |
| CAWT | CAWT – Ref. D = 2.0 m | 3.14 | 1.5 | 6.5 | 0.21 | 192 ± 11 |
| BIWT | BIWT – Ref. D = 2.0 m | 3.14 | 2.2 | 9 | 0.31 | 232 ± 30 |
- -
- DAWT reaches the highest AEP under reference winds due to high Cpmax and low vci;
- -
- BIWT and VAWT-D perform well;
- -
- VAWT-S and CAWT remain competitive at low speeds (low vci) despite lower Cpmax;
- -
- HAWT is disadvantaged in low/turbulent winds because of higher vr, despite a high Cpmax.
- -
- Absolute AEPs are lower (no 2 kW rescaling);
- -
- DAWT leads at rooftop-relevant winds, followed by BIWT and VAWT-S;
- -
- HAWT approaches the leaders only at higher speeds (benefiting from large vr);
- -
- Rankings shift because A is equalized and typology-specific vci, vr, Cpmax govern the usable part of the distribution.
| Location | HAWT | VAWT-D | VAWT-S | DAWT | CAWT | BIWT |
|---|---|---|---|---|---|---|
| B1M | 841 | 697 | 524 | 1065 | 421 | 679 |
| B2P | 978 | 811 | 599 | 1227 | 486 | 790 |
| B2M | 1022 | 861 | 648 | 1355 | 525 | 845 |
| B3M | 1104 | 921 | 693 | 1463 | 561 | 904 |
| B4P | 1166 | 972 | 732 | 1545 | 591 | 954 |
| B4M | 1215 | 1012 | 764 | 1609 | 617 | 992 |
| B5M | 1350 | 1125 | 847 | 1792 | 687 | 1102 |
| B6M | 1428 | 1190 | 896 | 1895 | 727 | 1165 |
| B7M | 965 | 805 | 605 | 1280 | 491 | 780 |
- AEP increases with mounting height and exposure. In the lowest site (B1M), most typologies produce < 950 kWh/year, with DAWT ≈ 1065 kWh as the only exception (Table 7). This confirms the limited feasibility of MAWT on low-rise buildings without access to free flow.
- Top yields occur in B5M–B6M. The highest AEP values are delivered by DAWT, reaching ≈ 1.8–1.9 MWh/year (e.g., 1895 kWh in B6M). HAWT peaks around 1.43 MWh/year (B6M), i.e., does not reach the 1.8–2.0 MWh range (Table 7). For the 2 kW class, this corresponds to capacity factors ≈ 0.06–0.11, not ~0.25.
- DAWT is the top performer across all locations (B1M–B7M). HAWT typically ranks second in stronger-wind sites (e.g., B5M–B6M), while VAWT-D is consistently moderate, above VAWT-S and CAWT but below HAWT/DAWT (Table 7).
- BIWT sits in the mid-range; generally above VAWT-S and CAWT and below HAWT and DAWT, with a relative advantage in mid-to-strong wind settings (e.g., B4–B6) (Table 7).
- B2P vs. B2M show consistent, modest differences (≈4–10%) with the modeled series tending higher, reflecting differences in height reference, turbulence intensity, and local morphology (Table 7).
- Design/placement implications: Turbine choice should follow site characteristics. Tall buildings (B5–B6) enable efficient use of HAWT/DAWT; in space- or noise-constrained settings, VAWT-S, BIWT, or CAWT may be preferable despite lower AEP, owing to compactness and lower acoustic impact.
3.4. The Impact of Turbines on User Comfort and the Environment
- Noise and acoustic profile—Expressed as sound pressure level ranges in dB(A) at a standard reference distance of 10 m, measured under conditions close to rated wind speed. The ranges reflect typical variability with wind speed, blade geometry, and mounting configuration. Data are derived from manufacturer documentation, field measurement reports, and peer-reviewed literature on small turbine aeroacoustics [18,19,24,30,31,34,44].
3.5. Multi-Criteria Evaluation of the Effectiveness and Usefulness of MAWTs
- Energy efficiency (E)—Based on annual energy production (AEP).
- Environmental impact and user comfort (C)—Including noise, vibration, stroboscopic effect, and social acceptance. In urban contexts, this axis is dominated by three constraints: LAeq noise at 10 m, structural vibration, and shadow flicker.
- Suitable for local conditions (L)—Taking into account the impact of turbulence, installation height, openness, and regulatory compliance.
- Energy efficiency (AEP): Mapped from the relative ranking and spread established in Table 6a,b (reference-site and fixed-footprint views).
- Acoustic comfort (noise): Informed by the small-wind noise and annoyance literature, including low-frequency effects. Reported values are based on LAeq levels at 10 m distance; higher scores reflect quieter designs and lower tip speeds [34].
- Shadow flicker: Qualitative risk reflecting rotor diameter/TSR and urban geometry, following recent syntheses on urban wind environmental effects [17].
- Structural vibration and shake: Based on feasibility evidence for building-mounted small-wind and rooftop transmission considerations [31].
- Operational safety: Referenced to small-wind design and safety guidance [24] (IEC 61400-2).
- Architectural and technical integration: Guided by interdisciplinary reviews of wind-powered building skins and integration aspects [21].
- Educational potential: Expert judgment (public-facing safety/visibility, demonstrability) where formal benchmarks are sparse.
- Set 1 (balanced)
- wE = 0.25, wN = 0.12, wF = 0.06, wV = 0.10, wS = 0.12, wA = 0.07, wSA = 0.15, wI = 0.08, wED = 0.05
- Set 2 (urban, noise-sensitive)
- wE = 0.20, wN = 0.20, wF = 0.10, wV = 0.12, wS = 0.10, wA = 0.06, wSA = 0.13, wI = 0.06, wED = 0.03
- Set 3 (off-grid, energy-first)
- wE = 0.35, wN = 0.08, wF = 0.04, wV = 0.08, wS = 0.12, wA = 0.05, wSA = 0.17, wI = 0.06, wED = 0.05
4. Discussions
- BIWT and CAWT turbines were characterized by the highest user comfort ratings, with minimal noise and good architectural integration.
- HAWT and DAWT, despite their high efficiency, generated significant tonal noise (50–65 dB, evaluated as LAeq at 10 m), which could lead to neighbor conflicts if inappropriately located.
- VAWT-S (Savonius) demonstrated the lowest noise levels (evaluated as LAeq at 10 m) and the highest social acceptance—confirming the data from [48].
- A commercial investor can prioritize energy efficiency.
- A municipality or school can focus on social acceptance, aesthetics, and educational potential.
- A designer can assess compliance with building regulations and noise restrictions.
- Meteorological data were based on annual wind speed histograms and Weibull parameters, which do not account for short-term variability and extremes.
- The influence of adjacent dynamic obstacles (e.g., deciduous trees that seasonally change their aerodynamic structure) was not considered.
- User comfort was assessed based on the literature and expert data, without formal public perception studies.
- Turbine acoustics depend on the specific manufacturer’s model and can vary significantly even within the same technology class.
- Incorporating hourly and seasonal data;
- Integration with PV and heat pump models in hybrid systems;
- Assessment of LCOE (levelized cost of energy) in the context of the economic viability of different MAWT types;
- Development of a decision-making application (e.g., in the form of an interactive online platform for prosumers).
5. Conclusions
- MAWT efficiency strongly depends on location, mounting height, and turbulent airflow characteristics. Locations with high building height and good wind exposure (B5–B6) enable achieving annual energy yields (AEP) exceeding 1800 kWh for 2 kW turbines, while in single-family homes (B1), these values fall below 900 kWh/year (Table 7).
- The turbine type should be closely matched to the environmental conditions. DAWTs and HAWTs achieve the highest AEP values in locations with stable airflow, but require good exposure (Table 7). In the built environment, BIWTs, CAWTs, and VAWTs are the better choice, demonstrating greater tolerance to turbulence and improved user comfort (Table 8).
- Environmental impact and user comfort play a key role in the acceptance of MAWT technology in residential environments. Low noise levels, lack of shadow flicker, and architectural integration increase public acceptance, especially in densely built-up urban areas. Savonius, BIWT, and CAWT turbines achieved the highest comfort and aesthetic ratings (Table 8).
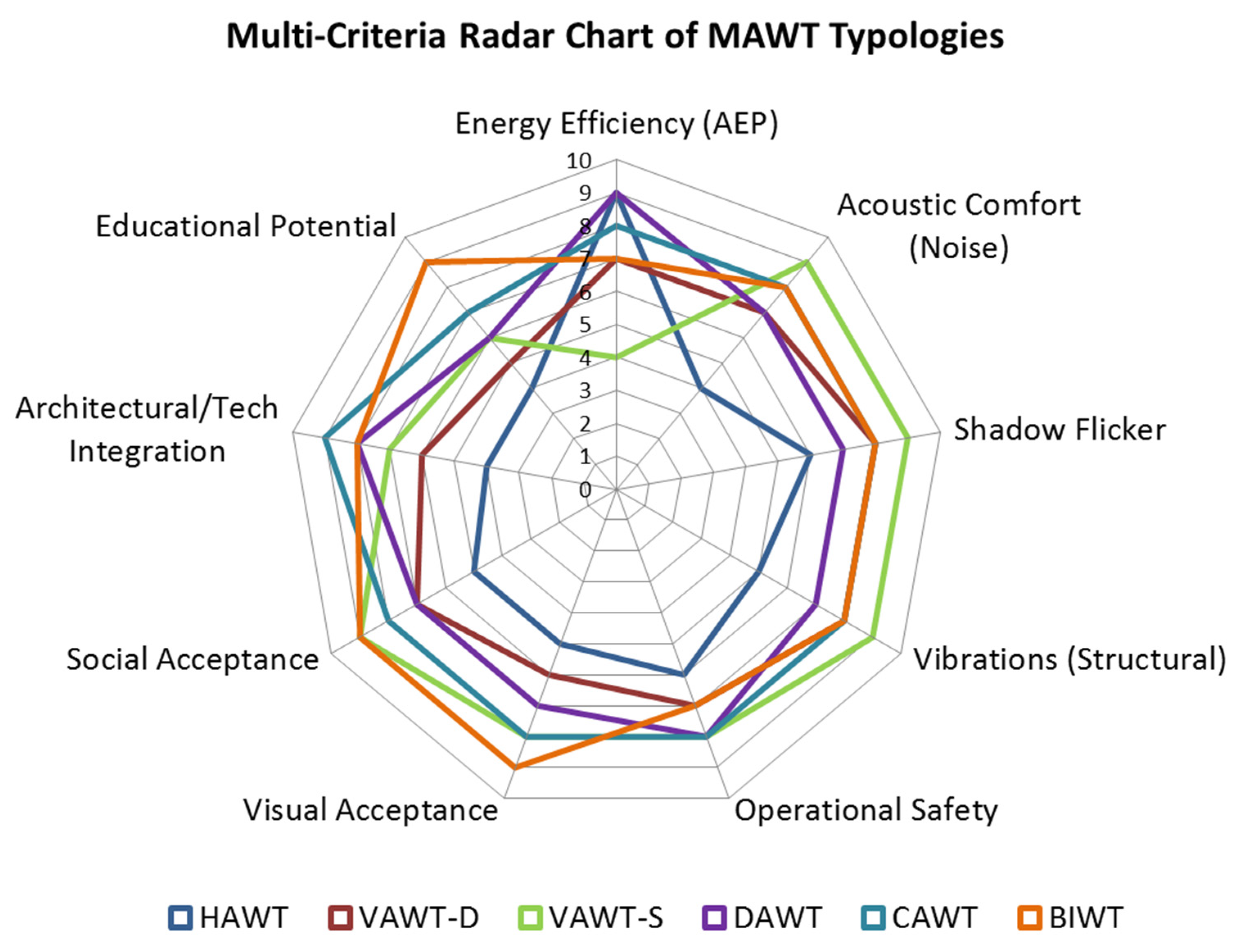
- The proposed MAWT-Score assessment methodology, supplemented by a radar chart for nine qualitative criteria (Figure 4), enables a transparent and scalable assessment of various turbine types. This framework allows tailoring technology selection to the investor’s needs, local conditions, and social and legal requirements.
- The assessment model can be expanded to include additional aspects, such as levelized cost of energy (LCOE), integration with PV and storage, and life-cycle assessment (LCA) for a comprehensive sustainability assessment. This opens up opportunities for integrating the method into planning tools and decision-making applications for prosumers and local government units.
- The MAWT industry requires further standardization and research into micro-scale environmental impacts. This particularly applies to acoustics, structural vibrations, and the stroboscopic effect in urban environments, which are currently not clearly regulated but can significantly impact the perception of installations (Table 8).
- Although the methodology was developed using wind and urban conditions typical of Central Europe, it is applicable in other climatic regions provided that key input parameters—such as terrain roughness, turbulence intensity (TI), and atmospheric stability—are localized to reflect site-specific conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anup, K.C.; Whale, J.; Urmee, T. Urban wind conditions and small wind turbines in the built environment: A review. Renew. Energy 2019, 131, 268–283. [Google Scholar] [CrossRef]
- Sunderland, K.; Woolmington, T.; Blackledge, J.; Conlon, M. Small wind turbines in turbulent (urban) environments: A consideration of normal and Weibull distributions for power prediction. J. Wind. Eng. Ind. Aerodyn. 2013, 121, 70–81. [Google Scholar] [CrossRef]
- Teimourian, H.; Abubakar, M.; Yildiz, M.; Teimourian, A. A Comparative Study on Wind Energy Assessment Distribution Models: A Case Study on Weibull Distribution. Energies 2022, 15, 5684. [Google Scholar] [CrossRef]
- Moreira, R.; Sousa, J.; Camus, C. Challenges and Opportunities in the Integration of Wind Turbines in Urban Areas: A Technical and Economic Analysis. In Proceedings of the 2025 21st International Conference on the European Energy Market (EEM), Lisbon, Portugal, 27–29 May 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Anjan, P.S.; Pranav, A.P.; Venugopal, A.; Yashwanth, V.; Champa, P.N. Energy Generation using vertical Axis Wind Turbine. In Proceedings of the 2025 International Conference on Intelligent and Innovative Technologies in Computing, Electrical and Electronics (IITCEE), Bengaluru, India, 16–17 January 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Ghosh, M.K.; Gupta, S.; Sharma, T. Wind Power from Vehicle-Induced Flow: A Sustainable Solution of Bi-Directional Vertical Wind Turbines in Renewable Energy Generation. In Proceedings of the 2025 International Conference in Advances in Power, Signal, and Information Technology (APSIT), Bhubaneswar, India, 23–25 May 2025; pp. 1–7. [Google Scholar] [CrossRef]
- Apu, A.R.; Mazumder, G.C.; Dey, D.; Ashiquzzaman, M.; Pathik, B.B.; Ghosh, H.R. Development and Performance Analysis of Darrieus and Savonius Turbines Using QBlade. In Proceedings of the 2025 4th International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 11–12 January 2025; pp. 146–150. [Google Scholar] [CrossRef]
- Marinić-Kragić, I.; Pehnec, I.; Bulić, D.; Čolović, T. Genetic Algorithm-Optimized Wind Tunnel for Experimental Validation of High-Efficiency Savonius Wind Turbines. In Proceedings of the 2025 10th International Conference on Smart and Sustainable Technologies (SpliTech), Bol, Croatia, 16–20 June 2025; pp. 1–4. [Google Scholar] [CrossRef]
- Kardous, M.; Chaker, R.; Aloui, F.; Abidi, I. Locations of vortices and their impacts on the aerodynamic performances of a diffuser and a DAWT. In Proceedings of the 2016 3rd International Conference on Renewable Energies for Developing Countries (REDEC), Zouk Mosbeh, Lebanon, 13–15 July 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Michal, L.; Maciej, K.; Krzysztof, J. Analysis and comparison of numerical methods for design and development of small Diffuser-Augmented Wind Turbine (DAWT). In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 5525–5531. [Google Scholar] [CrossRef]
- Nasution, A.; Purwanto, D.W. Optimized curvature interior profile for Diffuser Augmented Wind Turbine (DAWT) to increase its energy-conversion performance. In Proceedings of the 2011 IEEE Conference on Clean Energy and Technology (CET), Kuala Lumpur, Malaysia, 27–29 June 2011; pp. 315–320. [Google Scholar] [CrossRef]
- Elfante, P.B.M.; Santiago, C.T.K.; Tan, R.E.G.; Revalde, J.C.M.; Augusto, G.L.; Gonzaga, J.A.; Chua, J.A.T.; Lim, L.A.G. Numerical Simulation of a Double-Layer H-Darrieus Cross-Axis Wind Turbine. In Proceedings of the 2023 IEEE 15th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment, and Management (HNICEM), Coron, Palawan, Philippines, 19–23 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Seralathan, S.; Revanth Gupta, J.S.; Micha Premkumar, T.; Balaji, R.; Prasanth, D.; Hariram, V. Experimental and Numerical Studies on a Cross Axis Wind Turbine. In Proceedings of the 2019 2nd International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 21–23 August 2019; pp. 185–190. [Google Scholar] [CrossRef]
- Bao, D.; Shi, Z.; Li, C.; Jiang, A.; Han, Q.; Luo, Y.; Zhang, S. A Study on the Influence of Different Inflow Conditions on the Output Power and Dynamic Response Characteristics of a Variable Pitch Wind Turbine Structure. Energies 2024, 17, 5818. [Google Scholar] [CrossRef]
- Gan, S.; Li, G.; Li, H. Assessment of wind energy potential within through-building openings under twisted wind flows. Build. Environ. 2023, 244, 110773. [Google Scholar] [CrossRef]
- Darvishyadegari, M.; Hassanzadeh, R. Evaluation of a Savonius wind turbine in the vicinity of a circular cross-sectional building. J. Build. Eng. 2024, 93, 109818. [Google Scholar] [CrossRef]
- Tsionas, I.; Llaguno-Munitxa, M.; Stephan, A. Environmental effects of urban wind energy harvesting: A review. Build. Cities 2025, 6, 2087. [Google Scholar] [CrossRef]
- Zagubień, A.; Wolniewicz, K. Energy Efficiency of Small Wind Turbines in an Urbanized Area—Case Studies. Energies 2022, 15, 5287. [Google Scholar] [CrossRef]
- Dar, A.S.; Waridel, F.; Porté-Agel, F. Effect of roof fence shape on flow over a building and its impact on wind turbine performance. Renew. Energy 2025, 238, 121859. [Google Scholar] [CrossRef]
- Brandi, A.; Manoli, G. Meteorological assessment of vertical axis wind turbine energy generation potentials across two Swiss cities in complex terrain. arXiv 2025, arXiv:2501.11117. [Google Scholar]
- Chen, X.; Wang, X.; Qiu, Y.; Hu, H.; Xu, Z.; Wang, X. An interdisciplinary review of the wind-powered building skin. J. Build. Eng. 2024, 95, 110324. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, C.; Jia, Y.; Sui, S.; Zuo, C.; Liu, X. Studies on Performance of Distributed Vertical Axis Wind Turbine under Building Turbulence. Energy Eng. 2023, 120, 729–742. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, H.; Du, B.; Ge, M. Effects of a rooftop wind turbine on the dispersion of air pollutant behind a cube-shaped building. Theor. Appl. Mech. Lett. 2021, 11, 100296. [Google Scholar] [CrossRef]
- IEC 61400-2:2013; Wind Turbines—Part 2: Small Wind Turbines. International Standard; International Electrotechnical Commission: Geneva, Switzerland, 11 December 2013. Available online: https://webstore.iec.ch/en/publication/5433 (accessed on 1 August 2025).
- Seguro, J.V.; Lambert, T.W. Modern Estimation of the Parameters of the Weibull Wind Speed Distribution for Wind Energy Analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- Justus, C.G.; Hargraves, W.R.; Mikhail, A.; Graber, D. Methods for Estimating Wind Speed Frequency Distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov–Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Stephens, M.A. EDF Statistics for Goodness of Fit and Some Comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Sorensen, J.N. Aerodynamic Aspects of Wind Energy Conversion. Annu. Rev. Fluid Mech. 2011, 43, 427–448. [Google Scholar] [CrossRef]
- IEC 61400-1:2019; Wind Energy Generation Systems—Part 1: Design Requirements. International Standard; International Electrotechnical Commission: Geneva, Switzerland, 22 February 2019. Available online: https://webstore.iec.ch/publication/64374 (accessed on 1 August 2025).
- Dutton, A.G.; Halliday, J.A.; Blanch, M.J. The Feasibility of Building-Mounted/Integrated Wind Turbines (BUWTs): Achieving Their Potential for Carbon Emission Reductions; Energy Research Unit; CCLRC: London, UK, 2005; Available online: https://ukerc9.rl.ac.uk/cgi-bin/publicationsDiscover.pl?Action=detail&publicationid=4e7c4ab7-ef49-4dd2-90cc-a1af66759db2 (accessed on 25 July 2025).
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Masters, G.M. Renewable and Efficient Electric Power Systems; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Leventhall, H.G. Low frequency noise and annoyance. Noise Health 2004, 6, 59–72. [Google Scholar] [PubMed]
- Saidur, R.; Rahim, N.A.; Islam, M.R.; Solangi, K.H. Environmental impact of wind energy. Renew. Sustain. Energy Rev. 2011, 15, 2423–2430. [Google Scholar] [CrossRef]
- Building Law Act of 7 July 1994 (Ustawa z dnia 7 lipca 1994 r.—Prawo Budowlane). Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu19940890414 (accessed on 3 August 2025).
- Regulation of the Minister of Infrastructure of 12 April 2002 on the Technical Conditions to Be Met by Buildings and Their Location (Rozporządzenie Ministra Infrastruktury z dnia 12 Kwietnia 2002 r. w Sprawie Warunków Technicznych, Jakim Powinny Odpowiadać Budynki i ich Usytuowanie), Journal of Laws 2002 No. 75, Item 690. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu20020750690 (accessed on 3 August 2025).
- European Commission. Energy. Available online: https://commission.europa.eu/topics/energy_en (accessed on 3 August 2025).
- BauGB—Building Code. Available online: https://www.gesetze-im-internet.de/bbaug/BJNR003410960.html (accessed on 3 August 2025).
- Ordinance on the Building Use of Land. Available online: https://www.gesetze-im-internet.de/baunvo/ (accessed on 3 August 2025).
- Permitted Development Rights—Planning Permission—Planning Portal. Available online: https://www.planningportal.co.uk/permission/responsibilities/planning-permission/permitted-development-rights (accessed on 3 August 2025).
- The Department of Energy’s Energy.gov. Department of Energy. Available online: https://www.energy.gov/ (accessed on 3 August 2025).
- Troen, I.; Petersen, L.E. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989; ISBN 87-550-1482-8. [Google Scholar]
- Blocken, B.; Stathopoulos, T.; van Beeck, J.P.A.J. Pedestrian-level wind conditions around buildings: Review of wind-tunnel and CFD techniques and their accuracy for wind comfort assessment. Build. Environ. 2016, 100, 50–81. [Google Scholar] [CrossRef]
- Westerlund, M. Social Acceptance of Wind Energy in Urban Landscapes. TIM Rev. 2020, 10, 49–62. [Google Scholar] [CrossRef]
- Bereziartua-Gonzalez, L.; Retegi, A.; Ukar, O. Human-centered integration of small wind turbines in urban environments: A semi-systematic review from an industrial design perspective. Front. Sustain. Cities 2025, 7, 42703. [Google Scholar] [CrossRef]
- Pasqualetti, M.J. Opposing Wind Energy Landscapes: A Search for Common Cause. Ann. Assoc. Am. Geogr. 2011, 101, 907–917. [Google Scholar] [CrossRef]
- Wolsink, M. Planning of renewables schemes: Deliberative and fair decision-making on landscape issues instead of reproachful accusations of non-cooperation. Energy Policy 2007, 35, 2692–2704. [Google Scholar] [CrossRef]
- Abdelsalam, A.M.; Abdelmordy, M.; Ibrahim, K.A.; Sakr, I.M. An investigation on flow behavior and performance of a wind turbine integrated within a building tunnel. Energy 2023, 280, 128153. [Google Scholar] [CrossRef]
- Naji, M.M.; Jabbar, B.A. Diffuser augmented wind turbine: A review study. In Proceedings of the 3rd International Conference on Engineering and Science, Al-Samawa, Iraq, 3–4 May 2023; p. 100015. [Google Scholar] [CrossRef]
- Didane, D.H.; Behery, M.R.; Al-Ghriybah, M.; Manshoor, B. Recent Progress in Design and Performance Analysis of Vertical-Axis Wind Turbines—A Comprehensive Review. Processes 2024, 12, 1094. [Google Scholar] [CrossRef]
| Class | Average Annual Velocity Vavg [m/s] | Typical Locations | Example of MAWT Application | Expected AEP for a 2 kW Turbine [kWh/Year] |
|---|---|---|---|---|
| A—high | >6.0 m/s | Open areas, coastlines, high roofs | MAWT HAWT/VAWT in independent installations | >3000 |
| B—moderate | 4.5–6.0 m/s | Suburbs, mid-rise roofs | MAWT CAWT, DAWT, BIWT with buffer | 1500–3000 |
| C—low | 3.0–4.5 m/s | Urban roofs, compact development | MAWT WLT, Savonius, integrated systems | <1500 |
| D—marginal | <3.0 m/s | Deep downtown development | Rarely profitable—only educationally | <500 |
| (a) | |||||||
| Turbine Type | Aerodynamics | Axis of Rotation | TSR | Cpmax | vci [m/s] | vr [m/s] | Tolerance TI |
| HAWT 3-blade | Load-bearing | Horizontal | 6–8 | 0.35–0.40 | 3 | 10–12 | Low–Medium |
| HAWT multi-blade | Resistance | Horizontal | ~1 | 0.25 | 1.5–2.5 | 8–10 | High |
| VAWT—Darrieus | Load-bearing | Vertical | 3–5 | 0.28–0.32 | 3–5 | 10–12 | Medium |
| VAWT—Helical | Load-bearing | Vertical | 2–5 | 0.26–0.30 | 2.5–4 | 9–11 | Medium–High |
| VAWT—Savonius | Resistance | Vertical | <1 | 0.12–0.18 | 1–2 | 6–8 | Very High |
| VAWT—Hybrid | Mixed | Vertical | 1–3 | 0.20–0.30 | 1.5–3 | 8–10 | High |
| DAWT | Diffuser | Horizontal | 4–6 | 0.42–0.48 | 2 | 8–10 | Medium–High |
| CAWT | Transverse | Horizontal | 2–3 | 0.25–0.30 | 2 | 8–10 | High |
| WLT (lenticular) | Load-bearing + lens | Horizontal | 4–6 | 0.45–0.50 | 2 | 8–11 | High |
| BIWT | Integrated | Any | 1–4 | 0.28–0.35 | 2–5 | Depending on location | Very High |
| (b) | |||||||
| Turbine Type | Noise LAeq [dB(A) @ 10 m] | Installation | Aesthetics | Integration | Educational Potential | Capex Index (1–5) | Installation Complexity |
| HAWT 3-blade | 50–60 @50 m | Mast | Moderate | Low | Medium | 4 | High |
| HAWT multi-blade | ~60 | Mast/pumps | Low | Low | Medium | 3 | Medium |
| VAWT—Darrieus | 42–48 @15 m | Low Mast | High | Medium | High | 3 | Medium |
| VAWT—Helical | <45 | Roof/Mast | High | Medium | High | 3 | Medium |
| VAWT—Savonius | ~38 | Roof/floor | Medium | High | Very High | 2 | Low |
| VAWT—Hybrid | Different | Different | High | Medium | High | 3 | Medium |
| DAWT | ~50 | Mast or Roof | Low | Medium | Medium | 5 | High |
| CAWT | <45 | Roof | High | High | High | 3 | Medium |
| WLT (lenticular) | 46–52 | Mast/Roof | Moderate | Medium | Medium | 4 | High |
| BIWT | Niesłyszalny | Elevation/Roof | High | Very High | Very High | 4 | Medium |
| Turbine Type | Noise | Vibrations | Strobe Effect | Risk to Birds | Visual Integration | Social Acceptance |
|---|---|---|---|---|---|---|
| HAWT 3-blade | Medium | Medium | High | Moderate | Low–Moderate | Medium |
| HAWT multi-blade | High | High | High | Moderate | Low | Low |
| VAWT—Darrieus | Low | Low | Medium | Low | High | High |
| VAWT—Helical | Low | Low | Low | Very Low | High | High |
| VAWT—Savonius | Very Low | Very Low | None | Very Low | Medium–High | Very High |
| VAWT—Hybrid | Low | Medium | Medium | Low | Medium–High | High |
| DAWT | Medium | Medium | High | Moderate | Moderate | Medium |
| CAWT | Low | Low | Low | Low | High | High |
| WLT (lenticular) | Medium | Low | Low | Low | High | Medium–High |
| BIWT | Inaudible | Very Low | None | None | Very High | Very High |
| Type | Building Description /Location | Sample Height | Urban Characteristics | Notes on MAWT |
|---|---|---|---|---|
| B1 | Single-family home | 6–8 m | Open or semi-open areas, low building density | Limited access to even wind conditions, but easy rooftop installation. |
| B2 | Low-rise urban building | 10–12 m | Denser development, apartment complexes, e.g., Gdynia Redłowo | Significant impact of wind disturbances, but typical urban conditions require analysis. |
| B3 | Public building | 12–15 m | Schools, clinics, municipal buildings—medium exposure | Stable energy demand, possible integration with PV and MAWT. |
| B4 | 4-5-story residential building | 15–20 m | Medium or high-rise housing development | Height allows for better wind conditions (roof). |
| B5 | Industrial/technical building | 25–35 m | Warehouses, technical industrial buildings | Large roof area, good MAWT location. |
| B6 | High-rise urban building (office, hotel) | 30–60 m | Skyscrapers, hotels, commercial buildings | Very good wind exposure, but risk of noise and resonance. |
| B7 | Autonomous/off-grid building | 5–15 m | Passive houses, shelters, mobile homes in open spaces | Ideal wind conditions, MAWT as the main energy source. |
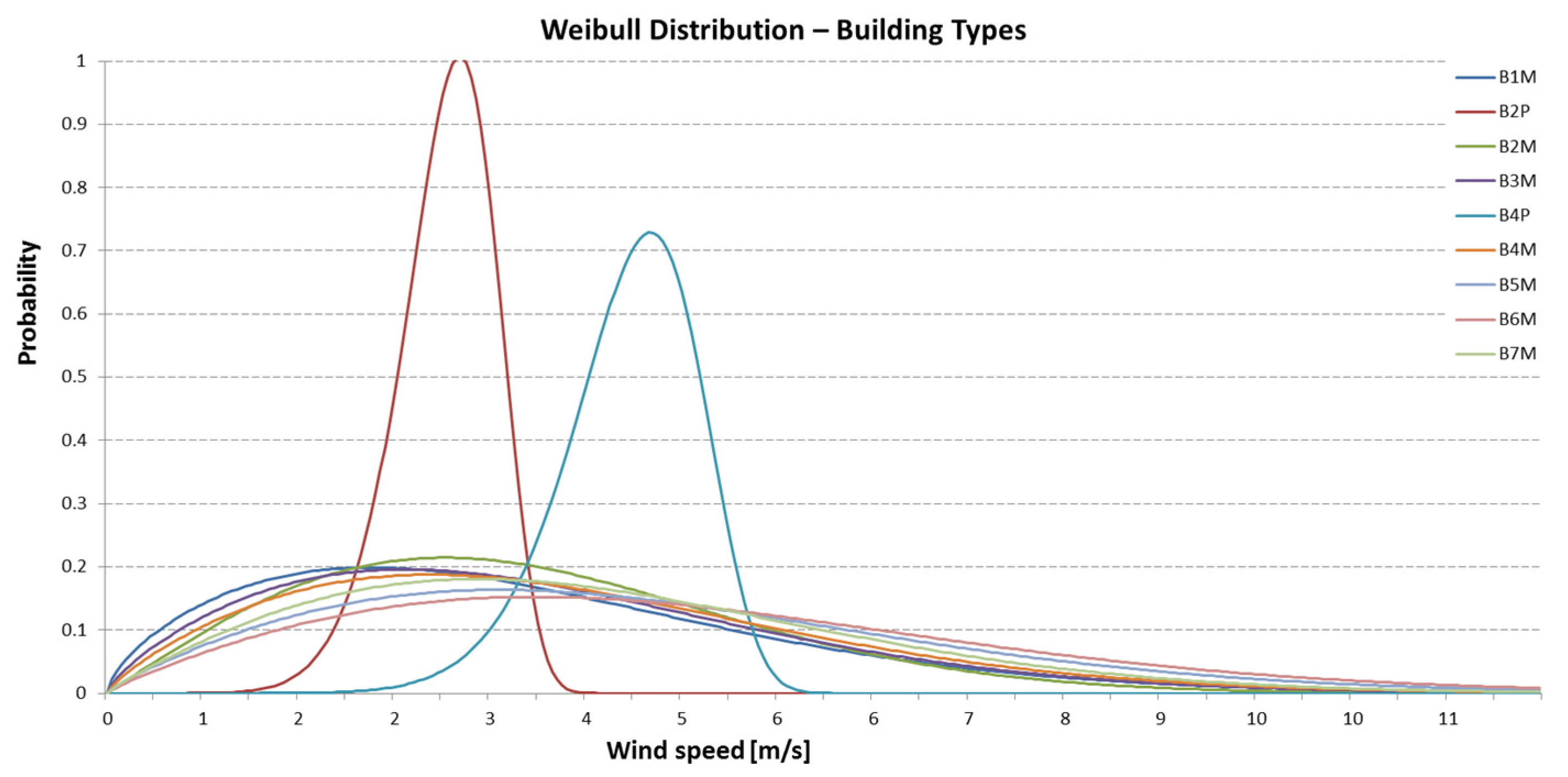
| Building Type | Location | Data Source | k (95% CI) [–] | c (95% CI) [m/s] | Vavg [m/s] | Height Measurement [m] | KS Statistic | AD Statistic |
|---|---|---|---|---|---|---|---|---|
| B1M | Northern Poland—single-family homes | Model | 1.65 (1.52–1.78) | 3.88 (3.74–4.02) | 3.42 | 15 | 0.076 | 0.482 |
| B2P | Gdynia–Rełowo | Measurement | 8.15 (7.92–8.38) | 3 (2.86–3.14) | 2.7 | 12 | 0.082 | 0.501 |
| B2M | Gdynia–Rełowo | Model | 2 (1.88–2.12) | 4 (3.87–4.13) | 3.6 | 15 | 0.069 | 0.463 |
| B3M | Luzino—school | Model | 1.75 (1.63–1.87) | 4.05 (3.92–4.18) | 3.65 | 15 | 0.073 | 0.476 |
| B4P | Kołobrzeg—apartment building | Measurement | 9.08 (8.84–9.32) | 4.61 (4.45–4.77) | 4.1 | 15 | 0.081 | 0.498 |
| B4M | Kołobrzeg—apartment building | Model | 1.79 (1.67–1.91) | 4.28 (4.14–4.42) | 3.76 | 15 | 0.070 | 0.469 |
| B5M | Gdynia—sports hall | Model | 1.85 (1.73–1.97) | 5 (4.85–5.15) | 4.72 | 30 | 0.066 | 0.454 |
| B6M | Gdańsk Wrzeszcz | Model | 1.87 (1.75–1.99) | 5.4 (5.25–5.55) | 5.12 | 40 | 0.064 | 0.447 |
| B7M | Northern Poland | Model | 1.9 (1.78–2.02) | 4.6 (4.46–4.74) | 4 | 15 | 0.068 | 0.459 |
| Turbine Type | Noise Level [LAeq dB(A) @ 10 m] | Stroboscopic Effect | Vibration | Social Acceptance | Installation Notes |
|---|---|---|---|---|---|
| HAWT | 55–65 | High (horizontal rotor) | Moderate (mast- mounted) | Low in densely built-up areas | Requires free space, visually dominant |
| VAWT-D | 45–58 | Low | Moderate | Medium—beneficial for flat roofs | Height may affect resonance |
| VAWT-S | 42–55 | None | Low | High in off-grid locations | Low efficiency but quiet profile |
| DAWT | 50–60 | Medium (rotor cover) | Low–Medium | Medium | Precise tunnel installation required |
| CAWT | 45–52 | Negligible | Very Low | High | Ideal for green or urban roofs |
| BIWT | 48–55 | Configuration dependent | Medium | High in urban areas | High aesthetics and modularity |
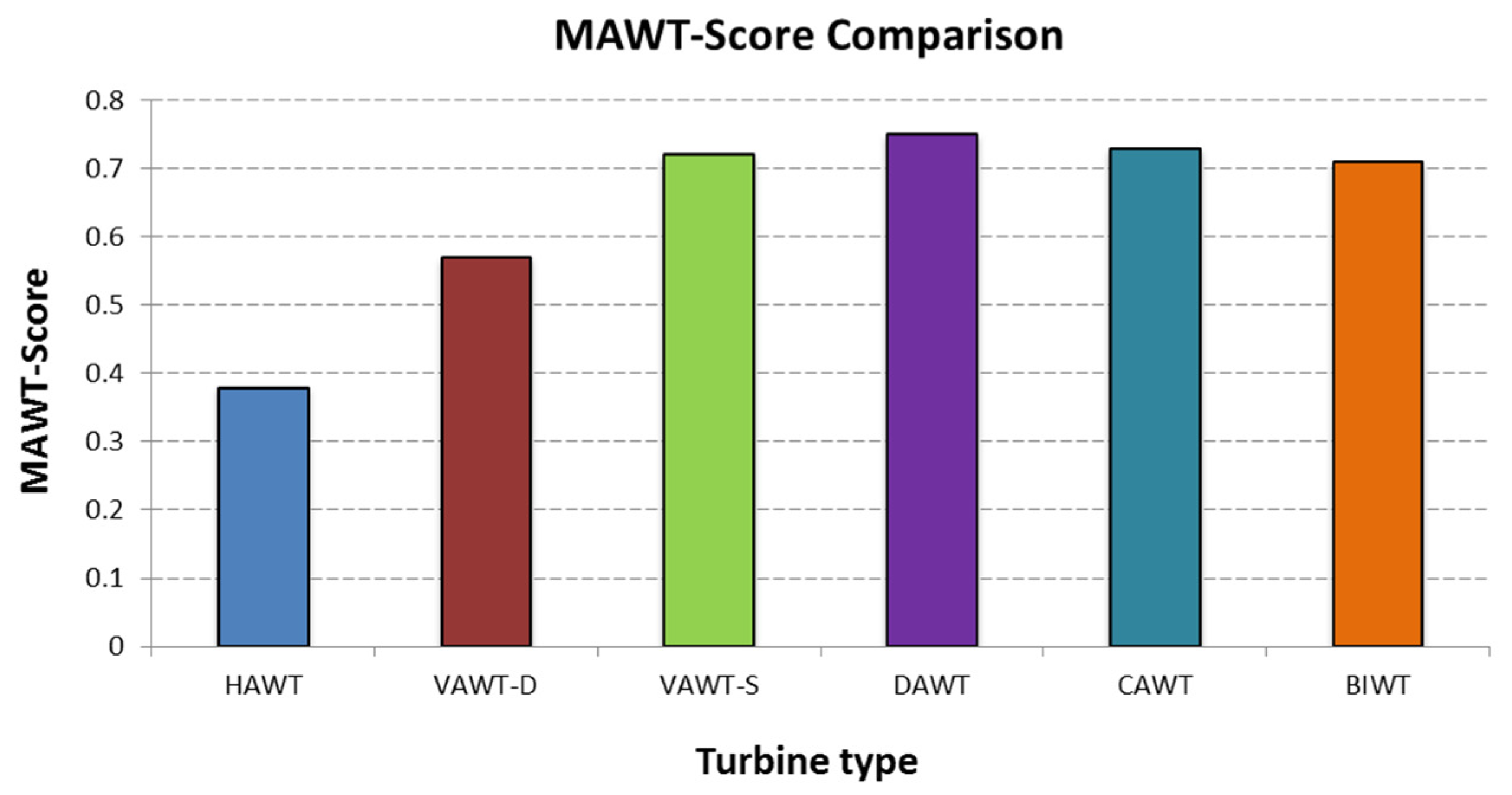
| Turbine Type | AEP Score | Comfort Score | Environmental Score | MAWT-Score |
|---|---|---|---|---|
| HAWT | 0.65 | 0.3 | 0.2 | 0.38 |
| VAWT-D | 0.53 | 0.65 | 0.55 | 0.57 |
| VAWT-S | 0.42 | 0.85 | 0.8 | 0.72 |
| DAWT | 0.81 | 0.65 | 0.75 | 0.75 |
| CAWT | 0.73 | 0.85 | 0.75 | 0.73 |
| BIWT | 0.63 | 0.75 | 0.85 | 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moska, W.; Piechowski, L.; Łebkowski, A. Selection and Classification of Small Wind Turbines for Local Energy Systems: Balancing Efficiency, Climate Conditions, and User Comfort. Energies 2025, 18, 4575. https://doi.org/10.3390/en18174575
Moska W, Piechowski L, Łebkowski A. Selection and Classification of Small Wind Turbines for Local Energy Systems: Balancing Efficiency, Climate Conditions, and User Comfort. Energies. 2025; 18(17):4575. https://doi.org/10.3390/en18174575
Chicago/Turabian StyleMoska, Waldemar, Leszek Piechowski, and Andrzej Łebkowski. 2025. "Selection and Classification of Small Wind Turbines for Local Energy Systems: Balancing Efficiency, Climate Conditions, and User Comfort" Energies 18, no. 17: 4575. https://doi.org/10.3390/en18174575
APA StyleMoska, W., Piechowski, L., & Łebkowski, A. (2025). Selection and Classification of Small Wind Turbines for Local Energy Systems: Balancing Efficiency, Climate Conditions, and User Comfort. Energies, 18(17), 4575. https://doi.org/10.3390/en18174575







