Power Factor Adaptive DPWM Control Strategy for T-Type Three-Level Inverters
Abstract
1. Introduction
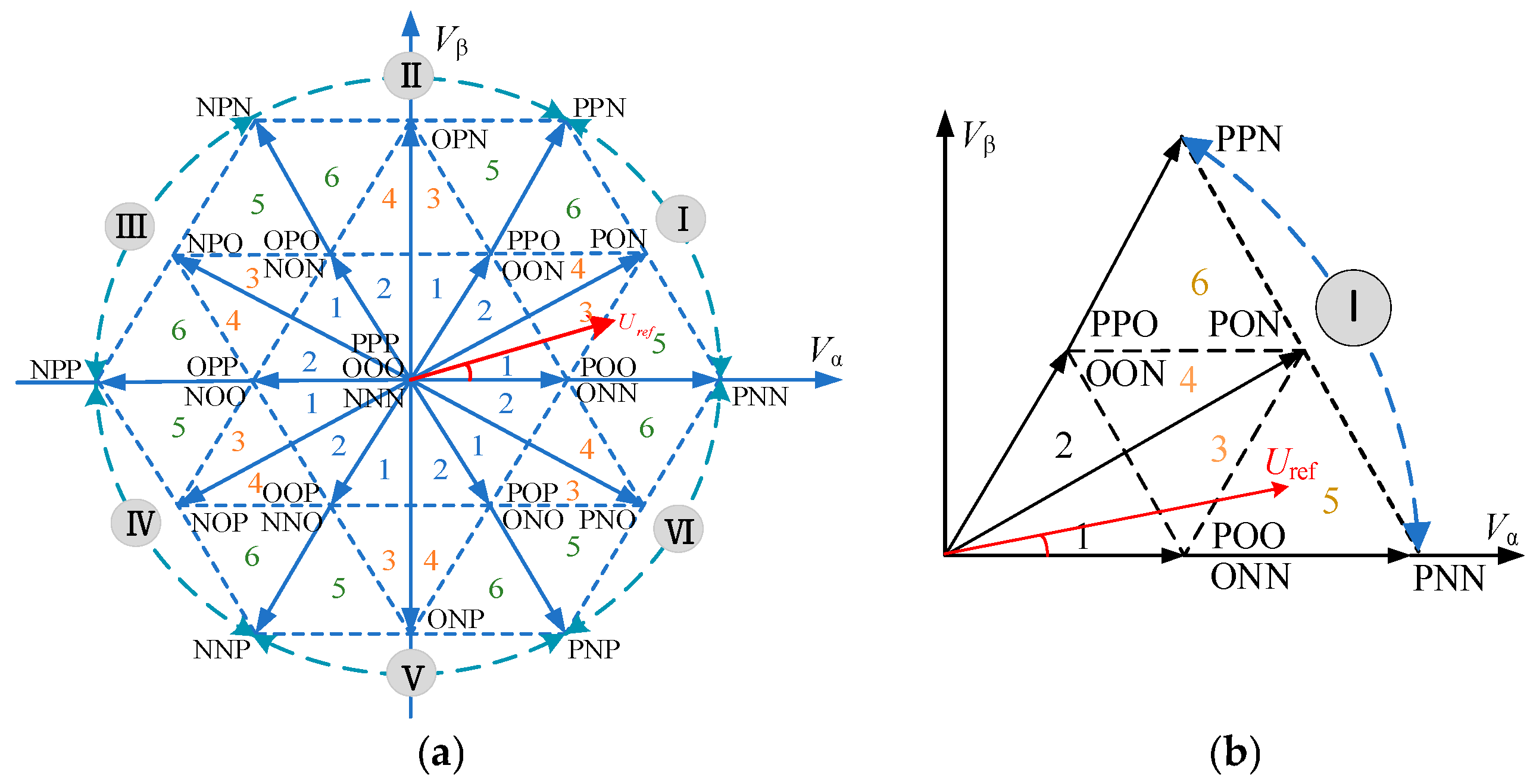
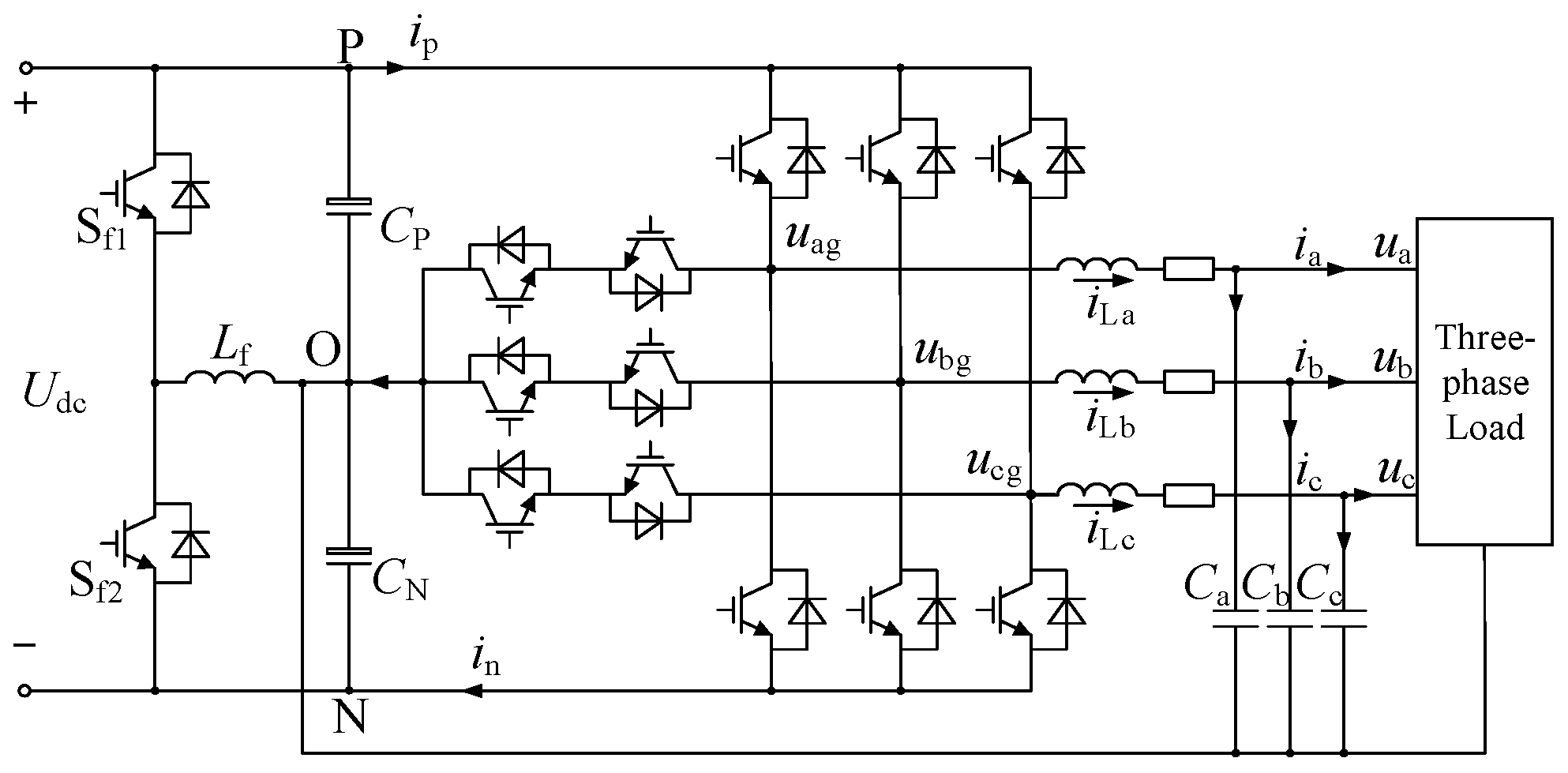
2. Three-Level PFA-DPWM Strategy
2.1. Basic Principle of Three-Level DPWM
2.2. Mathematical Model of Traditional Three-Level DPWM Strategy
2.3. Mathematical Model of Three-Level PFA-DPWM Strategy
3. Analysis of Different Three-Level Carrier Modulation Schemes
- (1)
- PD: All carrier signals are mutually in phase.
- (2)
- POD: The carriers above the zero reference are phase-shifted by 180° relative to those below it.
- (3)
- APOD: Each carrier is phase-shifted by 180° with respect to its adjacent carriers.
- (1)
- The phase voltage contains abundant harmonic components at the carrier frequency. These carrier harmonics are common-mode components and are inherently canceled in the line-to-line voltage.
- (2)
- Harmonics with even-order sidebands are present around odd multiples of the carrier frequency, and harmonics with odd-order sidebands are present around even multiples of the carrier frequency.
- (1)
- The phase voltage spectrum does not contain odd-order carrier frequency harmonics; only their sideband harmonic components are present. Consequently, the harmonic energy is dispersed among them.
- (2)
- The odd-order sideband harmonics surrounding even multiples of the carrier frequency are identical to those produced by the PD scheme.
4. Performance Analysis of Three-Level DPWM Strategies
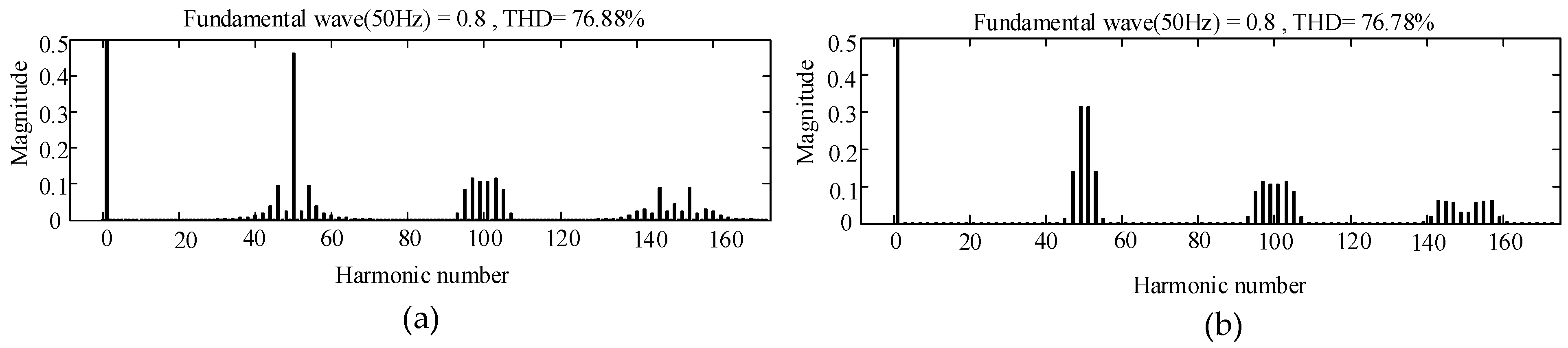
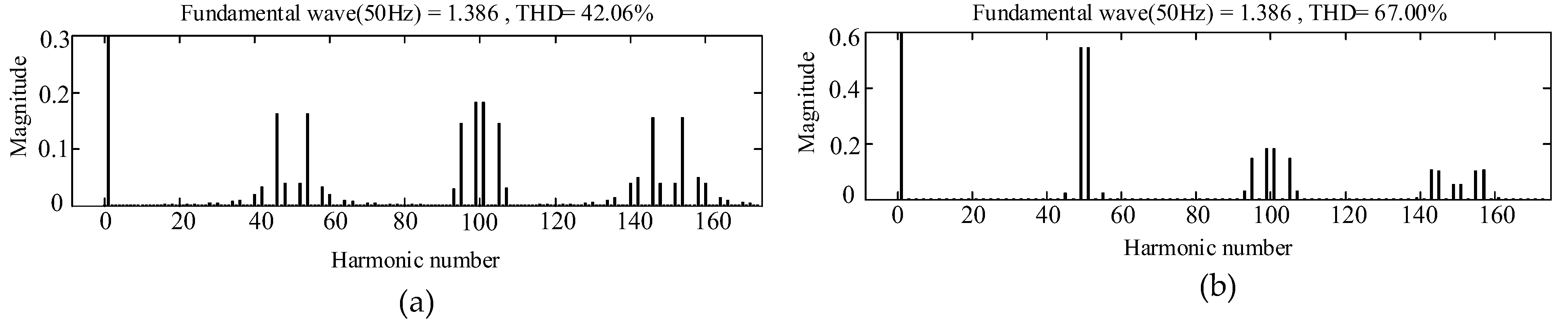
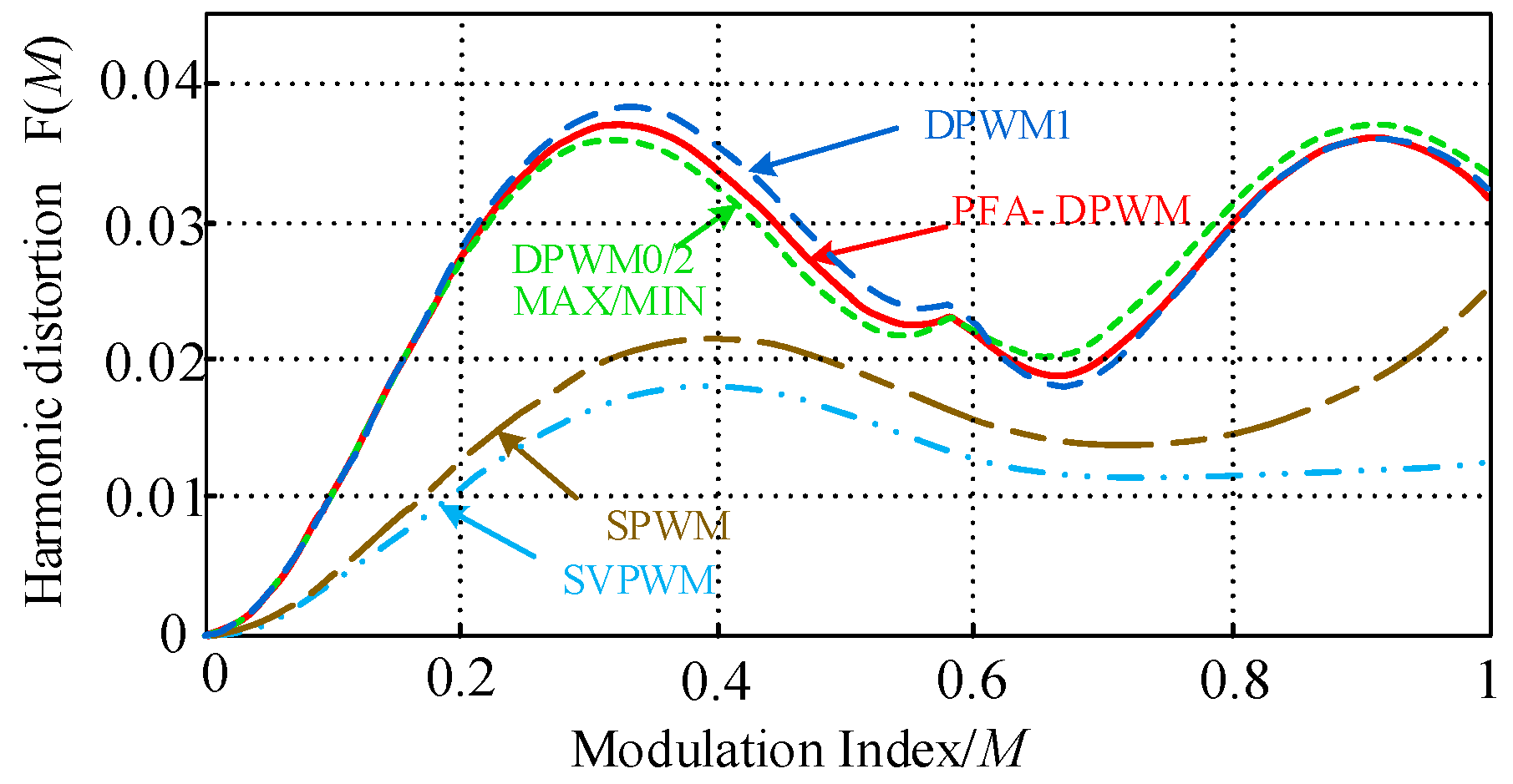
4.1. Harmonic Distortion
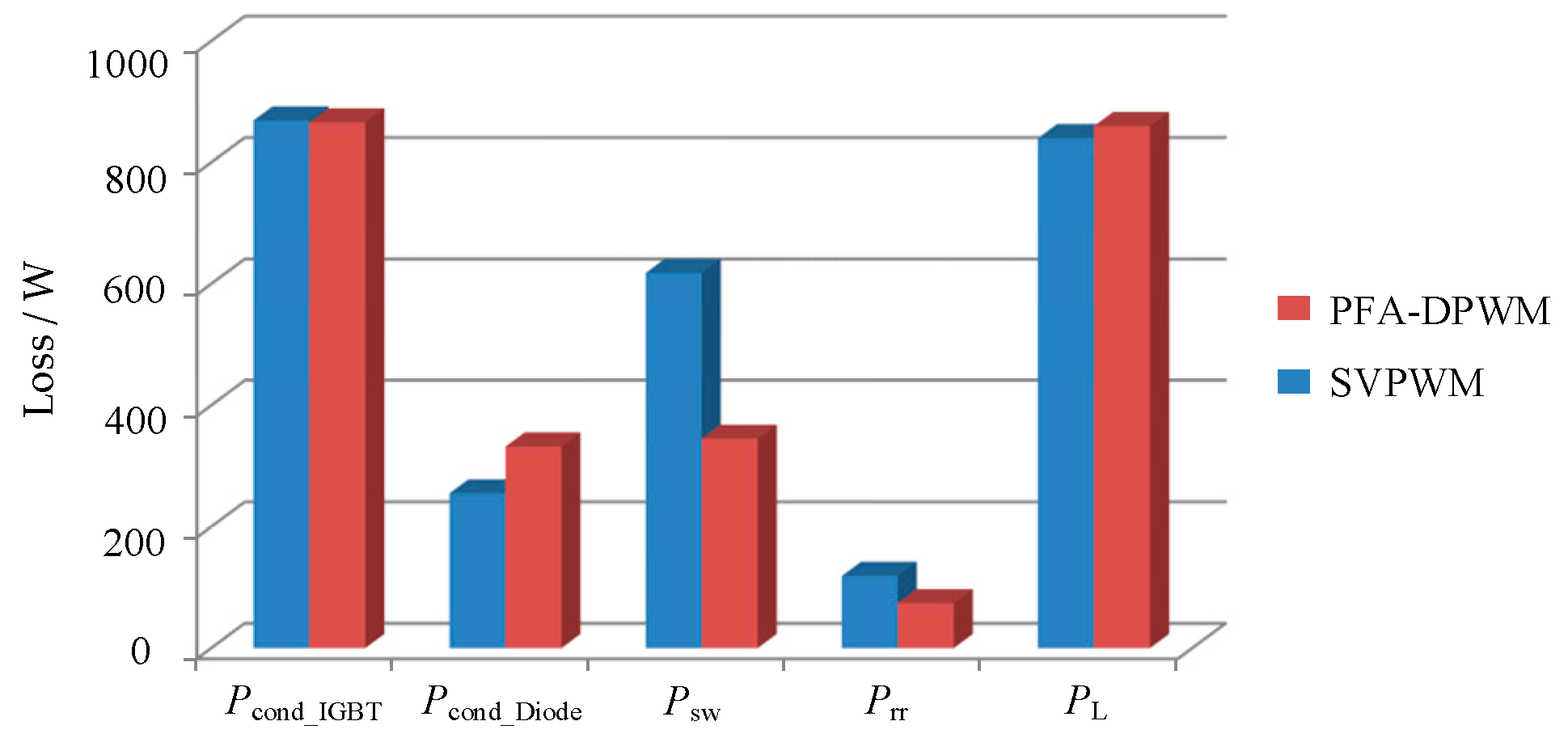
4.2. Switching Losses
4.3. Loss Model and Efficiency Analysis
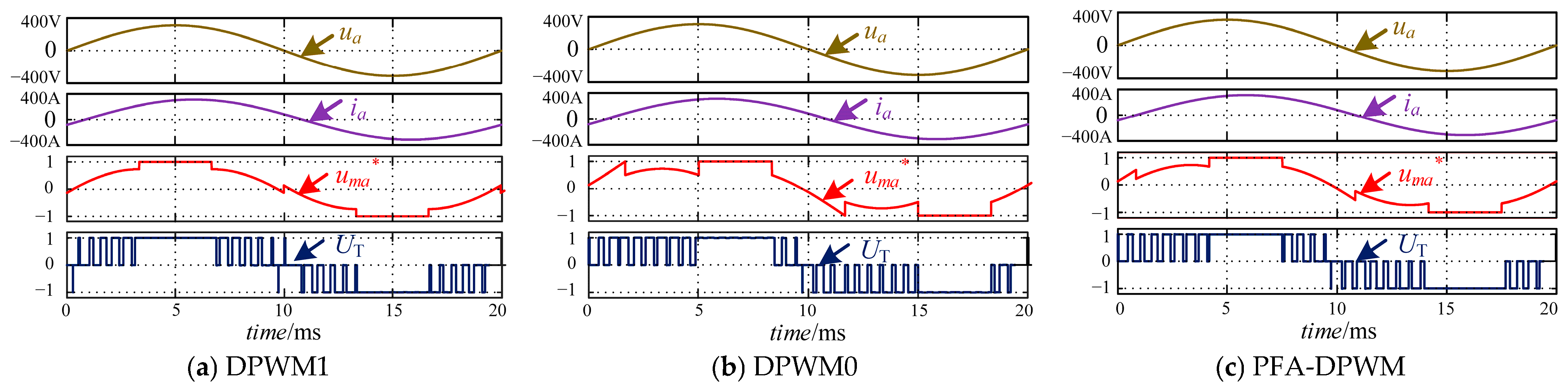
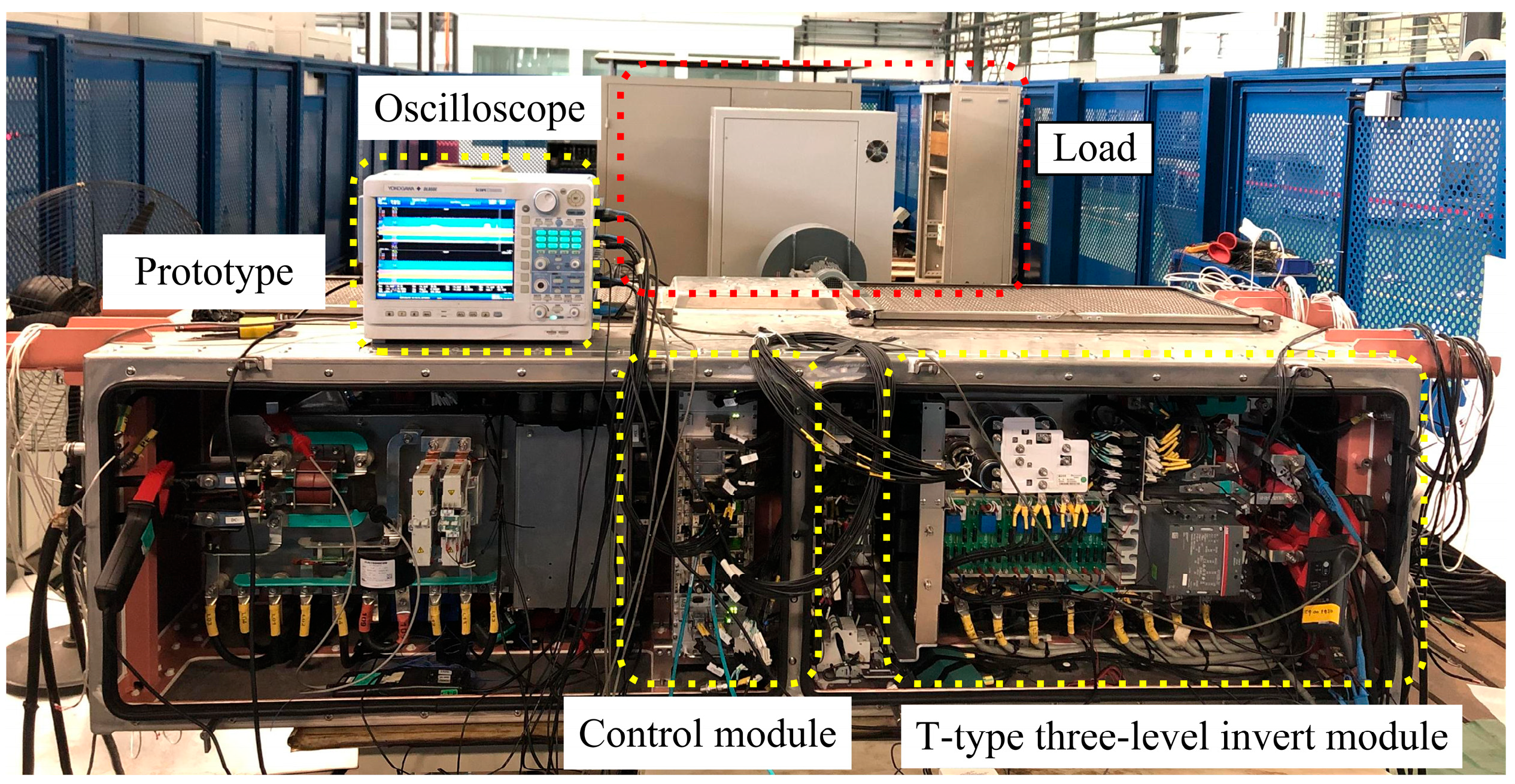
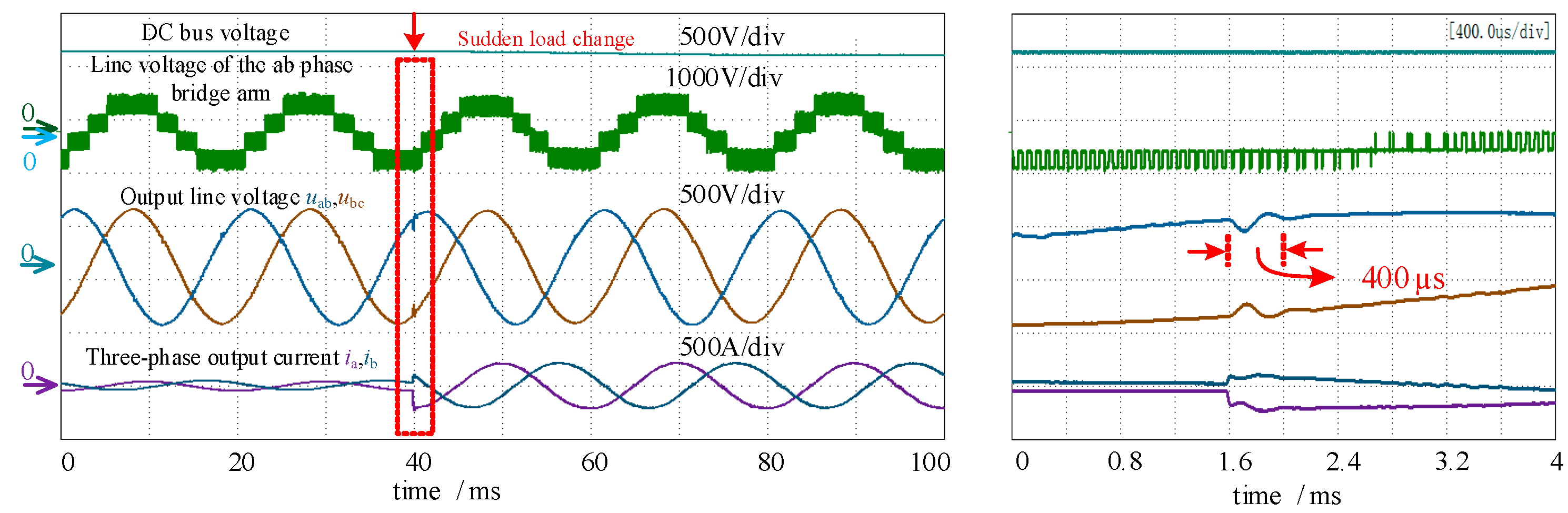
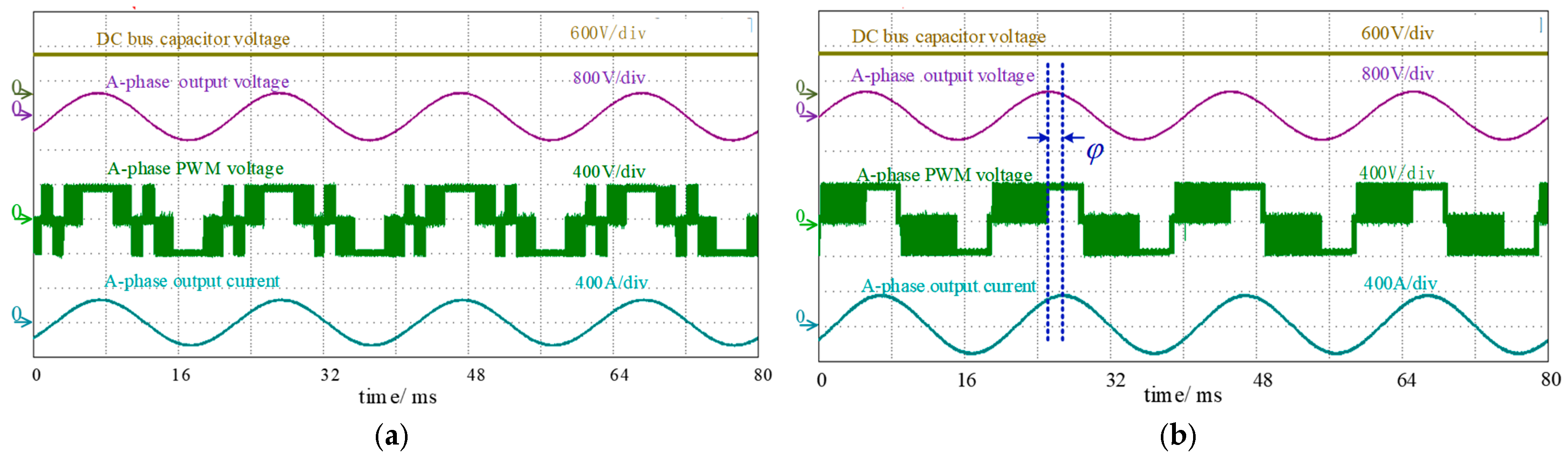
5. Simulation and Experimental Results
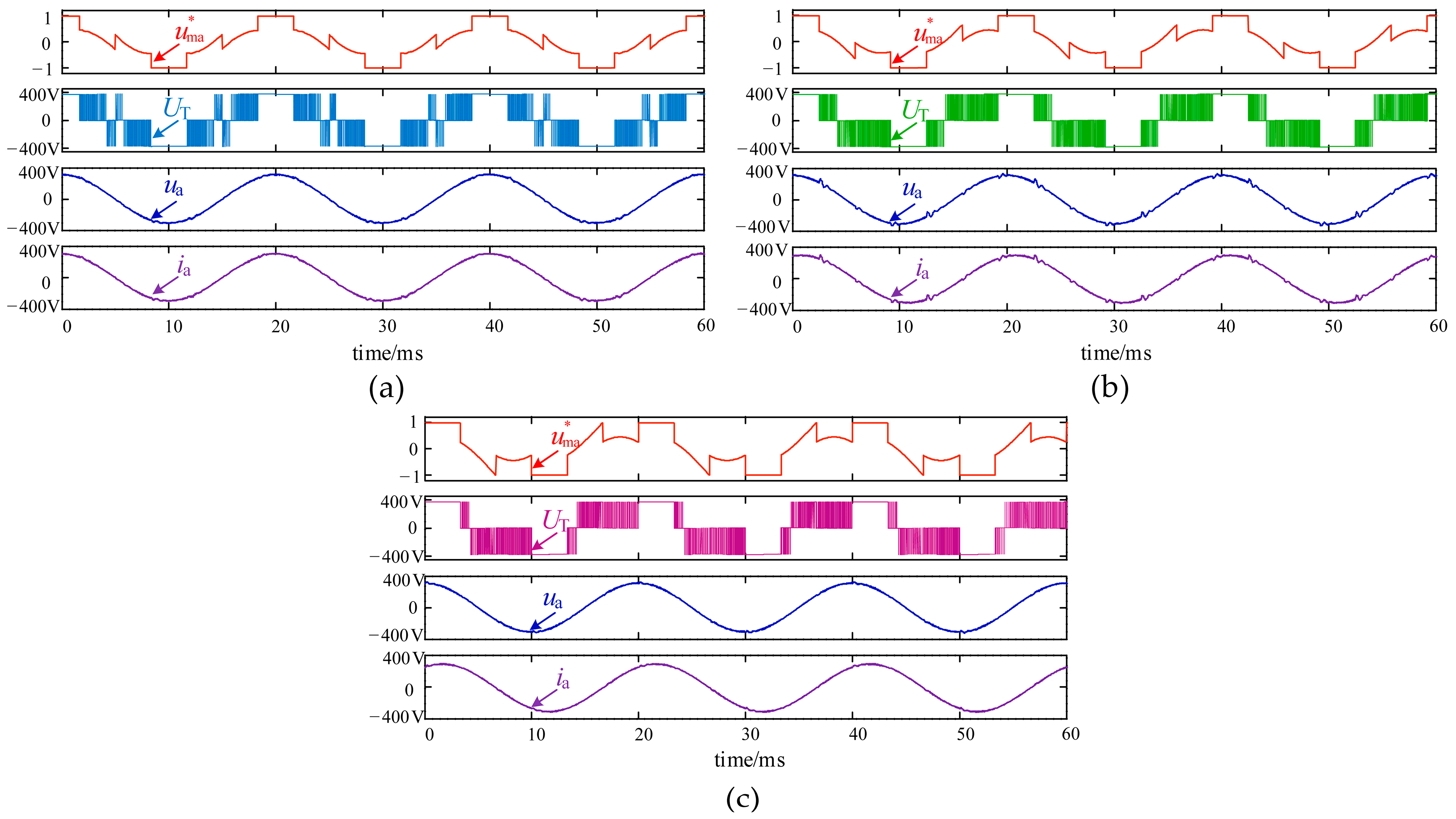
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbols | |
| Parameters | Definitions |
| udc | DC bus voltage |
| M | Modulation index |
| and | Modulation signals of three-phase voltages |
| uz | Zero-sequence component |
| ua, ub, and uc | Original phase voltages |
| φ | Load power factor angle |
| , and | Phase voltages after being phase-shifted by the φ |
| Zero-sequence voltage of three-level PFA-DPWM | |
| , , and | Modulation voltages of three-level PFA-DPWM |
| fc/fm | Carrier ratio |
| Lσ | Line-to-line equivalent leakage inductance |
| exy | The average internal electromotive force of the load |
| Abbreviations | |
| DPWM | Discontinuous pulse width modulation |
| SPWM | Sinusoidal pulse-width modulation |
| SVPWM | Space vector pulse-width modulation |
| PFA | Power factor adaptive |
| PD | Phase disposition |
| POD | Phase opposition disposition |
| APOD | Alternative phase opposition disposition |
| NP | Neutral point |
| ZSV | Zero-sequence voltage |
| THD | Total harmonic distortion |
| EMF | Electromotive force |
| DSP | Digital signal processor |
| FPGA | Field-programmable gate array |
Appendix A
References
- Alshahrani, S.; Khan, K.; Abido, M.; Khalid, M. Muhammad Khalid Grid-forming converter and stability aspects of renewable-based low-inertia power networks: Modern trends and challenges. Arab. J. Sci. Eng. 2024, 49, 6187–6216. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Ma, C. An overview of grid-forming technology and its application in new-type power system. Glob. Energy Interconnect. 2024, 7, 541–552. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, J.; Ren, Q.; Wu, L.; Liao, Z. A Semi Discontinuous PWM Method for Mitigating Oscillation in a Three-Level Grid-Tied PV Inverter. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, Z.; Sudhoff, S.; Gu, C.; Li, Y. Reduction of Common-Mode Voltage in Multiphase Two-Level Inverters Using SPWM with Phase-Shifted Carriers. IEEE Trans. Power Electron. 2016, 31, 6631–6645. [Google Scholar] [CrossRef]
- Yan, Q.; Zhou, Z.; Wu, M.; Yuan, X.; Zhao, R.; Xu, H. A Simplified Analytical Algorithm in abc Coordinate for the Three-Level SVPWM. IEEE Trans. Power Electron. 2021, 36, 3622–3627. [Google Scholar] [CrossRef]
- Srivastava, S.; Chaudhari, M.A. Comparison of SVPWM and SPWM Schemes for NPC Multilevel Inverter. In Proceedings of the IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 22–23 February 2020. [Google Scholar] [CrossRef]
- Wen, X.; Yin, X.; Zhang, Z. Unified Space Vector PWM Implementation Method for Three-Phase Inverters. Trans. China Electrotech. Soc. 2009, 24, 87–93. [Google Scholar] [CrossRef]
- An, S.; Sun, X.; Chen, Y.; Zhong, Y.; Ren, B. A New Generalized Implementation Method of Discontinuous PWM. Proc. CSEE 2012, 32, 59–66. [Google Scholar]
- Ojo, O. The Generalized Discontinuous PWM Scheme for Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Electron. 2004, 51, 1280–1289. [Google Scholar] [CrossRef]
- Li, K.; Wei, M.; Xie, C.; Deng, F.; Guerrero, J.; Vasquez, J. Triangle Carrier-Based DPWM for Three-Level NPC Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1966–1978. [Google Scholar] [CrossRef]
- Song, X.; Tian, J.; Li, L.; Li, S.; Zheng, Y.; Zhang, F. A Carrier-Based DPWM for T-Type Three-Level Inverter with ZSV Injected by Searching Neutral Point Current. In Proceedings of the IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, G.; Yan, Y.; Gu, X.; Shi, T.; He, X. Discontinuous Space Vector PWM Strategy of Neutral-Point-Clamped Three-Level Inverters for Output Current Ripple Reduction. IEEE Trans. Power Electron. 2017, 32, 5109–5121. [Google Scholar] [CrossRef]
- Jiang, W.; Jiang, H.; Liu, S.; Ji, S.; Wang, J. A Carrier-Based Discontinuous PWM Strategy for T-Type Three-Level Converter With Reduced Common Mode Voltage, Switching Loss, and Neutral Point Voltage Control. IEEE Trans. Power Electron. 2022, 37, 1761–1771. [Google Scholar] [CrossRef]
- Wang, J.; Ji, S.; Jiang, W.; Liu, S.; Jiang, H. A Novel Discontinuous PWM Strategy to Achieve Switching Loss Reduction and Neutral Point Voltage Balance for Vienna Rectifier. Proc. CSEE 2022, 42, 4125–4138. [Google Scholar] [CrossRef]
- Zou, Y.; Xing, Y.; Zhang, L.; Zheng, Z.; Liu, X.; Hu, H. Dynamic-Space-Vector Discontinuous PWM for Three-Phase Vienna Rectifiers with Unbalanced Neutral-Point Voltage. IEEE Trans. Power Electron. 2021, 36, 9015–9026. [Google Scholar] [CrossRef]
- Hossain, S.; Biswas, S.P.; Mondal, S.; Nath, J.; Islam, M.R. Advanced Voltage Balancing Discontinuous PWM Technique for Solar PV Fed Grid-Tied NPC Inverters. IEEE Trans. Appl. Supercond. 2024, 34, 1–5. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, J.; Ren, Q.; Wu, L.; Liao, Z. Research on Neutral-Point Balance Control of Three-Level Inverter Based on Hybrid DPWM. In Proceedings of the IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 19–21 June 2019. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, J.; Xin, Z.; Liu, H. A Hybrid DPWM Based Variable Switching Frequency Scheme for ZVS Three-Phase Three-Level Neutral-Point-Clamped Inverter. IEEE Trans. Ind. Electron. 2024, 71, 14276–14286. [Google Scholar] [CrossRef]
- Pham, K.D.; Nguyen, Q.V.; Nguyen, N.-V. PWM Strategy to Alleviate Common-Mode Voltage with Minimized Output Harmonic Distortion for Five-Level Cascaded H-Bridge Converters. Energies 2021, 14, 4476. [Google Scholar] [CrossRef]
- Busacca, A.; Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Schettino, G.; Scaglione, G.; Viola, F.; Colak, I. Switching Frequency Effects on the Efficiency and Harmonic Distortion in a Three-Phase Five-Level CHBMI Prototype with Multicarrier PWM Schemes: Experimental Analysis. Energies 2022, 15, 586. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, L.; Xing, Y.; Zhuge, H.; Shen, X.; Zhang, Y. An Optimized DPWM With Reduced Leakage Current for Three-Phase Three-Level Inverters with Unbalanced Neutral-Point Voltage. IEEE Trans. Power Electron. 2024, 39, 16346–16360. [Google Scholar] [CrossRef]
- Hu, Z.; Xing, X.; Liu, C.; Zhang, R.; Blaabjerg, F. A Modified Discontinuous PWM Method for Three-Level Inverters with the Improved LCL Filter. IEEE Trans. Power Electron. 2024, 39, 5498–5509. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Schutten, M.; De Leon, C.F.; Prabhakaran, S. Common-Mode EMI Comparison of SPWM, DPWM, and SVPWM Modulation Approaches. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Baltimore, MD, USA, 29 September–3 October 2019. [Google Scholar] [CrossRef]
- An, S.; Sun, X.; Zhong, Y.; Matsui, M. Research on a new and generalized method of discontinuous PWM strategies to minimize the switching loss. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012. [Google Scholar] [CrossRef]
- Addin, A.S.; Sahan, B.; Brueckner, T. Comparison of Different PWM Methods Assuming Equal Harmonic Loss Conditions. In Proceedings of the PCIM International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Online, 3–7 May 2021. [Google Scholar]
- Wang, M.; Xu, L.; Yang, B.; Li, J.; Gu, C.; Zhang, H. Optimized Carrier Disposition Based Discontinuous Pulse-width Modulation Method for three-level NPC Converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Baltimore, MD, USA, 29 September–3 October 2019. [Google Scholar] [CrossRef]
- Shin, H.; Lee, K.; Choi, J.; Seo, S.; Lee, J. Power loss comparison with different PWM methods for 3L-NPC inverter and 3L-T type inverter. In Proceedings of the International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014. [Google Scholar] [CrossRef]
- Xu, M.; Li, C.; Wang, Z.; Ge, Y.; Li, G.; Wang, N. DPWM Control Strategy of Auxiliary Inverter for Urban Rail Transit Based on Adaptive Power Factor. Proc. CSEE 2021, 41, 356–365. [Google Scholar] [CrossRef]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2003; pp. 453–484. [Google Scholar]
- Ali Iftekhar, M.; Tafti, H. Advanced Multilevel Converters and Applications in Grid Integration; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 243–254. [Google Scholar]
- Wu, W.-J.; Hu, L.-D.; Xin, Z.-Y.; Guo, C. Modeling and Analysis of Voltage Harmonic for Three-Level Neutral-Point-Clamped H-Bridge Inverter Considering Dead-Time. Energies 2022, 15, 5937. [Google Scholar] [CrossRef]







| PD | |||
| POD/APOD |
| 0 | ||
| 0 | ||
| Conditions | T1, T2, T3 | RMS of Current Ripple |
|---|---|---|
| Parameters | Value |
|---|---|
| DC bus voltage | 750 VDC |
| Three-phase output voltage | 380 VAC |
| Rated power | 120 kVA |
| Switching frequency | 8 kHz |
| Output frequency | 50 Hz |
| Three-phase filter inductor | 40 μH |
| Three-phase filter capacitor | 20 μF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, J.; Xu, Y.; Xu, M.; Liu, Z.; Zhou, Y. Power Factor Adaptive DPWM Control Strategy for T-Type Three-Level Inverters. Energies 2025, 18, 4574. https://doi.org/10.3390/en18174574
Tian J, Xu Y, Xu M, Liu Z, Zhou Y. Power Factor Adaptive DPWM Control Strategy for T-Type Three-Level Inverters. Energies. 2025; 18(17):4574. https://doi.org/10.3390/en18174574
Chicago/Turabian StyleTian, Jialiang, Yingying Xu, Mingxia Xu, Zhenjiang Liu, and Yuchi Zhou. 2025. "Power Factor Adaptive DPWM Control Strategy for T-Type Three-Level Inverters" Energies 18, no. 17: 4574. https://doi.org/10.3390/en18174574
APA StyleTian, J., Xu, Y., Xu, M., Liu, Z., & Zhou, Y. (2025). Power Factor Adaptive DPWM Control Strategy for T-Type Three-Level Inverters. Energies, 18(17), 4574. https://doi.org/10.3390/en18174574






