Model-Free Predictive Control of Inverter Based on Ultra-Local Model and Adaptive Super-Twisting Sliding Mode Observer
Abstract
1. Introduction
2. Problem Formulation
2.1. Mathematical Model and MPC Strategy
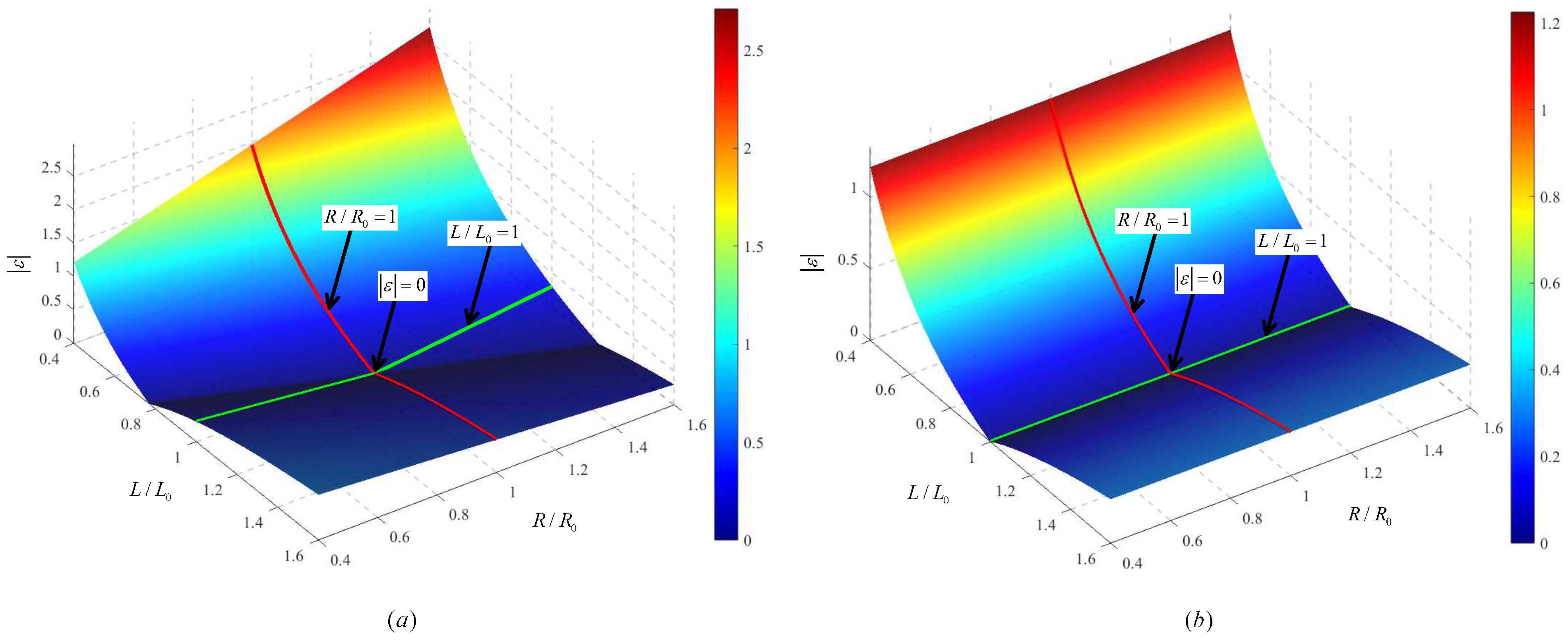
2.2. The Effect of Parameter Mismatch
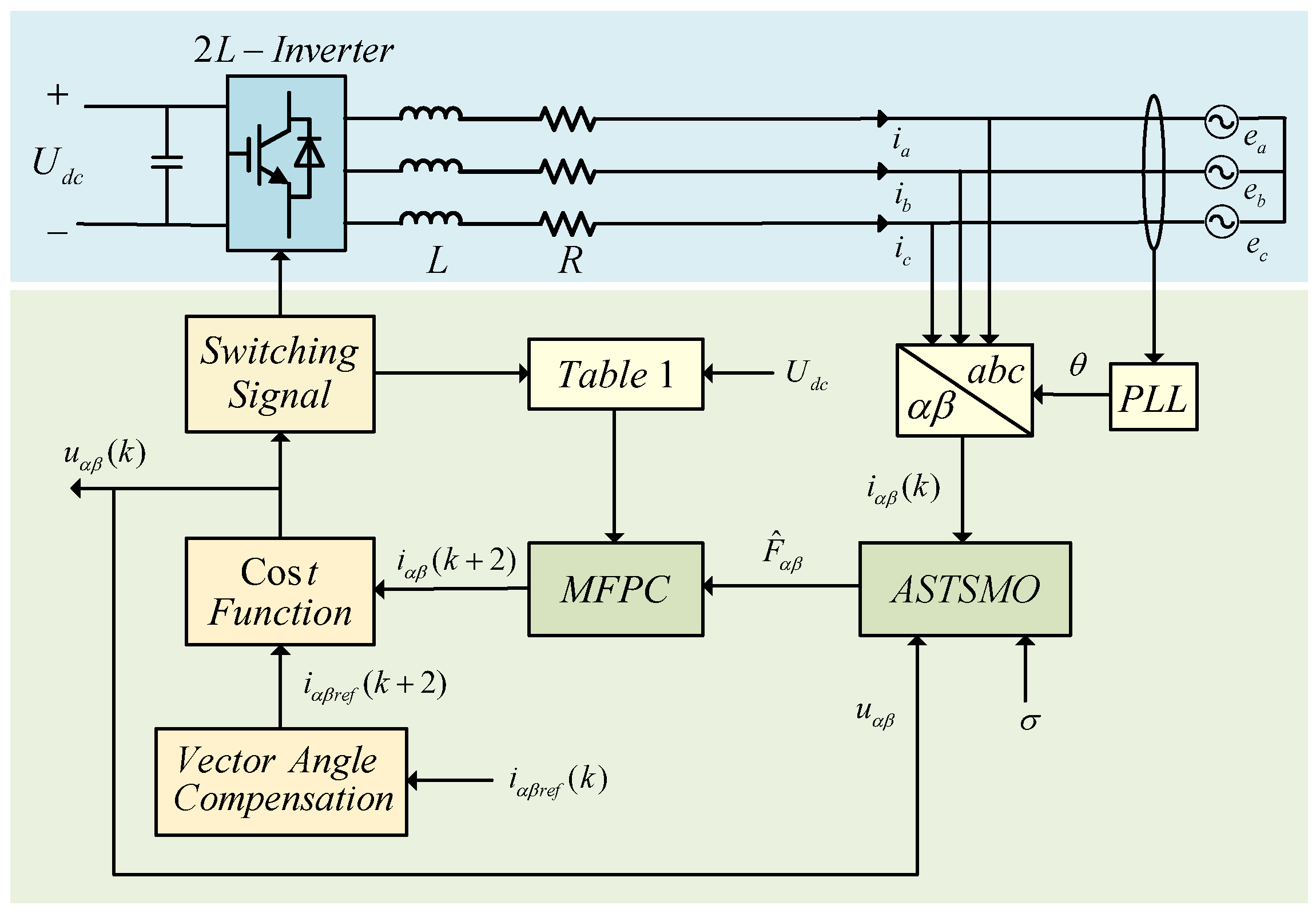
3. Proposed Control Strategy
3.1. Ultra-Local Model
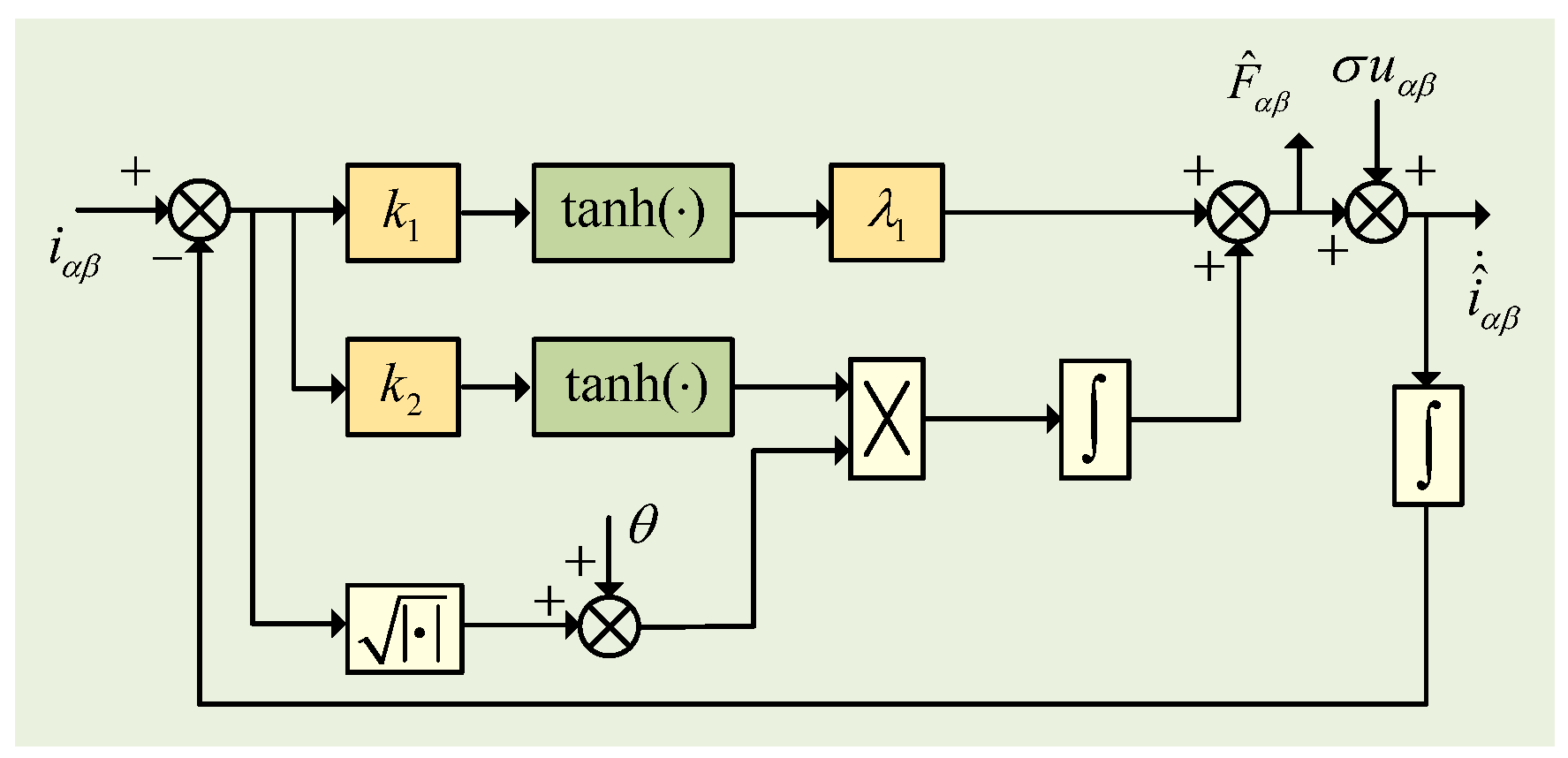
3.2. Adaptive Super-Twisting Sliding Mode Observer
3.3. Stability Proof
3.4. ASTSMO-MFPC Strategy
4. Simulation Verification
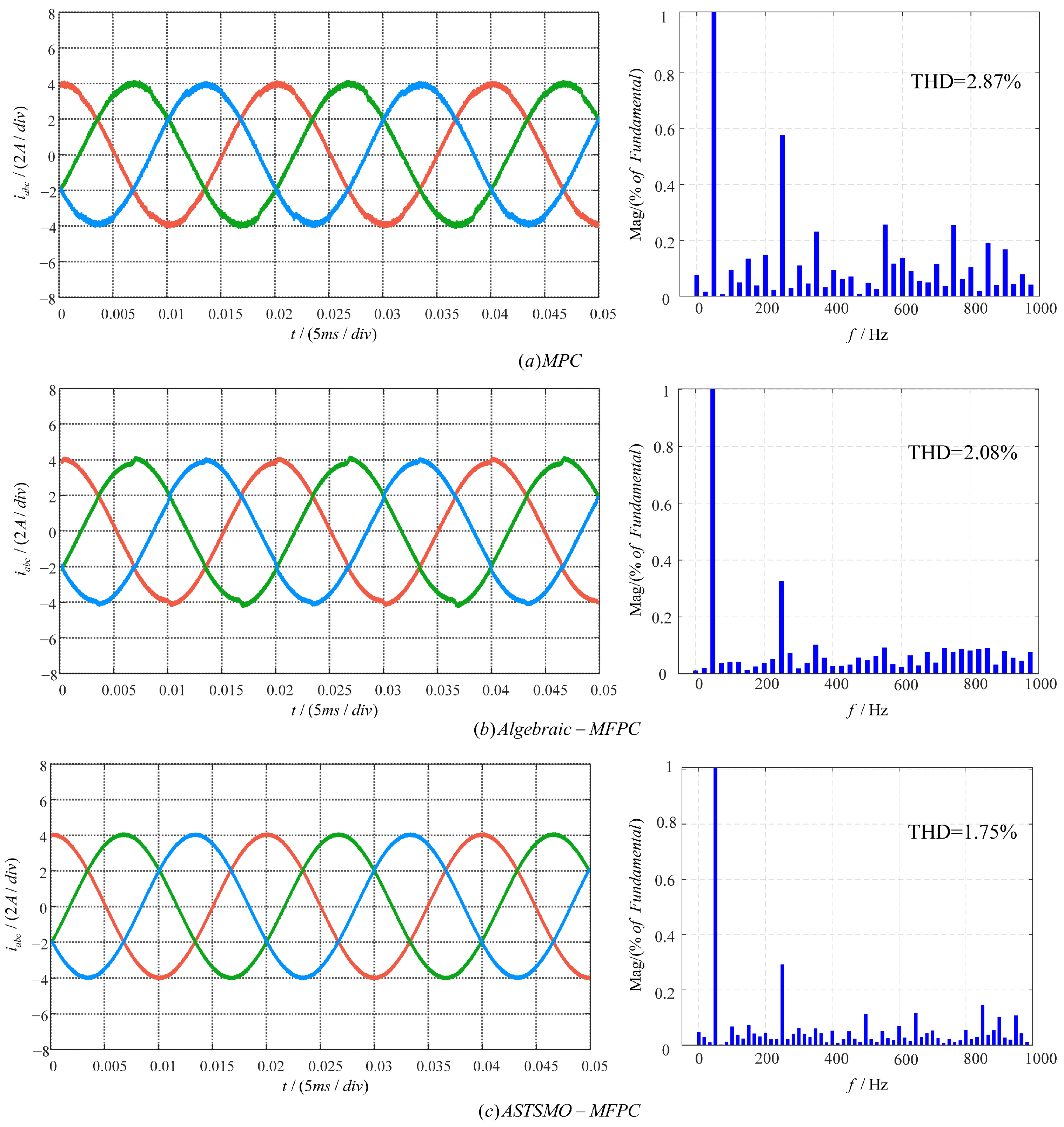
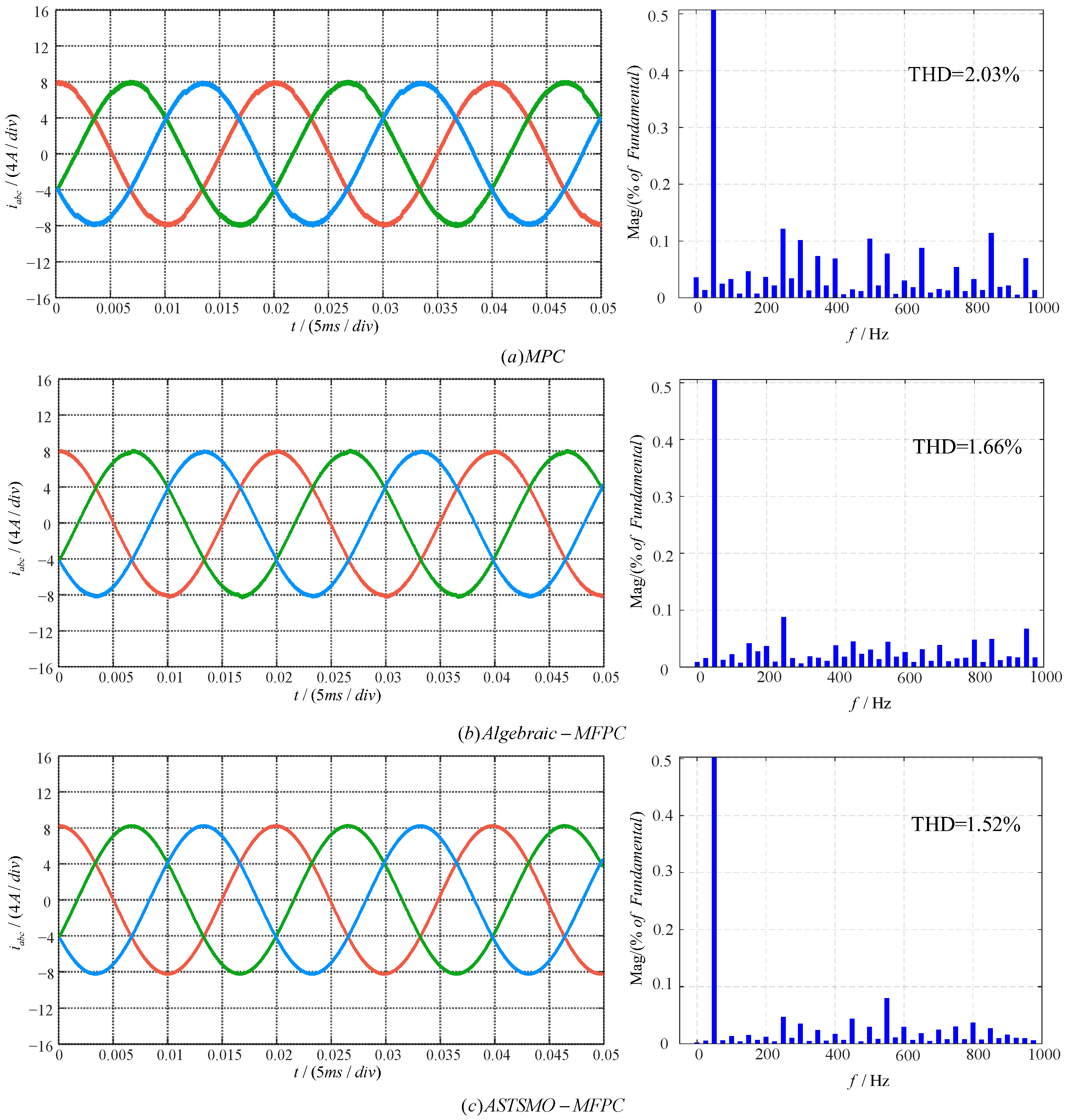
4.1. Steady-State Results Under Parameter Matching
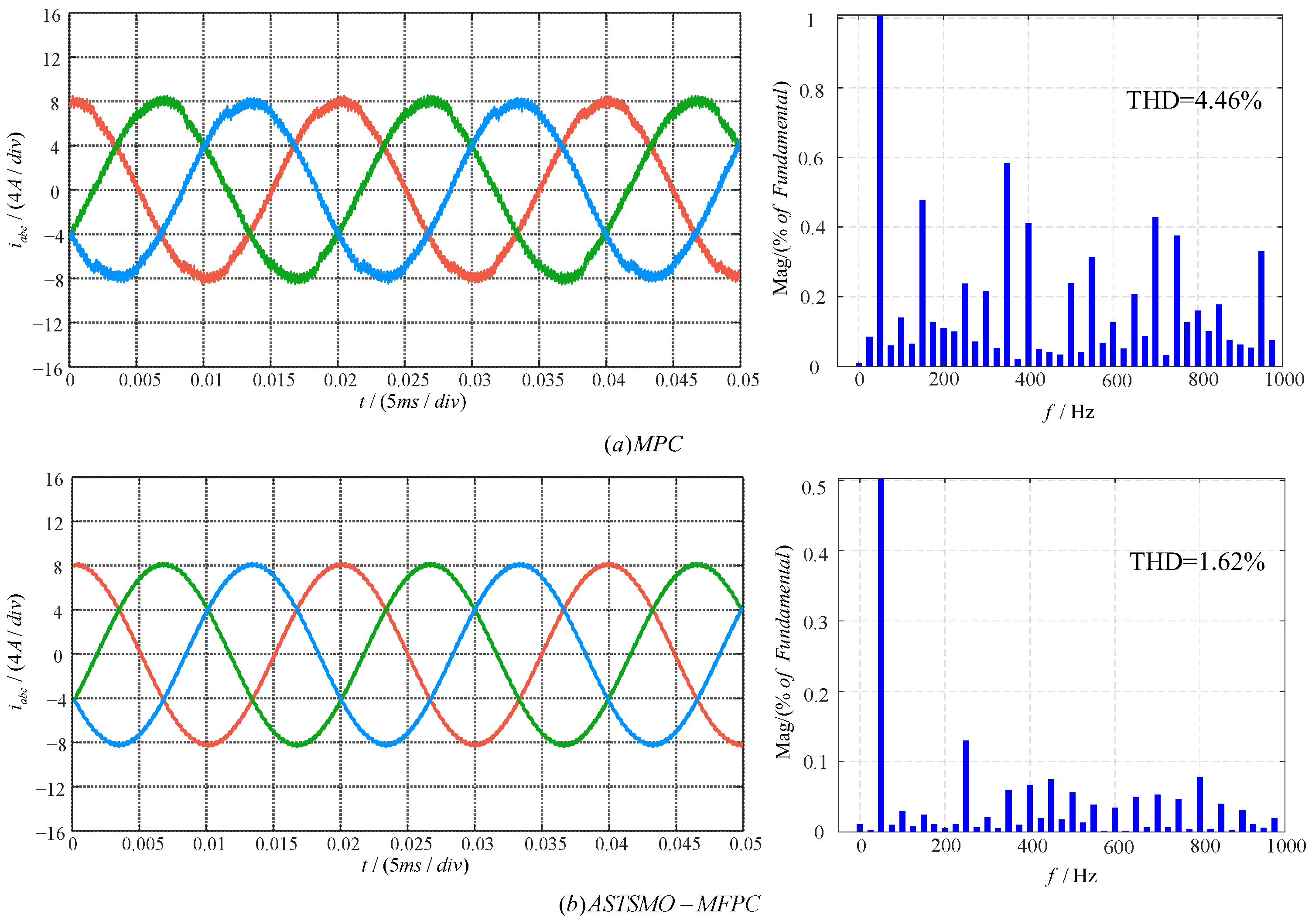
4.2. Results Under Parameter Mismatching
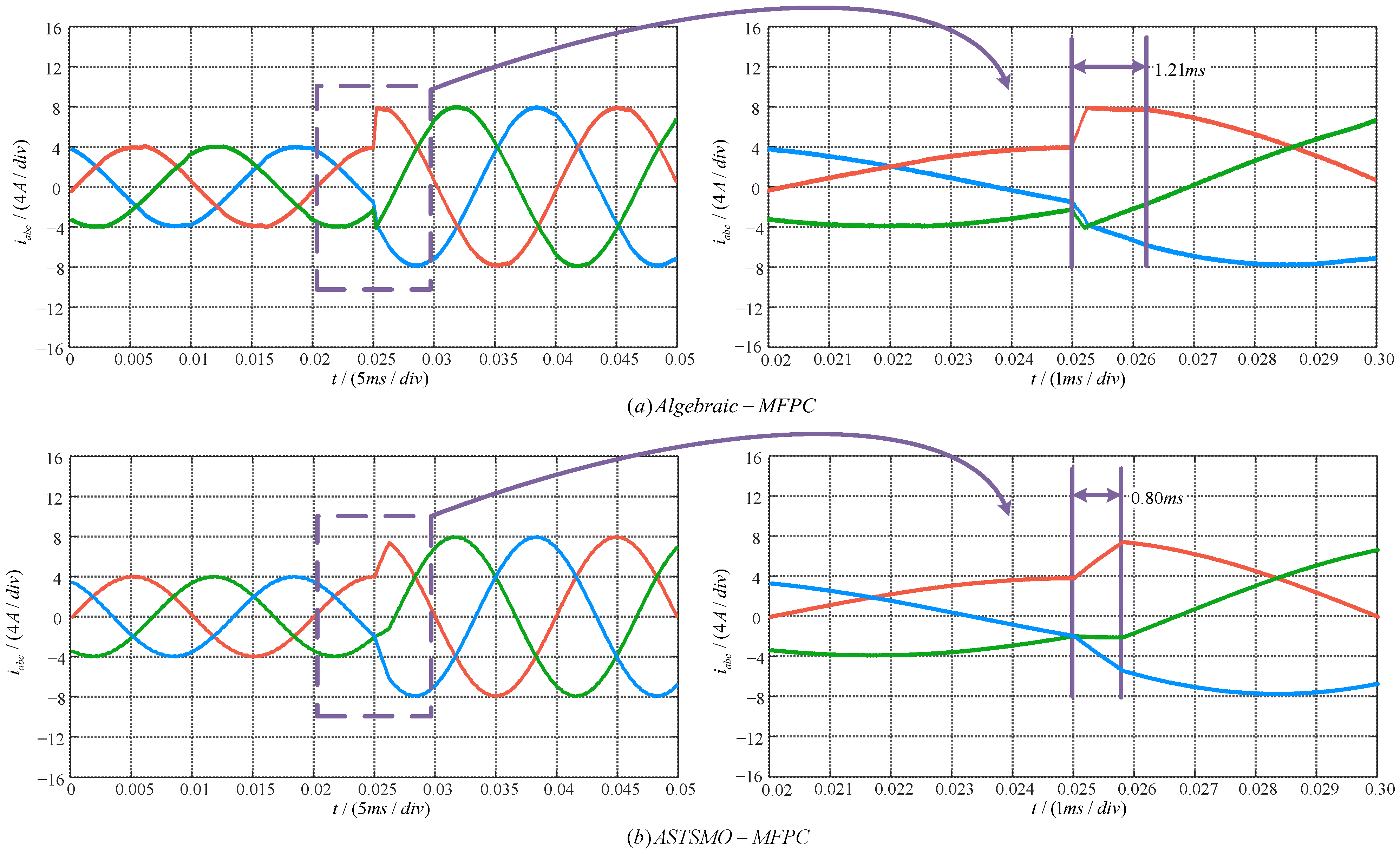
4.3. Dynamic Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, W.; Stynski, S.; Chub, A.; Franquelo, L.G.; Malinowski, M.; Vinnikov, D. Utility-Scale Energy Storage Systems: A Comprehensive Review of Their Applications, Challenges, and Future Directions. IEEE Ind. Electron. Mag. 2021, 15, 17–27. [Google Scholar] [CrossRef]
- Sui, Z.; Sun, Q.; Wang, R.; Li, D.; Wang, P. The Grid-Connected Inverter Stability Enhancement Control Based on Impedance Instability Region Elimination. IEEE Trans. Power Electron. 2025, 40, 9606–9624. [Google Scholar] [CrossRef]
- Alharbi, Y.; Darwish, A.; Ma, X. A Review of Model Predictive Control for Grid-Connected PV Applications. Electronics 2025, 14, 667. [Google Scholar] [CrossRef]
- Zafra, E.; Granado, J.; Lecuyer, V.B.; Vazquez, S.; Alcaide, A.M.; Leon, J.I.; Franquelo, L.G. Computationally Efficient Sphere Decoding Algorithm Based on Artificial Neural Networks for Long-Horizon FCS-MPC. IEEE Trans. Ind. Electron. 2024, 71, 39–48. [Google Scholar] [CrossRef]
- Shin, E.C.; Chae, H.G.; Roh, C. Advancing Discontinuous-Model Predictive Control for High Performance Inverters via Optimized Zero-Voltage State Selection Based on Offset Voltage. Appl. Sci. 2025, 15, 5532. [Google Scholar] [CrossRef]
- Liu, T.; Wang, X. Unified Voltage Control for Grid-Forming Inverters. IEEE Trans. Ind. Electron. 2024, 71, 2578–2589. [Google Scholar] [CrossRef]
- Guazzelli, P.R.U.; Pereira, W.C.; Oliveira, C.M.R.; Castro, A.G.; Aguiar, M.L. Weighting Factors Optimization of Predictive Torque Control of Induction Motor by Multiobjective Genetic Algorithm. IEEE Trans. Power Electron. 2018, 34, 6628–6638. [Google Scholar] [CrossRef]
- Shi, X.; Zhu, J.; Li, L.; Lu, D.D.C. Model-Predictive-Based Duty Cycle Control with Simplified Calculation and Mutual Influence Elimination for AC/DC Converter. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 504–514. [Google Scholar] [CrossRef]
- Shen, X.; Liu, J.; Liu, G.; Zhang, J.; Leon, J.I.; Wu, L.; Franquelo, L.G. Finite-Time Sliding Mode Control for NPC Converters with Enhanced Disturbance Compensation. IEEE Trans. Circuits Syst. I: Regul. Pap. 2025, 72, 1822–1831. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, J.; Jin, M. Adaptive Finite-Control-Set Model Predictive Current Control for IPMSM Drives with Inductance Variation. IET Electr. Power Appl. 2017, 11, 874–884. [Google Scholar] [CrossRef]
- Lin, C.K.; Yu, J.; Lai, Y.S.; Yu, H.C. Improved Model-Free Predictive Current Control for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2016, 63, 3942–3953. [Google Scholar] [CrossRef]
- Guo, F.; Yang, T.; Diab, A.M.; Yeoh, S.S.; Bozhko, S.; Wheeler, P. An Enhanced Virtual Space Vector Modulation Scheme of Three-Level NPC Converters for More-Electric-Aircraft Applications. IEEE Trans. Ind. Appl. 2021, 57, 5239–5251. [Google Scholar] [CrossRef]
- Michel, F.; Cédric, J. Model-Free Control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar]
- Guo, L.; Jin, N.; Gan, C.; Luo, K. Hybrid Voltage Vector Preselection-Based Model Predictive Control for Two-Level Voltage Source Inverters to Reduce the Common-Mode Voltage. IEEE Trans. Ind. Electron. 2019, 67, 4680–4691. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Chen, Z.; Mao, J.; Huang, J. Model-Free Adaptive Integral Backstepping Control for PMSM Drive Systems. J. Power Electron. 2019, 19, 1193–1202. [Google Scholar]
- Zhang, Y.; Jiang, T.; Jiao, J. Model-Free Predictive Current Control of a DFIG Using an Ultra-Local Model for Grid Synchronization and Power Regulation. IEEE Trans. Energy Convers. 2020, 35, 2269–2280. [Google Scholar] [CrossRef]
- Liu, J.; Shen, X.; Alcaide, A.M.; Yin, Y.; Leon, J.I.; Vazquez, S.; Wu, L.; Franquelo, L.G. Sliding Mode Control of Grid-Connected Neutral-Point-Clamped Converters Via High-Gain Observer. IEEE Trans. Ind. Electron. 2022, 69, 4010–4021. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Liu, R.; Yang, L.; Wang, X. Modulated Model-Free Predictive Control with Minimum Switching Losses for PMSM Drive System. IEEE Access 2020, 8, 20942–20953. [Google Scholar] [CrossRef]
- Cao, Y.L.; Cao, J.A.; Song, X.; Liu, Y.J. Research on Vector Control of PMSM Based on an Improved Sliding Mode Observer. Power Syst. Prot. Control 2021, 49, 104–111. [Google Scholar]
- Bagheri, F.; Bonaldo, J.; Guler, N.; Rivera, M.; Wheeler, P.; Lima, R. Enhanced Sliding Mode Control for Dual MPPT Systems Integrated with Three-Level T-Type PV Inverters. Energies 2025, 18, 3344. [Google Scholar] [CrossRef]
- Do, T.A.; Pham, Q.H.; Giap, V.N.; Nguyen, Q.D.; Vu, P. Homogeneous disturbance observer based on sliding mode observer and controller for T-type inverter. J. Electr. Eng. Technol. 2024, 19, 1671–1683. [Google Scholar] [CrossRef]
- Luo, W.; Vazquez, S.; Liu, J.; Gordillo, F.; Franquelo, L.G.; Wu, L. Control System Design of a Three-Phase Active Front End Using a Sliding-Mode Observer. IEEE Trans. Syst. Man, Cybern. Syst. 2020, 52, 739–748. [Google Scholar] [CrossRef]
- Ma, C.; Li, H.; Yao, X.; Zhang, Z.; Belie, F.D. An Improved Model-Free Predictive Current Control with Advanced Current Gradient Updating Mechanism. IEEE Trans. Ind. Electron. 2020, 68, 11968–11979. [Google Scholar] [CrossRef]
- Li, F.; Zheng, T.; He, N.; Cao, Q. Data-Driven Hybrid Neural Fuzzy Network and ARX Modeling Approach to Practical Industrial Process Identification. IEEE/CAA J. Autom. Sin. 2022, 9, 1702–1705. [Google Scholar] [CrossRef]
- Jin, N.; Chen, M.; Guo, L.; Li, Y.; Chen, Y. Double-Vector Model-Free Predictive Control Method for Voltage Source Inverter with Visualization Analysis. IEEE Trans. Ind. Electron. 2021, 69, 10066–10078. [Google Scholar] [CrossRef]
- Wang, D.; Liu, X. Sensorless control of PMSM with improved adaptive super-twisting sliding mode observer and IST-QSG. IEEE Trans. Transp. Electrif. 2024, 11, 721–731. [Google Scholar] [CrossRef]
- Chalanga, A.; Kamal, S.; Fridman, L.M.; Bandyopadhyay, B.; Moreno, J.A. Implementation of Super-Twisting Control: Super-Twisting and Higher Order Sliding-Mode Observer-Based Approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
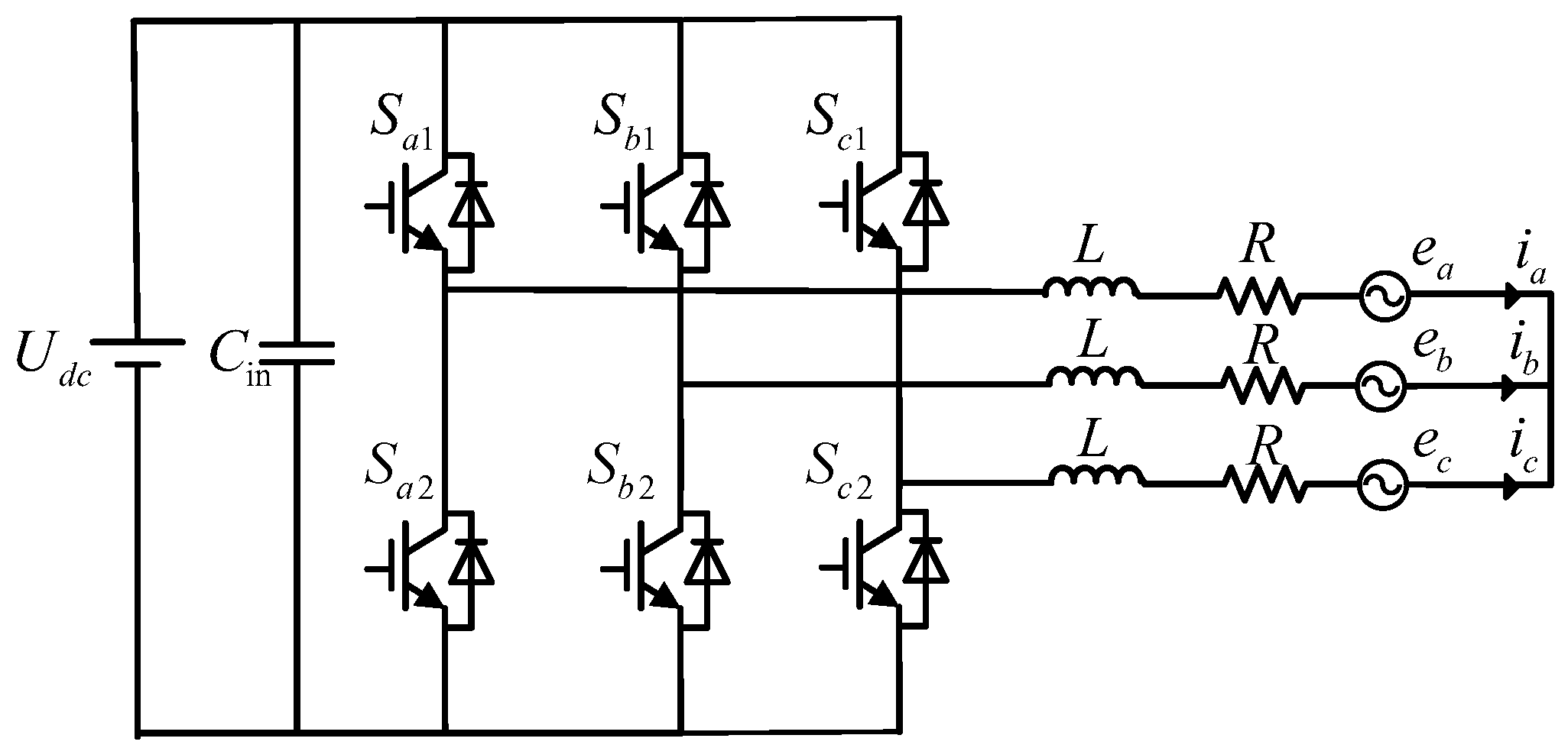
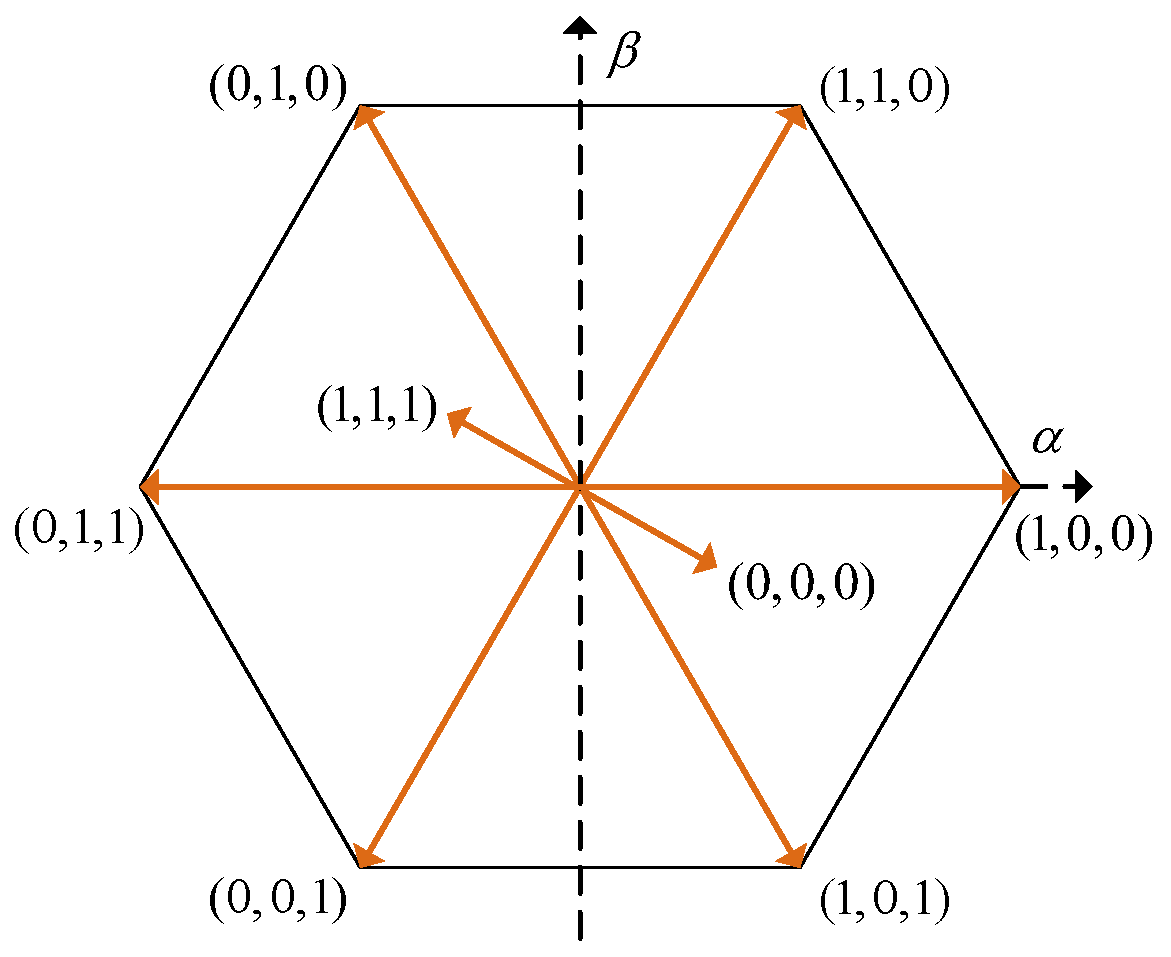
| Switching States (,,) | ||
|---|---|---|
| (0,0,0) | 0 | 0 |
| (0,0,1) | − | − |
| (0,1,0) | − | |
| (0,1,1) | −2 | 0 |
| (1,0,0) | 2 | 0 |
| (1,0,1) | − | |
| (1,1,0) | ||
| (1,1,1) | 0 | 0 |
| Parameter | Value |
|---|---|
| DC voltage | 120 |
| Effective value of AC line voltage | 60 |
| Filter inductor | 0.005 |
| Parasitic resistance | 0.05 |
| Sampling frequency | 20 |
| Scale factor | 500 |
| Basic gain | 25 |
| Proportional gain | 150 |
| Nonlinear coefficient | 80 |
| Nonlinear coefficient | 120 |
| Adaptive coefficient | 16 |
| Reference | THD of MPC | THD of Algebraic-MFPC | THD of ASTSMO-MFPC |
|---|---|---|---|
| 4 A | 2.87% | 2.08% | 1.75% |
| 6 A | 2.35% | 1.79% | 1.67% |
| 8 A | 2.03% | 1.66% | 1.52% |
| 10 A | 1.90% | 1.54% | 1.37% |
| 12 A | 1.80% | 1.44% | 1.30% |
| Reference | THD of MPC | THD of ASTSMO-MFPC |
|---|---|---|
| 4 A | 5.88% | 1.80% |
| 6 A | 5.06% | 1.72% |
| 8 A | 4.46% | 1.62% |
| 10 A | 3.98% | 1.42% |
| 12 A | 3.85% | 1.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, W.; Shu, Z.; Zhang, R.; Leon, J.I.; Alcaide, A.M.; Franquelo, L.G. Model-Free Predictive Control of Inverter Based on Ultra-Local Model and Adaptive Super-Twisting Sliding Mode Observer. Energies 2025, 18, 4570. https://doi.org/10.3390/en18174570
Luo W, Shu Z, Zhang R, Leon JI, Alcaide AM, Franquelo LG. Model-Free Predictive Control of Inverter Based on Ultra-Local Model and Adaptive Super-Twisting Sliding Mode Observer. Energies. 2025; 18(17):4570. https://doi.org/10.3390/en18174570
Chicago/Turabian StyleLuo, Wensheng, Zejian Shu, Ruifang Zhang, Jose I. Leon, Abraham M. Alcaide, and Leopoldo G. Franquelo. 2025. "Model-Free Predictive Control of Inverter Based on Ultra-Local Model and Adaptive Super-Twisting Sliding Mode Observer" Energies 18, no. 17: 4570. https://doi.org/10.3390/en18174570
APA StyleLuo, W., Shu, Z., Zhang, R., Leon, J. I., Alcaide, A. M., & Franquelo, L. G. (2025). Model-Free Predictive Control of Inverter Based on Ultra-Local Model and Adaptive Super-Twisting Sliding Mode Observer. Energies, 18(17), 4570. https://doi.org/10.3390/en18174570







