Numerical Study on the Vapor–Liquid Interface in the Evaporator of Loop Heat Pipes with Multiscale Wicks Using Pore Network Simulation
Abstract
1. Introduction
2. Numerical Study
2.1. Numerical Modeling
2.2. Modified Pore Network Simulation Model
3. Experimental Study
3.1. Fabrication of Multiscale Wicks
3.2. Measurement of Wick Characteristics
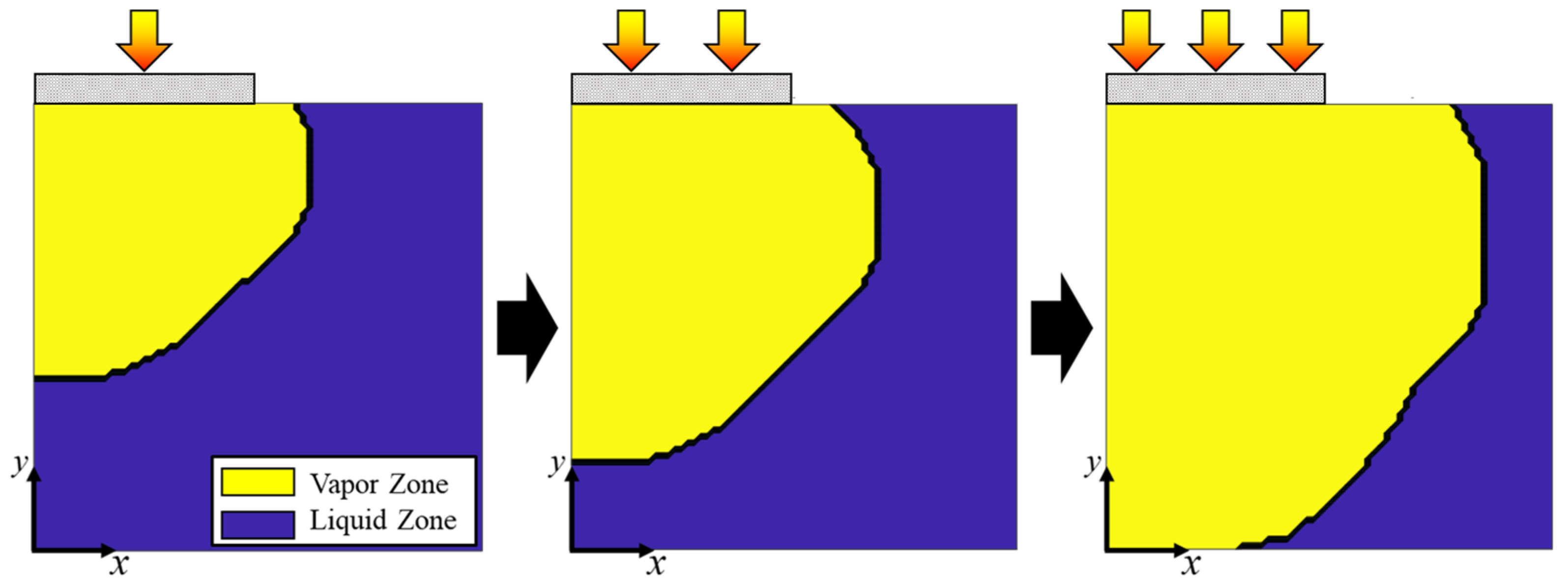
4. Results and Discussion
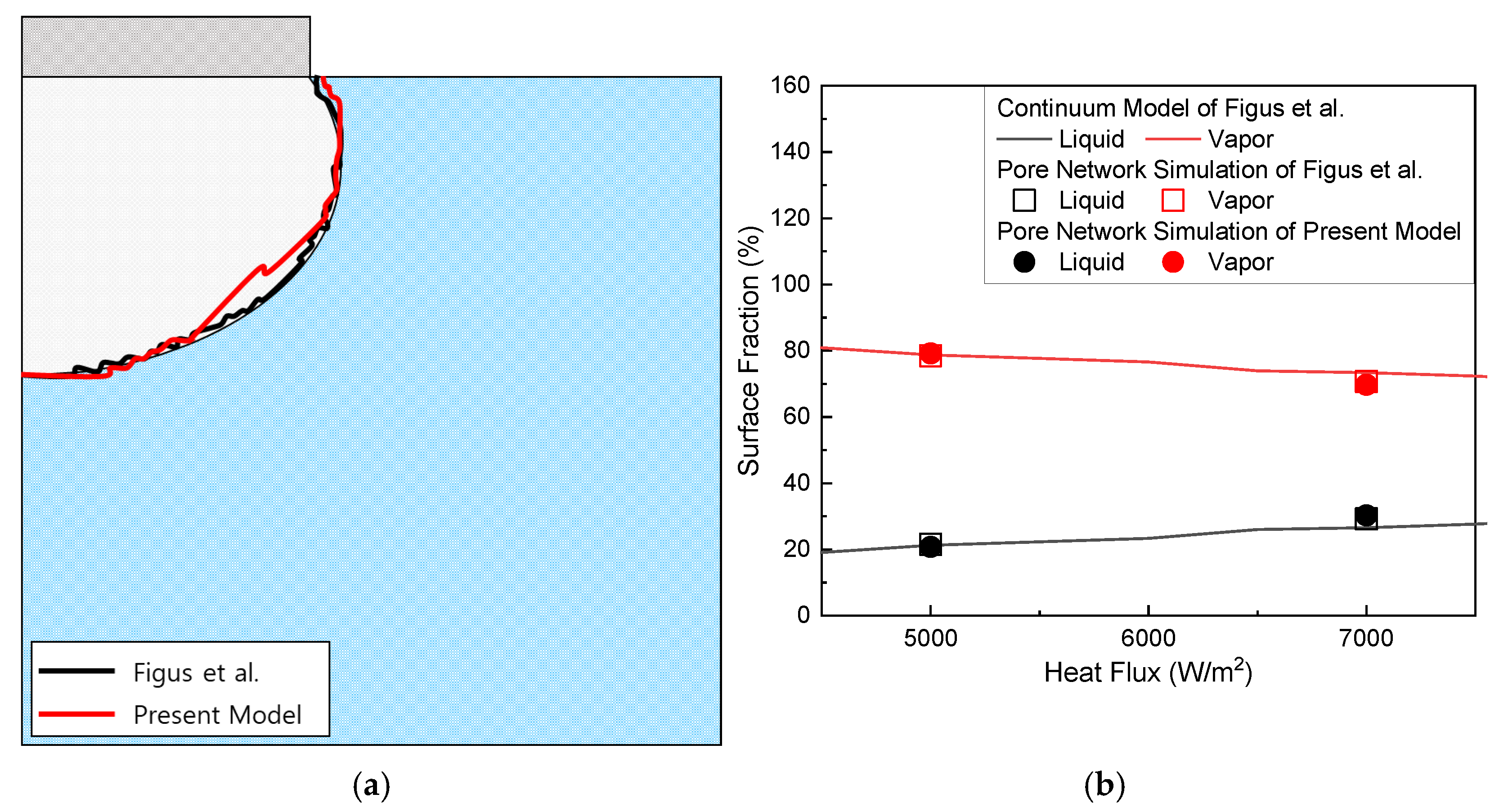
4.1. Validation Results
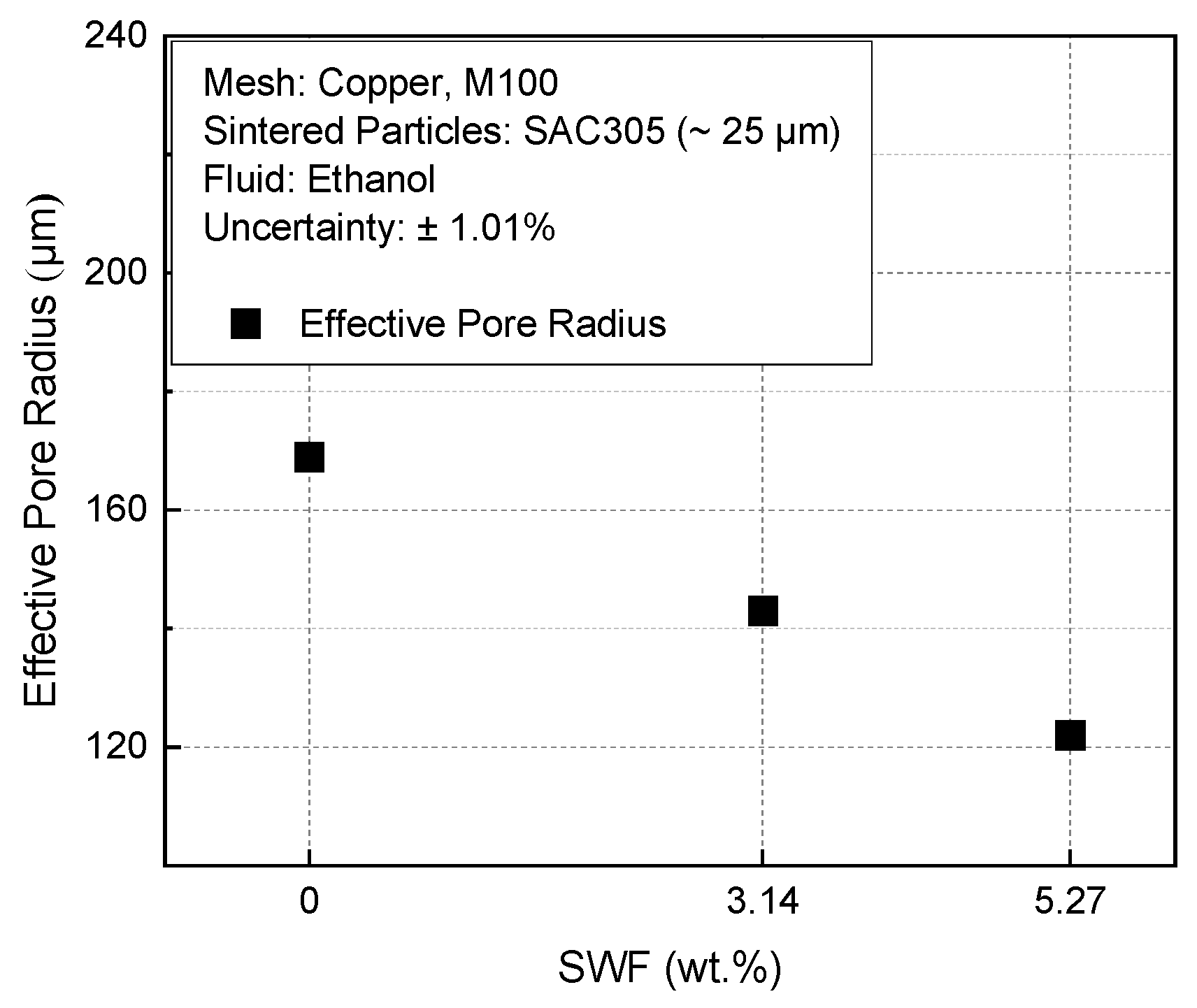
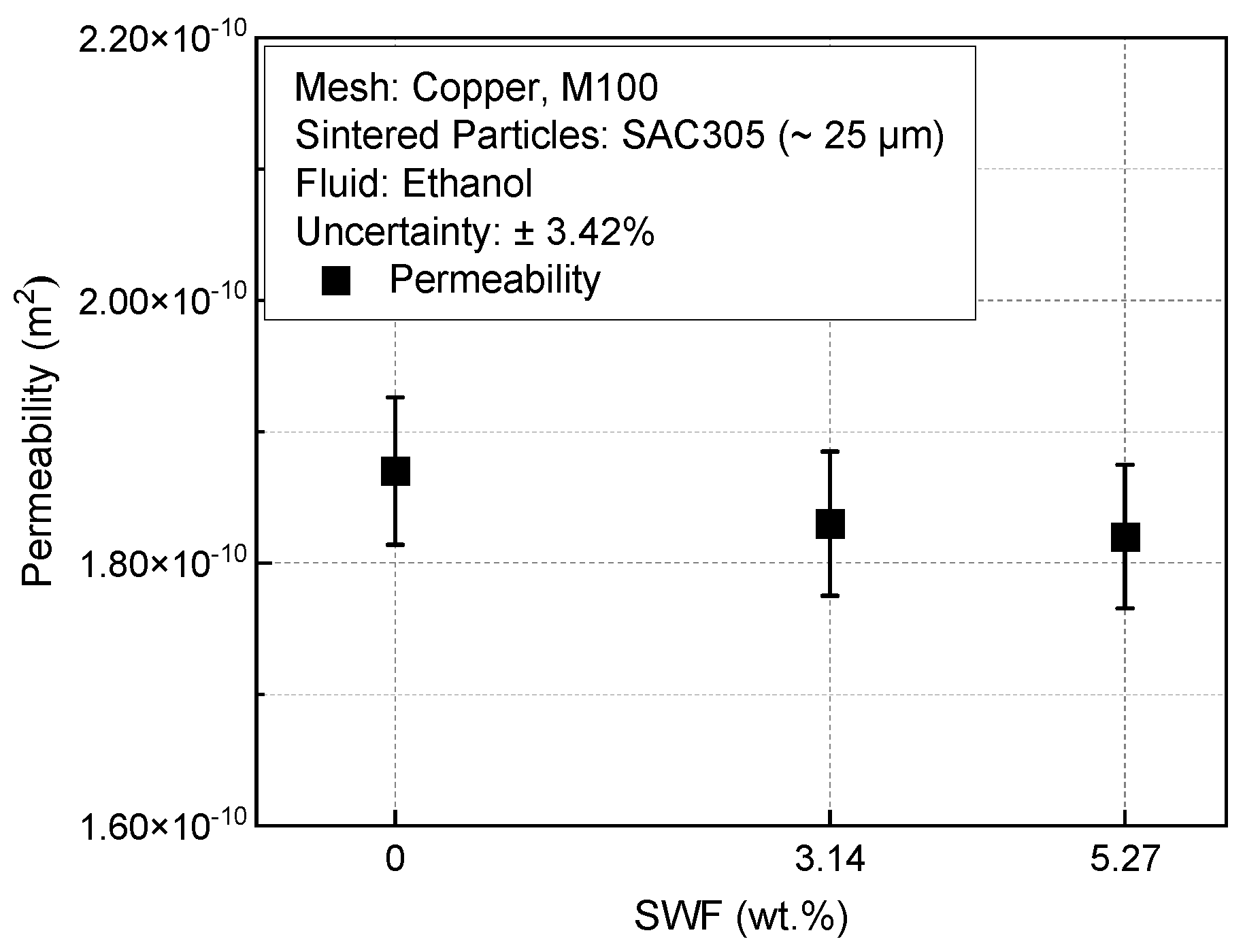
4.2. Wick Characteristics of Multiscale Wicks
4.3. Effect of Evaporator Parameters on Maximum Heat Transfer Rate
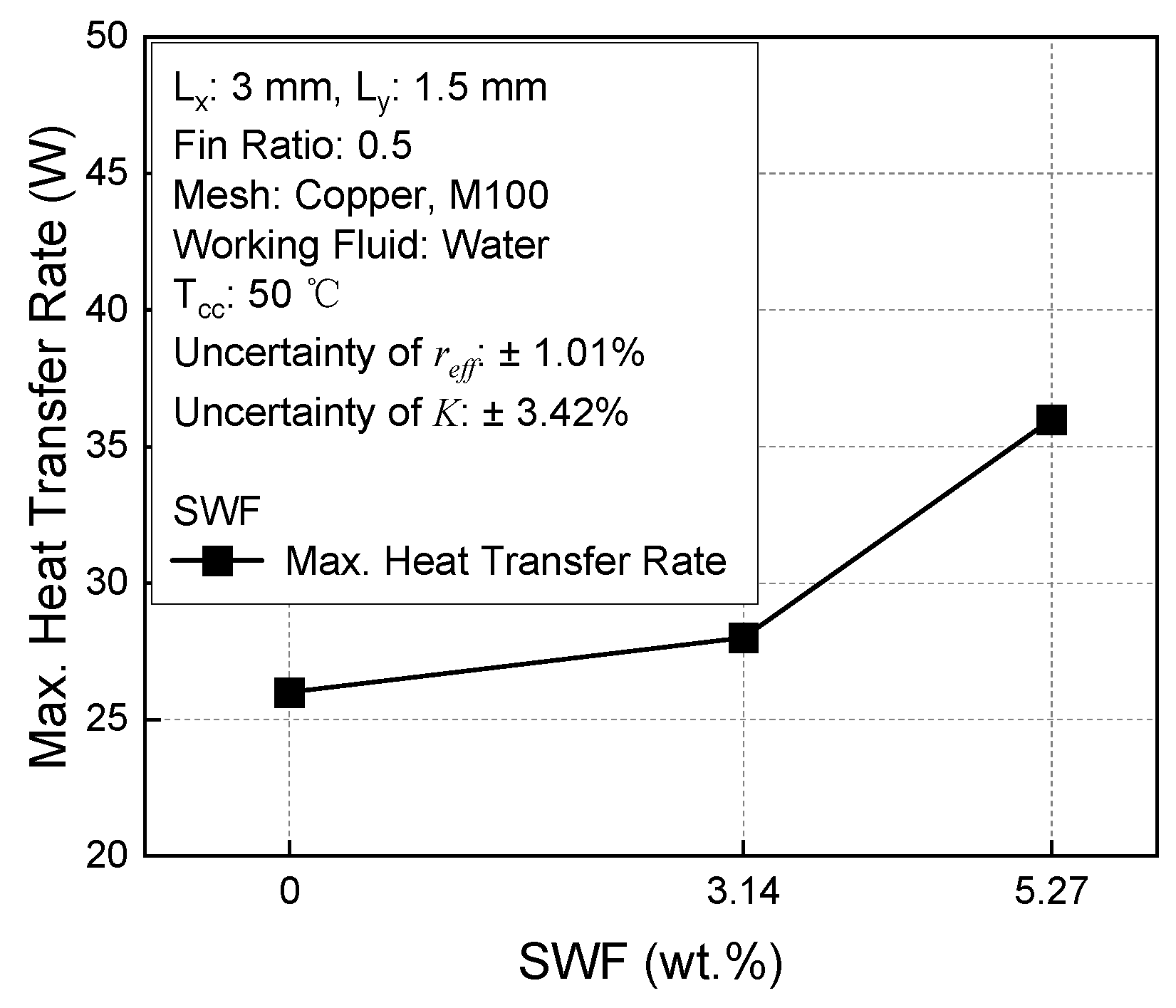
4.3.1. Effect of SWF of the Multiscale Wick
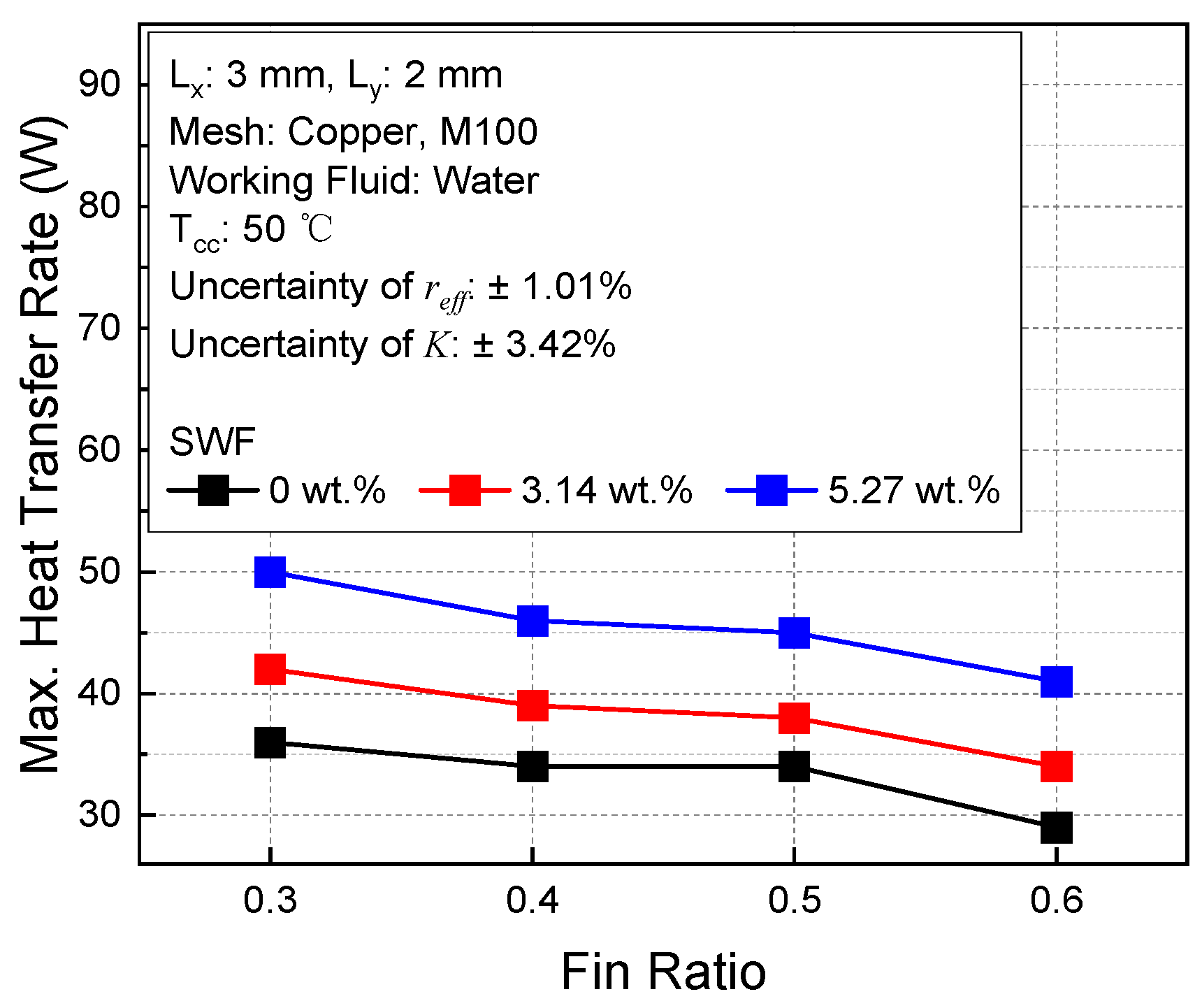
4.3.2. Effect of Fin Ratio
4.3.3. Effect of Wick Thickness
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Awick | Cross-sectional area of wick [m2] |
| B | Bias error |
| D | Wire diameter [m] |
| Dh | Hydraulic diameter [m] |
| d | Hydraulic distance [m] |
| dkf | Fluid thermal distance [m] |
| dks | Solid thermal distance [m] |
| d* | Thermal distance [m] |
| G | Hydraulic conductance [m2] |
| g | Gravitational acceleration [m/s2] |
| h | Height of the fluid absorbed in the wick [m] |
| hc | Convective heat transfer coefficient [W/m2·K] |
| hfg | Latent heat of vaporization [J/kg] |
| K | Permeability [m2] |
| k | Thermal conductivity [W/m∙K] |
| keff | Effective thermal conductivity of porous material [W/m∙K] |
| keff,f | Effective thermal conductivity of fluid [W/m∙K] |
| kf | Thermal conductivity of fluid [W/m∙K] |
| ks | Thermal conductivity of solid [W/m∙K] |
| Lfin | Fin width [m] |
| Lint | Vapor–liquid interface width [m] |
| Lwick | Length of wick [m] |
| Lx | Wick width [m] |
| Ly | Wick thickness [m] |
| lint | Length of the vapor–liquid interface [m] |
| m | Mass [kg] |
| mabs | Mass of fluid absorbed by the wick [kg] |
| Unit normal vector | |
| P | Pressure [Pa] |
| ΔP | Pressure drop [Pa] |
| q | Heat flux [W/m2] |
| R | Gas constant [J/kg∙K] |
| S | Cross-sectional area [m2] |
| S* | Heat transfer area [m2] |
| T | Temperature [K] |
| twick | Wick thickness [m] |
| U | Uncertainty |
| u | Velocity [m/s] |
| W | Wire separation distance [m] |
| Greek Symbols | |
| α | Constant |
| β | Slope |
| ε | Porosity |
| μ | Viscosity [Pa∙s] |
| ν | Kinematic viscosity [m2/s] |
| θ | Contact angle [rad] |
| ρ | Density [kg/m3] |
| Subscripts | |
| abs | Absorbed in the wick |
| cap | Capillary |
| cc | Compensation chamber |
| eff | Effective |
| gr | Vapor groove |
| int | Vapor–liquid interface |
| l | Liquid |
| mesh | Conventional screen mesh wick |
| particles | Sintered particles on the wick |
| ref | Reference |
| sat | Saturation |
| s | Solid |
| v | Vapor |
| x | x-directional coordinate |
| y | y-directional coordinate |
References
- Abdoli, A.; Jimenez, G.; Dulikravich, G.S. Thermo-fluid analysis of micro pin-fin array cooling configurations for high heat fluxes with a hot spot. Int. J. Therm. Sci. 2015, 90, 290–297. [Google Scholar] [CrossRef]
- Zhang, L.-Y.; Zhang, Y.-F.; Chen, J.-Q.; Bai, S.-L. Fluid flow and heat transfer characteristics of liquid cooling microchannels in LTCC multilayered packaging substrate. Int. J. Heat Mass Transf. 2015, 84, 339–345. [Google Scholar] [CrossRef]
- Khandekar, S.; Sahu, G.; Muralidhar, K.; Gatapova, E.Y.; Kabov, O.A.; Hu, R.; Zhao, L. Cooling of high-power LEDs by liquid sprays: Challenges and prospects. Appl. Therm. Eng. 2021, 184, 115640. [Google Scholar] [CrossRef]
- Lee, Y.J.; Kim, S.J. Experimental investigation on thermal-hydraulic performance of manifold microchannel with pin-fins for ultra-high heat flux cooling. Int. J. Heat Mass Transf. 2024, 224, 125336. [Google Scholar] [CrossRef]
- Wu, Z.; Xiao, W.; Song, B. Efficient thermal management of high-power electronics via jet-enhanced HU-type manifold microchannel. Int. J. Heat Mass Transf. 2023, 221, 125113. [Google Scholar] [CrossRef]
- Cui, Q.; You, Z.; Ni, Y.; Yang, X.; Zhou, Y.; Wei, J.; Liu, J. A comprehensive review of loop heat pipe: From fundamental re-searches to applications. Int. J. Heat Fluid Flow 2025, 115, 109880. [Google Scholar] [CrossRef]
- Ku, J.; Birur, G.C. Testing of a loop heat pipe with two evaporators and two condensers. In Proceedings of the 31st International Conference on Environmental Systems, Orlando, FL, USA, 31 July 2001. [Google Scholar]
- Ku, J.; Ottenstein, L.; Rogers, P.; Cheung, K.; Obenschain, A.F. Investigation of capillary limit in a loop heat pipe. In Proceedings of the 12th International Heat Transfer Conference, Grenoble, France, 18–23 August 2002. [Google Scholar]
- Caruana, R.; Guilizzoni, M. Modeling of Conventional Heat Pipes with Capillary Wicks: A Review. Energies 2025, 18, 2213. [Google Scholar] [CrossRef]
- Sudhakar, S.; Weibel, J.A.; Zhou, F.; Dede, E.M.; Garimella, S.V. The role of vapor venting and liquid feeding on the dryout limit of two-layer evaporator wicks. Int. J. Heat Mass Transf. 2020, 148, 119063. [Google Scholar] [CrossRef]
- Bai, L.; Lin, G.; Zhang, H.; Wen, D. Mathematical modeling of steady-state operation of a loop heat pipe. Appl. Therm. Eng. 2009, 29, 2643–2654. [Google Scholar] [CrossRef]
- Jung, E.G.; Boo, J.H. A Novel Analytical Modeling of a Loop Heat Pipe Employing the Thin-Film Theory: Part I—Modeling and Simulation. Energies 2019, 12, 2408. [Google Scholar] [CrossRef]
- Figus, C.; Le Bray, Y.; Bories, S.; Prat, M. Heat and mass transfer with phase change in aporous structure partially heated: Continuum model andpore network simulations. Int. J. Heat Mass Transf. 1999, 42, 2557–2569. [Google Scholar] [CrossRef]
- Mottet, L.; Coquard, T.; Prat, M. Three dimensional liquid and vapour distribution in the wick of capillary evaporators. Int. J. Heat Mass Transf. 2015, 83, 636–651. [Google Scholar] [CrossRef]
- Kang, S.Y.; Kim, S.H.; Park, J.; Jang, S.P. Thermal performance of a thin flat vapor chamber with a multiscale wick fabricated by SAC305/Sn58Bi micro-sized particles. Int. J. Heat Mass Transf. 2023, 212, 124305. [Google Scholar] [CrossRef]
- Wang, C.; Mehmani, Y.; Xu, K. Capillary equilibrium of bubbles in porous media. Proc. Natl. Acad. Sci. USA 2021, 118, e2024069118. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.J.; Jang, S.P. Effects of the Darcy number, the Prandtl number, and the Reynolds number on local thermal non-equilibrium. Int. J. Heat Mass Transf. 2002, 45, 3885–3896. [Google Scholar] [CrossRef]
- Chang, W.S. Porosity and effective thermal conductivity of wire screens. J. Heat Transf. 1990, 112, 5–9. [Google Scholar] [CrossRef]
- Holley, B.M.; Faghri, A. Permeability and effective pore radius measurements for heat pipe and fuel cell applications. Appl. Therm. Eng. 2006, 26, 448–462. [Google Scholar] [CrossRef]



| Wick properties | |
| Parameters | Specification |
| Wick width (Lx) | 5.0 mm |
| Wick thickness (Ly) | 5.0 mm |
| Fin length (Lfin) | 2.0 mm |
| Porosity (ε) | 0.4 |
| Effective pore radius (reff) | 5.0 μm |
| Thermal conductivity of solid (ks) | 0.4 W/m·K |
| Working fluid | |
| Parameters | Specification |
| Thermal conductivity of vapor (kv) | 0.05 W/m·K |
| Thermal conductivity of liquid (kl) | 0.50 W/m·K |
| Latent heat of vaporization (hfg) | 1.13 × 106 J/kg |
| Kinematic viscosity of vapor (νv) | 1.10 × 10−6 m2/s |
| Kinematic viscosity of liquid (νl) | 2.00 × 10−7 m2/s |
| Wick properties | |||
| Parameters | Specification | ||
| Sintered weight fraction (SWF) | 0 wt.% | 3.14 wt.% | 5.27 wt.% |
| Effective pore radius (reff) | 166 μm | 143 μm | 122 μm |
| Permeability (K) | 1.87 × 10−10 m2 | 1.83 × 10−10 m2 | 1.82 × 10−10 m2 |
| Porosity (ε) | 0.6753 | ||
| Thermal conductivity of solid (ks) | 400 W/m·K | ||
| Working fluid | |||
| Parameters | Specification | ||
| Thermal conductivity of vapor (kv) | 0.02 W/m·K | ||
| Thermal conductivity of liquid (kl) | 0.64 W/m·K | ||
| Latent heat of vaporization (hfg) | 2.38 × 106 J/kg | ||
| Kinematic viscosity of vapor (νv) | 1.26 × 10−4 m2/s | ||
| Kinematic viscosity of liquid (νl) | 5.53 × 10−7 m2/s | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, S.; Kang, S.Y.; Park, S.J.; Myeong, H.S.; Jang, S.P. Numerical Study on the Vapor–Liquid Interface in the Evaporator of Loop Heat Pipes with Multiscale Wicks Using Pore Network Simulation. Energies 2025, 18, 4526. https://doi.org/10.3390/en18174526
Jeon S, Kang SY, Park SJ, Myeong HS, Jang SP. Numerical Study on the Vapor–Liquid Interface in the Evaporator of Loop Heat Pipes with Multiscale Wicks Using Pore Network Simulation. Energies. 2025; 18(17):4526. https://doi.org/10.3390/en18174526
Chicago/Turabian StyleJeon, Seunghyeok, Seo Yeon Kang, Sung Jun Park, Hee Soo Myeong, and Seok Pil Jang. 2025. "Numerical Study on the Vapor–Liquid Interface in the Evaporator of Loop Heat Pipes with Multiscale Wicks Using Pore Network Simulation" Energies 18, no. 17: 4526. https://doi.org/10.3390/en18174526
APA StyleJeon, S., Kang, S. Y., Park, S. J., Myeong, H. S., & Jang, S. P. (2025). Numerical Study on the Vapor–Liquid Interface in the Evaporator of Loop Heat Pipes with Multiscale Wicks Using Pore Network Simulation. Energies, 18(17), 4526. https://doi.org/10.3390/en18174526






