Novel Single-Core Phase-Shifting Transformer: Configuration, Analysis and Application in Loop Closing
Abstract
1. Introduction
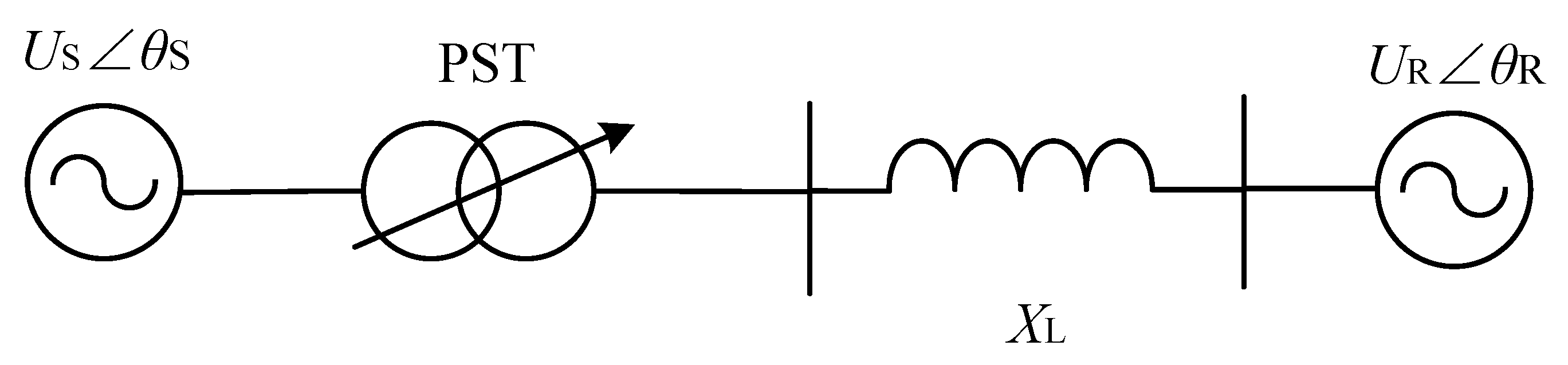
2. Basic Principle of PST
2.1. Power Flow Control Mechanism
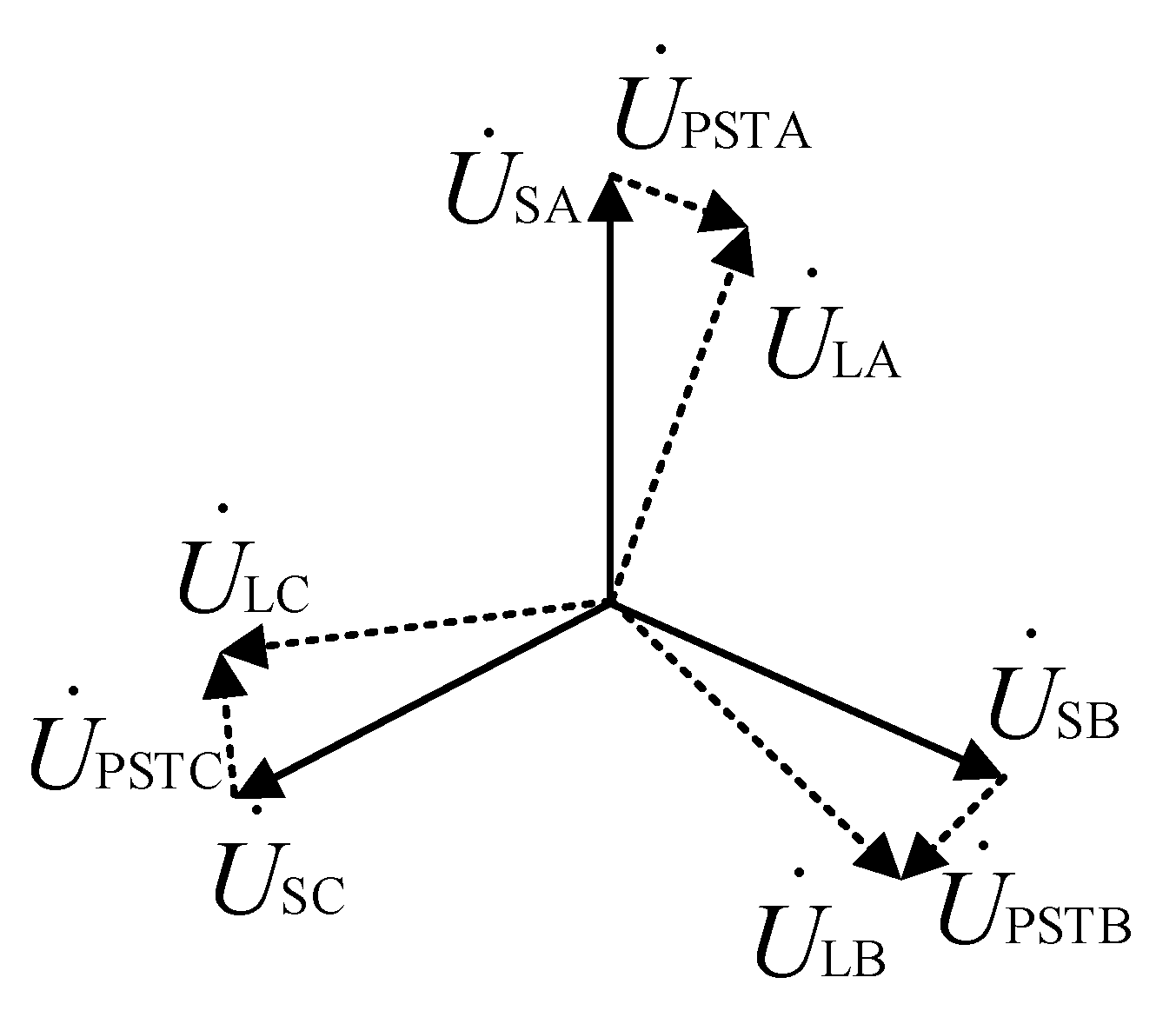
2.2. Voltage-Phasor Relationships
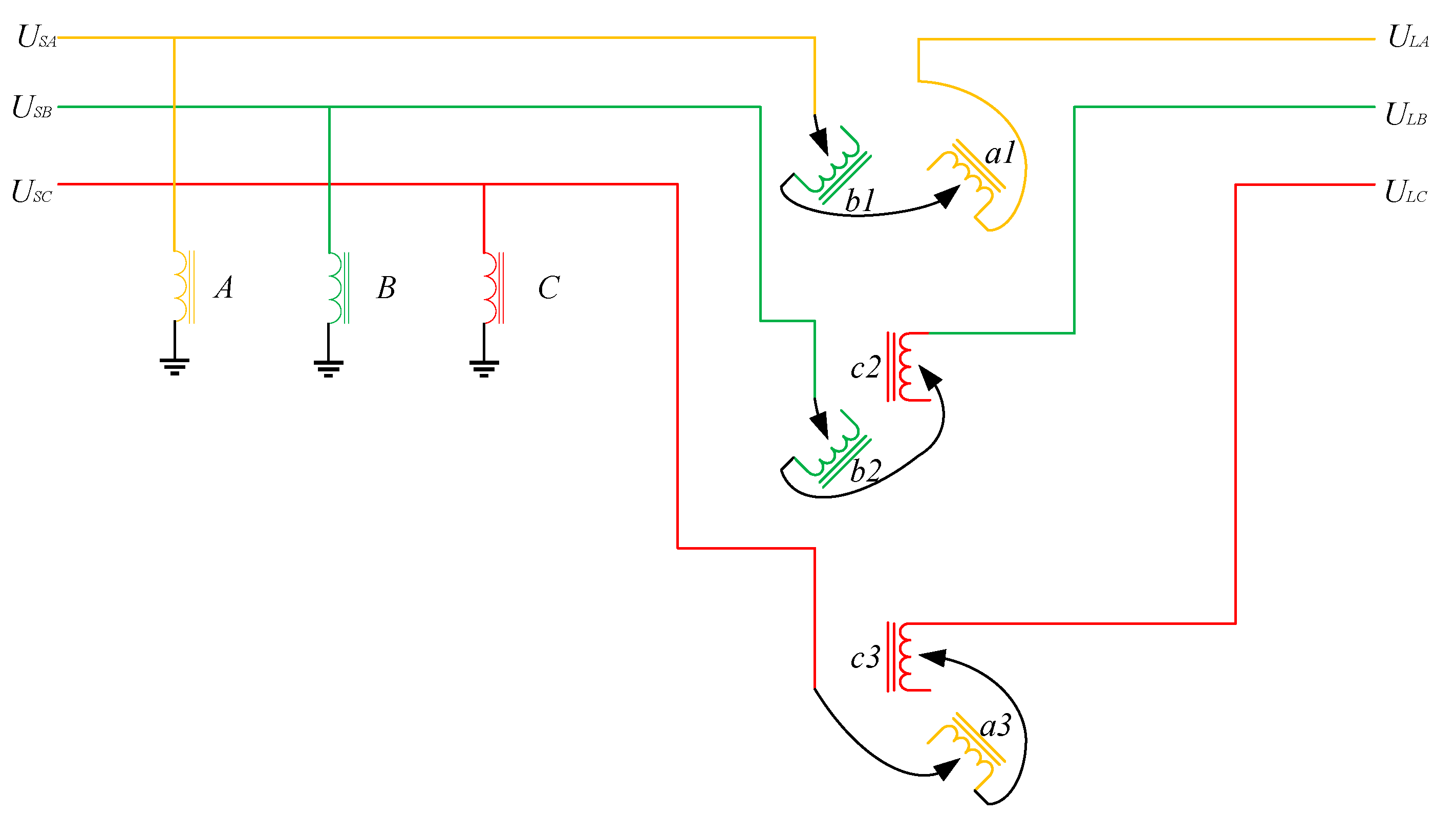
3. Topology Structure of the Novel Single-Core PST
- Phase A core limb: windings a1 and a3
- Phase B core limb: windings b1 and b2
- Phase C core limb: windings c2 and c3
- For phase A output: windings a1 and b1 in series
- For phase B output: windings b2 and c2 in series
- For phase C output: windings c3 and a3 in series
- Voltage regulation windings (a1, b2, c3): Provide voltage components in phase with their respective excitation voltages
- Phase-shifting windings (b1, c2, a3): Contribute voltage components from adjacent phases
4. Phase-Shifting and Voltage Regulation Capability Analysis
4.1. Analytical Derivation of Turns Ratios
4.2. Boundary Conditions on nE1 and nE2 for Total Phase Coverage
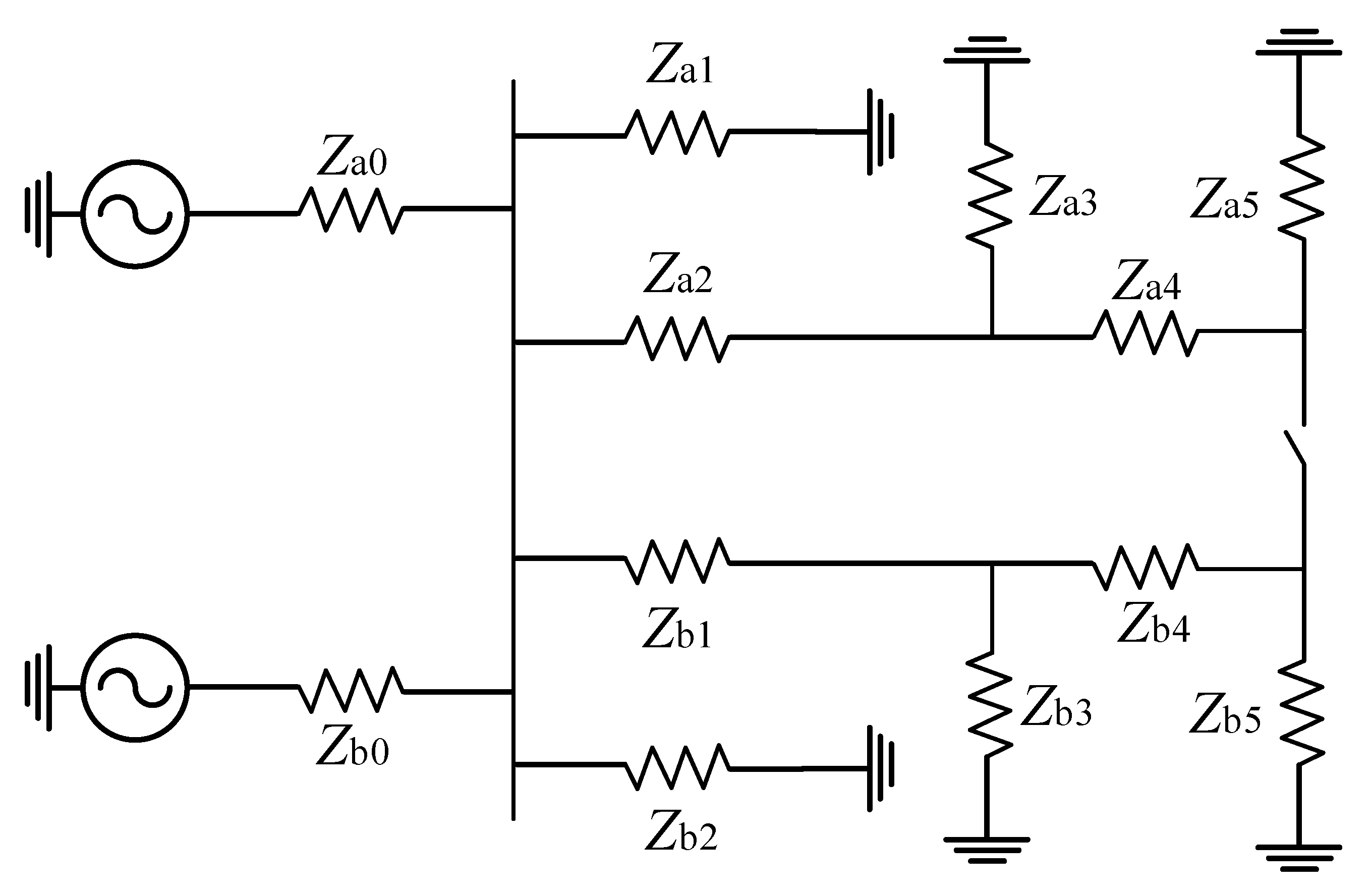
5. Loop Closing Current Control Method Based on the Single-Core Phase-Shifting Transformer
5.1. Loop Closing Challenges in Distribution Networks
5.2. Mechanism of Loop Closing Current and Control Objective
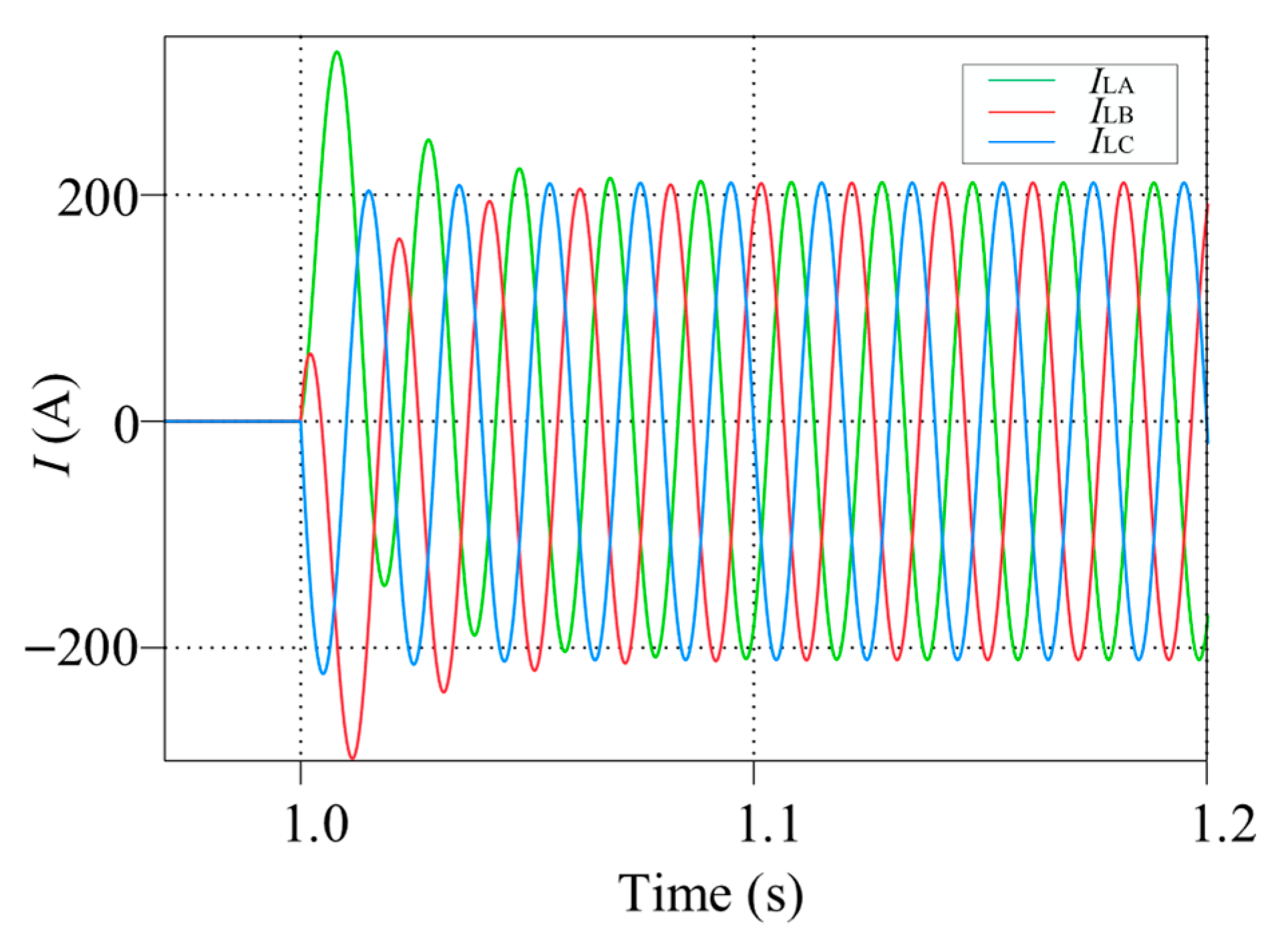
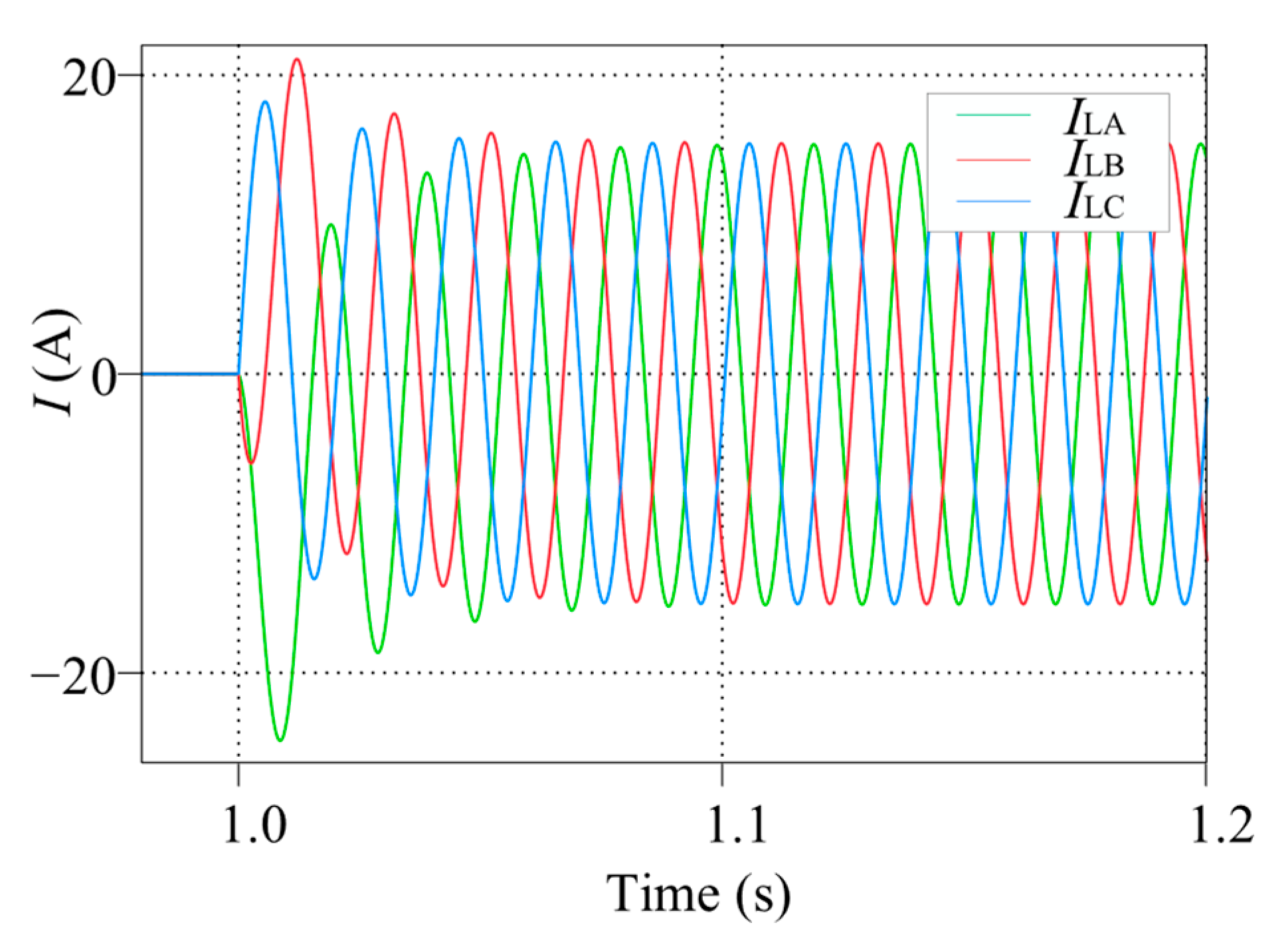
6. Simulation and Experiment
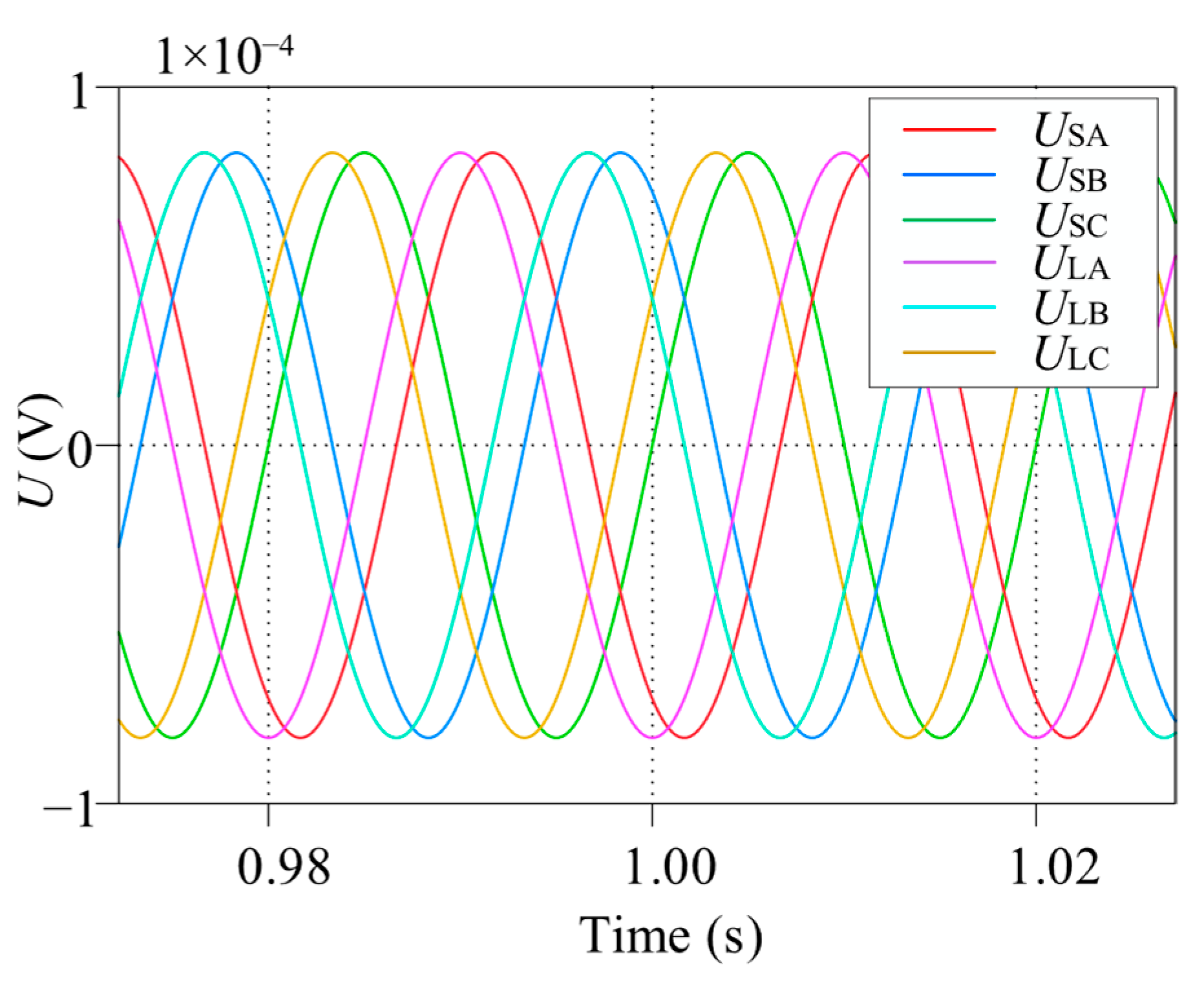
6.1. Simulation
6.2. Experiment
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, W.; Liu, H.; Zhang, W.; Yuan, J. Power Flow Regulation Effect and Parameter Design Method of Phase-Shifting Transformer. Energies 2024, 17, 1622. [Google Scholar] [CrossRef]
- Sakallıoğlu, B.; Esenboğa, B.; Demirdelen, T.; Tümay, M. Performance Evaluation of Phase-shifting Transformer for Integration of Renewable Energy Sources. Electr. Eng. 2020, 102, 2025–2039. [Google Scholar] [CrossRef]
- Jagtap, P.; Chandrakar, V.K. Advanced UPFC Controllers to Improve Transient and Dynamic Stability of Power System. In Proceedings of the International Conference on “Advances in Mechanical Engineering” 2023 (ICAME-2023), Nagpur, India, 22–23 December 2023. [Google Scholar]
- Ammr, S.M.; Asghar, M.S.; Ashraf, I.; Meraj, M. A Comprehensive Review of Power Flow Controllers in Interconnected Power System Networks. IEEE Access 2020, 8, 18036–18063. [Google Scholar] [CrossRef]
- Liu, J.; Hao, X.; Wang, X.; Chen, Y.; Fang, W.; Niu, S. Application of Thyristor Controlled Phase Shifting Transformer Excitation Impedance Switching Control to Suppress Short-Circuit Fault Current Level. J. Mod. Power Syst. Clean Energy 2018, 6, 821–832. [Google Scholar] [CrossRef]
- Brilinskii, A.S.; Badura, M.A.; Evdokunin, G.A.; Chudny, V.S.; Mingazov, R.I. Phase-Shifting Transformer Application for Dynamic Stability Enhancement of Electric Power Stations Generators. In Proceedings of the 2020 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 27–30 January 2020. [Google Scholar]
- Albrechtowicz, P.; Rozegnał, B.; Cisek, P. Comparison of Phase-Shifting Transformers Properties. Energies 2022, 15, 6224. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, W.; Mei, J.; Gan, D.; Zhou, H.; Zheng, Y. Independent Fast Phase Shifting Transformer: A Flexible and High-Precision Power Flow Controller. IEEE Trans. Power Deliv. 2023, 38, 4410–4421. [Google Scholar] [CrossRef]
- Li, J.; Lin, S.; Li, J.; Luo, Y.; Mao, C.; Li, H.; Guan, Z. Risk Assessment Method of Loop Closing Operation in Low-Voltage Distribution Network Based on Fuzzy Comprehensive Evaluation. Energy Rep. 2023, 9, 312–319. [Google Scholar] [CrossRef]
- Yan, X.; Peng, W.; Wang, Y.; Aslam, W.; Shao, C.; Li, T. Flexible Loop Closing Control Method for an Active Distribution Network Based on Dual Rotary Phase Shifting Transformers. IET Gener. Transm. Distrib. 2022, 16, 4204–4214. [Google Scholar] [CrossRef]
- Singh, P.; Tiwari, R.; Sangwan, V.; Gupta, A.K. Optimal Allocation of Thyristor-Controlled Series Capacitor (TCSC) and Thyristor-Controlled Phase-Shifting Transformer (TCPST). In Proceedings of the 2020 International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), Mathura, India, 28–29 February 2020. [Google Scholar]
- Zhang, N.; Chen, B.; Gao, X.; Gao, S.; Zhao, X. Modeling and Simulation of a Distribution Network with a Controllable Phase-Shifting Transformer for Loop Closing. Sci. Technol. Innov. 2024, 2, 23–26. (In Chinese) [Google Scholar]
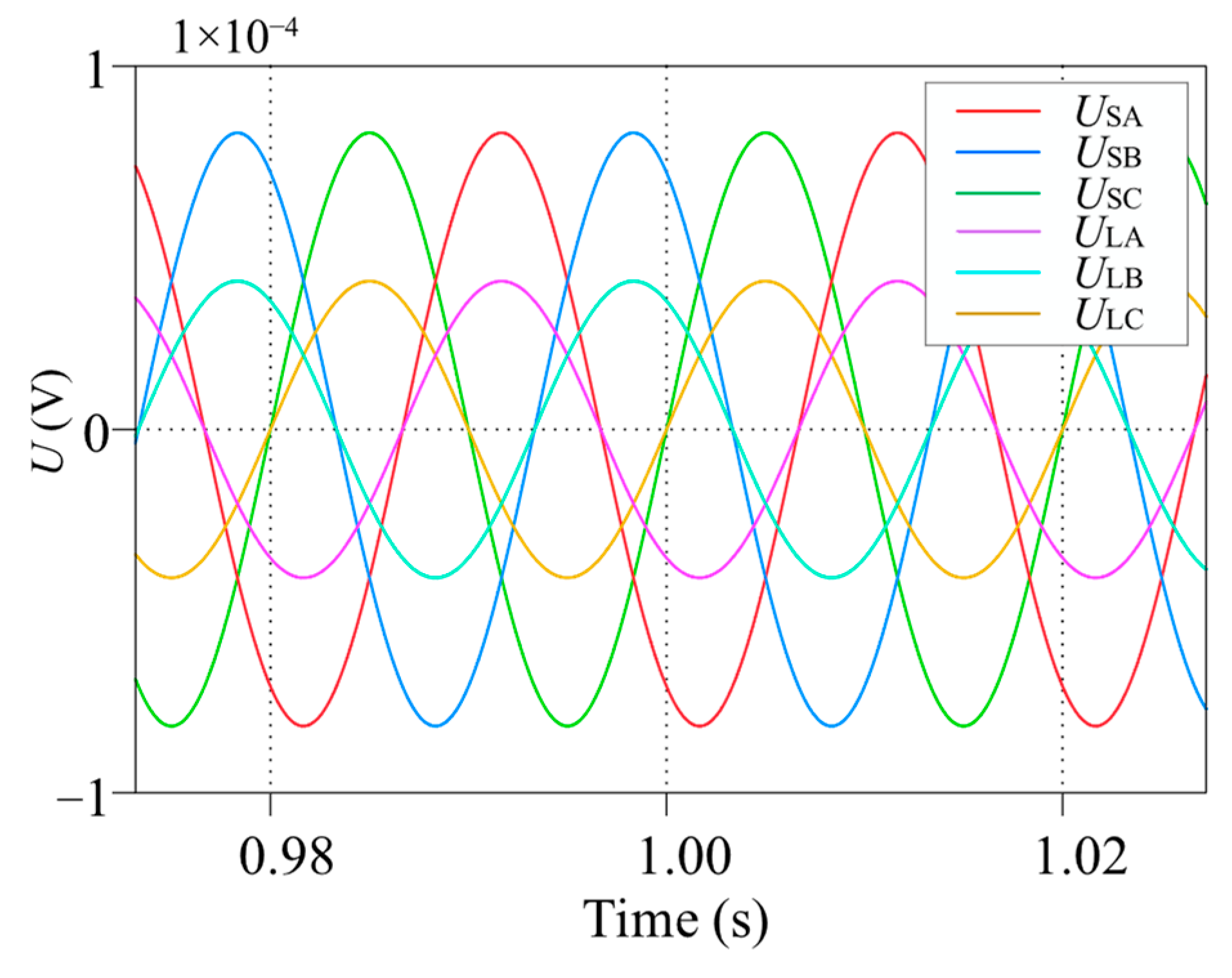






| Figure | nE1 | nE2 |
|---|---|---|
| Figure 3 | −0.423 | −0.577 |
| Figure 4 | −0.5 | 0 |
| Figure 5 | −0.736 → −0.288 | −0.841 → −0.431 |
| Feeder Line of Side a | Equivalent Impedance/Ω | Feeder Line of Side b | Equivalent Impedance/Ω |
|---|---|---|---|
| Za0 | 10 + j0.314 | Zb0 | 10 + j0.314 |
| Za1 | 12.03 + j2.450 | Zb1 | 3.50 + j1.018 |
| Za2 | 0.10 + j0.603 | Zb2 | 0.05 + j0.302 |
| Za3 | 8.60 + j2.752 | Zb3 | 16.24 + j2.714 |
| Za4 | 0.05 + j0.302 | Zb4 | 0.03 + j0.151 |
| Za5 | 10.64 + j2.224 | Zb5 | 8.06 + j2.865 |
| Parameter of PST | Value |
|---|---|
| Leakage inductance of primary windings (mH) | 2.56 |
| Leakage inductance of secondary windings (mH) | 0.64 |
| Primary winding resistance (Ω) | 0.0805 |
| Secondary winding resistance (Ω) | 0.0202 |
| Magnetizing curve (T, A/m) | (0, 0), (0.2, 12), (0.4, 24), (0.6, 38), (0.8, 55), (1.0, 80), |
| (1.2, 120), (1.4, 200), (1.6, 430), (1.7, 800), (1.8, 2000) | |
| Rated Capacity (MVA) | 400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Huang, F.; Diao, Y.; Bi, C.; Jin, X.; Wang, J. Novel Single-Core Phase-Shifting Transformer: Configuration, Analysis and Application in Loop Closing. Energies 2025, 18, 4500. https://doi.org/10.3390/en18174500
Xu Y, Huang F, Diao Y, Bi C, Jin X, Wang J. Novel Single-Core Phase-Shifting Transformer: Configuration, Analysis and Application in Loop Closing. Energies. 2025; 18(17):4500. https://doi.org/10.3390/en18174500
Chicago/Turabian StyleXu, Yong, Fangchen Huang, Yu Diao, Chongze Bi, Xiaokuan Jin, and Jianhua Wang. 2025. "Novel Single-Core Phase-Shifting Transformer: Configuration, Analysis and Application in Loop Closing" Energies 18, no. 17: 4500. https://doi.org/10.3390/en18174500
APA StyleXu, Y., Huang, F., Diao, Y., Bi, C., Jin, X., & Wang, J. (2025). Novel Single-Core Phase-Shifting Transformer: Configuration, Analysis and Application in Loop Closing. Energies, 18(17), 4500. https://doi.org/10.3390/en18174500






