Thermal Performance Enhancement in Pool Boiling on Copper Surfaces: Contact Angle and Surface Tension Analysis

Abstract

The electronics industry has significantly contributed to the development of efficient heat dissipation systems. One widely used technique is pool boiling, a simple method requiring no moving parts or complex structures. It enables the removal of large amounts of heat at relatively low temperature differences. Enhancing pool boiling performance involves increasing the critical heat flux and the heat transfer coefficient, which defines how effectively a surface can transfer heat to a cooling fluid. This method is commonly applied in cooling electronic devices, digital circuits, and power systems. In this study, pool boiling at atmospheric pressure was investigated using copper surfaces. To validate the Rohsenow model used to estimate the maximum bubble departure diameter, a planimetric approach was applied. Measurements included average contact angle (CA), surface tension (σ), and droplet diameter for four working fluids: deionised water, ethanol, Novec-649, and FC-72. For each fluid, at least 15 measurements of CA and σ were conducted using the Young–Laplace model. This study provides a comprehensive analysis of the influence of contact angle and surface tension on nucleate boiling using four different fluids on copper surfaces. The novelty lies in combining high-precision experimental measurements with validation of the Rohsenow model, offering new insights into surface-fluid interactions critical for thermal system performance.

1. Introduction

Heat dissipators are essential in industry and technology, where precise temperature control ensures the reliable operation of devices and processes. With the growing demand for high-performance electronic systems, effective heat management has become critical. Devices such as heat sinks, heat exchangers, and thermal coatings efficiently remove excess heat, preventing component overheating, performance degradation, and potential failure. Their application extends from consumer electronics to industrial systems, enhancing device lifespan and reducing electronic waste by limiting the need for replacements. Nucleate boiling represents a highly efficient cooling method, employed in sectors such as power generation, refrigeration, electronics, and chemical engineering. It occurs when a liquid at its boiling point forms vapor bubbles on a heated surface, enabling rapid heat removal through bubble detachment and liquid replenishment. This mechanism delivers high heat transfer rates from small surfaces under significant thermal loads—an advantage in cooling processors, computer components, and compact heat exchangers. Compared to conventional air or liquid convective cooling, nucleate boiling offers superior thermal performance and allows for the miniaturization of cooling systems.

However, controlling the nucleate boiling process poses challenges. If temperatures become too high, it can lead to superheating or film boiling, which decreases the cooling efficiency. Proper heating surface design and control of operating conditions are essential for stable nucleate boiling. Owing to its capacity for rapid, high-intensity heat removal, this method is increasingly applied in advanced industrial and electronic systems, ensuring efficiency and operational safety [1].

Wetting of solid surfaces by various liquids occurs in numerous technological processes (e.g., adhesion, nanotechnology, heat transfer) as well as in everyday activities (drying, washing, pharmaceutical applications) [2,3]. It involves partial or complete displacement of the liquid or gas phase from the solid surface. A key parameter characterizing liquid–solid interactions is the contact angle (CA), determined by the equilibrium of interfacial tensions between the liquid, solid, and gas phases. CA, together with surface tension (σ), reflects wettability and depends on the liquid and surface type as well as their physical and geometric properties [4]. Upon droplet deposition, a dynamic contact angle forms and evolves as the droplet spreads, decreasing in height until an equilibrium contact angle is reached. Specific CA ranges are used to classify surface wettability:

-

θ_z ≈ 0°—super hydrophilic surface;

-

θ_z < 5–10°—hydrophilic surface (the surface is entirely wetted);

-

~10° < θ_z < 90°—partially hydrophilic surface;

-

θ_z > 90°—hydrophobic surface (liquid droplet easily attaches to an air bubble);

-

θ_z > 150°—super hydrophobic surface [5].

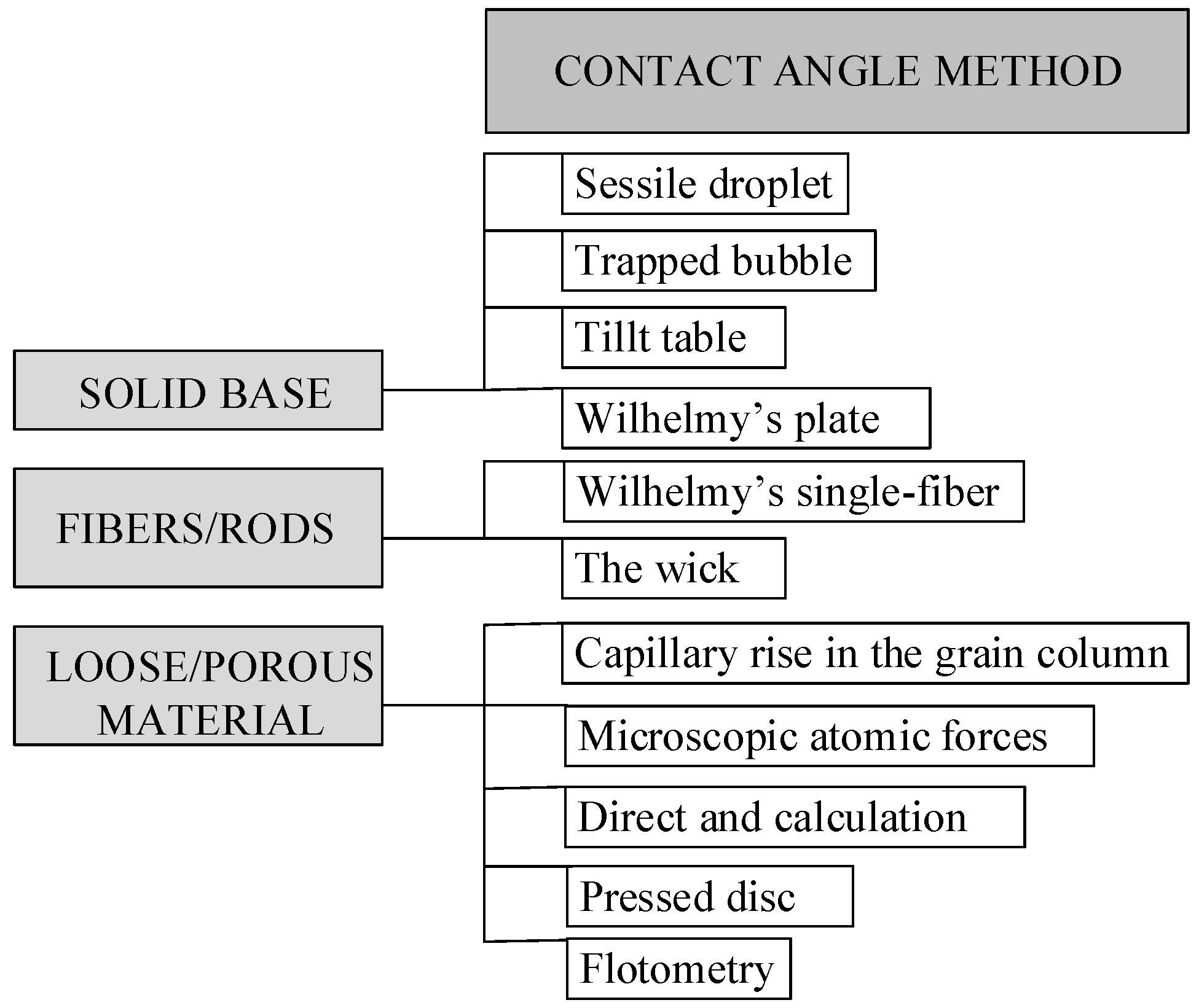
Most recommended methods for CA and surface tension research concern solid, flat surfaces, and a few methods, including sessile droplet or trapped bubbles, inclined plate, and Wilhelmy’s plate (Figure 1) [6].

There are many chemical and physical factors that, to some extent, may influence the contact angle and surface tension results concerning any fluid [7]. These mainly include the following:

-

Kind of fluid, its purity, and thermodynamic parameters (e.g., viscosity, density and even thermal conductivity);

-

Temperature of the process;

-

Presence of the surfactant and its type;

-

Voltage or electrical conductivity;

-

Stability of the working fluid;

-

Microwave radiation;

-

Presence of possible inclusions, e.g., nanoparticles.

Accurate contact angle determination requires considering surface and thermal conditions, boiling curve temperature range, fluid type, and process dynamics, as well as precise mapping of droplet geometry. Modern digital goniometry offers several shape approximations, with polynomial or elliptical fits used for dynamic measurements depending on the CA range; however, the ellipse method is unsuitable for axially asymmetric droplets. For small static CAs, the Young–Laplace and circular approximations are most effective, though only the Young–Laplace model yields surface tension values. Not all models accurately capture evaporation processes, and, for example, ellipse fitting is unsuitable for nanofluid evaporation [2].

The uncertainties of goniometry measurements depend mainly on the pixel size and are connected with image resolution [8]. Furthermore, kind of the solid base, droplet size, and dosing parameters are also meaningful [9].

Research on surface properties such as surface tension and wettability is gaining importance in heat transfer studies. In thermal engineering, the Rohsenow model is widely applied to predict heat transfer coefficients during nucleate boiling in systems like heat exchangers, reactors, and boilers, though it does not account for wetting angle [10]. Modified Mikic–Rohsenow correlations incorporating wettability effects have shown improved agreement with experimental data [11]. However, there remains a shortage of experimental studies addressing the combined influence of wettability, surface tension, and viscosity on heat transfer performance. As it turns out, the Mikic–Rohsenow model [12] gives even 100% discrepancy in relation to the experimental data and requires modification. Wen and Wang in [11] made an attempt to modify the active nucleate site correlation to include the effects of surface wettability [13]. In this case, Wen and Wang’s [11] proposition is as follows:

$${\mathrm{n}}_{\mathrm{a}}=\mathrm{C}{\left({\displaystyle \frac{1}{{\mathrm{r}}_{\mathrm{c}}}}\right)}^{\mathrm{m}}\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\theta }\right),$$

(1)

where n_a is active nucleate site density, r_c is the critical site radius for nucleation, which depends on superheat and surface tension, C and m are constants of the experiment; C = 5 × 10⁵, m = 6, θ is the contact angle.

$${\mathrm{r}}_{\mathrm{c}}={\displaystyle \frac{2{\mathrm{T}}_{\mathrm{s}}\mathsf{\sigma }}{{\mathrm{h}}_{\mathrm{f}\mathrm{g}}{\mathsf{\rho }}_{\mathrm{v}}\Delta {\mathrm{T}}_{\mathrm{s}}}},$$

(2)

where T_s is saturated temperature, σ is surface tension, h_fg means enthalpy of vaporization, and ρ_v is vapour density.

$$\mathrm{q}=\mathrm{B}{\left[\mathsf{\varphi }\left({\mathrm{T}}_{\mathrm{w}}-{\mathrm{T}}_{\mathrm{s}}\right)\right]}^{\mathrm{m}+1}\mathrm{C}\left(1-\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\theta }\right){\mathsf{\mu }}_{\mathrm{l}}{\mathrm{h}}_{\mathrm{l}\mathrm{v}}{\left[{\displaystyle \frac{\mathsf{\sigma }}{{\mathsf{\rho }}_{\mathrm{l}}{\mathsf{\rho }}_{\mathrm{v}}}}\right]}^{-0.5},$$

(3)

where $\mathrm{q}$ is the heat flux, $\mathrm{B}$ is a constant of the Mikic–Rohsenow experimental model [14], $\mathsf{\varphi }$ is the distribution of temperature differences, ${\mathrm{T}}_{\mathrm{w}}$ is wall temperature, ${\mathsf{\mu }}_{\mathrm{l}}$ and ${\mathsf{\rho }}_{\mathrm{l}}$ are kinematic viscosity and density of liquid phase, ${\mathrm{h}}_{\mathrm{l}\mathrm{v}}$ is liquid-vapour enthalpy, and ${\mathsf{\rho }}_{\mathrm{v}}$ refers to vapour density.

As it turns out, the use of a modified form of correlation, which takes into account surface conditions and wettability, causes the results of the heat flux density for superheating ΔT = 10 K in the case of liquids with the addition of Triton X-100 to be greater than 50% lower than the data from the literature [15], where the same substance was analyzed according to the assumptions of the Mikic–Rohsenow correlation. In turn, the difference in the results for liquids with the addition of sodium dodecyl sulfate (SDS) was slightly smaller and amounted to about 34%.

In [11] it is indicated that wettability is an important parameter in the boiling phenomenon and that it should undoubtedly be taken into account. However, there is a lack of sufficient experimental data conducted on a large scale in this area for many types of working fluids subjected to nucleate boiling.

Kim et al. [16] investigated the influence of copper surface roughness (Ra = 0.041–2.36 μm) on pool boiling heat transfer coefficient and critical heat flux (CHF). Static and dynamic contact angles were measured for nine surfaces using parallel and normal camera orientations. While roughness had a moderate effect on contact angles, it significantly increased heat transfer: the highest roughness yielded a CHF 50% greater than the smoothest surface (1.63 MW/m²). The enhancement was attributed to intensified capillary wicking and heat flux density. A modified Rohsenow correlation was proposed, replacing the empirical coefficient C with a function of surface roughness:

$${\displaystyle \frac{1}{{\mathrm{C}}_{\mathrm{s}\mathrm{f}}}}=84.3{\left({\displaystyle \frac{\mathrm{R}\mathrm{a}}{{\mathrm{R}\mathrm{a}}_0}}\right)}^{0.109},$$

(4)

where ${\mathrm{R}\mathrm{a}}_{\mathrm{a}}$ is the current surface roughness and ${\mathrm{R}\mathrm{a}}_0$ is representative surface roughness for typical metal surfaces.

The modified Rohsenow correlation proposed by Kim et al. [16] did not explicitly include contact angle, though its variation with roughness and measurement direction was examined using a Krüss DSA30 goniometer. Advancing contact angles were measured with 11.5 µdm³ droplets, receding angles with 50 µdm³ droplets. Values remained similar before and after boiling but differed by 5–15° depending on orientation: for Ra ≈ 1.5 µm, advancing angles were 90° (parallel) and 70° (normal), while receding angles were 11° and 9°, respectively. In the Rohsenow model, surface properties such as contact angle influence bubble distribution, nucleation frequency, and the surface tension term σ. Small angles yield flatter, less detachable bubbles and more nucleation sites, while large angles promote rapid detachment but reduce active nucleation areas. Surface tension, dependent on contact angle, affects bubble geometry, stability, and capillary forces in boiling.

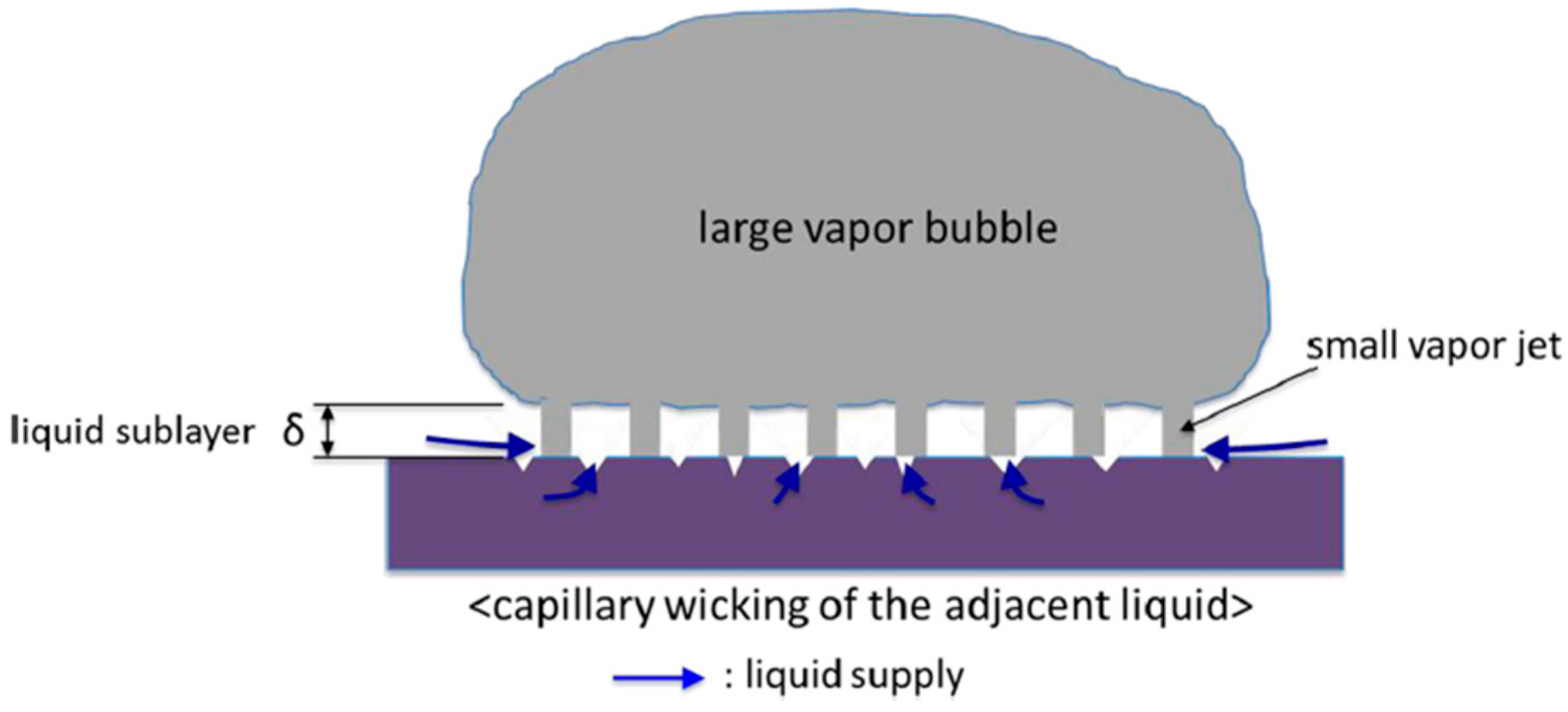
Figure 2 [16] shows how the structure, mainly the surface roughness, affects the formation of the vapor bubble during nucleation boiling. The static and dynamic contact angles decline with increasing Ra due to the capillary wicking, which results from the model proposed by Haramura and Katto in [17].

The classical Rohsenow model omits microstructural phenomena such as individual bubble dynamics, despite the contact angle’s key role in nucleate boiling. As a measure of liquid–solid interaction, the contact angle influences both thermodynamic and hydrodynamic boiling mechanisms. Empirical modifications introduce the contact angle into parameters C and n, with formulations such as C ∝ (1 + cos θ) to more accurately describe liquid behavior on various surfaces.

In addition to water and ethanol, refrigeration applications often use FC-72, valued for its high chemical stability, low boiling point (~56 °C), and low viscosity, enabling efficient convective flow. Its low surface tension—about 10% lower than that of deionized water—produces very small wetting angles, e.g., 2–3° for smooth copper under ambient conditions, facilitating bubble generation during boiling. Due to these properties, FC-72 is frequently employed in nucleate boiling and Rohsenow model studies [18,19,20,21].

Raj et al. [18] studied the wetting behavior of highly hydrophilic liquids like FC-72 on heated surfaces. For an oxidized, nearly smooth copper plate (Ra = 0.03 μm), the wetting angle ranged from 5 to 10°. High wettability enhances liquid adhesion, increasing active nucleation sites and improving cooling efficiency. According to the Wenzel model, surface roughness can further reduce the effective wetting angle (θ*) as the liquid fills microscopic surface irregularities:

$$\mathrm{c}\mathrm{o}\mathrm{s}{\mathsf{\theta }}^{*}=\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\theta }$$

(5)

where r is the roughness coefficient, and θ is the contact angle.

Since in the case of FC-72 droplet placed on copper, the increase in r lowers the effective wetting angle, with higher roughness, the liquid can penetrate micro-cracks and increase the contact with the surface, which leads to even better wetting.

The wetting angle varies with pressure and droplet size [2,22]. Fabien et al. [22] found that for water on stainless steel (R_a = 0.0335–0.1464 μm), the contact angle increased from 65° to 128° with pressure, while ethanol remained below 10° regardless of pressure. Novec-649 is commonly used in electronic cooling; Falsetti et al. [23] showed that pool boiling heat flux on copper (Ra 0.1–0.9 μm) rises with roughness and overheating, e.g., ΔT = 20 °C yields ~87% higher flux for 0.9 μm than smoother surfaces. Li et al. [24] proposed a universal relationship for the heat transfer coefficient α and the Rohsenow correlation constant C, accounting for contact angle, surface roughness, and coolant properties:

$$\mathsf{\alpha }=518503 \mathrm{C}{\displaystyle \frac{\mathsf{\Delta }{\mathrm{T}}_{\mathrm{e}}^{2.03}}{{\mathsf{\mu }}_{\mathrm{l}}{\mathrm{h}}_{\mathrm{f}\mathrm{g}}}}{\left.\left[\mathrm{g}{\displaystyle \frac{\left({\mathsf{\rho }}_{\mathrm{l}}-{\mathsf{\rho }}_{\mathrm{v}}\right)}{\mathsf{\sigma }}}\right.\right]}^{0.5}{\mathrm{k}}_{\mathrm{l}}^{3.03},$$

(6)

$$\mathrm{C}={(1-\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\theta })}^{0.5}\left\{0.5\right\}{\mathsf{\gamma }}^{-0.04}\left.\left[1+{\displaystyle \frac{5.45}{{\left({\mathrm{R}}_{\mathrm{a}}-3.5\right)}^2+2.61}}\right.\right],$$

(7)

where ${\mathrm{k}}_{\mathrm{l}},{\mathsf{\mu }}_{\mathrm{l}},{\mathsf{\rho }}_{\mathrm{l}}$ is thermal conductivity, viscosity, and density of the liquid; $\mathrm{g}$ is gravitational acceleration; ${\mathsf{\rho }}_{\mathrm{v}}$ is density of the vapor; $\mathsf{\theta }$ and $\mathsf{\gamma }$ are the contact angle and surface tension, respectively.

The contact angle is a key parameter influencing heat transfer in thermal systems. This study determines the wetting conditions and surface tension of four working fluids—deionized water, ethanol, FC-72, and Novec-649—on a copper base using the Young–Laplace method and a Krüss DSA25Expert goniometer, and presents the droplets’ geometric characteristics. The planimetric method is applied to validate the Rohsenow model for estimating the maximum bubble departure diameter. The work addresses a literature gap concerning the effect of contact angle on nucleate boiling for various fluids in contact with copper, a material widely used in heat exchangers [25,26,27].

2. Materials and Methods

2.1. Contact Angle Measurement and Wettability Characterization

The wetting angle and surface tension are determined using the sessile drop method and the Young–Laplace formulas:

$$\mathrm{c}\mathrm{o}\mathrm{s}{\mathsf{\theta }}_{\mathrm{D}}={\displaystyle \frac{{\mathsf{\gamma }}_{\mathrm{W}\mathrm{V}-}{\mathsf{\gamma }}_{\mathrm{W}\mathrm{L}}}{{\mathsf{\gamma }}_{\mathrm{L}\mathrm{V}}}},$$

(8)

$${\mathsf{\gamma }}_{\mathrm{W}\mathrm{V}}={\mathsf{\gamma }}_{\mathrm{W}\mathrm{L}}+{\mathsf{\gamma }}_{\mathrm{L}\mathrm{V}}\hspace{0.17em}\mathrm{c}\mathrm{o}\mathrm{s}{\mathsf{\theta }}_{\mathrm{D}}$$

(9)

where γ_LV—droplet surface tension, γ_WV—substrate free energy, γ_WL—droplet/substrate interfacial tension, θ_D—contact angle.

An angle that exists between the vector that determines the liquid to solid substrate interfacial tension γ_WL and the liquid surface tension γ_LV is called the contact angle, θ_D. The more fluid spreads over the solid substrate, the lower the contact angle. The equilibrium of the projections of forces on the horizontal plane is shown in Figure 3.

The dedicated software enables capturing, visualizing, and analyzing obtained metadata, also in the form of digital photos.

The droplet diameter is determined using a gonimeter set equipped with a high-resolution digital camera, based on the photograph.

In order to estimate the possible error in reading the diameter, resulting from the size of a single pixel Δr on the digital camera matrix, it is defined as the derivative of the area with respect to the droplet radius and is expressed by the equation:

$$\Delta \mathrm{A}={\displaystyle \frac{\partial \mathrm{A}}{\partial \mathrm{r}}}\Delta \mathrm{r}=2\mathsf{\pi }\sqrt{{\displaystyle \frac{\mathsf{\pi }{\mathrm{R}}^2}{\mathsf{\pi }}}}\Delta \mathrm{r}=2\mathsf{\pi }\sqrt{{\mathrm{R}}^2}\Delta \mathrm{r}=2\mathsf{\pi }\mathrm{R}\Delta \mathrm{r}=2\mathsf{\pi }\mathrm{R}\pm 1\mathrm{p}\mathrm{x}$$

(10)

where Δr is the size of a single pixel for a digital camera, depending on the current optical settings (the technical parameters of the camera are given in the next chapter). Each time the device was calibrated and the visual acuity was changed, the size of a single pixel was also determined, which did not exceed 0.0000147 m. The error in the measurement of the wetting angle was determined based on the following relationship:

The error of the contact angle measurement was determined based on the following relationship:

$$\Delta {\mathsf{\theta }}_{\mathrm{D}}={\displaystyle \frac{{\mathsf{\theta }}_{\mathrm{D}}-{\mathsf{\theta }}_{\mathrm{D},\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathsf{\theta }}_{\mathrm{D},\mathrm{m}\mathrm{a}\mathrm{x}}}}·100\%,$$

(11)

where ${\mathsf{\theta }}_{\mathrm{D},\mathrm{m}\mathrm{i}\mathrm{n}} \mathrm{a}\mathrm{n}\mathrm{d} {\mathsf{\theta }}_{\mathrm{D},\mathrm{m}\mathrm{a}\mathrm{x}}$ are minimum and maximum values of measured CA, respectively.

An estimate of the maximum absolute error was also provided:

$$\Delta {\mathsf{\theta }}_{\mathrm{D}}=\left|{{\mathsf{\theta }}_{\mathrm{D}}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}}-{{\mathsf{\theta }}_{\mathrm{D}}}_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}\right|,$$

(12)

where ${{\mathsf{\theta }}_{\mathrm{D}}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}},{{\mathsf{\theta }}_{\mathrm{D}}}_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}$ are measured and real values of CA, respectively.

2.2. Measuring Techniques

The research is implemented in a measurement station, the diagram of which is presented in Figure 4. Three main systems are distinguished: optical, digital, and dosing.

The technical parameters of the individual systems are as follows:

-

The optical system: LED technology, the dominant wavelength is 470 nm, the illumination area is 42 mm;

-

The digital camera system: five fields of resolution, from 160 fps at 1200 × 1200 px to 3400 fps at 640 × 50 px; the optics are characterized by view area for two ranges (3.2 mm × 3.2 mm to 18.5 mm × 18.5 mm and 1.4 mm × 1 mm to 8.1 mm × 6 mm) and resolutions (2.5 to 16.2 µm and 2.1 to 13.3 µm),

-

The automatic dosing system: glass syringe with a total capacity of 500 μdm³ equipped with a steel needle with a diameter of 1.063 mm; the resolution of the dosing system is 0.1 µdm³.

The research is conducted for four types of liquids: deionised water (DI), ethanol, FC-72, and Novec-649. Drops of these liquids of a given volume were dosed onto a previously leveled copper plate with a roughness coefficient of R_a = 123 μm, which was placed in the optical axis of the camera, on the goniometer table (marked 2 according to Figure 4). Due to the high hydrophilicity of the FC-72 and Novec-649 drops (drops of these substances ‘spread’ over the surface), their size and dosing speed were determined by the geometric dimensions of the copper plate and were 2–20 μdm³, 5–10 μdm³/s, respectively.

Static contact angle measurements are performed from the left and right side of the droplet; on this basis, its mean value (CA(m) = CA(l) + CA(r)) and surface tension for the given time step dt = 0.5 s is determined. The droplet shape analyzer used in the tests returns the contact angle values with an accuracy of 0.1°, while its sensitivity is 0.01°. Moreover, the droplet volume and diameter over time (dV/dt and dD/dt) are also obtained. At least twenty measurement series are carried out under Young–Laplace method for each fluid in two stages. Some results were rejected. The contact angles were measured under ambient conditions.

In the first stage, the tests were carried out for a ‘raw’ copper substrate, and in the second after a few minutes of heating. This allowed for checking whether copper oxides precipitated during heating could affect the wettability conditions and surface tension. The annealing process is shown in Figure 5. At first, the copper plate turned darker due to surface oxidation and the formation of a thin layer of copper oxides. At first, copper(I) oxide (CuO₂) is formed, which is reddish in colour. With further heating and the access of oxygen, copper (II) oxide (CuO) is formed, which is black. After convective cooling, the oxide layer flaked off.

2.3. Boiling Curve Determination

The experimental setup shown in Figure 6 [28] was designed to determine the boiling curves under gradually increasing heat flux conditions. The experiments focused on the nucleate boiling of water on smooth surfaces, starting from the onset of nucleate boiling (ONB) and continuing up to the occurrence of the first boiling crisis characteristic of pool boiling. All measurements were conducted under atmospheric pressure conditions.

The measurement process began with the activation of a water-cooled condenser to facilitate vapor condensation. Subsequently, the heating system was switched on, and the liquid was heated until the saturation temperature was reached. This state was maintained for 10 min to allow complete degassing of the liquid in the glass vessel. The next step involved setting the appropriate voltage on the autotransformer, corresponding to the desired heat flux. After approximately 15 min—until the temperature readings stabilized (no change for at least 5 min)—data acquisition began.

Temperature measurements were carried out using sheathed type-K thermocouples with a diameter of 0.5 mm. The copper cylinder had a diameter of d_cyl = 45 mm, and the active edge length of the sample was a = 37 mm. A thermal conductivity of copper equal to 380 W/(m·K) was assumed. The heat source was a cartridge heater with a power of 1600 W, a diameter of 16 mm, and a length of 100 mm.

Measurements were carried out using a FLUKE Hydra Series II 2635A (Everett, WA, USA) data acquisition system. The recorded variables included the temperatures within the copper heating rod (sensors T3 to T8) and the saturation temperatures of the liquid (sensors T1 and T2). Type K sheathed thermocouples with a diameter of 0.5 mm were used for temperature measurement. Prior to the experiments, all sensors were calibrated using an Altek 422 calibrator (Birmingham, AL, USA). The calibration range for the thermocouples extended from 40 °C to 300 °C in 5 °C increments, with an absolute measurement error not exceeding 0.1 K.

To ensure the repeatability of results and minimize errors in determining the heat flux and heat transfer coefficient, a one-dimensional heat conduction model was applied. The cylindrical heater was thermally insulated with a thick layer of insulating material, eliminating lateral heat losses. Consequently, Fourier’s law was used to calculate the heat flux.

$$\mathrm{q}={\mathsf{\lambda }}_{\mathrm{C}\mathrm{u}}{\displaystyle \frac{{\mathrm{T}}_{\mathrm{T}8}+{\mathrm{T}}_{\mathrm{T}5}}{{\mathsf{\delta }}_{\mathrm{T}8-\mathrm{T}5}}}{\displaystyle \frac{\mathsf{\pi }{\mathrm{d}}_{\mathrm{c}\mathrm{y}\mathrm{l}}^2}{{4\mathrm{a}}^2}}$$

(13)

The distance between the thermocouples, as shown in Figure 7, was δ_T8−T5 = 35 mm. The diameter of the copper cylinder was d_cyl = 45 mm, and the active side length of the sample was a = 37 mm. The thermal conductivity of copper used in the calculations was assumed to be −380 W/mK.

The heat transfer coefficient between the heat-exchanging surface and the liquid was determined based on an appropriate analytical relationship:

$$\mathsf{\alpha }={\displaystyle \frac{\mathrm{q}}{\mathsf{\Delta }\mathrm{T}}}$$

(14)

The temperature difference was determined, in accordance with Figure 7, as follows:

$$\Delta \mathrm{T}={\displaystyle \frac{{\mathrm{T}}_{\mathrm{T}3}+{\mathrm{T}}_{\mathrm{T}4}}{2}}-\mathrm{q}{\displaystyle \frac{{\mathsf{\delta }}_{\mathrm{b}\mathrm{s}}}{{\mathsf{\lambda }}_{\mathrm{C}\mathrm{u}}}}-{\displaystyle \frac{{\mathrm{T}}_{\mathrm{T}1}+{\mathrm{T}}_{\mathrm{T}2}}{2}}$$

(15)

where ${\delta }_{bs}$ is sample thickness, mm.

3. Results

3.1. Contact Angle Measurement and Wettability Characterization

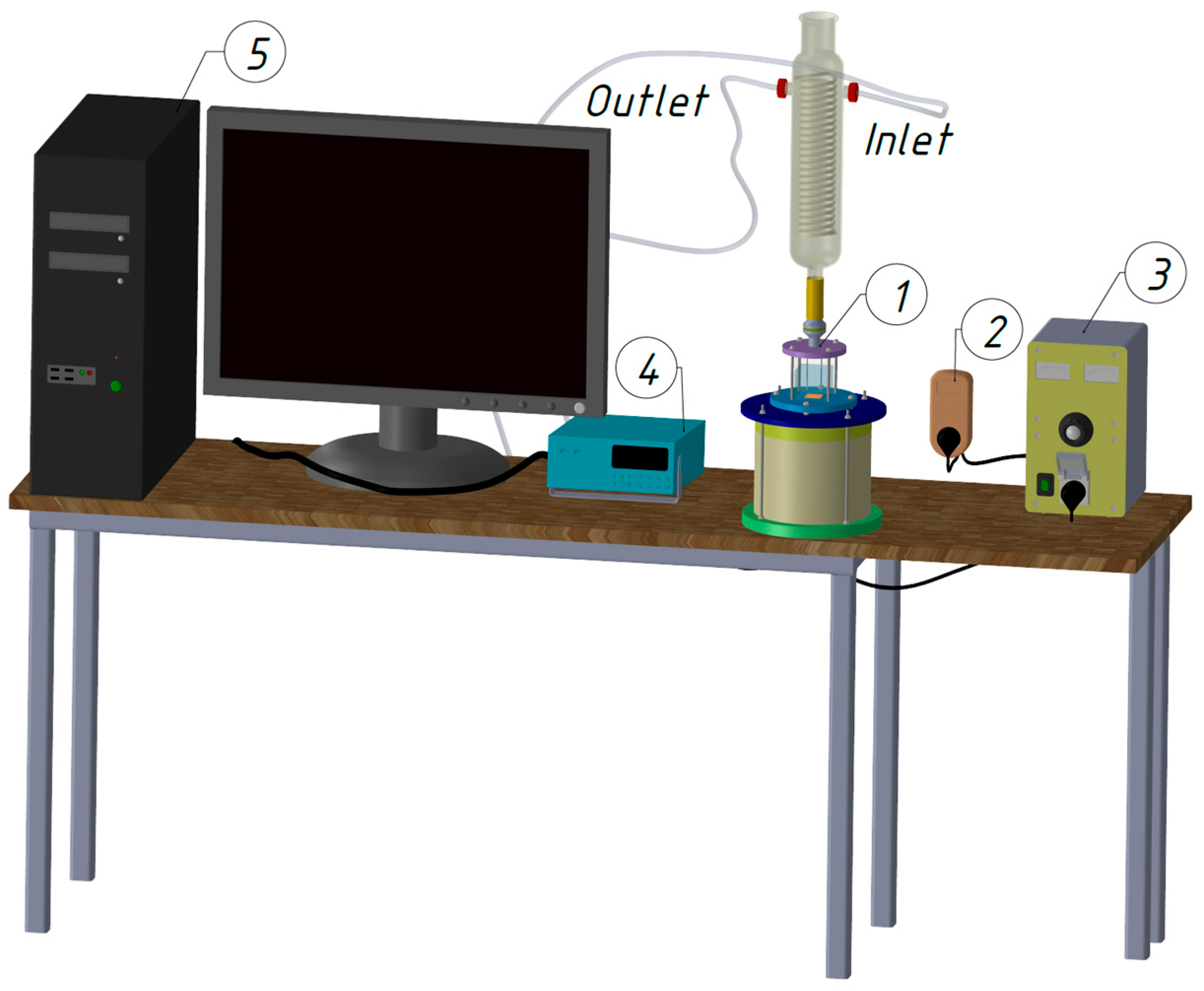
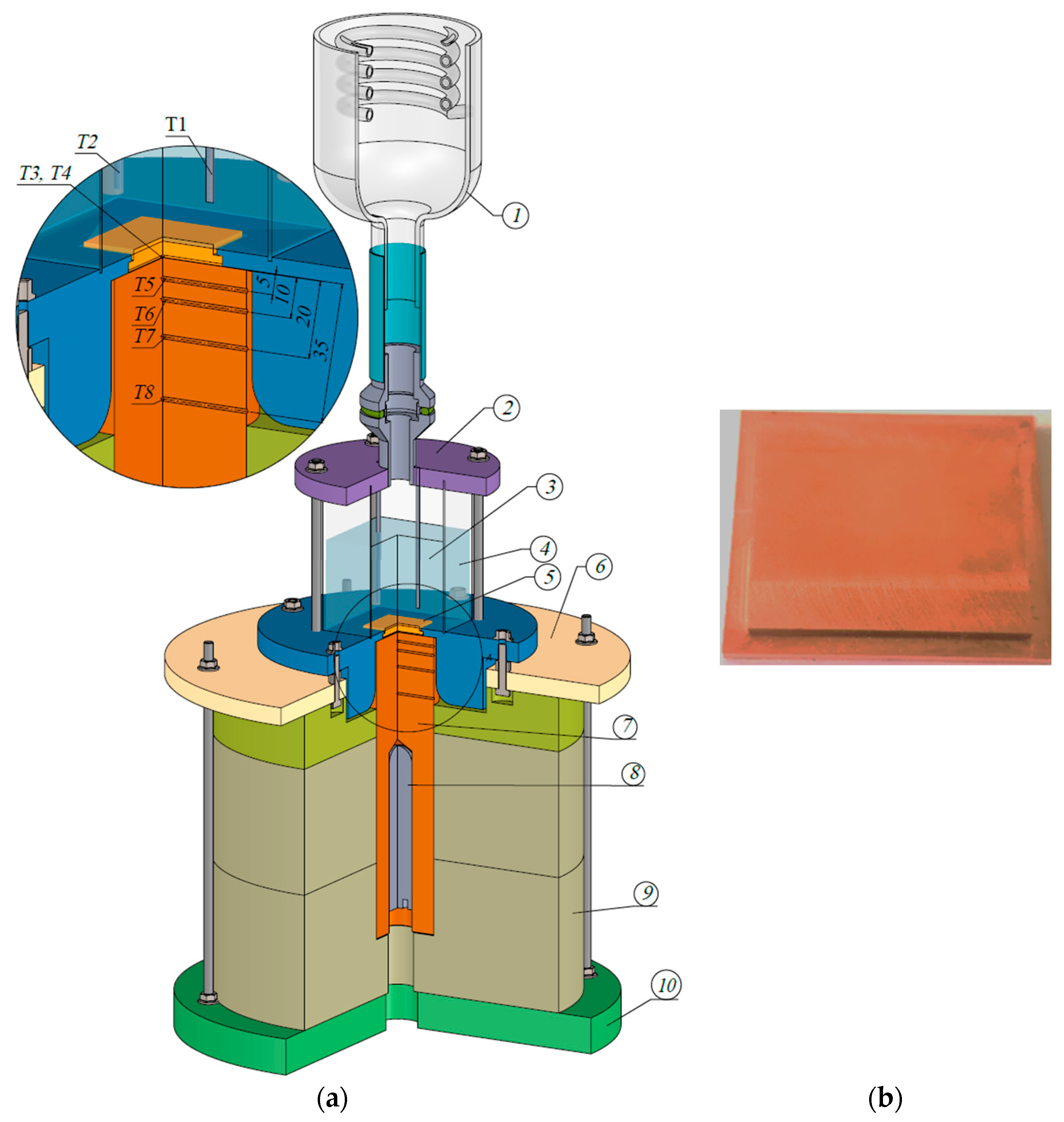
In the setup shown in Figure 4, a series of at least 20 measurements was performed for each liquid before and after heating the copper plate. Because of the observed instabilities and measurement errors resulting from the very rapid evaporation of the droplets, some of the measurements were rejected. Such a quantity of data allows for verification of repeatability and statistical analysis with sufficient confidence.

The research implemented allows for direct measurement and recording of the angle of the left CA(l), right CA(r), and mean contact angle CA(m) of a droplet over time, its current volume, diameter, and surface tension. The mean value of the difference between CA(M) and CA(L) or CA(M) and CA(R) does not exceed 0.30°, as confirmed in the paper [2].

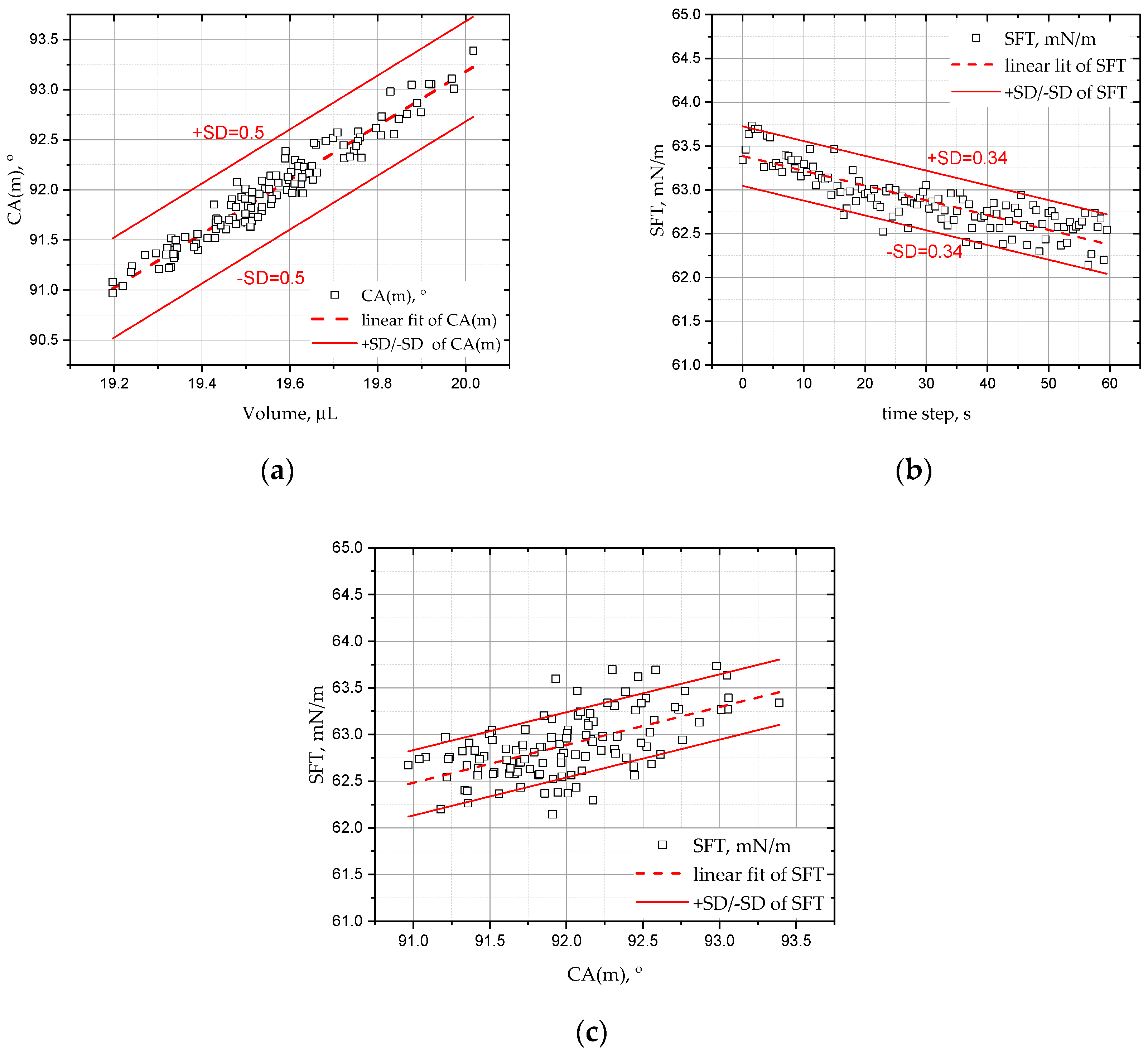
An example of a measurement series is demonstrated in Figure 8, which presents the change in the mean contact angle of the deionized water droplet over volume, time, and surface tension CA(m) (t, Vol, SFT) for the sample 1—copper surface before heating (Cu 1). The research was carried out with the DSA25E Krüss goniometer (Hamburg, Germany), by the use of the Young–Laplace approximation method.

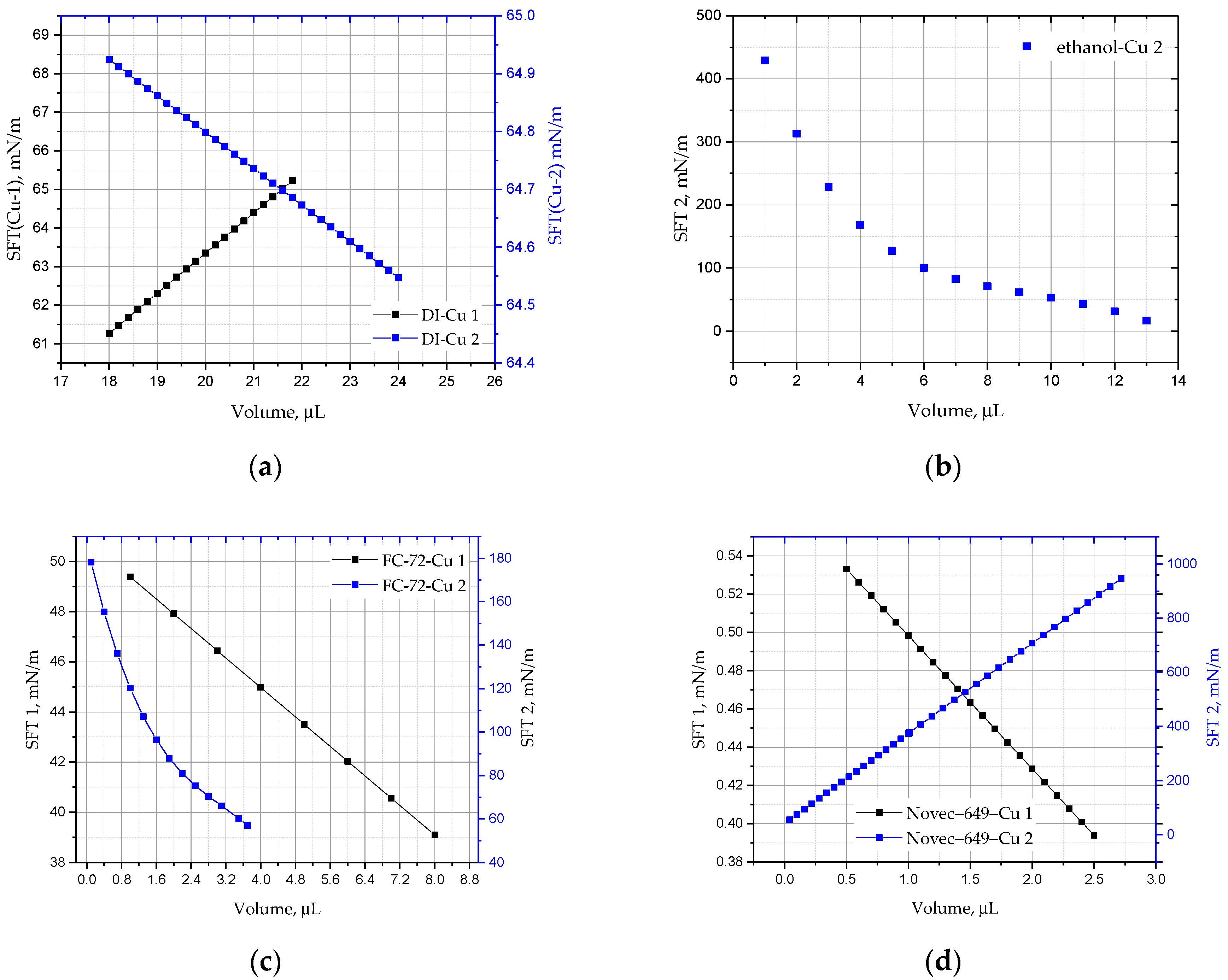
The following graphs (Figure 9 and Figure 10) show the cumulative results for the drops of all analysed liquids, DI water, ethanol, FC-72, and Novec-649 before (red marker) and after the annealing process (blue marker) of the copper substrate. In the case of Novec-649 drops, it was necessary to adopt two ranges of functions. The marking of the substrate with the numbers 1 or 2 refers to the copper plate before and after annealing, respectively.

Figure 9 shows the change in the mean contact angle CA(m) of the DI, ethanol, FC-72, and Novec-649 droplets as a function of their volume for the copper surface before (Cu 1) and after heating (Cu 2). For all liquids, a change in the dynamics of evaporation and surface wettability is observed before and after the heating process; moreover, apart from Novec-649 drops, lower values of the initial contact angles are also visible. The drops evaporate very quickly, and in the case of the Cu 2 substrate, it is not possible to ‘place’ a drop of a larger volume, similar to the one applied to the Cu 1 surface. Figure 11 shows the hydrophobic properties of a copper surface in contact with water. The remaining liquids tested could not be photographed in this way due to their superhydrophilic properties (CA~10°).

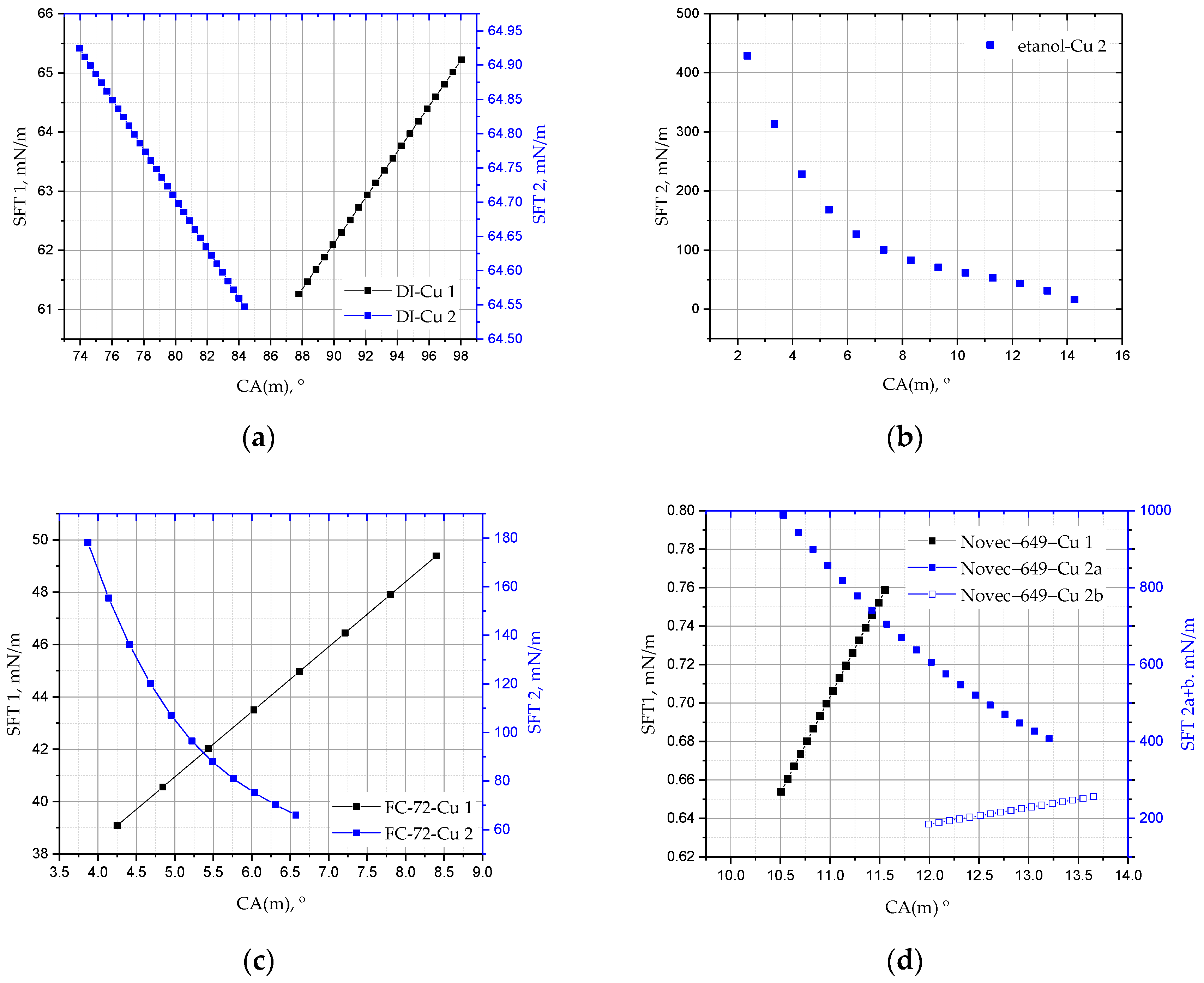
The following Figure 10 and Figure 12 show how the surface tension changes with the drop volume and the wetting angle, respectively. For Cu 2 samples, it is always inversely proportional to the drop volume, except for the Novec-649 liquid. It is also inversely proportional to the average wetting angle CA(m) and higher for samples after annealing, which explains the rapid evaporation process.

3.2. Measurement Errors Analysis

The wetting angle and surface tension measurements were performed using a Krüss Expert 25 digital goniometer and the Young–Laplace method. The digital camera system has five fields of resolution, from 160 fps at 1200 × 1200 px to 3400 fps at 640 × 50 px, which provides very good conditions for detecting the image of a liquid drop on a copper surface. The resolution of the goniometer camera has a significant impact on the accuracy of the wetting angle measurement because the liquid-surface contact line is detected based on the image. The more pixels there are in this area, the smaller the error in determining the actual angle. In addition, at very small wetting angles (<10°), differences in a few pixels can significantly affect the result. It is also worth adding that with rapidly evaporating liquids such as ethanol, FC-72, or Novec-649, the time to take a picture is limited, and the drop changes shape very quickly. The high-resolution camera allows for very dynamic and more precise capture of the droplet shape before evaporation affects the result, although for some liquids, this is still difficult. Other factors that can distort the CA measurement results may be poor lighting conditions (e.g., low contrast), an inaccurate droplet contour matching algorithm, uneven or contaminated surface. In the research presented here, an advanced optical system made in LED technology was used, which has a dominant wavelength of 470 nm, and the illumination area is 42 mm and provides very good image contrast.

To calculate the error in the detection of the diameter, resulting from the size of a single pixel Δr on the digital camera matrix, we used Equation (10). The size of a single pixel for a digital camera depends on the current optical settings. The single pixel size of the DC camera depends on the current optical settings. Every time the device is calibrated, visual clarity changes, and the size of a single pixel is calculated, and is not higher than 0.0000147 m.

Additionally, the relative error in the measurement of the wetting angle (percentage difference between the values) was determined based on the relationship (11).

Figure 13 shows the relative error of the contact angle measurements for the three analysed liquids, ethanol, FC-72, and Novec-649. The value of the error varies from 0% for low CA(m) values up to 65% for the FC-72-Cu 2 sample, i.e., after annealing. This process appears to noticeably modify the surface energy and increase hydrophobicity in the case of FC-72, which in turn causes the droplet lifetime to be extremely short and makes precise measurement more challenging. Due to the high hydrophobicity, it was not possible to deposit a droplet of a similar size as for the unannealed sample—the droplet diameter was approximately half that obtained before annealing.

In each case except for the Novec-649 liquid drop, the error is higher for the copper sample after annealing and is, on average 3% more for ethanol drops and 1.34% for FC-72 than for copper before the oxidation process; the maximum difference can reach 12% for FC-72. In the case of water, this error does not exceed 4% both before and after the plate annealing process, although in the latter case it is half as low. In most cases, the relative error decreases with the increase of the drop size except for the Novec-649 drop, where it first really increases and then decreases. The highest absolute error ($\Delta \mathrm{C}\mathrm{A}\left(\mathrm{m}\right)=\left|{\mathrm{C}\mathrm{A}\left(\mathrm{m}\right)}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}}-{\mathrm{C}\mathrm{A}\left(\mathrm{m}\right)}_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}\right|$), was recorded for FC-72 droplets, and the lowest for water droplets, which were 1.17° and 0.56°, respectively. In turn, the average relative error of surface tension measurement, SFT, in no case exceeds 38% for ethanol, FC-72, and Novec-649 droplets and 0.6% for water droplets. The value of the error resulting from the size of a single pixel is insignificant and does not exceed $\Delta \mathrm{A}=4\times {10}^{-7} {\mathrm{m}}^2$. Often, the uncertainty of measurements of contact angles is not even given [16].

The error in the measurement of the contact angle made with a digital goniometer depends on the camera resolution—the higher the resolution, the greater the precision of determining the wetting angle. It is particularly important for small angles and rapidly evaporating liquids, but the accuracy of the measurement also depends on other factors, such as software, measurement conditions, and surface properties. The selection of the droplet contact points with the substrate—automatic or manual marking of the measurement area can lead to discrepancies. In addition, contamination and surface irregularities can change the local surface tension and lead to errors, although in this case, the measurements were carried out with great care, and the surface was degreased before each droplet was placed. It should also be mentioned that in the case of volatile liquids, such as ethanol, FC-72, and Novec-649, the volume of the droplet and its geometry change very dynamically. Differences in the initial volume of the droplet can lead to different wetting angles (the effect of the dependence on the size of the droplet). Droplet evaporation can be limited by minimizing the measurement time and quickly taking pictures after the droplet has been deposited, or at least by using a closed measuring chamber, which limits air circulation and evaporation.

3.3. Pool Boiling

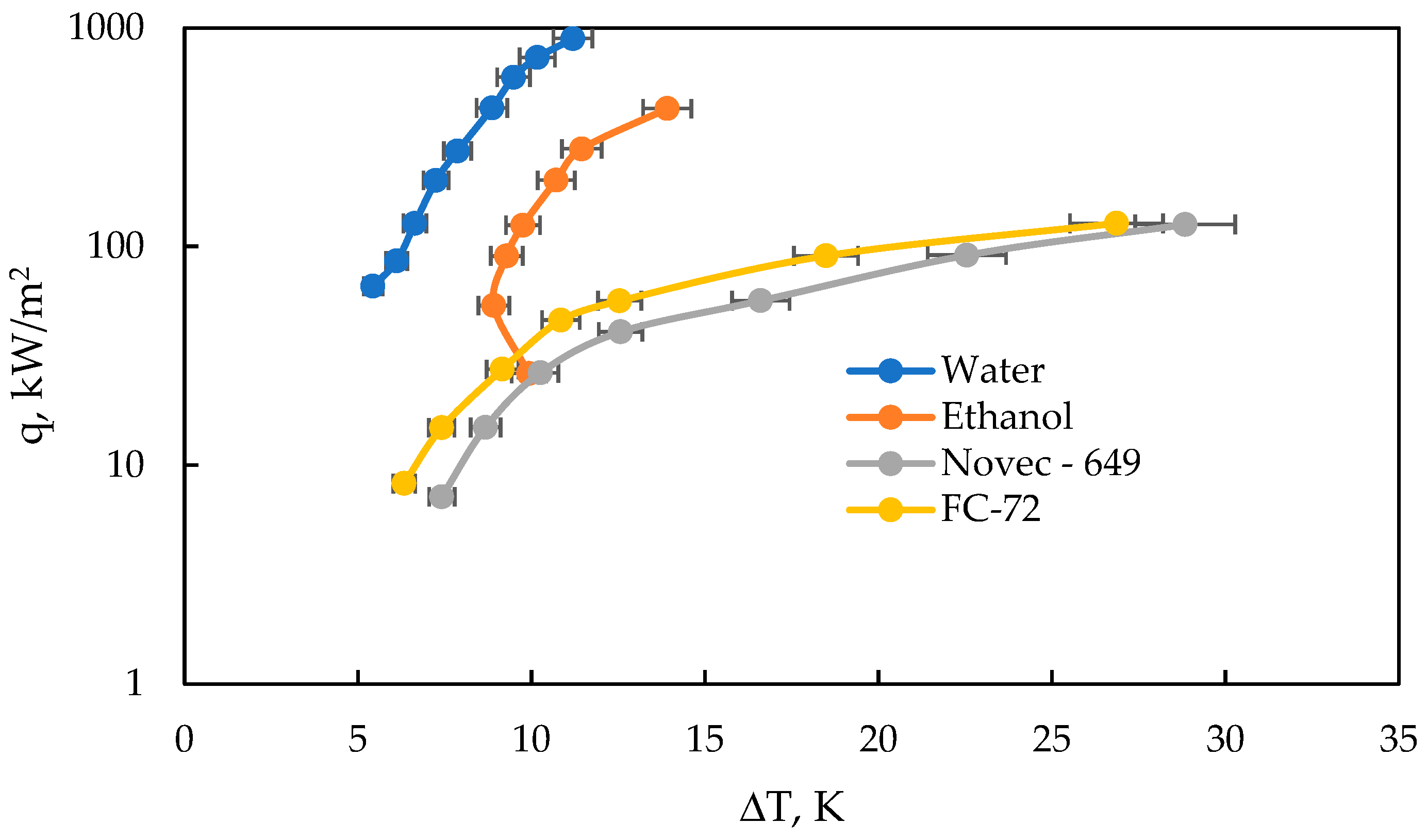
Experimental studies of the heat transfer process were conducted for four liquids: deionised water, ethanol, FC-72, and Novec-649. Measurements were carried out under atmospheric pressure during nucleate boiling on a smooth, flat surface, with a gradual increase in heat flux density. Pool boiling [29] is a complex phenomenon governed primarily by three mechanisms: evaporation of the microlayer, heat conduction, and forced convection. The boiling curves obtained for all tested fluids are presented in Figure 14.

An increase in surface roughness typically leads to a significant rise in the heat transfer coefficient (HTC), primarily due to a greater number of active microcavities that serve as nucleation sites for bubble formation. In studies conducted by Kim et al. [16,30], it was found that increasing the roughness parameter Ra from 0.041 µm to 2.36 µm resulted in a twofold increase in the critical heat flux (CHF)—reaching approximately 1625 kW/m²—as well as an enhancement in HTC. However, as shown by Pereira et al. [31] and Orman et al. [26,32], excessive surface roughness can slow down the boiling process due to the early formation of a vapor blanket.

Based on the boiling curves (q vs. ΔT) presented for four fluids (water, ethanol, FC-72, and Novec-649), clear differences can be observed in their boiling characteristics on a surface with a roughness of Ra = 123 µm. Water reaches the highest heat flux (q) values at relatively low surface superheat (ΔT), indicating its high efficiency in heat dissipation. This is consistent with theory, as water has a high surface tension and a large latent heat of vaporization, which promotes intense nucleate boiling. Ethanol also achieves relatively high q values, but requires a slightly higher ΔT. This results from its lower surface tension and higher volatility compared to that of water, leading to faster bubble detachment but a lower critical heat flux (CHF). FC-72 and Novec-649 exhibit similar curve behavior, characterized by lower heat transfer coefficients (HTC) and CHF. These fluids have very low surface tension and low latent heat of vaporization, which limits the intensity of the boiling process. The conclusions from the graph align with the predictions of the Rohsenow correlation, though accurate modeling requires calibration of the empirical parameter C_sf for the given surface.

For the range of heat fluxes analyzed, which varied from 8 to 892 kW/m², the calculated relative error ranged between 15.6% and 2.3%, showing a clear dependence on the magnitude of the heat flux. In the case of the heat transfer coefficient, evaluated within the range of 1 to 80 kW/m² K, the relative error was found to lie between 4.6% and 19.5%. These findings indicate that while the model provides a reasonable prediction accuracy across a wide operating range, certain deviations are more pronounced at lower heat flux values. Comparable levels of relative error were reported in the study conducted by Jaikumar [33] and his collaborators, which further supports the reliability and repeatability of the applied methodology for heat transfer modeling in pool boiling.

One of the most widely used correlations for describing heat transfer phenomena during pool boiling is the Rohsenow correlation. This model is based on the assumption that the key mechanisms enhancing heat transfer are the formation, growth, and departure of vapor bubbles from the heated surface. These processes cause localized disturbances in the boundary layer, inducing fluid mixing and significantly increasing the rate of heat transfer from the surface to the liquid. Rohsenow proposed that the efficiency of the boiling process could be expressed through a semi-empirical relation incorporating fluid and surface properties, the degree of superheat, and the thermal characteristics of the heating material. The correlation links heat flux to surface superheat, surface tension, thermal conductivity, fluid density, and viscosity. A crucial element of the model is the empirical coefficient that depends on the specific fluid–surface combination and the flow conditions. Its value was obtained by fitting the Rohsenow model to the measured boiling characteristics. The Rohsenow correlation can be expressed as follows [34]:

$${\displaystyle \frac{{\mathrm{c}}_{\mathrm{p}}\mathsf{\Delta }\mathrm{T}}{{\mathrm{h}}_{\mathrm{l}\mathrm{v}}}}={\mathrm{C}}_{\mathrm{s}\mathrm{f}}{\left[{\displaystyle \frac{\mathrm{q}}{{\mathrm{h}}_{\mathrm{l}\mathrm{v}}{\mathsf{\mu }}_{\mathrm{l}}}}{\mathrm{L}}_{\mathrm{c}\mathrm{a}\mathrm{p}}\right]}^{0.33}{\mathrm{P}\mathrm{r}}^{\mathrm{n}}$$

(16)

where ${\mathrm{L}}_{\mathrm{c}\mathrm{a}\mathrm{p}}=\sqrt{{\displaystyle \frac{\sigma }{\mathrm{g}\left({\rho }_{\mathrm{l}}-{\rho }_{\mathrm{v}}\right)}}}$

-

c_p—specific heat capacity of the liquid at constant pressure [J/(kg·K)]

-

ΔT—surface superheat, difference between surface and liquid temperature [K]

-

h_lv—latent heat of vaporization [J/kg]

-

C_sf—empirical coefficient depending on the fluid–surface combination

-

q—heat flux [W/m²]

-

μ_l—dynamic viscosity of the liquid [Pa·s]

-

L_cap—capillary length [m]

-

σ—surface tension [N/m]

-

g—gravitational acceleration [m/s²]

-

ρ_l—liquid density [kg/m³]

-

ρ_v—vapor density [kg/m³]

-

Pr—Prandtl number (dimensionless number characterizing heat conduction)

-

n—exponent depending on the fluid type (e.g., 1 for organic fluids, 1.7 for water)

This correlation is widely applied in the analysis and design of nucleate-based cooling systems, particularly in industrial processes, power engineering, and electronic device cooling. Despite its empirical nature and simplicity, the Rohsenow equation remains one of the most commonly used models in thermal engineering. Lower surface tension promotes the formation of smaller vapor bubbles and their quicker detachment from the surface, resulting in a higher bubble departure frequency and an increased heat transfer coefficient (HTC). In semi-empirical models, such as the Rohsenow correlation, surface tension appears in the denominator and influences the predicted heat flux.

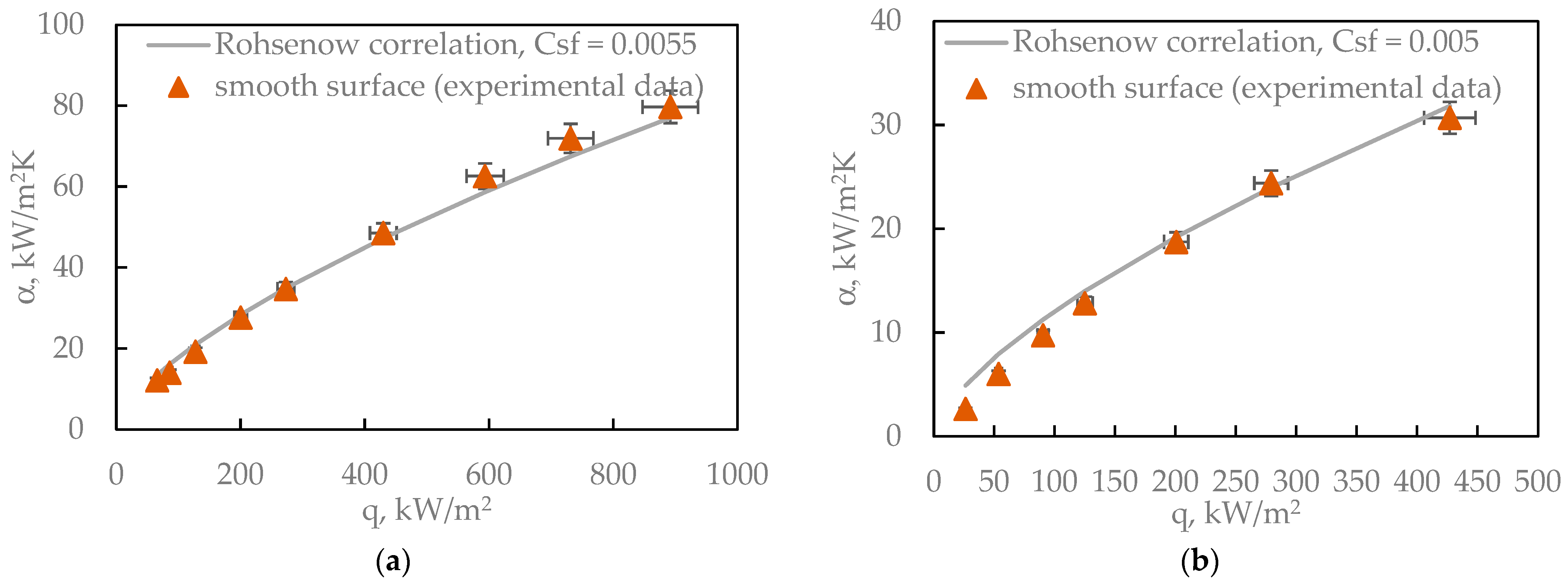
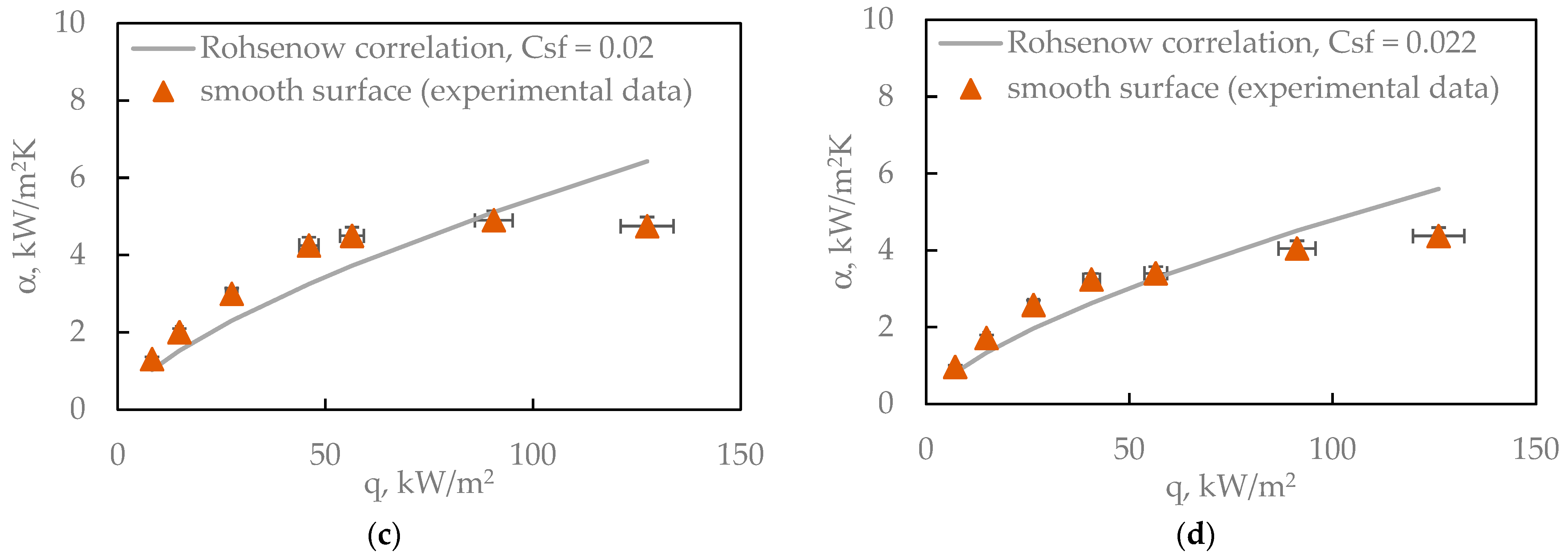
The boiling curves shown in Figure 15 can be related to the Rohsenow correlation, which describes the relationship between heat flux and surface superheat (ΔT), taking into account fluid and surface properties such as surface tension, viscosity, and the Prandtl number. This model assumes that the boiling intensity is governed by the formation and departure of vapor bubbles—a process strongly influenced by surface wettability and roughness. Water, in accordance with the Rohsenow model, shows the highest heat transfer coefficient (HTC) and critical heat flux (CHF) at low ΔT—precisely as the model predicts for a fluid with high surface tension and high latent heat of vaporization. Ethanol, with lower surface tension and greater volatility, boils more easily (at lower ΔT), but exhibits lower CHF—also consistent with Rohsenow’s predictions. FC-72 and Novec-649, which have very low surface tension and low latent heat, display the lowest HTC and CHF values. This behavior is reflected in the Rohsenow equation, where these properties appear in the denominator [35].

The Rohsenow model does not directly account for surface roughness, but it influences the empirical parameter C_sf, which must be determined experimentally. Therefore, although the correlation correctly predicts general trends (i.e., the relative boiling performance of each fluid), an accurate reproduction of the data in Figure 15 requires a calibration of C_sf for the specific surface roughness Ra = 123 µm.

4. Conclusions

Based on experimental studies of nucleate boiling conducted on copper surfaces before and after the annealing process, using four different working fluids, the following conclusions can be drawn:

▪

The annealing process significantly altered the surface wettability—in all cases, a decrease in contact angle (CA) was observed, while for most fluids an increase in surface tension (SFT) was noted, which accelerated droplet evaporation.

▪

Fluids with low contact angles and high volatility (ethanol, FC-72, Novec-649) evaporated very rapidly, making accurate measurements difficult. Water evaporated the slowest and yielded the lowest measurement errors.

▪

The measured CA and SFT values were within the following ranges:

-

Contact angle (°): approximately 90° for deionised water; from 2° to 12° for ethanol; from 0° to 8° for FC-72; and from 10° to 13° for Novec-649;

-

Surface tension (mN/m): from 61 to 65 for deionised water; from 0 to 440 for ethanol; from 39 to 49 for FC-72 before annealing and up to 180 after annealing of the copper surface; and from 0.39 to 0.53 for Novec-649 before annealing and reaching up to 900 after annealing.

▪

The high-resolution digital goniometer enabled precise measurements using the Young–Laplace method; however, for rapidly evaporating liquids, significant errors occurred—for FC-72 after annealing, errors reached up to 65%.

▪

The Rohsenow correlation, often modified to include wettability parameters (contact angle, CA) and surface tension, remains one of the fundamental engineering tools for predicting the heat transfer coefficient (HTC) in nucleate boiling. Models that account for the capillary wicking effect resulting from surface roughness show better agreement with experimental data, particularly in the critical heat flux (CHF) regime.

▪

Future work should include alternative methods for contact angle measurement (e.g., ADSA, tilting plate method) and a broader investigation of copper surface finishes and other substrate materials.