Simulation of a Natural Gas Solid Oxide Fuel Cell System Based on Rated Current Density Input
Abstract
1. Introduction
2. Materials and Methods
2.1. SOFC Electrochemical Model
2.1.1. SOFC Output Current
- is the molar flow rate of hydrogen actually participating in the electrochemical reaction (mol/h)
- is the rated current density of the system (A/m2)
- is the number of single SOFC cells
- is the total activation area for the electrochemical reaction in the SOFC (m2)
- is Faraday’s constant, valued at 96,485 C/mol
- is the number of electrons transferred per mole of hydrogen undergoing electrochemical oxidation
- is the total molar flow rate of the inlet fuel (mol/h)
- is the mole fraction of each gaseous component X in the inlet fuel
- is the specified fuel utilization rate
2.1.2. SOFC Output Voltage
- is the output voltage of the SOFC under actual operating conditions (V)
- is the baseline voltage of the SOFC under specific reference conditions (V). In this study, the reference operating conditions are based on experimental data from the literature: inlet fuel composition of 67% H2, 22% CO, and 11% H2O; fuel utilization of 0.85; air utilization of 0.25; stack operating temperature of 1000 °C; and stack operating pressure of 1 bar. Under these reference conditions, is taken as 0.7 V.
- is the voltage loss due to the deviation of the actual operating temperature from the reference temperature (V)
- is the voltage loss due to the deviation of the actual operating pressure from the reference pressure (V)
- is the voltage loss due to the deviation of the anode-side fuel composition from the reference state (V)
- is the voltage loss due to the deviation of the cathode-side oxidant composition from the reference state (V)
- is the absolute operating pressure of the SOFC under actual working conditions (bar)
- is the absolute operating pressure under reference conditions (1 bar)
- is the operating temperature of the SOFC under actual working conditions (°C)
- is the operating temperature under reference conditions (1000 °C)
- is the input current density to the SOFC (mA/cm2)
- is the ratio of the partial pressure of H2 to the partial pressure of H2O in the anode stream under actual SOFC operating conditions. In this model, this value is taken as the arithmetic mean of the corresponding ratios at the anode inlet and outlet.
- is the ratio of the partial pressure of H2 to the partial pressure of H2O in the anode stream under reference conditions (0.15)
- is the average partial pressure of O2 on the cathode side under actual SOFC operating conditions (bar). In this model, this value is taken as the arithmetic mean of the O2 partial pressures at the cathode inlet and outlet.
- is the average partial pressure of O2 on the cathode side under reference conditions (0.164 bar)
2.1.3. SOFC Output Power
- is the DC output power of the SOFC power generation system (W)
- is the input current density to the SOFC (A/m2)
- is the total activation area for the electrochemical reaction in the SOFC (m2), which is set to 96.1 m2 in this study
- is the output voltage of the SOFC under actual operating conditions (V)
- is the electrical efficiency of the SOFC
- is the total molar flow rate of the inlet fuel (mol/h), the calculation of which is detailed in Equation (2)
- is the average lower heating value of the inlet fuel (J/mol). In this study, this value is calculated as the weighted average of the standard LHV of each gaseous component in the inlet fuel, based on their respective mole fractions.
- The factor “3600” in the denominator is used to convert the hourly molar flow rate () to a per-second basis, to align with the unit of power (W, J/s).
2.2. System Process Modeling in Aspen Plus
2.2.1. Model Hypothesis
2.2.2. System Flow
2.3. Simulation Input Parameters
3. Results and Discussion
3.1. Simulation Results and Validation
3.1.1. Simulation Results
3.1.2. Simulation Verification
3.2. Sensitivity Analysis of SOFC Unit Parameters
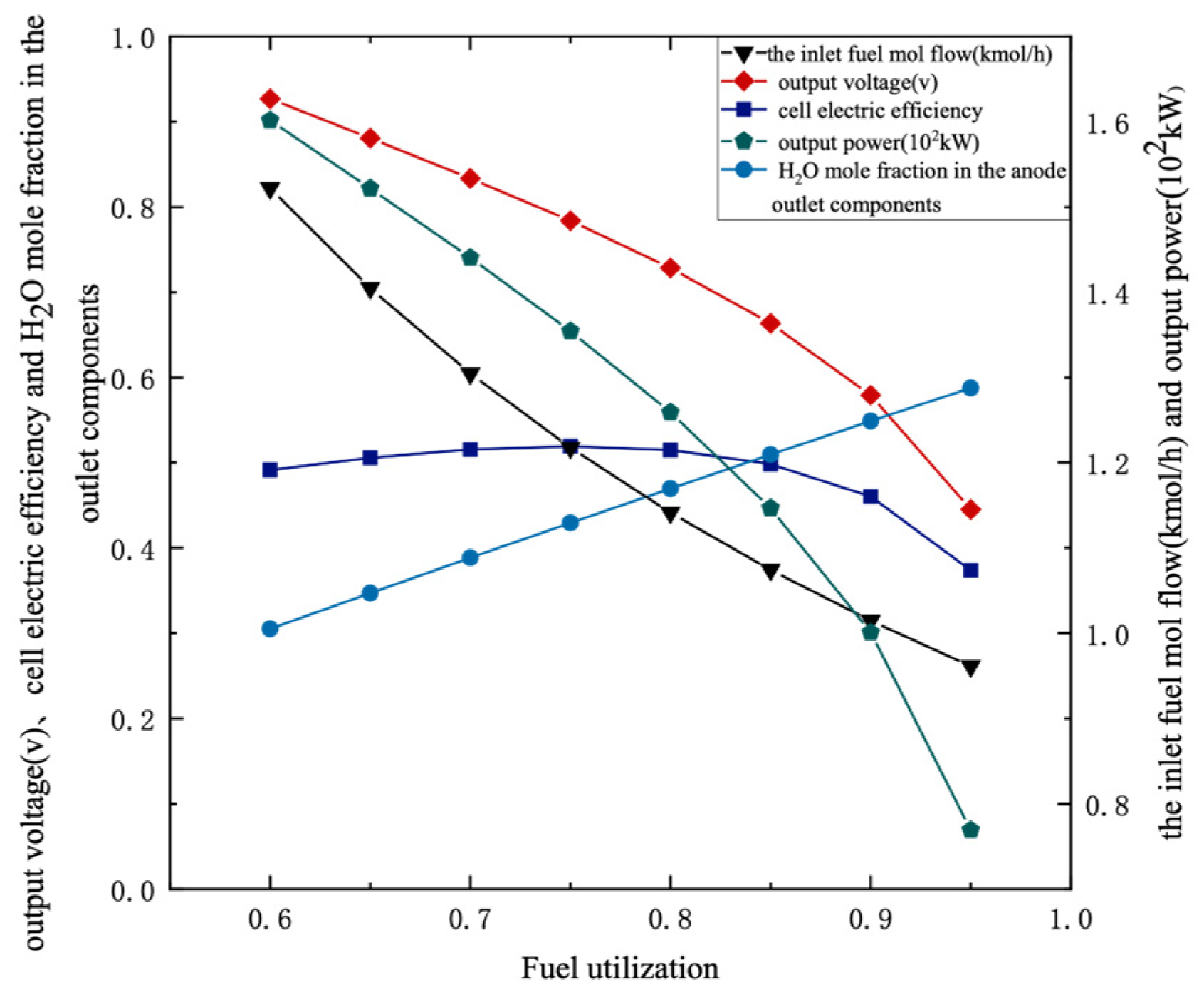
3.2.1. Fuel Utilization
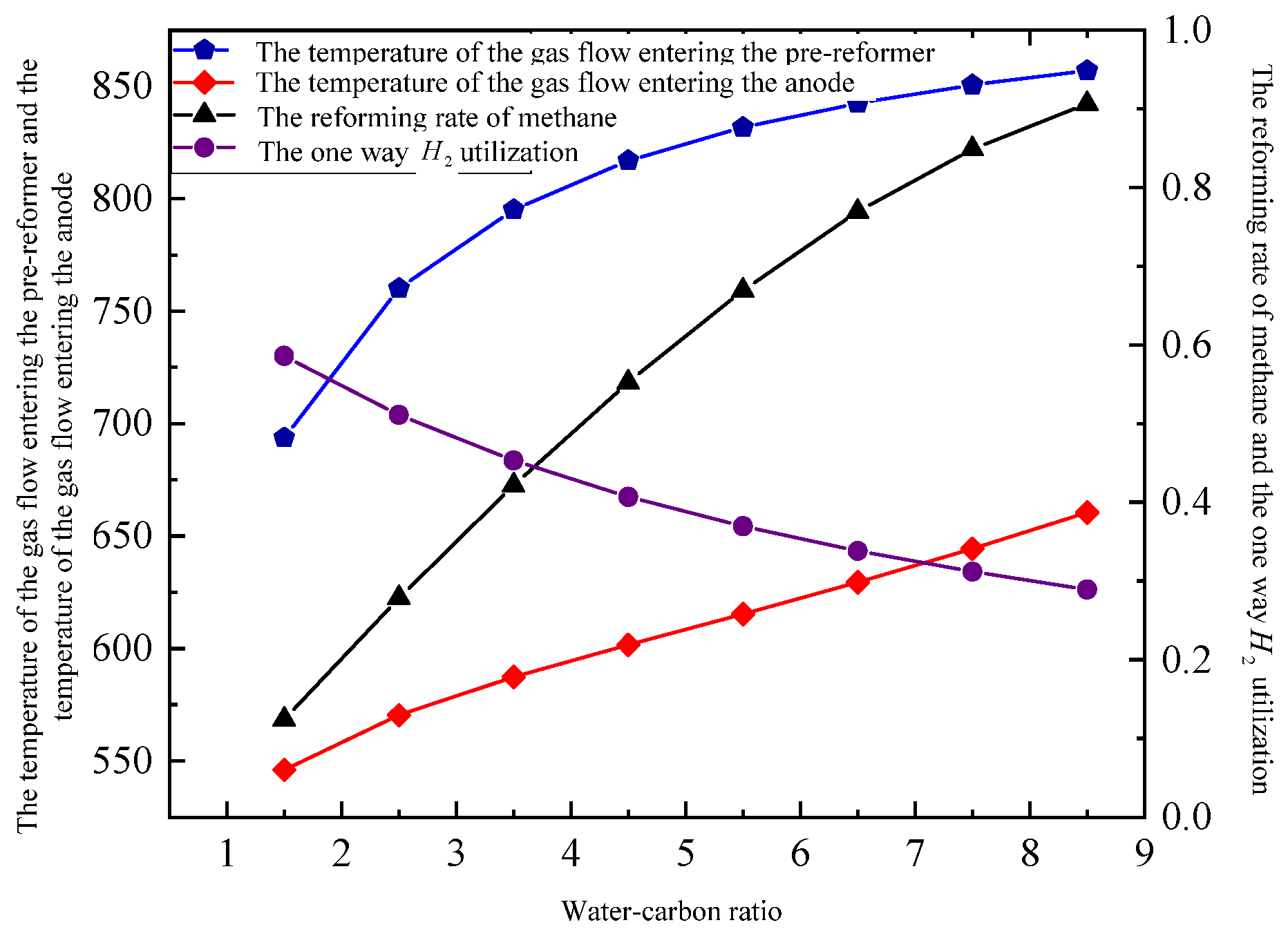
3.2.2. Water-Carbon Ratio
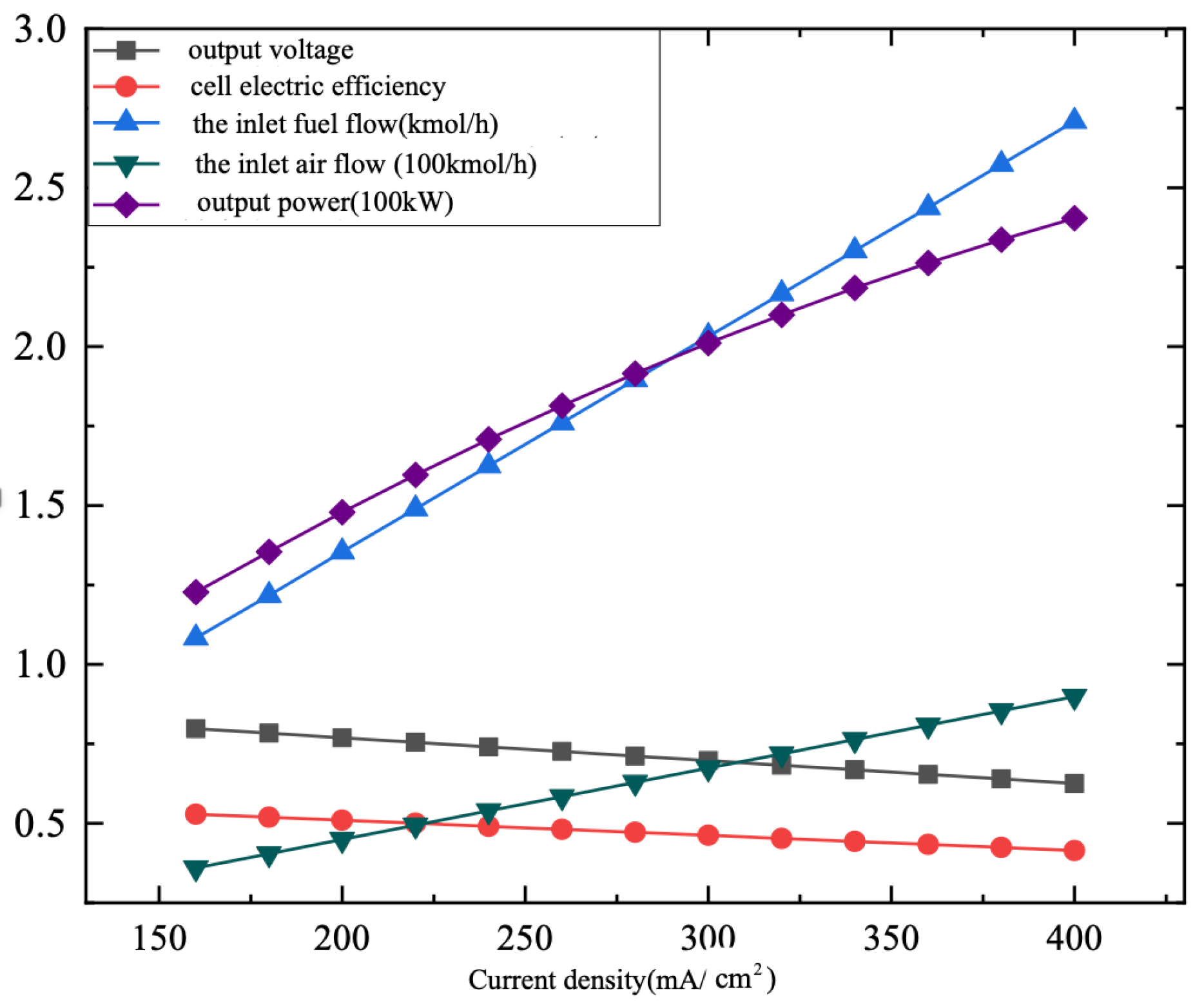
3.2.3. Current Density
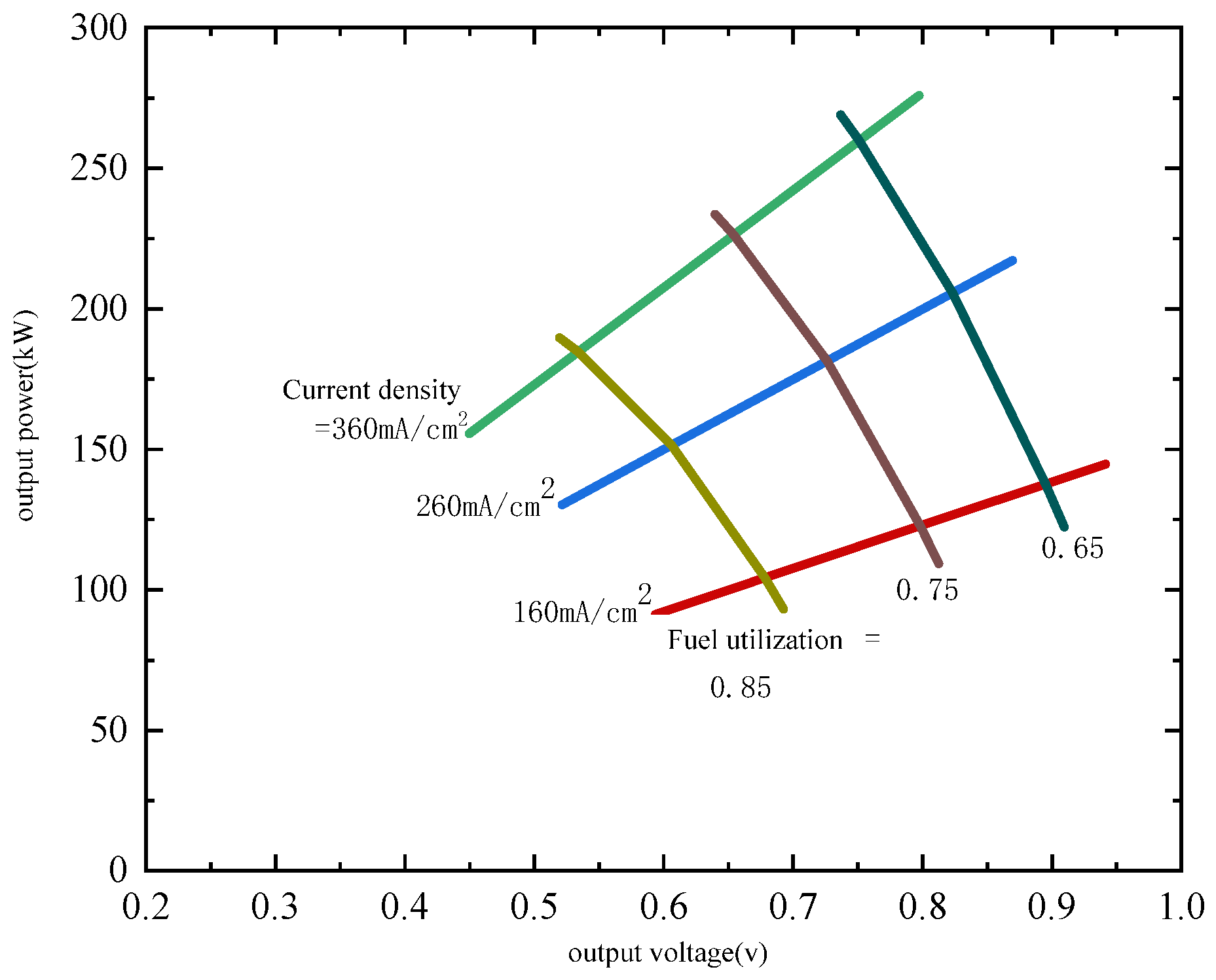
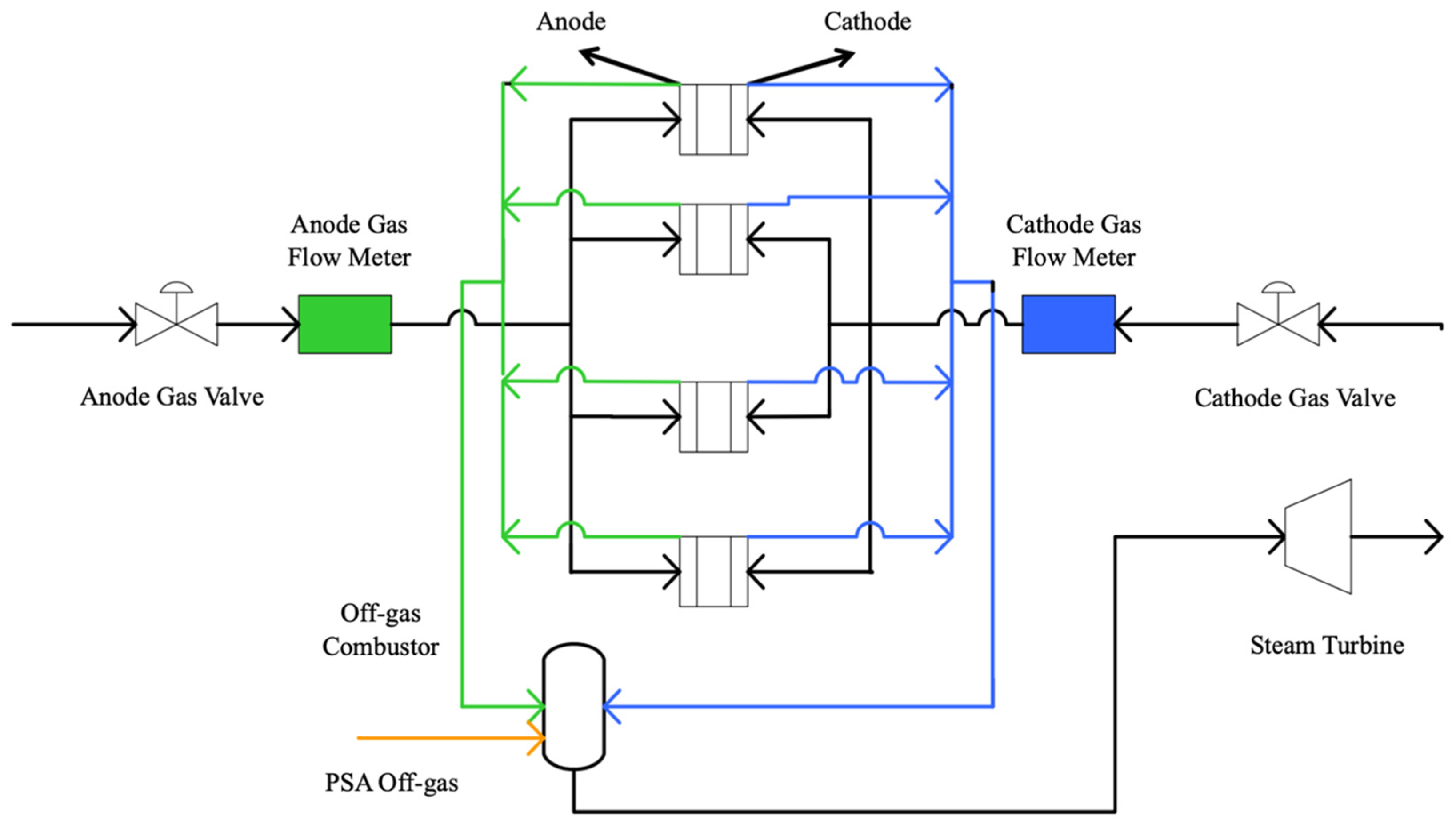
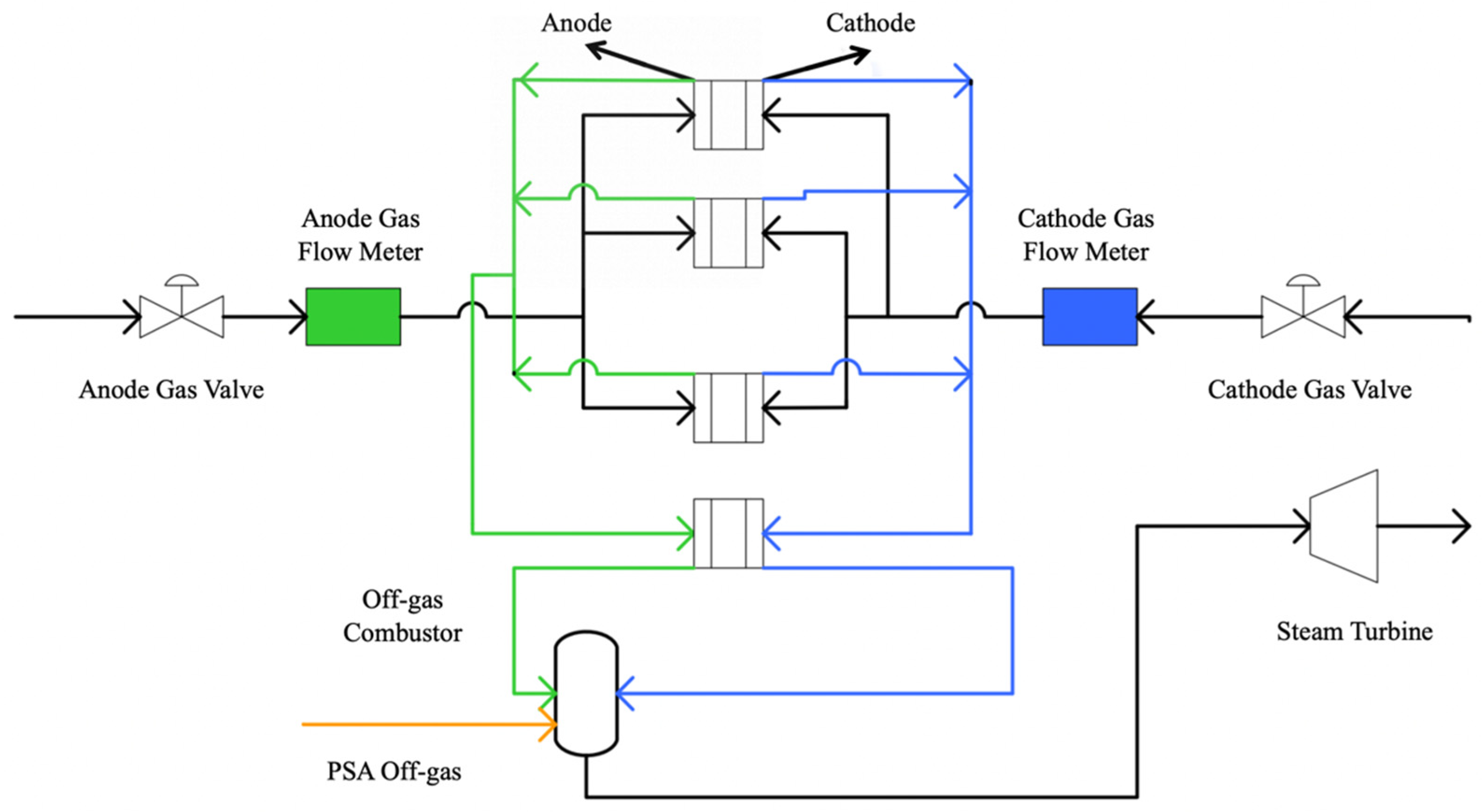
3.3. Multi-Unit SOFC Configuration Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Laky, D.J.; Cortes, N.P.; Eslick, J.C.; Noring, A.A.; Susarla, N.; Okoli, C.; Zamarripa, M.A.; Allan, D.A.; Brewer, J.H.; Iyengar, A.K.S.; et al. Market Optimization and Technoeconomic Analysis of Hydrogen-Electricity Coproduction Systems. Energy Environ. Sci. 2024, 17, 9509–9525. [Google Scholar] [CrossRef]
- Chitgar, N.; Hemmati, A.; Sadrzadeh, M. A Comparative Performance Analysis, Working Fluid Selection, and Machine Learning Optimization of ORC Systems Driven by Geothermal Energy. Energy Convers. Manag. 2023, 286, 117072. [Google Scholar] [CrossRef]
- Perna, A.; Minutillo, M.; Jannelli, E.; Cigolotti, V.; Nam, S.W.; Yoon, K.J. Performance Assessment of a Hybrid SOFC/MGT Cogeneration Power Plant Fed by Syngas from a Biomass down-Draft Gasifier. Appl. Energy 2018, 227, 80–91. [Google Scholar] [CrossRef]
- Chitgar, N.; Emadi, M.A. Development and Exergoeconomic Evaluation of a SOFC-GT Driven Multi-Generation System to Supply Residential Demands: Electricity, Fresh Water and Hydrogen. Int. J. Hydrogen Energy 2021, 46, 17932–17954. [Google Scholar] [CrossRef]
- Lai, H.; Adams, T.A. Eco-Technoeconomic Analyses of Natural Gas-Powered SOFC/GT Hybrid Plants Accounting for Long-Term Degradation Effects via Pseudo-Steady-State Model Simulations. J. Electrochem. Energy Convers. Storage 2024, 21, 021004. [Google Scholar] [CrossRef]
- Yang, B.; Hao, X.; Shen, X.; Shi, W.; Xie, Y.; Li, L. Design and Performance Analysis of a Coupled Burner for the Solid Oxide Fuel Cell System. Energy Convers. Manag. 2024, 322, 119181. [Google Scholar] [CrossRef]
- Ali, S.; Sørensen, K.; Nielsen, M.P. Modeling a Novel Combined Solid Oxide Electrolysis Cell (SOEC)-Biomass Gasification Renewable Methanol Production System. Renew. Energy 2020, 154, 1025–1034. [Google Scholar] [CrossRef]
- Saebea, D.; Arpornwichanop, A.; Patcharavorachot, Y. Thermodynamic Analysis of a Proton Conducting SOFC Integrated System Fuelled by Different Renewable Fuels. Int. J. Hydrogen Energy 2021, 46, 11445–11457. [Google Scholar] [CrossRef]
- Kumuk, B.; Atak, N.N.; Dogan, B.; Ozer, S.; Demircioglu, P.; Bogrekci, I. Numerical and Thermodynamic Analysis of the Effect of Operating Temperature in Methane-Fueled SOFC. Energies 2024, 17, 2603. [Google Scholar] [CrossRef]
- Zhu, P.; Yao, J.; Qian, C.; Yang, F.; Porpatham, E.; Zhang, Z.; Wu, Z. High-Efficiency Conversion of Natural Gas Fuel to Power by an Integrated System of SOFC, HCCI Engine, and Waste Heat Recovery: Thermodynamic and Thermo-Economic Analyses. Fuel 2020, 275, 117883. [Google Scholar] [CrossRef]
- Iliev, I.K.; Filimonova, A.A.; Chichirov, A.A.; Chichirova, N.D.; Kangalov, P.G. Computational and Experimental Research on the Influence of Supplied Gas Fuel Mixture on High-Temperature Fuel Cell Performance Characteristics. Energies 2024, 17, 2452. [Google Scholar] [CrossRef]
- Marcantonio, V.; Monarca, D.; Villarini, M.; Di Carlo, A.; Del Zotto, L.; Bocci, E. Biomass Steam Gasification, High-Temperature Gas Cleaning, and SOFC Model: A Parametric Analysis. Energies 2020, 13, 5936. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. Computer Simulation of a Biomass Gasification-Solid Oxide Fuel Cell Power System Using Aspen Plus. Energy 2010, 35, 4545–4555. [Google Scholar] [CrossRef]
- Han, W.; Jin, H.; Lin, R. A Novel Power Generation System Based on Moderate Conversion of Chemical Energy of Coal and Natural Gas. Fuel 2011, 90, 263–271. [Google Scholar] [CrossRef]
- Zhang, W.; Croiset, E.; Douglas, P.L.; Fowler, M.W.; Entchev, E. Simulation of a Tubular Solid Oxide Fuel Cell Stack Using AspenPlusTM Unit Operation Models. Energy Convers. Manag. 2005, 46, 181–196. [Google Scholar] [CrossRef]
- Batista, C.-T.N.; Mohammed, K.A.; Amiri, A.; Azimi, N.; Steinberger-Wilckens, R. Comparison of Equilibrium-Based and Kinetics-Based Models for Evaluating the Impact of Hydrogen Carrier Reforming on SOFC System. Energy Convers. Manag. 2025, 332, 119733. [Google Scholar] [CrossRef]
- Campanari, S. Thermodynamic Model and Parametric Analysis of a Tubular SOFC Module. J. Power Sources 2001, 92, 26–34. [Google Scholar] [CrossRef]
- Koo, T.; Kim, Y.S.; Lee, D.; Yu, S.; Lee, Y.D. System Simulation and Exergetic Analysis of Solid Oxide Fuel Cell Power Generation System with Cascade Configuration. Energy 2021, 214, 119087. [Google Scholar] [CrossRef]
- Zhuang, Q.; Geddis, P.; Runstedtler, A.; Clements, B. An Integrated Natural Gas Power Cycle Using Hydrogen and Carbon Fuel Cells. Fuel 2017, 209, 76–84. [Google Scholar] [CrossRef]
- Yang, L.; Fan, S.; Liu, P.; Han, X.; Liu, Y.; Jin, Z. Effect of Gas Flow Configurations on the Performance of MOLB-Type SOFC. Int. J. Electrochem. Sci. 2022, 17, 220538. [Google Scholar] [CrossRef]
- Niu, B.; Han, X.; Ding, J.; Yan, B.; Chen, G.; Yao, J. Energy, Efficiency, Economy, Environmental Assessment of Hydrogen Production via Solar-Driven Steam Gasification of Fresh Cow Manure Using Aspen plus Simulation Model. Int. J. Hydrogen Energy 2025, 98, 308–320. [Google Scholar] [CrossRef]
- Zhao, Y.; Yao, J.; Chen, G.; Liu, J.; Cheng, Z.; Wang, L.; Yi, W.; Xu, S. Energy, Efficiency, and Environmental Analysis of Hydrogen Generation via Plasma Co-Gasification of Biomass and Plastics Based on Parameter Simulation Using Aspen Plus. Energy Convers. Manag. 2023, 295, 117623. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Gallorini, F.; Ottaviano, A. An Energetic–Exergetic Comparison between PEMFC and SOFC-Based Micro-CHP Systems. Int. J. Hydrogen Energy 2011, 36, 3206–3214. [Google Scholar] [CrossRef]
- Yan, L.; He, B.; Pei, X.; Song, W.; Chen, Q.; Song, J. Simulation Research of Solid Oxide Fuel Cell Integrated in Zero-Emission Coal Systems. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2012, 32, 94–103. [Google Scholar]
- Su, X.; Zhang, F.; Yin, Y.; Tu, B.; Cheng, M. Thermodynamic Analysis and Fuel Processing Strategies for Propane-Fueled Solid Oxide Fuel Cell. Energy Convers. Manag. 2020, 204, 112279. [Google Scholar] [CrossRef]
- Chen, H.; Yang, C.; Zhou, N.; Farida Harun, N.; Oryshchyn, D.; Tucker, D. High Efficiencies with Low Fuel Utilization and Thermally Integrated Fuel Reforming in a Hybrid Solid Oxide Fuel Cell Gas Turbine System. Appl. Energy 2020, 272, 115160. [Google Scholar] [CrossRef]
- Li, M.; Brouwer, J.; Rao, A.D.; Samuelsen, G.S. Application of a Detailed Dimensional Solid Oxide Fuel Cell Model in Integrated Gasification Fuel Cell System Design and Analysis. J. Power Sources 2011, 196, 5903–5912. [Google Scholar] [CrossRef]
- Mahisanana, C.; Authayanun, S.; Patcharavorachot, Y.; Arpornwichanop, A. Design of SOFC Based Oxyfuel Combustion Systems with Anode Recycling and Steam Recycling Options. Energy Convers. Manag. 2017, 151, 723–736. [Google Scholar] [CrossRef]
- Soleimanpour, M.; Ebrahimi, M. Energy and Exergy Analysis of Dry and Steam External Reformers for a Power Cycle Based on Biogas-Fueled Solid Oxide Fuel Cell. Energy 2024, 305, 132382. [Google Scholar] [CrossRef]
- Li, K.; Zou, Q.; Zhang, J.; Jiang, C.; Liang, Z. Mixed Reforming of Methane with CO2 and H2O: Thermodynamic Analysis and ReaxFF Molecular Dynamics Simulation. J. Energy Inst. 2025, 121, 102188. [Google Scholar] [CrossRef]
- Yang, S.; Wang, G.; Liu, Z.; Deng, C.; Xie, N. Energy, Exergy and Exergo-Economic Analysis of a Novel SOFC Based CHP System Integrated with Organic Rankine Cycle and Biomass Co-Gasification. Int. J. Hydrogen Energy 2024, 53, 1155–1169. [Google Scholar] [CrossRef]
- Yonekura, T.; Tachikawa, Y.; Yoshizumi, T.; Shiratori, Y.; Ito, K.; Sasaki, K. Exchange Current Density of Solid Oxide Fuel Cell Electrodes. ECS Trans. 2011, 35, 1007–1014. [Google Scholar] [CrossRef]
- Cordova, J.L.; Heshmat, H. Development of a Ceramic Heat Exchanger for Application as Solid Oxide Fuel Cell Cathode Air Preheater. In Proceedings of the ASME Power Conference, Charlotte, NC, USA, 26–30 June 2016; Amer Soc Mechanical Engineers: New York, NY, USA, 2016; p. UNSP V001T04A006. [Google Scholar]
- Chen, D.; Zeng, Q.; Su, S.; Bi, W.; Ren, Z. Geometric Optimization of a 10-Cell Modular Planar Solid Oxide Fuel Cell Stack Manifold. Appl. Energy 2013, 112, 1100–1107. [Google Scholar] [CrossRef]
- Gandiglio, M.; Marocco, P.; Nieminen, A.; Santarelli, M.; Kiviaho, J. Energy and Environmental Performance from Field Operation of Commercial-Scale SOFC Systems. Int. J. Hydrogen Energy 2024, 85, 997–1009. [Google Scholar] [CrossRef]


| Assumed Input Parameters | Input Parameter Value |
|---|---|
| Inlet fuel components | 81.3%CH4, 2.9%C2H6, 0.4%C3H8, 0.2%C4H10, 14.3%N2, 0.9%CO |
| Cell operation temperature | 910 °C |
| Cell operation pressure | 1.08 atm |
| Input current density | 180 mA/cm2 |
| Activating reaction area | 96.1 m2 (1152 sets of mono-cells) |
| Cell outlet temperature | 910 °C |
| Inlet air temperature | 630 °C |
| Inlet fuel temperature | 200 °C |
| Afterburner reaction rate | 100% |
| Air use ratio | 19% |
| DC-AC conversion efficiency | 92% |
| Overall fuel utilization | 85% |
| Water-carbon ratio | 2.5 |
| Commingler fresh fuel-pressure ratio | 3 |
| SOFC internal pressure drop | 0 |
| SOFC heat loss | 2% |
| Stream | Temperature (℃) | Pressure (atm) | Mol Flow | Mole Fraction (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (kmol/h) | H2 | CH4 | H2O | CO | CO2 | O2 | N2 | |||
| 1 | 200.00 | 3.28 | 1.07 | - | 81.30 | - | 0.90 | - | - | 14.30 |
| 2 | 745.29 | 1.09 | 5.82 | 9.42 | 15.01 | 41.55 | 6.15 | 20.39 | - | 6.83 |
| 3 | 536.25 | 1.09 | 5.82 | 9.42 | 15.01 | 41.55 | 6.15 | 20.39 | - | 6.83 |
| 4 | 537.27 | 1.09 | 6.45 | 27.19 | 9.94 | 27.87 | 5.68 | 23.17 | - | 6.16 |
| 5 | 910.00 | 1.09 | 7.73 | 11.55 | - | 50.96 | 7.34 | 25.01 | - | 5.14 |
| 6 | 910.00 | 1.09 | 4.74 | 11.55 | - | 50.96 | 7.34 | 25.01 | - | 5.14 |
| 7 | 910.00 | 1.09 | 2.99 | 11.55 | - | 50.96 | 7.34 | 25.01 | - | 5.14 |
| 8 | 910.00 | 1.09 | 41.19 | - | - | 4.50 | - | 2.33 | 15.88 | 77.29 |
| 9 | 630.00 | 1.09 | 40.10 | - | - | - | - | - | 21.00 | 79.00 |
| 10 | 822.37 | 1.09 | 40.10 | - | - | - | - | - | 21.00 | 79.00 |
| 11 | 822.37 | 1.09 | 1.61 | - | - | - | - | - | 1.0000 | - |
| 12 | 822.37 | 1.09 | 38.78 | - | - | - | - | - | 17.72 | 82.28 |
| 13 | 910.00 | 1.09 | 38.78 | - | - | - | - | - | 17.72 | 82.28 |
| 14 | 1011.25 | 1.09 | 41.49 | - | - | 4.50 | - | 2.33 | 15.88 | 77.29 |
| 15 | 833.85 | 1.09 | 41.49 | - | - | 4.50 | - | 2.33 | 15.88 | 77.29 |
| Indicators | Lab Data | Reference [24] Simulation Results | Simulation Results | Simulation Errors |
|---|---|---|---|---|
| Cell power | - | - | 119.059 kW | - |
| Cell voltage | - | 0.685 V | 0.689 V | 5.8% |
| Current density | 180 mA/cm2 | 179.5 mA/cm2 | - | - |
| Anode gas output component | 48%H2O/28%CO2/ 14%H2/5%CO/5.0%N2 | 50.8%H2O/25%CO2/ 11.7%H2/7.3%CO/5.0%N2 | 51.0%H2O/25.0%CO2/ 11.5%H2/7.3%CO/5.1%N2 | - |
| Fuel cell electric efficiency | 50% | 50% | 49.8% | 0.4% |
| System Output | Method 1 Output Value | Method 2 Output Value |
|---|---|---|
| SOFC Anode Inlet Total Fuel Flow Rate (kmol/h) | 18.64 | 15.05 |
| SOFC Cathode Inlet Total Oxygen Flow Rate (kmol/h) | 6.40 | 5.80 |
| SOFC Maximum Power Output (kW) (DC) | 498.38 | 471.21 |
| SOFC Maximum Power Output (kW) (AC) | 458.51 | 433.51 |
| SOFC Single Cell Voltage (V) | 0.70 | 0.64/0.73 |
| System Net Electrical Efficiency (%) | 54 | 59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, W.; Sun, X.; Qin, Y. Simulation of a Natural Gas Solid Oxide Fuel Cell System Based on Rated Current Density Input. Energies 2025, 18, 4456. https://doi.org/10.3390/en18164456
Hu W, Sun X, Qin Y. Simulation of a Natural Gas Solid Oxide Fuel Cell System Based on Rated Current Density Input. Energies. 2025; 18(16):4456. https://doi.org/10.3390/en18164456
Chicago/Turabian StyleHu, Wenxian, Xudong Sun, and Yating Qin. 2025. "Simulation of a Natural Gas Solid Oxide Fuel Cell System Based on Rated Current Density Input" Energies 18, no. 16: 4456. https://doi.org/10.3390/en18164456
APA StyleHu, W., Sun, X., & Qin, Y. (2025). Simulation of a Natural Gas Solid Oxide Fuel Cell System Based on Rated Current Density Input. Energies, 18(16), 4456. https://doi.org/10.3390/en18164456




