Development and Optimization of Chemical Kinetic Mechanisms for Ethanol–Gasoline Blends Using Genetic Algorithms
Abstract
1. Introduction
2. Materials and Methods
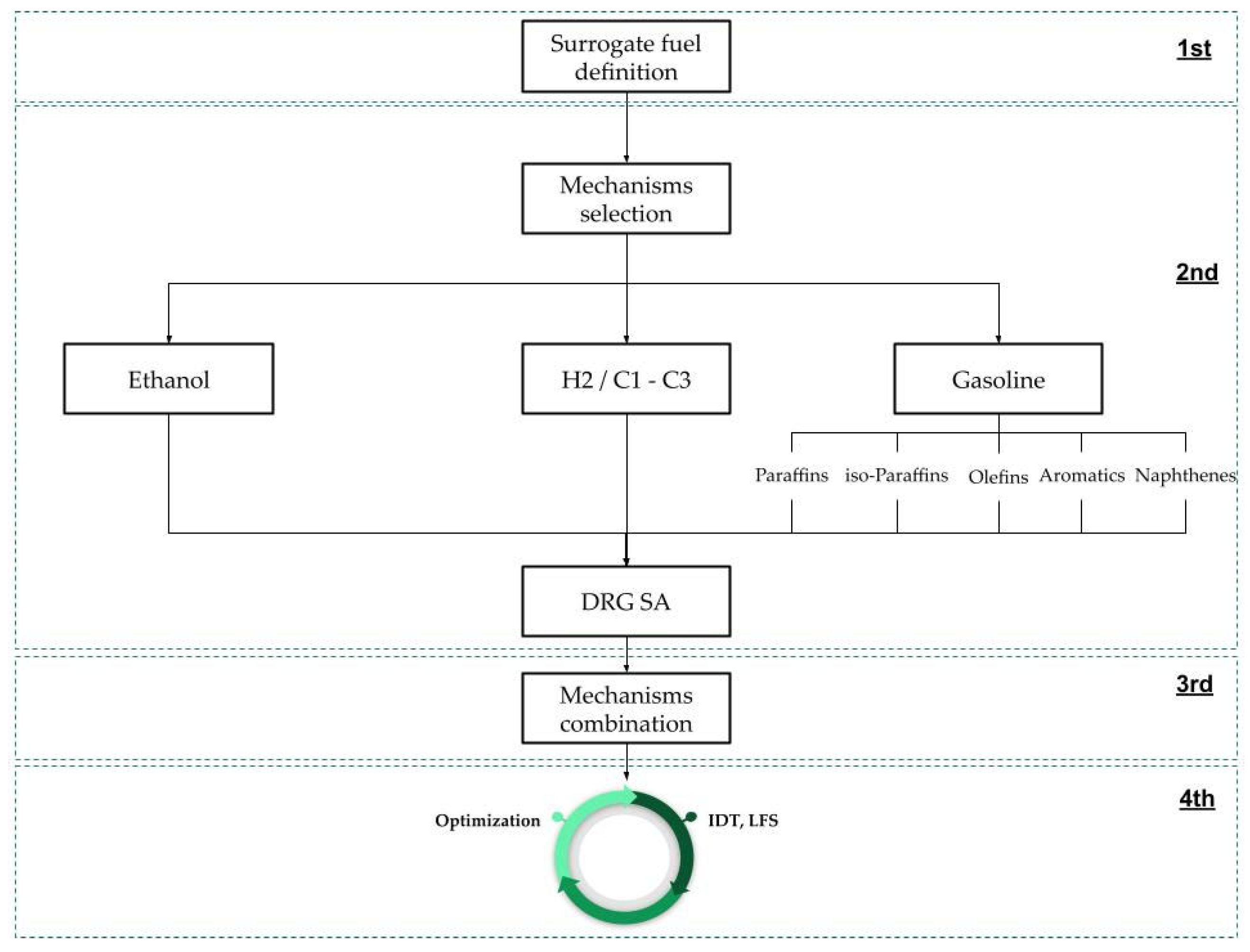
2.1. Surrogate Fuel Definition
2.2. Individual Mechanisms Selection
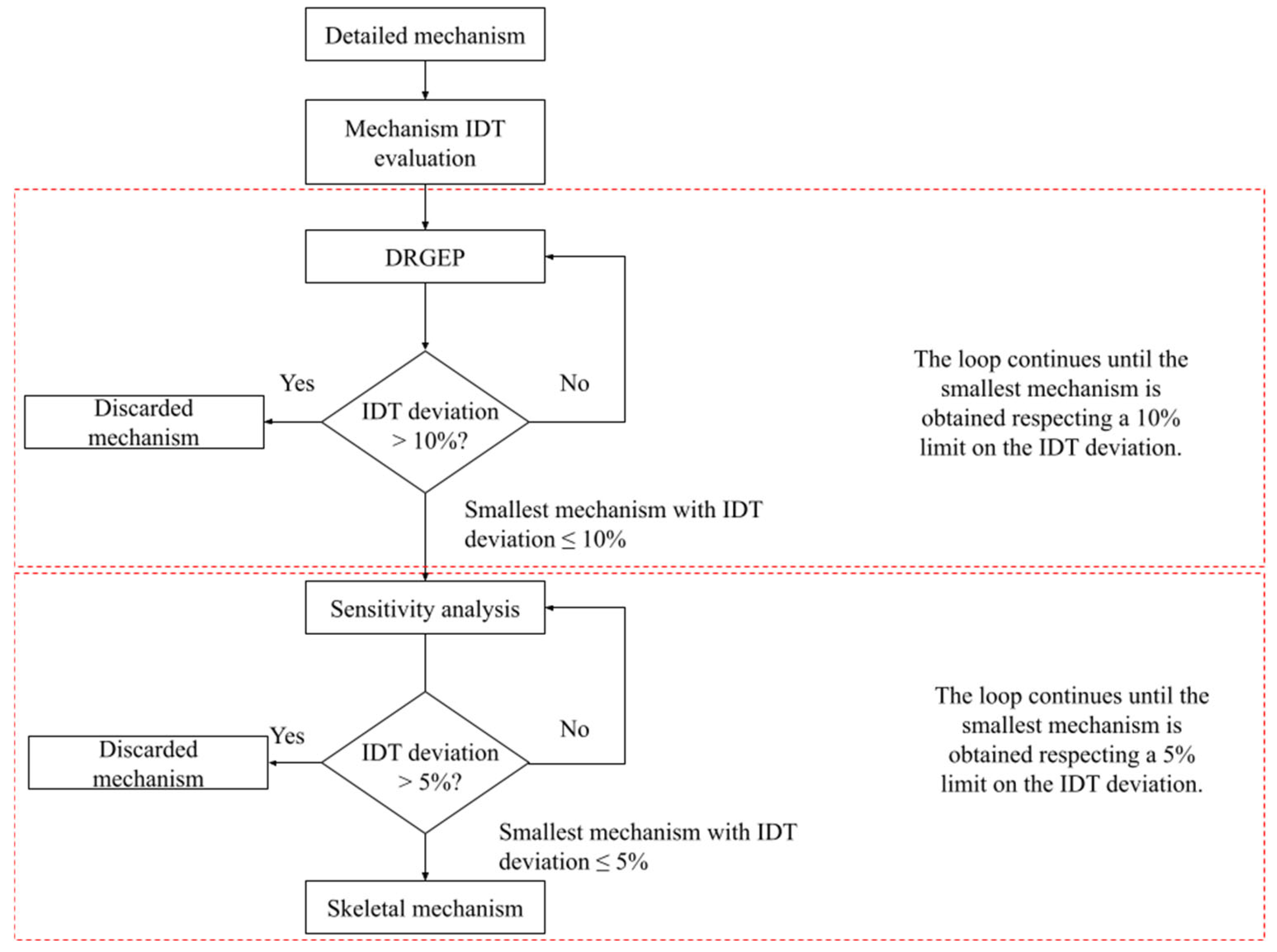
Mechanism Reduction/Extraction
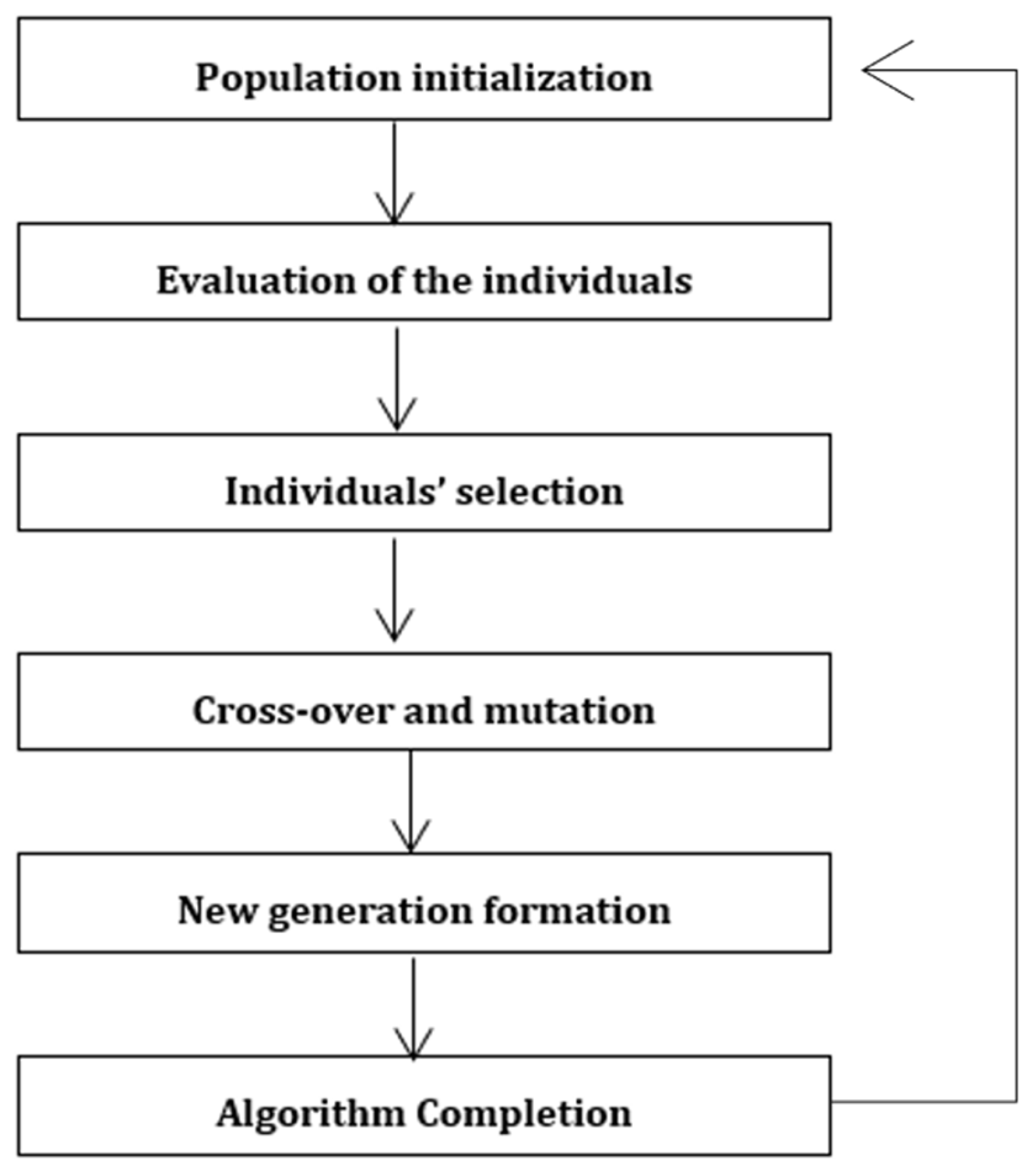
2.3. Mechanism Optimization Using Genetic Algorithm
3. Results
3.1. Surrogate Definition
3.2. Individual Mechanism Selection
3.3. Mechanism Optimization
4. Discussion
5. Conclusions
- 1-
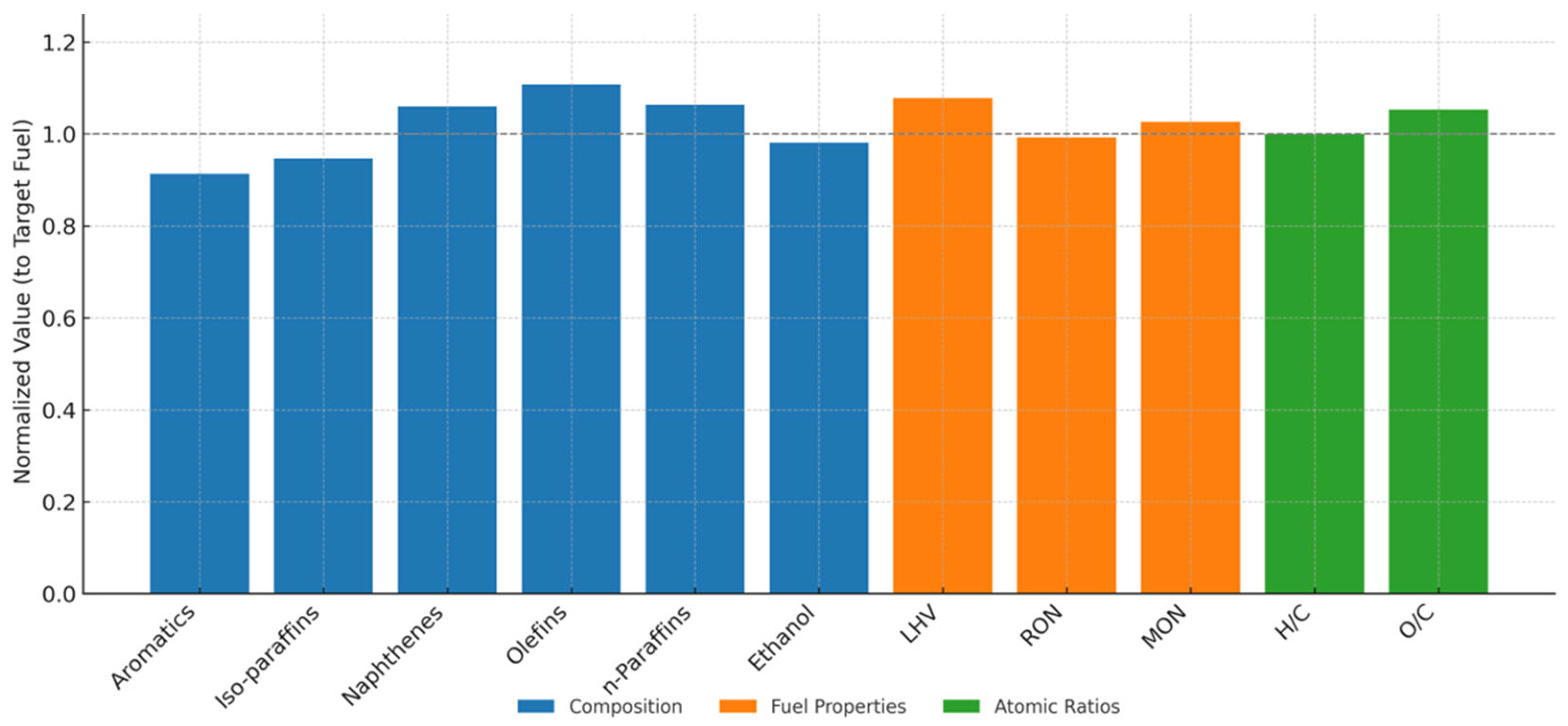
- The corresponding v/v% for each species was: 12.5%, 20.58%, 11.38%, 13.72%, 15.07%, 26.75% for toluene, iso-octane, methyl cyclohexane, 1-hexene, n-heptane, and ethanol, respectively. This surrogate presented a good correlation with experimental data of organic groups composition, lower heating value, research octane number, motor octane number, H/C, and O/C.
- 2-
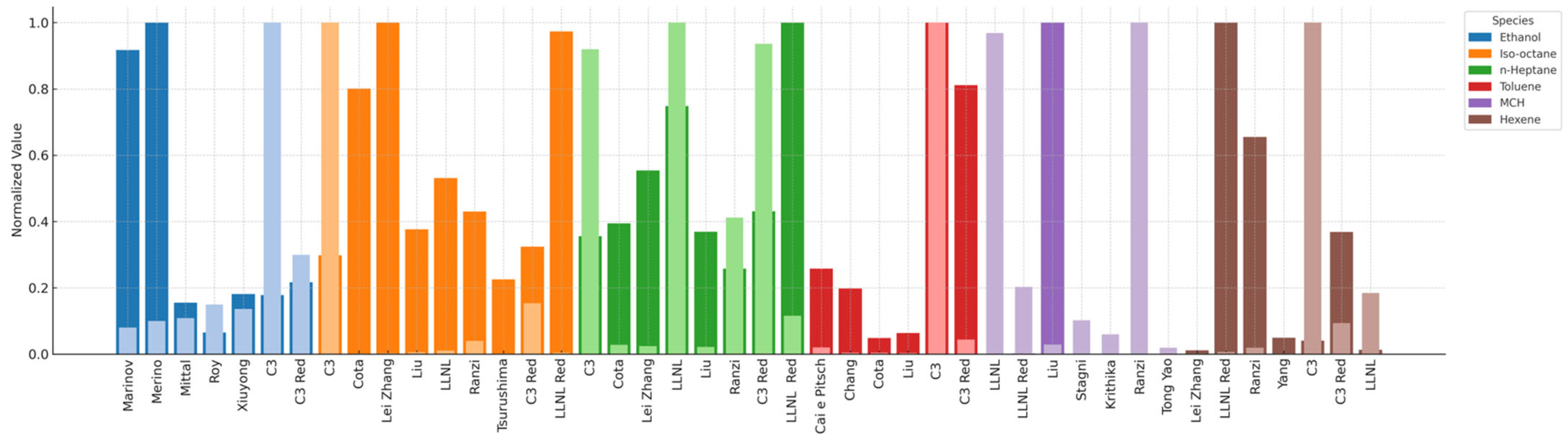
- Several mechanisms were tested for the individual species and compared with experimental data of ignition delay time and laminar flame speed. A square mean error analysis, together with simulation time, was used to select one mechanism for each species.
- 3-
- 4-
- 5-
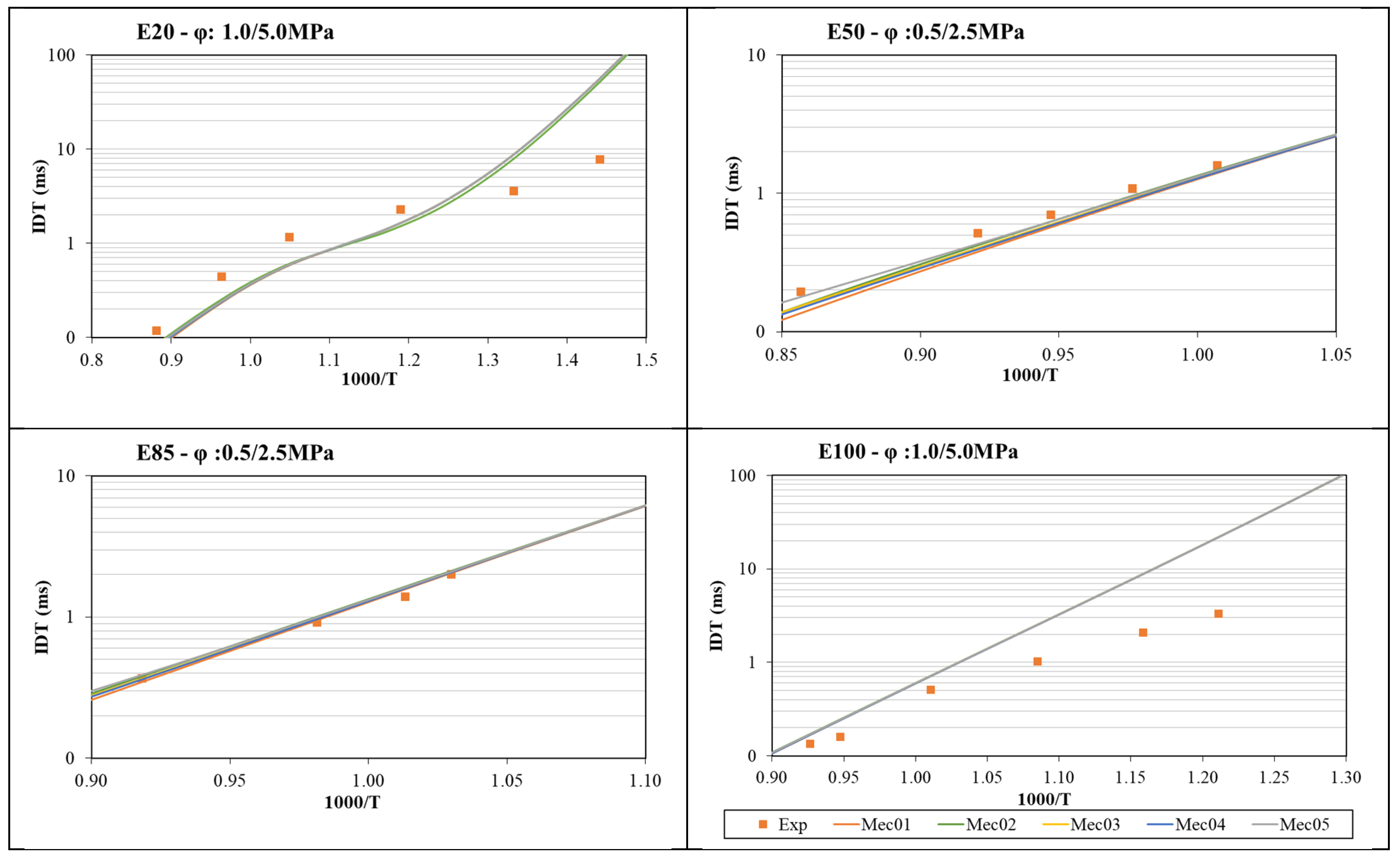
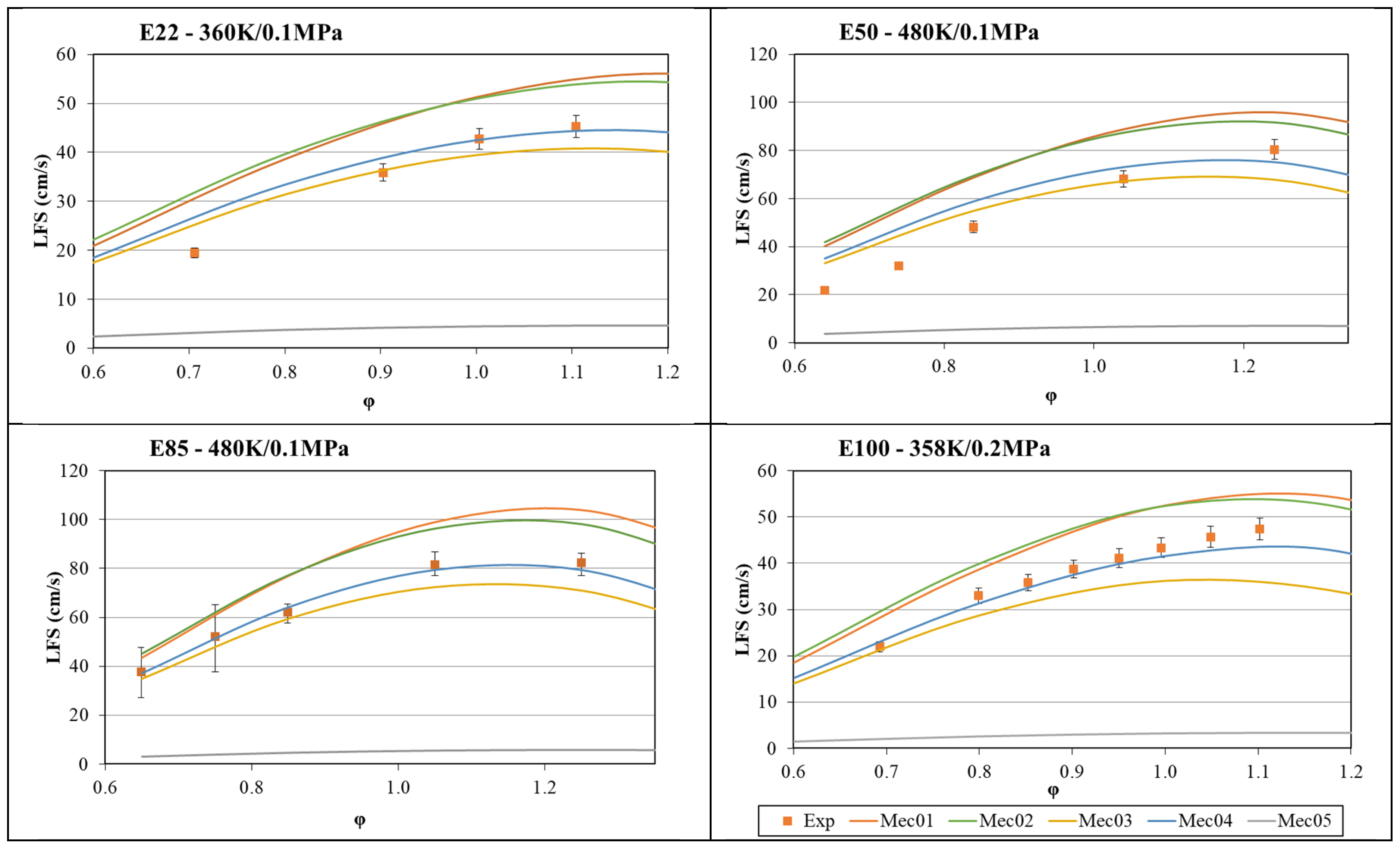
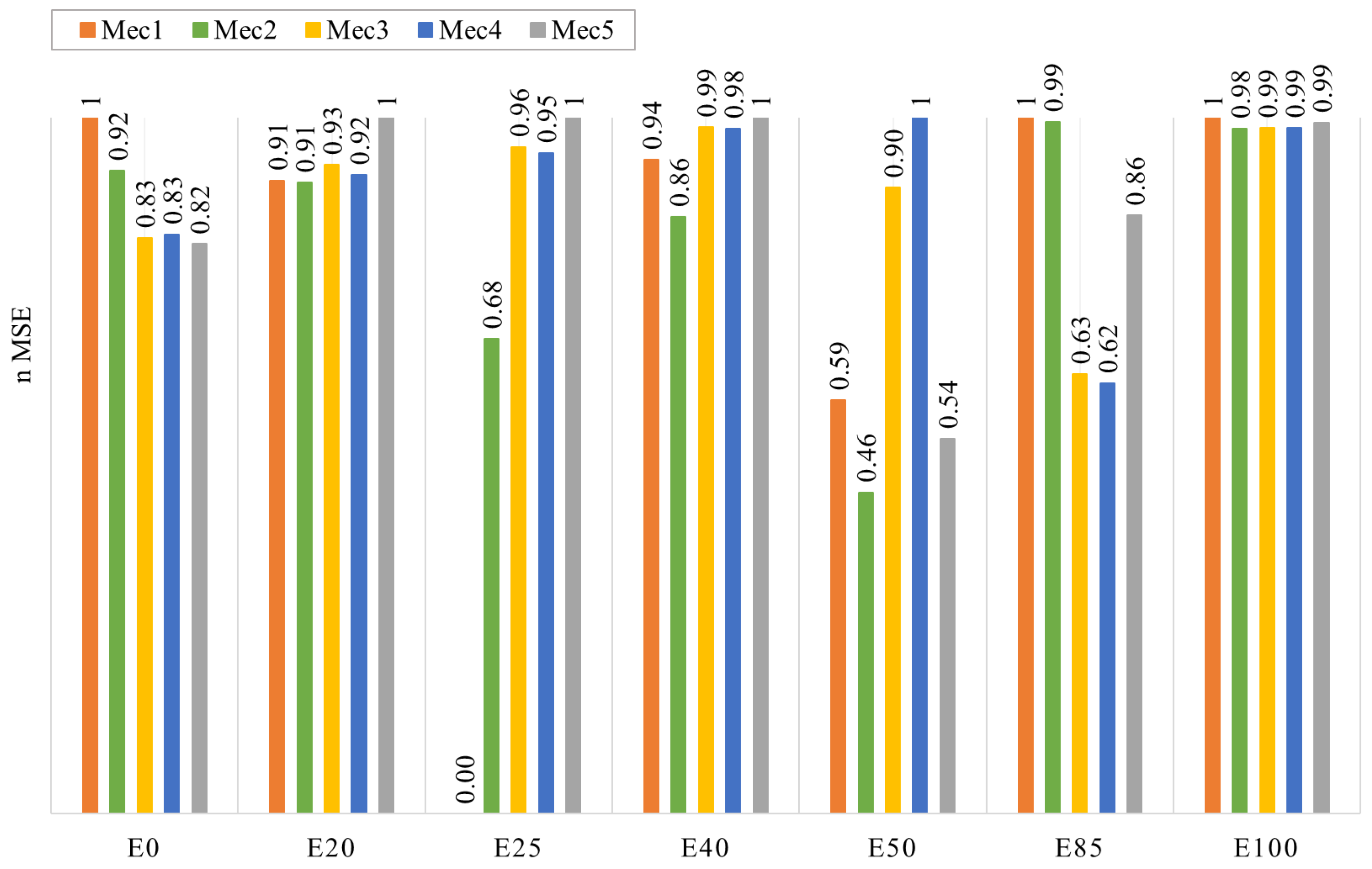
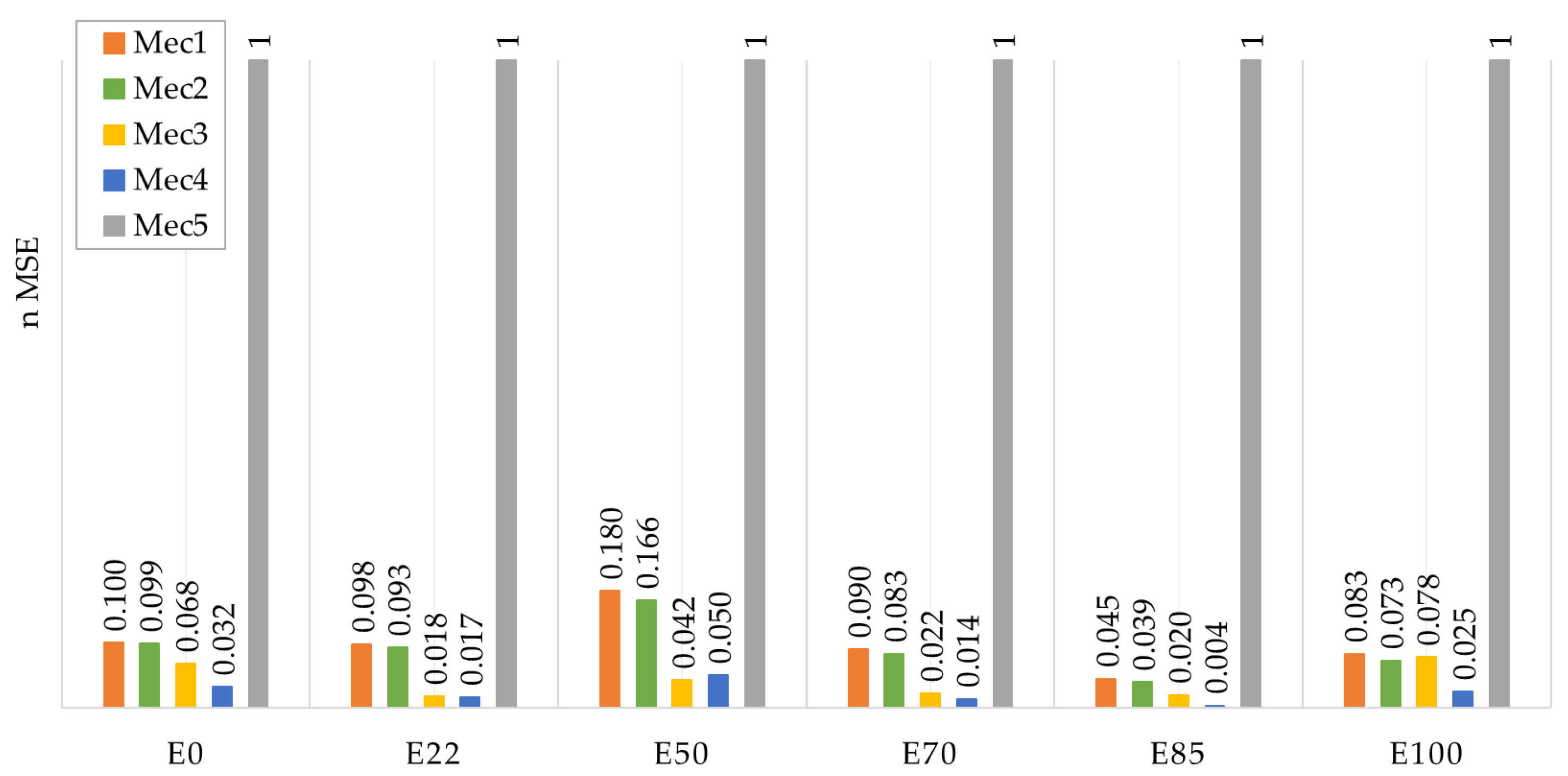
- The global mechanism was optimized, starting with Mec1, in four iterations of a genetic algorithm using ignition delay time and laminar flame speed experimental data as targets, with a weight factor of 0.7 for ignition delay time and 1.0 for laminar flame speed. A clear improvement in each iteration was observed until Mec4 was created. After that, the final iteration created Mec5, which lost its capability to represent laminar flame speed data, even though the results for ignition delay time were comparable to the previous versions of the mechanism.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DHA | Detailed Hydrocarbon Analysis |
| DRGEP | Directed Relation Graph with Error Propagation |
| E0–E100 | Ethanol–Gasoline Blends 0% to 100% Ethanol by Volume |
| GA | Genetic Algorithm |
| GHG | Greenhouse Gases |
| HCCI | Homogeneous Charge Compression Ignition |
| H/C | Hydrogen-to-Carbon Ratio |
| IDT | Ignition Delay Time |
| LFS | Laminar Flame Speed |
| LHV | Lower Heating Value |
| LLNL | Lawrence Livermore National Laboratory |
| MCH | Methylcyclohexane |
| MON | Motor Octane Number |
| nMSE | Normalized Mean Square Error |
| O/C | Oxygen-to-Carbon Ratio |
| PRF | Primary Reference Fuel |
| RON | Research Octane Number |
References
- Glyniadakis, S.; Balestieri, J.A.P. Brazilian light vehicle fleet decarbonization scenarios for 2050. Energy Policy 2023, 181, 113682. [Google Scholar] [CrossRef]
- Pacheco, A.F. Analysis and Reduction of Detailed Chemical Kinetics Mechanisms for Combustion of Ethanol and Air. Dissertação de Mestrado, Universidade Federal de Santa Catarina, Centro Tecnológico, Florianópolis, Santa Catarina, Brazil, 2016. [Google Scholar]
- Santos, N.D.S.A.; Roso, V.R.; Malaquias, A.C.T.; Baeta, J.G.C. Internal combustion engines and biofuels: Examining why this robust combination should not be ignored for future sustainable transportation. Renew. Sustain. Energy Rev. 2021, 148, 111292. [Google Scholar] [CrossRef]
- Eaglin, J. The History of Ethanol Production in Brazil with a Focus on Environmental Health. In Oxford Research Encyclopedia of Latin American History; Oxford University Press: Oxford, UK, 2024. [Google Scholar]
- Aguiar, D.R.D.; Taheripour, F.; Silva, D.A.L. Ethanol fuel in Brazil: Policies and carbon emission avoidance. Biofuels 2025, 16, 248–258. [Google Scholar] [CrossRef]
- Stolf, R.; de Oliveira, A.P.R. The success of the Brazilian alcohol program (PROÁLCOOL)-a decade-by-decade brief history of ethanol in Brazil. Eng. Agrícola 2020, 40, 243–248. [Google Scholar] [CrossRef]
- Malaquias, A.C.T.; de Paula Araújo, G.H.; Amaral, L.V.; de Carvalho Torres Filho, M.; Chavda, N.B.; Pujatti, F.J.P.; Baêta, J.G.C. Experimental characterization of ethanol controlled auto-ignition in a single-cylinder research engine. Case Stud. Therm. Eng. 2025, 70, 106128. [Google Scholar] [CrossRef]
- Roy, S.; Askari, O. A New Detailed Ethanol Kinetic Mechanism at Engine-Relevant Conditions. Energy Fuels 2020, 34, 3691–3708. [Google Scholar] [CrossRef]
- Cieplinski, A. O Potencial de Descarbonização do Programa MOVER: Explorando Variações nas Vendas de Veículos de Diferentes Tecnologias até 2027; International Council on Clean Transportation (ICCT): Brasília, Brasil, 2024; Available online: https://theicct.org/publication/o-potencial-de-descarbonizacao-do-programa-mover-explorando-variacoes-nas-vendas-de-veiculos-de-diferentes-tecnologias-ate-2027-jul24/ (accessed on 15 July 2024).
- Instituto de Pesquisa Econômica Aplicada (IPEA). Programa Mobilidade Verde e Inovação (Programa MOVER); Catálogo de Políticas Públicas, Ficha nº 995; IPEA: Brasília, Brazil, 2024. Available online: https://catalogo.ipea.gov.br/politica/995/programa-mobilidade-verde-e-inovacao-programa-mover (accessed on 27 April 2025).
- de Oliveira Gonçalves, F.; Perna, R.F.; Lopes, E.S.; Tovar, L.P.; Filho, R.M.; Lopes, M.S. Strategies to ensure fuel security in Brazil considering a forecast of ethanol production. Biomass 2023, 3, 1–17. [Google Scholar] [CrossRef]
- Olm, C.; Varga, T.; Valkó, É.; Hartl, S.; Hasse, C.; Turányi, T. Development of an ethanol combustion mechanism based on a hierarchical optimization approach. Int. J. Chem. Kinet. 2016, 48, 423–441. [Google Scholar] [CrossRef]
- Hockett, A.; Hampson, G.; Marchese, A.J. Development and validation of a reduced chemical kinetic mechanism for computational fluid dynamics simulations of natural gas/diesel dual-fuel engines. Energy Fuels 2016, 30, 2414–2427. [Google Scholar] [CrossRef]
- Kobayashi, K.; Tomioka, S.; Takahashi, M.; Kodera, M. Reaction mechanism reduction for ethylene-fueled supersonic combustion CFD. CEAS Space J. 2023, 15, 845–866. [Google Scholar] [CrossRef]
- Saraee, H.S.; Hughes, K.J.; Pourkashanian, M. Construction of a small-sized simplified chemical kinetics model for the simulation of n-propylcyclohexane combustion properties. Energies 2024, 17, 1103. [Google Scholar] [CrossRef]
- Marinov, N.M. A detailed chemical kinetic model for high temperature ethanol oxidation. Int. J. Chem. Kinet. 1999, 31, 183–220. [Google Scholar] [CrossRef]
- Wang, Q.-D.; Panigrahy, S.; Yang, S.; Martinez, S.; Liang, J.; Curran, H.J. Development of Multipurpose Skeletal Core Combustion Chemical Kinetic Mechanisms. Energy Fuels 2021, 35, 6921–6927. [Google Scholar] [CrossRef]
- Bellemans, A.; Kincaid, N.; Deak, N.; Pepiot, P.; Bisetti, F. P-DRGEP: A novel methodology for the reduction of kinetics mechanisms for plasma-assisted combustion applications. Proc. Combust. Inst. 2021, 38, 6631–6639. [Google Scholar] [CrossRef]
- Zhu, J.; Zhou, D.; Yu, L.; Qian, Y.; Lu, X. Construction of a skeletal multi-component diesel surrogate model by integrating chemical lumping and genetic algorithm. Fuel 2022, 313, 122711. [Google Scholar] [CrossRef]
- Shirazi, S.A.; Abdollahipoor, B.; Windom, B.; Reardon, K.F.; Foust, T.D. Effects of blending C3-C4 alcohol on motor gasoline properties and performance of spark ignition engines: A review. Fuel Process. Technol. 2020, 197, 106194. [Google Scholar] [CrossRef]
- Silva, A.P.; Bahú, J.O.; Soccol, R., Jr.; Rodríguez-Urrego, L.; Fajardo-Moreno, W.S.; Moya, H.; León-Pulido, J.; Concha, V.O.C. Naphtha characterization (PIONA, density, distillation curve and sulfur content): An origin comparison. Energies 2023, 16, 3568. [Google Scholar] [CrossRef]
- Li, C.; Hu, Y.; Guo, H. Study on the Simplified Chemical Kinetic Combustion Mechanism of Mixed Methanol/PODE Fuel for Marine Diesel Engines. Processes 2024, 12, 594. [Google Scholar] [CrossRef]
- NBR 13992; Produtos líquidos derivados de petróleo–Determinação do teor de etanol anidro combustível (AEAC)–Método da proveta. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brasil, 2017.
- ASTM D4809-18; Standard Test Method for Heat of Combustion of Liquid Hydrocarbon Fuels by Bomb Calorimeter (Precision Method). ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM D240-17; Standard Test Method for Heat of Combustion of Liquid Hydrocarbon Fuels by Bomb Calorimeter. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D2700-19; Standard Test Method for Research Octane Number of Spark-Ignition Engine Fuel. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM D2699-19; Standard Test Method for Motor Octane Number of Spark-Ignition Engine Fuel. ASTM International: West Conshohocken, PA, USA, 2019.
- Richards, K.J.; Senecal, P.K.; Pomraning, E. CONVERGE 4.1; Convergent Science: Madison, WI, USA, 2025. [Google Scholar]
- Mittal, G.; Burke, S.M.; Davies, V.A.; Parajuli, B.; Metcalfe, W.K.; Curran, H.J. Autoignition of ethanol in a rapid compression machine. Combust. Flame 2014, 161, 1164–1171. [Google Scholar] [CrossRef]
- Dong, S.; Wagnon, S.W.; Maffei, L.P.; Kukkadapu, G.; Nobili, A.; Mao, Q.; Pelucchi, M.; Cai, L.; Zhang, K.; Raju, M. A new detailed kinetic model for surrogate fuels: C3MechV3.3. Appl. Energy Combust. Sci. 2022, 9, 100043. [Google Scholar] [CrossRef]
- Shi, X.; Qian, W.; Wang, Q.; Luo, H.; Kang, Y.; Ni, J. Effect of water content of hydrous ethanol on chemical kinetic characteristics based on the new developed reduced ethanol-toluene reference fuels mechanism. Fuel 2021, 303, 121201. [Google Scholar] [CrossRef]
- Millán-Merino, A.; Fernández-Tarrazo, E.; Sánchez-Sanz, M.; Williams, F.A. A multipurpose reduced mechanism for ethanol combustion. Combust. Flame 2018, 193, 112–122. [Google Scholar] [CrossRef]
- Zhang, L.; Qi, Q. A reduced mechanism for the combustion of gasoline-ethanol blend on advanced engine combustion modes. Fuel 2021, 300, 120951. [Google Scholar] [CrossRef]
- Mehl, M.; Pitz, W.J.; Westbrook, C.K.; Curran, H.J. Kinetic modeling of gasoline surrogate components and mixtures under engine conditions. Proc. Combust. Inst. 2011, 33, 193–200. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Stagni, A.; Pelucchi, M.; Cuoci, A.; Faravelli, T. Reduced kinetic schemes of complex reaction systems: Fossil and biomass-derived transportation fuels. Int. J. Chem. Kinet. 2014, 46, 512–542. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Q.; Curran, H.J.; Jia, M. Development of a 5-component gasoline surrogate model using recent advancements in the detailed H2/O2/CO/C1-C3 mechanism for decoupling methodology. Fuel 2021, 283, 118793. [Google Scholar] [CrossRef]
- Liu, Y.-D.; Jia, M.; Xie, M.-Z.; Pang, B. Development of a new skeletal chemical kinetic model of toluene reference fuel with application to gasoline surrogate fuels for computational fluid dynamics engine simulation. Energy Fuels 2013, 27, 4899–4909. [Google Scholar] [CrossRef]
- Tsurushima, T. A new skeletal PRF kinetic model for HCCI combustion. Proc. Combust. Inst. 2009, 32, 2835–2841. [Google Scholar] [CrossRef]
- Cota, F.S. Desenvolvimento de Mecanismos Cinéticos Químicos Reduzidos para Diferentes Misturas de Gasolina e Etanol. Master’s Thesis, Universidade Federal de Minas Gerais, Belo Horizonte, Brazil, 2018. [Google Scholar]
- Narayanaswamy, K.; Pitsch, H.; Pepiot, P. A chemical mechanism for low to high temperature oxidation of methylcyclohexane as a component of transportation fuel surrogates. Combust. Flame 2015, 162, 1193–1213. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Grana, R.; Cuoci, A.; Faravelli, T.; Kelley, A.P.; Law, C.K. Hierarchical and comparative kinetic modeling of laminar flame speeds of hydrocarbon and oxygenated fuels. Prog. Energy Combust. Sci. 2012, 38, 468–501. [Google Scholar] [CrossRef]
- Yao, T.; Zhong, B.-J.; Luo, K.H. Compact chemical mechanism for autoignition and combustion of methylcyclohexane under engine relevant conditions. Energy Fuels 2017, 31, 11337–11347. [Google Scholar] [CrossRef]
- Stagni, A.; Frassoldati, A.; Cuoci, A.; Faravelli, T.; Ranzi, E. Skeletal mechanism reduction through species-targeted sensitivity analysis. Combust. Flame 2016, 163, 382–393. [Google Scholar] [CrossRef]
- Chang, Y.; Jia, M.; Li, Y.; Liu, Y.; Xie, M.; Wang, H.; Reitz, R.D. Development of a skeletal mechanism for diesel surrogate fuel by using a decoupling methodology. Combust. Flame 2015, 162, 3785–3802. [Google Scholar] [CrossRef]
- Cai, L.; Pitsch, H. Optimized chemical mechanism for combustion of gasoline surrogate fuels. Combust. Flame 2015, 162, 1623–1637. [Google Scholar] [CrossRef]
- Fikri, M.; Herzler, J.; Starke, R.; Schulz, C.; Roth, P.; Kalghatgi, G.T. Autoignition of gasoline surrogates mixtures at intermediate temperatures and high pressures. Combust. Flame 2008, 152, 276–281. [Google Scholar] [CrossRef]
- Cooper, S.P.; Mathieu, O.; Schoegl, I.; Petersen, E.L. High-pressure ignition delay time measurements of a four-component gasoline surrogate and its high-level blends with ethanol and methyl acetate. Fuel 2020, 275, 118016. [Google Scholar] [CrossRef]
- Cancino, L.R. Desenvolvimento e Aplicação de Modelos Cinéticos Detalhados para Etanol e Combustíveis Hidrocarbonetos Contendo Etanol. Ph.D. Thesis, Universidade Federal de Santa Catarina, Centro Tecnológico, Florianópolis, Florianópolis, Brazil, 2013. [Google Scholar]
- Zhu, Z.; Liang, K.; Chen, X.; Meng, Z.; He, W.; Song, H. Laminar flame characteristics of premixed methanol–water–air mixture. Energies 2020, 13, 6504. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI-Mech 3.0; 1999. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 15 May 2024).
- Pandey, H.M.; Chaudhary, A.; Mehrotra, D. A comparative review of approaches to prevent premature convergence in GA. Appl. Soft Comput. 2014, 24, 1047–1077. [Google Scholar] [CrossRef]
- Žegklitz, J.; Pošík, P. Model selection and overfitting in genetic programming: Empirical study. In Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation; Association for Computing Machinery: New York, NY, USA, 2015; pp. 1527–1528. [Google Scholar]

| Parameters | Value |
|---|---|
| Population size | 10 |
| Number of genes | 20 |
| Mutation factor | 0.2 |
| Maximum number of generations | 1000 |
| Correlation factor | 0.95 |
| Experiment | Surrogate | ||
|---|---|---|---|
| Group | v/v% | Species | v/v% |
| Aromatics | 16.00 | Toluene | 12.5 |
| iso-paraffins | 30.50 | iso-octane | 20.58 |
| Naphthenes | 13.53 | MCH | 11.38 |
| Olefins | 4.50 | 1-hexene | 13.72 |
| n-paraffins | 8.74 | n-heptane | 15.07 |
| Ethanol | 26.73 | Ethanol | 26.75 |
| Component | Mechanism | Species | Reactions | Reference |
|---|---|---|---|---|
| Ethanol | Marinov et al. (1999) | 57 | 383 | [16] |
| Mittal et al. (2014) | 113 | 710 | [29] | |
| Roy et al. (2020) | 67 | 1016 | [8] | |
| C3 (2022) | 3761 | 16,522 | [30] | |
| Shi et al. (2021) | 76 | 280 | [31] | |
| Merino et al. (2018) | 34 | 69 | [32] | |
| 1-Hexene | C3 (2022) | 3761 | 16,522 | [30] |
| Lei Zhang et al. (2021) | 145 | 653 | [33] | |
| LLNL (2011) | 1393 | 5969 | [34] | |
| Ranzi et al. (2014) | 339 | 9781 | [35] | |
| Yang et al. (2021) | 97 | 308 | [36] | |
| isoOctane | C3 (2022) | 3761 | 16,522 | [30] |
| Lei Zhang et al. (2021) | 145 | 653 | [33] | |
| LLNL (2011) | 1393 | 5969 | [34] | |
| Liu et al. (2013) | 56 | 168 | [37] | |
| Ranzi et al. (2014) | 339 | 9781 | [35] | |
| Tsurushima et al. (2009) | 33 | 38 | [38] | |
| Cota (2018) | 75 | 331 | [39] | |
| MCH | LLNL (2011) | 1393 | 5969 | [34] |
| Krithika et al. (2015) | 3761 | 16,522 | [40] | |
| Ranzi et al. (2012) | 492 | 17,790 | [41] | |
| Tong Yao et al. (2017) | 70 | 377 | [42] | |
| Liu et al. (2013) | 56 | 168 | [37] | |
| Stagni et al. (2016) | 201 | 4417 | [43] | |
| Toluene | Liu et al. (2013) | 56 | 168 | [37] |
| C3 (2022) | 3761 | 16,522 | [30] | |
| Chang et al. (2015) | 70 | 220 | [44] | |
| Cota (2018) | 75 | 331 | [39] | |
| Cai e Pitsch (2015) | 339 | 2791 | [45] | |
| n Heptane | C3 (2022) | 3761 | 16,522 | [30] |
| Lei Zhang et al. (2021) | 145 | 653 | [33] | |
| LLNL (2011) | 1393 | 5969 | [34] | |
| Liu et al. (2013) | 56 | 168 | [37] | |
| Ranzi et al. (2014) | 339 | 9781 | [35] | |
| Cota (2018) | 75 | 331 | [39] | |
| Tsurushima et al. (2009) | 33 | 38 | [38] |
| IDT | LFS | |||||
|---|---|---|---|---|---|---|
| Species | P [bar] | T [K] | phi | P [bar] | T [K] | phi |
| Ethanol | 10–50 | 750–1300 | 1.0 | 1; 2; 7; 10 | 298–428 | 0.6–1.8 |
| Toluene | 16–50 | 900–1450 | 0.25; 0.5; 1.0 | 1; 5 | 298–358 | 0.6–1.6 |
| 1-Hexene | 10–30 | 650–1250 | 1.0 | 1.0; 10 | 373 | 0.6–1.5 |
| Iso-Octane | 10–40 | 625–1450 | 0.5; 1.0; 2.0 | 1.0; 5; 10 | 298–470 | 0.6–1.4 |
| MCH | 12–50 | 650–1250 | 1.0 | 1.0; 5; 10 | 353 | 0.6–1.6 |
| n-Heptane | 13–43 | 550–1450 | 0.25; 0.5; 1.0 | 1.0; 2.5; 5.0 | 328–600 | 0.6–1.6 |
| IDT | LFS | |||||
|---|---|---|---|---|---|---|
| Mixture | P [bar] | T [K] | phi | P [bar] | T [K] | phi |
| E0 | 25–55 | 650–1450 | 1.0 | 1.0; 2.5 | 373 | 0.6–1.4 |
| E22 | 12–50 | 650–1250 | 0.25; 0.5; 1.0 | 1.0 | 360 | 0.6–1.2 |
| E40 | 10–50 | 750–1250 | 1.0 | - | - | - |
| E50 | 25 | 750–1150 | 0.5 | 1.0 | 360; 480 | 0.6–1.4 |
| E85 | 25 | 750–1100 | 0.5 | 1.0 | 353 | 0.6–1.6 |
| E100 | 10–50 | 750–1250 | 1.0 | 1.0–7.0 | 298–420 | 0.6–1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cota, F.; Martins, C.; Braga, R.; Baeta, J. Development and Optimization of Chemical Kinetic Mechanisms for Ethanol–Gasoline Blends Using Genetic Algorithms. Energies 2025, 18, 4444. https://doi.org/10.3390/en18164444
Cota F, Martins C, Braga R, Baeta J. Development and Optimization of Chemical Kinetic Mechanisms for Ethanol–Gasoline Blends Using Genetic Algorithms. Energies. 2025; 18(16):4444. https://doi.org/10.3390/en18164444
Chicago/Turabian StyleCota, Filipe, Clarissa Martins, Raphael Braga, and José Baeta. 2025. "Development and Optimization of Chemical Kinetic Mechanisms for Ethanol–Gasoline Blends Using Genetic Algorithms" Energies 18, no. 16: 4444. https://doi.org/10.3390/en18164444
APA StyleCota, F., Martins, C., Braga, R., & Baeta, J. (2025). Development and Optimization of Chemical Kinetic Mechanisms for Ethanol–Gasoline Blends Using Genetic Algorithms. Energies, 18(16), 4444. https://doi.org/10.3390/en18164444






