Interactive Optimization of Electric Bus Scheduling and Overnight Charging
Abstract
1. Introduction
2. Problem Definition
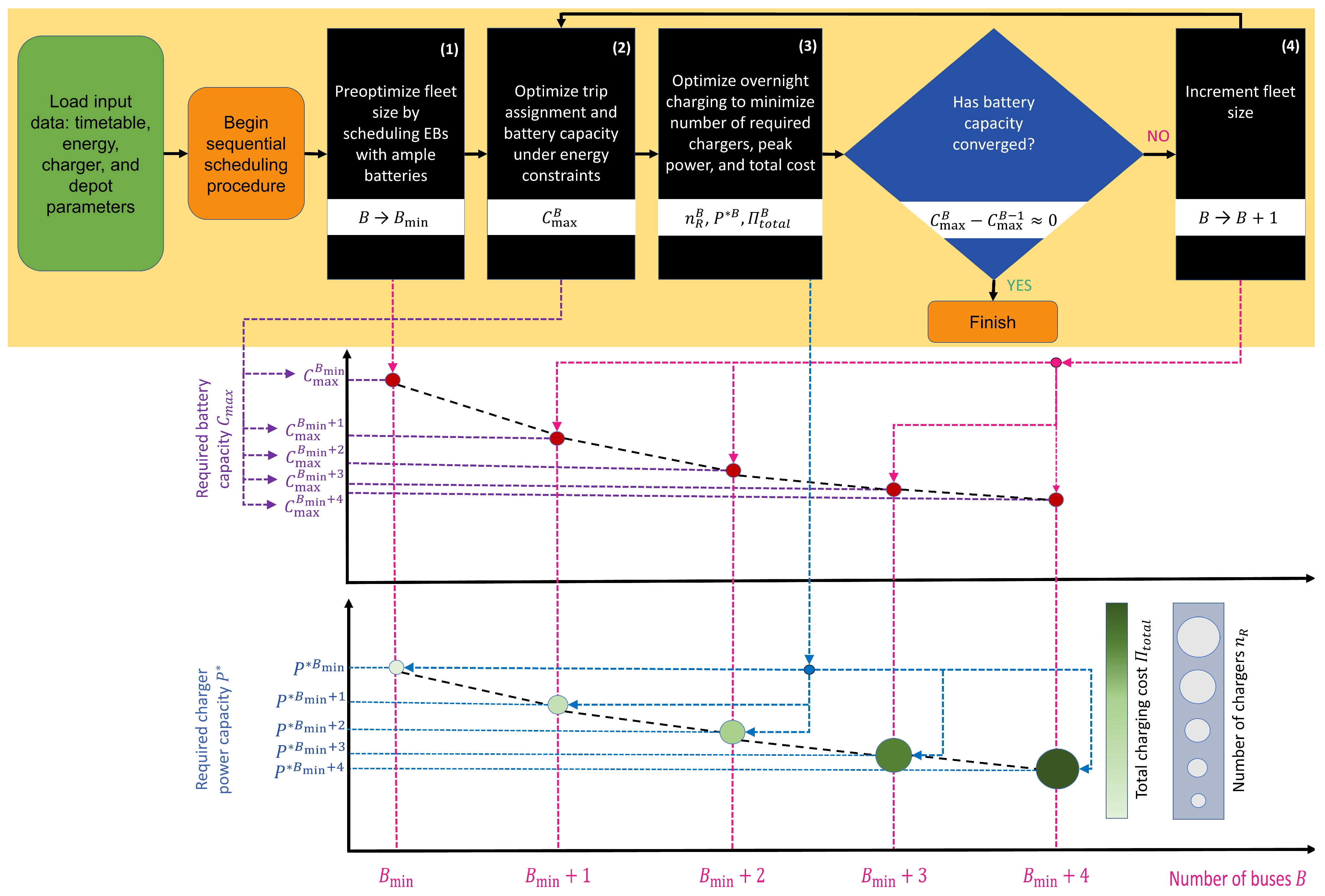
2.1. Electric City Bus Scheduling and Overnight Charging Framework
2.2. Problem Formulation
2.2.1. Input Parameters and Feasibility Constraints
- start time: (in minutes from midnight);
- duration: (in minutes);
- energy consumption: (in kWh);
- start location: ;
- end location: .
2.2.2. Fleet Size Minimization Formulation
2.2.3. Required Battery Capacity Minimization Formulation
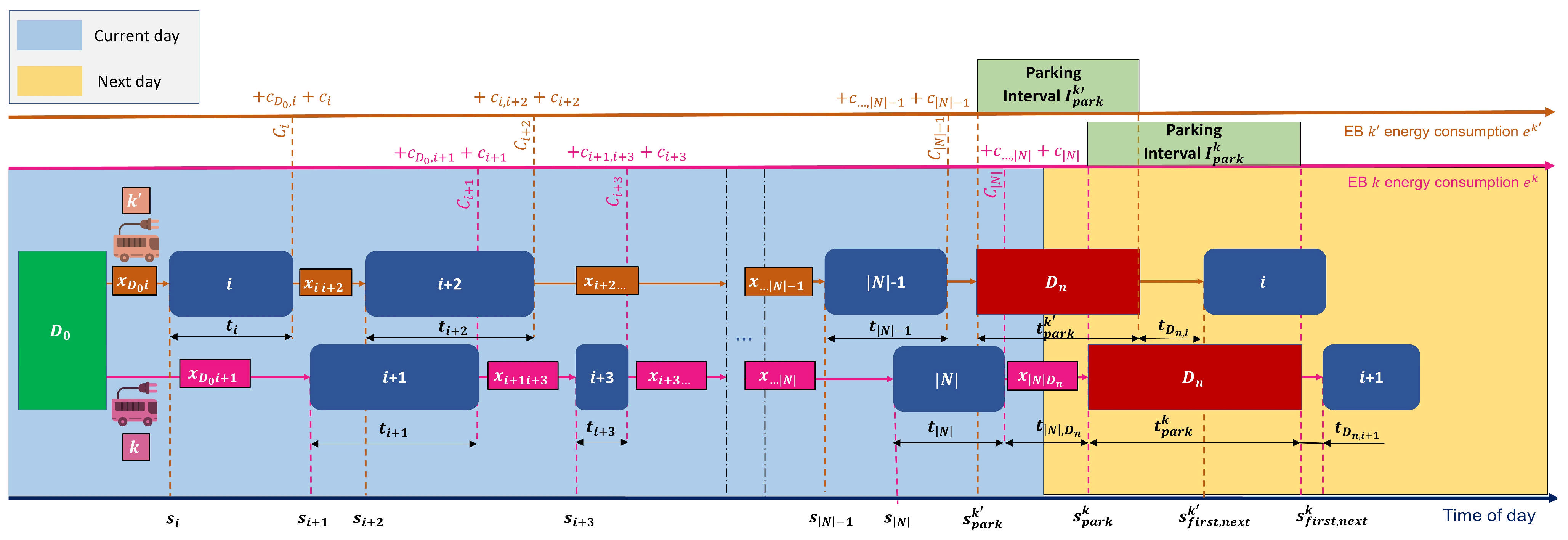
2.2.4. Overnight Charging Scheduling Formulation
3. Methodology
3.1. General MILP Formulation
3.2. Fleet Size Optimization
3.3. Required Battery Capacity Minimization
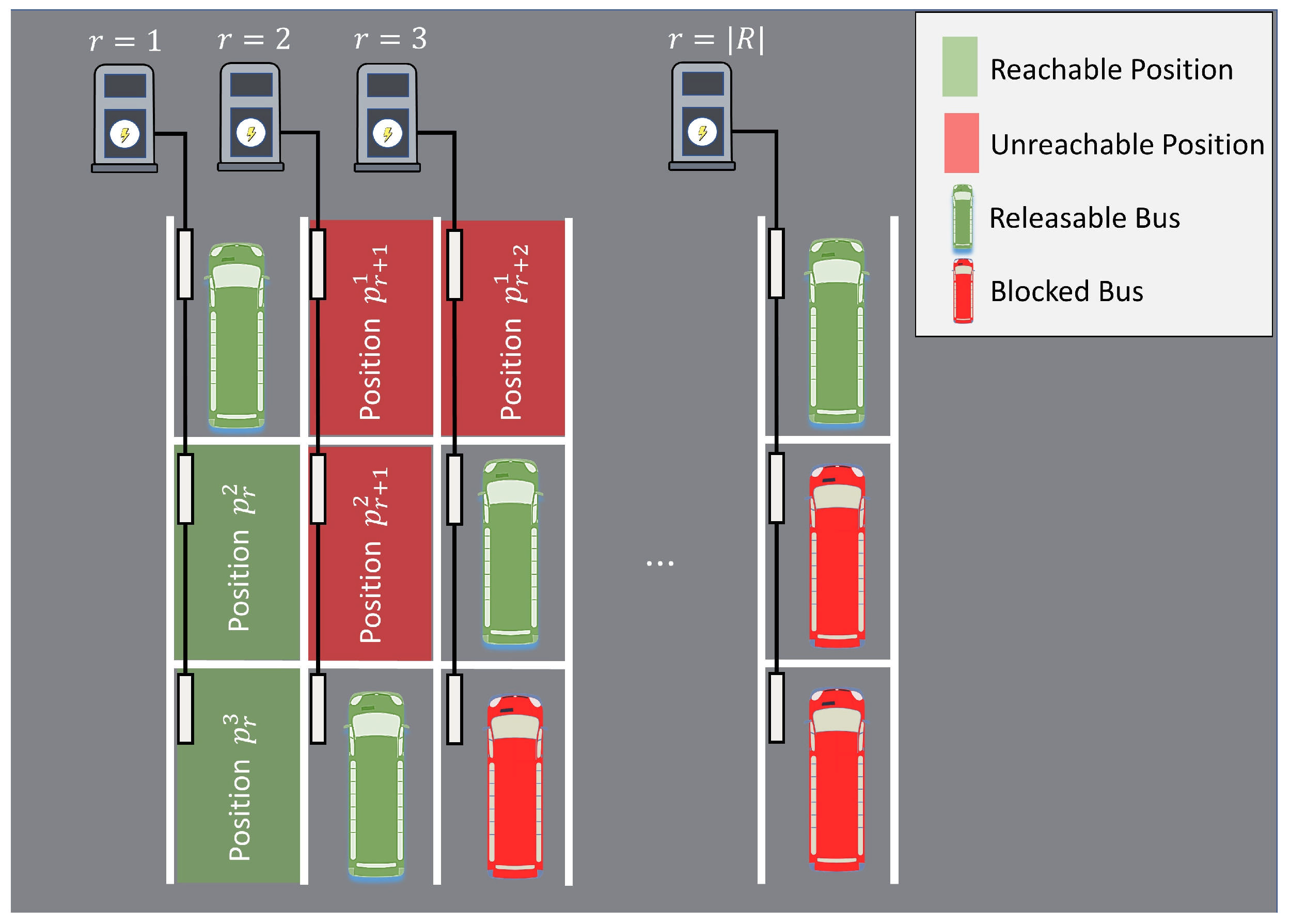
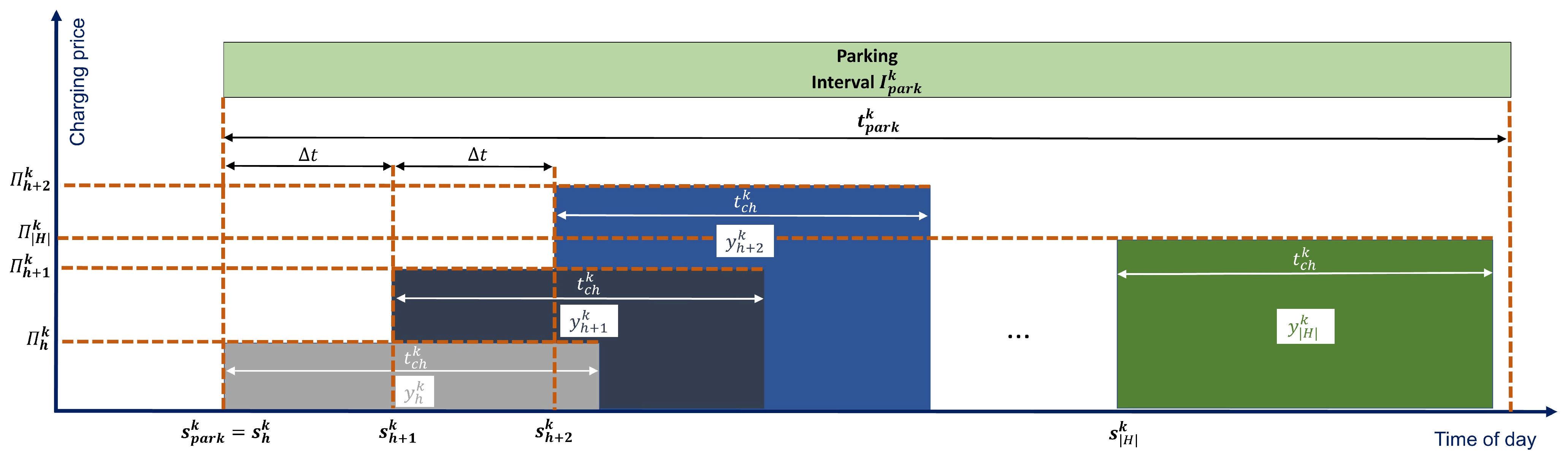
3.4. Overnight Charging Scheduling
| Algorithm 1. Joint optimization of charger count and charger power via nested search |
| PROCEDURE Find_Minimum_Chargers_and_Power ( |
| , // smallest power level to test (kW) |
| // largest power level to test (kW) |
| // convergence tolerance (kW) |
| ): // maximum number of chargers to try |
| // outer loop: grow charger pool |
| // current lower power bound |
| // current upper power bound |
| found ← FALSE // flag: feasibility for this r? |
| ) // inner loop: bisection on power |
| // midpoint candidate power |
| ) = FEASIBLE THEN |
| // current upper power bound |
| found ← TRUE |
| ELSE |
| // infeasible → raise lower bound |
| END IF END WHILE |
that works → global answer |
| ) for this |
| END IF |
| END FOR |
| RETURN “No feasible configuration within given limits” |
| END PROCEDURE |
4. Case Study
4.1. Nominal Service Data
4.2. Operational and Ambient Data
4.2.1. Data Processing
4.2.2. Energy Demand Model
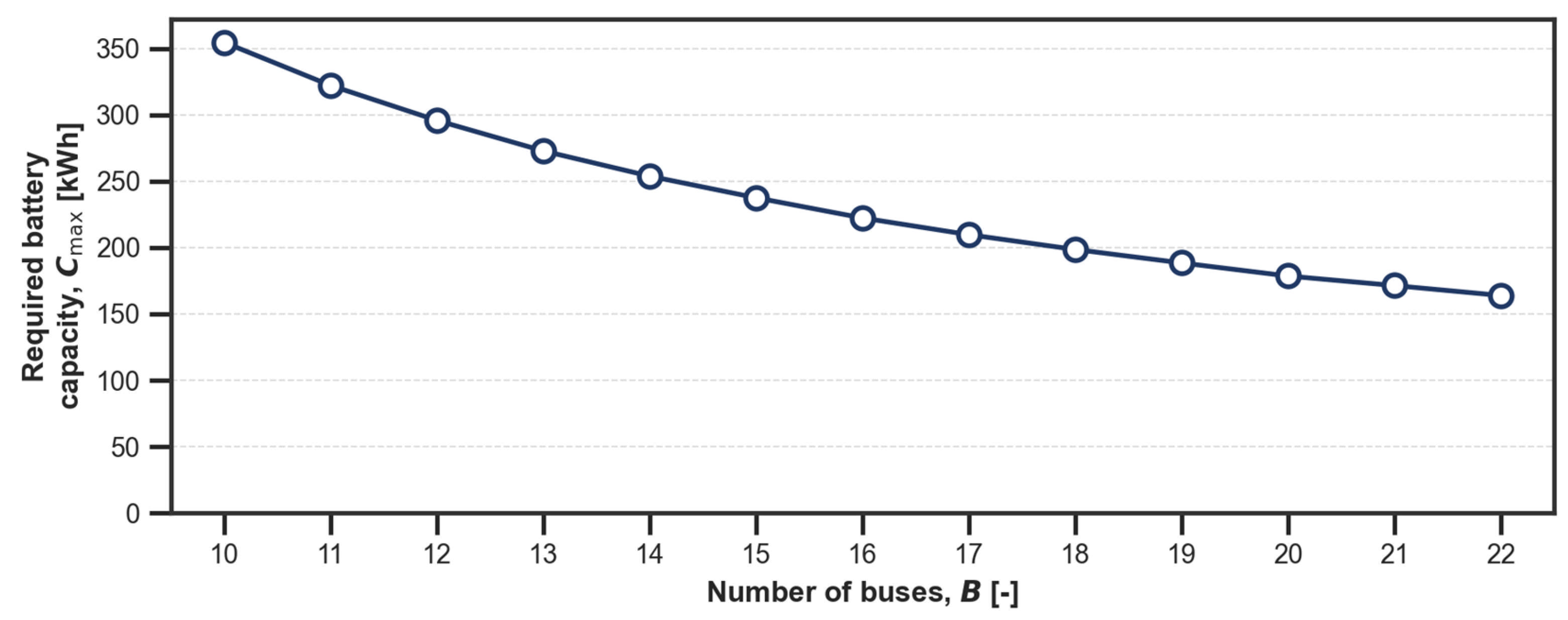
5. Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALNS–BB | Adaptive Large Neighborhood Search and Branch and Bound |
| CDG | Charles de Gaulle |
| CSP | Charging Scheduling Problem |
| EB | Electric Bus |
| EBSP | Electric Bus Scheduling Problem |
| HEB | Hybrid Electric Buses |
| HVAC | Heating, Ventilation, and Air Conditioning |
| MILP | Mixed-Integer Linear Program |
| TEA | Techno-Economic Analysis |
| TCO | Total Cost of Ownership |
| ToU | Time-of-Use |
| VSP | Vehicle Scheduling Problem |
References
- Braun, A.; Rid, W. Energy consumption of an electric and an internal combustion passenger car: A comparative case study from real-world data on the Erfurt circuit in Germany. Transp. Res. Procedia 2017, 27, 468–475. [Google Scholar] [CrossRef]
- Kalghatgi, G. Is it really the end of internal combustion engines and petroleum in transport? Appl. Energy 2018, 225, 965–974. [Google Scholar] [CrossRef]
- Paul, T.; Yamada, H. Operation and charging scheduling of electric buses in a city bus route network. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 2780–2786. [Google Scholar]
- Li, J.Q. Battery-electric transit bus developments and operations: A review. Int. J. Sustain. Transp. 2014, 10, 157–169. [Google Scholar] [CrossRef]
- Topić, J.; Soldo, J.; Maletić, F.; Škugor, B.; Deur, J. Virtual simulation of electric bus fleets for city bus transport electrification planning. Energies 2020, 13, 23. [Google Scholar] [CrossRef]
- Dabčević, Z.; Škugor, B.; Cvok, I.; Deur, J. A trip-based data-driven model for predicting battery energy consumption of electric city buses. Energies 2024, 17, 911. [Google Scholar] [CrossRef]
- Dabčević, Z.; Škugor, B.; Topić, J.; Deur, J. Synthesis of driving cycles based on low-sampling-rate vehicle-tracking data and Markov chain methodology. Energies 2022, 15, 4108. [Google Scholar] [CrossRef]
- Matković, D.; Topić, J.; Škugor, B.; Deur, J. Search space reduction-supported multi-objective optimization of charging system configuration for electrified city bus transport system. In Proceedings of the 17th Conference on Sustainable Development of Energy, Water and Environment Systems (SDEWES), Paphos, Cyprus, 6–10 November 2022. [Google Scholar]
- Xiang, Y.; Wang, S.; Su, T.; Li, J.; Mao, S.S.; Geimer, M. KIT Bus: A Shuttle Model for CARLA Simulator. In Proceedings of the 2021 IEEE Industrial Electronics and Applications Conference (IEACon), Penang, Malaysia, 21–22 November 2021; pp. 7–12. [Google Scholar]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problems with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Sung, Y.W.; Chu, J.C.; Chang, Y.J.; Yeh, J.C.; Chou, Y.H. Optimizing mix of heterogeneous buses and chargers in electric bus scheduling problems. Simul. Model. Pract. Theory 2022, 119, 102584. [Google Scholar] [CrossRef]
- Jiang, M.; Zhang, Y.; Zhang, Y. Multi-depot electric bus scheduling considering operational constraints and partial charging: A case study in Shenzhen, China. Sustainability 2022, 14, 255. [Google Scholar] [CrossRef]
- Brinkel, N.; Zijlstra, M.; van Bezu, R.; van Twuijver, T.; Lampropoulos, I.; van Sark, W. A comparative analysis of charging strategies for battery electric buses in wholesale electricity and ancillary services markets. Transp. Res. Part E Logist. Transp. Rev. 2023, 172, 103085. [Google Scholar] [CrossRef]
- Behnia, F.; Schuelke-Leech, B.A.; Mirhassani, M. Optimizing sustainable urban mobility: A comprehensive review of electric bus scheduling strategies and future directions. Sustain. Cities Soc. 2024, 108, 104297. [Google Scholar] [CrossRef]
- Dabčević, Z.; Škugor, B.; Deur, J. Pareto optimization of electric city bus scheduling. In Proceedings of the 18th Conference on Sustainable Development of Energy, Water and Environment Systems (SDEWES), Dubrovnik, Croatia, 24–29 September 2023. [Google Scholar]
- Sobhani, E.; Yassine, A.; Ameli, A.; Riahinia, S. Overnight Charging Mechanism of Battery Electric Buses for a Transit Network in Smart Cities. In Proceedings of the 2024 5th Technology Innovation Management and Engineering Science International Conference (TIMES-iCON), Bangkok, Thailand, 19–21 January 2024; pp. 1–5. [Google Scholar]
- Rinaldi, M.; Parisi, F.; Laskaris, G.; D’Ariano, A.; Viti, F. Optimal dispatching of electric and hybrid buses subject to scheduling and charging constraints. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 41–46. [Google Scholar]
- Škugor, B.; Grden, L.; Deur, J. Hierarchical model predictive control-based electric vehicle fleet charging management. Energy Convers. Manag. 2025, 342, 120119. [Google Scholar] [CrossRef]
- Moradipari, A.; Tucker, N.; Zhang, T.; Cezar, G.; Alizadeh, M. Mobility-aware smart charging of electric bus fleets. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Zhou, G.-J.; Xie, D.-F.; Zhao, X.-M.; Lu, C. Collaborative optimization of vehicle and charging scheduling for a bus fleet mixed with electric and traditional buses. IEEE Access 2020, 8, 8056–8072. [Google Scholar] [CrossRef]
- Wu, W.; Lin, Y.; Liu, R.; Jin, W. The multi-depot electric vehicle scheduling problem with power grid characteristics. Transp. Res. Part B Methodol. 2022, 155, 322–347. [Google Scholar] [CrossRef]
- Li, P.; Jiang, M.; Zhang, Y.; Zhang, Y. Cooperative optimization of bus service and charging schedules for a fast-charging battery electric bus network. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5362–5375. [Google Scholar] [CrossRef]
- Duan, M.; Liao, F.; Qi, G.; Guan, W. Integrated optimization of electric bus scheduling and charging planning incorporating flexible charging and timetable shifting strategies. Transp. Res. Part C Emerg. Technol. 2023, 152, 104175. [Google Scholar] [CrossRef]
- Li, X.; Wang, T.; Li, L.; Feng, F.; Wang, W.; Cheng, C. Joint optimization of regular charging electric bus transit network schedule and stationary charger deployment considering partial charging policy and time-of-use electricity prices. J. Adv. Transp. 2020, 2020, 8863905. [Google Scholar] [CrossRef]
- Perumal, S.S.G.; Dollevoet, T.; Huisman, D.; Lusby, R.M.; Larsen, J.; Riis, M. Solution approaches for integrated vehicle and crew scheduling with electric buses. Comput. Oper. Res. 2021, 132, 105268. [Google Scholar] [CrossRef]
- Perumal, S.S.G.; Lusby, R.M.; Larsen, J. Electric bus planning and scheduling: A review of related problems and methodologies. Eur. J. Oper. Res. 2022, 301, 395–413. [Google Scholar] [CrossRef]
- Garcia-Valle, R.; Lopes, J.A.P. Electric Vehicle Integration into Modern Power Networks; Springer: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- ABB Group. HVC-Overnight Charging—Electric Vehicle Infrastructure; Product Leaflet; ABB: Zurich, Switzerland, 2018. [Google Scholar]
- Gkiotsalitis, K.; Iliopoulou, C.; Kepaptsoglou, K. An exact approach for the multi-depot electric bus scheduling problem with time windows. Eur. J. Oper. Res. 2023, 306, 189–206. [Google Scholar] [CrossRef]
- Ceder, A. Public Transit Planning and Operation: Theory, Modeling and Practice; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Nemhauser, G.L.; Wolsey, L.A. Integer and Combinatorial Optimization; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
- Gurobi Optimization LLC. Gurobi Optimizer Reference Manual. 2024. Available online: https://www.gurobi.com (accessed on 5 March 2025).
- Williams, H.P. Model Building in Mathematical Programming, 5th ed.; Wiley: Chichester, UK, 2013. [Google Scholar]
- RTE France Spot Electricity Exchange. Available online: https://www.services-rte.com/en/view-data-published-by-rte/france-spot-electricity-exchange.html (accessed on 5 March 2025).

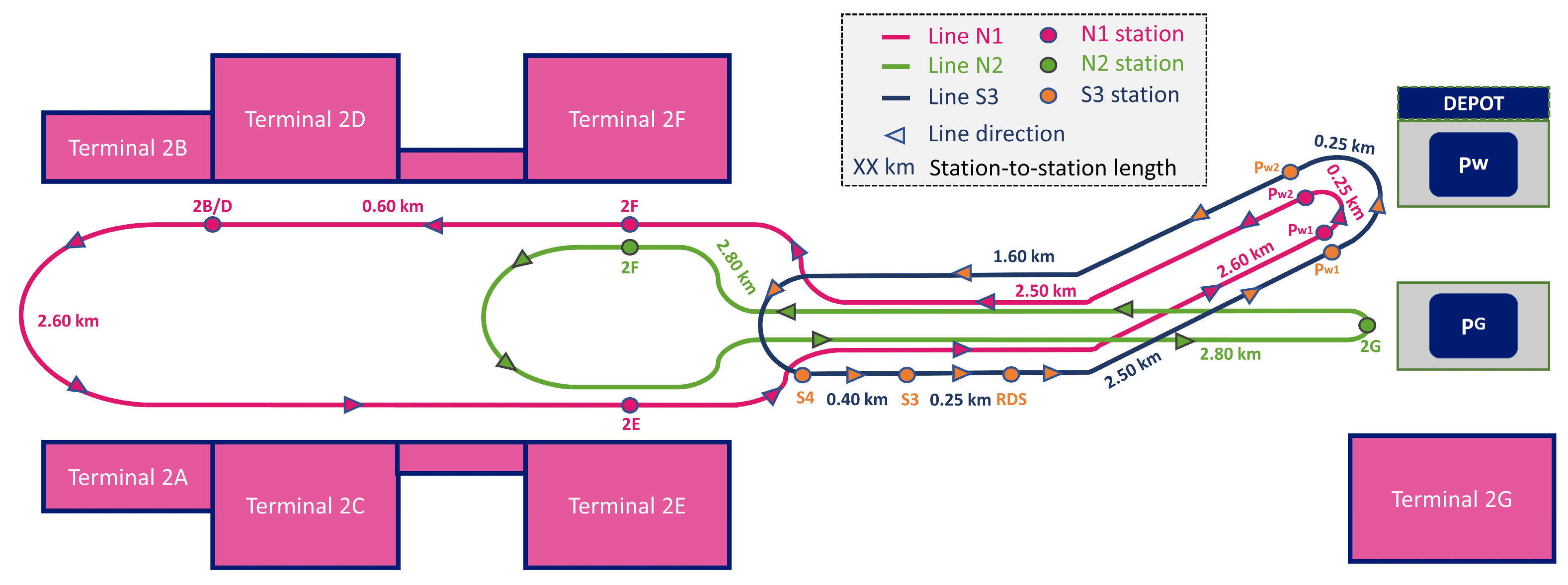

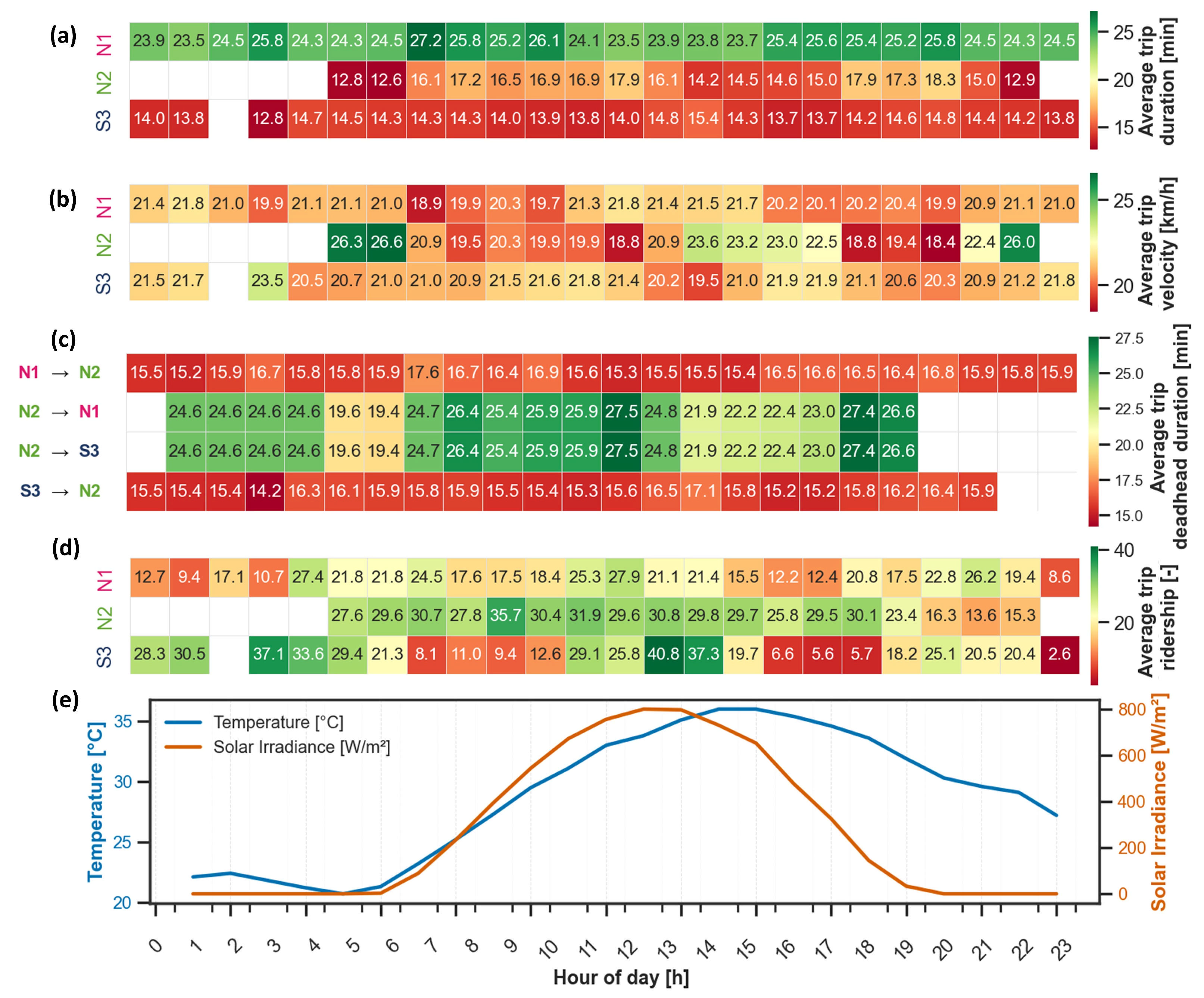
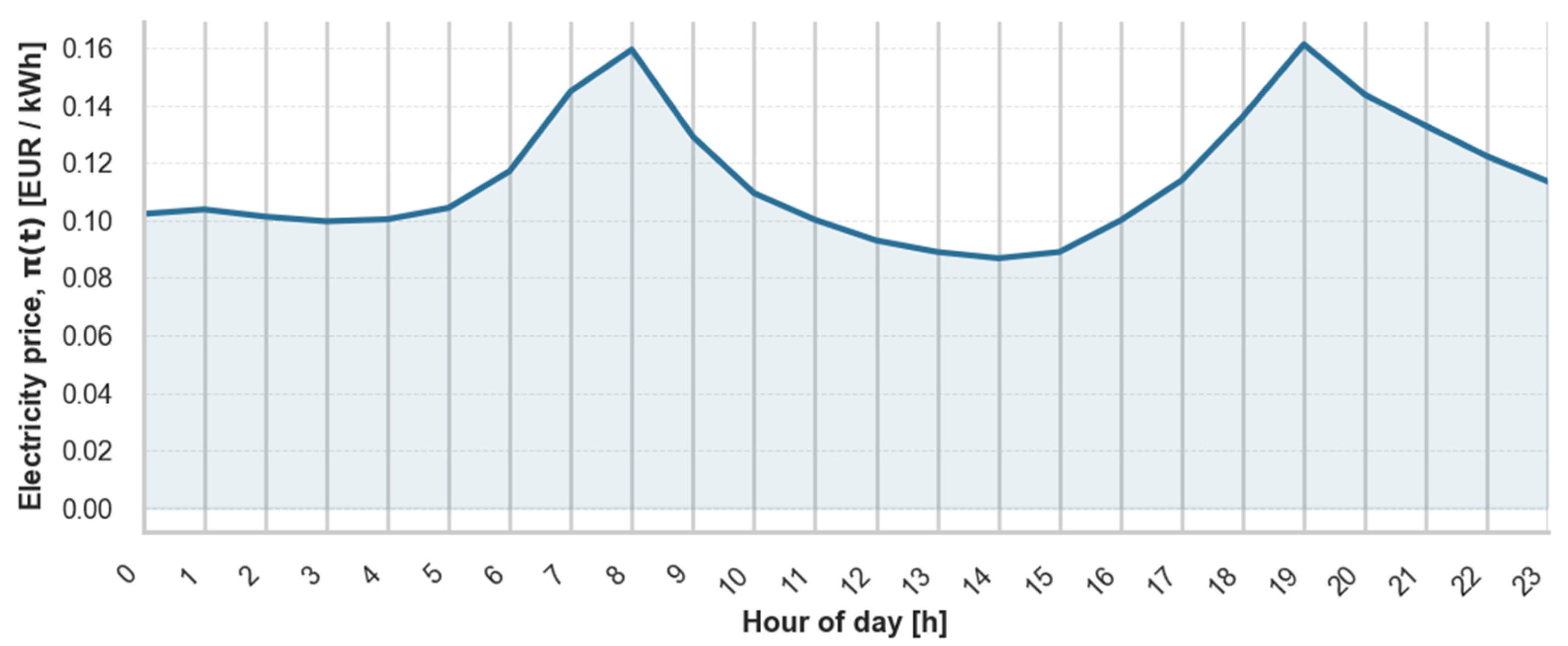
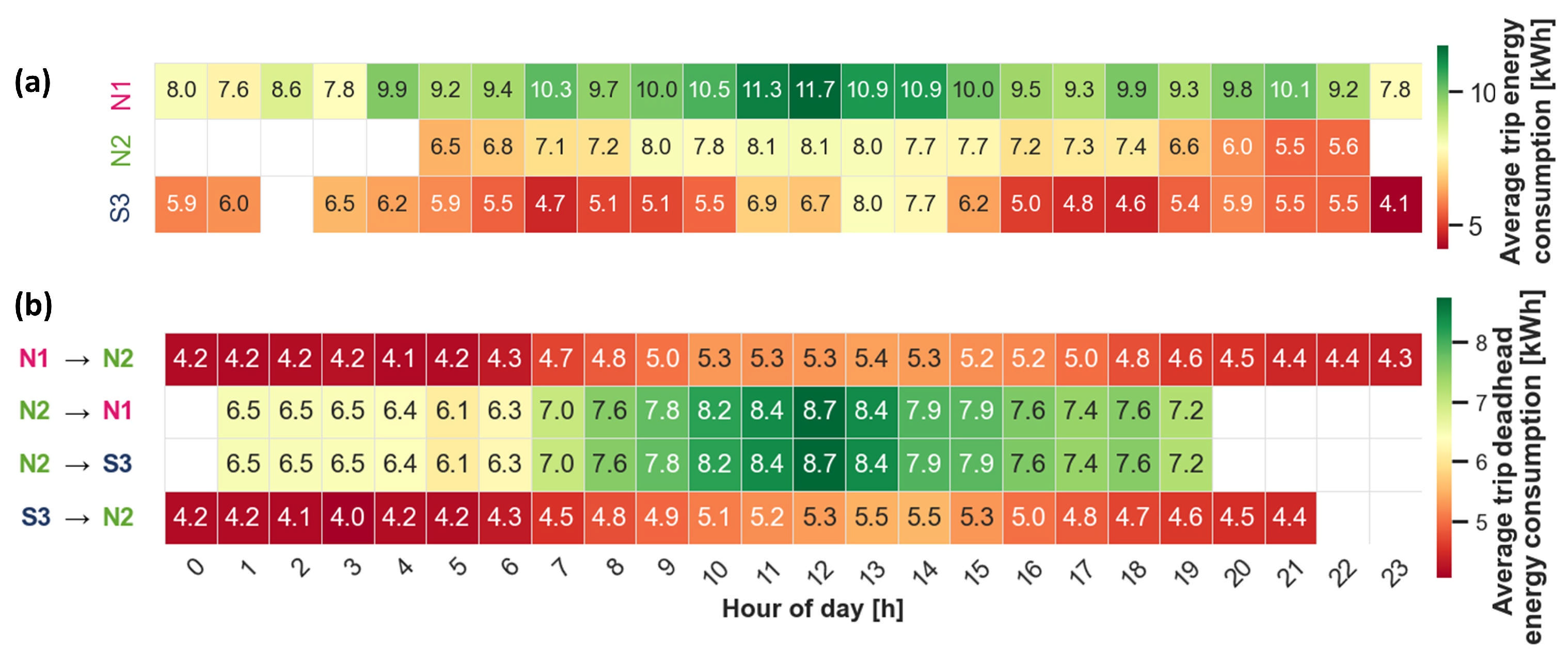
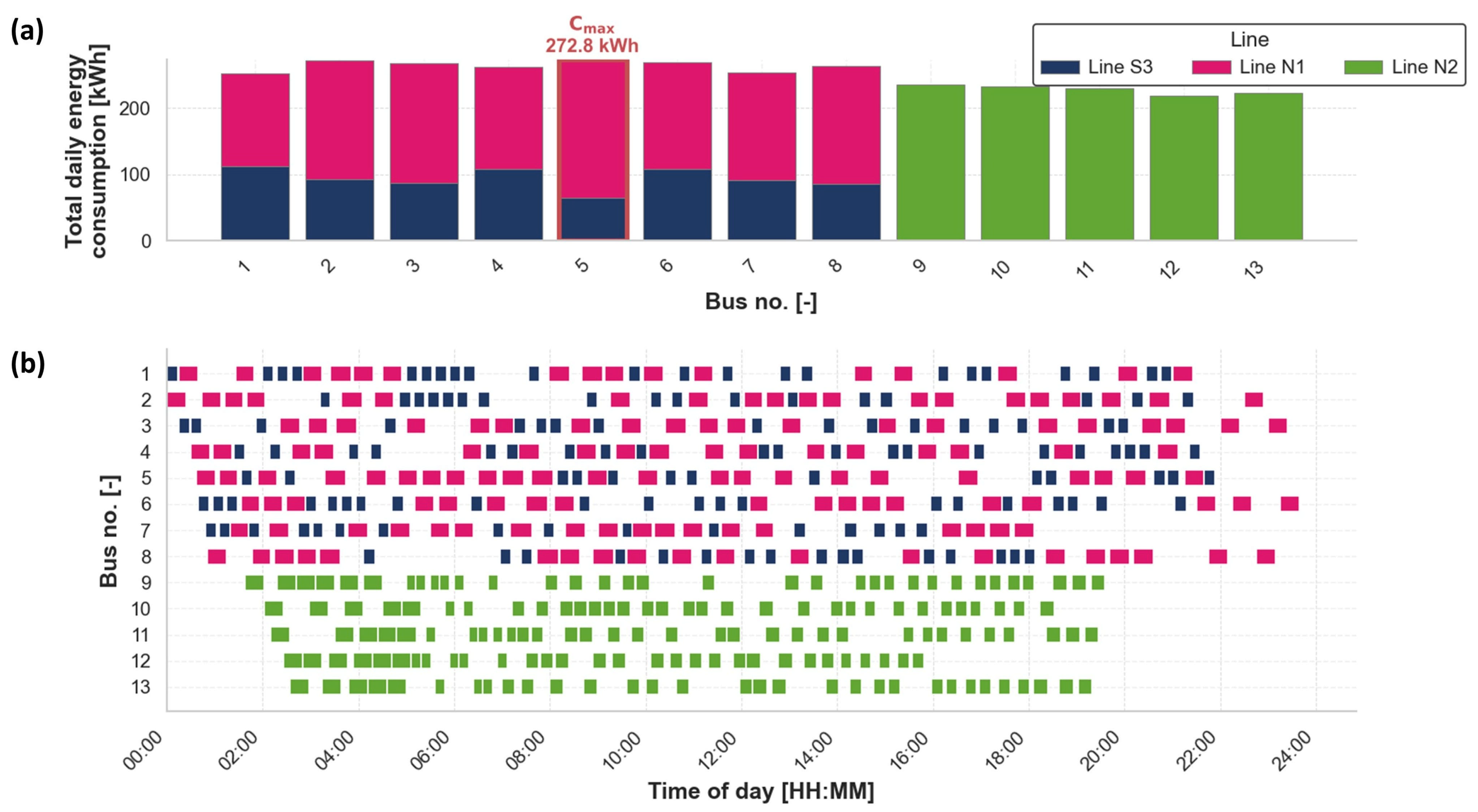

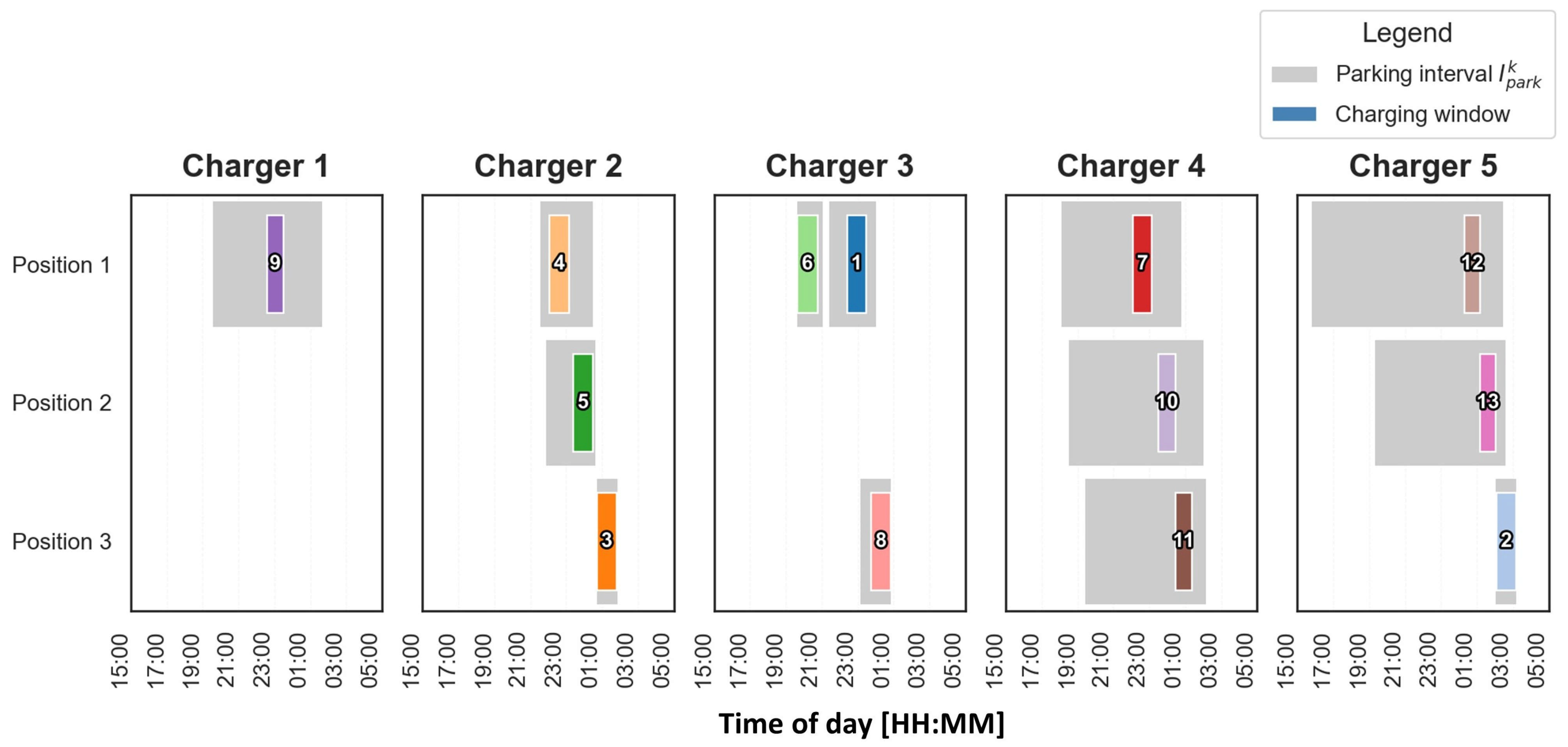
| Line | Connected Terminals/Stations | Route Type | Total Line Distance (km) | Avg. Distance Between Stations (km) | No. of Stations | No. of Trips per Day | Departure Frequency | No. of Buses |
|---|---|---|---|---|---|---|---|---|
| N1 | Pw1–Pw2–T2F–T2B/D–T2E–Pw1 | Circular, counterclockwise | 8.55 | 1.71 | 5 | 157 | ~7 min (before 16:00), ~10 min (after) | 5 |
| N2 | T2G–T2F–T2G | Circular, counterclockwise | 5.60 | 2.80 | 2 | 158 | ~6–8 min | 3 |
| S3 | Pw1–Pw2–S4–S3–RDS–Pw1 | Circular, counterclockwise | 5.00 | 1.00 | 5 | 143 | ~9 min | 3 |
| Scheduling Approach | Fleet Size B [-] | Required Battery Capacity [kWh] | Change vs. Baseline [%] |
|---|---|---|---|
| Baseline | 11 | 398 | 0% |
| Optimized | 11 | 322 | −19% |
| Optimized (minimum fleet) | 10 | 355 | −11% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabčević, Z.; Deur, J. Interactive Optimization of Electric Bus Scheduling and Overnight Charging. Energies 2025, 18, 4440. https://doi.org/10.3390/en18164440
Dabčević Z, Deur J. Interactive Optimization of Electric Bus Scheduling and Overnight Charging. Energies. 2025; 18(16):4440. https://doi.org/10.3390/en18164440
Chicago/Turabian StyleDabčević, Zvonimir, and Joško Deur. 2025. "Interactive Optimization of Electric Bus Scheduling and Overnight Charging" Energies 18, no. 16: 4440. https://doi.org/10.3390/en18164440
APA StyleDabčević, Z., & Deur, J. (2025). Interactive Optimization of Electric Bus Scheduling and Overnight Charging. Energies, 18(16), 4440. https://doi.org/10.3390/en18164440







