Research on Mode Transition Control of Power-Split Hybrid Electric Vehicle Based on Fixed Time
Abstract
1. Introduction
2. Modeling of PS-HEV
2.1. Transient Modeling of Power-Train
2.2. Transient Modeling of Engine and Motor
2.3. Mode Transition Logic
3. Mode Transition Problem Description for PS-HEVs
3.1. PS-HEV Mode Transition Problem
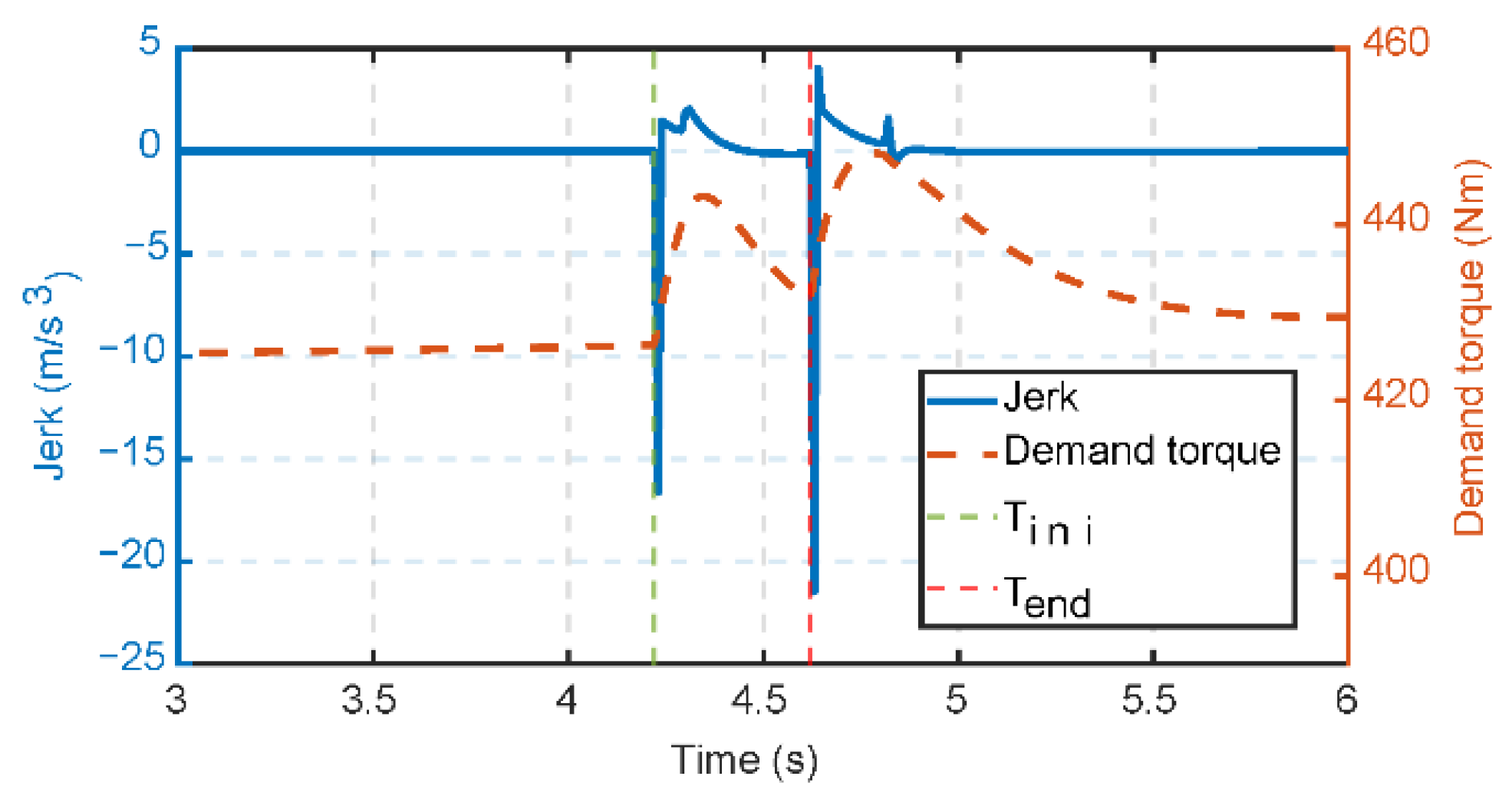
3.2. PS-HEV Mode Transition with Disturbance
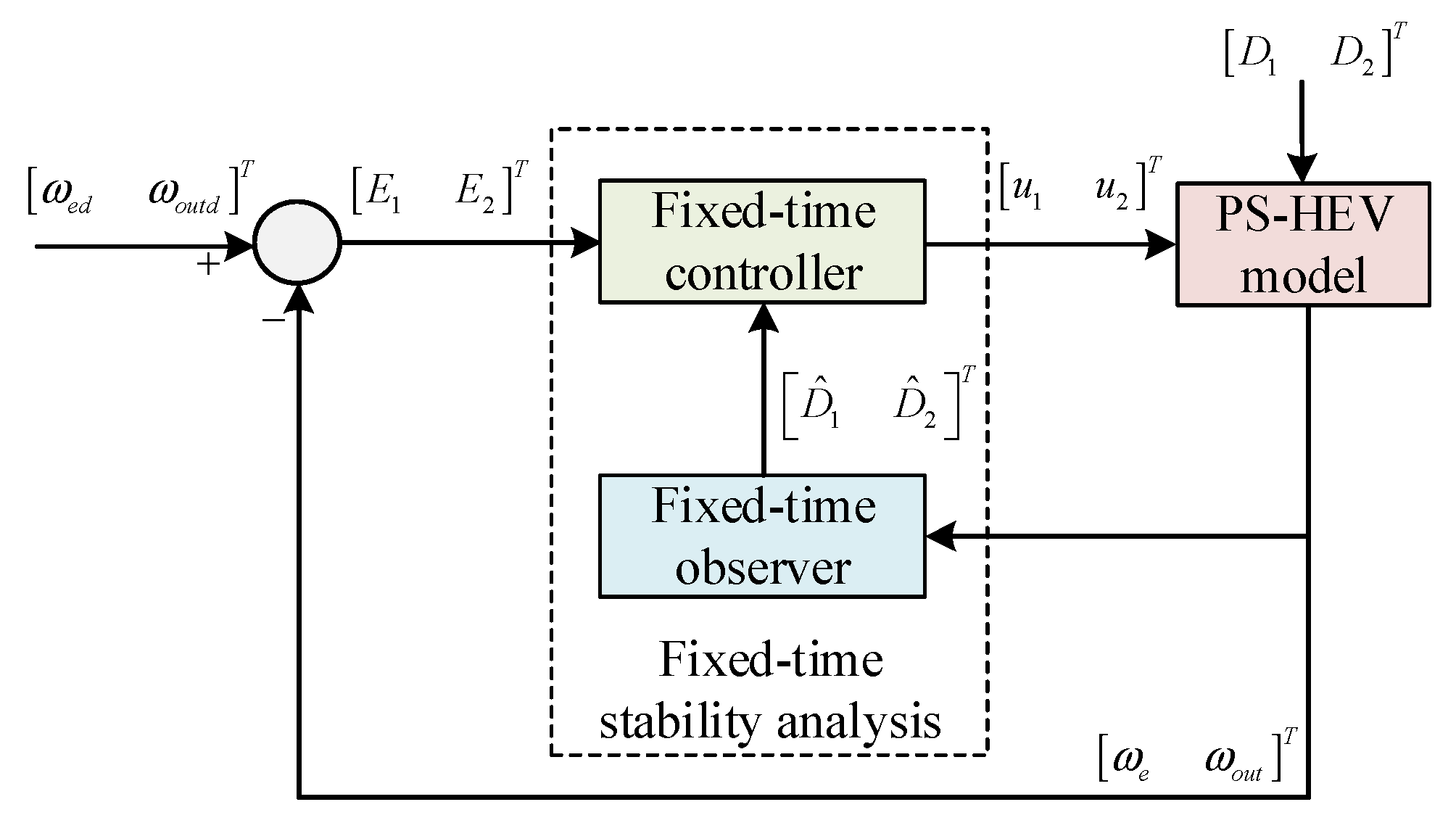
4. Design of PS-HEV Coordinated Control Strategy Based on Fixed-Time Theory
4.1. Fixed-Time Terminal Sliding Mode Controller Design
4.2. Fixed-Time Extended State Observer Design
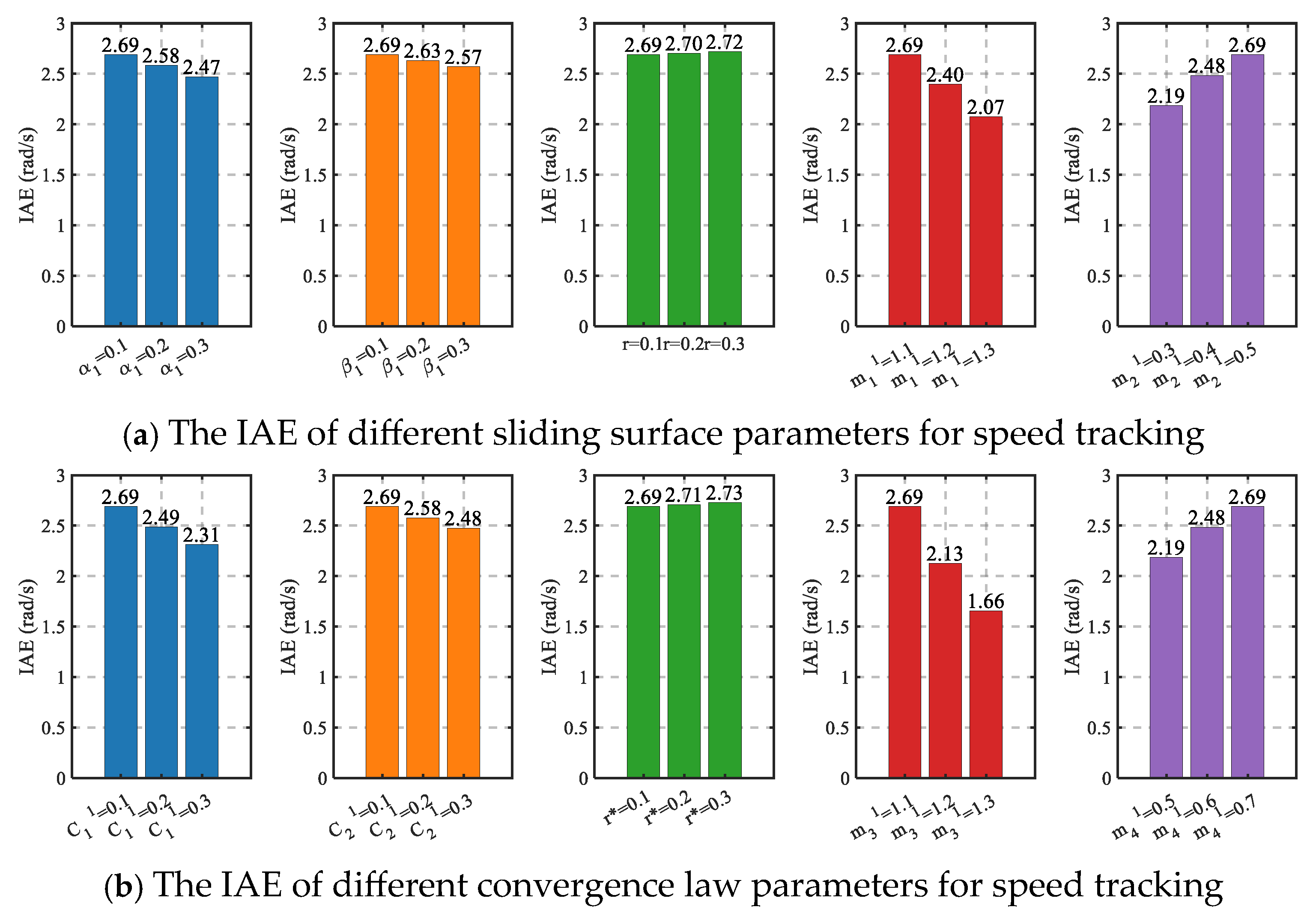
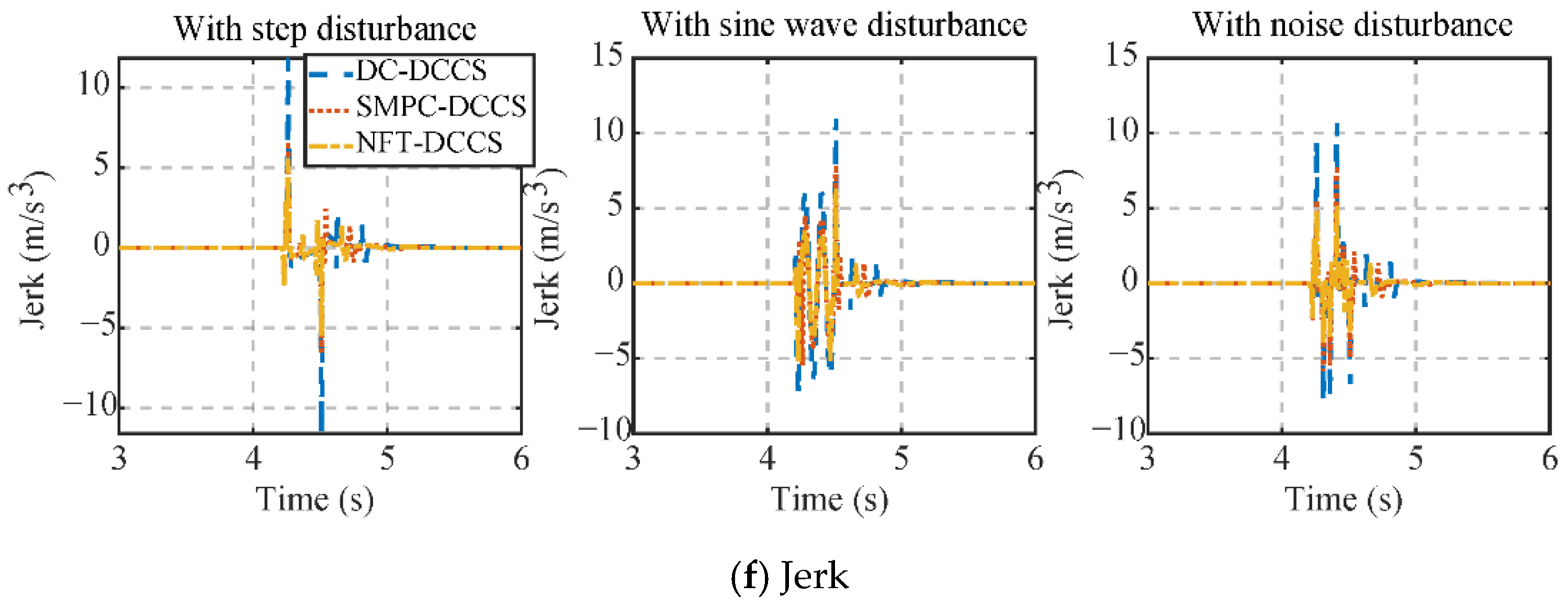
5. Simulation and HIL Test Results
5.1. Simulation Results
5.2. HIL Test Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, S.; Qiu, J.; Lin, J.; Yao, Z.; Liang, Q.; Lu, X. Planning of a multi-agent mobile robot-based adaptive charging network for enhancing power system resilience under extreme conditions. Appl. Energy 2025, 395, 126252. [Google Scholar] [CrossRef]
- Rong, X.; Shi, D.; Wang, S.; Yin, C.; Li, C. Control allocation-based adaptive dynamic coordinated control of compound power-split hybrid electric vehicles. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024. [Google Scholar] [CrossRef]
- Sabri, M.F.M.; Danapalasingam, K.A.; Rahmat, M.F. A review on hybrid electric vehicles architecture and energy management strategies. Renew. Sustain. Energy Rev. 2016, 53, 1433–1442. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Coskun, S.; Pang, H.; Cui, Y.; Xi, J. Energy management strategies for hybrid electric vehicles: Review, classification, comparison, and outlook. Energies 2020, 13, 3352. [Google Scholar] [CrossRef]
- Chen, B.; Pan, X.; Evangelou, S.A. Optimal energy management of series hybrid electric vehicles with engine start–stop system. IEEE Trans. Control Syst. Technol. 2022, 31, 660–675. [Google Scholar] [CrossRef]
- Zhao, Q.; Rong, X.; Shi, D. Research on switching control based sliding mode coordination strategy of hybrid electric vehicle. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2024, 238, 1872–1887. [Google Scholar] [CrossRef]
- Rong, X.; Shi, D.; Wang, S. Adaptive anti-saturation fixed-time control for PS-HEV mode transition with predefined performance. IEEE Trans. Power Electron. 2025, 40, 13852–13865. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; Li, B.; Ji, J.; Zhao, K.; Hu, C. A review of power management strategies and component sizing methods for hybrid vehicles. Renew. Sustain. Energy Rev. 2018, 96, 132–144. [Google Scholar] [CrossRef]
- Zhu, F.; Chen, L.; Yin, C.; Shu, J. Dynamic modelling and systematic control during the mode transition for a multi-mode hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1007–1023. [Google Scholar] [CrossRef]
- Sahu, R.K.; Srivastava, D.K. Model-Based Calibration of a Gasoline-Fueled Spark Ignition Engine for Torque Control Application Using Mean Value Engine Modeling. SAE Int. J. Engines 2023, 16, 855–870. [Google Scholar] [CrossRef]
- Zheng, T.; Zhang, Y.; Li, Y.; Shi, L. Real-time combustion torque estimation and dynamic misfire fault diagnosis in gasoline engine. Mech. Syst. Signal Process. 2019, 126, 521–535. [Google Scholar] [CrossRef]
- Feng, S.; Li, X.; Zhang, S.; Jian, Z.; Duan, H.; Wang, Z. A review: State estimation based on hybrid models of Kalman filter and neural network. Syst. Sci. Control Eng. 2023, 11, 2173682. [Google Scholar] [CrossRef]
- Gao, A.; Fu, Z.; Tao, F. Dynamic coordinated control based on sliding mode controller during mode transition with ICE starting for an HEV. IEEE Access 2020, 8, 60428–60443. [Google Scholar] [CrossRef]
- Chen, L.; Xi, G.; Sun, J. Torque coordination control during mode transition for a series–parallel hybrid electric vehicle. IEEE Trans. Veh. Technol. 2012, 61, 2936–2949. [Google Scholar] [CrossRef]
- Yin, C.; Xie, Y.; Shi, D.; Wang, S.; Zhang, K.; Li, M. Sliding mode coordinated control of hybrid electric vehicle via finite-time control technique. ISA Trans. 2024, 146, 541–554. [Google Scholar] [CrossRef]
- Ding, J.; Jiao, X. Mode transition prescribed performance control of connected hybrid electric vehicles based on driver intention fuzzy prediction. Control Eng. Pract. 2024, 142, 105748. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Cai, Y.; Shi, D.; Wang, R. Mode transition control of a power-split hybrid electric vehicle based on improved extended state observer. IEEE Access 2020, 8, 207260–207274. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Sun, X.; Xiang, C.; Yang, C. Model-based double closed-loop coordinated control strategy for the electro-mechanical transmission system of heavy power-split HEVs. Automot. Innov. 2021, 4, 44–55. [Google Scholar] [CrossRef]
- Wang, J.; Cai, Y.; Chen, L.; Shi, D.; Wang, S.; Zhu, Z. Research on compound coordinated control for a power-split hybrid electric vehicle based on compensation of non-ideal communication network. IEEE Trans. Veh. Technol. 2020, 69, 14818–14833. [Google Scholar] [CrossRef]
- Xue, H.; Wang, X. Prescribed Performance Ship Tracking Control with a Novel Predefined-Time Performance Function. IET Intell. Transp. Syst. 2025, 19, e70014. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, K.; Jiang, B.; Ding, S.X. Fixed-time fault-tolerant formation control for heterogeneous multi-agent systems with parameter uncertainties and disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2121–2133. [Google Scholar] [CrossRef]
- Cui, G.; Yang, W.; Yu, J.; Li, Z.; Tao, C. Fixed-time prescribed performance adaptive trajectory tracking control for a QUAV. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 494–498. [Google Scholar] [CrossRef]
- Chen, X.; Gong, P. Transient and steady-state performance improvement of IM drives based on dual-torque model. Machines 2023, 11, 490. [Google Scholar] [CrossRef]
- Yu, L.; He, G.; Wang, X.; Zhao, S. Robust fixed-time sliding mode attitude control of tilt trirotor UAV in helicopter mode. IEEE Trans. Ind. Electron. 2021, 69, 10322–10332. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, S.; Yan, Y. Fixed-time extended state observer-based trajectory tracking and point stabilization control for marine surface vessels with uncertainties and disturbances. Ocean Eng. 2019, 186, 106109. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, C.; Wu, R.; Cui, N. Fixed-time extended state observer based non-singular fast terminal sliding mode control for a VTVL reusable launch vehicle. Aerosp. Sci. Technol. 2018, 82–83, 70–79. [Google Scholar] [CrossRef]
- Basin, M.; Yu, P.; Shtessel, Y. Finite-and fixed-time differentiators utilising HOSM techniques. IET Control Theory Appl. 2017, 11, 1144–1152. [Google Scholar] [CrossRef]
- Hu, J.; He, H.; Wang, Z.; Ji, S.; Duan, Z. A switched model predictive control with parametric weights-based mode transition strategy for a novel parallel hybrid electric vehicle. Control Eng. Pract. 2025, 155, 106161. [Google Scholar] [CrossRef]
- Wang, S.; Rong, X.; Shi, D.; Yin, C. Research on fixed-time robust control allocation of the mode transition for CPS-HEV considering actuator uncertainties. IEEE Trans. Transp. Electrif. 2025. [Google Scholar] [CrossRef]











| Parameters | Value |
|---|---|
| Vehicle mass m | 1525 kg |
| Air resistance coefficient CD | 0.31 |
| Air density ρ | 1.23 m3/kg |
| Frontal area A | 2.02 m2 |
| Rolling resistance coefficient f | 0.008 |
| The radius of wheel r | 0.317 m |
| The ratio of the final drive ifd | 3.269 |
| Characteristic parameter of PG1 and PG2 K1/K2 | 2.6/2.639 |
| Engine maximum power Pe | 73 kW |
| MG1 maximum power PMG1 | 23 kW |
| MG2 maximum power PMG2 | 60 kW |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| α1 | 0.1 | m11 | 1.1 |
| α2 | 0.1 | m21 | 0.3 |
| β1 | 0.1 | m31 | 1.1 |
| β2 | 0.1 | m41 | 0.5 |
| C11 | 0.1 | m12 | 1.1 |
| C21 | 0.07 | m22 | 0.5 |
| C12 | 0.1 | m32 | 1.1 |
| C22 | 0.1 | m42 | 0.5 |
| r1 | 0.5 | r1* | 0.5 |
| r2 | 0.6 | r2* | 0.6 |
| μ1 | 100 | γ1 | 200 |
| μ2 | 70 | γ2 | 100 |
| μ3 | 100 | γ3 | 200 |
| μ4 | 50 | γ4 | 80 |
| η1 | 2 | η2 | 0.5 |
| 0.7 | 1.3 | ||
| 0.9 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yang, H.; Zhang, F.; Liao, X.; Zuo, Y. Research on Mode Transition Control of Power-Split Hybrid Electric Vehicle Based on Fixed Time. Energies 2025, 18, 4438. https://doi.org/10.3390/en18164438
Zhang H, Yang H, Zhang F, Liao X, Zuo Y. Research on Mode Transition Control of Power-Split Hybrid Electric Vehicle Based on Fixed Time. Energies. 2025; 18(16):4438. https://doi.org/10.3390/en18164438
Chicago/Turabian StyleZhang, Hongdang, Hongtu Yang, Fengjiao Zhang, Xuhui Liao, and Yanyan Zuo. 2025. "Research on Mode Transition Control of Power-Split Hybrid Electric Vehicle Based on Fixed Time" Energies 18, no. 16: 4438. https://doi.org/10.3390/en18164438
APA StyleZhang, H., Yang, H., Zhang, F., Liao, X., & Zuo, Y. (2025). Research on Mode Transition Control of Power-Split Hybrid Electric Vehicle Based on Fixed Time. Energies, 18(16), 4438. https://doi.org/10.3390/en18164438





