Abstract
Meta-learning has demonstrated significant advantages in small-sample tasks and has attracted considerable attention in wind turbine fault diagnosis. However, due to extreme operating conditions and equipment aging, the monitoring data of wind turbines often contain false alarms or missed detections. This results in inaccurate fault sample labeling. In meta-learning, these erroneous labels not only fail to help models quickly adapt to new meta-test tasks, but they also interfere with learning for new tasks, which leads to “negative transfer” phenomena. To address this, this paper proposes a novel method called Online Soft-Labeled Meta-learning with Gaussian Prototype Networks (SL-GPN). During training, the method dynamically aggregates feature similarities across multiple tasks or samples to form online soft labels. They guide model training process and effectively solve small-sample bearing fault diagnosis challenges. Experimental tests on small-sample data under various operating conditions and error labels were carried out. The results show that the proposed method improves diagnostic accuracy in small-sample environments, reduces false alarm rates, and demonstrates excellent generalization performance.
1. Introduction
Wind energy is considered one of the fastest-growing fields in renewable energy and is crucial for improving environmental quality. Wind turbines are typically installed in remote and harsh environments. Therefore, improving the reliability of wind turbines has become increasingly important [1]. The pitch control system is an important execution device for wind turbine control and protection, which plays a crucial role in ensuring the safe, stable, and efficient operation of wind turbines [2]. Pitch bearings are one of the key components of wind turbines. Due to the harsh working environment, high operating loads, and long running time of wind turbines, pitch bearings are prone to failure and cause economic losses and even personal injuries [3]. According to statistics, the proportion of wind turbine downtime caused by pitch bearing failures is as high as 23.32%. Therefore, it is of great significance to develop accurate and reliable methods for fault warning and diagnosis in pitch systems [4].
Wind turbines typically operate under normal conditions. When a fault occurs, they need to be shut down or inspected, which makes fault samples in monitoring data relatively rare. Researchers urgently need to address the challenge of conducting mechanical fault detection and condition monitoring with scarce samples. Meta-learning methods, which can quickly learn new tasks using previously acquired knowledge, have become one of the solutions to the problem of fault diagnosis with small sample sizes. Feng et al. conducted a comprehensive investigation of deep meta-learning in the context of fault diagnosis from three perspectives: algorithms, applications, and future prospects. Furthermore, the authors identified existing challenges and discussed potential future directions for advancing research in this area [5]. Liu et al. proposed a novel one-shot fault diagnosis method for wind turbines based on an improved momentum contrastive learning framework, demonstrating superior performance compared to conventional models [6]. Hu et al. proposed a data simulation resampling algorithm to expand the training datasets and used fast Fourier transform for feature extraction; they then aligned data distributions across different domains, which significantly enhanced few-shot learning capability and cross-domain diagnostic performance [7]. Zhang et al. explored a prior knowledge-informed multi-task dynamic learning framework for few-shot machinery fault diagnosis, thereby improving the model’s adaptability and effectiveness in few-shot fault diagnosis scenarios [8]. Zheng et al. proposed a domain-discrepancy-guided contrastive feature learning method for few-shot industrial fault diagnosis under variable working conditions [9]. Zhang et al.’s proposed method leverages a limited amount of labeled data along with abundant unlabeled data, which employ consistency regularization at the feature level and data augmentation techniques to enhance the diagnostic performance of models in small-sample scenarios [10].
In recent years, meta-learning has played a positive role not only in solving small-sample problems but also in cross-domain fault diagnosis and imbalanced data processing. Zhang et al. proposed a data synthesis method for rolling bearing fault diagnosis, which improves the accuracy and robustness of imbalanced fault diagnosis by generating diverse and realistic fault samples [11]. Lin et al. investigated a generalized model-agnostic meta-learning approach for few-shot cross-domain fault diagnosis of bearings driven by heterogeneous signals, thereby enabling improved adaptability and generalization across different domains in bearing fault diagnosis tasks [12]. Pang et al. proposed a time-frequency supervised contrastive learning framework via pseudo-labeling for unsupervised domain adaptation in rolling bearing fault diagnosis under time-varying speeds [13]. Liu et al. addressed the challenge of few-shot learning under domain shift by proposing an attention contrastive calibrated Transformer for time-series fault diagnosis under sharp speed variation, which improves diagnostic performance in scenarios involving abrupt changes in rotational speed [14]. Meng et al.’s proposed a method aims to capture more comprehensive fault representations through multi-source feature fusion and enhance the model’s generalization and diagnostic accuracy by leveraging guided adversarial learning, thereby improving performance in complex and variable industrial scenarios [15]. Ye et al. proposed a novel cross-domain fault diagnosis method based on model-agnostic meta-learning embedded within an adaptive threshold network, thereby enhancing the model’s performance in cross-domain fault diagnosis tasks [16]. Rehman et al. comprehensively analyzed the effectiveness and limitations of various deep learning models, including convolutional neural networks and auto-encoders in fault classification tasks [17]. These studies mainly use meta-learning and data enhancement techniques to transform the original data and generate new and diverse samples so as to expand the size of the dataset. These models possess a learning capability to rapidly identify fault characteristics from limited samples. When faced with new fault diagnosis tasks, they can leverage this pre-trained generalization ability to accurately determine new fault types through minor adjustments using minimal annotated data. Essentially, this approach enhances the model’s learning efficiency and generalization capacity, thereby indirectly compensating for insufficient data volume.
The Gaussian Prototype Network (GPN) is an improved architecture based on the prototype network, which is often used in small-sample learning tasks. It has been widely used in image classification, mechanical fault diagnosis, and other fields. Its core is to introduce the Gaussian covariance matrix to more effectively represent data features and uncertainties. Xu et al. effectively addressed the challenge of limited data availability and improved classification accuracy, providing a new paradigm for mechanical fault diagnosis under scarce sample conditions [18]. Su et al. proposed a meta-learning-based method, reconstructing input data with an improved stacked denoising auto-encoder and integrating it with a regularized meta-learning algorithm, effectively addressing the challenges of limited data [19]. Sun et al. proposed an intelligent open set fault diagnosis method for rolling bearings based on prototype and reconstruction network integration, which judged the fault according to the correlation between reconstruction signal and input signal [20]. Hou et al. proposed an embedded enhanced Gaussian Prototype Network, which optimizes the training mechanism from the perspective of meta-learning and builds prototypes for untrained categories through the Gaussian covariance matrix, and it maintain high robustness under small sample conditions [21]. Thus, the Gaussian Prototype Network can solve the problem of small-sample fault diagnosis. The Gaussian covariance matrix is mainly introduced to improve the representation ability and classification performance of the model on samples. The covariance matrix is used to represent the confidence interval of the encoded vector, reflecting the quality of each sample and the prediction ability of the model.
However, monitoring data in the field of wind power mainly uses threshold or algorithm fitting to report abnormal states of wind turbines and label monitoring data samples. In extreme working conditions such as wind turbine start stop, typhoon, rain, and snow, monitoring data may suddenly change. This results in abnormal situations beyond the threshold or fitting values, which are marked as false positive when there is no fault. At the same time, the wind turbine sensors may experience aging, drift, decreased sensitivity, or physical damage, which can cause distortion of the collected signal or result in ineffective collection of fault characteristics. If the signal amplitude does not reach the alarm threshold, the system will misjudge it as “no fault”, that is, a false-negative phenomenon. All of these make the fault sample labels inaccurate. Overall, the scarcity and labeling errors of wind power monitoring fault data affect the generalization ability of meta-learning. To this end, we propose a Gaussian Prototype Network based on online soft labels (SL-GPN). This model first inputs the original vibration signal samples of the bearing into an embedding space and then calculates the mean vector of the embedded vectors and simultaneously obtains a Gaussian covariance matrix that indicates the category position of the embedded vector. During the training process, the model dynamically aggregates the feature similarities of multiple task covariance matrices to form online soft labels. When soft-label parameters positively influence model training, SL-GPN enhances current parameter settings and the training process. Conversely, if existing soft-label configurations hinder model progress, the system automatically adjusts these parameters to guide the training process effectively. These soft labels guide the training process, effectively addressing the issue of over fitting caused by labeling errors. Experiments have shown that under different operating conditions, when sample labeling errors occur, the proposed method can improve the accuracy of bearing fault diagnosis in small sample scenarios, reduce the false alarm rate of fault diagnosis, and demonstrate good generalization capabilities.
The structure of the remainder of this paper is as follows: Section 2 introduces the fundamental concepts of meta-learning and Gaussian process networks. Section 3 introduces a new model for fault diagnosis of wind turbine pitch bearings, named SL-GPN. Section 4 trains and tests the proposed model using data from on-site wind turbines and analyzes the results. Section 5 provides a summary of the paper.
2. Online Soft-Label Meta-Learning
2.1. Meta-Learning
Meta-learning, referred to as “learning how to learn”, simulates the ability of organisms to rapidly acquire new knowledge by using existing prior knowledge. In the face of only a few labeled samples, this learning mechanism can still maintain the high accuracy of the model by a few-shot and multi-task training approach. The main steps of the meta-learning are illustrated in Figure 1.
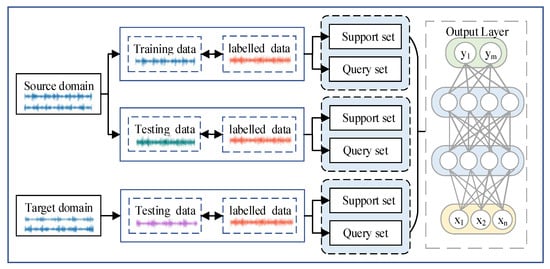
Figure 1.
Process of meta-learning.
Meta-learning is divided into two steps: meta-training and meta-testing. Each step is constructed based on a small number of sample task units. These tasks contain a support set S and query set Q. During the meta-learning phase, a series of training task sets are divided, where represents the number of classification tasks. For any given classification task , it includes a support set S and query set Q, which defines an N-way K-shot task. Specifically, N categories are randomly selected from the meta-learning dataset , and K samples are randomly chosen from each selected category to form the support set . Then, the query set is formed by extracting one sample from each of the N classes, and . For each task, the loss is obtained based on and During the training phase of meta-learning, the goal is to minimize the loss generated by all tasks.
In meta-learning tasks, it commonly includes a dataset with a total sample size of m, which will then be divided into a training set and test set :
In Equations (1) and (2), the number of samples in the training set is t. The model parameter is optimized by the training set . Then, this parameter is applied to the test set data for evaluating the performance and effect of the model. This process can be summarized as a function with parameter as the variable:
In Equations (3) and (4), L is defined as the loss function that measures the gap between the model’s predicted output and the actual label y of the sample. Additionally, the parameters’ update of the model depends on the optimization process of this loss function.
In the testing phase of meta-learning, the meta-test dataset is used to update and fine-tune the model parameters, and . The above steps are also followed to evaluate the effect of the model on , as shown in Equation (5):
Based on meta-learning, the central concept of the deep neural network is to decompose the model’s training process into two levels of optimization processes, namely, an internal one and external one. In internal optimization, the model uses strategies such as the gradient descent method to learn specific tasks and master prior knowledge. In external optimization, the focus is to improve the learning effect of the model across tasks, and the goal is to determine an optimal set of initial model parameters . Therefore, during the model testing phase, only a few samples are needed to fine-tune , which enable one to quickly adapt the model to the task and achieve a high classification accuracy.
2.2. Online Soft-Label Algorithm
In meta-learning, the accuracy of sample labels directly affects the computed loss, while the precision of the loss value influences the model’s generalization ability. In practical engineering scenarios, training datasets often contain a small number of mislabeled samples, which can lead to significant functional loss deviations in few-shot learning settings. This results in unstable model training and ultimately degrades prediction performance. To address this issue, we propose an online soft-label strategy to guide model training. The core idea is to assume the presence of potential label noise during training, thereby preventing the model from over-relying on the provided labels of training samples.
In training datasets , the samples from K different classes, denotes the raw vibration signal sample from the bearing, and represents its corresponding label. By utilizing the softmax layer, the model can generate an intermediate class prediction for each input sample . We represent the distribution of hard labels as d, where and . Accordingly, the loss for sample can be computed as shown in Equation (6):
Soft labels are commonly used for classification tasks to represent the probability distribution over classes. For a sample belonging to class , its class probability distribution is defined as shown in Equation (7), where is a smoothing parameter, typically set to 0.1 during training. This soft labeling strategy is designed under the assumption that the non-target classes share equal probability:
During the meta-learning training phase, given an input vibration signal , if the model’s predicted probability aligns with the true label , the soft label is updated based on the predicted probability . Then, the prediction result from the previous epoch is used as the soft label to supervise the current training epoch. Let the number of training epochs be T and define the set , where denotes the soft labels generated at the t-th training epoch. Each is a K × K matrix, where each row of the matrix represents a class-wise soft-label distribution. Given a sample , the soft-label distribution from the previous epoch is used to guide the model training. As shown in Equation (8), the training loss for sample , guided by , is calculated as
Then, both soft and hard labels are used jointly to update the model parameters. The final joint loss function is defined in Equation (9).
In the formula, is the variable used to balance and . The soft label can be updated using the model’s predicted probabilities during the t-th training iteration, and then the current label is used to guide the t + 1-th training iteration. At the beginning of the t-th iteration, the soft-label matrix is initialized to a zero matrix. If the input signal sample was correctly predicted in the previous round, the probability obtained is used to update the column of S, with the specific calculation process shown in Equation (10):
In the equation, k is the index of . After the current iteration, Equation (11) is used to normalize the column:
The current distribution can then be obtained. Summarizing the above, the soft-label matrix obtained in the t + 1-th iteration is
Here, N represents the number of samples accurately classified by the model during the training process, and indicates the probability that sample belongs to category k in the t−1-th training iteration. Therefore, as shown in Equation (13), the soft-label loss is rewritten as
2.3. Gaussian Prototype Network
The Gaussian Prototypical Network is a model designed for few-shot learning. It maps input data into embedding vectors while simultaneously generating an estimate of quality and a confidence region around the embedding, which is characterized by a Gaussian covariance matrix. As illustrated in Figure 2, P1, P2, P3, and P4 represent different categories of prototypes, each with a set of feature distributions. In the figure, circles of the same color surrounded by stars represent the prototype representations of the features for each category. Q1 and Q2 are the query samples to be classified. According to the distance between the query samples and each prototype, the category embedded samples are formed to determine the category to which they belong.
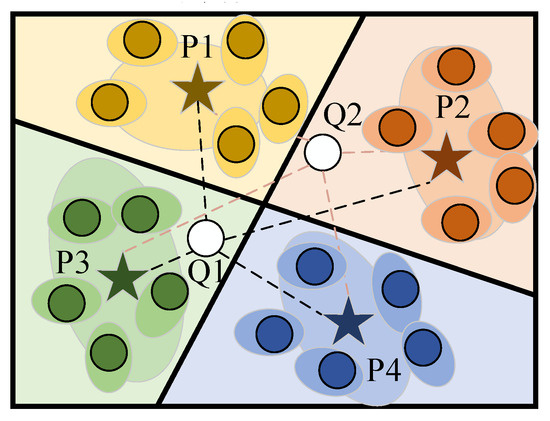
Figure 2.
Process of Gaussian Prototype Network.
The Gaussian Prototypical Network maps input samples into M-dimensional embedding vectors using an embedding network. The specific computation process is defined in Equation (14).
In the formula, represents the weight parameters of the GPN, variable denotes the input samples to the network, H and W represent the height and width of the input samples, respectively, and C represents the number of channels of the input. represents the embedded vector, and M represents the dimensional of the embedded vector .
During the training phase, the Gaussian Prototype Network uses the embedding network to transform the input samples into two core components: one is the embedded vector representing the sample features, and the other is the matrix atoms that form the covariance matrix, with the specific calculation process shown in Equation (15):
In the equation, represents the raw matrix atoms, and represents the matrix atoms’ dimensionality. By passing through the matrix atoms, the Gaussian covariance matrix is calculated.
The Gaussian Prototype Network incorporates the concept of Gaussian covariance matrices when defining the prototype. In this model architecture, the computation of the Gaussian prototype for each category is denoted as :
Here, represents the i-th sample in the support set that belongs to the k-th category, represents the Gaussian covariance matrix output corresponding to the sample, and ∘ denotes the dot product operation. Next, the Euclidean distances between the Gaussian prototypes of each class and the feature representations of the query samples are further computed.
In the equation, denotes the Gaussian prototype corresponding to the class, and represents the embedding vector of the j-th query sample. denotes the summed Gaussian covariance matrix of all samples belonging to class k:
By measuring the Euclidean distance of the sample features to the Gaussian prototypes of different categories, the predicted labels for the samples in the query set are obtained. The label is the category represented by the Gaussian prototype closest to the sample. The Gaussian Prototype Network implements this functionality using a distance-based softmax function. Specifically, given an input sample in the query set and its true label , we can calculate the probability that is classified into the k-th category:
In this study, the cross-entropy function is employed as the loss function. The loss is computed based on the probability of correctly predicting the labels of signal samples. The loss function of the classifier is defined in Equation (20):
Finally, the model parameters are updated using the Adam gradient optimization method to minimize the loss function. During the testing phase on the target domain, a task generation algorithm is employed to randomly select N classes from the test dataset. For each selected class, K samples are drawn to form the support set for the current task, while the remaining samples constitute the query set. The embedding network is then used to construct Gaussian prototypes from the support set samples. Classification is performed by computing the Euclidean distances between the query sample features and the corresponding Gaussian prototypes.
3. Fault Diagnosis Model with SL-GPN
For the small-sample fault diagnosis method based on the SL-GPN model proposed in this paper, the main idea is to construct meta-learning tasks using raw bearing vibration signals collected under varying operating conditions and optimize its initialization parameters by leveraging multiple known fault classification tasks across different conditions, thereby acquiring optimal prior knowledge. Additionally, an online soft-label strategy is incorporated during training to dynamically generate soft labels based on the similarity among samples, which guides the model’s training and parameter updates. This enables the SL-GPN model to obtain optimal prior knowledge with only a limited number of samples from variable operating conditions while preventing overconfidence in the training process. The diagnostic procedure consists of five stages: data acquisition, meta-task partitioning, model construction, meta-training, and meta-testing. The overall fault diagnosis framework is depicted in Figure 3.
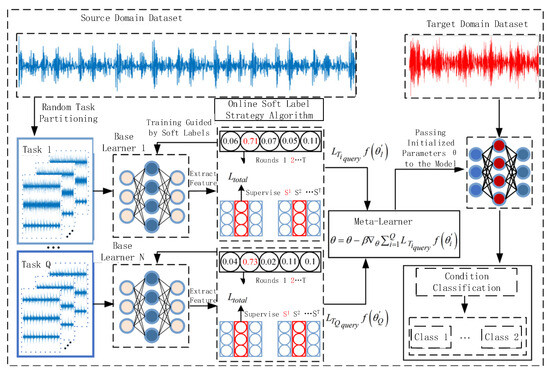
Figure 3.
Process of bearing fault diagnosis method based on SL-GPN model.
- (1)
- Data Acquisition: Raw vibration signals of rolling bearings under different operating conditions are collected using sensors, forming the dataset D.
- (2)
- Meta-Learning Task Partitioning: The dataset D is divided into training datasets and testing datasets. The training dataset includes support set and query set, and, similarly, the testing set also comprises support sets and query sets.
- (3)
- GPN Model Construction: A few-shot mechanical fault diagnosis model based on the Gaussian Prototype Network (GPN) is constructed. This model mainly consists of an embedding module, a distance metric module, and a classification module.
- (4)
- Meta-Training Phase: Support and query samples from the training set are fed into the model. During multi-task training, the model is optimized via an online soft-label strategy, where the model parameters and prior knowledge are obtained by minimizing the training loss computed between predicted labels and ground truth labels.
- (5)
- Meta-Testing Phase: Support and query samples from the testing set are input into the network trained in the previous phase. Gaussian prototypes for each class in the testing set are obtained, and classification is performed by calculating the Euclidean distance between sample features and the corresponding Gaussian prototypes.
The SL-GPN employs a convolutional neural network as the feature extractor to obtain sample representations. During the meta-training process, multiple batches of fault diagnosis tasks are trained in a multi-task manner. The model maps the input samples into a nonlinear feature space, and the mapping function is defined as shown in Equation (21):
In the formula, represents the feature mapping of the vibration signal with neural network parameters , and b denotes the bias vector. In this section, parameters and b are collectively represented as θ, and ReLU is used as the activation function. The SL-GPN is composed of multiple convolutional layers, with each convolutional layer’s output represented as , where represents the model parameters. When the model adapts to a new task the parameters for each task will become , which are updated using a gradient descent method, as specifically calculated in Equation (22):
In the equation, represents the learning rate of the base learner, and is the gradient of the loss on the support set of tasks . After obtaining Q parameters θ where , the loss of the query set is calculated as shown in Equation (23):
In this study, the loss function of the base learner is a cross-entropy loss optimized by the online soft-label strategy. Specifically, soft labels generated by the strategy are used to replace hard labels for guiding the model training process. The parameters of each base learner are trained by optimizing the classification performance within each training episode and can be computed as follows:
The meta-learner is primarily responsible for capturing the commonalities across different tasks and providing the initial model parameters θ for the base learner. Subsequently, the parameters θ are updated based on the performance of the base learner, which can be described as follows:
In the equation, f ( ) represents the mapping function of different task parameters . The update of the parameters θ is as follows, where β is the learning rate.
In the target-domain testing, the model parameters can be fine-tuned using the support set of the meta-testing set in order to identify model parameters that can achieve accurate fault classification on the corresponding query set.
4. Experimental Validation
4.1. Dataset Introduction and Experimental Setup
To verify the fault diagnosis performance of the SL-GPN model under complex operating conditions, experiments were conducted using the rolling bearing datasets provided by Case Western Reserve University (CWRU). This dataset was collected from the bearing fault test bench illustrated in Figure 4. The experimental setup primarily consists of a motor, drive-end bearing, fan-end bearing, torque sensor, and dynamo meter. By applying loads ranging from 0 to 3 horsepower (HP), motor speeds between 1797 rpm and 1730 rpm were simulated to generate bearing faults on the inner race, outer race, and rolling elements of both the drive-end and fan-end bearings. The fault diameters include 0.007 inch, 0.014 inch, and 0.021 inch. The data acquisition sampling frequency is 12 kHz.

Figure 4.
CWRU bearing test bench.
In the experiments, the raw vibration signals were collected from the drive-end bearing. Each sample consists of 1024 data points, with a sliding window stride of 256. The detailed datasets partitioning is presented in Table 1. Specifically, 0 HP, 1 HP, 2 HP, and 3 HP represent four different load conditions. The bearing fault types include inner race fault, outer race fault, and rolling element fault, each with three fault diameters: 0.007 inch, 0.014 inch, and 0.021 inch. For each load condition, the datasets contain 10 training samples and 200 testing samples per fault class.

Table 1.
Experimental dataset description.
Since the samples are one-dimensional vibration signals, a one-dimensional convolutional neural network (1D-CNN) was employed as the embedding module in the Gaussian Prototype Network. In the experiment, each sample was constructed from the original signal by sliding window extraction. Each sample contains 1024 data points with a sliding window step size of 256. For every layer, the number of convolutional kernels determines the feature dimensionality of the layer output and reflects the model’s focus on different features. For the shallow convolutional layers, basic features such as local fluctuations are extracted in the time-domain waveform. So, the model typically uses fewer kernels (set to 32) to avoid excessive redundant information. For the deep convolutional layers near the output layer, it processes higher-order abstract features like fault pattern combinations. The number of convolution kernels should be increased to 128 and 256, respectively, to accommodate more complex feature representations. In general, the entire network structure increases by two times from shallow to deep (32→64→128→256) to balance feature richness and computing cost.
As for the size of the convolution kernel, its size should match the feature scale of the data so as to extract the local features of the sample. Since the sample size in this paper is 1 × 1024, the shallow convolution kernel size is selected to be a larger size (1 × 9) to capture global features or a wide range of correlation information. Then, the size of the convolution kernel is reduced layer by layer to extract the detailed features in the signal. Therefore, the size of the convolution kernel is 1 × 9, 1 × 6, 1 × 4, and 1 × 2 successively. In this way, the detailed features are extracted and stacked instead of large convolution kernels so as to improve the feature extraction capability while reducing the parameters.
The detailed parameters of the network are shown in Table 2. The network consists of four convolutional layers, each followed by a corresponding pooling layer. Conv1 uses a large kernel of size 1 × 10 to extract high-level signal features and reduce the loss of informative patterns. Other convolutional layers use smaller kernels of sizes 1 × 6 and 1 × 4, aiming to capture local features while reducing the number of network parameters and computational complexity. Each convolutional layer output is processed using Batch Normalization (BN) to accelerate training and mitigate the risk of gradient explosion during optimization. In the experiment, both the support set and query set contained five samples. For the test set, the support set was selected with 1, 3, 5, 10, and 20 samples, respectively, meaning the training set used 6, 8, 10, 15, and 25 samples per category. The query set followed the same configuration as the support set. The initial coefficient for soft labels was set to 0.1. The ReLU function is applied as the nonlinear activation function. To preserve essential feature information while reducing computational load and parameter count, max pooling is adopted in all pooling layers. The initial learning rate of the model is set to 0.001. A total of 30,000 training episodes are conducted, and the network parameters and structure are optimized using the Adam optimizer. The learning rate is decayed by a factor of 0.5 every 5000 episodes. After training, the test samples are fed into the trained fault diagnosis model, and the average result over 10 runs is reported as the final performance. During both the training and testing phases, the few-shot learning tasks are constructed following the N-way K-shot setting.

Table 2.
Embed network parameters.
To validate the effectiveness of the proposed method, several classical few-shot learning approaches are selected for comparison. First, we compare with a conventional pretraining–fine-tuning transfer learning algorithm (CNN-FT) to demonstrate the advantages of meta-learning. Second, we compare with two representative metric-based meta-learning algorithms: the Prototypical Network (ProtoNet) and the Relation Network (RelationNet), as well as a Gaussian Prototype Network based on soft labels (SL-GPN), to further evaluate the performance of the proposed approach. In addition, Meta-Stochastic Gradient Descent (Meta-SGD) is an adaptive optimizer that integrates meta-learning concepts, dynamically adjusting learning rates through mapping historical gradient information. Model-Agnostic Meta-Learning (MAML-CNN), a model-agnostic framework, enables CNNs to rapidly adapt to new tasks and data distributions. For the Almost No Inner Loop (ANIL-CNN) model, a variant of model-agnostic meta-learning, it freezes the feature extraction layer and only updates parameters such as the classifier in the last layer.
In order to ensure the reliability and comparability of the experimental results, all comparison methods adopt the backbone network architecture in Table 2. This can eliminate the interference caused by differences in the network infrastructure. Both the hierarchical design of the feature extraction module and the configuration of the convolution kernel size and number, as well as the selection of the pooling method and activation function, are strictly consistent. Through this control variable experimental design, it can be ensured that the final observed performance differences are only due to the core logic of the algorithm, such as meta-learning strategy and parameter update mechanism, rather than the advantages and disadvantages of the network architecture itself, thus providing a solid foundation for the verification of the effectiveness of the method. At the same time, considering the random initialization of neural network parameters, it may have a significant impact on the model training process and final performance. This study conducted ten independent training and testing sessions for each comparative experiment. In each iteration, the model’s initial parameters and data partitioning random seeds were reset to cover a broader range of random variable distributions. The final evaluation metric was calculated as the average of these ten experiments, which maximizes the smoothing effect of random errors and brings experimental data closer to the model’s true performance level, thereby enhancing the statistical significance and persuasiveness of the conclusions.
4.2. Experiments with Different Pseudo-Label Quantities
In order to fully verify the practical effectiveness and robustness of the proposed method in the case of a label error, this study selects the vibration signal under the 1 HP load condition in Table 1 as the core experimental dataset. The reason for selecting this dataset is that the mechanical operating state under 1 HP load is typical and representative. Its vibration signals not only contain the stable characteristics of normal operation but also cover various common and critical fault types such as inner ring failure and outer ring failure, which can comprehensively simulate the possible fault modes in actual industrial scenarios.
Under the 1 HP load condition, the composition of the dataset mainly includes ten kinds of faults and health types such as normal state, inner circle faults, and outer circle faults. Each type is equipped with 10 training samples and 200 test samples, that is, each group of experiments contains 10 categories of samples and a total of 100 training samples and 2000 test samples. This sample size setting not only ensures that there is enough basic data to support model learning during the training process but also ensures the accuracy of evaluation on the generalization ability of the model through a large proportion of test samples.
In order to systematically explore the influence of label error ratio on model performance, four groups of control experiments were designed to build a pseudo-label scenario by tampering with the labels of the training samples to different degrees. For the first group of experiments, three samples are randomly selected from 10 training samples of each category to tamper with their labels (that is, incorrectly label them as other categories) so that the proportion of pseudo-labels reaches 30%. For the second experiment, each category was altered with two training samples’ labels, maintaining a 20% pseudo-label ratio. For the third experiment, each category was modified with only one training sample’s label, reducing the pseudo-label ratio to 10%. For the fourth experiment, no labels were altered, keeping them in their original state with a 0% pseudo-label ratio as the baseline control. This gradient-based labeling error ratio adjustment allows clear tracking of model performance trends with varying label contamination levels. Table 3 shows the experimental results with different numbers of pseudo-labels.

Table 3.
Test accuracy with different pseudo-label quantities.
As shown in Table 3, CNN-FT achieves 33.63% accuracy when pseudo-labels account for 30%; this rises to 41.25% at 20%, reaches 52.81% at 10%, and stands at 78.36% when no labels are used. The performance shows a gradual improvement as the proportion of pseudo-labels decreases, though the overall performance remains relatively weak. For ProtoNet, when the proportion of pseudo-labels was 30%, the result was 45.12%; when it was 20%, it was 56.38%; when it was 10%, it was 68.75%; and when it was 0%, it was 89.21%. The performance showed a steady upward trend, and the performance under each proportion was better than that of CNN-FT. For RelationshipNet, the results were 42.35% at the 30% pseudo-label ratio, 53.12% at 20%, 65.47% at 10%, and 86.58% at 0%. Its performance was similar to ProtoNet but slightly lower. For Meta-SGD, when the proportion of pseudo-labels was 30%, the result was 51.28%; when it was 20%, it was 63.57%; when it was 10%, it was 75.32%; and when it was 0%, it was 90.15%. The performance under each proportion of pseudo-labels was better than the previous three models, demonstrating good anti-interference capability. For MAML-CNN, when the proportion of pseudo-labels was 30%, the result was 55.63%; 68.42% at 20%; 79.86% at 10%; and 92.34% at 0%. Its performance outperforms Meta-SGD, demonstrating stronger stability under label errors. For ANIL-CNN, at 30% pseudo-labels, the result was 53.27%; 65.89% at 20%; 77.63% at 10%; and 91.08% at 0%. While slightly inferior to MAML-CNN, it maintained a relatively high overall performance. For SL-GPN, under 30% pseudo-labels, the result was 78.52%; 85.36% at 20%; 92.17% at 10%; and it reached 99.80% at 0%. This model outperformed all other models across all pseudo-label proportions, achieving near-perfect performance even at 0% and maintaining high performance even with 30% pseudo-labels, demonstrating significantly better anti-interference capability than other models. It can be clearly seen from these data that SL-GPN shows strong robustness in dealing with the problem of label errors, while the performance of other models is generally greatly affected by the proportion of pseudo-labels, and the gap between different models presents a certain regularity under different proportions of pseudo-labels.
Figure 5 shows the F1 index bar chart of each model under different pseudo-labels. Blue represents the index with 30% pseudo-labels, orange represents the index with 20% pseudo-labels, gray represents the index with 10% pseudo-labels, and yellow represents the index with 0% pseudo-labels.
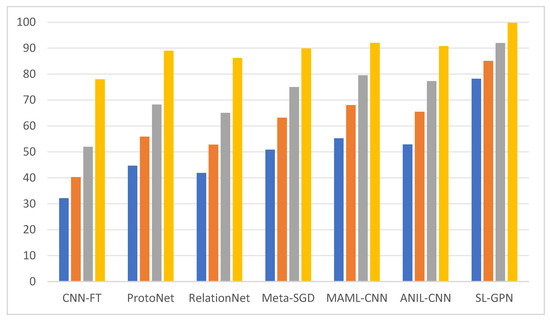
Figure 5.
The F1 index bar chart of each model under different pseudo-labels.
Under the four pseudo-labels, the column heights of CNN-FT are 32.15%, 40.32%, 51.98%, and 77.95%, respectively. The overall trend and relative position are similar to the performance of this model in the recall rate bar chart, slightly higher than the recall rate of the same model with the same proportion. The column heights of ProtoNet are 44.68%, 55.87%, 68.21%, and 88.96%, respectively, which are all higher than the recall rate of the same model, and the relative positions in each model are consistent with the recall rate bar chart. The Meta-SGD model demonstrates column heights of 41.89%, 52.78%, 65.03%, and 86.21%; it is slightly higher than the recall rate of its counterpart model and consistently lower than ProtoNet’s F1 index at corresponding proportions. Its Meta-SGD indices show 50.87%, 63.12%, 74.98%, and 89.87%, respectively, and it surpasses the recall rate of its model. Notably, when pseudo-label proportions were 30% and 20%, the gap with MAML-CNN became more pronounced. MAML-CNN’s indices reached 55.21%, 68.03%, 79.52%, and 92.05%, respectively, outperforming both Meta-SGD and ANIL-CNN across all proportions while maintaining higher recall rates. The ANIL-CNN model showed column heights of 52.86%, 65.47%, 77.28%, and 90.76%, slightly lower than the F1 index of MAML-CNN. Its overall performance trend aligns with the model’s performance in the recall rate bar chart. The SL-GPN model achieved index values of 78.21%, 85.07%, 91.93%, and 99.76%, respectively, all representing the highest scores within their respective ratio ranges. Notably, its recall rates showed minimal deviation from those of the same model, demonstrating excellent comprehensive performance.
4.3. Different Sample Size Experiments
To verify the effectiveness of the proposed method, we conducted experiments by adjusting the sample size of the support set. As shown in Table 4, there were five groups of experiments, each containing samples from ten categories. Each time, one training sample label was randomly altered. All experimental comparisons followed the unified model framework described earlier. Each experiment was run 10 times, with the average of 10 runs serving as the final result. Table 4 presents the experimental outcomes of seven models across five different sample sizes. The initial coefficient for soft labels was set to 0.1. The ReLU function was applied as the nonlinear activation function. To preserve essential feature information while reducing the computational load and parameter count, max pooling was adopted in all pooling layers. The initial learning rate of the model was set to 0.001. A total of 30,000 training episodes were conducted, and the network parameters and structure were optimized using the Adam optimizer. The learning rate is decayed by a factor of 0.5 every 5000 episodes.

Table 4.
Experimental results of samples from different support sets of a pseudo-label.
As shown in the table, under the 20-shot experimental setting, the total number of training samples reaches 200, and all methods achieve classification accuracies above 97%. Notably, the SL-GPN model attains an accuracy of 99.95%, meeting the accuracy requirements for intelligent diagnosis. In the 10-shot experiment, where the total training samples reduce to 100, all methods maintain high accuracy, and only the CNN-FT method shows a 2% decrease in accuracy, while the accuracy of the other three meta-learning-based methods remains above 97%. In the five-shot experiment, where the total training samples reduce to 50, all methods experience varying degrees of accuracy degradation. The CNN-FT method shows a more pronounced decrease, while the SL-GPN method maintains accuracy above 99%. In the three-shot setting, with only 30 training samples, the accuracies of CNN-FT, ProtoNet, and RelationNet decline to 94.65% and 97.23%, respectively, whereas the SL-GPN model still maintains an accuracy exceeding 99%. When the sample size further decreases to one-shot, using only 10 training samples in total, the CNN-FT accuracy drops to 89.63%, the ProtoNet and RelationNet accuracies remain around 95%, and the SL-GPN model still achieves 99.13%. These results demonstrate the effectiveness of the proposed model for bearing fault diagnosis under extremely limited sample conditions. Meta-SGD obtained the following results: 96.23% at 1-shot, 96.25% at 3-shot, 97.35% at 5-shot, 98.25% at 10-shot, and 98.75% at 20-shot. The metrics progressively improved with increasing shot counts. MAML-CNN obtained the following results: 96.38% at 1-shot, 96.83% at 3-shot, 98.28% at 5-shot, 98.36% at 10-shot, and 99.64% at 20-shot, showing significant growth in later stages with outstanding performance at 20-shot. ANIL-CNN obtained the following results: 95.52% at 1-shot, 96.75% at 3-shot, 97.75% at 5-shot, 97.58% at 10-shot, and 98.55% at 20-shot. The data showed some fluctuations but maintained an upward trend overall.
To evaluate the performance of the SL-GPN model under few-shot conditions, we plotted the training accuracy curves, as shown in Figure 6. The blue curve represents the change in accuracy over training iterations under the 10-way one-shot setting, while the red curve corresponds to the 10-way five-shot setting. In both experiments, the model achieves satisfactory performance after approximately 400 training iterations. Specifically, the blue curve shows a gradual increase from a low accuracy level, eventually stabilizing with some fluctuations in the later stages. The red curve exhibits generally higher accuracy, faster convergence, and greater stability during the later training phase. At around 200 training iterations, a notable difference between the two settings is observed: the red curve, benefiting from more abundant samples, attains significantly higher accuracy with reduced fluctuations compared to the blue curve, demonstrating the impact of the sample size on the training dynamics of the few-shot learning models.
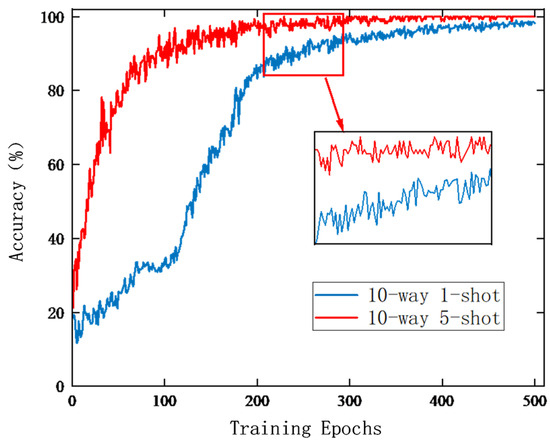
Figure 6.
Convergence of SL-GPN diagnostic accuracy during training process.
4.4. Model Generalization Experiment Under Variable Working Conditions
During the operation of rotating machinery, bearings are typically subjected to variable working conditions. Variations in load induce changes in the amplitude and impulse intervals of the bearing vibration signals, resulting in dynamic variations of fault characteristics. Relevant studies have demonstrated that fault data distributions differ across varying operating conditions, which leads to degraded diagnostic performance of models when applied to unseen conditions.
This experimental series primarily investigates the performance of the SL-GPN model under variable load conditions. Using all data from Table 1, we constructed a 10 × 10 training dataset and a 200 × 10 test set. By randomly altering labels in one sample within the training set, six variation experiments were conducted to evaluate the impact of pseudo-labeling on the model’s performance. To simulate practical scenarios where the distributions of training and testing samples differ, six cross-domain scenarios were designed to validate the effectiveness of the proposed method under few-shot conditions, as shown in Table 5.

Table 5.
Six different cross-domain scene settings.
Scenario 1 uses bearing data under 0 HP load for source-domain training and bearing data under 1 HP load for target-domain testing. Scenario 2 employs 0 HP load data as the source domain and 2 HP load data as the target domain. Scenario 3 uses 1 HP load data for the source domain and 0 HP load data for the target domain. Scenario 4 uses 1 HP load data as the source domain and 2 HP load data as the target domain. Scenario 5 takes 2 HP load data as the source domain and 0 HP load data as the target domain. Scenario 6 uses 2 HP load data for the source domain and 1 HP load data for the target domain. From the source-domain data, batches of 10-way five-shot meta-learning tasks were constructed to train the classification model, which was then evaluated on the target-domain data for cross-domain testing. The experimental results are presented in Figure 7.
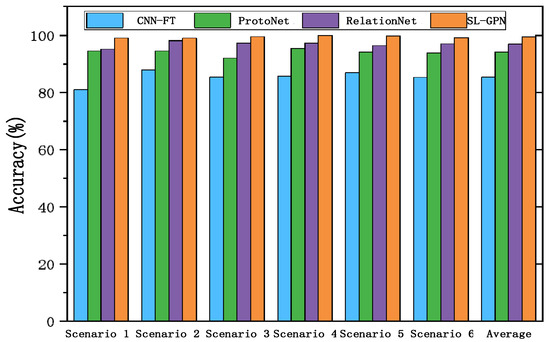
Figure 7.
Cross-domain experimental results.
In six scenarios, the accuracy rates of CNN-FT were 81.00%, 87.90%, 85.34%, 85.60%, 86.83%, and 85.28%, with an average of 85.33%. ProtoNet achieved 94.51%, 94.55%, 91.95%, 95.50%, 94.15%, and 93.75%, with an average of 94.07%. RelationNet reached 95.17%, 98.13%, 97.30%, 97.26%, 96.35%, and 96.96%, with an average of 96.86%. SL-GPN had an accuracy rate of 98.97%, 98.95%, 99.55%, 99.97%, 99.85%, and 99.14%, with an average of 99.41%. Among them, the average accuracy difference between CNN-FT and SL-GPN is 14.08%, indicating that in the iterative process of small-sample cross-domain learning technology, it is challenging to improve accuracy solely through pre-training and fine-tuning of model architectures. Both ProtoNet (94.07%) and RelationNet (96.86%) are classic small-sample methods, with an average difference of 2.79%. This is because RelationNet introduces feature relationship modeling, which makes it more adaptable to the distribution differences of cross-domain data compared to ProtoNet’s simple prototype clustering. SL-GPN achieves nearly 100% accuracy across multiple scenarios (for example, Scenario 4 reaches 99.97%), demonstrating its ability to efficiently utilize a very small amount of labeled data, making it particularly suitable for real-world scenarios with scarce defect samples, such as industrial fault diagnosis. In the six experiments, the accuracy of CNN-FT fluctuated by 6.90% (from 81.00% to 87.90%). This is because traditional fine-tuning relies on pre-trained knowledge from the source domain, while the sample distribution and fault characteristics in cross-domain scenarios vary. Traditional meta-learning models struggle to quickly adapt to these changes, leading to significant fluctuations in performance. In contrast, the fluctuation of SL-GPN was only 0.83% (from 98.95% to 99.97%), indicating that the model dynamically updates its label values during training, guiding it to adapt promptly to changes in sample characteristics. This significantly reduces the impact of scenario changes on predictions, making it notably more robust than other methods.
To further demonstrate the model’s performance, we selected the experimental results from Scenario 6 and constructed classification confusion matrices for four models to illustrate the alignment between predicted and actual labels. As shown in Figure 8, the x-axis represents the predicted label, while the y-axis represents the actual label. The cell values (or color intensity, corresponding to the color scale on the right) indicate the proportion of actual labels that were correctly predicted by the model.
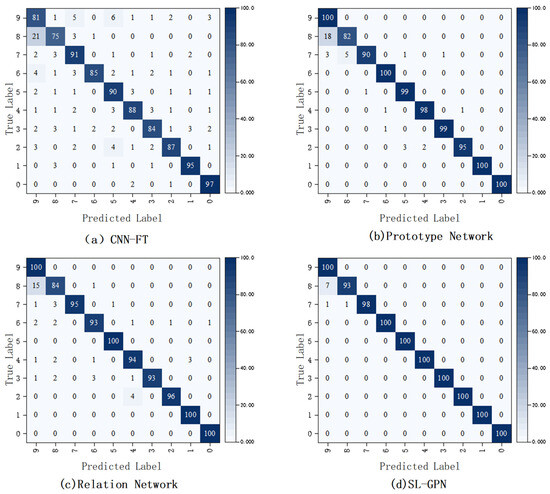
Figure 8.
Confusion matrix experiment in Scenario 6.
In Figure 8a, the diagonal values of CNN-FT are low, with only 81 instances where the true label 0 is correctly predicted as 0. In contrast, there are many off-diagonal values, with 21 instances where the true label 1 is incorrectly predicted as 0. This indicates that the model has more classification errors and weaker performance. In Figure 8b, the diagonal values of the Prototype Network are relatively high, mostly between 90 and 100, but there are still some misclassifications, such as five instances where the true label 1 is incorrectly predicted as 2. This suggests that the model’s performance is slightly better than that of CNN-FT. In Figure 8c, the diagonal values of the Relation Network have further improved, reaching up to 100 in some cases, with fewer misclassifications, for example, only 15 instances where the true label 7 is incorrectly predicted as 8, indicating more accurate classification. In Figure 8d, the diagonal values of the SL-GPN are mostly 100, with only one instance where the true label 8 is incorrectly predicted as 7. This indicates that the model has a lower misclassification rate and the best classification performance.
CNN-FT refines convolutional neural networks by using pre-trained weights to adapt to new tasks. However, when the scenario becomes more complex, such as with significant differences in cross-domain data, it is difficult to quickly adapt, which can affect accuracy. ProtoNet relies on prototype feature classification, while RelationNet focuses on learning feature relationships. SL-GPN offers superior cross-domain feature alignment and a small-sample learning mechanism, making it more robust to changes in the scenario. Advanced models like SL-GPN, after being optimized, exhibit strong generalization in cross-domain and small-sample scenarios. They can still stably extract effective features even when the data distribution varies across different scenarios. In contrast, traditional or basic models have weaker generalization capabilities, and any shift in the data distribution can lead to fluctuations in accuracy. However, SL-GPN involves complex operations such as inverse operation of the covariance matrix when processing data. Especially in high-dimensional data, the calculation cost will increase significantly, resulting in a large time overhead for model training and prediction and high hardware requirements, which affect its application in some scenarios with high real-time requirements or limited computing resources.
5. Conclusions
Current Gaussian Prototype Networks primarily employ Gaussian covariance matrices to enhance model representation capabilities and classification performance. These matrices represent confidence intervals for encoded vectors and reflect both sample quality and model prediction accuracy. However, when labels in small-sample data are inherently erroneous, they can significantly distort the mean and covariance matrices of Gaussian Prototype Networks, which cause “bias” in prototype distributions and reduce model robustness. To address this problem, the paper proposed the SL-GPN model, which dynamically generates soft labels for mitigating the impact of raw labels on training and optimizes the training process of the model. Specifically, mechanical vibration signal samples are first embedded in a space to compute mean vectors and Gaussian covariance matrices containing category information. Then, during each training session, the model dynamically generates soft labels based on the similarity between samples. When soft-label parameters prove beneficial for model training, SL-GPN enhances the current parameter settings and training process. Conversely, if existing soft-label configurations hinder model progress, the system automatically adjusts these parameters to guide the training process effectively. The experimental results using open datasets demonstrate that the SL-GPN model achieves 99.41% accuracy in small-sample mechanical fault diagnosis, significantly outperforming other small-sample learning methods. In the future AI equipment fault prediction, the proposed method has good fault tolerance, and it can quickly learn key features based on a small number of fault samples so that the results of the fault diagnosis can be more understandable and trusted by human users.
Author Contributions
Conceptualization, L.W.; Methodology, L.W., Z.B. and J.T.; Software, H.L.; Validation, J.T.; Formal analysis, J.Z. and C.W.; Resources, P.Y.; Data curation, H.L., P.Y., J.Z. and C.W.; Writing—original draft, X.Z.; Writing—review & editing, J.T. and X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key Research and Development Program of People’s Republic of China (Grant No. 2022YFF0608702), National Key R&D Program of China (Grant No. 2022YFF0608700), the science and technology program of the State Administration for Market Regulation (Grant No. 2021MK078), and the Hunan Provincial Department of Education Scientific Research Project (Grant No. 22C0262).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Authors Lianghong Wang, Zhongzhuang Bai, Hongxiang Li and Panpan Yang were employed by the company Yunnan Dianneng Smart Energy Co., Ltd. Authors Jinliang Zhao and Chunwei Wang were employed by the company Shanghai Electric Power Electronics Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ML-CNN | Convolutional Neural Network based on Meta Learning |
| GPN | Gaussian Prototypical Network |
| SL-GPN | Gaussian Prototype Network based on Soft Labels |
| CWRU | Case Western Reserve University |
| HP | Horsepower |
| 1D-CNN | One-Dimensional Convolutional Neural Network |
| BN | Batch Normalization |
| ProtoNet | Prototypical Network |
| RelationNet | Relation Network |
| CNN-FT | Conventional Pretraining–Fine-Tuning Transfer Learning Algorithm |
References
- Alagha, N.; Khairuddin, A.S.M.; Haitaamar, Z.N.; Al-Khatib, O.; Kanesan, J. Artificial Intelligence in Wind Turbine Fault Detection and Diagnosis: Advances and Perspectives. Energies 2025, 16, 1680. [Google Scholar] [CrossRef]
- Chen, Q.; Li, L.; Liu, R. Research Progress on Fault Diagnosis Methods and Technologies for Pitch Control Systems of High-Power Wind Turbines. Power Syst. Eng. 2020, 36, 1–7. [Google Scholar]
- Saci, A.; Nadour, M.; Cherroun, L.; Hafaifa, A.; Kouzou, A.; Rodriguez, J.; Abdelrahem, M. Condition Monitoring Using Digital Fault-Detection Approach for Pitch System in Wind Turbines. Energies 2024, 17, 4016. [Google Scholar] [CrossRef]
- Kjeld, J.G.; Avendaño-Valencia, L.D.; Vestermark, J. Effect of wind and wave properties in modal parameter estimates of an idling offshore wind turbine from long-term monitoring data. Mech. Syst. Signal Process. 2023, 187, 109934. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, J.; Xie, J.; Zhang, T.; Lv, H.; Pan, T. Meta-learning as a promising approach for few-shot cross-domain fault diagnosis: Algorithms, applications, and prospects. Knowl. Based Syst. 2022, 235, 107646. [Google Scholar] [CrossRef]
- Liu, X.; Guo, H.; Liu, Y. One-shot fault diagnosis of wind turbines based on meta-analogical momentum contrast learning. Energies 2022, 15, 3133. [Google Scholar] [CrossRef]
- Hu, T.; Tang, T.; Lin, R.; Chen, M.; Han, S.; Wu, J. A simple data augmentation algorithm and a self-adaptive convolutional architecture for few-shot fault diagnosis under different working conditions. Measurement 2020, 156, 107539. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, J.; Ye, Z.; Liu, W.; Tang, J. Prior knowledge-informed multi-task dynamic learning for few-shot machinery fault diagnosis. Expert Syst. Appl. 2025, 271, 126439. [Google Scholar] [CrossRef]
- Zheng, T.; Song, L.; Wang, J.; Teng, W.; Xu, X.; Ma, C. Data synthesis using dual discriminator conditional generative adversarial networks for imbalanced fault diagnosis of rolling bearings. Measurement 2020, 158, 107741. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, J.; Liu, S.; Liu, Z. Domain discrepancy-guided contrastive feature learning for few-shot industrial fault diagnosis under variable working conditions. IEEE Trans. Ind. Inform. 2023, 19, 10277–10287. [Google Scholar] [CrossRef]
- Zhang, T.; Li, C.; Chen, J.; He, S.; Zhou, Z. Feature-level consistency regularized semi-supervised scheme with data augmentation for intelligent fault diagnosis under small samples. Mech. Syst. Signal Process. 2023, 203, 110747. [Google Scholar] [CrossRef]
- Lin, J.; Shao, H.; Zhou, X.; Cai, B.; Liu, B. Generalized MAML for few-shot cross-domain fault diagnosis of bearing driven by heterogeneous signals. Expert Syst. Appl. 2023, 230, 120696. [Google Scholar] [CrossRef]
- Pang, B.; Liu, Q.; Sun, Z.; Xu, Z.; Hao, Z. Time-frequency supervised contrastive learning via pseudo-labeling: An unsupervised domain adaptation network for rolling bearing fault diagnosis under time-varying speeds. Adv. Eng. Inform. 2024, 59, 102304. [Google Scholar] [CrossRef]
- Liu, S.; Chen, J.; He, S.; Shi, Z.; Zhou, Z. Few-shot learning under domain shift: Attentional contrastive calibrated transformer of time series for fault diagnosis under sharp speed variation. Mech. Syst. Signal Process. 2023, 189, 110071. [Google Scholar] [CrossRef]
- Meng, Z.; He, H.; Cao, W.; Li, J.; Cao, L.; Fan, J.; Fan, F. A novel generation network using feature fusion and guided adversarial learning for fault diagnosis of rotating machinery. Expert Syst. Appl. 2023, 234, 121058. [Google Scholar] [CrossRef]
- Ye, C.; Wang, J.; Peng, C.; Ju, Z.; Geng, X.; Zhang, L.; Zhang, F. Novel cross-domain fault diagnosis method based on model-agnostic meta-learning embedded in adaptive threshold network. Measurement 2023, 222, 113677. [Google Scholar] [CrossRef]
- Rehman, A.U.; Jiao, W.; Jiang, Y.; Wei, J.; Sohaib, M.; Sun, J.; Chi, Y. Deep Learning in Industrial Machinery: A Critical Review of Bearing Fault Classification Methods. Appl. Soft Comput. 2025, 171, 112785. [Google Scholar] [CrossRef]
- Xu, Z.; Gao, X.; Fu, J.; Li, Q.; Tan, C. A novel fault diagnosis method under limited samples based on an extreme learning machine and meta-learning. J. Taiwan Inst. Chem. Eng. 2024, 161, 105522. [Google Scholar] [CrossRef]
- Su, H.; Xiang, L.; Hu, A.; Xu, Y.; Yang, X. A novel method based on meta-learning for bearing fault diagnosis with small sample learning under different working conditions. Mech. Syst. Signal Process. 2022, 169, 108765. [Google Scholar] [CrossRef]
- Sun, H.; Yang, B.; Lin, S. An Open Set Diagnosis Method for Rolling Bearing Faults Based on Prototype and Reconstructed Integrated Network. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Hou, R.; Chen, Z.; Chen, J.; He, S.; Zhou, Z. Imbalanced fault identification via embedding-augmented Gaussian prototype network with meta-learning perspective. Meas. Sci. Technol. 2022, 33, 055102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).