Multi-Level Coordination-Level Evaluation Study of Source-Grid-Load-Storage Based on AHP-Entropy Weighting
Abstract
1. Introduction
2. Multi-Level Coordination-Level Evaluation of Source-Grid-Load-Storage
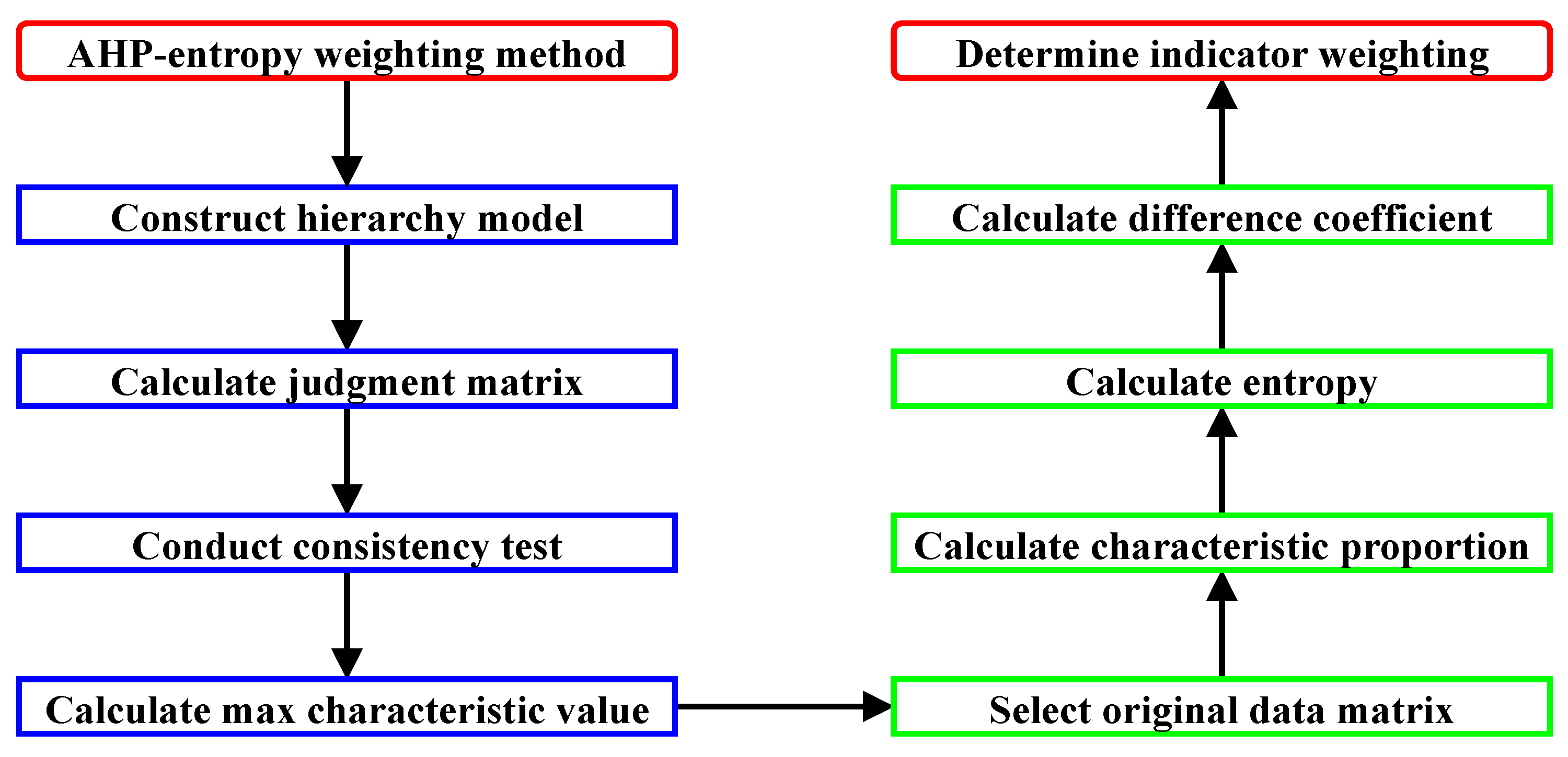
3. Ahp-Entropy Weighting Method
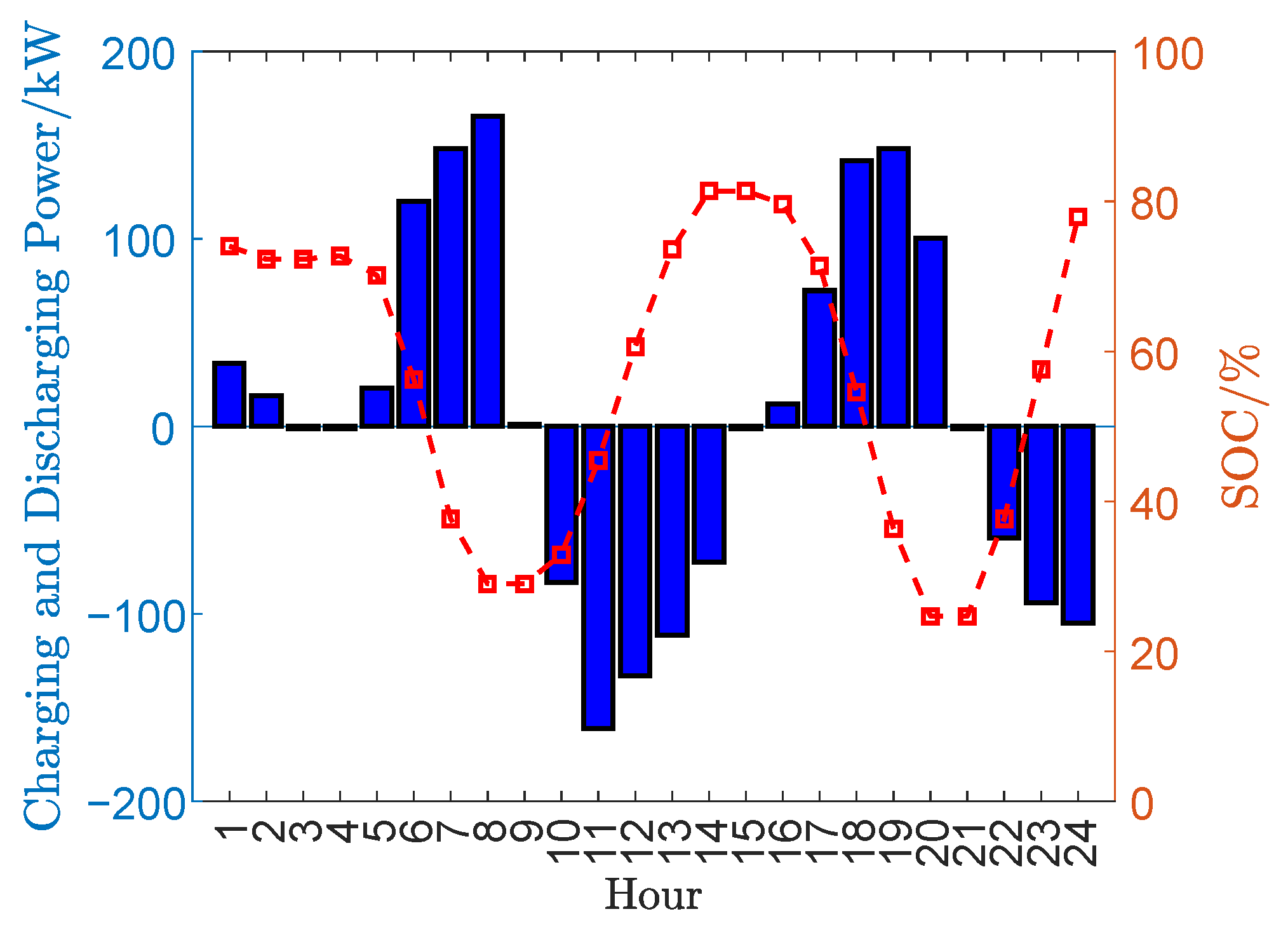
4. Case Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, G.; Qian, A.; Muhammad, Y.; Wang, X. Source-load-storage consistency collaborative optimization control of flexible DC distribution network considering multi-energy complementarity. Int. J. Electr. Power Energy Syst. 2019, 107, 273. [Google Scholar]
- Ni, S.; Zhang, L.; Hu, Z. Active distribution network source coordination planning method considering the timing characteristics of power supply and load. Power Syst. Prot. Control 2020, 48, 12. [Google Scholar]
- Huang, H.; Li, Y.; Liu, H. Collaborative optimization strategy of source-grid-load-storage considering dynamic time series complementarity of multiple storages. IET Gener. Transm. Distrib. 2023, 17, 4007. [Google Scholar] [CrossRef]
- Simonic, E.; Seme, S.; Sredensek, K. Research on the modelling and analysis of the penetration of renewable sources and storage into electrical networks. Energies 2025, 18, 2263. [Google Scholar] [CrossRef]
- Huang, J.; Xu, Y.; Ghias, A. Wind power plant dispatch for power grid frequency dynamics improvement: A surrogate model-based method. IEEE Trans. Power Syst. 2025, 40, 3261. [Google Scholar] [CrossRef]
- Wei, J.; Wei, L.; Huang, S.; Wang, B.; Huang, G.; Shen, F. Optimal coordinated post-event voltage control with energy storage boundary analysis for large-scale wind farms. IEEE Trans. Power Syst. 2025, 40, 3374. [Google Scholar] [CrossRef]
- Bogdan, M.; David, P. Three-level coordination in power system stabilization. Electr. Power Syst. Res. 2014, 111, 40. [Google Scholar] [CrossRef]
- Gong, Y.; Qin, H.; Fu, H. Optimal dispatch strategy of photovoltaic power-generation system considering source load uncertainty. J. Electr. Power Sci. Technol. 2019, 34, 112. [Google Scholar]
- Gao, N.; Zhang, H.; Wang, Z. Location and capacity planning for distributed energy storage in regional power grids. High Volt. Appar. 2020, 56, 52. [Google Scholar]
- Jiang, T.; Li, Y.; Ju, P. Overview of flexible load control and model research. Smart Electr. Power 2020, 48, 1. [Google Scholar]
- Shao, Z.; Zou, X.; Yuan, X. A review of energy storage applications under the background of flexible distribution networks. Electr. Meas. Instrum. 2020, 57, 86. [Google Scholar]
- Armghan, H.; Xu, Y.; Ali, N.; Farooq, U. Coordination control in hybrid energy storage based microgrids providing ancillary services: A three-layer control approach. J. Energy Storage 2024, 93, 112221. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, L.; Liu, J. Multi-time-scale coordinated optimum scheduling technique for a multi-source complementary power-generating system with uncertainty in the source-load. Energies 2023, 16, 3020. [Google Scholar] [CrossRef]
- Mi, Y.; Chen, Y.; Yuan, M.; Li, Z.; Tao, B.; Han, Y. Multi-timescale optimal dispatching strategy for coordinated source-grid-load-storage interaction in active distribution networks based on second-order cone planning. Energies 2023, 16, 1356. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Z.; Yi, H.; Li, Y.; Wang, X.; Xiao, Y.; Hu, Z.; Zhou, H.; Zhang, X. Source-storage-load flexible scheduling strategy considering characteristics complementary of hydrogen storage system and flexible carbon-capture system. Energies 2024, 17, 3894. [Google Scholar] [CrossRef]
- Wang, B.; Tian, Z.; Yang, H.; Li, C.; Xu, X.; Zhu, S.; Du, E.; Zhang, N. Collaborative planning of source-grid-load-storage considering wind and photovoltaic support capabilities. Energies 2025, 18, 2045. [Google Scholar] [CrossRef]
- Che, B.; Zhang, Z.; Wei, D.; Jin, P.; Yang, Y. Coordinated planning of source-grid-load-storage power system to promote large-scale renewable energy consumption. Asian Conf. Front. Power Energy 2022, 2022, 694. [Google Scholar]
- Qi, X.; Liu, L.; Zhang, Z.; Pan, Z.; Wu, W. Study on the cooperative optimized operation of power system source-grid-load-storage based on Gurobi mathematical programming. In Proceedings of the IEEE 7th Information Technology and Mechatronics Engineering Conference, Chongqing, China, 15–17 September 2023; p. 1085. [Google Scholar]
- Liu, X.; Li, J.; Huang, C.; Li, X.; Wang, Y.; Chen, X. Research on source-grid-load-storage coordination planning method of centralized-distributed form. In Proceedings of the IEEE PES 16th Asia-Pacific Power and Energy Engineering Conference, Nanjing, China, 25–27 October 2024; p. 1. [Google Scholar]
- Wang, H.; Guo, P.; Liu, G. Optimization of source-grid-load-storage coordination of power systems based on multiple time scale model. In Proceedings of the 4th International Conference on New Energy System and Power Engineering, Fuzhou, China, 25–27 April 2025; p. 112. [Google Scholar]
- Hirankittiwong, P.; Thanh, N.; Pattanaporkratana, A.; Chattham, N.; Jeenanunta, C.; Seng, V. Intelligent fuzzy multi-criteria decision-making for energy-saving building designs in construction. Energies 2025, 18, 2726. [Google Scholar] [CrossRef]
- Xie, F.; Yin, Z.; Luo, A.; Yuan, J. Prediction of distribution network line loss based on grey relation analysis and XGboost. In Proceedings of the IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering, Nanchang, China, 26–28 March 2021; p. 279. [Google Scholar]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of entropy weight method in decision-making. Math. Probl. Eng. 2020, 2020, 3564835. [Google Scholar] [CrossRef]
- Jaworski, S.; Chrzanowska, M.; Monica, Z.; Robert, P.; Aleksandra, J.; Piotr, Z. Evaluating the progress of renewable energy sources in Poland: A multidimensional analysis. Energies 2023, 16, 6431. [Google Scholar] [CrossRef]
- Zhan, Q.; Su, J.; Lin, J.; Guo, S. Coordinated optimization of source-storage–load in distribution network based on edge computation. Energy Rep. 2023, 9, 492. [Google Scholar] [CrossRef]
- Li, M.; Tian, Y.; Zhang, H.; Zhang, N. The source-load-storage coordination and optimal dispatch from the high proportion of distributed photovoltaic connected to power grids. J. Eng. Res. 2024, 12, 421. [Google Scholar] [CrossRef]
- Xie, L.; Jiang, J.; Huang, A.; Tang, Y.; Liu, Y.; Zhou, H.; Xing, Z. Calorimetric Evaluation of Thermal Stability of Organic Liquid Hydrogen Storage Materials and Metal Oxide Additives. Energies 2022, 15, 2236. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, J.; Yuan, F.; Shi, Y.; Li, Z. Research on Denoising Method for Hydroelectric Unit Vibration Signal Based on ICEEMDAN–PE–SVD. Sensors 2023, 23, 6368. [Google Scholar] [CrossRef] [PubMed]
- Rogge, N. Composite indicators as generalized benefit-of-the-doubt weighted averages. Eur. J. Oper. Res. 2018, 267, 381. [Google Scholar] [CrossRef]
- Hashem, O.; Mahsa, V.; Saeid, J. Construct a composite indicator based on integrating common weight data envelopment analysis and principal component analysis models: An application for finding development degree of provinces in Iran. Soc. Econ. Plan. Sci. 2019, 68, 100618. [Google Scholar]
- Bao, Q.; Zhu, Y.; Wang, Y.; Feng, Y. Can entropy weight method correctly reflect the distinction of water quality indices. Water Resour. Manag. 2020, 34, 3667. [Google Scholar] [CrossRef]
- Galym, T.; Aidana, T.; Serdar, D.; Nurlan, O.; Mert, G.; Ali, T.; Ferhat, K. Stakeholder based weights of new sustainability indicators providing pandemic resilience for residential buildings. Sustain. Cities Soc. 2021, 75, 103300. [Google Scholar] [CrossRef]
- Chintala, B.; Kumar, D. Multiobjective meter placement in active distribution system state estimation using inverse-model-based multilabel Gaussian classification with adaptive reference point method. Int. Transation Electr. Energy Syst. 2021, 31, 12935. [Google Scholar]
- Chen, L.; Miettinen, K.; Xin, B.; Vesa, O. Comparing reference point based interactive multiobjective optimization methods without a human decision maker. J. Glob. Optim. 2023, 85, 757. [Google Scholar] [CrossRef]


| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0.00 | 0.00 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 |
| Single Link | Characteristic Vector | Indicator Weighting | Maximum Characteristic Value | CI |
|---|---|---|---|---|
| power sources | 0.415 | 8.296% | 5.114 | 0.029 |
| power grids | 2.613 | 52.26% | ||
| load resources | 1.154 | 23.07% | ||
| energy storage | 0.253 | 5.057% |
| Link Interaction | Characteristic Vector | Indicator Weighting | Maximum Characteristic Value | CI |
|---|---|---|---|---|
| source-grid | 0.429 | 7.140% | 3.000 | 0.000 |
| source-load | 0.857 | 14.28% | ||
| source-storage | 1.714 | 28.57% | ||
| grid-load | 1.000 | 14.28% | ||
| grid-storage | 0.500 | 7.140% | ||
| load-storage | 2.000 | 28.57% |
| Region | Single Link | Link Interaction | Indirect Indicators |
|---|---|---|---|
| A | 0.585 | 0.593 | 0.773 |
| B | 0.606 | 0.595 | 0.783 |
| C | 0.542 | 0.530 | 0.765 |
| Region | Comprehensive Indicator Score | Coordination Level Evaluation |
|---|---|---|
| A | 0.627 | slightly high |
| B | 0.631 | slightly high |
| C | 0.582 | medium |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wu, L.; Zhang, P.; Zhang, F.; Guo, J. Multi-Level Coordination-Level Evaluation Study of Source-Grid-Load-Storage Based on AHP-Entropy Weighting. Energies 2025, 18, 4321. https://doi.org/10.3390/en18164321
Wang B, Wu L, Zhang P, Zhang F, Guo J. Multi-Level Coordination-Level Evaluation Study of Source-Grid-Load-Storage Based on AHP-Entropy Weighting. Energies. 2025; 18(16):4321. https://doi.org/10.3390/en18164321
Chicago/Turabian StyleWang, Benhong, Ligui Wu, Peng Zhang, Fangqing Zhang, and Jiang Guo. 2025. "Multi-Level Coordination-Level Evaluation Study of Source-Grid-Load-Storage Based on AHP-Entropy Weighting" Energies 18, no. 16: 4321. https://doi.org/10.3390/en18164321
APA StyleWang, B., Wu, L., Zhang, P., Zhang, F., & Guo, J. (2025). Multi-Level Coordination-Level Evaluation Study of Source-Grid-Load-Storage Based on AHP-Entropy Weighting. Energies, 18(16), 4321. https://doi.org/10.3390/en18164321









