Design of a High-Performance Current Controller for Permanent Magnet Synchronous Motors via Multi-Frequency Sweep Adjustment
Abstract
1. Introduction
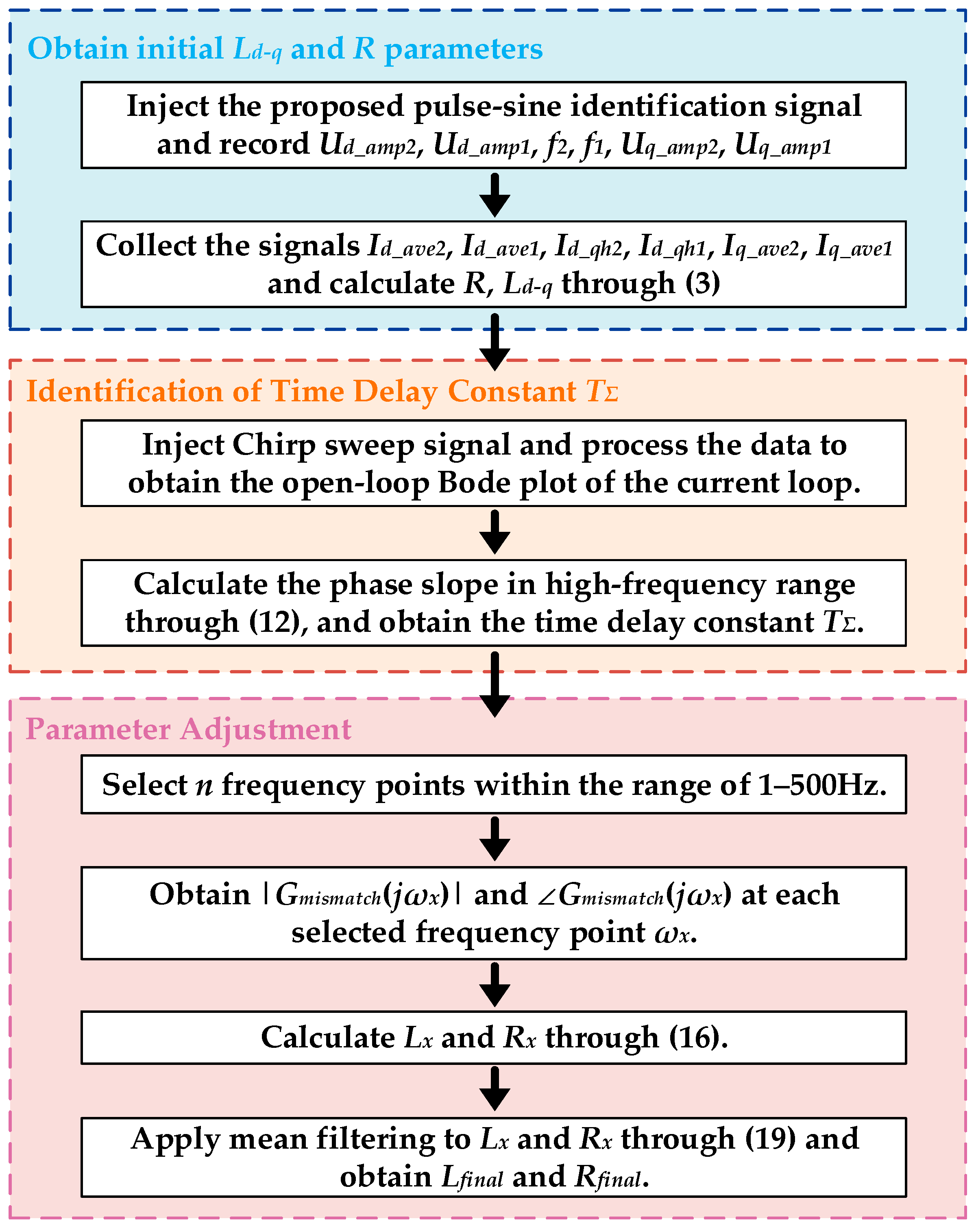
2. Preliminary Motor Parameter Identification
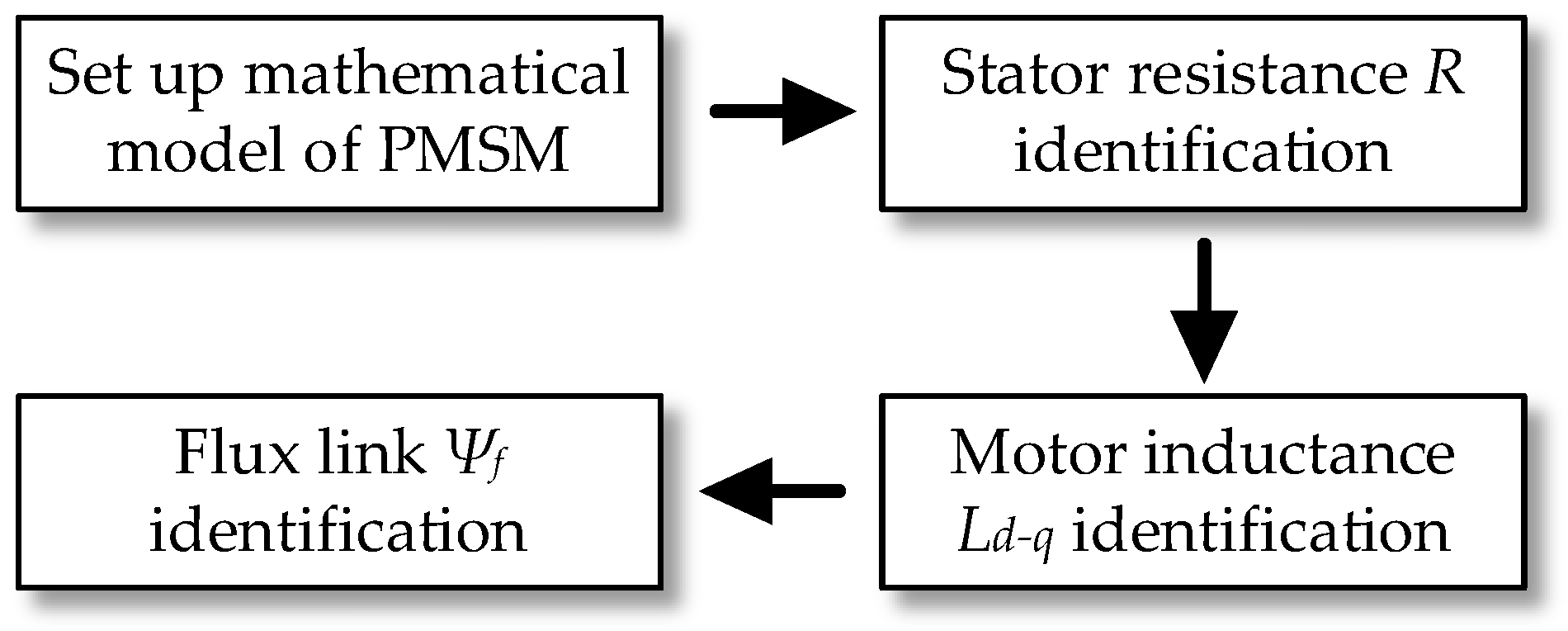
2.1. Current Loop Modeling and Parameter Identification Sequence
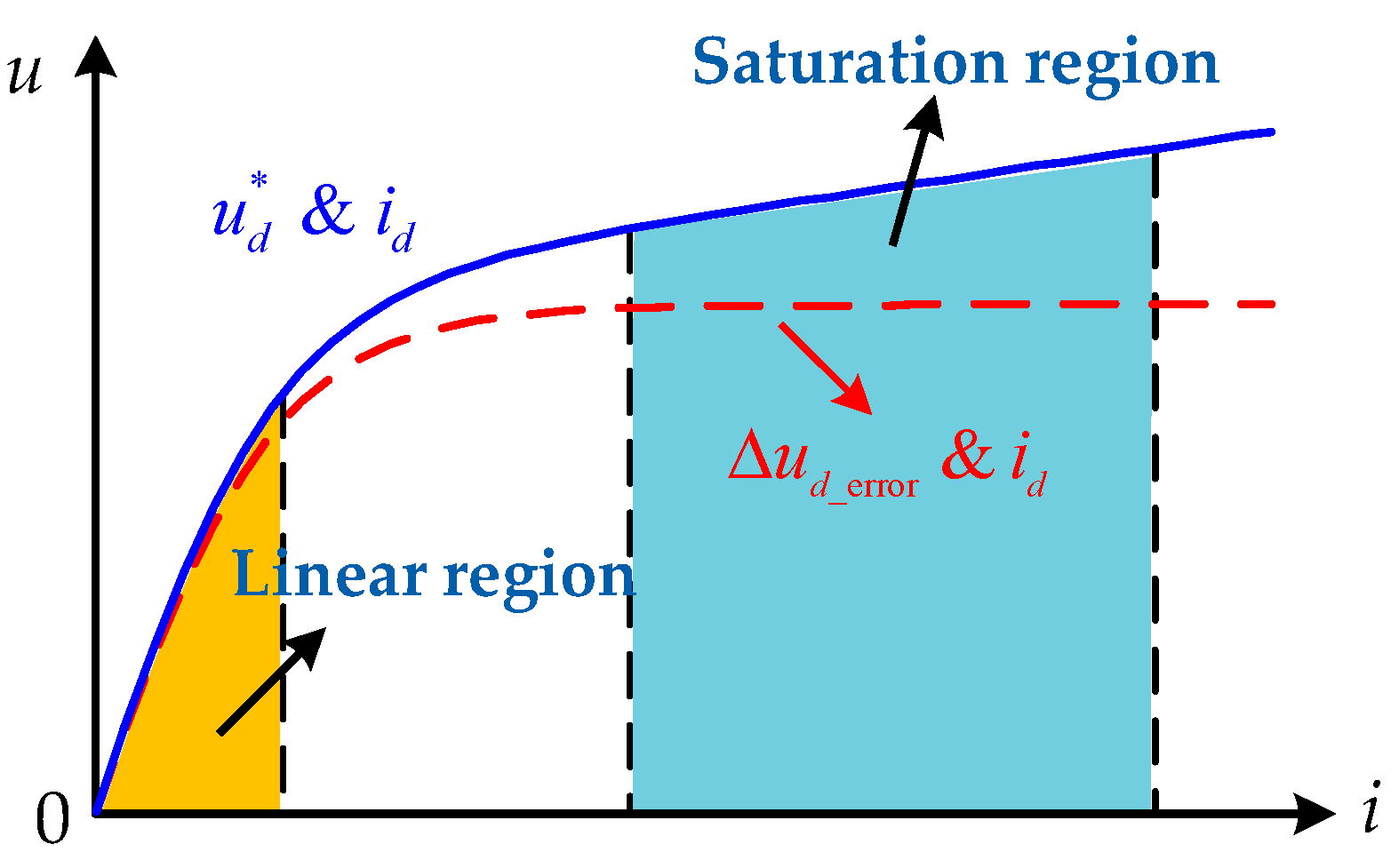
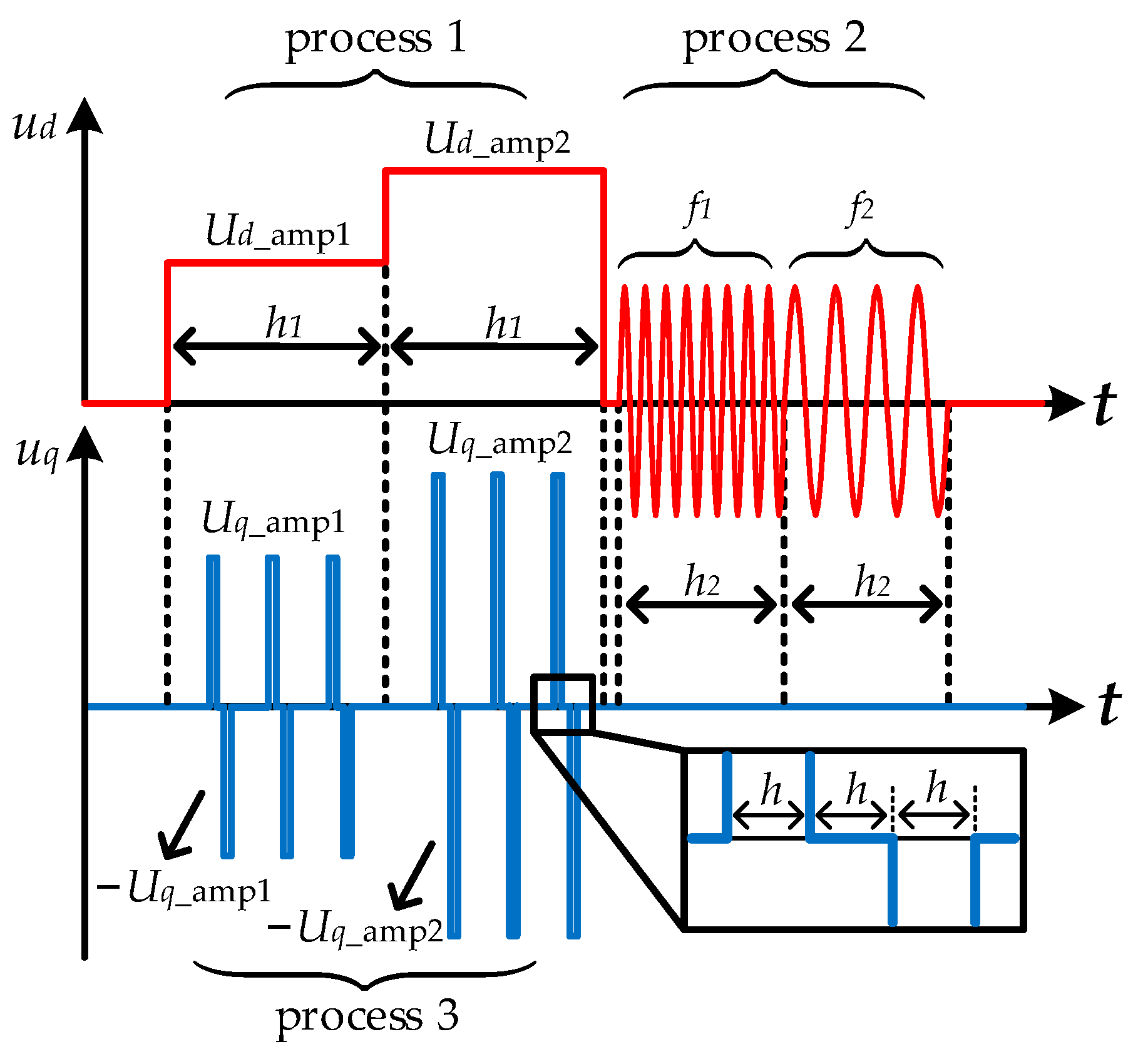
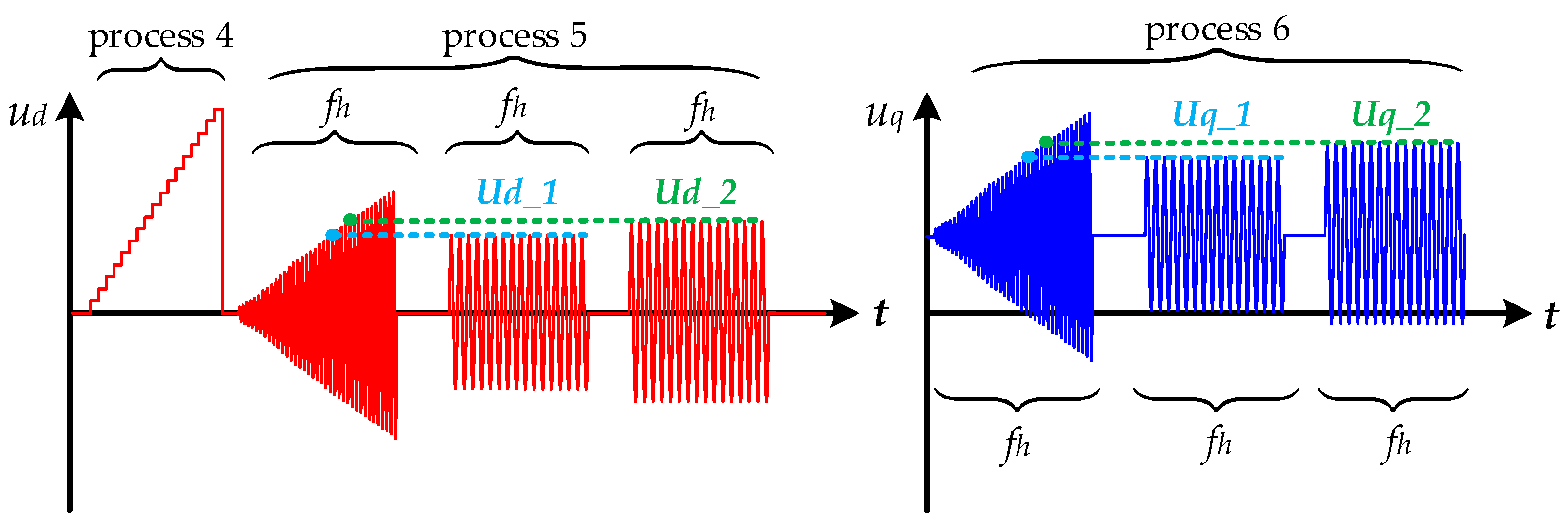
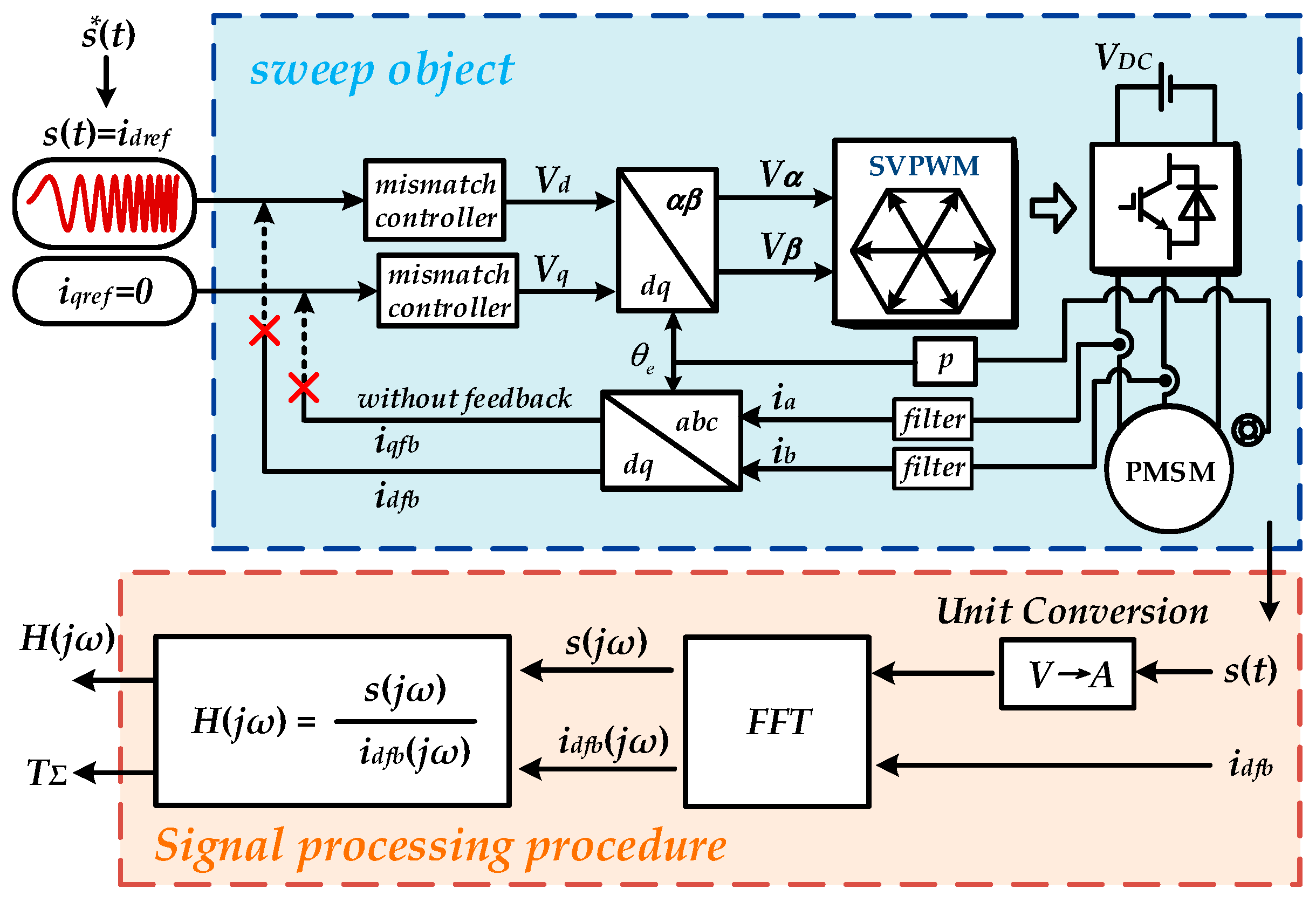
2.2. The Proposed Sinusoidal–Pulse Identification Strategy and Conventional Method
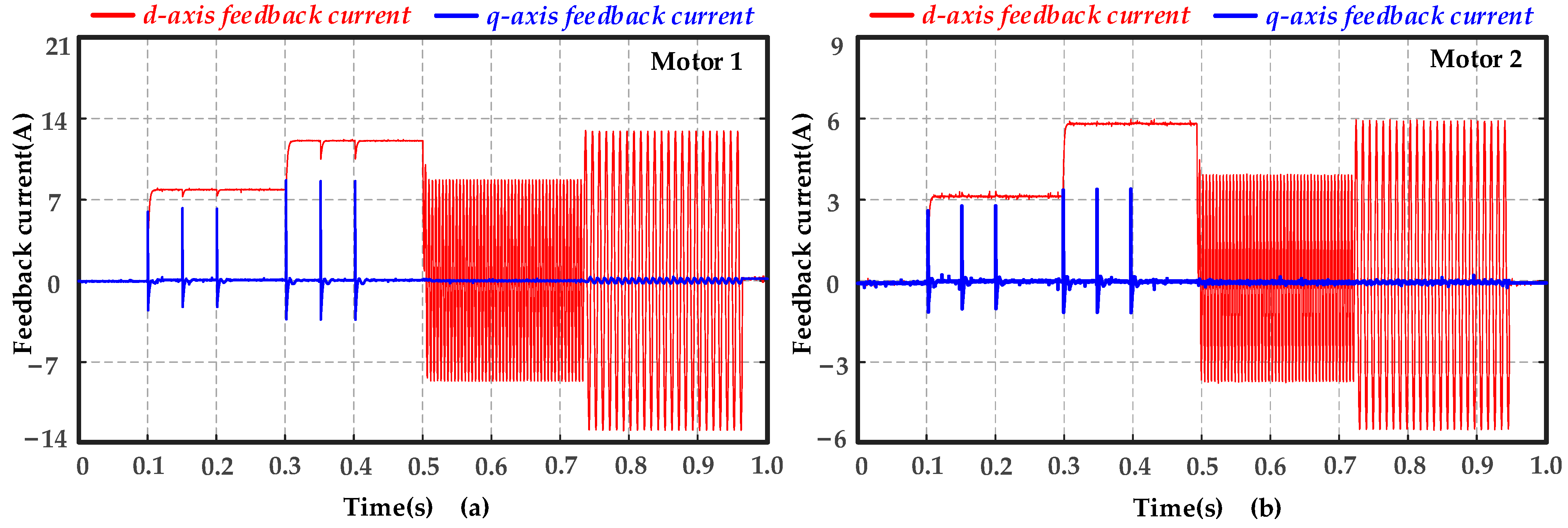
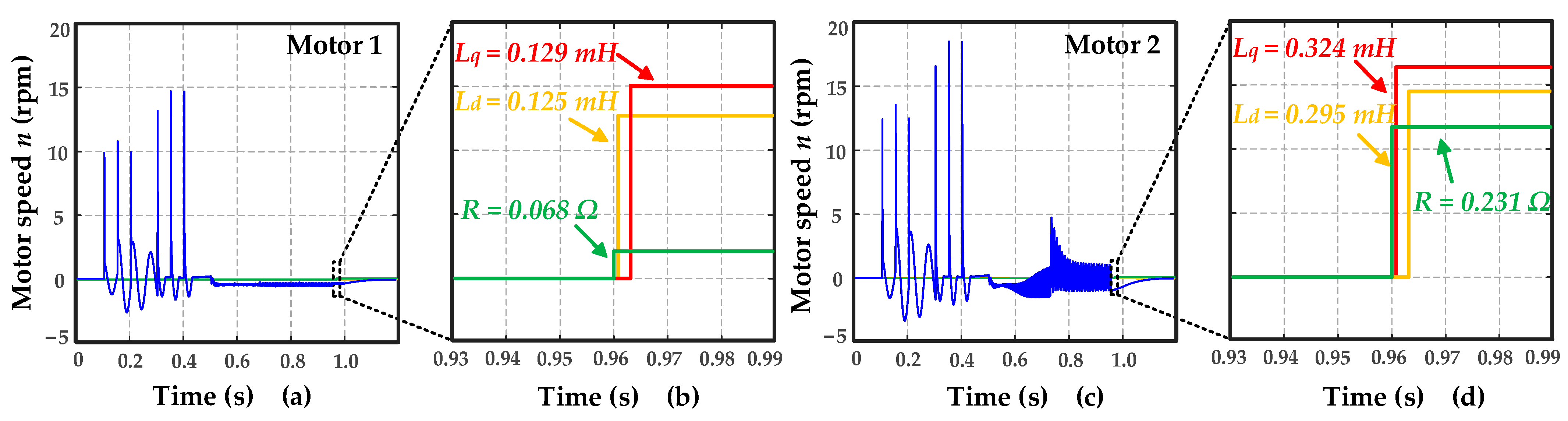
2.3. Experimental Verification
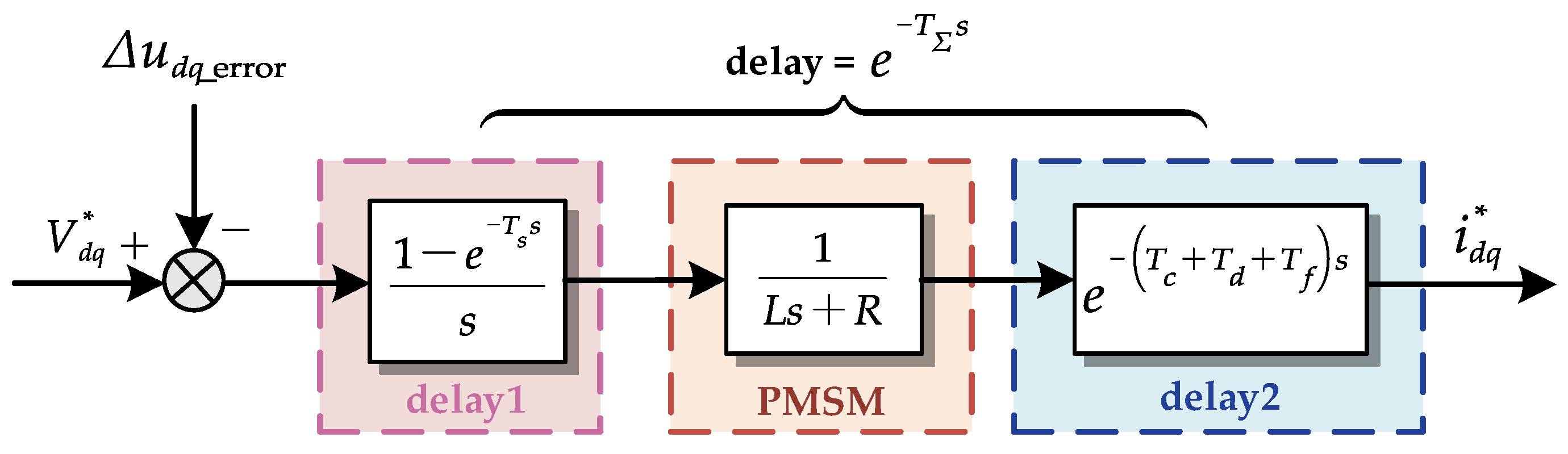
3. Identification of Current Loop Delay Time Constant
3.1. Delay Model of the Current Loop
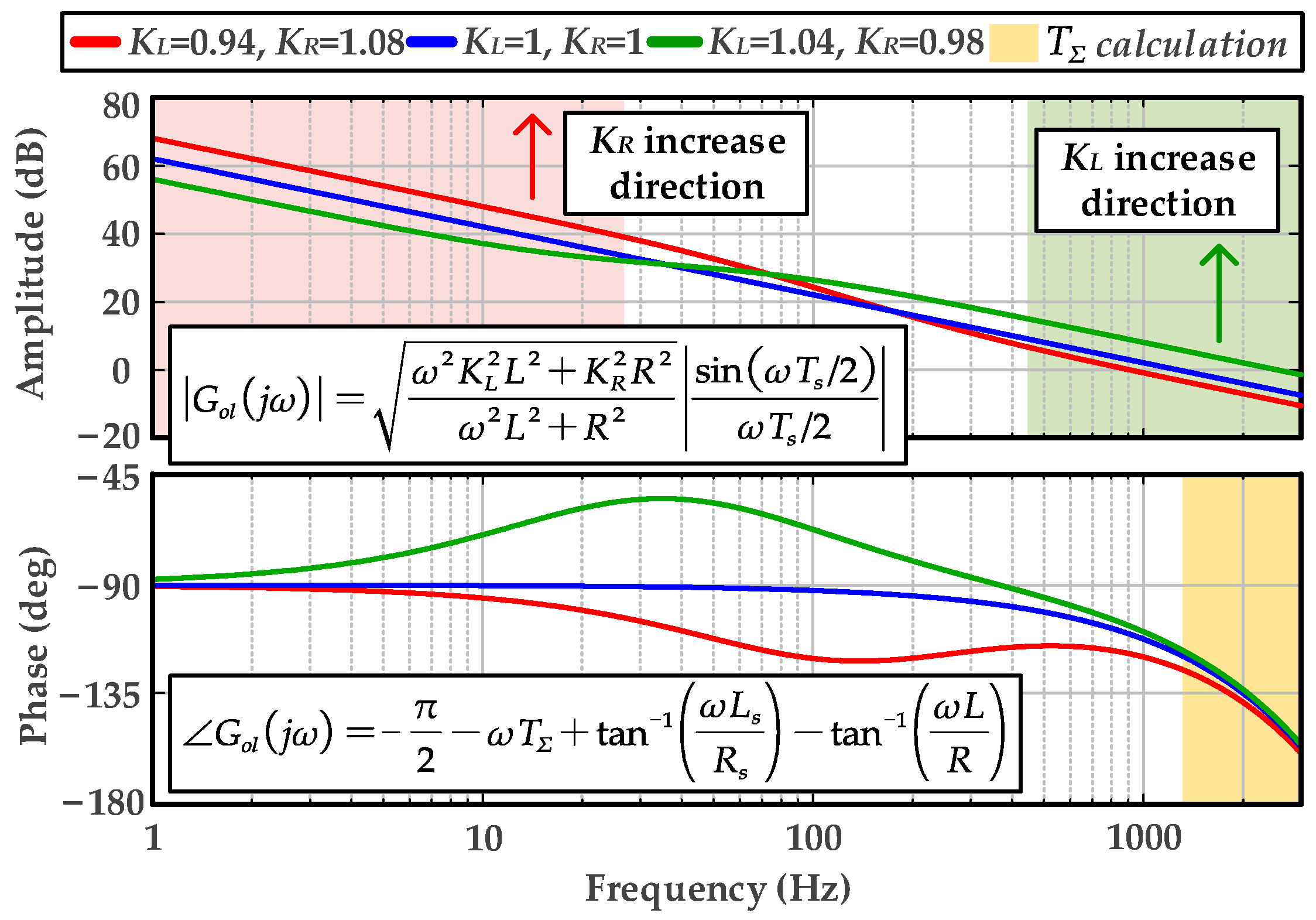
3.2. Identification of Delay Time Constant in the High-Frequency Range
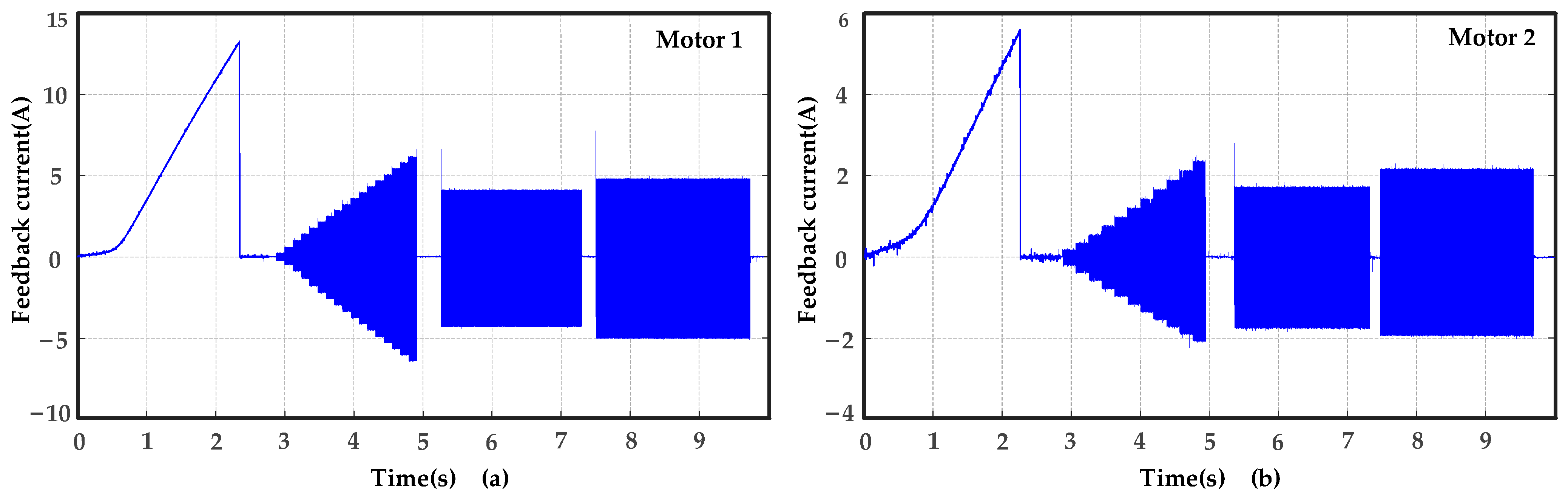
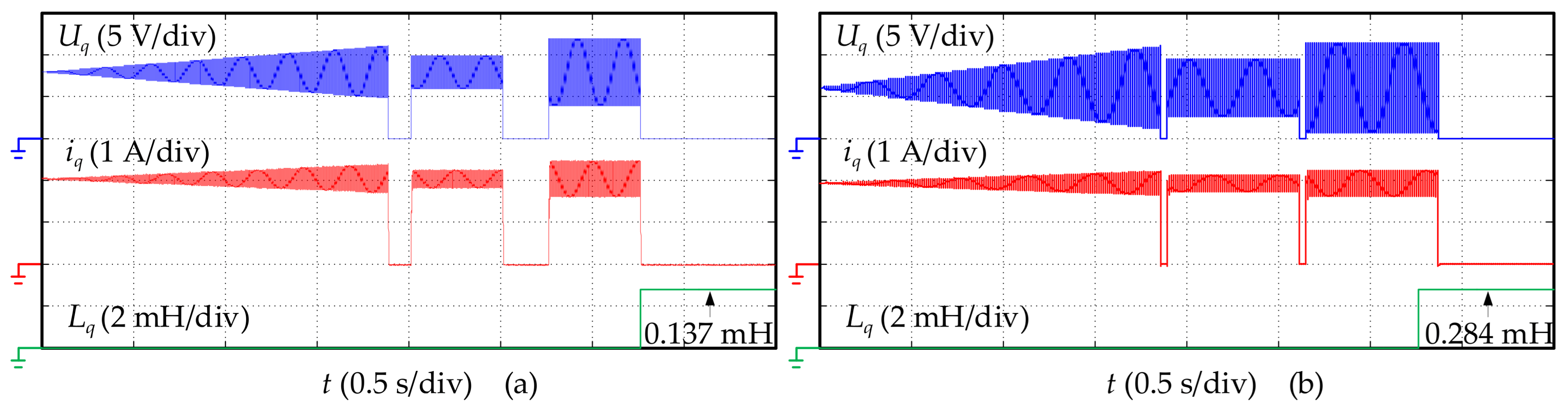
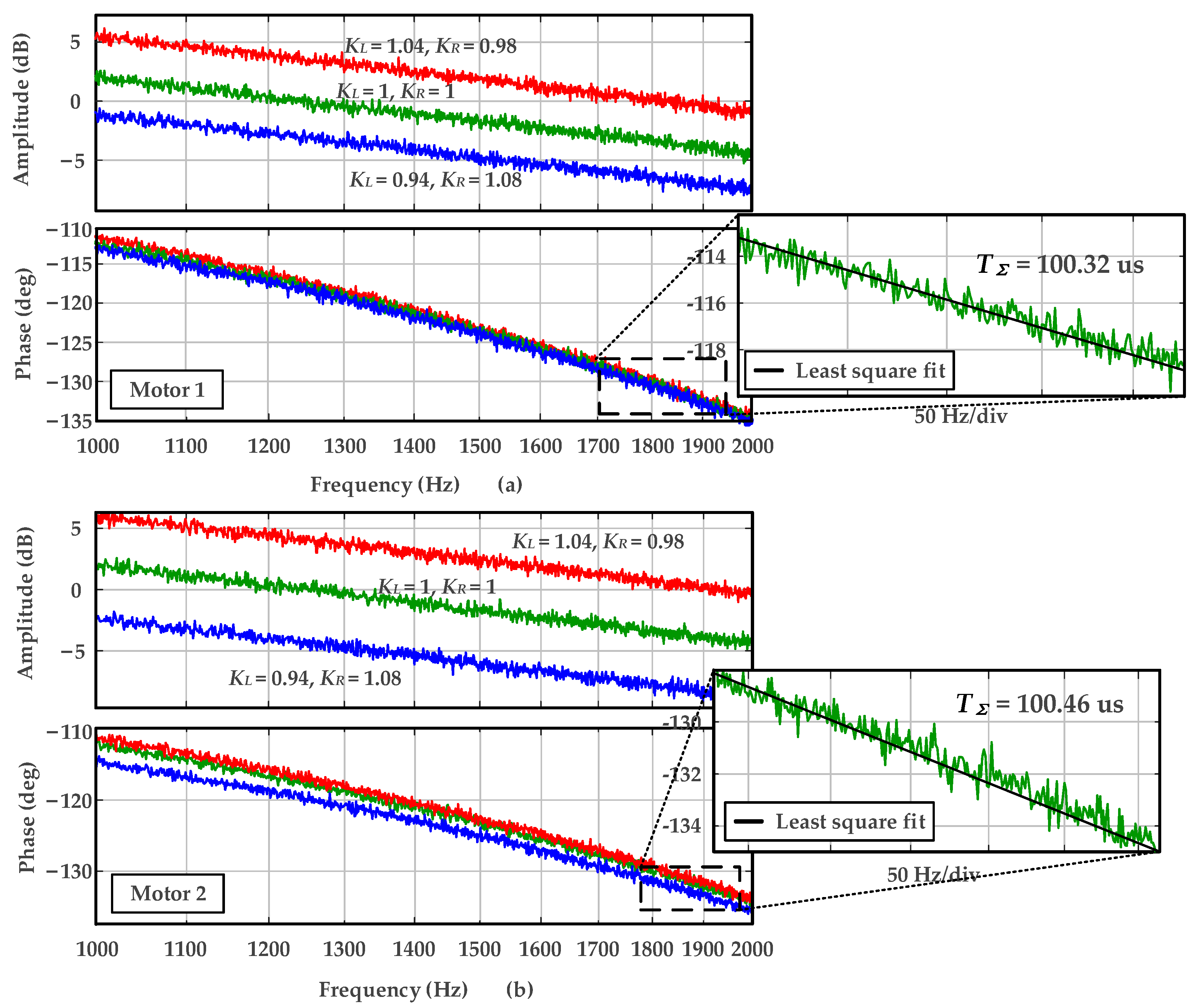
3.3. Experimental Verification
4. Bandwidth Adjustment Scheme Under Open-Loop Control
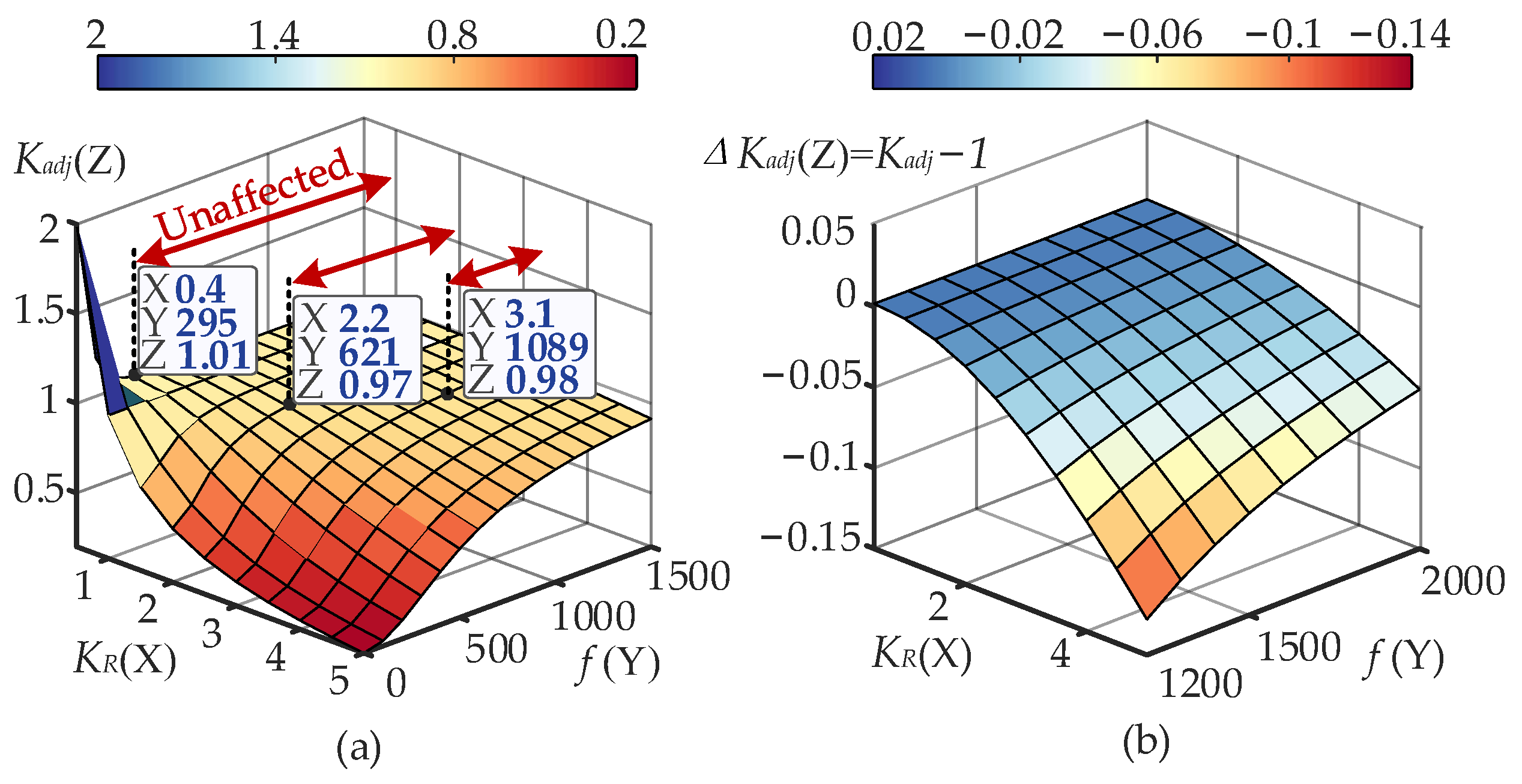
4.1. Multi-Frequency Parameter Adjustment Scheme
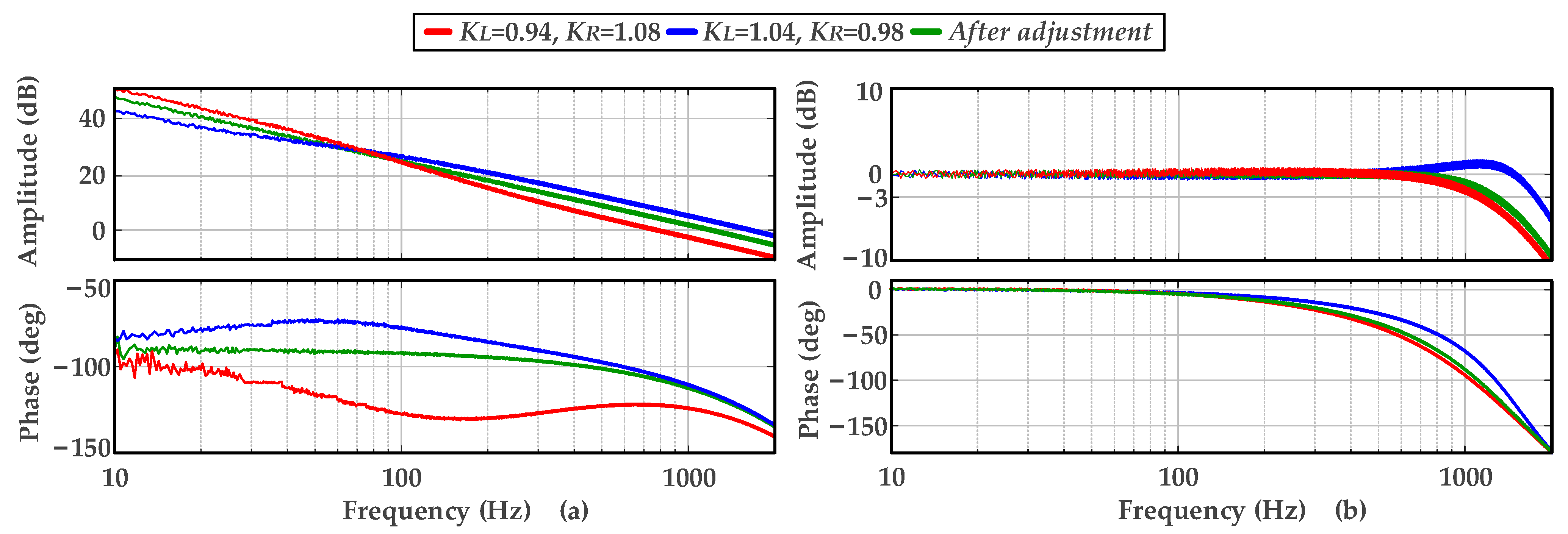
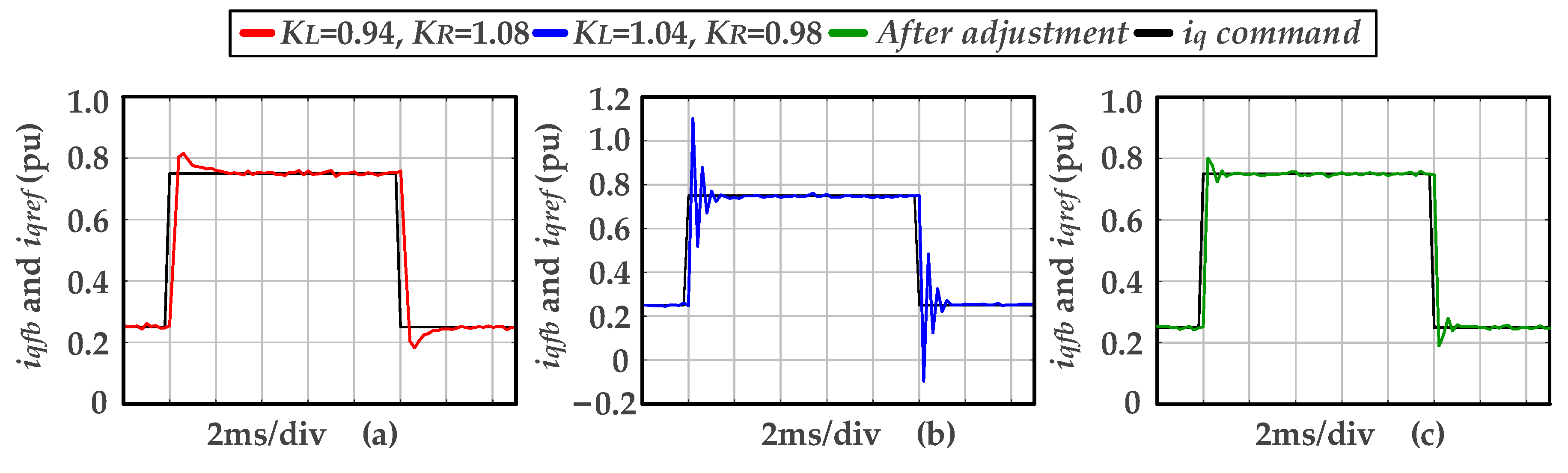
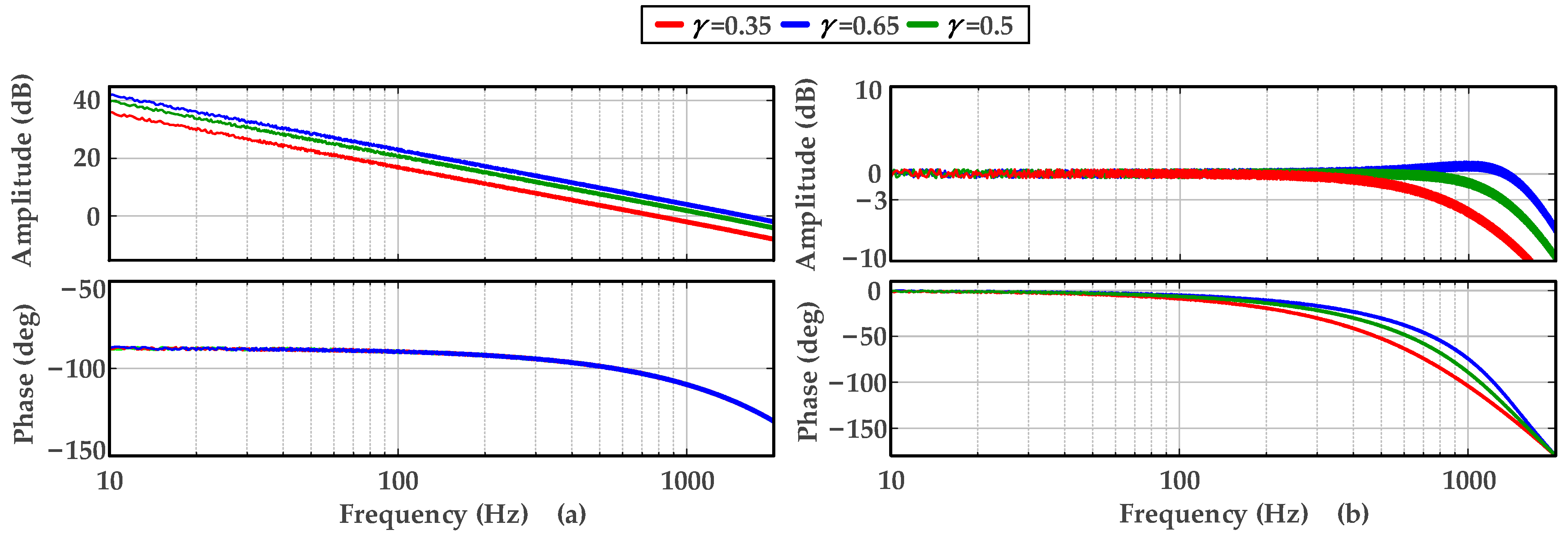
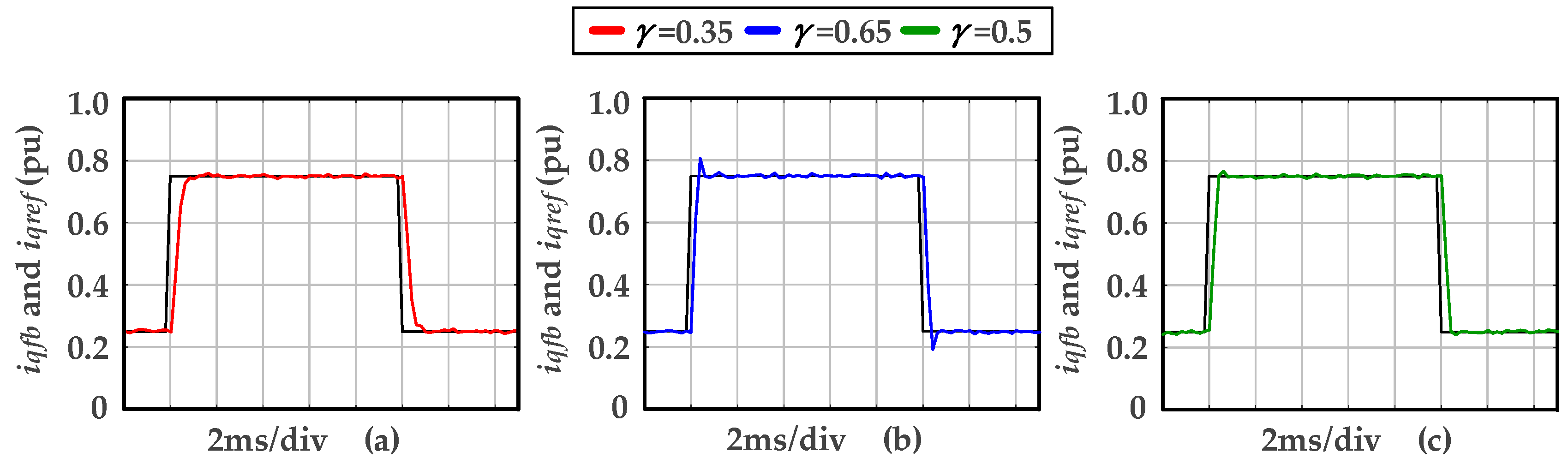
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maeda, Y.; Iwasaki, M. Rolling Friction Model-Based Analyses and Compensation for Slow Settling Response in Precise Positioning. IEEE Trans. Ind. Electron. 2013, 60, 5841–5853. [Google Scholar] [CrossRef]
- Ohishi, K.; Furusawa, R. Actuators for Motion Control: Fine Actuator Force Control for Electric Injection Molding Machines. IEEE Ind. Electron. Mag. 2012, 6, 4–13. [Google Scholar] [CrossRef]
- Montonen, J.-H.; Nevaranta, N.; Lindh, T.; Alho, J.; Immonen, P.; Pyrhönen, O. Experimental Identification and Parameter Estimation of the Mechanical Driveline of a Hybrid Bus. IEEE Trans. Ind. Electron. 2018, 65, 5921–5930. [Google Scholar] [CrossRef]
- Östring, M.; Gunnarsson, S.; Norrlöf, M. Closed-loop identification of an industrial robot containing flexibilities. Control Eng. Pract. 2003, 11, 291–300. [Google Scholar] [CrossRef]
- Cameron, F.; Seborg, D.E. A self-tuning controller with a PID structure. Int. J. Control 1983, 38, 401–417. [Google Scholar] [CrossRef]
- Hang, C.C.; Åström, K.J.; Ho, W.K. Refinements of the Ziegler-Nichols tuning formula. Proc. Inst. Elect. Eng. 1991, 138, 111–118. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. J. Fluids Eng. 1942, 64, 759–765. [Google Scholar] [CrossRef]
- Rad, A.B.; Lo, W.L.; Tsang, K.M. Self-tuning PID controller using Newton-Raphson search method. IEEE Trans. Ind. Electron. 1997, 44, 717–725. [Google Scholar]
- MartÃn, D.; Caballero, B.; Haber, R. Optimal tuning of a networked linear controller using a multi-objective genetic algorithm. Application to a complex electromechanical process. In Proceedings of the International Conference on Intelligent Data Communication Technologies and Internet of Things, Dalian, China, 18–20 June 2008; p. 91. [Google Scholar]
- Cheng, K.Y.; Tzou, Y.Y. Fuzzy optimization techniques applied to the design of a digital PMSM servo drive. IEEE Trans. Power Electron. 2004, 19, 1085–1099. [Google Scholar] [CrossRef]
- Tursini, M.; Parasiliti, F.; Zhang, D. Real-time gain tuning of PI controllers for high-performance PMSM drives. IEEE Trans. Ind. Appl. 2002, 38, 1018–1026. [Google Scholar] [CrossRef]
- Yepes, A.G.; Vidal, A.; Malvar, J.; López, O.; Doval-Gandoy, J. Tuning method aimed at optimized settling time and overshoot for synchronous proportional-integral current control in electric machine. IEEE Trans. Power Electron. 2014, 29, 3041–3054. [Google Scholar] [CrossRef]
- Boshi, C. Electric Drag Automatic Control System: Motion Control System; Machinery Ind. Press: South Norwalk, CT, USA, 2003. [Google Scholar]
- Kim, H.; Degner, M.; Guerrero, J.; Briz, F.; Lorenz, R. Discrete-time current regulator design for AC machine drives. IEEE Trans. Ind. Appl. 2010, 46, 1425–1435. [Google Scholar] [CrossRef]
- Yang, S.M.; Lin, K.W. Automatic control loop tuning for permanent-magnet AC servo motor drives. IEEE Trans. Ind. Electron. 2016, 63, 1499–1506. [Google Scholar] [CrossRef]
- Erturk, F.; Akin, B. Spatial Inductance Estimation for Current Loop Auto-Tuning in IPMSM Self-Commissioning. IEEE Trans. Ind. Electron. 2020, 67, 3911–3920. [Google Scholar] [CrossRef]
- Shang, C.; Yang, M.; You, J. High Bandwidth Current Regulator Design for PMSM Based on Frequency Sweep Correction. IEEE Trans. Ind. Electron. 2024, 71, 1768–1778. [Google Scholar] [CrossRef]
- Franklin, G.; Powel, J.; Emami-Naeini, A. Feedback Control of Dynamical Systems; Prentice Hall: Hoboken, NJ, USA, 2015. [Google Scholar]
- Aström, K.J.; Hagglund, T. Automatic tuning of simple regulators with specifications on phase and amplitude margins. Automatica 1984, 20, 645–651. [Google Scholar] [CrossRef]
- Li, K. PID tuning for optimal closed-loop performance with specified gain and phase margins. IEEE Trans. Control Syst. Technol. 2013, 21, 1024–2030. [Google Scholar] [CrossRef]
- Chen, P.; Luo, Y. Analytical Fractional-Order PID Controller Design With Bode’s Ideal Cutoff Filter for PMSM Speed Servo System. IEEE Trans. Ind. Electron. 2023, 70, 1783–1793. [Google Scholar] [CrossRef]
- Elso, J.; Gil-Martinez, M.; Garcia-Sanz, M. Quantitative feedback control for multivariable model matching and disturbance rejection. Int. J. Robust Nonlinear Control 2017, 27, 121–134. [Google Scholar] [CrossRef]
- Fan, Y.; Cheng, Y.; Zhang, P.; Lu, G. An active disturbance rejection control design for the distillation process with input saturation via quantitative feedback theory. J. Process Control 2023, 128, 103029. [Google Scholar] [CrossRef]
- Maeda, Y.; Iwasaki, M. Circle Condition-Based Feedback Compensa-tion With Frequency Shaping for Improvement of Settling Performance. IEEE Trans. Ind. Electron. 2014, 61, 5500–5508. [Google Scholar] [CrossRef]
- Balestrino, A.; Corsanini, D.; Landi, A.; Sani, L. Circle-based criteria for performance evaluation of controlled dc–dc switching converters. IEEE Trans. Ind. Electron. 2006, 53, 1862–1869. [Google Scholar] [CrossRef]
- Balestrino, A.; Landi, A.; Sani, L. Complete root contours for circle criteria and relay autotune implementation. IEEE Control Syst. Mag. 2002, 22, 82–91. [Google Scholar]
- Chen, Y.; Moore, K.L. Relay feedback tuning of robust PID controllers with iso-damping property. IEEE Trans. Syst. 2005, 35, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Yaniv, O.; Mollov, S. Synthesizing all filtered proportional-integral and PID controllers satisfying gain, phase, and sensitivity specifications. IEEE Trans. Ind. Electron. 2023, 70, 2939–2947. [Google Scholar] [CrossRef]
- Tan, K.K.; Guo, W.Q.; Chieh, H.C.; Hagglund, T. Advances in PID Controllers; Advances in Industrial Control; Springer: London, UK, 2000. [Google Scholar]
- Mercader, P. Robust PID design based on QFT and convex-concave optimization. IEEE Trans. Control Syst. Technol. 2016, 25, 441–452. [Google Scholar] [CrossRef]
- Shang, C.; Yang, M.; You, J. A General Parallel Disturbance Controller for PMSM Drives Based on Frequency Domain Design. IEEE Trans. Ind. Electron. 2025, 72, 768–780. [Google Scholar] [CrossRef]
- Xia, B.; Huang, S.; Zhang, J.; Zhang, W.J.; Liao, W.; Huang, X.H.; Huang, S.D. Encoderless Deadbeat Predictive Current Control for SPMSM Drives With Online Parameter Identification. IEEE Trans. Transp. Electrif. 2025, 11, 761–773. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Hang, J.; Ding, S.C. Parallel Iron Loss Resistance Equivalent Impedance Model Method for Online Full Parameters Identification of PMSM. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 1783–1791. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, Z.Q.; Liang, D.W. Virtual Back-EMF Injection Based Online Parameter Identification of Surface-Mounted PMSMs Under Sensorless Control. IEEE Trans. Ind. Electron. 2025, 72, 5579–5590. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, M.; Shang, C.; Zeng, Q. A Frequency Domain Identification Method of General Mechanical Drive System. In Proceedings of the 2023 IEEE 4th China International Youth Conference on Electrical Engineering (CIYCEE), Chengdu, China, 8–10 December 2023; pp. 1–7. [Google Scholar]
- Novak, M.; Grobelna, I.; Nyman, U.; Blaabjerg, F. Application of Statistical Model Checking for Robustness Comparison of Power Electronics Controllers. In Proceedings of the 2024 IEEE 15th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Luxembourg, 18 September 2024; pp. 1–6. [Google Scholar]

| Key Parameter | Motor 1 | Motor 2 |
|---|---|---|
| Stator resistance | 0.063 Ω | 0.232 Ω |
| d-q axis inductance | 0.13 mH | 0.31 mH |
| Rated torque | 2.39 N·m | 1.92 N·m |
| Rated current | 7.07 A | 6.54 A |
| Rated speed | 3000 rpm | 2800 rpm |
| Power | 750 W | 600 W |
| Motor inertia | 1.64 × 10−4 kg·m2 | 3.62 × 10−4 kg·m2 |
| Pole pairs | 5 | 4 |
| Parameter | Motor 1 | Motor 2 |
|---|---|---|
| R/Ω | 0.068 Ω | 0.231 Ω |
| R error | 7.936% | 0.431% |
| Ld/mH | 0.125 mH | 0.295 mH |
| Ld error | 3.846% | 4.839% |
| Lq/mH | 0.129 mH | 0.324 mH |
| Lq error | 0.769% | 4.516% |
| Parameter | Motor 1 | Motor 2 |
|---|---|---|
| R/Ω | 0.069 Ω | 0.234 Ω |
| R error | 9.524% | 0.862% |
| Ld/mH | 0.121 mH | 0.353 mH |
| Ld error | 6.923% | 13.87% |
| Lq/mH | 0.137 mH | 0.284 mH |
| Lq error | 5.372% | 8.46% |
| Parameter Matching Degree | Cutoff Frequency | Bandwidth |
|---|---|---|
| Case 1: KL = 0.94, KR = 1.08 | 807.2 Hz | 1231.8 Hz |
| Case 2: KL = 1.04, KR = 0.98 | 1532.6 Hz | 1785.4 Hz |
| After Adjustment | 1186.4 Hz | 1446.5 Hz |
| Normalized Gain | Cutoff Frequency | Bandwidth |
| γ = 0.35 | 764.6 Hz | 810.4 Hz |
| γ = 0.5 | 1186.4 Hz | 1446.5 Hz |
| γ = 0.65 | 1623.8 Hz | 1843.0 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, P.; Yang, M.; Shang, C. Design of a High-Performance Current Controller for Permanent Magnet Synchronous Motors via Multi-Frequency Sweep Adjustment. Energies 2025, 18, 4306. https://doi.org/10.3390/en18164306
Lan P, Yang M, Shang C. Design of a High-Performance Current Controller for Permanent Magnet Synchronous Motors via Multi-Frequency Sweep Adjustment. Energies. 2025; 18(16):4306. https://doi.org/10.3390/en18164306
Chicago/Turabian StyleLan, Pengcheng, Ming Yang, and Chaoyi Shang. 2025. "Design of a High-Performance Current Controller for Permanent Magnet Synchronous Motors via Multi-Frequency Sweep Adjustment" Energies 18, no. 16: 4306. https://doi.org/10.3390/en18164306
APA StyleLan, P., Yang, M., & Shang, C. (2025). Design of a High-Performance Current Controller for Permanent Magnet Synchronous Motors via Multi-Frequency Sweep Adjustment. Energies, 18(16), 4306. https://doi.org/10.3390/en18164306






