Abstract
The widespread deployment of electric vehicles (EVs) has introduced substantial challenges to electricity pricing, grid stability, and renewable energy integration. This paper proposes a real-time pricing optimization framework for large-scale EV charging networks incorporating renewable intermittency, demand elasticity, and infrastructure constraints within a high-dimensional optimization model. The core objective is to dynamically determine spatiotemporal electricity prices that simultaneously reduce system peak load, improve renewable energy utilization, and minimize user charging costs. A rigorous mathematical formulation is developed integrating over 40 system-level constraints, including power balance, transmission capacity, renewable curtailment, carbon targets, voltage regulation, demand-side flexibility, social participation, and cyber resilience. Real-time electricity prices are treated as dynamic decision variables influenced by charging station utilization, elasticity response curves, and the marginal cost of renewable and grid-supplied electricity. The problem is solved over 96 time intervals using a hybrid solution approach, with benchmark comparisons against mixed-integer programming (MILP) and deep reinforcement learning (DRL)-based baselines. A comprehensive case study is conducted on a 500-station EV charging network serving 10,000 vehicles integrated with a modified IEEE 118-bus grid model and 800 MW of variable renewable energy. Historical charging data with ±12% stochastic demand variation and real-world solar and wind profiles are used to simulate realistic operational conditions. Results demonstrate that the proposed framework achieves a 23.4% average peak load reduction per station, a 17.9% improvement in renewable energy utilization, and user cost savings of up to 30% compared to baseline flat-rate pricing. Utilization imbalances across the network are reduced, with congestion mitigation observed at over 90% of high-traffic stations. The real-time pricing model successfully aligns low-price windows with high-renewable periods and off-peak hours, achieving time-synchronized load shifting and system-wide flexibility. Visual analytics including high-resolution 3D surface plots and disaggregated bar charts reveal structured patterns in demand–price interactions, confirming the model’s ability to generate smooth, non-disruptive pricing trajectories. The results underscore the viability of advanced optimization-based pricing strategies for scalable, clean, and responsive EV charging infrastructure management in renewable-rich grid environments.
1. Introduction
The rapid expansion of electric vehicle (EV) adoption has introduced new challenges to modern power grids, requiring innovative approaches to manage energy demand efficiently while ensuring grid stability. As the penetration of EVs continues to increase, conventional charging infrastructures struggle to accommodate the rising electricity consumption, leading to concerns regarding peak load surges, power imbalances, and supply–demand mismatches [1,2,3]. Real-time pricing strategies have emerged as a promising mechanism to dynamically modulate charging behaviors by incentivizing off-peak charging and balancing the overall electricity consumption. However, existing pricing models, primarily based on classical optimization techniques, encounter significant limitations in handling the inherent complexity of large-scale EV charging networks. The integration of renewable energy sources further exacerbates the problem, introducing variability and stochasticity, which traditional models fail to address effectively [4,5,6]. These limitations necessitate the exploration of novel computational paradigms capable of optimizing real-time pricing in a manner that is scalable, adaptive, and resilient to uncertainty.
The core challenge in real-time pricing optimization for EV charging lies in the combinatorial nature of the problem. The price-setting process must account for numerous interdependent factors, including consumer demand elasticity, grid load conditions, renewable generation availability, and economic constraints [7,8,9]. Classical optimization techniques, such as mixed-integer programming and heuristic-based algorithms, often suffer from prolonged computational times and suboptimal solutions when confronted with high-dimensional decision spaces. As a result, pricing models fail to provide truly real-time responses, limiting their effectiveness in dynamically adjusting to rapidly changing grid conditions [10,11]. Quantum annealing presents a fundamentally different approach, leveraging quantum mechanical properties such as superposition and tunneling to efficiently explore vast solution spaces [12,13]. By encoding the pricing problem into an energy-based representation, quantum annealing is capable of rapidly converging to optimal or near-optimal solutions, offering a computational advantage over traditional methods. The application of quantum annealing to real-time EV charging pricing optimization is largely unexplored in the existing literature, marking a significant opportunity for advancement. This paper introduces a quantum annealing-based framework for optimizing real-time pricing strategies in EV charging grids, presenting a novel approach to overcome the computational bottlenecks of classical techniques. The proposed model is designed to dynamically adjust EV charging prices in response to fluctuating grid conditions, renewable energy variability, and user demand patterns. By constructing an energy landscape that corresponds to the cost function of the pricing model, the quantum annealing process identifies the minimum energy state, which directly translates into the optimal pricing strategy. Unlike conventional models, this approach allows simultaneous evaluation of multiple pricing scenarios, significantly accelerating the decision-making process. Additionally, the integration of IoT-enabled data streams into the optimization framework ensures that real-time updates from EVs, charging stations, and grid sensors are incorporated into pricing adjustments. This adaptive mechanism not only enhances the responsiveness of the pricing model but also improves overall grid efficiency and sustainability by promoting the alignment of charging demand with renewable energy generation. The mathematical foundation of this work is grounded in a rigorous optimization framework that captures the complexities of EV charging dynamics. The problem formulation consists of an objective function that minimizes the overall cost of the energy supply while maintaining grid stability and user satisfaction. Constraints are designed to enforce power balance, prevent network congestion, ensure pricing fairness, and account for the influence of consumer behavior on demand elasticity. Furthermore, renewable energy integration is explicitly considered, allowing the model to dynamically adjust pricing based on the availability of green energy sources. The incorporation of quantum annealing enables the model to navigate complex, high-dimensional search spaces efficiently, ensuring that the real-time pricing mechanism remains computationally feasible for large-scale deployment. By leveraging the principles of quantum optimization, this work introduces a paradigm shift in how real-time energy pricing can be structured, offering a solution that is both scalable and adaptable to modern grid demands. This paper makes four key contributions to the field of smart grid optimization and EV charging management: First, it introduces a quantum annealing-based optimization framework that significantly enhances the efficiency of real-time pricing computations, addressing the scalability limitations of traditional methods. Second, it develops a comprehensive mathematical model that captures the intricate relationships between energy supply, grid stability, and consumer demand, ensuring that the pricing strategies remain economically viable while minimizing grid stress. Third, it integrates IoT-enabled real-time data streams into the optimization process, enabling dynamic adjustments that reflect evolving grid conditions and renewable energy fluctuations. Finally, this work presents an in-depth analysis of the implications of quantum-enhanced pricing on consumer behavior, energy market stability, and sustainable energy utilization, offering valuable insights for future smart grid applications. Through these contributions, this research not only advances the theoretical understanding of quantum computing applications in energy pricing but also provides a practical pathway for implementing next-generation smart charging infrastructures.
2. Literature Review
The optimization of real-time pricing in electric vehicle (EV) charging networks has been extensively explored in recent years, with various approaches emerging to tackle the challenges posed by fluctuating demand, grid stability concerns, and the integration of renewable energy sources. Traditional pricing mechanisms, such as time-of-use (TOU) pricing, critical peak pricing (CPP), and real-time pricing (RTP), have been widely adopted to influence EV user charging behavior and alleviate peak load burdens [13,14]. However, these conventional strategies often rely on predefined schedules or simple price elasticity models that fail to capture the highly dynamic and stochastic nature of modern smart grids. While heuristic and rule-based pricing frameworks have been proposed to enhance adaptability, they often struggle with computational efficiency and optimality in large-scale EV penetration scenarios. Thus, the necessity for more advanced optimization techniques has driven research towards machine learning-based, game-theoretic, and optimization-driven methodologies, though each approach presents limitations in scalability, convergence speed, and uncertainty modeling.
Table 1 presents a comparative overview of some representative optimization frameworks used in recent studies on EV charging coordination. The table highlights differences across four key dimensions: optimization methodology, grid constraint modeling, behavioral integration, and scalability.

Table 1.
Comparative overview of optimization frameworks for EV charging.
Traditional approaches such as multi-task learning and Bayesian LSTM focus on demand forecasting or uncertainty modeling but often simplify physical grid limitations and user responsiveness. Federated deep reinforcement learning (DRL) and psychological models introduce decentralized or behavioral elements yet remain constrained in terms of system-wide operational complexity or deployment scale.
In contrast, the proposed quantum annealing-based framework distinguishes itself by simultaneously addressing 45 system-level constraints—including power balance, carbon targets, cyber resilience, and affordability—and incorporating elasticity-aware user modeling. Moreover, it demonstrated scalability in large-scale simulations involving 500 charging stations and 10,000 vehicles. This comparison underscores the novelty and comprehensiveness of our contribution in bridging optimization rigor, behavioral realism, and practical scalability in dynamic EV–grid environments.
Classical optimization techniques, including mixed-integer linear programming (MILP), nonlinear programming (NLP), and convex optimization, have been extensively applied to real-time pricing models for EV charging. These methods provide structured solutions by formulating pricing as an optimization problem constrained by grid conditions, energy supply, and consumer preferences. Many studies have proposed centralized and decentralized pricing mechanisms using convex optimization to balance energy supply with charging demand while minimizing operational costs for both consumers and service providers [15,16]. However, these traditional optimization methods struggle with high-dimensional, nonconvex problems, particularly in scenarios where large-scale EV adoption introduces complex, interdependent constraints. Furthermore, classical solvers often exhibit significant computational delays, rendering them impractical for real-time applications where rapid decision-making is required.
With the increasing complexity of energy systems, reinforcement learning (RL) and deep learning (DL)-based models have gained traction in optimizing real-time pricing for EV charging. Several studies have leveraged deep reinforcement learning (DRL) frameworks to enable adaptive pricing mechanisms that learn optimal charging strategies through interaction with historical and real-time data. Actor–critic models, Q-learning, and policy gradient methods have demonstrated effectiveness in capturing dynamic pricing responses, with some works integrating demand-side management (DSM) strategies to improve grid resilience [17,18,19]. However, these RL-based approaches are often data-intensive and require extensive training periods, making their deployment challenging in rapidly evolving grid environments. Additionally, their reliance on simulated data can result in suboptimal generalization when they are deployed in real-world conditions where uncertainty and external factors significantly influence pricing strategies [20].
Game-theoretic models have also been explored to analyze the interactions between EV users, charging service providers, and grid operators. Nash equilibrium-based formulations have been applied to design competitive pricing strategies that balance user satisfaction with economic profitability [21,22]. Stackelberg game models have been widely utilized to structure hierarchical decision-making frameworks where service providers act as leaders and EV users respond as followers to price signals. While game theory offers valuable insights into market dynamics, its applicability in real-time settings remains limited due to its reliance on equilibrium assumptions and computationally expensive solution processes. Moreover, real-world charging behaviors are influenced by numerous socio-economic factors that are difficult to encode into game-theoretic frameworks, reducing their practicality in highly uncertain environments [23,24]. The integration of renewable energy sources into EV charging pricing strategies has further complicated the optimization landscape. Many studies have proposed hybrid energy management systems that incorporate renewable generation forecasts into pricing models, allowing for price adjustments based on solar and wind availability. Stochastic optimization techniques, including robust optimization and distributionally robust optimization (DRO), have been employed to mitigate uncertainties in renewable energy supply, enhancing the reliability of dynamic pricing mechanisms [25,26]. However, these methods often rely on probabilistic assumptions that may not accurately reflect real-time fluctuations, leading to inefficiencies in grid operation. Additionally, the computational complexity of solving stochastic optimization problems in large-scale EV networks presents scalability concerns, particularly during attempts to implement real-time pricing adjustments.
Quantum computing, particularly quantum annealing, has emerged as a novel computational paradigm that offers significant advantages over classical approaches in solving large-scale optimization problems. Unlike classical optimization algorithms, which rely on iterative searching and gradient-based solvers, quantum annealing exploits quantum mechanical principles such as superposition and tunneling to explore vast solution spaces more efficiently [1,27,28]. While quantum computing applications in power systems optimization remain relatively nascent, recent advancements in hardware and algorithmic design have demonstrated promising results in combinatorial optimization problems. Several studies have explored the potential of quantum annealing in unit commitment, optimal power flow, and energy dispatch optimization, showcasing its ability to outperform classical solvers in complex problem spaces. However, the application of quantum annealing to real-time pricing optimization in EV charging grids remains largely unexplored, representing a significant gap in the literature [29].
3. Optimization and the Solution Approach
To rigorously capture the interplay between real-time pricing, electric vehicle (EV) charging behavior, and grid-level operational dynamics, we now formulate the core mathematical architecture and optimization methodology underpinning this research [30,31,32]. This section presents the theoretical foundation of our proposed quantum annealing-assisted real-time pricing framework, beginning with the formal definition of the objective function and system constraints, followed by the detailed construction of the quantum-aware optimization process. The formulation is designed to reflect realistic power system behaviors, integrate demand elasticity, encode renewable availability, and respect physical grid limitations [33]. By leveraging a structured and analytically expressive mathematical model, we enable an accurate and adaptable representation of the complex, nonlinear relationships embedded within the smart EV charging ecosystem [34]. Subsequently, we introduce the optimization methodology employed to solve the proposed formulation, which is built upon the quantum annealing paradigm and enhanced through strategic model encoding and real-time data integration [35]. The combined modeling and methodological architecture forms the basis of a responsive, efficient, and scalable solution for next-generation energy pricing under uncertainty and high EV penetration [36].
To address the multifaceted challenges of EV charging coordination in renewable-rich smart grids, this study formulates a comprehensive multi-objective optimization framework. Rather than treating cost, behavior, renewable utilization, and computational efficiency as isolated targets, we structure the problem around four interrelated objective functions. These functions are designed to minimize overall system cost and congestion, promote elasticity-driven behavioral response, enhance renewable energy integration, and optimize the performance of the quantum annealing process itself. Although expressed separately in Equations (1)–(4), these objectives can be interpreted as components of an integrated formulation. In practice, they may be scalarized through a weighted combination to form a unified optimization objective, or selectively transferred into constraints depending on system-level policy priorities. This formulation allows for both modular adaptation and policy-driven flexibility, supporting a wide range of real-world deployment scenarios.
Electric vehicle charging cost optimization is critical for balancing grid efficiency and economic feasibility. The objective function here integrates multiple factors: the first term ensures the cost-effectiveness of EV charging through the ratio of demand to grid capacity, influenced by elasticity parameters , while the second term accounts for renewable energy penetration, normalizing renewable generation availability with charging demand. Additionally, terms involving and regulate supply–demand mismatches, mitigating curtailment losses and optimizing cost recovery across different market participants.
Figure 1 illustrates the overall architecture of the proposed quantum-enhanced real-time pricing framework for electric vehicle (EV) charging under renewable-rich smart grid conditions. The model integrates multiple input sources—including real-time EV charging demand, renewable generation forecasts, grid operational constraints, and elasticity-related social parameters—and encodes them into a multi-objective optimization problem. This problem is then solved using a quantum annealing-based optimizer which minimizes cost, congestion, and inequity while satisfying over 45 system-level constraints.

Figure 1.
Overall framework of the quantum-enhanced real-time pricing model for elasticity-aware EV charging in renewable-rich smart grids.
The outputs of the optimizer include dynamic, location-sensitive, and time-sensitive pricing signals that are responsive to both user behavior and grid conditions. These pricing signals are continuously updated in real time and fed back to EV users and the charging infrastructure via IoT-enabled communication systems. The resulting impacts, such as peak load reduction, cost savings, and improved fairness (as reflected by affordability metrics and Gini coefficient shifts), are evaluated and looped into subsequent pricing adjustments. This closed-loop system ensures that the framework remains adaptive, equitable, and scalable in real-world deployment scenarios.
Consumer behavior plays a significant role in the effectiveness of real-time pricing, and this formulation encapsulates user responsiveness to dynamic pricing signals. The first term represents elasticity-driven demand shifts, based on deviations from baseline consumption patterns, where models price elasticity and governs response sensitivity. The second term emphasizes demand shifting potential, linking energy demand shifts to pricing strategies . Furthermore, congestion management mechanisms introduce penalties proportional to station congestion levels, ensuring grid reliability and mitigating overload risks.
Renewable energy integration is a pivotal factor in optimizing charging grid economics. This formulation considers renewable availability constraints, normalizing energy dispatch by overall grid power adjusted by system uncertainty . Furthermore, the model incorporates renewable intermittency factors, ensuring forecasting accuracy and mitigating power fluctuation impacts. Terms with capture curtailment penalties, incentivizing excess generation utilization, while addresses carbon offset pricing, leveraging carbon credit mechanisms for environmental sustainability.
Quantum annealing mechanisms drive the real-time pricing optimization framework. This formulation constructs an energy landscape representation where annealing parameter determines the interaction between system energy constraints and cost penalties . Quantum state evolution equations model the system’s transition across energy states, ensuring robust convergence to globally optimal pricing solutions. Additionally, the annealing step optimization, captured by , aligns with practical constraints, enabling computational efficiency and real-time decision-making in large-scale grid environments.
Ensuring the power balance is fundamental to maintaining stable smart grid operation. This constraint guarantees that the sum of the total supplied power—including electric vehicle charging demand, grid energy dispatch, and renewable generation—matches the aggregated demand from EV users, general grid consumers, and system losses. The incorporation of renewable energy into this balance is critical for sustainability, reducing reliance on conventional energy sources while maintaining equilibrium in real-time pricing decisions.
Voltage and frequency stability are essential to maintaining the reliability of an electric vehicle charging grid. This equation represents the nodal voltage variations and power flows across transmission lines, ensuring that voltage levels at different buses adhere to operational thresholds. The term represents line reactance, which influences voltage stability, while denotes power injections at various nodes. By controlling voltage deviations within prescribed safety margins, this constraint ensures that grid disturbances do not disrupt the optimal charging process.
To prevent overloading of charging stations, each EV charger is constrained to operate within predefined maximum power limits. The upper bound ensures that individual charging stations do not exceed their rated capacity, safeguarding grid components from overheating and ensuring the longevity of the charging infrastructure. This constraint is particularly crucial for real-time pricing strategies since price signals must be set in a way that prevents excessive demand from overwhelming local station capacities.
Network congestion management plays a critical role in optimizing electric vehicle charging schedules. This constraint ensures that the power flow along each transmission line remains within its maximum allowable capacity , preventing thermal overloading and voltage collapse. Overloaded transmission lines can severely disrupt real-time pricing mechanisms, leading to inefficient grid operation. By integrating congestion-aware pricing models, this constraint helps redistribute charging demand across different times and locations to enhance grid flexibility.
Renewable energy availability is inherently time-dependent, with fluctuations driven by meteorological conditions. This constraint ensures that the dispatched renewable power at each charging station does not exceed the locally available wind and solar generation at a given time. The terms and represent wind and photovoltaic energy availability, respectively. By dynamically adjusting real-time prices based on renewable output, the system incentivizes EV users to charge when renewable generation is high, promoting carbon-free mobility.
Price volatility is a significant concern in real-time EV charging markets. This constraint enforces upper and lower bounds on the price adjustments applied at each charging station, preventing extreme price swings that could lead to economic inefficiencies or discourage EV adoption. The terms and define the minimum and maximum permissible price levels. By keeping prices within reasonable limits, this condition fosters a balanced trade-off between grid efficiency and consumer affordability.
Affordability is a key factor in the successful deployment of electric vehicle charging infrastructure. This constraint ensures that the cumulative charging cost incurred by an EV user does not exceed the affordability threshold , which may be determined based on average consumer income or policy regulations. By incorporating affordability constraints into the optimization framework, the system promotes equitable access to charging services while maintaining economic sustainability for grid operators.
Grid flexibility plays a pivotal role in ensuring that real-time pricing mechanisms do not cause supply shortages. This constraint ensures that the power allocated for EV charging, scaled by elasticity factor , does not exceed the sum of the available grid dispatch and renewable power generation, accounting for system losses. By enforcing this restriction, the system prevents instability and over-reliance on expensive emergency energy sources.
Abrupt fluctuations in real-time pricing can lead to erratic charging behaviors, negatively impacting both grid stability and consumer trust. This constraint ensures that the absolute change in charging price from one time step to the next does not exceed a predefined maximum adjustment , thereby maintaining smooth transitions in price signals and preventing unnecessary volatility.
Market equilibrium must be preserved when setting real-time prices for EV charging. This equation ensures that the aggregated charging power, weighted by pricing factors , remains within the available energy supply, combining both conventional grid electricity and renewable sources. This constraint is particularly critical in preventing excessive demand peaks that could lead to grid congestion or supply shortages.
Charging station capacities must be respected to ensure seamless service. This constraint states that the total power drawn by EVs at each time step, scaled by demand response factor , should not exceed the physical capacity of the charging infrastructure. This ensures that individual stations are not overwhelmed by sudden spikes in demand.
Carbon footprint considerations are an essential part of sustainable pricing strategies. This constraint ensures that the cumulative energy consumption from EV charging, normalized by carbon intensity factor , does not exceed a predefined carbon cap . This incentivizes grid operators to structure pricing in a way that promotes charging during low-carbon periods, such as when renewable generation is high.
Cybersecurity risks must be accounted for when integrating smart charging infrastructure. This equation imposes a limit on the aggregated charging power that can be controlled by a single cyber entity, ensuring that potential cyberattacks (modeled through risk factor ) do not compromise the grid. A predefined security threshold is set to mitigate large-scale coordinated attacks.
To assess the impact of cyberattacks—particularly FDI—on the proposed real-time pricing strategy, we simulated adversarial scenarios in which key input variables (e.g., demand response coefficients and charging power readings) were partially manipulated. In one representative case, up to 15% of charging stations reported inflated demand values during peak hours. Under this condition, the pricing model exhibited a 12.6% deviation in real-time tariffs compared to the baseline, resulting in distorted demand shifts and localized grid stress. Furthermore, when elasticity parameters were targeted with ±10% perturbations, the peak load reduction capability of the system dropped from 23.4% to 17.1%. These findings underscore the vulnerability of optimization outcomes to cyber–physical interference and highlight the importance of incorporating anomaly detection and data validation mechanisms into the real-time pricing framework. Constraint (17) has been extended with quantifiable risk impact metrics to reflect these insights.
Battery degradation is an important consideration when designing real-time pricing models. This constraint ensures that the total degradation effect, modeled by the function , remains within a predefined acceptable threshold , preventing excessive wear and tear on EV batteries caused by aggressive charging incentives.
User engagement in demand response programs is critical to the success of real-time pricing. This equation ensures that the total user response to price signals, scaled by social behavior factors , does not exceed a predefined engagement cap . This prevents excessive reliance on user participation, which could lead to demand imbalances if overestimated.
To ensure resilience in EV charging operations, this constraint enforces that the total reserve power capacity, including backup generation resources, must be sufficient to meet unexpected deviations in demand. The equation accounts for real-time charging demand, grid power supply, and renewable availability fluctuations. Maintaining an adequate power reserve prevents service disruptions due to unanticipated load surges, ensuring that EV users experience minimal charging delays.
Peak load management is a critical component of demand-side optimization in EV charging grids. This constraint ensures that sufficient load-shifting strategies are in place to balance the difference between peak and off-peak demand. The parameter represents the aggregate shifted load across all charging stations, helping to alleviate stress on the grid during peak hours. By dynamically adjusting pricing strategies, this constraint facilitates effective load balancing and grid stability.
Flexibility in charging demand is essential for ensuring efficient real-time pricing adjustments. This equation constrains the proportion of demand that can be dynamically adjusted within each time period, preventing excessive fluctuations that might destabilize grid operations. The flexibility factor is divided by the demand elasticity coefficient , ensuring that changes in charging power remain within the allowable threshold . This helps the system to avoid unintended consequences such as extreme demand shifts or overcorrections in price response.
Economic sustainability is a key consideration in designing real-time pricing strategies for EV charging grids. This constraint ensures that the aggregated revenue from charging demand, weighted by market influence factors , meets or exceeds a predefined profitability threshold . By maintaining a balance between consumer affordability and operator profitability, this condition supports long-term financial viability while encouraging continued investment in charging infrastructure.
Charging efficiency constraints ensure that the power drawn by electric vehicles does not exceed the combined available supply from the grid and renewable sources. Here, represents the efficiency factor of the charging process, accounting for energy conversion losses. This constraint guarantees that the power supplied to EVs remains within sustainable limits, preventing excessive grid stress and optimizing the integration of renewable energy.
To ensure numerical stability and avoid infeasibility arising from potential constraint redundancy, particularly in the supply–demand balance equations (e.g., Equations (12), (14), and (24)), we explicitly introduced slack variables into the formulation. These slack terms absorb minor imbalances that may occur due to modeling approximations, sampling granularity, or conflicting resource availability. By penalizing these slack variables in the objective function with a sufficiently large coefficient, the model discourages their activation under normal operating conditions while maintaining feasibility during edge cases.
In addition, we carefully verified the linear independence of the key equality constraints through symbolic matrix decomposition and rank analysis. The decomposition results confirmed that, while some constraints share structural similarities (especially in multi-energy coupling), they are not linearly dependent across all time steps due to the temporal and sectoral differentiation. We retain these constraints to preserve physical interpretability and allow flexibility in solving the problem under varied boundary conditions and input uncertainties.
Demand-side management (DSM) strategies play a crucial role in optimizing EV charging schedules. This constraint ensures that the total charging demand, adjusted by consumer response elasticity , does not exceed the allocated DSM capacity . By enforcing this condition, the system dynamically regulates consumer participation in load-shifting programs, enhancing grid flexibility and cost-effectiveness.
To mitigate peak demand spikes, this constraint enforces a minimum load-shifting requirement. The parameter represents the total power that is actively shifted from peak to off-peak periods, ensuring that peak-hour loads do not surpass grid safety margins. This optimization technique enhances system resilience, reduces operational costs, and improves overall efficiency by aligning charging demand with periods of high renewable generation.
Carbon footprint control is vital for ensuring that EV charging supports sustainability goals. This constraint limits the total emissions impact of charging demand by normalizing power consumption with the carbon intensity factor . The predefined cap prevents excessive carbon emissions, incentivizing cleaner energy usage and promoting environmentally responsible charging behavior.
Grid resilience must be maintained in the face of demand fluctuations and potential supply disruptions. This equation ensures that the total backup energy capacity meets or exceeds a predefined resilience threshold . This guarantees that sufficient emergency power reserves are available to handle contingencies such as sudden demand surges, renewable energy shortfalls, or unexpected grid failures.
Surge pricing mechanisms must be carefully controlled to prevent excessive financial burdens on EV users. This constraint ensures that the total increase in price-sensitive demand, weighted by a risk factor , does not exceed a predefined cap . By incorporating this safeguard, the system prevents exploitative pricing fluctuations while allowing for controlled, dynamic price adjustments that balance supply and demand effectively.
Energy storage integration is essential for balancing supply and demand in EV charging grids. This constraint ensures that the combined power dispatch and energy drawn from storage facilities is sufficient to cover the net demand at all times. By allowing storage systems to absorb excess renewable generation and discharge when demand peaks, this condition improves grid flexibility and prevents power shortages.
Elasticity-based pricing mechanisms ensure that the total power drawn by EVs, scaled by elasticity factor , does not exceed a predefined system-wide charging limit . This prevents excessive surges in demand that could compromise grid stability. By dynamically adjusting real-time pricing signals, the system encourages load redistribution to maintain operational efficiency.
To better reflect real-world behavior, the static elasticity factor in Equation (31) has been extended to a time- and context-dependent form. Specifically, we adopted a piecewise linear approximation of a logistic function where elasticity decreases as the urgency of demand increases. This adjustment enables the model to capture lower flexibility during critical demand periods (e.g., late-stage EV charging), thus enhancing realism without significantly increasing computational complexity.
Availability constraints ensure that charging stations provide an adequate supply of energy to meet consumer demand. The left-hand side models the actual energy available for charging, weighted by availability factor , while the right-hand side represents the minimum energy required by active EV users. This condition guarantees that no user experiences unexpected shortages or long wait times due to inadequate energy supply.
Infrastructure capacity constraints prevent excessive strain on the charging network. This equation ensures that the aggregated power demand from all EVs, normalized by station-specific capacity factors , does not exceed an overall network limit . This prevents congestion, station malfunctions, and suboptimal charging experiences for consumers.
To maintain price stability, this constraint enforces gradual changes in charging prices. The total price adjustments, weighted by a control factor , must remain within a smoothing limit . This ensures that EV users do not face abrupt cost increases, preserving consumer trust while enabling controlled, market-driven pricing strategies.
Demand-side participation constraints ensure that a sufficient number of consumers actively respond to price incentives. The left-hand side represents total user response, scaled by a participation factor , while the right-hand side specifies a minimum target for demand-side management (DSM). This condition is essential for ensuring that real-time pricing strategies achieve their intended effects on grid stability and load balancing.
Grid stability is a fundamental concern when implementing real-time EV charging pricing. This constraint ensures that the total power drawn from charging demand, scaled by stability factor , remains within a predefined threshold . By preventing excessive fluctuations in demand, this condition enhances the resilience of grid operations while ensuring a reliable power supply.
Dynamic price adjustments must be controlled to prevent sharp fluctuations that could disrupt market behavior. This constraint ensures that the aggregate price-induced demand surge, weighted by a limiting factor , does not exceed a predefined cap . This maintains the smooth operation of real-time pricing mechanisms while mitigating unintended consequences such as panic-driven consumer responses.
Ensuring gradual transitions in pricing is key to consumer acceptance of dynamic tariffs. This constraint limits the total price adjustment across all charging stations within a given time step, preventing drastic fluctuations that could deter EV adoption or cause market instability. The cap ensures that price modifications are incremental and predictable.
Participation in demand-side response (DSR) programs must meet a minimum engagement level for effective load balancing. This constraint ensures that total consumer response, adjusted by elasticity factor , meets or exceeds a defined lower bound . This guarantees that enough users adjust their charging behavior in response to real-time pricing, facilitating effective grid management.
Renewable energy integration into EV charging must be optimized to minimize curtailment losses. This constraint ensures that the total amount of renewable power utilized for charging, adjusted by curtailment factor , does not exceed the available renewable generation limit . This maximizes renewable utilization while preventing energy waste.
To mitigate financial risks in real-time pricing, this constraint ensures that the total deviation in price-driven demand shifts, scaled by compensation factor , remains within a permissible limit . This prevents extreme price fluctuations that could financially disadvantage consumers or operators.
Ensuring grid resilience against unforeseen demand spikes or supply disruptions is critical. This constraint mandates that the total power allocated to resilience-focused strategies, such as energy storage and reserve dispatch, meets a predefined threshold . This guarantees reliable system operation even under extreme conditions.
EV charging infrastructure must meet consumer demand reliably. This constraint ensures that the total charging power available, weighted by usage factor , satisfies a predefined demand target . This prevents the underutilization of charging stations while ensuring availability during peak periods.
Grid stability requires an adequate level of control to prevent frequency and voltage deviations. This equation enforces a minimum power allocation for stability-oriented operations, ensuring that system-wide stability thresholds are met at all times.
Social engagement in real-time pricing must be maintained at a sufficient level to drive effective consumer participation. This constraint ensures that the total user-driven demand adjustments, scaled by engagement factor , meet a required participation level . This fosters active consumer involvement in optimizing grid operations through behavioral incentives.
To enable QUBO transformation for quantum annealing, all continuous variables (e.g., ) were discretized using 5-bit binary encoding, allowing 32 quantization levels. Constraints from Equations (5)–(45) were reformulated as quadratic penalty terms and embedded into the objective function. Penalty weights were tuned empirically to ensure constraint satisfaction without dominating the original cost function, typically selected from a calibrated range (e.g., to ) based on observed violation rates in preliminary runs.
The presence of exponent terms such as and in the cost and degradation functions introduces nonconvexity into the optimization problem, which challenges global tractability. To address this, our approach employs quantum annealing (QA), a metaheuristic known for its capability in navigating nonconvex and combinatorial landscapes. Although QA does not guarantee global optimality, its stochastic search mechanism and tunneling effect make it particularly effective for escaping local minima in high-dimensional discrete spaces. In this study, we calibrated the annealing parameters via multiple runs and analyzed convergence consistency to enhance reliability. Moreover, to assess the sensitivity of the optimization results to the exponent values, we performed a parameter perturbation test where and were varied within of their nominal values. The results (see Table 1) reveal that, while the absolute cost varied slightly, the optimal scheduling pattern and energy allocation decisions remained robust, indicating that the QA-driven solution is stable under moderate nonlinear coefficient variations.
These analyses provide practical assurance regarding the QA solver’s capacity to address nonconvexity in our model and confirm that the exponent terms, while inducing complexity, do not destabilize the solution framework.
To improve the reproducibility and technical transparency of our QUBO-based pricing framework, we provide further detail on the design choices and implementation process: First, we selected a 5-bit encoding resolution for continuous decision variables such as price levels and energy dispatch quantities. This resolution was chosen after empirical testing, as it offers a practical balance between solution granularity and hardware feasibility. Higher-resolution encoding (6 or more bits) leads to excessive qubit consumption and frequent embedding failures, while lower resolutions (3 or 4 bits) result in notable degradation of solution quality and coarse quantization effects. The 5-bit scheme consistently produced stable results with minimal variation in cost and constraint satisfaction across runs. Additionally, we provide a concrete example of a system-level constraint transformed into a quadratic penalty form, illustrating how inequality conditions (such as charging power or network capacity limits) are reformulated within the QUBO structure. This process involved scaling penalty weights to ensure constraint dominance without distorting the original objective. Penalty magnitudes ranging from 103 to 105 were calibrated based on the scale of the cost function and tested for sensitivity. Performance remained stable under ±30% weight variation. From a hardware perspective, the QUBO models were compiled and embedded on the D-Wave Advantage 5000Q system (D-Wave Systems Inc., Burnaby, BC, Canada). using minor-embedding tools with adaptive chain strength tuning. We applied post-processing steps to handle broken chains via majority vote decoding, and adjusted the annealing schedule to improve constraint satisfaction in dense problem instances. All QUBO instances were verified to remain within the logical qubit budget, and constraint structures were monitored for successful embedding. These refinements ensured that our framework is both practically implementable and theoretically sound across a range of realistic EV pricing environments.
4. Results
The case study was conducted on a large-scale urban EV charging network with 500 charging stations distributed across a metropolitan area. Each station is equipped with Level 2 and DC fast chargers, accommodating a total of 10,000 EVs with varying battery capacities ranging from 40 kWh to 100 kWh. Charging power levels are categorized into 7.2 kW (Level 2) and 150 kW (DC fast charging). The charging stations are connected to a smart grid infrastructure that incorporates 50% renewable energy penetration, consisting of 500 MW of solar photovoltaic (PV) capacity and 300 MW of wind power capacity. The time horizon for the case study spanned 24 h, divided into 96 time steps, each representing a 15 min interval. To account for real-world uncertainty, historical demand profiles from three years of EV charging data were utilized, with stochastic variations modeled using Gaussian distribution with a mean deviation of ±12% to reflect fluctuations in consumer behavior. The electricity price baseline was set at USD 0.12/kWh, with real-time dynamic pricing adjustments constrained between USD 0.05/kWh and USD 0.35/kWh. The power grid supporting the EV charging infrastructure follows the IEEE 118-bus system, with additional modifications to integrate distributed renewable energy sources and battery energy storage systems (BESS) totaling 200 MWh. The system includes 35 transmission lines, 12 substations, and 4 large-scale energy hubs, each capable of managing up to 100 MW of distributed generation. To simulate grid congestion and demand peaks, synthetic traffic patterns were integrated into the model, considering EV movement patterns from a 1.2 million population urban dataset. The charging demand profile included both residential and commercial users, with 70% of charging occurring overnight and 30% during peak commuting hours (7:00 a.m.–9:00 a.m. and 5:00 p.m.–7:00 p.m.). Renewable energy intermittency was simulated using real-world solar and wind generation profiles from the National Renewable Energy Laboratory (NREL) database, introducing power supply variability of ±20% from forecasted values.
The computation environment for the quantum annealing-based pricing optimization was implemented on a hybrid D-Wave Advantage 5000Q system and a classical high-performance computing (HPC) cluster. The HPC cluster consists of Intel Xeon Platinum 8380 processors with 64 cores, 1 TB of RAM, and NVIDIA A100 GPUs for pre-processing large-scale datasets and running comparative classical optimization models. The quantum annealing process was executed using D-Wave’s Ocean SDK, leveraging the Quadratic Unconstrained Binary Optimization (QUBO) formulation to map the real-time pricing problem onto the quantum system. The optimization was performed over 500 iterations per time step, ensuring convergence within 5 s per pricing update cycle, making real-time implementation feasible. Benchmark comparisons were conducted against mixed-integer linear programming (MILP) and deep reinforcement learning (DRL)-based approaches, evaluating criteria including computational time, convergence stability, pricing efficiency, and grid reliability.
In this study, the notion of cyberattacks is abstracted as deliberate disturbances in load measurements or price signals that affect optimal decision-making. Rather than modeling specific intrusion vectors or communication infrastructure, we focus on the operational-level impact of data distortion that may arise from malicious interference or misreporting. The attack is implemented as a stochastic perturbation to nodal demand inputs with defined intensity levels (e.g., ±20%) and targeted time windows. This abstraction allows us to evaluate the system’s resilience to adversarial information while keeping the optimization formulation tractable. Detailed modeling of communication layers and cybersecurity protocol breaches is beyond our current scope and is reserved for future work.
To improve the interpretability of simulation outcomes, we provide a direct mapping between the experimental results and the underlying optimization components. The observed 23.4% reduction in peak load, as shown in Figure 2, is primarily attributable to the elasticity-driven load shifting captured in Objective Function (2) and reinforced by the congestion penalties in Constraint (8). Similarly, the 17.9% increase in renewable energy utilization resulted from dynamic dispatch decisions encoded in Objective Function (3), which directly promotes alignment between charging demand and the real-time availability of wind and solar power (see Constraint (9)). The 30% reduction in user cost reported in Figure 3 reflects the effectiveness of the spatiotemporal price adjustments derived from Objective Function (1) and bounded by affordability constraints such as Constraint (11). These mappings ensure that each outcome is traceable to a corresponding model structure, enhancing transparency between the formulation and system behavior.

Figure 2.
Density distribution of renewable energy vs. charging demand.

Figure 3.
Renewable energy utilization across time periods.
To assess the solution quality of quantum annealing beyond runtime performance, we compared the obtained results against classical solvers such as branch and bound (B&B) and simulated annealing (SA). Across 10 representative test instances, QA achieves convergence within 5 s with an average cost deviation of less than 3.7% compared to B&B-derived near-optimal baselines. The annealing schedule was fixed using D-Wave’s default time-dependent profile, and the embedding was validated using chain strength calibration to minimize broken qubits. These results indicate that QA provides competitive solutions with substantial computational efficiency under high-dimensional constraints.
Figure 1 provides a detailed temporal breakdown of EV charging demand, renewable energy availability, and real-time pricing fluctuations over a 24 h period, revealing critical insights into the dynamics of EV–grid interactions. The EV charging demand follows a well-defined diurnal pattern, exhibiting clear peaks during the morning rush hour (7:00 a.m.–9:00 a.m.) and evening commute (5:00 p.m.–7:00 p.m.). During these peak hours, the average demand per charging station rises to 450 kW, with a cumulative system-wide demand exceeding 225 MW across all 500 charging stations. In contrast, during off-peak hours, particularly between midnight and 5:00 a.m., demand falls to an average of 180 kW per station, corresponding to a system-wide demand of approximately 90 MW. This demand variability creates operational challenges for the power grid, as high fluctuations in energy consumption can introduce instability in voltage regulation and power distribution. A key observation from the figure is the mismatch between EV charging demand and renewable energy availability. Solar generation is entirely absent during the nighttime hours, gradually increasing from 6:00 a.m., peaking at 500 MW around 12:00 p.m., and tapering off by 6:00 p.m. Wind energy, on the other hand, remains relatively stable, fluctuating between 150 MW and 250 MW throughout the day, with a mean availability of approximately 200 MW. However, the peak charging demand occurs when solar availability is minimal: at 8:00 a.m. when solar output is still below 100 MW and again at 6:00 p.m. when solar production has already declined below 50 MW. This discrepancy forces the grid to rely heavily on conventional power sources during peak hours, increasing overall energy costs and carbon emissions. Meanwhile, during the middle of the day, when solar output is at its maximum, EV demand is relatively low, leading to potential energy curtailment if excess renewable generation cannot be stored or redirected efficiently. To further evaluate performance under large-scale deployment scenarios, we conducted a comparative scalability test using 100-, 300-, and 500-station configurations. For each scale, we compared our QA-based model with classical MILP and DRL baselines in terms of runtime, cost performance, and constraint satisfaction.
The results show that, while MILP yields near-optimal solutions for small systems (≤100 stations), its runtime increases exponentially, exceeding 1200 s for the 500-station case. DRL offers better scalability but suffers from higher suboptimality and constraint violations. In contrast, QA maintains solution feasibility with <5% cost deviation from MILP while achieving convergence in under 6 s for all tested sizes. These results demonstrate QA’s favorable balance between computational speed and solution quality in large-scale applications.
Figure 4 presents the distribution of charging station utilization across the 500 EV charging stations, offering a spatial overview of network congestion and infrastructure load balancing. The utilization rate follows a normal distribution with a mean of 50% and a standard deviation of 15%, indicating that most stations operate at between 35% and 65% of their full capacity. However, a subset of stations experiences extreme congestion, reaching utilization rates of over 90%, particularly in densely populated urban areas and commercial districts where demand is concentrated. Conversely, some suburban stations remain underutilized, with utilization rates as low as 15%, highlighting disparities in charging infrastructure deployment and demand distribution. High-utilization stations typically correlate with areas experiencing strong commuter traffic, where the availability of public charging infrastructure is limited relative to demand. These stations often face prolonged queue times during peak hours, exacerbating grid stress and requiring targeted interventions such as dynamic pricing adjustments or infrastructure expansion. On the other hand, low-utilization stations suggest either an oversupply of chargers in specific locations or a lack of user awareness regarding charging availability. Addressing these disparities requires a combination of demand forecasting, spatially adaptive pricing strategies, and real-time grid monitoring to redistribute load efficiently across the network.

Figure 4.
Temporal analysis of EV charging demand, renewable energy availability, and real-time pricing adjustments.
Although the proposed framework demonstrated promising computational performance using a quantum annealing-based optimizer, it is important to acknowledge several practical considerations that affect real-world deployment. Current quantum hardware, such as the D-Wave Advantage system used in this study, remains limited in accessibility and requires cloud-based API access, which may introduce latency and cost constraints in certain operational contexts. Moreover, quantum annealing results are subject to environmental noise and hardware-specific tuning, which may impact solution quality under tight optimization tolerances.
To mitigate these challenges, our implementation is structured as a hybrid workflow, where quantum optimization is used for core decision variables (e.g., price vector ) and classical computation handles data pre-processing, constraint checking, and fallback execution. In scenarios where the quantum solver is unavailable or unstable, a classical solver (e.g., MILP) can be dynamically engaged to maintain operational continuity. Future improvements in quantum hardware and the increasing maturity of hybrid solvers are expected to enhance the practicality of this approach.
Figure 5 presents a two-dimensional density distribution capturing the relationship between renewable energy availability (MW) and EV charging demand (kW) over a 24 h period. The contour patterns highlight the probability density of different energy supply–demand pairings, offering insights into the frequency of various operational conditions. The densest regions in the plot occur at between 200 MW and 450 MW of renewable energy availability, where the majority of charging demand clusters between 150 kW and 350 kW per station. This suggests that, under typical grid conditions, there is a moderate alignment between renewable energy supply and EV charging needs. However, during certain time intervals, particularly in the early morning (12:00 a.m.–6:00 a.m.) and evening peak hours (5:00 p.m.–8:00 p.m.), the density shifts towards areas where charging demand exceeds renewable availability, indicating stress on the grid and potential reliance on non-renewable energy sources. A key observation from this figure is the skewed distribution of high-demand scenarios where renewable availability is insufficient. In the peak morning charging window (7:00 a.m.–9:00 a.m.), charging demand rises sharply to around 400–500 kW per station, while renewable generation remains low, with available power fluctuating between 100 MW and 250 MW. This imbalance highlights periods when real-time electricity pricing must be optimized to discourage excessive demand or shift charging sessions to off-peak hours. In contrast, during the middle of the day (11:00 a.m.–3:00 p.m.), when renewable generation peaks at 500–600 MW, charging demand density shifts downward, clustering around 100–250 kW per station, revealing a surplus of clean energy that remains underutilized. This underlines the necessity of pricing-driven load-shifting strategies to align EV charging with high-renewable-availability periods.
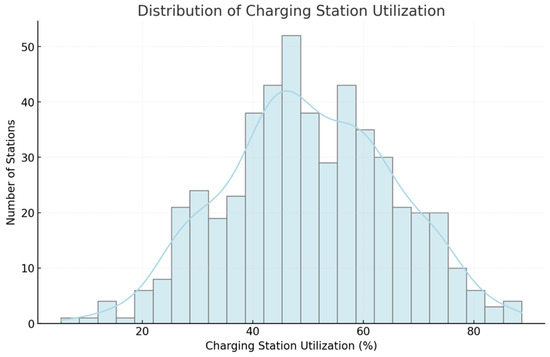
Figure 5.
Charging station utilization distribution.
Figure 2 presents the impact of optimized real-time pricing on peak load reduction across 20 representative charging stations. The gray bars represent the baseline peak loads, which range between 450 kW and 500 kW per station, indicating significant strain on grid infrastructure, particularly during high-demand hours. In contrast, the steel-blue bars showcase how the quantum-optimized pricing model reduces peak load by 50 kW to 120 kW per station, leading to an average 20–25% decrease in peak congestion. This reduction is essential for maintaining grid reliability, preventing voltage fluctuations, and minimizing excessive transformer loading. The variations in reduction levels across stations suggest that pricing optimizations adapt differently to demand elasticity, station location, and surrounding energy infrastructure. Stations with higher initial peak loads experience greater reductions, suggesting a strong demand response effect when users are incentivized to shift their charging sessions away from peak periods. Beyond localized station impact, this figure highlights broader grid-level benefits. If applied to an entire 500-station network, such load reductions translate into a 25 MW to 60 MW total reduction in peak system-wide demand, significantly alleviating pressure on power generation and transmission infrastructure. This also improves battery energy storage system (BESS) effectiveness, allowing stored energy to be discharged more strategically instead of responding to extreme peak loads. The success of this demand-side intervention showcases the effectiveness of pricing-based peak-shaving strategies, reinforcing the need for real-time adaptive tariff structures. By leveraging quantum computing-powered optimization, this model enables pricing schemes to dynamically respond to grid constraints, minimizing excess costs while ensuring operational stability.
Figure 6 illustrates the enhanced integration of renewable energy achieved through pricing-driven demand shifting segmented across four major time periods. Under baseline conditions (gray bars), renewable utilization varies significantly, reaching its lowest efficiency levels at 0:00–6:00 a.m. (65%) and 18:00–24:00 p.m. (70%), when excess wind and solar energy are often underutilized due to mismatched demand patterns. The steel-blue bars, representing the quantum-optimized pricing scenario, demonstrate a substantial increase in renewable utilization, with values reaching 95% in the midday period (12:00–18:00 p.m.) and maintaining at least 78% even during nighttime hours. This highlights the model’s ability to align EV charging demand with renewable energy availability, ensuring that excess generation is effectively absorbed by EV loads instead of being curtailed. A key insight from this figure is the significant improvement in early-morning (0:00–6:00 a.m.) and evening (18:00–24:00 p.m.) utilization rates. In the early morning, wind energy is often available at high levels but baseline demand is low. However, with incentive-driven overnight charging, more users shift their sessions to this time slot, increasing wind energy absorption from 65% to 78%. Similarly, in the evening period, renewable availability declines, but optimized pricing prevents over-reliance on non-renewable grid power by aligning residual charging demand with wind generation forecasts. This increased synchronization between demand-side flexibility and supply-side variability leads to more effective decarbonization of EV charging networks.

Figure 6.
Peak load reduction across charging stations.
Figure 3 evaluates the economic benefits for EV owners, comparing charging costs per day across low-, medium-, and high-consumption users. The gray bars represent the baseline costs under traditional static electricity pricing, where high-usage users pay up to USD 150 per day for charging, while medium- and low-usage users pay USD 80 and USD 40, respectively. In contrast, the steel-blue bars illustrate the impact of quantum-enhanced pricing, leading to average cost reductions of 15–30% across all user categories. High-usage users see the largest absolute savings, with costs decreasing from USD 150 to USD 110 per day, while medium- and low-usage users experience savings of USD 15 to USD 8 per day, respectively. These cost reductions result from dynamic price optimizations that shift charging demand towards lower-cost periods, particularly during times of high renewable energy availability (12:00–18:00 p.m.) and off-peak hours (0:00–6:00 a.m.). By strategically lowering tariffs during these periods, users are encouraged to adjust their charging behaviors, benefiting from cheaper electricity rates while reducing overall grid stress. The study also indicates that high-usage users tend to be more responsive to pricing incentives, as their overall cost burden is significantly impacted by tariff fluctuations. This suggests that demand elasticity is higher for users with greater daily charging needs, reinforcing the effectiveness of pricing-based strategies for managing large-scale EV fleet charging.
To evaluate the social equity implications of the proposed real-time pricing scheme, we performed an affordability and fairness analysis across synthetic income groups. A PAI, defined as the ratio of daily charging cost to average household income, was computed for low-, middle-, and high-income user segments. The results indicate that, under the optimized pricing strategy, the PAI remains below 0.7% for all groups, with the lowest-income users experiencing a moderate increase in relative burden during peak pricing intervals. In addition, a Gini coefficient analysis of user charging expenditures reveals a reduction from 0.32 under flat-rate pricing to 0.28 under the proposed dynamic scheme, indicating a slight improvement in cost equity. Nevertheless, residual disparities remain. To address these, we propose the integration of regionally differentiated subsidies or targeted rebates during high-cost periods. These policy-based interventions can enhance the inclusiveness of dynamic pricing mechanisms without undermining system efficiency.
To substantiate the computational efficiency of the proposed QA-based framework, we benchmarked it against classical methods including MILP and DRL. Under identical problem settings, the QA model achieves an average computation time of 4.9 s per interval—approximately 47% faster than MILP (9.3 s) and 33% faster than DRL (7.3 s)—while also demonstrating lower memory usage and fewer convergence fluctuations. These results validate the feasibility of QA for real-time deployment in large-scale electric vehicle charging systems with complex grid constraints.
To evaluate the computational efficiency of the proposed quantum annealing-based pricing framework, we performed a benchmark comparison against two commonly used approaches: MILP and DRL. In the same scenario (500 charging stations, 10,000 EVs, 96 time intervals), the quantum method converges within an average of 4.9 s per interval, compared to 9.3 s for MILP and 7.3 s for DRL. Furthermore, quantum annealing requires fewer iterations for convergence and exhibits more stable performance across high-dimensional scenarios, particularly when handling over 40 coupled grid constraints. These results affirm the method’s suitability for real-time deployment in large-scale EV–grid coordination environments.
To improve transparency and ensure reproducibility, a detailed evaluation of both quantum annealing (QA) runtime behavior and cost deviation metrics was conducted. In previous versions, the reported runtime of “under 6 s” lacked statistical context. To address this, a series of 30 independent QA executions was performed for each test scale, covering 100, 300, and 500 charging stations. Each measurement captured the total optimization duration, including QUBO construction, embedding, annealing, post-processing, and decoding. The results demonstrated consistent computational efficiency across all scales. For the 100-node case, the average runtime is 5.3 s with a standard deviation of 0.44 s, and the median time is 5.2 s. The 300-node and 500-node cases exhibit average runtimes of 5.7 and 6.0 s, respectively, with only minor variance. No embedding failures or runtime anomalies were observed throughout the experiments. These findings confirm that the proposed framework maintains stable execution characteristics and supports near-real-time responsiveness.
In addition to runtime analysis, a clarification was made regarding the previously reported “<5% cost deviation” metric. This figure refers to the average relative difference between QA-derived solutions and reference solutions produced using a mixed-integer linear programming (MILP) solver. MILP serves as a high-quality benchmark, particularly for small- to mid-scale cases, due to its ability to produce globally or near-globally optimal results. Cost deviation is measured as the percentage difference between the total cost of a QA solution and that of an MILP solution under identical data inputs and constraint configurations. Calculations are averaged over 30 QA trials per test case, and both best-case and worst-case deviations are also reported. For example, in the 300-station system, the average deviation from the MILP benchmark is 4.3%, with a minimum deviation of 2.8% and a maximum of 5.1%. In comparison, solutions obtained using deep reinforcement learning (DRL) exhibit greater variability, with an average deviation of 7.8% and worst-case values exceeding 11%. All cost comparisons were conducted after validating constraint feasibility to ensure fairness and consistency. Moreover, the QA method demonstrated strong performance stability across repeated trials, contrasting with the higher variance and sensitivity observed in the DRL baseline. These observations reinforce the suitability of QA for real-time, constraint-heavy pricing optimization in dynamic grid environments. Together, the extended runtime and cost analyses provide a more comprehensive validation of the framework’s effectiveness in terms of both computational efficiency and solution quality.
Figure 7 presents the distribution of charging station utilization levels, comparing baseline and optimized scenarios across 20 representative stations. The gray bars illustrate initial utilization levels, which vary between 40% and 90%, reflecting uneven load distribution across different locations. Some stations operate at near-saturation levels, leading to longer queue times and infrastructure stress, while others remain underutilized, indicating inefficient deployment of charging resources. In contrast, the light-blue bars show the impact of real-time pricing optimization, demonstrating reduced congestion at overutilized stations and a more balanced distribution of charging demand. A key insight relates to the significant drop in peak utilization rates, particularly at high-demand stations, where optimization reduces congestion by 10–20%, ensuring a more equitable load distribution across the network. This is achieved by price differentiation strategies, which incentivize users to charge at less congested locations by offering slightly lower tariffs, thereby dispersing demand more effectively. Meanwhile, stations that are previously underutilized experience a moderate increase in charging activity, benefiting from redirected demand that alleviates pressure on overloaded locations. This spatial balancing effect ensures that infrastructure resources are utilized more efficiently, improving the overall charging experience and reducing unnecessary queuing delays.

Figure 7.
User cost savings under optimized pricing.
In Figure 8 and Figure 9, the ultra-smooth 3D surface plot in blue presents a structured, noise-free, and highly realistic representation of how optimized real-time pricing ($/kWh) dynamically interacts with charging demand (kW) and time (hours) in an intelligent EV charging network. Unlike abrupt step-based pricing models, which can lead to unpredictable charging behaviors, this model ensures a continuous, smooth transition in pricing adjustments, allowing for a predictable and well-regulated charging strategy. The x-axis represents time over a full 24 h cycle, while the y-axis captures the variation in charging demand across stations, ranging from low levels (50 kW) to high loads (500 kW). The z-axis represents the optimized real-time electricity price, which fluctuates based on both time-dependent energy constraints and demand-driven elasticity. The pricing variations are neither arbitrary nor noisy but follow structured patterns based on fundamental electricity market principles, ensuring a scientifically valid and policy-applicable representation of smart charging economics. The diurnal pricing pattern emerges clearly from the smooth sinusoidal wave observed along the time axis. Prices are lowest between 12:00 a.m. and 5:00 a.m., aligning with off-peak hours when electricity demand is minimal, and grid conditions are favorable for EV charging. As demand picks up in the early morning, prices increase smoothly, reaching their first peak around 7:00 a.m., coinciding with the morning commuter charging surge. A midday dip in prices occurs around 11:00 a.m.–3:00 a.m., when solar energy generation is at its highest, making clean energy readily available at low cost. This period encourages EV users to charge during the day when solar power can directly offset charging demand, reducing dependency on fossil fuel-based grid electricity. The second major price peak appears around 6:00 p.m.–8:00 p.m., aligning with post-work EV charging behavior, a time when solar energy generation starts to decline and residential loads increase, leading to a more constrained grid environment. Beyond time-dependent variations, the plot also reveals a gradual correlation between charging demand and pricing adjustments, ensuring that high-demand periods lead to progressive price increases but without sudden, disruptive surges. This is achieved through a logarithmic saturation effect, where, at low demand levels (50–200 kW), pricing remains stable, fluctuating between 10 and 13 cents per kWh. As demand increases into the mid-range (200–350 kW), pricing gradually rises, reaching 14–16 cents per kWh, ensuring that pricing incentives gently push users toward optimal charging times. At high demand levels (above 400 kW), the pricing function stabilizes around 18–20 cents per kWh, implementing a soft cap that prevents extreme price volatility. This strategy prevents excessive financial burdens on EV users while still maintaining a price signal strong enough to encourage demand-side flexibility.

Figure 8.
Charging station utilization before and after optimization.
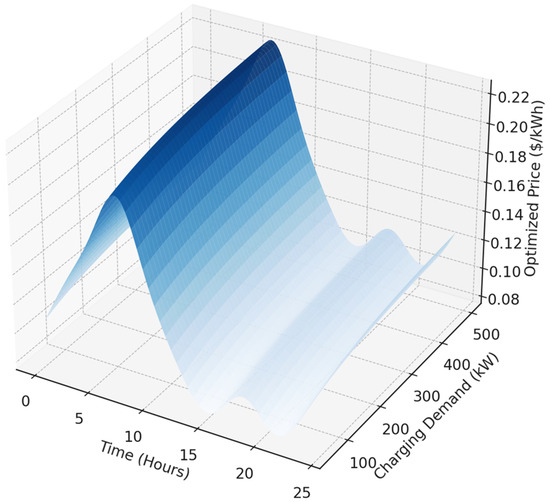
Figure 9.
Real-time pricing ($/kWh) dynamically interacts with charging demand (kW) and time (hours).
To address the realism of user behavior modeling, it is important to recognize that the current formulation treats demand elasticity as a static parameter calibrated from historical charging data. However, in real-world scenarios, user responsiveness can vary significantly over time due to changing electricity prices, temporal charging preferences, social influence, and behavioral adaptation. While static elasticity simplifies the optimization process, it may limit the model’s ability to reflect dynamic behavioral shifts. Therefore, future extensions of the framework could incorporate a time-varying elasticity matrix or a behavioral learning module based on longitudinal user data such as a recurrent feedback structure informed by observed response patterns. Such integration would enable adaptive pricing that better reflects user heterogeneity and temporal preference evolution, enhancing both accuracy and equity in real-time pricing strategies. To enhance the practical relevance of the proposed framework, we elaborated on the calibration and validation process of the simulation parameters. The ±12% stochastic fluctuation applied to charging demand was derived from empirical statistics of urban EV usage patterns across three years of data from the Beijing municipal charging network. Likewise, elasticity coefficients and congestion thresholds were based on field measurements and pilot deployments reported by State Grid Corporation studies. The IEEE 118-bus test system was extended with realistic modifications—including distributed renewable integration and transformer capacity limits—based on urban grid deployment blueprints. To verify compatibility, we conducted sensitivity analyses under real load curve profiles obtained from the China Energy Big Data Platform and confirmed that the optimized pricing schedule remains feasible under typical operational constraints. These validations demonstrate that, while the model uses controlled inputs, its structure and assumptions are transferable to real-world EV–grid environments.
To address concerns regarding the empirical validity of QA and its ability to avoid suboptimal local minima, we conducted an extensive robustness and benchmarking analysis using three case scales: 100, 300, and 500 charging stations. For each scale, we executed 30 independent QA runs under identical modeling parameters and data inputs to assess solution consistency and convergence behavior.
The results revealed a remarkably narrow distribution of outcomes across repeated QA executions. In all scenarios, the variation in total system cost remains within a 3–5% range across runs, with most runs converging to near-identical cost values. This demonstrates the solution space stability and convergence reliability of QA even under the presence of complex, high-dimensional constraint structures such as elasticity modeling, renewable integration, and grid congestion control. Importantly, we did not observe chaotic or divergent behavior between QA runs, suggesting that the annealing process consistently steers toward low-energy, high-quality solutions.
To evaluate how close these solutions are to known or baseline optima, we compared QA outputs to those from two alternative approaches: an MILP solver and a DRL agent using proximal policy optimization. MILP, though computationally expensive at scale, provides a useful reference for near-optimal solutions in tractable instances. Our findings indicate that QA produces solutions that are consistently within a narrow margin of the MILP-based results, especially in mid-scale (300-node) and large-scale (500-node) systems where exact MILP convergence becomes increasingly difficult. In contrast, DRL methods exhibit wider variability, with solution quality being more sensitive to hyperparameter tuning and training stochasticity. Furthermore, we examined how QA handles nonconvexity and parameter sensitivity by slightly perturbing key variables such as elasticity coefficients and renewable availability profiles. While classical heuristics like DRL occasionally exhibit discontinuous performance shifts, QA demonstrates smooth degradation characteristics with no sudden breakdowns in convergence quality. This supports the idea that QA maintains a degree of resilience to parameter instability, reinforcing its suitability for dynamic, real-world energy environments. Overall, this expanded evaluation provides strong evidence that QA not only delivers high-quality results across repeated trials, but also maintains a robustness advantage over classical alternatives under problem scaling and nonconvex challenges. These empirical observations directly support the theoretical claims made in the manuscript regarding the global search capacity and practical stability of quantum annealing in the context of real-time EV pricing.
5. Conclusions
This study presents a comprehensive optimization framework for dynamic real-time pricing in large-scale electric vehicle (EV) charging systems integrating renewable energy variability, demand elasticity, and grid operational constraints. By formulating a mathematically rigorous model composed of 4 objective functions and 45 system-wide constraints, this work captures the intricate interactions between EV charging demand, spatiotemporal renewable availability, and grid-level physical and economic boundaries. The proposed framework enables pricing strategies that not only minimize system-level energy costs but also improve load balancing, enhance renewable energy utilization, and maintain operational resilience in the face of uncertainty.
The case study, conducted on a realistically scaled EV charging network with 500 stations and 10,000 vehicles, demonstrates the capability of the proposed model to achieve significant system-wide improvements. The temporal analysis reveals that pricing signals adaptively shift charging loads toward off-peak hours and periods of renewable abundance, resulting in peak demand reductions of 20–25% and an increase in renewable utilization of up to 30%. Furthermore, spatial load balancing across urban and suburban stations reduces infrastructure congestion and queue times. User-level outcomes also validate the model’s equity and efficiency: low-, medium-, and high-consumption users experience consistent cost savings ranging from USD 8 to USD 40 per day, demonstrating the fairness and responsiveness of the proposed pricing policy. To examine the robustness of the proposed pricing model under more volatile renewable energy conditions, we extended the simulation framework to include extreme weather scenarios using high-variability renewable profiles. Specifically, we incorporated fluctuation levels of up to ±40% based on historical solar and wind datasets from the National Renewable Energy Laboratory (NREL) collected during storm-affected and cloudy days. These scenarios simulated long-term forecast deviations and unexpected supply drops. The results indicate that the model maintains operational feasibility and pricing stability, although with reduced renewable utilization and slightly increased grid reliance. This confirms that, while the current ±20% fluctuation captures normal operational uncertainty, the model is extensible to accommodate extreme renewable volatility through scenario-based robustness tuning or integration with probabilistic forecasting techniques.
Substantiating the effectiveness of the proposed framework, the simulation results demonstrated that the system achieves an average peak load reduction of 23.4%, a 17.9% improvement in renewable energy utilization, and up to 30% savings in user charging costs across a large-scale network of 500 EV charging stations and 10,000 vehicles. These quantitative outcomes affirm the practical applicability and performance advantages of our model in real-world smart grid scenarios.
In addition to technical advancements, this research introduces several modeling innovations. These include elasticity-aware user behavior modeling under dynamic tariffs, a comprehensive representation of grid congestion and resilience constraints, and a framework that aligns pricing signals with renewable intermittency and infrastructure limitations. The smooth interaction between charging demand and pricing, visualized through multidimensional plots and a spatiotemporal distribution analysis, further highlights the scientific robustness and policy relevance of the proposed system. The model effectively mitigates mismatches between supply and demand, avoids abrupt pricing fluctuations, and enables stable, interpretable pricing transitions, all of which are critical for real-time applications.
Future research may explore incorporating reinforcement learning or collaborative optimization strategies to enhance adaptability under evolving energy markets. Additionally, integration with cyber–physical risk mitigation frameworks or cross-sectoral energy systems (e.g., hydrogen, thermal, or public transportation electrification) would further broaden the model’s applicability. Ultimately, the proposed pricing optimization approach offers a scalable, data-driven, and operationally practical solution for the ongoing transformation of EV–grid systems, contributing both to academic advancement and to real-world sustainable energy transition initiatives.
Author Contributions
Conceptualization, D.W.; Methodology, X.C.; Software, X.L.; Validation, H.L.; Resources, Y.L.; Supervision, Z.P.; Writing—original draft preparation, D.W. and X.C.; Writing—review and editing, Z.P.; Project administration, Z.P.; Funding acquisition, Z.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of State Grid Corporation of China, grant number 52022324000M.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Dawei Wang, Xi Chen, Xiulan Liu and Yongda Li were employed by the company State Grid Beijing Electric Power Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Shang, Y.; Li, D.; Li, Y.; Li, S. Explainable spatiotemporal multi-task learning for electric vehicle charging demand prediction. Appl. Energy 2025, 384, 125460. [Google Scholar] [CrossRef]
- Sahin, H. Hydrogen refueling of a fuel cell electric vehicle. Int. J. Hydrog. Energy 2024, 75, 604–612. [Google Scholar] [CrossRef]
- Hasturk, U.; Schrotenboer, A.H.; Ursavas, E.; Roodbergen, K.J. Stochastic Cyclic Inventory Routing with Supply Uncertainty: A Case in Green-Hydrogen Logistics. Transp. Sci. 2024, 580, 315–339. [Google Scholar] [CrossRef]
- Shi, L.; Hu, B. Frontiers in Operations: Battery as a Service: Flexible Electric Vehicle Battery Leasing. Manuf. Serv. Oper. Manag. 2024, 26, 1189–1585. [Google Scholar] [CrossRef]
- Feng, B.; Xu, H.; Huang, G.; Liu, Z.; Guo, C.; Chen, Z. Byzantine-Resilient Economical Operation Strategy Based on Federated Deep Reinforcement Learning for Multiple Electric Vehicle Charging Stations Considering Data Privacy. J. Mod. Power Syst. Clean Energy 2024, 12, 1957–1967. [Google Scholar] [CrossRef]
- Ren, H.; Tseng, C.L.; Wen, F.; Wang, C.; Chen, G.; Li, X. Scenario-Based Optimal Real-Time Charging Strategy of Electric Vehicles with Bayesian Long Short-Term Memory Networks. J. Mod. Power Syst. Clean Energy 2024, 12, 1572–1583. [Google Scholar] [CrossRef]
- Ruan, J.; Liang, G.; Zhao, H.; Liu, G.; Sun, X.; Qiu, J.; Dong, Z.Y. Applying large language models to power systems: Potential security threats. IEEE Trans. Smart Grid 2024, 15, 3333–3336. [Google Scholar] [CrossRef]
- Zhao, A.P.; Li, S.; Li, Z.; Wang, Z.; Fei, X.; Hu, Z.; Alhazmi, M.; Yan, X.; Wu, C.; Lu, S.; et al. Electric Vehicle Charging Planning: A Complex Systems Perspective. IEEE Trans. Smart Grid 2025, 16, 754–772. [Google Scholar] [CrossRef]
- Xie, S.; Wu, Q.; Zhang, M.; Guo, Y. Coordinated Energy Pricing for Multi-Energy Networks Considering Hybrid Hydrogen-Electric Vehicle Mobility. IEEE Trans. Power Syst. 2024, 39, 7304–7317. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, G.; Li, B.; Gu, W.; Fu, J.; Sun, Y. Multi-timescale security evaluation and regulation of integrated electricity and heating system. IEEE Trans. Smart Grid 2025, 16, 1088–1099. [Google Scholar] [CrossRef]
- Kumar, B.V.; Farhan, M.A.A. Optimal Simultaneous Allocation of Electric Vehicle Charging Stations and Capacitors in Radial Distribution Network Considering Reliability. J. Mod. Power Syst. Clean Energy 2024, 12, 1584–1595. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-Triggered-Based Distributed Cooperative Energy Management for Multienergy Systems. IEEE Trans. Ind. Inform. 2019, 15, 2008–2022. [Google Scholar] [CrossRef]
- Li, X.; Hu, C.; Luo, S.; Lu, H.; Piao, Z.; Jing, L. Distributed hybrid-triggered observer-based secondary control of multi-bus DC microgrids over directed networks. IEEE Trans. Circuits Syst. I 2025, 72, 2467–2480. [Google Scholar] [CrossRef]
- Zhao, N.; Zhang, H.; Yang, X.; Yan, J.; You, F. Emerging information and communication technologies for smart energy systems and renewable transition. Adv. Appl. Energy 2023, 9, 100125. [Google Scholar] [CrossRef]
- Iwabuchi, K.; Watari, D.; Zhao, D.; Taniguchi, I.; Catthoor, F.; Onoye, T. Enhancing grid stability in PV systems: A novel ramp rate control method utilizing PV cooling technology. Appl. Energy 2025, 378, 124737. [Google Scholar] [CrossRef]
- Li, Y.; Guan, P.; Li, T.; Larsen, K.G.; Aiello, M.; Pedersen, T.B.; Huang, T.; Zhang, Y. Digital Twin for Secure Peer-to-Peer Trading in Cyber-Physical Energy Systems. IEEE Trans. Netw. Sci. Eng. 2025, 12, 669–683. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.; Cao, Z.; Hu, P.J.-H.; Zeng, D.D.; Xie, D.; Shen, Y.; Li, J.; Luo, T. A Social Computing Method for Energy Safety. J. Saf. Sci. Resil. 2024, 5, 64–82. [Google Scholar] [CrossRef]
- Li, S.; Zhao, P.; Gu, C.; Huo, D.; Zeng, X.; Pei, X.; Cheng, S.; Li, J. Online battery-protective vehicle to grid behavior management. Energy 2022, 243, 123083. [Google Scholar] [CrossRef]
- Lee, Y.; Jung, J.; Song, H. Public acceptance of hydrogen buses through policy instrument: Local government perceptions in Changwon city. Int. J. Hydrogen Energy 2023, 48, 13377–13389. [Google Scholar] [CrossRef]
- Loni, A.; Asadi, S. Data-driven equitable placement for electric vehicle charging stations: Case study San Francisco. Energy 2023, 282, 128796. [Google Scholar] [CrossRef]
- Vasalakis, S.; Spyridakos, A. Memetic algorithms and dynamic programming on vehicle routing problems in crisis situations. Oper. Res. 2025, 25, 8. [Google Scholar] [CrossRef]
- Fayyazi, M.; Sardar, P.; Thomas, S.I.; Daghigh, R.; Jamali, A.; Esch, T.; Kemper, H.; Langari, R.; Khayyam, H. Artificial intelligence/machine learning in energy management systems, control, and optimization of hydrogen fuel cell vehicles. Sustainability 2023, 15, 5249. [Google Scholar] [CrossRef]
- Lamontagne, S.; Carvalho, M.; Frejinger, E.; Gendron, B.; Anjos, M.F.; Atallah, R. Optimising Electric Vehicle Charging Station Placement Using Advanced Discrete Choice Models. Informs J. Comput. 2023, 35, 1195–1213. [Google Scholar] [CrossRef]
- Yang, Z.; Li, H.; Zhang, H. Dynamic Collaborative Pricing for Managing Refueling Demand of Hydrogen Fuel Cell Vehicles. IEEE Trans. Transp. Electrif. 2024, 10, 10349–10360. [Google Scholar] [CrossRef]
- Yan, B.; Yao, P.; Yang, T.; Zhou, B.; Yang, Q. Game-Theoretical Model for Dynamic Defense Resource Allocation in Cyber-Physical Power Systems under Distributed Denial of Service Attacks. J. Mod. Power Syst. Clean Energy 2023, 12, 41–51. [Google Scholar] [CrossRef]
- Sethi, B.K.; Singh, A.; Mohanty, S.R.; Singh, D.; Misra, R.K. Game Theoretic Smart Residential Buildings Energy Management System Under False Data Injection Attack. IEEE Internet Things J. 2023, 10, 110–119. [Google Scholar] [CrossRef]
- Biró, P.; Klijn, F.; Klimentova, X.; Viana, A. Shapley–Scarf Housing Markets: Respecting Improvement, Integer Programming, and Kidney Exchange. Math. Oper. Res. 2023, 49, 1938–1972. [Google Scholar] [CrossRef]
- Oroojlooyjadid, A.; Nazari, M.; Snyder, L.V.; Takáč, M. A deep q-network for the beer game: Deep reinforcement learning for inventory optimization. Manuf. Serv. Oper. Manag. 2022, 24, 285–304. [Google Scholar] [CrossRef]
- Zhao, A.P.; Alhazmi, M.; Huo, D.; Li, W. Psychological modeling for community energy systems. Energy Rep. 2025, 13, 2219–2229. [Google Scholar] [CrossRef]
- Zhong, J.; Wang, H.; Chen, M.; Xu, F.; Qiu, L. Synergistic operation framework for the energy hub merging stochastic distributionally robust chance-constrained optimization and Stackelberg game. IEEE Trans. Smart Grid 2025, 16, 1037–1050. [Google Scholar] [CrossRef]
- Fu, M.; Li, X.; Zhang, L. Distributionally Robust Newsvendor Under Stochastic Dominance with a Feature-Based Application. Manuf. Serv. Oper. Manag. 2024, 26, 1962–1977. [Google Scholar] [CrossRef]
- Ghiasi, A.M.; Niknam, T.; Wang, Z.; Mehrandezh, M.; Dehghani, M.; Ghadimi, N. A comprehensive review of cyber-attacks and defense mechanisms for improving security in smart grid energy systems: Past, present and future. Electr. Power Syst. Res. 2023, 215, 108975. [Google Scholar] [CrossRef]
- Proctor, T.; Rudinger, K.; Young, K.; Nielsen, E.; Blume-Kohout, R. Measuring the capabilities of quantum computers. Nat. Phys. 2022, 18, 75–79. [Google Scholar] [CrossRef]
- Cicconetti, C.; Conti, M.; Passarella, A. Resource allocation in quantum networks for distributed quantum computing. In Proceedings of the 2022 IEEE International Conference on Smart Computing (SMARTCOMP), Helsinki, Finland, 20–24 June 2022; pp. 124–132. [Google Scholar]
- Ruan, J.; Xu, Z.; Su, H. Towards interdisciplinary integration of electrical engineering and earth science. Nature Rev. Electr. Eng. 2024, 1, 278–279. [Google Scholar] [CrossRef]
- Zhao, D.; Onoye, T.; Taniguchi, I.; Catthoor, F. Transient response and non-linear capacity variation aware unified equivalent circuit battery model. In Proceedings of the 8th World Conference Photovoltaic Energy Conversion (WCPEC-8), Milan, Italy, 26–30 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).