A P-Q Arc Suppression Method Based on DC-Link Voltage Stability for Hybrid Multifunctional Arc Suppression Devices

Abstract

The traditional arc suppression device suffers from high costs and low utilization. These problems can be effectively avoided by using a hybrid multi-function arc suppression device (HMF-ASD). However, an HMF-ASD will consume active power during arc suppression. Based on this, a P-Q arc suppression method based on DC-link voltage stability is proposed. The energy flow during a single line-to-ground (SLG) fault is analyzed to optimize operation of the HMF-ASD. The topology and principle of the HMF-ASD are introduced. Secondly, the influence mechanism of the traditional arc suppression method on the output active power and energy flow direction of the HMF-ASD is analyzed. The internal reason for the change in the DC-link voltage is clarified. Additionally, non-fault phases of the HMF-ASD are regulated to produce no active output, delivering only the reactive current required for arc suppression. This method effectively mitigates SLG faults while maintaining DC-link voltage stability. Non-fault phases exclusively supply reactive power, with the active power needed for arc suppression drawn directly from the grid. The validity of the proposed method is confirmed through both simulation and experiment.

1. Introduction

A distribution network serves as a vital component in constructing a new power system. Characterized by complex structures and frequent grounding faults, the SLG fault accounts for the highest proportion, approximately 80% [1,2,3,4]. With the massive expansion of power electronic devices and nonlinear loads on distribution networks, both active and reactive power components in grounding fault currents have significantly increased [5,6]. The reactive power component can be only compensated by traditional passive arc suppression devices. Arcs can be generated by the active component and the harmonic component [7,8]. When an SLG fault occurs in a coal mine power grid in China, the active component of the measured grounding current reaches 13.05 A [8]. The fault current of some distribution networks is still as high as tens of amperes after the compensation capacitor component of the passive arc suppression device. If the fault cannot be eliminated, it will seriously threaten the power grid.

Literature Review

The active arc suppression device can achieve full compensation of the fault current. The existing active arc suppression devices inject zero-sequence current to regulate the zero-sequence voltage to be the opposite of the fault phase voltage [9,10,11]. However, these active arc suppression devices only operate during an SLG fault in distribution networks, suffering from low equipment utilization efficiency.

To fully leverage the flexible regulation capabilities of power electronic devices, an HMF-ASD that combines power quality management and grounding fault regulation is proposed. An HMF-ASD can not only achieve arc suppression during an SLG fault in the power grid but it also performs reactive power compensation, harmonic control, and three-phase imbalance control, which significantly enhances the equipment utilization rate. In [12], an HMF-ASD based on cascaded H-bridges is proposed, which outputs arc suppression current and reactive power compensation current.

However, the voltage withstand requirement of the HMF-ASD during arc suppression reaches the line voltage. This has led to the problem of high device costs. In [13], an HMF-ASD is introduced which integrates cascaded H-bridge configurations with a passive arc suppression coil. The primary function of the arc suppression coil is to offset the predominant reactive portion of the fault current. Meanwhile, the active module is designed to compensate for the active power component, harmonic distortions, and a residual fraction of the reactive power in the fault current. Since an HMF-ASD needs to fully compensate for the reactive power demands of the load, the overall capacity tends to be large. In [14], an HMF-ASD based on cascaded H-bridges and single-phase converters is proposed, which achieves deep integration of power exchange, power quality management, and grounding fault regulation. However, when the magnitude of the active current component is considerable, a voltage shift occurs at the common point, consequently compromising the DC-link voltage.

It is crucial for realizing efficient fault current compensation to maintain stable DC-link voltage. Till now, there are two ways for an HMF-ASD to maintain the DC-link voltage. Scheme I is controlling the converter to absorb energy based on positive and negative sequence loops [15,16,17,18,19,20]. Scheme II is adding additional energy storage units [21,22,23,24,25]. As for Scheme I, the influence of a zero sequence loop is not considered. Further, the existing DC-link voltage control strategies for an arc suppression device are not applicable to the condition with ground resistance [19,20]. As for Scheme II, in [21], every H-bridge module in the HMF-ASD is linked to an energy storage unit, leading to a relatively high overall device cost. In [22], only a single energy storage device is integrated into the HMF-ASD. In [23], a method is introduced that achieves DC-link voltage stability by alternately conducting arc suppression and voltage regulation on the two non-fault phases. However, this approach falls short in simultaneously accomplishing reactive power compensation and arc suppression. The existing HMF-ASDs effectively improve equipment utilization and practicality, but additional energy supply devices are needed [24,25].

To further solve the problem of unstable DC-link voltage in HMF-ASDs, a P-Q arc suppression method is proposed. Firstly, the topological structure of the HMF-ASD is elaborated in this paper. Under normal grid conditions, the HMF-ASD provides reactive power to meet the load’s demands. When an SLG fault occurs, reactive power compensation and arc suppression are achieved simultaneously. Secondly, the energy flow characteristics during an SLG fault and the reason for the failure of the traditional DC-link voltage control method are analyzed. Further, by controlling the HMF-ASD to output only reactive power during arc suppression, the DC-link voltage is stable. Finally, the validity of the proposed method is confirmed through both simulation and experiment.

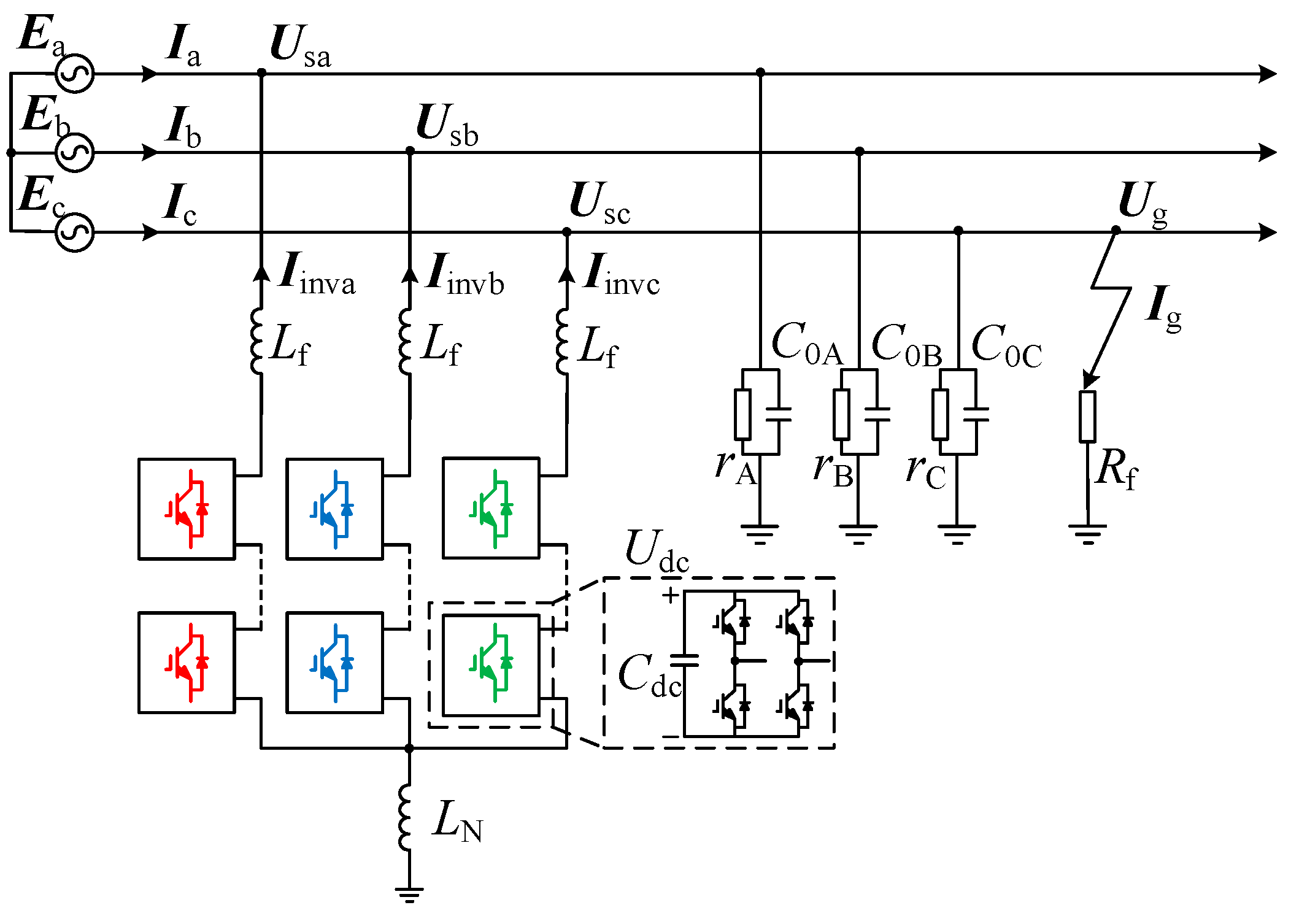
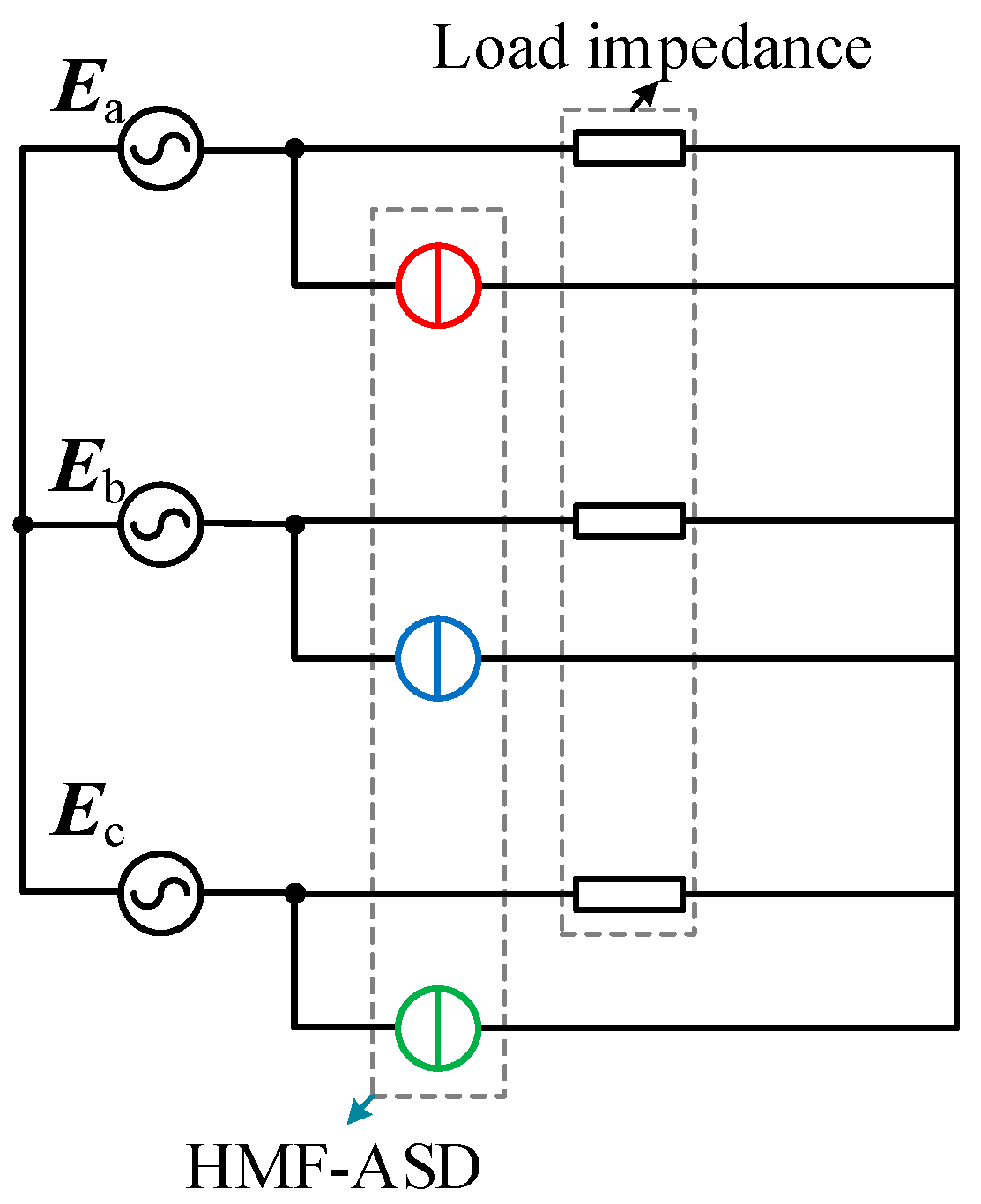
2. Topology and Working Principle of HMF-ASD

The rated voltage of the distribution network is 10 kV and the neutral point is ungrounded. A three-phase structure with symmetrical distribution among the three phases is used, and the arc suppression coil is linked to the common point. The topology of the HMF-ASD is shown in Figure 1. In Figure 1, I_g, I_x (x = a, b, c), and I_invx are the fault current, system current, and output current of the HMF-ASD, respectively. E_x, U_sx, U_g, and U_dc are the system voltage, busbar voltage, fault voltage, and DC-link voltage, respectively. r_x and C_0x are the ground resistance and capacitance, respectively. C_dc is the DC-link capacitance. R_f is the ground-fault resistance. L_f and L_N are filter inductance and arc suppression inductance, respectively.

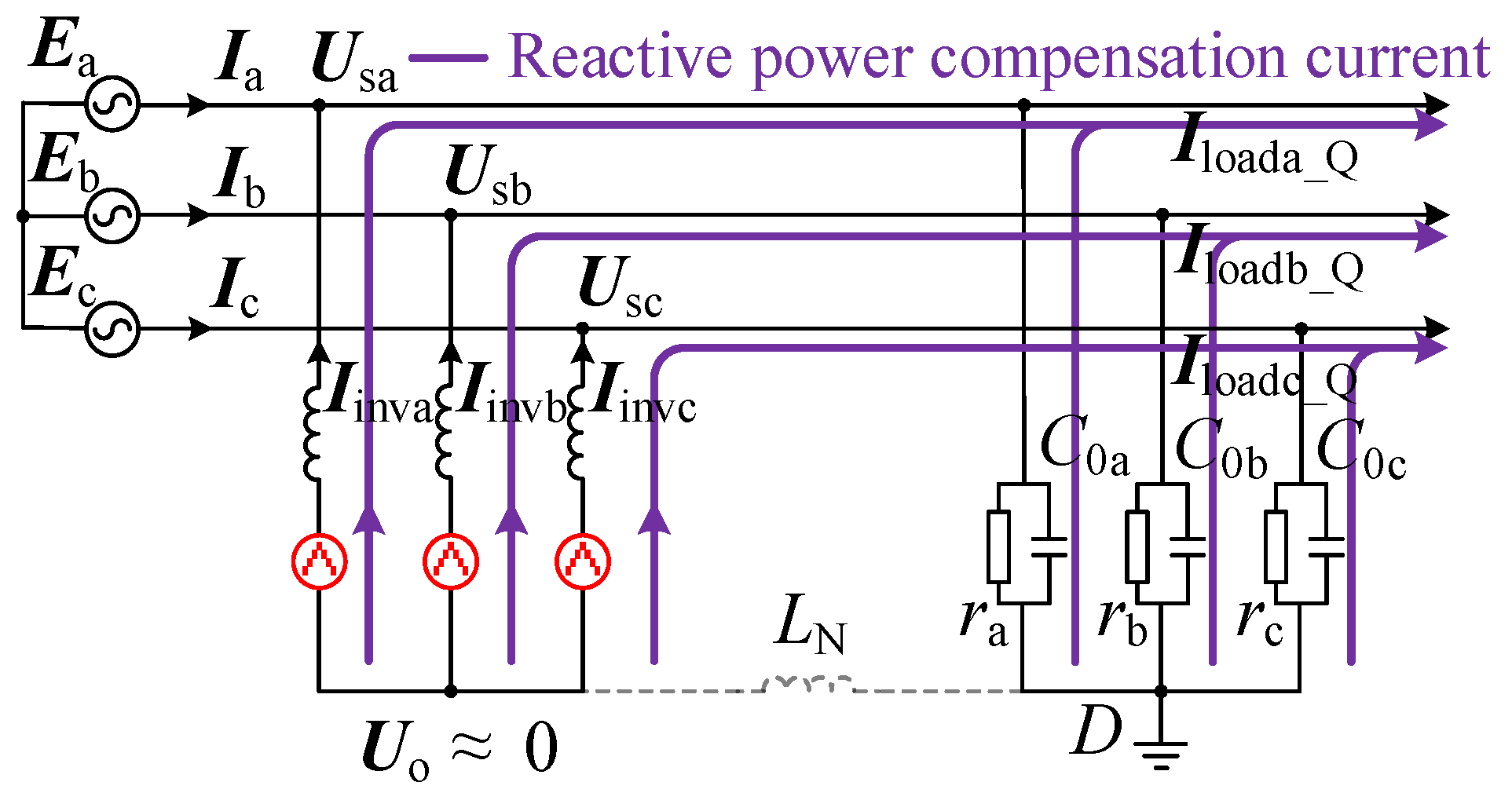
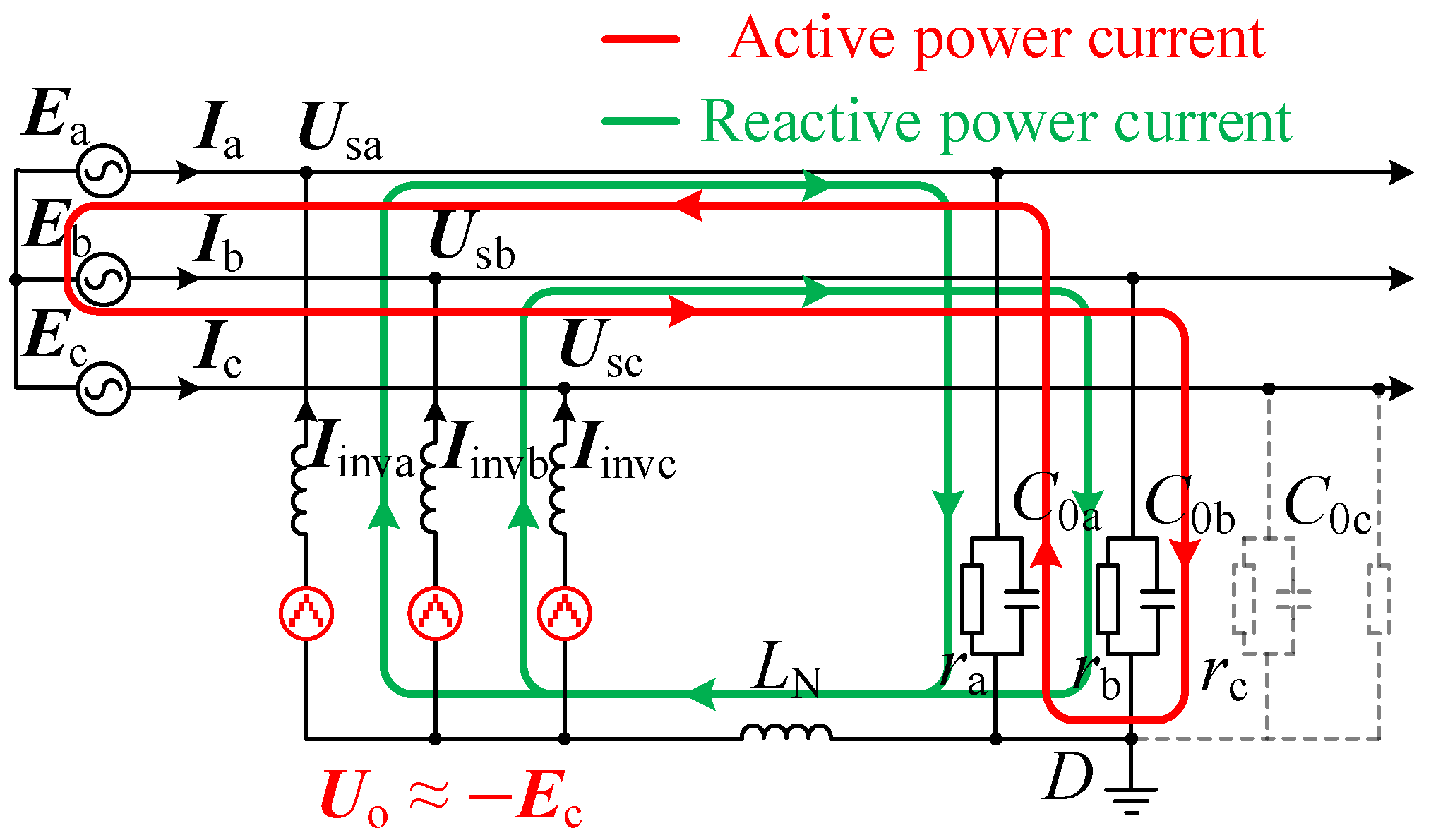
2.1. Analysis of Reactive Power Compensation Mode

Under normal conditions of the power grid, the HMF-ASD operates in a reactive power compensation state. The HMF-ASD compensates reactive power by load, which can be regarded as a controlled current source. The equivalent circuit diagram during normal conditions of a power grid is shown in Figure 2.

The voltage at the common connection point of the HMF-ASD Uo is regulated to 0 and the arc suppression inductance branch is equivalent to an open circuit. The HMF-ASD outputs reactive power compensation current and the HMF-ASD bears the phase voltage. The current flow diagram during normal operation of a power grid is shown in Figure 3.

The reactive power compensation current output by HMF-ASD is:

$$\left\{\begin{array}{l}{\mathit{I}}_{\mathrm{inva}}+{\mathit{I}}_{\mathrm{a}}={\mathit{I}}_{\mathrm{loada}\_\mathrm{Q}}-j\omega C_{0\mathrm{a}}{\mathit{E}}_{\mathrm{a}}\\ {\mathit{I}}_{\mathrm{invb}}+{\mathit{I}}_{\mathrm{b}}={\mathit{I}}_{\mathrm{loadb}\_\mathrm{Q}}-j\omega C_{0\mathrm{b}}{\mathit{E}}_{\mathrm{b}}\\ {\mathit{I}}_{\mathrm{invc}}+{\mathit{I}}_{\mathrm{c}}={\mathit{I}}_{\mathrm{loadc}\_\mathrm{Q}}-j\omega C_{0\mathrm{c}}{\mathit{E}}_{\mathrm{c}}\end{array}\right.$$

(1)

where I_{loada_Q}, I_{loadb_Q}, and I_{loadc_Q} are the reactive currents of the three-phase load.

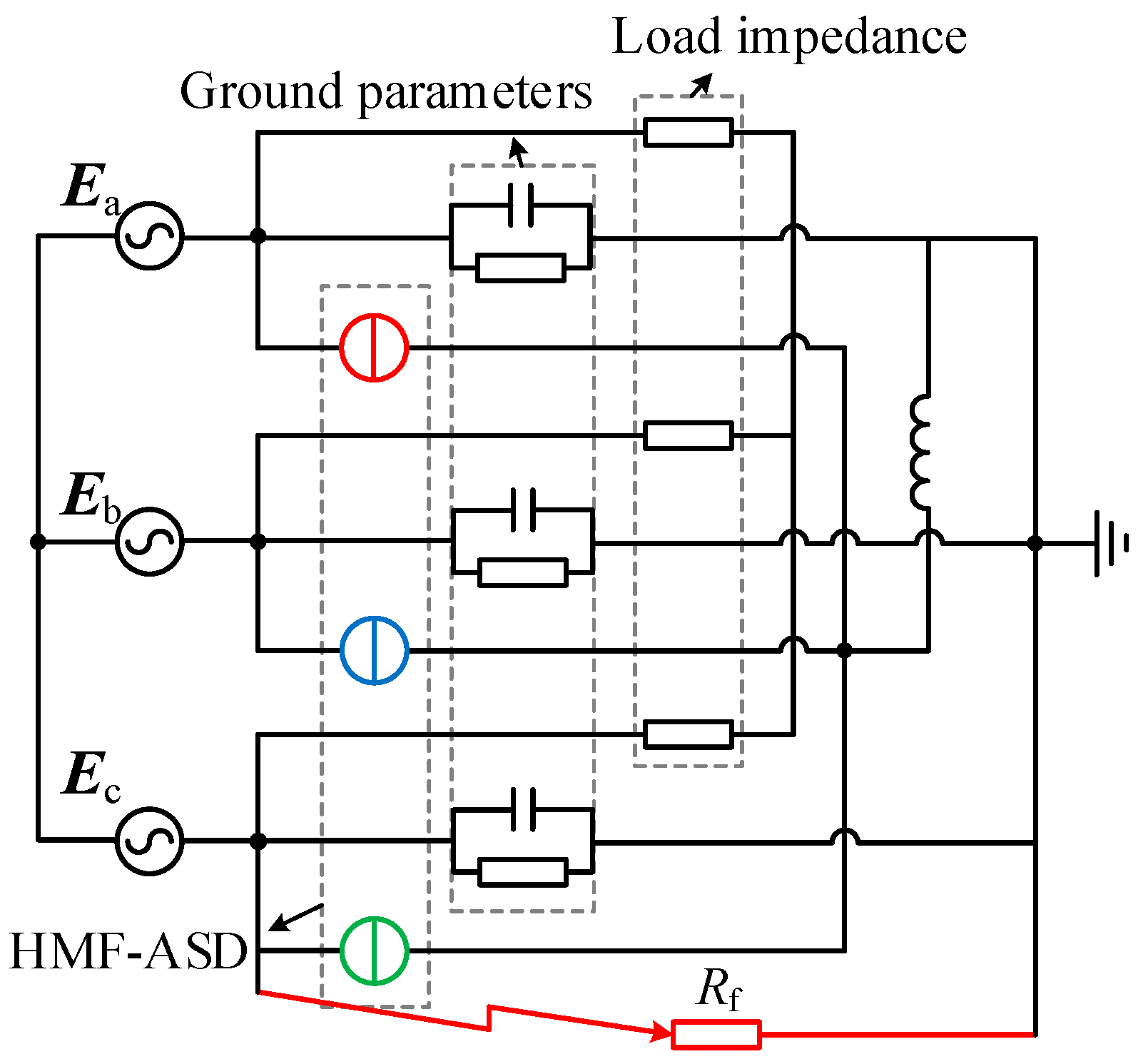
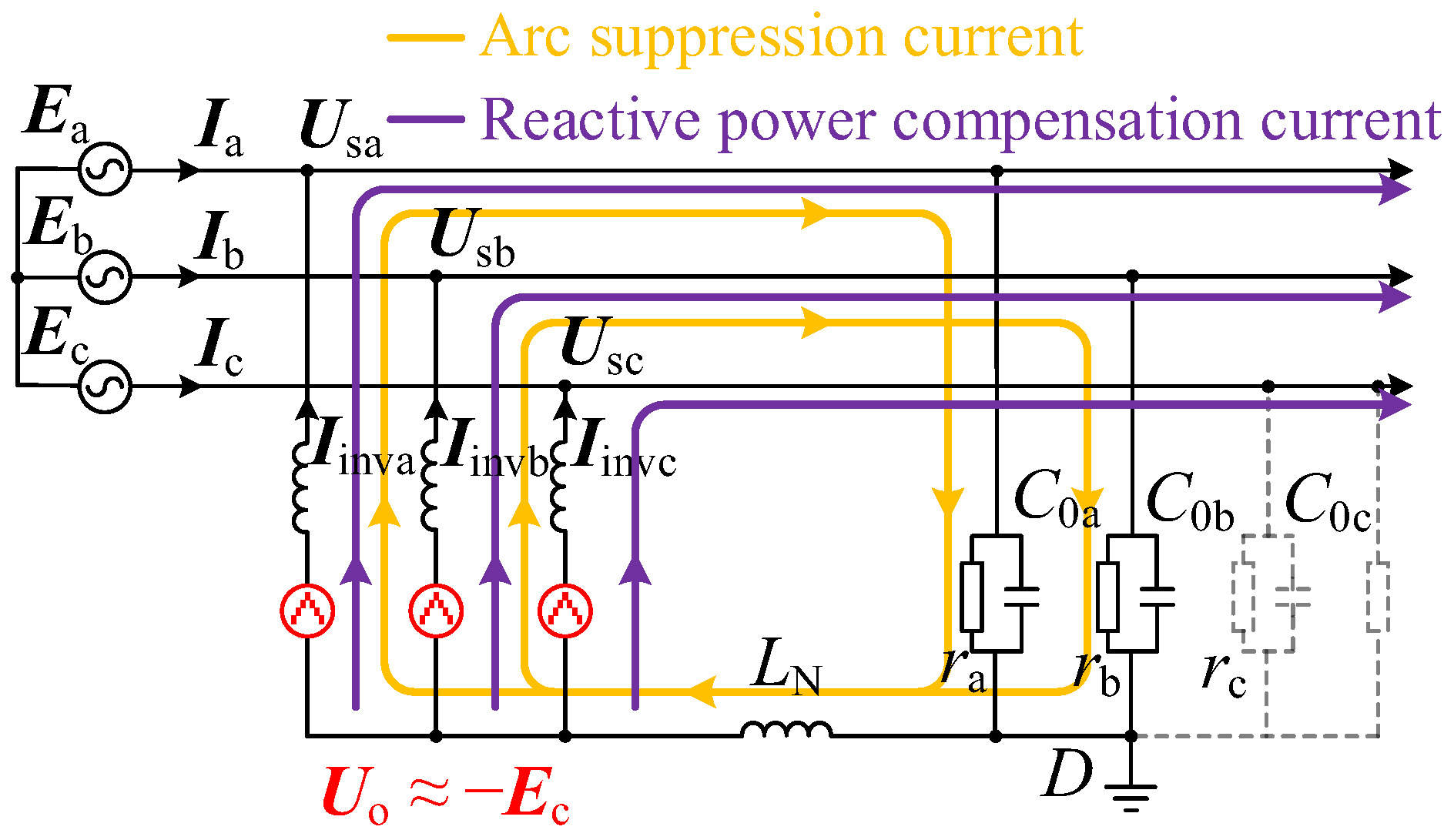
2.2. Analysis of Arc Suppression Mode

When an SLG fault occurs, the HMF-ASD switches to arc suppression mode. The ground fault point establishes a closed loop with the grounding characteristics of the distribution network, allowing the ground current to pass through the fault location. During this process, arc suppression and reactive power compensation are carried out concurrently. The equivalent schematic diagram is shown in Figure 4 and the HMF-ASD can still be equivalently regarded as a controlled current source,

The current flow diagram during an SLG fault is shown in Figure 5 and Uo is controlled to −Ec. The HMF-ASD outputs arc suppression current to effectively reduce the current at the fault point.

In order to obtain the arc suppression current of each phase output of the HMF-ASD, the current equation is written in the zero-sequence loop of the system. The following equation is obtained by formulating KCL at node D and substituting the network parameters:

$$\begin{array}{l}{\mathit{U}}_{\mathrm{sc}}({\displaystyle \frac{1}{r_{\mathrm{c}}}}+{\displaystyle \frac{1}{R_{\mathrm{f}}}}+j\omega C_{0\mathrm{c}})+{\mathit{U}}_{\mathrm{sb}}({\displaystyle \frac{1}{r_{\mathrm{b}}}}+j\omega C_{0\mathrm{b}})+\\ {\mathit{U}}_{\mathrm{sa}}({\displaystyle \frac{1}{r_{\mathrm{a}}}}+j\omega C_{0\mathrm{a}})-({\mathit{I}}_{\mathrm{oa}}+{\mathit{I}}_{\mathrm{ob}}+{\mathit{I}}_{\mathrm{oc}})=0\end{array}$$

(2)

Assuming that the three-phase voltage is balanced, the ground resistance and capacitance are r₀ and C₀, respectively. When using the traditional arc suppression method, the three-phase output arc suppression currents I_ox output by the HMF-ASD are as follows:

$$\left\{\begin{array}{l}{\mathit{I}}_{\mathrm{oa}}=({\mathit{E}}_{\mathrm{a}}-{\mathit{E}}_{\mathrm{c}})({\displaystyle \frac{1}{r_0}}+j\omega C_0)\\ {\mathit{I}}_{\mathrm{ob}}=({\mathit{E}}_{\mathrm{b}}-{\mathit{E}}_{\mathrm{c}})({\displaystyle \frac{1}{r_0}}+j\omega C_0)\\ {\mathit{I}}_{\mathrm{oc}}=0\end{array}\right.$$

(3)

The output currents of the HMF-ASD are as follows:

$$\left\{\begin{array}{l}{\mathit{I}}_{\mathrm{inva}}={\mathit{I}}_{\mathrm{loada}\_\mathrm{Q}}+{\mathit{I}}_{\mathrm{oa}}\\ {\mathit{I}}_{\mathrm{invb}}={\mathit{I}}_{\mathrm{loadb}\_\mathrm{Q}}+{\mathit{I}}_{\mathrm{ob}}\\ {\mathit{I}}_{\mathrm{invc}}={\mathit{I}}_{\mathrm{loadc}\_\mathrm{Q}}+{\mathit{I}}_{\mathrm{oc}}\end{array}\right.$$

(4)

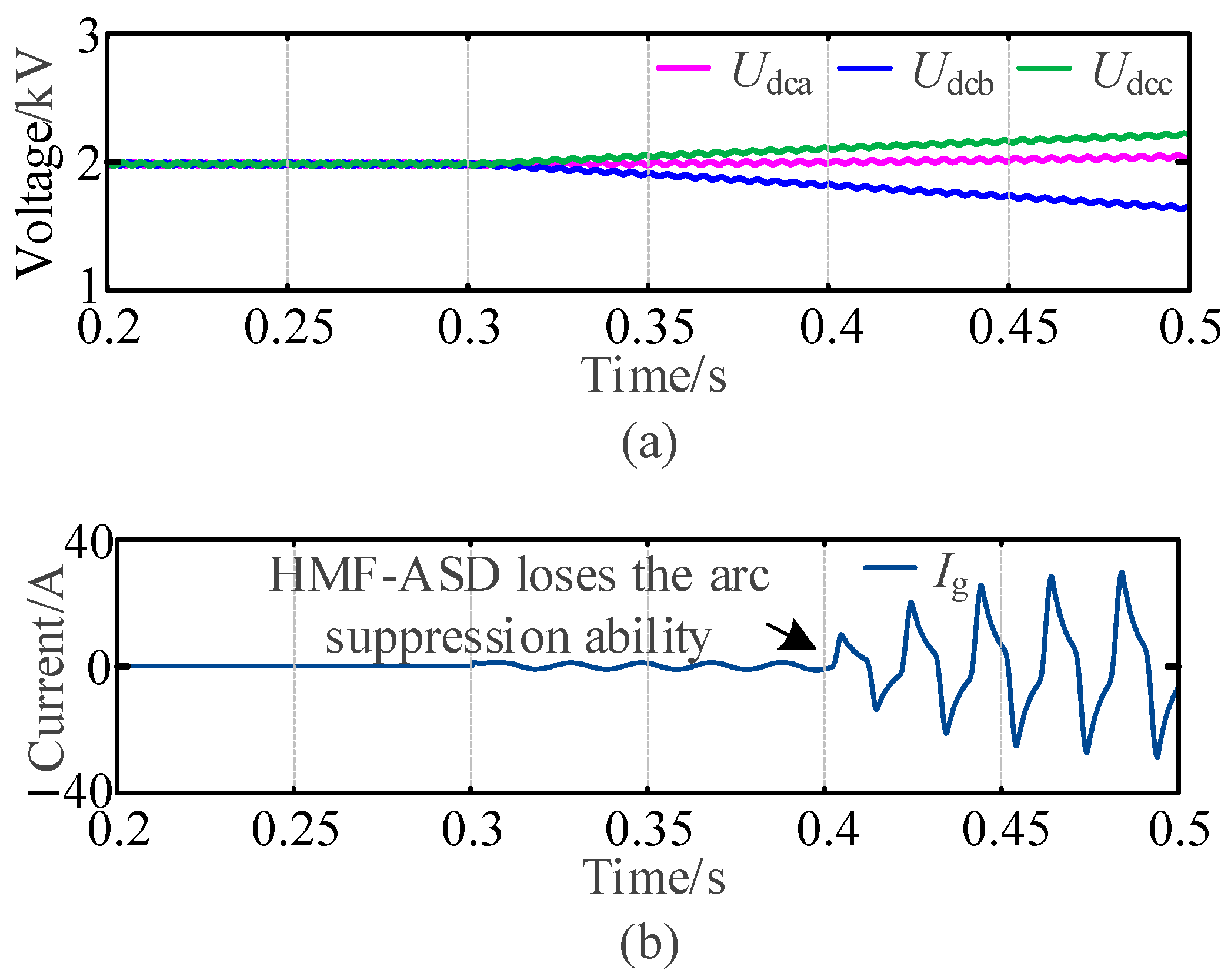
3. Failure Mechanism of Traditional Arc Suppression Method

This section examines how the conventional arc suppression approach affects the output active power and energy flow direction of the HMF-ASD, while also elucidating the underlying cause for variations in the DC-link voltage.

3.1. Power Characteristics of Traditional Arc Suppression Method

According to Figure 4 and Figure 5, it can be seen that the voltage borne by the active part of HMF-ASD U_invx during arc suppression is as follows:

$$\left\{\begin{array}{l}{\mathit{U}}_{\mathrm{inva}}={\mathit{U}}_{\mathrm{sa}}-{\mathit{U}}_{\mathrm{o}}={\mathit{E}}_{\mathrm{a}}\\ {\mathit{U}}_{\mathrm{invb}}={\mathit{U}}_{\mathrm{sb}}-{\mathit{U}}_{\mathrm{o}}={\mathit{E}}_{\mathrm{b}}\\ {\mathit{U}}_{\mathrm{invc}}={\mathit{U}}_{\mathrm{sc}}-{\mathit{U}}_{\mathrm{o}}={\mathit{E}}_{\mathrm{c}}\end{array}\right.$$

(5)

According to Equations (3)–(5), the active power transmitted by HMF-ASD P_invx during arc suppression can be obtained as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{inva}}=\sqrt{3}{E}^2\sqrt{{\displaystyle \frac{1}{{r_0}^2}}+{\omega }^2{C_0}^2}\cos \theta \\ P_{\mathrm{invb}}=\sqrt{3}{E}^2\sqrt{{\displaystyle \frac{1}{{r_0}^2}}+{\omega }^2{C_0}^2}\cos (\theta +{60}^{°})\\ P_{\mathrm{invc}}=0\end{array}\right.$$

(6)

where θ is the angle between I_oa and E_a, which is related to r_x and C_0x. The specific expression is as follows:

$$\theta =\arctan (\omega C_0{r}_0)-{30}^{°}$$

(7)

The specific variation is shown in

Table 1. Variation of energy of HMF-ASD with θ.

The Range of θ	Pinva	Pinvb	Pinvc
0 ≤ θ < 30°	+	+	0
θ = 30°	+	0	0
30° < θ ≤ 60°	+	−	0

. It can be seen from Equation (6) that θ can directly reflect the range of the active power absorbed and emitted by the HMF-ASD.

As can be seen from Table 1, when 0 ≤ θ ≤ 60°, P_inva > 0. Phase A consumes active power during arc suppression. When 0 ≤ θ < 30°, P_invb > 0. Phase B consumes active power. When θ = 30°, P_invb = 0. Phase B only transmits reactive power during arc suppression. When 30° < θ ≤ 60°, P_invb < 0. The HMF-ASD absorbs active power during arc suppression. During arc suppression, P_invc = 0, and phase C only outputs the load reactive current.

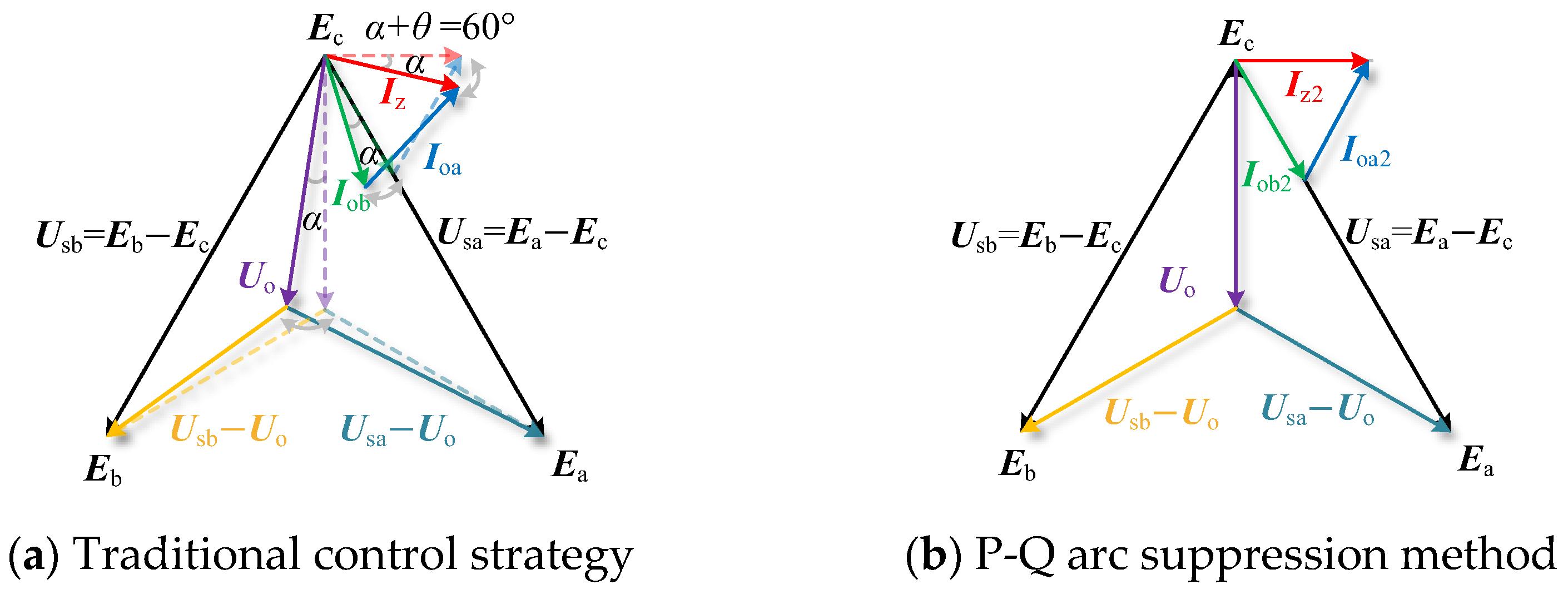
3.2. Control Strategy of the Traditional Arc Suppression Method

The reference value i_d._dc corresponding to the voltage loop is obtained by calculating the difference between the reference value U_dc._ref and the actual value U_dc through the voltage loop PI. The load current is sampled, and the reactive compensation reference current i_q._ref is subsequently calculated following dq transformation. The grid voltage components along the D-axis and Q-axis are combined with the controller outputs to produce the corresponding D-axis and Q-axis reference signals. The total arc suppression current I_z specified in Formula (3) is utilized as the reference value. The specific expression of I_z is I_z = I_oa + I_ob + I_oc. Additionally, the reference signal for the 0-axis is obtained by processing the difference in the zero-sequence current io through the current loop PI controller. Finally, the modulated signal U_sum is produced by performing an inverse dq transformation. The traditional arc suppression method is shown in Figure 6.

To compensate for the active power consumed during arc suppression and sustain DC-link voltage stability in the HMF-ASD, the system absorbs active power from the grid using a conventional arc suppression strategy. The active components of both the arc suppression current and the stabilizing current exhibit equal magnitudes but opposite polarities. Based on Equations (3)–(5), the stabilizing current of the HMF-ASD I_ox1 can be expressed as follows:

$$\left\{\begin{array}{l}{\mathit{I}}_{\mathrm{oa}1}=-\sqrt{{\displaystyle \frac{3}{{r_0}^2}}+3{\omega }^2{C_0}^2}\cos \theta {\mathit{E}}_{\mathrm{a}}\\ {\mathit{I}}_{\mathrm{ob}1}=-\sqrt{{\displaystyle \frac{3}{{r_0}^2}}+3{\omega }^2{C_0}^2}\cos (\theta +{60}^{\circ }){\mathit{E}}_{\mathrm{b}}\\ {\mathit{I}}_{\mathrm{oc}1}=0\end{array}\right.$$

(8)

where I_ox1 is the active component of the stabilizing current of the HMF-ASD.

The conventional arc suppression approach is limited to regulating only the active power exchanged between the HMF-ASD and the distribution network. According to Equation (8), it is known that I_oa1 + I_ob1 + I_oc1 = 0. At this time, the neutral point of the grid cannot satisfy KCL. There must be reactive power exchange between the HMF-ASD and the grid. Therefore, the traditional arc suppression method is unable to stabilize DC-link side voltage.

4. P-Q Arc Suppression Method Based on DC-Link Voltage Stability

Due to the large ground resistance, the active component of the arc suppression current only accounts for 5–10%. The variation range of α is from 0° to 10°, and the specific variation trajectory is shown in Figure 7a. As shown in the figure, the solid line and the dotted line represent the phasor relationship when α = 10° and α = 0°, respectively. The change trajectory is shown in the gray line.

To address the aforementioned issues, a P-Q arc suppression method is introduced. During an SLG fault, the HMF-ASD is controlled to output only reactive power, enabling complete compensation of the fault current and stabilization of the DC-link voltage without using external power supply devices. When the SLG fault occurs, non-fault phases jointly output arc suppression current. The phasor relationship is shown in Figure 7b, where α is the angle between the r_x and C_0x. The specific expression is as follows:

$$\alpha =\arctan ({\displaystyle \frac{1}{\omega C_0{r}_0}})$$

(9)

According to Figure 7, the zero-sequence power output by the HMF-ASD is as follows:

$$\left\{\begin{array}{c}{P}_{\mathrm{zab}}=-2E{I}_{\mathrm{z}}\sin \alpha \\ Q_{\mathrm{zab}}=2E{I}_{\mathrm{z}}\cos \alpha \end{array}\right.$$

(10)

where P_zab and Q_zab are the zero-sequence active power and reactive power using the traditional arc suppression method, respectively.

When the traditional arc suppression method is adopted, the HMF-ASD is required to simultaneously output both active and reactive power. To stabilize the DC-link voltage, supplementary energy supply units become necessary. The P-Q arc suppression method can attain complete compensation of the fault current and ensure the stability of the DC-link voltage by regulating the HMF-ASD to output solely reactive power, thereby eliminating the need for additional energy supply devices. Since the active and reactive components of the arc suppression current are respectively provided by the power grid and the HMF-ASD, the value of the arc suppression current remains unchanged. The value of the arc suppression current will not be affected by the HMF-ASD.

The zero-sequence power of the HMF-ASD is as follows:

$$\left\{\begin{array}{l}{P}_{\mathrm{zab}}^{\prime }=0\hfill \\ Q_{\mathrm{zab}}^{\prime }=2E{I}_{\mathrm{z}}\cos \alpha \hfill \end{array}\right.$$

(11)

where P′_zab and Q′_zab are the zero-sequence active power and reactive power using the P-Q arc suppression method, respectively.

Therefore, when the P-Q arc suppression method is adopted, the phase A and phase B of the HMF-ASD compensate the zero-sequence reactive power. Meanwhile, the grid side undertakes the compensation for the active power. Both active power and reactive power flow along the line. The diagram illustrating the zero-sequence power flow is shown in Figure 8.

The proposed control strategy is shown in Figure 9. The control strategy of the HMF-ASD mainly includes a power loop and a voltage stability loop. Q_b^* and Q_a^* are the reactive power reference values of phase B and A, respectively. Q_b and Q_a are the actual reactive power values of phase B and A, respectively. i_zb and i_za are the current reference values corresponding to the power loops of phase B and A, respectively. i_dcb and i_dca are the current reference values corresponding to the voltage stabilizing loops of phase B and A, respectively. E_bc and E_ac are the line voltage of the BC phase and the AC phase, respectively. U_dcx._ref and ∑U_dcxi are the reference values of the actual value of the DC-link voltage. N is the number of cascades.

(1)

Power loop

During the fault, the Q_a^* and Q_b^* needed for arc suppression in phases A and B are calculated, and the reference values of arc suppression currents i_za and i_zb are obtained through the power loop PI using the difference between them and the actual value.

(2)

Voltage stabilizing loop

i_dca and i_dcb of the voltage stabilizing are obtained through the voltage stabilizing PI. The actual output current is regulated by calculating the deviation between the combined current references and the measured current.

(3)

Current loop

i_za, i_zb, i_dca, and i_dcb serve as the input to the current loop PI regulator, whose output is superimposed on the busbar voltage of the HMF-ASD. The resulting signal undergoes carrier phase shift PWM (CPS-PWM) to generate the signals for the HMF-ASD.

Till now, two ways are proposed to stabilize the DC-link voltage in an HMF-ASD. Scheme I is controlling the converter to absorb energy based on positive and negative sequence loops. Scheme II is adding auxiliary DC power supply units.

(1)

As for Scheme I, the influence of a zero sequence loop is not considered. Further, the existing DC-link voltage control strategies for arc suppression devices are not applicable to the condition with ground resistance. As the DC-link voltage of the HMF-ASD progressively decreases, fault current escalates, ultimately compromising arc suppression capability.

(2)

As for Scheme II, the DC side of the HMF-ASD is connected to auxiliary DC power supplies to provide arc suppression energy. While this method enables complete fault current compensation with minimal control complexity, it incurs relatively high costs.

(3)

To achieve DC-link voltage stability and full fault current compensation without auxiliary power supplies, this paper introduces a P-Q-based arc suppression strategy. A comparative analysis with existing methods is presented in

Table 2. The comparison between existing methods and P-Q arc suppression method.

Contrast Type	Scheme I	Scheme II	P-Q Arc Suppression Method
Cost	Low	High	Low
The effect of arc suppression	Little	Great	Great
Complexity	Medium	Low	Medium

. The proposed method demonstrates superior cost-effectiveness and arc suppression performance compared to conventional approaches, though its control complexity exceeds that of Scheme II.

5. Simulation Results

To evaluate the practicality and performance of the proposed HMF-ASD topology and its operational functions, a simulation model is developed using the MATLAB 2021a/Simulink environment. Detailed simulation parameters are provided in

Table 3. Simulation Parameters.

Parameters	Values	Parameters	Values
Distribution network voltage (kV)	10	Filter inductance (mH)	5
Ground resistance (kΩ)	30	Active power of load (MW)	1
Ground capacitance (uF)	10	Power factor of load	0.97
Ground-fault resistance (Ω)	1	DC-link capacitance (mF)	3
Arc suppression inductance (mH)	330	Number of cascaded modules	5
Proportional coefficient of the power loop	0.0175	Integral coefficient of the power loop	15
Proportional coefficient of the stabilizing loop	0.2	Integral coefficient of the stabilizing loop	20
Proportional coefficient of the current loop	5	Integral coefficient of the current loop	30

.

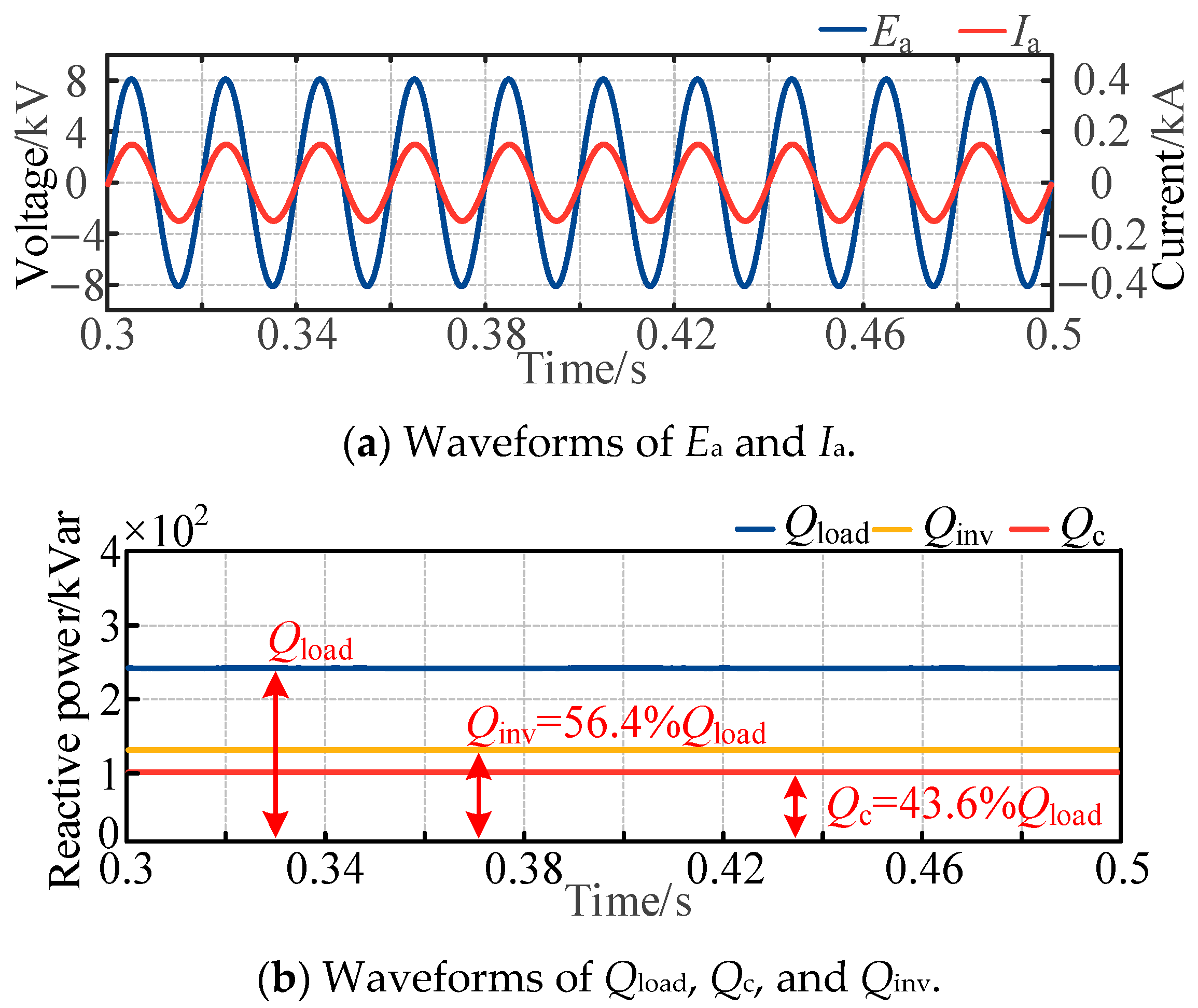
5.1. Simulation of Reactive Power Compensation Mode

During 0–0.1 s, the HMF-ASD is not put into operation. During 0.1–0.5 s, the HMF-ASD operates in reactive power compensation mode. Comprehensive simulation waveforms for the reactive power compensation mode are provided in Figure 10. E_a and I_a waveforms are shown in Figure 10a. E_a = 8165 V and I_a = 173 A. The in-phase alignment of voltage and current confirms the system’s effective reactive power compensation capability. The reactive power distribution is further analyzed in Figure 10b, showing the load reactive power (Q_load = 241 kVar), the reactive power of the ground capacitance (Q_c = 105 kVar), and the reactive power of the HMF-ASD (Q_inv = 136 kVar). The ground capacitance accounts for 43.6% of the total compensation, while the HMF-ASD contributes 56.4%.

5.2. Simulation of Arc Suppression Mode

In order to further verify the performance of the HMF-ASD using the traditional control strategy, a simulation model of a 10 kV distribution network is built. The waveforms using the traditional control strategy are shown in Figure 11a,b. The HMF-ASD operates in arc suppression mode from 0.3–0.5 s, switching to reactive power compensation mode during other times.

As shown in Figure 11a, the DC-link voltage of the CHB remains stable at 2000 V between 0.2 s and 0.3 s. At 0.3 s, non-fault phases initiate arc suppression current injection. During this period, phase B consumes active power, causing its DC-link voltage to decrease, while phase C absorbs active power, resulting in an increase in its CHB DC-link voltage. Figure 11b demonstrates that the HMF-ASD achieves effective arc suppression between 0.3 s and 0.4 s. However, as DC-link voltages continue to decline, the fault current rises, ultimately compromising the HMF-ASD arc suppression capability. These findings indicate that the conventional control strategy fails to maintain effective arc suppression under conditions involving ground resistance.

The simulated waveforms of the HMF-ASD using the P-Q arc suppression method are presented in Figure 12. For fault resistances R_f = 1 Ω and R_f = 1000 Ω, the corresponding fault current I_g waveforms are displayed in Figure 12a,b. After the HMF-ASD is switched to the arc suppression mode, the fault current I_g is reduced to zero within 100 ms. The DC-link voltages of phases B and C, as shown in Figure 12c,d, stabilize near 2 kV for each sub-module after mode transition, ensuring precise delivery of arc suppression current. The output currents (I_inva, I_invb, and I_invc) are illustrated in Figure 12e. During reactive power compensation mode, the system accurately injects compensation current, while in arc suppression mode, phases B and C deliver 73.7∠-30.8° A and 75.1∠-149.6° A, respectively, enabling effective SLG fault mitigation.

To assess the impact of arc suppression inductance, the HMF-ASD operates without current injection during 0.2–0.3 s. From 0.3–0.4 s, direct grounding is employed to inject arc suppression current, followed by inductance-based grounding from 0.4–0.5 s. The voltage waveforms for the HMF-ASD and arc suppression inductance are depicted in Figure 12f. Under normal grid conditions, the HMF-ASD output voltage matches the phase voltage. At 0.2 s, an SLG fault in phase A causes neutral point voltage deviation, elevating the HMF-ASD output above the phase voltage. Direct grounding at 0.3 s shifts the neutral point voltage to approximately −E_a, raising the HMF-ASD output to line voltage. At 0.4 s, inductance-based grounding reduces the inductance voltage U_LN to near −E_a, restoring the HMF-ASD output to phase voltage. Simulation results confirm that inductance-based grounding significantly decreases inductor capacity requirements in arc suppression mode, thereby minimizing power device usage.

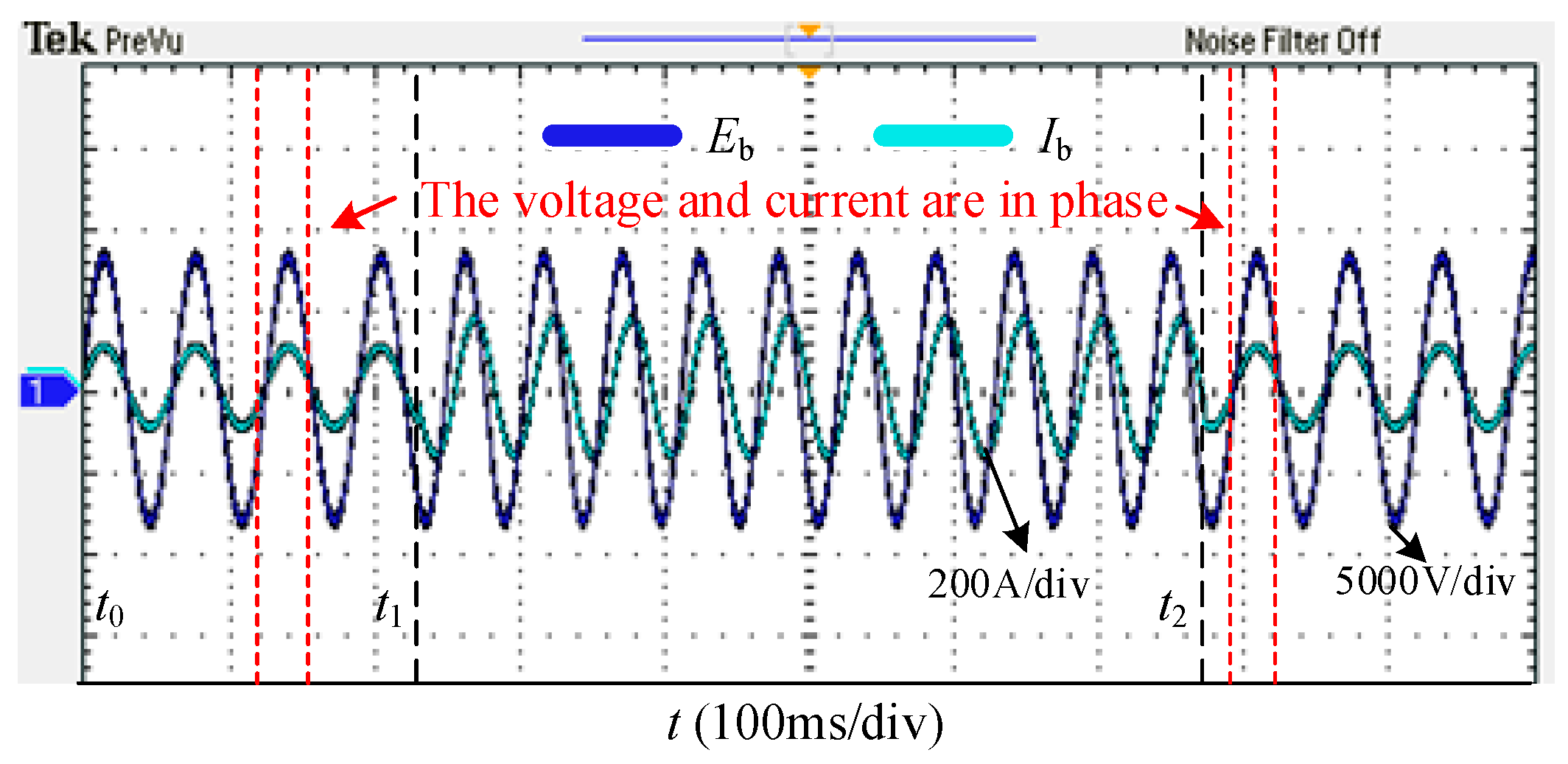
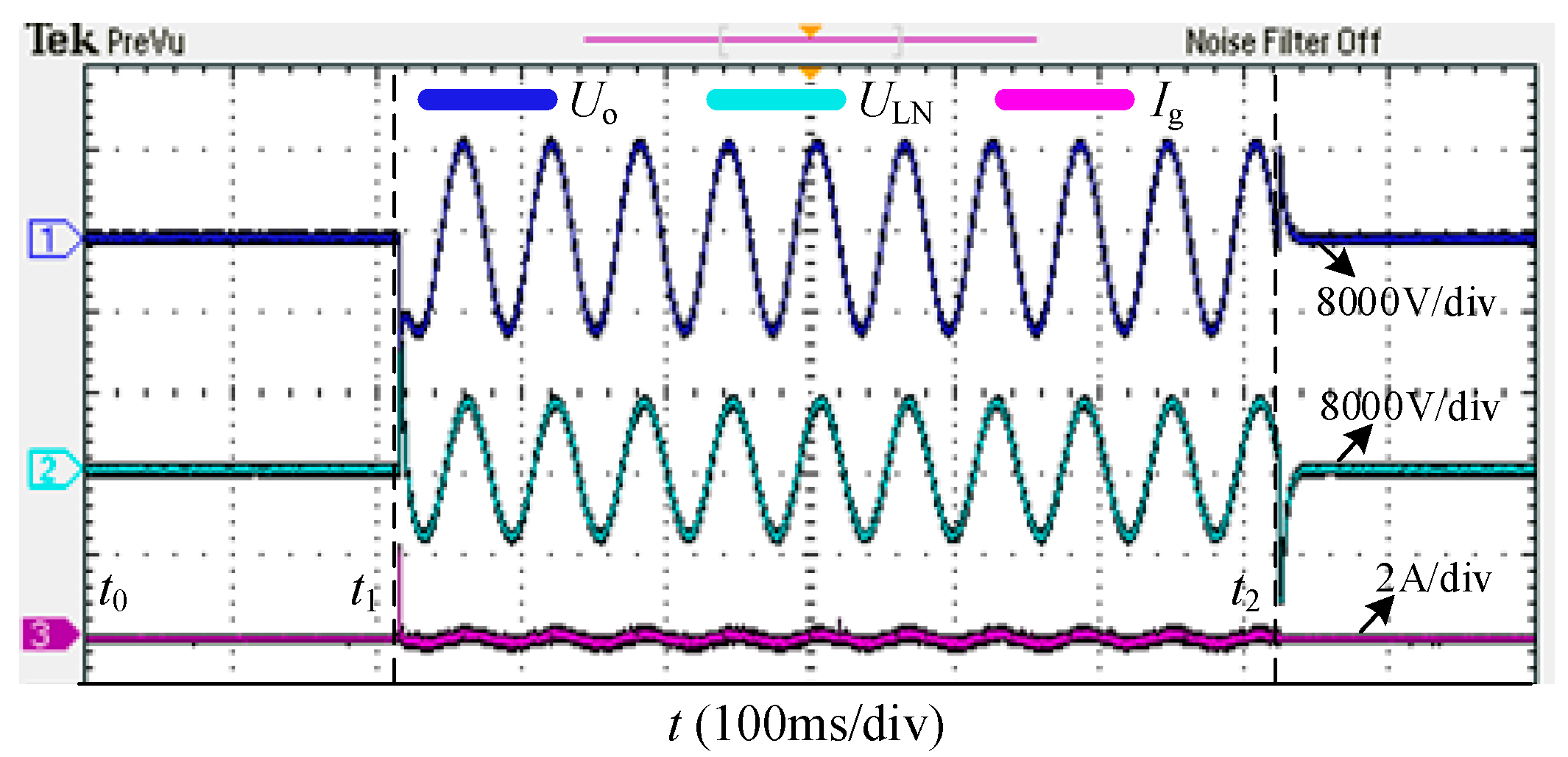
6. Experimental Results

To validate the effectiveness and precision of the proposed P-Q arc suppression method, an experimental assessment is conducted using a Control Hardware-in-the-Loop (CHIL) testbed built on the RT-LAB OP5600 platform (Opal-RT). Figure 13 illustrates the configuration of this RT-LAB-based CHIL testing system.

An SLG fault is assumed to occur in Phase A at t₁. During the t₀-t₁, the HMF-ASD operates in reactive power compensation mode. From t₁-t₂, the system transitions to arc suppression mode, and after t₂, it reverts to reactive power compensation. All other experimental parameters remain consistent with those used in the simulation.

Figure 14 displays the experimental waveforms of U_dca, U_dcb, and U_dcc. Using the proposed P-Q arc suppression method, the DC-link voltage of the HMF-ASD remains stable at 2000 V during arc suppression, with voltage fluctuations constrained within 50 V. Figure 15 presents the experimental waveforms of E_b and I_b. When the HMF-ASD operates in reactive power compensation mode, it supplies the load’s reactive power demand, ensuring in-phase alignment between grid voltage and current. Figure 16 illustrates the experimental waveforms of U_o, U_LN, and I_g. During arc suppression mode, the HMF-ASD reduces the fault current to 0.1 A, while the voltage across the arc suppression inductance reaches approximately 8000 V. Figure 17 shows the experimental waveforms of I_inva, I_invb, and I_invc. The reactive current required for reactive power compensation is delivered in compensation mode, whereas the reactive current for arc suppression is provided in suppression mode.

7. Conclusions

Aiming at the problem that HMF-ASDs need to add additional power supply units to maintain DC-link voltage, a P-Q arc suppression method based on DC-link voltage stability is proposed. The conclusions are as follows:

(1)

The working principle of the HMF-ASD is introduced and the current flow of the HMF-ASD in two modes is analyzed.

(2)

The influence mechanism of the traditional arc suppression method on the output active power and energy flow direction of the HMF-ASD is analyzed. The internal causes of DC link voltage changes are clarified.

(3)

The phase relationship between voltage and current under arc suppression mode is analyzed, and a P-Q arc suppression method is proposed. By controlling the HMF-ASD to compensate only zero-sequence reactive power, the HMF-ASD can stabilize the DC-link voltage.

(4)

Compared with existing methods, the proposed method has lower cost and better arc suppression effect, but the control complexity is relatively high.

(5)

In the future, the performance improvement of PLL under unbalanced and fault conditions will be further studied.