Study on a Hierarchical Game-Based Model for Generation Rights Trading in Multi-Park CCHP-Based Integrated Energy Systems Accounting for New Energy Grid Integration

Abstract

To address the challenges of power generation rights trading and profit distribution in the integrated energy system of multi-park combined cooling, heating, and power (CCHP) with new energy grid integration, we constructed a hierarchical game model involving multi-energy system aggregators. By having aggregators price electricity, heat, cold, and carbon costs, the model establishes a hierarchical game framework with the linkage of the four prices (electricity, heat, cold, and carbon), achieving inter-park peer-to-peer (P2P) multi-energy dynamic price matching for the first time. It aims to coordinate distribution network dispatching, renewable energy, energy storage, gas turbine units, demand response, cooling–heating–power coupling, and inter-park P2P multi-energy interaction. With the goal of optimizing the profits of integrated energy aggregators, a hierarchical game mechanism is established, which integrates power generation rights trading models and incentive-based demand response. The upper layer of this mechanism is the profit function of integrated energy aggregators, while the lower layer is the cost function of park microgrid alliances. A hierarchical game mechanism with Two-Level Optimization, integrating the Adaptive Disturbance Quantum Particle Swarm Optimization (ADQPSO) algorithm and the branch and bound method (ADQPSO-Driven Branch and Bound Two-Level Optimization), is used to determine dynamic prices, thereby realizing dynamic matching of energy supply and demand and cross-park collaborative optimal allocation. Under the hierarchical game mechanism, the convergence speed of the ADQPSO-driven branch and bound method is 40% faster than that of traditional methods, and the optimization profit accuracy is improved by 1.59%. Moreover, compared with a single mechanism, the hierarchical game mechanism (Scenario 4) increases profits by 17.17%. This study provides technical support for the efficient operation of new energy grid integration and the achievement of “dual-carbon” goals.

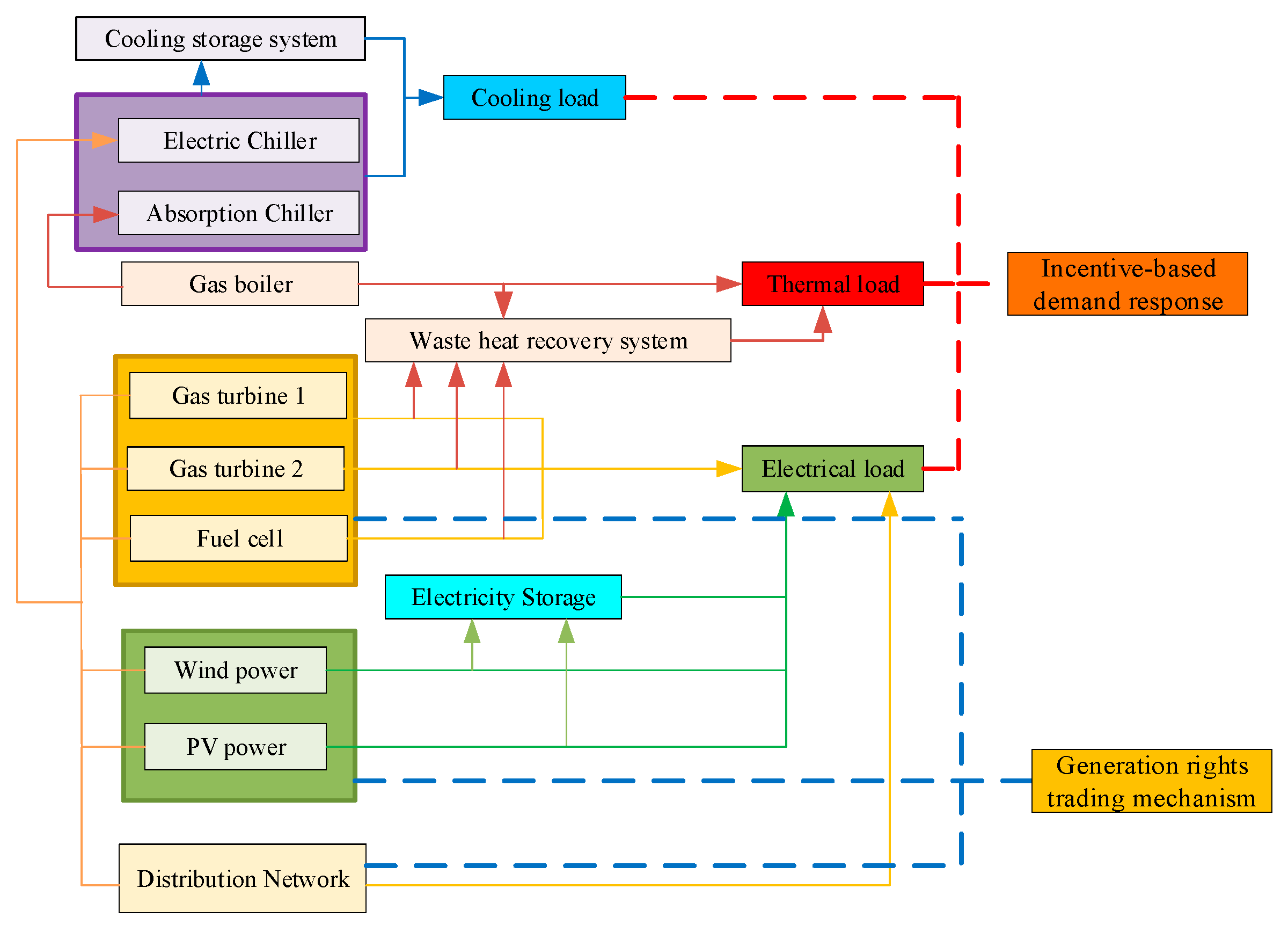
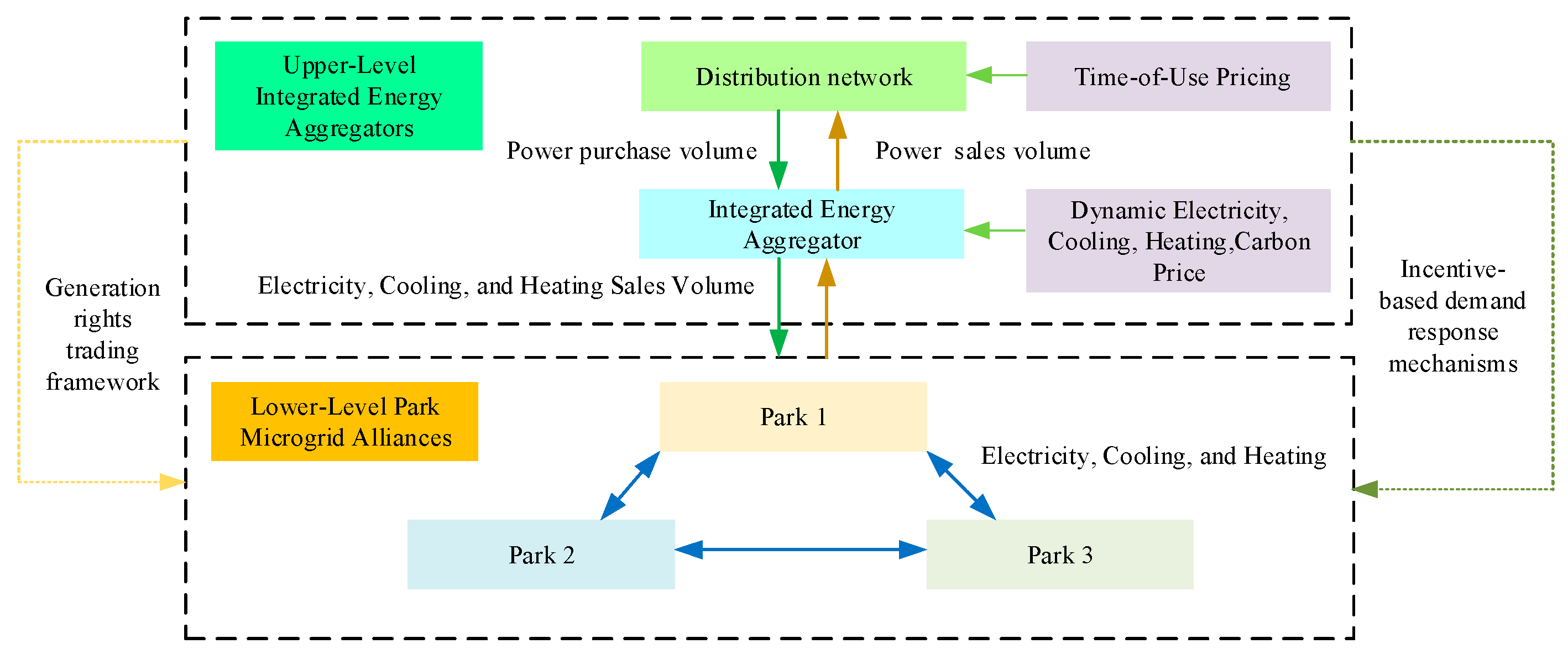
1. Introduction

With the advancement of new energy grid integration and the escalating enhancement of dual-carbon goals, multi-park combined cooling, heating, and power (CCHP)-based integrated energy systems, by virtue of their multi-energy synergy characteristics, have an important role in improving energy utilization efficiency and promoting low-carbon transition, thus becoming a core carrier. Against this backdrop, scholars at home and abroad have conducted research on this system, laying a foundation for further research. Current relevant studies mainly focus on the application of game theory and optimal scheduling in integrated energy systems, which can be categorized based on differences in research objects, core methods, and objectives.

In the field of local integrated energy systems, Reference [1] addresses the insufficient research on the application of shared energy storage (SES) in local integrated energy systems (LIESs). The authors constructed a day-ahead scheduling model for LIESs with SES based on cooperative game theory and solved it using the ADMM-W-D distributed algorithm. This model effectively reduces the operating costs of the system, improves the absorption of renewable energy, and features better algorithm convergence and scalability. Studies on energy interaction among park-level systems and multi-agent clusters include several works. Reference [2] focuses on energy sharing among multiple park-level integrated energy systems (PIESs). It combines cooperative game theory with distributed optimization algorithms, integrates demand response and carbon trading mechanisms, and improves the Shapley value method for benefit distribution, achieving significant results in emission reduction, economic efficiency enhancement, and stakeholder coordination. Reference [3] proposes a hierarchical game approach considering bounded rationality, which realizes collaborative optimization of clusters while protecting privacy through designs such as the Stackelberg game, mild altruism function, evolutionary game, and prosumer role switching. Reference [4] targets the “energy–carbon” interconnection characteristics of integrated energy systems, adopts the Stackelberg game to coordinate the goals of energy service providers and prosumers, and combines integrated pricing to improve efficiency and reduce emissions. The authors of Reference [5] developed a data-driven stochastic game model, used spatiotemporal graph convolutional networks to learn social attributes, and clarified their impact on P2P energy sharing. Regarding the coordination between integrated energy microgrids and distribution networks, Reference [6] proposes a two-stage planning model involving mixed games. The first stage integrates the Stackelberg game and nested cooperative game, while the second stage incorporates a demand response model considering carbon emission flow (CEF) and step carbon pricing. With the help of algorithms like PCB-ADMM, it enhances convergence and protects the privacy of multiple subjects, realizing coordinated planning between distribution networks and multiple microgrids. Regarding scheduling and benefit distribution in multi-energy systems, Reference [7] constructs an optimal scheduling model based on non-cooperative game theory and combines it with the Particle Swarm Optimization (PSO) algorithm to improve energy utilization efficiency, ensuring reliable system operation and reasonable benefit distribution among energy systems. Reference [8] addresses the issue of the computation time of the nucleolus mechanism in cooperative games increasing exponentially with the number of participants. It introduces clustering techniques to optimize nucleolus estimation, significantly reducing computation time. Reference [9] coordinates the conflict between overall optimization and investors’ profits through a two-layer game model: the inner layer uses a master–slave game to optimize the planned output, and the outer layer combines non-cooperative games and cooperative games led by the wind–photovoltaic alliance to determine optimal capacity allocation, obtaining an equilibrium solution through iteration. Reference [10] proposes a new energy pricing and sharing strategy for virtual energy stations (VESs) in multi-carrier energy systems, optimizing energy management and market bidding.

Regarding research on energy aggregators, the following works in the literature mainly focus on the functions and strategies of aggregators in energy systems, which can be divided into four categories. The first category focuses on energy system management and optimization. Reference [11] proposes a day-ahead microgrid energy management framework with demand response aggregators as intermediate coordinators, aiming to maximize the social welfare of the system. It develops the FAST-PP-ADMM accelerated distributed optimization method, constructs a data-driven risk-adjusted uncertainty set, and adopts the C&CG method to solve the two-stage robust energy management model. Reference [12] introduces customer aggregators to meet downstream demand in the most economical manner and establishes a two-level optimization problem (TLOP). The system operator maximizes social welfare under the constraint of the aggregator’s strategy to minimize energy purchase costs. Its innovation lies in integrating customers’ flexible demand with Two-Level Optimization, simplifying the scheduling process through transformation, and achieving parameter internalization and efficient scheduling. Reference [13] proposes a hydrogen–electricity integrated energy sharing model, taking aggregators capable of consuming electricity or hydrogen as a new coupling point between the power grid and gas grid, with the objective of maximizing the total social welfare of cross-system energy dispatch. It adopts a distributed optimization method to reduce computational complexity and concludes that hydrogen–electricity sharing can achieve the lowest system cost and maximum social welfare, and that distributed energy storage can improve system stability. The second category revolves around multi-energy collaboration and aggregation models. Reference [14] explores the coordinated scheduling of renewable energy and multi-type loads using aggregators in multi-park microgrids. With aggregators as the core, it integrates user-side demand response and zero-marginal-cost new energy and constructs an optimization model considering carbon emission reduction targets to enhance the low-carbon performance and resilience of the system. Reference [15] studies the multi-energy collaborative operation of cooling, heating, and electricity led by integrated energy aggregators, coordinating cooling, heating, and electricity loads in the region with the output of distributed energy sources. It adopts a mixed-integer programming model to optimize energy conversion and transmission paths, balancing the economy and environmental protection of the system. Reference [16] establishes a cooperation mechanism between aggregators and distributed energy producers (such as wind power, photovoltaics, and small-scale energy storage), encouraging multi-subject participation in energy aggregation through contract design and benefit-sharing models to improve the absorption rate of distributed energy and its market participation. The third category focuses on market transaction strategies and game interactions: Reference [17] studies the impact of strategic bidding by distributed energy aggregators on the distribution network, constructs a bi-level mixed-integer nonlinear programming model, solves the equilibrium solution through heuristic algorithms, and verifies the regulatory effect of bidding strategies on distribution network node prices and load distribution. Reference [18] proposes the concept of the “optimal absorption interval” for new energy, establishes a leader–follower game model between regional energy aggregators and the main power grid, solves the strategy equilibrium between the two parties through numerical methods, and improves the absorption rate of new energy and the overall benefits of the system. Reference [19] designs a single-level optimization model transformed based on KKT conditions for local electricity markets involving multiple distributed energy aggregators, solving the transaction strategies and benefit distribution schemes among aggregators to promote the efficient participation of distributed energy in market transactions. The fourth category focuses on interest balance in system fault recovery: Reference [20] addresses the scenario of distribution network fault recovery, studying the interest coordination mechanism between integrated energy aggregators and distribution network operators. Through the optimization of emergency power supply strategies and cost-sharing models, it balances the interests of both parties while ensuring the efficiency of fault recovery, providing a solution for the participation of aggregators in the system’s emergency state.

The value of the method used in this paper is as follows: algorithmically, it is the first to integrate adaptive perturbation and dynamic weights, solving the traditional convergence problem; application-wise, it focuses on the hierarchical game of multi-park CCHP, enabling cross-park resource optimization. It forms a hierarchical complementarity of “system optimization–equipment control” with existing methods, providing support for the efficient operation of integrated energy systems and offering methodological references for cross-park collaboration.

According to the above, existing research on optimal scheduling of multi-park combined cooling, heating, and power (CCHP)-based integrated energy systems has three significant shortcomings: In terms of hierarchical game mechanisms, most studies [7,8,9] only focus on the pricing of a single energy source (electricity), failing to reflect the linkage logic of electricity, heat, cooling, and carbon prices, and ignoring the impact of multi-energy coupling on game strategies. In terms of cross-park dynamic price matching, although references [2,6] mention cross-park interaction, they do not establish a quantitative model for P2P multi-energy real-time supply–demand response, lacking a dynamic price adjustment mechanism. In terms of algorithm limitations and research object positioning, traditional PSO algorithms [7] tend to fall into local optima in scenarios with strong constraints, and compared with reference [15], existing studies do not fully consider the coupling of carbon prices with multi-energy prices. They insufficiently depict hierarchical game mechanisms involving multi-energy aggregators (including the pricing logic of electricity, heat, cooling, and carbon) and lack exploration of dynamic price matching models for cross-park multi-energy interaction, power generation rights trading, and demand response mechanisms; additionally, traditional algorithms have limited convergence in handling nonlinear constraints. Reference [17] emphasizes the restriction of distribution network security checks on bidding strategies and the effectiveness of the RBRD algorithm. In contrast, this study employs multi-level collaborative optimization, where the upper layer aims to maximize profits and the lower layer aims to minimize operating costs, pursuing a multi-objective balance. Its core verifies the synergistic effect of “power generation rights trading + demand response” and the advantages of the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm.

To address the aforementioned shortcomings, this study constructs a hierarchical game mechanism based on multi-energy dynamic pricing, integrating the linkage logic of electricity, heat, cooling, and carbon prices to break through the limitations of single-energy pricing. Guided by the optimal interests of energy aggregators, it integrates the ADQPSO algorithm with the branch and bound method to solve the local optima problem of traditional PSO algorithms. Adopting the core framework of the hierarchical game model, based on power generation rights trading and demand response mechanisms, it collaborates with distribution networks, wind–solar storage systems, gas turbines, and cross-park P2P multi-energy coupling systems to achieve dynamic price matching and optimal resource allocation. Through Two-Level Optimization, it realizes the dynamic matching of electricity–heat–cooling supply and demand, providing methodological support for the efficient solution of optimal configuration in new energy grid-connected multi-park combined cooling, heating, and power (CCHP) systems.

2. Hierarchical Game Model Involving Integrated Energy Aggregators in Multi-Park Systems

In the multi-park system, each sub-park has established a multi-energy complementary CCHP-type system of energy supply and regulation mechanisms. Energy production includes Gas Turbine 1, Gas Turbine 2, and fuel cells for combined heat and power generation, wind power generation, and photovoltaic power generation to provide renewable electricity, as well as externally purchased electricity. The electricity generated thereby supplies the electrical load; on the other hand, supply and demand are regulated through the electricity storage system.

Regarding heat energy utilization, the waste heat from gas turbines and fuel cells is collected by the waste heat recovery system and, together with a gas boiler, meets the heat load. Regarding cooling, electric chillers and absorption chillers (which can be driven by thermal energy) work in conjunction with the cooling storage system to meet the cooling load.

In demand side management, incentive-based demand response implements flexible regulation for heat load, cooling load, and electrical load. The generation rights trading mechanism optimizes the market allocation of power resources. All modules are interconnected and intercommunicated through energy flows and regulation mechanisms, forming an efficient and collaborative multi-park CCHP-type integrated energy system. The system structure topology is shown in Figure 1.

2.1. Hierarchical Game Framework Design

In the context of electricity–carbon linkage, the value of generation rights trading is primarily reflected in the following two aspects:

Incremental profits for both trading parties: As there is a difference in power generation costs between the sellers and buyers participating in generation rights trading, the value is embodied in the incremental profits generated by both sides through the transaction.

Extra profits in the carbon emission rights trading market: Under the electricity–carbon linkage framework, power generation enterprises are allowed to freely trade carbon emission rights within the regional total carbon emission cap, so the value of generation rights trading is also reflected in the additional profits from the carbon market.

Since the power generation cost of clean energy is far lower than that of thermal power and no carbon emissions are generated during the power generation process, when the transferee of generation rights trading is a clean energy entity, the substantial cost difference and significant remaining carbon emission rights form the basis for the feasibility of clean energy generation rights trading. Therefore, the game model established in this study fully considers the impact of the generation rights trading mechanism under the electricity–carbon linkage environment on system operation costs.

In incentive-based demand response, users’ response strategies for different energy sources also exhibit mutually coupled characteristics, which are manifested as mutually restrictive relationships between the response volumes of different energy sources. To account for such coupling characteristics, this paper establishes a user-side electricity–heat–cooling coupling demand response mechanism.

The hierarchical game framework for multi-park CCHP (combined cooling, heating and power) systems constructed in this paper is as shown in Figure 2.

2.1.1. Upper-Level Integrated Energy Aggregators (IEAs)

Based on Nash bargaining theory, integrated energy aggregators dynamically determine 24-hour electricity/heat/cold prices and carbon prices to maximize their profits, guiding energy scheduling across parks through price signals. This strategy coordinates multi-energy flows (electricity, heat, and cold) and carbon quota transactions, balancing market competitiveness and operational sustainability while forming a two-way interaction mechanism of “price guidance–response adjustment”.

2.1.2. Lower-Level Park Microgrid Alliances

Through cooperative game optimization, park microgrid alliances integrate distributed energy resources (renewable generation, fuel cells, and gas turbines), energy storage systems, and cold–heat–electricity coupling devices to achieve source–load–storage coordination and minimize alliance operational costs. The model further incorporates incentive-based demand response mechanisms and establishes a generation rights trading framework under electricity–carbon linkage, aiming to maximize social benefits by optimizing resource allocation among renewable energy integration (e.g., flexible accommodation of wind/solar power), dynamic adjustment of flexible loads, and carbon emission reduction targets. This approach balances economic efficiency with environmental benefits, ensuring sustainable and cost-effective operation of the alliance.

The proposed hierarchical game model promotes efficient interaction among multi-level energy systems through the collaborative linkage of price guidance by aggregators and cost optimization by microgrid alliances, significantly enhancing comprehensive energy utilization efficiency and system operational economy.

2.2. Game-Driven Integrated Energy Aggregator

2.2.1. Objective Function

The integrated energy aggregator, acting as the game leader, formulates dynamic energy purchase and sale prices based on the actual quantities of energy purchased/sold and associated costs.

The objective function of the upper-level integrated energy aggregator is set as follows:

$$\max B^{\mathrm{IEA}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}(l_{i,t}^{\mathrm{e}}·p_t^{\mathrm{e}}+l_{i,t}^{\mathrm{h}}·p_t^{\mathrm{h}}+l_{i,t}^{\mathrm{c}}·p_t^{\mathrm{c}})}}-C_{\mathrm{total}}$$

(1)

In Formula (1), $B^{\mathrm{IEA}}$ denotes the profit of the integrated energy aggregator, N represents the total number of park microgrid alliances, and T is the time period, representing 24 h. $l_{i,t}^{\mathrm{e}}$, $l_{i,t}^{\mathrm{h}}$, and $l_{i,t}^{\mathrm{c}}$ denote the electrical load, thermal load, and cooling load, respectively. $p_t^{\mathrm{e}}$, $p_t^{\mathrm{h}}$, and $p_t^{\mathrm{c}}$ represent the dynamic time-of-use electricity price, dynamic time-of-use thermal price, and dynamic time-of-use cooling price, respectively. $C_{\mathrm{total}}$ denotes the total cost of the park microgrid alliances.

The total cost of the park microgrid alliance is represented by the total energy consumption cost of the park microgrid alliance; the total environmental cost of the park microgrid alliance; the incentive-based demand response costs for electricity, heating, and cooling of the park microgrid alliance; and the income from generation rights trading. Among these, the income from generation rights trading consists of carbon subsidies, fuel savings, and profits from renewable energy, as expressed in Formulas (2) and (3):

$$\min C_{\mathrm{total}}=F_{\mathrm{ener}}+F_{\mathrm{envi}}+F_{\mathrm{dr}}-F_{\mathrm{link}}$$

(2)

$$F_{\mathrm{link}}=F_{\mathrm{carbon}}+F_{\mathrm{fuel}}+F_{\mathrm{ren}}$$

(3)

In Formula (2), $F_{\mathrm{ener}}$ represents the total energy consumption cost of the park microgrid alliance, and $F_{\mathrm{envi}}$ denotes the total environmental cost of the park microgrid alliance. $F_{\mathrm{dr}}$ represents incentive-based demand response costs for electricity, heating, and cooling of the park microgrid alliance. $F_{\mathrm{link}}$ denotes the generation rights trading income function. In Formula (3), $F_{\mathrm{carbon}}$ denotes the profit from carbon allowances, $F_{\mathrm{fuel}}$ denotes the fuel cost savings, and $F_{\mathrm{ren}}$ denotes the profit from renewable energy.

The total energy consumption cost of the park microgrid alliance is expressed as shown in Formula (4):

$$\begin{array}{l}{F}_{\mathrm{ener}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{\alpha }_1·w_{i,t}+{\beta }_1}}·v_{i,t}+{\delta }_t·g_{i,t}-{\gamma }_t·s_{i,t}+{\alpha }_2·(f_{i,t}^{\mathrm{dis}}+f_{i,t}^{\mathrm{c}\mathrm{h}})+{\alpha }_3·(q_{i,t}^1+q_{i,t}^2)+{\alpha }_4·r_{i,t}+{\alpha }_5·d_{i,t}+\\ {\alpha }_6·k_{i,t}+{\alpha }_7·(m_{i,t}^{\mathrm{dis}}+m_{i,t}^{\mathrm{c}\mathrm{h}})\end{array}$$

(4)

In Formula (4), ${\alpha }_1$ represents the wind power operation and maintenance cost coefficient, $w_{i,t}$ denotes the wind power utilization of park i at time t, ${\beta }_1$ is the photovoltaic (PV) operation and maintenance cost coefficient, $v_{i,t}$ is the PV power utilization, ${\delta }_t$ is the electricity purchase price at time t, $g_{i,t}$ is the electricity purchase volume, ${\gamma }_t$ is the electricity selling price, $s_{i,t}$ is the electricity selling volume, ${\alpha }_2$ is the power storage operation and maintenance cost coefficient, $f_{i,t}^{\mathrm{dis}}$ and $f_{i,t}^{\mathrm{c}\mathrm{h}}$ are the discharge/charge volumes of energy storage battery, ${\alpha }_3$ is the operation cost coefficient of the gas turbine, $q_{i,t}^1$ is the power generation of gas turbine 1 in park i at time t, $q_{i,t}^2$ is the power generation of gas turbine 2, ${\alpha }_4$ is the operation cost coefficient of the fuel cell, $r_{i,t}$ is the power generation of the fuel cell, ${\alpha }_5$ is the operation cost coefficient of the electric chiller, $d_{i,t}$ is the cooling capacity of the electric chiller, ${\alpha }_6$ is the operation cost coefficient of the gas boiler, $k_{i,t}$ is the heat output of the gas boiler, ${\alpha }_7$ is the cooling storage operation and maintenance cost coefficient, and $m_{i,t}^{\mathrm{dis}}$ and $m_{i,t}^{\mathrm{c}\mathrm{h}}$ are the cooling discharge/charge volumes of the cooling storage system.

The total environmental cost of the park microgrid alliance is expressed as shown in Formula (5):

$$F_{\mathrm{envi}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}(q_{i,t}^1}}+q_{i,t}^2)·{\lambda }_1+r_{i,t}·{\lambda }_2+g_{i,t}·{\lambda }_3$$

(5)

In Formula (5), ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are the environmental cost coefficients of the gas turbine, fuel cell, and distribution network, respectively.

This paper considers incentive-based electrical, thermal, and cooling demand response, where the demand response cost is mainly influenced by reducible loads.

$$F_{\mathrm{dr}}={\lambda }_{\mathrm{e}}^{\mathrm{cut}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{P}_{i,t}^{\mathrm{cut}}}}+{\lambda }_{\mathrm{h}}^{\mathrm{cut}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{Q}_{i,t}^{\mathrm{cut}}}}+{\lambda }_{\mathrm{c}}^{\mathrm{cut}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{R}_{i,t}^{\mathrm{cut}}}}$$

(6)

In Formula (6), $P_{i,t}^{\mathrm{cut}}$, $Q_{i,t}^{\mathrm{cut}}$, and $R_{i,t}^{\mathrm{cut}}$ denote the incentive-based reducible electrical load, thermal load, and cooling load demand response values of park i at time t, respectively. ${\lambda }_{\mathrm{e}}^{\mathrm{cut}}$, ${\lambda }_{\mathrm{h}}^{\mathrm{cut}}$, and ${\lambda }_{\mathrm{c}}^{\mathrm{cut}}$ denote the reducible cost coefficients for the electrical load, thermal load, and cooling load, respectively.

Profit from carbon allowances is expressed as shown in Formula (7):

$$F_{\mathrm{carbon}}=({\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}(E_r-(q_{i,t}^1+q_{i,t}^2-K_{i,t})}}·{\phi }_r)+(E_{\mathrm{c}}-r_{i,t}\cdot {\phi }_{\mathrm{c}}))\cdot p_t^{\mathrm{car}}$$

(7)

In Formula (7), $E_r$ denotes the carbon allowance of the gas turbine, $K_{i,t}$ denotes the trading volume of new energy power generation rights for park i at time t, ${\phi }_r$ denotes the carbon emission factor of the gas turbine, $E_{\mathrm{c}}$ denotes the carbon allowance of the fuel cell, ${\phi }_{\mathrm{c}}$ denotes the carbon emission factor of the fuel cell, and $p_t^{\mathrm{car}}$ denotes the dynamic time-of-use carbon price at time t.

Fuel cost savings are expressed as shown in Formula (8), and the profit from renewable energy is as shown in Formula (9):

$$F_{\mathrm{fuel}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{\varphi }_{\mathrm{fuel}}\cdot K_{i,t}}}$$

(8)

$$F_{\mathrm{ren}}={\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}(w_{i,t}}}+v_{i,t}+K_{i,t})\cdot {\gamma }_{\mathrm{ro}}$$

(9)

In Formula (8), ${\varphi }_{\mathrm{fuel}}$ denotes the fuel cost saving coefficient. In Formula (9), ${\gamma }_{\mathrm{ro}}$ denotes the renewable energy income coefficient.

The trading volume of new energy power generation rights is as shown in Formula (10):

$$K_{i,t}=W_{i,t}+V_{i,t}-w_{i,t}-v_{i,t}$$

(10)

In Formula (10), $W_{i,t}$ denotes the predicted wind power output of park i at time t, and $V_{i,t}$ denotes the predicted photovoltaic (PV) power output.

The integrated energy aggregator aims to maximize its own benefits, which include the costs and revenues associated with energy purchase and sale with the power grid and the park microgrid alliance.

2.2.2. Constraint Conditions

The electric power balance constraints for each park are as follows:

$$\begin{array}{l}{P}_{i,t}^{\mathrm{netbuy}}+w_{i,t}+v_{i,t}+q_{i,t}^1+q_{i,t}^2+r_{i,t}+P_{i,t}^{\mathrm{cut}}+P_{i,t}^{\mathrm{exfrom}}+f_{i,t}^{\mathrm{dis}}=l_{i,t}^{\mathrm{e}}+f_{i,t}^{\mathrm{c}\mathrm{h}}+P_{i,t}^{\mathrm{cool}}+P_{i,t}^{\mathrm{netsell}}+P_{i,t}^{\mathrm{exto}}\\ P_{i,t}^{\mathrm{cool}}=\Upsilon \cdot d_{i,t}\end{array}$$

(11)

In Formula (11), $P_{i,t}^{\mathrm{netbuy}}$ and $P_{i,t}^{\mathrm{netsell}}$, respectively, represent the electric power purchased and sold in the interactive power between park i and the distribution network at time t. $P_{i,t}^{\mathrm{exfrom}}$ and $P_{i,t}^{\mathrm{exto}}$, respectively, represent the electric power imported and exported in the power exchanged between park i and other microgrids. $P_{i,t}^{\mathrm{cool}}$ is the power consumption of the electrical chiller, and $\Upsilon$ is the cooling-to-electricity conversion coefficient.

The thermal power balance constraints for each park are as follows:

$$\begin{array}{l}{P}_{i,t}^{\mathrm{yure}}+P_{i,t}^{\mathrm{ranqi}}+Q_{i,t}^{\mathrm{cut}}+P_{i,t}^{\mathrm{hotexfrom}}=l_{i,t}^{\mathrm{h}}+P_{i,t}^{\mathrm{hotrequest}}+P_{i,t}^{\mathrm{hotexto}}\\ P_{i,t}^{\mathrm{hotrequest}}=\varsigma \cdot P_{i,t}^{\mathrm{xscool}}\end{array}$$

(12)

In Formula (12), $P_{i,t}^{\mathrm{yure}}$ represents the thermal power of the waste heat recovery system. $P_{i,t}^{\mathrm{ranqi}}$ denotes the thermal power generated by the gas boiler. $P_{i,t}^{\mathrm{hotexfrom}}$ and $P_{i,t}^{\mathrm{hotexto}}$ are the imported and exported thermal power exchanged among parks. $P_{i,t}^{\mathrm{hotrequest}}$ is the thermal demand of the waste heat recovery system. $P_{i,t}^{\mathrm{xscool}}$ is the cooling power of the absorption chiller, and $\varsigma$ is the cooling-to-heat conversion coefficient.

The cooling power balance constraints for each park are as follows:

$$d_{i,t}+P_{i,t}^{\mathrm{xscool}}+R_{i,t}^{\mathrm{cut}}+P_{i,t}^{\mathrm{coolexfrom}}+m_{i,t}^{\mathrm{dis}}=l_{i,t}^{\mathrm{c}}+m_{i,t}^{\mathrm{c}\mathrm{h}}+P_{i,t}^{\mathrm{coolexto}}$$

(13)

In Formula (13), $P_{i,t}^{\mathrm{coolcut}}$ represents the incentive-based cooling load demand response. $P_{i,t}^{\mathrm{coolexfrom}}$ and $P_{i,t}^{\mathrm{coolexto}}$, respectively, denote the imported and exported cooling power exchanged among parks.

Generally speaking, the constraints of the energy storage unit in operation include the following [21]:

$$0\le f_{i,t}^{\mathrm{dis}}\le U_{i,t}{f}_{\max }$$

(14)

$$0\le f_{i,t}^{\mathrm{c}\mathrm{h}}\le (1-U_{i,t})f_{\max }$$

(15)

$${\eta }_E{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{f}_{i,t}^{\mathrm{c}\mathrm{h}}-{\eta }_E^{\prime }}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{f}_{i,t}^{\mathrm{dis}}}}=0$$

(16)

$$f_{\min }\le f(0)+{\eta }_E{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{f}_{i,t}^{\mathrm{c}\mathrm{h}}}}-{\eta }_E^{\prime }{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{f}_{i,t}^{\mathrm{dis}}}}\le f_{\max }$$

(17)

$$0\le m_{i,t}^{\mathrm{dis}}\le U_{i,t}{m}_{\max }$$

(18)

$${\eta }_{\mathrm{c}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{m}_{i,t}^{\mathrm{c}\mathrm{h}}-{\eta }_{\mathrm{c}}^{\prime }}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{m}_{i,t}^{\mathrm{dis}}}}=0$$

(19)

$$m_{\min }\le m(0)+{\eta }_{\mathrm{c}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{m}_{i,t}^{\mathrm{c}\mathrm{h}}}}-{\eta }_{\mathrm{c}}^{\prime }{\displaystyle \sum _{i=1}^{\mathrm{N}}{\displaystyle \sum _{t=1}^{\mathrm{T}}{m}_{i,t}^{\mathrm{dis}}}}\le m_{\max }$$

(20)

In Formulas (14)–(20), $U_{i,t}$ denotes the charge–discharge state of energy storage, where a value of 1 indicates discharge and a value of 0 indicates charging; ${\eta }_E$ and ${\eta }_E^{\prime }$ are the charge–discharge efficiencies of the energy storage unit; and $f_{\max }$ and $f_{\min }$ are the allowed maximum/minimum remaining capacity of the energy storage during the scheduling process. ${\eta }_{\mathrm{c}}$ and ${\eta }_{\mathrm{c}}^{\prime }$ are the charge and discharge cold efficiencies of the energy storage unit; $m_{\min }$ and $m_{\max }$ are the allowed maximum/minimum remaining capacity of the cold storage system during the scheduling process.

3. ADQPSO Algorithm

The multi-park CCHP system involves multi-energy coupling of electricity, heat, and cold; cross-park peer-to-peer (P2P) interaction; and multi-mechanism collaboration, including demand response and power generation rights trading, which is a complex optimization problem characterized by high dimensionality, strong nonlinearity, and multiple constraints. Traditional Particle Swarm Optimization (PSO) tends to fall into local optima. Although Quantum Particle Swarm Optimization (QPSO) enhances search capability through quantum behavior, it still has issues such as a slow convergence speed and insufficient adaptability to constraints when dealing with multi-mechanism coupling (e.g., the linkage of “hierarchical game model–demand response–power generation rights trading”). ADQPSO is an improvement based on traditional PSO and QPSO. By introducing hybrid disturbances of Cauchy distribution and Gaussian distribution, dynamic disturbances are applied to the average optimal position of particles in the late iteration stage, effectively avoiding falling into local optima. The dynamic inertia weight (DECC) linearly adjusts the expansion–contraction coefficient $\alpha$; it enhances global search capability in the early iteration stage and improves local optimization accuracy in the later stage, thus adapting to the “global collaboration–local fine-tuning” optimization requirements of multi-energy systems. Next, the principle of this method will be explained.

Assume that particle m is moving at a high speed in a d-dimensional space to search for the optimal solution. When the k-th iteration is completed, the potential well of particle m in the d-th dimension is $p_{m\mathrm{d}}\left(k\right)$, that is [22],

$$p_{m\mathrm{d}}\left(k\right)={\phi }_{m\mathrm{d}}\left(k\right)P_{m\mathrm{d}}\left(k\right)+\left[1-{\phi }_{m\mathrm{d}}\left(k\right)\right]P_{\mathrm{a}\mathrm{d}}\left(k\right)$$

(21)

In Equation (21), ${\phi }_{m\mathrm{d}}\left(k\right)$ is a random number uniformly distributed over (0, 1), and $P_{\mathrm{a}\mathrm{d}}\left(k\right)$ represents the global optimal position of the population.

In the (k + 1)-th iteration of particle m, its position in the d-dimensional coordinate is expressed by the following equation:

$$x_{m\mathrm{d}}\left(k+1\right)=P_{m\mathrm{d}}\left(k\right)\pm 0.5L_{m\mathrm{d}}\left(k\right)\ln (1/u_{m\mathrm{d}}\left(k\right))$$

(22)

$$L_{m\mathrm{d}}\left(k\right)=2\alpha \left|S_{\mathrm{d}}\left(k\right)-x_{m\mathrm{d}}\left(k\right)\right|$$

(23)

In Equation (23), $u_{m\mathrm{d}}$ is a random number uniformly distributed over (0, 1); $\alpha$ is the expansion–contraction coefficient; and $S_{\mathrm{d}}$ is the average optimal position.

The center of the global optimal positions of particles is solved using the following equation:

$$S_{\mathrm{d}}\left(k\right)=\left({\displaystyle \frac{1}{\mathrm{M}}}{\displaystyle \sum }_{m=1}^{\mathrm{M}}{P}_{m1}\left(k\right),{\displaystyle \frac{1}{\mathrm{M}}}{\displaystyle \sum }_{m=1}^{\mathrm{M}}{P}_{m2}\left(k\right),\dots ,{\displaystyle \frac{1}{\mathrm{M}}}{\displaystyle \sum }_{m=1}^{\mathrm{M}}{P}_{m\mathrm{d}}\left(k\right)\right)$$

(24)

In Formula (24), M denotes the population size.

By combining Equations (22)–(24), the position update equation of the particle is obtained as follows:

$$x_{m\mathrm{d}}\left(k+1\right)=p_{m\mathrm{d}}\left(k\right)\pm \alpha \mid S_{\mathrm{d}}\left(k\right)-x_{m\mathrm{d}}\left(k\right)\mid \ln \left[1/u_{m\mathrm{d}}\left(k\right)\right]$$

(25)

This algorithm introduces an adaptive prematurity judgment criterion as follows.

Let M denote the population size, let $f_m$ denote the fitness of particle m, let $f_{\mathrm{avr}}$ be the mean of the fitness of all particles, and let $S^2$ be the variance of the fitness. Then, $S^2$ is given by

$$S^2={\displaystyle \sum }_{m=1}^{\mathrm{M}}{\left({\displaystyle \frac{f_m-f_{\mathrm{avr}}}{f}}\right)}^2$$

(26)

$$f=\left\{\begin{array}{ll}\max \left|f_m-f_{avr}\right|>1\hfill & 1⩽m⩽\mathrm{M}\hfill \\ 1\hfill & \mathrm{else}\hfill \end{array}\right.$$

(27)

In Formula (27), $f$ denotes the normalization scaling factor.

During the iteration process of the QPSO algorithm, different particles gradually converge toward the position corresponding to the same optimal fitness as the number of iterations increases. The fitness variance corresponding to $S^2$ will gradually decrease, and the entire population eventually tends to converge. In this process, a threshold $\lambda$ is given as a criterion to determine whether to enter the late-stage search.

During the late-stage optimization process, particles are highly prone to falling into local minima. At this point, applying the Blended Disturbance Operation (BDO) can effectively prevent this optimization issue, enabling particles to enter a broader solution set space for optimization, thus significantly improving prediction accuracy. When QPSO enters the late stage of the iteration process, the BDO process is typically performed on the average best position to effectively overcome the problem of converging to a local optimum. The BDO formula is as follows:

$${\beta }_k=C_1\left[C_k\left(0,1\right)+C_2{N}_k\left(0,1\right)\right]$$

(28)

$$\left\{\begin{array}{l}{C}_1=C_{1\min }+\left(C_{1\max }-C_{1\min }\right)k/k_{\max }\hfill \\ C_2=C_{2\max }-\left(C_{2\max }-C_{2\min }\right)k/k_{\max }\hfill \end{array}\right.$$

(29)

In Equations (28) and (29), $C_k\left(0,1\right)$ denotes a random number following a standard Cauchy distribution; $N_k\left(0,1\right)$ represents a random number from a Gaussian distribution. Both C₁ and C₂ are perturbation coefficients in the algorithm execution; $C_{1\max }$ and $C_{1\min }$ are, respectively, the upper and lower bounds of Disturbance Coefficient 1; $C_{2\max }$ and $C_{2\min }$ are, respectively, the upper and lower bounds of Disturbance Coefficient 2; $k_{\max }$ is the maximum number of iterations; and $k$ is the current iteration number being executed.

After BDO is executed, the optimal average position of all particles during the optimization process is denoted as $\widehat{S_{\mathrm{d}}}\left(k\right)$:

$$\widehat{S_{\mathrm{d}}}\left(k\right)=S_{\mathrm{d}}\left(k\right)\left(1+{\beta }_k\right)$$

(30)

During the Blended Disturbance Operation (BDO), the value of $C_1$ is directly proportional to the number of iterations. In the early stage of BDO, when the number of iterations is small, a lower $C_1$ value facilitates optimization within the current search region, promoting algorithm convergence. In the late iteration stage, a larger $C_1$ value helps skip local minimum points, enhancing the global search capability.

The expansion–contraction coefficient $\alpha$ can regulate the convergence process of the QPSO algorithm. Meanwhile, by introducing the theory of dynamic inertia weight (DECC) from the PSO algorithm in the calculation process, the DECC expression in the QPSO process is as follows:

$$\alpha ={\alpha }_{\min }+\left({\alpha }_{\max }-{\alpha }_{\min }\right)\left(k_{\max }-k\right)/k_{\max }$$

(31)

When the value of $\alpha$ is larger during the middle-early stage of the iteration process, it enhances the particles’ global optimization capability. Conversely, when the value of $\alpha$ is smaller, it overcomes the premature convergence state where the algorithm tends to fall into local minima during the convergence process.

4. Simulation Case Study

In the hierarchical game model for new energy grid-integrated multi-park CCHP (combined cooling, heating, and power)-based integrated energy systems, the output characteristics of renewable energy act as the core factors influencing system dispatching, generation rights trading, and pricing decisions.

As shown in Figure 3, Figure 4 and Figure 5, which present the dynamic characteristics of renewable energy output, comprehensive load of multiple parks, and time-of-use electricity price, respectively, the acquisition of data volume should match the volatility and complexity of these dimensions. Overall, the data volume needs to cover the cross dynamics of four dimensions: “time (24 h), energy types (electricity/heat/cold/wind/photovoltaic), 3 parks, and electricity price types (purchase/sale)”. Only by doing so can it support the model to accurately depict the fluctuation correlations among various variables (such as the linkage between wind and photovoltaic power output and electricity price and the response of load demand to electricity price), thereby ensuring calculation accuracy.

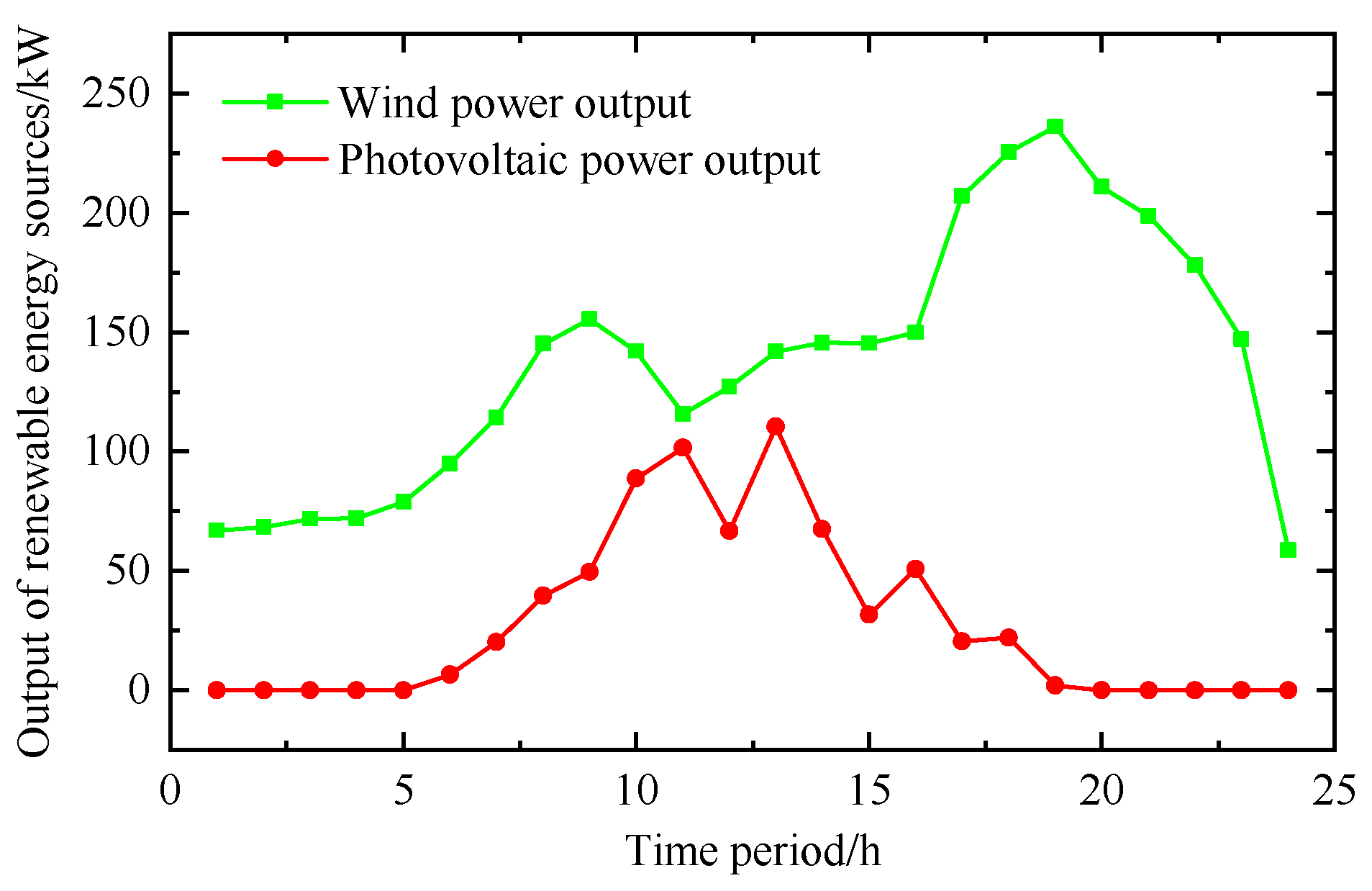
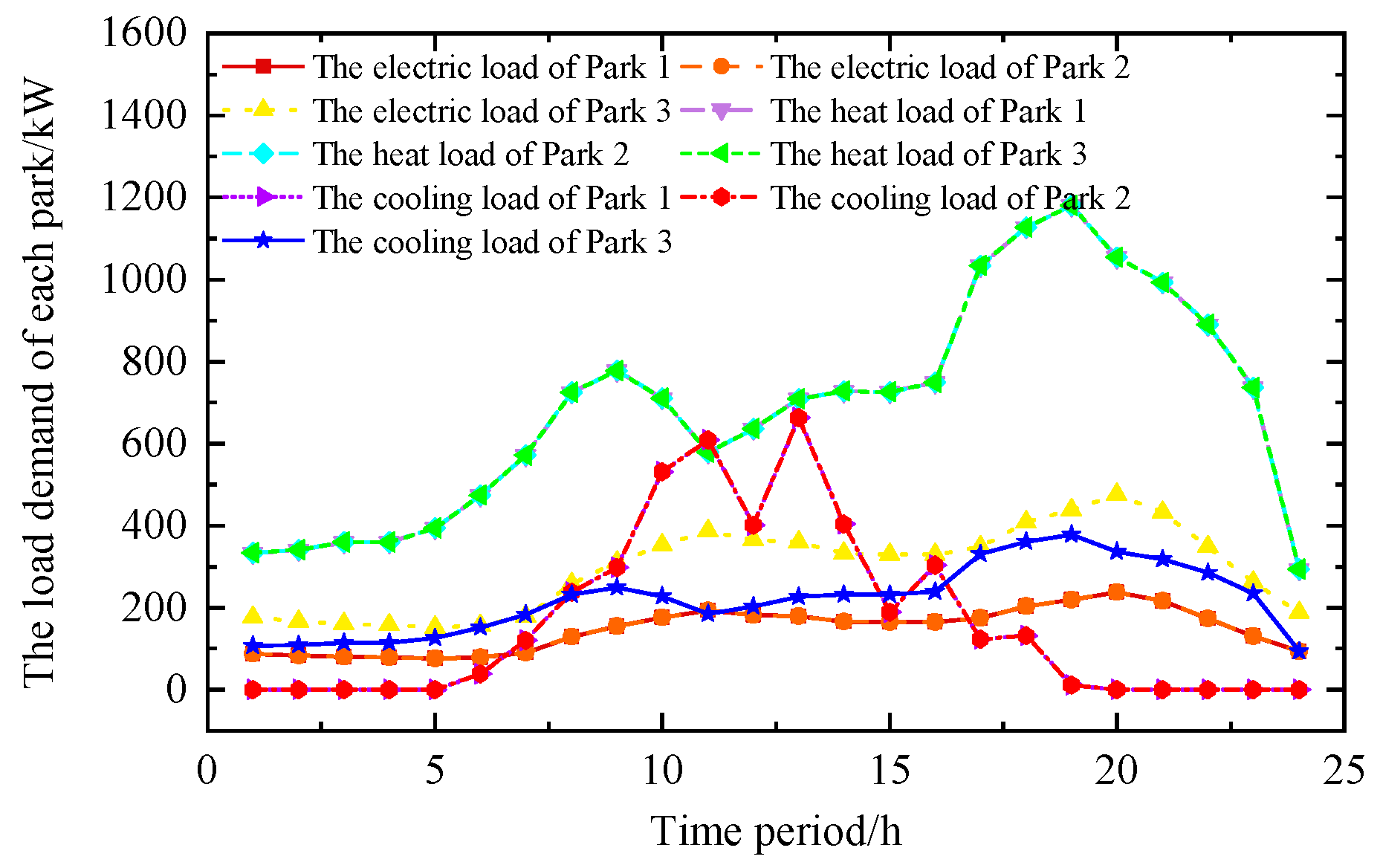
The forecast data of wind power (from a specific wind farm) and photovoltaic power (from a photovoltaic power station) adopted in this study, as illustrated in Figure 3, demonstrate distinct intermittency and temporal heterogeneity. Figure 4 presents the dynamic characteristics of electricity, heat, and cold loads within 24 h in three parks, respectively: in terms of electricity load, the demand of Park 3 is slightly higher than that of Park 1 and Park 2, and the fluctuation in the three parks throughout the day is gentle. The heat load demand is the same in each park, while in terms of cold load, Park 1 and Park 2 are the same, and Park 3 is characterized by spatial heterogeneity compared with other parks. 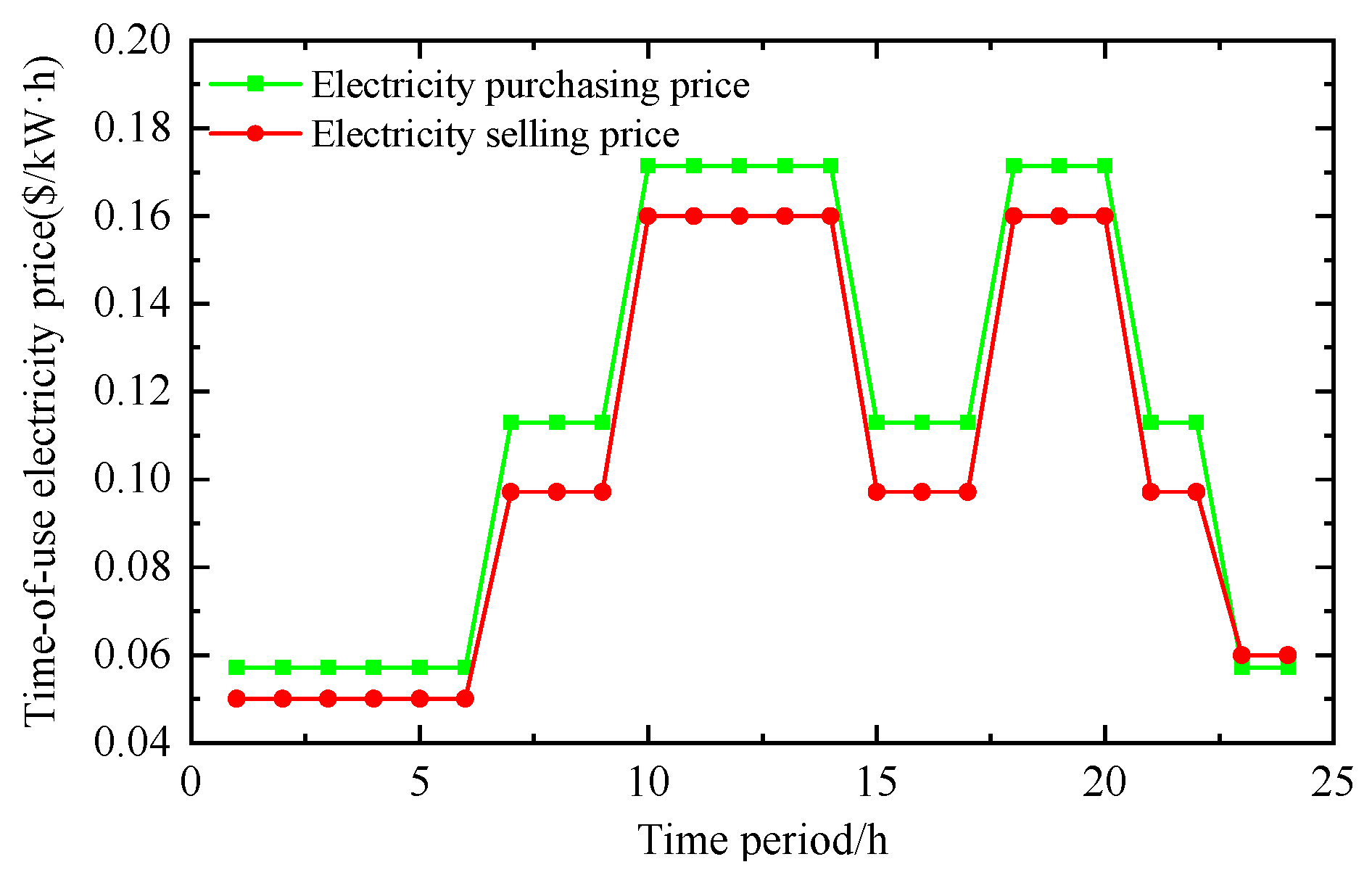Figure 5 shows a statistical chart of time-of-use electricity pricing, with the green curve representing the electricity purchasing price and the red curve representing the electricity selling price. It can be seen from the chart that the electricity prices exhibit obvious time period differences, reflecting the mechanism of time-of-use electricity pricing in guiding users to “peak shaving and valley filling” and optimizing the power supply and demand. Therefore, the aforementioned data are adopted for case verification.

This paper considers establishing four scenarios to systematically isolate and verify the independent effects and synergistic effects of the incentive-based demand response mechanism and the generation rights trading mechanism. Scenario 1: Neither the incentive-based demand response mechanism nor the generation rights trading mechanism is considered. Scenario 2: The incentive-based demand response mechanism is considered, while the generation rights trading mechanism is not. Scenario 3: The incentive-based demand response mechanism is not considered, while the generation rights trading mechanism is considered. Scenario 4: Both the incentive-based demand response mechanism and the generation rights trading mechanism are considered.

Scenario 1 serves as the baseline, where neither of the two mechanisms is introduced. The load is fixed with no generation rights transfer, reflecting the system state under the traditional operation mode and providing a reference for other scenarios. Scenario 2 only enables the incentive-based demand response for electricity, heat, and cooling, allowing users to adjust their electricity, heat, and cooling loads according to dynamic prices. It is used to independently evaluate the impact of demand-side flexibility on supply–demand matching and cost optimization. Scenario 3 only activates the generation rights trading mechanism, combined with electricity–carbon linkage, focusing on the mutual support role of the trading mechanism in promoting low-carbon transition and improving cross-park resource allocation efficiency. Scenario 4 enables both mechanisms simultaneously to verify the superimposed optimization effect when they are coupled. Through the comparison of the four scenarios, the marginal benefits of a single mechanism and the synergistic gains of the combined mechanisms can be clearly quantified, providing a basis for the mechanism design of multi-park CCHP systems.

CCHP systems involve multi-energy flow coupling, dynamic cross-park interaction, and two-way feedback of hierarchical games, where traditional algorithms tend to fall into local optima or converge slowly. Thus, the QPSO and ADQPSO algorithms are selected for comparison. QPSO, as a basic algorithm, has certain global search capabilities, but its optimization accuracy is limited when facing strong constraints. ADQPSO, on the other hand, expands the solution space by introducing adaptive disturbance operations and balances search capabilities through dynamic inertia weights, making it more suitable for the complex characteristics of the system. This further supports the effectiveness of system optimization under the coupling of algorithms and mechanisms.

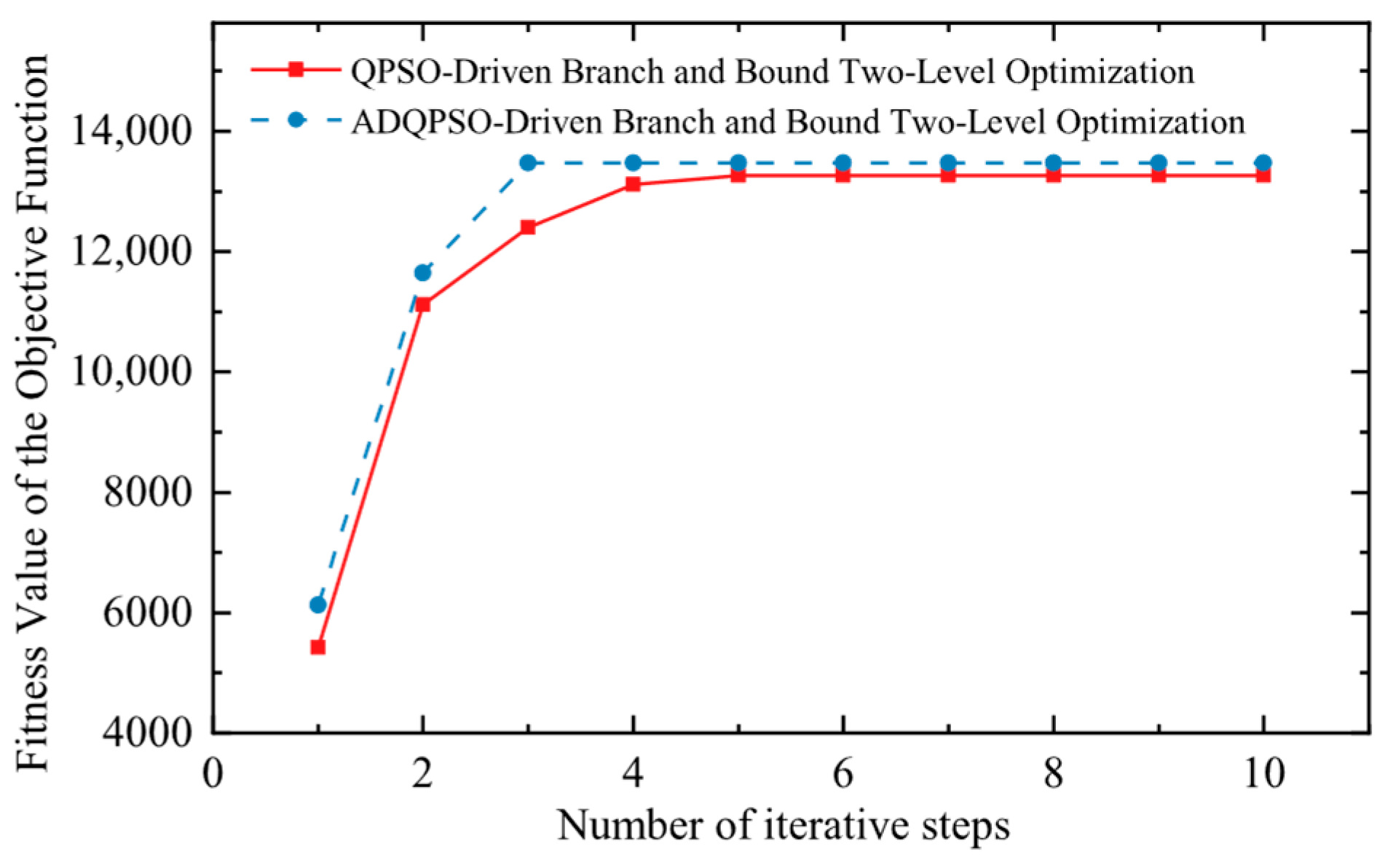
Figure 6 presents the comparison results of the optimization convergence curves of the two algorithms in Scenario 4. In the figure, the horizontal axis represents the number of iterative steps, and the vertical axis denotes the fitness value of the objective function, which reflects the optimization performance (a higher value generally corresponds to better benefits for the aggregator). The red curve stands for the QPSO-driven branch and bound Two-Level Optimization, while the blue curve represents ADQPSO-driven branch and bound Two-Level Optimization. From the curve trends, the optimization driven by ADQPSO converges faster and achieves superior fitness gains. Thus, it can be further concluded that the coupling of the generation rights trading mechanism and the electricity–heat–cold incentive demand response mechanism constructs a trans-temporal and spatial regulation game system for multi-energy resources for aggregators and expands the decision-making solution space. Relying on the resource allocation flexibility endowed by this coupled mechanism, the ADQPSO algorithm accurately characterizes the interaction constraints of multi-energy flows, improves the optimization precision and convergence rate, and accelerates the convergence to the optimal benefit solution for energy aggregators. The collaborative game between the ADQPSO algorithm and the coupled mechanism drives the Pareto improvement of energy aggregators.

From the data in Figure 6, it can be concluded that under the electricity–carbon linkage mechanism, the operation convergence speed of the ADQPSO-Driven Branch and Bound method is 40% faster than that of the QPSO-Driven Branch and Bound method, and the optimization profit accuracy is improved by 1.59%.

Table 1. Optimization of operational results in different scenarios based on QPSO.

Scenarios	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Profit of IEA (Upper-Level)/USD	12,434.99	12,655.21	13,362.87	13,259.79
Energy Consumption Cost of Park 1/USD	−552	−325.57	−525.14	−328.71
Environmental Cost of Park 1/USD	246.14	285.14	287	314.57
Profit from Carbon Emission Allowances of Park 1/USD	-	-	113.80	132.40
Fuel Cost Savings of Park 1/USD	-	-	95.84	95.84
Revenue from Renewable Energy Output of Park 1/USD	-	-	238.43	238.43
Electricity, Heat, and Cooling Demand Response Cost of Park 1/USD	308.43	14.06	309	15.80
Microgrid Cost of Park 1 (Lower-Level)/USD	−305.71	−26.39	−686.29	−465.14
Energy Consumption Cost of Park 2/USD	−537.14	−458.57	−535.57	−442.57
Environmental Cost of Park 2/USD	280	289.57	272.14	307.86
Profit from Carbon Emission Allowances of Park 2/USD	-	-	110.36	129.66
Fuel Cost Savings of Park 2/USD	-	-	14.24	14.24
Revenue from Renewable Energy Output of Park 2/USD	-	-	40.67	40.67
Electricity, Heat, and Cooling Demand Response Cost of Park 2/USD	601.86	35.14	593.43	39.51
Microgrid Cost of Park 2 (Lower-Level)/USD	−257.14	−133.9	−428.57	−279.86
Energy Consumption Cost of Park 3/USD	−6.63	−112.03	27.16	−80.33
Environmental Cost of Park 3/USD	341.71	313	367.57	341.71
Profit from Carbon Emission Allowances of Park 3/USD	-	-	110.21	128.36
Fuel Cost Savings of Park 3/USD	-	-	95.84	95.84
Revenue from Renewable Energy Output of Park 3/USD	-	-	238.43	238.43
Electricity, Heat, and Cooling Demand Response Cost of Park 3/USD	674.71	35.14	653	39.51
Microgrid Cost of Park 3 (Lower-Level)/USD	335.14	236.14	−49.81	−161.86

presents the optimization results of the QPSO algorithm under four scenarios. The total profit of integrated energy aggregators is as follows: Scenario 3 (only power generation rights trading, USD 13,362.87) > Scenario 4 (demand response–power generation rights trading, USD 13,259.79) > Scenario 2 (only demand response, USD 12,655.21) > Scenario 1 (no mechanism, USD 12,434.99). This indicates that single power generation rights trading has the most significant effect on profit improvement. Profit slightly decreases after combination with demand response, but it is still higher than the scenario without the power generation rights trading mechanism.

Therefore, it can be observed that the QPSO algorithm is more suitable for the single generation rights trading mechanism. The incentive demand response mechanism can help reduce energy consumption and regulation costs; however, when coupled with the generation rights trading mechanism, the synergistic benefits are not fully unleashed due to the limited capability of QPSO in handling constraints.

Table 2. Optimization of operational results in different scenarios based on ADQPSO.

Scenarios	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Profit of IEA (Upper-Level)/USD	12,305.98	12,087.90	11,496.54	13,470.06
Energy Consumption Cost of Park 1/USD	−552	−345.14	−348.86	−363.57
Environmental Cost of Park 1/USD	246.14	252.57	308	296.86
Profit from Carbon Emission Allowances of Park 1/USD	-	-	132.61	117.77
Fuel Cost Savings of Park 1/USD	-	-	95.84	95.84
Revenue from Renewable Energy Output of Park 1/USD	-	-	238.43	238.43
Electricity, Heat, and Cooling Demand Response Cost of Park 1/USD	332	25.89	307	19.61
Microgrid Cost of Park 1 (Lower-Level)/USD	−305.71	−66.69	−507.86	−499.14
Energy Consumption Cost of Park 2/USD	−537.14	−462.14	−516.86	−444.86
Environmental Cost of Park 2/USD	280	289.43	293.14	306.43
Profit from Carbon Emission Allowances of Park 2/USD	-	-	129.76	115.67
Fuel Cost Savings of Park 2/USD	-	-	14.24	14.24
Revenue from Renewable Energy Output of Park 2/USD	-	-	40.67	40.67
Electricity, Heat, and Cooling Demand Response Cost of Park 2/USD	681.29	64.73	561.14	49.03
Microgrid Cost of Park 2 (Lower-Level)/USD	−257.14	−108.01	−408.43	−259.86
Energy Consumption Cost of Park 3/USD	−6.63	−179	−167.71	−82.77
Environmental Cost of Park 3/USD	341.71	311.43	325.57	349.71
Profit from Carbon Emission Allowances of Park 3/USD	-	-	129.21	114.37
Fuel Cost Savings of Park 3/USD	-	-	95.84	95.84
Revenue from Renewable Energy Output of Park 3/USD	-	-	238.43	238.43
Electricity, Heat, and Cooling Demand Response Cost of Park 3/USD	730.71	64.73	634.43	49.03
Microgrid Cost of Park 3 (Lower-Level)/USD	335.14	197.14	−305.57	−132.69

presents the optimization results of the ADQPSO algorithm under four scenarios. The total profit of the integrated energy aggregator is as follows: Scenario 4 (demand response–generation rights trading, USD 13,470.06) > Scenario 1 (no mechanism, USD 12,305.98) > Scenario 2 (only demand response, USD 12,087.90) > Scenario 3 (only generation rights trading, USD 11,496.54). This indicates that profit is the highest when the two mechanisms are combined, while profit from single generation rights trading is the lowest. Moreover, compared with a single mechanism (Scenario 3), the hierarchical game mechanism (Scenario 4) increases profits by 17.17%.

By comparing the operational data of Scenario 4 in Table 2 based on ADQPSO with that of Scenario 4 in Table 1 based on QPSO, the optimization advantages of the ADQPSO algorithm in the “demand response–generation rights trading” coupled scenario can be clearly observed. In Scenario 4, as shown in Table 2, the upper-level profit (Profit of IEA (Upper-Level)) reaches USD 13,470.06, showing a significant increase compared to USD 13,259.79 in the same scenario in Table 1, with an improvement accuracy of 1.59%. The optimization of this core revenue indicator stems from the synergistic regulation of multi-dimensional costs and revenues.

From the perspective of energy consumption cost in Scenario 4, compared with QPSO, ADQPSO exhibits outstanding performance in energy consumption savings in individual parks through synergistic scheduling among parks, achieving total savings of USD 39.59 across the three parks. The ADQPSO-driven method demonstrates stronger capability in environmental cost control, with total savings of USD 11.14 across the three parks, effectively reducing the overall environmental governance expenditure of the system. Although the investment of the ADQPSO-driven method in electricity–heat–cooling demand response cost is USD 22.91 higher than that of the QPSO method, resulting in an additional investment of USD 15.17 in the total microgrid cost across the three parks for the ADQPSO-driven method, this investment has promoted energy consumption savings and environmental cost control, laying a foundation for the growth of upper-level profits.

Overall, the linkage optimization of various indicators in Scenario 4, as shown in Table 2 (energy consumption cost, environmental cost, profit from carbon emission allowances, fuel saving cost, renewable energy revenue, and electricity–heat–cooling demand response cost), fully confirms the optimal effect of the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm in this coupled scenario (Scenario 4), providing a more competitive optimization path for the revenue of park integrated energy aggregators in the context of new energy grid integration.

Therefore, it can be analyzed that the ADQPSO algorithm is more suitable for the coupling mechanism of “demand response–generation rights trading”. It captures the synergistic benefits of “flexible load adjustment–generation rights trading” through its global search capability. In contrast, single generation rights trading, due to the lack of constraints from demand response, is prone to resource misallocation, leading to a decline in benefits.

Both algorithms show that the incentive-based demand response mechanism can effectively reduce demand response costs (Scenario 2 vs. Scenario 1), and generation rights trading can bring carbon quota benefits and save fuel costs (Scenario 3 vs. Scenario 1), verifying the independent value of both mechanisms.

QPSO excels in handling a single mechanism (generation rights trading). Its local search efficiency is superior under simple constraints, making Scenario 3 yield the highest profit; however, when faced with the coupling mechanism (Scenario 4), the underestimation of synergistic benefits can occur. ADQPSO excels in handling coupling mechanisms. Its global search capability (adaptive disturbance–dynamic weight) can parse dynamic correlations such as “load adjustment quantity–dynamic energy prices–carbon quotas”, resulting in the highest profit in Scenario 4; however, under a single mechanism, it is inefficient due to search redundancy.

Therefore, game optimization based on multi-park CCHP systems needs to match “mechanism complexity–algorithm capability”: if only generation rights trading is introduced, QPSO is more efficient; if it is necessary to achieve the synergy of “demand response–generation rights trading”, ADQPSO is a better choice as it can fully unleash the synergistic potential of “economic benefits and low-carbon goals”.

Overall, the strategy of Scenario 4 that adopts ADQPSO-driven branch and bound Two-Level Optimization enables the energy aggregator to achieve the optimal revenue.

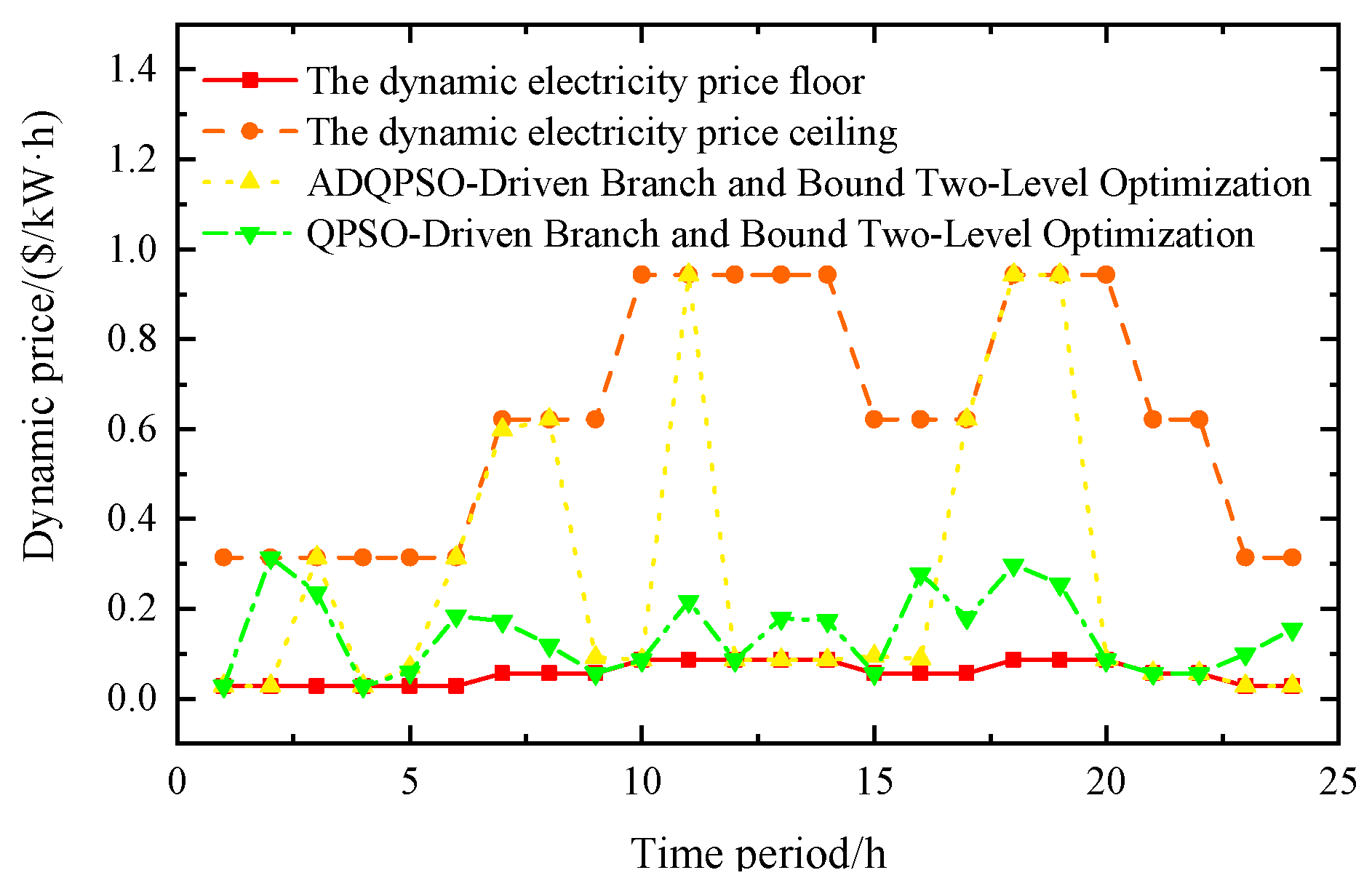
Figure 7 presents the results of optimizing the dynamic electricity prices in the park using different algorithms under Scenario 4. The yellow dotted line (representing ADQPSO-Driven Branch and Bound Two-Level Optimization) sees a notable surge in electricity prices during peak periods (e.g., around the 6–8th and 17–19th hours), approaching the upper bound. This demonstrates the algorithm’s price response to time-varying supply–demand tightness, guiding the adjustment of electricity loads by increasing prices. In contrast, the green triangular line (representing the QPSO-Driven Branch and Bound Two-Level Optimization) consistently fluctuates near the lower bound, with the electricity price generally remaining below 0.4 USD/kWh, focusing on maintaining the stability of low prices.

Taking the electricity price peak during the 17th–19th hours as an example, the electricity price under ADQPSO-Driven Branch and Bound Two-Level Optimization almost touches the electricity price ceiling represented by the orange dashed line, while the electricity price under QPSO-Driven Branch and Bound Two-Level Optimization remains at a relatively low level. This intuitive difference reflects the divergence in strategic logic between the two algorithms when responding to peak electricity loads; ADQPSO tends to benefit optimization through price mechanisms, while QPSO leans toward “price stabilization and supply guarantee”. The essence of this difference lies in the algorithms’ varying depths in depicting supply–demand dynamics in multi-energy coupling systems. Relying on improved Particle Swarm Optimization (PSO) logic, ADQPSO can more accurately match real-time supply–demand gaps with users’ price elasticity, thereby releasing stronger price regulation signals during peak periods. Compared with the QPSO-Driven Branch and Bound Two-Level Optimization algorithm, the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm is more aggressive, better suited for peak electricity load regulation, excels at capturing the price elasticity during peak periods, and regulates supply and demand via price signals to attain favorable electricity profits.

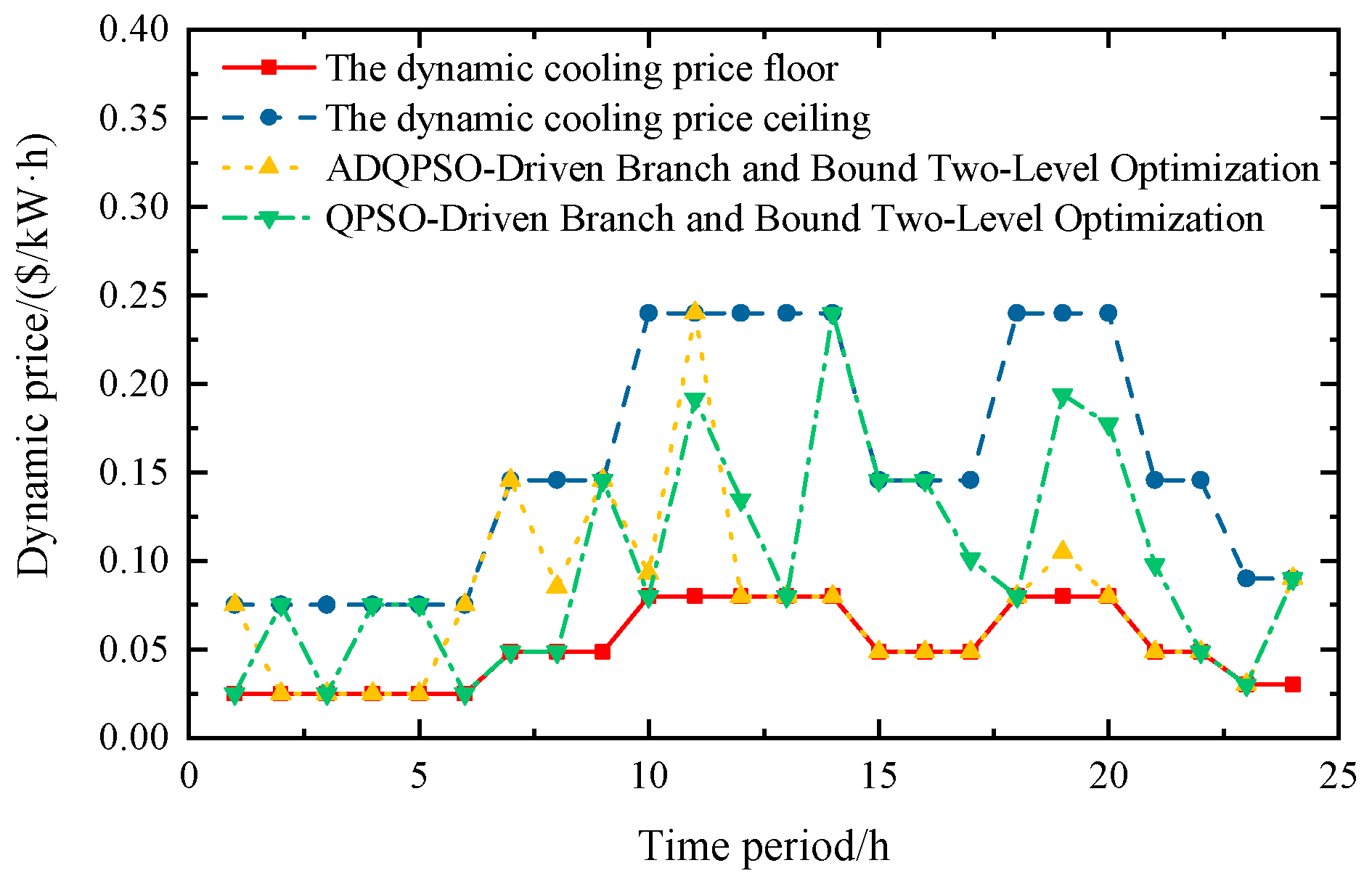
Figure 8 presents the optimization results of the dynamic cooling price in the park under Scenario 4. The yellow dotted–dashed line (representing ADQPSO-Driven Branch and Bound Two-Level Optimization) shows a trend of rapid surging in cooling prices during peak cooling demand periods (approximately the 6th–7th and 9th hours), even briefly touching the price upper limit. The underlying principle is that the ADQPSO-Driven Branch and Bound Two-Level Optimization method enhances the global search capability through quantum behavior, enabling it to acutely capture peak periods with surging cooling loads and intensified supply–demand contradictions, thus pushing prices closer to the upper limit. This high-price signal, on one hand, guides users to proactively reduce unnecessary cooling loads through the demand-side response mechanism. On the other hand, it reflects the algorithm’s response capability to the tension of time-varying cooling demand while leveraging price leverage to guide users to shift cooling loads. In contrast, the green dotted–dashed line (representing QPSO-Driven Branch and Bound Two-Level Optimization) fluctuates slightly near the price lower limit throughout the process, and the price mostly stays below USD 0.2 per kWh. Its strategy focuses on stabilizing prices and controlling costs to mitigate the impact of price fluctuations on users. Overall, the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm is suitable for peak cooling load regulation scenarios. It performs excellently in capturing price elasticity during peak periods and can help energy aggregators achieve better revenues from cooling services.

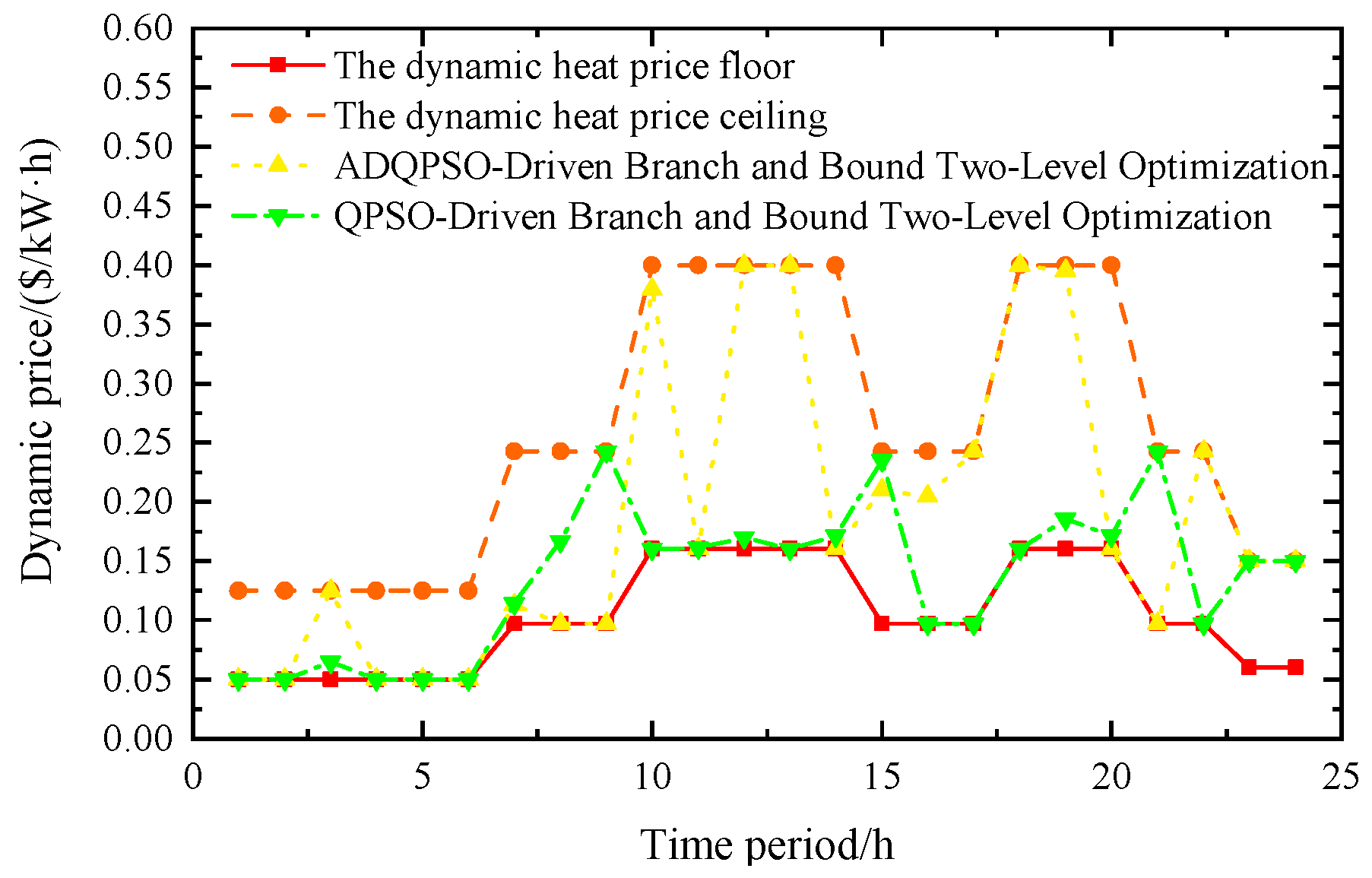
Figure 9 presents the optimization results of the dynamic heat price in the park under Scenario 4. Among them, the yellow dotted line corresponds to ADQPSO-Driven Branch and Bound Two-Level Optimization, while the green dotted line represents QPSO-Driven Branch and Bound Two-Level Optimization. It can be observed that the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm can significantly increase the heat price during specific periods, even approaching or briefly touching the dynamic heat price upper limit. This helps energy aggregators “lock in high prices” to improve the revenue from heating services during tight heat load periods. In contrast, the QPSO-Driven Branch and Bound Two-Level Optimization algorithm always fluctuates near the dynamic heat price lower limit, and the overall heat price remains at a relatively low level with mild fluctuation characteristics. Its pricing logic focuses more on “stabilizing prices and controlling costs”. Overall, the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm is like a “proactive regulator”, and it is good at capturing price elasticity during peak periods to achieve revenue optimization.

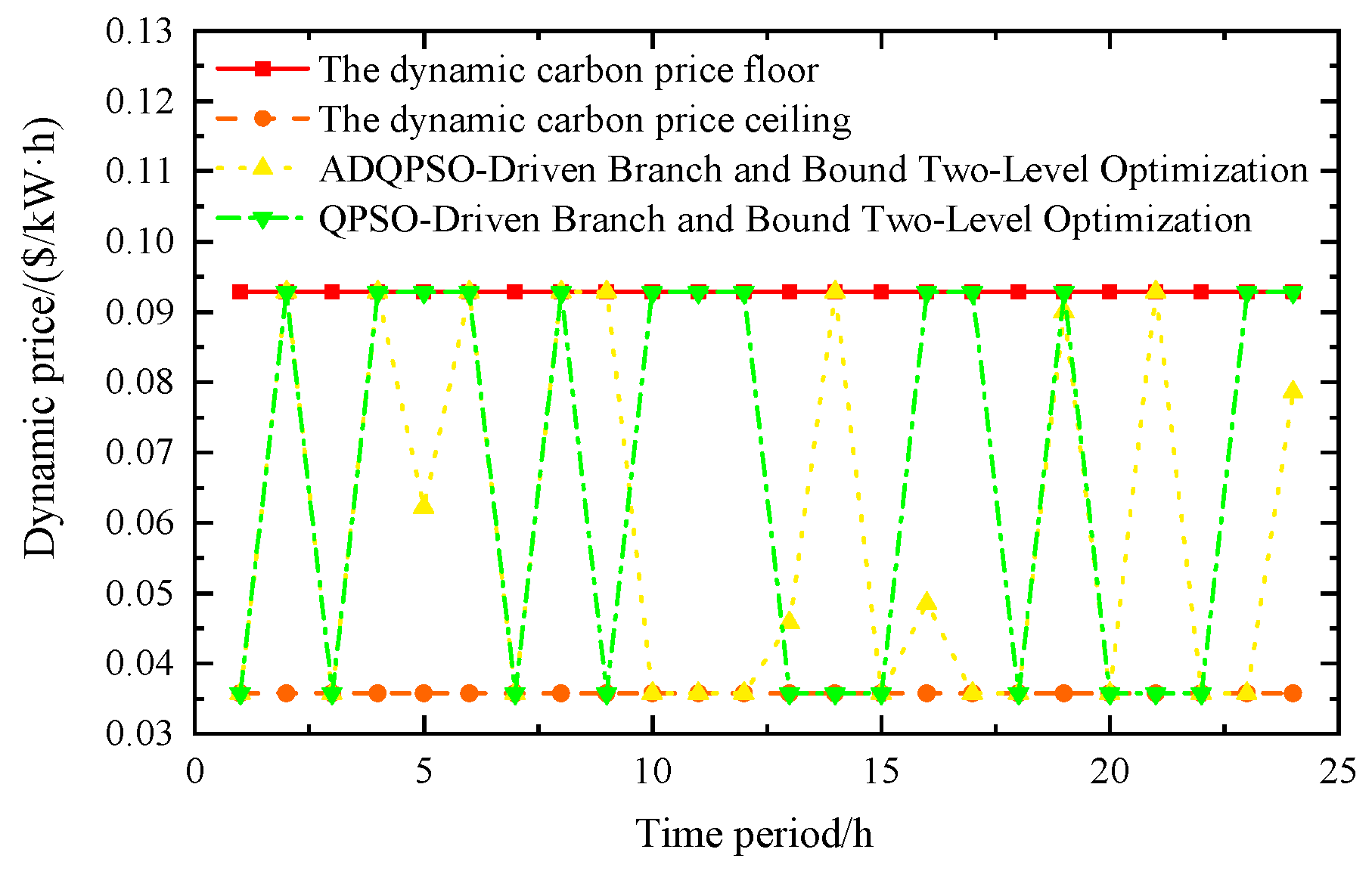
Figure 10 presents the optimization results of dynamic carbon prices in the park under Scenario 4. The carbon price under the ADQPSO-Driven Branch and Bound Two-Level Optimization algorithm exhibits characteristics of drastic fluctuations and even temporarily approaches the upper bound, which reflects its price response mechanism to the park’s high-carbon emission behaviors. By raising carbon prices, it optimizes the energy structure (e.g., increasing the consumption of green electricity and reducing fossil energy consumption) and strengthens the incentives for carbon emission reduction through price leverage.

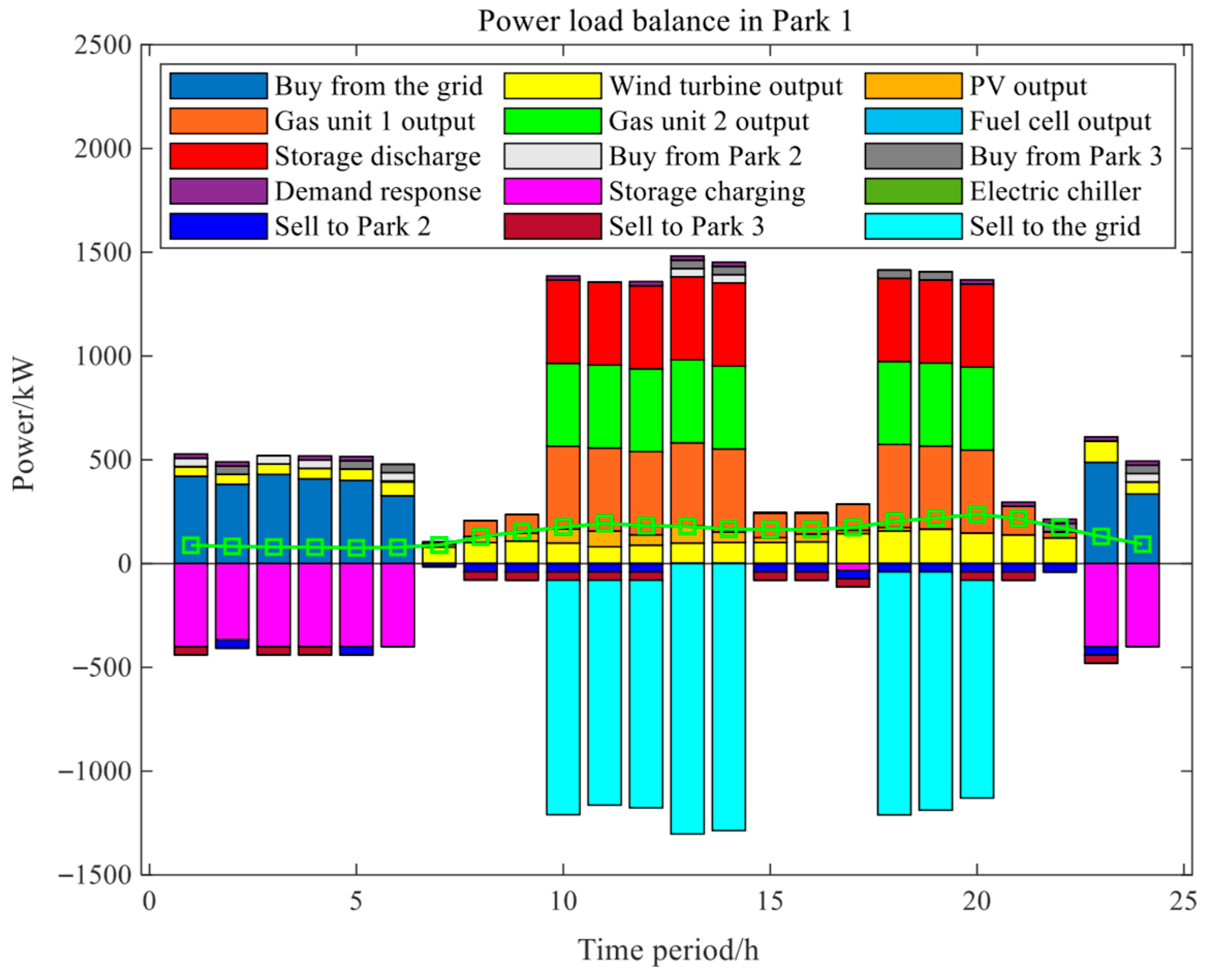
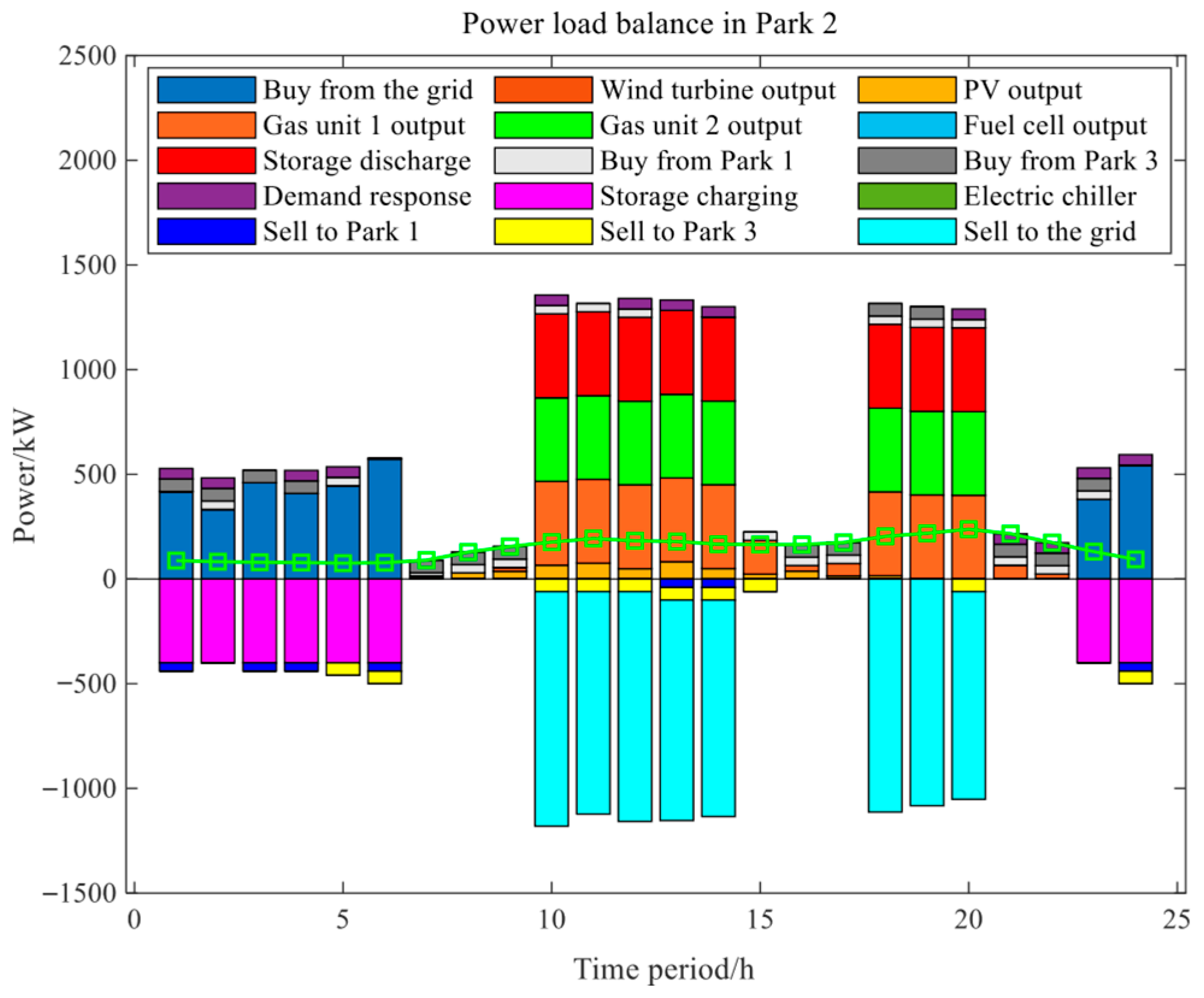
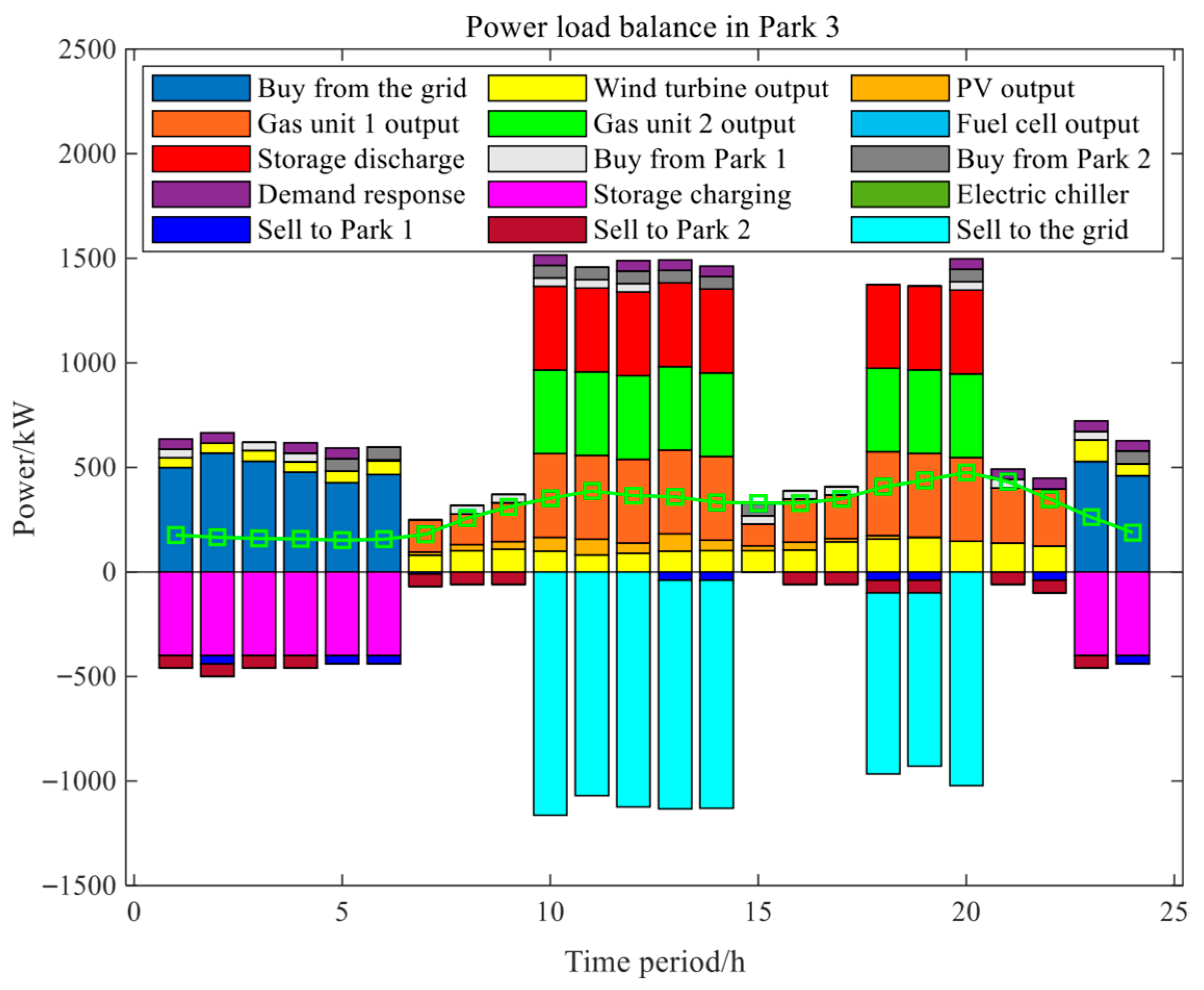
The power load balance of Park 1, Park 2, and Park 3 is shown in Figure 11, Figure 12, and Figure 13, respectively, based on ADQPSO-Driven Branch and Bound Two-Level Optimization under Scenario 4. The system presents the dynamic operation characteristics of the multi-park power system within the 0–24 h period. From the perspective of the changes in various quantities in different time periods, the three parks show a highly consistent time-varying law: during low-load periods (0–8 h and 22–25 h), “Buy from the grid” serves as the core support, accompanied by a low output of gas units to ensure the basic load. Energy storage systems mainly focus on charging to absorb surplus electricity, while photovoltaics (PV) have almost zero output due to night or low-light conditions.

During peak hours (9–21 h), the operation switches to a “multi-energy synergy” mode. Gas-fired units operate at full output to take on the main power supply responsibility. Wind power and photovoltaics (PV) achieve high-efficiency output due to optimized daytime environmental conditions. Energy storage systems switch to discharging to supplement peak loads. Demand response is activated simultaneously for peak shaving and load reduction. Surplus electricity is absorbed through selling to other parks or the grid, thus forming a multi-element balance mechanism integrating “conventional power sources–renewable energy–energy storage discharge–demand-side regulation”.

Overall, under optimization Scenario 4, the three parks achieved a smooth transition of load from “low-load reserve” to “peak-load collaborative supply” through the time-periodic dynamic adaptation of power production and consumption links (such as power purchase, self-generation, energy storage, and mutual power sales). This not only reflects the role of gas-fired units as a stable power source for bottom-line support and the advantage of renewable energy like wind and solar in daytime output but also highlights the key value of energy storage in “peak shaving and valley filling” and demand response in “flexible regulation”. This characteristic provides a quantitative basis for the optimal dispatching, energy complementarity, and stable operation of multi-park power systems and also offers practical reference for cross-park energy collaborative management.

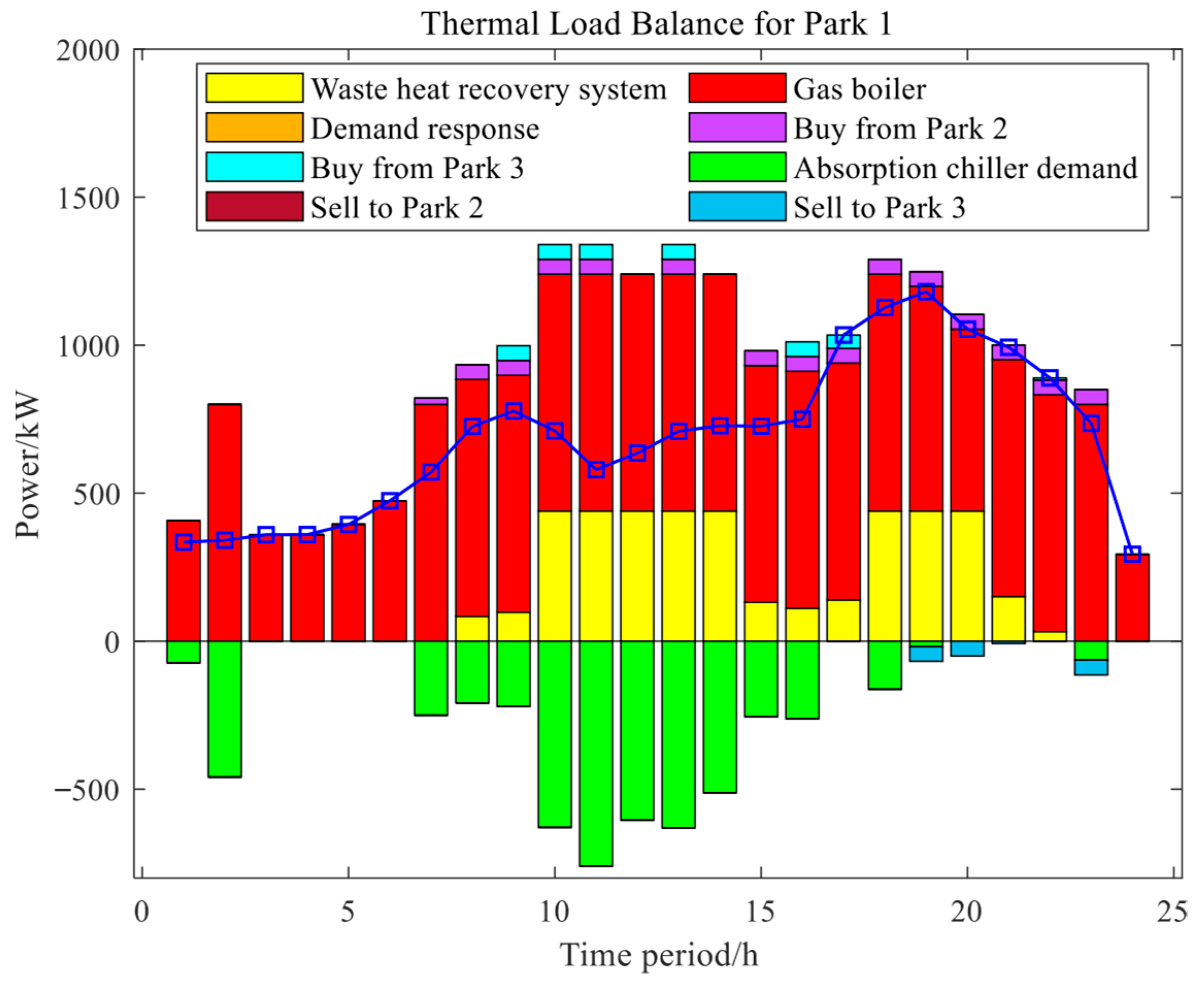
Figure 14 illustrates the thermal load balance characteristics of Park 1 under Scenario 4. The red-colored gas boiler plays a core role in peak shaving during the thermal peak period from 10 to 20 h; the yellow waste heat recovery system continuously and stably supplies energy, with output maintained across most time intervals, thus unlocking the valorization potential of waste heat. The green bars represent absorption chiller demand, appearing as negative-valued bars, coinciding with the peak output of the gas boiler since the refrigeration process consumes thermal energy and indirectly drives up thermal demand, reflecting the coupled relationship between cooling and heating loads. Overall, the ADQPSO-Driven Branch and Bound Two-Level Optimization strategy achieves the dynamic balance of the thermal network through the synergy of “waste heat as a baseline support, boiler-based peak shaving, inter-park heat mutual assistance”, thereby verifying the adaptability of multi-energy coupling to thermal load fluctuations.

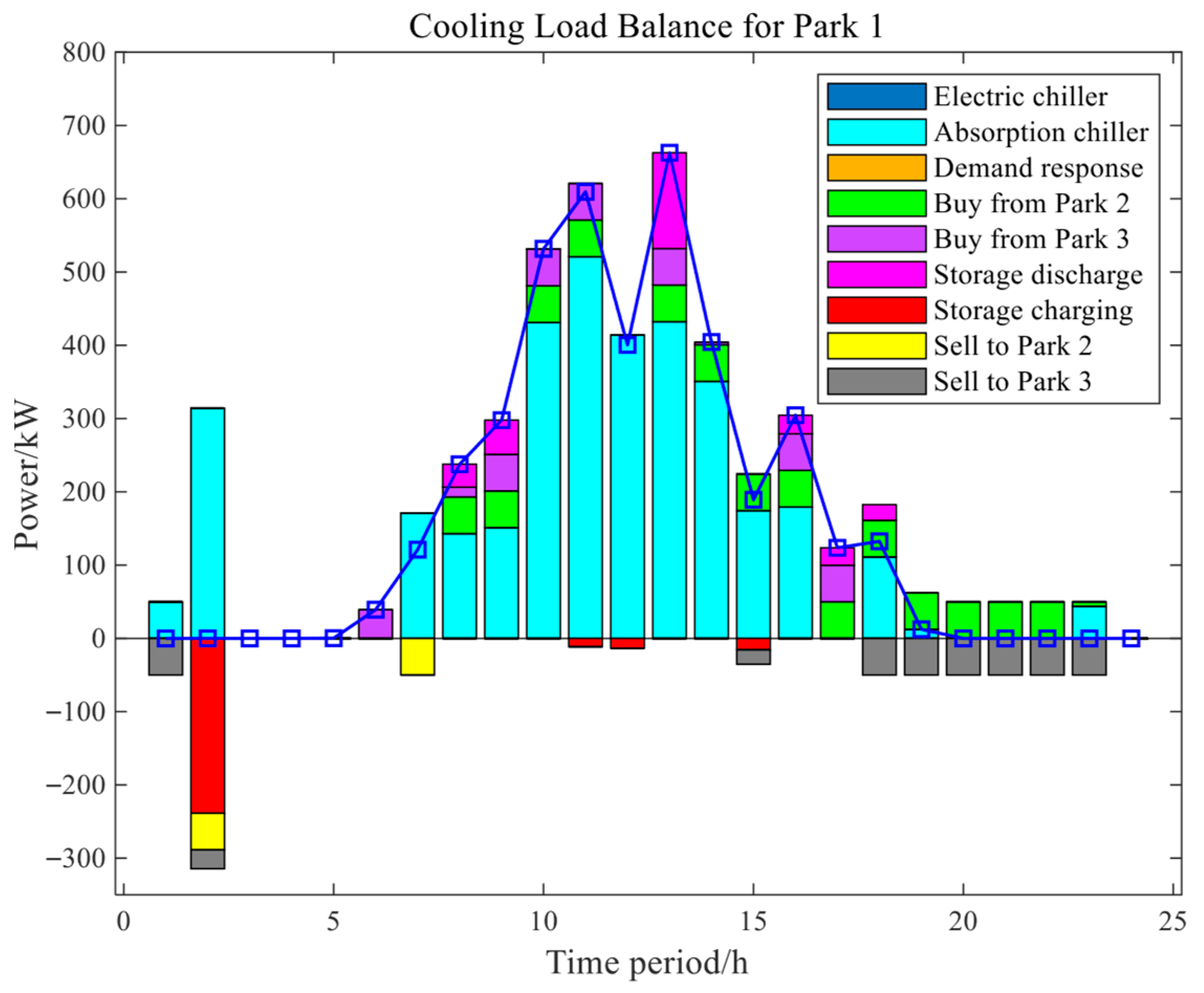
Figure 15 illustrates the cooling load balance characteristics of Park 1 under Scenario 4. During peak hours (9–17 h), the light blue absorption chiller, serving as the primary cooling unit, maintains continuous and efficient operation, with its output flexibly supplemented by the cooling capacity imported from Park 3; concurrently, the pink indicates storage discharge and synchronously releases the cold energy stored during off-peak periods. In off-peak periods (e.g., 0–8 h, 18–24 h), the red-colored cold storage system capitalizes on low-load intervals to store cold energy, and when there is a surplus of cold energy, it facilitates the yellow-marked mutual cooling supply to Park 2 and the gray-marked mutual cooling supply to Park 3.

The ADQPSO-Driven Two-Level Optimization strategy achieves the dynamic balance of the cooling load through multi-dimensional synergy, which includes coordination among various types of chillers, peak-shaving and valley-filling by energy storage, and the inter-park mutual support of cold energy. This provides a practical reference for the optimal scheduling of cold energy and the enhancement of resilience in the multi-park CCHP-type integrated energy system.

5. Conclusions

The conclusions of this paper are as follows:

(1)

The constructed hierarchical game model for new energy grid-integrated multi-park CCHP-type integrated energy systems effectively realizes multi-energy synergy and cross-park interaction. Through the hierarchical linkage between the dynamic pricing (electricity, heat, cooling, and carbon prices) by upper-level integrated energy aggregators and cost optimization by lower-level park microgrid alliances, the model successfully coordinates multiple elements such as distributed energy resources (wind, PV, energy storage, gas turbines, etc.), demand response, and generation rights trading. This verifies its feasibility in achieving dynamic supply–demand matching and collaborative optimization in complex energy systems. The synergistic effect of demand response and generation rights trading is crucial for improving system efficiency. A single mechanism (whether it is demand response alone or generation rights trading alone) can produce a certain optimization effect, but the synergistic mechanism can further reduce system costs and improve benefits through the electricity–carbon linkage of dynamic price guidance. Compared with a single mechanism, the hierarchical game mechanism (Scenario 4) increases profits by 17.17%.

(2)

The dynamic pricing mechanism effectively guides the optimization of energy structure and load regulation. By means of price leverage, it promotes the absorption of renewable energy and the reduction in fossil energy consumption, providing a quantitative regulation path for the low-carbon transition of the system.

(3)

The two-layer optimization method that combines the ADQPSO algorithm with the Branch and Bound method performs significantly better than traditional algorithms in handling multi-mechanism coupling problems. Especially in the “demand response–generation rights trading” coupling scenario (Scenario 4), compared with the QPSO algorithm, ADQPSO effectively improved the convergence speed and optimization accuracy through adaptive disturbance operations and dynamic inertia weight adjustment: specifically, the convergence speed of the Branch and Bound method driven by ADQPSO is 40% faster than that driven by QPSO, and the accuracy of optimization benefits is improved by 1.59%. Against the background of new energy grid integration, this method helps aggregators not only achieve the highest returns but also fully release the synergistic potential of multiple mechanisms.