Stochastic Optimization Scheduling Method for Mine Electricity–Heat Energy Systems Considering Power-to-Gas and Conditional Value-at-Risk
Abstract
1. Introduction
- A Cholesky decomposition technique is employed to analyze source–load correlations in the mining-area integrated energy system (MIES). Building upon this correlation structure, Latin hypercube sampling (LHS) is implemented to generate a source–load sample matrix with predetermined correlation coefficients, followed by Affinity Propagation clustering to produce representative scenarios.
- With the objective of minimizing the total cost, which is constituted by dispatching cost, expected adjustment cost, and CVaR, a stochastic optimization dispatch model for the mining area energy system incorporating P2G technology is formulated. This model enables the reduction in operational costs of the mining area energy system and the enhancement of the renewable energy utilization rate while effectively addressing the impact of uncertain power outputs on both the supply and demand sides.
- A simulation study of the proposed optimal dispatch model was conducted on a typical mining area energy system to verify the model’s performance in terms of reducing operational costs and enhancing renewable energy accommodation, as well as the necessity of considering the correlation between supply and demand sides.
2. The MIES Structure and Source–Load Risk Measurement
2.1. Analysis of the Architecture of the MIES Containing P2G
2.2. Generation of Typical Scenes on Both Sides of the Source and Load
2.3. Risk Measurement of the MIES
3. Optimization Scheduling Model for MIES
3.1. Objective Function
3.2. Operating Constraints
3.2.1. Two-Stage P2G System
3.2.2. Micro Gas Turbine Unit (MT)
3.2.3. Exhausted Air Heat Storage Oxidation Unit (RT)
3.2.4. Water Source Heat Pump Unit (WS) and Air Source Heat Pump Unit (AS)
3.2.5. Battery and Thermal Energy Storage Unit (BT, TT)
3.2.6. Renewable Energy and Purchased Energy Constraint
3.2.7. Power Balance Constraint
3.2.8. CVaR Constraint
3.3. Model Solving
4. System Simulation
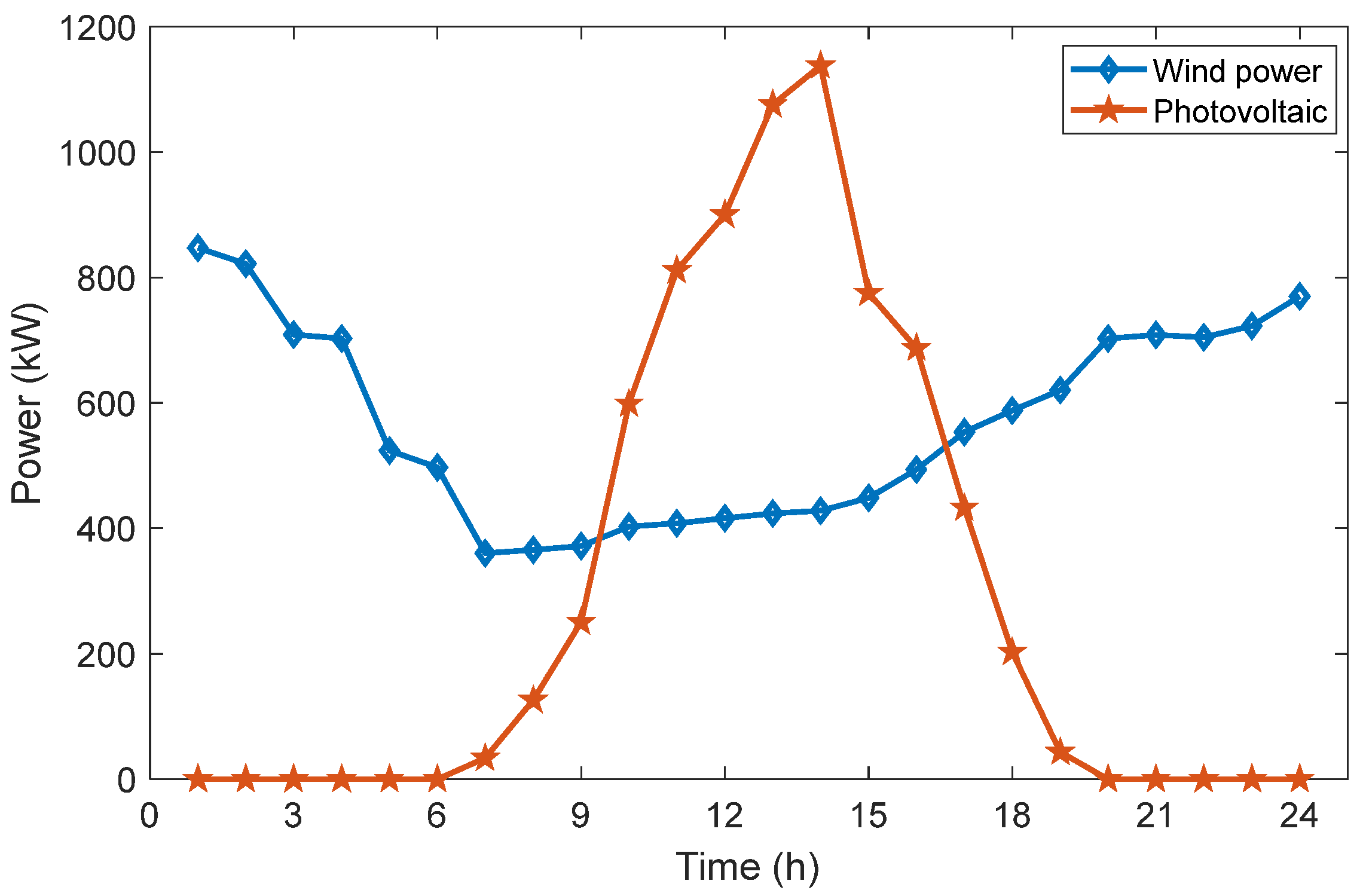
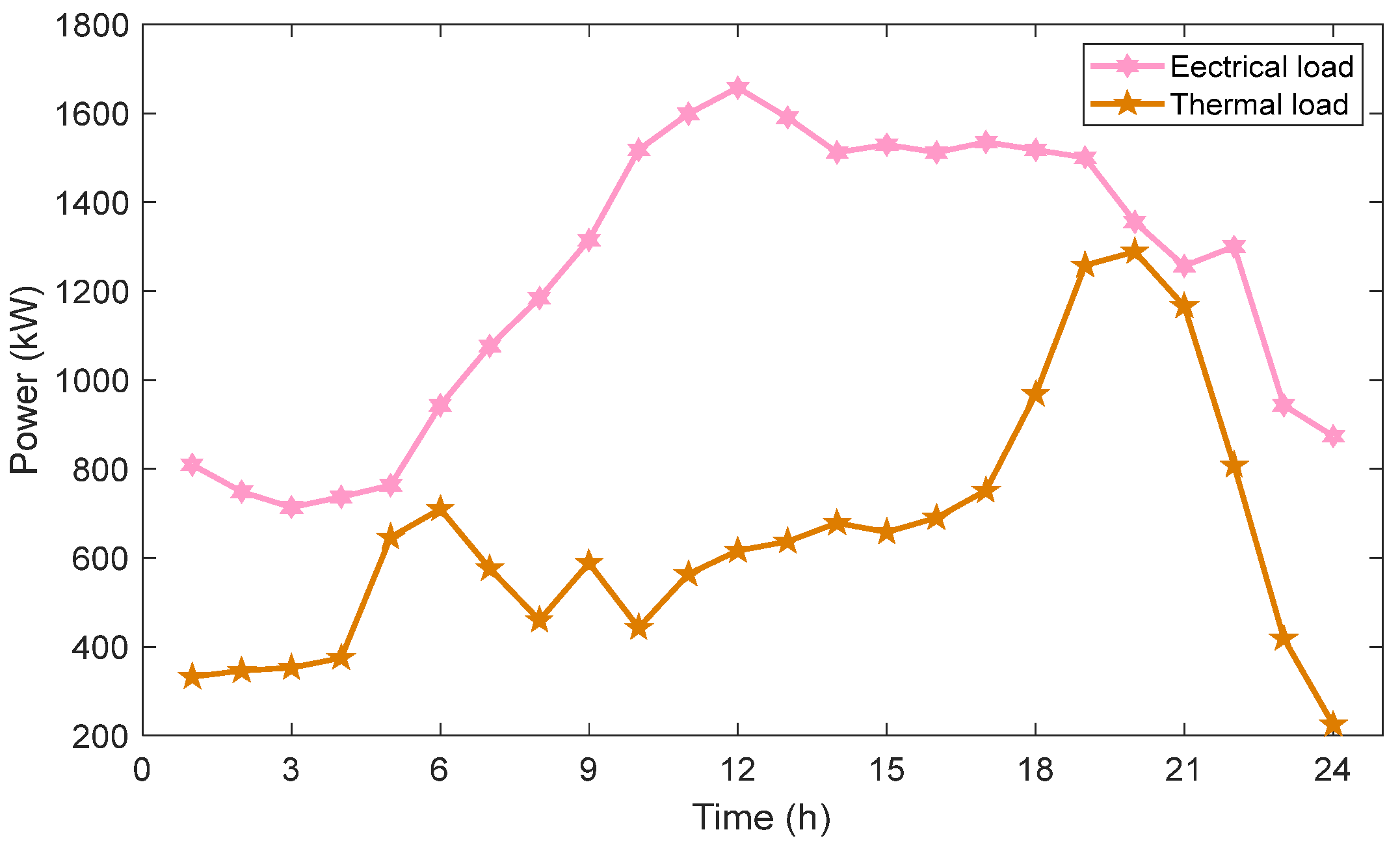
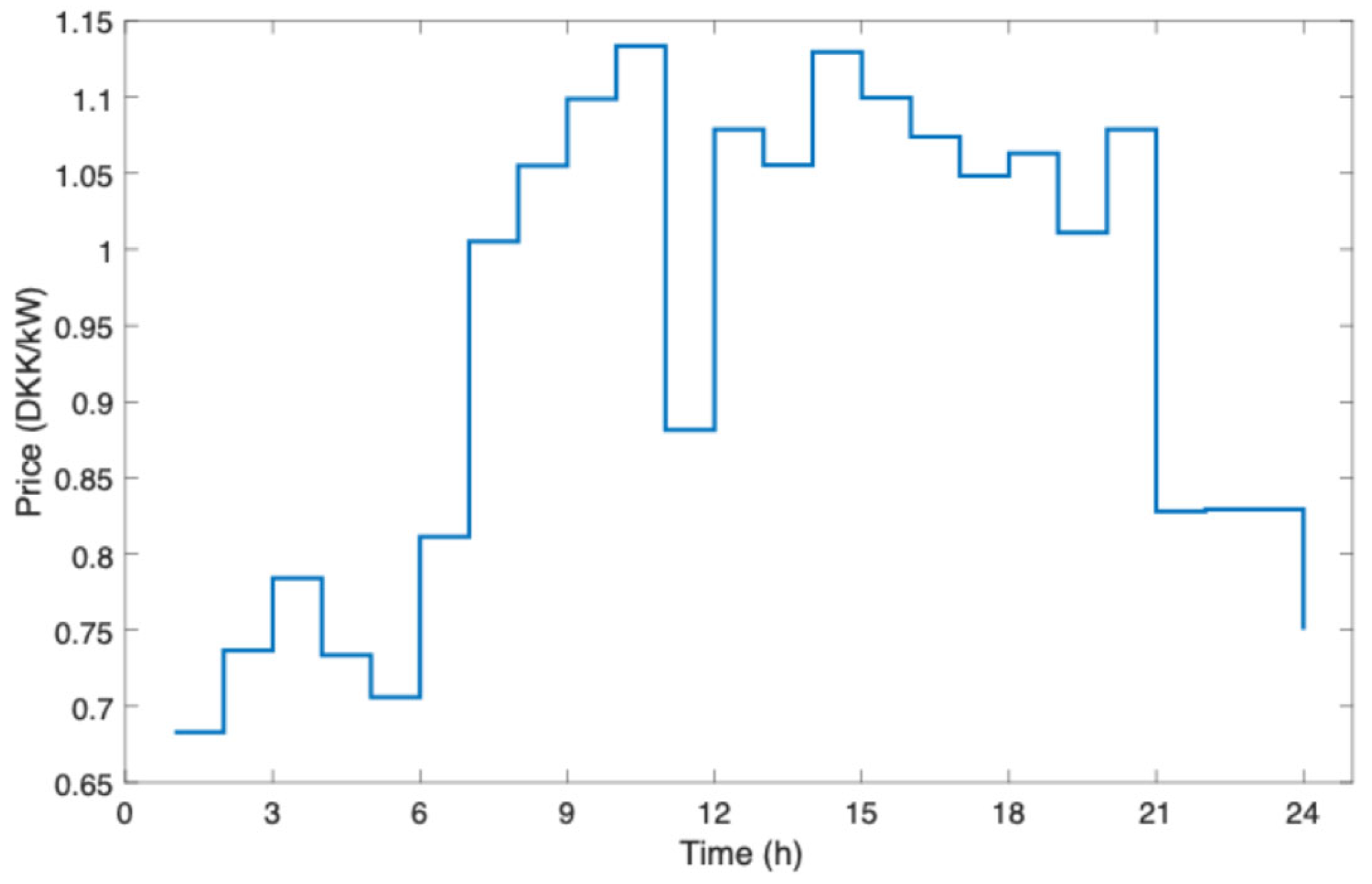
4.1. Parameter Settings
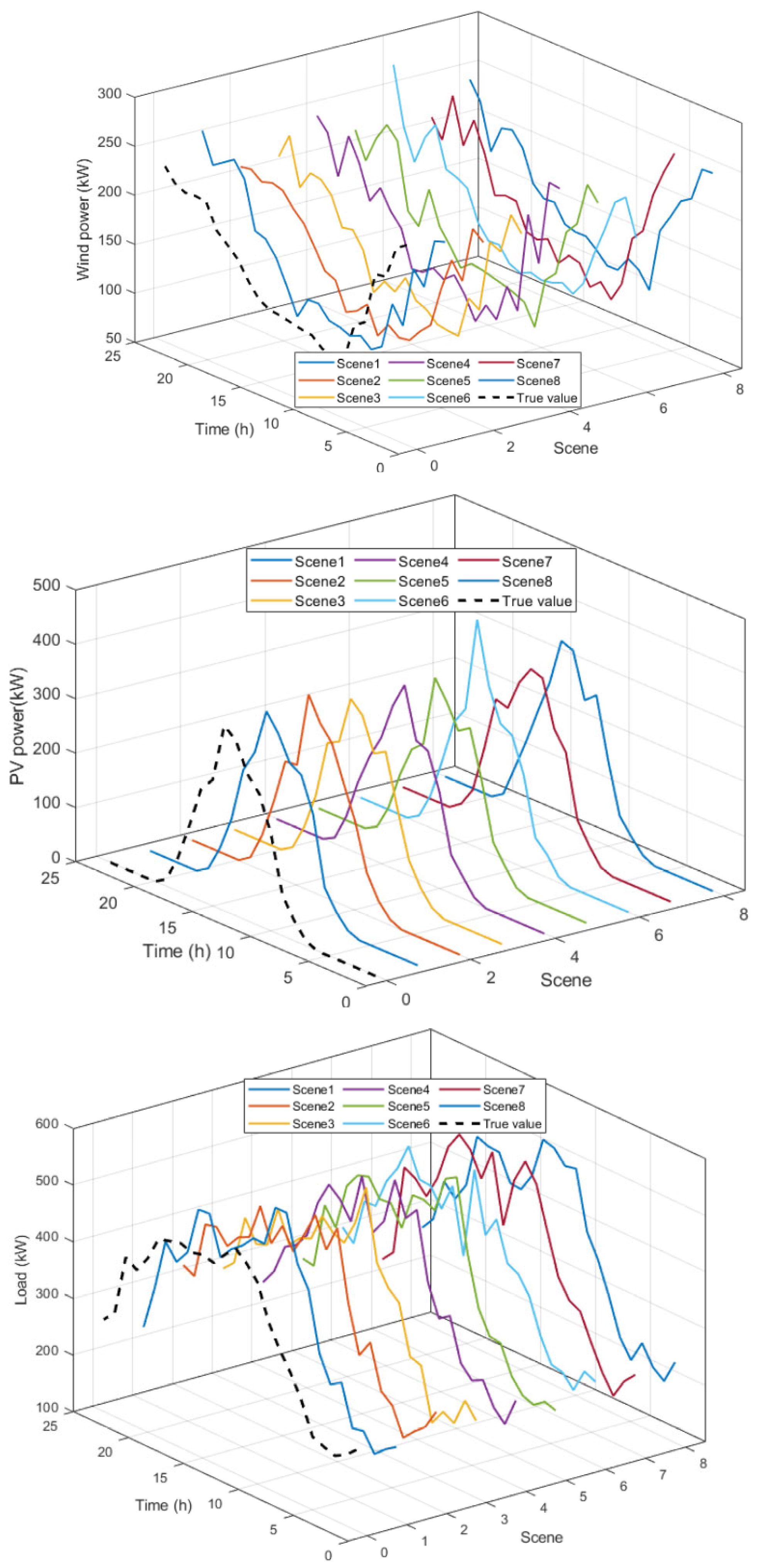
4.2. Analysis of Source–Load Bilateral Parameter Clustering Results
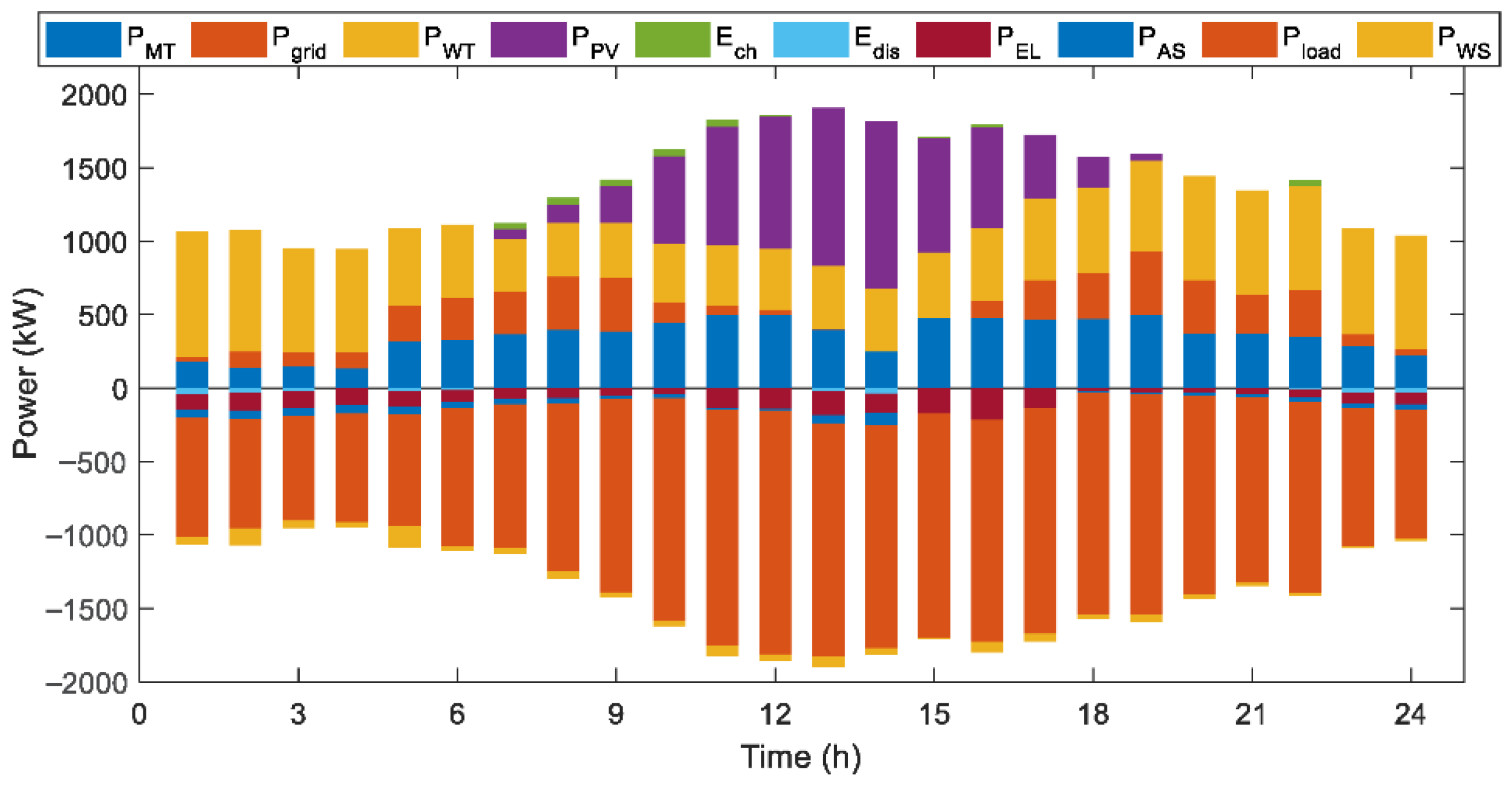
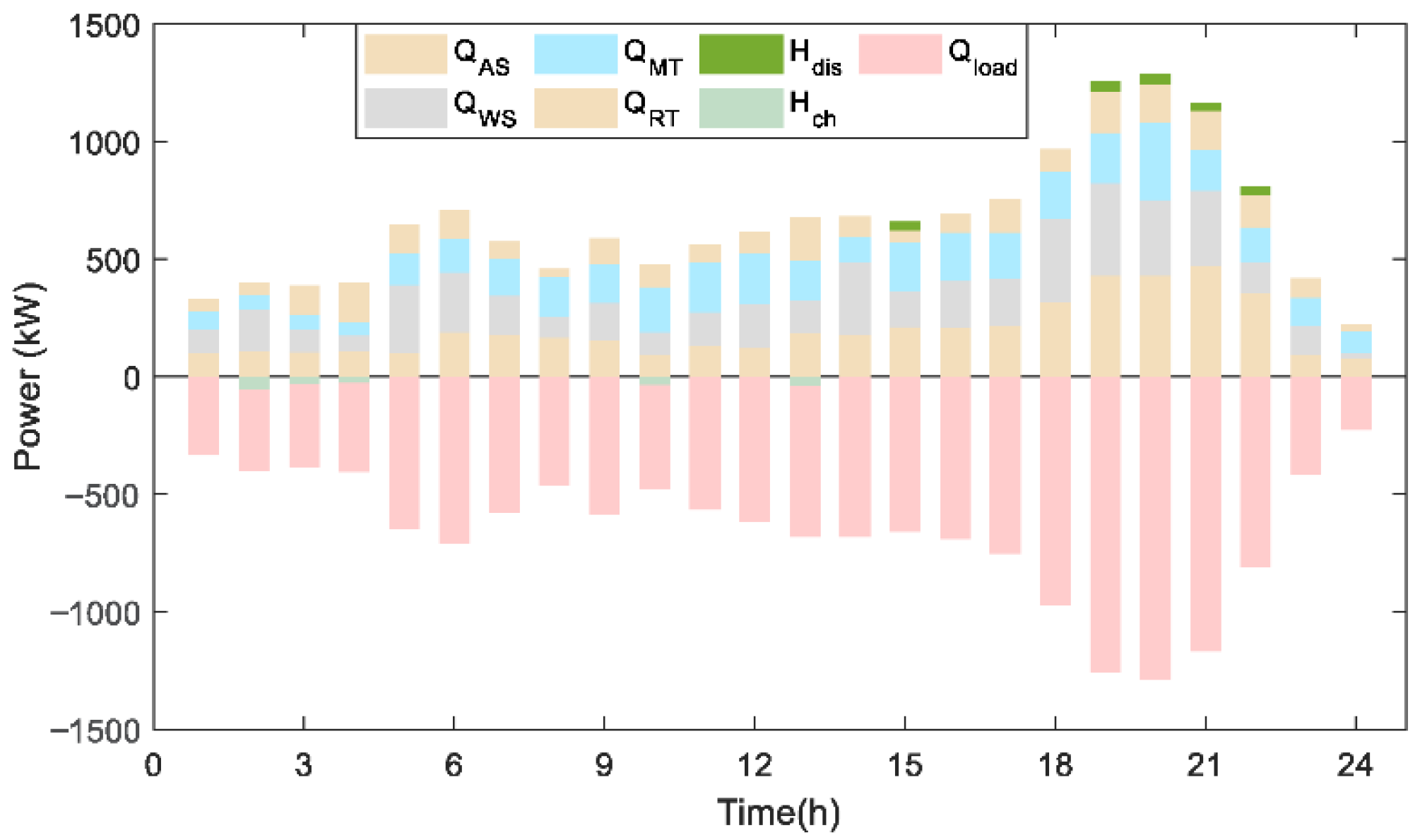
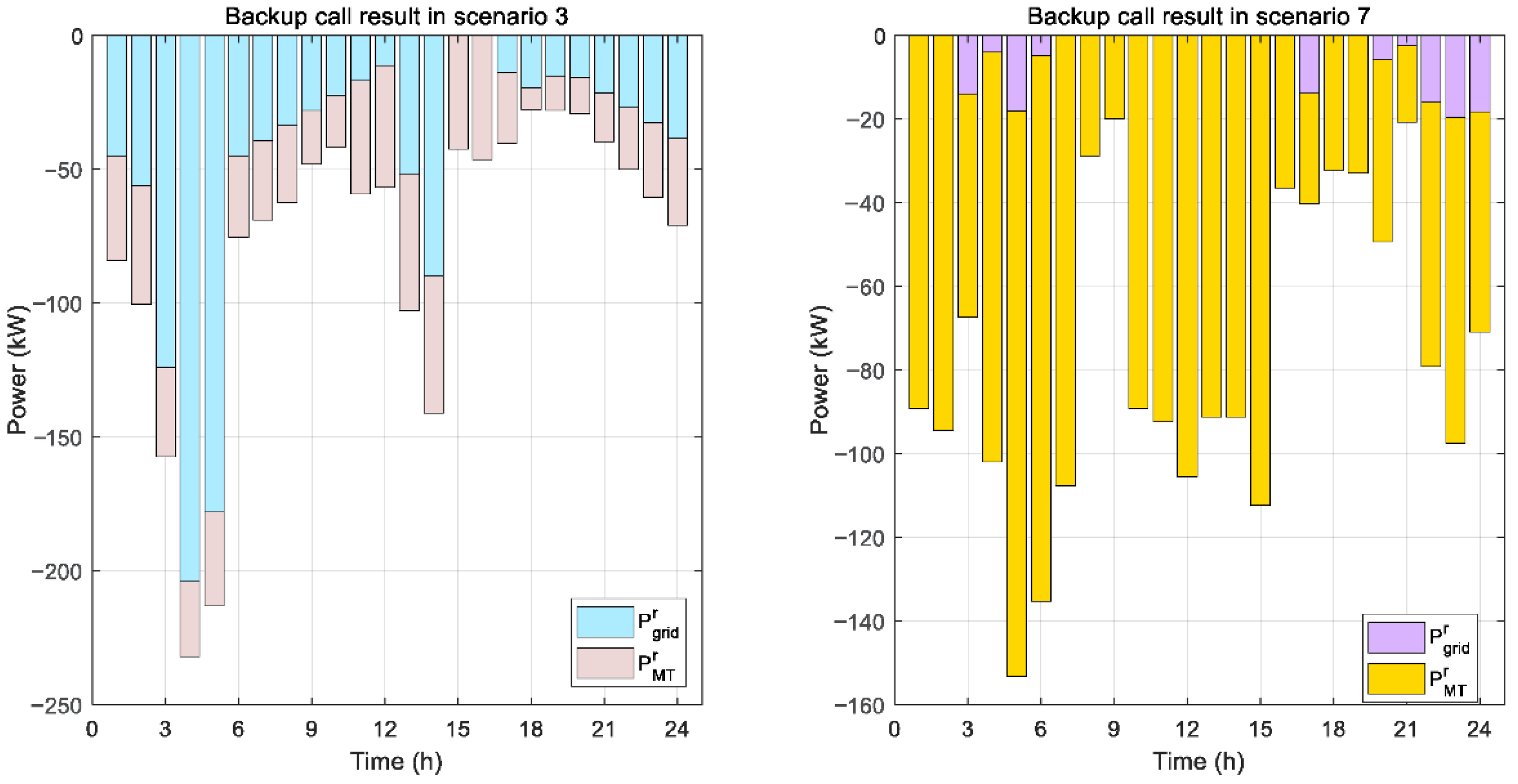
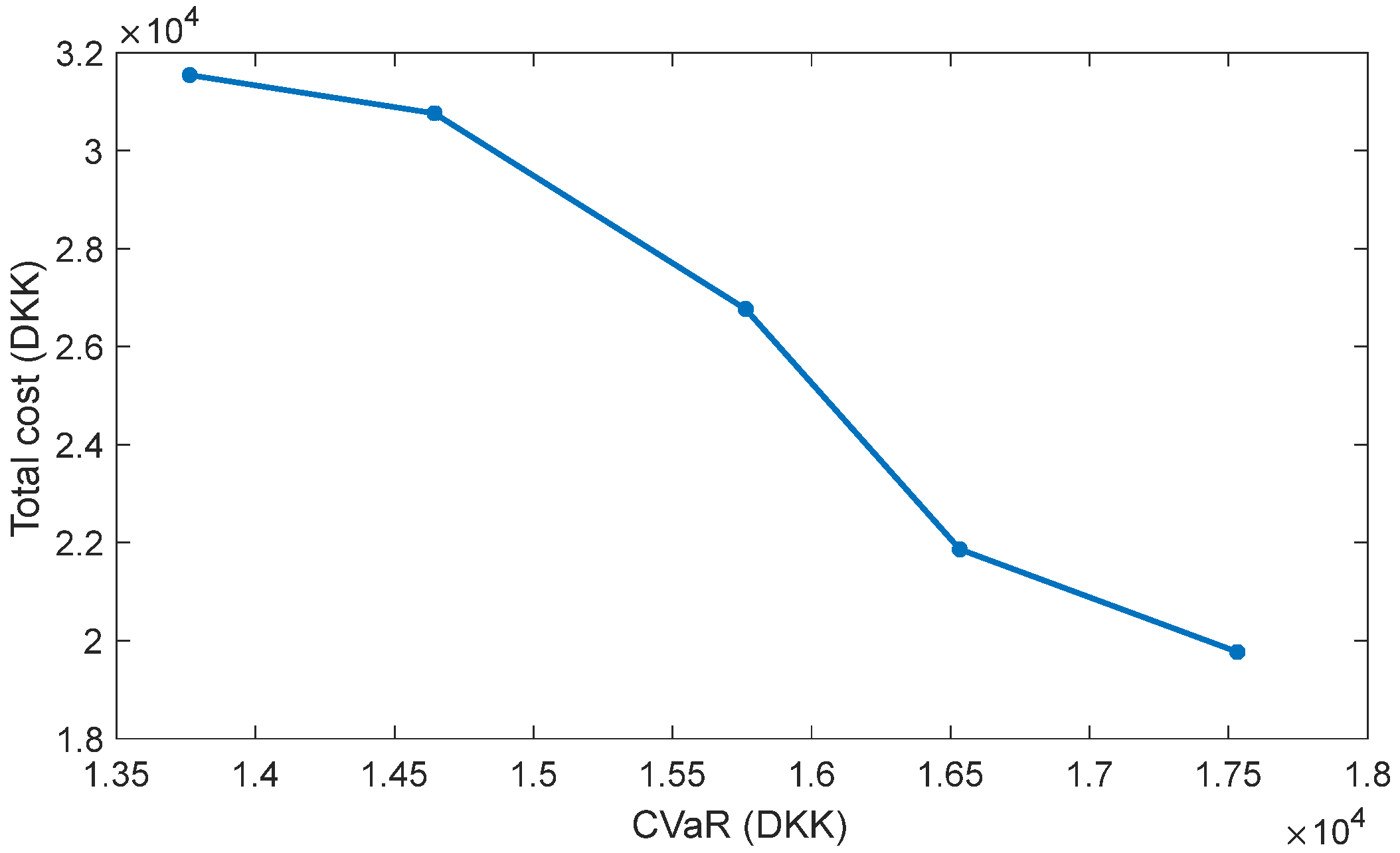
4.3. Results of Optimized Dispatch of Mining Area Energy System
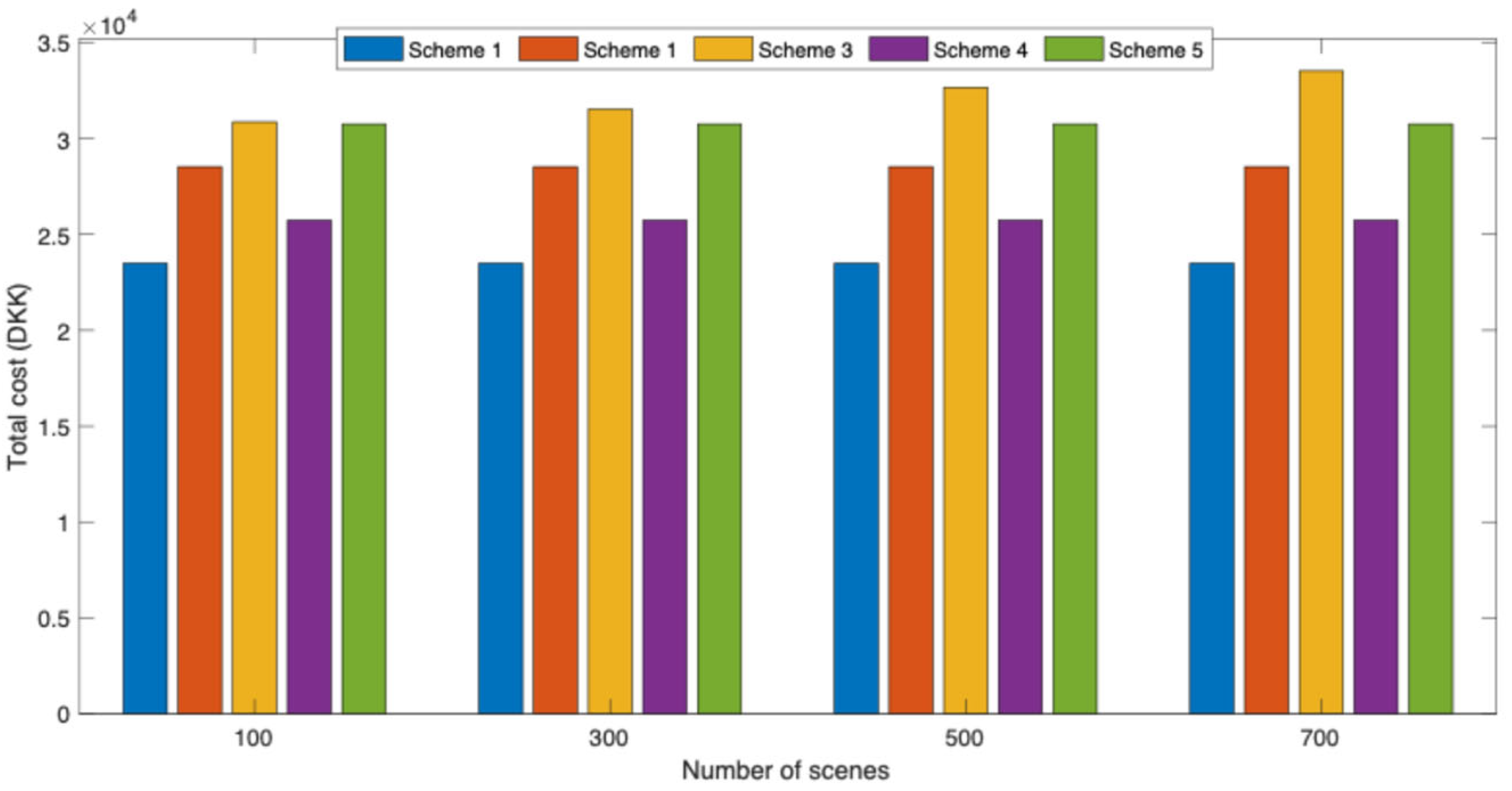
4.4. Model Comparison and Analysis
5. Conclusions
- (1)
- The Latin hypercube sampling (LHS) method based on the correlation coefficient matrix can more accurately characterize the uncertainty and interdependencies of multiple random variables in the mine energy system. The Affinity Propagation (AP) clustering algorithm adaptively determines the number of cluster centers and selects actual scenarios from the original dataset as representative scenarios, resulting in clustering outcomes with strong representativeness.
- (2)
- By considering the correlation between supply and load and optimizing the operational power of adjustment devices based on the complementary characteristics of multiple uncertainties, the total operational cost of the mine energy system is reduced by 1.4%, thereby enhancing the system’s economic performance. The integration of the P2G unit into the traditional mine energy system effectively addresses issues such as renewable energy surplus and high carbon emissions.
- (3)
- The economic dispatch model of the mine energy system incorporating CVaR enables decision-makers to formulate reasonable operating strategies according to their risk preferences, achieving a balance between economic efficiency and operational robustness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Li, B.; Wang, Y.; Lu, H.; Zhao, H.; Xue, W. A bargaining game-based profit allocation method for the wind-hydrogen-storage combined system. Appl. Energy 2022, 310, 118472. [Google Scholar] [CrossRef]
- Adom, S.; Matsui, K. Investigating Barriers to Low-Carbon Policy Implementation among Mining Companies in Ghana. Sustainability 2024, 16, 1798. [Google Scholar] [CrossRef]
- Xue, D.; Shao, Z. Patent text mining based hydrogen energy technology evolution path identification. Int. J. Hydrogen Energy 2024, 49, 699–710. [Google Scholar] [CrossRef]
- Zhu, Y.; An, Y.; Li, X.; Cheng, L.; Lv, S. Geochemical characteristics and health risks of heavy metals in agricultural soils and crops from a coal mining area in Anhui province, China. Environ. Res. 2024, 241, 117670. [Google Scholar] [CrossRef] [PubMed]
- Gong, X.; Li, X.; Zhong, Z. Strategic bidding of hydrogen-wind-photovoltaic energy system in integrated energy and flexible ramping markets with renewable energy uncertainty. Int. J. Hydrogen Energy 2024, 80, 1406–1423. [Google Scholar] [CrossRef]
- Lei, H.; Liu, P.; Cheng, Q.; Xu, H.; Liu, W.; Zheng, Y.; Chen, X.; Zhou, Y. Frequency, duration, severity of energy drought and its propagation in hydro-wind-photovoltaic complementary systems. Renew. Energy 2024, 230, 120845. [Google Scholar] [CrossRef]
- Ofélia de Queiroz, F.A.; Morte, I.B.B.; Borges, C.L.; Morgado, C.R.; de Medeiros, J.L. Beyond clean and affordable transition pathways: A review of issues and strategies to sustainable energy supply. Int. J. Electr. Power Energy Syst. 2024, 155, 109544. [Google Scholar]
- Kim, Y.; Moon, I.; Kim, J.; Lee, J. Renewable natural gas value chain based on cryogenic carbon capture, utilization and storage, and power-to-gas for a net-zero CO2 economy. Renew. Sustain. Energy Rev. 2025, 212, 115425. [Google Scholar] [CrossRef]
- Hu, J.; Zou, Y.; Zhao, Y. Robust operation of hydrogen-fueled power-to-gas system within feasible operating zone considering carbon-dioxide recycling process. Int. J. Hydrogen Energy 2024, 58, 1429–1442. [Google Scholar] [CrossRef]
- Liang, R.; Li, J.; Gong, D.; Huang, H.; Liang, K.; Liu, H.; Li, X. Optimal planning method for the high-quality coal mine energy system with complete clean energy supply. J. China Coal Soc. 2024, 49, 1669–1679. [Google Scholar]
- Miao, Q.; Sun, X.; Ma, C.; Zhang, Y.; Gong, D. Rescheduling costs and adaptive asymmetric errors guided closed-loop prediction of power loads in mine integrated energy systems. Energy AI 2025, 21, 100516. [Google Scholar] [CrossRef]
- Liu, J.; Li, R.; Wu, T. Short-term multi-objective optimal scheduling of the integrated power grid-abandoned coal mine energy system. Results Eng. 2024, 22, 102103. [Google Scholar] [CrossRef]
- Wu, F.; Liu, Y.; Gao, R. Challenges and opportunities of energy storage technology in abandoned coal mines: A systematic review. J. Energy Storage 2024, 83, 110613. [Google Scholar] [CrossRef]
- Xiong, Y.; Kong, D.; Song, G. Research hotspots and development trends of green coal mining: Exploring the path to sustainable development of coal mines. Resour. Policy 2024, 92, 105039. [Google Scholar] [CrossRef]
- Li, C.; Han, S.; Zeng, S.; Yang, S. Robust optimization. In Intelligent Optimization: Principles, Algorithms and Applications; Springer Nature: Singapore, 2024; pp. 239–251. [Google Scholar]
- Yang, C.; Xia, Y. Interval Pareto front-based multi-objective robust optimization for sensor placement in structural modal identification. Reliab. Eng. Syst. Saf. 2024, 242, 109703. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.; Park, J.; Adams, D.; Heo, S.; Lee, J.H. Multi-period, multi-timescale stochastic optimization model for simultaneous capacity investment and energy management decisions for hybrid Micro-Grids with green hydrogen production under uncertainty. Renew. Sustain. Energy Rev. 2024, 190, 114049. [Google Scholar] [CrossRef]
- Wu, M.; Yan, R.; Zhang, J.; Fan, J.; Wang, J.; Bai, Z.; He, Y.; Cao, G.; Hu, K. An enhanced stochastic optimization for more flexibility on integrated energy system with flexible loads and a high penetration level of renewables. Renew. Energy 2024, 227, 120502. [Google Scholar] [CrossRef]
- Sarkar, D.; Srivastava, P.K. Recent development and applications of neutrosophic fuzzy optimization approach. Int. J. Syst. Assur. Eng. Manag. 2024, 15, 2042–2066. [Google Scholar] [CrossRef]
- Wang, S.; Tan, Q.; Ding, X.; Li, J. Efficient microgrid energy management with neural-fuzzy optimization. Int. J. Hydrogen Energy 2024, 64, 269–281. [Google Scholar] [CrossRef]
- Ran, X.; Suyaroj, N.; Tepsan, W.; Ma, J.; Zhou, X.; Deng, W. A hybrid genetic-fuzzy ant colony optimization algorithm for automatic K-means clustering in urban global positioning system. Eng. Appl. Artif. Intell. 2024, 137, 109237. [Google Scholar] [CrossRef]
- Xiang, Y.; Tang, Q.; Xu, W.; Hu, S.; Zhao, P.; Guo, J.; Liu, J. A multi-factor spatio-temporal correlation analysis method for PV development potential estimation. Renew. Energy 2024, 223, 119962. [Google Scholar] [CrossRef]
- Ru, Y.; Wang, Y.; Mao, W.; Zheng, D.; Fang, W. Dynamic Environmental Economic Dispatch Considering the Uncertainty and Correlation of Photovoltaic–Wind Joint Power. Energies 2024, 17, 6247. [Google Scholar] [CrossRef]
- Zhong, M.; Fan, J.; Luo, J.; Xiao, X.; He, G.; Cai, R. InfoCAVB-MemoryFormer: Forecasting of wind and photovoltaic power through the interaction of data reconstruction and data augmentation. Appl. Energy 2024, 371, 123745. [Google Scholar] [CrossRef]
- Zhang, Q.; Leng, S.; Ma, X.; Liu, Q.; Wang, X.; Liang, B.; Liu, Y.; Yang, J. CVaR-constrained policy optimization for safe reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 830–841. [Google Scholar] [CrossRef] [PubMed]
- Elias, I.I.; Ali, T.H. Optimal level and order of the Coiflets wavelet in the VAR time series denoise analysis. Front. Appl. Math. Stat. 2025, 11, 1526540. [Google Scholar] [CrossRef]
- Pedersen, T.B.; Lehtola, S.; Fdez Galván, I.; Lindh, R. The versatility of the Cholesky decomposition in electronic structure theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2024, 14, e1692. [Google Scholar] [CrossRef]
- Iordanis, I.; Koukouvinos, C.; Silou, I. On the efficacy of conditioned and progressive Latin hypercube sampling in supervised machine learning. Appl. Numer. Math. 2025, 208, 256–270. [Google Scholar] [CrossRef]
- Zhao, M.K.; Guo, J.; Xu, Z.S.; Wu, X.H. A large-scale group decision-making method based on improved affinity propagation algorithm and adjustable minimum-cost consensus model in social networks. Comput. Ind. Eng. 2024, 187, 109819. [Google Scholar] [CrossRef]
- Brehm, P.A.; Johnston, S.; Milton, R. Backup power: Public implications of private substitutes for electric grid reliability. J. Assoc. Environ. Resour. Econ. 2024, 11, 1419–1445. [Google Scholar] [CrossRef]



| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 50 kW | 400 kW | ||
| 1.08 | 30 kW | ||
| 500 kW | |||
| 0.82 | 3 | ||
| 0.8 | 0.8 | ||
| 50 kWh | 50 kW | ||
| 0.75 | 0.75 | ||
| 30 kWh | 30 kW | ||
| 1000 kW | 0.65 | ||
| 0.351 DKK/kWh | |||
| 0.085 DKK/kWh | 0.127 DKK/kWh | ||
| 50 kW | |||
| 50 kW | 30 kW | ||
| 2.7 | 50 kW | ||
| 300 kWh | 200 kWh | ||
| 30 kW | 0.462 DKK/kWh | ||
| 0.1 | 0.032 DKK/kWh |
| Number of Categories | K-Means Clustering Silhouette Coefficient | AP Clustering Silhouette Coefficient |
|---|---|---|
| 3 | 0.374 | 0.598 |
| 6 | 0.275 | 0.418 |
| 10 | 0.151 | 0.275 |
| Scenario | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Probability Value | 0.080 | 0.075 | 0.070 | 0.165 | 0.080 | 0.145 | 0.215 | 0.170 |
| Operation and Scheduling Costs (DKK) | Adjusting Expected Costs (DKK) | Total Cost (DKK) | |
|---|---|---|---|
| Scheme 1 | 21,047.5 | 2451.9 | 23,499.4 |
| Scheme 2 | 25,578.4 | 2955.4 | 28,533.8 |
| Scheme 3 | 29,304.9 | 3369.4 | 32,674.3 |
| Scheme 4 | 23,067.5 | 2676.4 | 25,743.9 |
| Scheme 5 | 27,585.1 | 3178.3 | 30,763.4 |
| EUD (kW) | LOLP (%) | |
|---|---|---|
| Scheme 1 | 14.2 | 12.3 |
| Scheme 3 | 0 | 0 |
| Scheme 5 | 2.7 | 1.8 |
| Operation and Scheduling Costs (DKK) | Adjusting Expected Costs (DKK) | Total Cost (DKK) | |
|---|---|---|---|
| Scheme 6 | 27,585.1 | 3178.3 | 30,763.4 |
| Scheme 7 | 27,999.2 | 3224.4 | 31,223.5 |
| Cost reduction rate | 1.5% | 1.4% | 1.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Zhu, Y.; Zhou, X.; Wang, X. Stochastic Optimization Scheduling Method for Mine Electricity–Heat Energy Systems Considering Power-to-Gas and Conditional Value-at-Risk. Energies 2025, 18, 4146. https://doi.org/10.3390/en18154146
Han C, Zhu Y, Zhou X, Wang X. Stochastic Optimization Scheduling Method for Mine Electricity–Heat Energy Systems Considering Power-to-Gas and Conditional Value-at-Risk. Energies. 2025; 18(15):4146. https://doi.org/10.3390/en18154146
Chicago/Turabian StyleHan, Chao, Yun Zhu, Xing Zhou, and Xuejie Wang. 2025. "Stochastic Optimization Scheduling Method for Mine Electricity–Heat Energy Systems Considering Power-to-Gas and Conditional Value-at-Risk" Energies 18, no. 15: 4146. https://doi.org/10.3390/en18154146
APA StyleHan, C., Zhu, Y., Zhou, X., & Wang, X. (2025). Stochastic Optimization Scheduling Method for Mine Electricity–Heat Energy Systems Considering Power-to-Gas and Conditional Value-at-Risk. Energies, 18(15), 4146. https://doi.org/10.3390/en18154146





