Abstract
The gyroid minimal surface is one type of triply periodic minimal surface (TPMS). TPMS is a minimal surface replicated in the three main directions of the Cartesian coordinate system. The minimal surface is a surface stretched between two objects, known as the smallest possible area (e.g., a soap bubble with a saddle shape stretched between two parallel circles). The complicated shape of the TPMS makes its production possible only by additive methods (3D printing). This article presents the results of experimental studies on heat transfer and flow resistance in a heat exchanger made of stainless steel. The heat exchange surface, a TPMS gyroid, separates two working media: hot and cold water. The water flow rate was varied in the range from 8 kg/h to 25 kg/h (Re = 246–1171). The water temperature at the inlet to the exchanger was maintained at a constant level of 8.8 ± 0.3 °C and 49.5 ± 0.5 °C for cold and hot water, respectively. The effect of water flow rate on the change in its temperature, the heat output of the exchanger, the average heat transfer coefficient, pressure drop, and overall resistance factor was presented.
1. Introduction
1.1. Context and Motivation
Relying on intelligent manufacturing technologies is a key feature of modern industry. One such technology is additive manufacturing (AM). Additive manufacturing was first developed in the late 1980s [1]. It involves combining materials (including metal) to produce a coherent part with a shape that cannot be obtained using other manufacturing techniques [2]. Additive manufacturing has become popular due to its apparent advantages, which include the possibility of rapid prototyping [3], the production of complex or impossible-to-produce elements using other technologies [4], the creation of finished elements without the need to produce subassemblies [5], no need to use many different machines, the possibility to produce components with diametrically different shapes on a single device [6], and the possibility to ensure the continuity of production by printing missing subassemblies [7]. Additive manufacturing techniques have also expanded into the field of thermal engineering, enabling the production of heat exchangers with shapes that were previously impossible to produce or economically unfeasible [8]. Some of these shapes were created by nature; an example is the minimum surface area. The first example of a minimal surface was the Neovius surface, discovered in 1833 (named after its discoverer). In 1865, a surface called diamond was found by Schwarz. In 1970, Schoen presented many types of minimal surfaces, the most famous of which is the so-called gyroid [4]. The elementary form of a minimal surface replicated in the three main directions of the Cartesian coordinate system is the so-called triply periodic minimal surface (TPMS). Studies of TPMS structures show that, due to the high surface to volume ratio [9], they are known by low mass [10], high stiffness [11], and strength [12]. The first reports on the use of printed structures, including TPMS in the construction of heat exchangers (HX) appear.
1.2. Review of the State of the Art
A study by [13] presented the thermal performance of a TPMS-based heat exchanger. A gyroid structure was used as the filling of the heat exchanger. The authors demonstrated a 13% increase in the Nusselt number compared to a straight tube heat exchanger, using the same pumping power. Samson et al. [14] experimentally tested TPMS structures for heating systems purposes. The authors found that cell size does not affect thermal performance as porosity does. Wang et al. [15] investigated heat transfer in triply periodic minimal surface-based channels. It was found that flow characteristics have the most significant impact on heat transfer in TPMS-based heat exchangers. The authors proposed a prediction model for the Nusselt number. TPMS geometries were also tested by Iasiello et al. [16]. The authors used an open-cell foam. The Kelvin tetrakaidecahedron foam model was used. The authors of [17] showed the thermal performance of complexed cell topologies, lattice cubes. They used air as the working medium. A 10–20-times increase was obtained in heat transfer compared to the smooth channel counterparts. In study [18], gyroid heat exchangers were tested for superconducting electric motors. It was found that the gyroid HX generates higher heat transfer performance compared to standard constructions. Tang et al. [19,20] tested heat transfer diamond, gyroid, and IWP TPMS structures in heat exchangers. The individual structures showed slight differences in heat exchange in a narrow range of parameter changes. Several papers describe the results of experimental studies on a wide range of changes in thermal flow parameters using TPMS structures. However, there are many papers describing numerical simulations of TPMS-based heat exchangers that were conducted by [21,22,23,24,25,26,27,28,29,30].
A literature review reveals that there are publications devoted to experimental studies of heat transfer on TPMS-type surfaces; however, these differ from those presented in this article. For example, in [13], the heat exchanger was printed from a material not typically used for heat exchanger construction—resin; studies [14,15,19,20] concern a heat sink in which heat transfer takes place from the TPMS to the fluid; Iasiello et al. [16] examined a heat exchanger with a Kelvin core; in study by Aider et al. [17]—the metal heat exchanger was printed as lattices with four different unit cell topologies; and in study by Bonner-Hutton et al. [18]—the heat exchanger was printed using Selective Laser Melting (SLM) technology to melt and fuse metallic powders with a powerful laser beam. This article presents the results of experimental studies of heat transfer between two fluids in a gyroid-type TPMS-based heat exchanger. The results of heat transfer and flow resistance tests obtained using a heat exchanger with an industrially feasible design, conventional hydraulic channel diameter (dh = 11.3 mm), and AISI 316L stainless steel are described. Due to the material used, the 3D printing technique, and the dimensions of the exchanger, the presented results and the characteristics derived from them constitute a significant contribution to the modest database of experimental results available in the literature. The studies were conducted at four fixed levels and measurements were carried out in the steady states of one of the media (Re = 245; 342; 589; 719) and several abruptly changed values of the second medium flow rate (Re = 482–1171). The results of comprehensive studies constitute comparative material for the validation of computer simulations planned by the authors and are suitable for use by other authors dealing with simulations in the area of CFD.
2. The Experimental Set-Up
2.1. Research Station
The test stand, the diagram of which is shown in Figure 1, consisted of the tested heat exchanger (6) and two independent working fluid circuits.
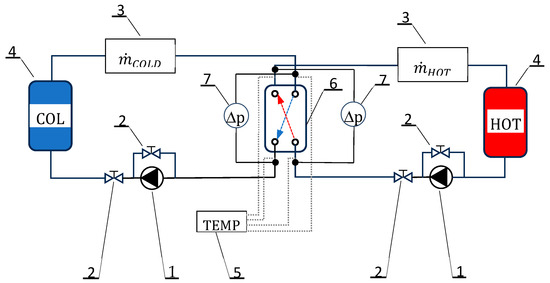
Figure 1.
Schematic diagram of the heat exchanger testing station. 1—pump; 2—control valve; 3—flow meter; 4—ultrathermostat; 5—temperature recorder; 6—tested heat exchanger; 7—pressure drop sensor.
Both the hot and cold water circuits were equipped with the same elements. A miniature gear pump (1) was used to force the water flow. The water flow rate was regulated using control valves (2) installed in the primary working medium circuit and in the bypass. The water flow rate was measured using mass flow meters (3). The water temperature in the hot and cold water circuits was determined using an ultrathermostat (4). The ultrathermostats could heat the water and, thanks to integrated cooling devices, cool it. The initial water temperature (TCOLD in, THOT in) was measured at the inlet to the exchanger, while its final temperature (TCOLD out, THOT out) was measured at the outlet. The temperature values were displayed and archived in the recorder (5). Additionally, sensors with transducers were connected at the inlet and outlet nozzles to measure the pressure drop (7). In this way, it was possible to measure the flow resistance of the working fluid along the length of the heat exchanger.
2.2. The Heat Exchanger
The heat exchanger, with an external shape resembling a cuboid and dimensions of 40 × 40 × 200 mm (Figure 2), was the most crucial element of the research installation.

Figure 2.
View of the printed heat exchanger subjected to experimental tests.
The innovative nature of the heat exchanger resulted from two elements. First, the heat exchanger was manufactured using the DMLS (Direct Metal Laser Sintering) method. The method involves creating 3D objects by melting successive layers of metal powder in precisely selected areas using a laser beam. As a result, the surface roughness of the solid made by the DMLS method differs significantly from the surface roughness produced by “classical” methods. Tests conducted with a HOMMELTESTER T8000 profilometer show that the surface of the printed exchanger was characterized by an average arithmetic roughness of Ra = 11.9 μm (class Ra3) and an average roughness profile height of Rz = 6.2 μm. Tests conducted with the same device show that the surface of the copper hydraulic pipe had an average arithmetic roughness over 100 times lower (Ra = 0.112 μm—class Ra11) and an average roughness profile height approximately 4 times lower (Rz = 1.495 μm).
Another innovative feature of the heat exchanger stems from the fact that the heat transfer surface is a so-called TPMS (Triply Periodic Minimal Surface), which can only be produced using additive methods. In the tested heat exchanger, the minimum surface area was defined by the equation f(x,y,z) = cos(x)·sin(y) + cos(y)·sin(z) + cos(z)·sin(x) = C. This is a Schoen gyroid surface. A single gyroid cell with dimensions of 20 × 20 × 20 mm was replicated in the x, y, and z directions 2, 2, and 10 times, respectively, creating a triply periodic minimal surface—the heat transfer surface in the tested heat exchanger (Figure 3).

Figure 3.
CAD drawings: triple-periodic gyroid minimal surface (a) used as heat transfer surface in the tested heat exchanger (b).
The minimum surface wall thickness was 0.5 mm. The entire exchanger was printed from AISI 316L stainless steel. The working medium was supplied to the interior of the heat exchanger using connecting pipes with a diameter of do = 9 mm (internal diameter) and di = 6 mm (internal diameter). The entire structure was thermally insulated with a 13 mm thick self-adhesive rubber mat.
2.3. Experimental Apparatus
K-type thermoelectric thermometers were used to measure the water temperature at the inlet and outlet of the exchanger. The thermometers were individually calibrated against a reference thermometer, allowing for temperature measurements with an accuracy of ±0.2 °C. Coriolis flowmeters were used to measure the water flow rate. These were Endress & Hauser flowmeters with a measurement range of 0–250 L/h. They allowed us to measure the flow rate with an accuracy of ±0.1 % of the estimated value; hence, the maximum possible error in flow rate measurement was ±0.25 L/h. Endress & Hauser devices were used to measure the flow resistance through the heat exchanger. These were differential pressure sensors with a measurement range of 0–30 kPa. The measurement error of the devices used was ±0.075% of the maximum reading. Hence, the error of a single pressure drop measurement was ±22.5 Pa.
3. Methods and Procedures
All measurements were carried out in steady states. Cold water with a constant mass flow rate ( = 7.94, 10.97, 18.87, and 23.02 kg/h) flowed through the heat exchanger. For each mass flow rate of cold water, several different values of the flow rate of hot water were set ( = 8–25 kg/h). The measurement of the water temperature at the inlet (TCOLD in) and outlet (TCOLD out) allowed, with a known flow rate [kg/s], to determine the heat flux Q [W] supplied to the cold water:
where cp [J/(kg·K)] is the specific heat of water at constant pressure. Assuming an ideal process (no heat exchange with the environment), it can be assumed that the heat added to the cold water is equal to the heat given off by the hot water.
Knowledge of the temperature of the media at the inlet and outlet of the exchanger allowed the calculation of the logarithmic mean temperature difference (LMTD).
The value of the heat transfer coefficient k [W/(m2K)] for the tested exchanger was calculated from the transformed relationship for its thermal power:
where A = 49.5 × 10−3 m2 is the heat exchange surface of the tested heat exchanger structure determined using CAD software.
The heat exchanger characteristics, in order to compare with the results of studies by other authors, are presented as a function of the dimensionless flow—the Reynolds number (Re)
where dh [mm]—hydraulic diameter of the channel through which the working fluid flows; w [m/s]—average flow velocity of the working fluid in the exchanger channel; and ν [m2/s]—kinematic coefficient of water viscosity depending on its average temperature. The hydraulic diameter of the channel was calculated from the relationship
where V [m3] is the volume occupied by the liquid in one space of the exchanger, and A is the heat exchange surface. For the tested heat exchanger, dh = 11.3 mm. To determine the average velocity of water flowing through the heat exchanger channel, the flow rate measurement was used and hence,
where ρ [kg/m3]—the density of water depends on its average temperature; and Ac [m2]—cross-sectional area of the channel.
dh = 4V/A
Overall resistance factor:
here Δp [Pa] is pressure drop measured at the connectors before and after the exchanger; L [m] is the distance that water travels between the pressure drop measurement points.
4. Experimental Data
Figure 4 presents the results of calculations of the heat flux given off by hot water and taken up by cold water (Formulas (1) and (2)). Assuming that the heat exchange process between the fluids took place without heat exchange with the environment, the results should be arranged along the line QHOT = QCOLD. The presented comparison shows that hot water gave off more heat than cold water took in. This indicates heat losses to the environment through the thermal insulation of the heat exchanger. It is noted that heat losses to the environment were minimal, reaching a maximum of 5%.

Figure 4.
Comparison of heat transfer between media flowing through the heat exchanger.
Figure 5 illustrates the effect of the Reynolds number (Formula (5)) on the current thermal power of the exchanger (Formula (1)). It can be seen that, with the increase in the flow rate of hot water, the value of the heat flux exchanged between the fluids increased. It changed from 250 W to 330 W at the lowest flow rate of cold water to a value from 330 W to 500 W at the highest flow rate of cold water.
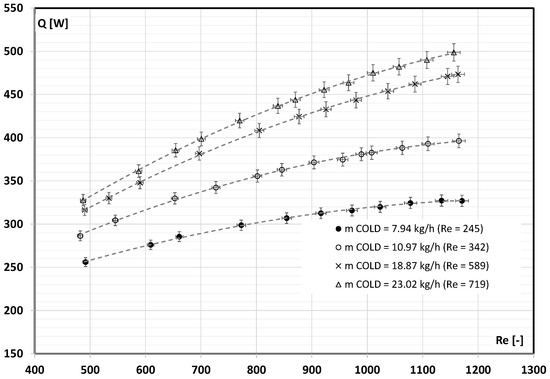
Figure 5.
The influence of the Reynolds number on the heat exchange flux.
Figure 6 presents the results of calculations of the heat transfer coefficient k (Formula (4)) from the Re of the fluids. As a result of the obtained characteristics, the value of the heat transfer coefficient of the printed exchanger with the liquid flow shaped by the triple-periodic minimal surface of the gyroid type varied in the range from approximately 300 W/(m2K) to 450 W/(m2K). The value of the coefficient increased as the flow rate of the fluids increased.
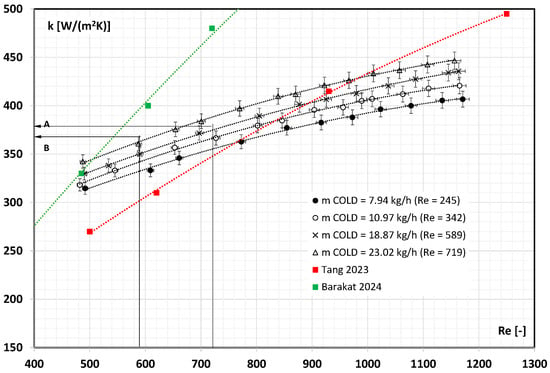
Figure 6.
The influence of the Reynolds number on the overall heat transfer coefficient [20,31].
It is noted that, within a certain range, the Re numbers are consistent with experimental results obtained during studies using printed Gyroid structures. The results of experimental studies according to [20,31] were obtained for a heat sink with TPMS of the gyroid type (1 × 1 × 4 and dimensions 20 mm × 20 mm × 80 mm) printed from aluminum alloy (AiSi10Mg). The surface roughness was Ra7 (Ra ≈ 2 μm). Therefore, the surface of the tested exchanger had a higher roughness in comparison to the heat sink of the authors [20,31]. Moreover, the authors of the cited studies used air as the working medium. Different surface roughness and a fluid with different physical properties resulted in the fact that rate of change in the overall heat transfer coefficient (k) is not as rapid as indicated by studies by other authors. Our own studies indicate that an increase in the Reynolds number from Re = 500 to Re = 1200 for hot water flow resulted in an increase in the overall heat transfer coefficient by approximately 30%. For example, a similar increase in Re according to [20] resulted in an increase in k by approximately 75%.
Another fact also follows from Figure 6. The gyroid surface divides the heat exchanger into two symmetrical flows. It is observed that, when = 719 kg/h, = 589 kg/h, the heat transfer coefficient k is approximately 375 W/(m2K)—point A in Figure 6. For the same values of the medium flow rate, but this time = 719 kg/h, and = 589 kg/h, the heat transfer coefficient k is approximately 360 W/(m2K)—point B in Figure 6. This observation confirms that the value of the heat transfer coefficient is influenced by the thermophysical properties of the fluid, which depend on its temperature, and the value of the heat transfer coefficient, despite the flow symmetry, is different on the hot and cold water sides.
The influence of the flow rate of the medium (Re)on the flow resistance is shown in Figure 7. It is observed that the higher the flow rate of the medium, the higher the resistance to its flow. The parabolic course of the characteristics indicates that the flow of the medium inside the exchanger was turbulent. The research results of other authors confirm these observations. According to [32,33], turbulent flow of the medium in printed TPMS structures can occur at Re = 300.

Figure 7.
The influence of the Reynolds number on the flow resistance.
From Figure 7, the influence of the working medium temperature on the flow resistance is clearly visible. Hot and cold water flowed in approximately equal amounts, i.e., 8–25 kg/h. Consideration of the physical properties of water, depending on its temperature, revealed that the flows occurred within a different range of Reynolds numbers. It was clearly shown that, for hot water, the flow resistance was lower than for cold water with the same Re number. The lower flow resistance resulted from the lower viscosity of water at a higher temperature.
Figure 8 presents a summary of overall resistance factor (Formula (8)) calculation results using hydrodynamic quantities measured during flow tests. In addition to our own results, the results of experimental studies by other authors [20,22,34] are presented. It is noted that the overall resistance factor value is higher than those obtained by other authors. This is due to the fact that the measured pressure drop includes not only flow resistance along the TPMS walls but also flow resistance through the connection ports and local flow resistance at the port–heat exchanger interface, both at the inlet and outlet sides of the fluid inside the heat exchanger. It is noted that the higher the Re, the lower the overall resistance factor value. In the case of hot water, the overall resistance factor results are arranged along a straight line, indicating the possibility of turbulent water flow. This is confirmed by the results and analyzes presented in [20]. In the case of cold water, the overall resistance factor results obtained for Re = 245 and Re = 342 vary from 24.65 to 19.76, while for higher Re values, they are numerically close to the results obtained for warm water (the overall resistance factor is about 15). The obtained trend indicates that the results for low Re values were obtained in laminar flow of cold water, while the next values (Re > 500) correspond to turbulent water flow. This fact is confirmed by the results taken from [34].

Figure 8.
The influence of the Reynolds number on the overall resistance factor [20,22,34].
5. Summary and Conclusions
In this article, the results of experimental studies on heat transfer and flow resistance in a heat exchanger based on a triple-periodic minimal surface of the gyroid type were presented. The exchanger was printed using the Direct Metal Laser Sintering (DMLS) method from AISI 316L steel. Detailed thermal and flow studies were conducted in the range of Re = 246–1171. A liquid with well-known physical properties—water—was used as the working medium. Cold water, with an initial temperature of 8.8 ± 0.3 °C, flowed counter-currently to warm water, with an initial temperature of 49.5 ± 0.5 °C. As a result of the conducted studies, it was found that
- The thermal power of the tested heat exchanger changed from Q = 250 W to Q = 350 W (for cold water: Re = 245) and increased to change in the range from Q = 330 W to Q = 500 W (for cold water: Re = 719).
- The value of the average heat transfer coefficient k changed analogously to the changes in the thermal power of the exchanger. It ranged from about 300 W/(m2K) at the lowest values of the flow of agents to 450 W/(m2K) at the maximum values of the flow of agents.
- The pressure drop of water flow through the tested heat exchanger ranged from 300 Pa to 1.5 kPa. The maximum value of the heat flow resistance was achieved by water at Re = 1171, while cold water reached it at a Reynolds number of approximately Re = 700.
The presented results of detailed studies constitute material for further analyses. It is planned to prepare a
- Correlation enabling the calculation of heat transfer coefficients from the working medium to the printed partition based on TPMS.
- Multi-variant CFD simulations. The presented experimental data are intended to be used to validate the obtained results of numerical calculations. These data expand the so far modest base of laboratory research results and can be used to validate computer models prepared by other authors.
Author Contributions
Conceptualization, K.D. and M.K.; methodology, K.D.; software, M.W.; validation, K.D., M.K. and M.W.; formal analysis, K.D.; investigation, M.W.; resources, M.K.; data curation, K.D.; writing—original draft preparation, K.D.; writing—review and editing, M.K.; visualization, M.W.; supervision, K.D.; project admin-istration, M.W.; funding acquisition, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
Authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Dutkowski, K.; Kruzel, M.; Rokosz, K. Review of the State-of-the-Art Uses of Minimal Surfaces in Heat Transfer. Energies 2022, 15, 7994. [Google Scholar] [CrossRef]
- Padrão, D.; Hancock, D.; Paterson, J.; Schoofs, F.; Tuck, C.; Maskery, I. New structure-performance relationships for surface-based lattice heat sinks. Appl. Therm. Eng. 2024, 236, 121572. [Google Scholar] [CrossRef]
- Cramer, C.L.; Ionescu, E.; Graczyk-Zajac, M.; Nelson, A.T.; Katoh, Y.; Haslam, J.J.; Wondraczek, L.; Aguirre, T.G.; LeBlanc, S.; Wang, H.; et al. Additive manufacturing of ceramic materials for energy applications: Road map and opportunities. J. Eur. Ceram. Soc. 2022, 42, 3049–3088. [Google Scholar] [CrossRef]
- Yeranee, K.; Rao, Y. A Review of Recent Investigations on Flow and Heat Transfer Enhancement in Cooling Channels Embedded with Triply Periodic Minimal Surfaces (TPMS). Energies 2022, 15, 8994. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, F.; Jia, H.; Zhao, Z.; Wang, P.; Duan, S.; Lei, H. Conformal geometric design and additive manufacturing for special-shaped TPMS heat exchangers. Int. J. Heat Mass Transf. 2025, 247, 127146. [Google Scholar] [CrossRef]
- Kruzel, M.; Bohdal, T.; Dutkowski, K.; Kuczyński, W.; Chliszcz, K. Current Research Trends in the Process of Condensation of Cooling Zeotropic Mixtures in Compact Condensers. Energies 2022, 15, 2241. [Google Scholar] [CrossRef]
- Kruzel, M.; Bohdal, T.; Dutkowski, K. Heat Transfer Enhancement in a 3D-Printed Compact Heat Exchanger. Energies 2024, 17, 4754. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, D.J. 3D printed compact heat exchangers with mathematically defined core structures. J. Comput. Des. Eng. 2020, 7, 527–550. [Google Scholar] [CrossRef]
- Thomas, N.; Sreedhar, N.; Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R.K.; Arafat, H. 3D printed triply periodic minimal surfaces as spacers for enhanced heat and mass transfer in membrane distillation. Desalination 2018, 443, 256–271. [Google Scholar] [CrossRef]
- Saito, S.; Baba, S.; Kinoshita, K.; Takada, N.; Someya, S. Thermal–hydraulic performance of additively manufactured crossflow minichannel heat exchangers. Appl. Therm. Eng. 2025, 274, 126543. [Google Scholar] [CrossRef]
- Heisel, C.; Caliot, C.; Chartier, T.; Chupin, S.; David, P.; Rochais, D. Digital design and 3D printing of innovative SiC architectures for high temperature volumetric solar receivers. Sol. Energy Mater. Sol. Cells 2021, 232, 111336. [Google Scholar] [CrossRef]
- Li, W.; Yu, G.; Yu, Z. Bioinspired heat exchangers based on triply periodic minimal surfaces for supercritical CO2 cycles. Appl. Therm. Eng. 2020, 179, 115686. [Google Scholar] [CrossRef]
- Reynolds, B.W.; Fee, C.J.; Morison, K.R.; Holland, D.J. Characterisation of Heat Transfer within 3D Printed TPMS Heat Exchangers. Int. J. Heat Mass Transf. 2023, 212, 124264. [Google Scholar] [CrossRef]
- Samson, S.; Tran, P.; Marzocca, P. Design and modelling of porous gyroid heatsinks: Influences of cell size, porosity and material variation. Appl. Therm. Eng. 2023, 235, 121296. [Google Scholar] [CrossRef]
- Wang, J.; Chen, K.; Zeng, M.; Ma, T.; Wang, Q.; Cheng, Z. Investigation on flow and heat transfer in various channels based on triply periodic minimal surfaces (TPMS). Energy Convers. Manag. 2023, 283, 116955. [Google Scholar] [CrossRef]
- Iasiello, M.; Cunsolo, S.; Bianco, N.; Chiu, W.K.S.; Naso, V. Developing thermal flow in open-cell foams. Int. J. Therm. Sci. 2017, 111, 129–137. [Google Scholar] [CrossRef]
- Aider, Y.; Kaur, I.; Cho, H.; Singh, P. Periodic heat transfer characteristics of additively manufactured lattices. Int. J. Heat Mass Transf. 2022, 189, 122692. [Google Scholar] [CrossRef]
- Bonner-Hutton, O.; Busch, B.; Lv, Y.; Caughley, A.; Badcock, R.; Lumsden, G.; Weijers, H.; Singamneni, S. Analysis of gyroid heat exchangers for superconducting electric motors. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Tang, W.; Zhou, H.; Zeng, Y.; Yan, M.; Jiang, C.; Yang, P.; Li, Q.; Li, Z.; Fu, J.; Huang, Y.; et al. Analysis on the convective heat transfer process and performance evaluation of Triply Periodic Minimal Surface (TPMS) based on Diamond, Gyroid and Iwp. Int. J. Heat Mass Transf. 2023, 201, 123642. [Google Scholar] [CrossRef]
- Tang, W.; Zou, C.; Zhou, H.; Zhang, L.; Zeng, Y.; Sun, L.; Zhao, Y.; Yan, M.; Fu, J.; Hu, J.; et al. A novel convective heat transfer enhancement method based on precise control of Gyroid-type TPMS lattice structure. Appl. Therm. Eng. 2023, 230, 120797. [Google Scholar] [CrossRef]
- Oh, S.H.; An, C.H.; Seo, B.; Kim, J.; Park, C.Y.; Park, K. Functional morphology change of TPMS structures for design and additive manufacturing of compact heat exchangers. Addit. Manuf. 2023, 76, 103778. [Google Scholar] [CrossRef]
- Qin, K.; Zhuang, N.; Shao, C.; Zhao, H.; Tang, X. Gyroid-type TPMS structure optimization based on mathematical function control and its convective heat transfer performance study. Int. Commun. Heat Mass Transf. 2025, 162, 108682. [Google Scholar] [CrossRef]
- Yan, K.; Wang, J.; Li, L.; Deng, H. Numerical investigation into thermo-hydraulic characteristics and mixing performance of triply periodic minimal surface-structured heat exchangers. Appl. Therm. Eng. 2023, 230, 120748. [Google Scholar] [CrossRef]
- Li, W.; Li, W.; Yu, Z. Heat transfer enhancement of water-cooled triply periodic minimal surface heat exchangers. Appl. Therm. Eng. 2022, 217, 119198. [Google Scholar] [CrossRef]
- Sun, J.; Li, X.; Mao, H.; Ma, Y.; Liu, J.; Chen, X. Numerical analysis of the mechanism of porosity effect on the thermal–hydraulic performance of Gyroid-type TPMS structures in combined aero engines. Appl. Therm. Eng. 2025, 264, 125453. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Rovira, M.; Duwig, C. Design analysis of the “Schwartz D” based heat exchanger: A numerical study. Int. J. Heat Mass Transf. 2021, 177, 121415. [Google Scholar] [CrossRef]
- Zhianmanesh, M.; Varmazyar, M.; Montazerian, H. Fluid Permeability of Graded Porosity Scaffolds Architectured with Minimal Surfaces. ACS Biomater. Sci. Eng. 2019, 5, 1228–1237. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, P. Flow and thermal transport characteristics of Triply-Periodic Minimal Surface (TPMS)-based gyroid and Schwarz-P cellular materials. Numer. Heat Transf. Part A Appl. 2021, 79, 553–569. [Google Scholar] [CrossRef]
- Cheng, Z.; Li, X.; Xu, R.; Jiang, P. Investigations on porous media customized by triply periodic minimal surface: Heat transfer correlations and strength performance. Int. Commun. Heat Mass Transf. 2021, 129, 105713. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Attarzadeh-Niaki, S.H.; Duwig, C. Multi-objective optimization of TPMS-based heat exchangers for low-temperature waste heat recovery. Appl. Therm. Eng. 2022, 212, 118448. [Google Scholar] [CrossRef]
- Barakat, A.; Sun, B.B. Controlling TPMS lattice deformation for enhanced convective heat transfer: A comparative study of Diamond and Gyroid structures. Int. Commun. Heat Mass Transf. 2024, 154, 107443. [Google Scholar] [CrossRef]
- El Khadiri, I.; Abouelmajd, M.; Zemzami, M.; Hmina, N.; Lagache, M.; Belhouideg, S. Comprehensive analysis of flow and heat transfer performance in triply periodic minimal surface (TPMS) heat exchangers based on Fischer-Koch S, PMY, FRD, and Gyroid structures. Int. Commun. Heat Mass Transf. 2024, 156, 107617. [Google Scholar] [CrossRef]
- Khalil, M.; Hassan Ali, M.I.; Khan, K.A.; Abu Al-Rub, R. Forced convection heat transfer in heat sinks with topologies based on triply periodic minimal surfaces. Case Stud. Therm. Eng. 2022, 38, 102313. [Google Scholar] [CrossRef]
- Iyer, J.; Moore, T.; Nguyen, D.; Roy, P.; Stolaroff, J. Heat transfer and pressure drop characteristics of heat exchangers based on triply periodic minimal and periodic nodal surfaces. Appl. Therm. Eng. 2022, 209, 118192. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).