Grid-Forming Buck-Type Current-Source Inverter Using Hybrid Model-Predictive Control
Abstract
1. Introduction
2. Materials and Methods
2.1. Buck-Type CSI
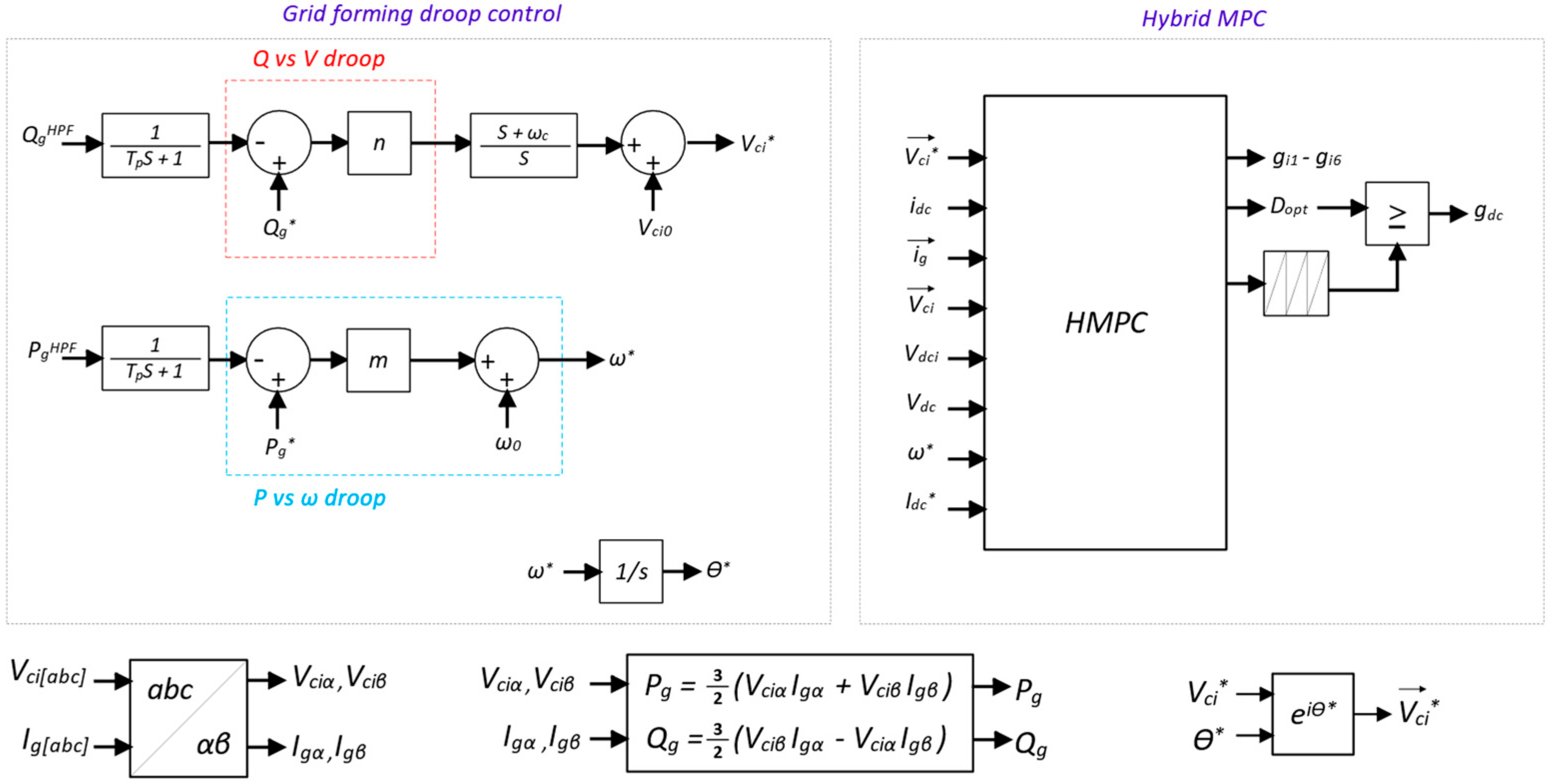
2.2. Grid-Forming Functionality
2.3. Hybrid Model-Predictive Control
3. Results
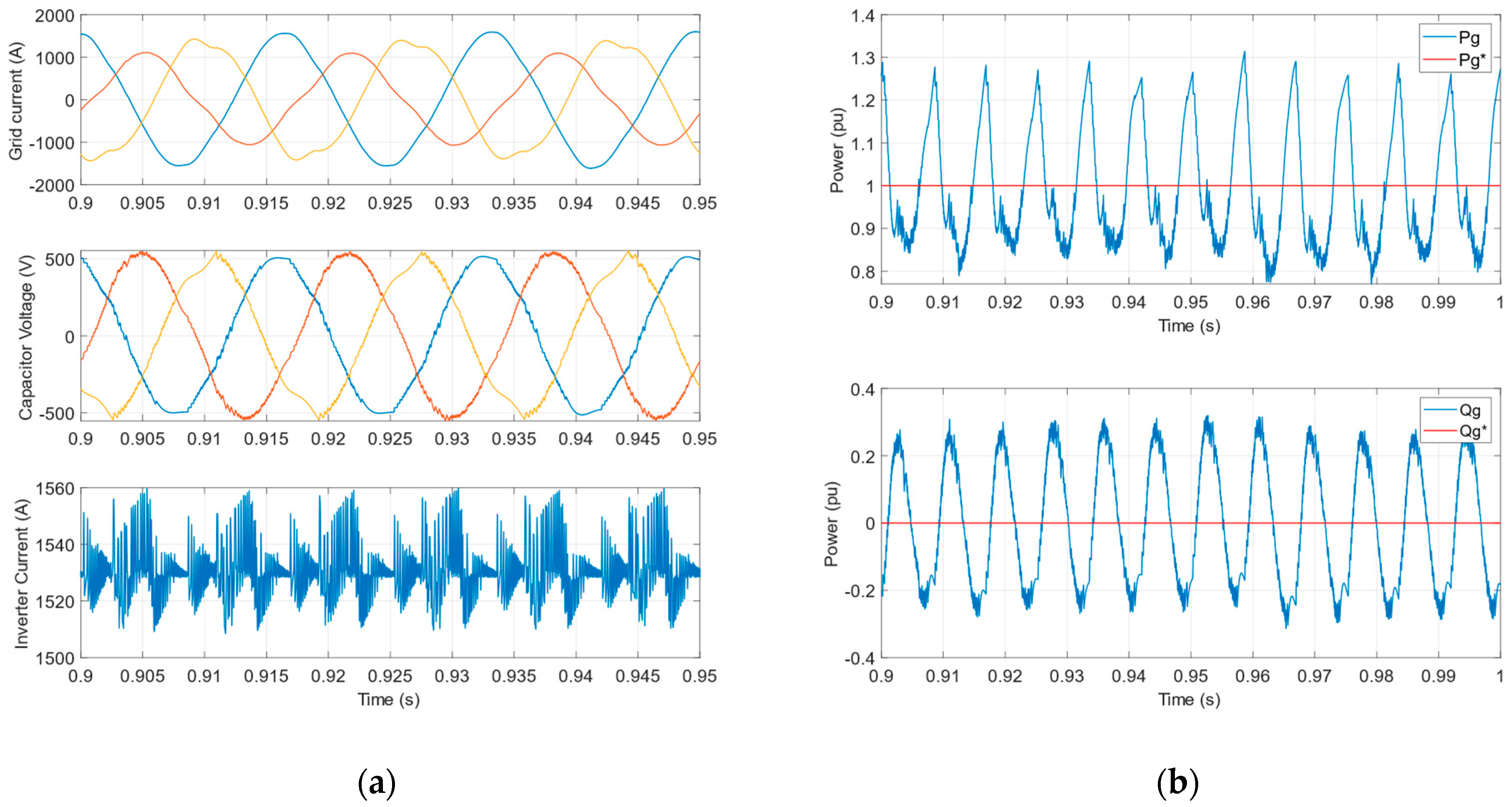
3.1. Steady-State Operation
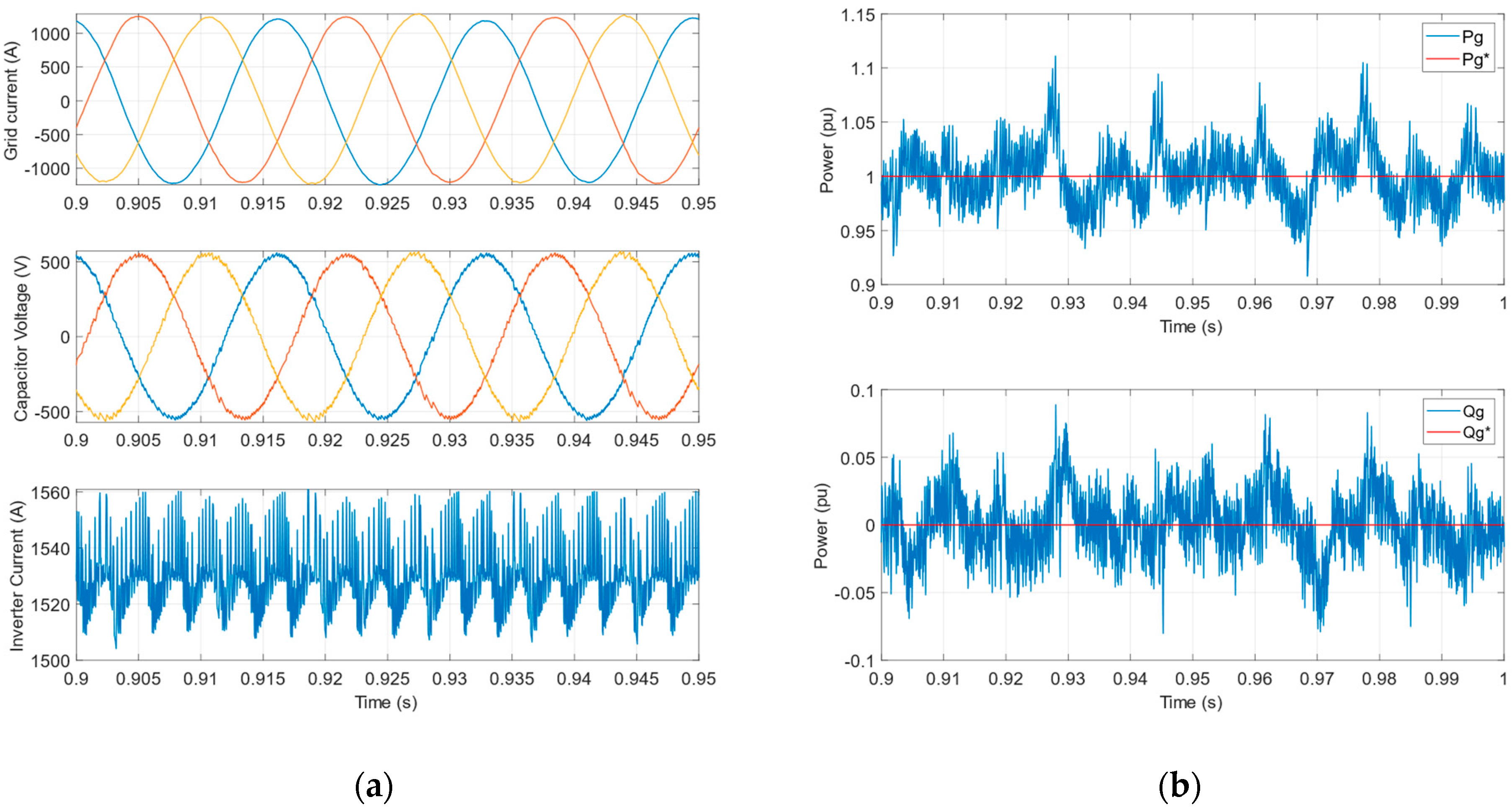
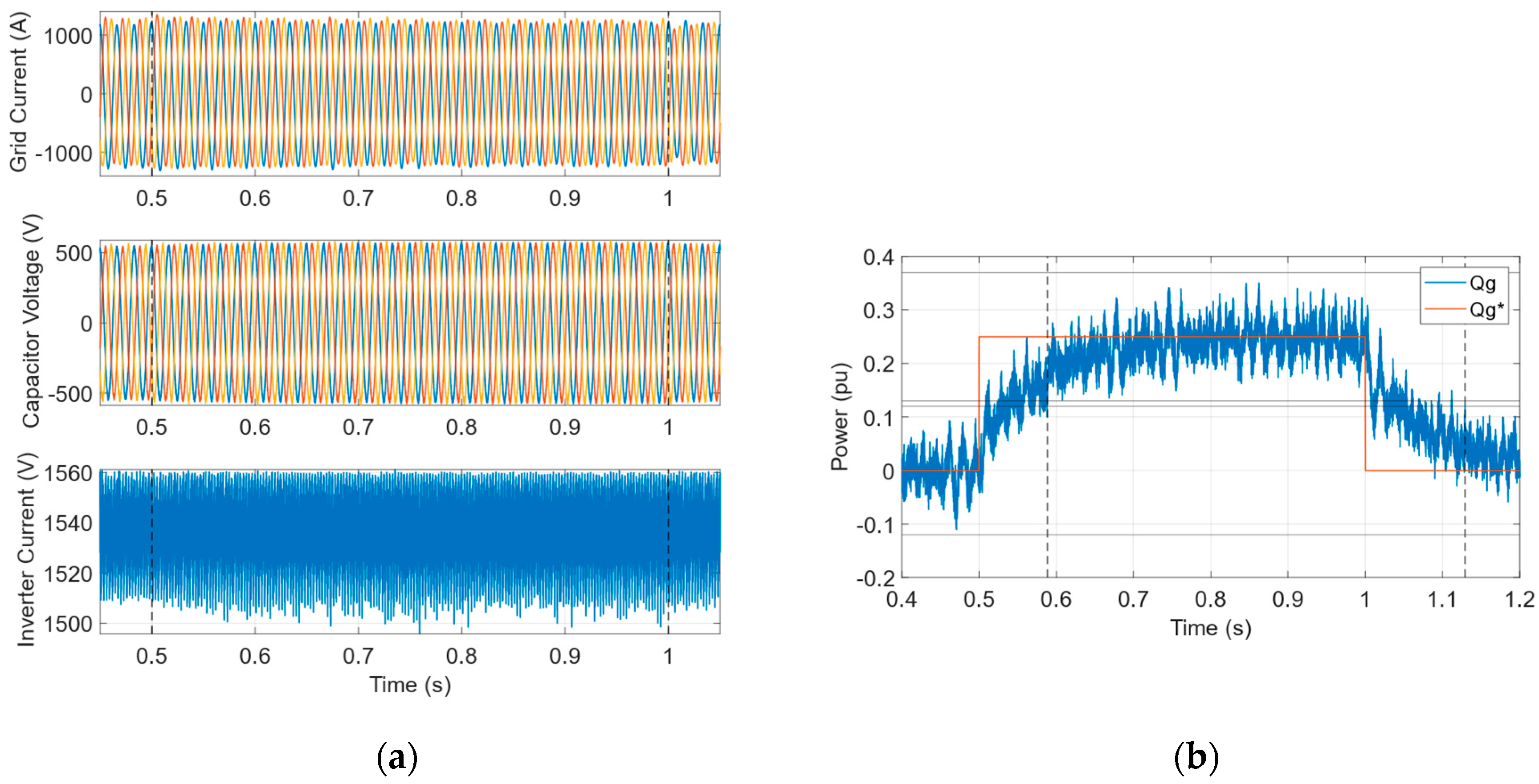
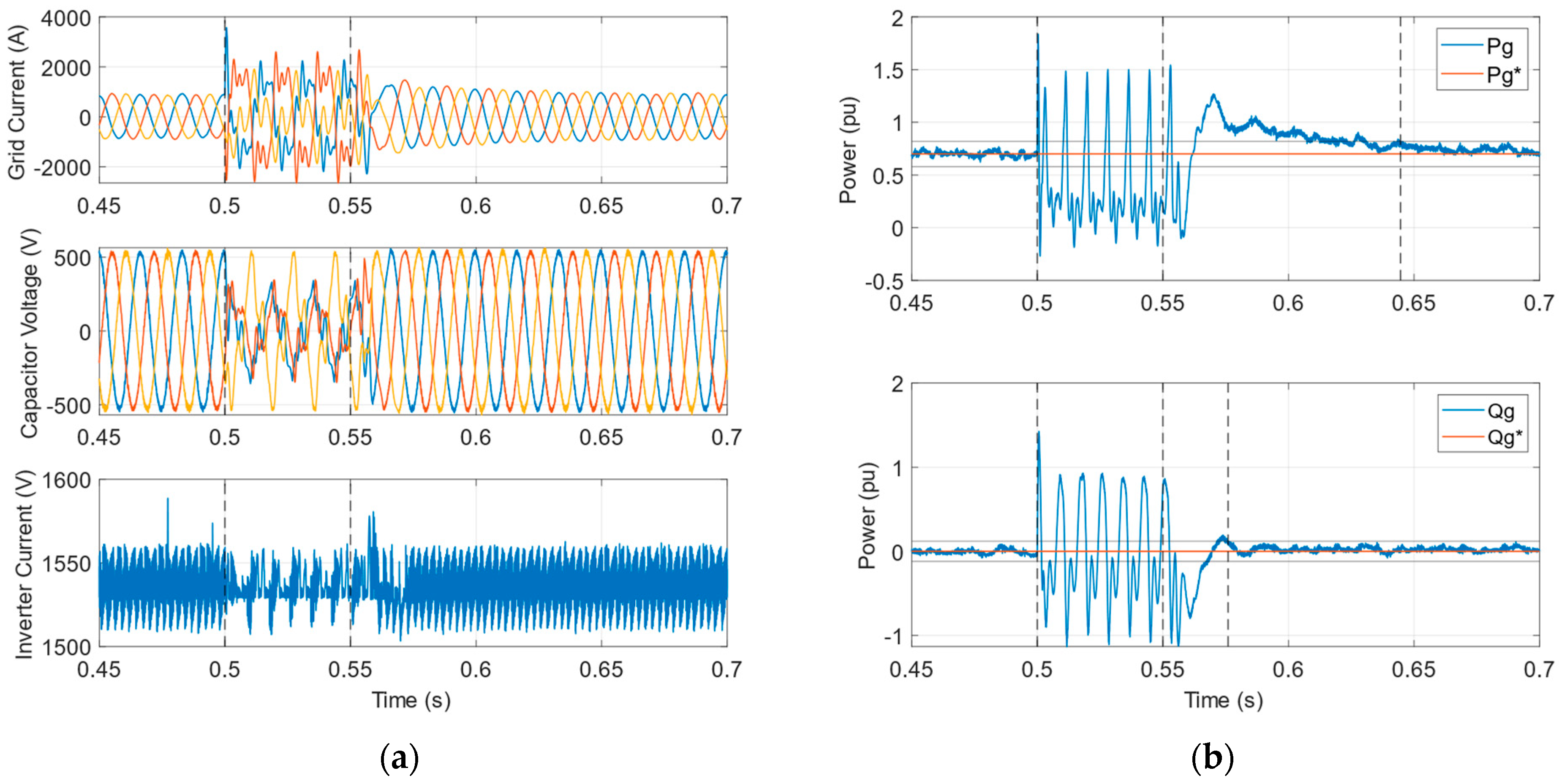
3.2. Transient Response
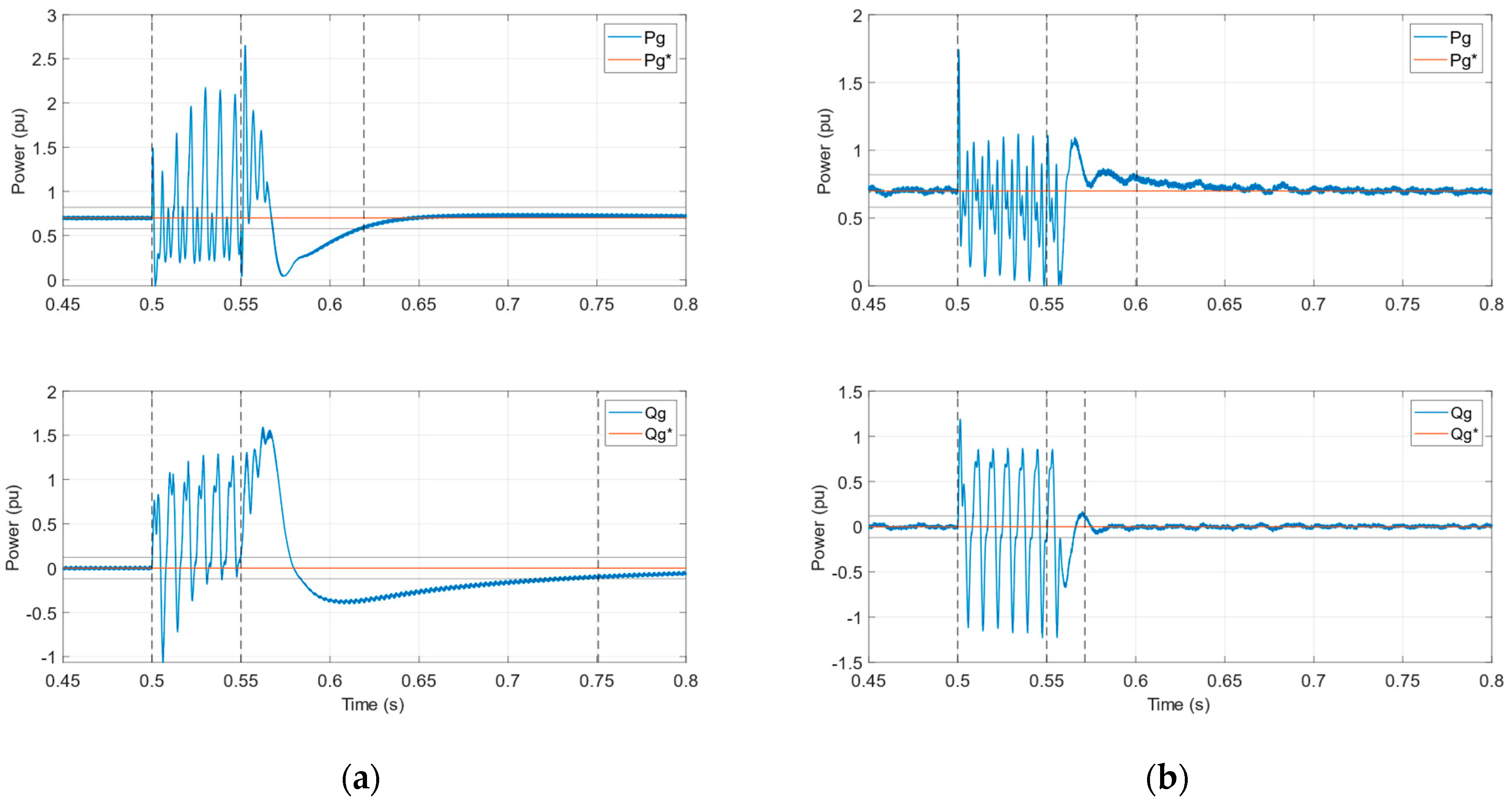
3.3. Fault Response
3.4. Comparison to Classic Linear Control
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, Y.; Eto, J.; Johnson, B.; Flicker, J.; Lasseter, R.; Pico, H.V.; Seo, G.-S.; Pierre, B.; Ellis, A. Research Roadmap on Grid-Forming Inverters. 2020. Available online: https://docs.nrel.gov/docs/fy21osti/73476.pdf (accessed on 28 May 2025).
- Matevosyan, J.; Badrzadeh, B.; Prevost, T.; Quitmann, E.; Ramasubramanian, D.; Urdal, H.; Achilles, S.; Macdowell, J.; Huang, S.H.; Vital, V.; et al. Grid-Forming Inverters: Are They the Key for High Renewable Penetration? IEEE Power Energy Mag. 2019, 17, 89–98. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-Forming Inverters: A Critical Asset for the Power Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
- Simulating the Role of Grid-Forming Inverters in the Future Electric Grid. Available online: https://www.pnnl.gov/news-media/simulating-role-grid-forming-inverters-future-electric-grid (accessed on 4 July 2025).
- Geekiyanage, V.; Seppänen, J. Power System Stability Improvements Through Grid Forming Inverters for Systems with High Penetration of Grid Following Inverters. In Proceedings of the 2024 IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE), Dubrovnik, Croatia, 14–17 October 2024; pp. 1–5. [Google Scholar]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid Forming Converters in Renewable Energy Sources Dominated Power Grid: Control Strategy, Stability, Application, and Challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Mirmohammad, M.; Azad, S.P. Control and Stability of Grid-Forming Inverters: A Comprehensive Review. Energies 2024, 17, 3186. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, S.; Li, Y.; Yang, F.; Zhao, Z. Fault Tolerant Control of Grid Connected Inverters Based on Low-Voltage Ride Through. Int. J. Mech. Electr. Eng. 2024, 3, 78–83. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Razzaghi, R.; Bahrani, B. Generalized Virtual Synchronous Generator Control Design for Renewable Power Systems. IEEE Trans. Sustain. Energy 2022, 13, 1021–1036. [Google Scholar] [CrossRef]
- Pattabiraman, D. Current Source Inverter with Grid Forming Control. Electr. Power Syst. Res. 2024, 226, 109910. [Google Scholar] [CrossRef]
- Fidone, G.L.; Migliazza, G.; Carfagna, E.; Benatti, D.; Immovilli, F.; Buticchi, G.; Lorenzani, E. Common Architectures and Devices for Current Source Inverter in Motor-Drive Applications: A Comprehensive Review. Energies 2023, 16, 5645. [Google Scholar] [CrossRef]
- Wu, B.; Pontt, J.; Rodriguez, J.; Bernet, S.; Kouro, S. Current-Source Converter and Cycloconverter Topologies for Industrial Medium-Voltage Drives. IEEE Trans. Ind. Electron. 2008, 55, 2786–2797. [Google Scholar] [CrossRef]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems, 1st ed.; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-0-470-59365-3. [Google Scholar]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model Predictive Control: A Review of Its Applications in Power Electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Young, H.A.; Marin, V.A.; Pesce, C.; Rodriguez, J. Simple Finite-Control-Set Model Predictive Control of Grid-Forming Inverters With LCL Filters. IEEE Access 2020, 8, 81246–81256. [Google Scholar] [CrossRef]
- Gao, H.; Mahmud, T. High-Frequency Common-Mode Voltage Reduced Space Vector Modulation for Grid-Connected Current-Source Inverter. World Electr. Veh. J. 2022, 13, 236. [Google Scholar] [CrossRef]
- Wu, B.; Narimani, M. High-Power Converters and AC Drives, 2nd ed.; Wiley: Hoboken, NJ, USA, 2016; Available online: https://www.wiley.com/en-us/High-Power+Converters+and+AC+Drives%2C+2nd+Edition-p-9781119156031 (accessed on 4 July 2025).








| Control Methodology | Current-Limiting | Simple Control Algorithm | PLL Independent |
|---|---|---|---|
| ✗ | ✔ | ✔ | |
| ✔ | ✗ | ✔ | |
| ✗ | ✗ | ✔ | |
| ✔ | ✗ | ✔ | |
| MPC | ✔ | ✔ | ✔ |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.01 pu | 1.1 pu | ||
| 0.1 pu | 1.0 pu | ||
| 0.05 pu | 377 rad/s | ||
| 0.5 pu | 0.01 | ||
| 0.15 pu | 0.05 | ||
| 0.95 pu | 50 rad/s | ||
| 1.0 pu | 50 μs |
| Conditions | THD () | THD () | Max | Max/min | Max/min | |
|---|---|---|---|---|---|---|
| Normal | 1.52% | 2.57% | 1561.65 A | 1.11 pu | 0.12 pu | 2489 Hz |
| Unbalanced Three-Phase Voltage | 7.01% | 5.37% | 1568.12 A | 1.34 pu | 0.35 pu | 2199 Hz |
| X/R Ratio: 20 | 1.51% | 2.41% | 1560.90 A | 1.11 pu | −0.10 pu | 2514 Hz |
| Condition | |||||||
|---|---|---|---|---|---|---|---|
| Steady-state | n/a | n/a | 1561.65 A | 1.11 pu | 0.12 pu | n/a | n/a |
| 401.05 A | n/a | 1615.05 A | n/a | n/a | 274.51 ms 118.92 ms | n/a | |
| n/a | n/a | 1561.19 A | n/a | n/a | n/a | 88.40 ms 129.21 ms | |
| L-G Fault | 2826.50 A 1148.99 A 1605.57 A | n/a | 1607.35 A | 1.70 pu | −1.20 pu | 61.67 ms | 20.61 ms |
| L-L-G Fault | 3564.71 A 2606.32 A 1909.11 A | n/a | 1593.67 A | 1.84 pu | 1.42 pu | 94.06 ms | 25.95 ms |
| L-L-L-G Fault | 4290.47 A 2321.01 A 2286.37 A | n/a | 1712.27 A | 2.25 pu | −1.38 pu | 219.58 ms | 241.05 ms |
| L-L-L-G Fault (Weak Grid) | 4070.67 A 2534.34 A 2428.82 A | n/a | 1747.62 A | 2.23 pu | 0.98 pu | 134.82 ms | 35.80 ms |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| Droop Control | 2967.60 A | 805.90 V | 1599.80 A | 2.65 pu | 1.59 pu | 69.06 ms | 200.68 ms |
| Buck-Type MPC | 2870.30 A | 550.04 V | 958.33 A | 1.74 pu | 1.19 pu | 50.66 ms | 21.46 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avilan-Losee, G.; Gao, H. Grid-Forming Buck-Type Current-Source Inverter Using Hybrid Model-Predictive Control. Energies 2025, 18, 4124. https://doi.org/10.3390/en18154124
Avilan-Losee G, Gao H. Grid-Forming Buck-Type Current-Source Inverter Using Hybrid Model-Predictive Control. Energies. 2025; 18(15):4124. https://doi.org/10.3390/en18154124
Chicago/Turabian StyleAvilan-Losee, Gianni, and Hang Gao. 2025. "Grid-Forming Buck-Type Current-Source Inverter Using Hybrid Model-Predictive Control" Energies 18, no. 15: 4124. https://doi.org/10.3390/en18154124
APA StyleAvilan-Losee, G., & Gao, H. (2025). Grid-Forming Buck-Type Current-Source Inverter Using Hybrid Model-Predictive Control. Energies, 18(15), 4124. https://doi.org/10.3390/en18154124







